Global Dynamics of a Diffusive Within-Host HTLV/HIV Co-Infection Model with Latency

Abstract

In several publications, the dynamical system of HIV and HTLV mono-infections taking into account diffusion, as well as latently infected cells in cellular transmission has been mathematically analyzed. However, no work has been conducted on HTLV/HIV co-infection dynamics taking both factors into consideration. In this paper, a partial differential equations (PDEs) model of HTLV/HIV dual infection was developed and analyzed, considering the cells’ and viruses’ spatial mobility. CD$4^{+}$T cells are the primary target of both HTLV and HIV. For HIV, there are three routes of transmission: free-to-cell (FTC), latent infected-to-cell (ITC), and active ITC. In contrast, HTLV transmits horizontally through ITC contact and vertically through the mitosis of active HTLV-infected cells. In the beginning, the well-posedness of the model was investigated by proving the existence of global solutions and the boundedness. Eight threshold parameters that determine the existence and stability of the eight equilibria of the model were obtained. Lyapunov functions together with the Lyapunov–LaSalle asymptotic stability theorem were used to investigate the global stability of all equilibria. Finally, the theoretical results were verified utilizing numerical simulations.

1. Introduction

Mathematical models and their analysis are efficient and important means of comprehending the dynamics of within-host viral infections. This contributes to a deeper understanding of viral disease structures caused by many viruses such as human immunodeficiency virus (HIV) and human T-lymphotropic virus (HTLV), as well as other viruses such as dengue virus (DENV), hepatitis C virus (HCV), hepatitis B virus (HBV), and, most recently, coronavirus (COVID-19). In fact, this may lead to an improvement in therapeutic interferences and control infectious diseases. HTLV and HIV are transmitted in similar ways from one infected person to another. Both viruses share in common the ability to infect specific immune cells, which are the CD$4^{+}$T cells. HTLV does not cause acquired immunodeficiency syndrome (AIDS) as in the case of HIV; however, it causes fatal diseases such as HTLV-associated myelopathy/tropical spastic paraparesis (HAM/TSP) and adult T-cell leukemia (ATL).

In a groundbreaking study, Nowak and Bangham developed a fundamental model of HIV dynamics [1]. Since then, many works have been published that involved expanded models of this model. Lai and Zou [2] have proposed a mathematical model that describes the dynamics of HIV-1 infection, where direct cell-to-cell transmission and virus-to-cell transmission are considered, as two forms of viral infection. Mojaver and Kheiri [3] developed a model of HIV infection that takes into account cell-to-cell transmission and antiretroviral therapies (HAART) that can be used to treat and control HIV infection. They reported that HAART uses the inhibitors of reverse transcriptase and protease to prevent HIV infection from becoming a fatal disease (AIDS) [3]. A multi-pathway and multi-delay HIV-1 infection model was studied by Adak and Bairagi [4]. It was found that the system exhibited different switching phenomena even without delays. A mathematical model of HIV dynamics was developed by Guo and Qiu [5] to analyze the effect of cytotoxic T lymphocyte (CTL) immune response on the infection dynamics. In this study, the potent therapy, latently infected cells, and cell-to-cell viral transmission were taken into account. Liu and Zhang [6] investigated the dynamics of a two-times delay differential equation model that investigates the dynamics of HIV infection with latency and considering a nonlinear type of HIV infection rate. Chen et al. [7] presented a complete study on the global dynamics of an HIV viral infection model with a saturated incidence rate of infection, as well as a wild-type and a drug-resistant strain of influenza virus.

In the above-mentioned works, all the mathematical models were based on ordinary or delay differential equations without considering the cells’ and viruses’ spatial mobility. In 2007, Wang and Wang [8] incorporated a spatial dependence into the model presented in [1]. Several considerations have been incorporated into the model presented by [8], and these include time delay, different forms of the incidence rate, and immune responses (see [9,10,11]).

It is important to note that the model introduced by [8] has neglected two crucial aspects:

• Viral latent reservoirs: A major impediment to eliminating HIV infection by antiretroviral therapy is the presence of latent HIV-infected cells. Cells that are latently infected carry the virions, but do not generate them until they are activated. There are many studies that have dealt with the development of HIV infection models with active and latent infected cells without taking spatial dependence into account, e.g., [12,13,14,15].
• Cellular transmission: Wang and Wang [8] considered only one mode of transmission of the infection occurring when the HIV particles infect the healthy CD$4^{+}$T cells (FTC), but several studies have indicated that infected-to-cell (ITC) is another method of transmission, carried out through virological synapses between HIV-infected and healthy CD$4^{+}$T cells [16]. Wang et al. [17] extended the work of [8] by including ITC transmission. Following that, Sun and Wang [18] incorporated time delay into the model presented in [17] and considered the incidence rate $f(U,H)$ in a general form.

Based on the work presented in [8], Xu et al. [19] included the ITC infection in their model. In this study, ITC infection arises from the contact between active infected cells and healthy cells. Recently, according to [20], latent and active HIV-infected cells are capable of infecting healthy CD$4^{+}$T cells through the HIV ITC mechanism. Elaiw and AlShamrani [21] assumed nonlinear general forms of ITC and FTC transmissions in the HIV infection model. It was assumed that virus particles can move according to Fickian diffusion, whereas cells cannot in all of the above-mentioned models.

In several recent studies, the assumption was made that viruses, healthy cells, infected cells, and immune cells were capable of diffusing [22,23,24,25,26,27,28]. Gao and Wang [22] investigated a reaction–diffusion HIV-1 dynamics model with time delay and cell-to-cell dissemination. It was assumed in [23] that viruses, uninfected cells, infected cells, and humoral immune cells can diffuse. In [24], the authors examined the global asymptotic stability of a reaction–diffusion virus infection model with homogeneous environments, nonlinear incidence in heterogeneous environments, and humoral immunity. AlAgha and Elaiw [25] presented a study of the global stability of an HIV-1 model with humoral immune response and heterogeneous diffusion. In [26], Elaiw and AlAgha analyzed the dynamics of a system with discrete time delays and three types of infected cells: latently, short-lived productively, and long-lived productively infected cells. The models in [25,26] contain some parameters that measure the efficiency of highly active antiretroviral therapies (HAARTs). Wang et al. [27] proposed a diffusive viral infection model incorporating cell-to-cell infection mode, nonlinear incidences, incubation period, and spatial heterogeneity. Ren et al. [28] discussed the impact of cell-to-cell transmission and the mobility of viruses and cells on HIV-1 dynamics. The following model that considers the mobility of HIV particles and cells was presented by Wang et al. [27]:

$$\left\{\begin{array}{c}\frac{\partial U(s,t)}{\partial t}=d_U\Delta U(s,t)+\varrho -\varsigma U(s,t)-U(s,t)\left[{\omega }_{1}H(s,t)+{\omega }_{2}L(s,t)+{\omega }_{3}I(s,t)\right],\hfill \\ \frac{\partial L(s,t)}{\partial t}=d_L\Delta L(s,t)+U(s,t)\left[{\omega }_{1}H(s,t)+{\omega }_{2}L(s,t)+{\omega }_{3}I(s,t)\right]-\left(\beta +\eta \right)L(s,t),\hfill \\ \frac{\partial I(s,t)}{\partial t}=d_I\Delta I(s,t)+\beta L(s,t)-\alpha I(s,t),\hfill \\ \frac{\partial H(s,t)}{\partial t}=d_H\Delta H(s,t)+\varpi I(s,t)-\vartheta H(s,t).\hfill \end{array}\right.$$

In this model, at position $s=\left(s_1,s_2,\dots ,s_k\right)$ and time t, the densities of healthy CD$4^{+}$T cells, latent infected cells, active infected cells, and free virus particles are represented by $U(s,t),L(s,t),I(s,t)$, and $H(s,t),$ respectively. $d_U$, $d_L$, $d_I$, and $d_H$ are the diffusion coefficients of the corresponding compartments, and $\Delta$ is the Laplacian operator. Cells that are healthy are created at a rate $\varrho .$ Healthy cells are infected by the viral particles through FTC transmission at a rate ${\omega }_{1}UH$. The terms ${\omega }_{2}UL$ and ${\omega }_{3}UI$ represent the ITC incidence rates that occur when healthy CD$4^{+}$T cells come into contact with latent or active infected cells, respectively. Cells that have been latently infected become active at a rate $\beta L.$ Viruses are produced by active infected cells at a rate of $\varpi I.$ The rates of death for healthy cells, latent infected cells, active infected cells, and viral particles are $\varsigma U$, $\eta L,\alpha I$, and $\vartheta H$, respectively.

Additionally, in several studies, the dynamics of HTLV mono-infections have been modeled and analyzed [29,30,31,32,33,34,35,36]. Vargas-De-Leon [29] provided a complete classification of the global dynamics for an HTLV mono-infection model taking the latently infected cells into consideration. Lim and Maini [30] formulated a model for HTLV-I dynamics under the consideration of CTL immunity and mitotic division of active HTLV-infected cells. Pan et al. [31] proposed a model to describe the dynamics of HTLV infection with CTL immunity and time delays. Wang et al. [32] developed an HTLV-I infection model with nonlinear lytic and nonlytic CTL immunity, nonlinear incidence rate, distributed delay, and immune impairment. Wang et al. [33] studied a model of HTLV-I infection with two time delays: an intracellular delay and a CTL immune response delay. Refs. [34,35] discussed HTLV infection with the presence of CTL immunity, as well as the mitotic division of the active infected cells. Except for Wang and Ma [36], all of these HTLV dynamics models neglected the diffusion of viruses and cells. In [36], CTL immunity and the mitotic division of active infected cells were included in a diffusive HTLV infection model.

In the past decade, there has been considerable reporting on HTLV and HIV co-infections. Infection by both viruses concurrently affects pathogenic development and associated chronic disease outcomes [37]. There has been documentation of HTLV/HIV co-infection in certain areas where both retroviruses appear endemic [38] and in individuals who are of a certain ethnicity as well. In highly endemic regions such as South America and Sub-Saharan Africa, co-infections with HIV and HTLV are common. Further, the rate of concurrent HTLV and HIV infections is high in areas where people swap needles and participate in unprotected sexual relationships. According to statistics from some parts of Brazil, 16% of HIV patients in some areas have co-infection [39].

According to a recent study, the results showed that HIV-infected individuals are more likely to be co-infected with HTLV 100- to 500-times more often than people who are not infected [40]. Additionally, several studies have shown that HTLV-infected individuals have a higher likelihood of concomitant HIV infection, and vice versa, as compared to the general population who is infection-free [38]. HTLV and HIV affect primarily CD$4^{+}$T cells and cause immune dysfunction, but their etiologies and clinical outcomes are also in conflict [41]. According to many researchers, HIV-infected patients who possibly have concurrent HTLV infection are at risk of developing AIDS. While the progression of HTLV in co-infected individuals is modified by HIV, resulting in diseases such as HAM∖TSP and ATL [38,40].

Although many mathematical models and analyses have been developed for HTLV and HIV mono-infections, very few works have considered the dynamics of co-infection with HTLV and HIV. There are a few exceptions, namely the very recent papers in [42,43,44,45].

As a consequence of the above, co-infection of HTLV/HIV; involving both latent and active infected cells sharing ITC infection, as well as the diffusion of viruses and cells; has never been mathematically studied. Therefore, in light of the works of [44,45], this study aims to develop and analyze an HTLV/HIV co-infection model taking into account the following considerations:

(C1) 

The hosts of both HIV and HTLV are healthy CD$4^{+}$T cells;

(C2) 

The presence of latently infected HIV and HTLV cells;

(C3) 

Both HTLV and HIV have a specific bilinear CTL immune response;

(C4) 

Several factors can lead to CD$4^{+}$T cells becoming infected with HIV, including free HIV particles, latent HIV-infected cells, and active HIV-infected cells;

(C5) 

HTLV has two routes of transmission: (i) horizontally through the straight ITC contact over the virological synapse and (ii) vertically where the active HTLV-infected cells can transmit HTLV via mitotic division;

(C6) 

All types of cells and viruses diffuse spatially.

The novelty and advantages of the developed model are generalization and improvement of many mathematical models existing in the literature describing HTLV/HIV co-infection by considering three routes of transmission and other biological factors.

The well-posedness of the model has been verified by proving the non-negativity and the boundedness of the model’s solutions. Our analysis yielded a number of threshold parameters that set the presence of the equilibria and their stability. We formulated Lyapunov functions and used the Lyapunov–LaSalle asymptotic stability theorem (L-LAST) to demonstrate the global stability of all equilibria. To assert our analytical results, we supply numerical simulations of the model. Due to the possibility of an individual having two or more infections at the same time, our model may be useful for studying co-infections such as COVID-19 with influenza and HIV with HCV or HBV. Our proposed model and its mathematical analysis will assist clinicians in estimating when to initiate treatment in patients who have co-infections with more than one virus.

2. Model Formulation

We propose the following partial differential equations model based on the statements (C1)–(C6) mentioned in Section 1:

$$\left\{\begin{array}{c}\frac{\partial U(s,t)}{\partial t}=d_U\Delta U(s,t)+\varrho -\varsigma U(s,t)-U(s,t)\left[{\omega }_{1}H(s,t)+{\omega }_{2}L(s,t)\right.\hfill \\ \left.+{\omega }_{3}I(s,t)+{\omega }_{4}E(s,t)\right],\hfill \\ \frac{\partial L(s,t)}{\partial t}=d_L\Delta L(s,t)+U(s,t)\left[{\omega }_{1}H(s,t)+{\omega }_{2}L(s,t)+{\omega }_{3}I(s,t)\right]\hfill \\ -\left(\beta +\eta \right)L(s,t),\hfill \\ \frac{\partial I(s,t)}{\partial t}=d_I\Delta I(s,t)+\beta L(s,t)-\alpha I(s,t)-{\varkappa }_1{Z}^I(s,t)I(s,t),\hfill \\ \frac{\partial P(s,t)}{\partial t}=d_P\Delta P(s,t)+\phi {\omega }_{4}U(s,t)E(s,t)+\epsilon bE(s,t)-\left(\theta +b_1\right)P(s,t),\hfill \\ \frac{\partial E(s,t)}{\partial t}=d_E\Delta E(s,t)+\theta P(s,t)+\left(1-\epsilon \right)bE(s,t)-b_{2}E(s,t)\hfill \\ -{\varkappa }_2{Z}^E(s,t)E(s,t),\hfill \\ \frac{\partial H(s,t)}{\partial t}=d_H\Delta H(s,t)+\varpi I(s,t)-\vartheta H(s,t),\hfill \\ \frac{\partial Z^I(s,t)}{\partial t}=d_{Z^I}\Delta Z^I(s,t)+{\upsilon }_1{Z}^I(s,t)I(s,t)-c_1{Z}^I(s,t),\hfill \\ \frac{\partial Z^E(s,t)}{\partial t}=d_{Z^E}\Delta Z^E(s,t)+{\upsilon }_2{Z}^E(s,t)E(s,t)-c_2{Z}^E(s,t),\hfill \end{array}\right.$$

(1)

where $t\in [0,\infty )$ and $s\in \mathsf{\Omega }$, with boundary conditions:

$$\frac{\partial U}{\partial \overrightarrow{\rho }}=\frac{\partial L}{\partial \overrightarrow{\rho }}=\frac{\partial I}{\partial \overrightarrow{\rho }}=\frac{\partial P}{\partial \overrightarrow{\rho }}=\frac{\partial E}{\partial \overrightarrow{\rho }}=\frac{\partial H}{\partial \overrightarrow{\rho }}=\frac{\partial Z^I}{\partial \overrightarrow{\rho }}=\frac{\partial Z^E}{\partial \overrightarrow{\rho }}=0,t>0,s\in \partial \mathsf{\Omega },$$

(2)

and initial conditions:

$$\begin{array}{cc}\hfill U(s,0)={\mathsf{{\rm Y}}}_1\left(s\right),& L(s,0)={\mathsf{{\rm Y}}}_2\left(s\right),I(s,0)={\mathsf{{\rm Y}}}_3\left(s\right),P(s,0)={\mathsf{{\rm Y}}}_4\left(s\right),E(s,0)={\mathsf{{\rm Y}}}_5\left(s\right),\hfill \\ \hfill H(s,0)={\mathsf{{\rm Y}}}_6\left(s\right),& Z^I(s,0)={\mathsf{{\rm Y}}}_7\left(s\right),Z^E(s,0)={\mathsf{{\rm Y}}}_8\left(s\right),s\in \overline{\mathsf{\Omega }}.\hfill \end{array}$$

(3)

The following is a description of Model (1) with Conditions (2) and (3): At position $s\in \mathsf{\Omega }$ and time $t>0,$ the compartments $P(s,t)$ and $E(s,t)$ represent the density of latent and active HTLV-infected cells. $Z^I(s,t)$ and $Z^E(s,t)$ are the CTLs specific for HIV and for HTLV, respectively. Through ITC contact, healthy CD$4^{+}$T cells become infected with HTLV at a rate ${\omega }_{4}UE$. The ratio $\phi \in (0,1)$ identifies the possibility that HTLV infections will be latent. $\epsilon bE,$ $\epsilon \in \left(0,1\right)$ denotes the rate at which active HTLV-infected cells are passed to become latently infected and escape the immune system [35]. The mortality rates of latent and active HTLV-infected cells are $b_{1}P$ and $b_{2}E$, respectively. $\theta P$ is the rate at which latent HTLV-infected cells are activated. HIV-infected cells and HTLV-infected cells die, respectively, at rates ${\varkappa }_1{Z}^{I}I$ $,{\varkappa }_2{Z}^{E}E,$ as a result of their specific immunity. CTLs particular to HIV and HTLV expand at distinct rates ${\upsilon }_1{Z}^{I}I$, ${\upsilon }_2{Z}^{E}E$, and they decay at rates $c_1{Z}^I,c_2{Z}^E$, respectively. The diffusion coefficients of the compartments P, $E,Z^I$, $Z^E$ are $d_P$, $d_E,d_{Z^I}$, and $d_{Z^E}$. As illustrated in Section 1, all remaining parameters have the same name and explanation.

The boundary conditions (2) are the homogeneous Neumann boundary conditions, which can provide a natural spreading limit and ensure that viruses and cells are unable to escape through the isolated boundaries [46]. The open domain $\mathsf{\Omega }\subset {\mathbb{R}}^k,$ $k\ge 1$ is connected and bounded with a smooth boundary $\partial \mathsf{\Omega }$, and the unit vector $\overrightarrow{\rho }$ is the outward normal vector on $\partial \mathsf{\Omega }$. The functions ${\mathsf{{\rm Y}}}_i\left(s\right)$, $i=1,\dots ,8,$ are non-negative and continuous.

We will assume that $b<min\left\{\varsigma ,b_1,b_2\right\}$ [30]. It follows that $\left(1-\epsilon \right)b<b_2$ and then

$$b_2-\left(1-\epsilon \right)b>0.$$

Let $a=b_2-\left(1-\epsilon \right)b$ and $w=\epsilon b$. Therefore, Model (1) can be written as

$$\left\{\begin{array}{c}\frac{\partial U(s,t)}{\partial t}=d_U\Delta U(s,t)+\varrho -\varsigma U(s,t)-U(s,t)\left[{\omega }_{1}H(s,t)+{\omega }_{2}L(s,t)\right.\hfill \\ \left.+{\omega }_{3}I(s,t)+{\omega }_{4}E(s,t)\right],\hfill \\ \frac{\partial L(s,t)}{\partial t}=d_L\Delta L(s,t)+U(s,t)\left[{\omega }_{1}H(s,t)+{\omega }_{2}L(s,t)+{\omega }_{3}I(s,t)\right]\hfill \\ -\left(\beta +\eta \right)L(s,t),\hfill \\ \frac{\partial I(s,t)}{\partial t}=d_I\Delta I(s,t)+\beta L(s,t)-\alpha I(s,t)-{\varkappa }_1{Z}^I(s,t)I(s,t),\hfill \\ \frac{\partial P(s,t)}{\partial t}=d_P\Delta P(s,t)+\phi {\omega }_{4}U(s,t)E(s,t)+wE(s,t)\hfill \\ -\left(\theta +b_1\right)P(s,t),\hfill \\ \frac{\partial E(s,t)}{\partial t}=d_E\Delta E(s,t)+\theta P(s,t)-aE(s,t)-{\varkappa }_2{Z}^E(s,t)E(s,t),\hfill \\ \frac{\partial H(s,t)}{\partial t}=d_H\Delta H(s,t)+\varpi I(s,t)-\vartheta H(s,t),\hfill \\ \frac{\partial Z^I(s,t)}{\partial t}=d_{Z^I}\Delta Z^I(s,t)+{\upsilon }_1{Z}^I(s,t)I(s,t)-c_1{Z}^I(s,t),\hfill \\ \frac{\partial Z^E(s,t)}{\partial t}=d_{Z^E}\Delta Z^E(s,t)+{\upsilon }_2{Z}^E(s,t)E(s,t)-c_2{Z}^E(s,t).\hfill \end{array}\right.$$

(4)

3. Properties of Solutions

Proposition 1.

Suppose that $d_U=d_L=d_I=d_P=d_E=d_H=d_{Z^I}=d_{Z^E}=\tilde{d}$. Then, there exists a unique solution $Sol(s,t)=(U\left(s,t\right),L\left(s,t\right),I\left(s,t\right),P\left(s,t\right),E\left(s,t\right),H\left(s,t\right),$ $Z^I\left(s,t\right),Z^E\left(s,t\right))$ for System (4) with the boundary and initial conditions (2)–(3). Moreover, this solution remains non-negative and bounded on $\overline{\mathsf{\Omega }}\times [0,+\infty )$.

Proof. 

Define the norm ${\parallel \lambda \parallel }_{\mathcal{Y}}=\underset{s\in \overline{\mathsf{\Omega }}}{sup}\left|\lambda \left(s\right)\right|,$ where the set $\mathcal{Y}=BUC\left(\overline{\mathsf{\Omega }},{\mathbb{R}}^8\right)$ comprises all uniformly bounded and continuous functions from $\overline{\mathsf{\Omega }}$ to ${\mathbb{R}}^8$. Consider a positive cone ${\mathcal{Y}}_{+}=BUC\left(\overline{\mathsf{\Omega }},{\mathbb{R}}_{+}^8\right)\subset \mathcal{Y}$ that leads to partial order on $\mathcal{Y}$. As a result, the space $\left({\mathcal{Y},\parallel ·\parallel }_{\mathcal{Y}}\right)$ is a Banach lattice [47,48].

Let $\mathsf{\Phi }={({\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2,{\mathsf{\Phi }}_3,{\mathsf{\Phi }}_4,{\mathsf{\Phi }}_5,{\mathsf{\Phi }}_6,{\mathsf{\Phi }}_7,{\mathsf{\Phi }}_8)}^{tr}:{\mathcal{Y}}_{+}\to \mathcal{Y}$ with any initial data $\mathsf{{\rm Y}}=({\mathsf{{\rm Y}}}_1,{\mathsf{{\rm Y}}}_2,{\mathsf{{\rm Y}}}_3,$ ${\mathsf{{\rm Y}}}_4,{\mathsf{{\rm Y}}}_5,{\mathsf{{\rm Y}}}_6,{\mathsf{{\rm Y}}}_7,{\mathsf{{\rm Y}}}_8{)}^{tr}\in {\mathcal{Y}}_{+}$, given by

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_1\left(\mathsf{{\rm Y}}\right)\left(s\right)& =\varrho -\varsigma {\mathsf{{\rm Y}}}_1\left(s\right)-{\mathsf{{\rm Y}}}_1\left(s\right)\left[{\omega }_1{\mathsf{{\rm Y}}}_6\left(s\right)+{\omega }_2{\mathsf{{\rm Y}}}_2\left(s\right)+{\omega }_3{\mathsf{{\rm Y}}}_3\left(s\right)+{\omega }_4{\mathsf{{\rm Y}}}_5\left(s\right)\right],\hfill \\ \hfill {\mathsf{\Phi }}_2\left(\mathsf{{\rm Y}}\right)\left(s\right)& ={\mathsf{{\rm Y}}}_1\left(s\right)\left[{\omega }_1{\mathsf{{\rm Y}}}_6\left(s\right)+{\omega }_2{\mathsf{{\rm Y}}}_2\left(s\right)+{\omega }_3{\mathsf{{\rm Y}}}_3\left(s\right)\right]-\left(\beta +\eta \right){\mathsf{{\rm Y}}}_2\left(s\right),\hfill \\ \hfill {\mathsf{\Phi }}_3\left(\mathsf{{\rm Y}}\right)\left(s\right)& =\beta {\mathsf{{\rm Y}}}_2\left(s\right)-\alpha {\mathsf{{\rm Y}}}_3\left(s\right)-{\varkappa }_1{\mathsf{{\rm Y}}}_7\left(s\right){\mathsf{{\rm Y}}}_3\left(s\right),\hfill \\ \hfill {\mathsf{\Phi }}_4\left(\mathsf{{\rm Y}}\right)\left(s\right)& =\phi {\omega }_4{\mathsf{{\rm Y}}}_1\left(s\right){\mathsf{{\rm Y}}}_5\left(s\right)+w{\mathsf{{\rm Y}}}_5\left(s\right)-\left(\theta +b_1\right){\mathsf{{\rm Y}}}_4\left(s\right),\hfill \\ \hfill {\mathsf{\Phi }}_5\left(\mathsf{{\rm Y}}\right)\left(s\right)& =\theta {\mathsf{{\rm Y}}}_4\left(s\right)-a{\mathsf{{\rm Y}}}_5\left(s\right)-{\varkappa }_2{\mathsf{{\rm Y}}}_8\left(s\right){\mathsf{{\rm Y}}}_5\left(s\right),\hfill \\ \hfill {\mathsf{\Phi }}_6\left(\mathsf{{\rm Y}}\right)\left(s\right)& =\varpi {\mathsf{{\rm Y}}}_3\left(s\right)-\vartheta {\mathsf{{\rm Y}}}_6\left(s\right),\hfill \\ \hfill {\mathsf{\Phi }}_7\left(\mathsf{{\rm Y}}\right)\left(s\right)& ={\upsilon }_1{\mathsf{{\rm Y}}}_7\left(s\right){\mathsf{{\rm Y}}}_3\left(s\right)-c_1{\mathsf{{\rm Y}}}_7\left(s\right),\hfill \\ \hfill {\mathsf{\Phi }}_8\left(\mathsf{{\rm Y}}\right)\left(s\right)& ={\upsilon }_2{\mathsf{{\rm Y}}}_8\left(s\right){\mathsf{{\rm Y}}}_5\left(s\right)-c_2{\mathsf{{\rm Y}}}_8\left(s\right).\hfill \end{array}$$

Clearly, $\mathsf{\Phi }$ is locally Lipschitz on ${\mathcal{Y}}_{+}$. It is possible to rewrite System (4) with the boundary conditions (2) and initial conditions (3) as the following abstract functional differential equation:

$$\left\{\begin{array}{c}\frac{d\overline{\mathcal{G}}}{dt}=\mathsf{\Theta }\overline{\mathcal{G}}+\mathsf{\Phi }\left(\overline{\mathcal{G}}\right),t>0,\hfill \\ \overline{\mathcal{G}}\left(0\right)=\mathsf{{\rm Y}}\in {\mathcal{Y}}_{+},\hfill \end{array}\right.$$

where $\overline{\mathcal{G}}={(U,L,I,P,E,H,Z^I,Z^E)}^{tr}$ and $\mathsf{\Theta }\overline{\mathcal{G}}=\left(d_U\Delta U,d_L\Delta L,d_I\Delta I,d_P\Delta P,d_E\Delta E,d_H\Delta H,d_{Z^I}\Delta Z^I,\right.{\left.d_{Z^E}\Delta Z^E\right)}^{tr}.$ In this case,

$$\underset{h\to 0^{+}}{lim}\frac{1}{h}\mathrm{dist}\left(\mathsf{{\rm Y}}\left(0\right)+h\mathsf{\Phi }\left(\mathsf{{\rm Y}}\right),{\mathcal{Y}}_{+}\right)=0,\mathrm{for}\mathrm{all}\mathsf{{\rm Y}}\in {\mathcal{Y}}_{+}.$$

According to [47,48,49], System (4) with (2)–(3) has a unique non-negative mild solution $Sol(s,t)$ defined on $\overline{\mathsf{\Omega }}\times [0,{\mathcal{L}}_k)$ for any $\mathsf{{\rm Y}}\in {\mathcal{Y}}_{+}$, where the maximum time interval during which $Sol(s,t)$ exists is $[0,{\mathcal{L}}_k)$. Additionally, $Sol(s,t)$ is a classical solution.

In order to establish that solutions are bounded, let

$$G\left(s,t\right)=U\left(s,t\right)+L\left(s,t\right)+I\left(s,t\right)+\frac{1}{\phi }\left[P\left(s,t\right)+E\left(s,t\right)\right]+\frac{\alpha }{2\varpi }H\left(s,t\right)+\frac{{\varkappa }_1}{{\upsilon }_1}{Z}^I\left(s,t\right)+\frac{{\varkappa }_2}{\phi {\upsilon }_2}{Z}^E\left(s,t\right).$$

Since $d_U=d_L=d_I=d_P=d_E=d_H=d_{Z^I}=d_{Z^E}=\tilde{d}$, then using System (4), we obtain

$$\begin{array}{cc}\hfill \frac{\partial G(s,t)}{\partial t}-\tilde{d}\Delta G(s,t)& =\varrho -\varsigma U(s,t)-\eta L(s,t)-\frac{\alpha }{2}I(s,t)-\frac{b_1}{\phi }P(s,t)\hfill \\ \hfill & -\frac{a-w}{\phi }E(s,t)-\frac{\alpha \vartheta }{2\varpi }H(s,t)-\frac{{\varkappa }_1{c}_1}{{\upsilon }_1}{Z}^I(s,t)-\frac{{\varkappa }_2{c}_2}{\phi {\upsilon }_2}{Z}^E(s,t).\hfill \end{array}$$

We have $a-w=b_2-b>0$. Hence,

$$\begin{array}{cc}\hfill \frac{\partial G(s,t)}{\partial t}-\tilde{d}\Delta G(s,t)& =\varrho -\varsigma U(s,t)-\eta L(s,t)-\frac{\alpha }{2}I(s,t)-\frac{b_1}{\phi }P(s,t)\hfill \\ \hfill & -\frac{b_2-b}{\phi }E(s,t)-\frac{\alpha \vartheta }{2\varpi }H(s,t)-\frac{{\varkappa }_1{c}_1}{{\upsilon }_1}{Z}^I(s,t)-\frac{{\varkappa }_2{c}_2}{\phi {\upsilon }_2}{Z}^E(s,t)\hfill \\ \hfill & \le \varrho -\varphi \left[U(s,t)+L(s,t)+I(s,t)+\frac{1}{\phi }\left\{P(s,t)+E(s,t)\right\}\right.\hfill \\ \hfill & \left.+\frac{\alpha }{2\varpi }H(s,t)+\frac{{\varkappa }_1}{{\upsilon }_1}{Z}^I(s,t)+\frac{{\varkappa }_2}{\phi {\upsilon }_2}{Z}^E(s,t)\right]=\varrho -\varphi G(s,t),\hfill \end{array}$$

where $\varphi =min\{\varsigma ,\eta ,\frac{\alpha }{2},b_1,b_2-b,\vartheta ,c_1,c_2\}$. Therefore, $G(s,t)$ satisfies the following system:

$$\left\{\begin{array}{c}\frac{\partial G(s,t)}{\partial t}-\tilde{d}\Delta G(s,t)\le \varrho -\varphi G(s,t),\hfill \\ G(s,0)={\mathsf{{\rm Y}}}_1\left(s\right)+{\mathsf{{\rm Y}}}_2\left(s\right)+{\mathsf{{\rm Y}}}_3\left(s\right)+\frac{1}{\phi }\left[{\mathsf{{\rm Y}}}_4\left(s\right)+{\mathsf{{\rm Y}}}_5\left(s\right)\right]+\frac{\alpha }{2\varpi }{\mathsf{{\rm Y}}}_6\left(s\right)+\frac{{\varkappa }_1}{{\upsilon }_1}{\mathsf{{\rm Y}}}_7\left(s\right)+\frac{{\varkappa }_2}{\phi {\upsilon }_2}{\mathsf{{\rm Y}}}_8\left(s\right)\ge 0,\hfill \\ \frac{\partial G}{\partial \overrightarrow{\rho }}=0.\hfill \end{array}\right.$$

Assume $\tilde{G}\left(t\right)$ is a solution of the ordinary differential equation system given below:

$$\left\{\begin{array}{c}\frac{d\tilde{G}\left(t\right)}{dt}=\varrho -\varphi \tilde{G}\left(t\right),\hfill \\ \tilde{G}\left(0\right)={\displaystyle \underset{s\in \overline{\mathsf{\Omega }}}{max}}G(s,0).\hfill \end{array}\right.$$

Accordingly, this gives $\tilde{G}\left(t\right)\le max\left\{\frac{\varrho }{\varphi },{\displaystyle \underset{s\in \overline{\mathsf{\Omega }}}{max}}G(s,0)\right\}$. In accordance with the comparison principle (see [50]), we obtain $G(s,t)\le \tilde{G}\left(t\right)$. Thus,

$$G(s,t)\le max\left\{\frac{\varrho }{\varphi },\underset{s\in \overline{\mathsf{\Omega }}}{max}G(s,0)\right\},$$

and this implies that $U\left(s,t\right),$ $L\left(s,t\right),$ $I\left(s,t\right),$ $P\left(s,t\right),$ $E\left(s,t\right),$ $H\left(s,t\right),$ $Z^I\left(s,t\right),$ and $Z^E\left(s,t\right)$ are bounded on $\overline{\mathsf{\Omega }}\times [0,{\mathcal{L}}_k)$. Using the standard theory for semi-linear parabolic systems, we concluded that ${\mathcal{L}}_k=+\infty$ [51]. As a result, the solution $Sol(s,t)$ is defined for all $s\in \mathsf{\Omega },$ $t>0$, unique, non-negative, and bounded.   □

4. Equilibrium Analysis

This section is devoted to the study of computing the model’s threshold parameters and equilibria. Model (4) satisfies the following equations:

$$\begin{array}{cc}\hfill 0& =\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE,\hfill \\ \hfill 0& ={\omega }_{1}UH+{\omega }_{2}UL+{\omega }_{3}UI-\left(\beta +\eta \right)L,\hfill \\ \hfill 0& =\beta L-\alpha I-{\varkappa }_1{Z}^{I}I,\hfill \\ \hfill 0& =\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P,\hfill \\ \hfill 0& =\theta P-aE-{\varkappa }_2{Z}^{E}E,\hfill \\ \hfill 0& =\varpi I-\vartheta H,\hfill \\ \hfill 0& =\left({\upsilon }_{1}I-c_1\right)Z^I,\hfill \\ \hfill 0& =\left({\upsilon }_{2}E-c_2\right)Z^E.\hfill \end{array}$$

The results of the calculations show that there are eight equilibrium points for Model (4):

• Infection-free equilibrium, ${\check{S}}_0=(U_0,0,0,0,0,0,0,0)$ and $U_0=\varrho /\varsigma$. Both HIV and HTLV are not present in this case.
• Persistent HIV mono-infection equilibrium accompanied by an inefficient immune response, ${\check{S}}_1=(U_1,L_1,I_1,0,0,H_1,0,0),$ with components given by

  $$\begin{array}{cc}\hfill U_1& ={\displaystyle \frac{U_0}{{\mathcal{R}}_1}},L_1=\frac{\alpha \varsigma \vartheta }{\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)}\left({\mathcal{R}}_1-1\right),\hfill \\ \hfill I_1& =\frac{\varsigma \vartheta \beta }{\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)}\left({\mathcal{R}}_1-1\right),H_1=\frac{\varsigma \varpi \beta }{\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)}\left({\mathcal{R}}_1-1\right).\hfill \end{array}$$

  The parameter ${\mathcal{R}}_1$ defines the basic HIV mono-infection reproductive number for Model (4), which is given as

  $${\mathcal{R}}_1=\frac{U_0\left[\alpha \vartheta {\omega }_2+\beta \left(\varpi {\omega }_1+\vartheta {\omega }_3\right)\right]}{\alpha \vartheta (\beta +\eta )}=\frac{U_0\beta \varpi {\omega }_1}{\alpha \vartheta (\beta +\eta )}+\frac{U_0{\omega }_2}{\beta +\eta }+\frac{U_0\beta {\omega }_3}{\alpha (\beta +\eta )}.$$

  ${\mathcal{R}}_1$ is responsible for determining whether or not a persistent HIV mono-infection is possible. In the meantime, the immune system is unable to respond effectively. In addition, ${\check{S}}_1$ exists if ${\mathcal{R}}_1>1$.
• Persistent HTLV mono-infection equilibrium accompanied by an inefficient immune response, ${\check{S}}_2=(U_2,0,0,P_2,E_2,0,0,0)$, with components given by

  $$U_2={\displaystyle \frac{U_0}{{\mathcal{R}}_2}},P_2=\frac{\varsigma a}{{\omega }_4\theta }\left({\mathcal{R}}_2-1\right),E_2=\frac{\varsigma }{{\omega }_4}\left({\mathcal{R}}_2-1\right).$$

  The parameter ${\mathcal{R}}_2$ specifies the basic HTLV mono-infection reproductive number for Model (4) and is given as

  $${\mathcal{R}}_2=\frac{\phi {\omega }_4\theta U_0}{\left(a-w\right)\theta +a{b}_1}.$$

  ${\mathcal{R}}_2$ is responsible for determining whether or not a persistent HTLV mono-infection is possible. In the meantime, the immune system is unable to work effectively. Further, ${\check{S}}_2$ exists if ${\mathcal{R}}_2>1$.
• Persistent HIV mono-infection equilibrium accompanied only by efficient HIV-specific CTL, ${\check{S}}_3=(U_3,L_3,I_3,0,0,H_3,Z_3^I,0)$, with components given by

  $$U_3=\frac{\varrho \vartheta {\upsilon }_1}{\varpi c_1{\omega }_1+\vartheta \left(c_1{\omega }_3+\varsigma {\upsilon }_1+{\upsilon }_1{\omega }_2{L}_3\right)},I_3=\frac{c_1}{{\upsilon }_1},H_3=\frac{\varpi }{\vartheta }{I}_3=\frac{\varpi c_1}{\vartheta {\upsilon }_1},Z_3^I={\displaystyle \frac{\alpha }{{\varkappa }_1}}({\mathcal{R}}_3-1),$$

  and

  $${\mathcal{R}}_3=\frac{\beta {\upsilon }_1{L}_3}{\alpha c_1},$$

  represents the HIV-specific CTL immunity reproductive number for HIV mono-infection. In the case of HIV mono-infection, ${\mathcal{R}}_3$ indicates whether or not HIV-specific CTL immunity is efficient in the case of HIV mono-infection where the HTLV infection is not present. The component $L_3$ satisfies the quadratic equation:

  $$A_1{L}_3^2+B_1{L}_3+C_1=0,$$

  (5)

  where

  $$\begin{array}{cc}\hfill A_1& =\vartheta {\omega }_2{\upsilon }_1\left(\beta +\eta \right),\hfill \\ \hfill B_1& =c_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)\left(\beta +\eta \right)+\vartheta {\upsilon }_1\left[\varsigma \left(\beta +\eta \right)-{\omega }_2\varrho \right],\hfill \\ \hfill C_1& =-c_1\varrho \left(\varpi {\omega }_1+\vartheta {\omega }_3\right).\hfill \end{array}$$

  (6)

  Since $A_1>0$ and $C_1<0$, then $B_1^2-4A_1{C}_1>0,$ and the positive real root of Equation (5) is calculated as follows:

  $$L_3=\frac{-B_1+\sqrt{B_1^2-4A_1{C}_1}}{2A_1}.$$

  ${\check{S}}_3$ exists if ${\mathcal{R}}_3>1$.
• Persistent HTLV mono-infection equilibrium accompanied only by efficient HTLV-specific CTL, ${\check{S}}_4=(U_4,0,0,P_4,E_4,0,0,Z_4^E)$, with components given by

  $$\begin{array}{cc}\hfill U_4& ={\displaystyle \frac{{\upsilon }_2\varrho }{c_2{\omega }_4+\varsigma {\upsilon }_2}},P_4={\displaystyle \frac{c_2\left[w\left(c_2{\omega }_4+\varsigma {\upsilon }_2\right)+{\omega }_4\varrho \phi {\upsilon }_2\right]}{{\upsilon }_2\left(\theta +b_1\right)\left(c_2{\omega }_4+\varsigma {\upsilon }_2\right)}},\hfill \\ \hfill E_4& =\frac{c_2}{{\upsilon }_2},Z_4^E=\frac{(a-w)\theta +a{b}_1}{{\varkappa }_2(\theta +b_1)}({\mathcal{R}}_4-1).\hfill \end{array}$$

  The term ${\mathcal{R}}_4$ is introduced as the HTLV-specific CTL immunity reproductive number for HTLV mono-infection and is defined as

  $${\mathcal{R}}_4=\frac{{\upsilon }_2\varrho \phi {\omega }_4\theta }{\left(c_2{\omega }_4+\varsigma {\upsilon }_2\right)\left[(a-w)\theta +a{b}_1\right]}.$$

  In fact, ${\mathcal{R}}_4$ indicates whether or not HTLV-specific CTL immunity is efficient in the case HTLV mono-infection where the HIV infection is not present. On the other hand, ${\check{S}}_4$ exists if ${\mathcal{R}}_4>1$.
• Persistent HTLV/HIV co-infection equilibrium accompanied only by efficient HIV-specific CTL, ${\check{S}}_5=(U_5,L_5,I_5,P_5,E_5,H_5,Z_5^I,0)$, with components given by

  $$\begin{array}{cc}\hfill U_5& ={\displaystyle \frac{\left(a-w\right)\theta +a{b}_1}{\phi {\omega }_4\theta }}=U_2,L_5=\frac{c_1(\varpi {\omega }_1+\vartheta {\omega }_3)}{\vartheta {{\upsilon }_1\omega }_2({\widehat{\mathcal{R}}}_5-1)},\hfill \\ \hfill I_5& =\frac{c_1}{{\upsilon }_1}=I_3,H_5=\frac{\varpi c_1}{\vartheta {\upsilon }_1}=H_3,\hfill \\ \hfill P_5& =\frac{a\left[c_1{\omega }_4\theta \phi (\varpi {\omega }_1+\vartheta {\omega }_3)(\beta +\eta )+\varsigma \vartheta {{\upsilon }_1\omega }_2\left\{(a-w)\theta +a{b}_1\right\}({\widehat{\mathcal{R}}}_5-1)\right]}{\vartheta {{\upsilon }_1\omega }_4\theta {\omega }_2\left[(a-w)\theta +a{b}_1\right]}\left(\frac{{\mathcal{R}}_5-1}{{\widehat{\mathcal{R}}}_5-1}\right),\hfill \\ \hfill E_5& =\frac{c_1\phi \theta {\omega }_4(\varpi {\omega }_1+\vartheta {\omega }_3)(\beta +\eta )+\varsigma \vartheta {{\upsilon }_1\omega }_2\left[(a-w)\theta +a{b}_1\right]({\widehat{\mathcal{R}}}_5-1)}{\vartheta {{\upsilon }_1{\omega }_4\omega }_2\left[(a-w)\theta +a{b}_1\right]}\left(\frac{{\mathcal{R}}_5-1}{{\widehat{\mathcal{R}}}_5-1}\right),\hfill \\ \hfill Z_5^I& =\frac{\alpha {\omega }_4\phi \theta (\beta +\eta )}{{{\varkappa }_1\omega }_2\left[(a-w)\theta +a{b}_1\right]\left({\widehat{\mathcal{R}}}_5-1\right)}\left({\mathcal{R}}_1/{\mathcal{R}}_2-1\right).\hfill \end{array}$$

  Here, ${\mathcal{R}}_5$ is the HTLV infection reproductive number when the HIV infection exists, and

  $${\mathcal{R}}_5=\frac{\varrho \phi \theta \vartheta {{\upsilon }_1{\omega }_4\omega }_2({\widehat{\mathcal{R}}}_5-1)}{c_1\phi \theta {\omega }_4(\varpi {\omega }_1+\vartheta {\omega }_3)(\beta +\eta )+\varsigma \vartheta {{\upsilon }_1\omega }_2\left[(a-w)\theta +a{b}_1\right]({\widehat{\mathcal{R}}}_5-1)},$$

  where

  $${\widehat{\mathcal{R}}}_5=\frac{{\omega }_4\phi \theta (\beta +\eta )}{{\omega }_2\left[(a-w)\theta +a{b}_1\right]}.$$

  In fact, ${\mathcal{R}}_5$ determines whether or not HIV-infected individuals can further be dually infected with HTLV.
• Persistent HTLV/HIV co-infection equilibrium accompanied only by efficient HTLV-specific CTL, ${\check{S}}_6=(U_6,L_6,I_6,P_6,E_6,H_6,0,Z_6^E)$, with components given by

  $$\begin{array}{cc}\hfill U_6& =\frac{\alpha \vartheta (\beta +\eta )}{\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)}=U_1,L_6=\frac{\alpha \vartheta (c_2{\omega }_4+\varsigma {\upsilon }_2)}{{\upsilon }_2\left[\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)\right]}\left({\mathcal{R}}_6-1\right),\hfill \\ \hfill I_6& =\frac{\beta \vartheta (c_2{\omega }_4+\varsigma {\upsilon }_2)}{{\upsilon }_2\left[\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)\right]}\left({\mathcal{R}}_6-1\right),\hfill \\ \hfill P_6& =\frac{c_2\left[w\left\{\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)\right\}+\alpha \vartheta {\omega }_4\phi (\beta +\eta )\right]}{{\upsilon }_2(\theta +b_1)\left[\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)\right]},\hfill \\ \hfill E_6& =\frac{c_2}{{\upsilon }_2}=E_4,H_6=\frac{\varpi \beta (c_2{\omega }_4+\varsigma {\upsilon }_2)}{{\upsilon }_2\left[\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)\right]}\left({\mathcal{R}}_6-1\right),\hfill \\ \hfill Z_6^E& ={\displaystyle \frac{(a-w)\theta +a{b}_1}{{\varkappa }_2\left(\theta +b_1\right)}}\left({\mathcal{R}}_2/{\mathcal{R}}_1-1\right).\hfill \end{array}$$

  ${\mathcal{R}}_6$ represents the HIV infection reproductive number when HTLV infection exists, and

  $${\mathcal{R}}_6=\frac{\varrho {\upsilon }_2\left[\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)\right]}{\alpha \vartheta (\beta +\eta )(c_2{\omega }_4+\varsigma {\upsilon }_2)}.$$

  The parameter ${\mathcal{R}}_6$ indicates whether or not an HTLV-infected individual can further be dually infected with HIV.
• Persistent HTLV/HIV co-infection equilibrium accompanied by efficient HIV-specific CTL and HTLV-specific CTL, ${\check{S}}_7=(U_7,L_7,I_7,P_7,E_7,H_7,Z_7^I,Z_7^E)$, with components given by

  $$\begin{array}{cc}\hfill U_7& ={\displaystyle \frac{\vartheta {\upsilon }_1{\upsilon }_2\varrho }{c_1{\upsilon }_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)+\vartheta {\upsilon }_1\left(c_2{\omega }_4+\varsigma {\upsilon }_2+{{\omega }_2\upsilon }_2{L}_7\right)}},\hfill \\ \hfill P_7& =\frac{c_2\vartheta {\omega }_4\varrho {{\upsilon }_1\upsilon }_2\phi +c_{2}w\left[c_1{\upsilon }_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)+\vartheta {\upsilon }_1(c_2{\omega }_4+\varsigma {\upsilon }_2+{{\omega }_2\upsilon }_2{L}_7)\right]}{{\upsilon }_2(\theta +b_1)\left[c_1{\upsilon }_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)+\vartheta {\upsilon }_1(c_2{\omega }_4+\varsigma {\upsilon }_2+{\omega }_2{\upsilon }_2{L}_7)\right]},\hfill \\ \hfill I_7& =\frac{c_1}{{\upsilon }_1}=I_3=I_5,E_7=\frac{c_2}{{\upsilon }_2}=E_4=E_6,H_7=\frac{\varpi c_1}{\vartheta {\upsilon }_1}=H_3=H_5,\hfill \\ \hfill Z_7^I& ={\displaystyle \frac{\alpha }{{\varkappa }_1}}\left({\mathcal{R}}_7-1\right),Z_7^E=\frac{(a-w)\theta +a{b}_1}{{\varkappa }_2(\theta +b_1)}\left({\mathcal{R}}_8-1\right),\hfill \end{array}$$

  and

  $$\begin{array}{cc}\hfill {\mathcal{R}}_7& ={\displaystyle \frac{\beta {\upsilon }_1{L}_7}{\alpha c_1}},\hfill \\ \hfill {\mathcal{R}}_8& =\frac{\vartheta {\omega }_4\varrho {\upsilon }_1{\upsilon }_2\phi \theta }{((a-w)\theta +a{b}_1)\left[c_1{\upsilon }_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)+\vartheta {\upsilon }_1(c_2{\omega }_4+\varsigma {\upsilon }_2+{\omega }_2{\upsilon }_2{L}_7)\right]}.\hfill \end{array}$$

  The parameters ${\mathcal{R}}_7$ and ${\mathcal{R}}_8$ represent, respectively, the competingHIV-specific CTL and HTLV-specific CTL reproductive numbers in the case of HTLV/HIV co-infection. Here, $L_7$ satisfies the equation:

  $$A_2{L}_7^2+B_2{L}_7+C_2=0,$$

  (7)

  where

  $$\begin{array}{cc}\hfill A_2& =\vartheta {\omega }_2{\upsilon }_1\upsilon {}_2(\beta +\eta ),\hfill \\ \hfill B_2& =c_2\vartheta {\omega }_4{\upsilon }_1(\beta +\eta )+c_1{\upsilon }_2(\varpi {\omega }_1+\vartheta {\omega }_3)(\beta +\eta )+\varsigma \vartheta {\upsilon }_1{\upsilon }_2(\beta +\eta )-\vartheta {\omega }_2\varrho {\upsilon }_1{\upsilon }_2,\hfill \\ \hfill C_2& =-c_1\varrho {\upsilon }_2(\varpi {\omega }_1+\vartheta {\omega }_3).\hfill \end{array}$$

  (8)

  Since $A_2>0$ and $C_2<0$, then $B_2^2-4A_2{C}_2>0,$ and the positive real root of Equation (7) is calculated as follows:

  $$L_7=\frac{-B_2+\sqrt{B_2^2-4A_2{C}_2}}{2A_2}.$$

  It is obvious that if ${\mathcal{R}}_7>1$ and ${\mathcal{R}}_8>1,$ then ${\check{S}}_7$ exists.

5. Global Properties

This section is devoted to the implementation of a Lyapunov method to check the global stability of the equilibria of Model (4). To do so, we constructed Lyapunov functions as described in the works [52,53]. We further considered the following concepts:

-

According to the arithmetic–geometric mean inequality:

$$\frac{1}{m}\sum _{i=1}^m{F}_i\ge \sqrt[m]{\prod _{i=1}^m{F}_i},F_i\ge 0,i=1,2,\dots$$

we have

$$\begin{array}{cc}\hfill \frac{U_i}{U}+\frac{UI{L}_i}{U_i{I}_{i}L}+\frac{L{I}_i}{L_{i}I}& \ge 3,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \frac{U_i}{U}+\frac{HU{L}_i}{H_i{U}_{i}L}+\frac{L{I}_i}{L_{i}I}+\frac{I{H}_i}{I_{i}H}& \ge 4,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \frac{U_i}{U}+\frac{UE{P}_i}{U_i{E}_{i}P}+\frac{P{E}_i}{P_{i}E}& \ge 3.\hfill \end{array}$$

(11)

-

Consider a function ${\mathsf{\Psi }}_j(U,L,I,P,E,H,Z^I,Z^E)$ in which

$${\widehat{\mathsf{\Psi }}}_j\left(t\right)={\int }_{\mathsf{\Omega }}{\mathsf{\Psi }}_j(s,t)\mathrm{d}s,j=0,1,2,\dots ,7.$$

-

Denote

$${\mathsf{\Gamma }}_j=\left\{(U,L,I,P,E,H,Z^I,Z^E):\frac{d{\widehat{\mathsf{\Psi }}}_j}{dt}=0\right\},j=0,1,2,\dots ,7,$$

and let ${\mathsf{\Gamma }}_j^{\prime }$ represent the largest invariant subset of ${\mathsf{\Gamma }}_j.$

-

Define a function $ϝ\left(x\right)=x-1-lnx$. We have that $ϝ\left(x\right)\ge 0$ for all $x>0$ and $ϝ\left(x\right)=0$ if and only if $x=1$.

-

Based on the condition (2) and the divergence theorem, we derive

$$\begin{array}{cc}\hfill 0& ={\int }_{\partial \mathsf{\Omega }}\nabla \mathcal{S}·\overrightarrow{\rho }\mathrm{d}s={\int }_{\mathsf{\Omega }}\mathrm{div}(\nabla \mathcal{S})\mathrm{d}s={\int }_{\mathsf{\Omega }}\Delta \mathcal{S}\mathrm{d}s,\hfill \\ \hfill 0& ={\int }_{\partial \mathsf{\Omega }}\frac{1}{\mathcal{S}}\nabla \mathcal{S}·\overrightarrow{\rho }\mathrm{d}s={\int }_{\mathsf{\Omega }}\mathrm{div}(\frac{1}{\mathcal{S}}\nabla \mathcal{S})\mathrm{d}s={\int }_{\mathsf{\Omega }}\left(\frac{\Delta \mathcal{S}}{\mathcal{S}}-\frac{{\parallel ▿\mathcal{S}\parallel }^2}{{\mathcal{S}}^2}\right)\mathrm{d}s,\hfill \end{array}$$

for $\mathcal{S}\in \{U,L,I,P,E,H,Z^I,Z^E\}.$ Thus, we obtain

$$\begin{array}{cc}\hfill {\int }_{\mathsf{\Omega }}\Delta \mathcal{S}\mathrm{d}s& =0,\hfill \\ \hfill {\int }_{\mathsf{\Omega }}\frac{\Delta \mathcal{S}}{\mathcal{S}}\mathrm{d}s& ={\int }_{\mathsf{\Omega }}\frac{{\parallel ▿\mathcal{S}\parallel }^2}{{\mathcal{S}}^2}\mathrm{d}s.\hfill \end{array}$$

(12)

In order to simplify the notation, we denote $\mathcal{S}(s,t)$ by $\mathcal{S}$. Based on the above concepts, the following subsections will deal with proving the global stability analysis of each equilibrium point.

5.1. Stability of Equilibrium ${\check{S}}_0$

Theorem 1.

The equilibrium ${\check{S}}_0$ of Model (4) is globally asymptotically stable (GAS) when ${\mathcal{R}}_1\le 1$ and ${\mathcal{R}}_2\le 1.$

Proof. 

Define a Lyapunov function ${\mathsf{\Psi }}_0(s,t)$ as

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_0(s,t)& =U_0ϝ\left(\frac{U}{U_0}\right)+L+\frac{U_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }I+\frac{1}{\phi }P+\frac{\theta +b_1}{\phi \theta }E\hfill \\ \hfill & +\frac{{\omega }_1{U}_0}{\vartheta }H+\frac{{\varkappa }_1{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E.\hfill \end{array}$$

Clearly, ${\widehat{\mathsf{\Psi }}}_0(U,L,I,P,E,H,Z^I,Z^E)>0$ for all $U,L,I,P,E,H,Z^I,Z^E>0,$ and ${\widehat{\mathsf{\Psi }}}_0=0$ at ${\check{S}}_0$. Calculating $\frac{\partial {\mathsf{\Psi }}_0}{\partial t}$ along the solutions of Model (4) as follows:

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_0}{\partial t}& =\left(1-\frac{U_0}{U}\right)\left(d_U\Delta U+\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE\right)+d_L\Delta L+{\omega }_{1}UH\hfill \\ \hfill & +{\omega }_{2}UL+{\omega }_{3}UI-\left(\beta +\eta \right)L+\frac{U_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(d_I\Delta I+\beta L-\alpha I-{\varkappa }_1{Z}^{I}I\right)\hfill \\ \hfill & +\frac{1}{\phi }\left[d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\right]+\frac{\theta +b_1}{\phi \theta }\left(d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_0}{\vartheta }\left(d_H\Delta H+\varpi I-\vartheta H\right)+\frac{{\varkappa }_1{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\left(d_{Z^I}\Delta Z^I+{\upsilon }_1{Z}^{I}I-c_1{Z}^I\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(d_{Z^E}\Delta Z^E+{\upsilon }_2{Z}^{E}E-c_2{Z}^E\right)\hfill \\ \hfill & =\left(1-\frac{U_0}{U}\right)\left(\varrho -\varsigma U\right)+{\omega }_2{U}_{0}L+{\omega }_4{U}_{0}E-\left(\beta +\eta \right)L+\frac{\beta U_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L\hfill \\ \hfill & +\frac{w}{\phi }E-\frac{a\left(\theta +b_1\right)}{\phi \theta }E-\frac{{\varkappa }_1{c}_1{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E\hfill \\ \hfill & +d_U\left(1-\frac{U_0}{U}\right)\Delta U+d_L\Delta L+\frac{d_I{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I+\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E\hfill \\ \hfill & +\frac{{\omega }_1{d}_H{U}_0}{\vartheta }\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

Using $U_0=\varrho /\varsigma$, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_0}{\partial t}& =-\varsigma \frac{{(U-U_0)}^2}{U}+\left(\beta +\eta \right)\left({\mathcal{R}}_1-1\right)L+\frac{\left(a-w\right)\theta +a{b}_1}{\phi \theta }\left({\mathcal{R}}_2-1\right)E\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E+d_U\left(1-\frac{U_0}{U}\right)\Delta U\hfill \\ \hfill & +d_L\Delta L+\frac{d_I{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I+\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E\hfill \\ \hfill & +\frac{{\omega }_1{d}_H{U}_0}{\vartheta }\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

Therefore, we calculate $\frac{d{\widehat{\mathsf{\Psi }}}_0}{dt}$ as follows:

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_0}{dt}& =-\varsigma {\int }_{\mathsf{\Omega }}\frac{{(U-U_0)}^2}{U}\mathrm{d}s+\left(\beta +\eta \right)\left({\mathcal{R}}_1-1\right){\int }_{\mathsf{\Omega }}L\mathrm{d}s+\frac{\left[\left(a-w\right)\theta +a{b}_1\right]\left({\mathcal{R}}_2-1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}E\mathrm{d}s\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{\int }_{\mathsf{\Omega }}{Z}^I\mathrm{d}s-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{\int }_{\mathsf{\Omega }}{Z}^E\mathrm{d}s+d_U{\int }_{\mathsf{\Omega }}\left(1-\frac{U_0}{U}\right)\Delta U\mathrm{d}s\hfill \\ \hfill & +d_L{\int }_{\mathsf{\Omega }}\Delta L\mathrm{d}s+\frac{d_I{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{\int }_{\mathsf{\Omega }}\Delta I\mathrm{d}s+\frac{d_P}{\phi }{\int }_{\mathsf{\Omega }}\Delta P\mathrm{d}s+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}\Delta E\mathrm{d}s\hfill \\ \hfill & +\frac{{\omega }_1{d}_H{U}_0}{\vartheta }{\int }_{\mathsf{\Omega }}\Delta H\mathrm{d}s+\frac{{\varkappa }_1{d}_{Z^I}{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{\int }_{\mathsf{\Omega }}\Delta Z^I\mathrm{d}s+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{\int }_{\mathsf{\Omega }}\Delta Z^E\mathrm{d}s.\hfill \end{array}$$

(13)

By using Equality (12), Equation (13) is simplified as the following form:

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_0}{dt}& =-\varsigma {\int }_{\mathsf{\Omega }}\frac{{(U-U_0)}^2}{U}\mathrm{d}s+\left(\beta +\eta \right)\left({\mathcal{R}}_1-1\right){\int }_{\mathsf{\Omega }}L\mathrm{d}s+\frac{\left[\left(a-w\right)\theta +a{b}_1\right]\left({\mathcal{R}}_2-1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}E\mathrm{d}s\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_0\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{\int }_{\mathsf{\Omega }}{Z}^I\mathrm{d}s-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{\int }_{\mathsf{\Omega }}{Z}^E\mathrm{d}s-d_U{U}_0{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}s.\hfill \end{array}$$

Hence, $\frac{d{\widehat{\mathsf{\Psi }}}_0}{dt}\le 0$ for any $U,L,E,Z^I,Z^E>0$ and $\frac{d{\widehat{\mathsf{\Psi }}}_0}{dt}=0$ when $(U,L,E,Z^I,Z^E)=(U_0,0,0,0,0)$. The solutions of Model (4) are limited to ${\mathsf{\Gamma }}_0^{\prime }$. It can be seen that the elements of the set ${\mathsf{\Gamma }}_0^{\prime }$ satisfy $(U,L,E,Z^I,Z^E)=(U_0,0,0,0,0)$. Then, $\frac{\partial E}{\partial t}=\Delta E=0$, and the fifth equation of Model (4) becomes

$$0=\frac{\partial E}{\partial t}=\theta P.$$

Thus, $P=0$. The third and sixth equations of Model (4) yield

$$\left\{\begin{array}{cc}\frac{\partial I}{\partial t}\hfill & =d_I\Delta I-\alpha I,\hfill \\ \frac{\partial H}{\partial t}\hfill & =d_H\Delta H+\varpi I-\vartheta H.\hfill \end{array}\right.$$

(14)

We can define a Lyapunov function as follows

$${\tilde{\mathsf{\Psi }}}_0={\int }_{\mathsf{\Omega }}I\mathrm{d}s+\frac{\alpha }{2\varpi }{\int }_{\mathsf{\Omega }}H\mathrm{d}s.$$

Then, $\frac{d{\tilde{\mathsf{\Psi }}}_0}{dt}$ can be computed along the solutions of Model (14) as follows

$$\frac{d{\tilde{\mathsf{\Psi }}}_0}{dt}=-\frac{\alpha }{2}{\int }_{\mathsf{\Omega }}\left(I+\frac{\vartheta }{\varpi }H\right)\mathrm{d}s\le 0.$$

Clearly, $\frac{d{\tilde{\mathsf{\Psi }}}_0}{dt}=0$ when $I=H=0$. Let

$${\mathsf{\Gamma }}_0^{″}=\left\{(U,L,I,P,E,H,Z^I,Z^E)\in {\mathsf{\Gamma }}_0^{\prime }:\frac{d{\tilde{\mathsf{\Psi }}}_0}{dt}=0\right\}.$$

Thus

$${\mathsf{\Gamma }}_0^{″}=\left\{(U,L,I,P,E,H,Z^I,Z^E)\in {\mathsf{\Gamma }}_0^{\prime }:(U,L,I,P,E,H,Z^I,Z^E)=\left(U_0,0,0,0,0,0,0,0\right)\right\}=\left\{{\check{S}}_0\right\}.$$

As a result of applying L-LAST, we concluded that ${\check{S}}_0$ is GAS [54,55,56].   □

5.2. Stability of Equilibrium ${\check{S}}_1$

To prove the global stability of ${\check{S}}_1$, we need the following lemma:

Lemma 1.

If ${\mathcal{R}}_3\le 1$, then $I_1\le I_3$.

Proof. 

Let ${\mathcal{R}}_3\le 1$; hence, $\frac{\beta {\upsilon }_1{L}_3}{\alpha c_1}\le 1$, and therefore,

$$\begin{array}{cc}\hfill & L_3\le \frac{\alpha c_1}{\beta {\upsilon }_1}⟹\frac{-B_1+\sqrt{B_1^2-4A_1{C}_1}}{2A_1}\le \frac{\alpha c_1}{\beta {\upsilon }_1}\hfill \\ \hfill & ⟹\sqrt{B_1^2-4A_1{C}_1}\le \frac{2A_1\alpha c_1+\beta {\upsilon }_1{B}_1}{\beta {\upsilon }_1}\hfill \\ \hfill & ⟹{\left(\frac{2A_1\alpha c_1+\beta {\upsilon }_1{B}_1}{\beta {\upsilon }_1}\right)}^2+4A_1{C}_1-B_1^2\ge 0.\hfill \end{array}$$

Using Equation (6), we obtain

$$\frac{4\alpha c_1\vartheta {\omega }_2{\upsilon }_1{(\beta +\eta )}^2\left[\alpha \vartheta {\omega }_2+\beta \left(\varpi {\omega }_1+\vartheta {\omega }_3\right)\right]}{{\beta }^2}\left(I_3-I_1\right)\ge 0.$$

Hence, $I_1\le I_3$.   □

Theorem 2.

The equilibrium ${\check{S}}_1$ of Model (4) is GAS when ${\mathcal{R}}_1>1$, ${\mathcal{R}}_2/$ ${\mathcal{R}}_1\le 1$ and ${\mathcal{R}}_3\le 1.$

Proof. 

Construct a Lyapunov function ${\mathsf{\Psi }}_1(s,t)$ as follows:

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_1(s,t)& =U_1ϝ\left(\frac{U}{U_1}\right)+L_1ϝ\left(\frac{L}{L_1}\right)+\frac{U_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{I}_1ϝ\left(\frac{I}{I_1}\right)+\frac{1}{\phi }P\hfill \\ \hfill & +\frac{\theta +b_1}{\phi \theta }E+\frac{{\omega }_1{U}_1}{\vartheta }{H}_1ϝ\left(\frac{H}{H_1}\right)+\frac{{\varkappa }_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E.\hfill \end{array}$$

Calculating ${\displaystyle \frac{\partial {\mathsf{\Psi }}_1}{\partial t}}$ as

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_1}{\partial t}& =\left(1-\frac{U_1}{U}\right)\left(d_U\Delta U+\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE\right)\hfill \\ \hfill & +\left(1-\frac{L_1}{L}\right)\left[d_L\Delta L+{\omega }_{1}UH+{\omega }_{2}UL+{\omega }_{3}UI-\left(\beta +\eta \right)L\right]+\frac{U_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\hfill \\ \hfill & \times \left(1-\frac{I_1}{I}\right)\left(d_I\Delta I+\beta L-\alpha I-{\varkappa }_1{Z}^{I}I\right)+\frac{1}{\phi }\left[d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\right]\hfill \\ \hfill & +\frac{\theta +b_1}{\phi \theta }\left(d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\right)+\frac{{\omega }_1{U}_1}{\vartheta }\left(1-\frac{H_1}{H}\right)\left(d_H\Delta H+\varpi I-\vartheta H\right)\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\left(d_{Z^I}\Delta Z^I+{\upsilon }_1{Z}^{I}I-c_1{Z}^I\right)+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(d_{Z^E}\Delta Z^E+{\upsilon }_2{Z}^{E}E-c_2{Z}^E\right)\hfill \\ \hfill & =\left(1-\frac{U_1}{U}\right)\left(\varrho -\varsigma U\right)+{\omega }_2{U}_{1}L+{\omega }_4{U}_{1}E-\left(\beta +\eta \right)L-{\omega }_{1}UH\frac{L_1}{L}-{\omega }_{2}U{L}_1\hfill \\ \hfill & -{\omega }_{3}UI\frac{L_1}{L}+\left(\beta +\eta \right)L_1+\frac{\beta U_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L-\frac{\beta U_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L\frac{I_1}{I}\hfill \\ \hfill & +\frac{U_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta }{I}_1+\frac{{\varkappa }_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{Z}^I{I}_1+\frac{w}{\phi }E-\frac{a\left(\theta +b_1\right)}{\phi \theta }E-{\omega }_1{U}_1\frac{\varpi I}{\vartheta }\frac{H_1}{H}\hfill \\ \hfill & +{\omega }_1{U}_1{H}_1-\frac{{\varkappa }_1{c}_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E+d_U\left(1-\frac{U_1}{U}\right)\Delta U\hfill \\ \hfill & +d_L\left(1-\frac{L_1}{L}\right)\Delta L+\frac{d_I{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(1-\frac{I_1}{I}\right)\Delta I+\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E\hfill \\ \hfill & +\frac{d_H{\omega }_1{U}_1}{\vartheta }\left(1-\frac{H_1}{H}\right)\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

Applying the equilibrium conditions for ${\check{S}}_1$:

$$\begin{array}{cc}\hfill & \varrho =\varsigma U_1+{\omega }_1{U}_1{H}_1+{\omega }_2{U}_1{L}_1+{\omega }_3{U}_1{I}_1,\hfill \\ \hfill & {\omega }_1{U}_1{H}_1+{\omega }_2{U}_1{L}_1+{\omega }_3{U}_1{I}_1=\left(\beta +\eta \right)L_1,\hfill \\ \hfill & \frac{\beta L_1}{\alpha }=I_1,H_1=\frac{\varpi I_1}{\vartheta },\hfill \end{array}$$

we have

$${\omega }_1{U}_1{H}_1+{\omega }_3{U}_1{I}_1=\frac{U_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta }{I}_1=\frac{\beta U_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{L}_1.$$

Further, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_1}{\partial t}& =\left(1-\frac{U_1}{U}\right)\left(\varsigma U_1-\varsigma U\right)+\left({\omega }_1{U}_1{H}_1+{\omega }_2{U}_1{L}_1+{\omega }_3{U}_1{I}_1\right)\left(1-\frac{U_1}{U}\right)\hfill \\ \hfill & +{\omega }_4{U}_{1}E-{\omega }_1{U}_1{H}_1\frac{UH{L}_1}{U_1{H}_{1}L}-{\omega }_2{U}_1{L}_1\frac{U}{U_1}-{\omega }_3{U}_1{I}_1\frac{UI{L}_1}{U_1{I}_{1}L}+{\omega }_1{U}_1{H}_1\hfill \\ \hfill & +{\omega }_2{U}_1{L}_1+{\omega }_3{U}_1{I}_1-\left({\omega }_1{U}_1{H}_1+{\omega }_3{U}_1{I}_1\right)\frac{L{I}_1}{L_{1}I}+{\omega }_1{U}_1{H}_1+{\omega }_3{U}_1{I}_1\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{Z}^I{I}_1+\frac{w}{\phi }E-\frac{a\left(\theta +b_1\right)}{\phi \theta }E-{\omega }_1{U}_1{H}_1\frac{I{H}_1}{I_{1}H}+{\omega }_1{U}_1{H}_1\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E+d_U\left(1-\frac{U_1}{U}\right)\Delta U\hfill \\ \hfill & +d_L\left(1-\frac{L_1}{L}\right)\Delta L+\frac{d_I{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(1-\frac{I_1}{I}\right)\Delta I+\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E\hfill \\ \hfill & +\frac{d_H{\omega }_1{U}_1}{\vartheta }\left(1-\frac{H_1}{H}\right)\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E\hfill \\ \hfill & =-\varsigma \frac{{(U-U_1)}^2}{U}+{\omega }_1{U}_1{H}_1\left(4-\frac{U_1}{U}-\frac{UH{L}_1}{U_1{H}_{1}L}-\frac{I{H}_1}{I_{1}H}-\frac{L{I}_1}{L_{1}I}\right)\hfill \\ \hfill & +{\omega }_2{U}_1{L}_1\left(2-\frac{U_1}{U}-\frac{U}{U_1}\right)+{\omega }_3{U}_1{I}_1\left(3-\frac{U_1}{U}-\frac{UI{L}_1}{U_1{I}_{1}L}-\frac{L{I}_1}{L_{1}I}\right)\hfill \\ \hfill & +\frac{\left(a-w\right)\theta +a{b}_1}{\phi \theta }\left(\frac{\phi {\omega }_4\theta U_1}{\left(a-w\right)\theta +a{b}_1}-1\right)E+\frac{{\varkappa }_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(I_1-\frac{c_1}{{\upsilon }_1}\right)Z^I\hfill \\ \hfill & -\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E+d_U\left(1-\frac{U_1}{U}\right)\Delta U+d_L\left(1-\frac{L_1}{L}\right)\Delta L+\frac{d_I{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\hfill \\ \hfill & \times \left(1-\frac{I_1}{I}\right)\Delta I+\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E+\frac{d_H{\omega }_1{U}_1}{\vartheta }\left(1-\frac{H_1}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

(15)

Therefore, Equation (15) becomes

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_1}{\partial t}& =-\left(\varsigma +{\omega }_2{L}_1\right)\frac{{(U-U_1)}^2}{U}+{\omega }_1{U}_1{H}_1\left(4-\frac{U_1}{U}-\frac{UH{L}_1}{U_1{H}_{1}L}-\frac{I{H}_1}{I_{1}H}-\frac{L{I}_1}{L_{1}I}\right)\hfill \\ \hfill & +{\omega }_3{U}_1{I}_1\left(3-\frac{U_1}{U}-\frac{UI{L}_1}{U_1{I}_{1}L}-\frac{L{I}_1}{L_{1}I}\right)+\frac{\left(a-w\right)\theta +a{b}_1}{\phi \theta }\left({\mathcal{R}}_2/{\mathcal{R}}_1-1\right)E\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(I_1-I_3\right)Z^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E+d_U\left(1-\frac{U_1}{U}\right)\Delta U\hfill \\ \hfill & +d_L\left(1-\frac{L_1}{L}\right)\Delta L+\frac{d_I{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(1-\frac{I_1}{I}\right)\Delta I+\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E\hfill \\ \hfill & +\frac{d_H{\omega }_1{U}_1}{\vartheta }\left(1-\frac{H_1}{H}\right)\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

(16)

Calculating ${\displaystyle \frac{d{\widehat{\mathsf{\Psi }}}_1}{dt}}$ and using Equality (12) to obtain

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_1}{dt}& =-\left(\varsigma +{\omega }_2{L}_1\right){\int }_{\mathsf{\Omega }}\frac{{(U-U_1)}^2}{U}\mathrm{d}s+{\omega }_1{U}_1{H}_1{\int }_{\mathsf{\Omega }}\left(4-\frac{U_1}{U}-\frac{UH{L}_1}{U_1{H}_{1}L}-\frac{I{H}_1}{I_{1}H}-\frac{L{I}_1}{L_{1}I}\right)\mathrm{d}s\hfill \\ \hfill & +{\omega }_3{U}_1{I}_1{\int }_{\mathsf{\Omega }}\left(3-\frac{U_1}{U}-\frac{UI{L}_1}{U_1{I}_{1}L}-\frac{L{I}_1}{L_{1}I}\right)\mathrm{d}s+\frac{\left[\left(a-w\right)\theta +a{b}_1\right]\left({\mathcal{R}}_2/{\mathcal{R}}_1-1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}E\mathrm{d}s\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)\left(I_1-I_3\right)}{\alpha \vartheta }{\int }_{\mathsf{\Omega }}{Z}^I\mathrm{d}s-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{\int }_{\mathsf{\Omega }}{Z}^E\mathrm{d}s-d_U{U}_1{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}s\hfill \\ \hfill & -d_L{L}_1{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿L\parallel }^2}{L^2}\mathrm{d}s-\frac{d_I{U}_1{I}_1\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}s-\frac{d_H{\omega }_1{U}_1{H}_1}{\vartheta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿H\parallel }^2}{H^2}\mathrm{d}s.\hfill \end{array}$$

Using Lemma 1, we obtain that $I_1\le I_3$ whenever ${\mathcal{R}}_3\le 1$. Moreover, since ${\mathcal{R}}_2/$ ${\mathcal{R}}_1\le 1$, then utilizing Inequalities (9)–(10), we obtain $\frac{d{\widehat{\mathsf{\Psi }}}_1}{dt}\le 0$ for any $U,L,I,E,H,Z^I,Z^E>0$. Moreover, $\frac{d{\widehat{\mathsf{\Psi }}}_1}{dt}=0$ at $(U,L,I,H,E,Z^I,Z^E)=(U_1,L_1,I_1,H_1,0,0,0).$ The trajectories of Model (4) tend to ${\mathsf{\Gamma }}_1^{\prime }$, which consists of the element where $E=0.$ Hence, $\frac{\partial E}{\partial t}=\Delta E=0$, and the fifth equation of Model (4) reduces to

$$0=\frac{\partial E}{\partial t}=\theta P,$$

and gives $P=0$. Hence, ${\mathsf{\Gamma }}_1^{\prime }=\left\{\check{S}{}_1\right\}$ and ${\check{S}}_1$ is GAS by using L-LAST.   □

5.3. Stability of Equilibrium ${\check{S}}_2$

Theorem 3.

The equilibrium ${\check{S}}_2$ of Model (4) is GAS when ${\mathcal{R}}_2>1$, ${\mathcal{R}}_1/$ ${\mathcal{R}}_2\le 1$, and ${\mathcal{R}}_4\le 1.$

Proof. 

Assume ${\mathsf{\Psi }}_2(s,t)$ is defined as follows:

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_2(s,t)& =U_2ϝ\left(\frac{U}{U_2}\right)+L+\frac{U_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }I+\frac{1}{\phi }{P}_2ϝ\left(\frac{P}{P_2}\right)+\frac{\theta +b_1}{\phi \theta }{E}_2ϝ\left(\frac{E}{E_2}\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_2}{\vartheta }H+\frac{{\varkappa }_1{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E.\hfill \end{array}$$

We calculate ${\displaystyle \frac{\partial {\mathsf{\Psi }}_2}{\partial t}}$ as

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_2}{\partial t}& =\left(1-\frac{U_2}{U}\right)\left(d_U\Delta U+\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE\right)+d_L\Delta L+{\omega }_{1}UH+{\omega }_{2}UL\hfill \\ \hfill & +{\omega }_{3}UI-\left(\beta +\eta \right)L+\frac{U_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(d_I\Delta I+\beta L-\alpha I-{\varkappa }_1{Z}^{I}I\right)+\frac{1}{\phi }\left(1-\frac{P_2}{P}\right)\hfill \\ \hfill & \times \left[d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\right]+\frac{\theta +b_1}{\phi \theta }\left(1-\frac{E_2}{E}\right)\left(d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_2}{\vartheta }\left(d_H\Delta H+\varpi I-\vartheta H\right)+\frac{{\varkappa }_1{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\left(d_{Z^I}\Delta Z^I+{\upsilon }_1{Z}^{I}I-c_1{Z}^I\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(d_{Z^E}\Delta Z^E+{\upsilon }_2{Z}^{E}E-c_2{Z}^E\right)\hfill \\ \hfill & =\left(1-\frac{U_2}{U}\right)\left(\varrho -\varsigma U\right)+{\omega }_2{U}_{2}L+{\omega }_4{U}_{2}E-\left(\beta +\eta \right)L+\frac{\beta U_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L+\frac{w}{\phi }E\hfill \\ \hfill & -{\omega }_{4}UE\frac{P_2}{P}-\frac{w}{\phi }E\frac{P_2}{P}+\frac{\theta +b_1}{\phi }{P}_2-\frac{a\left(\theta +b_1\right)}{\phi \theta }E-\frac{\theta +b_1}{\phi }P\frac{E_2}{E}+\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_2\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}^E{E}_2-\frac{{\varkappa }_1{c}_1{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E+d_U\left(1-\frac{U_2}{U}\right)\Delta U\hfill \\ \hfill & +d_L\Delta L+\frac{d_I{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_2}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_2}{E}\right)\Delta E\hfill \\ \hfill & +\frac{d_H{\omega }_1{U}_2}{\vartheta }\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

Using the equilibrium conditions for ${\check{S}}_2$:

$$\varrho =\varsigma U_2+{\omega }_4{U}_2{E}_2,{\omega }_4{U}_2{E}_2+\frac{w}{\phi }{E}_2=\frac{\theta +b_1}{\phi }{P}_2=\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_2,$$

(17)

We obtain

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_2}{\partial t}& =\left(1-\frac{U_2}{U}\right)\left(\varsigma U_2-\varsigma U\right)+{\omega }_4{U}_2{E}_2\left(1-\frac{U_2}{U}\right)+{\omega }_2{U}_{2}L-\left(\beta +\eta \right)L\hfill \\ \hfill & +\frac{\beta U_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L-{\omega }_4{U}_2{E}_2\frac{UE{P}_2}{U_2{E}_{2}P}-\frac{w}{\phi }{E}_2\frac{E{P}_2}{E_{2}P}+{\omega }_4{U}_2{E}_2+\frac{w}{\phi }{E}_2\hfill \\ \hfill & -{\omega }_4{U}_2{E}_2\frac{P{E}_2}{P_{2}E}-\frac{w}{\phi }{E}_2\frac{P{E}_2}{P_{2}E}+{\omega }_4{U}_2{E}_2+\frac{w}{\phi }{E}_2+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}^E{E}_2\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E+d_U\left(1-\frac{U_2}{U}\right)\Delta U+d_L\Delta L\hfill \\ \hfill & +\frac{d_I{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_2}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_2}{E}\right)\Delta E\hfill \\ \hfill & +\frac{d_H{\omega }_1{U}_2}{\vartheta }\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E\hfill \\ \hfill & =-\varsigma \frac{{\left(U-U_2\right)}^2}{U}+{\omega }_4{U}_2{E}_2\left(3-\frac{U_2}{U}-\frac{UE{P}_2}{U_2{E}_{2}P}-\frac{P{E}_2}{P_{2}E}\right)\hfill \\ \hfill & +\frac{w}{\phi }{E}_2\left(2-\frac{E{P}_2}{E_{2}P}-\frac{P{E}_2}{P_{2}E}\right)+\left(\beta +\eta \right)\left[\frac{U_2\left\{\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)\right\}}{\alpha \vartheta \left(\beta +\eta \right)}-1\right]L\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }\left(E_2-\frac{c_2}{{\upsilon }_2}\right)Z^E+d_U\left(1-\frac{U_2}{U}\right)\Delta U\hfill \\ \hfill & +d_L\Delta L+\frac{d_I{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_2}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_2}{E}\right)\Delta E\hfill \\ \hfill & +\frac{d_H{\omega }_1{U}_2}{\vartheta }\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E\hfill \\ \hfill & =-\varsigma \frac{{\left(U-U_2\right)}^2}{U}-\frac{w}{\phi }\frac{{(E{P}_2-P{E}_2)}^2}{P{P}_{2}E}+{\omega }_4{U}_2{E}_2\left(3-\frac{U_2}{U}-\frac{UE{P}_2}{U_2{E}_{2}P}-\frac{P{E}_2}{P_{2}E}\right)\hfill \\ \hfill & +\left(\beta +\eta \right)\left({\mathcal{R}}_1/{\mathcal{R}}_2-1\right)L-\frac{{\varkappa }_1{c}_1{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+\frac{{\varkappa }_2\left(\theta +b_1\right)\left(\varsigma {\upsilon }_2+{\omega }_4{c}_2\right)}{\phi \theta {\omega }_4{\upsilon }_2}\hfill \\ \hfill & \times \left({\mathcal{R}}_4-1\right)Z^E+d_U\left(1-\frac{U_2}{U}\right)\Delta U+d_L\Delta L+\frac{d_I{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I\hfill \\ \hfill & +\frac{d_P}{\phi }\left(1-\frac{P_2}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_2}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_2}{\vartheta }\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

(18)

By calculating ${\displaystyle \frac{d{\widehat{\mathsf{\Psi }}}_2}{dt}}$ along the positive solutions of Model (4) and applying Equality (12), we find

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_2}{dt}& =-\varsigma {\int }_{\mathsf{\Omega }}\frac{{\left(U-U_2\right)}^2}{U}\mathrm{d}s-\frac{w}{\phi }{\int }_{\mathsf{\Omega }}\frac{{(E{P}_2-P{E}_2)}^2}{P{P}_{2}E}\mathrm{d}s\hfill \\ \hfill & +{\omega }_4{U}_2{E}_2{\int }_{\mathsf{\Omega }}\left(3-\frac{U_2}{U}-\frac{UE{P}_2}{U_2{E}_{2}P}-\frac{P{E}_2}{P_{2}E}\right)\mathrm{d}s+\left(\beta +\eta \right)\left({\mathcal{R}}_1/{\mathcal{R}}_2-1\right){\int }_{\mathsf{\Omega }}L\mathrm{d}s\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_2\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{\int }_{\mathsf{\Omega }}{Z}^I\mathrm{d}s+\frac{{\varkappa }_2\left(\theta +b_1\right)\left(\varsigma {\upsilon }_2+{\omega }_4{c}_2\right)\left({\mathcal{R}}_4-1\right)}{\phi \theta {\omega }_4{\upsilon }_2}{\int }_{\mathsf{\Omega }}{Z}^E\mathrm{d}s\hfill \\ \hfill & -d_U{U}_2{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}s-\frac{d_P{P}_2}{\phi }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿P\parallel }^2}{P^2}\mathrm{d}s-\frac{d_E{E}_2\left(\theta +b_1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿E\parallel }^2}{E^2}\mathrm{d}s.\hfill \end{array}$$

Thus, if ${\mathcal{R}}_1/$ ${\mathcal{R}}_2\le 1$ and ${\mathcal{R}}_4\le 1$, then from Inequality (11), we obtain $\frac{d{\widehat{\mathsf{\Psi }}}_2}{dt}\le 0$ for any $U,L,I,P,E,H,Z^I,Z^E>0$. In addition, $\frac{d{\widehat{\mathsf{\Psi }}}_2}{dt}=0$ at $(U,P,E,L,Z^I,Z^E)=(U_2,P_2,E_2,0,0,0).$ Similar to the proof of Theorem 1, one can demonstrate that ${\mathsf{\Gamma }}_2^{\prime }=\left\{\check{S}{}_2\right\}$, and L-LAST implies that ${\check{S}}_2$ is GAS.   □

5.4. Stability of Equilibrium ${\check{S}}_3$

Theorem 4.

The equilibrium ${\check{S}}_3$ of Model (4) is GAS when ${\mathcal{R}}_3>1$ and ${\mathcal{R}}_5\le 1.$

Proof. 

Define a function ${\mathsf{\Psi }}_3(s,t)$ as

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_3& =U_3ϝ\left(\frac{U}{U_3}\right)+L_3ϝ\left(\frac{L}{L_3}\right)+\frac{U_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}{I}_3ϝ\left(\frac{I}{I_3}\right)+\frac{1}{\phi }P+\frac{\theta +b_1}{\phi \theta }E\hfill \\ \hfill & +\frac{{\omega }_1{U}_3}{\vartheta }{H}_3ϝ\left(\frac{H}{H_3}\right)+\frac{{\varkappa }_1{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}{Z}_3^Iϝ\left(\frac{Z^I}{Z_3^I}\right)+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E.\hfill \end{array}$$

We calculate ${\displaystyle \frac{\partial {\mathsf{\Psi }}_3}{\partial t}}$ as

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_3}{\partial t}& =\left(1-\frac{U_3}{U}\right)\left(d_U\Delta U+\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE\right)\hfill \\ \hfill & +\left(1-\frac{L_3}{L}\right)\left[d_L\Delta L+{\omega }_{1}UH+{\omega }_{2}UL+{\omega }_{3}UI-\left(\beta +\eta \right)L\right]\hfill \\ \hfill & +\frac{U_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{I_3}{I}\right)\left(d_I\Delta I+\beta L-\alpha I-{\varkappa }_1{Z}^{I}I\right)\hfill \\ \hfill & +\frac{1}{\phi }\left[d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\right]\hfill \\ \hfill & +\frac{\theta +b_1}{\phi \theta }\left(d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\right)+\frac{{\omega }_1{U}_3}{\vartheta }\left(1-\frac{H_3}{H}\right)\left(d_H\Delta H+\varpi I-\vartheta H\right)\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{Z_3^I}{Z^I}\right)\left(d_{Z^I}\Delta Z^I+{\upsilon }_1{Z}^{I}I-c_1{Z}^I\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(d_{Z^E}\Delta Z^E+{\upsilon }_2{Z}^{E}E-c_2{Z}^E\right).\hfill \end{array}$$

(19)

Equation (19) can be simplified as

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_3}{\partial t}& =\left(1-\frac{U_3}{U}\right)\left(\varrho -\varsigma U\right)+{\omega }_2{U}_{3}L+{\omega }_3{U}_{3}I+{\omega }_4{U}_{3}E-\left(\beta +\eta \right)L-{\omega }_{1}UH\frac{L_3}{L}\hfill \\ \hfill & -{\omega }_{2}U{L}_3-{\omega }_{3}UI\frac{L_3}{L}+\left(\beta +\eta \right)L_3+\frac{\beta U_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}L-\frac{\alpha U_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}I\hfill \\ \hfill & -\frac{\beta U_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}L\frac{I_3}{I}+\frac{\alpha U_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}{I}_3+\frac{{\varkappa }_1{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}{Z}^I{I}_3+\frac{w}{\phi }E\hfill \\ \hfill & -\frac{a\left(\theta +b_1\right)}{\phi \theta }E+\frac{{\omega }_1{U}_3}{\vartheta }\varpi I-\frac{{\omega }_1{U}_3}{\vartheta }\varpi I\frac{H_3}{H}+{\omega }_1{U}_3{H}_3-\frac{{\varkappa }_1{c}_1{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}{Z}^I\hfill \\ \hfill & -\frac{{\varkappa }_1{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}{Z}_3^{I}I+\frac{{\varkappa }_1{c}_1{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}{Z}_3^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E\hfill \\ \hfill & +d_U\left(1-\frac{U_3}{U}\right)\Delta U+d_L\left(1-\frac{L_3}{L}\right)\Delta L+\frac{d_I{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{I_3}{I}\right)\Delta I+\frac{d_P}{\phi }\Delta P\hfill \\ \hfill & +\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E+\frac{d_H{\omega }_1{U}_3}{\vartheta }\left(1-\frac{H_3}{H}\right)\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{Z_3^I}{Z^I}\right)\Delta Z^I\hfill \\ \hfill & +\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

Applying the equilibrium conditions for ${\check{S}}_3$:

$$\begin{array}{cc}\hfill & \varrho =\varsigma U_3+{\omega }_1{U}_3{H}_3+{\omega }_2{U}_3{L}_3+{\omega }_3{U}_3{I}_3,\hfill \\ \hfill & {\omega }_1{U}_3{H}_3+{\omega }_2{U}_3{L}_3+{\omega }_3{U}_3{I}_3=\left(\beta +\eta \right)L_3,\hfill \\ \hfill & \beta L_3=\left(\alpha +{\varkappa }_1{Z}_3^I\right)I_3,I_3=\frac{c_1}{{\upsilon }_1},H_3=\frac{\varpi }{\vartheta }{I}_3,\hfill \end{array}$$

we have

$${\omega }_1{U}_3{H}_3+{\omega }_3{U}_3{I}_3=\frac{U_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta }{I}_3=\frac{\beta U_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}{L}_3.$$

Moreover, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_3}{\partial t}& =\left(1-\frac{U_3}{U}\right)\left(\varsigma U_3-\varsigma U\right)+\left({\omega }_1{U}_3{H}_3+{\omega }_2{U}_3{L}_3+{\omega }_3{U}_3{I}_3\right)\left(1-\frac{U_3}{U}\right)\hfill \\ \hfill & +{\omega }_4{U}_{3}E-{\omega }_1{U}_3{H}_3\frac{UH{L}_3}{U_3{H}_{3}L}-{\omega }_2{U}_3{L}_3\frac{U}{U_3}-{\omega }_3{U}_3{I}_3\frac{UI{L}_3}{U_3{I}_{3}L}+{\omega }_1{U}_3{H}_3\hfill \\ \hfill & +{\omega }_2{U}_3{L}_3+{\omega }_3{U}_3{I}_3-\left({\omega }_1{U}_3{H}_3+{\omega }_3{U}_3{I}_3\right)\frac{L{I}_3}{L_{3}I}+{\omega }_1{U}_3{H}_3+{\omega }_3{U}_3{I}_3\hfill \\ \hfill & -\frac{\left(a-w\right)\theta +a{b}_1}{\phi \theta }E-{\omega }_1{U}_3{H}_3\frac{I{H}_3}{I_{3}H}+{\omega }_1{U}_3{H}_3-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E\hfill \\ \hfill & +d_U\left(1-\frac{U_3}{U}\right)\Delta U+d_L\left(1-\frac{L_3}{L}\right)\Delta L+\frac{d_I{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}\hfill \\ \hfill & \times \left(1-\frac{I_3}{I}\right)\Delta I+\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E+\frac{d_H{\omega }_1{U}_3}{\vartheta }\left(1-\frac{H_3}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{Z_3^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E\hfill \\ \hfill & =-\varsigma \frac{{\left(U-U_3\right)}^2}{U}+{\omega }_1{U}_3{H}_3\left(4-\frac{U_3}{U}-\frac{UH{L}_3}{U_3{H}_{3}L}-\frac{L{I}_3}{L_{3}I}-\frac{I{H}_3}{I_{3}H}\right)\hfill \\ \hfill & +{\omega }_2{U}_3{L}_3\left(2-\frac{U_3}{U}-\frac{U}{U_3}\right)+{\omega }_3{U}_3{I}_3\left(3-\frac{U_3}{U}-\frac{UI{L}_3}{U_3{I}_{3}L}-\frac{L{I}_3}{L_{3}I}\right)\hfill \\ \hfill & +{\omega }_4\left(U_3-\frac{\left(a-w\right)\theta +a{b}_1}{{\omega }_4\phi \theta }\right)E-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E\hfill \\ \hfill & +d_U\left(1-\frac{U_3}{U}\right)\Delta U+d_L\left(1-\frac{L_3}{L}\right)\Delta L+\frac{d_I{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{I_3}{I}\right)\Delta I\hfill \\ \hfill & +\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E+\frac{d_H{\omega }_1{U}_3}{\vartheta }\left(1-\frac{H_3}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{Z_3^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E\hfill \\ \hfill & =-\left(\varsigma +{\omega }_2{L}_3\right)\frac{{\left(U-U_3\right)}^2}{U}+{\omega }_1{U}_3{H}_3\left(4-\frac{U_3}{U}-\frac{UH{L}_3}{U_3{H}_{3}L}-\frac{L{I}_3}{L_{3}I}-\frac{I{H}_3}{I_{3}H}\right)\hfill \\ \hfill & +{\omega }_3{U}_3{I}_3\left(3-\frac{U_3}{U}-\frac{UI{L}_3}{U_3{I}_{3}L}-\frac{L{I}_3}{L_{3}I}\right)+{\omega }_4\left(U_3-U_5\right)E-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E\hfill \\ \hfill & +d_U\left(1-\frac{U_3}{U}\right)\Delta U+d_L\left(1-\frac{L_3}{L}\right)\Delta L+\frac{d_I{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{I_3}{I}\right)\Delta I\hfill \\ \hfill & +\frac{d_P}{\phi }\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\Delta E+\frac{d_H{\omega }_1{U}_3}{\vartheta }\left(1-\frac{H_3}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}\left(1-\frac{Z_3^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

(20)

Computing the time derivative of ${\widehat{\mathsf{\Psi }}}_3\left(t\right)$ and applying Equality (12), Equation (20) will take the following form:

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_3}{dt}& =-\left(\varsigma +{\omega }_2{L}_3\right){\int }_{\mathsf{\Omega }}\frac{{\left(U-U_3\right)}^2}{U}\mathrm{d}s+{\omega }_1{U}_3{H}_3{\int }_{\mathsf{\Omega }}\left(4-\frac{U_3}{U}-\frac{UH{L}_3}{U_3{H}_{3}L}-\frac{L{I}_3}{L_{3}I}-\frac{I{H}_3}{I_{3}H}\right)\mathrm{d}s\hfill \\ \hfill & +{\omega }_3{U}_3{I}_3{\int }_{\mathsf{\Omega }}\left(3-\frac{U_3}{U}-\frac{UI{L}_3}{U_3{I}_{3}L}-\frac{L{I}_3}{L_{3}I}\right)\mathrm{d}s+{\omega }_4\left(U_3-U_5\right){\int }_{\mathsf{\Omega }}E\mathrm{d}s-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{\int }_{\mathsf{\Omega }}{Z}^E\mathrm{d}s\hfill \\ \hfill & -d_U{U}_3{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}s-d_L{L}_3{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿L\parallel }^2}{L^2}\mathrm{d}s-\frac{d_I{U}_3{I}_3\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_3^I\right)}{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}s\hfill \\ \hfill & -\frac{d_H{\omega }_1{U}_3{H}_3}{\vartheta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿H\parallel }^2}{H^2}\mathrm{d}s-\frac{{\varkappa }_1{d}_{Z^I}{U}_3{Z}_3^I\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_3^I\right)}{\int }_{\mathsf{\Omega }}\frac{\parallel ▿Z^I{\parallel }^2}{{\left(Z^I\right)}^2}\mathrm{d}s.\hfill \end{array}$$

Obviously, if ${\mathcal{R}}_5\le 1$, then ${\check{S}}_5$ does not exist since $P_5\le 0$ and $E_5\le 0$. Accordingly, in this case, we have

$$\begin{array}{cc}\hfill \frac{\partial P}{\partial t}& =d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\le 0,\hfill \\ \hfill \frac{\partial E}{\partial t}& =d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\le 0.\hfill \end{array}$$

The next step is to find the value $\overline{U}$ with $0<U\left(t\right)\le \overline{U}$ such that $\frac{\partial P}{\partial t}\le 0$ and $\frac{\partial E}{\partial t}\le 0$. Let us consider

$$\begin{array}{cc}\hfill & \frac{d}{dt}\left(P+\frac{\theta +b_1}{\theta }E\right)\hfill \\ \hfill & ={\int }_{\mathsf{\Omega }}\left[d_P\Delta P+\frac{\left(\theta +b_1\right)d_E}{\theta }\Delta E+\phi {\omega }_{4}UE-\frac{\left(a-w\right)\theta +a{b}_1}{\theta }E-\frac{{\varkappa }_2\left(\theta +b_1\right)}{\theta }{Z}^{E}E\right]\mathrm{d}s\hfill \\ \hfill & =\phi {\omega }_4{\int }_{\mathsf{\Omega }}\left[U-\frac{\left(a-w\right)\theta +a{b}_1}{{\omega }_4\phi \theta }\right]E\mathrm{d}s-\frac{{\varkappa }_2\left(\theta +b_1\right)}{\theta }{\int }_{\mathsf{\Omega }}{Z}^{E}E\mathrm{d}s\le 0\mathrm{for}\mathrm{all}{Z}^E,E>0.\hfill \end{array}$$

This occurs when $U_3\le \overline{U}=\frac{\left(a-w\right)\theta +a{b}_1}{{\omega }_4\phi \theta }=U_5$. Then, from Inequalities (9)–(10), we have $\frac{d{\widehat{\mathsf{\Psi }}}_3}{dt}\le 0$ for any $U,L,I,E,H,Z^I,Z^E>0$. In addition, $\frac{d{\widehat{\mathsf{\Psi }}}_3}{dt}=0$ at $(U,L,I,H,Z^I,E,Z^E)=(U_3,L_3,I_3,H_3,Z_3^I,0,0).$ The solutions of Model (4) are limited to ${\mathsf{\Gamma }}_3^{\prime }$, which has elements satisfying $E=0$. Hence, $\frac{\partial E}{\partial t}=\Delta E=0$, and the fifth equation of Model (4) becomes

$$0=\frac{\partial E}{\partial t}=\theta P,$$

which yields $P=0$,and hence, ${\mathsf{\Gamma }}_3^{\prime }=\left\{\check{S}{}_3\right\}$. As a result of applying L-LAST, ${\check{S}}_3$ is GAS.   □

5.5. Stability of Equilibrium ${\check{S}}_4$

Theorem 5.

The equilibrium ${\check{S}}_4$ of Model (4) is GAS when ${\mathcal{R}}_4>1$ and ${\mathcal{R}}_6\le 1.$

Proof. 

Define ${\mathsf{\Psi }}_4(s,t)$ as follows:

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_4& =U_4ϝ\left(\frac{U}{U_4}\right)+L+\frac{U_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }I+\frac{1}{\phi }{P}_4ϝ\left(\frac{P}{P_4}\right)+\frac{\theta +b_1}{\phi \theta }{E}_4ϝ\left(\frac{E}{E_4}\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_4}{\vartheta }H+\frac{{\varkappa }_1{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}_4^Eϝ\left(\frac{Z^E}{Z_4^E}\right).\hfill \end{array}$$

Calculating ${\displaystyle \frac{\partial {\mathsf{\Psi }}_4}{\partial t}}$ as given below:

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_4}{\partial t}& =\left(1-\frac{U_4}{U}\right)\left(d_U\Delta U+\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE\right)+d_L\Delta L+{\omega }_{1}UH+{\omega }_{2}UL\hfill \\ \hfill & +{\omega }_{3}UI-\left(\beta +\eta \right)L+\frac{U_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(d_I\Delta I+\beta L-\alpha I-{\varkappa }_1{Z}^{I}I\right)+\frac{1}{\phi }\left(1-\frac{P_4}{P}\right)\hfill \\ \hfill & \times \left[d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\right]+\frac{\theta +b_1}{\phi \theta }\left(1-\frac{E_4}{E}\right)\left(d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_4}{\vartheta }\left(d_H\Delta H+\varpi I-\vartheta H\right)+\frac{{\varkappa }_1{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\left(d_{Z^I}\Delta Z^I+{\upsilon }_1{Z}^{I}I-c_1{Z}^I\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_4^E}{Z^E}\right)\left(d_{Z^E}\Delta Z^E+{\upsilon }_2{Z}^{E}E-c_2{Z}^E\right)\hfill \\ \hfill & =\left(1-\frac{U_4}{U}\right)\left(\varrho -\varsigma U\right)+{\omega }_2{U}_{4}L+{\omega }_4{U}_{4}E-\left(\beta +\eta \right)L+\frac{\beta U_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L\hfill \\ \hfill & +\frac{w}{\phi }E-{\omega }_{4}UE\frac{P_4}{P}-\frac{w}{\phi }E\frac{P_4}{P}+\frac{\theta +b_1}{\phi }{P}_4-\frac{a\left(\theta +b_1\right)}{\phi \theta }E-\frac{\theta +b_1}{\phi }P\frac{E_4}{E}\hfill \\ \hfill & +\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_4+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}^E{E}_4-\frac{{\varkappa }_1{c}_1{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E\hfill \\ \hfill & -\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}_4^{E}E+\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}_4^E+d_U\left(1-\frac{U_4}{U}\right)\Delta U+d_L\Delta L\hfill \\ \hfill & +\frac{d_I{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_4}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_4}{E}\right)\Delta E\hfill \\ \hfill & +\frac{d_H{\omega }_1{U}_4}{\vartheta }\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_4^E}{Z^E}\right)\Delta Z^E.\hfill \end{array}$$

Using the equilibrium conditions for ${\check{S}}_4$:

$$\begin{array}{cc}\hfill \varrho & =\varsigma U_4+{\omega }_4{U}_4{E}_4,E_4=\frac{c_2}{{\upsilon }_2},\hfill \\ \hfill {\omega }_4{U}_4{E}_4+\frac{w}{\phi }{E}_4& =\frac{\theta +b_1}{\phi }{P}_4=\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_4+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}_4^E{E}_4.\hfill \end{array}$$

Then, we find

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_4}{\partial t}& =\left(1-\frac{U_4}{U}\right)\left(\varsigma U_4-\varsigma U\right)+{\omega }_4{U}_4{E}_4\left(1-\frac{U_4}{U}\right)+{\omega }_2{U}_{4}L-\left(\beta +\eta \right)L+\frac{\beta U_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L\hfill \\ \hfill & -{\omega }_4{U}_4{E}_4\frac{UE{P}_4}{U_4{E}_{4}P}-\frac{w}{\phi }{E}_4\frac{E{P}_4}{E_{4}P}+{\omega }_4{U}_4{E}_4+\frac{w}{\phi }{E}_4-{\omega }_4{U}_4{E}_4\frac{P{E}_4}{P_{4}E}-\frac{w}{\phi }{E}_4\frac{P{E}_4}{P_{4}E}+{\omega }_4{U}_4{E}_4\hfill \\ \hfill & +\frac{w}{\phi }{E}_4-\frac{{\varkappa }_1{c}_1{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+d_U\left(1-\frac{U_4}{U}\right)\Delta U+d_L\Delta L+\frac{d_I{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I\hfill \\ \hfill & +\frac{d_P}{\phi }\left(1-\frac{P_4}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_4}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_4}{\vartheta }\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_4^E}{Z^E}\right)\Delta Z^E\hfill \\ \hfill & =-\varsigma \frac{{\left(U-U_4\right)}^2}{U}+{\omega }_4{U}_4{E}_4\left(3-\frac{U_4}{U}-\frac{UE{P}_4}{U_4{E}_{4}P}-\frac{P{E}_4}{P_{4}E}\right)+\frac{w}{\phi }{E}_4\left(2-\frac{E{P}_4}{E_{4}P}-\frac{P{E}_4}{P_{4}E}\right)\hfill \\ \hfill & +\left(\beta +\eta \right)\left[\frac{U_4\left\{\alpha \vartheta {\omega }_2+\beta (\varpi {\omega }_1+\vartheta {\omega }_3)\right\}}{\alpha \vartheta \left(\beta +\eta \right)}-1\right]L-\frac{{\varkappa }_1{c}_1{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I\hfill \\ \hfill & +d_U\left(1-\frac{U_4}{U}\right)\Delta U+d_L\Delta L+\frac{d_I{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_4}{P}\right)\Delta P\hfill \\ \hfill & +\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_4}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_4}{\vartheta }\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I\hfill \\ \hfill & +\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_4^E}{Z^E}\right)\Delta Z^E\hfill \\ \hfill & =-\varsigma \frac{{\left(U-U_4\right)}^2}{U}-\frac{w}{\phi }\frac{{(E{P}_4-P{E}_4)}^2}{P{P}_{4}E}+{\omega }_4{U}_4{E}_4\left(3-\frac{U_4}{U}-\frac{UE{P}_4}{U_4{E}_{4}P}-\frac{P{E}_4}{P_{4}E}\right)\hfill \\ \hfill & +\left(\beta +\eta \right)\left({\mathcal{R}}_6-1\right)L-\frac{{\varkappa }_1{c}_1{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+d_U\left(1-\frac{U_4}{U}\right)\Delta U+d_L\Delta L\hfill \\ \hfill & +\frac{d_I{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_4}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_4}{E}\right)\Delta E\hfill \\ \hfill & +\frac{d_H{\omega }_1{U}_4}{\vartheta }\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_4^E}{Z^E}\right)\Delta Z^E.\hfill \end{array}$$

Calculating ${\displaystyle \frac{d{\widehat{\mathsf{\Psi }}}_4}{dt}}$ along the positive solutions of System (4) and using Equality (12), then we obtain

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_4}{dt}& =-\varsigma {\int }_{\mathsf{\Omega }}\frac{{\left(U-U_4\right)}^2}{U}\mathrm{d}s-\frac{w}{\phi }{\int }_{\mathsf{\Omega }}\frac{{(E{P}_4-P{E}_4)}^2}{P{P}_{4}E}\mathrm{d}s\hfill \\ \hfill & +{\omega }_4{U}_4{E}_4{\int }_{\mathsf{\Omega }}\left(3-\frac{U_4}{U}-\frac{UE{P}_4}{U_4{E}_{4}P}-\frac{P{E}_4}{P_{4}E}\right)\mathrm{d}s+\left(\beta +\eta \right)\left({\mathcal{R}}_6-1\right){\int }_{\mathsf{\Omega }}L\mathrm{d}s\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_4\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{\int }_{\mathsf{\Omega }}{Z}^I\mathrm{d}s-d_U{U}_4{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}s-\frac{d_P{P}_4}{\phi }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿P\parallel }^2}{P^2}\mathrm{d}s\hfill \\ \hfill & -\frac{d_E{E}_4\left(\theta +b_1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿E\parallel }^2}{E^2}\mathrm{d}s-\frac{{\varkappa }_2{d}_{Z^E}{Z}_4^E\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{\int }_{\mathsf{\Omega }}\frac{\parallel ▿Z^E{\parallel }^2}{{\left(Z^E\right)}^2}\mathrm{d}s.\hfill \end{array}$$

Hence, if ${\mathcal{R}}_6\le 1$, then from Inequality (11), we obtain $\frac{d{\widehat{\mathsf{\Psi }}}_4}{dt}\le 0$, for any $U,L,I,P,E,H,Z^I$, $Z^E>0$. In addition, $\frac{d{\widehat{\mathsf{\Psi }}}_4}{dt}=0$ at $(U,P,E,Z^E,L,Z^I)=(U_4,P_4,E_4,Z_4^E,0,0).$ The solutions of Model (4) are limited to ${\mathsf{\Gamma }}_4^{\prime }$. Therefore, in the same way that Theorem 1 was proven, one can demonstrate that ${\mathsf{\Gamma }}_4^{\prime }=\left\{{\check{S}}_4\right\}$. Applying L-LAST, we obtain that ${\check{S}}_4$ is GAS.   □

5.6. Stability of Equilibrium ${\check{S}}_5$

Theorem 6.

The equilibrium ${\check{S}}_5$ of Model (4) is GAS when ${\mathcal{R}}_5>1,$ ${\widehat{\mathcal{R}}}_5>1$, ${\mathcal{R}}_8\le 1$, and ${\mathcal{R}}_1/{\mathcal{R}}_2>1.$

Proof. 

Define ${\mathsf{\Psi }}_5(s,t)$ as follows:

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_5& =U_5ϝ\left(\frac{U}{U_5}\right)+L_5ϝ\left(\frac{L}{L_5}\right)+\frac{U_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}{I}_5ϝ\left(\frac{I}{I_5}\right)+\frac{1}{\phi }{P}_5ϝ\left(\frac{P}{P_5}\right)\hfill \\ \hfill & +\frac{\theta +b_1}{\phi \theta }{E}_5ϝ\left(\frac{E}{E_5}\right)+\frac{{\omega }_1{U}_5}{\vartheta }{H}_5ϝ\left(\frac{H}{H_5}\right)+\frac{{\varkappa }_1{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}{Z}_5^Iϝ\left(\frac{Z^I}{Z_5^I}\right)+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E.\hfill \end{array}$$

Calculating ${\displaystyle \frac{\partial {\mathsf{\Psi }}_5}{\partial t}}$ as stated below:

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_5}{\partial t}& =\left(1-\frac{U_5}{U}\right)\left(d_U\Delta U+\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE\right)\hfill \\ \hfill & +\left(1-\frac{L_5}{L}\right)\left[d_L\Delta L+{\omega }_{1}UH+{\omega }_{2}UL+{\omega }_{3}UI-\left(\beta +\eta \right)L\right]\hfill \\ \hfill & +\frac{U_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{I_5}{I}\right)\left(d_I\Delta I+\beta L-\alpha I-{\varkappa }_1{Z}^{I}I\right)\hfill \\ \hfill & +\frac{1}{\phi }\left(1-\frac{P_5}{P}\right)\left[d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\right]\hfill \\ \hfill & +\frac{\theta +b_1}{\phi \theta }\left(1-\frac{E_5}{E}\right)\left(d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_5}{\vartheta }\left(1-\frac{H_5}{H}\right)\left(d_H\Delta H+\varpi I-\vartheta H\right)\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{Z_5^I}{Z^I}\right)\left(d_{Z^I}\Delta Z^I+{\upsilon }_1{Z}^{I}I-c_1{Z}^I\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(d_{Z^E}\Delta Z^E+{\upsilon }_2{Z}^{E}E-c_2{Z}^E\right).\hfill \end{array}$$

(21)

Equation (21) can be simplified as

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_5}{\partial t}& =\left(1-\frac{U_5}{U}\right)\left(\varrho -\varsigma U\right)+{\omega }_2{U}_{5}L+{\omega }_3{U}_{5}I+{\omega }_4{U}_{5}E-\left(\beta +\eta \right)L-{\omega }_{1}UH\frac{L_5}{L}\hfill \\ \hfill & -{\omega }_{2}U{L}_5-{\omega }_{3}UI\frac{L_5}{L}+\left(\beta +\eta \right)L_5+\frac{\beta U_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}L-\frac{\alpha U_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}I\hfill \\ \hfill & -\frac{\beta U_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}L\frac{I_5}{I}+\frac{\alpha U_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}{I}_5+\frac{{\varkappa }_1{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}{Z}^I{I}_5+\frac{w}{\phi }E\hfill \\ \hfill & -{\omega }_{4}UE\frac{P_5}{P}-\frac{w}{\phi }E\frac{P_5}{P}+\frac{\theta +b_1}{\phi }{P}_5-\frac{a\left(\theta +b_1\right)}{\phi \theta }E-\frac{\theta +b_1}{\phi }P\frac{E_5}{E}+\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_5\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}^E{E}_5+{\omega }_1{U}_5\frac{\varpi I}{\vartheta }-{\omega }_1{U}_5{H}_5\frac{\varpi I}{\vartheta H}+{\omega }_1{U}_5{H}_5-\frac{{\varkappa }_1{c}_1{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}{Z}^I\hfill \\ \hfill & -\frac{{\varkappa }_1{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}{Z}_5^{I}I+\frac{{\varkappa }_1{c}_1{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}{Z}_5^I-\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E\hfill \\ \hfill & +d_U\left(1-\frac{U_5}{U}\right)\Delta U+d_L\left(1-\frac{L_5}{L}\right)\Delta L+\frac{d_I{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{I_5}{I}\right)\Delta I\hfill \\ \hfill & +\frac{d_P}{\phi }\left(1-\frac{P_5}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_5}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_5}{\vartheta }\left(1-\frac{H_5}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{Z_5^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

Using the equilibrium conditions for ${\check{S}}_5$:

$$\begin{array}{cc}\hfill & \varrho =\varsigma U_5+{\omega }_1{U}_5{H}_5+{\omega }_2{U}_5{L}_5+{\omega }_3{U}_5{I}_5+{\omega }_4{U}_5{E}_5,\hfill \\ \hfill & {\omega }_1{U}_5{H}_5+{\omega }_2{U}_5{L}_5+{\omega }_3{U}_5{I}_5=\left(\beta +\eta \right)L_5,\hfill \\ \hfill & \beta L_5=\left(\alpha +{\varkappa }_1{Z}_5^I\right)I_5,I_5=\frac{c_1}{{\upsilon }_1},H_5=\frac{\varpi }{\vartheta }{I}_5,\hfill \\ \hfill & {\omega }_4{U}_5{E}_5+\frac{w}{\phi }{E}_5=\frac{\theta +b_1}{\phi }{P}_5=\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_5.\hfill \end{array}$$

We obtain

$${\omega }_1{U}_5{H}_5+{\omega }_3{U}_5{I}_5=\frac{U_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta }{I}_5=\frac{\beta U_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}{L}_5.$$

Further, we have

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_5}{\partial t}& =\left(1-\frac{U_5}{U}\right)\left(\varsigma U_5-\varsigma U\right)+\left({\omega }_1{U}_5{H}_5+{\omega }_2{U}_5{L}_5+{\omega }_3{U}_5{I}_5+{\omega }_4{U}_5{E}_5\right)\hfill \\ \hfill & \times \left(1-\frac{U_5}{U}\right)-{\omega }_1{U}_5{H}_5\frac{UH{L}_5}{U_5{H}_{5}L}-{\omega }_2{U}_5{L}_5\frac{U}{U_5}-{\omega }_3{U}_5{I}_5\frac{UI{L}_5}{U_5{I}_{5}L}\hfill \\ \hfill & +{\omega }_1{U}_5{H}_5+{\omega }_2{U}_5{L}_5+{\omega }_3{U}_5{I}_5-\left({\omega }_1{U}_5{H}_5+{\omega }_3{U}_5{I}_5\right)\frac{L{I}_5}{L_{5}I}+{\omega }_1{U}_5{H}_5\hfill \\ \hfill & +{\omega }_3{U}_5{I}_5-{\omega }_4{U}_5{E}_5\frac{UE{P}_5}{U_5{E}_{5}P}-\frac{w}{\phi }{E}_5\frac{E{P}_5}{E_{5}P}+{\omega }_4{U}_5{E}_5+\frac{w}{\phi }{E}_5\hfill \\ \hfill & -{\omega }_4{U}_5{E}_5\frac{P{E}_5}{P_{5}E}-\frac{w}{\phi }{E}_5\frac{P{E}_5}{P_{5}E}+{\omega }_4{U}_5{E}_5+\frac{w}{\phi }{E}_5-{\omega }_1{U}_5{H}_5\frac{I{H}_5}{I_{5}H}\hfill \\ \hfill & +{\omega }_1{U}_5{H}_5+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }\left(E_5-\frac{c_2}{{\upsilon }_2}\right)Z^E+d_U\left(1-\frac{U_5}{U}\right)\Delta U\hfill \\ \hfill & +d_L\left(1-\frac{L_5}{L}\right)\Delta L+\frac{d_I{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{I_5}{I}\right)\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_5}{P}\right)\hfill \\ \hfill & \times \Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_5}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_5}{\vartheta }\left(1-\frac{H_5}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{Z_5^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E\hfill \\ \hfill & =-\varsigma \frac{{\left(U-U_5\right)}^2}{U}+{\omega }_1{U}_5{H}_5\left(4-\frac{U_5}{U}-\frac{UH{L}_5}{U_5{H}_{5}L}-\frac{L{I}_5}{L_{5}I}-\frac{I{H}_5}{I_{5}H}\right)\hfill \\ \hfill & +{\omega }_2{U}_5{L}_5\left(2-\frac{U_5}{U}-\frac{U}{U_5}\right)+{\omega }_3{U}_5{I}_5\left(3-\frac{U_5}{U}-\frac{UI{L}_5}{U_5{I}_{5}L}-\frac{L{I}_5}{L_{5}I}\right)\hfill \\ \hfill & +{\omega }_4{U}_5{E}_5\left(3-\frac{U_5}{U}-\frac{UE{P}_5}{U_5{E}_{5}P}-\frac{P{E}_5}{P_{5}E}\right)+\frac{w}{\phi }{E}_5\left(2-\frac{E{P}_5}{E_{5}P}-\frac{P{E}_5}{P_{5}E}\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }\left(E_5-\frac{c_2}{{\upsilon }_2}\right)Z^E+d_U\left(1-\frac{U_5}{U}\right)\Delta U+d_L\left(1-\frac{L_5}{L}\right)\Delta L\hfill \\ \hfill & +\frac{d_I{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{I_5}{I}\right)\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_5}{P}\right)\Delta P\hfill \\ \hfill & +\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_5}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_5}{\vartheta }\left(1-\frac{H_5}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{Z_5^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

(22)

Then, Equation (22) will be simplified as follows:

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_5}{\partial t}& =-\left(\varsigma +{\omega }_2{L}_5\right)\frac{{\left(U-U_5\right)}^2}{U}-\frac{w}{\phi }\frac{{(E{P}_5-P{E}_5)}^2}{P{P}_{5}E}\hfill \\ \hfill & +{\omega }_1{U}_5{H}_5\left(4-\frac{U_5}{U}-\frac{UH{L}_5}{U_5{H}_{5}L}-\frac{L{I}_5}{L_{5}I}-\frac{I{H}_5}{I_{5}H}\right)\hfill \\ \hfill & +{\omega }_3{U}_5{I}_5\left(3-\frac{U_5}{U}-\frac{UI{L}_5}{U_5{I}_{5}L}-\frac{L{I}_5}{L_{5}I}\right)+{\omega }_4{U}_5{E}_5\left(3-\frac{U_5}{U}-\frac{UE{P}_5}{U_5{E}_{5}P}-\frac{P{E}_5}{P_{5}E}\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }\left(E_5-E_7\right)Z^E+d_U\left(1-\frac{U_5}{U}\right)\Delta U+d_L\left(1-\frac{L_5}{L}\right)\Delta L\hfill \\ \hfill & +\frac{d_I{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{I_5}{I}\right)\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_5}{P}\right)\Delta P\hfill \\ \hfill & +\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_5}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_5}{\vartheta }\left(1-\frac{H_5}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}\left(1-\frac{Z_5^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\Delta Z^E.\hfill \end{array}$$

Now, along the solution trajectories of Model (4), we calculate ${\displaystyle \frac{d{\widehat{\mathsf{\Psi }}}_5}{dt}}$ and utilize Equality (12) to obtain the following result:

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_5}{dt}& =-\left(\varsigma +{\omega }_2{L}_5\right){\int }_{\mathsf{\Omega }}\frac{{\left(U-U_5\right)}^2}{U}\mathrm{d}s-\frac{w}{\phi }{\int }_{\mathsf{\Omega }}\frac{{(E{P}_5-P{E}_5)}^2}{P{P}_{5}E}\mathrm{d}s\hfill \\ \hfill & +{\omega }_1{U}_5{H}_5{\int }_{\mathsf{\Omega }}\left(4-\frac{U_5}{U}-\frac{UH{L}_5}{U_5{H}_{5}L}-\frac{L{I}_5}{L_{5}I}-\frac{I{H}_5}{I_{5}H}\right)\mathrm{d}s\hfill \\ \hfill & +{\omega }_3{U}_5{I}_5{\int }_{\mathsf{\Omega }}\left(3-\frac{U_5}{U}-\frac{UI{L}_5}{U_5{I}_{5}L}-\frac{L{I}_5}{L_{5}I}\right)\mathrm{d}s\hfill \\ \hfill & +{\omega }_4{U}_5{E}_5{\int }_{\mathsf{\Omega }}\left(3-\frac{U_5}{U}-\frac{UE{P}_5}{U_5{E}_{5}P}-\frac{P{E}_5}{P_{5}E}\right)\mathrm{d}s\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }\left(E_5-E_7\right){\int }_{\mathsf{\Omega }}{Z}^E\mathrm{d}s-d_U{U}_5{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}s\hfill \\ \hfill & -d_L{L}_5{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿L\parallel }^2}{L^2}\mathrm{d}s-\frac{d_I{U}_5{I}_5\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_5^I\right)}{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}s\hfill \\ \hfill & -\frac{d_P{P}_5}{\phi }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿P\parallel }^2}{P^2}\mathrm{d}s-\frac{d_E{E}_5\left(\theta +b_1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿E\parallel }^2}{E^2}\mathrm{d}s\hfill \\ \hfill & -\frac{d_H{\omega }_1{U}_5{H}_5}{\vartheta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿H\parallel }^2}{H^2}\mathrm{d}s-\frac{{\varkappa }_1{d}_{Z^I}{U}_5{Z}_5^I\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_5^I\right)}{\int }_{\mathsf{\Omega }}\frac{\parallel ▿Z^I{\parallel }^2}{{\left(Z^I\right)}^2}\mathrm{d}s.\hfill \end{array}$$

Hence, if ${\mathcal{R}}_8\le 1$, then ${\check{S}}_7$ does not exists since $Z_7^E=\frac{(a-w)\theta +a{b}_1}{{\varkappa }_2(\theta +b_1)}\left({\mathcal{R}}_8-1\right)\le 0$. Since the existence of the equilibria does not depend on the diffusion terms, therefore, in the absence of diffusion, we can say $\frac{d{Z}^E}{dt}={\upsilon }_2\left(E-\frac{c_2}{{\upsilon }_2}\right)Z^E\le 0$ for all $Z^E>0$. Thus, $E_5\le \frac{c_2}{{\upsilon }_2}=E_7$. Hence, from Inequalities (9)–(11), we obtain $\frac{d{\widehat{\mathsf{\Psi }}}_5}{dt}\le 0$ for all $U,L,I,P,E,H,Z^I,Z^E>0$. We also have $\frac{d{\widehat{\mathsf{\Psi }}}_5}{dt}=0$ at $(U,L,I,P,E,H,Z^I,Z^E)=(U_5,L_5,I_5,P_5,E_5,H_5,Z_5^I,0)$. The trajectories of Model (4) are limited to ${\mathsf{\Gamma }}_5^{\prime }$, and hence, ${\mathsf{\Gamma }}_5^{\prime }=\left\{\check{S}{}_5\right\}$. Applying L-LAST, we obtain ${\check{S}}_5$ is GAS.   □

5.7. Stability of Equilibrium ${\check{S}}_6$

To prove the global stability of ${\check{S}}_6$, we need the following lemma:

Lemma 2.

If ${\mathcal{R}}_7\le 1$, then $I_6\le I_7$.

Proof. 

Let ${\mathcal{R}}_7\le 1$; hence, ${\displaystyle \frac{\beta {\upsilon }_1{L}_7}{\alpha c_1}}\le 1$, and therefore,

$$\begin{array}{cc}\hfill & L_7\le \frac{\alpha c_1}{\beta {\upsilon }_1}⟹\frac{-B_2+\sqrt{B_2^2-4A_2{C}_2}}{2A_2}\le \frac{\alpha c_1}{\beta {\upsilon }_1}\hfill \\ \hfill & ⟹\sqrt{B_2^2-4A_2{C}_2}\le \frac{2A_2\alpha c_1+\beta {\upsilon }_1{B}_2}{\beta {\upsilon }_1}\hfill \\ \hfill & ⟹{\left(\frac{2A_2\alpha c_1+\beta {\upsilon }_1{B}_2}{\beta {\upsilon }_1}\right)}^2+4A_2{C}_2-B_2^2\ge 0.\hfill \end{array}$$

Using Equation (8), we obtain

$$\frac{4\alpha c_1\vartheta {\omega }_2{{\upsilon }_1\upsilon }_2^2{(\beta +\eta )}^2\left[\alpha \vartheta {\omega }_2+\beta \left(\varpi {\omega }_1+\vartheta {\omega }_3\right)\right]}{{\beta }^2}\left(I_7-I_6\right)\ge 0.$$

Hence, $I_6\le I_7$.   □

Theorem 7.

The equilibrium ${\check{S}}_6$ of Model (4) is GAS when ${\mathcal{R}}_6>1$, ${\mathcal{R}}_7\le 1$, and ${\mathcal{R}}_2/{\mathcal{R}}_1>1.$

Proof. 

Define ${\mathsf{\Psi }}_6(s,t)$ as follows:

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_6& =U_6ϝ\left(\frac{U}{U_6}\right)+L_6ϝ\left(\frac{L}{L_6}\right)+\frac{U_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{I}_6ϝ\left(\frac{I}{I_6}\right)+\frac{1}{\phi }{P}_6ϝ\left(\frac{P}{P_6}\right)+\frac{\theta +b_1}{\phi \theta }{E}_6ϝ\left(\frac{E}{E_6}\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_6}{\vartheta }{H}_6ϝ\left(\frac{H}{H_6}\right)+\frac{{\varkappa }_1{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}_6^Eϝ\left(\frac{Z^E}{Z_6^E}\right).\hfill \end{array}$$

Calculating ${\displaystyle \frac{\partial {\mathsf{\Psi }}_6}{\partial t}}$ as follows:

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_6}{\partial t}& =\left(1-\frac{U_6}{U}\right)\left(d_U\Delta U+\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE\right)\hfill \\ \hfill & +\left(1-\frac{L_6}{L}\right)\left[d_L\Delta L+{\omega }_{1}UH+{\omega }_{2}UL+{\omega }_{3}UI-\left(\beta +\eta \right)L\right]\hfill \\ \hfill & +\frac{U_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(1-\frac{I_6}{I}\right)\left(d_I\Delta I+\beta L-\alpha I-{\varkappa }_1{Z}^{I}I\right)\hfill \\ \hfill & +\frac{1}{\phi }\left(1-\frac{P_6}{P}\right)\left[d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\right]\hfill \\ \hfill & +\frac{\theta +b_1}{\phi \theta }\left(1-\frac{E_6}{E}\right)\left(d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_6}{\vartheta }\left(1-\frac{H_6}{H}\right)\left(d_H\Delta H+\varpi I-\vartheta H\right)\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\left(d_{Z^I}\Delta Z^I+{\upsilon }_1{Z}^{I}I-c_1{Z}^I\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_6^E}{Z^E}\right)\left(d_{Z^E}\Delta Z^E+{\upsilon }_2{Z}^{E}E-c_2{Z}^E\right).\hfill \end{array}$$

(23)

Simplifying Equation (23), we derive

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_6}{\partial t}& =\left(1-\frac{U_6}{U}\right)\left(\varrho -\varsigma U\right)+{\omega }_2{U}_{6}L+{\omega }_3{U}_{6}I+{\omega }_4{U}_{6}E-\left(\beta +\eta \right)L-{\omega }_{1}UH\frac{L_6}{L}\hfill \\ \hfill & -{\omega }_{2}U{L}_6-{\omega }_{3}UI\frac{L_6}{L}+\left(\beta +\eta \right)L_6+\frac{\beta U_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L-\frac{U_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta }I\hfill \\ \hfill & -\frac{\beta U_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }L\frac{I_6}{I}+\frac{U_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta }{I}_6+\frac{{\varkappa }_1{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{Z}^I{I}_6+\frac{w}{\phi }E\hfill \\ \hfill & -{\omega }_{4}UE\frac{P_6}{P}-\frac{w}{\phi }E\frac{P_6}{P}+\frac{\theta +b_1}{\phi }{P}_6-\frac{a\left(\theta +b_1\right)}{\phi \theta }E-\frac{\theta +b_1}{\phi }P\frac{E_6}{E}+\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_6\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}^E{E}_6+{\omega }_1{U}_6\frac{\varpi I}{\vartheta }-{\omega }_1{U}_6{H}_6\frac{\varpi I}{\vartheta H}+{\omega }_1{U}_6{H}_6-\frac{{\varkappa }_1{c}_1{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}{Z}^I\hfill \\ \hfill & -\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E-\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}_6^{E}E+\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}_6^E+d_U\left(1-\frac{U_6}{U}\right)\Delta U\hfill \\ \hfill & +d_L\left(1-\frac{L_6}{L}\right)\Delta L+\frac{d_I{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(1-\frac{I_6}{I}\right)\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_6}{P}\right)\Delta P\hfill \\ \hfill & +\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_6}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_6}{\vartheta }\left(1-\frac{H_6}{H}\right)\Delta H+\frac{{\varkappa }_1{d}_{Z^I}{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I\hfill \\ \hfill & +\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_6^E}{Z^E}\right)\Delta Z^E.\hfill \end{array}$$

Using the equilibrium conditions for ${\check{S}}_6$:

$$\begin{array}{cc}\hfill & \varrho =\varsigma U_6+{\omega }_1{U}_6{H}_6+{\omega }_2{U}_6{L}_6+{\omega }_3{U}_6{I}_6+{\omega }_4{U}_6{E}_6,\hfill \\ \hfill & {\omega }_1{U}_6{H}_6+{\omega }_2{U}_6{L}_6+{\omega }_3{U}_6{I}_6=\left(\beta +\eta \right)L_6,\hfill \\ \hfill & E_6=\frac{c_2}{{\upsilon }_2},H_6={\displaystyle \frac{\varpi I_6}{\vartheta }},\frac{\beta }{\alpha }{L}_6=I_6,\hfill \\ \hfill & {\omega }_4{U}_6{E}_6+\frac{w}{\phi }{E}_6=\frac{\theta +b_1}{\phi }{P}_6=\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_6+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}_6^E{E}_6.\hfill \end{array}$$

It follows that

$${\omega }_1{U}_6{H}_6+{\omega }_3{U}_6{I}_6=\frac{U_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta }{I}_6=\frac{\beta U_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{L}_6.$$

As a result, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_6}{\partial t}& =\left(1-\frac{U_6}{U}\right)\left(\varsigma U_6-\varsigma U\right)+\left({\omega }_1{U}_6{H}_6+{\omega }_2{U}_6{L}_6+{\omega }_3{U}_6{I}_6+{\omega }_4{U}_6{E}_6\right)\left(1-\frac{U_6}{U}\right)\hfill \\ \hfill & -{\omega }_1{U}_6{H}_6\frac{UH{L}_6}{U_6{H}_{6}L}-{\omega }_2{U}_6{L}_6\frac{U}{U_6}-{\omega }_3{U}_6{I}_6\frac{UI{L}_6}{U_6{I}_{6}L}+{\omega }_1{U}_6{H}_6+{\omega }_2{U}_6{L}_6+{\omega }_3{U}_6{I}_6\hfill \\ \hfill & -\left({\omega }_1{U}_6{H}_6+{\omega }_3{U}_6{I}_6\right)\frac{L{I}_6}{L_{6}I}+{\omega }_1{U}_6{H}_6+{\omega }_3{U}_6{I}_6-{\omega }_4{U}_6{E}_6\frac{UE{P}_6}{U_6{E}_{6}P}-\frac{w}{\phi }{E}_6\frac{E{P}_6}{E_{6}P}\hfill \\ \hfill & +{\omega }_4{U}_6{E}_6+\frac{w}{\phi }{E}_6-{\omega }_4{U}_6{E}_6\frac{P{E}_6}{P_{6}E}-\frac{w}{\phi }{E}_6\frac{P{E}_6}{P_{6}E}+{\omega }_4{U}_6{E}_6+\frac{w}{\phi }{E}_6\hfill \\ \hfill & -{\omega }_1{U}_6{H}_6\frac{I{H}_6}{I_{6}H}+{\omega }_1{U}_6{H}_6+\frac{{\varkappa }_1{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(I_6-\frac{c_1}{{\upsilon }_1}\right)Z^I\hfill \\ \hfill & +d_U\left(1-\frac{U_6}{U}\right)\Delta U+d_L\left(1-\frac{L_6}{L}\right)\Delta L+\frac{d_I{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(1-\frac{I_6}{I}\right)\Delta I\hfill \\ \hfill & +\frac{d_P}{\phi }\left(1-\frac{P_6}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_6}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_6}{\vartheta }\left(1-\frac{H_6}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_6^E}{Z^E}\right)\Delta Z^E\hfill \\ \hfill & =-\varsigma \frac{{\left(U-U_6\right)}^2}{U}+{\omega }_1{U}_6{H}_6\left(4-\frac{U_6}{U}-\frac{UH{L}_6}{U_6{H}_{6}L}-\frac{L{I}_6}{L_{6}I}-\frac{I{H}_6}{I_{6}H}\right)\hfill \\ \hfill & +{\omega }_2{U}_6{L}_6\left(2-\frac{U_6}{U}-\frac{U}{U_6}\right)+{\omega }_3{U}_6{I}_6\left(3-\frac{U_6}{U}-\frac{UI{L}_6}{U_6{I}_{6}L}-\frac{L{I}_6}{L_{6}I}\right)\hfill \\ \hfill & +{\omega }_4{U}_6{E}_6\left(3-\frac{U_6}{U}-\frac{UE{P}_6}{U_6{E}_{6}P}-\frac{P{E}_6}{P_{6}E}\right)+\frac{w}{\phi }{E}_6\left(2-\frac{E{P}_6}{E_{6}P}-\frac{P{E}_6}{P_{6}E}\right)\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(I_6-\frac{c_1}{{\upsilon }_1}\right)Z^I+d_U\left(1-\frac{U_6}{U}\right)\Delta U+d_L\left(1-\frac{L_6}{L}\right)\Delta L\hfill \\ \hfill & +\frac{d_I{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(1-\frac{I_6}{I}\right)\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_6}{P}\right)\Delta P\hfill \\ \hfill & +\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_6}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_6}{\vartheta }\left(1-\frac{H_6}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_6^E}{Z^E}\right)\Delta Z^E.\hfill \end{array}$$

(24)

Then, Equation (24) will be simplified to

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_6}{\partial t}& =-\left(\varsigma +{\omega }_2{L}_6\right)\frac{{\left(U-U_6\right)}^2}{U}-\frac{w}{\phi }\frac{{(E{P}_6-P{E}_6)}^2}{P{P}_{6}E}\hfill \\ \hfill & +{\omega }_1{U}_6{H}_6\left(4-\frac{U_6}{U}-\frac{UH{L}_6}{U_6{H}_{6}L}-\frac{L{I}_6}{L_{6}I}-\frac{I{H}_6}{I_{6}H}\right)\hfill \\ \hfill & +{\omega }_3{U}_6{I}_6\left(3-\frac{U_6}{U}-\frac{UI{L}_6}{U_6{I}_{6}L}-\frac{L{I}_6}{L_{6}I}\right)+{\omega }_4{U}_6{E}_6\left(3-\frac{U_6}{U}-\frac{UE{P}_6}{U_6{E}_{6}P}-\frac{P{E}_6}{P_{6}E}\right)\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(I_6-I_7\right)Z^I+d_U\left(1-\frac{U_6}{U}\right)\Delta U+d_L\left(1-\frac{L_6}{L}\right)\Delta L\hfill \\ \hfill & +\frac{d_I{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }\left(1-\frac{I_6}{I}\right)\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_6}{P}\right)\Delta P\hfill \\ \hfill & +\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_6}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_6}{\vartheta }\left(1-\frac{H_6}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta {\upsilon }_1}\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_6^E}{Z^E}\right)\Delta Z^E.\hfill \end{array}$$

Now, along the solution trajectories of Model (4), we calculate ${\displaystyle \frac{d{\widehat{\mathsf{\Psi }}}_6}{dt}}$ and utilize Equality (12) to obtain the following result:

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_6}{dt}& =-\left(\varsigma +{\omega }_2{L}_6\right){\int }_{\mathsf{\Omega }}\frac{{\left(U-U_6\right)}^2}{U}\mathrm{d}s-\frac{w}{\phi }{\int }_{\mathsf{\Omega }}\frac{{(E{P}_6-P{E}_6)}^2}{P{P}_{6}E}\mathrm{d}s\hfill \\ \hfill & +{\omega }_1{U}_6{H}_6{\int }_{\mathsf{\Omega }}\left(4-\frac{U_6}{U}-\frac{UH{L}_6}{U_6{H}_{6}L}-\frac{L{I}_6}{L_{6}I}-\frac{I{H}_6}{I_{6}H}\right)\mathrm{d}s\hfill \\ \hfill & +{\omega }_3{U}_6{I}_6{\int }_{\mathsf{\Omega }}\left(3-\frac{U_6}{U}-\frac{UI{L}_6}{U_6{I}_{6}L}-\frac{L{I}_6}{L_{6}I}\right)\mathrm{d}s\hfill \\ \hfill & +{\omega }_4{U}_6{E}_6{\int }_{\mathsf{\Omega }}\left(3-\frac{U_6}{U}-\frac{UE{P}_6}{U_6{E}_{6}P}-\frac{P{E}_6}{P_{6}E}\right)\mathrm{d}s\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)\left(I_6-I_7\right)}{\alpha \vartheta }{\int }_{\mathsf{\Omega }}{Z}^I\mathrm{d}s-d_U{U}_6{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}s\hfill \\ \hfill & -d_L{L}_6{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿L\parallel }^2}{L^2}\mathrm{d}s-\frac{d_I{U}_6{I}_6\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\alpha \vartheta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}s\hfill \\ \hfill & -\frac{d_P{P}_6}{\phi }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿P\parallel }^2}{P^2}\mathrm{d}s-\frac{d_E{E}_6\left(\theta +b_1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿E\parallel }^2}{E^2}\mathrm{d}s\hfill \\ \hfill & -\frac{d_H{\omega }_1{U}_6{H}_6}{\vartheta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿H\parallel }^2}{H^2}\mathrm{d}s-\frac{{\varkappa }_2{d}_{Z^E}{Z}_6^E\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{\int }_{\mathsf{\Omega }}\frac{\parallel ▿Z^E{\parallel }^2}{{\left(Z^E\right)}^2}\mathrm{d}s.\hfill \end{array}$$

Hence, if ${\mathcal{R}}_7\le 1$, then using Lemma 2 to obtain $I_6\le I_7$, therefore, using Inequalities (9)–(11), we conclude that $\frac{d{\widehat{\mathsf{\Psi }}}_6}{dt}\le 0$; furthermore, $\frac{d{\widehat{\mathsf{\Psi }}}_6}{dt}=0$ when $(U,L,I,P,E,H,Z^E,Z^I)=(U_6,L_6,I_6,P_6,$ $E_6,H_6,Z_6^E,0)$. The solutions of Model (4) tend to ${\mathsf{\Gamma }}_6^{\prime }$, and hence, ${\mathsf{\Gamma }}_6^{\prime }=\left\{{\check{S}}_6\right\}$. Applying L-LAST, we obtain that ${\check{S}}_6$ is GAS.   □

5.8. Stability of Equilibrium ${\check{S}}_7$

Theorem 8.

The equilibrium ${\check{S}}_7$ of Model (4) is GAS when ${\mathcal{R}}_7>1$ and ${\mathcal{R}}_8>1.$

Proof. 

Define ${\mathsf{\Psi }}_7(s,t)$ as follows:

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_7& =U_7ϝ\left(\frac{U}{U_7}\right)+L_7ϝ\left(\frac{L}{L_7}\right)+\frac{U_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}{I}_7ϝ\left(\frac{I}{I_7}\right)+\frac{1}{\phi }{P}_7ϝ\left(\frac{P}{P_7}\right)+\frac{\theta +b_1}{\phi \theta }{E}_7ϝ\left(\frac{E}{E_7}\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_7}{\vartheta }{H}_7ϝ\left(\frac{H}{H_7}\right)+\frac{{\varkappa }_1{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_7^I\right)}{Z}_7^Iϝ\left(\frac{Z^I}{Z_7^I}\right)+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}_7^Eϝ\left(\frac{Z^E}{Z_7^E}\right).\hfill \end{array}$$

Calculating ${\displaystyle \frac{\partial {\mathsf{\Psi }}_7}{\partial t}}$ as follows:

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_7}{\partial t}& =\left(1-\frac{U_7}{U}\right)\left(d_U\Delta U+\varrho -\varsigma U-{\omega }_{1}UH-{\omega }_{2}UL-{\omega }_{3}UI-{\omega }_{4}UE\right)\hfill \\ \hfill & +\left(1-\frac{L_7}{L}\right)\left[d_L\Delta L+{\omega }_{1}UH+{\omega }_{2}UL+{\omega }_{3}UI-\left(\beta +\eta \right)L\right]\hfill \\ \hfill & +\frac{U_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}\left(1-\frac{I_7}{I}\right)\left(d_I\Delta I+\beta L-\alpha I-{\varkappa }_1{Z}^{I}I\right)\hfill \\ \hfill & +\frac{1}{\phi }\left(1-\frac{P_7}{P}\right)\left[d_P\Delta P+\phi {\omega }_{4}UE+wE-\left(\theta +b_1\right)P\right]\hfill \\ \hfill & +\frac{\theta +b_1}{\phi \theta }\left(1-\frac{E_7}{E}\right)\left(d_E\Delta E+\theta P-aE-{\varkappa }_2{Z}^{E}E\right)\hfill \\ \hfill & +\frac{{\omega }_1{U}_7}{\vartheta }\left(1-\frac{H_7}{H}\right)\left(d_H\Delta H+\varpi I-\vartheta H\right)\hfill \\ \hfill & +\frac{{\varkappa }_1{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_7^I\right)}\left(1-\frac{Z_7^I}{Z^I}\right)\left(d_{Z^I}\Delta Z^I+{\upsilon }_1{Z}^{I}I-c_1{Z}^I\right)\hfill \\ \hfill & +\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_7^E}{Z^E}\right)\left(d_{Z^E}\Delta Z^E+{\upsilon }_2{Z}^{E}E-c_2{Z}^E\right).\hfill \end{array}$$

(25)

Simplifying Equation (25), we derive

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_7}{\partial t}& =\left(1-\frac{U_7}{U}\right)\left(\varrho -\varsigma U\right)+{\omega }_2{U}_{7}L+{\omega }_3{U}_{7}I+{\omega }_4{U}_{7}E-\left(\beta +\eta \right)L-{\omega }_{1}UH\frac{L_7}{L}\hfill \\ \hfill & -{\omega }_{2}U{L}_7-{\omega }_{3}UI\frac{L_7}{L}+\left(\beta +\eta \right)L_7+\frac{\beta U_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}L-\frac{\alpha U_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}I\hfill \\ \hfill & -\frac{\beta U_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}L\frac{I_7}{I}+\frac{\alpha U_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}{I}_7+\frac{{\varkappa }_1{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}{Z}^I{I}_7\hfill \\ \hfill & +\frac{w}{\phi }E-{\omega }_{4}UE\frac{P_7}{P}-\frac{w}{\phi }E\frac{P_7}{P}+\frac{\theta +b_1}{\phi }{P}_7-\frac{a\left(\theta +b_1\right)}{\phi \theta }E-\frac{\theta +b_1}{\phi }P\frac{E_7}{E}\hfill \\ \hfill & +\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_7+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}^E{E}_7+{\omega }_1{U}_7\frac{\varpi I}{\vartheta }-{\omega }_1{U}_7{H}_7\frac{\varpi I}{\vartheta H}+{\omega }_1{U}_7{H}_7\hfill \\ \hfill & -\frac{{\varkappa }_1{c}_1{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_7^I\right)}{Z}^I-\frac{{\varkappa }_1{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}{Z}_7^{I}I+\frac{{\varkappa }_1{c}_1{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_7^I\right)}{Z}_7^I\hfill \\ \hfill & -\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}^E-\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}_7^{E}E+\frac{{\varkappa }_2{c}_2\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{Z}_7^E+d_U\left(1-\frac{U_7}{U}\right)\Delta U\hfill \\ \hfill & +d_L\left(1-\frac{L_7}{L}\right)\Delta L+\frac{d_I{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}\left(1-\frac{I_7}{I}\right)\Delta I+\frac{d_P}{\phi }\left(1-\frac{P_7}{P}\right)\Delta P\hfill \\ \hfill & +\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_7}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_7}{\vartheta }\left(1-\frac{H_7}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_7^I\right)}\left(1-\frac{Z_7^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_7^E}{Z^E}\right)\Delta Z^E.\hfill \end{array}$$

The equilibrium conditions for ${\check{S}}_7$ give

$$\begin{array}{cc}\hfill & \varrho =\varsigma U_7+{\omega }_1{U}_7{H}_7+{\omega }_2{U}_7{L}_7+{\omega }_3{U}_7{I}_7+{\omega }_4{U}_7{E}_7,\hfill \\ \hfill & {\omega }_1{U}_7{H}_7+{\omega }_2{U}_7{L}_7+{\omega }_3{U}_7{I}_7=\left(\beta +\eta \right)L_7,\hfill \\ \hfill & \beta L_7=\left(\alpha +{\varkappa }_1{Z}_7^I\right)I_7,I_7=\frac{c_1}{{\upsilon }_1},E_7=\frac{c_2}{{\upsilon }_2},H_7={\displaystyle \frac{\varpi I_7}{\vartheta }}\hfill \\ \hfill & {\omega }_4{U}_7{E}_7+\frac{w}{\phi }{E}_7=\frac{\theta +b_1}{\phi }{P}_7=\frac{a\left(\theta +b_1\right)}{\phi \theta }{E}_7+\frac{{\varkappa }_2\left(\theta +b_1\right)}{\phi \theta }{Z}_7^E{E}_7.\hfill \end{array}$$

This implies that

$${\omega }_1{U}_7{H}_7+{\omega }_3{U}_7{I}_7=\frac{U_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta }{I}_7=\frac{\beta U_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}{L}_7.$$

In addition, we obtain

$$\begin{array}{cc}\hfill \frac{\partial {\mathsf{\Psi }}_7}{\partial t}& =\left(1-\frac{U_7}{U}\right)\left(\varsigma U_7-\varsigma U\right)+\left({\omega }_1{U}_7{H}_7+{\omega }_2{U}_7{L}_7+{\omega }_3{U}_7{I}_7+{\omega }_4{U}_7{E}_7\right)\left(1-\frac{U_7}{U}\right)\hfill \\ \hfill & -{\omega }_1{U}_7{H}_7\frac{UH{L}_7}{U_7{H}_{7}L}-{\omega }_2{U}_7{L}_7\frac{U}{U_7}-{\omega }_3{U}_7{I}_7\frac{UI{L}_7}{U_7{I}_{7}L}+{\omega }_1{U}_7{H}_7+{\omega }_2{U}_7{L}_7+{\omega }_3{U}_7{I}_7\hfill \\ \hfill & -\left({\omega }_1{U}_7{H}_7+{\omega }_3{U}_7{I}_7\right)\frac{L{I}_7}{L_{7}I}+{\omega }_1{U}_7{H}_7+{\omega }_3{U}_7{I}_7-{\omega }_4{U}_7{E}_7\frac{UE{P}_7}{U_7{E}_{7}P}-\frac{w}{\phi }{E}_7\frac{E{P}_7}{E_{7}P}\hfill \\ \hfill & +{\omega }_4{U}_7{E}_7+\frac{w}{\phi }{E}_7-{\omega }_4{U}_7{E}_7\frac{P{E}_7}{P_{7}E}-\frac{w}{\phi }{E}_7\frac{P{E}_7}{P_{7}E}+{\omega }_4{U}_7{E}_7+\frac{w}{\phi }{E}_7-{\omega }_1{U}_7{H}_7\frac{I{H}_7}{I_{7}H}\hfill \\ \hfill & +{\omega }_1{U}_7{H}_7+d_U\left(1-\frac{U_7}{U}\right)\Delta U+d_L\left(1-\frac{L_7}{L}\right)\Delta L+\frac{d_I{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}\left(1-\frac{I_7}{I}\right)\Delta I\hfill \\ \hfill & +\frac{d_P}{\phi }\left(1-\frac{P_7}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_7}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_7}{\vartheta }\left(1-\frac{H_7}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_7^I\right)}\left(1-\frac{Z_7^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_7^E}{Z^E}\right)\Delta Z^E\hfill \\ \hfill & =-\left(\varsigma +{\omega }_2{L}_7\right)\frac{{\left(U-U_7\right)}^2}{U}-\frac{w}{\phi }\frac{{(E{P}_7-P{E}_7)}^2}{P{P}_{7}E}\hfill \\ \hfill & +{\omega }_1{U}_7{H}_7\left(4-\frac{U_7}{U}-\frac{UH{L}_7}{U_7{H}_{7}L}-\frac{L{I}_7}{L_{7}I}-\frac{I{H}_7}{I_{7}H}\right)\hfill \\ \hfill & +{\omega }_3{U}_7{I}_7\left(3-\frac{U_7}{U}-\frac{UI{L}_7}{U_7{I}_{7}L}-\frac{L{I}_7}{L_{7}I}\right)+{\omega }_4{U}_7{E}_7\left(3-\frac{U_7}{U}-\frac{UE{P}_7}{U_7{E}_{7}P}-\frac{P{E}_7}{P_{7}E}\right)\hfill \\ \hfill & +d_U\left(1-\frac{U_7}{U}\right)\Delta U+d_L\left(1-\frac{L_7}{L}\right)\Delta L+\frac{d_I{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}\left(1-\frac{I_7}{I}\right)\Delta I\hfill \\ \hfill & +\frac{d_P}{\phi }\left(1-\frac{P_7}{P}\right)\Delta P+\frac{d_E\left(\theta +b_1\right)}{\phi \theta }\left(1-\frac{E_7}{E}\right)\Delta E+\frac{d_H{\omega }_1{U}_7}{\vartheta }\left(1-\frac{H_7}{H}\right)\Delta H\hfill \\ \hfill & +\frac{{\varkappa }_1{d}_{Z^I}{U}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_7^I\right)}\left(1-\frac{Z_7^I}{Z^I}\right)\Delta Z^I+\frac{{\varkappa }_2{d}_{Z^E}\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}\left(1-\frac{Z_7^E}{Z^E}\right)\Delta Z^E.\hfill \end{array}$$

Calculating ${\displaystyle \frac{d{\widehat{\mathsf{\Psi }}}_7}{dt}}$ and using Equality (12), we find

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Psi }}}_7}{dt}& =-\left(\varsigma +{\omega }_2{L}_7\right){\int }_{\mathsf{\Omega }}\frac{{\left(U-U_7\right)}^2}{U}\mathrm{d}s-\frac{w}{\phi }{\int }_{\mathsf{\Omega }}\frac{{(E{P}_7-P{E}_7)}^2}{P{P}_{7}E}\mathrm{d}s\hfill \\ \hfill & +{\omega }_1{U}_7{H}_7{\int }_{\mathsf{\Omega }}\left(4-\frac{U_7}{U}-\frac{UH{L}_7}{U_7{H}_{7}L}-\frac{L{I}_7}{L_{7}I}-\frac{I{H}_7}{I_{7}H}\right)\mathrm{d}s\hfill \\ \hfill & +{\omega }_3{U}_7{I}_7{\int }_{\mathsf{\Omega }}\left(3-\frac{U_7}{U}-\frac{UI{L}_7}{U_7{I}_{7}L}-\frac{L{I}_7}{L_{7}I}\right)\mathrm{d}s+{\omega }_4{U}_7{E}_7{\int }_{\mathsf{\Omega }}\left(3-\frac{U_7}{U}-\frac{UE{P}_7}{U_7{E}_{7}P}-\frac{P{E}_7}{P_{7}E}\right)\mathrm{d}s\hfill \\ \hfill & -d_U{U}_7{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿U\parallel }^2}{U^2}\mathrm{d}s-d_L{L}_7{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿L\parallel }^2}{L^2}\mathrm{d}s-\frac{d_I{U}_7{I}_7\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta \left(\alpha +{\varkappa }_1{Z}_7^I\right)}{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿I\parallel }^2}{I^2}\mathrm{d}s\hfill \\ \hfill & -\frac{d_P{P}_7}{\phi }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿P\parallel }^2}{P^2}\mathrm{d}s-\frac{d_E{E}_7\left(\theta +b_1\right)}{\phi \theta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿E\parallel }^2}{E^2}\mathrm{d}s-\frac{d_H{\omega }_1{U}_7{H}_7}{\vartheta }{\int }_{\mathsf{\Omega }}\frac{{\parallel ▿H\parallel }^2}{H^2}\mathrm{d}s\hfill \\ \hfill & -\frac{{\varkappa }_1{d}_{Z^I}{U}_7{Z}_7^I\left(\varpi {\omega }_1+\vartheta {\omega }_3\right)}{\vartheta {\upsilon }_1\left(\alpha +{\varkappa }_1{Z}_7^I\right)}{\int }_{\mathsf{\Omega }}\frac{\parallel ▿Z^I{\parallel }^2}{{\left(Z^I\right)}^2}\mathrm{d}s-\frac{{\varkappa }_2{d}_{Z^E}{Z}_7^E\left(\theta +b_1\right)}{\phi \theta {\upsilon }_2}{\int }_{\mathsf{\Omega }}\frac{\parallel ▿Z^E{\parallel }^2}{{\left(Z^E\right)}^2}\mathrm{d}s.\hfill \end{array}$$

Inequalities (9)–(11) imply that $\frac{d{\widehat{\mathsf{\Psi }}}_7}{dt}\le 0$ where $\frac{d{\widehat{\mathsf{\Psi }}}_7}{dt}=0$ occurs at ${\check{S}}_7$. The solutions of Model (4) are limited to ${\mathsf{\Gamma }}_7^{\prime }=\left\{{\check{S}}_7\right\}$. Applying L-LAST, we obtain that ${\check{S}}_7$ is GAS.   □

Let $X=(U,L,I,P,E,H,Z^I,Z^E)\in {\mathbb{R}}^8$ with the norm $\parallel X\parallel =\left|U\right|+\left|L\right|+\left|I\right|+\left|P\right|+\left|E\right|+\left|H\right|+|Z^I|+|Z^E|$. By a simple computation, we have ${\mathsf{\Psi }}_i\left(X\right)\to \infty$ as $\parallel X\parallel \to \infty$. Hence, the Lyapunov functions ${\mathsf{\Psi }}_i$, i = 0, 1, …, 7 considered in the proofs of Theorems 1–8 are unbounded. In addition, Table 1 summarizes the results obtained in these theorems.

Table 1. Global stability conditions for the equilibria of Model (4).

Equilibrium	Global Stability$\mathbf{Conditions}$
${\check{S}}_0$	${\mathcal{R}}_1\le 1$ and ${\mathcal{R}}_2\le 1$
${\check{S}}_1$	${\mathcal{R}}_1>1$, ${\mathcal{R}}_2/{\mathcal{R}}_1\le 1$ and ${\mathcal{R}}_3\le 1$
${\check{S}}_2$	${\mathcal{R}}_2>1$, ${\mathcal{R}}_1/{\mathcal{R}}_2\le 1$ and ${\mathcal{R}}_4\le 1$
${\check{S}}_3$	${\mathcal{R}}_3>1$ and ${\mathcal{R}}_5\le 1$
${\check{S}}_4$	${\mathcal{R}}_4>1$ and ${\mathcal{R}}_6\le 1$
${\check{S}}_5$	${\widehat{\mathcal{R}}}_5,$ ${\mathcal{R}}_5>1$, ${\mathcal{R}}_8\le 1$ and ${\mathcal{R}}_1/{\mathcal{R}}_2>1$
${\check{S}}_6$	${\mathcal{R}}_6>1$, ${\mathcal{R}}_7\le 1$ and ${\mathcal{R}}_2/{\mathcal{R}}_1>1$
${\check{S}}_7$	${\mathcal{R}}_7>1$ and ${\mathcal{R}}_8>1$

6. Numerical Simulations

This part illustrates the global stability of equilibria using numerical simulations based on the parameters listed in Table 2; some values of these parameters for HIV were obtained from [57]. To numerically solve the system of PDEs, we used the solver PDEPE in MATLAB (see the code given in the link given in [58]: https://www.mdpi.com/article/10.3390/math10224390/s1 (accessed on 15 January 2023)). Additionally, a comparison study between mono-infection and co-infection dynamics will be demonstrated. We selected a step size of $0.1$ for time $t>0$ and a domain $\mathsf{\Omega }$ as $\mathsf{\Omega }=[0,2]$ with a step size of $0.02$. In addition, we considered Model (1) under the initial conditions:

$$\begin{array}{cc}\hfill & U(s,0)=500\left[1+0.2{cos}^2\left(\pi s\right)\right],L(s,0)=10\left[1+0.5{cos}^2\left(\pi s\right)\right],\hfill \\ \hfill & I(s,0)=2\left[1+0.5{cos}^2\left(\pi s\right)\right],P(s,0)=20\left[1+0.5{cos}^2\left(\pi s\right)\right],\hfill \\ \hfill & E(s,0)=0.2\left[1+0.5{cos}^2\left(\pi s\right)\right],H(s,0)=4\left[1+0.5{cos}^2\left(\pi s\right)\right],\hfill \\ \hfill & Z^I(s,0)=4\left[1+0.5{cos}^2\left(\pi s\right)\right],Z^E(s,0)=1.5\left[1+0.5{cos}^2\left(\pi s\right)\right],s\in [0,2],\hfill \end{array}$$

(26)

and the homogeneous Neumann boundary conditions:

$$\frac{\partial U}{\partial \overrightarrow{\rho }}=\frac{\partial L}{\partial \overrightarrow{\rho }}=\frac{\partial I}{\partial \overrightarrow{\rho }}=\frac{\partial P}{\partial \overrightarrow{\rho }}=\frac{\partial E}{\partial \overrightarrow{\rho }}=\frac{\partial H}{\partial \overrightarrow{\rho }}=\frac{\partial Z^I}{\partial \overrightarrow{\rho }}=\frac{\partial Z^E}{\partial \overrightarrow{\rho }}=0,t>0,s=0,2.$$

(27)

Table 2. List of parameters of Model (1).

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
$\varrho$	10	$\epsilon$	$0.9$	$\vartheta$	2	$d_L$	$0.1$
$\varsigma$	$0.01$	b	$0.008$	$\eta$	$0.02$	$d_I$	$0.01$
${\omega }_1$	Varied	$b_2$	$0.2$	${\upsilon }_1$	Varied	$d_P$	$0.01$
${\omega }_2$	Varied	$\varpi$	5	${\upsilon }_2$	Varied	$d_E$	$0.2$
${\omega }_3$	Varied	$c_1$	$0.1$	$\beta$	$0.2$	$d_H$	$0.01$
${\omega }_4$	Varied	$c_2$	$0.1$	$b_1$	$0.01$	$d_{Z^I}$	$0.2$
$\alpha$	$0.5$	${\varkappa }_1$	$0.2$	$\theta$	$0.003$	$d_{Z^E}$	$0.2$
$\phi$	$0.2$	${\varkappa }_2$	$0.2$	$d_U$	$0.1$

6.1. Stability of the Equilibria

Under the above initial and boundary conditions, we chose various values of the parameters ${\omega }_1$, ${\omega }_2$, ${\omega }_3$, ${\omega }_4$, ${\upsilon }_1,$ and ${\upsilon }_2$, which yielded the following cases:

(1)

We picked ${\omega }_1=0.00006,$ ${\omega }_2=0.00005,$ ${\omega }_3=0.00007,$ ${\omega }_4=0.001,$ ${\upsilon }_1=0.3,$ and ${\upsilon }_2=0.5$. For this set of parameters, we have ${\mathcal{R}}_1=0.63<1$ and ${\mathcal{R}}_2=0.23<1$. As shown in Figure 1, the solution of Model (1) reaches the equilibrium ${\check{S}}_0=(1000,0,0,0,0,0,0,0)$. This shows that ${\check{S}}_0$ is GAS in accordance with Theorem 1. Both HTLV and HIV will be removed in this case.

Figure 1. The solution behavior of Model (1) with the initial conditions (26) and boundary conditions (27). Taking ${\omega }_1=0.00006,{\omega }_2=0.00005,{\omega }_3=0.00007,{\omega }_4=0.001,{\upsilon }_1=0.3,{\upsilon }_2=0.5$, we have ${\mathcal{R}}_1=0.63<1,$ ${\mathcal{R}}_2=0.23<1,$ and the equilibrium ${\check{S}}_0=(1000,0,0,0,0,0,0,0)$ is asymptotically stable.

(2)

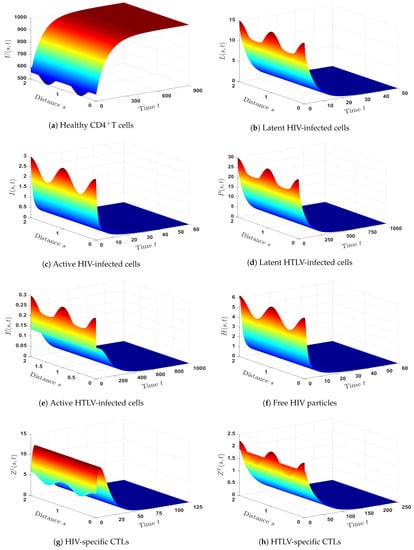
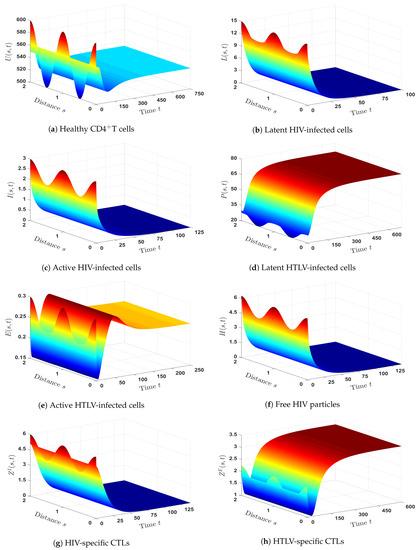
We selected ${\omega }_1=0.0001,$ ${\omega }_2=0.0002,$ ${\omega }_3=0.0003,$ ${\omega }_4=0.0005,$ ${\upsilon }_1=0.003,$ and${\upsilon }_2=0.2$. With such a choice, we obtained ${\mathcal{R}}_2=0.12<1<1.91={\mathcal{R}}_1$, ${\mathcal{R}}_3=0.39<1$, and hence, ${\mathcal{R}}_2/{\mathcal{R}}_1=0.06<1$. Theorem 2 implies that ${\check{S}}_1=\left(523.81,21.65,8.66,0,0,21.65,0,0\right)$ is GAS, which is displayed in Figure 2. As a result, HIV mono-infection will persist, but with an inefficient CTL immune response.

Figure 2. The solution behavior of Model (1) with the initial conditions (26) and boundary conditions (27). Taking ${\omega }_1=0.0001,{\omega }_2=0.0002,{\omega }_3=0.0003,{\omega }_4=0.0005,{\upsilon }_1=0.003,{\upsilon }_2=0.2$, we have ${\mathcal{R}}_1=1.91>1,{\mathcal{R}}_2/{\mathcal{R}}_1=0.063<1,{\mathcal{R}}_3=0.39<1,$ and the equilibrium ${\check{S}}_1=\left(523.81,21.65,8.66,0,0,21.65,0,0\right)$ is asymptotically stable.

(3)

We set ${\omega }_1=0.0001,$ ${\omega }_2=0.00005,$ ${\omega }_3=0.00007,$ ${\omega }_4=0.006,$ ${\upsilon }_1=0.001,$ and ${\upsilon }_2=0.05$. Then, we calculated ${\mathcal{R}}_1=0.81<1<1.4={\mathcal{R}}_2$, ${\mathcal{R}}_4=0.64<1,$ and then, ${\mathcal{R}}_1/{\mathcal{R}}_2=0.58<1$. The numerical results showed that ${\check{S}}_2=\left(713.33,0,0,44.47,0.67,0,0,0\right)$ exists. Figure 3 illustrates that ${\check{S}}_2$ is GAS. It is evident from this that the numerical outcomes and the theoretical finding of Theorem 3 are consistent. Therefore, a persistent HTLV mono-infection with an inefficient CTL immunity is present.

Figure 3. The solution behavior of Model (1) with the initial conditions (26) and boundary conditions (27). Taking ${\omega }_1=0.0001,{\omega }_2=0.00005,{\omega }_3=0.00007,{\omega }_4=0.006,{\upsilon }_1=0.001,{\upsilon }_2=0.05,$ we have ${\mathcal{R}}_2=1.4>1,{\mathcal{R}}_1/{\mathcal{R}}_2=0.58<1,{\mathcal{R}}_4=0.64<1,$ and the equilibrium ${\check{S}}_2=\left(713.33,0,0,44.47,0.67,0,0,0\right)$ is asymptotically stable.

(4)

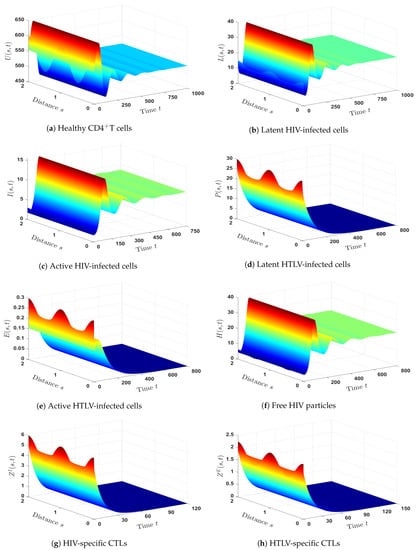
We took ${\omega }_1=0.001,$ ${\omega }_2=0.0001,$ ${\omega }_3=0.0003,$ ${\omega }_4=0.001,$ ${\upsilon }_1=0.05,$ and ${\upsilon }_2=0.005$ to yield ${\mathcal{R}}_3=3.91>1$ and ${\mathcal{R}}_5=0.22<1$. Figure 4 shows that ${\check{S}}_3=\left(569.59,19.56,2,0,0,5,7.28,0\right)$ is GAS based on Theorem 4. Therefore, a persistent HIV mono-infection with an efficient HIV-specific CTL immune response is reached.

Figure 4. The solution behavior of Model (1) with the initial conditions (26) and boundary conditions (27). Taking ${\omega }_1=0.001,{\omega }_2=0.0001,{\omega }_3=0.0003,{\omega }_4=0.001,{\upsilon }_1=0.05,{\upsilon }_2=0.005$, we have ${\mathcal{R}}_3=3.91>1,$ ${\mathcal{R}}_5=0.22<1,$ and the equilibrium ${\check{S}}_3=\left(569.59,19.56,2,0,0,5,7.28,0\right)$ is asymptotically stable.

(5)

We set ${\omega }_1={\omega }_2=0.0001,$ ${\omega }_3=0.0002,$ ${\omega }_4=0.035,$ ${\upsilon }_1=0.05,$ and ${\upsilon }_2=0.4$. Then, we calculated ${\mathcal{R}}_4=4.35>1$ and ${\mathcal{R}}_6=0.68<1$. According to these data, ${\check{S}}_4$ exists and is given by ${\check{S}}_4=\left(533.33,0,0,71.93,0.25,0,0,3.32\right)$. In Figure 5, we show that ${\check{S}}_4$ is GAS, which is consistent with Theorem 5. There is a persistent HTLV mono-infection in this case, with efficient HTLV-specific CTL immunity.

Figure 5. The solution behavior of Model (1) with the initial conditions (26) and boundary conditions (27). Taking ${\omega }_1={\omega }_2=0.0001,{\omega }_3=0.0002,{\omega }_4=0.035,{\upsilon }_1=0.05,{\upsilon }_2=0.4$, we have ${\mathcal{R}}_4=4.35>1,$ ${\mathcal{R}}_6=0.68<1,$ and the equilibrium ${\check{S}}_4=\left(533.33,0,0,71.93,0.25,0,0,3.32\right)$ is asymptotically stable.

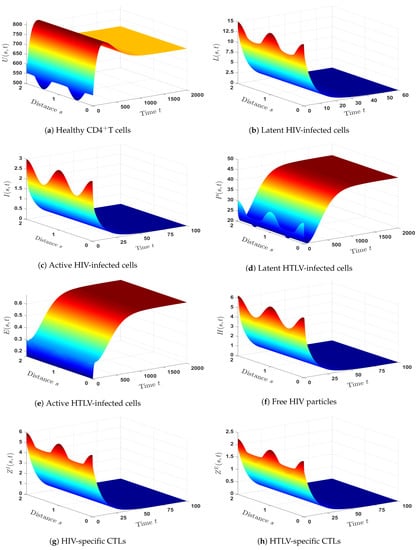
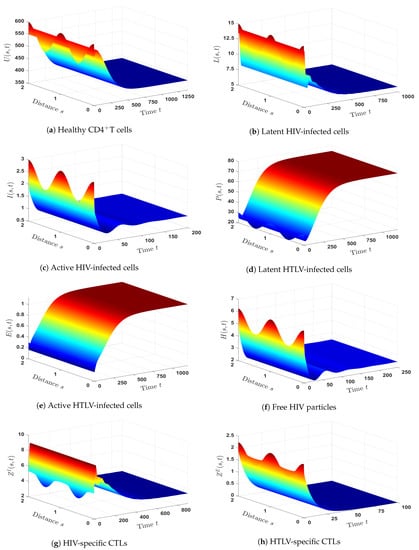
(6)

We chose ${\omega }_1=0.001,$ ${\omega }_2=0.0001,$ ${\omega }_3=0.0002,$ ${\omega }_4=0.011,$ ${\upsilon }_1=0.1,$ and ${\upsilon }_2=0.01$. Hence, we have ${\widehat{\mathcal{R}}}_5=5.64>1$, ${\mathcal{R}}_5=1.93>1$, ${\mathcal{R}}_8=0.21<1,$ and ${\mathcal{R}}_1/{\mathcal{R}}_2=2.09>1$. The numerical outcomes displayed in Figure 6 confirmed the existence and global stability of ${\check{S}}_5=\left(389.09,5.80,1,74.98,1.13,2.5,3.30,0\right)$. Theorem 6 is, therefore, affirmed by this result. In this case, there is a persistent co-infection with HTLV and HIV together with an efficient HIV-specific CTL immunity, whereas the HTLV-specific CTL immunity is an inefficient.

Figure 6. The solution behavior of Model (1) with the initial conditions (26) and boundary conditions (27). Taking ${\omega }_1=0.001,{\omega }_2=0.0001,{\omega }_3=0.0002,{\omega }_4=0.011,{\upsilon }_1=0.1,{\upsilon }_2=0.01$, we have ${\widehat{\mathcal{R}}}_5=5.64>1,{\mathcal{R}}_5=1.93>1,{\mathcal{R}}_8=0.21<1,{\mathcal{R}}_1/{\mathcal{R}}_2=2.09>1,$ and the equilibrium ${\check{S}}_5=\left(389.09,5.80,1,74.98,1.13,2.5,3.30,0\right)$ is asymptotically stable.

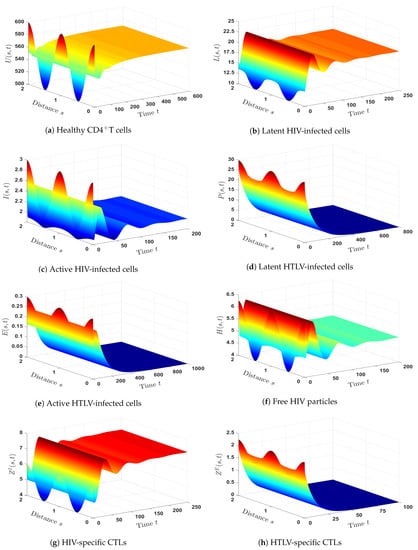
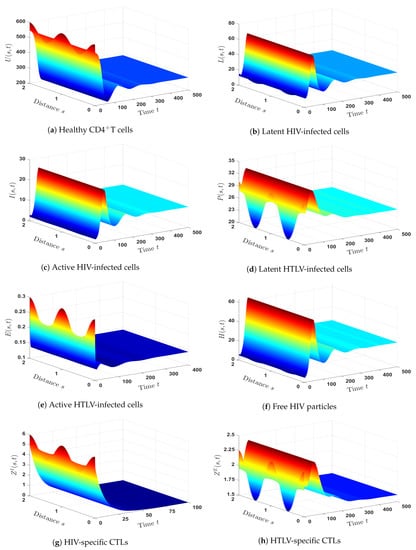
(7)

We picked ${\omega }_1=0.0006,$ ${\omega }_2=0.0001,$ ${\omega }_3=0.0002,$ ${\omega }_4=0.04,$ ${\upsilon }_1=0.001,$ and ${\upsilon }_2=0.7$. This gives ${\mathcal{R}}_6=2.26>1$, ${\mathcal{R}}_7=0.17<1,$ and ${\mathcal{R}}_2/{\mathcal{R}}_1=2.63>1$. As can be seen from Figure 7, the equilibrium ${\check{S}}_6=\left(282.05,25.31,10.12,24.87,0.143,25.31,0,1.62\right)$ is GAS, and this is a confirmation of Theorem 7. In such a case, a persistent co-infection with HTLV and HIV occurs together with the effective HTLV-specific CTL immunity; however, the HIV-specific CTL immunity is not working.

Figure 7. The solution behavior of Model (1) with the initial conditions (26) and boundary conditions (27). Taking ${\omega }_1=0.0006,{\omega }_2=0.0001,{\omega }_3=0.0002,{\omega }_4=0.04,{\upsilon }_1=0.001,{\upsilon }_2=0.7$, we have ${\mathcal{R}}_6=2.26>1,{\mathcal{R}}_7=0.17<1,{\mathcal{R}}_2/{\mathcal{R}}_1=2.63>1,$ and the equilibrium ${\check{S}}_6=\left(282.05,25.31,10.12,24.87,0.143,25.31,0,1.62\right)$ is asymptotically stable.

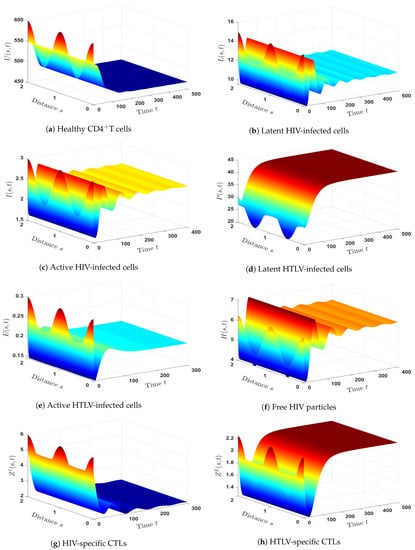
(8)

We chose ${\omega }_1=0.0006,$ ${\omega }_2=0.0001,$ ${\omega }_3=0.0002,$ ${\omega }_4=0.03,$ ${\upsilon }_1=0.04,$ and ${\upsilon }_2=0.5$. These data give ${\mathcal{R}}_7=1.83>1$ and ${\mathcal{R}}_8=3.27>1$. Figure 8 illustrates that ${\check{S}}_7=\left(467.37,11.46,2.5,43.25,0.2,6.25,2.09,2.25\right)$ is GAS. Theorem 8 is, therefore, confirmed. Consequently, a persistent co-infection with HTLV and HIV occurs where the immune system is functioning well.

Figure 8. The solution behavior of Model (1) with the initial conditions (26) and boundary conditions (27). Taking ${\omega }_1=0.0006,{\omega }_2=0.0001,{\omega }_3=0.0002,{\omega }_4=0.03,{\upsilon }_1=0.04,{\upsilon }_2=0.5$, we have ${\mathcal{R}}_7=1.83>1,{\mathcal{R}}_8=3.27>1,$ and the equilibrium ${\check{S}}_7=\left(467.37,11.46,2.5,43.25,0.2,6.25,2.09,2.25\right)$ is asymptotically stable.

6.2. Comparison Study

We compare mono- and co-infection dynamics in this part, through studying the effect of one of the infections (HIV infection or HTLV infection) on the dynamical behavior of the other mono-infection as in the following points:

(i) 

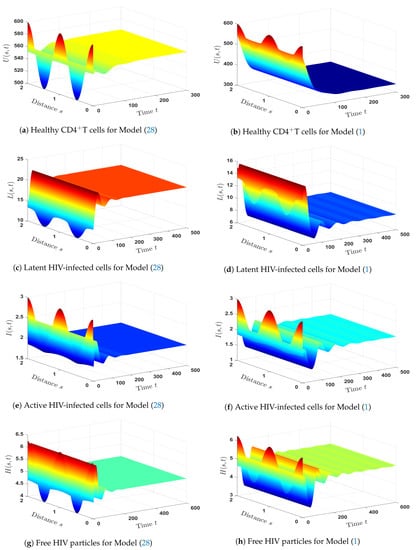
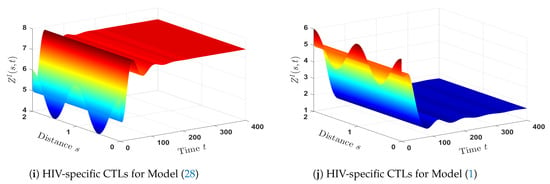
The impact of HTLV infection on the dynamical behavior of HIV mono-infection:

The following HIV mono-infection model was compared with Model (1) in order to determine the impact of HTLV infections on HIV mono-infection dynamics:

$$\left\{\begin{array}{c}\frac{\partial U(s,t)}{\partial t}=d_U\Delta U(s,t)+\varrho -\varsigma U(s,t)-{\omega }_{1}U(s,t)H(s,t)\hfill \\ -{\omega }_{2}U(s,t)L(s,t)-{\omega }_{3}U(s,t)I(s,t),\hfill \\ \frac{\partial L(s,t)}{\partial t}=d_L\Delta L(s,t)+{\omega }_{1}U(s,t)H(s,t)+{\omega }_{2}U(s,t)L(s,t)\hfill \\ +{\omega }_{3}U(s,t)I(s,t)-\left(\beta +\eta \right)L(s,t),\hfill \\ \frac{\partial I(s,t)}{\partial t}=d_I\Delta I(s,t)+\beta L(s,t)-\alpha I(s,t)-{\varkappa }_1{Z}^I(s,t)I(s,t),\hfill \\ \frac{\partial H(s,t)}{\partial t}=d_H\Delta H(s,t)+\varpi I(s,t)-\vartheta H(s,t),\hfill \\ \frac{\partial Z^I(s,t)}{\partial t}=d_{Z^I}\Delta Z^I(s,t)+{\upsilon }_1{Z}^I(s,t)I(s,t)-c_1{Z}^I(s,t).\hfill \end{array}\right.$$

(28)

The comparison was made through the following considerations:

• The parameters ${\omega }_1=0.0006$, ${\omega }_2=0.0002$, ${\omega }_3=0.0004$, ${\upsilon }_1=0.05$, and ${\upsilon }_2=0.5$ are fixed.
• Both the initial conditions (26) and boundary conditions (27) were taken into consideration.
• We chose ${\omega }_4=0.07$ (in the case of HTLV/HIV co-infection dynamics).

As shown in Figure 9, patients with only HIV who are co-infected with HTLV have lower levels of CD$4^{+}$T cells (both latent and healthy), as well as HIV-specific CTLs. On the other hand, the concentration of free HIV particles reaches the same level in both HIV mono-infection and HTLV/HIV co-infection. Actually, this finding is compatible with the results of a recently published paper [59], where the study indicated that there are no discernible contrasts between HIV mono-infected and HTLV/HIV co-infected in terms of the number of HIV particles.

Figure 9. Comparison between the solutions of two models: HIV mono-infection Model (28) and HTLV/HIV co-infection Model (1), under the initial conditions (26) and boundary conditions (27), taking ${\omega }_1=0.0006,{\omega }_2=0.0002,{\omega }_3=0.0004,{\omega }_4=0.07,{\upsilon }_1=0.05,{\upsilon }_2=0.5$.

(ii) 

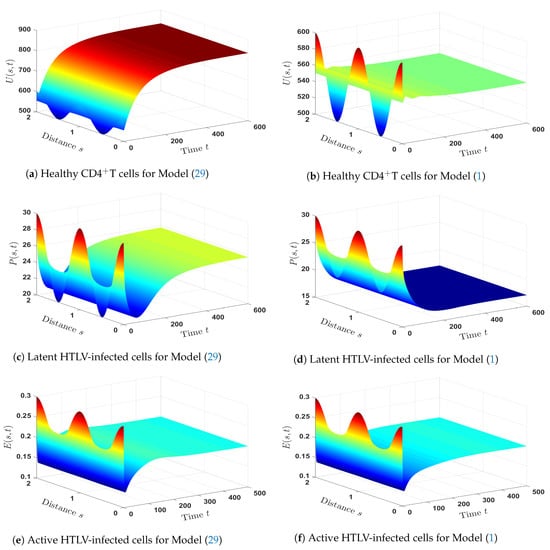
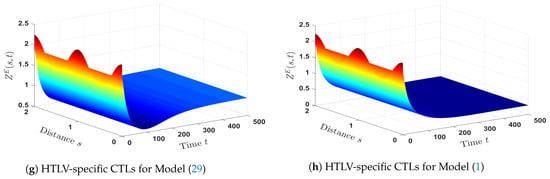
The impact of HIV infection on the dynamical behavior of HTLV mono-infection:

In order to know how HIV infection influences the HTLV mono-infection dynamics, we compared Model (1) with an HTLV mono-infection model as given below:

$$\left\{\begin{array}{c}\frac{\partial U(s,t)}{\partial t}=d_U\Delta U(s,t)+\varrho -\varsigma U(s,t)-{\omega }_{4}U(s,t)E(s,t),\hfill \\ \frac{\partial P(s,t)}{\partial t}=d_P\Delta P(s,t)+\phi {\omega }_{4}U(s,t)E(s,t)+\epsilon bE(s,t)\hfill \\ -\left(\theta +b_1\right)P(s,t),\hfill \\ \frac{\partial E(s,t)}{\partial t}=d_E\Delta E(s,t)+\theta P(s,t)+\left(1-\epsilon \right)bE(s,t)\hfill \\ -b_{2}E(s,t)-{\varkappa }_2{Z}^E(s,t)E(s,t),\hfill \\ \frac{\partial Z^E(s,t)}{\partial t}=d_{Z^E}\Delta Z^E(s,t)+{\upsilon }_2{Z}^E(s,t)E(s,t)-c_2{Z}^E(s,t).\hfill \end{array}\right.$$

(29)

To make the comparison, we took into account the following factors:

• The parameters ${\omega }_4=0.01$, ${\upsilon }_1=0.05$, and ${\upsilon }_2=0.5$ are fixed.
• The initial conditions (26) and boundary conditions (27) were considered.
• We picked ${\omega }_1=$ $0.0005,$ ${\omega }_2=0.0002,$ and ${\omega }_3=0.0003$ (in the case of HTLV/HIV co-infection dynamics).

The solutions of Models (1) and (29) are shown by Figure 10. We noticed that, in the case of co-infection, the densities of CD$4^{+}$T cells (both latent and healthy) and HTLV-specific CTLs are less than those in the case of HTLV mono-infection. However, both HTLV mono-infection and HTLV/HIV co-infection have the same level of density of active HTLV-infected cells.

Figure 10. Comparison between the solutions of two models: HTLV mono-infection Model (29) and HTLV/HIV co-infection Model (1), under the initial conditions (26) and boundary conditions (27), taking ${\omega }_1=0.0005,{\omega }_2=0.0002,{\omega }_3=0.0003,{\omega }_4=0.01,{\upsilon }_1=0.05,{\upsilon }_2=0.5$.

7. Conclusions

In this work, we developed and analyzed the spatiotemporal dynamics of a mathematical PDE model for HTLV/HIV co-infection in the presence of three routes of transmission, which are FTC, latent ITC, and active ITC. The developed PDE model also incorporated latent infected cells, which represent reservoirs for both HTLV and HIV, as well as the cellular immunity mediated by CTL cells in order to control the HTLV/HIV co-infection. We first studied the properties of the solutions including the existence, uniqueness, non-negativity, and boundedness to guarantee that our developed model is biologically and mathematically well-posed. Furthermore, we proved that the dynamics of the model is fully determined by eight threshold parameters: ${\mathcal{R}}_i$, i = 1, 2,…, 8. More precisely, the infection-free equilibrium is globally asymptotically stable when ${\mathcal{R}}_1\le 1$ and ${\mathcal{R}}_2\le 1$, which biologically means that both HIV and HTLV are cleared and the co-infection dies out. However, when ${\mathcal{R}}_1>1$ or ${\mathcal{R}}_2>1$, one or both viruses persist in the host and seven steady states appear; their global stability conditions are summarized in Table 1.

The reaction in the present model was modeled by the classical temporal derivative, and the diffusion was described by the Laplacian operator. Further, the model considered only one arm of adaptive immunity. Therefore, the study of the impact of immunological memory on the dynamics of the PDEs model by means of the new generalized Hattaf fractional (GHF) derivative introduced in [60,61] and the modeling the role of the second arm of adaptive immunity exercised antibodies as in [62] will be the main aims of our future works.