Abstract
Recently, a variety of non-systematic satisfiability studies on Discrete Hopfield Neural Networks have been introduced to overcome a lack of interpretation. Although a flexible structure was established to assist in the generation of a wide range of spatial solutions that converge on global minima, the fundamental problem is that the existing logic completely ignores the probability dataset’s distribution and features, as well as the literal status distribution. Thus, this study considers a new type of non-systematic logic termed S-type Random k Satisfiability, which employs a creative layer of a Discrete Hopfield Neural Network, and which plays a significant role in the identification of the prevailing attribute likelihood of a binomial distribution dataset. The goal of the probability logic phase is to establish the logical structure and assign negative literals based on two given statistical parameters. The performance of the proposed logic structure was investigated using the comparison of a proposed metric to current state-of-the-art logical rules; consequently, was found that the models have a high value in two parameters that efficiently introduce a logical structure in the probability logic phase. Additionally, by implementing a Discrete Hopfield Neural Network, it has been observed that the cost function experiences a reduction. A new form of synaptic weight assessment via statistical methods was applied to investigate the effect of the two proposed parameters in the logic structure. Overall, the investigation demonstrated that controlling the two proposed parameters has a good effect on synaptic weight management and the generation of global minima solutions.
Keywords:
discrete hopfield neural network; non-systematic satisfiability; probability distribution; binomial distribution; statistical learning; optimization problems; travelling salesman problem; evolutionary computation MSC:
37M22; 37M05
1. Introduction
A Discrete Hopfield Neural Network (DHNN) is a significant type of Artificial Neural Network (ANN) that employs a learning model based on association features formulated by Hopfield and Tank [1]. ANNs have long been used as a mathematical method with which to solve a range of issues [2,3,4,5,6,7,8]. DHNN is a recurrent ANN with feedforward connections that comprise interconnected neurons in which every neuron output is fed back into every neuron input. Neurons are stored in either a binary or bipolar form in the input and output neurons of the DHNN structure [9]. Further, to approximate optimization solutions for problems, the structures of DHNN have been extensively modified. This network has many interesting behaviors. Fault tolerance is also a feature of the Content Addressable Memory (CAM) technique, which has an infinite capacity for pattern storage and is useful for its converging iterative process [10]. Numerous applications have made use of DHNNs, including optimization problems [1], clinical diagnosis [11,12,13], the electric power sector [14], the investment sector [15], location detectors [16], and others. Despite the importance of using the intelligent decision systems of the DHNN to solve optimization problems, it is necessary to implement the symbolic rule to guarantee that the DHNN always converges to the ideal solution, because recent studies failed to conduct a thorough analysis of a DHNN based on neural connections. This issue was solved by Wan Abdullah [17], who suggested a logical rule for ANNs by associating each neuron’s connection with a true or plausible interpretation.
The Wan Abdullah approach is a novel approach, and it is interesting to note that the synaptic weight is determined by matching the logic cost function and the Lyapunov energy function. This approach led to better performance than traditional teaching techniques such as Hebbian learning with respect to obtaining the synaptic weight during the training phase. A more specific logical rule has been developed since the logical rule was first introduced in the original DHNN. Sathasivam [18] decided to expand the work of Wan Abdullah and proposed Horn Satisfiability (HORNSAT) as a new Satisfiability (SAT) concept. This study introduced the Sathasivam method of relaxation to improve the finalized state of neurons. This proposal demonstrates the strong capabilities of the HORNSAT in terms of reaching the absolute minimum amount of energy. The outcome demonstrates that logical rules can be included in DHNNs. Nevertheless, because DHNNs relax too quickly and offer fewer possibilities for neurons to interchange information, more local minimum solutions result, which makes it difficult to understand how different logical rules affect DHNNs. This motivated the emergence of a new era of research with different perspectives, beginning with Kasihmuddin et al. [9], who introduced systematic k Satisfiability (kSAT) for k = 2, 2 Satisfiability (2SAT). With each clause containing two literals and all clauses joined by a disjunction, the implementation of 2SAT in a DHNN was reported to achieve a high global minima ratio while keeping computational time to a minimum. Subsequently, Mansor et al. [19] continued the research by proposing a high degree of order of kSAT for k = 3, namely, 3 Satisfiability (3SAT), in a DHNN. With each clause containing three literals and all clauses joined by a disjunction, the proposed 3SAT in a DHNN increases the storage capacity of a network because each neuron’s number of local minimum solutions tends to be low. Despite the success of the implementation of systematic logic in DHNNs, this approach lacks control with respect to distributing the number of negative literals as well as regarding a variety of clauses. Furthermore, as the number of such neurons increases, the efficiency of the training phase in the DHNN decreases. During the testing phase of DHNNs, there is less neuronal variation. Sathasivam et al. [20] clarified that the rigidity of the logical structure contributes to overfitting solutions in DHNNs. When the number of neurons is large, the restricted number of literals per clause results in suboptimal synaptic weight values, thereby decreasing the likelihood of locating diverse global minima solutions. The necessity of variance in the recovered solutions ensures that the search space is well-explored. Further stated by [21], DHNNs are still vulnerable to various challenges, including a lack of generality as a result of non-flexible logical rules and a strict logic structure, despite the fact that the accuracy of research acquired from the real-world dataset has been satisfactory.
Due to the need for a different logical clause set that contributes to the degree of connection between the logical formulae, Sathasivam et al. [20] proposed a non-systematic SAT called Random k Satisfiability (RANkSAT) by using first-order and second-order logic 2SAT in conjunction, where k = 1, 2; Random 2 Satisfiability (RAN2SAT); and all clauses are connected by disjunction. RAN2SAT introduces a flexible logic structure that contributes to the generation of more logical inconsistency, which expands the diversity of synaptic weights. The proposed RAN2SAT in a DHNN achieved about 90% of the global minima ratio with fewer neurons. Due to the necessity of increasing the storage capacity of RAN2SAT and dealing with the absence of interpretation in a typical systematic satisfiability logic and limited k ≤ 2, Karim et al. [22] were inspired to resolve this problem and thus proposed a flexible logic structure that increases storage capacity by incorporating third-order clauses into the formulation. Random 3 Satisfiability (RAN3SAT) suggests three logical (k = 1, 3; k = 2, 3; and k = 1, 2, 3) literal structures per clause, and for all clauses to be joined by a disjunction. This increases the capacity of the DHNN to recover neuronal states based on different logical orders, which can lead to a variety of convergent interpretations of global minimum solutions. Both RANkSAT types experience difficulty regarding the selection system in terms of the composition represented by the first, second, and third logical formulations, which is still poorly defined. Thus, the combination of correct interpretations is restricted to the number of k-order clauses with a predefined term assigned in the logical formula.
Another fascinating study on non-systematic logic with a different perspective was introduced by Alway et al. [23]; this solution increases the representation of 2SAT compared to 3SAT clauses in non-systematic SAT logic through an assigned 2SAT ratio (r*) in DHNN in order to decrease the duplication of final neuron state patterns. The proposed Major 2 Satisfiability (MAJ2SAT) in the DHNN successfully provides more neuronal variation. Zamri et al. [24] introduced Weighted Random k Satisfiability (rSAT) as a non-systematic method with a proposed logical structure that ideally produces the proper rSAT logical structure using a Genetic Algorithm (GA) by taking into account the desired proportion of negative literals (r). Another method introduced by Sidik et al. [25] consisted of altering the rSAT logic phase by adding a binary Artificial Bee Colony algorithm to guarantee that negative literals are distributed properly. The proposed rSAT in a DHNN with a weighted ratio of negative literals leads to a significant global minima ratio. Nonetheless, despite this significant advancement in controlling the logical structure of selecting clauses and using a metaheuristic approach to distribute the number of negative literals, these techniques fail to account for the representation of the probability distribution of the dataset in the selection system.
Unique, flexible logical systems were formed by combining systematic and non-systematic approaches with a unique perspective. This approach leads to a great potential for solution diversity as it randomly generates a number of clauses. Guo et al. [26] proposed Y-Type Random 2 Satisfiability (YRAN2SAT), in which a number is randomly assigned to the first-order and second-order clauses, while further final states can be retrieved by YRAN2SAT in a DHNN with the minimum global energy. With high order logic, Gao et al. [27] proposed a G-Type Random k Satisfiability (GRAN3SAT) system, in which a set of clauses of first, second, and third orders is randomly generated. In a DHNN, GRAN3SAT can exhibit a larger storage capacity and is capable of investigating complex dimensional issues. Despite this success, its system of selection still has a flaw: there is no clear system with which to control a distribution over the desired number of negative literals based on the probability distribution of a dataset.
The Probabilistic Satisfiability problem (PSAT) involves assigning probabilities to a set of propositional formulations and deciding whether this assignment is consistent. The pioneering work was introduced by George Boole [28] as another perspective. He proposed the PSAT to determine if he could discover a probability measure for truth assignments that satisfy all assessments. The PSAT framework was developed to demonstrate these details as logical sentences with linked probabilities to infer the likelihood of a query sentence. The PSAT was initially suggested by George Boole and, subsequently, was refined by Nilsson [29]. This intelligent perspective was followed by different studies [30,31,32,33], which all aimed to integrate the probability tools into satisfiability without considering their implementation in a DHNN. The present study addresses this gap by introducing a probability distribution to the prevailing attribute in the data set, which is represented in a DHNN through desire logic.
There are no studies in this area regarding the way in which the probability distribution for literals with SAT may be represented in a DHNN. Thus, the findings addressing this issue can be used to guarantee the most effective search for satisfying interpretations. Therefore, this study introduces S-type Random k Satisfiability (), where k = 1, 2 () and with the probability distribution of the prevailing attribute in the simulation dataset. It aims to address the problem regarding RANkSAT, where k randomizes structural issues by utilizing two statistical features, the probability distribution and the sample size formula, to obtain an estimator for the binomial distribution dataset. In addition to helping to assign the negative literal that was mapped to the prevailing attribute in a dataset with a non-systematic logical RAN2SAT, the main feature of RAN2SAT is its structural flexibility, which takes advantage of another logical rule, 2SAT, whereas the non-systematic logical rule provides a more diversified solution [34,35]. Furthermore, the probability distribution is used to control the composition’s probability of appearing in first- and second-order logic to avoid a poorly explained or lack of interpretation in non-systematic SAT by providing suitable logical combinations depending on the dataset’s distribution. Moreover, the logic system uses the binomial distribution’s sample size to determine the appropriate number of negative literals based on the predetermined proportion appearing in the dataset. Then, the clauses are distributed in each order depending on the probability distribution governing appearance. This approach will help us determine the appropriate weight of a negative literal number in logic systems based on the distributed clauses in order to create suitable solutions [24]. Notably, researchers tend to neglect negative literals because they are indirectly mapped errors in a logical structure [36]; however, in this study, negative literals represent the prevailing attribute in a binomial distribution that has only two characteristics.
Our proposed logical rule will provide flexibility with respect to controlling the overall structure of in terms of the dataset’s characteristics by combining both the effects of statistical parameters and non-systematic features to identify suitable neuronal variation and diversity in the proposed logic. The main aims of this study are as follows:
- (a)
- To formulate a novel logical rule called S-Type Random k Satisfiability, where k = 1, 2 and statistical tools are integrated to structure first- and second-order logic in order to select the most suitable number of negative literals.
- (b)
- To propose a probability logic phase to determine the probability of the appearance of the number of the first- and second-order literals and the distribution of the desired number of negative literals on every clause by considering the selected dataset.
- (c)
- To implement the proposed S-Type Random 2 Satisfiability as a symbolic structure in the Discrete Hopfield Neural Network by reducing the logical inconsistency of the corresponding zero-cost function’s logical rule, as well as determine the synaptic weight of the DHNN that achieves the cost function equivalent to the satisfied .
- (d)
- To compare the effectiveness of with respect to producing the appropriate logical structure during the probability logic phase before training in the Discrete Hopfield Neural Network by using three proposal metrics in accordance with the existing benchmark works.
- (e)
- To examine the capability of the proposed under the current logical rules with respect to the training and testing phase, demonstrate synaptic weight management, and ascertain the quality of neuronal states’ efficiency in the DHNN via well-known performance metrics.
- (f)
- To investigate the proposed system’s structural behavior during the training phase and thereby demonstrate the flexibility of this logical structure by using a novel form of analysis—synaptic weight analysis—via the mean of the synaptic weights.
The framework of this paper is as follows: The motivation for this study is described in detail in Section 2. An overview of ’s structure is given in Section 3. The integration of into a DHNN is described in Section 4. Section 5 explains the experimental setup and performance assessment metrics incorporated into the simulation. In Section 6, the effectiveness of the proposal logic in a DHNN is discussed and analyzed, with comparisons made to several existing logical structures with regard to various parameters and phases. The conclusions and future work are presented in Section 7 at the end of the article.
2. Motivation
2.1. Issue with the Identified Probability Distribution
With reference to the structural issue regarding existing systematic and non-systematic satisfiability, that is, the systematic logic kSAT [19,37], the relevant approaches in this respect implement random selection for the literal states from within clauses, where the clauses are selected uniformly, without regard to the individual probability or chance of appearing in the required population dataset. Whereas the non-systematic logic RANkSAT [20,22] structure is defined randomly, wherein the clauses are selected uniformly. Moreover, the chance of obtaining both negative and positive literals is uniformly distributed [38], with both outcome having an equally likely chance of appearing. This implies that the population follows a uniform distribution and is thus considered a limited option. In this study, we address this research gap by giving the clauses and negative literals inside clauses the priority of a population dataset’s probability distribution, and when the dataset has two characteristics, i.e., negative and positive literals, we assign the negative literal for the prevailing attribute that is withdrawn from a binomial distribution.
2.2. Initialization for the Number of Clauses and Number of Neuron
The investigation into controlling the general structure of SAT is still ongoing. Cai and Lei’s [39] work proposed a Partial Maximum Satisfiability (PMAXSAT) clausal weighting mechanism, with a positive integer as its weight. This method demonstrated the power of weight in terms of controlling the distribution of a logical structure based on the desired result. Conversely, Always et al. [23] suggested a non-systematic logical rule, MAJ2SAT, which seeks to create bias in the selection of 2SAT over 3SAT via the r* ratio. The MAJ2SAT system successfully provides more neuronal variations that increase the composition of the 2SAT with the same number of neurons. Despite the benefit of extracting information from real datasets that exhibit the behaviors of 2SAT and 3SAT, the persistent issue is the system of selection, which limits the value of r in the set of limited pre-defined intervals and is chosen randomly without considering a dataset’s probability distribution. Therefore, we propose the non-systematic logical rule , which incorporates a probability logic phase to calculate the probability of first- and second-order clauses appearing from the dataset by determining the required number of literal and clauses.
2.3. Initialization for the Number of Negative Literals
The structure of SAT should be subjected to a systematic analysis to avoid the poor description of a dataset. Dubois and Prade [40] examined the role of logic in dealing with uncertainty in an ANN. The work concluded that it was crucial to use the generalization method to determine how many negative literals should be distributed for technical convenience. Zamri et al. [24] introduced rSAT with the (logic phase) as a new phase to produce a non-systematic logical structure based on the ratio of negative literals. The ratio is generated in the logic phase by employing GA to increase the logic phase’s effectiveness. Nevertheless, the findings showed that the proposed model performed well, indicating that having a dynamic distribution of negative literals will benefit the generation of global minimum solutions with different states of the final neurons. One of the limitations of the weighting scheme is the method of choosing the number of negative literals, where the value of r is in the set of limited pre-defined intervals and is subject to the issue of random system selection without considering the probability distribution of literals.
Alway and Zamri’s studies motivated the current study, in which we propose the non-systematic logical rule , which incorporates a probability logic phase to calculate the appearance-related probability distribution in the first-order and second-order clauses from the real dataset by predetermining the required number of neurons or number of clauses via harnessing the behavior of 2SAT so as to explore a wider solution space and extract information from datasets, as well as assign the number of negative literals required for logic by using the sample size formula with a predefined, prevailing attribute proportion from the dataset that will be exposed in the logic.
2.4. Synaptic Weight Performance Using Statistical Analysis
The research on satisfiability in DHNNs suffers from a lack of statistical analysis, especially in terms of synaptic weight, which is considered the backbone for the global minimum solution achieved during testing phases. We determine synaptic weight by contrasting the cost function with Lyapunov energy. The previous studies on systematic and non-systematic approaches were limited in terms of assessing the performance accuracy of the logic in different phases, as mentioned in [9,21,22]. The synaptic weight was analyzed at several points in this study since they were not completely comprehensible in [20,26], wherein the authors describe the dimensions of the synaptic weight values. In addition, [27] measured the accuracy of the error in the synaptic weight by evaluating the differences between the synaptic weight obtained by Wan’s method and the synaptic weight achieved in the training phase. The gap was addressed in this study by using new statistical tests to capture the impact of changing the synaptic weight during training phases due to the absence of statistical tools in the synaptic weight analysis.
3. S-Type Random 2 Satisfiability Logic
S-Type Random 2 Satisfiability () is a new category of non-systematic-clause SAT in which the probability distribution is used to assign prevailing attributes in the dataset via two methods: First, depending on the dataset requirements, we assigned the probability of the appearance of first- and second-order logic. Second, we used the sample size from a binomial population [41] to ascertain the appropriate number of negation literals inside each clause based on its assigned probability since the probability of a negative literal appearing follows a binomial distribution. The novelty of the mentioned methods is that they determine the suitable weight of negative literal numbers () in logic depending on the probability clauses distributed, which will lead to greater structural diversity. In addition, the negative literal number is not fixed, and by increasing or decreasing the probability of obtaining a literal number in the logic system, there is greater flexibility in the dataset.
Our approach can be introduced as a form of non-systematic logic comprising n literals per clauses. It is a general form of RANkSAT logic, where k = 1,2 is expressed in the k Conjunctive Normal Form (kCNF). The components of the S-Type Random 2 Satisfiability Logic problem are as follows:
- (a)
- A set of variables, , where for all items in our logic system;
- (b)
- A set of non-redundant literals , where is the positive () or a negative nature of a literal;
- (c)
- A set of distinguishable clauses, , where every clause is composed of literals joined by ∧ logical (AND) Booleans, which is distributed as follows:
- A set of first-order clauses:
- A set of second-order clauses: where
The general formulation of S-Type Random 2 Satisfiability is given as follows:
where in Equation (1) is for k = 1, 2. The difference between and RAN2SAT lies in the selection system for the number of clauses and the number of negative literals in . This system is established under the condition that the number of clauses corresponds to:
where denotes the total number of literals or total number of clauses ; and denote the number of literals in the first- and second-order clauses or the number of clauses when , respectively; represent clauses for different values of ; and and denote the probability of first- and second-order logic appearing, which is calculated by the Laplace formula [42] to find the probability from population expressed as follows:
represents a number of elements that contain a prevailing attribute from the total number of a dataset in this study. We will denote the probability of second-order by , which is considered as the first parameter in .
The number of negated literals that exist in each will be determined by , where is the negative literal number used to obtain in the dataset [41] and is calculated as follows:
where:
: The pre-defined negative literal proportion required in the logic system (Second parameter in Logic).
: the negative literal proportion in the population (which is available before the survey; if no estimate of is available prior to the survey, a worst-case value of can be used to determine the sample size).
: the margin of error (or the maximum error) of the negative literal proportion, which is calculated as follows:
: the upper point of the normal distribution when , where Significance Level = P (type I error) = .
The distribution of the number of negated literals in each order logic clause is dependent on the value , where:
In (7), and denote first- and second-order logic, respectively, and is the total number of negated literals existing in logic, where:
The structure of is believed to provide more variations and greater diversity of the final neuron states and to be able to find more global solutions in other solution spaces via two effective parameters: and . The implementation of S-type Random k Satisfiability logic in this study is outlined in Figure 1.
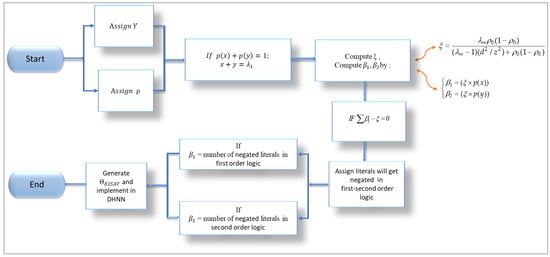
Figure 1.
Block diagram of the proposed S-type Random 2 Satisfiability logic .
Probability Logic Phase in
The probability logic phase was developed to assess the features of a prevailing attribute in the dataset via probability distribution, which are then reflected in the logic system by the two parameters and ; this differs from the logic phase in rSAT [24], where the phase is established to allocate the correct ratio of the negative literals and the position in the rSAT logic via metaheuristics. The main purpose for the probability logic phase is to extract the required information from the dataset, and then generate the correct structure of RAN2SAT logic depending on the dataset features assigned by the two probability Equations (3) and (5). Subsequently, once the desired logic has been attained, the probability logic phase is complete. This section will introduce some logic generated from the dataset using the two parameters and ; the restriction in the probability logic phase is as follows:
whose probability function can be defined as follows (Nilsson 1986) [29]:
According to the applied method for the determination of probability, there are two types of : First, there is the type of probability logic phase that determines the probability of the appearance of the number of first-order logic and second-order logic literals and the distribution of the desired number of negative literals in each clause depending on the selected dataset. Second, there is the type of probability logic phase that determines the probability of the appearance of the number of first-order logic and second-order logic clauses and the distribution of the desired number of negative literals in each clause depending on the selected dataset. Table 1 introduces some possible examples of two cases of the logic of that can be used to generate the dataset using Equations (4), (5) and (7) when .

Table 1.
Possible structures of when .
We observe that applying the same probability to more clauses results in a reduced number of first-order logic items than applying it to a greater number of neurons ; notably, the number of unique logic combinations that a probability logic phase can create by using a specific value of the two parameters and is . Algorithm 1 presents the pseudocode for the steps taken to generate the , which starts with the determination of the value of the two parameters and ; then, by applying the constraint of the logic in Equation (9), the probability logic phases operate under the following conditions: (a) , because we need to expose the prevailing attribute. (b) The z is a random number generated to ensure the negative values will be distributed in the logic phase randomly. (c) The loop will run w times to ensure that the logic system will be correctly generated. (d) The probability logic phase ends when Equation (8) is satisfied, at which point the DHNN training phase begins.
The limitation that we observed in ’s logic structure is the position of negative literals; these are selected randomly depending on random numbers, and this randomization clearly effects results in an inconsistent interpretation. In addition, there are no redundant literals. Also, due to the high probability of 2SAT, the Exhaustive Search (ES) algorithm is unable to find the best number of instances of first-order logic for a small number of clauses that satisfies Equation (9). The utilization of in a DHNN is presented as . In the next section, we clarify how functions as a representational command to control the neurons of the DHNN mappings.
| Algorithm1: Pseudocode for generating the probability of logic phases |
| Input: , , , Set of |
| Output: The best |
| Begin |
| Generate |
| Initialized ; |
| Initialized Proportion ; |
| Initialized Second-order clauses ; |
| Calculate The number of first- and second-order clauses |
| While |
| Do |
| Calculate , by Equation (3); |
| Calculate by Equation (5); |
| Calculate & by Equation (7); |
| End while |
| distributed negative literal in logic |
| While do |
| While do |
| for do |
| Generate random number z; |
| Generate proportion to be initial negative literal ; |
| IF () THEN |
| ; (); |
| ELSE |
| ; |
| End IF |
| End for |
| for do |
| Generate random number z; |
| Generate proportion to be initial negative literal ; |
| IF () THEN |
| -B; (); |
| Else |
| B; |
| End IF |
| End for |
| End While End While |
| End |
| Note: , is a counter. |
4. in Discrete Hopfield Neural Network
A DHNN is a type of free, self-feedback information comprising N interconnected neurons with no hidden layers. The neurons are updated one at a time; Ref. [23] asserts that the possibility of neuronal oscillations is eliminated by asynchronous updating. This network has parallel computing, quick convergence, and is also effective in terms of its CAM capacity, which has encouraged researchers to use DHNNs as mediums for solving challenging optimization problems. A general description of the state of activated neurons in a DHNN is provided below:
where the synaptic weight from unit to unit is . The synaptic weight of a DHNN is always symmetrical, whereby , and has no self-looping, . represents the state of neuron ; is a predetermined threshold value, and in this study, to guarantee a uniform decrease in DHNN energy [18]; and is the number of logic variables. The is implemented in a DHNN according to the following equation (), due to the requirement for a symbolic rule that can control the network’s output and decrease logical inconsistency by minimizing the network’s cost function. To derive the cost function of , the following formula can be used:
where and are the number of clauses. The inconsistency of , denoted as , is specified in Equation (13), as literals are possible in :
where denotes the random literals assigned in . If , which leads to ; this indicates that all clauses in are satisfied with the value of the mean task for the logic program during the training phase (i.e., a consistent interpretation is found). A consistent interpretation will help the logic program to derive the correct synaptic weight of clauses, and the Wan Abdullah (WA) method [17] can be used to directly compare the cost function and Lyapunov energy function of the DHNN to determine the values of . However, it is noted that the DHNN’s synaptic weight can be effectively trained using a traditional approach such as Hebbian learning [1]; nevertheless, Ref. [43] demonstrated that the (WA) method, when compared to Hebbian learning, can achieve the optimal synaptic weight with minimal neuron oscillation. Synaptic weight is a building block (matrix) of CAM. Therefore, a specific output-squashing mechanism will be applied to every neuron in via the Hyperbolic Tangent Activation Function (HTAF) to retrieve the correct logic pattern of the CAM; according to Karim et al. [22], the equation is expressed as follows:
A DHNN’s testing phase allows for the asynchronous updating of the neuronal state based on the following equation:
represents the network’s local field, where is the second-order synaptic weight and is the first-order synaptic weight. By applying the HTAF to the values, the final state of the neurons is retrieved, and the neuron states are updated by:
The information that results in must be present in the neuron’s final state [44], which corresponds to , the Lyapunov energy function [18]:
The convergence of the energy will indicate when the degree of convergence has reached a stable state according to [22]. This is supported by Sathasivam [18], who states that if a DHNN is stable and oscillation-free, the Lyapunov energy will reach its lowest value (the equilibrium state). Hence, [45] a DHNN will always converge to the global minimum energy. One can see the convergence of the final neuron state based on the following Equation:
where , the final neuron state, produces the anticipated global minimum energy and is calculated as follows:
where and denote the number of first- and second-order clauses, respectively. Algorithm 2 is an example of the given in pseudocode, which explains the processes of the training phase and testing phase of . Conventionally, the logic program employs a search space to find consistent interpretations by ES in the training phase.
Figure 2 illustrates the schematic diagram of . Different orders of k = 1, 2 are shown in two different blocks. In the orange block, there are two inputs and an output (I/O) line, which are green and yellow, representing the two types of logic distributed by clauses and neuron, respectively. Inside the orange box, the second-order clauses are depicted, and every line represents the connection of the neuron state via weights. On the right side, the dashed blue line denotes the first-order clause that is present in this phase as well, with two (I/O) lines: green and yellow. On the inside, the line represents the connection of the neuron state via weights. The satisfied clauses from the two boxes will result in ; the figure only represents the satisfied clauses of
| Algorithm2: Pseudocode of |
| Begin |
| Probability logic phase |
| Initialized ; |
| Training phase |
| do According to Equation (12), minimize cost function; |
| Use WA method to calculate Synaptic weight and store it in CAM; |
| According to Equation (19), calculate global minimum energy ; |
| End |
| Testing phase |
| Initialize Random neuron state; |
| do |
| According to Equation (14), calculate the HTAF; |
| According to Equation (15), calculate the local field; |
| According to Equation (16), update neuron state; |
| End |
| According to Equation (17), calculate the final neuron energy; |
| By using Equation (18), confirm global or local minimum energy; |
| Recognize global or local minimum solutions; |
| Global minima solutions |
| Else |
| Local minima solutions |
| End |
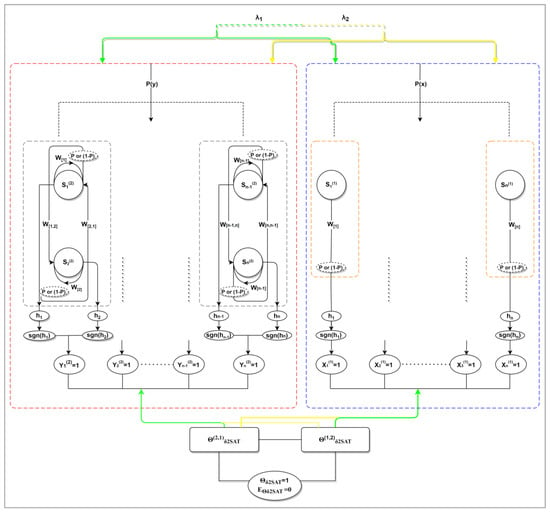
Figure 2.
Schematic diagram of for both types of logic; the total of literal is n for first-second-order logic.
5. Experimental Procedure for Testing
In this section, we explain the proposed logic output and evaluate it using several evaluation metrics at all phases to guarantee the effectiveness of adding statistical parameters in RAN2SAT, which aimed to produce logic. Furthermore, the simulation platform, the assignment of parameters, and the metrics for performance are all explained. All models were used with the ES algorithm, where the algorithm utilizes trial and error to achieve a cost function that is minimized () [23].
5.1. Simulation Platform
All simulations were carried out using an open-source software, visual basic C++ (Version 2022), and a 64-bit Windows 10 operating system. To avoid biases in the interpretation of the results, the simulations were run on a single personal computer equipped with an Intel Core i5 processor. The open-source software R studio was used to perform the statistical analysis. Eight different simulations—depending on the statistical parameters (probability and proportion)—were conducted, including those involving different numbers of clauses and neurons. In addition, different numbers of logic combinations () were tested in this study.
Each simulation’s specifics are as follows:
- (a)
- Various range of parameter . This section assesses and examines the effects of the various probabilities that can be obtained from the dataset applied to . The performance metrics at each phase and the effect of parameter alterations on were determined.
- (b)
- Various proportions of negative literals, . In this section, we evaluate the impact of different proportions of negative literals on , evaluating the performance metrics at each phase and determining the effects of parameter alterations on the proposed logic.
- (c)
- A variety of logic structure analyses. In this section, we compare with a number of well-known logical rules in terms of the diversity-satisfying clauses of the logical rule.
- (d)
- Synaptic weight mean analysis for models’ simulation includes boxplot and whiskers and a probability function curve.
5.2. The Parameter Setting in Probability Logic Phase
The proposed model incorporates a probability logic phase. As we previously mentioned, there are two types of depending on the probability that is applied to the number of neurons or the number of clauses. Numerous types of simulations are conducted to examine the impacts of different probabilities and several types of expected negative literal proportions on the dataset, in which the probability logic phase is dependent upon the dataset. The different probability logic phase will be denoted as , where (1 refers to the probability with respect to the number of neurons and 2 refers to the probability of the number of clauses), and refers to the negative literal proportion; the overall model can be denoted as . Another type of logic is possible if the range of the probability parameter with respect to the number of neurons or clauses stated in the simulation step generates only one type of neuron or clause state, and this will yield a systematic 2SAT during initialization, which is not covered in this study; alternatively, the first-order logic clauses will correspond to more than second-order logic. When this occurs, the proposed system’s structural benefit cannot be seen because only one specific type of solution can be found in the final neuron state. In order to prevent these two types of logic, it is proposed that , wherein more features of second-order as opposed to first-order logic are implemented in the DHNN. In parallel, to determine the range proportion, we proposed to determine the correct number of negative literals that represent the prevailing attribute in the dataset, and we also considered since there is no available information prior to the survey; the symbols of the stages are presented in Table 2.

Table 2.
Parameter list for probability logic phases.
5.3. Parameter Setup of
All simulations were run with 100 logical combinations (). This method aids the DHNN model’s analysis and the approximate evaluation of the efficacy of the proposed logic in a DHNN with various distributions of the two parameters and . The number of total literals in the logic system is represented by the number of neurons () in the DHNN. We chose a specific number of neurons: . For the DHNN, we apply a relaxation procedure in accordance with [18]. We select R = 3 in this context because a further reduction in the potential neuron oscillation has been observed, and a value of R greater than 4 will yield the same outcome as [27]. Table 3 summarizes the establishment of all the parameters necessary for . In addition, it is notable that each has a neuron combination that is equivalent to the other DHNN logic systems, which eliminates the issue of a small sample size.

Table 3.
List of parameters for .
5.4. Performance Metrics
The objective of each phase includes the evaluation of the performance of the proposed model. Therefore, this study will utilize several performance metrics to assess the efficacy of each simulation in the different phases with respect to the model to verify the effectiveness of the proposed logic system in terms of the probability logic, learning, and testing analysis phases.
5.4.1. Assessment Logic Structure
The probability logic phase is the phase in which the correct logic sequence is generated and that controls the number of clauses and negative literals by solving Equations (3), (5) and (7). We attempt to evaluate the features of the output logic by comparing it with other models to guarantee well-produced logic in terms of clauses and negative numbers, which will the acquirement of the minimum cost function given in Equation (12). To determine the appropriate synaptic weight based on the main objective of this phase, we express three features: (a) the number of negative literals affected by parameter , (b) the weights of the second-order logic clauses affected by parameter , and (c) the full-negativity second-order logic clauses affected by the two parameters and . The goal is to compare these features to determine whether the probability logic phase will be successful in achieving the desired logic system by changing this parameter and demonstrating its excellence with respect to expressing the logic features. The parameter controls the proportion of negative literals; hence, in this section, we test the effectiveness of this parameter based on several different aspects, which are provided below.
The proportion of negativity: in the probability logic phase, the optimal value of negative literals in the logic system will be assigned , which is a constant ratio that is dependent on , and the probability of negative literals in the logic system will be computed using the following equation:
Probability Of total Negativity (PON):
Equation (20) is derived from a Laplace formula [42]; we need to test whether the change in will affect the probability of a negative literal structure occurring in the two types of logic compared to other forms of logic that introduce random proportions of negative literals in the logic structure. When compared to other types of logic, this matrix’s scale, if corresponding to the necessary proportion, gives us the correct negative literal probability in the logic structure. While analyzing the deviation of the negative literal in terms of the whole logic system, we introduce a second measure to determine the state of the negative literals in the whole logic system, as shown below:
Negativity Absolute Error (NAE):
The proposed NAE scale measures the amount of error that is not negative if it fits the desired proportion in Equation (5). The optimal NAE is zero, which is equivalent to the required number of negative literals.
The probability of the full negativity of second-order logic: Full negativity second-order logic helps us to represent a greater number of the attributes in the final solution. The main objective of the is to control the number of negative literals and second-order logical items in the logic structure. We need to expose the features of second-order logic as mentioned previously to fully enjoy the benefits of 2SAT in terms of our proposed logic system. Therefore, the next measure is presented as follows:
Full-Negativity Absolute Error second clauses (FNAE):
where is the number of full negativity second-order clauses and is the number of second-order clauses in a specific string of logic. The accuracy of the logic will be measured by the FNAE scale in terms of generating the full-negative second-order clauses, which are expressed as , from the rest of the second-order clauses, that is, , , and . Similarly, using this scale, we will address the effectiveness degree of the two factor parameters and with respect to their significance in terms of altering the second-order clauses. We can determine if the required logic can represent the prevailing attributes by the properties of this measure. The optimal best of FNAE scale is zero, which is equivalent to the required number fully negative second-order clauses.
To address the effect of a parameter in the second-order weight, we propose the weighted error measure, which gives the accuracy of the changing of the effect of in both proposed logic types when compared to other logic systems, as follows:
Weight Full-Negativity Absolute Error (WFNAE):
where is the mean number of second-order clauses, and is the weight of second-order clauses, which equals because the Laplace formula determines an equally likely probability for all the elements. Using this measure, we can determine the effect of on the amount of deviation of the full negative clauses from the mean. We can calculate the real weight for this deviation by multiplying it with the weighted . A large scale signifies a high degree of representation in terms of the weight of the negative strings, which greatly improves our understanding of the weight of dominating attribute in logic. By comparing the scale to the other reasoning and assigning weight to that prioritized (completely negative sentences), the deviance is biased towards. Table 4 lists the symbols that we require during this phase.

Table 4.
List of parameters used in experimental setup.
5.4.2. Assessment during the Training Phase
In the training phase, we achieved satisfying assignments of the clauses, which generated the optimal synaptic weights in terms of by minimizing Equation (12). The Root-Mean-Square Error (RMSE) has been used as a basic statistical metric for measuring the quality of a model’s prediction in many fields [24], and it is utilized to identify the quality of the training phase, wherein the value of RMSE training (RMSEtrain) signifies the root square of the error between the neurons’ desired fitness value generated and their current fitness [22]. The RMSEtrain formula is:
The optimal value of the RMSE in the DHNN model is achieved when it is zero, which means the WA method derived the correct synaptic weight. Furthermore, a good model is achieved when the measure is between 0–60. Whereas the Root-Mean-Square Error in synaptic weight (RMSEweight) used will be assessed based on the following formula
where denotes the Expected synaptic weight obtained by the WA method, and is the actual synaptic weight obtained in the testing phases; this measure gives us a complete understanding of the error produced by the WA method, wherein the best result is 0, which corresponds to Equation (12).
5.4.3. Assessment for Testing Phase
In the event that the suggested network satisfies the requirement in Equation (18), the proposed will act in conformance with the embedded logical rule during the testing phase. The final neuron state will enter a state of minimum energy, which corresponds to the cost function of the proposed logical rule. Therefore, based on the synaptic weight generated in the training phase, we evaluate the quality of the retrieved final neuron states (global), namely, the minima solutions. Thus, we apply the next measure as follows: Global minima ratio ()—the goal of the global minima ratio is to assess the retrieval efficiency of the . The formula of the is:
where is the number of global minimum solutions that satisfy condition (18) after being distributed in Equation (19), is the number of trials in the training phase, and is the logical combination for each run. This metric was frequently used in articles such as [21,38] to assess the proposed ’s convergence property.
The second measure in the testing phase is the Root-Mean-Square Error energy (RMSEenergy) [22], which is used to evaluate the minimization of energy achieved by . The energy profile can be determined using RMSEenergy:
We use RMSEenergy to analyze the converge of to determine the actual energy difference between the absolute minimum energy and the final minimum energy .
5.4.4. Similarity Index
The similarity index [38] and cumulative neuronal variation [24] can be used to evaluate SAT performance using a DHNN. The similarity index values will be compared with benchmark neuron states to determine the quality of each optimal final neuron state that achieved global lowest energy, as indicated in the following formula:
where 1 denotes a positive literal of , and −1 denotes a negative literal of in each clause. It should be noted that the benchmark neuron states are the DHNN model’s ideal neuron states that satisfy the conditions in Equation (18). The retrieved final neuron states are compared to the benchmark neuron states indicated in Table 5 to provide a comprehensive comparison of the benchmark neuron states and final neuron states.

Table 5.
Variables’ similarity index specifications.
The overall comparison of the benchmark and final neuron states is conducted as follows [9]:
According to Case 1 in given in the examples in Table 1, the final neuron states are generalizable, as follows:
In this study, we selected a well-known measure with which to determine the similarity index for diverse perspectives, namely, that developed by Sokal and Michener (Sokal) [46], which will be employed to evaluate the viability of the recovered final neuron states. It should be noted that Sokal measures the similarity of negative cases of with over a range of (0, 1). The formulation is as follows:
The Ratio of Cumulative Neuronal variation () is used because the testing phase uses the DHNN’s ability to directly memorize the final neuron states ratio without the need to create a new state. This is expressed as follows:
where denotes the points scores used to assess the difference between newly recovered final neuron states and the benchmark neuron states. The symbol that we require for this Testing and Training phase is shown in Table 4.
5.5. Comparison of Method and Baseline Models
Since this study focuses on investigating performance with respect to its logical behavior, we need to investigate the ’s performance in terms of and with regard to constructing a good logical structure in the probability logic phase. Therefore, we compare with the existing logic systems in DHNNs based on the logic structures, testing phases, and the quality of the solution to examine two behaviors relating to logic:
- (a)
- The effects of controlling a number of clauses on the second-order weight and non-systematic logic structure.
- (b)
- The capability of to control the negative literals and accurately reflect the behavior of the dataset.
In order to examine the logic in a DHNN after its implementation, we also compare its final neuron state’s quality to that of RAN2SAT. We also evaluate the variation introduced by the testing phase, global minima solutions, and variation of neurons. The most recent logic systems with a 2SAT structure were selected for this reason, and one of their features was the decision to compare the logic systems’ structures. Each clause contains two literals and all clauses are joined by a disjunction.
- (a)
- 2SAT [37]: This is a systematic logical rule that was implemented into a DHNN, with each clause containing two literals. It is a special type of logic of general Boolean satisfiability. Each phrase in the 2SAT model can withstand no more than one suboptimal neuron update, leaving it more akin to a two-dimensional decision-making system. When included into logic mining, this logic system has demonstrated good applicability in task classification. Neuron counts varied from .
- (b)
- MAJ2SAT [23]: The initial focus of the effort was on developing the current non-systematic SAT logic structure. MAJ2SAT suggests structural modifications when considering unbalanced clauses. The unbalanced feature result from different compositions of 2SAT and 3SAT. As a result, MAJ2SAT prefers a greater number of 2SAT clauses. Moreover, to avoid any bases, we limited the number of neurons ranging from .
- (c)
- RAN2SAT [20]: This system is a second-order and first-order clause logical rule that was implemented in a DHNN as an initial form of non-systematic logic. The has no structural differences compared to RAN2SAT but consists of a logic probability phase. Due to the connection of the first-order clause, RAN2SAT is reported to provide a greater variety in terms of synaptic weight. Although each literal state was chosen at random, the number of clauses in each order can be determined in advance. Specifically, the number of neurons ranged from .
- (d)
- RAN3SAT [22]: This work expanded on the previous work by [20], incorporating higher-order logic of 3SAT clauses in a non-systematic SAT structure, which improved the lack of interpretability of the current non-systematic SAT by storing more neurons per clause. Although the number of clauses for each sequence was selected at random, each literal state was defined. In this case, again, we restricted the number of neurons; the range was .
- (e)
- YRAN2SAT [26]: This system is known as the Y-Type Random 2-Satisfiability logical rule. YRAN2SAT’s novelty is introduced by randomly generating first- and second-order clauses. It is a combination of systematic and non-systematic logic. YRAN2SAT can explore the search area with a high potential for solution diversity by adding the features of both clauses. YRAN2SAT introduces remarkable logical flexibility, while the number of all clauses is predefined by the user and the literal states are defined at random. The range of the number of neurons is .
- (f)
- rSAT [24]: This is a new, non-systematic satisfiability logic class, known as Weighted Random k Satisfiability for k = 1, 2, which includes a weighted ratio of negative literals and adds a new logic phase to produce a non-systematic logical structure based on the number of negative literals specified. More diverse final neuron states were obtained by integrating rSAT into a DHNN. The proposed model showed outstanding promise as an advanced logic-mining model that can be used further in the forecasting and prediction of real-world problems. In this study, we select (r = 0.5) because it has been discovered that it performs well in the logic phase of the rSAT [24]. The range of the number of neurons was .
5.6. Benchmark Dataset
In this study, the proposed model generated bipolar interpretations randomly from a simulated dataset. More specifically, the logical illustration that was used in the simulations will serve as the foundation for the structure of the simulated data. The simulated dataset is commonly used in the modeling and evaluation of the efficacy of SAT logic programming, as demonstrated in the work of [18,22,27].
5.7. Statistical Test
This section provides a brief definition of the statistical measures that will be used in this study for two purposes (description and testing):
- (a)
- The measure of central tendency is defined as “the statistical measure that designates a single value as being indicative of a whole distribution” [47]. Therefore, we selected two measures: (a) The average, which is known as the arithmetic mean (or, simply, “Mean”). It is calculated by adding all of the values in the dataset and dividing them by the number of observations. One of the most significant measures is the central tendency measure. The mean has the disadvantage of being sensitive to extreme values/outliers, especially when the sample size is small. As a result, it is ineffective as a measure of central tendency for a skewed distribution [48]. Its formula is expressed as follows:
- (b)
- The measure of dispersion: Variability measures inform us about the distribution of the data and allow us to compare the dispersion of two or more sets of data. We can determine whether the data are stretched or compressed using dispersion metrics, namely, the Standard Deviation (SD), which evaluates variability by considering the distance between each score and the distribution’s mean as a reference point. It is a variance square root and gives an indication of the standard deviation or average separation from the mean. It is presented as follows:
- (c)
- The boxplot and whiskers (measure of position): The boxplot (Tukey1977) [50] is a well-known tool for displaying significant distributional features of a dataset. The classical box-plot displays the quartiles , and whiskers, where the median is equal , which is used to estimate the 25th () and 75th () quantiles, thus providing an estimate of the interquartile range The range of the majority of the data (the whisker’s length) ends at those values just inside the whisker’s “limits” (referred to as “fences” and defined by and , lower (LF) and upper (UF) respectively. Observations outside the whiskers (the outliers), observations beyond the fences [51], plotted individually, are defined as the data points outside the boundaries. When comparing different datasets, the boxplot is particularly helpful. Instead of using a Table of Values, we can quickly compare all reported statistics across numerous datasets. The simple, effective design of the boxplot aids the comparison of summary statistics (location, spread, and range of the data in the sample or batch).
- (d)
- The Laplace Principle of Probability states that in a space of elementary events , where each element has the same chance of appearing, the probability of a compound event, A, is equal to the ratio of outcomes that are favorable to the occurrence of all other outcomes. This is demonstrated by the formula in Equation (4):
- (e)
- The probability density function curve is a schematic illustration of the probability of random variable density function that is given by:
- (f)
- The Wilcoxon signed-rank test: The Wilcoxon signed-rank test was introduced for the first time by Frank Wilcoxon in 1945 [52]. It is a one-sample location problem-based nonparametric test that is used to test the null hypothesis wherein the median of a distribution equals some value () for data that are skewed or otherwise (i.e., do not follow a normal distribution). It can be used instead of a one-sample t-test or paired t-test, or for ordered categorical data with a normal distribution. If (p-value ≤ ), the null hypothesis is rejected; this is strong evidence that the null hypothesis is invalid, i.e., the result of the median is significant. The Formula for the Wilcoxon Rank Sum Test () for independent random variable is:

Table 6.
Parameters List for .
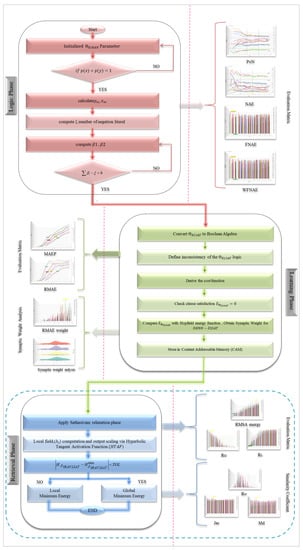
Figure 3.
Flowchart of and Experimental evaluation.
6. Results and Discussion
In this section, we describe the suggested logical output and evaluate it using a variety of evaluation metrics throughout all three phases to ensure that the addition of statistical tools to the RAN2SAT structure and the produced logic was effective. Furthermore, the simulation platform, assigned parameters, and the metrics’ performance are discussed in this section. It is important to note that we have not considered any optimization during the probability logic phase, as in Zamri et al.’s [24] work; the training phase, as proposed in [21,38]; or the testing phase, as proposed in [9,53].
6.1. Logic Structure Capability
The probability phases give us different models in terms of negative literals and second-order logic with respect to the two parameters and . Since both parameters fall within the [0,1] interval, we can generate an endless (infinite) number of 2SAT models using both parameters. For the majority of the representations of 2SAT, we chose to use () more frequently than so that the results would be in the range (0.6–0.9). In this study, we chose values of greater than 0.5 in the range (0.6–0.9) of the probability logic phases to obtain a greater representation of the negative numbers in order to study the predominating attributes in the dataset, as we previously mentioned.
We selected the most significant differences from the two intervals and designated them as models, which are illustrated in Table 7, in order to examine the efficacy of the two parameters with different numbers of , where so at improve the benefits compared with other recently developed produced logic systems. Subsequently, we will test two types with different numbers of , , and ; these values are selected considering the significant change in probability and negative literals. Notably, values of will be disregarded because we do not need all literals to be negative because the structure will not represent the Binomial distribution dataset. Moreover, the will give one satisfied interpretation of a first-order clause [54]; on the other hand, will give us second-order logic. It is important to emphasize that we do not consider a systematic logical system in this study. Table 7 shows the names of two types for different possible models depending on the two parameters and , as well as other logic symbols.

Table 7.
The logical symbols in the experiment.
The negativity representation: The PON measure in the different logic models has been tested by Equation (20). The PON represents the probability of the appearance of a negative literal in the entire logic system in all combinations with different . It is necessary to control the negative literals in order to determine the prevailing attributes in the dataset, as negative literals will ensure more negativity in the final neurons; then, we can ensure that the attribute will appear in the solution space by helping the DHNN find the optimal solution [24].
The Figure 4, a line representation, shows different layers of logic in different proportions for both types of . At the same time, for other groups, for rSAT logic, and random for other logic systems (YRAN2SAT, MAJ2SAT, RAN3SAT, 2SAT, and RAN2SAT). The reason why this is in the minimum levels of the proposed logic for the is because, as was already noted, the probability of receiving a negative literal for the SAT is incredibly low. The highest two layers were recorded as and in both types of , respectively. By applying Equation (5), we obtain the best number of negative literals for all , which is similar to the third layer for the other two groups, where and were the lowest probabilities in both types of , which, by the change in the proportional parameter , indicates the success in terms of producing the desired number of negative literals in the logic system, representing the predominate attributes in our dataset. Additionally, there was a direct correlation between the number of neurons in each class of the desired proportion and the proportions where a high PON recorded low probability when the number corresponded to . When the number is less than 17 and after 31 for , the PON becomes approximately stable. This is because the in Equation (6) in the sample size equation always selects the optimal sample that reflects the number of negative literals, even if the number of neurons is low. Table 8 provides detailed information on the PON in each proportion group for the two types of logic. Note that group () recorded the maximum PON and highest mean value of the PON with low in both types of ; the small indicates a different number of neurons , and this provides the nearest value of the PON means, and that result is highly similar within each group for all models and increases in accordance with the increasing in the models for both types, namely, and . the small indicate, with different number of neuron , it provides the nearest value of PON mean’s, and that result is highly similar within each group for all models and increases in accordance with the increasing in models for both types, namely, , . However, we can also note that the PON mean of the other logic systems is closest, indicating that the minimal PON value was recorded in YRANSAT with a minimum mean of 0.4966 and a low SD() = (0.015), which indicates that it was also the lowest for different numbers of neurons, but we can also notice that the PON mean of other logic systems is closest, showing low values for different numbers of neurons that were less than or equal to 0.5. The PON results prove the flexibility of ’s structure in terms of controlling the literals’ states.
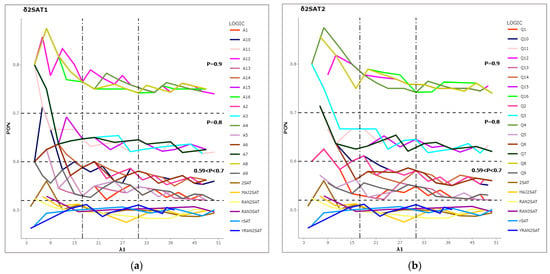
Figure 4.
PON line representation for models in both types of logic (a) , (b) , and recently developed logic systems.

Table 8.
PNO results for models with both types of logic, and , and recently developed logic systems’ details determined by Wilcoxon test for median divided by value.
The accuracy of the models is evaluated by the NAE measure in Equation (21) in terms of the amount of error that is non-negative or the quantity of the negative literal status for the entire logic system in each proportion group for both types of models. According to Figure 5, in the line representation, note that the effect of the proportional changes in the logic restructure guarantees that the best RAN2SAT is required, or effective of the prevailing attribute in the dataset where different proportions give us different layers. The details of Figure 5 can be found in Table 9, which shows the minimum values of the NAE that were recorded in a group where A4 in was recorded as the lowest error by (0.1429). It should be observed that the median value (0.3090) was the lowest possible value, indicating that the A4 for all n neurons of always had a lesser error in the middle sections. Additionally, it should be noted that all models in the same group, A16, A12, and A8, have very similar median values (0.333, 0.31, and 0.320), which is because, as shown in the PON, this group has the highest probability for the representation of a negative literal, which is accomplished by the proportion . Similarly, in , Q4 recorded the lowest error as 0.1429, but the least median was recorded by Q16 (0.13125), which means the minimum error lies in the middle values with respect to the number of neurons . Moreover, it can be noted from Figure 5 that for a small number of neurons , Q4 has fewer NAE values than Q8, Q12, and Q16. However, the reverse is true for the middle values of Q16 compared to Q12, Q8, and Q4, as mentioned before regarding the effect of in . However, in Table 9 the value of the median has very small differences from the model in group . As discussed in terms of the PON, this indicates the successfulness of the proportion of representation in the logic system. The highest NAE value was observed to be for rSAT with a high median, where r = 0.5 with the nearest value of NAE for the other logic systems (YRAN2SAT, MAJ2SAT, RAN3SAT, 2SAT, and RAN2SAT); as previously mentioned, there was a lack of representation of the negative literals in the logic system, as they recorded the least degree of the probability of the appearance of negative literals.
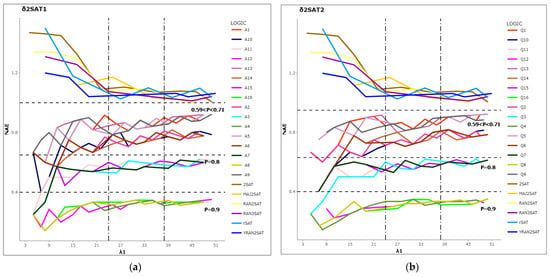
Figure 5.
NAE line representation for models in both types of logic (a) , (b) , and recently developed logic systems.

Table 9.
Maximum and minimum NAE results for models with both types of logic , , and recently developed logic systems with details determined by Wilcoxon test for median divided by value.
The probability of full negativity of second-order logic: We examined the ability of several models incorporating the two types of to produce full-negativity second-order clauses with greater accuracy compared to other recently developed logic systems by manipulating two parameters, and , using the FNAE measure for the second-order clause in Equation (22). Obtaining full negativity second-order logic guarantees that the prevailing attribute in the desired logic structure is represented. Figure 6, a columnar representation, shows the result of the FNAE measure, the higher accuracy achieved by A8 and A4 in , and Q4 in that obtained a value of (0) for FNAE. This is due to the effect of the two parameters in this model, for which the proportion of negative number is , with a lower probability than other models in second-order logic where , which means that all second-order clauses are satisfied by negative numbers because of the small representation of second-order clauses. Based on the same figure, the low accuracy obtained by A1 and Q1, which obtain the maximum number in terms of the FNAE logic (0.8930, 0.8650), is the reason for the low representation of the negative proportion in the logic system. Thus, if we need greater representation of the prevailing attributes in the desired logic structure, we should choose the A8 and A16 from and Q4 from . Model A4 recorded higher accuracy using the lowest value of the FNAE median (0.3995), which means the minimum error lies is in the middle values for all neuron quantities . We also note the proportion of negative literals is , which means there are more second-order negative clauses in the models in recorded in model Q12, where the lowest FNAE median was (0.4147). The accurate results regarding the FNAE measure are listed in Table 10. It is evident that the ratios of the negative literals are and , indicating that the model has a higher fraction of negative, second-order representations. Comparing these results to those of other state-of-the-art logic systems, all of them provide low accuracy due to a higher median value, which indicates that the mean lacks the ability to accurately represent the full-negative second-order values in this model. RAN2SAT performs the best among the logic systems. The latest logic systems give higher errors because the fluctuation in predetermine for assigning second-order logic and low represent for negative literal that indicate the and is flexible more than the recent logic systems in controlling of two parameters.
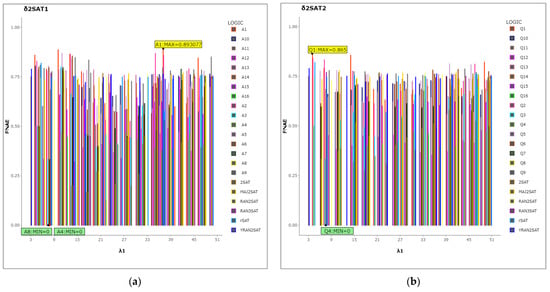
Figure 6.
FNAE column representation for models in both types of logic (a) , (b) , and recently developed logic systems.

Table 10.
Maximum and minimum FNAE results for models in both types of logic , , and recently developed logic systems with details determined by Wilcoxon test for median.
A high result in the WFNAE measure in Equation (23) indicates that full-negative second-order logic is more greatly represented. By using this scale, the weight of the sentences in the logic has been evaluated, and the parameter may be used to determine whether the model is desirable because the highest probability gives the highest weight. The maximum probability, as shown in Figure 7, is the highest weight represented and is obtained by A16, Q16 in , and , respectively, and 0 for YRANSAT, because it also produces first-order logic. In Table 11, note the highest significant median value was achieved by the A16 and Q16 models (0.4477 and 0.4691, respectively), and the lowest significant median value was achieved by the YRANSAT (0) WFNAE value. This would ensure that the prevailing attribute has the highest representation in our logic compared to other state-of-the-art logic systems, in addition to its ability to minimize and maximize changes in . In conclusion, it is evident that the two parameters, and , have a direct impact on the probability distribution dataset in the logic structure.
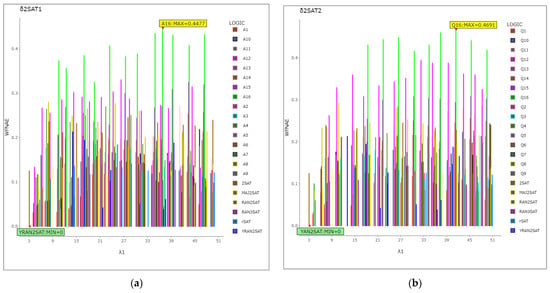
Figure 7.
WFNA column representation for models in both types of logic (a) , (b) and recently developed logic systems.

Table 11.
Maximum and minimum WFNAE results for models in both types of logic , and recently developed logic systems with details determined by Wilcoxon test for median.
6.2. Training Phase Capability
This phase’s objective is to evaluate the efficiency of various structures produced in the probability logic phase, which were trained in a DHNN and minimize the logical inconsistencies using Equation (12), to obtain the correct synaptic weight. In this phase, ES obtained consistent interpretations for and derived the correct synaptic weight for the logic system. If the model arrived at an inconsistent interpretation (), the model will reset the whole search space and generate a new one until . The error of the maximum fitness of logic, which is represented by the total clause from the achieved fitness, is calculated by employing RMSEtrain and RMSEweight to quantify the error in the training phase via Equations (24) and (25), respectively. Figure 8 and Figure 9 show different RMSEtrain, and RMSEweight results for both types of , when (); for both types of , RMSEtrain was described to undergo an exponential increase (logistic growth) with a rate of growth equal to and a linear positive increase in RMSEweight. According to [26], the error value in the training phase starts off low when the learning set is small because it is more difficult to fit the larger learning set. In this instance, as rises, more iterations are required for the DHNN to locate SAT structures with satisfying interpretations, and the training phase metrics obtain 0 value when is small. When the value of is high, there is always low error because the structure of second-order logic helps ES by becoming satisfied () to a greater extent than first-order logic and because the probability of finding a consistent interpretation for each clause follows a binomial distribution, which measures the effect of flexible structure by changing in two parameters and in terms of the RMSEtrain and RMSEweight results [24]. As shown in Figure 8 and Figure 9, high probability of obtaining second-order makes it easier to locate optimal interpretations [22], which means the WA method will derive the correct synaptic weight. On the other hand, when decreases, it signifies that the probability of the first-order clauses being satisfied is very low for 2SAT. Due to its limited number of interpretations, the non-systematic logical rule with first-order clauses reduces the cost function of the logic.
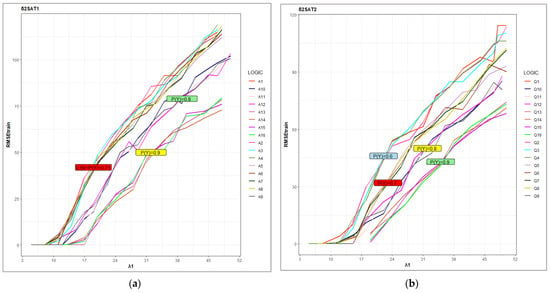
Figure 8.
RMSEtrain line representation for models in both types of logic (a) , (b) .
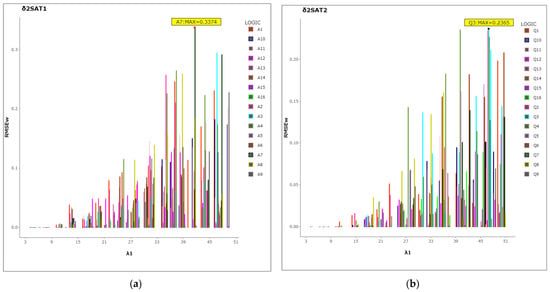
Figure 9.
RMSEweight column representation for models in both types of logic (a) ,(b) .
Table 12 records the values in Figure 8; in the line representation, it is noted for large RMSEtrain reported for A4 (118.895) that follows group , have the smallest number for 2SAT at the same time, the result of the RMSEtrain median gives us the more significant result reported by group , whereas A8(68.5274) has a large RMSEtrain value without any effect by outlier for all ; thus, when decreases, the ES could not find a consistent interpretation for first-order logic. The low RMSEtrain median go for group were A14 (38.16665), which also indicates a large number of 2SAT that make it simpler for ES to achieve consistent interpretation. For a large error was reported for the group in Q1(114.342) because of a small number of 2SAT. For the median result, we note that Q3(64.7599) reported a high RMSEtrain in the same group, and group reported a lower value with respect to Q16 (41.0488), which indicates it has the same behavior for ; it is worth noting here that large and have large fitness errors. It is clear in Q(4,8,12,16) that when in both measures, that means it is difficult for ES to become satisfied for negative literals, because the extreme value for negative literal makes it difficult to achieve optimal fitness, as mentioned in [24]. Due to the limited room for searching, it is challenging for ES to be applied to large in small . Finally, the mechanism of ES in the training phase of DHNN is only effective when is small and effected by a high number of neurons because of the non-randomized operator [24]. The training phase can be improved further by embedding a learning algorithm in a DHNN and using global and local search operators [26]. This approach may aid in the search for optimal interpretations and ensures that logical inconsistencies are minimized.

Table 12.
Maximum and minimum RMSEtrain results for models in both type of logic , details by Wilcoxon test for median.
From Figure 9, column representation, the RMSEweight for two types models help to better understand the fitness of the neuron state. Based on the results, the value of 0 was obtained in different quantities of in the interval [5,18] in different models in both types of ; then, the values started to fluctuate at large —the maximum RMSEweight values were reported for A7 and Q3, where the values of the negative literals were large () and where was large. In Table 13, which corresponds Figure 9, it is reported that the maximum RMSEweight values in terms of the median are A1(0.0791) and Q10(0.0548), wherein the is small. In addition, a small result was reported for A16 (0.0075) and Q14(0.0048), where the negative numbers are large, which is clearly the result of the RMSEweight being affected by the fitness clauses that were measured by RMSEtrain, because the ES is could not find the interpretation for a clause with a high value of then the DHNN could not derive the correct synaptic weight by WA methods when the result was more than zero. The fluctuation in the result is because the DHNN is selected the random number for weight if after the number of iterations reaches the maximum. In conclusion, it is evident that two parameters, and , have a direct impact on the probability distribution dataset during the testing phases.

Table 13.
Maximum and minimum RMSEweight results for models in both types of logic , and details by Wilcoxon test for median.
6.3. Testing Phase Capability
Optimal testing phase is achieved when retrieved optimal synaptic weight, after completing checking clause satisfaction and generating optimal synaptic weight through the WA method. The final state of the neuron will converge towards the global minimum energy. It is important to evaluate testing phase because DHNN frequently produces similar final neuron states as opposed to novel final neuron states [55]. Therefore, we compare the logic with the recent logic systems by global minima ratio matric. If the model is unable to reach a global solution, this indicates that it is trapped in a local solution, which makes it impossible to determine whether the proposed is satisfied or not.
Figure 10, column representation, shows the global minima ratio results, calculated by Equation (26) for two types and state-of-the-art logic systems, without considering any optimizer, to assess the actual testing phase capability for of . Where the optimal result for global minima ratio is 1, we can note in Figure 10 that all are capable of retrieving the optimal synaptic weight values in small and then it decreases linearity with large , because the ES is unable to manage synaptic weight in the training phase and will be susceptible to retrieving non-optimal neuron states and ensnared in local minima. A model’s ability to achieve maximum global minima ratio demonstrates that the suggested SAT is effectively integrated into DHNN. Maximum global minima ratio reported for YRAN2SAT, rSAT, and (A1, A11, Q11) models in . The reason for YRAN2SAT recorded the high global minima ratio for small [26] because the flexibility in the structure offers an accurate result. Table 14 gives the Figure 10 numerical result, from the median results without effect from the outliers, note both type achieve near result to other latest logic systems. High median goes for MAJ2SAT because the structure of logic that (2SAT,3SAT) [23], also the fare literals state represent in rSAT [24] make it achieved highly . Based on Table 14, from median, there is a high effect for two parameters and in , small in the DHNN for small and can retrieval the right synaptic weight such as (A1,Q1), but from median, the high and achieved more global minimum than other such as A(13,14,15), Q(9,10,13,14). It can say the proposed models showcased the efficiency of to control DHNN as a symbolic structure that causes network convergence. Since the local field in Equation (15) drives the neuron’s final state in accordance with the behavior of the second and first-order clause, it exhibits the same behavior as the non-systematic RAN2SAT structure presented by [20].
Figure 10.
Column representation for models in both types of logic (a) , (b) and recently developed logic systems.

Table 14.
Maximum results for models in both type of logic , and RAN2SAT details by Wilcoxon test for median.
The purpose of finding the RMSEenergy in Equation (27) is to calculate the difference between the final energy and the absolute minimum energy, as stated in condition Equation (18). indicates whether or not the solutions produced by are optimal, it must assess the flexibility of by determining the value of RMSEenergy. Based on Figure 11 column representation, was reported to small achieve less RMAEenergy value for all models, which indicates a successful convergence towards the optimal final neuron state, after which the final energy difference fluctuates as the number of increased. This phenomenon occurs as a result of the decreased probability of receiving cost function , as clear in RMSEtrain which leads to higher energy, and ’s ineffective learning strategy. As the number of increases, some synaptic weights become suboptimal, resulting in final neuron states stuck in local minimum energy. Additionally, Sathasivam [18] claims that during the DHNN testing phase, suboptimal neuron updates are what caused the local minimum energy to exist. Suboptimal neuron updates in this situation will result in more incomplete sentences, which raises the energy gap. When the logical formulation containing 2SAT was incorporated into we said the behaved like the traditional non-systematic logical rule RAN2SAT. As shown in Figure 11 it can be observed that the adverse impact of negative literal with high number of in logic where A4 Q12 recorded the highest value of RMSEenergy and A1 Q1 when number of small is the opposite, from Table 15 gives from the Figure 11 the median of RMSEenergy gives us the accurate result where the small median go for A13, Q9 with low value parameter and A8, A16 with high value parameter give high RMSEenergy error. This demonstrates that when most neuron states are negative, tend to converge towards local minimum energy. In conclusion, it is evident that two parameters, and , have a direct impact on the probability distribution dataset during the testing phases.
Figure 11.
RMSEenergy column representation for models in both types of logic (a) , (b) .

Table 15.
Maximum and minimum RMSEenergy results for models in both type of logic , details by Wilcoxon test for median.
6.4. Similarity Index Analysis
For final neurons’ quality states only compare both type of with RAN2SAT because consider the enhancement and developing for RAN2SAT, also, they have the same structure behavior, we tested the variation introduced by the testing phase for models and final neurons’ quality state compared with RAN2SAT, where the degree of state redundancy for the DHNN model training phases is indicated by the similarity index of the final neuron state. A standard has been introduced indexing metrics, which is Sokal index, and consider the effective metric known as the ratio of total neurons variation .
Firstly, consider the lower Sokal in Equation (30) in the similarity index matrices indicates that the final neuron states obtained are highly distinct to the benchmark states. According to Figure 12, a column representation to both types of reported low values, which imply higher more variety solution than other recorded by A16, Q16m but Q1, A5 recorded high value, due to parameter . Table 16 translates Figure 12, which clarifies numerically, where the A16, Q16 reported low median value. Where all logic has the and record low value, it indicates that there is more negative neuron and less first-order logic provides the final neuron state and the benchmark state distinction as shown in blue numbers in Table 16, Q, A (4,8,12,16). In other words, the low negativity and greater representation for first-order logic give us a high Sokal, as shown in Q, A (1,5,9,13) with a red number.
Figure 12.
Sokal column representation for models in both types of logic (a) , (b) and RAN2SAT.

Table 16.
Maximum and minimum Sokal results for models in both types of logic , and RAN2SAT details by Wilcoxon test for median.
Secondly, the effective parameter known as the ratio total variation of neurons In Equation (31). From the Figure 13 its clearly a column representation to both types giving us different number of variation solution for different number of because of the effect of two parameter and in the training phase. The highly oscillation recorded for in and for models and the highest oscillation value is recorded for A16 in . For . The highly oscillation recorded in for models and the highest oscillation value is traced for Q15 in . At the same time both type of models affected by a number of neurons, they start the ups and downs in different according to the effect of two parameter and . The total oscillation for some of models is rich to zero when , such as A (1,3,4,5,8,10,12) and so low for others models , also Q1,Q4 when , for , we can be said there are no significant variations for high than 37, also we can note here the effect of , it can’t achieve the global solution for low because the ES will disturb the model in order to reach the optimal training phase (known as learn inconsistent interpretation), from Figure 10, global solutions acquired by models grow as decrease as introduce previously. Table 17 for numerical result for Figure 13 note the effect of increase where the logic has recorded the highest high number of , where the highest variation go for A16 (0.2149) and Q15 (0.2084), and also can see the record high than in general, the reason her the give less number of first-order logic than for the same that was mention previously in Table 1, then the ES will deal with fewer numbers for first-order logic where it difficult to reach the optimal training phase. Moreover, Figure 13 presents the reason for the decrease when increases the hard achieved global solution. It was observed that the RAN2SAT behave similarly to the , with a high recorded of (0.1764) at the same time as its increase in the interval and then decrease with a high . The impact of the global minimum solution is related to the number of neurons. As rises, the probability of the number of global solutions reduces. We can conclude from the above results that is related to the occurrence of other neuron states that lead to global minimum solutions in other domain adaptations [22].
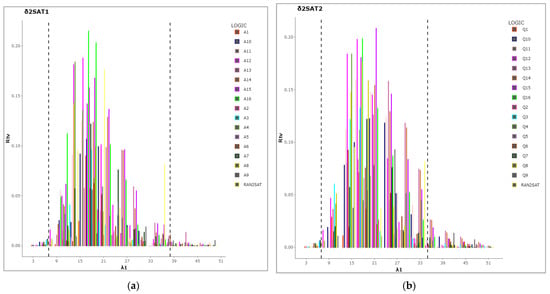
Figure 13.
Column representation for models in both types of logic (a) , (b) and RAN2SAT.

Table 17.
Maximum and minimum results for models in both types of logic , and RAN2SAT.
6.5. Synaptic Weight Analysis
The mean is important because it signifies the location of the dataset’s centre value, it contains information from each observation in a dataset. When a dataset is skewed or contains outliers, the mean may be untrue. We are utilizing various statistical tests to aid us comprehend the behaviors of synaptic weight to deduce information about the performance of logic in the training phases for further inquiry in synaptic weight distribution. The descriptive statistic of mean synaptic weight is a novel perspective in synaptic weight analysis, and we consider the mean of full logic to obtain a meaningful result in this analysis of our study by using the following formula:
where synaptic weight for first-order logic, synaptic weight for second-order logic literals, synaptic weight for second-order logic clauses. An example of the formula is shown as follows:
The center value located in a dataset is carries a piece of information from every observation in a dataset; accordingly the mean will give the information of the center value for all synaptic weight in logic, where they affect together in cos function on training phases, in this study the mean for 100 combinations been calculated in training phase as sampling size for each logic in both type of , so we have 100 individual results for the means that have the same characteristic in two parameters and . It is worth noting that all means’ values were tested first using appropriate tests that yielded significant p-values to ensure a correct outcome. The logic value signifies that features will be statistically defined by the curve of probability density function , representing points and (boxplot and whiskers), denoted as (Raincloud Plot), and we want to achieve the following by using these figures:
- (a)
- The probability density function the curve will give an accurate result data behaviors (symmetric or skewness) so that we can determine if there is an outlier or if all value is distributed normality in the and logic (a normal bell curve indicating there is no outlier, and this logic has a high probability of achieving satisfaction in terms of and ).
- (b)
- The representing points the spread of mean values, while the boxplot and whiskers explain the amount of spread around the median, along with the details of an outlier from the median value given by whiskers sides.
This investigation will look at the impact of mean value analysis in evaluating the during the training phase. We consider the highest in each logic systems combination to calculate the mean, so we have between 48,50 to obtain more accurate results. In the training phase, the synaptic mean value was determined using the ES effect to uncover inconsistent interpretations that offer us a basic understanding about the behavior of logic and achieving satisfied. There are 4 figures for both types of , each figure includes a probability density function curve, the representing point, and (boxplot and whiskers), its classification depending on the values in both types of , where they have the same structure because it is the key affected parameter in the mean values discussed as follows: For both and :
- (a)
- When noted the following from Figure 14:
 Figure 14. The Raincloud Plot analysis for (a) , (b) synaptic weight means when .
Figure 14. The Raincloud Plot analysis for (a) , (b) synaptic weight means when .
probability function curve shows thin-tailed on two sides, so it is fairly to be a symmetric ship, which indicates that outliers are infrequent (an observation is considered an outlier if it differs numerically from the rest of the data), and the values for the mean tend to be normal for A (1,2,3,4), whereas the probability function curve Q3,4 are similar in behavior for . It is fairly to a symmetric ship, so it has thin tailed on two sides and rare outliers, but Q1,2 shows different results because it tends to be non-symmetric by the heavier tail on the left which means that there are a lot of outliers. This result will be supported by the boxplot and whiskers. When we look at interquartile ranges, IQR (the lengths of the boxes), the longer it is, the more dispersed the data are, and the shorter it is, the less dispersed the data are. It can be observed that the is highly dispersed from the median compared to since the IQR range is higher in A (1,2,3,4) than Q (1,2,3,4). In addition, in terms of outlier, when checking a box plot, an outlier is defined as a data point that lies outside the box plot’s whiskers, the and have the approximate behavior of a huge outlier, but it can be noted that the has more outlier than because ES could not achieve inconsistent interpretation in the training phase due to the models structure that leads to a random value for synaptic weight. Finally, the boxplot clearly shows that the distribution is nonsymmetric for and , as previously explained (the distribution is symmetric when the median is in the center of the box and the whiskers are nearly the same on both sides of the box), in both logic systems. The reasons for these results are:
In terms of parameter, the number of first-order logic that has a in logic value that pulls the logic curve to the sides because the suboptimal synaptic weight for first-order logic is clearly in the distribution tail and box-whiskers plot also has more 2SAT than for the same parameter, and that reflects in the spread of value in the boxplot, which is high in . This indicates a high variation between the mean values ES failed to find a consistent interpretation. In terms of parameter, from the boxplot also, we can observe that the effect of gives more negative synaptic weight, but we should also consider the value of WBB that was positive in clauses , and that affected 2SAT clauses mean values, because it is noted in there is no effect for , as mentioned previously, it has more 2SAT clauses than for the same . Therefore, the ES tend to obtain consistent interpretation that is reflected in the mean values of whole synaptic weight logic. Conversely, for the effect of is clearer in the mean values, with most points of the values located on the negative side.
- (b)
- When noted the following from Figure 15 as follows:
 Figure 15. The Raincloud Plot analysis for (a) , (b) synaptic weight means when .
Figure 15. The Raincloud Plot analysis for (a) , (b) synaptic weight means when .
The probability function curve for exhibits the same behavior for , indicating that it is a symmetric ship with normal mean values. It has a thin tailed on two sides, so outliers are infrequent. For it is a little different, all Q (5,6,7,8) is symmetric. Then, the mean values tend to be normal and have a light tail, except for Q6, as we see in the curve, it is a fat tail, therefore there are a lot of outliers on both sides. The boxplot and whiskers tell the same story for . When we look at the box side, we can see that the is highly dispersed from the median compared than the because the value of IQR is higher in A (4,5,6,7) than the Q (4,5,6,7). Moreover, in terms of an outlier, we can observe that the and both have the approximate behavior of a huge outlier, but the is more outlier than except for Q6. Most logic has an outlier and, at the same time, is a short box (which implies that high-frequency data tends to be more fat-tailed). Finally, from the boxplot, the non-symmetric shape in both for and can be seen clearly. The reasons for these results are justified as follows:
In terms of parameter, the number of second-order logic clauses that have a is considered a bit high, especially in high which generates that pulls the logic curve to the two sides because the suboptimal synaptic weight is clearly in the tail of probability curve distribution and boxplot-whiskers. For , it has more 2SAT clauses than , for the same parameter. This reflects in the spread of value in the boxplot at its highest more than in . Therefore, it shows a high variation between mean values because ES failed to find consistent interpretations. In terms of parameter, boxplot in and are reflected in a negative synaptic weight value. Both models have the parameter of , the spread of data affected by in 2SAT clauses and it affects the value of the mean which tends to be positive, as we mentioned previously. Finally, as seen in the Q6, the reasons for right fat-tailed the number of high second-order logic sentences that generate suboptimal synaptic weight, resulting in positive mean values.
- (c)
- When is observed from Figure 16 as follows:
 Figure 16. The Raincloud Plot analysis for (a) , (b) synaptic weight means when.
Figure 16. The Raincloud Plot analysis for (a) , (b) synaptic weight means when.
Where the 2SAT clauses are the common clauses, for the curve shows semi normal ship in A (9.11,12) with a semi skewed in A10, the light tail on the two sides with less outlier is in all . On the other side, gives near result where Q (10,12) is fairly to be symmetric ship, the mean values tend to be normal, it has a thin-tailed in two sides, Q (9.11) tend to be non-symmetric, the light tail in the two sides with less outlier is on all The boxplot and whiskers for and , is highly sparse from the median comparison because the IQR range is higher in A (9,10,11,12) than Q (9,11,12), and shorter in Q10. In the terms outlier, from a box plot whiskers, the and have approximate behavior of huge outliers on both sides, but we can note the Q11 is more outlier on the left than others and Q9 is more outlier on the right. Finally, based on the boxplot, it clarifies both logic systems have non symmetric curves. The reasons for these results are justified as follows:
In terms of parameter, the number of first-order logic clauses that have a small appearance probability that makes the range values of mean is high in the two previous Figure 14 and Figure 15. It is clear here in these figures the obtaining (0.5) synaptic weight is small, so most of the means value range is small that led to less spread curve line, on the other side, the high representation of 2SAT clauses makes the length of the box highest because the volatile in the mean values of 2SAT clauses it gives a different result depending on negative literal, where , and have the mean values different from the effect also by ES algorithm searching and that effect in cost function in Equation (12), that pull the logic curve and boxplot-whiskers into sides, that reflects in the spread of values in boxplot its highest than in . In terms of parameter, its high effect here, in boxplot in and is clearly in the range of values, most of it full in the negative side, more clearly in Q, A( 11,12) because the mean values of full negative second-order logic clauses it is highest here as we clarify in FNAE matric. It is also noted for Q (9,10), A10 is in the positive side because the is small therefore, the mean will be positive and ES algorithm searching tend to find inconsistent interpretation. This indicates the effect of the parameter but A9 still has first-order logic, which makes the data spread in two sides with light tail. However, in Q10 and Q12, the tail because the extreme mean values that come from full negative clauses and first-order logic clauses.
- (d)
- When is observed from Figure 17 as follows:
 Figure 17. The Raincloud Plot analysis for (a) , (b) synaptic weight means when .
Figure 17. The Raincloud Plot analysis for (a) , (b) synaptic weight means when .
The probability function curve indicates that it is reasonable to be a symmetric shape in A(15,16), but A14 tends to be non-symmetric, with a thin tail in two sides, implying that outliers are infrequent. Whereas A13 is left–right skewed and heavy-tailed, which implies that there a lot of outliers on the left, but in , Q (13,14,16) is symmetrical. While Q15 tends to be non-symmetric, they have a thin tailed on two sides, implying that outliers are infrequent. Moreover, Q14 is heavily tailed which indicates there is a lot of outliers, but Q13, 16 have light tails and outliers are infrequent. When we look at interquartile ranges, we can observe that , A (15,16) is considerably distributed from the median compared to A (13,14) because the IQR range is similarly high in . Meanwhile, Q (13,15,16) is highly dispersed from the median compared to Q (14) because the IQR range is highest in terms of an outlier. When reviewing box whiskers, the and have the approximate behavior of a huge outlier however, we can note that Q, A (13,14,) is more outlier than Q, A (15,16). Finally, from the boxplot, it is clearly the non-symmetric for and as we previously mentioned. The reasons for these results are justified as follows:
In terms of parameter, the number of second-order logic clauses that have the smallest appearance, so the mean values are high, is clear in the , figures. Moreover, the majority of 2SAT clauses representing, make the spread in all length box highest in , because of the volatility in the mean of 2SAT clauses, as mentioned previously. This effect in the logic curve and pulling the logic curve into the two sides also for boxplot-whiskers, which reflect in the dispersion of value in boxplot is more than . In terms of the parameter, it has a high effect as well, in the boxplot in and , it is clearly in the range of value, most of it fails in the negative side also more clearly in Q, A (15,16) because the mean of full negative second-order logic clauses is highest here. As we explain in the FNAE metric, for other logic A, Q (14, 13) still has more first-order logic, which causes the mean spread in two directions and a heavy tail in Q14 and A13 due to the extrema value that occurs due to the full negative clauses and second-order logic clauses.
From this result, we can note the significance of the synaptic weight analysis; it gives a summary of the search space area for a specific algorithm in training phases, and it is clarified by the mean synaptic weight results, which give the center of search space (optimal) and the wide by the range of spread (suboptimal) from the previous result the mean synaptic weight gives a general perspective for the mechanism of ES algorithm in this search space. Thus, we can observe the behavior of working in this limited space, as well as the behaviors of obtaining a solution using optimal and suboptimal synaptic weights. The ES has a unique search space that is heavily influenced by the number of neurons and the structure of logic.
6.6. The Limitation of the DHNN-δ2SAT
One of the limitations of in this study is that the proposed hybrid network DHNN only considers propositional logic programming. The DHNN is unable to embed other variant of logic, such as predicate logic, fuzzy logic, or probabilistic logic due to the nature of Hopfield Neural Network proposed by Pinkas [56] that are limited to symmetric connectionist network, as well as the DHNN’s low storage capacity and the cost function proposed by Wan Abdullah (1992), which only considers bipolar neurons. Conversely, this study takes a number of neurons limits is less than 52 because of ES. Consequently, as we improve, will replace ES by metaheuristics such as Artificial Bee Colony Algorithm [57] and Election Algorithm [58]. Despite DHNN flexibility, ’s the quality of solutions offered needed to be improved. We can increase the iterations numbers required in our simulations by increasing the number of learning. The proposed model may yield more variation neurons, less errors, and a global minimum solution with more iterations.
6.7. Summary
In this section, we provide a brief summary of the beneficial properties of the logical structure of the proposed model; moreover, we provide a simple summary of the most important accomplishments of the proposed logic system, clarifying the findings given in the Results and Discussion section with respect to the following points:
- (a)
- Probability logic phases were applied to introduce various models to address dataset-related requirements. Notably, one of the most significant advantages of is that it can generate multifarious models by controlling parameters that are revealed from the dataset features in the logic system. It is a flexible logic system, but this is not discussed in this study. The parameters can be used to generate models of logic that can be systematic when , transforming to 2SAT and when , it becomes first-order logic or it can be high-order non-systematic when k = 3, and it can be SRAN3SAT for order k = 1, 2, 3 or k = 2, 3 or k = 1, 3 by adding a new parameter . In this case, regarding the probability of third clauses, we consider the probability concept , when and , it becomes 3SAT. The main differences between and other logic systems such as YRAN2SAT, RAN3SAT, and RAN2SAT, as well as other systematic logic systems such as 2SAT and 3SAT, are the factors of probability, wherein the dataset will choose the best structure by controlling the probability parameter; in addition, the terms of negative literals determined from the dataset and distributed in clauses depend on the probability parameter, whose two main features render the unique.
- (b)
- The testing and the training phases were examined. By applying Equations (24) and (25) in the testing phase, the results show that the proposed model obtained optimal synaptic weight after checking the clauses’ satisfaction. It also generated optimal synaptic weight through the WA method for the small number of neurons and high parameter values. Equations (26) and (27) in the training phase showed that the efficiency of the probability logic phase produced various logical structures in the DHNN compared to the current systems.
- (c)
- A novel analysis of the synaptic weight for was introduced, which was termed the descriptive statistic of mean synaptic weight. Previously, there have been various statistical tests used to study the behaviors of synaptic weight to deduce information about the performance of a proposed logic system in the training phases. Whereas, in this study, the descriptive statistical method analyzed the synaptic weight distribution by obtaining the mean of the synaptic weight in the testing phase.
- (d)
- Notably, in the Results and Discussion section, the sample size in Equation (5) gives us the best number of negative literals for the desired logic needed to obtain satisfaction. Of particular significance are the models and , which have a high proportion () and high probability () introduced by probability logic phases, have the best structure as clarified by the measures used in the study (PON, NAE, and FNAE), and tended to be the best models in the training and testing phases, which are also shown by the similarity index measures. This result is the opposite of that obtained by Zamri et al. [24], which concluded a value of r = 0.5 for negative literal works efficiently in the logic phase and yielded a better structure than (r = 0.1, 0.9). The reason behind these contrary findings is that the proportion is dependent on the value in Equation (6), which gives a margin of error dependent on the value; additionally, there is the probability of second-order logic drawn from the dataset, which affected the models—all these factors rendered it the best in terms of logic structure.
- (e)
- In this study, the probability distribution from the contributed data set successfully generated an efficient, new logical structure for a DHNN. The discussion section considered the introduction of the comparative analysis of the with other existing SATs, for which the proposed model was superior in several aspects, as shown in Table 18.
 Table 18. A summary of comparative analysis between and other SATs.
Table 18. A summary of comparative analysis between and other SATs.
7. Conclusions and Future Work
It is critical to create a non-systematic logical framework in a DHNN, employing parameters conducive to building a flexible final neuronal state. This study introduced a new probability logic phase that assigns the probability of the first- and second-order clauses and the desired negative literals appearing in each sentence, which helped to address the requirements of datasets. Statistical tools govern the creation of during the probability logic phase. The novel logic probability phase of the proposed model provides a new enhancement with which to shape the logic structure according to the dataset, for which it was found that these models have high values in two parameters () of two types, which introduced efficient logic structures in the probability logic phase. The new logic was embedded in the by reducing the logical inconsistency of the corresponding zero-cost function’s logical rule. The achieved cost function that corresponds to satisfaction was used to calculate the synaptic weight of the DHNN’s effectiveness with a logical structure, which was examined using three proposal metrics in comparison with state-of-the-art methods, such as 2SAT, MAJ2SAT, RAN2SAT, RAN3SAT, YRAN2SAT, and rSAT. The final neuron state was assessed based on various initial neuron states, statical method parameters, and various metric performances, such as learning errors, synaptic weight errors, energy profiles, testing errors, and similarity metrics, which were compared with existing benchmark works. To further demonstrate the efficiency and robustness of the proposed , it was validated using four different second-order probability distributions with four different proportions of extensive simulations. Further, a new prospective logical investigation was introduced in this study, which consisted of the analysis of the mean of synaptic weight for to evaluate the existence of a flexible logical structure. The findings demonstrated that the proposed was successful in achieving a flexible logical structure with a prevailing attribute dataset compared to other state-of-the-art SAT. For future work: (1) A metaheuristic analysis of the probability logic phase would aid the selection of the negative literals’ positions in a logic system. (2) A metaheuristic analysis of the training phases would aid the satisfaction of Equation (12). (3) A metaheuristic analysis of the testing phases would aid the generation of a vast range of space solutions. (4) Synaptic weight analysis can be applied in the training phases to address the effects of the energy function and global solutions on the synaptic weight. Moreover, we can add the measure of variability to address the deviation in the results. Notably, the robust architecture of ANNs integrated with our proposed logic would serve as a good foundation for real-life applications such as Natural Disaster prediction. In this context, each neuron would represent the attributes from the data, such as rainfall trends, river levels, and drainage and ground conditions. These attributes will be embedded into the logic-mining approach proposed by [45], which will lead to the formation of induced logic, which, in turn, has predictive and classificatory abilities. In other developments, the proposed logic system would be indispensable in finding the optimal route in the Travelling Salesman Problem.
Author Contributions
Conceptualization, methodology, software, writing—original draft preparation, S.A.; formal analysis, validation, N.E.Z.; supervision and funding acquisition, M.S.M.K.; writing—review and editing, G.M.; visualization, N.A.; project administration, M.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Ministry of Higher Education Malaysia for Transdisciplinary Research Grant Scheme (TRGS) with Project Code: TRGS/1/2022/USM/02/3/3.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to express special thanks to all researchers in the Artificial Intelligence Research Development Group (AIRDG) for their continued support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Notation | Explanation |
| AI | Artificial Intelligence |
| DHNN | Discrete Hopfield Neural Network |
| ANN | Artificial Neural Network |
| CAM | Content addressable memory |
| SAT | Satisfiability |
| HORNSAT | Horn Satisfiability |
| 2SAT | 2 Satisfiability |
| 3SAT | 3 Satisfiability |
| RAN2SAT | Random 2 Satisfiability |
| RAN3SAT | Random 3 Satisfiability |
| MAJ2SAT | Major 2 Satisfiability |
| YRAN2SAT | Y-Type Random 2 Satisfiability |
| GRAN3SAT | G-Type Random k Satisfiability |
| PSAT | Probabilistic Satisfiability Problem |
| rSAT | Weighted Random k Satisfiability |
| PMAXSAT | partial maximum satisfiability |
| GA | Genetic Algorithm |
| ES | Exhaustive Search |
| HTAF | Hyperbolic Tangent Activation Function |
| WA | Wan Abdullah method |
| CNF | Conjunctive Normal Form |
| RMSE | Root-Mean-Square Error |
| PON | Probability of total negative |
| NAE | Negativity Absolut Error |
| FNAE | Full negativity Absolut Error second clauses |
| WFNAE | Weight Full negativity Absolut Error |
| pre-defined proportion range | |
| negative literal proportion | |
| Significance Level | |
| the upper α/2 point of the normal distribution | |
| Number of learning in probability logic phases | |
| literal | |
| First-order clause | |
| Second order clause | |
| Probability second-order logic range | |
| Number of literals/neurons | |
| Total clauses | |
| Number of the second-order clauses | |
| Number of the first-order logic clauses | |
| General formula of | |
| Synaptic weight between i and j | |
| Synaptic weight of neuron i | |
| Maximum fitness | |
| Current fitness | |
| Expected Synaptic weight that obtained by Wan method | |
| Actual synaptic weight | |
| The Total of negative literal in logic | |
| The probability of obtaining second-order clauses | |
| The number full negativity second-order clauses | |
| The number of second-order | |
| The mean number of second-order clauses | |
| Minimum energy value | |
| Final energy | |
| Ratio of global minimum solutions | |
| Number of global minimum solutions | |
| Neuron state | |
| Benchmark neuron state | |
| Sokal and Michener Index | |
| The Ratio of cumulative neuronal variation | |
| local field | |
| , | Counter |
| Number of Learning | |
| Number of neuron combination | |
| Number of Trials | |
| Tolerance value | |
| R | Relaxation rate |
| Learning iteration | |
| Threshold constraint of DHNN | |
| The cost function of the DHNN-YRAN2SAT | |
| The arithmetic mean | |
| The median | |
| Standard deviation | |
| First quartile | |
| Second quartile | |
| Third quartile | |
| Interquartile range | |
| LF | Lower fences |
| UF | Upper fences |
| Probability density function for random variables | |
| Smallest of absolute values of the sum of in Wilcoxon test | |
| Wilcoxon test value (sum of smallest and biggest of absolute values of the sum ) |
References
- Hopfield, J.J.; Tank, D.W. “Neural” computation of decisions in optimization problems. Biol. Cybern. 1985, 52, 141–152. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef] [PubMed]
- Egrioglu, E.; Baş, E.; Chen, M.-Y. Recurrent Dendritic Neuron Model Artificial Neural Network for Time Series Forecasting. Inf. Sci. 2022, 607, 572–584. [Google Scholar] [CrossRef]
- Gonzalez-Fernandez, I.; Iglesias-Otero, M.; Esteki, M.; Moldes, O.; Mejuto, J.; Simal-Gandara, J. A critical review on the use of artificial neural networks in olive oil production, characterization and authentication. Crit. Rev. Food Sci. Nutr. 2019, 59, 1913–1926. [Google Scholar] [CrossRef]
- Juan, N.P.; Valdecantos, V.N. Review of the application of Artificial Neural Networks in ocean engineering. Ocean Eng. 2022, 259, 111947. [Google Scholar] [CrossRef]
- Liao, Z.; Wang, B.; Xia, X.; Hannam, P.M. Environmental emergency decision support system based on Artificial Neural Network. Saf. Sci. 2012, 50, 150–163. [Google Scholar] [CrossRef]
- Shafiq, A.; Çolak, A.B.; Sindhu, T.N.; Lone, S.A.; Alsubie, A.; Jarad, F. Comparative Study of Artificial Neural Network versus Parametric Method in COVID-19 data Analysis. Results Phys. 2022, 38, 105613. [Google Scholar] [CrossRef]
- Tran, L.; Bonti, A.; Chi, L.; Abdelrazek, M.; Chen, Y.-P.P. Advanced calibration of mortality prediction on cardiovascular disease using feature-based artificial neural network. Expert Syst. Appl. 2022, 203, 117393. [Google Scholar] [CrossRef]
- Mohd Kasihmuddin, M.S.; Mansor, M.; Md Basir, M.F.; Sathasivam, S. Discrete mutation Hopfield neural network in propositional satisfiability. Mathematics 2019, 7, 1133. [Google Scholar] [CrossRef]
- Gosti, G.; Folli, V.; Leonetti, M.; Ruocco, G. Beyond the maximum storage capacity limit in Hopfield recurrent neural networks. Entropy 2019, 21, 726. [Google Scholar] [CrossRef] [PubMed]
- Hemanth, D.J.; Anitha, J.; Son, L.H.; Mittal, M. Diabetic retinopathy diagnosis from retinal images using modified hopfield neural network. J. Med. Syst. 2018, 42, 1–6. [Google Scholar] [CrossRef]
- Channa, A.; Ifrim, R.-C.; Popescu, D.; Popescu, N. A-WEAR bracelet for detection of hand tremor and bradykinesia in Parkinson’s patients. Sensors 2021, 21, 981. [Google Scholar] [CrossRef] [PubMed]
- Channa, A.; Popescu, N.; Ciobanu, V. Wearable solutions for patients with Parkinson’s disease and neurocognitive disorder: A systematic review. Sensors 2020, 20, 2713. [Google Scholar] [CrossRef] [PubMed]
- Veerasamy, V.; Wahab, N.I.A.; Ramachandran, R.; Madasamy, B.; Mansoor, M.; Othman, M.L.; Hizam, H. A novel rk4-hopfield neural network for power flow analysis of power system. Appl. Soft Comput. 2020, 93, 106346. [Google Scholar] [CrossRef]
- Chen, H.; Lian, Q. Poverty/investment slow distribution effect analysis based on Hopfield neural network. Future Gener. Comput. Syst. 2021, 122, 63–68. [Google Scholar] [CrossRef]
- Dang, X.; Tang, X.; Hao, Z.; Ren, J. Discrete Hopfield neural network based indoor Wi-Fi localization using CSI. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Abdullah, W.A.T.W. Logic programming on a neural network. Int. J. Intell. Syst. 1992, 7, 513–519. [Google Scholar] [CrossRef]
- Sathasivam, S. Upgrading logic programming in Hopfield network. Sains Malays. 2010, 39, 115–118. [Google Scholar]
- Mansor, M.; Kasihmuddin, M.; Sathasivam, S. Artificial Immune System Paradigm in the Hopfield Network for 3-Satisfiability Problem. Pertanika J. Sci. Technol. 2017, 25, 1173–1188. [Google Scholar]
- Sathasivam, S.; Mansor, M.A.; Ismail, A.I.M.; Jamaludin, S.Z.M.; Kasihmuddin, M.S.M.; Mamat, M. Novel Random k Satisfiability for k ≤ 2 in Hopfield Neural Network. Sains Malays. 2020, 49, 2847–2857. [Google Scholar] [CrossRef]
- Bazuhair, M.M.; Jamaludin, S.Z.M.; Zamri, N.E.; Kasihmuddin, M.S.M.; Mansor, M.; Alway, A.; Karim, S.A. Novel Hopfield Neural Network Model with Election Algorithm for Random 3 Satisfiability. Processes 2021, 9, 1292. [Google Scholar] [CrossRef]
- Karim, S.A.; Zamri, N.E.; Alway, A.; Kasihmuddin, M.S.M.; Ismail, A.I.M.; Mansor, M.A.; Hassan, N.F.A. Random satisfiability: A higher-order logical approach in discrete Hopfield Neural Network. IEEE Access 2021, 9, 50831–50845. [Google Scholar] [CrossRef]
- Alway, A.; Zamri, N.E.; Karim, S.A.; Mansor, M.A.; Mohd Kasihmuddin, M.S.; Mohammed Bazuhair, M. Major 2 satisfiability logic in discrete Hopfield neural network. Int. J. Comput. Math. 2022, 99, 924–948. [Google Scholar] [CrossRef]
- Zamri, N.E.; Azhar, S.A.; Mansor, M.A.; Alway, A.; Kasihmuddin, M.S.M. Weighted Random k Satisfiability for k = 1, 2 (r2SAT) in Discrete Hopfield Neural Network. Appl. Soft Comput. 2022, 126, 109312. [Google Scholar] [CrossRef]
- Muhammad Sidik, S.S.; Zamri, N.E.; Mohd Kasihmuddin, M.S.; Wahab, H.A.; Guo, Y.; Mansor, M.A. Non-Systematic Weighted Satisfiability in Discrete Hopfield Neural Network Using Binary Artificial Bee Colony Optimization. Mathematics 2022, 10, 1129. [Google Scholar] [CrossRef]
- Guo, Y.; Kasihmuddin, M.S.M.; Gao, Y.; Mansor, M.A.; Wahab, H.A.; Zamri, N.E.; Chen, J. YRAN2SAT: A novel flexible random satisfiability logical rule in discrete hopfield neural network. Adv. Eng. Softw. 2022, 171, 103169. [Google Scholar] [CrossRef]
- Gao, Y.; Guo, Y.; Romli, N.A.; Kasihmuddin, M.S.M.; Chen, W.; Mansor, M.A.; Chen, J. GRAN3SAT: Creating Flexible Higher-Order Logic Satisfiability in the Discrete Hopfield Neural Network. Mathematics 2022, 10, 1899. [Google Scholar] [CrossRef]
- Boole, G. The Laws of Thought (1854). Walt. Mabe. 1911, 2, 450–461. [Google Scholar]
- Nilsson, N.J. Probabilistic logic. Artif. Intell. 1986, 28, 71–87. [Google Scholar] [CrossRef]
- Andersen, K.A.; Pretolani, D. Easy cases of probabilistic satisfiability. Ann. Math. Artif. Intell. 2001, 33, 69–91. [Google Scholar] [CrossRef]
- Caleiro, C.; Casal, F.; Mordido, A. Generalized probabilistic satisfiability. Electron. Notes Theor. Comput. Sci. 2017, 332, 39–56. [Google Scholar] [CrossRef]
- Semenov, A.; Pavlenko, A.; Chivilikhin, D.; Kochemazov, S. On Probabilistic Generalization of Backdoors in Boolean Satisfiability. In Proceedings of the Thirty-Sixth AAAI Conference on Artificial Intelligence (AAAI-22), Virtual, 22 February–1 March 2022. [Google Scholar]
- Fu, H.; Liu, J.; Wu, G.; Xu, Y.; Sutcliffe, G. Improving probability selection based weights for satisfiability problems. Knowl.-Based Syst. 2022, 245, 108572. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, D. Properties of the satisfiability threshold of the strictly d-regular random (3, 2s)-SAT problem. Front. Comput. Sci. 2020, 14, 1–14. [Google Scholar] [CrossRef]
- Schawe, H.; Bleim, R.; Hartmann, A.K. Phase transitions of the typical algorithmic complexity of the random satisfiability problem studied with linear programming. PLoS ONE 2019, 14, e0215309. [Google Scholar] [CrossRef] [PubMed]
- Saribatur, Z.G.; Eiter, T. Omission-based abstraction for answer set programs. Theory Pract. Log. Program. 2021, 21, 145–195. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.M.; Mansor, M.A.; Sathasivam, S. Hybrid Genetic Algorithm in the Hopfield Network for Logic Satisfiability Problem. Pertanika J. Sci. Technol. 2017, 25, 139–152. [Google Scholar]
- Sathasivam, S.; Mansor, M.A.; Kasihmuddin, M.S.M.; Abubakar, H. Election Algorithm for Random k Satisfiability in the Hopfield Neural Network. Processes 2020, 8, 568. [Google Scholar] [CrossRef]
- Cai, S.; Lei, Z. Old techniques in new ways: Clause weighting, unit propagation and hybridization for maximum satisfiability. Artif. Intell. 2020, 287, 103354. [Google Scholar] [CrossRef]
- Dubois, D.; Godo, L.; Prade, H. Weighted logics for artificial intelligence—An introductory discussion. Int. J. Approx. Reason. 2014, 55, 1819–1829. [Google Scholar] [CrossRef]
- Thompson, S.K. Sample size for estimating multinomial proportions. Am. Stat. 1987, 41, 42–46. [Google Scholar]
- Sheynin, O.B.P.S. Laplace’s Work on Probability. Arch. Hist. Exact Sci. 1976, 16, 137–187. [Google Scholar] [CrossRef]
- Sathasivam, S.; Wan Abdullah, W.A.T. Logic mining in neural network: Reverse analysis method. Computing 2011, 91, 119–133. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.M.; Jamaludin, S.Z.M.; Mansor, M.A.; Wahab, H.A.; Ghadzi, S.M.S. Supervised Learning Perspective in Logic Mining. Mathematics 2022, 10, 915. [Google Scholar] [CrossRef]
- Bruck, J.; Goodman, J.W. A generalized convergence theorem for neural networks. IEEE Trans. Inf. Theory 1988, 34, 1089–1092. [Google Scholar] [CrossRef]
- Sokal, R.R. A statistical methods for evaluating systematic relationships. Univ. Kans. Sci. Bull. 1958, 38, 1409–1438. [Google Scholar]
- Gravetter, F.J.; Wallnau, L.B.; Forzano, L.-A.B.; Witnauer, J.E. Essentials of Statistics for the Behavioral Sciences; Cengage Learning: Boston, MA, USA, 2020. [Google Scholar]
- Manikandan, S. Measures of central tendency: The mean. J. Pharmacol. Pharmacother. 2011, 2, 140. [Google Scholar] [PubMed]
- Manikandan, S. Measures of central tendency: Median and mode. J. Pharmacol. Pharmacother. 2011, 2, 214. [Google Scholar]
- Tukey, J.W. Exploratory data analysis. In Addison-Wesley Series in Behavioral Science: Quantitative Methods; Addison-Wesley: Reading, MA, USA, 1977; Volume 2. [Google Scholar]
- Hoaglin, D.C.; Iglewicz, B.; Tukey, J.W. Performance of some resistant rules for outlier labeling. J. Am. Stat. Assoc. 1986, 81, 991–999. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Zamri, N.E.; Azhar, S.A.; Sidik, S.S.M.; Mansor, M.A.; Kasihmuddin, M.S.M.; Pakruddin, S.P.A.; Pauzi, N.A.; Nawi, S.N.M. Multi-discrete genetic algorithm in hopfield neural network with weighted random k satisfiability. Neural Comput. Appl. 2022, 34, 19283–19311. [Google Scholar] [CrossRef]
- Darmann, A.; Döcker, J. On simplified NP-complete variants of monotone 3-sat. Discret. Appl. Math. 2021, 292, 45–58. [Google Scholar] [CrossRef]
- Ong, P.; Zainuddin, Z. Optimizing wavelet neural networks using modified cuckoo search for multi-step ahead chaotic time series prediction. Appl. Soft Comput. 2019, 80, 374–386. [Google Scholar] [CrossRef]
- Pinkas, G. Symmetric neural networks and propositional logic satisfiability. Neural Comput. 1991, 3, 282–291. [Google Scholar] [CrossRef] [PubMed]
- Karaboga, D.; Basturk, B. Artificial Bee Colony (ABC) Optimization Algorithm for Solving Constrained Optimization Problems. Found. Fuzzy Log. Soft Comput. 2007, 4529, 789–798. [Google Scholar]
- Emami, H.; Derakhshan, F. Election algorithm: A new socio-politically inspired strategy. AI Commun. 2015, 28, 591–603. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).