Abstract
For a class of multiagent systems with an unknown time-varying input dead-zone, a prescribed settling time adaptive neural network consensus control method is developed. In practical applications, some control signals are difficult to use effectively due to the extensive existence of an input dead-zone. Moreover, the time-varying input gains further seriously degrade the performance of the systems and even cause system instability. In addition, multiagent systems need frequent communication to ensure a system’s consistency. This may lead to communication congestion. To solve this problem, an event-triggered adaptive neural network control method is proposed. Further, combined with the prescribed settling time transform function, the developed consensus method greatly increases the convergence rate. It is demonstrated that all followers of multiagent systems can track the virtual leader within a prescribed time and not exhibit Zeno behavior. Finally, the theoretical analysis and simulation verify the effectiveness of the designed control method.
Keywords:
multiagent systems; input dead-zone; event-triggered control; prescribed settling time; neural network MSC:
37M05
1. Introduction
Multiagent systems’ consensus control is a research hotspot [1,2,3], as a superior control effect is needed in many practical applications, such as unmanned aerial vehicles [4,5,6], microgrid systems [7,8,9], unmanned surface vehicles [10,11,12], and so on. The goal of consensus control is to converge the states of followers to a common quantity by constructing suitable controllers [13]; many methods have been proposed to achieve this. For the control problem of fixed-wing unmanned aerial vehicles with model uncertainty and disturbances, a learning-based consensus protocol was constructed in [5]. Studying the economic dispatch problem of an Energy Internet, a distributed economic dispatch algorithm based on consensus control and incremental power exchange was proposed in [9]. For unmanned surface vehicle systems with fading channels and time-varying transmission delay, the sampled-data consensus control problem was discussed in [10]. It is important to enhance a system’s convergence rate while ensuring the system’s convergence. Thus, finite-time control was proposed and has attracted the attention of researchers [14,15,16,17,18]. To deal with the control problem of nonlinear systems, a decentralized adaptive fuzzy output feedback finite-time control scheme was designed in [17]. An NN-based event-triggered finite-time control strategy was published in [18] for multiagent systems.
Although the above control methods could ensure that the systems converged within a finite time, the question remained as to how to prescribe the settling time as required. A novel prescribed settling time control method has also been investigated [19,20,21,22,23]. It is worth noting that the control methods can meet the upper bound of the systems’ settling time without any limitation. A prescribed-time bipartite consensus was constructed for first-order multiagent systems in [19]. For the the affine formation control problem, a prescribed-time distributed control protocol was proposed in [21]. Moreover, for the leader-following consensus tracking control problem for second-order multiagent systems, a prescribed-time tracking controller was constructed in [22]. The above results all achieved the prescription of the settling time. However, systems have several nonlinear characteristics, such as a dead-zone and disturbances, and the problem of how to compensate these quickly and effectively remains.
In practical engineering systems, since some electronic components are not sensitive to small signals, an input dead-zone exists. In addition, due to the varying unpredictable faults and mass property, systems’ input gains are unknown and time-varying. Moreover, due to the unknown external disturbances and unmodeled parts, the systems unavoidably include uncertainty and nonlinearity. These problems all seriously degrade a system’s performance. Regarding the uncertain nonlinear characteristics of systems, many interesting results were presented in [24,25,26,27,28,29,30,31]. For unknown nonlinear systems with an input dead-zone, an adaptive fuzzy control was proposed in [24]. For uncertain nonlinear systems with unknown and time-varying gains, radial basis function neural networks and some ingenious treatments were used to compensate in [30]. For the control problem of pure-feedback multiagent systems with a dynamic disturbance and a dead-zone, an adaptive neural network consensus control method was established in [31]. A system’s uncertain nonlinear characteristics influence the system’s control performance and even cause system instability. Therefore, it is important to determine how to enable effective compensation within a prescribed time.
In addition, to guarantee the effective compensation and consistency of the followers, it is necessary to have frequent communication. This may cause communication congestion, as communication resources are extremely limited in a host of practical systems. Setting a triggered threshold to reduce unnecessary signal transmission, as shown in [32,33,34,35,36,37], is a useful way to save communication resources. Differing from the traditional scheme that updates the control signal every fixed period, event-triggered mechanisms work when the systems satisfy preset trigger thresholds. A novel combination of a tracking error-based and event-triggered control method was designed for random differential equation systems in [36]. With a new threshold that included the relative output measurement and the states of all followers, an adaptive event-triggered scheme was constructed in [37]. All of these strategies save communication resources. However, when the systems need to quickly converge, a shorter settling time can be selected, and a a large amount of communication is inevitable. Our aim is to design a suitable event-triggered control strategy that ensures rapid convergence without a large amount of communication pressure.
Based on the previous discussions, for uncertain nonlinear multiagent systems with an unknown time-varying dead-zone, an event-triggered prescribed settling time adaptive neural network consensus control is proposed, and the main contributions are summarized as follows:
- 1.
- Input gains and external disturbances exist in multiagent systems. Both of these are unknown and time-varying. To reduce their impact, a consensus control method is proposed based on boundary information. Moreover, in combination with transform technology, the system’s convergence rate is remarkably increased.
- 2.
- Due to its existence in systems and its serious impact on control performance, the dead-zone is a factor that cannot be ignored. At the same time, a dead-zone exists in time-varying form, which makes compensation difficult. Thus, an adaptive event-triggered mechanism is constructed to compensate for such a dead-zone. Meanwhile, the problem of the large amount of communication resources is addressed.
2. Preliminaries and Problem Description
2.1. Systems Model
A class of uncertain nonlinear multiagent systems constructed by one virtual leader and followers is discussed. The i-th follower model is described as
where represents the i-th follower’s states, and . and are the unknown external disturbances and input gains, respectively. and are the output and control signal of i-th follower, respectively. is the nonlinear dead-zone input. The sketch map of the input dead-zone is shown in Figure 1.
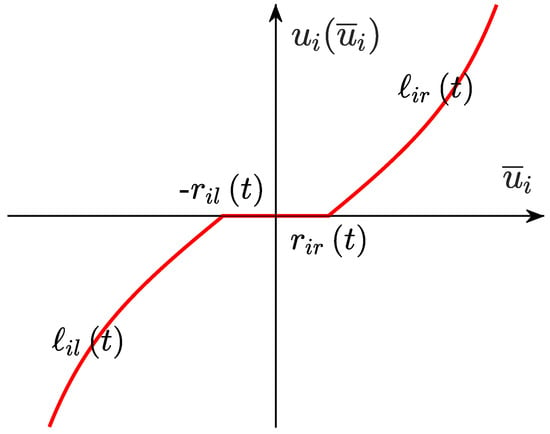
Figure 1.
Dead-zone nonlinearity.
According to the sketch map, the model of the dead-zone can be described as
where and are the right slope and the left slope, respectively. and are the right breakpoint and the left breakpoint of the dead zones, respectively. They satisfy , , , . When the control signal is in the dead-zone interval , the actual input is zero. The actuator works when the input signal exceeds the dead-zone interval. The dead-zone model (2) can be rewritten as
where
This paper aims to solve the prescribed time consensus problem of multiagent systems (1) with an unknown time-varying dead zone (3). To achieve the aim and make sense practically, the following common and necessary assumptions are introduced:
Assumption 1 ([34]).
For the time-varying input gains function , there exist two position constants and that express the input gains upper bound and lower bound, respectively; it is satisfied that .
Assumption 2 ([17]).
The output signal of the virtual leader is known, bounded, continues, and has n-th order derivatives.
2.2. Graph Theory
The information interaction of the directed communication topology graph, which includes followers, can be represented by , where denotes followers , and is the edge set from follower j to follower i. The adjacency matrix among all followers is ; if follower j receives information from follower i, , otherwise, . The in-degree of follower i is described as , and the diagonal matrix is . The augmented graph is described as , where denotes leader 0 and followers , and .
Assumption 3.
The augmented graph contains a spanning tree, and the root of the spanning tree is the virtual leader 0.
Definition 1.
The i-th follower of the multiagent systems’ synchronization error is defined as:
where denotes the output of the virtual leader. denotes the adjacency matrix between the leader and the followers. If the follower i can receive information from the leader, . Otherwise, .
2.3. Radial Basis Function Neural Network
A neural network can be used to handle the uncertain nonlinear functions in multiagent systems. The radial basis function neural network (RBFNN) can be described as , where is the input vector, is the weight vector, and m is the number of neurons. The radial basis function vector , and each vector is expressed as
where . is the width of the radial basis function, and is the center of the radial basis function.
Lemma 1 ([32]).
A continuous function on set can be modeled with arbitrary positive precision
where is the approximation error, which satisfies . The ideal weight vectors are described as:
2.4. Prescribed Settling Time Transform Function
To reach systems convergence within the prescribed time, a transform function is introduced to map and scale the systems. The transform function is defined as:
where T is the prescribed time, , , and all are design constants, and it is obvious that .
The derivation of the function is
It is obvious that in is a continuous function, and the function derivative is positive and bounded.
Remark 1.
It is worth noting that the systems convergence rate is greatly enhanced in combination with the transform function. Using the proposed control method, the systems settling time can be directly prescribed according to the actual requirement, and it is unaffected by the system’s initial states and various controller parameters.
2.5. Other Preliminaries
This paper aims to design a consensus control method to make systems converge within a prescribed time in the case of the existence of unknown time-varying dead-zone and gains. To facilitate the control design and stability analysis, the following lemmas are introduced:
Lemma 2 ([17]).
For Laplacian matrix and adjacency matrix , there exists at least one that satisfies , and it follows that is nonsingular.
Lemma 3 ([38]).
Defining , , and , one has
where presents the minimum eigenvalue of the matrix .
Lemma 4 ([39]).
For any constant and , one has
where , , and it satisfies .
Lemma 5 ([40]).
For and , one has
Lemma 6 ([41]).
There exist constants and , for a semi-positively determinable derivative function , where the one-order derivative satisfies the relationship ; there exists the following relationship:
3. Controller Design and Ability Analysis
3.1. Prescribed Settling Time Adaptive Neural Network Control Design
By utilizing n steps backstepping technology, the prescribed settling time adaptive neural network control is constructed. Firstly, we define the i-th follower error variable as follows:
where is the i-th follower error variable, and the virtual controller of the i-th follower is denoted as .
Step 1: The Lyapunov function is selected as
where is the design positive parameter, using to estimate , expresses the parameter estimation error, and the definition of will be shown later.
Taking the time derivation of (19) yields
Taking the into (20) yields
where .
According to Lemma 1, RBFNN is used to model with error
where , and .
According to Lemma 4, the following results hold:
where and are the design parameters.
We construct the virtual controller and the parameter updating law as follows
where , are the design parameters, and is the lower bound of the gains function .
Remark 2.
The unknown and uncertain parts widely exist in multiagent systems, which introduces difficulties into the design of the control method. Thus, neural networks are introduced to deal with these. As there are many states in multiagent systems, it is hard to obtain the ideal weight vectors. The adaptive law is designed to estimate these, which simplifies the control design. In addition, considering the unknown time-varying input gains , the boundary information is introduced into the virtual controller to reduce the impact.
Step k : Similarly, the Lyapunov function is selected as
where is the design positive parameter, using to estimate , expresses the parameter estimation error, and the definition of will be shown later.
Taking the time derivation of in (33) yields
We define the continue function , which is modeled by RBFNN with error ; it can be expressed as
where , and . It can be deduced that
According to Lemma 4, the following results hold:
where and are the design positive parameters.
By substituting (39)–(41) into (38), one has
where , , and is the upper bound of the input gains function . We construct the virtual controller and the parameter updating law as
where and are the design parameters, and is the lower bound of the gains function.
Adaptive event-triggered mechanism: To reduce the communication stress, an adaptive event-triggered mechanism is established. The event-triggered control input is as follows:
where , , and are the design parameters. We define the intermediate signal as
where , . To redress the impact of the input dead-zone by utilizing to estimate , the parameter estimation error can be expressed as . Thus, (47) can be rewritten as
Further, it is important to design a suitable event-triggered threshold, constructing a relative threshold
When the moment , in which the relative error satisfies the triggered condition , the input signal will be updated as the event-triggered signal .
Remark 3.
Considering the frequent signal transmission of multiagent systems, an event-triggered scheme is established to relieve the communication stress. At the same time, an intermediate signal is established in (47) to compensate for the impact of the dead-zone. Due to the parameters of an unknown and time-varying dead-zone being difficult to determine, an intermediate signal is designed to compensate them. Moreover, a correction term is added to enhance the precision.
Step n: The Lyapunov function is selected as
where is expressed as a 2∗2 positive matrix, and the inverse matrix is expressed as . Using to estimate , expresses the parameter estimation error, the definition of is shown later, and is a design parameter.
Taking the time derivation of in (50) yields
Substituting (50) into (49) yields
From (46), due to , , it can be obtained that
As and , it is true that
Subsequently,
From Lemma 5, (57) can be rewritten as
Defining the continuous function , which is similarly modeled by the RBFNN with error , it can be expressed as
where and .
According to Lemma 4, the following results hold:
where and are the design positive parameters.
We construct the virtual controller and the parameter updating law as
where and are the design parameters, is the lower bound of the gains function , and it satisfies .
We design the parameter updating law as
where is design parameter. Substituting (45) and (67) into (66) yields
Applying Lemma 4 and the definitions of adaptive laws, the following inequalities hold:
3.2. System Stability Analysis
Theorem 1.
For uncertain nonlinear multiagent systems (1) with an unknown time-varying input dead-zone (3), a prescribed settling time transform function (10), virtual control (30), (43), and (64), a parameter updating law (31), (44), and (65), (67), an event-triggered mechanism (46) and (49), the following goals can be achieved:
- 1.
- 2.
- In the interval time between any twice triggering , the existing satisfies , so that the systems do not experience Zeno.
Proof of Theorem 1.
The total Lyapunov function V is selected as
Based on (70), it can be known that
where , .
Using Lemma 6, it can be obtained that
According to the definition of , it is proof that all the signals of multiagent systems are semi-globally uniformly ultimately bounded. It is obvious that
We define ; it follows that
We can obtain the synchronization error of multiagent systems’ coverage on set . Furthermore, according to Lemma 3, the tracking error of multiagent systems’ coverages in , and the decay rate is not less than .
Based on the above analysis, it can be proved that , and are all bounded. From and , it can be known that and are bounded. According to (64), the virtual controller is bounded. Combined with (48), we know that input signal is bounded too; so, all states of are bounded. Similarly, all states of multiagent systems are bounded.
Remark 4.
Based on the above analysis, the settling time T up bound can be prescribed, which is independent of initial states and design parameters. Moreover, the convergence set of systems error can be adjusted by setting the relevant parameters Φ, Ψ and Υ, then the Υ can be preset by adjusting the designed parameters , , , , , and , , .
From the event-triggered mechanism (49), one obtains
It is obvious that is continuous and bounded, and the existing constant satisfies
For ,
Taking the time derivate of yields
Therefore,
It is proven that the existing time lower bound guarantees multiagent systems avoid Zeno. □
4. Simulation
In this section, the proposed control method is validated by two simulation experiments.
4.1. Numerical Simulation
We considered the multiagent systems constructed by one virtual leader and four followers, the communication topology graph is shown in Figure 2, and each follower (similar to [24]) was modeled as follows
where , the time-varying input gains functions and , and the unknown external disturbance is expressed as and .
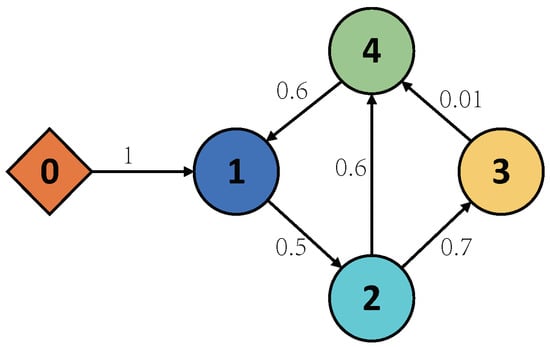
Figure 2.
The multiagent systems’ communication topology graph.
The right breakpoint of the input dead-zone was , and the right breakpoint was , The dead-zone slope functions were and . The reference signal of the virtual leader was selected as .
The adaptive event-triggered mechanism was designed as:
The prescribed setting adaptive neural network controllers were as follows:
The proposed consensus control method was applied to multiagent systems with input dead zones (84). The parameters of the prescribed settling time preference function were , , , and . The related parameters were set to , . The parameters of the event-triggered mechanism were selected as , , , and , where . The systems’ initial states and designed parameters are listed in Table 1.

Table 1.
The systems’ initial states and designed parameters.
The simulation results are shown in Figure 3. Figure 3a shows the virtual leader’s reference signal and the four followers’ output tracking signals, and Figure 3b shows the synchronization error of the four followers. The followers converged to the virtual leader, and the synchronization error converged within the presetting time of 0.3 s. Figure 3c exhibits the event-triggered mechanism inputs and the nonlinear dead-zone inputs of the four followers, where the event-triggered mechanism inputs were continuous, and the dead-zone inputs were rectangular. Figure 3d shows the event-triggered time interval, and there was no Zeno phenomenon. The trigger numbers of the event-triggered mechanism were 765, 703, 792, and 754. The trigger number of the traditional periodic sampled-data control was 2000. This indicates the event-triggered mechanism saved more than 60% of communication resources.
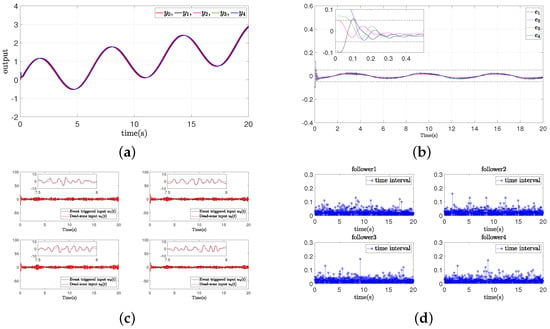
Figure 3.
The simulation results of Example A case I. (a) Outputs of leader and followers; (b) synchronization error ; (c) event-triggered and dead-zone input; (d) time intervals.
To further verify the practicality of the constructed method and confirm that the convergence time was independent of the designed parameters and the systems’ initial states, two simulation experiments were conducted for different initial states and different design parameters. These simulation results are presented in Figure 4 and Figure 5. For the conditions of different initial states and different design parameters, there were similar results: All followers quickly tracked the leader, and the synchronization errors converged within the prescribed time.
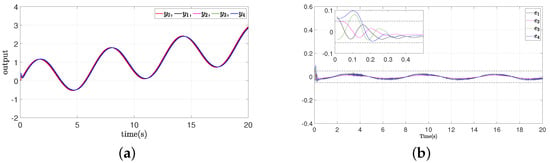
Figure 4.
The simulation results of Example A case II. (a) Outputs of leader and followers; (b) synchronization error .
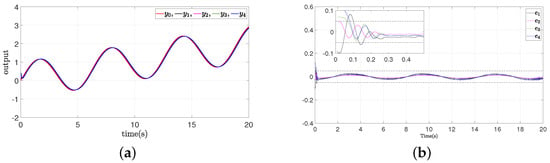
Figure 5.
The simulation results of Example A case III. (a) Outputs of leader and followers; (b) synchronization error .
4.2. Application Simulation
With practicality and high-efficiency characteristics, the robotic arm has been widely used in engineering, including welding, grinding, and carrying. Robotic arms are usually constructed by a base, several rigid links, joints, and an end effector. Here, the developed method was applied in four robotic arms to further validate its practicality. The diagrammatic sketch of each robotic arm is shown in Figure 6. The controller output the control signal and transmitted it to the actuator. The actuator produced the generalized force and acted on the link through the gears.
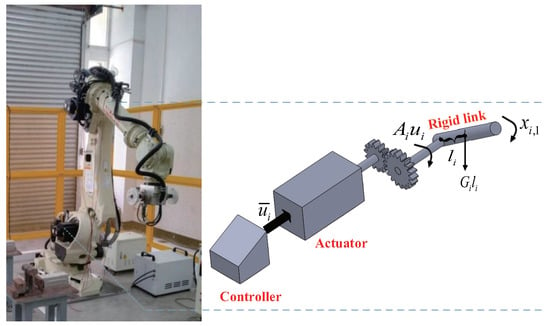
Figure 6.
Robotic arms diagrammatic sketch.
Then, the robotic arm with the input dead-zone model (similar to [25,42]) was formulated as follows:
where represents the i-th link angle, expresses the i-th link angular velocity, represents the control signal input, represents the dead-zone input, and represents the output of the i-th link. Then, is the input gains function. is the viscous friction coefficient, and and represent the mass and length of the link, respectively. is the inertia moment, where . The systems’ initial states and relevant parameters setting were the same as in the previous numerical simulation.
The simulation results are shown in Figure 7. Figure 7a displays the reference angle and the four robotic arms’ angle, which shows that the angles of the four robotic arms achieved consensus quickly. Figure 7b depicts the synchronization error of the four robotic arms, which entered the 5% error band within the prescribed time. This indicates that the prescribed time consensus control performance of the robotic arm can be guaranteed, irrespective of the existence of the time-varying input dead-zone and gains. Figure 7c shows the event-triggered input and the dead-zone input; it can be seen that the system inputs suffered from dead-zone nonlinearity. Figure 7d presents the triggered interval time of the event-trigger mechanism, and the total trigger number of the event-triggered mechanism was 3069. It saved almost 60% of the communication resources for the systems; hence, the communication pressure was greatly reduced.
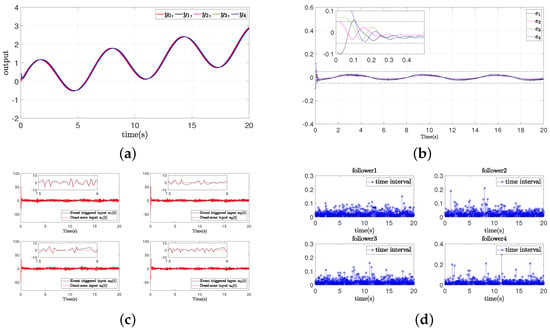
Figure 7.
The simulation results of Example B case I. (a) Outputs of leader and followers; (b) synchronization error ; (c) event-triggered and dead-zone input; (d) time intervals.
For different initial states and different design parameters in Table 1, two simulation experiments were conducted. The similar results are presented in Figure 8 and Figure 9. Comparing the simulation results for the two classes of multiagent systems, similar control performances were shown. This indicates that the proposed method is not only applicable to specific systems. For the uncertainty of nonlinear multiagent systems with an unknown time-varying dead zone, the prescribed settling time consensus control problem of effective compensation within the prescribed time is solved.
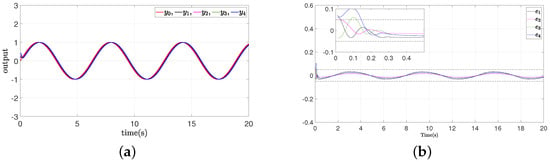
Figure 8.
The simulation results of Example B case II. (a) Outputs of leader and followers; (b) synchronization error .
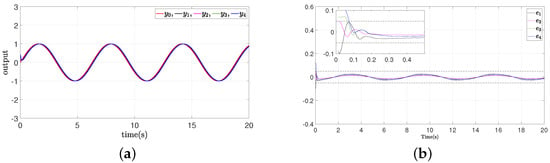
Figure 9.
The simulation results of Example B case III. (a) Outputs of leader and followers; (b) synchronization error .
5. Conclusions
This paper established a novel prescribed settling time adaptive neural network consensus control method for uncertain nonlinear multiagent systems with an input dead-zone. Due to the uncertainty and nonlinearity, the existing prescribed settling time consensus control methods are difficult to use effectively in uncertain nonlinear multiagent systems. For the issues of the systems’ unknown time-varying disturbances and input gains, an adaptive RBFNN control was constructed to handle them; furthermore, an adaptive event-triggered mechanism was designed, which reduced the unnecessary communications while compensating for the dead-zone. Combined with the transform function, the established control method succeeded in the followers being able to track the virtual leader within the prescribed time, and the settling time was not affected by the initial states or the designed parameters. Simulations were conducted to confirm the effectiveness of the developed control method. In prescribed settling time control, a lot of energy is used to ensure the systems quickly converge, especially when a shorter settling time is selected. However, systems can have actuator saturation as a restriction on the elements. How to guarantee systems’ converge within the prescribed time, while systems suffer from actuator saturation, remains a challenging question.
Author Contributions
Methodology, W.W. and J.L.; validation, W.W., J.L., and F.L.; formal analysis, Y.Z.; data curation, Y.Z.; writing—original draft preparation, J.L. and Z.H.; writing—review and editing, W.W. and J.L.; supervision, F.L.; project administration, J.L. and Z.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Programme of Guangzhou (Grant Number 202102010428), the Tertiary Education Scientific research project of Guangzhou Municipal Education Bureau, China (Grant Number 202235199, 202235237), the Open Fund of Key Laboratory of Bridge Engineering Safety Control by Department of Education (Grant Number 19KB06), the Special Funds for the Cultivation of Guangdong College Students’ Scientific and the Technological Innovation (Grant Number pdjh2022a0404), and the College Students’ Innovative Entrepreneurial Training Plan Program (Grant Number 202211078101), the “Challenge Cup” National College Student Curricular Academic Science and Technology Works Competition (Grant Number 2022TZBNAH0819).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All relevant data are within the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zou, W.; Ahn, C.K.; Xiang, Z. Fuzzy-Approximation-Based Distributed Fault-Tolerant Consensus for Heterogeneous Switched Nonlinear Multiagent Systems. IEEE Trans. Fuzzy Syst. 2021, 29, 2916–2925. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Wang, Z.; Fu, C.C.; Song, S. Distributed Event-Triggered Control for Cooperative Output Regulation of Multiagent Systems With an Online Estimation Algorithm. IEEE Trans. Cybern. 2022, 52, 1911–1923. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wu, Y.; Chen, M. Adaptive Fault-Tolerant Tracking Control for Discrete-Time Multiagent Systems via Reinforcement Learning Algorithm. IEEE Trans. Cybern. 2021, 51, 1163–1174. [Google Scholar] [CrossRef]
- Wu, Y.; Gou, J.; Hu, X.; Huang, Y. A new consensus theory-based method for formation control and obstacle avoidance of UAVs. Aerosp. Sci. Technol. 2020, 107, 106332. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, S.; Wang, X. Distributed Control for Coordinated Tracking of Fixed-Wing Unmanned Aerial Vehicles under Model Uncertainty and Disturbances. Appl. Sci. 2021, 11, 9830. [Google Scholar] [CrossRef]
- Du, B.; Mao, R.; Kong, N.; Sun, D. Distributed Data Fusion for On-Scene Signal Sensing With a Multi-UAV System. IEEE Trans. Control Netw. Syst. 2020, 7, 1330–1341. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, X.; Xu, W.; Wen, G. Modeling and Control of Islanded DC Microgrid Clusters With Hierarchical Event-Triggered Consensus Algorithm. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 376–386. [Google Scholar] [CrossRef]
- Chen, X.; Shi, M.; Zhou, J.; Zuo, W.; Chen, Y.; Wen, J.; He, H. Consensus-Based Distributed Control for Photovoltaic-Battery Units in a DC Microgrid. IEEE Trans. Ind. Electron. 2019, 66, 7778–7787. [Google Scholar] [CrossRef]
- Chen, W.; Li, T. Distributed Economic Dispatch for Energy Internet Based on Multiagent Consensus Control. IEEE Trans. Autom. Control 2021, 66, 137–152. [Google Scholar] [CrossRef]
- Wang, L.; Yue, W.; Zhang, R. Sampled-data consensus control of MUSV systems with channel fading and transmission delay. China Commun. 2020, 17, 36–45. [Google Scholar] [CrossRef]
- Gu, N.; Wang, D.; Peng, Z.; Liu, L. Observer-Based Finite-Time Control for Distributed Path Maneuvering of Underactuated Unmanned Surface Vehicles With Collision Avoidance and Connectivity Preservation. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5105–5115. [Google Scholar] [CrossRef]
- Zhou, W.; Fu, J.; Yan, H.; Du, X.; Wang, Y.; Zhou, H. Event-Triggered Approximate Optimal Path-Following Control for Unmanned Surface Vehicles With State Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 104–118. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Han, Q.; Ge, X.; Zhang, X. An Overview of Recent Advances in Event-Triggered Consensus of Multiagent Systems. IEEE Trans. Cybern. 2018, 48, 1110–1123. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Y.; Liu, Z.; Chen, C.L.P.; Zhang, C.; Chen, K. Finite-time consensus control for multi-agent systems with full-state constraints and actuator failures. Neural Netw. Off. J. Int. Neural Netw. Soc. 2022, 157, 350–363. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Wang, L.; Liu, Y.; Sun, J.; Pan, Y. Finite-time adaptive optimal consensus control for multi-agent systems subject to time-varying output constraints. Appl. Math. Comput. 2022, 427, 127176. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, B.; Lin, C.; Shang, Y. Fuzzy adaptive finite-time consensus tracking control for nonlinear multi-agent systems. Int. J. Syst. Sci. 2021, 52, 1346–1358. [Google Scholar] [CrossRef]
- Du, P.; Pan, Y.; Li, H.; Lam, H.K. Nonsingular Finite-Time Event-Triggered Fuzzy Control for Large-Scale Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2021, 29, 2088–2099. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Y.; Liu, Z.; Chen, C.L.P.; Zhang, C.; Chen, K. Neural network-based event-triggered finite-time control of uncertain nonlinear systems with full-state constraints and actuator failures. Int. J. Robust Nonlinear Control 2022, 33, 1683–1703. [Google Scholar] [CrossRef]
- Chen, X.; Yu, H.; Hao, F. Prescribed-Time Event-Triggered Bipartite Consensus of Multiagent Systems. IEEE Trans. Cybern. 2022, 52, 2589–2598. [Google Scholar] [CrossRef]
- Wang, J.; Gong, Q.; Huang, K.C.; Liu, Z.; Chen, C.L.P.; Liu, J. Event-Triggered Prescribed Settling Time Consensus Compensation Control for a Class of Uncertain Nonlinear Systems With Actuator Failures. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Wang, J.; Ding, X.; Wang, C.; Liang, L.; Hu, H. Affine formation control for multi-agent systems with prescribed convergence time. J. Frankl. Inst. 2021, 358, 7055–7072. [Google Scholar] [CrossRef]
- Ge, S.; Zhou, Y.; Jiang, G.; Liu, S.; Li, H. Prescribed-Time Leader-Following Consensus Tracking Control for Second-Order Multi-agent Systems. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 945–950. [Google Scholar]
- Lin, Q.; Zhou, Y.; Jiang, G.; Ge, S.; Ye, S. Prescribed-time containment control based on distributed observer for multi-agent systems. Neurocomputing 2021, 431, 69–77. [Google Scholar] [CrossRef]
- Li, S.; Ding, L.; Gao, H.; Liu, Y.; Huang, L.; Deng, Z. Adaptive Fuzzy Finite-Time Tracking Control for Nonstrict Full States Constrained Nonlinear System With Coupled Dead-Zone Input. IEEE Trans. Cybern. 2022, 52, 1138–1149. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Park, J.H.; Xie, X.; Liu, Y.; Yang, Z. Event-triggered adaptive asymptotic tracking control of uncertain nonlinear systems with unknown dead-zone constraints. Appl. Math. Comput. 2020, 386, 125528. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Z.; Wang, J.; Liu, Z.; Chen, C.L.P. Fuzzy Adaptive Two-Bit-Triggered Control for a Class of Uncertain Nonlinear Systems With Actuator Failures and Dead-Zone Constraint. IEEE Trans. Cybern. 2020, 51, 210–221. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhao, S.; Li, H.; Lu, R.; Wu, C. Adaptive Neural Network Tracking Control for Robotic Manipulators With Dead Zone. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3611–3620. [Google Scholar] [CrossRef]
- Li, H.; Zhao, S.; He, W.; Lu, R. Adaptive finite-time tracking control of full state constrained nonlinear systems with dead-zone. Automatica 2019, 100, 99–107. [Google Scholar] [CrossRef]
- Ding, L.; Li, S.; Gao, H.; Liu, Y.; Huang, L.; Deng, Z. Adaptive Neural Network-Based Finite-Time Online Optimal Tracking Control of the Nonlinear System With Dead Zone. IEEE Trans. Cybern. 2021, 51, 382–392. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Liu, Z.; Chen, C.L.P.; Zhang, Y. Distributed Adaptive Neural Fixed-Time Tracking Control of Multiple Uncertain Mechanical Systems With Actuation Dead Zones. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3859–3872. [Google Scholar] [CrossRef]
- Liang, H.; Liu, G.; Zhang, H.; Huang, T. Neural-Network-Based Event-Triggered Adaptive Control of Nonaffine Nonlinear Multiagent Systems With Dynamic Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2239–2250. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.; Chen, C.L.P.; Liu, Z.; Zhang, C. Fast Finite-Time Event-Triggered Consensus Control for Uncertain Nonlinear Multiagent Systems With Full-State Constraints. IEEE Trans. Circuits Syst. I Regul. Pap. 2022. [Google Scholar] [CrossRef]
- Zhao, G.; Cao, L.; Li, X.; Zhou, Q. Observer-based dynamic event-triggered control for nonstrict-feedback stochastic nonlinear multiagent systems. Appl. Math. Comput. 2022, 430, 127289. [Google Scholar] [CrossRef]
- Deng, C.; Che, W.; Wu, Z. A Dynamic Periodic Event-Triggered Approach to Consensus of Heterogeneous Linear Multiagent Systems With Time-Varying Communication Delays. IEEE Trans. Cybern. 2021, 51, 1812–1821. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Ma, K.; Liu, Z.; Chen, C.L.P. Neural Adaptive Self-Triggered Control for Uncertain Nonlinear Systems With Input Hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6206–6214. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Xi, R.; Wang, Y.; Sun, S.; Sun, J. Event-Triggered Adaptive Tracking Control for Random Systems With Coexisting Parametric Uncertainties and Severe Nonlinearities. IEEE Trans. Autom. Control 2022, 67, 2011–2018. [Google Scholar] [CrossRef]
- Wang, W.; Li, M.Y.; Tong, S. Neural-Network-Based Adaptive Event-Triggered Consensus Control of Nonstrict-Feedback Nonlinear Systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1750–1764. [Google Scholar] [CrossRef]
- Wu, Y.; Liang, H.; Zhang, Y.; Ahn, C.K. Cooperative Adaptive Dynamic Surface Control for a Class of High-Order Stochastic Nonlinear Multiagent Systems. IEEE Trans. Cybern. 2021, 51, 5214–5224. [Google Scholar] [CrossRef]
- Jin, X. Adaptive Fixed-Time Control for MIMO Nonlinear Systems With Asymmetric Output Constraints Using Universal Barrier Functions. IEEE Trans. Autom. Control 2019, 64, 3046–3053. [Google Scholar] [CrossRef]
- Li, M.; Li, S.; Ahn, C.K.; Xiang, Z. Adaptive Fuzzy Event-Triggered Command-Filtered Control for Nonlinear Time-Delay Systems. IEEE Trans. Fuzzy Syst. 2022, 30, 1025–1035. [Google Scholar] [CrossRef]
- Xing, L.; Wen, C.; Liu, Z.; Su, H.; Cai, J. Event-Triggered Adaptive Control for a Class of Uncertain Nonlinear Systems. IEEE Trans. Autom. Control 2017, 62, 2071–2076. [Google Scholar] [CrossRef]
- Mi, X.; Zou, Y.; Li, S.; Karimi, H.R. Self-Triggered DMPC Design for Cooperative Multiagent Systems. IEEE Trans. Ind. Electron. 2020, 67, 512–520. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).