Abstract
The main objective of this work was to develop a tuning method for PID controllers suitable for use in an industrial environment. Therefore, a computationally simple tuning method is presented based on a simple experiment on the process without requiring any input from the user. Essentially, the method matches the closed-loop response to the response obtained in the steady-state change experiment. The proposed method requires no prior knowledge of the process and, in its basic form, only the measurement of the change in the steady state of the process in the manually or automatically performed experiment is needed, which is not limited to step-like process input signals. The user does not need to provide any prior information about the process or any information about the closed-loop behavior. Although the control loop dynamics is not defined by the user, it is still known in advance because it is implicitly defined by the process open-loop response. Therefore, no exaggerated control signal swings are expected when the reference signal changes, which is an advantage in many industrial plants. The presented method was designed to be computationally undemanding and can be easily implemented on less powerful hardware, such as lower-end PLC controllers. The work has shown that the proposed model-free method is relatively insensitive to process output noise. Another advantage of the proposed tuning method is that it automatically handles the tuning of highly delayed processes, since the method discards the initial process response. The simplicity and efficiency of the tuning method is demonstrated on several process models and on a laboratory thermal system. The method was also compared to a tuning method based on a similar closed-loop criterion. In addition, all necessary Matlab/Octave files for the calculation of the controller parameters are provided online.
MSC:
47N70; 58E25
1. Introduction
The tuning of control systems has attracted the interest of researchers for eight decades. It is, therefore, not surprising that the number of published tuning methods is very high. All methods use some specific information from the process to achieve controller tuning. Most tuning methods require the process model (or an estimated lower-order model), and model quality is a key factor in successful controller tuning. The most commonly used tuning methods in practice are those that require the least amount of information from the process to achieve the desired control performance.
In general, controller tuning methods can be divided into those that require an explicit process model and those that do not. The latter can be referred to as data-driven methods because the tuning is based on input and output measurements of the process in the time domain without identifying an explicit process model. Recently, data-driven methods have received increasing attention from researchers because the only information required from the process is the input and output signals, which are usually available.
Some typical representatives of data-driven methods are Virtual Reference Feedback Tuning (VRFT) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15], Fictitious Reference Iterative Tuning (FRIT) [16,17,18,19,20], Direct Adaptive Controller (DIRAC) [21], Balanced method [22], model-free approaches with ultra-local models [23,24,25], and Magnitude Optimum Multiple Integration (MOMI) tuning methods [26,27,28,29,30]. All these methods use the process input and output signals to calculate the controller parameters.
In the VRFT method, the controller parameters are determined by comparing the measured and calculated controller output signals after calculating the “virtual reference signal” from the measured process output signal and the inverse of the desired closed-loop transfer function. The controller parameters can be calculated by a regression method. The VRFT method has been adapted for MIMO processes [2,12], for nonlinear processes [3,5], and for IMC-based PID controllers [9,13,14].
The FRIT method is similar to the VRFT method except that it compares the measured and desired process outputs. The “fictitious reference” is calculated from the measured process input and output signals and the inverse of the controller’s transfer function. Some of FRIT methods have been extended by improving robustness with desired maximum sensitivity (MS) [16], using cascade control structures [18,19], and optimizing disturbance-rejection performance [20].
DIRAC method [21] is similar to the VRFT method, where the discrete controller parameters are calculated by a regression method by comparing the filtered process input signal with the difference between the filtered and the original process output signal, where filter is the desired closed-loop transfer function.
The Balanced method [22] is an iterative tuning method for PI controllers that calculates the controller parameters by balancing the contribution of the proportional and integral terms. This is achieved using an extended performance index ITAEX and a “sign criterion” in the optimization loop.
Model-free approaches with ultra-local models are based on describing the process with a very simple process model (e.g., integrator or double integrator), while considering the rest of the process behavior is considered to be disturbance (compensated with closed-loop inner control). By estimating the n-th derivative of the process output and the reference, the controller parameters can be calculated. The user should select the desired closed-loop speed [23].
The MOMI tuning method is based on multiple integrals of the process input and output signals. These integrals are used to evaluate the process moments (areas), which are then used to calculate the controller parameters (e.g., PID [26,27,28], higher-order controllers [29], multivariable controllers [30], etc.).
One of the basic requirements for VRFT, FRIT, DIRAC and model-free methods is the definition of the desired closed-loop transfer function or desired closed-loop speed. However, it is not always easy to define this for an unknown process. The disadvantage of the Balanced method is the iterative procedure required to determine the optimal balance between the proportional and integral terms of the controller. The MOMI tuning method does not require the desired closed-loop transfer function or an iterative procedure to calculate the controller parameters. However, the calculation of repeated integrals on the input and output signals of the process is prone to error if the process does not settle during the experiment.
Therefore, we decided to propose a novel PID controller tuning method (but not limited to the PID controllers), based on the VRFT method, which addresses most of the mentioned shortcomings. The main advantages of the proposed method are the following:
- -
- The tuning method requires only the measurement of the manually or automatically controlled experiment on the process, where the process changes the steady state (the process input signal is not limited to step-like signals).
- -
- The user does not need to provide any prior information about the process, such as the process transfer function, the desired control loop transfer function or time constants.
- -
- Although the closed-loop response is not defined by the user, it is implicitly defined by the open-loop response. The advantage of matching the responses is that there are no exaggerated swings of the controller output signal in response to the setpoint change, which is often preferred by plant operators in many industrial plants.
- -
- Because the tuning method discards the initial response of the process (e.g., during process time delay of the process), the method slows the closed-loop response for processes with larger time delays and therefore inherently stabilizes the closed-loop response.
- -
- Due to the regression method used, the proposed method is relatively insensitive to process measurement noise.
- -
- The proposed method is simple, does not require optimization, is not computationally intensive, and therefore can be implemented on less powerful hardware, such as lower-end PLC controllers.
- -
- All scripts (Matlab/Octave) for calculating the controller parameters are available online, allowing the user to immediately calculate the controller parameters for any selected process model or from provided process input and output signals. The scripts are open-source, can be copied and modified as needed.
- -
- The method can be extended to include an additional velocity factor that speeds up or slows down the closed-loop response compared to the open-loop response accordingly. This extension requires an additional estimate of the process time delay and process average residence time, which can be trivially determined from the open-loop response.
Therefore, the proposed tuning method could be particularly welcome in industrial environments.
The remainder of the paper is organized as follows. The VRFT method is described in Section 2. The proposed equalization method based on an implicitly defined closed-loop transfer function is described in Section 3. In Section 4, the effects of measurement noise at the process output are tested. The generalization of the proposed method to obtain faster or slower closed-loop responses than open-loop responses is explained in Section 5, while examples on different process models and a laboratory temperature plant are given in Section 6. A comparison with other tuning methods based on similar desired closed-loop response is presented in Section 7. Some conclusions are drawn in the last section.
2. VRFT Method
The original VRFT method calculates the controller parameters using a “virtual reference signal” derived from the measured process output signal and the inverse of the desired closed-loop transfer function. Figure 1 shows the main principle of the VFT tuning method, where u and y represent the measured process input and output signals (from any open-loop or closed-loop experiment), GCL−1 is the inverse of the desired closed-loop transfer function, and r* and e* are the fictitious reference and control error, respectively.
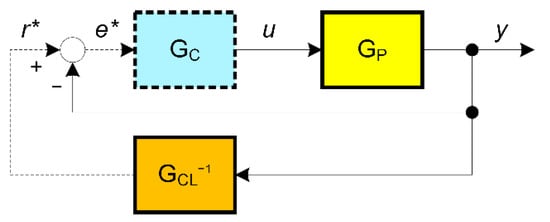
Figure 1.
VRFT controller tuning principle.
The controller parameters (GC) can be calculated by regression from the following expression:
where the fictitious reference r* is calculated from the process output measurement filtered by the inverse of the desired closed-loop transfer function:
The capital letters U, R* and Y denote the Laplace transforms of the signals u, r* and y, respectively. The bias in the estimation of the controller parameters can be reduced by additional filtering of the input and output signals of the process with the following filters [7]:
where
Please note that ωC is a cutoff frequency of the low-pass filter WLP(s) and G*CL is the desired closed-loop transfer function without time delay. Therefore, the final equation used by the regression method to calculate the controller parameters is as follows:
As mentioned in the introduction, the VRFT method requires an explicit definition of the desired closed-loop transfer function, which is not always an easy task. Therefore, the solution proposed here is to avoid selecting the closed-loop transfer function by implicitly using the measured process open-loop response, instead.
3. Equalization Method
The equalization method is based on two-degrees-of-freedom (2-DOF) controller structure [31,32,33] as shown in Figure 2.
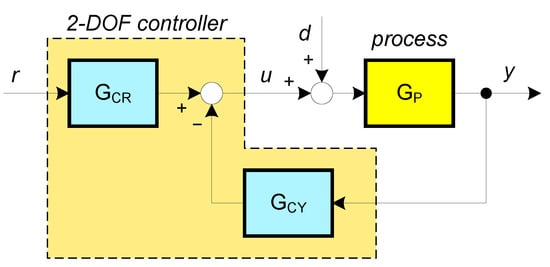
Figure 2.
2-DOF controller structure used in equalization method.
The controller output (U) signal can be calculated as follows (assuming that the disturbance signal is d = 0):
where R and Y are the Laplace transforms of the reference signal and the process output, respectively. The 2-DOF structure is defined by the feedforward (GCR) and feedback (GCY) transfer function blocks. Assume that the process is defined by the following unknown transfer function:
where KPR is the steady-state process gain, Tdelay is the time delay, and a1, a2, …, b1, b2, … are the dynamic process parameters. The parameters of the 2-DOF controller can be calculated from expression (6) when the reference signal R is calculated from the process output signal and the desired closed-loop transfer function:
However, as mentioned above, selecting the desired closed-loop transfer function is not always a simple task. To skip the calculation of the desired closed-loop transfer function and simplify the derivation of the controller parameters, one can choose the desired closed-loop transfer function similar to the process open-loop transfer function:
Please note that the process transfer function is divided by the steady-state process gain KPR, since the steady-state closed-loop gain must equal one. In this case, the reference signal (8) becomes
Now, the calculation of the controller parameters is simplified significantly, since expression (6), considering expression (10), becomes:
Therefore, if the steady-state process gain is known, the controller parameters can be calculated directly by regression from the measured input and output signals of the process. Figure 3 shows typical process input and output signals during the steady-state change. The steady-state process gain can be easily calculated as follows:
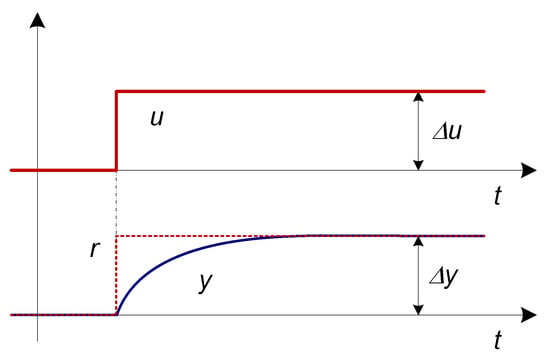
Figure 3.
Typical process input (u) and output (y) signals during the open-loop or closed-loop steady-state change in the process, where r = KPR∙u.
The calculation of the controller parameters depends on the controller structure. When choosing the following 2-DOF controller:
where KP, KI, KD and TF are the proportional, integral, and derivative gains of the controller and the filter time constant of the controller, respectively. The chosen 2-DOF controller structure is one of the most common structures in process control. Considering (13), the expression (11) becomes:
The choice of the controller filter time constant TF depends on the desired high-frequency gain of the controller, which corresponds to KD/TF. Similar to the VRFT method, the process input and output signals can be additionally filtered (4) to reduce the bias in noisy signals, as shown in Section 4.
The controller gains (KI, KP and KD) can be calculated using a regression or optimization method. For process input and output signals, represented by n discrete measurements, the regression matrix Ψ is as follows:
where iF, eF, and yF are time equivalents of the Laplace signals IF(s), EF(s) and YF(s), respectively, which can be derived by filtering process signals as shown in Figure 4.
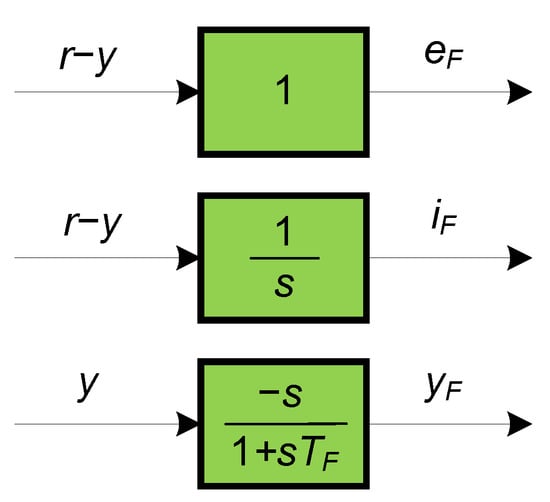
Figure 4.
Filtering process input (u) and output (y) signals to obtain the regression signals eF, iF and yF, where r = KPR u.
The controller parameters are then calculated using the least-squares regression method:
where u is the vector of the process input measurements:
In practice, however, expression (14) is not perfectly satisfied. The largest differences between the left and right sides of the above expression usually occur in the first moments after the process input (u) changes. These differences are unavoidable, for example, in delayed processes where the left side of the expression increases steadily (due to IF(s)) even though the process input signal is constant during the time delay. To alleviate the mentioned problems, expression (14) should be considered only from the time when the process output (y) starts to change (e.g., after reaching 10% of the total steady-state change), as shown in Figure 5.
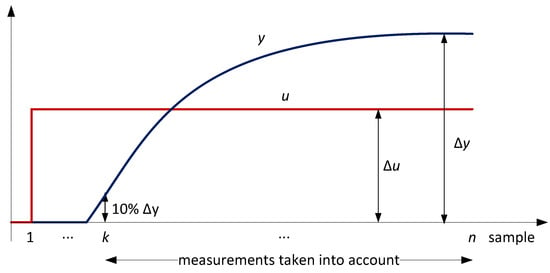
Figure 5.
Time range of measurements considered in the regression method.
Therefore, the weighted least-squares regression method should be used instead:
where W is a square diagonal matrix whose diagonal elements are zero for samples 1…k − 1 (see Figure 5), where the change in process output is less than 10% of the total change in steady state, and one for the remaining diagonal elements:
where w1…wk−1 = 0 and wk…wn = 1.
As mentioned in the previous section, all signals used in regression methods should be additionally filtered (4) if the process measurement noise is present. However, the problem with this is that the additional filter (4) includes the desired closed-loop transfer function GCL. The advantage of the proposed tuning method is that it does not require the definition of the desired closed-loop transfer function. Fortunately, for the purposes of signal filtering, the desired closed-loop transfer function need not be exact. In fact, it is sufficient to estimate the desired closed-loop dynamics by the first-order transfer function with steady-state gain 1 without time delay:
where the desired closed-loop time constant TCL is equal to the process time constant TOL. The latter can be estimated as the sum of the process time constants without pure time delay, which, according to expression (7), is equivalent to:
In practice, the sum of the process time constants and the time delay corresponds to the first process moment or the average residence time tar [34], which can be easily calculated or estimated from the process step response as shown in Figure 6.
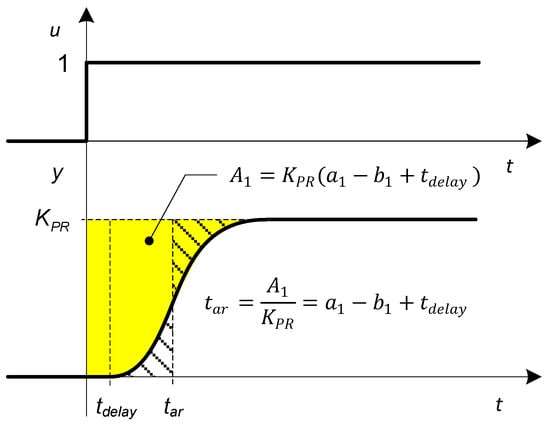
Figure 6.
The average residence time tar can be determined from the process open-loop response by means of integrating the yellow area or by estimating the position of the vertical line tar so that the shaded areas are equal.
The desired closed-loop time constant is thus:
Once the closed-loop time constant is determined, the additional filter F(s) can be calculated using expression (4). The only remaining parameter is the high-frequency filter, whose cutoff frequency can be pragmatically set to the reciprocal of the controller filter time constant:
Thus, the additional signal filter is the following:
The controller parameters are then calculated using the following expression:
where the regression matrix ΨF contains additional filtered signals eF, iF, and yF, as shown in Figure 7.
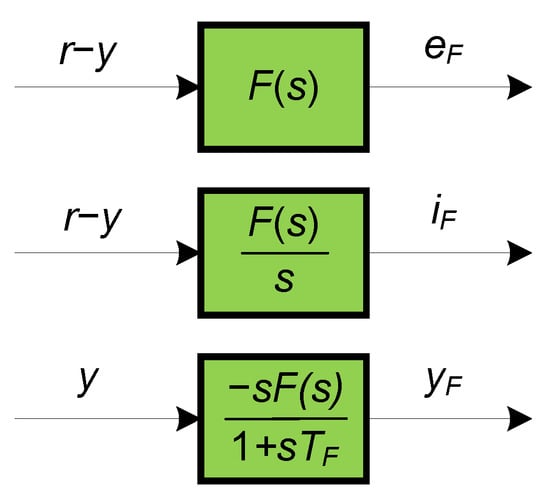
Figure 7.
Filtering of input (u) and output (y) signals to obtain additionally filtered regression signals eF, iF and yF, where r = KPR u.
The signal vector uF contains the measured values of the filtered signal u:
Therefore, the signals eF, iF and yF in the regression matrix Ψ (15), including the signal vector u should be additionally filtered with F(s) before calculating the controller parameters by the regression method (25). This method will be referred to as Filtered WLS (FWLS) method.
Remark 1.
If the calculated derivative time constant TD = KD/KP is negative, the derivative gain must be set to KD = 0. The last column (−yF) in the regression matrices Ψ (15) or ΨF (25) should be deleted. Of course, the resulting controller vector in (18) and (25) reduces only to the integrating (KI) and proportional (KP) gain.
Remark 2.
When using the WLS and FLWS methods, all signals during process time delay, including the time it takes for the process output to change by 10% (see Figure 5), are ignored in the regression calculation. For highly delayed processes and/or higher-order processes with PID control, this means that the process input signals are generally smaller than the open-loop input signals before the process reaches 10% of the total steady-state change. Therefore, for highly delayed processes or higher-order processes, slower closed-loop responses can be expected compared to open-loop responses. This is an advantage, since such processes generally require slower closed-loop responses to remain stable.
The entire procedure for calculating the controller parameters is as follows:
- Measure the open-loop response of the process and obtain the process input (uOL) and output (yOL) signals and subtract the initial steady-state values of the signals.
- Estimate the process gain KPR from the steady-states values of the input and output signals of the process.
- Calculate the reference signal r from (10) or Figure 3 (can be calculated automatically).
- Find the time when the process output has risen to 10% of the final steady-state value (see Figure 5) and calculate the controller parameters from (18) or (25).
Please note that the calculation of the controller parameters can be automated using Matlab/Octave scripts available online. These scripts are described in Section 6.
Example 1.
Consider the following second-order delayed process:
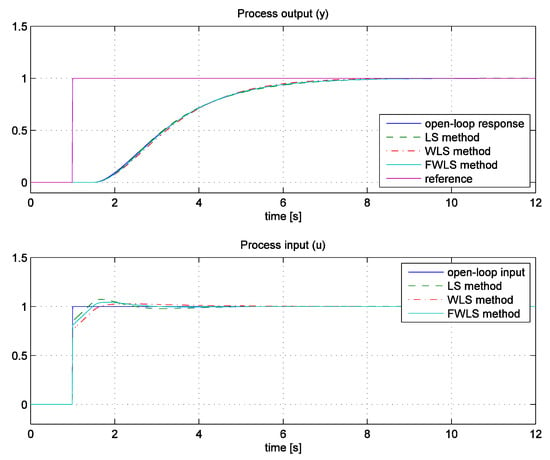
Please note that the actual process transfer function is not known and only the input and output measurements of the process are used to calculate the controller parameters. The process open-loop response on the input step-change is shown in Figure 8(blue solid lines).

Figure 8.
The comparison between the open-loop and closed-loop responses using LS, WLS and FLWS tuning methods.
The steady-state process gain KPR is then calculated from (12) and the signals iF, eF and yF are then calculated according to Figure 4, where the filter time constant of the controller is chosen to be TF = 0.1. The open-loop process output response reaches 10% of the steady-state change at t = 2.3 s, so all diagonal elements of matrix W (19) are set to zero prior to t = 2.3 s. The estimated time delay was tdelay = 0.5 and the average residence time tar = 2.5, so the desired closed-loop time was TCL ≈ tar − tdelay = 2 s.
The calculated controller parameters, using the ordinary least-squares (LS) method (16), the WLS method (18) and FWLS method (25) are given in Table 1.

Table 1.
The calculated PID controller parameters when using the LS, WLS and FWLS methods.
The closed-loop responses to a step-change in the reference signal (r) are shown in Figure 8, where the dashed green lines correspond to the LS method, the dash-dotted red lines to the WLS method and the solid cyan lines to the FWLS method. From this figure, it can be seen that all three methods lead to a relatively close fitting between the open-loop and the closed-loop responses. It should be noted that that, as expected, the LS method leads to the largest overshoots in the process input signal, since the process contains a pure time delay. Therefore, in the rest of the paper, the WLS and FWLS methods are used to calculate the controller parameters.
The presented method works well for noise-free processes. However, in practice, the measurement noise may reduce the accuracy of the calculated controller parameters. The noise sensitivity of the presented method is tested in Section 4.
4. Noise Sensitivity
Any tuning method is sensitive to process measurement noise. The influence of noise is therefore important for the practical implementation of the method. With this in mind, we decided to add a band-limited white noise with a power of 10−5 and a sampling time of 0.01 s (the open-loop and closed-loop sampling time) to the process output using the Simulink block “Band-limited white noise”. The same process as in Example 1 (27) was used. The calculation of the controller parameters was repeated 100 times with different values of the random generator. All 100 open-loop responses to the input step-change are shown in Figure 9 (upper figure). As can be seen, the noise amplitude is about 0.1 (about 10% of the process steady-state change during the experiment). Therefore, the considered samples by WLS and FWLS methods were the ones when the process output reached 20% of the process steady-state change. The controller parameters are first calculated using the WLS method for each noisy open-loop response as described in the previous section. The histogram of the controller parameters for all 100 runs is shown in Figure 10. It is obvious that the calculated controller gains (with the exception of KI) are far from the values obtained with the undisturbed process signals (see red circles in the histograms). The bias caused by the process measurement noise is particularly visible in the calculation of the derivative gain KD, where all values were 0 (according to Remark 1, all originally calculated KD were negative, so the KD parameter was fixed at 0 and the remaining two controller parameters were recalculated).
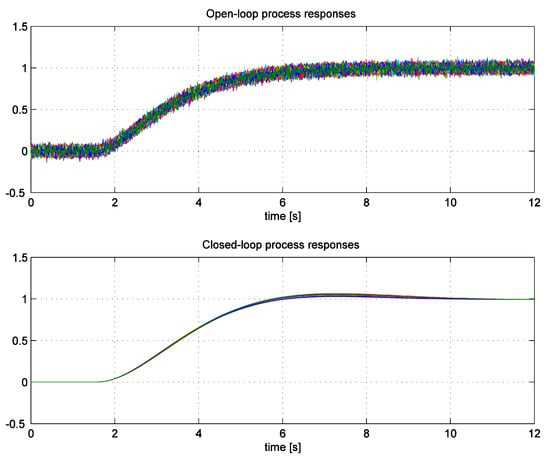
Figure 9.
One hundred process open-loop responses with measurement noise (top figure) and closed-loop responses (bottom figure) using the WLS tuning method without additional noise (for clarity).
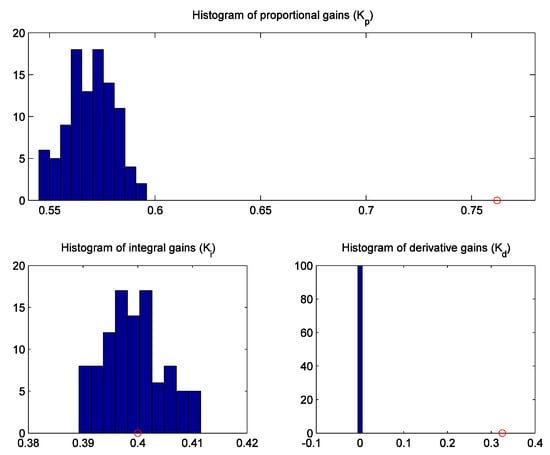
Figure 10.
Histograms of the calculated controller parameters for 100 runs with noisy open-loop responses obtained using the WLS method. The values of the controller parameters obtained with undisturbed open-loop responses without noise are represented by red circles.
The closed-loop process output responses using the calculated controller parameters, are shown in Figure 9 (bottom panel). Please note that no noise was added to the process output in the closed-loop configuration to more clearly show the effects of process noise. The dispersion of the closed-loop responses is relatively small, but all of the closed-loop responses exhibit some overshoot that was not present in the original response in the case without noise (see Figure 8).
The controller parameters are then calculated using the FWLS method for each noisy open-loop response. The histogram of the controller parameters for all 100 runs is shown in Figure 11. The advantage of the additional signal filtering is more than obvious. The obtained histograms of the controller parameters are now scattered around the values obtained for the unperturbed process signals (indicated by red circles in the histograms).
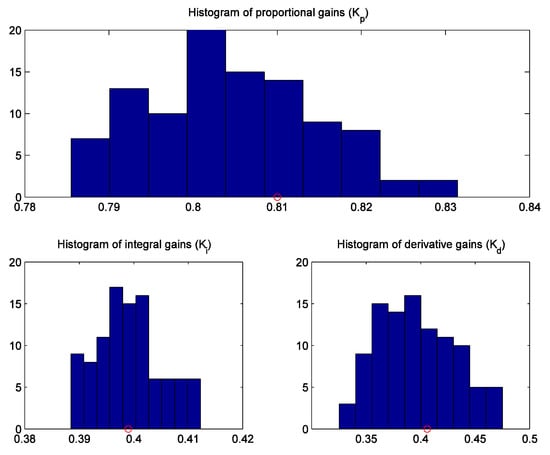
Figure 11.
Histograms of the calculated controller parameters for 100 runs in noisy open-loop responses obtained using the FWLS method. The values of the controller parameters obtained with undisturbed open-loop responses without noise are represented by red circles.
The closed-loop output responses of the process, using the controller parameters calculated by the FWLS method are shown in Figure 12 (bottom panel). Again, note that no noise was added to the process output in the closed-loop configuration to more clearly show the effects of process noise. The scatter of the closed-loop responses is now even lower than before, and all 100 closed-loop responses are very similar to the closed-loop response obtained using the FWLS method in Figure 8 with no visible overshoots.
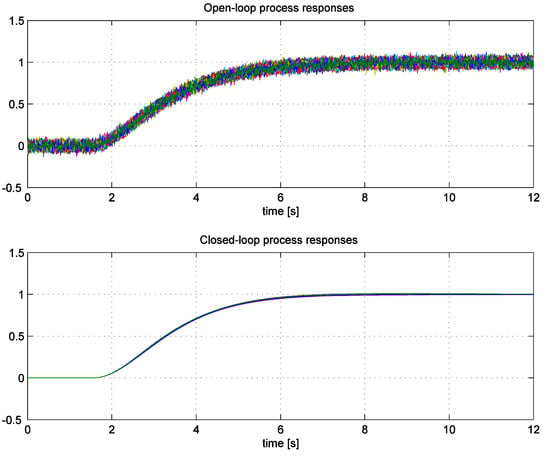
Figure 12.
One hundred process open-loop responses with measurement noise (top figure) and closed-loop responses (bottom figure) using FWLS tuning method without additional noise (for clarity).
Due to the significantly improved closed-loop responses in the presence of process measurement noise, the FWLS method is used in the following derivations.
5. Adaptive Equalization Method
In the previous sections, the FWLS method was derived and tested, based on equating the open-loop and closed-loop responses of the process. The remaining question is whether the proposed equalization method is limited only to the closed-loop transfer functions that are equal to the scaled open-loop process transfer functions. Indeed, in practice, a faster or even slower closed-loop behavior is often required. On the other hand, the advantage of the proposed method is that it does not require an explicit definition of the closed-loop transfer function, since it is implicitly defined by the existing open-loop response. Thus, the question arises whether it is possible to achieve faster or slower control response without explicitly defining the desired control transfer function? The answer to this question is positive, but with some limitations, as will be explained below.
One possible solution to change the closed-loop speed is to change the measured signals u and y while keeping the already calculated reference signal r (10). Figure 13 illustrates the basic idea. Specifically, the input and output signals of the process can be accelerated (or slowed down) by applying appropriate filters. If the signals u* and y* are used instead of the measured signals u and y, the closed-loop response of the process input should be similar to that of u*. Therefore, the closed-loop response of the process output should be similar to y*. Therefore, using a suitable filter, the closed-loop response can become faster or slower than the open-loop response when the u and y signals are replaced by y* and u*.
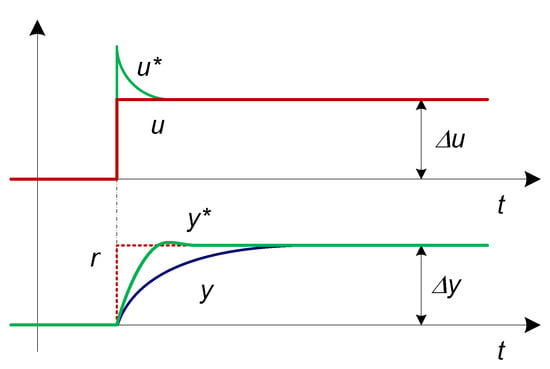
Figure 13.
Measured process input (u) and output (y) signals with artificially calculated reference signal (r) (dashed line) represented by r = KPR∙u and filtered process input (u*) and output (y*) signals (solid green lines) during the open-loop experiment.
What kind of filter should be used? The simplest solution would be to filter the process input and output signals with the following filter:
However, in this case, the process transfer function GP should be known and the desired closed-loop transfer function GCL should be defined as in the VRFT method. Therefore, all the advantages of the proposed equalization method would be lost. On the other hand, the process transfer function could be approximated by the first-order process with estimated time delay and average residence time tar (sum of process time constants), while the desired closed-loop transfer function GCL could be defined similarly to the process transfer function but with faster or slower time constant:
where kS stands for speed factor (kS > 1 means that the closed-loop response is faster than the open-loop response and vice versa) and t*ar is given in (22). In this case, expression (28) simplifies to:
The signals r, u* and y* can then be easily calculated as follows:
corresponding to the desired speed factor kS. However, if the desired closed-loop response is faster than the open-loop response (kS > 1), the high-frequency measurement noise in y will be amplified by an additional factor kS when y* is calculated. This can be avoided by filtering all three signals in (31) by the additional inverse filter GF−1(s) = GF1(s):
Therefore, only the reference signal (KPR∙u) must be additionally filtered with GF1(s), and the desired closed-loop speed can be modified according to the speed factor kS. The new signal r is shown in Figure 14. The controller parameters are then calculated by first filtering all three signals in (32) by (24), where the desired closed-loop time constant is:
and then apply the regression formula (25).
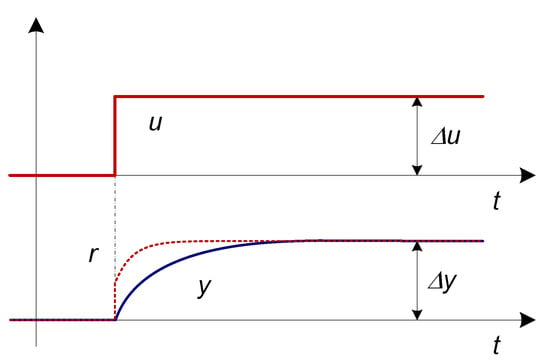
Figure 14.
Measured process input (u) and output (y) signals with artificially calculated reference (r) signal (dashed line) represented by r = GF1(s)KPR∙u.
Due to the approximated values for the average residence time and time delay, the complexity of the actual process, and the fixed PID controller structure, the process input closed-loop signal u*CL:
generally differ from the filtered actual process input signal uF (26). Increasing the closed-loop speed factor kS generally increases the difference between the u*CL and uF. Therefore, the speed factor kS should not be increased too much. The proposed method for automatically determining the speed factor kS increases it until the difference between u*CL (34) and the filtered process input signal uF (26) becomes larger than a certain threshold:
where σ denotes the standard deviation of the signal and σUR is a relative standard deviation. The suggested value for σURmax is 0.1.
In addition to limiting the relative standard deviation of the signal difference, the closed-loop process output should not have large overshoots for a step-like reference. According to Figure 13, the maximum overshoot (oy) of the filtered process output signal y* (31) should be limited:
where typical values are 0.02 ≤ oymax ≤ 0.1.
Therefore, an automatic procedure for determining the speed factor kS is to increase it from the initial value kS = 1 until the relative standard deviation (35) exceeds the value 0.1 or the relative filtered overshoot y* (36) exceeds a certain value (e.g., 0.05). Of course, the upper value of speed factor kS should also be limited to a maximum value (i.e., if the closed-loop response should be up to 10-times faster than the open-loop response, the maximum value of kS can be set to 10).
If the process already exceeds one of the set values at speed factor 1, the speed should be reduced until both values, the deviation and the overshoot, are within the specified limits (see flow chart in Figure 15). Again, the lowest value of the speed factor kS should be set. In practice, the minimum value of kS should be set to 0.2. Please note that the limitation of the factor kS is not explicitly shown in the flow chart (Figure 16).
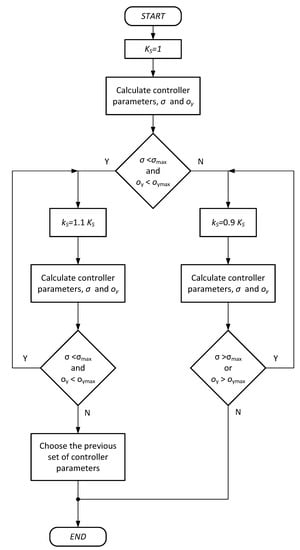
Figure 15.
Flowchart of the applied algorithm for automatic calculation of the controller parameters.
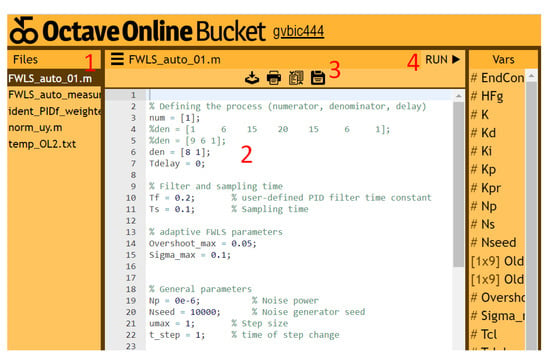
Figure 16.
The Octave Bucket screen which runs the script for the calculation of the controller parameters.
The calculation of the controller parameters can be automated using Matlab/Octave scripts, which are available online [35]. The link to the scripts opens the window shown in Figure 16. The calculation of the controller parameters using the online scripts proceeds as follows:
- Select the appropriate Octave (MATLAB) script (FWLS_auto_01.m if you are calculating the parameters from the process transfer function or FWLS_auto_measurements_01.m if you are calculating the parameters directly from the measured process open-loop response).
- Modify the process and the user-defined parameters.
- Press the “Save” button, and
- Press the “Run” button. The results will be displayed in the lower part of the right window.
- If the script does not finish in time (display “!!! OUT OF TIME !!!” at the bottom of the right window), click the “Run” button again and then click the “Add 15 s” link at the bottom of the right window while the script is running. Click the “Add 15 s” link several times if necessary.
6. Examples and Experiments
The proposed FWLS method and the FWLS method with adaptive calculation of controller parameters were tested on several, significantly different process models:
Thus, the studied process models cover a wide range of dynamics: first-order process, second-order process with delay, non-minimum phase process, high-order process with time delay and second-order process with high time delay.
The PID controller parameters were calculated from the processes open-loop responses with a fixed filter time constant TF = 0.2, according to expressions (25) and Figure 16 or directly using the Matlab/Octave script [35], as mentioned in the previous section.
The chosen maximum values of relative standard deviation (35) and overshoot (36) are σURmax = 0.1 and oymax = 0.05, respectively. The obtained controller parameters are listed in Table 2.

Table 2.
PID controller parameters for considered models.
Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 show the closed-loop tracking and control responses. The step input disturbance was added in the middle of the experiment. The response of the first-order process GP1 (Figure 17) shows an ideal match between the open-loop and the closed-loop tracking responses using the FWLS method. The adaptive method automatically increased the closed-loop response by a factor of KS = 9.85 since the maximum allowable speed factor was 10.
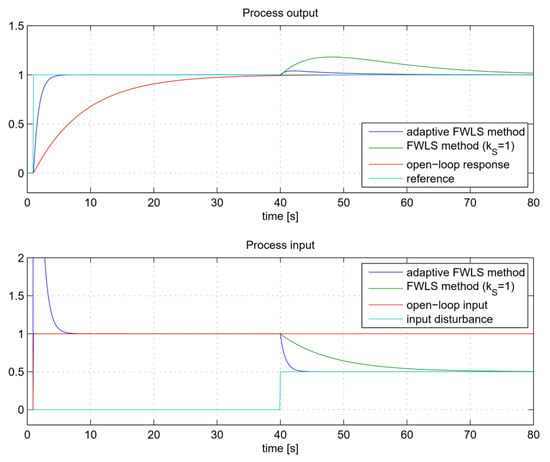
Figure 17.
The closed-loop tracking and control signals for process GP1.
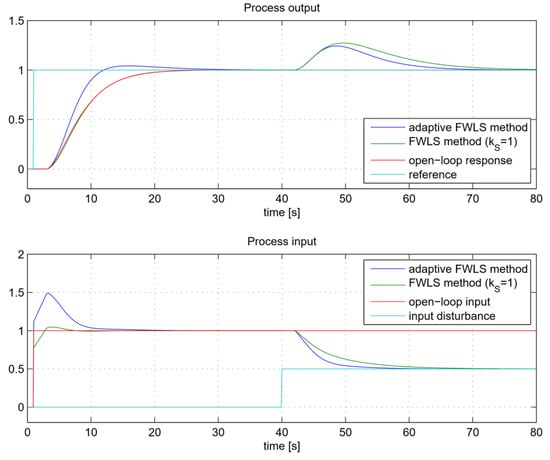
Figure 18.
The closed-loop tracking and control signals for process GP2.
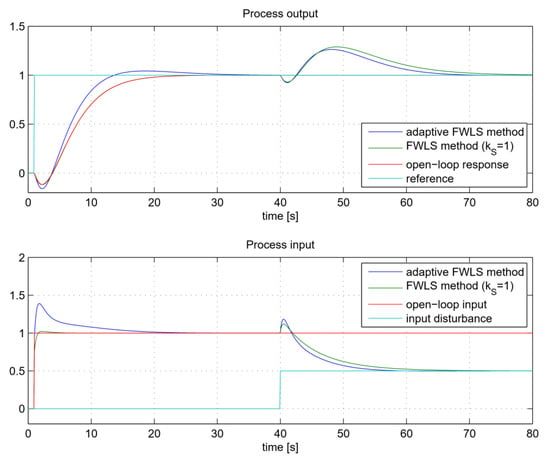
Figure 19.
The closed-loop tracking and control signals for process GP3.
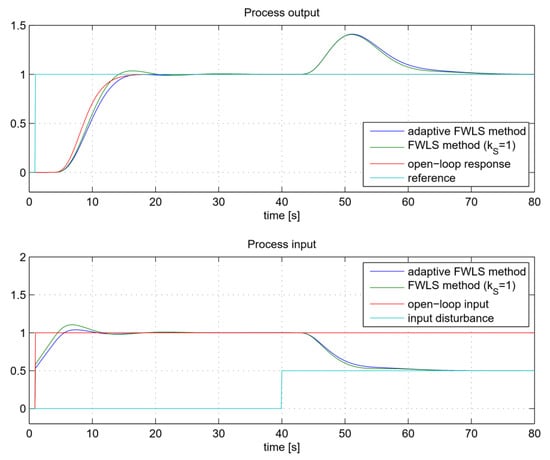
Figure 20.
The closed-loop tracking and control signals for process GP4.
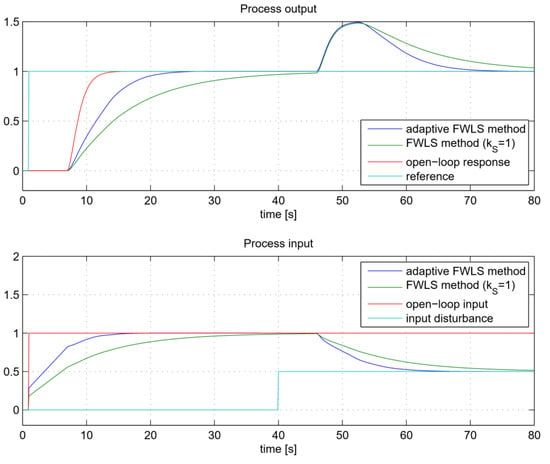
Figure 21.
The closed-loop tracking and control signals for process GP5.
The response of the second-order process with delay GP2 (Figure 18) also shows an almost ideal match between the open-loop and the closed-loop tracking response when using the FWLS method. The adaptive FWLS method increased the closed-loop response by a factor of KS = 1.61. A lower process output overshoot is observed, which is lower than the prescribed limit (5%).
Similarly, the open-loop and the closed-loop responses of the phase non-minimum process GP3 (Figure 19) are almost indistinguishable when the FWLS method is used. The adaptive FWLS method slightly increases the closed-loop response by a factor of KS = 1.33. Again, a smaller process output overshoot of less than 5% can be seen.
On the other hand, the closed-loop responses of the higher-order process GP4 (Figure 20) is slower than the open-loop response when the FWLS method is used. This is consistent with observations in Remark 2. Due to the larger difference (relative standard deviation) between the process open-loop and the closed-loop signals, the adaptive FWLS method slightly reduced the closed-loop speed by 10%.
The responses of the highly delayed second-order process GP5 are shown in Figure 21. It can be seen that the closed-loop response with the FWLS method is much slower than the process open-loop response. The adaptive FWLS method significantly improves the closed-loop response without affecting the closed-loop stability.
In addition to the tests on the process models, the proposed tuning method was also tested on a thermal laboratory process based on the Arduino platform The thermal process was built by the first author of the paper to test SISO and MIMO thermal processes.
The image of the thermal process can be seen in Figure 22.

Figure 22.
The laboratory thermal process based on the Arduino hardware platform.
The electronic scheme of the thermal process, connected to Arduino UNO development board, is shown in Figure 23.
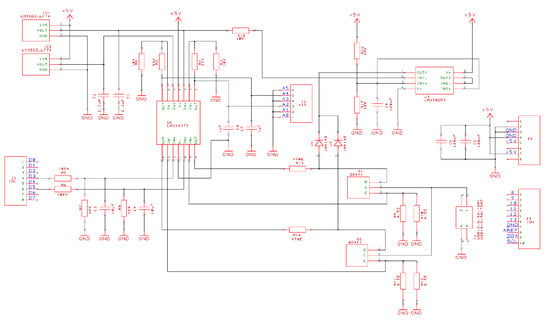
Figure 23.
The electronic scheme of the laboratory thermal process connected to Arduino UNO development board.
The thermal process consists of two NPN transistors BD 441 connected to a 5 V power supply from a separate USB charger. The actual current through the transistors, and thus the power consumed at the transistors, is controlled by the PWM (pulse width modulation) outputs on the Arduino board. The PWM signals are also filtered by the first-order analog filters on the thermal process board.
The thermal process communicates with the computer via the USB port and the GNU Octave program. Communication between Arduino and GNU Octave is established by the open-source library GNU “Arduino” (available at GNU Octave). The “Arduino” library can also upload the required program (firmware) to the Arduino board.
The process input is the heating power of the power transistors (between 0 and 100% with 8-bit resolution) and the process outputs are the temperatures (in degrees Celsius) measured by two temperature sensors with a resolution of about 0.1 degrees Celsius. In our case, the process output was the first temperature sensor output. It was additionally filtered with a first-order filter with a time constant of 20 s to make it more difficult for control.
First, the process open-loop step response was measured. The process input (heating power) was changed from 0 to 80%. The selected sampling time was TS = 0.5 s. Figure 24 shows the open-loop response.
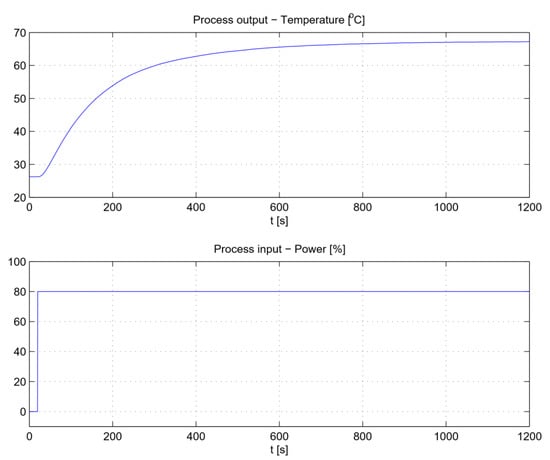
Figure 24.
The thermal process open-loop response.
The response of the process is smooth because of the additional filtering. The open-loop response is then used to calculate the controller parameters. Three sets of PID controller parameters were calculated: (a) applying the FWLS method with kS = 1, (b) applying the adaptive FWLS method with σURmax = 0.1 and oymax = 0.05, and (c) applying the adaptive FWLS method with σURmax = 0.15 and oymax = 0.10. In the following text, cases (b) and (c) will be referred to as “adaptive FWLS 1” and “adaptive FWLS 2”, respectively. In all cases, the derivative filter TF = 2 s was chosen.
The calculated PID controller parameters for all 3 cases are listed in Table 3. It should be noted that the automatic calculation of the PID controller parameters is also available online as a Matlab/Octave script [35] by running the script “FWLS_auto_measurements_01.m”.

Table 3.
The closed-loop parameters for FWLS, adaptive FWLS 1 and adaptive FWLS 2 methods.
The closed-loop responses for all three cases, to the reference change from 35 °C to 45 °C at t = 1000 s and to the −10% process input disturbance at t = 2000 s, are shown in Figure 25. The sampling time was TS = 0.5 s. It can be seen that the closed-loop response of the original FWLS method (blue solid line) is virtually identical to the amplitude-scaled process open-loop response (cyan dash-dotted line). The adaptive algorithms provide significantly faster responses. The adaptive FWLS 1 response is slower than the adaptive FWLS 2 response. On the other hand, the adaptive FWLS 1 method exhibits a smaller overshoot (less than 5%) for a reference change, all according to the selected maximum overshoot. The adaptive FWLS 2 method has the best disturbance-rejection performance.
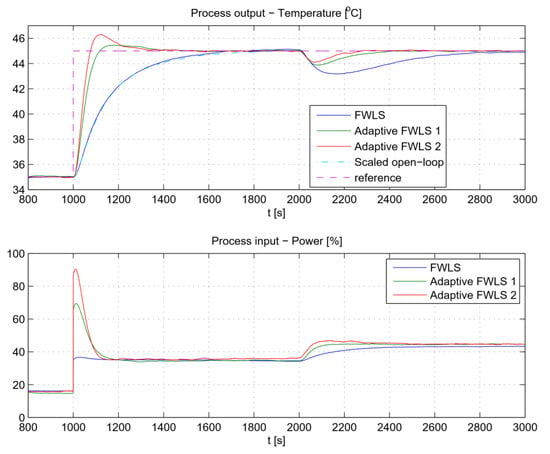
Figure 25.
The thermal process closed-loop responses.
7. Comparison to Other Methods
The FWLS method is based entirely on measuring the input and output signals of the open-loop process, with the desired closed-loop response implicitly defined by the open-loop dynamics. As mentioned earlier, only the adaptive FLWS method and/or the presence of measurement noise requires a rough estimate of the average open-loop residence time, which can be easily obtained from the process open-loop response. To our knowledge, there are no other tuning methods based on a similar tuning procedure. The closest tuning method seems to be the Balanced method [22], which leads to closed-loop dynamics similar to the open-loop dynamics. However, as mentioned earlier, the Balanced method requires iterative closed-loop experiments to compute the PI controller parameters.
Nevertheless, we decided to compare the proposed FWLS method and, for illustrative purposes, the adaptive FWLS method with the Balanced method. The compared processes were selected from the processes tested with the Balanced method [22]:
The parameters of the PID controller were calculated from the processes open-loop responses with a fixed filter time constant TF = 0.1, according to the expressions (25) and Figure 16 or directly using the Matlab/Octave script [35]. The chosen maximum values of relative standard deviation (35) and overshoot (36) are σURmax = 0.1 and oymax = 0.05, respectively. The obtained controller parameters are listed in Table 4. Please note that in the Balanced method, PI controllers are used, so the derivative gain KD = 0.

Table 4.
PID controller parameters for considered models.
The closed-loop responses for all three methods are shown in Figure 26, Figure 27 and Figure 28. It can be seen that the Balanced method results in similar closed-loop responses to the open-loop ones for all three processes considered. However, it can also be seen that the FWLS method leads to much better fitting between the open-loop and closed-loop responses. As expected, the process input responses are also closer to the process open-loop step responses when using the FWLS. In all three cases, the adaptive FWLS method results in a slight increase in closed-loop speed and a slight overshoot.
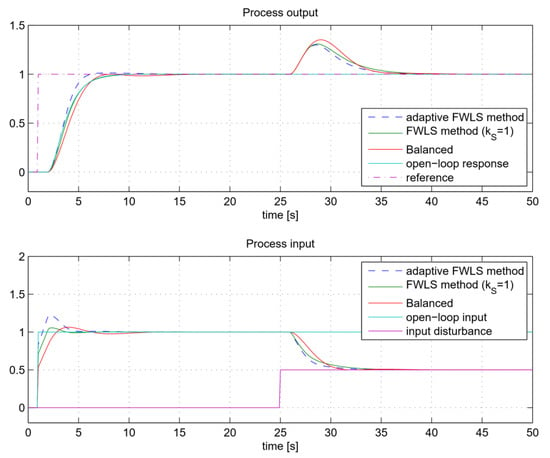
Figure 26.
The closed-loop tracking and control signals for process GP6 when using FLWS, adaptive FLWS and Balanced method.
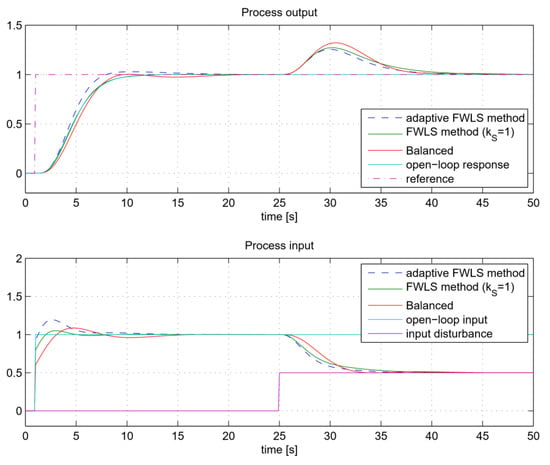
Figure 27.
The closed-loop tracking and control signals for process GP7 when using FLWS, adaptive FLWS and Balanced method.
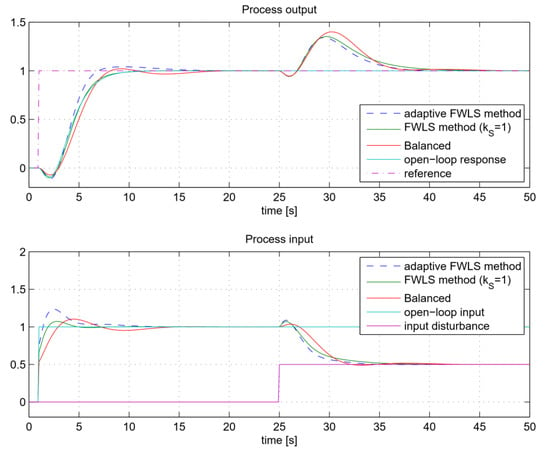
Figure 28.
The closed-loop tracking and control signals for process GP8 when using FLWS, adaptive FLWS and Balanced method.
The values of the integral of the squared error (ISE) were calculated to quantify the similarity between the open-loop (yOL) and closed-loop (yCL) responses during the reference change (ISEy) and to measure the tracking and disturbance-rejection performance (ISEe):
ISEy values were, of course, calculated only for the FWLS and Balanced method, since they are based on equating the open-loop and closed-loop responses. ISEe values were calculated separately for tracking (ISEer) and disturbance rejection (ISEed). All ISE values are listed in Table 5.

Table 5.
ISE values for tracking and disturbance rejection for considered models.
As shown in Table 5, the FWLS responses, according to the ISEy values, fit the open-loop responses better than the Balanced method. As can already be seen from Figure 26, Figure 27 and Figure 28, the adaptive FWLS method is superior in tracking and disturbance rejection. This is to be expected, since the adaptive FWLS method can achieve faster closed-loop responses. Although the FWLS and Balanced method are based on the same tuning criteria, the FWLS method has better tracking and disturbance-rejection ISE values.
8. Conclusions
The main purpose of the proposed method was to develop a tuning method that does not require any information from the user (about the process or the desired closed-loop response), that is based on a simple experiment on the process where the process input signal is not limited to step-like signals during the steady-state change, that is computationally extremely simple, and that does not cause excessive kicks to the process input when the reference signal is changed.
By cleverly manipulating some calculations, such as implicitly defining the closed-loop response from the steady-state response, neglecting the initial process response (during the time delay), and using additional filtering of the measured signals, we were able to solve several problems associated with many other existing tuning methods.
The proposed method is based on a regression, similar to the VRFT method, where an additional signal weighting is introduced to improve the closed-loop responses, especially for highly delayed processes or higher-order processes.
The closed-loop response could be additionally adjusted using the proposed adaptive algorithm, which estimates the process input signal fitting and the process output overshoot. The only parameters required from the user, besides the measured process open-loop time responses, is a rough estimate of the time delay and the average residence time, which can be easily estimated from the process open-loop response even by an untrained user. The mentioned parameters are not required if the adaptive algorithm is not used and the process noise is relatively low. The tuning results for noisy measurements showed a relatively small influence of the noise.
The proposed FWLS and adaptive FWLS algorithms were tested on six different process models, including lower- and higher-order processes, processes without minimum phase, and highly delayed processes, as well as on a temperature laboratory plant. The closed-loop responses obtained were smooth and stable. The method was also compared with the Balanced method and the proposed method showed better agreement between the open-loop and closed-loop responses.
We believe that the proposed method can be successfully applied in industrial practice due to its advantageous properties.
The Matlab/Octave scripts for calculating the PID controller parameters are available online, allowing users to immediately calculate the controller parameters either from the steady-state measurements of the process or from the process transfer function (if available).
Author Contributions
Writing-original draft preparation, D.V., P.M.O., P.B. and M.H. Simulations, D.V., P.B. and M.H. Editing, D.V., P.M.O. and M.H. Project administration, D.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the grants P2-0001 financed by the Slovenian Research Agency, by Clean Hydrogen Partnership (EU Horizon 2020) under Grant Agreement No 101007175 (project REACTT), Advancing University Capacity and Competence in Research, Development and Innovation“ (ITMS project code: 313021X329) supported by Operational Programme Integrated Infrastructure and funded by the European Regional Development Fund and the National Funds through the Portuguese funding agency, FCT—Fundação para a Ciência e a Tecnologia, within project LA/P/0063/2020.
Data Availability Statement
The data presented in this study are available in [35].
Acknowledgments
Supported by Slovenská e-akadémia, n. o.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Campi, M.; Lecchini, A.; Savaresi, S. Virtual reference feedback tuning: A direct method for the design of feedback controllers. Automatica 2002, 38, 1337–1346. [Google Scholar] [CrossRef]
- Campestrini, L.; Eckhard, D.; Chía, L.A.; Boeira, E. Unbiased MIMO VRFT with application to process control. J. Process. Control. 2016, 39, 35–49. [Google Scholar] [CrossRef]
- Jeng, J.-C.; Yeh, C.-H. Coordinated control design for a PEMFC power system using adaptive VRFT method. J. Taiwan Inst. Chem. Eng. 2017, 73, 102–111. [Google Scholar] [CrossRef]
- Jeng, J.-C. Data-Based Tuning of PID Controllers: A Combined Model- Reference and VRFT Method. In PID Control for Industrial Processes; IntechOpen: London, UK, 2018; Available online: https://www.intechopen.com/chapters/63028 (accessed on 23 October 2022).
- Radac, M.-B.; Precup, R.-E.; Roman, R.-C. Data-driven model reference control of MIMO vertical tank systems with model-free VRFT and Q-Learning. ISA Trans. 2018, 73, 227–238. [Google Scholar] [CrossRef]
- Care, A.; Torricelli, F.; Campi, M.C.; Savaresi, S.M. A Toolbox for Virtual Reference Feedback Tuning (VRFT). In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 4252–4257. [Google Scholar] [CrossRef]
- Formentin, S.; Campi, M.C.; Carè, A.; Savaresi, S.M. Deterministic continuous-time Virtual Reference Feedback Tuning (VRFT) with application to PID design. Syst. Control. Lett. 2019, 127, 25–34. [Google Scholar] [CrossRef]
- Ota, N.; Masuda, S.; Matsui, Y. Simultaneous Design of Reference Model and Controller for VRFT using Closed-loop Step Response Data. In Proceedings of the 2019 16th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Pattaya, Thailand, 10–13 July 2019; pp. 866–869. [Google Scholar] [CrossRef]
- Chiluka, S.K.; Ambati, S.R.; Seepana, M.; Gara, U.B.B. A New VRFT Approach for IMC-PID Feedback-Feedforward Controller Design based on Robustness. IFAC PapersOnLine 2020, 53, 147–152. [Google Scholar] [CrossRef]
- Kumar, A.; Zhang, Y.; Chiu, M.-S. VRFT-based digital controller design using a generalized second-order reference model. Comput. Chem. Eng. 2020, 142, 107049. [Google Scholar] [CrossRef]
- Kinoshita, T.; Morota, Y.; Yamamoto, T. Design of a Data-Driven Multi PID Controllers using Ensemble Learning and VRFT. J. Robot. Netw. Artif. Life 2020, 7, 68–72. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, G. Data-driven Two Degrees of Freedom Controller Design for MIMO System via VRFT Approach. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 981–986. [Google Scholar] [CrossRef]
- Condrachi, L.; Vilanova, R.; Barbu, M. Data-Driven Internal Model Control of an Anaerobic Digestion Process. In Proceedings of the 2021 25th International Conference on System Theory, Control and Computing (ICSTCC), Iași, Romania, 20–23 October 2021; pp. 504–509. [Google Scholar] [CrossRef]
- Condrachi, L.; Vilanova, R.; Meneses, M.; Barbu, M. Anaerobic Digestion Process Control Using a Data-Driven Internal Model Control Method. Energies 2021, 14, 6746. [Google Scholar] [CrossRef]
- Zhang, Y.; Kumar, A.; Chiu, M.-S. VRFT-based predictor design for processes with inverse response. J. Taiwan Inst. Chem. Eng. 2021, 130, 104113. [Google Scholar] [CrossRef]
- Kurokawa, R.; Sato, T.; Vilanova, R.; Konishi, Y. Closed-loop Data-driven Trade-off PID Control Design. IFAC PapersOnLine 2018, 51, 244–249. [Google Scholar] [CrossRef]
- Kaneko, O. Data-Driven Controller Tuning: FRIT approach. IFAC Proc. Vol. 2013, 46, 326–336. [Google Scholar] [CrossRef]
- Silawatchananai, C.; Lapanaphan, N.; Ruangurai, P. Double-Loop Controller Tuning Based Fictitious Reference Iterative Tuning (FRIT) for Unmanned Ground Vehicle. In Proceedings of the 2018 7th International Congress on Advanced Applied Informatics (IIAI-AAI), Tottori, Japan, 8–13 July 2018; pp. 554–558. [Google Scholar] [CrossRef]
- Julkananusart, A.; Nilkhamhang, I. Quadrotor tuning for attitude control based on double-loop PID controller using fictitious reference iterative tuning (FRIT). In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 004865–004870. [Google Scholar] [CrossRef]
- Masuda, S. PID controller tuning based on disturbance attenuation FRIT using one-shot experimental data due to a load change disturbance. IFAC Proc. Vol. 2012, 45, 92–97. [Google Scholar] [CrossRef]
- DeKeyser, R. DIRAC: A direct adaptive controller. In Proceedings of the IFAC Workshop on Digital Control, Terrassa, Spain, 5–7 April 2000; pp. 199–204. [Google Scholar]
- Klàn, P.; Gorez, R. Balanced tuning of PI controllers. Eur. J. Control. 2000, 6, 541–550. [Google Scholar] [CrossRef]
- Condrachi, L.; Vilanova, R.; Ceanga, E.; Barbu, M. The Tuning of a Model-Free Controller for an Anaerobic Digestion Process using ADM1 as Virtual Plant. IFAC-PapersOnLine 2019, 52, 99–104. [Google Scholar] [CrossRef]
- Lv, M.; Gao, S.; Wei, Y.; Zhang, D.; Qi, H.; Wei, Y. Model-Free Parallel Predictive Torque Control Based on Ultra-Local Model of Permanent Magnet Synchronous Machine. Actuators 2022, 11, 31. [Google Scholar] [CrossRef]
- Boubakir, A.; Touil, S.A.; Labiod, S.; Boudjerda, N. A robust model-free controller for a three-phase grid-connected photovoltaic system based on ultra-local model. Prot. Control. Mod. Power Syst. 2021, 6, 43. [Google Scholar] [CrossRef]
- Vrančić, D.; Strmčnik, S.; Juričić, Đ. A magnitude optimum multiple integration method for filtered PID controller. Automatica 2001, 37, 1473–1479. [Google Scholar] [CrossRef]
- Vrančić, D.; Strmčnik, S.; Kocijan, J.; de Moura Oliveira, P.B. Improving disturbance rejection of PID controllers by means of the magnitude optimum method. ISA Trans. 2010, 49, 47–56. [Google Scholar] [CrossRef]
- Vrančić, D. Magnitude optimum techniques for PID controllers. In Introduction to PID Controllers: Theory, Tuning and Application to Frontiers Areas; Panda, R.C., Ed.; InTech: Rijeka, Croatia, 2011; pp. 75–102. [Google Scholar]
- Vrančić, D.; Huba, M. High-Order Filtered PID Controller Tuning Based on Magnitude Optimum. Mathematics 2021, 9, 1340. [Google Scholar] [CrossRef]
- Vrančić, D.; Lieslehto, J.; Strmcnik, S. Designing a MIMO PI controller using the multiple integration approach. Process. Control. Qual. 2001, 11, 455–468. [Google Scholar] [CrossRef]
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar] [CrossRef]
- Vilanova, R.; Visioli, A. PID Control in the Third Millennium, 1st ed.; Vilanova, R., Visioli, A., Eds.; Advances in Industrial Control; Springer: London, UK, 2012; ISBN 978-1-4471-2424-5. [Google Scholar]
- Vítečkova, M.; Víteček, A. 2DOF PI and PID controllers tuning. In Proceedings of the 9th IFAC Workshop on Time Delay Systems, Prague, Czech Republic, 7–9 June 2010; Volume 9, pp. 343–348. [Google Scholar]
- Åström, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tuning, 2nd ed.; Instrument Society of America: Pittsburgh, PA, USA, 1995. [Google Scholar]
- Octave Online Bucket Website. Available online: https://octav.onl/gvbic444 (accessed on 20 October 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).