Convergence of the Euler Method for Impulsive Neutral Delay Differential Equations

Abstract

In this paper, we are concerned with a fixed stepsize Euler method for a class of linear impulsive neutral delay differential equations. By taking the partition nodes for the Euler scheme and employing the linear interpolation, we strictly prove the method is convergent of order one. Two examples illustrating the efficiency results are also presented.

1. Introduction

Neutral delay differential equations (NDDEs) arise widely in the study of circuit theory [1], control theory [2,3,4,5], population dynamics [6], bioengineering [7] and so on; some researchers also considered the delayed neural networks [8], the stochastic area [9], etc. In particular, the mathematical theories of impulsive neutral delay differential equations (INDDEs) have been developed by a large number of researchers in recent years. For example, their existence, uniqueness and oscillation have been studied by some professors in [10,11,12], their stability has also been studied extensively. In [13], Xiaodi Li and Feiqi Deng used the Razumikhin method for impulsive functional differential equations of neutral type. In [14], Baînov Drumi Dimitrov, Stamova and Ivanka M. studied the uniform asymptotic stability of impulsive differential difference equations of neutral type by Lyapunov’s direct method. In [15,16], both authors found the asymptotic behavior of solutions for INDDEs. In [17,18], the authors discussed the exponential stability of INDDEs. However, their explicit solutions are considerably difficult or even impossible to obtain. This is why we need to investigate the numerical methods of INDDEs and use these works for mathematical simulations.

For non-neutral-type differential equations, there are lots of publications dealing with their numerical methods. In paper [19], Zhuo Xue, Xinxin Han and Kaining Wu studied the stability of the Runge–Kutta method for linear impulsive differential equations (IDEs). In paper [20], Shujin Wu investigated the Euler method for random impulsive differential equations. In [21], Covachev et al. obtained a convergent difference approximation for a nonlinear impulsive system in a Banach space. Bainov et al. [22] studied some difference methods for the first-order partial impulsive functional differential equations and proved the convergence for general numerical methods. Then, Ding, Wu and Liu [23] used their idea to investigate the Euler scheme and its convergence for impulsive delay differential equations (IDDEs). Our work was in part motivated by this. So far, however, only few papers have studied numerical methods for INDDEs. It is the purpose of this paper to investigate numerical solutions for INDDEs using the Euler scheme. The difficulty is caused by the neutral term and delay term, which should be simulated with another stepsize in case of the effect of impulse.

The aim of the present paper is as follows. First, we establish the Euler scheme of linear systems for INDDEs. After assuming the conditions, we present a method to take the fixed stepsize and design a new interpolation idea to deal with those non-integer partition nodes. Our main result first proves the convergence order by means of the induction and the technique of inequality within the first interval, and then uses mathematical induction to reach the final conclusion. Finally, based on the idea discussed before, we offer explicit solutions and Euler schemes of two examples, using MATLAB R2023b to verify their convergence orders, respectively, which are illustrated clearly in two tables and figures.

2. Main Result

In this paper, we consider the INDDE

$$\left\{\begin{array}{cc}{x}^{\prime }\left(t\right)=ax\left(t\right)+bx(t-\tau )-c{x}^{\prime }(t-\sigma ),\hfill & t\ge 0,t\ne {\tau }_k,\hfill \\ \Delta x\left({\tau }_k\right)=l_k,\hfill & k\in {\mathbb{Z}}^{+},\hfill \\ x\left(t\right)=\varphi \left(t\right),\hfill & -r\le t\le 0,\hfill \end{array}\right.$$

(1)

where a, b, c, $\sigma ,\tau$ and $l_k$ are real constants, $\sigma >0,\tau >0$ and ${\mathbb{Z}}^{+}=\{1,2,\cdots \}$, $x^{\prime }\left(t\right)$ denotes the right-hand derivative of $x\left(t\right)$, $\varphi \left(t\right)\in C^1$, $r=max\{\sigma ,\tau \}$ and $\Delta x\left({\tau }_k\right)=x\left({\tau }_k^{+}\right)-x\left({\tau }_k^{-}\right)$, $x\left({\tau }_k^{+}\right)=x\left({\tau }_k\right)$. The impulse times ${\tau }_k$ satisfy $0<{\tau }_1<\cdots <{\tau }_k<\cdots$ and ${lim}_{k\to \infty }{\tau }_k=\infty$.

We let ${\tau }_k-\sigma$ and ${\tau }_k-\tau$ be not impulsive points, ∀$k\in {\mathbb{Z}}^{+}$, ${\tau }_k-{\tau }_{k-1}>r$. The Euler scheme for Equation (1) is

$$\left\{\begin{array}{c}{X}_{n+1}=X_n+ah{X}_n+bh{X}_{n-m_1+{\delta }_1}-c{X}_{n-m_2+1+{\delta }_2}+c{X}_{n-m_2+{\delta }_2},n\ne {\eta }_k-1,\hfill \\ X_{{\eta }_k}=X_{{\eta }_k-1}+l_k,\hfill \\ X_i=\varphi \left(ih\right),ih\in \left[-r,0\right],i\in \left[-m,0\right],\hfill \end{array}\right.$$

(2)

where $\left(m_1-{\delta }_1\right)h=\tau ,\left(m_2-{\delta }_2\right)h=\sigma$, $m_1,m_2\in {\mathbb{Z}}^{+},{\delta }_1,{\delta }_2\in \left[0,1\right)$, h is a stepsize, $0<h\le \tau$ and $X_{n-m_j+{\delta }_j}(j=1,2)$ are defined by interpolations

$$X_{n-m_j+{\delta }_j}={\delta }_j{X}_{n-m_j+1}+(1-{\delta }_j)X_{n-m_j}.$$

(3)

Let ${\eta }_0=0$ and

$$\begin{array}{c}\hfill {\eta }_k=\left\{\begin{array}{cc}\frac{{\tau }_k}{h},\hfill & \frac{{\tau }_k}{h}\in {\mathbb{Z}}^{+},\hfill \\ \lfloor \frac{{\tau }_k}{h}\rfloor +1,\hfill & Otherwise.\hfill \end{array}\right.\end{array}$$

(4)

Note that $\lfloor ·\rfloor$ is the greatest integer function.

Given $T>0$, there exist $p,N\in {\mathbb{Z}}^{+}$, which makes $T=pmh$, $0<{\tau }_1<\cdots <{\tau }_k<\cdots <{\tau }_N\le T<{\tau }_{N+1}$, where $m=max\{m_1,m_2\}$. From [11], we know that $x\left(t\right)$ and $x^{\prime }\left(t\right)$ are bounded. Therefore, we assume that there exits an $M>0$ such that the solution $x\left(t\right)$ of Equation (1) satisfies $\left|x\right(t\left)\right|\le M$ and $\left|x^{\prime }\left(t\right)\right|\le M$ for $t\in [-r,T]$. For the sake of simplicity, we also assume $\left|\varphi \right(t)-\varphi (s\left)\right|\le M|t-s|$ and $|{\varphi }^{\prime }\left(t\right)-{\varphi }^{\prime }\left(s\right)|\le M|t-s|$.

The exact solutions $x\left(t_n\right)$ are approximated by $X_n$ at $t_n=nh,n\in {\mathbb{Z}}^{+},0\le n\le pm$. The initial function is $X_i=\varphi \left(ih\right),ih\in [-r,0]$.

We let $e_n=|x\left(nh\right)-X_n|$, which denotes the global error. The following theorem illustrates that the convergence order of the Euler method for Equation (1) is one by analyzing the global error $e_n$.

Theorem 1.

The convergent order of Euler scheme Equation (2) is one, if there exists a $C>0$, such that $e_n\le Ch$, $1\le n\le sm$.

Proof. 

We show there exists a $C_k>0$ such that

$$e_n\le C_{k}h,n\in I_k=[{\eta }_{k-1}+1,{\eta }_k]\bigcap \mathbb{Z},k=1,2,3,\cdots ,N.$$

(5)

First, we show that there exists a $C_1>0$ such that $e_n\le C_{1}h$, $n\in I_1$. For the sake of simplicity, we assume that $r=max\{\sigma ,\tau \}=\sigma$, $m=m_2$ and $0<\tau <\sigma <{\tau }_1$.

When $0\le t_n\le \tau <\sigma <{\tau }_1$, $1\le n\le m_1-{\delta }_1<m_2-{\delta }_2<{\eta }_1$, we have

$$\begin{array}{cc}{e}_n\hfill & =|x\left(nh\right)-X_n|\hfill \\ \hfill & =|x\left((n-1)h\right)+{\int }_{(n-1)h}^{nh}ax\left(t\right)+bx(t-\tau )-c{x}^{\prime }(t-\sigma )dt-X_{n-1}-ah{X}_{n-1}\hfill \\ \hfill & -bh{X}_{n-m_1-1+{\delta }_1}+c{X}_{n-m_2+{\delta }_2}-c{X}_{n-m_2-1+{\delta }_2}|\hfill \\ \hfill & \le e_{n-1}+|{\int }_0^{h}ax((n-1)h+t)+bx((n-m_1-1+{\delta }_1)h+t)-c{x}^{\prime }\left(\right(n-m_2\hfill \\ \hfill & -1+{\delta }_2)h+t)dt-ah{X}_{n-1}-bh{X}_{n-m_1-1+{\delta }_1}+c{X}_{n-m_2+{\delta }_2}-c{X}_{n-m_2-1+{\delta }_2}|\hfill \\ \hfill & \le e_{n-1}+{\int }_0^h\left|a\right||x((n-1)h+t)-X_{n-1}|+\left|b\right||x((n-m_1-1+{\delta }_1)h+t)\hfill \\ \hfill & -X_{n-m_1-1+{\delta }_1}|dt+\left|c\right||{\int }_0^h-x^{\prime }((n-m_2-1+{\delta }_2)h+t)dt+X_{n-m_2+{\delta }_2}\hfill \\ \hfill & -X_{n-m_2-1+{\delta }_2}|,\hfill \end{array}$$

(6)

where

$$\begin{array}{cc}\hfill & |x((n-1)h+t)-X_{n-1}|\hfill \\ \hfill & =|x\left((n-1)h\right)+{\int }_{(n-1)h}^{t+(n-1)h}ax\left(u\right)+bx(u-\tau )-c{x}^{\prime }(u-\sigma )du-X_{n-1}|\hfill \\ \hfill & \le e_{n-1}+{\int }_0^t\left|a\right|\left|x((n-1)h+u)\right|+\left|b\right|\left|x((n-m_1-1+{\delta }_1)h+u)\right|+\left|c\right||x^{\prime }\hfill \\ \hfill & ((n-m_2-1+{\delta }_2)h+u)|du\hfill \\ \hfill & \le e_{n-1}+(\left|a\right|+\left|b\right|+\left|c\right|)Mh,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & |x((n-m_1-1+{\delta }_1)h+t)-X_{n-m_1-1+{\delta }_1}|\hfill \\ \hfill & =|\varphi (t+(n-m_1-1+{\delta }_1)h)-\varphi \left((n-m_1-1+{\delta }_1)h\right)|\hfill \\ \hfill & \le Mh,\hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill & |{\int }_0^h-x^{\prime }((n-m_2-1+{\delta }_2)h+t)dt+X_{n-m_2+{\delta }_2}-X_{n-m_2-1+{\delta }_2}|\hfill \\ \hfill & =|x\left((n-m_2-1+{\delta }_2)h\right)-x\left((n-m_2+{\delta }_2)h\right)+X_{n-m_2+{\delta }_2}-X_{n-m_2-1+{\delta }_2}|\hfill \\ \hfill & =|\varphi \left((n-m_2-1+{\delta }_2)h\right)-\varphi \left((n-m_2+{\delta }_2)h\right)+\varphi \left((n-m_2+{\delta }_2)h\right)-\varphi \hfill \\ \hfill & \left((n-m_2-1+{\delta }_2)h\right)|\hfill \\ \hfill & =0.\hfill \end{array}$$

(9)

Substituting Equations (7)–(9) into Equation (6), we obtain

$$\begin{array}{cc}{e}_n\hfill & \le e_{n-1}+\left|a\right|h[e_{n-1}+(\left|a\right|+\left|b\right|+\left|c\right|)Mh]+\left|b\right|M{h}^2+\left|c\right|·0\hfill \\ \hfill & =e_{n-1}(1+\left|a\right|h)+M{h}^2[\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|]\hfill \\ \hfill & \le C_{1,1,1}h,\hfill \end{array}$$

(10)

and letting $e_0=0$, by Gronwall inequality [24,25], we obtain

$$C_{1,1,1}=\frac{\left[\right|a\left|\right(\left|a\right|+\left|b\right|+\left|c\right|)+|b\left|\right]M}{\left|a\right|}{e}^{\left|a\right|T}.$$

When $\tau <t_n\le 2\tau <\sigma <{\tau }_1$, $m_1-{\delta }_1<n\le 2(m_1-{\delta }_1)<m_2-{\delta }_2<{\eta }_1$, we have

$$\begin{array}{cc}{e}_n\hfill & =|x\left(nh\right)-X_n|\hfill \\ \hfill & \le e_{n-1}+{\int }_0^h\left|a\right||x((n-1)h+t)-X_{n-1}|+\left|b\right||x((n-m_1-1+{\delta }_1)h+t)\hfill \\ \hfill & -X_{n-m_1-1+{\delta }_1}|dt+\left|c\right||{\int }_0^h-x^{\prime }((n-m_2-1+{\delta }_2)h+t)dt+X_{n-m_2+{\delta }_2}\hfill \\ \hfill & -X_{n-m_2-1+{\delta }_2}|.\hfill \end{array}$$

(11)

As discussed in Equation (7), for $t\in [0,h]$, we obtain

$$|x((n-1)h+t)-X_{n-1}|\le e_{n-1}+(\left|a\right|+\left|b\right|+\left|c\right|)Mh,$$

(12)

$$\begin{array}{cc}\hfill & |x((n-m_1-1+{\delta }_1)h+t)-X_{n-m_1-1+{\delta }_1}|\hfill \\ \hfill & =|x\left((n-m_1-1)h\right)+{\int }_{(n-m_1-1)h}^{(n-m_1-1+{\delta }_1)h+t}ax\left(u\right)+bx(u-\tau )-c{x}^{\prime }(u-\sigma )du\hfill \\ \hfill & -{\delta }_1{X}_{n-m_1}-(1-{\delta }_1)X_{n-m_1-1}|\hfill \\ \hfill & \le e_{n-m_1-1}+|{\int }_0^{{\delta }_{1}h+t}ax(u+(n-m_1-1)h)+bx(u+(n-2m_1-1+{\delta }_1)h)\hfill \\ \hfill & -c{x}^{\prime }(u+(n-m_1-m_2-1+{\delta }_2)h)du-{\delta }_1(X_{n-m_1}-X_{n-m_1-1})|\hfill \\ \hfill & \le e_{n-m_1-1}+|{\int }_0^{{\delta }_{1}h}ax(u+(n-m_1-1)h)+bx(u+(n-2m_1-1+{\delta }_1)h)\hfill \\ \hfill & -c{x}^{\prime }(u+(n-m_1-m_2-1+{\delta }_2)h)du+{\int }_{{\delta }_{1}h}^{{\delta }_{1}h+t}ax(u+(n-m_1-1)h)\hfill \\ \hfill & +bx(u+(n-2m_1-1+{\delta }_1)h)-c{x}^{\prime }(u+(n-m_1-m_2-1+{\delta }_2)h)du\hfill \\ \hfill & -{\delta }_1(ah{X}_{n-m_1-1}+bh{X}_{n-2m_1-1+{\delta }_1}-c{X}_{n-m_1-m_2+{\delta }_2}+c{X}_{n-m_1-m_2-1+{\delta }_2})|\hfill \\ \hfill & \le e_{n-m_1-1}+|{\int }_0^{{\delta }_{1}h}a(x(u+(n-m_1-1)h)-X_{n-m_1-1})+b\left(x\right(u+(n-2m_1\hfill \\ \hfill & -1+{\delta }_1\left)h\right)-X_{n-2m_1-1+{\delta }_1})du+{\int }_0^{{\delta }_{1}h}-c{x}^{\prime }(u+(n-m_1-m_2-1+{\delta }_2)h)du\hfill \\ \hfill & -{\delta }_1(-c{X}_{n-m_1-m_2+{\delta }_2}+c{X}_{n-m_1-m_2-1+{\delta }_2})|+(\left|a\right|+\left|b\right|+\left|c\right|)Mh\hfill \\ \hfill & \le e_{n-m_1-1}+\left|a\right|{\delta }_{1}h(e_{n-m_1-1}+(\left|a\right|+\left|b\right|+\left|c\right|)M{\delta }_{1}h)+\left|b\right|M{\delta }_1^2{h}^2+\left|c\right|\left|x\right((n\hfill \\ \hfill & -m_1-m_2-1+{\delta }_2\left)h\right)-x\left((n-m_1-m_2-1+{\delta }_1+{\delta }_2)h\right)+X_{n-m_1-m_2+{\delta }_2}\hfill \\ \hfill & -X_{n-m_1-m_2-1+{\delta }_2}|+(\left|a\right|+\left|b\right|+\left|c\right|)Mh\hfill \\ \hfill & \le e_{n-m_1-1}+\left|a\right|{\delta }_{1}h(e_{n-m_1-1}+(\left|a\right|+\left|b\right|+\left|c\right|)M{\delta }_{1}h)+\left|b\right|M{\delta }_1^2{h}^2+\left|c\right||-\varphi (\hfill \\ \hfill & (n-m_1-m_2-1+{\delta }_1+{\delta }_2)h)+\varphi \left((n-m_1-m_2+{\delta }_2)h\right)|+(\left|a\right|+\left|b\right|\hfill \\ \hfill & +\left|c\right|)Mh\hfill \\ \hfill & \le (1+\left|a\right|{\delta }_{1}h)e_{n-m_1-1}+Mh((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))\hfill \\ \hfill & +\left|b\right|M{\delta }_1^2{h}^2,\hfill \end{array}$$

(13)

and similarly to Equation (9),

$$|{\int }_0^h-x^{\prime }((n-m_2-1+{\delta }_2)h+t)dt+X_{n-m_2+{\delta }_2}-X_{n-m_2-1+{\delta }_2}|=0.$$

(14)

Substituting Equations (12)–(14) into Equation (11) yields

$$\begin{array}{cc}{e}_n\hfill & \le e_{n-1}+\left|a\right|h(e_{n-1}+(\left|a\right|+\left|b\right|+\left|c\right|)Mh)+\left|b\right|h((1+\left|a\right|{\delta }_{1}h)e_{n-m_1-1}+Mh\hfill \\ \hfill & ((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))+\left|b\right|M{\delta }_1^2{h}^2)+\left|c\right|·0\hfill \\ \hfill & \le e_{n-1}(1+\left|a\right|h)+M{h}^2(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)\hfill \\ \hfill & +\left|c\right|(1-{\delta }_1))+b^2{\delta }_1^{2}h)+\left|b\right|(1+\left|a\right|{\delta }_{1}h)C_{1,1,1}{h}^2\hfill \\ \hfill & \le C_{1,1,2}h,\hfill \end{array}$$

where

$$C_{1,1,2}=\frac{M(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|((\left|a\right|{\delta }_1^{2}T+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))+b^2{\delta }_1^{2}T)+\left|b\right|(1+\left|a\right|{\delta }_{1}T)C_{1,1,1}}{\left|a\right|}{e}^{\left|a\right|T}.$$

When $(k-1)\tau <t_n\le k\tau$, $(k-1)(m_1-{\delta }_1)<n\le k(m_1-{\delta }_1)$ for some $k\in [3,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor ]$, similarly to the discussion above, we can obtain $C_{1,1,k}=$ $(\frac{M(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|(\left|a\right|{\delta }_1^{2}T(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))(1+\left|b\right|{\delta }_{1}T+b^2{\delta }_1^2{T}^2+\cdots +{\left|b\right|}^{k-2}{\delta }_1^{k-2}{T}^{k-2})+{\left|b\right|}^k{\delta }_1^k{T}^{k-2})}{\left|a\right|}+\frac{\left|b\right|(1+\left|a\right|{\delta }_{1}T)(C_{1,1,k-1}+\left|b\right|{\delta }_{1}T{C}_{1,1,k-2}+b^2{\delta }_1^2{T}^2{C}_{1,1,k-3}+\cdots +{\left|b\right|}^{k-2}{\delta }_1^{k-2}{T}^{k-2}{C}_{1,1,1})}{\left|a\right|})e^{\left|a\right|T}$, such that $e_n\le C_{1,1,k}h$.

When $\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor \tau <t_n<\sigma$, $\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor (m_1-{\delta }_1)<n<m_2-{\delta }_2$, an analogous calculation can be performed to obtain $C_{1,1,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}$, such that inequality $e_n\le C_{1,1,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}h$ holds.

Taking $C_{1,1}=max\{C_{1,1,1},C_{1,1,2},\cdots ,C_{1,1,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}\}$, we have $e_n\le C_{1,1}h$ for $1\le n<m_2-{\delta }_2<{\eta }_1$.

When $\sigma \le t_n<2\sigma <{\tau }_1$, $m_2-{\delta }_2\le n<2(m_2-{\delta }_2)<{\eta }_1$, firstly we consider $\sigma \le t_n<\sigma +\tau <2\sigma <{\tau }_1$, $m_2-{\delta }_2\le n<m_2-{\delta }_2+m_1-{\delta }_1<2(m_2-{\delta }_2)<{\eta }_1$,

$$\begin{array}{cc}{e}_n\hfill & =|x\left(nh\right)-X_n|\hfill \\ \hfill & \le e_{n-1}+{\int }_0^h\left|a\right||x((n-1)h+t)-X_{n-1}|+\left|b\right||x((n-m_1-1+{\delta }_1)h+t)\hfill \\ \hfill & -X_{n-m_1-1+{\delta }_1}|dt+\left|c\right||{\int }_0^h-x^{\prime }((n-m_2-1+{\delta }_2)h+t)dt+X_{n-m_2+{\delta }_2}\hfill \\ \hfill & -X_{n-m_2-1+{\delta }_2}|.\hfill \end{array}$$

(15)

As discussed in Equations (7) and (13), for $t\in [0,h]$, we have

$$|x((n-1)h+t)-X_{n-1}|\le e_{n-1}+(\left|a\right|+\left|b\right|+\left|c\right|)Mh,$$

(16)

$$\begin{array}{cc}\hfill & |x((n-m_1-1+{\delta }_1)h+t)-X_{n-m_1-1+{\delta }_1}|\hfill \\ \hfill & \le (1+\left|a\right|{\delta }_{1}h)(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })C_{1,1}h\hfill \\ \hfill & +Mh((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots \hfill \\ \hfill & +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{)+M\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2}{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2},\hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill & |{\int }_0^h-x^{\prime }((n-m_2-1+{\delta }_2)h+t)dt+X_{n-m_2+{\delta }_2}-X_{n-m_2-1+{\delta }_2}|\hfill \\ \hfill & =|x\left((n-m_2-1+{\delta }_2)h\right)-x\left((n-m_2+{\delta }_2)h\right)+X_{n-m_2+{\delta }_2}-X_{n-m_2-1+{\delta }_2}|\hfill \\ \hfill & =|x\left((n-m_2-1)h\right)+{\int }_{(n-m_2-1)h}^{(n-m_2-1+{\delta }_2)h}ax\left(u\right)+bx(u-\tau )-c{x}^{\prime }(u-\sigma )du-x\left(\right(n\hfill \\ \hfill & -m_2\left)h\right)-{\int }_{(n-m_2)h}^{(n-m_2+{\delta }_2)h}ax\left(u\right)+bx(u-\tau )-c{x}^{\prime }(u-\sigma )du+{\delta }_2{X}_{n-m_2+1}+(1\hfill \\ \hfill & -{\delta }_2)X_{n-m_2}-{\delta }_2{X}_{n-m_2}-(1-{\delta }_2)X_{n-m_2-1}|\hfill \\ \hfill & \le |e_{n-m_2}-e_{n-m_2-1}|+|{\int }_0^{{\delta }_{2}h}ax(u+(n-m_2-1)h)+bx(u+(n-m_1-m_2-1\hfill \\ \hfill & +{\delta }_1\left)h\right)-c{x}^{\prime }(u+(n-2m_2-1+{\delta }_2)h)du-{\int }_0^{{\delta }_{2}h}ax(u+(n-m_2)h)+bx(u\hfill \\ \hfill & +(n-m_1-m_2+{\delta }_1)h)-c{x}^{\prime }(u+(n-2m_2+{\delta }_2)h)du+{\delta }_2(ah{X}_{n-m_2}\hfill \\ \hfill & +bh{X}_{n-m_2-m_1+{\delta }_1}-c{X}_{n-2m_2+1+{\delta }_2}+c{X}_{n-2m_2+{\delta }_2}-(ah{X}_{n-m_2-1}\hfill \\ \hfill & +bh{X}_{n-m_2-m_1-1+{\delta }_1}-c{X}_{n-2m_2+{\delta }_2}+c{X}_{n-2m_2-1+{\delta }_2}\left)\right)|\hfill \\ \hfill & \le |e_{n-m_2}-e_{n-m_2-1}|+|{\int }_0^{{\delta }_{2}h}a(x(u+(n-m_2-1)h)-X_{n-m_2-1})+b\left(x\right(u+(n\hfill \\ \hfill & -m_1-m_2-1+{\delta }_1\left)h\right)-X_{n-m_2-m_1-1+{\delta }_1})du-{\int }_0^{{\delta }_{2}h}a(x(u+(n-m_2)h)\hfill \\ \hfill & -X_{n-m_2})+b(x(u+(n-m_1-m_2+{\delta }_1)h)-X_{n-m_2-m_1+{\delta }_1})du+c{\int }_0^{{\delta }_{2}h}{x}^{\prime }(u+\hfill \\ \hfill & (n-2m_2+{\delta }_2)h)-x^{\prime }(u+(n-2m_2-1+{\delta }_2)h)du+c{\delta }_2(-X_{n-2m_2+1+{\delta }_2}\hfill \\ \hfill & +2X_{n-2m_2+{\delta }_2}-X_{n-2m_2-1+{\delta }_2}\left)\right|\hfill \\ \hfill & \le |e_{n-m_2}-e_{n-m_2-1}|+{\int }_0^{{\delta }_{2}h}\left|a\right||x(u+(n-m_2-1)h)-X_{n-m_2-1}|+\left|b\right|\left|x\right(u+\hfill \\ \hfill & (n-m_1-m_2-1+{\delta }_1)h)-X_{n-m_1-m_2-1+{\delta }_1}|du+{\int }_0^{{\delta }_{2}h}\left|a\right|\left|x\right(u+(n-m_2)h)\hfill \\ \hfill & -X_{n-m_2}|+\left|b\right||x(u+(n-m_1-m_2+{\delta }_1)h)-X_{n-m_1-m_2+{\delta }_1}|du+\left|c\right||{\int }_0^{{\delta }_{2}h}{x}^{\prime }(u\hfill \\ \hfill & +(n-2m_2+{\delta }_2)h)-x^{\prime }(u+(n-2m_2-1+{\delta }_2)h)du+{\delta }_2(-X_{n-2m_2+1+{\delta }_2}\hfill \\ \hfill & +2X_{n-2m_2+{\delta }_2}-X_{n-2m_2-1+{\delta }_2}\left)\right|\hfill \\ \hfill & \le e_{n-m_2-1}\left|a\right|h+M{h}^2(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|)+\left|a\right|{\delta }_{2}h(e_{n-m_2-1}+(\left|a\right|+\left|b\right|\hfill \\ \hfill & +\left|c\right|)M{\delta }_{2}h)+\left|a\right|{\delta }_{2}h(e_{n-m_2}+(\left|a\right|+\left|b\right|+\left|c\right|)M{\delta }_{2}h)+2\left|b\right|{\delta }_{2}h·M{\delta }_{1}h+\left|c\right|\hfill \\ \hfill & |-\varphi \left((n-2m_2+{\delta }_2)h\right)+\varphi \left((n-2m_2+2{\delta }_2)h\right)-\varphi \left((n-2m_2-1+2{\delta }_2)h\right)+\varphi \hfill \\ \hfill & \left((n-2m_2-1+{\delta }_2)h\right)-\varphi \left((n-2m_2+1+{\delta }_2)h\right)+2\varphi \left((n-2m_2+{\delta }_2)h\right)-\varphi \hfill \\ \hfill & \left((n-2m_2-1+{\delta }_2)h\right)|\hfill \\ \hfill & \le \left|a\right|(1+2{\delta }_2)C_{1,1}{h}^2+M{h}^2(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)(1+2{\delta }_2^2)+\left|b\right|(1+2{\delta }_1{\delta }_2))+\left|c\right|\hfill \\ \hfill & |\varphi \left((n-2m_2+2{\delta }_2)h\right)-\varphi \left((n-2m_2-1+2{\delta }_2)h\right)-\varphi \left((n-2m_2+1+{\delta }_2)h\right)\hfill \\ \hfill & +\varphi \left((n-2m_2+{\delta }_2)h\right)|\hfill \\ \hfill & \le \left|a\right|(1+2{\delta }_2)C_{1,1}{h}^2+M{h}^2(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)(1+2{\delta }_2^2)+\left|b\right|(1+2{\delta }_1{\delta }_2))+\left|c\right|\hfill \\ \hfill & |{\varphi }^{\prime }\left((n-2m_2-1+2{\delta }_2)h\right)h-{\varphi }^{\prime }\left((n-2m_2+{\delta }_2)h\right)h|\hfill \\ \hfill & \le \left|a\right|(1+2{\delta }_2)C_{1,1}{h}^2+M{h}^2(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)(1+2{\delta }_2^2)+\left|b\right|(1+2{\delta }_1{\delta }_2)+\left|c\right|(1\hfill \\ \hfill & -{\delta }_2\left)\right)\hfill \end{array}$$

(18)

Substituting Equations (16)–(18) into Equation (15) yields

$$\begin{array}{cc}{e}_n\hfill & \le e_{n-1}+\left|a\right|h(e_{n-1}+(\left|a\right|+\left|b\right|+\left|c\right|)Mh)+\left|b\right|h\left((1+\left|a\right|{\delta }_{1}h)\right(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots \hfill \\ \hfill & +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })C_{1,1}h+Mh((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))\hfill \\ \hfill & (1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })+M{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2}\hfill \\ \hfill & h^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2})+\left|c\right|(\left|a\right|(1+2{\delta }_2)C_{1,1}{h}^2+M{h}^2(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)(1+2{\delta }_2^2)+\left|b\right|(1\hfill \\ \hfill & +2{\delta }_1{\delta }_2)+\left|c\right|(1-{\delta }_2)\left)\right)\hfill \\ \hfill & \le e_{n-1}(1+\left|a\right|h)+M{h}^2(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|(((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|\hfill \\ \hfill & (1-{\delta }_1))(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })+{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}\hfill \\ \hfill & {\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2}{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })+\left|c\right|(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)(1+2{\delta }_2^2)+\left|b\right|(1+2{\delta }_1{\delta }_2)+\left|c\right|(1-{\delta }_2)))\hfill \\ \hfill & +(\left|b\right|(1+\left|a\right|{\delta }_{1}h)(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })+\left|c\right|\left|a\right|\hfill \\ \hfill & (1+2{\delta }_2))C_{1,1}{h}^2\hfill \\ \hfill & \le C_{1,2,1}h,\hfill \end{array}$$

where $$\begin{gathered} C_{1,2,1}=(M(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|(((\left|a\right|{\delta }_1^{2}T+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))(1+\left|b\right|{\delta }_{1}T+b^2{\delta }_1^2{T}^2+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{T}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })+{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2}{T}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })+ \\ \left|c\right|(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)(1+2{\delta }_2^2)+\left|b\right|(1+2{\delta }_1{\delta }_2)+\left|c\right|(1-{\delta }_2)))+(\left|b\right|(1+\left|a\right|{\delta }_{1}T)(1+\left|b\right|{\delta }_{1}T+b^2{\delta }_1^2{T}^2+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor }{T}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor })+\left|c\right|\left|a\right|(1+2{\delta }_2))C_{1,1}){\left|a\right|}^{-1}{e}^{\left|a\right|T} \end{gathered}$$.

When $\sigma +\tau \le t_n<\sigma +2\tau$, $m_2-{\delta }_2+m_1-{\delta }_1\le n<m_2-{\delta }_2+2(m_1-{\delta }_1)$, similarly to the discussion above, we can obtain

$$\begin{array}{cc}{e}_n\hfill & \le e_{n-1}+\left|a\right|h(e_{n-1}+(\left|a\right|+\left|b\right|+\left|c\right|)Mh)+\left|b\right|h\left((1+\left|a\right|{\delta }_{1}h)\right(e_{n-m_1-1}+\left|b\right|{\delta }_{1}h{e}_{n-2m_1-1}\hfill \\ \hfill & +b^2{\delta }_1^2{h}^2{e}_{n-3m_1-1}+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{e}_{n-(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2)m_1-1})\hfill \\ \hfill & +Mh((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots \hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{)+M\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2}{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +3}{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +3})+\left|c\right|(e_{n-m_2-1}\left|a\right|h\hfill \\ \hfill & +M{h}^2(\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))+b^2{\delta }_1^{2}h)\hfill \\ \hfill & +\left|b\right|(1+\left|a\right|{\delta }_{1}h)C_{1,1}{h}^2+\left|a\right|{\delta }_{2}h(e_{n-m_2-1}+(\left|a\right|+\left|b\right|+\left|c\right|)M{\delta }_{2}h)+\left|a\right|{\delta }_{2}h(e_{n-m_2}\hfill \\ \hfill & +(\left|a\right|+\left|b\right|+\left|c\right|)M{\delta }_{2}h)+2\left|b\right|{\delta }_{2}h(e_{n-m_2-m_1-1}(1+\left|a\right|{\delta }_{1}h)+Mh\left((\left|a\right|{\delta }_1^{2}h+1)\right(\left|a\right|\hfill \\ \hfill & +\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))+\left|b\right|M{\delta }_1^2{h}^2)+\left|c\right|(1-{\delta }_2)M{h}^2)\hfill \\ \hfill & \le e_{n-1}(1+\left|a\right|h)+M{h}^2(\left|a\right|(1+\left|c\right|+2\left|c\right|{\delta }_2^2)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|(\left|a\right|{\delta }_1^{2}h(\left|a\right|+\left|b\right|+\left|c\right|)\hfill \\ \hfill & +\left|c\right|(1-{\delta }_1))(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots +{\left(\left|b\right|{\delta }_{1}h\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1})+{\left(\left|b\right|{\delta }_{1}h\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +3}\hfill \\ \hfill & +\left|b\right|\left|c\right|((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))+b^2\left|c\right|{\delta }_1^{2}h+2\left|b\right|\left|c\right|{\delta }_2((\left|a\right|{\delta }_1^{2}h+1)\hfill \\ \hfill & (\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1)+\left|b\right|{\delta }_1^{2}h)+c^2(1-{\delta }_2))+(\left|b\right|(1+\left|a\right|{\delta }_{1}h)(C_{1,2,1}\hfill \\ \hfill & +\left|b\right|{\delta }_{1}h{C}_{1,1}+b^2{\delta }_1^2{h}^2{C}_{1,1}+\cdots +{\left(\left|b\right|{\delta }_{1}h\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{C}_{1,1})+\left|c\right|C_{1,1}(\left|a\right|(1+2{\delta }_2)+\left|b\right|\hfill \\ \hfill & (1+\left|a\right|{\delta }_{1}h+2{\delta }_2)\left)\right)h^2\hfill \\ \hfill & \le C_{1,2,2}h,\hfill \end{array}$$

where $$\begin{gathered} C_{1,2,2}=(M(\left|a\right|(1+\left|c\right|+2\left|c\right|{\delta }_2^2)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|((\left|a\right|{\delta }_1^{2}T+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))(1+\left|b\right|{\delta }_{1}T+b^2{\delta }_1^2{T}^2+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{T}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1})+ \\ {\left(\left|b\right|{\delta }_1\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +3}{T}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +2}+\left|b\right|\left|c\right|((\left|a\right|{\delta }_1^{2}T+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))+b^2\left|c\right|{\delta }_1^{2}T+2\left|b\right|\left|c\right|{\delta }_2((\left|a\right|{\delta }_1^{2}T+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1)+\left|b\right|{\delta }_1^{2}T)+c^2(1-{\delta }_2))+ \\ (\left|b\right|(1+\left|a\right|{\delta }_{1}T)(C_{1,2,1}+\left|b\right|{\delta }_{1}T{C}_{1,1}+b^2{\delta }_1^2{T}^2{C}_{1,1}+\cdots +{\left|b\right|}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{\delta }_1^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{T}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}{C}_{1,1})+\left|c\right|C_{1,1}(\left|a\right|(1+2{\delta }_2)+\left|b\right|(1+\left|a\right|{\delta }_{1}T+2{\delta }_2)))){\left|a\right|}^{-1}{e}^{\left|a\right|T}. \end{gathered}$$

When $\sigma +(k-1)\tau \le t_n<\sigma +k\tau$, $m_2-{\delta }_2+(k-1)(m_1-{\delta }_1)\le n<m_2-{\delta }_2+k(m_1-{\delta }_1)$ for some $k\in [3,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor ]$, similarly to the discussion above, we can obtain $$\begin{gathered} C_{1,2,k}=(M(\left|a\right|(1+\left|c\right|+2\left|c\right|{\delta }_2^2)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|((1+\left|c\right|)(1+\left|b\right|{\delta }_{1}T+\cdots +{\left(\left|b\right|{\delta }_{1}T\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +k-1})+2\left|c\right|{\delta }_2(1+\left|b\right|{\delta }_{1}T+\cdots +{\left(\left|b\right|{\delta }_{1}T\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +k-2})) \\ ((\left|a\right|{\delta }_1^{2}T+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))+{\left(\left|b\right|{\delta }_1\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +k}{h}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +k-1}((1+\left|c\right|)\left|b\right|{\delta }_1+2\left|c\right|{\delta }_2)+2\left|b\right|c^2{\delta }_2(1-{\delta }_2)T)+ \\ \left|b\right|(1+2\left|c\right|{\delta }_2)(1+\left|a\right|{\delta }_{1}T)(C_{1,2,k-1}+\cdots +{\left(\left|b\right|{\delta }_{1}T\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +k-1}{C}_{1,1})+(\left|a\right|\left|c\right|(1+2{\delta }_2)+\left|b\right|\left|c\right|(1+\left|a\right|{\delta }_{1}T)(1+\cdots +{\left(\left|b\right|{\delta }_{1}T\right)}^{\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +k-1}))C_{1,1}){\left|a\right|}^{-1}{e}^{\left|a\right|T} \end{gathered}$$.

When $\sigma +\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor \tau \le t_n<2\sigma$, $m_2-{\delta }_2+\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor (m_1-{\delta }_1)\le n<2(m_2-{\delta }_2)$, an analogous calculation can be performed to obtain $C_{1,2,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}$, such that inequality $e_n\le C_{1,2,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}h$ holds.

Taking $C_{1,2}=max\{C_{1,2,1},C_{1,2,2},\cdots ,C_{1,2,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}\}$, we have $e_n\le C_{1,2}h$ for $m_2-{\delta }_2\le n<2(m_2-{\delta }_2)<{\eta }_1$.

Let $B_{i+1}=\lfloor \frac{{\eta }_{i+1}-{\eta }_i}{m_2-{\delta }_2}\rfloor$. When $(j-1)\sigma <t_n\le j\sigma$, $(j-1)(m_2-{\delta }_2)<n\le j(m_2-{\delta }_2)$, $3\le j\le B_1$, $e_n\le C_{1,j}h$, where $C_{1,j}=max\{C_{1,j,1},C_{1,j,2},\cdots ,C_{1,j,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}\}$, and $C_{1,j,k}$ can be obtained by

$$\begin{array}{cc}{e}_n\hfill & \le e_{n-1}(1+\left|a\right|h)+M{h}^2(\left|a\right|(1+2\left|c\right|{\delta }_2^2)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|\left(\right(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots \hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{(j-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)+k-2})+2{\delta }_2(1+2\left|c\right|+\cdots +{\left(2\left|c\right|\right)}^{j-2})(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots \hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{(j-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)+k-3}\left)\right)((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))\hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{(j-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)+k-2}(b^2{\delta }_1^{2}h+2\left|b\right|{\delta }_1{\delta }_2(1+2\left|c\right|+\cdots +{\left(2\left|c\right|\right)}^{j-2}))+{\left(2\left|c\right|\right)}^{j-1}(1\hfill \\ \hfill & -{\delta }_2\left)\right)+h^2(\left|b\right|(1+\left|a\right|{\delta }_{1}h)(C_{1,j,k-1}+\cdots +{\left(\left|b\right|{\delta }_{1}h\right)}^{(j-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)+k-2}{C}_{1,1})+2\left|a\right|\left|c\right|{\delta }_2(1\hfill \\ \hfill & +2\left|c\right|+\cdots +{\left(2\left|c\right|\right)}^{j-2})(C_{1,j-1}+\cdots +C_{1,1})+2\left|b\right|{\delta }_2(1+2\left|c\right|+\cdots +{\left(2\left|c\right|\right)}^{j-2})(1+\left|a\right|{\delta }_{1}h)\hfill \\ \hfill & (C_{1,j,k-1}+\cdots +{\left(\left|b\right|{\delta }_{1}h\right)}^{(j-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)+k-3}{C}_{1,1}))+\left|c\right|(|e_{n-m_2}-e_{n-m_2-1}|+\cdots +{\left(2\left|c\right|\right)}^{j-2}\hfill \\ \hfill & |e_{n-(j-1)m_2}-e_{n-(j-1)m_2-1}|)\hfill \\ \hfill & \le C_{1,j,k}h,\hfill \end{array}$$

When $B_1\sigma \le t_n<{\tau }_1$, $B_1(m_2-{\delta }_2)\le n<{\eta }_1$, an analogous calculation can be performed to obtain $C_{1,B_1+1}$, such that inequality $e_n\le C_{1,B_1+1}h$ holds.

Taking $\widetilde{C_1}=max\{C_{1,1},C_{1,2},\cdots ,C_{1,B_1+1}\}$, we have $e_n\le \widetilde{C_1}h$ for $1\le n<{\eta }_1$.

When $t_n={\tau }_1$, $n={\eta }_1$,

$$\begin{array}{cc}{e}_n\hfill & =|x\left({\eta }_{1}h\right)-X_{{\eta }_1}|\hfill \\ \hfill & =|x\left({\tau }_1\right)+{\int }_{{\tau }_1}^{{\eta }_{1}h}ax\left(t\right)+bx(t-\tau )-c{x}^{\prime }(t-\sigma )dt-X_{{\eta }_1}|\hfill \\ \hfill & =|l_1+x\left({\tau }_1^{-}\right)+{\int }_0^{{\eta }_{1}h-{\tau }_1}ax(t+{\tau }_1)+bx({\tau }_1+t-\tau )-c{x}^{\prime }({\tau }_1+t-\sigma )dt\hfill \\ \hfill & -(l_1+X_{{\eta }_1-1})|\hfill \\ \hfill & \le |x\left(({\eta }_1-1)h\right)+{\int }_{({\eta }_1-1)h}^{{\tau }_1}ax\left(t\right)+bx(t-\tau )-c{x}^{\prime }(t-\sigma )dt-X_{{\eta }_1-1}|\hfill \\ \hfill & +|{\int }_0^{{\eta }_{1}h-{\tau }_1}ax(t+{\tau }_1)+bx({\tau }_1+t-\tau )-c{x}^{\prime }({\tau }_1+t-\sigma )dt|\hfill \\ \hfill & \le e_{{\eta }_1-1}+|{\int }_{({\eta }_1-1)h}^{{\tau }_1}ax\left(t\right)+bx(t-\tau )-c{x}^{\prime }(t-\sigma )dt|+(\left|a\right|+\left|b\right|+\left|c\right|)Mh\hfill \\ \hfill & \le e_{{\eta }_1-1}+2(\left|a\right|+\left|b\right|+\left|c\right|)Mh\hfill \\ \hfill & \le (\widetilde{C_1}+2(\left|a\right|+\left|b\right|+\left|c\right|)M)h.\hfill \end{array}$$

(19)

Letting $C_1=\widetilde{C_1}+2(\left|a\right|+\left|b\right|+\left|c\right|)M$, we obtain inequality $e_n\le C_{1}h$, holds for $n\in I_1$.

We assume that Equation (5) holds for $n\in I_{s-1}$, that is $e_n\le C_{s-1}h$ for $n\in I_{s-1}$. Now, we show Equation (5) holds for $n\in I_s$.

When ${\tau }_{s-1}\le t_n\le {\tau }_{s-1}+\tau <{\tau }_{s-1}+\sigma$, ${\eta }_{s-1}+1\le n\le {\eta }_{s-1}+m_1-{\delta }_1<{\eta }_{s-1}+m_2-{\delta }_2$,

$$\begin{array}{cc}{e}_n\hfill & =|x\left(nh\right)-X_n|\hfill \\ \hfill & \le e_{n-1}+{\int }_0^h\left|a\right||x((n-1)h+t)-X_{n-1}|+\left|b\right||x((n-m_1-1+{\delta }_1)h+t)\hfill \\ \hfill & -X_{n-m_1-1+{\delta }_1}|dt+\left|c\right||{\int }_0^h-x^{\prime }((n-m_2-1+{\delta }_2)h+t)dt+X_{n-m_2+{\delta }_2}\hfill \\ \hfill & -X_{n-m_2-1+{\delta }_2}|.\hfill \end{array}$$

As discussed in Equations (7), (13) and (18), for $t\in [0,h]$, we have

$$|x((n-1)h+t)-X_{n-1}|\le e_{n-1}+(\left|a\right|+\left|b\right|+\left|c\right|)Mh,$$

$$\begin{array}{cc}\hfill & |x((n-m_1+{\delta }_1-1)h+t)-X_{n-m_1+{\delta }_1-1}|\hfill \\ \hfill & \le (1+\left|a\right|{\delta }_{1}h)(C_{s-1}+\cdots +{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-1}{C}_1)h+Mh\hfill \\ \hfill & ((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots +\hfill \\ \hfill & {\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-1}{)+M\left|b\right|}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)}\hfill \\ \hfill & {\delta }_1^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)+1}{h}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)+1},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & |{\int }_0^h-x^{\prime }((n-m_2-1+{\delta }_2)h+t)dt+X_{n-m_2+{\delta }_2}-X_{n-m_2-1+{\delta }_2}|\hfill \\ \hfill & \le |e_{n-m_2}-e_{n-m_2-1}|+\cdots +{\left(2\left|c\right|\right)}^{B_1+\cdots +B_{s-1}+s-3}|e_{n-(B_1+\cdots +B_{s-1}+s-2)m_2}\hfill \\ \hfill & -e_{n-(B_1+\cdots +B_{s-1}+s-2)m_2-1}|+2\left|a\right|{\delta }_{2}h((1+\cdots +{\left(2\left|c\right|\right)}^{B_1+\cdots +B_{s-1}+s-3})\hfill \\ \hfill & (C_{s-1}+\cdots +C_1)h+(\left|a\right|+\left|b\right|+\left|c\right|)M{\delta }_{2}h)+2\left|b\right|{\delta }_{2}h(1\hfill \\ \hfill & +\cdots +{\left(2\left|c\right|\right)}^{B_1+\cdots +B_{s-1}+s-3}\left)\right((1+\left|a\right|{\delta }_{1}h)(C_{s-1}h+\cdots \hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-2}{C}_{1}h)+(1+\left|b\right|{\delta }_{1}h+\cdots \hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-2}\left)Mh\right((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)\hfill \\ \hfill & +\left|c\right|(1-{\delta }_1))+M{\delta }_{1}h{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-1})\hfill \\ \hfill & +{\left(2\left|c\right|\right)}^{B_1+\cdots +B_{s-1}+s-2}(1-{\delta }_2)M{h}^2,\hfill \end{array}$$

then, we obtain

$$\begin{array}{cc}{e}_n\hfill & \le e_{n-1}(1+\left|a\right|h)+M{h}^2\left|a\right|(\left|a\right|+\left|b\right|+\left|c\right|)+\left|b\right|h^2\left((1+\left|a\right|{\delta }_{1}h)\right(C_{s-1}+\cdots \hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-1}{C}_1)+M((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|\hfill \\ \hfill & (1-{\delta }_1))(1+\left|b\right|{\delta }_{1}h+b^2{\delta }_1^2{h}^2+\cdots +{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-1})\hfill \\ \hfill & +M{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)})+\left|c\right|(|e_{n-m_2}-e_{n-m_2-1}|+\cdots +\hfill \\ \hfill & {\left(2\left|c\right|\right)}^{B_1+\cdots +B_{s-1}+s-3}|e_{n-(B_1+\cdots +B_{s-1}+s-2)m_2}-e_{n-(B_1+\cdots +B_{s-1}+s-2)m_2-1}|+2\left|a\right|{\delta }_{2}h\hfill \\ \hfill & ((1+\cdots +{\left(2\left|c\right|\right)}^{B_1+\cdots +B_{s-1}+s-3})(C_{s-1}+\cdots +C_1)h+(\left|a\right|+\left|b\right|+\left|c\right|)M{\delta }_{2}h)\hfill \\ \hfill & +2\left|b\right|{\delta }_{2}h(1+\cdots +{\left(2\left|c\right|\right)}^{B_1+\cdots +B_{s-1}+s-3})\left((1+\left|a\right|{\delta }_{1}h)\right(C_{s-1}h+\cdots \hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-2}{C}_{1}h)+Mh(1+\left|b\right|{\delta }_{1}h+\cdots \hfill \\ \hfill & +{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-2})((\left|a\right|{\delta }_1^{2}h+1)(\left|a\right|+\left|b\right|+\left|c\right|)+\left|c\right|(1-{\delta }_1))\hfill \\ \hfill & +M{\delta }_{1}h{\left(\left|b\right|{\delta }_{1}h\right)}^{(B_1+\cdots +B_{s-1}+s-1)(\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1)-1})+{\left(2\left|c\right|\right)}^{B_1+\cdots +B_{s-1}+s-2}(1-{\delta }_2)M{h}^2)\hfill \\ \hfill & \le C_{s,1,1}h.\hfill \end{array}$$

Just as in the discussion of $C_{1,1,k}$, we can obtain $C_{s,1,k}$ such that $e_n\le C_{s,1,k}h,{\eta }_{s-1}+(k-1)(m_1-{\delta }_1)\le n<{\eta }_{s-1}+k(m_1-{\delta }_1)$ for $k=1,2,\cdots ,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor$. When ${\tau }_{s-1}+\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor \tau \le t_n<{\tau }_{s-1}+\sigma$, ${\eta }_{s-1}+\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor (m_1-{\delta }_1)\le n<{\eta }_{s-1}+m_2-{\delta }_2$, we also can obtain $C_{s,1,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}$ which satisfies $e_n\le C_{s,1,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}h$.

Taking $C_{s,1}=max\{C_{s,1,1},C_{s,1,2},\cdots ,C_{s,1,\lfloor \frac{m_2-{\delta }_2}{m_1-{\delta }_1}\rfloor +1}\}$, we have $e_n\le C_{s,1}h$, for ${\eta }_{s-1}+1\le n<{\eta }_{s-1}+m_2-{\delta }_2$. Then, there are finite $C_{s,j}$, and the number of $C_{s,j}$ does not depend on stepsize h.

Taking

$${\tilde{C}}_s=max\{C_{s,1},C_{s,2},\cdots ,C_{s,B_s+1}\};$$

we have

$$e_n\le {\tilde{C}}_{s}h,{\eta }_{s-1}+1\le n<{\eta }_s.$$

When $t_n={\tau }_s$, $n={\eta }_s$, an analogous calculation as in Equation (19) yields

$$\begin{array}{cc}{e}_n\hfill & =|x\left({\eta }_{s}h\right)-X_{{\eta }_s}|\hfill \\ \hfill & \le ({\tilde{C}}_s+2(\left|a\right|+\left|b\right|+\left|c\right|)M)h.\hfill \end{array}$$

(20)

Letting $C_s={\tilde{C}}_s+2(\left|a\right|+\left|b\right|+\left|c\right|)$, we obtain $e_n\le C_{s}h$ for $n\in I_s$.

When ${\eta }_N<n\le pm=\frac{T}{h}$, same as $n\in \left[{\eta }_{s-1}+1,{\eta }_s\right)$, we can obtain $C_{N+1,1}$ which satisfies $e_n\le C_{N+1,1}h$.

Taking

$$C=max\{C_1,C_2,\cdots ,C_N,C_{N+1,1}\},$$

we can obtain $e_n\le Ch$ which holds for $1\le n\le pm$. This completes the proof. □

3. Examples

In this section, we present two examples to show the efficiency of our work.

3.1. Example 1

We consider the following INDDE:

$$\left\{\begin{array}{cc}{x}^{\prime }\left(t\right)=-2x\left(t\right)-x(t-1)+x^{\prime }(t-\frac{3}{2}),\hfill & t\ge 0,t\ne 2k,\hfill \\ \Delta x\left(2k\right)=0.5,\hfill & k\in {\mathbb{Z}}^{+},\hfill \\ x\left(t\right)=1+t,\hfill & -\frac{3}{2}\le t\le 0,\hfill \end{array}\right.$$

(21)

The solution of Equation (21) for $t\in [-\frac{3}{2},\frac{5}{2}]$ is

$$x\left(t\right)=\left\{\begin{array}{cc}\frac{3}{4}-\frac{1}{2}t+\frac{1}{4}{e}^{-2t},\hfill & 0<t\le 1,\hfill \\ -\frac{1}{4}+\frac{1}{4}t-\frac{1}{4}t{e}^{2-2t}+\frac{1}{4}{e}^{-2t}+\frac{1}{2}{e}^{2-2t},\hfill & 1<t\le \frac{3}{2},\hfill \\ -1+\frac{1}{4}t-\frac{1}{4}t{e}^{2-2t}-\frac{1}{2}t{e}^{3-2t}+\frac{3}{2}{e}^{3-2t}+\frac{1}{2}{e}^{2-2t}+\frac{1}{4}{e}^{-2t},\hfill & \frac{3}{2}<t<2,\hfill \\ -\frac{1}{8}t+\frac{1}{16}+\frac{1}{8}{t}^2{e}^{4-2t}-\frac{3}{4}t{e}^{4-2t}-\frac{1}{4}t{e}^{2-2t}-\frac{1}{2}t{e}^{3-2t}\hfill \\ +\frac{3}{2}{e}^{3-2t}+\frac{1}{4}{e}^{-2t}+\frac{19}{16}{e}^{4-2t}+\frac{1}{2}{e}^{2-2t},\hfill & 2<t<\frac{5}{2}\hfill \end{array}\right.$$

(22)

Using Euler scheme (2), we obtain the global errors at $t=0.5$, $t=1.5$, $t=2$, and $t=2.5$, denoted by $e_{0.5}$, $e_{1.5}$, $e_2$ and $e_{2.5}$. Then, as can be seen from Table 1, as the stepsize halves, the error reduces by a factor approximately equal to $\frac{1}{2}$. The errors are also plotted in Figure 1. Obviously, we obtain that the numerical solution convergent to the exact solution with $h\to 0$ and the convergent order is one. This means our method is efficient.

Table 1. The global errors of Euler scheme (2) for INDDE (21).

Stepsize	${\mathit{e}}_{0.5}$	${\mathit{e}}_{1.5}$	${\mathit{e}}_2$	${\mathit{e}}_{2.5}$
1/10	0.0100	0.0189	0.0093	0.0211
1/20	0.0048	0.0091	0.0051	0.0104
1/40	0.0023	0.0045	0.0026	0.0052
1/80	0.0012	0.0022	0.0013	0.0026
1/160	0.000578	0.001100	0.000676	0.001293
1/320	0.000288	0.000549	0.000339	0.000646
1/640	0.000144	0.000274	0.000170	0.000323
1/1280	0.000072	0.000137	0.000085	0.000162

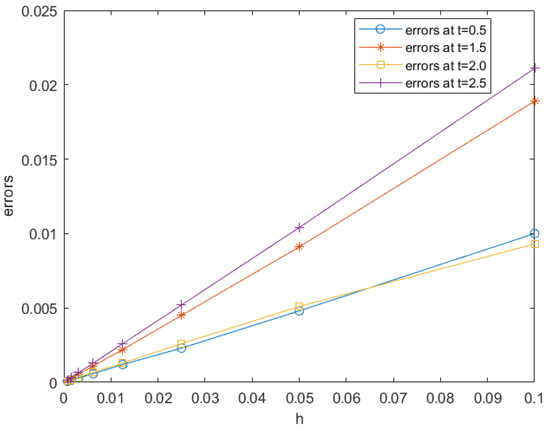
Figure 1. Errors vesus stepsize for Equation (21) at four alternative output points.

3.2. Example 2

We consider the following INDDE [26]:

$$\left\{\begin{array}{cc}{x}^{\prime }\left(t\right)=\frac{1}{3}x\left(t\right)-\frac{1}{e}x(t-\frac{1}{5})+\frac{1}{3e}{x}^{\prime }(t-\frac{1}{2}),\hfill & t\ge 0,t\ne k,\hfill \\ \Delta x\left(k\right)={(-\frac{1}{e})}^k,\hfill & k\in {\mathbb{Z}}^{+},\hfill \\ x\left(t\right)=0,\hfill & -\frac{1}{2}\le t\le 0,\hfill \end{array}\right.$$

(23)

The solution for $t\in [0,\frac{3}{2}]$ is

$$x\left(t\right)=\left\{\begin{array}{cc}0,\hfill & 0\le t<1,\hfill \\ -e^{\frac{t-4}{3}},\hfill & 1\le t<\frac{6}{5},\hfill \\ -(\frac{6e^{-\frac{12}{5}}}{5}+e^{-\frac{4}{3}})e^{\frac{t}{3}}+e^{-\frac{12}{5}}t{e}^{\frac{t}{3}},\hfill & \frac{6}{5}\le t<\frac{7}{5},\hfill \\ (\frac{6e^{-\frac{52}{15}}}{5}+e^{-\frac{12}{5}})t{e}^{\frac{t}{3}}-\frac{1}{2}{(t-\frac{1}{5})}^2{e}^{\frac{t}{3}-\frac{52}{15}}\hfill \\ +(-e^{-\frac{7}{5}}-\frac{24}{25}{e}^{-\frac{52}{15}}-\frac{7}{5}{e}^{-\frac{12}{5}})e^{\frac{t}{3}},\hfill & \frac{7}{5}\le t<\frac{3}{2}.\hfill \end{array}\right.$$

(24)

By Euler scheme (2), we similarly obtain the global errors at $t=1$, $t=11/10$, $t=13/10$, and $t=7/5$, denoted by $e_1$, $e_{11/10}$, $e_{13/10}$ and $e_{7/5}$. And from Table 2, as the stepsize halves, the error reduces by a factor approximately equal to $\frac{1}{2}$, too. The errors are plotted in Figure 2. We can easily see that with $h\to 0$, the numerical solution is convergent and the order is one, which proves our method again.

Table 2. The global errors of Euler scheme (2) for INDDE (23).

Stepsize	${\mathit{e}}_1$	${\mathit{e}}_{11/10}$	${\mathit{e}}_{13/10}$	${\mathit{e}}_{7/5}$
1/10	0	2.0667 × 10${}^{-4}$	2.0366 × 10${}^{-4}$	5.0877 × 10${}^{-5}$
1/20	0	1.0448 × 10${}^{-4}$	1.0179 × 10${}^{-4}$	2.8268 × 10${}^{-5}$
1/40	0	5.2531 × 10${}^{-5}$	5.0879 × 10${}^{-5}$	1.4867 × 10${}^{-5}$
1/80	0	2.6339 × 10${}^{-5}$	2.5435 × 10${}^{-5}$	7.6198 × 10${}^{-6}$
1/160	0	1.3188 × 10${}^{-5}$	1.2716 × 10${}^{-5}$	3.8569 × 10${}^{-6}$
1/320	0	6.5989 × 10${}^{-6}$	6.3579 × 10${}^{-6}$	1.9401 × 10${}^{-6}$
1/640	0	3.3007 × 10${}^{-6}$	3.1790 × 10${}^{-6}$	9.7293 × 10${}^{-7}$
1/1280	0	1.6507 × 10${}^{-6}$	1.5896 × 10${}^{-6}$	4.8710 × 10${}^{-7}$

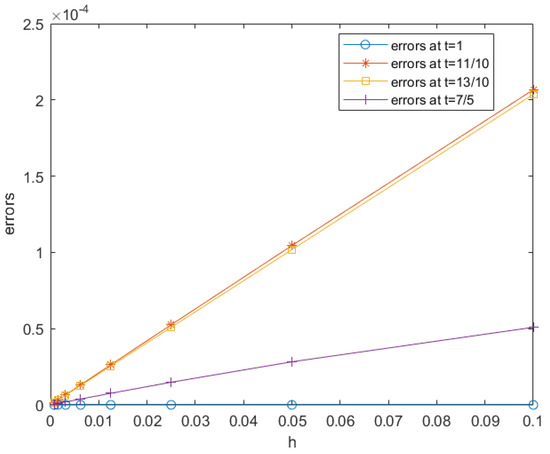
Figure 2. Errors vesus stepsize for Equation (23) at four alternative output points.

4. Conclusions

In this paper, we discuss the numerical solutions for the neutral delay differential equations with impulsive perturbations, we use a fixed stepsize Euler method for INDDEs and propose the Euler scheme which is a simple but most feasible scheme by taking the partition nodes and employing the linear interpolation. Then, we show how this method may be convergent by order one. To achieve this, mathematical induction is used to strictly prove the final conclusion, that is, the convergence order of the INDDEs is one. Lastly, we present two numerical results to verify their convergence orders, respectively.

From this paper, we know that the Euler method for INDDEs is convergent of order one. To find numerical methods with higher convergence order for INDDEs is the goal of our futher work. On the other hand, the current study actually is a kind of preparation for the stability of INDDEs. However, as far as we know, there are many studies on the stability of exact solutions, but few on the stability of numerical solutions. Therefore, we are going to focus on the properties of stability by these different choices of numerical methods. These will be new challenges for us.