On the Double-Zero Bifurcation of Jerk Systems

Abstract

In this paper, we construct approximate normal forms of the double-zero bifurcation for a two-parameter jerk system exhibiting a non-degenerate fold bifurcation. More precisely, using smooth invertible variable transformations and smooth invertible parameter changes, we obtain normal forms that are also jerk systems. In addition, we discuss some of their parametric portraits.

1. Introduction

The double-zero bifurcation, also called the Bogdanov–Takens bifurcation, can occur in a continuous-time dynamical system $\dot{x}=f(x,\mu ),x\in {\mathbb{R}}^n,\mu \in {\mathbb{R}}^2,n\ge 2$ when the system has at the critical value of $\mu$ an equilibrium point with two zero eigenvalues and no other eigenvalues on the imaginary axis (see, e.g., [1,2]).

The double-zero bifurcation can be met, for instance, in mechanical, electrical, and biological systems. For example, the analysis of mathematical models of an internally constrained planar beam equipped with a lumped visco–elastic device and loaded by a follower force [3] or of a non-linear cantilever beam that is externally damped and made of a visco–elastic material [4] reveals among other solutions the existence of a double-zero bifurcation. Oscillators and electronic circuits are modeled by differential equations, and in some cases, they experience a double-zero bifurcation (see, e.g., [5,6,7]). Also, a double-zero bifurcation appears in some chemical reactions (see, e.g., [8,9]) and in fluid mechanics (see, e.g., [10,11]).

The importance of the double-zero bifurcation is highlighted by the following remark: “One of the most important features of the Takens–Bogdanov bifurcation is that it warrants the existence of global connections in its vicinity (a homoclinic orbit in the non-symmetric case and a homoclinic or a heteroclinic orbit if the system is symmetric)” [12].

This local bifurcation was first analyzed by Bogdanov [13] and Takens [14] in the case $n=2.$ Several normal forms of this bifurcation were reported in this case (see, e.g., [1]). In fact, such a normal form is “the simplest parameter-dependent form to which any generic two-parameter system exhibiting the bifurcation can be transformed by smooth invertible changes of coordinates and parameters and (if necessary) time reparametrizations” [2]. Approximate normal forms are obtained by truncation of higher-order terms. In the n-dimensional case $n\ge 3$, the study of the double-zero bifurcation is carried out by reduction on a local center manifold to the planar case. It is natural to ask whether such a reduction can be avoided, i.e., whether $n-$dimensional normal forms can be obtained. We will give an affirmative answer for $n=3.$

In this paper, we consider the jerk system

$$\left\{\begin{array}{c}\dot{x}=y\hfill \\ \dot{y}=z\hfill \\ \dot{z}=j(x,y,z,\alpha ,\beta )\hfill \end{array}\right.,$$

(1)

where j is smooth and $\alpha ,\beta \in \mathbb{R}$ are parameters. Our goal is to obtain normal forms and approximate normal forms for the double-zero bifurcation of system (1), which is also a jerk system.

Particular cases of jerk systems have been widely investigated. Among topics, we recall local stability and bifurcations [15,16,17,18,19,20,21,22], chaotic behavior [23,24,25,26], and image encryption and cryptography [27,28].

The paper is organized as follows: In Section 2, we recall some results regarding non-degenerate fold bifurcations. In Section 3, we derive jerk approximate normal forms for system (1), and we discuss some of their parametric portraits.

2. The Fold Curve

Assume there are ${\alpha }_c,{\beta }_c$ such that system (1) displays a non-degenerate fold bifurcation when $\alpha$ passes through the critical value ${\alpha }_c$ and $\beta ={\beta }_c$ is fixed. Following [21], sufficient conditions are given below:

F1.

There is at the critical value $({\alpha }_c,{\beta }_c)$ an equilibrium point $E(x_c,0,0)$ of system (1) with a simple zero eigenvalue and no other eigenvalues on the imaginary axis, i.e., $j\left(E_c\right)=0$, $j_x\left(E_c\right)=0$, $j_y\left(E_c\right)\ne 0$, $j_z\left(E_c\right)\ne 0$;

F2.

The transversality condition $j_{\alpha }\left(E_c\right)\ne 0$;

F3.

The nondegeneracy condition $j_{x^2}\left(E_c\right)\ne 0$;

where $E_c=(x_c,0,0,{\alpha }_c,{\beta }_c).$ We have denoted: $j_x={\displaystyle \frac{\partial j}{\partial x}}$, $j_{\alpha }={\displaystyle \frac{\partial j}{\partial \alpha }}$, $j_{x^2}={\displaystyle \frac{{\partial }^{2}j}{\partial x^2}}.$

It is known that if the fold conditions hold, then “generically, there is a bifurcation curve $\mathcal{F}$ in the $(\alpha ,\beta )$-plane along which the system has an equilibrium exhibiting the same bifurcation” [2]. For the sake of completeness, we prove this result in our case.

Lemma 1.

Let ${\alpha }_c,{\beta }_c$ be such that $E(x_c,0,0)$ is an equilibrium point of system (1) and conditions $F1$–$F3$ are satisfied. Then the standard projection of the curve

$$\mathsf{\Gamma }:\left\{\begin{array}{c}j(x,0,0,\alpha ,\beta )=0\hfill \\ j_x(x,0,0,\alpha ,\beta )=0\hfill \end{array}\right.$$

in the $(\alpha ,\beta )$-plane is a curve $\mathcal{F}$ along which system (1) has an equilibrium exhibiting a non-degenerate fold bifurcation.

Proof. 

Considering the coordinates $(x,\alpha ,\beta )$, $\mathsf{\Gamma }$ is the intersection of two surfaces. Clearly, $(x_c,{\alpha }_c,{\beta }_c)$ belongs to this intersection. Since

$$rank{\left.\left[\begin{array}{ccc}{j}_x& j_{\alpha }& j_{\beta }\\ j_{x^2}& j_{x\alpha }& j_{x\beta }\end{array}\right]\right|}_{E_c}=2,$$

where $E_c=(x_c,0,0,{\alpha }_c,{\beta }_c)$, $\mathsf{\Gamma }$ is a curve passing through $(x_c,{\alpha }_c,{\beta }_c)$. Moreover, since $j\left(E_c\right)=0$, $j_x\left(E_c\right)=0,$ and ${\displaystyle \frac{D(j,j_x)}{D(x,\alpha )}}\left(E_c\right)=-j_{\alpha }\left(E_c\right)j_{x^2}\left(E_c\right)\ne 0,$ by the Implicit Function Theorem (IFT), there are the functions $x=x\left(\beta \right),\alpha =\alpha \left(\beta \right)$ in a neighborhood $\mathcal{V}$ of ${\beta }_c$ such that $x\left({\beta }_c\right)=x_c, \alpha \left({\beta }_c\right)={\alpha }_c$ and which verify the equations of $\mathsf{\Gamma }.$ Hence, $\left(x\right(\beta ),\alpha (\beta ),\beta )$ is a parametrization of $\mathsf{\Gamma }$ in a neighborhood of $(x_c,{\alpha }_c,{\beta }_c)$. In addition, for all $\beta \in \mathcal{V}$, $E_{\beta }(x\left(\beta \right),0,0)$ is an equilibrium point of system (1) and by continuity, the other fold conditions will be satisfied. Consequently, the construction can be repeated to extend the curve further.

The projection $(x,\alpha ,\beta )\mapsto (\alpha ,\beta )$ will give the fold bifurcation curve $\mathcal{F}$. □

3. The Double-Zero Bifurcation

In this section, we deduce jerk approximate normal forms for the double-zero bifurcation of a jerk system. Also, we give parametric portraits of these.

When the parameters $\alpha$ and $\beta$ vary simultaneously to track the bifurcation curve $\mathcal{F}$, another real eigenvalue can approach the imaginary axis, which leads to a double-zero bifurcation generally.

Consider the following mechanism of the double-zero bifurcation: Let $\mathcal{F}=\left\{\right(\alpha \left(\beta \right),\beta ):\beta \in \mathbb{R}\}$ be the fold bifurcation curve given by Lemma 1. The parameter $\beta$ varies such that $E\left(x\right(\beta ),0,0)$ is an equilibrium point that fulfills the conditions $F_1$–$F_3$. Taking into account the characteristic polynomial of the equilibrium $E\left(x\right(\beta ),0,0)$ of system (1), namely

$$P\left(\lambda \right)={\lambda }^3-j_z\left(E_{\beta }\right){\lambda }^2-j_y\left(E_{\beta }\right)\lambda ,$$

where $E_{\beta }=(x\left(\beta \right),0,0,\alpha \left(\beta \right),\beta ),$ we assume there is a unique $\beta ={\beta }_0$ and consequently a unique pair $({\alpha }_0,{\beta }_0)\in \mathcal{F},{\alpha }_0=\alpha \left({\beta }_0\right)$ such that

$$j_y(x\left({\beta }_0\right),0,0,{\alpha }_0,{\beta }_0)=0.$$

Therefore, we get the equilibrium $E_0(x\left({\beta }_0\right),0,0)$ with a double-zero eigenvalue when $\beta$ passes through the critical value ${\beta }_0$. Obviously, we can consider $\alpha$ instead of $\beta .$

In the following, we consider $E_0=O(0,0,0)$ and $({\alpha }_0,{\beta }_0)=(0,0)$; we denote $E=(0,0,0,\alpha ,\beta )$ and $\overline{0}=(0,0,0,0,0)$. We are concerned with local properties: that is, $(\alpha ,\beta )$ moves in the parametric plane with $\left|(\alpha ,\beta )\right|=\sqrt{{\alpha }^2+{\beta }^2}$ being sufficiently small.

First, we use Taylor’s expansion of the function j with respect to $(x,y,z)$ at $(0,0,0)$:

$$\begin{array}{cc}\hfill j(x,y,z,\alpha ,\beta )& =j\left(E\right)+j_x\left(E\right)x+j_y\left(E\right)y+j_z\left(E\right)z+{\displaystyle \frac{1}{2}}{j}_{x^2}\left(E\right)x^2+{\displaystyle \frac{1}{2}}{j}_{y^2}\left(E\right)y^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{j}_{z^2}\left(E\right)z^2+j_{xy}\left(E\right)xy+j_{xz}\left(E\right)xz+j_{yz}\left(E\right)yz+\mathcal{O}\left(x^i{y}^j{z}^k\right),\hfill \end{array}$$

where $i+j+k\ge 3$. We have $j\left(\overline{0}\right)=j_x\left(\overline{0}\right)=j_y\left(\overline{0}\right)=0$, $j_z\left(\overline{0}\right)\ne 0$, $j_{x^2}\left(\overline{0}\right)\ne 0.$

We perform the parameter-dependent shift of the first variable, i.e.,

$$x=\epsilon +\delta (\alpha ,\beta ), y=y, z=z,$$

and system (1) becomes

$$\left\{\begin{array}{c}\dot{\epsilon }=y\hfill \\ \dot{y}=z\hfill \\ \dot{z}=\tilde{j}(\epsilon ,y,z,\alpha ,\beta )\hfill \end{array}\right.,$$

(2)

where

$$\begin{array}{ll}\tilde{j}(\epsilon ,y,z,\alpha ,\beta )& =\left(j\left(E\right)+j_x\left(E\right)\delta +{\displaystyle \frac{1}{2}}{j}_{x^2}\left(E\right){\delta }^2+\mathcal{O}\left({\delta }^3\right)\right)+\left(j_x\left(E\right)+j_{x^2}\left(E\right)\delta +\mathcal{O}\left({\delta }^2\right)\right)\epsilon \\ & +\left(j_y\left(E\right)+j_{xy}\left(E\right)\delta +\mathcal{O}\left({\delta }^2\right)\right)y+\left(j_z\left(E\right)+j_{xz}\left(E\right)\delta +\mathcal{O}\left({\delta }^2\right)\right)z\\ & +{\displaystyle \frac{1}{2}}{j}_{x^2}\left(E\right){\epsilon }^2+{\displaystyle \frac{1}{2}}{j}_{y^2}\left(E\right)y^2+{\displaystyle \frac{1}{2}}{j}_{z^2}\left(E\right)z^2+j_{xy}\left(E\right)\epsilon y+j_{xz}\left(E\right)\epsilon z+j_{yz}\left(E\right)yz\\ & +\mathcal{O}\left({(\epsilon +\delta )}^i{y}^j{z}^k\right),i+j+k\ge 3.\end{array}$$

(3)

Now we try to find $\delta$ such that one of the linear terms vanishes via IFT. We have two cases.

Case I. The annihilation of the term proportional to y.

Let $f(\alpha ,\beta ,\delta )=j_y\left(E\right)+j_{xy}\left(E\right)\delta +\mathcal{O}\left({\delta }^2\right)=j_y\left(E\right)+j_{xy}\left(E\right)\delta +\phi (\alpha ,\beta ,\delta ){\delta }^2.$

We have $f(0,0,0)=j_y\left(\overline{0}\right)=0$ and $f_{\delta }(0,0,0)=j_{xy}\left(\overline{0}\right).$ Imposing the condition $j_{xy}\left(\overline{0}\right)\ne 0$, we can apply IFT; thus, there is the function $\delta =\delta (\alpha ,\beta )$ with $\delta (0,0)=0$ such that $f(\alpha ,\beta ,\delta (\alpha ,\beta \left)\right)=0$ in the neighborhood of $(0,0)$. Moreover

$$\delta (\alpha ,\beta )=-{\displaystyle \frac{j_{y\alpha }\left(\overline{0}\right)}{j_{xy}\left(\overline{0}\right)}}\alpha -{\displaystyle \frac{j_{y\beta }\left(\overline{0}\right)}{j_{xy}\left(\overline{0}\right)}}\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right),i+j\ge 2.$$

We replace the above $\delta$ in (3), and then we expand in Taylor series with respect to $(\alpha ,\beta )$ at $(0,0)$, knowing that $j\left(\overline{0}\right)=j_x\left(\overline{0}\right)=j_y\left(\overline{0}\right)=0$, $j_z\left(\overline{0}\right)\ne 0$, $j_{x^2}\left(\overline{0}\right)\ne 0$, $j_{xy}\left(\overline{0}\right)\ne 0$, $j_{\alpha }\ne 0$. We have

$$\begin{array}{cc}\hfill \tilde{j}(\epsilon ,y,z,\alpha ,\beta )& =\left(j_{\alpha }\left(\overline{0}\right)\alpha +j_{\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right)\hfill \\ \hfill & +\left({\displaystyle \frac{j_{x\alpha }\left(\overline{0}\right)j_{xy}\left(\overline{0}\right)-j_{x^2}\left(\overline{0}\right)j_{y\alpha }\left(\overline{0}\right)}{j_{xy}\left(\overline{0}\right)}}\alpha +{\displaystyle \frac{j_{x\beta }\left(\overline{0}\right)j_{xy}\left(\overline{0}\right)-j_{x^2}\left(\overline{0}\right)j_{y\beta }\left(\overline{0}\right)}{j_{xy}\left(\overline{0}\right)}}\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right)\epsilon \hfill \\ \hfill & +\left(j_z\left(\overline{0}\right)-{\displaystyle \frac{j_{y\alpha }\left(\overline{0}\right)j_{xz}\left(\overline{0}\right)}{j_{xy}\left(\overline{0}\right)}}\alpha -{\displaystyle \frac{j_{y\beta }\left(\overline{0}\right)j_{xz}\left(\overline{0}\right)}{j_{xy}\left(\overline{0}\right)}}\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right)z\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(j_{x^2}\left(\overline{0}\right)+j_{x^2\alpha }\left(\overline{0}\right)\alpha +j_{x^2\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right){\epsilon }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(j_{y^2}\left(\overline{0}\right)+j_{y^2\alpha }\left(\overline{0}\right)\alpha +j_{y^2\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right)y^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(j_{z^2}\left(\overline{0}\right)+j_{z^2\alpha }\left(\overline{0}\right)\alpha +j_{z^2\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right)z^2\hfill \\ \hfill & +\left(j_{xy}\left(\overline{0}\right)+j_{xy\alpha }\left(\overline{0}\right)\alpha +j_{xy\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right)\epsilon y\hfill \\ \hfill & +\left(j_{xz}\left(\overline{0}\right)+j_{xz\alpha }\left(\overline{0}\right)\alpha +j_{xz\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right)\epsilon z\hfill \\ \hfill & +\left(j_{yz}\left(\overline{0}\right)+j_{yz\alpha }\left(\overline{0}\right)\alpha +j_{yz\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\right)yz\hfill \\ \hfill & +\mathcal{O}\left({\epsilon }^k{y}^l{z}^m{\alpha }^n{\beta }^p\right), i+j\ge 2, k+l+m\ge 3, n+p\ge 0.\hfill \end{array}$$

Consider the change in parameters near the origin $(\alpha ,\beta )\mapsto ({\nu }_1,{\nu }_2)$ given by

$$\begin{array}{cc}\hfill & {\nu }_1=j_{\alpha }\left(\overline{0}\right)\alpha +j_{\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\hfill \\ \hfill & {\nu }_2={\displaystyle \frac{j_{x\alpha }\left(\overline{0}\right)j_{xy}\left(\overline{0}\right)-j_{x^2}\left(\overline{0}\right)j_{y\alpha }\left(\overline{0}\right)}{j_{xy}\left(\overline{0}\right)}}\alpha +{\displaystyle \frac{j_{x\beta }\left(\overline{0}\right)j_{xy}\left(\overline{0}\right)-j_{x^2}\left(\overline{0}\right)j_{y\beta }\left(\overline{0}\right)}{j_{xy}\left(\overline{0}\right)}}\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right).\hfill \end{array}$$

The above the map is regular if

$${\left.{\displaystyle \frac{D({\nu }_1,{\nu }_2)}{D(\alpha ,\beta )}}\right|}_{(0,0)}={\displaystyle \frac{1}{2j_{xy}\left(\overline{0}\right)}}\left|\begin{array}{cc}{j}_{\alpha }\left(\overline{0}\right)& j_{\beta }\left(\overline{0}\right)\\ j_{x\alpha }\left(\overline{0}\right)j_{xy}\left(\overline{0}\right)-j_{x^2}\left(\overline{0}\right)j_{y\alpha }\left(\overline{0}\right)& j_{x\beta }\left(\overline{0}\right)j_{xy}\left(\overline{0}\right)-j_{x^2}\left(\overline{0}\right)j_{y\beta }\left(\overline{0}\right)\end{array}\right|\ne 0,$$

which is equivalent in our hypothesis to the regularity of the map

$$(x,\alpha ,\beta )\mapsto (j(x,0,0,\alpha ,\beta ), j_x(x,0,0,\alpha ,\beta ), j_y(x,0,0,\alpha ,\beta ))$$

at the origin.

The above change in parameters transforms system (2) in

$$\left\{\begin{array}{c}\dot{\epsilon }=y\hfill \\ \dot{y}=z\hfill \\ \dot{z}=\tilde{j}(\epsilon ,y,z,{\nu }_1,{\nu }_2)\hfill \end{array}\right.,$$

(4)

where

$$\begin{array}{cc}\hfill \tilde{j}(\epsilon ,y,z,{\nu }_1,{\nu }_2)& ={\nu }_1+{\nu }_2\epsilon +\left(j_z\left(\overline{0}\right)z+\mathcal{O}\left({\nu }_1^g{\nu }_2^h\right)\right)+\left({\displaystyle \frac{1}{2}}{j}_{x^2}\left(\overline{0}\right)+\mathcal{O}\left({\nu }_1^g{\nu }_2^h\right)\right){\epsilon }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{j}_{y^2}\left(\overline{0}\right)y^2+{\displaystyle \frac{1}{2}}{j}_{z^2}\left(\overline{0}\right)z^2+j_{xy}\left(\overline{0}\right)\epsilon y+j_{xz}\left(\overline{0}\right)\epsilon z+j_{yz}\left(\overline{0}\right)yz\hfill \\ \hfill & +\mathcal{O}\left({\epsilon }^i{y}^j{z}^k{\mu }_1^l{\mu }_2^m\right)+\mathcal{O}\left({\epsilon }^n{y}^p{z}^q{\mu }_1^r{\mu }_2^s\right),\hfill \end{array}$$

$g+h\ge 1, i+j+k=2, (i,j,k)\ne (2,0,0), l+m\ge 1, n+p+q\ge 3, r+s\ge 0.$

We denote $A({\nu }_1,{\nu }_2)=\frac{1}{2}(j_{x^2}\left(\overline{0}\right)+\mathcal{O}\left({\nu }_1^i{\nu }_2^j\right)).$ Since $A(0,0)=\frac{1}{2}{j}_{x^2}\left(\overline{0}\right)\ne 0$, this results in $A({\nu }_1,{\nu }_2)\ne 0$ near $(0,0).$ Using the transformation

$$X=A({\nu }_1,{\nu }_2)\epsilon , Y=A({\nu }_1,{\nu }_2)y, Z=A({\nu }_1,{\nu }_2)z, {\mu }_1=A({\nu }_1,{\nu }_2){\nu }_1, {\mu }_2={\nu }_2,$$

and

$$\frac{1}{A({\nu }_1,{\nu }_2)}=\frac{2}{j_{x^2}\left(\overline{0}\right)}+\mathcal{O}\left({\nu }_1^i{\nu }_2^j\right),i+j\ge 1,$$

system (4) can be written as

$$\begin{array}{ccc}\dot{X}\hfill & =\hfill & Y\hfill \\ \dot{Y}\hfill & =\hfill & Z\hfill \\ \dot{Z}\hfill & =\hfill & {\mu }_1+{\mu }_{2}X+X^2+cZ+dXY+\phi ({\mu }_1,{\mu }_2)Z\hfill \\ \hfill & \hfill & +{\displaystyle \frac{j_{y^2}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}{Y}^2+{\displaystyle \frac{j_{z^2}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}{Z}^2+{\displaystyle \frac{2j_{xz}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}XZ+{\displaystyle \frac{2j_{yz}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}YZ\hfill \\ \hfill & \hfill & +\mathcal{O}\left(X^i{Y}^j{Z}^k{\mu }_1^l{\mu }_2^m\right)+\mathcal{O}\left(X^n{Y}^p{Z}^q{\mu }_1^r{\mu }_2^s\right),\hfill \end{array}$$

(5)

where $i+j+k=2, i\ne 2, l+m\ge 1, n+p+q\ge 3, r+s\ge 0$, $c=j_z\left(\overline{0}\right)\ne 0$, $d={\displaystyle \frac{2j_{xy}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}\ne 0$, $\phi (0,0)=0$.

In conclusion, we have obtained the following theorem.

Theorem 1.

Let the jerk system $\dot{x}=y, \dot{y}=z, \dot{z}=j(x,y,z,\alpha ,\beta ),$ where j is smooth.

Assume that the following conditions are fulfilled:

DZ1. 

$j\left(\overline{0}\right)=0$, $j_x\left(\overline{0}\right)=0$, $j_y\left(\overline{0}\right)=0$, $j_z\left(\overline{0}\right)\ne 0$;

DZ2. 

$j_{\alpha }\left(\overline{0}\right)\ne 0$;

DZ3. 

$j_{x^2}\left(\overline{0}\right)\ne 0$, $j_{xy}\left(\overline{0}\right)\ne 0$;

DZ4. 

The map $(x,\alpha ,\beta )\mapsto (j(x,0,0,\alpha ,\beta ),j_x(x,0,0,\alpha ,\beta ),j_y(x,0,0,\alpha ,\beta ))$ is regular at $(0,0,0)$.

Then the considered system has at $(\alpha ,\beta )=(0,0)$ the equilibrium $O(0,0,0)$ with a double-zero eigenvalue and there are smooth invertible variable transformations and smooth invertible parameter changes, which together reduce the system to

$$\left\{\begin{array}{c}\dot{X}=Y\hfill \\ \dot{Y}=Z\hfill \\ \dot{Z}={\mu }_1+{\mu }_{2}X+X^2+cZ+dXY+F(X,Y,Z,{\mu }_1,{\mu }_2)\hfill \end{array}\right.,$$

(6)

where $c=j_z\left(\overline{0}\right)\ne 0$, $d={\displaystyle \frac{2j_{xy}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}\ne 0$, $F(X,Y,Z,{\mu }_1,{\mu }_2)=\phi ({\mu }_1,{\mu }_2)Z+{\displaystyle \frac{j_{y^2}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}{Y}^2+{\displaystyle \frac{j_{z^2}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}{Z}^2+{\displaystyle \frac{2j_{xz}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}XZ+{\displaystyle \frac{2j_{yz}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}YZ+\mathcal{O}\left(X^i{Y}^j{Z}^k{\mu }_1^l{\mu }_2^m\right)+\mathcal{O}\left(X^n{Y}^p{Z}^q{\mu }_1^r{\mu }_2^s\right),$$i+j+k=2,i\ne 2,l+m\ge 1,n+p+q\ge 3,r+s\ge 0,$ and φ is a smooth function with $\phi (0,0)=0.$

Remark 1.

We notice the similarity between the reduced jerk system (6) and Bogdanov’s normal form of the double-zero bifurcation on ${\mathbb{R}}^2$ given by (see, e.g., [2])

$$\left\{\begin{array}{c}\dot{X}=Y\hfill \\ \dot{Y}={\mu }_1+{\mu }_{2}X+X^2\pm XY\hfill \end{array}\right..$$

(7)

Because $c,d\ne 0$ and the local stability and some local bifurcations are related to the coefficients of the characteristic polynomial, we conclude that for a jerk system, an approximate normal form for the double-zero bifurcation is given by the system

$$\left\{\begin{array}{c}\dot{x}=y\hfill \\ \dot{y}=z\hfill \\ \dot{z}={\mu }_1+{\mu }_{2}x+x^2+cz+dxy\hfill \end{array}\right.,$$

(8)

where $c,d\in \mathbb{R},c,d\ne 0$ are fixed.

It is easy to see that if ${\mu }_2^2-4{\mu }_1>0$, system (8) has two equilibria $E^{\pm }(x^{\pm },0,0)$, $x^{\pm }=\frac{-{\mu }_2\pm \sqrt{{\mu }_2^2-4{\mu }_1}}{2}$, which collide when ${\mu }_2^2-4{\mu }_1=0$ and then disappear for ${\mu }_2^2-4{\mu }_1<0$. Moreover, the characteristic polynomial at $E^{\pm }$ is given by

$$P_{E^{\pm }}\left(\lambda \right)={\lambda }^3-c{\lambda }^2-d{x}^{\pm }\lambda \mp \sqrt{{\mu }_2^2-4{\mu }_1}.$$

The fold curve is $\mathcal{F}=\{({\mu }_1,{\mu }_2):{\mu }_2^2-4{\mu }_1=0\}$, and ${\lambda }_1={\lambda }_2=0$ iff $({\mu }_1,{\mu }_2)=(0,0).$

Following [21], if the characteristic polynomial has the form $P\left(\lambda \right)={\lambda }^3-c{\lambda }^2-b\lambda -a,$ then the Hopf bifurcation occurs if $a<0, b<0, c<0, a+bc>0$; hence, it cannot occur at $E^{+}.$

For $E^{-}$, let $a=-\sqrt{{\mu }_2^2-4{\mu }_1}, b=d{x}^{-}=-\frac{{\mu }_2+\sqrt{{\mu }_2^2-4{\mu }_1}}{2}d.$

Assume $c<0$. At $E^{-}$, we obtain the Hopf bifurcation curve

$$\mathcal{H}=\{({\mu }_1,{\mu }_2):(2+cd)\sqrt{{\mu }_2^2-4{\mu }_1}+cd{\mu }_2=0\},$$

which depends on c and $d.$ In fact, $\mathcal{H}$ is half of the parabola ${\mu }_1=\frac{cd+1}{{(cd+2)}^2}{\mu }_2^2$ for $d\in (-\infty ,0)\cup (0,-\frac{1}{c})\cup (-\frac{1}{c},-\frac{2}{c})\cup (-\frac{2}{c},\infty ),$ the negative semi-axis ${\mu }_2=0$ for $d=-\frac{2}{c}$, and the positive semi-axis ${\mu }_1=0$ for $d=-\frac{2}{c}.$ Moreover, for $c<0$, we get that $E^{+}$ is an unstable equilibrium point with a two-dimensional stable manifold; thus, it does not bifurcate.

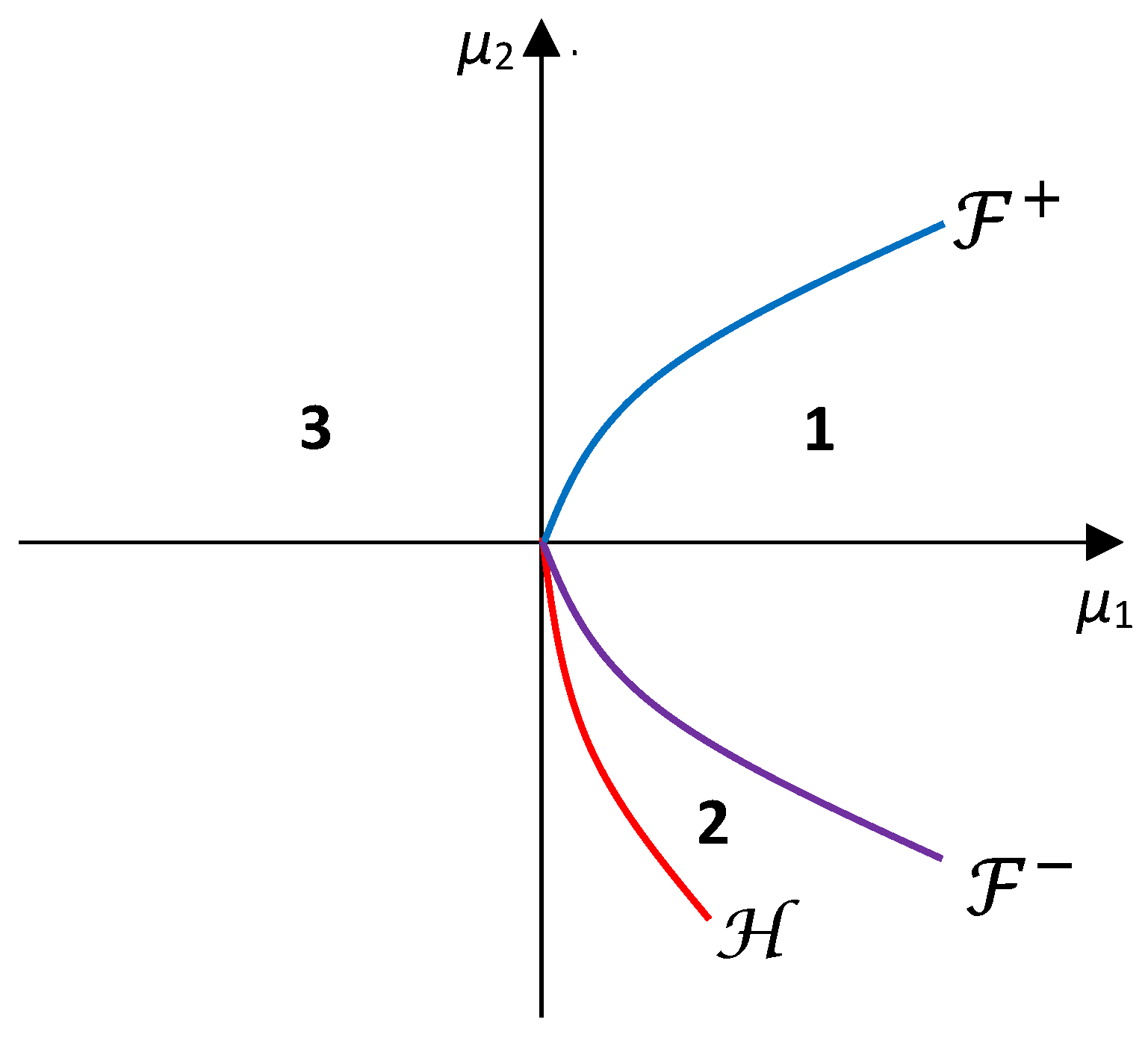
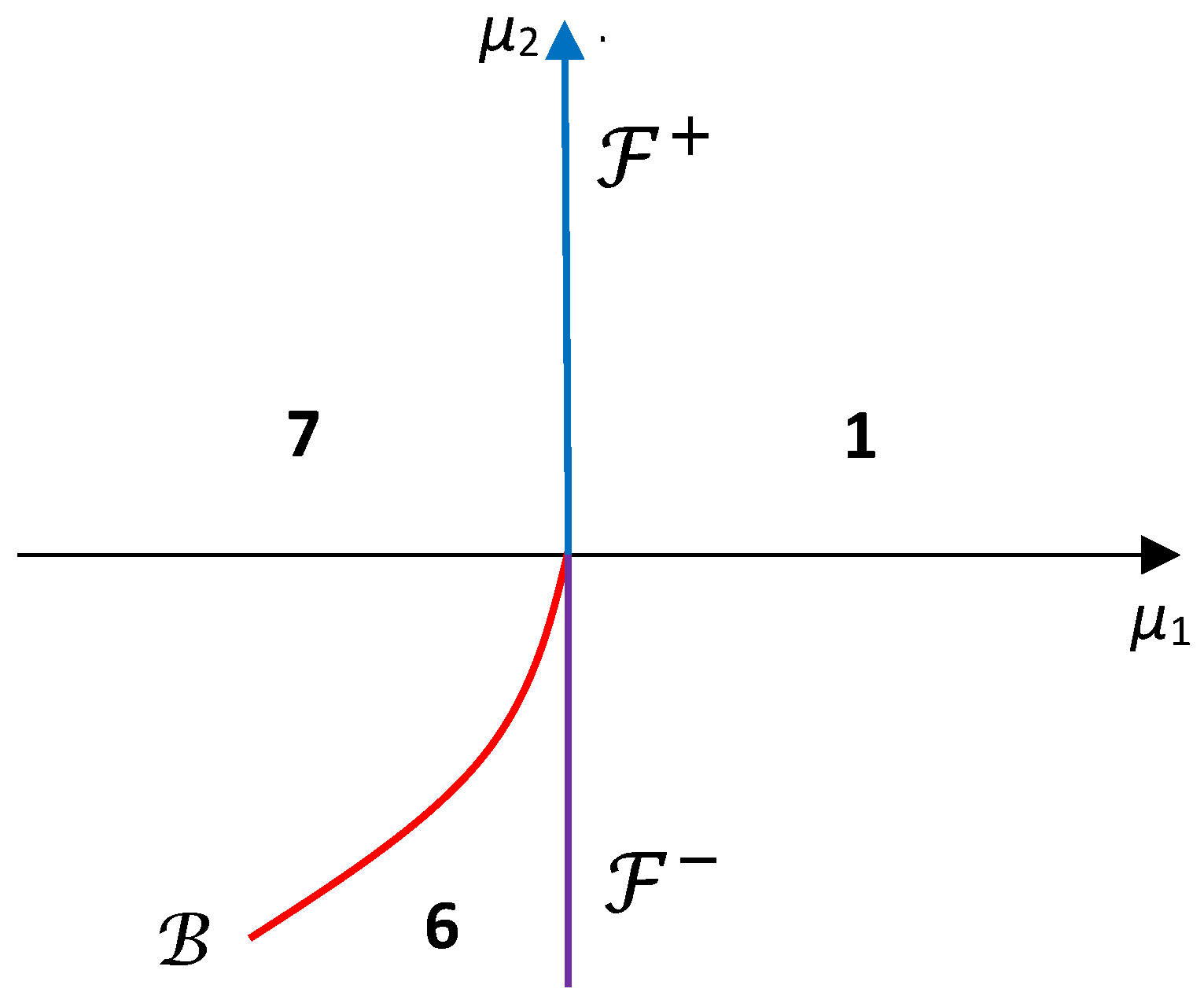
Now, let $d<0$. Consider the parametric portrait given in Figure 1, where $\mathcal{H}$ is the above Hopf curve and ${\mathcal{F}}^{+},{\mathcal{F}}^{-}$ are the branches of the fold curve $\mathcal{F}$ separated by the double-zero point $(0,0)$.

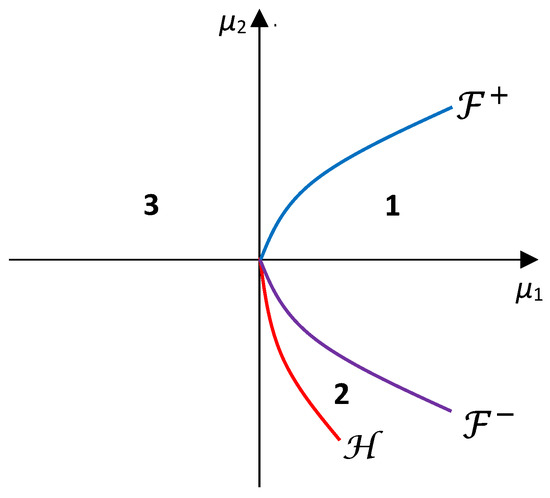
Figure 1. The parametric portrait for local bifurcations of system (8) for $c<0, d<0$.

In region 1, there are no equilibrium points. On the curve ${\mathcal{F}}^{-}$, an equilibrium is born and splits into the asymptotically stable node (or focus-node) $E^{-}$ and the unstable saddle (or saddle-focus) $E^{+}$ in the region 2. Hence system (8) displays a saddle–node bifurcation when $({\mu }_1,{\mu }_2)$ crosses the fold curve ${\mathcal{F}}^{-}$. In region 3, $E^{-}$ is an unstable equilibrium point with a one-dimensional stable manifold; hence, it loses stability when the curve $\mathcal{H}$ is crossed. Moreover, a Hopf bifurcation occurs, and a stable limit cycle is born (we assume that the first Lyapunov coefficient does not vanish). The unstable equilibria $E^{+}$ and $E^{-}$ collide when $({\mu }_1,{\mu }_2)\in {\mathcal{F}}^{+}$ and then disappear when returning to region 1; thus, a degenerate fold bifurcation occurs. We conclude that there are no other local bifurcations in the dynamics of system (8) in the case $c<0, d<0.$

We notice that the above scenario is similar to that which takes place for Bogdanov’s normal form (7) (see [2]). As is pointed out in [2], “…finally return to region 1, no limit cycles must remain. Therefore, there must be global bifurcations ’destroying’ the cycle somewhere between $\mathcal{H}$ and ${\mathcal{F}}^{+}$”. Consequently, a global bifurcation has to occur for system (8) in this case.

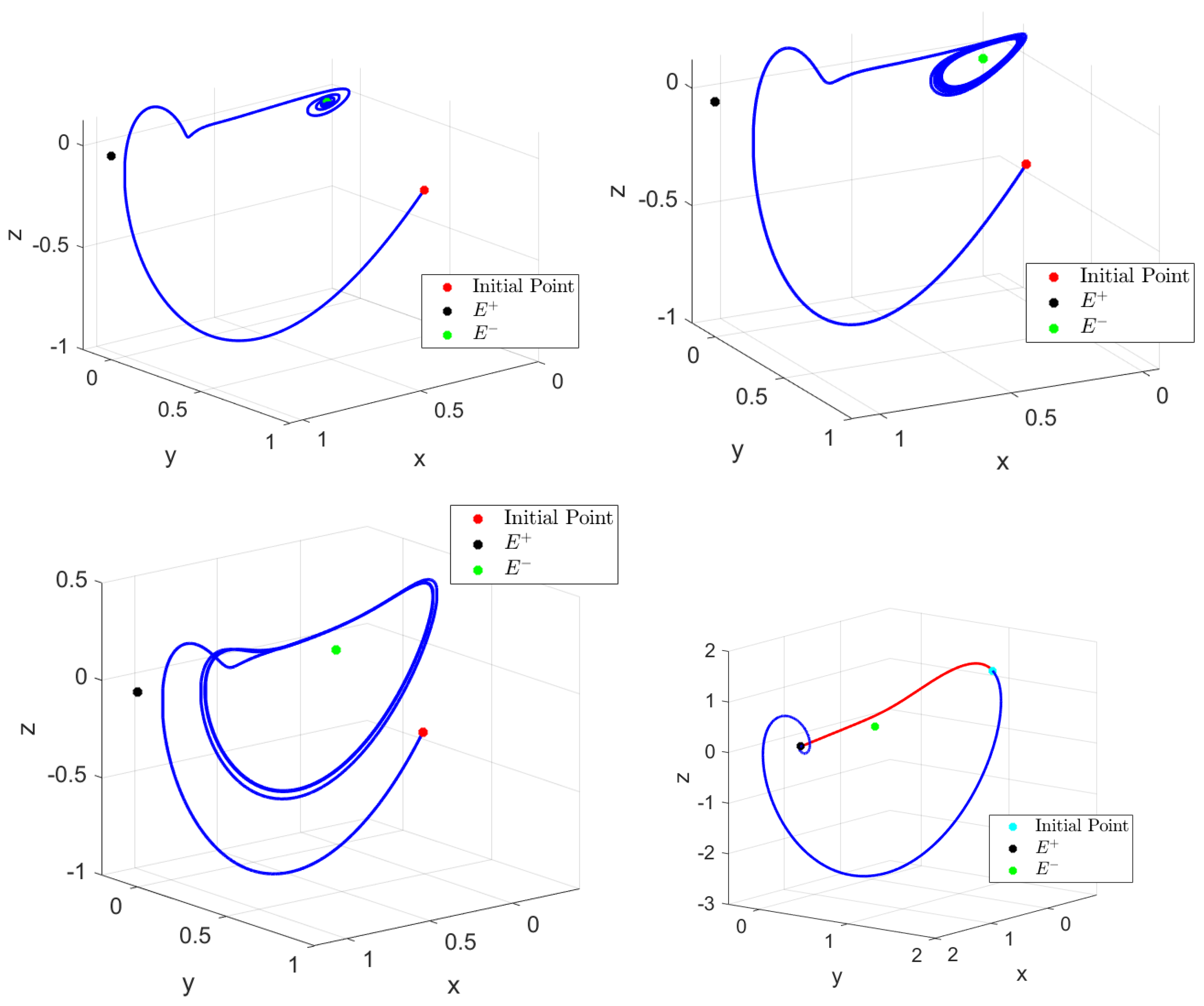
In Figure 2, we present such a homoclinic bifurcation obtained by numerical simulations. We fix $c=-2, d=-5, {\mu }_2=-1.2$, and we vary the parameter ${\mu }_1$. Considering the initial point $(0.3463,0.8131,-0.1167)$, we obtain an asymptotically stable orbit for ${\mu }_1=0.15$, which turns into a stable limit cycle at the above-mentioned Hopf curve. The limit cycle deforms (${\mu }_1=0.1$, ${\mu }_1=-0.01$) and finally becomes a homoclinic orbit (plotted here for ${\mu }_1=-0.0738$ using the initial point $(-0.3142,1.1737,1.3654)$: the red part of the homoclinic orbit corresponds to $t\in (-\infty ,0)$ and the blue one to $t\in [0,\infty )$).

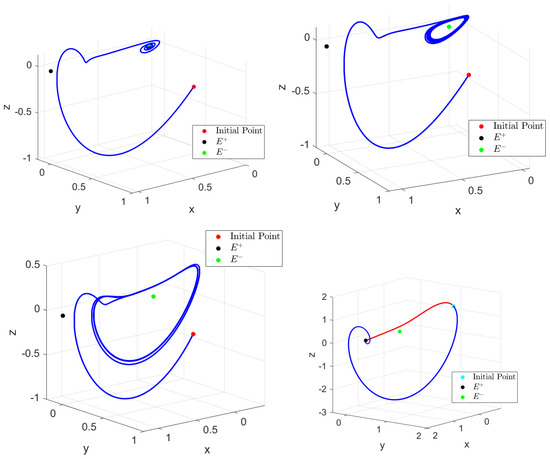
Figure 2. The transition from an asymptotically stable orbit to a homoclinic orbit of system (8) via limit cycles for $c<0, d<0$.

In the cases for which $d\in (0,-\frac{1}{c})\cup (-\frac{1}{c},-\frac{2}{c})\cup (-\frac{2}{c},\infty ),$ we obtain similar parametric portraits. The difference is that the regions 2 and 3 and the curves ${\mathcal{F}}^{-}$ and ${\mathcal{F}}^{+}$ change their roles.

Now, assume that $c>0$. We obtain that $E^{-}$ is an unstable equilibrium point with an one-dimensional stable manifold; thus, it does not bifurcate. Moreover, in this case system (8) does not experience a Hopf bifurcation.

Let $d>0$, and the parametric portrait given in Figure 3, where $\mathcal{B}$ is half of the parabola ${\mu }_1=\frac{cd+1}{{(cd+2)}^2}{\mu }_2^2$ with ${\mu }_2>0$ and ${\mathcal{F}}^{+},{\mathcal{F}}^{-}$, is as above.

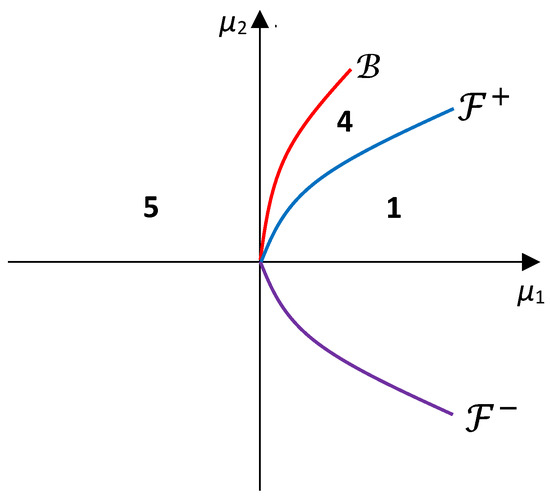
Figure 3. The parametric portrait for local bifurcations of system (8) for $c>0, d>0$.

Again, there are no equilibrium points in region 1. Crossing the curve ${\mathcal{F}}^{+}$, an equilibrium is born and separates into the unstable node (or focus-node) $E^{+}$ and the unstable saddle (or saddle-focus) $E^{-}$ in region 4. Since both equilibria are unstable, system (8) does not display a saddle–node bifurcation in the classic sense: that is, a stable node and a saddle coalesce. Anyway, a fold bifurcation occurs in the considered dynamics. In region 5, $E^{+}$ is an unstable equilibrium point with a two-dimensional stable manifold. Therefore, crossing the curve $\mathcal{B}$, the dimension of the stable manifold of $E^{+}$ changes. The saddles $E^{+}$ and $E^{-}$ collide when $({\mu }_1,{\mu }_2)$ crosses ${\mathcal{F}}^{-}$ and then disappear when returning to region 1; thus, a degenerate fold bifurcation occurs. We conclude that there are no other local bifurcations in the dynamics of system (8) in this case. Similar bifurcation diagrams are obtained when $d<0$.

Case II. The annihilation of the term proportional to $\epsilon$.

Let $g(\alpha ,\beta ,\delta )=j_x\left(E\right)+j_{x^2}\left(E\right)\delta +\mathcal{O}\left({\delta }^2\right)=j_x\left(E\right)+j_{x^2}\left(E\right)\delta +\phi (\alpha ,\beta ,\delta ){\delta }^2.$

We have $g(0,0,0)=j_x\left(\overline{0}\right)=0$ and $g_{\delta }(0,0,0)=j_{x^2}\left(\overline{0}\right)\ne 0.$ By IFT, there is a function $\delta =\delta (\alpha ,\beta )$ with $\delta (0,0)=0$ such that $g(\alpha ,\beta ,\delta (\alpha ,\beta \left)\right)=0$ in the neighborhood of $(0,0).$ Moreover,

$$\delta (\alpha ,\beta )=-{\displaystyle \frac{j_{x\alpha }\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}\alpha -{\displaystyle \frac{j_{x\beta }\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right),i+j\ge 2.$$

We proceed as in the previous case. Now we consider the change in parameters $(\alpha ,\beta )\mapsto ({\mu }_1,{\mu }_2)$ near the origin given by

$$\begin{array}{cc}\hfill & {\nu }_1=j_{\alpha }\left(\overline{0}\right)\alpha +j_{\beta }\left(\overline{0}\right)\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right)\hfill \\ \hfill & {\nu }_2=-{\displaystyle \frac{j_{x\alpha }\left(\overline{0}\right)j_{xy}\left(\overline{0}\right)-j_{x^2}\left(\overline{0}\right)j_{y\alpha }\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}\alpha -{\displaystyle \frac{j_{x\beta }\left(\overline{0}\right)j_{xy}\left(\overline{0}\right)-j_{x^2}\left(\overline{0}\right)j_{y\beta }\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}\beta +\mathcal{O}\left({\alpha }^i{\beta }^j\right).\hfill \end{array}$$

The above map is regular in $(0,0)$ if the map

$$(x,\alpha ,\beta )\mapsto (j(x,0,0,\alpha ,\beta ),j_x(x,0,0,\alpha ,\beta ),j_y(x,0,0,\alpha ,\beta ))$$

is also regular at $(0,0,0)$.

Consequently, system (2) is transformed into the system given in the next theorem.

Theorem 2.

Let the jerk system $\dot{x}=y, \dot{y}=z, \dot{z}=j(x,y,z,\alpha ,\beta ),$ where j is smooth.

Assume that the following conditions are fulfilled:

DZ1. 

$j\left(\overline{0}\right)=0$, $j_x\left(\overline{0}\right)=0$, $j_y\left(\overline{0}\right)=0$, $j_z\left(\overline{0}\right)\ne 0$;

DZ2. 

$j_{\alpha }\left(\overline{0}\right)\ne 0$;

DZ3. 

$j_{x^2}\left(\overline{0}\right)\ne 0$;

DZ4. 

The map $(x,\alpha ,\beta )\mapsto (j(x,0,0,\alpha ,\beta ), j_x(x,0,0,\alpha ,\beta ), j_y(x,0,0,\alpha ,\beta ))$ is regular at $(0,0,0)$.

Then the considered system has at $(\alpha ,\beta )=(0,0)$ the equilibrium $O(0,0,0)$ with a double-zero eigenvalue, and there are smooth invertible variable transformations and smooth invertible parameter changes, which together reduce the system to

$$\left\{\begin{array}{c}\dot{X}=Y\hfill \\ \dot{Y}=Z\hfill \\ \dot{Z}={\mu }_1+{\mu }_{2}Y+cZ+X^2+G(X,Y,Z,{\mu }_1,{\mu }_2)\hfill \end{array}\right.,$$

(9)

where $c=j_z\left(\overline{0}\right)\ne 0$, $G(X,Y,Z,{\mu }_1,{\mu }_2)=\phi ({\mu }_1,{\mu }_2)Z+{\displaystyle \frac{j_{y^2}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}{Y}^2+{\displaystyle \frac{j_{z^2}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}{Z}^2+{\displaystyle \frac{2j_{xy}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}XY+{\displaystyle \frac{2j_{xz}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}XZ+{\displaystyle \frac{2j_{yz}\left(\overline{0}\right)}{j_{x^2}\left(\overline{0}\right)}}YZ+\mathcal{O}\left(X^i{Y}^j{Z}^k{\mu }_1^l{\mu }_2^m\right)+\mathcal{O}\left(X^n{Y}^p{Z}^q{\mu }_1^r{\mu }_2^s\right)$, $i+j+k=2, i\ne 2, l+m\ge 1, n+p+q\ge 3, r+s\ge 0,$ and φ is a smooth function with $\phi (0,0)=0.$

Remark 2.

In this case, the reduced jerk system (9) is similar to the normal form of the double-zero bifurcation on ${\mathbb{R}}^2$ given by Guckenheimer and Holmes [1]:

$$\left\{\begin{array}{c}\dot{X}=Y\hfill \\ \dot{Y}={\mu }_1+{\mu }_{2}Y+X^2+dXY\hfill \end{array}\right..$$

Now, we consider for a jerk system another approximate normal form for the double-zero bifurcation given by the system

$$\left\{\begin{array}{c}\dot{x}=y\hfill \\ \dot{y}=z\hfill \\ \dot{z}={\mu }_1+{\mu }_{2}y+cz+x^2+dxy\hfill \end{array}\right.,$$

(10)

where $c,d\in \mathbb{R},c\ne 0$ are fixed.

If ${\mu }_1<0$, system (10) has two equilibria $E^{\pm }\left(x\right)(\pm \sqrt{-{\mu }_1},0,0)$, which coalesce when ${\mu }_1=0$ and then disappear for ${\mu }_1>0$. The characteristic polynomial at $E^{\pm }$ is given by

$$P_{E^{\pm }}\left(\lambda \right)={\lambda }^3-c{\lambda }^2-({\mu }_2\pm d\sqrt{-{\mu }_1})\lambda \mp 2\sqrt{-{\mu }_1}.$$

The fold curve is $\mathcal{F}=\{({\mu }_1,{\mu }_2):{\mu }_1=0\}$, and ${\lambda }_1={\lambda }_2=0$ iff $({\mu }_1,{\mu }_2)=(0,0).$

The Hopf bifurcation cannot occur at $E^{+}.$ For $E^{-}$, we denote $a=-2\sqrt{-{\mu }_1}$, $b={\mu }_2-d\sqrt{-{\mu }_1}.$

Let $c<0$. It follows that $E^{+}$ is an unstable equilibrium point with a two-dimensional stable manifold; thus, it does not bifurcate.

At $E^{-}$, we obtain the Hopf bifurcation curve

$$\mathcal{H}=\{({\mu }_1,{\mu }_2):c{\mu }_2-(2+cd)\sqrt{-{\mu }_1}=0\}.$$

In fact, $\mathcal{H}$ is half of the parabola ${\mu }_1=-\frac{c^2}{{(cd+2)}^2}{\mu }_2^2$ for $d\in (-\infty ,-\frac{2}{c})\cup (-\frac{2}{c},\infty ),$ and the negative semi-axis ${\mu }_2=0$ for $d=-\frac{2}{c}$.

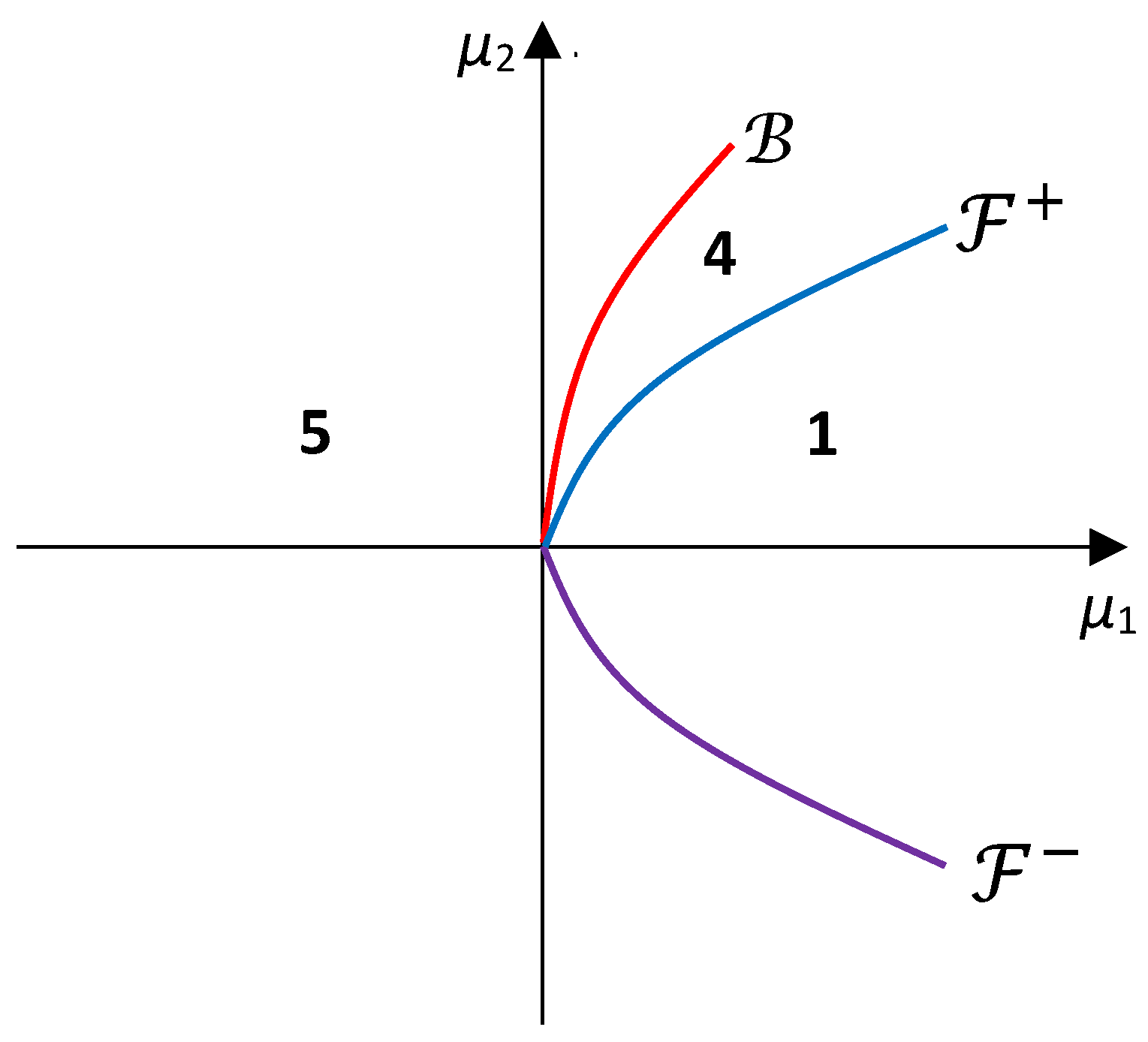
Now, let $d\le 0$. We obtain the parametric portrait given in Figure 4, where $\mathcal{H}$ is the above Hopf curve and ${\mathcal{F}}^{+},{\mathcal{F}}^{-}$ are the branches of the fold curve $\mathcal{F}$ separated by the double-zero point $(0,0)$. Also, the behavior of system (10) in each region is the same as of system (8) in the case $c<0, d<0$ (see Case 1). For $d\in (0,-\frac{2}{c})\cup (-\frac{2}{c},\infty ),$ we obtain similar parametric portraits.

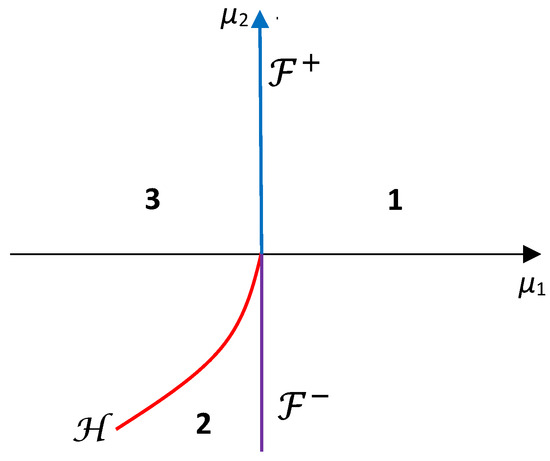
Figure 4. The parametric portrait for local bifurcations of system (10) for $c<0, d<0$.

In the case $c>0$, we obtain that $E^{-}$ is an unstable equilibrium point with a one-dimensional stable manifold; thus, it does not bifurcate. In addition, a Hopf bifurcation does not occur in the dynamics of system (10).

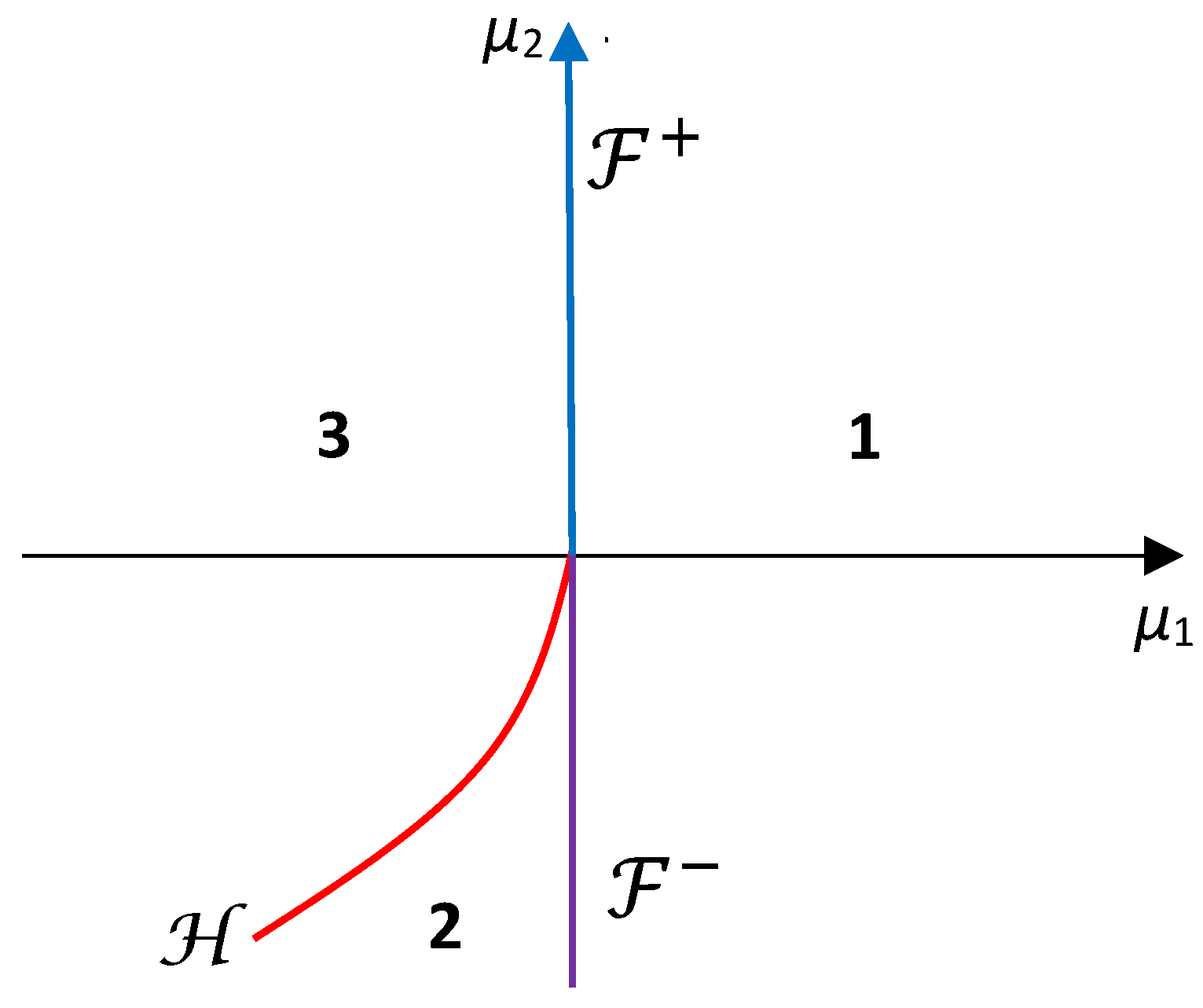
For $d>0$, we get the parametric portrait given in Figure 5, where $\mathcal{B}$ is the parabola ${\mu }_1=-\frac{c^2}{{(cd+2)}^2}{\mu }_2^2$ with ${\mu }_2<0$ and ${\mathcal{F}}^{+},{\mathcal{F}}^{-}$ are as above.

Figure 5. The parametric portrait for local bifurcations of system (10) for $c>0, d>0$.

In this case, there are no equilibrium points in region 1, and an equilibrium appears when $({\mu }_1,{\mu }_2)\in {\mathcal{F}}^{-}$. This point splits into the unstable node (or focus-node) $E^{+}$ and the unstable saddle (or saddle-focus) $E^{-}$ in the region 6. Crossing the curve $\mathcal{B}$, $E^{+}$ changes its number of negative eigenvalues, and in region 7, it has a two-dimensional stable manifold. The saddles $E^{+}$ and $E^{-}$ collide when $({\mu }_1,{\mu }_2)$ crosses ${\mathcal{F}}^{+}$ and then disappear when returning to region 1; thus, a degenerate fold bifurcation occurs. We conclude that there are no other local bifurcations in the dynamics of system (10) in this case. Similar bifurcation diagrams are obtained when $d\le 0$.

Remark 3.

It is known that the normal forms for the double-zero bifurcation given by Bogdanov [13], Takens [14], and Guckenheimer and Holmes [1] are equivalent. In our case, the approximate normal forms (8) and (10) have similar parametric portraits. Moreover, if $c<0, d<0,$ the local bifurcations are the same as those obtained for the Bogdanov normal form (see [2]) and Guckenheimer and Holmes (see [1]), respectively. It remains an open problem to establish if a jerk system and the corresponding approximate normal form are locally topologically equivalent: that is, the construction of a homeomorphism that maps orbits of the first system onto orbits of the second system.

4. Conclusions

In this paper, we have studied the double-zero bifurcation of an arbitrary two-parameter jerk system. This bifurcation is associated with the appearance of two zero eigenvalues. In the two-dimensional case, the behavior of a system that displays such a bifurcation near the critical values of the parameters is given by the behavior of a normal form. For an $n-$dimensional dynamical system, particularly a jerk system, a normal form is obtained by reduction on a local center manifold. To avoid this reduction, using invertible coordinate and parameter changes, we have derived approximate normal forms for a double-zero bifurcation of an arbitrary two-parameter jerk system that continues being a jerk system. We have obtained the simplest jerk systems that experience such a bifurcation. In addition, we have given some parametric portraits and have studied the local behavior of these systems.