New Criteria for Analyzing the Permanence, Periodic Solution, and Global Attractiveness of the Competition and Cooperation Model of Two Enterprises with Feedback Controls and Delays

Abstract

This paper studies a class of the non-autonomous competition and cooperation model of two enterprises involving discrete time delays and feedback controls. The paper proposes new criteria for analyzing the permanence, periodic solution, and global attractiveness of the model. The common mathematical techniques of the Lyapunov method, the continuation theorem, and the comparison principle are used in this paper. By means of the comparison principle and inequality techniques, the concept of permanence is investigated, which refers to the long-term survival of the enterprises within the competitive and cooperative framework. Meanwhile, using the continuation theorem, we establish conditions under which the system exhibits periodic behavior. Additionally, the global attractiveness of the system is derived by constructing multiple Lyapunov functionals. Finally, an example is presented to illustrate the applicability and validity of the proposed criteria in this paper. This example serves as a demonstration that showcases the main results derived from the analysis.

1. Introduction

It is well known that the survival of the species is crucial for maintaining ecosystems and coexistence is a fundamental aspect of nature. Similarly, in the business world, coexistence among enterprises is essential for the development and sustainability of enterprise clusters. In recent years, there has been growing interest among scholars in studying enterprise clusters using concepts and principles from ecological theory and dynamic system theory [1,2,3,4,5,6]. By applying these theories, researchers have proposed various models to explore the dynamic properties of enterprise clusters. For example, Tian and Nie [1] studied the following non-delayed autonomous model

$$\begin{array}{c}{\displaystyle \frac{d{y}_1\left(t\right)}{dt}=y_1\left(t\right)[c_1-\frac{c_1{y}_1\left(t\right)}{\mathcal{K}}-\frac{c_1{b}_1{(y_2\left(t\right)-d_2)}^2}{\mathcal{K}}],}\hfill \\ {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=y_2\left(t\right)[c_2-\frac{c_2{y}_2\left(t\right)}{\mathcal{K}}+\frac{c_2{b}_2{(y_1\left(t\right)-d_1)}^2}{\mathcal{K}}],}\hfill \end{array}$$

where $y_1\left(t\right)$ and $y_2\left(t\right)$ denote the output of the enterprises $E_1$ and $E_2$, $\mathcal{K}$ denotes the carrying capacity of mark under nature unlimited conditions, $c_1$ and $c_2$ are the intrinsic growth rates of enterprises $E_1$ and $E_2$, $b_1$ denotes the rate of intra-enterprise competition from $E_2$, $b_2$ denotes the rate of conversion of the commodity into the reproduction of enterprise $E_1$, and $d_1$ and $d_2$ are the initial productions of enterprises $E_1$ and $E_2$. Letting $a_{11}=\frac{c_1}{\mathcal{K}},a_{12}=\frac{c_1{b}_1}{\mathcal{K}},$ $a_{21}=\frac{c_2}{\mathcal{K}},a_{22}=\frac{c_2{b}_2}{K}$ in the above model, then system takes the form:

$$\begin{array}{c}{\displaystyle \frac{d{y}_1\left(t\right)}{dt}=y_1\left(t\right)[c_1-a_{11}{y}_1\left(t\right)-a_{12}{(y_2\left(t\right)-d_2)}^2],}\hfill \\ {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=y_2\left(t\right)[c_2-a_{21}{y}_2\left(t\right)+a_{22}{(y_1\left(t\right)-d_1)}^2].}\hfill \end{array}$$

(1)

Inspired by model (1) and considering time delays, Liao et al. [2] investigated the following two-time delayed autonomous model

$$\begin{array}{c}{\displaystyle \frac{d{y}_1\left(t\right)}{dt}=y_1\left(t\right)[c_1-a_{11}{y}_1(t-{\sigma }_1)-a_{12}{(y_2(t-{\sigma }_2)-d_2)}^2],}\hfill \\ {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=y_2\left(t\right)[c_2-a_{21}{y}_2(t-{\sigma }_1)+a_{22}{(y_1(t-{\sigma }_2)-d_1)}^2],}\hfill \end{array}$$

(2)

and discussed the dynamic behavior of system (2). When ${\sigma }_1={\sigma }_2=\sigma$, then we can derive the following model

$$\begin{array}{c}{\displaystyle \frac{d{y}_1\left(t\right)}{dt}=y_1\left(t\right)[c_1-a_{11}{y}_1(t-\sigma )-a_{12}{(y_2(t-\sigma )-d_2)}^2],}\hfill \\ {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=y_2\left(t\right)[c_2-a_{21}{y}_2(t-\sigma )+a_{22}{(y_1(t-\sigma )-d_1)}^2].}\hfill \end{array}$$

(3)

In [3], the authors investigated the bifurcation behavior and stability of system (3). In [4], Li et al., discussed the system with four time delays

$$\begin{array}{c}{\displaystyle \frac{d{y}_1\left(t\right)}{dt}=y_1\left(t\right)[c_1-a_{11}{y}_1(t-{\sigma }_1)-a_{21}{(y_2(t-{\sigma }_2)-d_2)}^2],}\hfill \\ {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=y_2\left(t\right)[c_2-a_{21}{y}_2(t-{\sigma }_3)+a_{22}{(y_1(t-{\sigma }_4)-d_1)}^2].}\hfill \end{array}$$

(4)

They restricted themselves to the case when ${\sigma }_1={\sigma }_2=0$, ${\sigma }_2+{\sigma }_4>0$ and denote ${\sigma }_2$ and ${\sigma }_4$ by ${\sigma }_1$ and ${\sigma }_2$, then by choosing $\sigma ={\sigma }_1+{\sigma }_2$ as the bifurcation parameter, they obtained some results on the bifurcation behavior and stability of system (4). Moreover, there have been some studies [7,8] related to the study of the dynamical behavior of autonomous fractional-order competition and cooperation models involving two enterprises with delays.

It is worth noting that the market carrying capacity, enterprise output, and resource availability within an enterprise cluster ecosystem change over time. These changes have a direct impact on the growth patterns and characteristics of the enterprise clusters. As a result, the mathematical models of enterprise clusters need to consider these time-varying factors to accurately describe the dynamics of the system. The existing models (1–4), may have limitations in fully describing the complex and dynamic nature of enterprise cluster systems. Therefore, it becomes necessary to study enterprise cluster models in a non-autonomous environment. Non-autonomous scenarios allow for the incorporation of time-varying factors, such as changing market demands, technological advancements, resource availability, and government policies. By considering these time-dependent influences, non-autonomous models can better reflect the real-world dynamics of enterprise clusters. For example, focused on model (1), in [9], the authors discussed the following non-autonomous model without time delay

$$\begin{array}{c}{\displaystyle \frac{d{y}_1\left(t\right)}{dt}=y_1\left(t\right)[c_1\left(t\right)-a_{11}\left(t\right)y_1\left(t\right)-a_{12}\left(t\right){(y_2\left(t\right)-d_2\left(t\right))}^2],}\hfill \\ {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=y_2\left(t\right)[c_2\left(t\right)-a_{21}\left(t\right)y_2\left(t\right)+a_{22}\left(t\right){(y_1\left(t\right)-d_1\left(t\right))}^2].}\hfill \end{array}$$

(5)

By means of the Lyapunov function method and useful inequality techniques, the authors in [9] derived several conditions on the dynamic properties of system (5).

On the other hand, feedback controls are widely used in various fields, including economics, engineering, electronics, automation, and process control. The main purpose of feedback controls is to maintain stability and accuracy in a system by continuously monitoring and adjusting its output. By comparing the actual output with the desired output, feedback controls help to identify and correct any errors or deviations, ensuring that the system operates as intended. Overall, the feedback controls play a crucial role in achieving precise and stable operation in complex systems, enabling efficient and reliable performance in a wide range of applications. Recently, there have been a few studies [10,11,12] about the delayed non-autonomous competition and cooperation model of two enterprises that consider dynamic behaviors for feedback control cases. Based on the above analysis and as an extension of previously works [1,2,3,4,5,6,9], this paper will consider the following non-autonomous model with feedback controls and time delays:

$$\begin{array}{c}{\displaystyle \frac{d{y}_1\left(t\right)}{dt}=y_1\left(t\right)[c_1\left(t\right)-b_{11}\left(t\right)y_1(t-{\zeta }_1)-b_{12}\left(t\right){(y_2(t-{\zeta }_2)-d_2\left(t\right))}^2-g_1\left(t\right)u_1(t-{\phi }_1)],}\hfill \\ {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=y_2\left(t\right)[c_2\left(t\right)-b_{21}\left(t\right)y_2(t-{\zeta }_3)+b_{22}\left(t\right){(y_1(t-{\zeta }_4)-d_1\left(t\right))}^2-g_2\left(t\right)u_2(t-{\phi }_2)],}\hfill \\ {\displaystyle \frac{d{u}_1\left(t\right)}{dt}=-f_1\left(t\right)u_1\left(t\right)+h_1\left(t\right)y_1(t-{\psi }_1),}\hfill \\ {\displaystyle \frac{d{u}_2\left(t\right)}{dt}=-f_2\left(t\right)u_2\left(t\right)+h_2\left(t\right)y_2(t-{\psi }_2),}\hfill \end{array}$$

(6)

where $y_1\left(t\right)$ and $y_2\left(t\right)$ represent the output of enterprise $E_1$ and enterprise $E_2$, $u_1\left(t\right)$ and $u_2\left(t\right)$ represent the indirect feedback control variables, and $g_i\left(t\right),f_i\left(t\right),h_i\left(t\right)$ represent the feedback control coefficients at time t, respectively.

The purpose of this study is to derive some conditions on the permanence, periodic solution, and global attractiveness for model (6).

2. Preliminaries

In this paper, we introduce the following assumptions for system (6):

(${\mathsf{\Lambda }}_1$)

$c_1\left(t\right)>0,c_2\left(t\right)>0$, $b_{11}\left(t\right)>,b_{12}\left(t\right)>0$, $b_{21}\left(t\right)>0{,}_{22}\left(t\right)>0$, $g_1\left(t\right),g_2\left(t\right)$, $f_1\left(t\right),f_2\left(t\right),h_1\left(t\right),h_2\left(t\right)$, and $d_1\left(t\right)>0,d_2\left(t\right)>0$ are continuous bounded functions, ${\phi }_i,{\psi }_i(i=1,2)$, ${\zeta }_i>0(i=1,2,3,4)$ are constants.

(${\mathsf{\Lambda }}_2$)

$c_1\left(t\right)>0,c_2\left(t\right)>0$, $b_{11}\left(t\right)>,b_{12}\left(t\right)>0$, $b_{21}\left(t\right)>0,b_{22}\left(t\right)>0$, $g_1\left(t\right),g_2\left(t\right)$, $f_1\left(t\right),f_2\left(t\right),h_1\left(t\right),h_2\left(t\right)$ and $d_1\left(t\right)>0,d_2\left(t\right)>0$ are continuous $\varpi$-periodic functions on $[0,\varpi ]$, ${\phi }_i,{\psi }_i(i=1,2)$, ${\zeta }_i>0(i=1,2,3,4)$ are constants.

Throughout the article, for system (6), we introduce the following initial conditions

$$y_1\left(t\right)={ϵ}_1\left(t\right),y_2\left(t\right)={ϵ}_2\left(t\right),u_1\left(t\right)={ϵ}_3\left(t\right),u_2\left(t\right)={ϵ}_4\left(t\right),t\in [-\zeta ,0],$$

where ${ϵ}_1\left(t\right),{ϵ}_2\left(t\right),{ϵ}_3\left(t\right),{ϵ}_4\left(t\right)$ are non-negative and continuous functions defined on $[-\zeta ,0]$ satisfying ${ϵ}_1\left(0\right)>0,{ϵ}_2\left(0\right)>0,{ϵ}_3\left(0\right)>0,{ϵ}_4\left(0\right)>0$ and

$\zeta =max\{{\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4,{\phi }_1,{\phi }_2,{\psi }_1,{\psi }_2\}$.

For a continuous and bounded function $F\left(t\right)$ defined on $[0,+\infty )$, we define $F^L={inf}_{t\in [0,+\infty )}\left\{F\left(t\right)\right\}$ and $F^M={sup}_{t\in [0,+\infty )}\left\{F\left(t\right)\right\}$.

Now, we present two useful lemmas.

Lemma 1

([13]). Assume that $w\left(t\right)\ge 0$ is a function defined on $[-q\theta ,+\infty )$ and satisfies that

$$\dot{w}\left(t\right)\le w\left(t\right)(\gamma -\sum _{n=0}^q{\sigma }^{p}w(t-p\theta ))+B,$$

where

$$\gamma >0,{\sigma }^k\ge 0(n=0,1,2,\cdots q),\tau =\sum _{n=0}^q{\sigma }^p>0,B\ge 0,$$

are constants. Then, there is a constant $M_w>0$ such that

$$\underset{t\to \infty }{lim\; sup}w\left(t\right)\le M_w=-\frac{B}{\gamma }+(\frac{B}{\gamma }+w^{*})exp\left(\gamma q\theta \right),$$

(7)

where $w=w^{*}>0$ is the unique positive solution of equation

$$w(\gamma -pw)+B=0.$$

Lemma 2

([13]). Assume that $w\left(t\right)\ge 0$ is a function defined on $[-q\theta ,+\infty )$ and satisfies that

$$\dot{w}\left(t\right)\ge w\left(t\right)(\gamma -\sum _{n=0}^q{\sigma }^{p}w(t-p\theta ))+B,$$

$$\gamma >0,{\sigma }^k\ge 0(n=0,1,2,\cdots q),\tau =\sum _{n=0}^q{\sigma }^p>0,B\ge 0,$$

are constants. If inequality (7) holds, then there is a constant $N_w>0$ such that

$$\underset{t\to \infty }{lim\; inf}w\left(t\right)\ge N_w=\frac{\gamma }{\sigma }exp\left\{(\gamma -\sigma M_w)q\theta \right\}.$$

3. Permanence and Periodic Solution

Firstly, we provide the two following lemmas.

Lemma 3.

Suppose that (${\mathsf{\Lambda }}_1$) holds, then for any positive solution $(y_1\left(t\right),y_2\left(t\right),u_1\left(t\right),u_2\left(t\right))$ of system (6), there exist real numbers $M_1>0,M_2>0,N_1>0,N_2>0$, and $T>0$ such that $y_1\left(t\right)\le M_1,y_2\left(t\right)\le M_2$ and $u_1\left(t\right)\le N_1,u_2\left(t\right)\le N_2$ as $t>T$.

Proof. 

First, from system (6), for $t>{\zeta }_1$, we have

$$\frac{d{y}_1\left(t\right)}{dt}\le y_1\left(t\right)\left(c_1^M-b_{11}^L{y}_1(t-{\zeta }_1)\right).$$

By Lemma 1, we have

$$\underset{t\to \infty }{lim\; sup}{y}_1\left(t\right)\le M_1\triangleq \frac{c_1^M}{b_{11}^L}exp\left(c_1^M{\zeta }_1\right),$$

then, for any constant ${\epsilon }_0>0$, there exists a constant $T_0>{\tau }_1$ such that

$$y_1\left(t\right)\le M_1+{\epsilon }_0,t\ge T_0,$$

then from system (6), we have

$$\frac{d{y}_2\left(t\right)}{dt}\le y_2\left(t\right)\left(c_2^M+M^{*}-b_{21}^L{y}_2(t-{\zeta }_3)\right),t\ge T_0,$$

where $M^{*}=b_{22}^M[{(M_1+{\epsilon }_0)}^2+{\left(d_1^M\right)}^2]$. Since ${\epsilon }_0$ is arbitrary, by Lemma 1, we have

$$\underset{t\to \infty }{lim\; sup}{y}_2\left(t\right)\le M_2\triangleq \frac{M_0}{b_{21}^L}exp\left\{M_0{\zeta }_3\right\},$$

where $M_0=c_2^M+b_{22}^M[{\left(M_1\right)}^2+{\left(d_1^M\right)}^2]$.

On the other hand, from system (6), we have

$$\frac{d{u}_i\left(t\right)}{dt}\le -f_i^L{u}_i\left(t\right)+h_i^M{M}_i,t\ge T_1,$$

where $i=1,2$ and $T_1\ge T_0$. Then, we have

$$\underset{t\to \infty }{lim\; sup}{u}_i\left(t\right)\le N_i\triangleq \frac{M_i{h}_i^M}{f_i^L}.$$

□

Lemma 4.

Suppose that (${\mathsf{\Lambda }}_1$) holds and $r>0(i=1,2)$, then for any positive solution $(y_1\left(t\right),y_2\left(t\right),u_1\left(t\right),u_2\left(t\right))$ of system (6), there exist real numbers $m_1>0,m_2>0,n_1>0,n_2>0$ and $T^M>0$ such that $y_1\left(t\right)\ge m_1,y_2\left(t\right)\ge m_2$ and $u_1\left(t\right)\ge n_1,u_2\left(t\right)\ge n_2$ as $t>T^M$. Where $r=min\{r_1,r_2\}$, $r_1=c_1^L-b_{12}^M(M_2^2+{\left(d_2^M\right)}^2)-g_1^M{N}_1$, $r_2=c_2^L-g_2^M{N}_2$.

Proof. 

From system (6) and Lemma 3 for $t>T_2>{\zeta }_3$, we have

$$\dot{y_1}\left(t\right)\ge y_1\left(t\right)\left(r_0-b_{11}^M{y}_1(t-{\zeta }_1)\right)\mathrm{a}\mathrm{n}\mathrm{d}\dot{y_2}\left(t\right)\ge y_2\left(t\right)\left(r_2-b_{21}^M{y}_2(t-{\zeta }_3)\right),$$

where $r_1=c_1^L-b_{12}^M(M_2^2+{\left(d_2^M\right)}^2)-g_1^M{N}_1$ and $r_2=c_2^L-g_2^M{N}_2$.

Using Lemma 2, we have

$$\underset{t\to \infty }{lim\; inf}{y}_1\left(t\right)\ge m_1\triangleq \frac{r_0}{b_{11}^M}exp\left\{(r_0-b_{11}^M{M}_1){\zeta }_1\right\},$$

and

$$\underset{t\to \infty }{lim\; inf}{y}_2\left(t\right)\ge m_2\triangleq \frac{c_2^L}{b_{21}^M}exp\left\{(c_2^L-b_{21}^M{M}_2){\zeta }_3\right\}.$$

Next, from system (6) for $t\ge T_3>T_2$, we have

$$\dot{u_i}\left(t\right)\ge h_i^L{m}_i-f_i^M{u}_i\left(t\right),i=1,2.$$

Then, we have

$$\underset{t\to \infty }{lim\; inf}{u}_1\left(t\right)\ge n_i\triangleq \frac{h_i^L{m}_i}{f_i^M},i=1,2.$$

□

Theorem 1.

Suppose that (${\mathsf{\Lambda }}_1$) holds and $r>0$; then, system (6) is permanent, where $r=min\{r_1,r_2\}$, $r_1=c_1^L-b_{12}^M(M_2^2+{\left(d_2^M\right)}^2)-g_1^M{N}_1$, $r_2=c_2^L-g_2^M{N}_2$.

From the above two lemmas, we can see the permanence of system (6). Next, in order to obtain the positive periodic solution of system (6), we need the following lemma.

Lemma 5.

If $(y_1^{*}\left(t\right),y_2^{*}\left(t\right),u_1^{*}\left(t\right),u_2^{*}\left(t\right))$ is an ϖ-periodic solution of (6), then $(y_1^{*}\left(t\right),y_2^{*}\left(t\right),u_1^{*}\left(t\right),$$u_2^{*}\left(t\right))$ satisfies the system

$$\begin{array}{c}{\displaystyle \frac{d{y}_1\left(t\right)}{dt}=y_1\left(t\right)[c_1\left(t\right)-b_{11}\left(t\right)y_1(t-{\zeta }_1)-b_{12}\left(t\right){(y_2(t-{\zeta }_2)-d_2\left(t\right))}^2-g_1\left(t\right)u_1(t-{\phi }_1)],}\hfill \\ {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=y_2\left(t\right)[c_2\left(t\right)-b_{21}\left(t\right)y_2(t-{\zeta }_3)+b_{22}\left(t\right){(y_1(t-{\zeta }_4)-d_1\left(t\right))}^2-g_2\left(t\right)u_2(t-{\phi }_2)],}\hfill \\ {\displaystyle u_i\left(t\right)={\int }_t^{t+\varpi }{h}_i\left(s\right)y_i(s-{\psi }_i)H_i(t,s)ds,i=1,2,}\hfill \end{array}$$

(8)

where

$$H_i(t,s)=\frac{exp\left\{{\int }_t^s{f}_i\left(\theta \right)d\theta \right\}}{exp\left\{{\int }_0^{\varpi }{f}_i\left(\theta \right)d\theta \right\}-1},i=1,2.$$

The converse is also true.

Proof. 

From system (6) with the initial conditions and the variation-constants formula in ordinary differential equations, we have

$$\begin{array}{cc}\hfill {\displaystyle u_i\left(t\right)=}& {\displaystyle \left({\int }_0^t{h}_i\left(s\right)y_i(s-{\psi }_i)H_i\left(s\right)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right)\right)}\hfill \\ & {\displaystyle \times exp\left\{-{\int }_0^t{f}_i\left(\theta \right)d\theta \right\},i=1,2.}\hfill \end{array}$$

(9)

Then, we obtain

$$\begin{array}{cc}\hfill {\displaystyle u_i(t+\varpi )=}& {\displaystyle \left({\int }_0^{t+\varpi }{h}_i\left(s\right)y_i(s-{\psi }_i)H_i\left(s\right)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right)\right)}\hfill \\ & {\displaystyle \times exp\left\{-{\int }_0^t{f}_i\left(\theta \right)d\theta \right\},i=1,2.}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\displaystyle u_i^{*}\left(t\right)=}& {\displaystyle \left({\int }_0^t{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)H_i\left(s\right)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right)\right)}\hfill \\ & {\displaystyle \times exp\left\{-{\int }_0^t{f}_i\left(\theta \right)d\theta \right\},i=1,2.}\hfill \end{array}$$

Considering that $(y_1^{*}\left(t\right),y_2^{*}\left(t\right),u_1^{*}\left(t\right),u_2^{*}\left(t\right))$ is a $\varpi$-periodic solution of system (6) with the initial conditions, we obtain

$$\begin{array}{cc}\hfill {\displaystyle (}& {\displaystyle {\int }_0^t{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right))exp\left\{-{\int }_0^t{h}_i\left(\theta \right)d\theta \right\}}\hfill \\ & {\displaystyle =\left({\int }_0^{t+\varpi }{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right)\right)}\hfill \\ & {\displaystyle \times exp\left\{-{\int }_0^{t+\varpi }{f}_i\left(\theta \right)d\theta \right\},i=1,2.}\hfill \end{array}$$

then

$$\begin{array}{cc}\hfill {\displaystyle (}& {\displaystyle {\int }_0^t{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right))exp\left\{{\int }_0^{\varpi }{f}_i\left(\theta \right)d\theta \right\}}\hfill \\ & {\displaystyle =\left({\int }_0^{t+\varpi }{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right)\right)}\hfill \\ & {\displaystyle ={\int }_0^t{h}_i\left(s\right)y_i^{*}(s-{\psi }_i))exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right)}\hfill \\ & {\displaystyle +{\int }_t^{t+\varpi }{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds,i=1,2.}\hfill \end{array}$$

which implies

$$\begin{array}{cc}\hfill {\displaystyle (}& {\displaystyle {\int }_0^t{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right))(e^{\overline{f}\varpi }-1)}\hfill \\ & {\displaystyle ={\int }_t^{t+\varpi }{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds,i=1,2.}\hfill \end{array}$$

that is,

$$\begin{array}{cc}& {\displaystyle {\int }_0^t{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds+{ϵ}_i\left(0\right)}\hfill \\ & {\displaystyle =u_i^{*}\left(t\right)exp\left\{{\int }_0^t{f}_i\left(\theta \right)d\theta \right\}}\hfill \\ & {\displaystyle =\frac{1}{e^{\overline{f}\varpi }-1}{\int }_t^{t+\varpi }{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)exp\left\{{\int }_0^s{f}_i\left(\theta \right)d\theta \right\}ds,i=1,2.}\hfill \end{array}$$

Thus, we have

$$u_i^{*}\left(t\right)={\int }_t^{t+\varpi }{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)\frac{exp\left\{{\int }_t^s{f}_i\left(\theta \right)d\theta \right\}}{exp\left\{{\int }_0^{\varpi }{f}_i\left(\theta \right)d\theta \right\}-1}ds.i=1,2.$$

Next, let $(y_1^{*}\left(t\right),y_2^{*}\left(t\right),u_1^{*}\left(t\right),u_2^{*}\left(t\right))$ be a $\varpi$-periodic solution of system (8), then

$$u_i^{*}\left(t\right)={\int }_t^{t+\varpi }{h}_i\left(s\right)x_i^{*}(s-{\psi }_i)\frac{exp\left\{{\int }_t^s{f}_i\left(\theta \right)d\theta \right\}}{exp\left\{{\int }_0^{\varpi }{f}_i\left(\theta \right)d\theta \right\}-1}ds,i=1,2.$$

Then, from direct calculation, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{u}^{*}\left(t\right)}{dt}=}& {\displaystyle -f_i\left(t\right){\int }_t^{t+\varpi }{h}_i\left(s\right)y_i^{*}(s-{\psi }_i)\frac{exp\left\{{\int }_t^s{f}_i\left(\theta \right)d\theta \right\}}{exp\left\{{\int }_0^{\varpi }{f}_i\left(\theta \right)d\theta \right\}-1}ds}\hfill \\ & {\displaystyle +h_i(t+\varpi )y_i^{*}(t+\varpi -{\psi }_i)\frac{exp\left\{{\int }_t^{t+\varpi }{f}_i\left(\theta \right)d\theta \right\}}{exp\left\{{\int }_0^{\varpi }{f}_i\left(\theta \right)d\theta \right\}-1}}\hfill \\ & {\displaystyle -h_i\left(t\right)y_i^{*}(t-{\psi }_i)\frac{1}{exp\left\{{\int }_0^{\varpi }{f}_i\left(\theta \right)d\theta \right\}-1}}\hfill \\ \hfill =& {\displaystyle -f_i\left(t\right)u_i\left(t\right)+h_i\left(t\right)y_i^{*}(t-{\psi }_i),i=1,2.}\hfill \end{array}$$

This completes the proof. □

One can see that, in order to prove that system (6) has at least one $\varpi$-periodic solution, we only need to prove that system (8) has at least one $\varpi$-periodic solution.

Now, for the convenience of statements, we denote

$${\overline{c}}_i=\frac{1}{\varpi }{\int }_0^{\varpi }{c}_i\left(t\right)dt,{\overline{R}}_i=\frac{1}{\varpi }{\int }_0^{\varpi }\left|c_i\left(t\right)\right|dt,i=1,2.$$

The following theorem is about the existence of positive periodic solutions of system (6).

Theorem 2.

Suppose that $\left({\mathsf{\Lambda }}_2\right)$ and ${\overline{c}}_1-{\overline{b}}_{12}{(M_2-{\overline{d}}_2)}^2>0$ hold; then, system (6) has at least one positive $\varpi -$ periodic solution, where $M_2$ is defined in Lemma 3.

Proof. 

Set

$$y_1\left(t\right)=exp\left\{z_1\left(t\right)\right\},y_2\left(t\right)=exp\left\{z_2\left(t\right)\right\}.$$

Then, by (8), we obtain

$$\begin{array}{c}{\displaystyle \frac{d{z}_1\left(t\right)}{dt}=c_1\left(t\right)-b_{11}\left(t\right)exp\left\{z_1(t-{\zeta }_1)\right\}-b_{12}\left(t\right){(exp\left\{z_2(t-{\zeta }_2)\right\}-d_2\left(t\right))}^2-g_1\left(t\right)U_1(t-{\phi }_1),}\hfill \\ {\displaystyle \frac{d{z}_2\left(t\right)}{dt}=c_2\left(t\right)-b_{21}\left(t\right)exp\left\{z_2(t-{\zeta }_3)\right\}+b_{22}\left(t\right){(exp\left\{z_1(t-{\zeta }_4)\right\}-d_1\left(t\right))}^2-g_2\left(t\right)U_2(t-{\phi }_2),}\hfill \\ {\displaystyle U_i\left(t\right)={\int }_t^{t+\varpi }{h}_i\left(s\right)exp\left\{z_i(s-{\psi }_i)\right\}{H}_i(t,s)ds,i=1,2.}\hfill \end{array}$$

(10)

Let $\mathcal{C}(\mathbb{R},{\mathbb{R}}^2)$ denote the space of all continuous functions $z\left(t\right)=(z_1\left(t\right),z_2\left(t\right)):\mathbb{R}\to {\mathbb{R}}^2$. We take

$$\mathcal{Y}=\mathcal{Z}=\{z\left(t\right)\in \mathcal{C}(\mathbb{R},{\mathbb{R}}^2):z\left(t\right)\mathrm{an}\varpi \mathrm{-periodic}\mathrm{function}\},$$

with norm

$$\Vert z\Vert =\underset{t\in [0,\varpi ]}{max}|z_1\left(t\right)|+\underset{t\in [0,\varpi ]}{max}\left|z_2\left(t\right)\right|.$$

Then, one can see that $\mathcal{Y}$ and $\mathcal{Z}$ are the Banach spaces.

Now, define a linear operator $\mathcal{L}:$ Dom$\mathcal{L}\subset \mathcal{Y}\to \mathcal{Z}$ and a continuous operator $\mathcal{N}:\mathcal{Y}\to \mathcal{Z}$ as follows.

$$\mathcal{L}z\left(t\right)=\dot{z}\left(t\right),$$

and

$$\mathcal{N}z\left(t\right)=(\mathcal{N}{z}_1\left(t\right),\mathcal{N}{z}_2\left(t\right)),$$

where

$$\begin{array}{cc}{\displaystyle \mathcal{N}{z}_1\left(t\right)=}\hfill & {\displaystyle c_1\left(t\right)-b_{11}\left(t\right)exp\left\{z_1(t-{\zeta }_1)\right\}-b_{12}\left(t\right){(exp\left\{z_2(t-{\zeta }_2)\right\}-d_2\left(t\right))}^2-g_1\left(t\right)U_1(t-{\phi }_1),}\hfill \\ \mathcal{N}{z}_2\left(t\right)=\hfill & {\displaystyle c_2\left(t\right)-b_{21}\left(t\right)exp\left\{z_2(t-{\zeta }_3)\right\}+b_{22}\left(t\right){(exp\left\{z_1(t-{\zeta }_4)\right\}-d_1\left(t\right))}^2-g_2\left(t\right)U_2(t-{\phi }_2).}\hfill \end{array}$$

(11)

Let $\mathcal{P}:\mathcal{Y}\to \mathcal{Y}$ and $\mathcal{Q}:\mathcal{Z}\to \mathcal{Z}$ be the continuous projector

$$\mathcal{P}z\left(t\right)=\frac{1}{\varpi }{\int }_0^{\varpi }z\left(t\right)dt,\mathcal{Q}\lambda \left(t\right)=\frac{1}{\varpi }{\int }_0^{\varpi }\lambda \left(t\right)dt.$$

Then, $\mathrm{I}\mathrm{m}\mathcal{L}=\{\lambda \in \mathcal{Z}:{\int }_0^{\omega }\lambda \left(t\right)dt=0\}$ and $\mathrm{K}\mathrm{e}\mathrm{r}\mathcal{L}={\mathbb{R}}^2$. Thus, obtain that Im$\mathcal{L}$ is closed in $\mathcal{Z}$ and dimKer$L=2$. Since, for any $\lambda \in \mathcal{Z}$, there are unique ${\lambda }_1\in {\mathbb{R}}^n$ and ${\lambda }_2\in \mathrm{I}\mathrm{m}\mathcal{L}$ with

$${\lambda }_1=\frac{1}{\varpi }{\int }_0^{\varpi }\lambda \left(t\right)dt,{\lambda }_2\left(t\right)=\lambda \left(t\right)-{\lambda }_1$$

such that $\lambda \left(t\right)={\lambda }_1+{\lambda }_2\left(t\right)$, we have codimIm$\mathcal{L}=2$. Therefore, $\mathcal{L}$ is a Fredholm mapping of index zero. Next, the generalized inverse (to $\mathcal{L}$) ${\mathcal{K}}_p:$ Im$\mathcal{L}\to$ Ker$\mathcal{P}\cap$ Dom$\mathcal{L}$ is given in the following form

$${\mathcal{K}}_p\lambda \left(t\right)={\int }_0^t\lambda \left(s\right)ds-\frac{1}{\varpi }{\int }_0^{\varpi }{\int }_0^t\lambda \left(s\right)dsdt.$$

Let $\mathcal{F}\left(t\right)=({\mathcal{F}}_1\left(t\right),{\mathcal{F}}_2\left(t\right))$, where

$$\begin{array}{cc}{\displaystyle {\mathcal{F}}_1\left(t\right)=}\hfill & {\displaystyle c_1\left(t\right)-b_{11}\left(t\right)exp\left\{z_1(t-{\zeta }_1)\right\}-b_{12}\left(t\right){(exp\left\{z_2(t-{\zeta }_2)\right\}-d_2\left(t\right))}^2-g_1\left(t\right)U_1(t-{\phi }_1),}\hfill \\ {\mathcal{F}}_2\left(t\right)=\hfill & {\displaystyle c_2\left(t\right)-b_{21}\left(t\right)exp\left\{z_2(t-{\zeta }_3)\right\}+b_{22}\left(t\right){(exp\left\{z_1(t-{\zeta }_4)\right\}-d_1\left(t\right))}^2-g_2\left(t\right)U_2(t-{\phi }_2).}\hfill \end{array}$$

(12)

Thus, we have

$$\mathcal{QN}z\left(t\right)=\frac{1}{\varpi }{\int }_0^{\varpi }\mathcal{F}\left(t\right)dt$$

(13)

and

$$\begin{array}{cc}\hfill {\mathcal{K}}_p(I-\mathcal{Q})\mathcal{N}z\left(t\right)=& {\mathcal{K}}_{p}I\mathcal{N}z\left(t\right)-{\mathcal{K}}_p\mathcal{Q}\mathcal{N}z\left(t\right)\hfill \\ \hfill =& {\displaystyle {\int }_0^t\mathcal{F}\left(s\right)ds-\frac{1}{\varpi }{\int }_0^{\varpi }{\int }_0^t\mathcal{F}\left(s\right)dsdt}\hfill \\ & {\displaystyle +\left(\frac{1}{2}-\frac{t}{\varpi }\right){\int }_0^{\varpi }\mathcal{F}\left(s\right)ds}\hfill \end{array}$$

(14)

From (13) and (14), one can see that $\mathcal{QN}$ and ${\mathcal{K}}_p(I-\mathcal{Q})\mathcal{N}$ are continuous operators and by using the Arzelà–Ascoli theorem, one can find that $\overline{{\mathcal{K}}_p(I-\mathcal{Q})\mathcal{N}\left(\overline{\mathsf{\Omega }}\right)}$ is compact for any open bounded set $\mathsf{\Psi }\subset \mathcal{Y}$ and $\mathcal{QN}\left(\overline{\mathsf{\Psi }}\right)$ is bounded. Thus, $\mathcal{N}$ is $\mathcal{L}$-compact on $\overline{\mathsf{\Psi }}$ for any open bounded subset $\mathsf{\Psi }\subset \mathcal{Y}$.

Let the following equation

$${\dot{z}}_i\left(t\right)=\gamma {\mathcal{F}}_i\left(t\right),i=1,2,$$

(15)

correspond to the operator equation $\mathcal{L}z\left(t\right)=\gamma \mathcal{N}z\left(t\right)$ with parameter $\gamma \in (0,1)$. Furthermore, assume that $z\left(t\right)=(z_1\left(t\right),z_2\left(t\right))\in \mathcal{Y}$ is a solution of system (15) for some parameter $\gamma \in (0,1)$. Then, by integrating system (15) over the interval $[0,\varpi ]$, we obtain

$$\begin{array}{cc}{\displaystyle }\hfill & {\displaystyle {\int }_0^{\varpi }[c_1\left(t\right)-b_{11}\left(t\right)exp\left\{z_1(t-{\zeta }_1)\right\}-b_{12}\left(t\right){(exp\left\{z_2(t-{\zeta }_2)\right\}-d_2\left(t\right))}^2}\hfill \\ & {\displaystyle -g_1\left(t\right)U_1(t-{\phi }_1)\left\}\right]dt=0,}\hfill \\ & {\displaystyle {\int }_0^{\varpi }[c_2\left(t\right)-b_{21}\left(t\right)exp\left\{z_2(t-{\zeta }_3)\right\}+b_{22}\left(t\right){(exp\left\{z_1(t-{\zeta }_4)\right\}-d_1\left(t\right))}^2}\hfill \\ & {\displaystyle -g_2\left(t\right)U_2(t-{\phi }_2)]dt=0.}\hfill \end{array}$$

(16)

By (16), we have

$$\begin{array}{cc}{\displaystyle }\hfill & {\displaystyle {\int }_0^{\varpi }[b_{11}\left(t\right)exp\left\{z_1(t-{\zeta }_1)\right\}+b_{12}\left(t\right){(exp\left\{z_2(t-{\zeta }_2)\right\}-d_2\left(t\right))}^2}\hfill \\ & {\displaystyle +g_1\left(t\right)U_1(t-{\phi }_1)\left\}\right]dt={\overline{c}}_1\varpi ,}\hfill \\ & {\displaystyle {\int }_0^{\varpi }[b_{21}\left(t\right)exp\left\{z_2(t-{\zeta }_3)\right\}-b_{22}\left(t\right){(exp\left\{z_1(t-{\zeta }_4)\right\}-d_1\left(t\right))}^2}\hfill \\ & {\displaystyle +g_2\left(t\right)U_2(t-{\phi }_2)]dt={\overline{c}}_2\varpi .}\hfill \end{array}$$

(17)

By (15) and (17), we obtain

$$\begin{array}{cc}{\displaystyle {\int }_0^{\varpi }\left|{\dot{z}}_1\left(t\right)\right|dt}\hfill & {\displaystyle =\gamma {\int }_0^{\varpi }|c_1\left(t\right)-b_{11}\left(t\right)exp\left\{z_1(t-{\zeta }_1)\right\}-b_{12}\left(t\right){(exp\left\{z_2(t-{\zeta }_2)\right\}-d_2\left(t\right))}^2}\hfill \\ & {\displaystyle -g_1\left(t\right)U_1(t-{\phi }_1)\left\}\right|dt}\hfill \\ & {\displaystyle \le {\int }_0^{\varpi }\left|c_1\left(t\right)\right|dt+{\int }_0^{\varpi }[b_{11}\left(t\right)exp\left\{z_1(t-{\zeta }_1)\right\}+b_{12}\left(t\right){(exp\left\{z_2(t-{\zeta }_2)\right\}-d_2\left(t\right))}^2}\hfill \\ & {\displaystyle +g_1\left(t\right)U_1(t-{\phi }_1)\left\}\right]dt}\hfill \\ & {\displaystyle \le (\overline{c_1}+{\overline{R}}_1)\omega ,}\hfill \end{array}$$

and

$$\begin{array}{cc}{\displaystyle {\int }_0^{\varpi }\left|{\dot{z}}_2\left(t\right)\right|dt}\hfill & {\displaystyle =\gamma {\int }_0^{\varpi }|c_2\left(t\right)-b_{21}\left(t\right)exp\left\{z_2(t-{\zeta }_3)\right\}+b_{22}\left(t\right){(exp\left\{z_1(t-{\zeta }_4)\right\}-d_1\left(t\right))}^2}\hfill \\ & {\displaystyle -g_2\left(t\right)U_2(t-{\phi }_2)\left\}\right|dt}\hfill \\ & {\displaystyle \le {\int }_0^{\varpi }\left|c_2\left(t\right)\right|dt+{\int }_0^{\varpi }[b_{21}\left(t\right)exp\left\{z_2(t-{\zeta }_3)\right\}+b_{22}\left(t\right){(exp\left\{z_1(t-{\zeta }_4)\right\}-d_1\left(t\right))}^2}\hfill \\ & {\displaystyle +g_2\left(t\right)U_2(t-{\phi }_2)\left\}\right]dt}\hfill \\ & {\displaystyle \le (\overline{c_2}+{\overline{R}}_2)\omega ,}\hfill \end{array}$$

that is,

$${\int }_0^{\varpi }\left|{\dot{z}}_i\left(t\right)\right|dt\le (\overline{c_i}+{\overline{R}}_i)\omega :={\mathsf{\Phi }}_i,i=1,2.$$

(18)

For $i=1,2$, we have

$$\begin{array}{cc}& {\displaystyle {\int }_0^{\varpi }{b}_{1i}\left(t\right)exp\left\{z_i(t-{\zeta }_i)\right\}dt}\hfill \\ \hfill =& {\displaystyle {\int }_{-{\zeta }_i}^{\varpi -{\zeta }_i}{b}_{1i}(s+{\zeta }_i)exp\left\{z_i\left(s\right)\right\}ds}\hfill \\ \hfill =& {\displaystyle {\int }_0^{\varpi }{b}_{1i}(s+{\zeta }_i)exp\left\{z_i\left(s\right)\right\}ds}\hfill \\ \hfill =& {\displaystyle {\int }_0^{\varpi }{b}_{1i}(t+{\zeta }_i)exp\left\{z_i\left(t\right)\right\}dt.}\hfill \end{array}$$

(19)

Similarly, we obtain

$$\begin{array}{cc}& {\displaystyle {\int }_0^{\varpi }{b}_{21}\left(t\right)exp\left\{z_2(t-{\zeta }_3)\right\}dt={\int }_0^{\varpi }{b}_{21}(t+{\zeta }_3)exp\left\{z_1\left(t\right)\right\}dt,}\hfill \\ & {\displaystyle {\int }_0^{\varpi }{b}_{22}\left(t\right)exp\left\{z_2(t-{\zeta }_4)\right\}dt={\int }_0^{\varpi }{b}_{22}(t+{\zeta }_4)exp\left\{z_2\left(t\right)\right\}dt,}\hfill \\ & {\displaystyle {\int }_0^{\varpi }{g}_1\left(t\right)exp\left\{U_1(t-{\phi }_1)\right\}dt={\int }_0^{\varpi }{g}_1(t+{\phi }_1)exp\left\{U_1\left(t\right)\right\}dt,}\hfill \\ & {\displaystyle {\int }_0^{\varpi }{g}_2\left(t\right)exp\left\{U_2(t-{\phi }_2)\right\}dt={\int }_0^{\varpi }{g}_2(t+{\phi }_2)exp\left\{U_2\left(t\right)\right\}dt.}\hfill \\ & {\displaystyle {\int }_0^{\varpi }{h}_1\left(t\right)exp\left\{z_1(t-{\psi }_1)\right\}dt={\int }_0^{\varpi }{h}_1(t+{\psi }_1)exp\left\{z_1\left(t\right)\right\}dt,}\hfill \\ & {\displaystyle {\int }_0^{\varpi }{h}_2\left(t\right)exp\left\{z_2(t-{\psi }_2)\right\}dt={\int }_0^{\varpi }{h}_2(t+{\psi }_2)exp\left\{z_2\left(t\right)\right\}dt.}\hfill \end{array}$$

(20)

From the continuity of $z\left(t\right)=(z_1\left(t\right),z_2\left(t\right))$, there exist constants ${\rho }_i,{\varrho }_i\in [0,\varpi ](i=1,2)$ such that

$$z_i\left({\rho }_i\right)=\underset{t\in [0,\varpi ]}{max}{z}_i\left(t\right),z_i\left({\varrho }_i\right)=\underset{t\in [0,\varpi ]}{min}{z}_i\left(t\right),i=1,2.$$

(21)

From (17), (19)–(21), and the boundedness of solutions, we further obtain

$$\begin{array}{cc}& {\displaystyle z_1\left({\varrho }_1\right)\le ln\left(\frac{{\overline{c}}_1}{{\overline{b}}_{11}}\right)=:B_1,z_2\left({\varrho }_2\right)\le ln\left(\sqrt{\frac{{\overline{c}}_1}{{\overline{b}}_{12}}}+{\overline{d}}_2\right)=:B_2,}\hfill \\ & {\displaystyle z_1\left({\rho }_2\right)\ge ln\left(\frac{{\overline{c}}_2}{{\overline{b}}_{21}+{\overline{G}}_1}\right)=:B_3,z_2\left({\rho }_2\right)\ge ln\left(\frac{{\overline{c}}_1-{\overline{b}}_{12}{(M_2-{\overline{d}}_2)}^2}{{\overline{b}}_{21}+{\overline{G}}_1}\right)=:B_4}\hfill \end{array}$$

(22)

where

$$G_1\left(t\right)={\int }_0^{\omega }{g}_1\left(t\right){\int }_t^{t+\varpi }{h}_1\left(s\right)H_1(t,s)dsdt,G_2\left(t\right)={\int }_0^{\omega }{g}_2\left(t\right){\int }_t^{t+\varpi }{h}_2\left(s\right)H_2(t,s)dsdt.$$

From (18) and (22), we have

$$z_i\left(t\right)\le z_i\left({\varrho }_i\right)+{\int }_0^{\varpi }\left|{\dot{z}}_i\left(t\right)\right|dt\le B_i+{\mathsf{\Phi }}_i=:{\mathcal{M}}_i,i=1,2,$$

(23)

and

$$z_i\left(t\right)\ge z_i\left({\rho }_i\right)-{\int }_0^{\varpi }\left|{\dot{z}}_i\left(t\right)\right|dt\ge B_{i+2}-{\mathsf{\Phi }}_i=:{\mathcal{N}}_i,i=1,2.$$

(24)

Therefore, from (23) and (24), we have

$$\underset{t\in [0,\varpi ]}{max}\left|z_i\left(t\right)\right|\le max\left\{|{\mathcal{M}}_i|,|{\mathcal{N}}_i|\right\}=:{\mathcal{H}}_i,i=1,2.$$

One can see that the constants ${\mathcal{H}}_i(i=1,2)$ are independent of parameter $\gamma \in (0,1)$.

For any $z=(z_1,z_2)\in {\mathbb{R}}^2$, from (12), we can obtain

$$\mathcal{QN}z=(\mathcal{QN}{z}_1,\mathcal{QN}{z}_2)$$

where

$$\begin{array}{cc}\mathcal{QN}{z}_1=& {\displaystyle {\overline{c}}_1-({\overline{b}}_{11}+{\overline{G}}_1)exp\left\{z_1\right\}-{\overline{b}}_{12}{(exp\left\{z_2\right\}-{\overline{d}}_2)}^2,}\hfill \\ \mathcal{QN}{z}_2=& {\displaystyle {\overline{c}}_2-({\overline{b}}_{21}+{\overline{G}}_2)exp\left\{z_1\right\}+{\overline{b}}_{22}{(exp\left\{z_1\right\}-{\overline{d}}_1)}^2.}\hfill \end{array}$$

Now, consider the following system of algebraic equations

$$\begin{array}{cc}& {\displaystyle {\overline{c}}_1-({\overline{b}}_{11}+{\overline{G}}_1){\pi }_1-{\overline{b}}_{12}{({\pi }_2-{\overline{d}}_2)}^2=0,}\hfill \\ & {\displaystyle {\overline{c}}_2-({\overline{b}}_{21}+{\overline{G}}_2){\pi }_2+{\overline{b}}_{22}{({\pi }_1-{\overline{d}}_1)}^2=0.}\hfill \end{array}$$

(25)

From the assumption of Theorem 1 and the similar method in [14], we can find that (25) has a unique positive solution $\pi =({\pi }_1,{\pi }_2)$. Thus, the equation $\mathcal{QN}z=0$ has a unique solution $z^{*}=(z_1^{*},z_2^{*})=(ln{\pi }_1,ln{\pi }_2)\in {\mathbb{R}}^2$.

Let $\mathcal{H}>0$ be large enough such that $|z_1^{*}|+|z_2^{*}|<\mathcal{H}$ and $\mathcal{H}>{\mathcal{H}}_1+{\mathcal{H}}_2$; then, a bounded open set $\mathsf{\Psi }\subset \mathcal{Y}$ can be defined as follows

$$\mathsf{\Psi }=\{z\in \mathcal{Y}:\parallel z\parallel <\mathcal{H}\}.$$

One can see that $\mathsf{\Psi }$ fulfills the first and second conditions of the coincidence degree theory [15].

On the other hand, we can obtain

$$\mathrm{d}\mathrm{e}\mathrm{g}\{JQN,\mathsf{\Omega }\cap KerL,(0,0\left)\right\}$$

$$=\mathrm{s}\mathrm{g}\mathrm{n}\left|\begin{array}{cc}-({\overline{b}}_{11}+{\overline{G}}_1){\mathcal{K}}_1& -2{\overline{b}}_{12}({\mathcal{K}}_2-{\overline{d}}_2){\mathcal{K}}_2\\ 2{\overline{b}}_{22}({\mathcal{K}}_1-{\overline{d}}_1){\mathcal{K}}_1& -({\overline{b}}_{21}+{\overline{G}}_2){\mathcal{K}}_2\end{array}\right|\ne 0,$$

where ${\mathcal{K}}_i=exp\left\{z_i\right\}(i=1,2)$.

This shows that $\mathsf{\Psi }$ satisfies the last condition of the coincidence degree theory [13]. Therefore, system (10) has a $\varpi$-periodic solution $z^{*}\left(t\right)=(z_1^{*}\left(t\right),z_2^{*}\left(t\right))\in \overline{\mathsf{\Psi }}$. Hence, system (6) has a positive $\varpi$-periodic solution $y^{*}\left(t\right)=(y_1^{*}\left(t\right),y_2^{*}\left(t\right),u_1^{*}\left(t\right),u_2^{*}\left(t\right))$.

□

4. Global Attractivity

Firstly, for convenience, we denote the following functions

$$\begin{array}{c}{\mathsf{\Omega }}_j\left(t\right)=y_j\left(t\right)-z_j\left(t\right),{\dot{\mathsf{\Omega }}}_j\left(t\right)={\dot{y}}_j\left(t\right)-{\dot{z}}_j\left(t\right),{\mathsf{\Omega }}_j(t-{\zeta }_j)=y_j(t-{\zeta }_j)-z_j(t-{\zeta }_j),j=1,2,\hfill \\ {\mathsf{\Omega }}_3(t-{\zeta }_3)=y_2(t-{\zeta }_3)-z_2(t-{\zeta }_3),{\mathsf{\Omega }}_4(t-{\zeta }_4)=y_1(t-{\zeta }_4)-z_1(t-{\zeta }_4),\hfill \\ Y_j(t-{\psi }_j)=y_j(t-{\psi }_j)-z_j(t-{\psi }_1),U_j(t-{\phi }_j)=u_j(t-{\phi }_j)-v_j(t-{\phi }_j),j=1,2,\hfill \\ A_1\left(t\right)=b_{11}\left(t\right)-{\zeta }_1{b}_{11}^M[c_1\left(t\right)+b_{11}\left(t\right)M_1+b_{12}\left(t\right){(M_2-d_2\left(t\right))}^2],B_1\left(t\right)={\zeta }_1{b}_{11}^M{M}_1{b}_{11}\left(t\right),\hfill \\ A_2\left(t\right)=b_{21}\left(t\right)-{\zeta }_3{b}_{21}^M[c_2\left(t\right)+b_{21}\left(t\right)M_2+b_{22}\left(t\right){(M_1-d_1\left(t\right))}^2],B_2\left(t\right)={\zeta }_3{b}_{21}^M{M}_2{b}_{21}\left(t\right),\hfill \\ C_1\left(t\right)=b_{22}\left(t\right)({\beta }^M+2d_1\left(t\right))(1+{\zeta }_3{b}_{21}^M{M}_2),\beta \left(t\right)=y_1(t-{\zeta }_4)+z_1(t-{\zeta }_4),{\beta }^M=2M_1,\hfill \\ C_2\left(t\right)=b_{12}\left(t\right)({\gamma }^M+2d_2\left(t\right))(1+{\zeta }_1{b}_{11}^M{M}_1),\gamma \left(t\right)=y_2(t-{\zeta }_2)+z_2(t-{\zeta }_2),{\gamma }^M=2M_2,\hfill \\ D_1\left(t\right)=A_1\left(t\right)-B_1(t+{\zeta }_1)-C_1(t+{\zeta }_4)-h_1(t+{\psi }_1),U_1\left(t\right)=u_1\left(t\right)-v_1\left(t\right),\hfill \\ D_2\left(t\right)=A_2\left(t\right)-B_2(t+{\zeta }_3)-C_2(t+{\zeta }_2)-h_2(t+{\psi }_2),U_2\left(t\right)=u_2\left(t\right)-v_2\left(t\right),\hfill \\ D_3\left(t\right)=f_1\left(t\right)-g_1(t+{\phi }_1),D_4\left(t\right)=f_2\left(t\right)-g_2(t+{\phi }_2).\hfill \end{array}$$

where $(y_1\left(t\right),y_2\left(t\right))$ and $(z_1\left(t\right),z_2\left(t\right))$ are any two positive solutions of system (6).

Theorem 3.

Assume that (${\mathsf{\Lambda }}_1$) hold and $D>0$, then

$$\underset{t\to +\infty }{lim}{\mathsf{\Omega }}_1\left(t\right)=0,\underset{t\to +\infty }{lim}{\mathsf{\Omega }}_2\left(t\right)=0,\underset{t\to +\infty }{lim}{U}_1\left(t\right)=0,\underset{t\to +\infty }{lim}{U}_2\left(t\right)=0,$$

where

$$D=min\left\{\underset{t\to +\infty }{lim\; inf}{D}_i\left(t\right)(i=1,2,3,4)\right\}.$$

Proof. 

For any two positive solutions $(y_1\left(t\right),y_2\left(t\right),u_1\left(t\right),u_2\left(t\right))$ and $(z_1\left(t\right),z_2\left(t\right),v_1\left(t\right),v_2\left(t\right))$ of system (6), there exist real numbers $T_4>0$ and $M_1>0,M_2>0,m_1>0,m_2>0,M_1>0,M_2>0,m_1>0,m_2>0$ such that $m_1\le y_1\left(t\right),z_1\left(t\right)\le M_1,m_2\le y_2\left(t\right),z_2\left(t\right)\le M_2$ as $t\ge T_1$. Let

$$W_1\left(t\right)=V_{11}\left(t\right)+V_{21}\left(t\right),$$

where

$$V_{11}=|ln\frac{y_1\left(t\right)}{z_1\left(t\right)}|,V_{21}=|ln\frac{y_2\left(t\right)}{z_2\left(t\right)}|.$$

By the calculation of $D^{+}{W}_1\left(t\right)$ and system (6), we have

$$\begin{array}{cc}\hfill D^{+}{W}_1(t)=& \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_1(t)[-b_{11}(t){\mathsf{\Omega }}_1(t-{\zeta }_1)-b_{12}(t)({(y_2(t-{\zeta }_2)-d_2(t))}^2\hfill \\ & -{(z_2(t-{\zeta }_2)-d_2(t))}^2)-g_1(t)(u_1(t-{\phi }_1)-v_1(t-{\phi }_1))]\hfill \\ & +\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_2(t)[-b_{21}(t){\mathsf{\Omega }}_3(t-{\zeta }_3)+b_{22}(t)({(y_1(t-{\zeta }_4)-d_1(t))}^2\hfill \\ & -{(z_1(t-{\zeta }_4)-d_1(t))}^2)-g_2(t)(u_2(t-{\phi }_2)-v_2(t-{\phi }_2))]\hfill \\ \hfill =& \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_1(t)[-b_{11}(t){\mathsf{\Omega }}_1(t-{\zeta }_1)-b_{12}(t)(y_2^2(t-{\zeta }_2)-z_2^2(t-{\zeta }_2))\hfill \\ & +2b_{12}(t)d_2(t){\mathsf{\Omega }}_2(t-{\zeta }_2)-g_1(t)U_1(t-{\phi }_1)]+\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_2(t)[-b_{21}(t){\mathsf{\Omega }}_3(t-{\zeta }_3)\hfill \\ & +b_{22}(t)(y_1^2(t-{\zeta }_4)-z_1^2(t-{\zeta }_4))-2b_{22}(t)d_1(t){\mathsf{\Omega }}_4(t-{\zeta }_4)-g_2(t)U_2(t-{\phi }_2)]\hfill \\ \hfill =& \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_1(t)[-b_{11}(t){\mathsf{\Omega }}_1(t-{\zeta }_1)-b_{12}(t)(y_2(t-{\zeta }_2)+z_2(t-{\zeta }_2)){\mathsf{\Omega }}_2(t-{\zeta }_2)\hfill \\ & +2b_{12}(t)d_2(t){\mathsf{\Omega }}_2(t-{\zeta }_2)]+\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_2(t)[-b_{21}(t){\mathsf{\Omega }}_3(t-{\zeta }_3)\hfill \\ & +b_{22}(t)(y_1(t-{\zeta }_4)+z_1(t-{\zeta }_4)){\mathsf{\Omega }}_4(t-{\zeta }_4)-2b_{22}(t)d_1(t){\mathsf{\Omega }}_4(t-{\zeta }_4)]\hfill \\ \hfill =& \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_1(t)[-b_{11}(t){\mathsf{\Omega }}_1(t)-b_{12}(t)\gamma (t){\mathsf{\Omega }}_2(t-{\zeta }_2)+2b_{12}(t)d_2(t){\mathsf{\Omega }}_2(t-{\zeta }_2)\hfill \\ & {\displaystyle +b_{11}(t){\int }_{t-{\zeta }_1}^t{\dot{\mathsf{\Omega }}}_1(u)du-g_1(t)U_1(t-{\phi }_1)]+\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_2(t)[-b_{21}(t){\mathsf{\Omega }}_2(t)}\hfill \\ & {\displaystyle +b_{22}(t)\beta (t){\mathsf{\Omega }}_4(t-{\zeta }_4)-2b_{22}(t)d_1(t){\mathsf{\Omega }}_4(t-{\zeta }_4)+b_{21}(t){\int }_{t-{\zeta }_3}^t{\dot{\mathsf{\Omega }}}_1(u)du-g_2(t)U_2(t-{\phi }_2)]}\hfill \\ \hfill =& \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_1(t)[-b_{11}(t){\mathsf{\Omega }}_1(t)-\gamma (t)b_{12}(t){\mathsf{\Omega }}_2(t-{\zeta }_2)+2d_2(t)b_{12}(t){\mathsf{\Omega }}_2(t-{\zeta }_2)\hfill \\ & {\displaystyle +b_{11}(t){\int }_{t-{\zeta }_1}^t(y_1(u)\left[c_1(u)-b_{11}(u)y_1(u-{\zeta }_1)-b_{12}(u){(y_2(u-{\zeta }_2)-d_2(t))}^2\right]}\hfill \\ & -z_1(u)\left[c_1(u)-b_{11}(u)z_1(u-{\zeta }_1)-b_{12}(u){(y_2(u-{\zeta }_2)-d_2(t))}^2\right])du-g_1(t)U_1(t-{\phi }_1)]\hfill \\ & +\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_2(t)[-b_{21}(t){\mathsf{\Omega }}_2(t)+\beta (t)b_{22}(t){\mathsf{\Omega }}_4(t-{\zeta }_4)-2b_{22}(t)d_1(t){\mathsf{\Omega }}_4(t-{\zeta }_4)\hfill \\ & {\displaystyle +b_{21}(t){\int }_{t-{\zeta }_3}^t(y_2(u)\left[c_2(u)-b_{21}(u)y_2(u-{\zeta }_3)+b_{22}(u){(y_1(u-{\zeta }_4)-d_1(t))}^2\right]}\hfill \\ & -z_2(u)\left[c_2(u)-b_{21}(u)z_2(u-{\zeta }_3)+b_{22}(u){(y_1(u-{\zeta }_4)-d_1(t))}^2\right])du-g_2(t)U_2(t-{\phi }_2)]\hfill \\ \hfill =& \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_1(t)[-b_{11}(t){\mathsf{\Omega }}_1(t)-b_{12}(t)\gamma (t){\mathsf{\Omega }}_2(t-{\zeta }_2)+2b_{12}(t)d_2(t){\mathsf{\Omega }}_2(t-{\zeta }_2)-g_1(t)U_1(t-{\phi }_1)\hfill \\ & {\displaystyle +b_{11}(t){\int }_{t-{\zeta }_1}^t({\mathsf{\Omega }}_1(u)\left[c_1(u)-d_{11}(u)z_1(u-{\zeta }_1)-b_{12}(u){(y_2(u-{\zeta }_2)-d_2(t))}^2\right]}\hfill \\ & +y_1(u)\left[-b_{11}(u){\mathsf{\Omega }}_1(u-{\zeta }_1)-b_{12}(t)\gamma (t){\mathsf{\Omega }}_2(u-{\zeta }_2)+2b_{12}(t)d_2(t){\mathsf{\Omega }}_2(u-{\zeta }_2)\right])du]\hfill \end{array}$$

$$\begin{array}{cc}& +\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}{\mathsf{\Omega }}_2(t)[-b_{21}(t){\mathsf{\Omega }}_2(t)+b_{22}(t)\beta (t){\mathsf{\Omega }}_4(u-{\zeta }_4)-2b_{22}(t)d_1(t){\mathsf{\Omega }}_4(u-{\zeta }_4)-g_2(t)U_2(t-{\phi }_2)\hfill \\ & {\displaystyle +b_{21}(t){\int }_{t-{\zeta }_3}^t({\mathsf{\Omega }}_2(u)\left[c_2(u)-b_{21}(u)z_2(u-{\zeta }_3)+b_{22}(u){(y_1(u-{\zeta }_4)-d_1(t))}^2\right]}\hfill \\ & +y_2(u)\left[-b_{21}(u){\mathsf{\Omega }}_3(u-{\zeta }_3)+b_{22}(t)\beta (t){\mathsf{\Omega }}_4(u-{\zeta }_4)-2b_{22}(t)d_1(t){\mathsf{\Omega }}_4(u-{\zeta }_4)\right])du]\hfill \\ \hfill \le & {\displaystyle -\sum _{j=1}^2{b}_{j1}(t)|{\mathsf{\Omega }}_j(t)|+(\gamma (t)+2d_2(t))b_{12}(t)\left|{\mathsf{\Omega }}_2(t-{\zeta }_2)\right|+(\beta (t)+2d_1(t))}\hfill \\ & {\displaystyle \times b_{22}(t)|{\mathsf{\Omega }}_4(t-{\zeta }_4)|+b_{11}(t){\int }_{t-{\zeta }_1}^t(\left|{\mathsf{\Omega }}_1(u)\right|[c_1(u)+b_{11}(u)z_1(u-{\zeta }_1)}\hfill \\ & {\displaystyle +b_{12}(u){(z_2(u-{\zeta }_2)-d_2(t))}^2]+y_1(u)[b_{11}(u)|{\mathsf{\Omega }}_1(u-{\zeta }_1)|+b_{12}(t)\gamma (t)\left|{\mathsf{\Omega }}_2(u-{\zeta }_2)\right|}\hfill \\ & {\displaystyle +2b_{12}(t)d_2(t)|{\mathsf{\Omega }}_2(u-{\zeta }_2)|])du]+b_{21}(t){\int }_{t-{\zeta }_3}^t(\left|{\mathsf{\Omega }}_2(u)\right|[c_2(u)+b_{21}(u)z_2(u-{\zeta }_3)}\hfill \\ & +b_{22}(u)|y_1(u-{\zeta }_4)-d_1(t){|}^2]+y_2(u)[b_{21}(u)|{\mathsf{\Omega }}_3(u-{\zeta }_3)|+b_{22}(t)\beta (t)\left|{\mathsf{\Omega }}_3(u-{\zeta }_3)\right|\hfill \\ & {\displaystyle +2b_{22}(t)d_1(t)|{\mathsf{\Omega }}_4(u-{\zeta }_4)|])du]+g_1(t)|U_1(t-{\phi }_1)|+g_2(t)\left|U_2(t-{\phi }_2)\right|.}\hfill \end{array}$$

(26)

Define

$$W_2(t)=V_{12}(t)+V_{22}(t),$$

where

$$\begin{array}{cc}\hfill V_{12}(t)=& {\displaystyle {\int }_{t-{\zeta }_1}^t{\int }_u^t{b}_{11}(u+{\zeta }_1)(\left[c_1(s)+b_{11}(s)z_1(s-{\zeta }_1)+b_{12}(u){(y_2(s-{\zeta }_2)-d_2(s))}^2\right]}\hfill \\ & \times |{\mathsf{\Omega }}_1(s)|+y_1(s)[b_{11}(s)|{\mathsf{\Omega }}_1(s-{\zeta }_1)|+b_{12}(t)\gamma (s)\left|{\mathsf{\Omega }}_2(s-{\zeta }_2)\right|\hfill \\ & {\displaystyle +2b_{12}(s)d_2(s)\left|{\mathsf{\Omega }}_2(s-{\zeta }_2)\right|])dsdu,}\hfill \end{array}$$

$$\begin{array}{cc}\hfill V_{22}(t)=& {\displaystyle {\int }_{t-{\zeta }_3}^t{\int }_u^t{b}_{21}(u+{\zeta }_3)(\left[c_2(s)+b_{21}(s)z_2(s-{\zeta }_3)+b_{22}(u){(y_1(s-{\zeta }_4)-d_1(s))}^2\right]}\hfill \\ & \times |{\mathsf{\Omega }}_2(s)|+y_2(s)[b_{21}(s)|{\mathsf{\Omega }}_3(s-{\zeta }_3)|+b_{22}(t)\beta (s)\left|{\mathsf{\Omega }}_4(s-{\zeta }_4)\right|\hfill \\ & {\displaystyle +2b_{22}(s)d_1(s)\left|{\mathsf{\Omega }}_4(s-{\zeta }_4)\right|])dsdu.}\hfill \end{array}$$

By calculation of $D^{+}{W}_2(t)$ and (26), we have

$$\begin{array}{cc}\hfill {\displaystyle D^{+}{W}_1(t)+D^{+}{W}_2(t)\le }& {\displaystyle -(b_{11}(t)|{\mathsf{\Omega }}_1(t)|+b_{21}(t)|{\mathsf{\Omega }}_2(t)|)+b_{12}(t)({\gamma }^M+2d_2(t))\left|{\mathsf{\Omega }}_2(t-{\zeta }_2)\right|}\hfill \\ & {\displaystyle +b_{22}(t)({\beta }^M+2d_1(t))\left|{\mathsf{\Omega }}_4(t-{\zeta }_4)\right|+{\zeta }_1{b}_{11}^M[c_1(t)}\hfill \\ & {\displaystyle +b_{11}(t)M_1+b_{12}(t){(M_2-d_2(t))}^2]|{\mathsf{\Omega }}_1(t)|}\hfill \\ & {\displaystyle +{\zeta }_1{b}_{11}^M{M}_1\left[b_{11}(t)|{\mathsf{\Omega }}_1(t-{\zeta }_1)|+b_{12}(t)({\gamma }^M+2d_2(t))\left|{\mathsf{\Omega }}_2(t-{\zeta }_2)\right|\right]}\hfill \\ & {\displaystyle +{\zeta }_3{b}_{21}^M[c_2(t)+b_{21}(t)M_2+b_{22}(t){(M_1-d_1(t))}^2]|{\mathsf{\Omega }}_2(t)|}\hfill \\ & {\displaystyle +{\zeta }_3{b}_{21}^M{M}_2\left[b_{21}(t)|{\mathsf{\Omega }}_3(t-{\zeta }_3)|+b_{22}(t)({\beta }^M+2d_1(t))\left|{\mathsf{\Omega }}_4(t-{\zeta }_4)\right|\right]}\hfill \\ & +g_1(t)|U_1(t-{\phi }_1)|+g_2(t)\left|U_2(t-{\phi }_2)\right|\hfill \\ & {\displaystyle =-(A_1(t)|{\mathsf{\Omega }}_1(t)|+A_2(t)|{\mathsf{\Omega }}_2(t)|)+B_1(t)\left|{\mathsf{\Omega }}_1(t-{\zeta }_1)\right|}\hfill \\ & {\displaystyle +B_2(t)|{\mathsf{\Omega }}_3(t-{\zeta }_3)|+C_1(t)|{\mathsf{\Omega }}_4(t-{\zeta }_4)|+C_2(t)\left|{\mathsf{\Omega }}_2(t-{\zeta }_2)\right|}\hfill \\ & +g_1(t)|U_1(t-{\phi }_1)|+g_2(t)\left|U_2(t-{\phi }_2)\right|.\hfill \end{array}$$

(27)

Define

$$W_3(t)=V_{13}(t)+V_{23}(t)+V_{33}(t),$$

where

$$V_{13}(t)={\int }_{t-{\zeta }_1}^t{B}_1(u+{\zeta }_1)|{\mathsf{\Omega }}_1(u)|du+{\int }_{t-{\zeta }_4}^t{C}_1(u+{\zeta }_4)\left|{\mathsf{\Omega }}_1(u)\right|du,$$

$$V_{23}(t)={\int }_{t-{\zeta }_2}^t{C}_2(u+{\zeta }_2)|{\mathsf{\Omega }}_2(u)|du+{\int }_{t-{\zeta }_3}^t{B}_2(u+{\zeta }_3)\left|{\mathsf{\Omega }}_2(u)\right|du.$$

and

$$\begin{array}{cc}\hfill V_{33}(t)=& {\displaystyle |u_1(t)-v_1(t)|+|u_2(t)-v_2(t)|+{\int }_{t-{\psi }_1}^t{h}_1(s+{\psi }_1)\left|Y_1(s)\right|ds}\hfill \\ & {\displaystyle +{\int }_{t-{\psi }_2}^t{h}_1(s+{\psi }_2)|Y_2(s)|ds+{\int }_{t-{\phi }_1}^t{g}_1(s+{\phi }_1)|U_1(s)|ds+{\int }_{t-{\phi }_2}^t{g}_2(s+{\phi }_2)\left|U_2(s)\right|ds,}\hfill \end{array}$$

By the calculation of $D^{+}{W}_3(t)$ and (27), we have

$$D^{+}{W}_1(t)+D^{+}{W}_2(t)+D^{+}{W}_3(t)\le -(D_1|{\mathsf{\Omega }}_1(t)|+D_2|{\mathsf{\Omega }}_2(t)|+D_3|U_1(t)|+D_4|U_1(t)|).$$

(28)

Next, we define

$$V(t)=W_1(t)+W_2(t)+W_3(t).$$

From the assumptions of Theorem 3 and by (28), for $t\ge T_4$ we derive

$$D^{+}V(t)\le -D(|{\mathsf{\Omega }}_1(t)|+|{\mathsf{\Omega }}_2(t)|+|U_1(t)|+|U_2(t)|).$$

(29)

Taking integral from $T_4$ to t on both sides of (29) we obtain

$$V(t)+D{\int }_{T^4}^t\left(|{\mathsf{\Omega }}_1(s)|+|{\mathsf{\Omega }}_2(s)|+|U_1(s)|+|U_2(s)|\right)ds\le V(T_4).$$

Then, we obtain

$${\int }_{T_4}^t\left(|{\mathsf{\Omega }}_1\left(s\right)|+|{\mathsf{\Omega }}_2\left(s\right)|+|U_1\left(s\right)|+|U_2\left(s\right)|\right)ds<\infty .$$

(30)

From the boundedness of system (6) and (30), we obtain that ${\mathsf{\Omega }}_1\left(t\right),{\mathsf{\Omega }}_2\left(t\right),U_1\left(t\right),U_2\left(t\right)$ and ${\dot{\mathsf{\Omega }}}_1\left(t\right),{\dot{\mathsf{\Omega }}}_2\left(t\right),{\dot{U}}_1\left(t\right),{\dot{U}}_2\left(t\right)$ bounded on $[T_4,+\infty )$. Thus, $|{\mathsf{\Omega }}_j\left(t\right)|(j=1,2)\in L^1[T_4,+\infty )$ and $|U_j\left(t\right)|(j=1,2)\in L^1[T_4,+\infty )$. Furthermore, from Barbalat’s theorem, we can obtain

$$\underset{t\to +\infty }{lim}{\mathsf{\Omega }}_1\left(t\right)=0,\underset{t\to +\infty }{lim}{\mathsf{\Omega }}_2\left(t\right)=0,\underset{t\to +\infty }{lim}{U}_1\left(t\right)=0,\underset{t\to +\infty }{lim}{U}_2\left(t\right)=0.$$

□

Corollary 1.

Assume that the conditions of Theorem 2 hold and $D>0$, then system (6) has a global attractive positive $\varpi -$ periodic solution.

Remark 1.

The theoretical results obtained in our article can be seen as supplementary and extended findings to previously known works [1,2,3,4,5,6,9,10] and provide a more comprehensive understanding of enterprise cluster dynamics and behaviors.

5. Numerical Example

Example 1.

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{y}_1\left(t\right)}{dt}=}& {\displaystyle y_1\left(t\right)[\frac{6.5+|cos(t\left)\right|}{10}-\frac{21+|cos(t\left)\right|}{10}{y}_1(t-{\zeta }_1)-\frac{1.15+|cos(t\left)\right|}{20}}\hfill \\ & {\displaystyle \times {\left(y_2(t-{\zeta }_2)-\frac{1+|cos(t\left)\right|}{10}\right)}^2-\frac{1+|cos(t\left)\right|}{15}{u}_1(t-{\phi }_1)],}\hfill \\ \hfill {\displaystyle \frac{d{y}_2\left(t\right)}{dt}=}& {\displaystyle y_2\left(t\right)[\frac{5.7+|sin(t\left)\right|}{10}-\frac{53+3|sin(t\left)\right|}{25}{y}_2(t-{\zeta }_3)+\frac{1.1+|sin(t\left)\right|}{20}}\hfill \\ & {\displaystyle \times {\left(y_1(t-{\zeta }_4)-\frac{1+|sin(t\left)\right|}{10}\right)}^2-\frac{1+|sin(t\left)\right|}{15}{u}_2(t-{\phi }_2)],}\hfill \\ \hfill {\displaystyle \frac{d{u}_1\left(t\right)}{dt}=}& {\displaystyle -\frac{5.5+|cos(t\left)\right|}{10}{u}_1\left(t\right)+\frac{1+|cos(t\left)\right|}{12}{y}_1(t-{\psi }_1),}\hfill \\ \hfill {\displaystyle \frac{d{u}_2\left(t\right)}{dt}=}& {\displaystyle -\frac{5.5+|sin(t\left)\right|}{10}{u}_2\left(t\right)+\frac{1+|sin(t\left)\right|}{12}{y}_2(t-{\psi }_2).}\hfill \end{array}$$

(31)

In system (31), firstly we let ${\zeta }_1=0.25,{\zeta }_2=0.5,{\zeta }_3=0.3,{\zeta }_4=0.6,{\phi }_1=0.35$, ${\phi }_1=0.33,{\psi }_1=0.15,{\psi }_1=0.18$, then we have

$$M_1\approx 0.4523,M_2\approx 0.3632,N_1\approx 0.1096,N_1\approx 0.0880,r\approx 0.2572,$$

$$r_1\approx 0.2572,r_2\approx 0.5583,{\overline{c}}_1-{\overline{b}}_{12}{(M_2-{\overline{d}}_2)}^2\approx 0.64,$$

$$\underset{t\to \infty }{lim\; inf}{D}_1\left(t\right)\approx 0.1516,\underset{t\to \infty }{lim\; inf}{D}_2\left(t\right)\approx 0.1297,\underset{t\to \infty }{lim\; inf}{D}_3\left(t\right)\approx 0.4167,\underset{t\to \infty }{lim\; inf}{D}_4\left(t\right)\approx 0.4167.$$

One can see that the conditions of Theorems 1–3 and Corollary 1 hold.

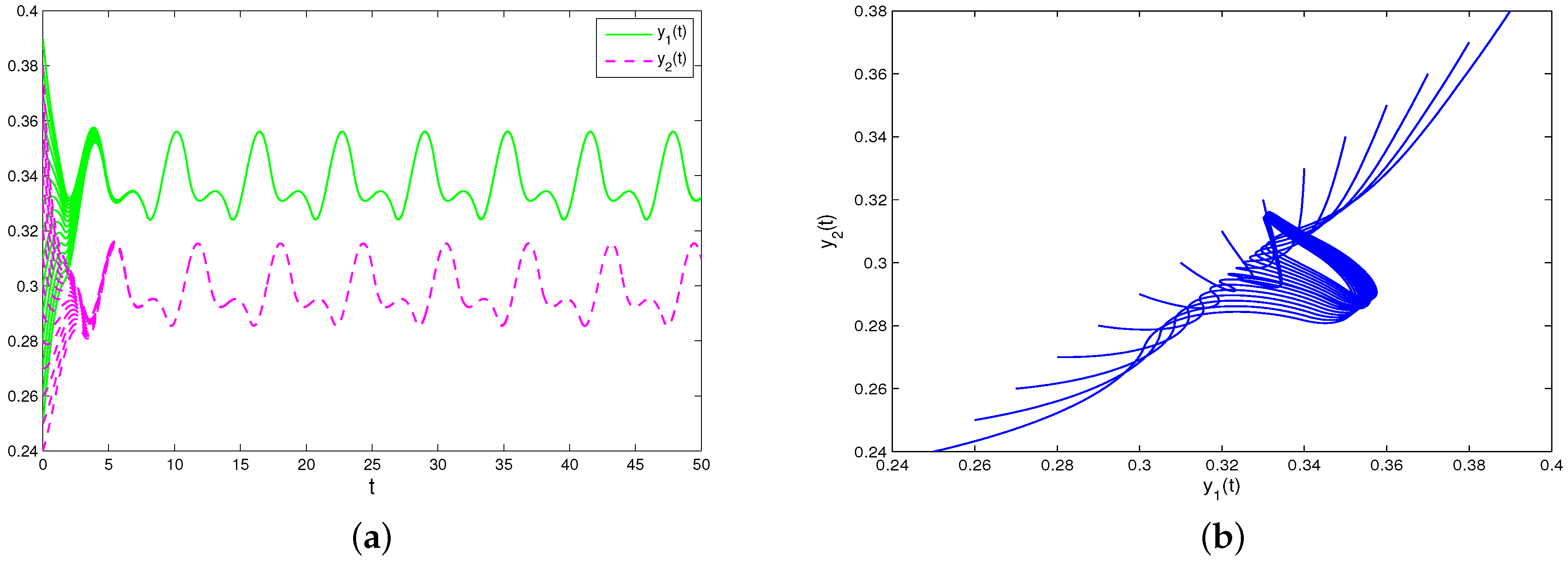
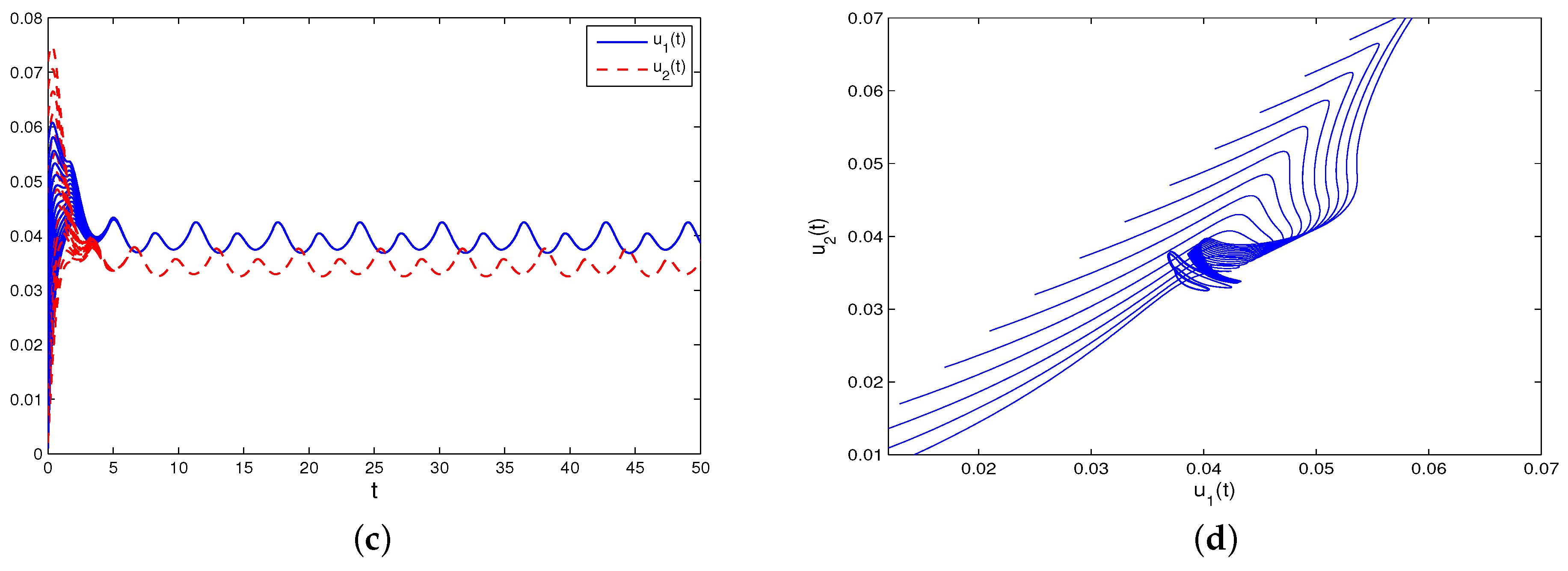
From Figure 1, one can find a permanent and globally attractive positive periodic solution for system (31).

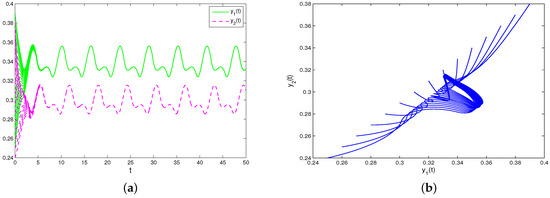
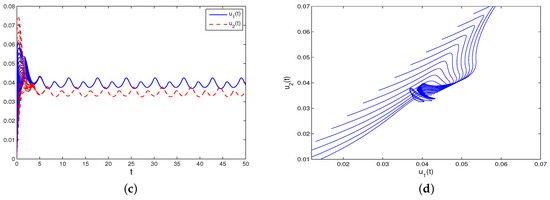
Figure 1. Permanence, periodic solution, and global attractivity of system (31). (a,b) Permanence, periodic solution, and global attractivity of $y_1\left(t\right)$ and $y_2\left(t\right)$. (c,d) Permanence, periodic solution, and global attractivity of $u_1\left(t\right)$ and $u_2\left(t\right)$.

Remark 2.

The numerical simulations in Figure 1a–d illustrate that if the coefficients (intrinsic growth rates $c_i\left(t\right)(i=1,2)$, intra-enterprise competition rate $b_1\left(t\right)$, conversion of commodity into the reproduction rate $b_2\left(t\right)$, initial productions $d_i\left(t\right)(i=1,2)$, and feedback control coefficients $g_i\left(t\right),f_i\left(t\right),h_i\left(t\right)(i=1,2)$) of model (31) satisfy the conditions of Theorems 1–3, and Corollary 1, then system (31) remains stable for a long time, which means the competition and cooperation of enterprises can reach a dynamical balance, and solutions $y_1\left(t\right)$ and $y_2\left(t\right)$ (output of enterprises) are also uniquely remnants between the determined quantities $m_i\left(t\right)(i=1,2)$ and $M_i\left(t\right)(i=1,2)$ for a long time.

Next, we take ${\zeta }_1=2.5,{\zeta }_2=0.5,{\zeta }_3=2.75,{\zeta }_4=0.6$; then, we have

$$M_1\approx 2.4453,M_2\approx 25.9726,\underset{t\to \infty }{lim\; inf}{D}_1\left(t\right)\approx -30.1637<0.$$

Evidently, the conditions of Theorem 3 are failed.

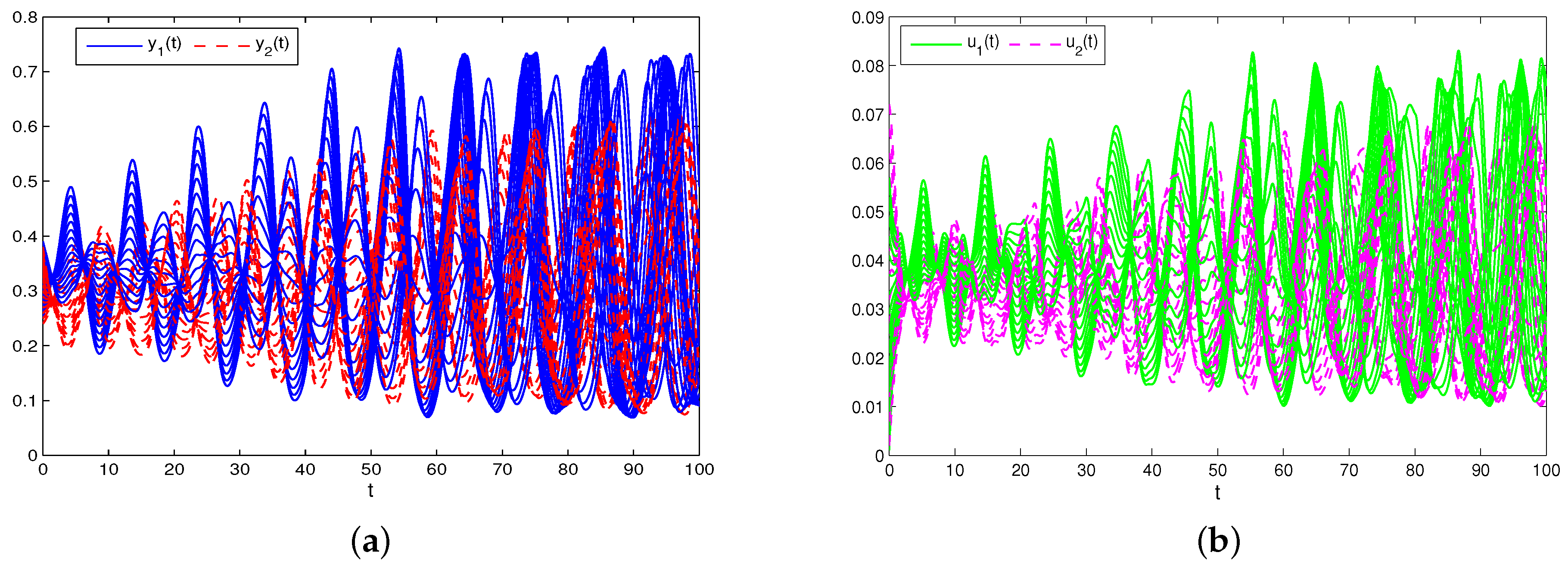
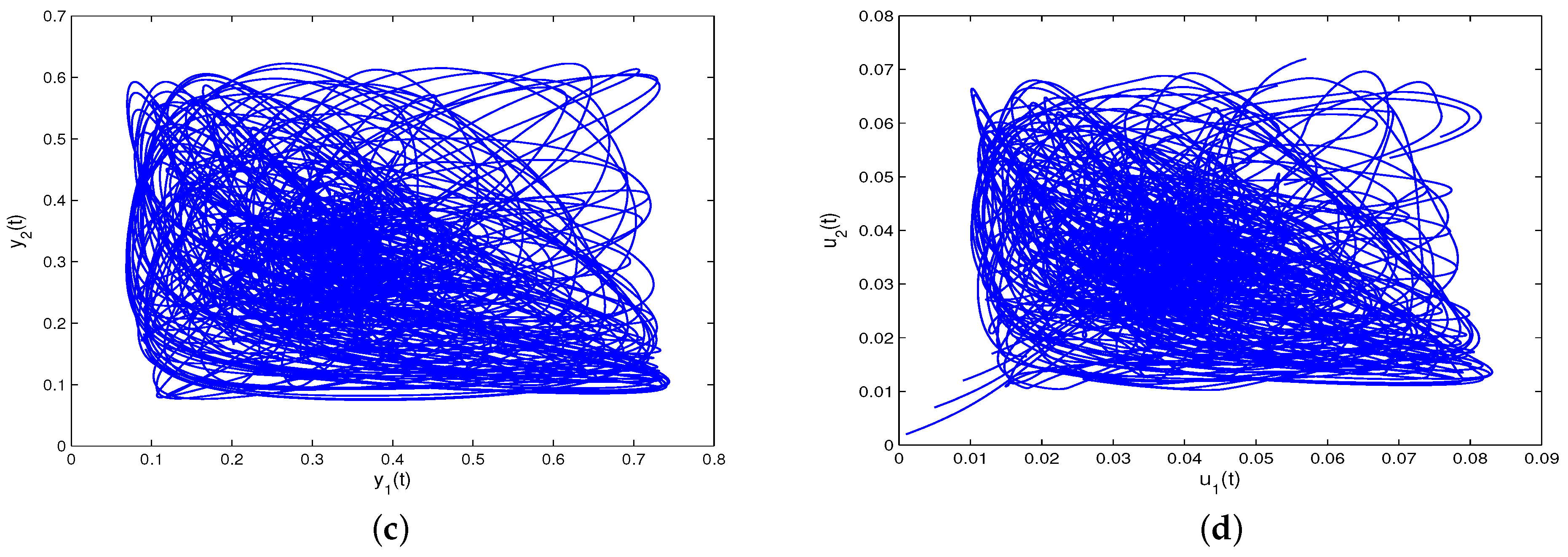
From Figure 2, one can find that system (31) is not globally attractive.

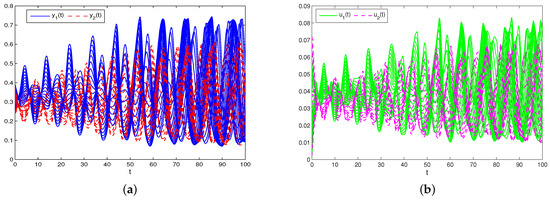
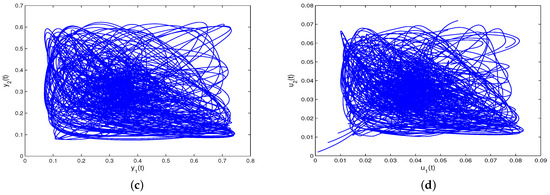
Figure 2. Non-global attractivity of system (31). (a,c) Non-global attractivity of $y_1\left(t\right)$ and $y_2\left(t\right)$. (b,d) Non-global attractivity of $u_1\left(t\right)$ and $u_2\left(t\right)$.

6. Conclusions

In this study, by proposing system (6), which incorporates time-varying coefficients and feedback controls, we expanded upon existing models (1–5) and enriched the understanding of enterprise clusters. The derived conditions for dynamic behaviors in system (6) offer new insights into the growth patterns, stability, and coexistence within enterprise clusters. Hence, the derivation of conditions for dynamic behaviors in system (6) contribute to the existing body of knowledge on enterprise cluster modeling. Additionally, we can see from the conditions and results of Theorems 1–3, Corollary 1, and Example 1, that discrete time delays ${\zeta }_i(i=1,2,3,4)$ and feedback control coefficients $g\left(t\right),f\left(t\right)$ and $h\left(t\right)$ have influence on the aforementioned dynamic behaviors of model (6). In conclusion, the fate of an enterprise cluster is influenced by multiple factors, including feedback control effects, time delay effects, self-development, market saturation degree, competition power, and varying economic environments. Understanding and effectively managing these factors can help enterprises navigate challenges, seize opportunities, and achieve sustainable growth in a competitive business landscape.