Abstract
The Internet of Things (IoT) is an emerging technology that has recently gained significant interest, especially with the dramatic increase in connected devices. However, IoT networks are not yet standardized, and the design of such networks faces many challenges, including scalability, flexibility, reliability, and availability of such networks. Routing is among the significant problems facing IoT network design because of the dramatic increase in connected devices and the network requirements regarding availability, reliability, latency, and flexibility. To this end, this work investigates deploying a multipath routing scheme for dense IoT networks. The proposed method selects a group of routes from all available routes to forward data at a maximum rate. The choice of data transmission routes is a complex problem for which numerical optimization methods can be used. A novel method for selecting the optimum group of routes and coefficients of traffic distribution along them is proposed. The proposed method is implemented using dynamic programming. The proposed method outperforms the traditional route selection methods, e.g., random route selection, especially for dense IoT networks. The model significantly reduced the number of intermediate nodes involved in routing paths over dense IoT networks by 34%. Moreover, it effectively demonstrated a significant decrease of 52% in communication overhead and 40% in data delivery time in dense IoT networks compared to traditional models.
Keywords:
Internet of Things; high-density network; multipath routing; route selection; achievable data rate MSC:
94A15
1. Introduction
The Internet of Things (IoT) has become integral to modern info-communication systems [1,2]. According to the forecasts of leading manufacturers, the number of wireless devices connected to communication networks will grow in the foreseeable future [3]. A large number of connected devices leads to the formation of high-density networks, which have several features associated with significant mutual influences between nodes [4,5,6].
Along with the complexities of organizing high-density networks, many features provide additional opportunities for network organization [7]. For example, when selecting the logical structure of the network, in conditions of a large number of nodes, there is the possibility of a more flexible approach to the solution of the problem [8]. In conditions of low density, the possibilities of choosing a logical structure are defined exclusively by the mutual placement of nodes [9]. However, in conditions of high density, a node can be found in proximity, practically, to any point of space. This allows one to choose to build the logical structure that some considerations require [10].
However, this freedom of choice requires methods for shaping the logical structure that best meets specific needs. In [11], the authors provided a method for selecting route parameters in IoT networks to obtain the maximum transmission speed. The authors proved that the transmission speed of the route decreases as the number of transits increases. If the length of the route (i.e., number of transits) is too high, which may be the case in large-scale networks, its transmission speed may be less than required and cannot be increased by the choice of its parameters. In such a case, the only way to increase the transmission speed is to use multipath routing.
The ultimate objective of this work is to develop a novel route selection scheme that selects the optimum routes over a communication network for a certain transmission to achieve the maximum transmission speed. The main contributions of this work as summarized as follows:
- Developing a multipath routing scheme for dense IoT networks.
- Developing a route selection model that selects a group of routes from available routes to transmit data at higher speeds.
- Optimizing the proposed route selection model to obtain the optimum routes that achieve the maximum transmission speed.
- Performance evaluation of the proposed route selection scheme for dense IoT networks.
The rest of the article is organized as follows. Section 2 presents the proposed multipath routing model for dense IoT networks. Section 3 presents the developed route selection scheme for the considered dense IoT network. Section 4 provides the optimization problem of the proposed model and introduces the solution. Section 5 presents the obtained results. Section 6 concludes the work and provides future directions.
2. Multipath Routing Model
Existing routing protocols in Internet protocol (IP) networks and multipath protocols allow the implementation of multiple route choices between the source and destination [12,13,14]. In a high-density network, the potential number of such routes can be extremely large. The routes to be selected may contain common sections (i.e., be dependent) or may not contain them and be independent [15]. In general, when independent routes are used, the data transmission speed equals the sum of the transmission speeds in each route [16].
In the case of dependent routes, it will be limited to the transmission speed of the slowest common section [17]. In wireless networks, routes are dependent if the transmission over any part of them depends on the activity of nodes of another route (i.e., sections do not necessarily have to be common); it is enough that the nodes are in a mutual communication (or influence) zone [18,19]. Therefore, it is impossible to construct completely independent routes. At least the first and the last sites should always be considered common because simultaneous transmission to them is possible only by one of the routes [20]. Figure 1 shows a graphical interpretation of the multipath routing model between the source node s and the destination node t.
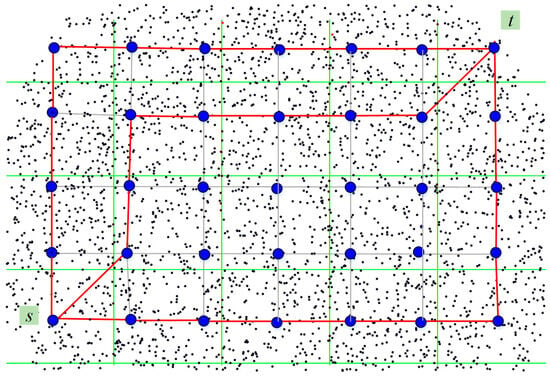
Figure 1.
Possible multipath routing structure.
The presence of dependent sections inevitably reduces the data transfer rate because the activity of the influencing node in the dependent route must suspend the transfer [21]. Thus, routes should be selected with no mutual influence to increase the transmission speed of communicated data, except for the first and last sections. These routes are assumed to be large enough for dense IoT networks. The geometric dimensions of such a network must be sufficiently large compared to the size of the communication zone of the node [22]. The problem naturally degenerates with small network sizes (i.e., small-scale networks) since, in some of the applications of such networks, there is no need to build a route or build simple routes. This is the case in some indoor IoT applications.
For the proposed multipath routing model, we assume the network has M different routes between the source node s and the destination node t. Routes can contain different numbers of transits and serve different traffic flows. Generally, the data transfer rate along each route is random. It depends on the number of nodes in the route (i.e., transit sections), the data transfer rate on each route, and the properties of the served traffic flows.
A set of n known available routes (R) can be used to transfer traffic from the source node s to the destination node t. The set R is defined as follows.
The received data rate on each available route i is random and equal to bi, where bi is defined in Equation (2).
where L is the amount of data (bits) and xi is the delivery time (s). Data transferred over a group of routes are processed in parallel. Simultaneous transmission over several routes is impossible in the case under consideration; however, this applies only to the route’s first and last links. When transmitting over several routes, it is necessary to distribute the data transmitted. The distribution is built on the basis that each route carries a fraction of the data.
where βi is the fraction of data carried by the ith route. The delivery time for the allocated fraction of data on each route used is a random variable with a distribution function Fi(X). Then, there is a set of distribution functions of the delivery time of available routes (F), defined as follows.
where x is a random value—delivery time. Since the routes are independent, the values of the delivery times in routes are also random and independent. The connection is realized using a set of routes W, which is a subset of available routes. The set W is defined as follows.
The delivery time over the group of routes T is also a random variable determined by the slowest route from W. The transmission process is terminated when all data transmission is complete. Figure 2 presents the transmission process over a route group.
where xwi is the delivery time for the ith route of the selected route group, and W is the set of selectable routes. The distribution function of the delivery time T is Gw(x) and is defined as follows.
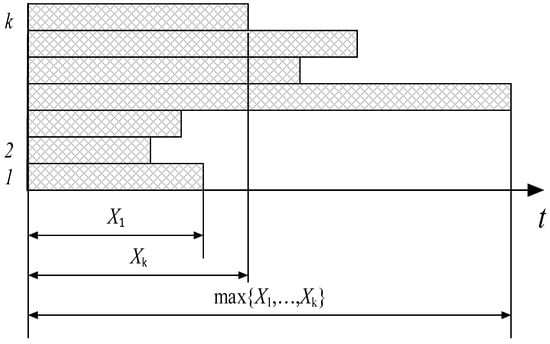
Figure 2.
A transmission process over a group of routes.
The mathematical expectation of the delivery time T is E(T) and is defined as follows.
The problem of selecting channels in a group is not trivial because Equations (8) and (9) depend on the distributions of delivery times of each selected route [23]. Moreover, the number of solutions when choosing a group of routes can be significant (e.g., for n = 20, the number of variants can reach tens of thousands). The proposed model in this work aims to solve this problem by minimizing the mean value of the selected groups. Most existing models seek to get the optimum group of routes; however, each considers different ways. We consider a novel method and novel objectives while selecting routes.
3. Route Selection Method
The purpose of developing a method for selecting routes in a group is to reduce the data delivery time (i.e., to increase the equivalent data transfer rate). According to Equations (6), (8) and (9), we can reduce the average data delivery time (i.e., increasing the transmission speed) by increasing the number of routes in group k, choosing specific values of traffic distribution coefficients βi, and selecting routes with certain distribution functions Fi(t).
When selecting a group of routes, the main objective is reducing the average data delivery time (i.e., minimizing Equation (9)).
We consider the gamma distribution for the proposed model with the probability density f(x) defined as follows [24].
where k and θ are distribution parameters. We consider plotting the probability density function for a network with three available routes (i.e., n = 3), where k = 2. We consider a random delivery time over the selected routes with the values x1, x2, and x3. The considered mathematical expectations of these random variables are introduced as follows.
The variances of the three variables are introduced as follows. Figure 3 presents the probability densities of the three routes.
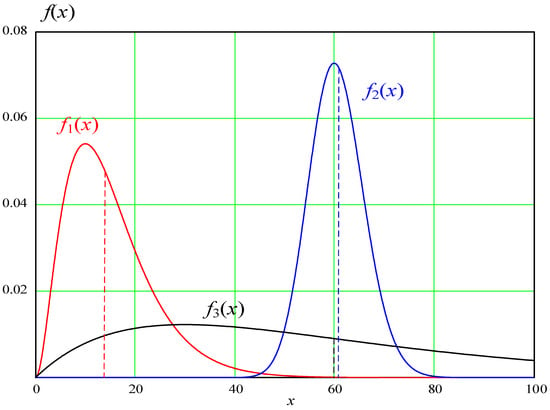
Figure 3.
Probability densities of the random variables x1, x2, and x3.
These random variables have different mathematical expectations (shown with dashed lines) and dispersions. Using the mathematical expectation value, you should choose the values with the lowest mathematical expectation values (i.e., x1 and x3).
Figure 4 shows the probability density functions of possible choice results: g1,2(x), g1,3(x), and g2,3(x). According to Equation (5), the probability density is defined for the resulting solutions as follows.
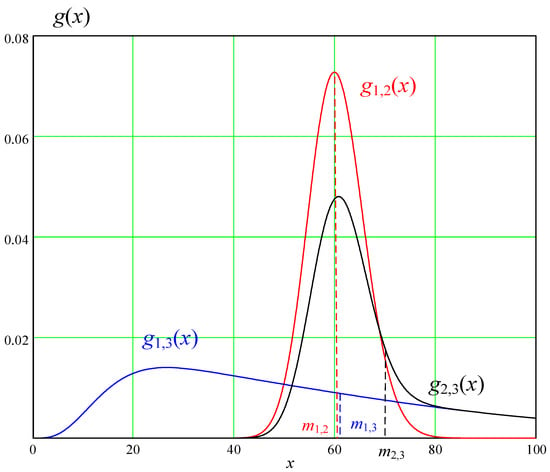
Figure 4.
Results of choosing two random variables (k = 2).
The mathematical expectation (mi,j(x)) is defined as follows.
The results indicate that the lowest mathematical expectation value of Equation (9) is achieved when selecting routes x1 and x2 since the lowest mi,j in Figure 4 is m1,2 (m1,2 = 60.0, 5.0). For other choices, the values of mathematical expectation, according to Equation (6), are m1,3 = 60.0, 9.0, and m2,3 = 76.0, 7.0.
4. Optimizing the Proposed Route Selection Model
However, evaluating the mathematical expectation of the delivery time is insufficient for choosing a route. The route selection problem should be considered as the minimization of the mathematical expectation of delivery time E(T) in a group of routes by selecting a set of k routes W from the total number of n available routes R. The problem’s solution is a set of selected routes at which the minimum value of mathematical expectation of data transfer time is achieved, according to Equation (6). The optimization problem can be formulated as follows.
The objective function is defined as follows to solve the previously introduced optimization problem.
The solution of the previously introduced optimization problem Equation (15), considering Equation (8), introduces a large computation complexity using traditional solution methods. The problem introduced in Equation (15) is formulated concerning the data delivery time (xi), which depends on the proportion of the data transmitted (βi), according to Equation (7). Thus, it is necessary to solve the problem of choosing βi that meets the problem’s solution, which significantly complicates the solution.
In this work, we propose to solve the problem sequentially in two stages. In the first stage, the problem of choosing k routes is solved under the assumption that all traffic distribution coefficients are equal (i.e., βi = β = 1/k, i = 1,…, k)). In the second stage, the problem of selecting values of distribution coefficients βi is solved. Algorithms 1 and 2 provide the pseudo-code of the proposed two stages.
| Algorithm 1 First stage of the optimum route selection | ||||
| Input data: | ||||
| R: Set of known routes. | ||||
| n: Number of known routes. | ||||
| W: Set-group of selected routes. | ||||
| K: Number of selected routes. | ||||
| Step 1. | Input initial data R, n, W, k and initialize variables i = j = s = 1, W = φ, T = φ. | |||
| Step 2. | Choose a route ri. | |||
| [This step selects a route from the set R to further evaluate its effect on the target function ri ∈ R, ri ∉ W.] | ||||
| Step 3. | Calculate the value of the target function (Solve Equation (16)), Then: | |||
| [This step calculates the next value of the target function and includes it in the set of values of the target function T. (At each iteration i (iteration of Phase I) the value of the target function is calculated for g selected routes, and g varies in Phase II from 1 to k.)] | ||||
| Step 4. | Check the end of Phase I. | |||
| If (i < n − g) | ||||
| i = i + 1 | ||||
| go to Step 2. | ||||
| Else | ||||
| perform the next step (go to step 5) | ||||
| End if | ||||
| [Phase I runs until all available routes from the set R that are not included in the set of selected routes W are checked] | ||||
| Step 5. | Include the route in a group of selected routes. | |||
| Calculate r: | ||||
| Then: | ||||
| [At this step, the set of target function values T is examined, and the minimum value is selected, and the route for which the corresponding value of the target function was obtained is included in the group of routes.] | ||||
| Step 6. | Ending Phase II: | |||
| If (g < k) | ||||
| g = g + 1, | ||||
| i = 1, | ||||
| go to step 2 | ||||
| Else | ||||
| Perform the next step (go to step 7). | ||||
| End if | ||||
| Step 7. | Output the set of selected routes W | |||
| End | ||||
| Algorithm 2 Second stage of the optimum route selection | |||||
| Input data: | |||||
| W: Set (group) of selected routes. | |||||
| β: Set of traffic distribution coefficients. | |||||
| b: Set of data transmission rate values for the selected channels. | |||||
| K: Number of chosen routes. | |||||
| Step 1. | Input initial data W, k and initialize variables i = j = s = 1, β = 1/k, T = φ. | ||||
| Step 2. | Choosing the βi coefficient | ||||
| [This step selects the coefficient βi from the set β to further evaluate its effect on the target function, βi ∈ β.] | |||||
| Step 3. | Calculation of the value of the target function for the changed traffic distribution coefficients βi. | ||||
| In this step, the value of βi is changed by Δβ, and all other values βj are corrected through multiplication by ηj coefficients so that the condition is: | |||||
| Then, calculate the objective function as follows. | |||||
| Where: | |||||
| [This step calculates the value of the target function and includes it in the set of values of the target function T. (At each iteration i (iteration of phase I) the value of the target function is calculated for k routes.)] | |||||
| Step 4. | Check the end of Phase I. | ||||
| If (i < k) | |||||
| i = i + 1 | |||||
| go to step 2. | |||||
| Else | |||||
| perform the next step (go to step 5) | |||||
| End if | |||||
| [Phase I is executed until all traffic distribution coefficients β have been checked.] | |||||
| Step 5. | Changing traffic distribution ratios. | ||||
| [In this step, the set of values of the target function T is examined and the minimum value is selected, the traffic distribution coefficients corresponding to this solution are chosen.] | |||||
| Step 6. | Ending Phase II: | ||||
| If the resulting solution gave the value of the target function t0, less than the value obtained at the previous iteration t0 < T0 | |||||
| i = 1, | |||||
| go to step 2 | |||||
| Else | |||||
| Perform the next step (go to step 7). | |||||
| End if | |||||
| Step 7. | Output the set of traffic distribution coefficients β. | ||||
| End | |||||
4.1. First Stage
The problem of the first stage is a knapsack problem, which has many variants. The solution of the first stage problem is complicated due to nonlinearity. This work proposes an approximate solution to the problem using dynamic programming. During the solution of the first stage of the problem, all traffic distribution coefficients are assumed to be equal. The problem’s solution is to select k traffic service routes from n available routes by the minimum data transfer time criterion.
The problem is solved iteratively, and the solution is organized into two nested phases: phase I and II. Algorithm 1 provides the pseudo-code of the first and second phases of the proposed method. In phase I, the route that leads to the greatest delivery time reduction is selected from all available routes, while in phase II, we compare the value of the target function with the value obtained in the previous phase and the number of selected routes. The phases are repeated every iteration until the optimum number of k routes is selected among the group of routes or when the new route selection does not reduce the data delivery time.
The result of executing Algorithm 1 is a group of routes that can be used for data transmission in multipath routing. However, this group is obtained when the traffic is evenly distributed among the selected routes, which is not the best solution when the route parameters are different. The obtained solution can be improved by rationally choosing the values of traffic distribution coefficients βi. The use of dynamic programming is also proposed to solve this problem [25].
4.2. Second Stage
The proposed method is similar in structure to the above-described method, and the main steps are presented in Algorithm 2. It is also organized in an iterative procedure with two main phases: phase I and II (internal and external cycles).
Phase I attempts to change the values of βi by small variations (±Δβ), taking into account the constraints, and chooses the value of i, for which the change has the greatest effect (i.e., the smallest value of the target function (delivery time) was obtained). Thus, phase I results in changing one of the values of βi by the value ±Δβ and adjusting the values of the others.
In phase II, we check if the value of the target function has changed compared to the previous phase. When the value decreases, the process passes to the next cycle; otherwise, the process stops, and the current values of βi are considered the problem’s solution. The considered variations (±Δβ) determine the results’ accuracy and the volume of calculations in the search for a solution. Algorithm 2 provides the pseudo-code for the selection of traffic distribution coefficients.
5. Numerical Evaluation and Analysis
The proposed model is simulated using the Matlab platform with an initial value of Δβ of 0.1. Table 1 provides the considered simulation parameters. The simulation was conducted utilizing an IoT network comprising a total of 30 nodes, randomly distributed within the network topology, with the characteristics introduced in Table 1. The proposed route selection algorithm was implemented for the network with twelve available routes, i.e., n = 12. A group of six routes, i.e., k = 6, was chosen as the selected routes, and the traffic distribution coefficients were calculated. The model was built in a discrete event modeling system. It implements traffic generation in the source node and the foreground traffic served by the network elements through which the selected routes pass [26].

Table 1.
Simulation parameters [13].
Figure 5 shows the structure of the considered model network, which is an ad hoc network consisting of 32 nodes, including source and destination nodes. All network nodes support the IEEE 802.11 protocol.
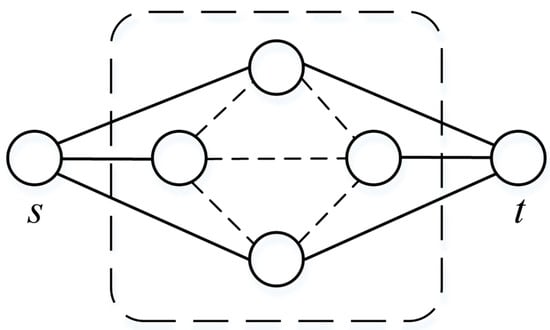
Figure 5.
Structure of the modeling network.
Figure 6 presents the obtained data rate of the simulation during the first ten seconds. The introduced results are for the network with the proposed route selection scheme and the traditional routing. The considered traditional routing scheme was the multipath optimized link state routing (OLSR) protocol [27]. The OLSR protocol supports the use of multiple parallel routes; however, the proposed method focuses on choosing a group of these routes. The developed route selection scheme increases the network speed by selecting the optimum routes and transferring data over them.
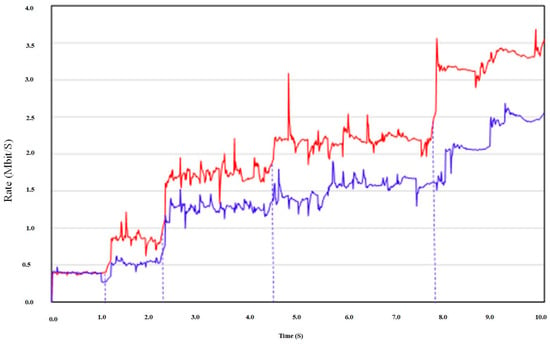
Figure 6.
Simulation results using the proposed method (red curve) and traditional method (blue curve).
Figure 6 shows five sections corresponding to the sequential solution of the route selection problem for different values of k = 1, 2, 3, 4, and 5 (red curve). Increasing the number of channels in the group increases the data transfer rate between the source and destination nodes.
The simulation was performed to evaluate the effectiveness of the proposed route group selection method when the route group was increased, without using the proposed algorithm, randomly and with an equal probability distribution of traffic over the routes (blue curve). The proposed route selection scheme improved the transmission rate, compared to random selection and equal-probability traffic distribution, by 40%. However, the proposed algorithm is limited by its computation cost, even with reduced computations.
The speed of data delivery using the proposed method was higher than with an arbitrary choice of a set of routes; it follows that the delay in data delivery using this method was decreased by the same value, i.e., by 40%.
Various performance metrics, including packet delivery rate (PDR), number of multiple relays (MPR), packet delivery time, routing latency, and energy consumption, were considered for assessing performance. We measured these parameters for the proposed and the other four multipath routing models. We considered four common routing algorithms for performance comparisons. These algorithms are the OLSR, directional OLSR (DOLSR), mobility and load aware OLSR (ML-OLSR), and multi-objective OLSR (MO-OLSR) [13,27,28].
Since packet delivery is used as a performance metric of routing schemes, we considered it as a key performance indicator of the proposed model. Packet delivery maps to communication overhead and route failure. Figure 7 provides the recorded PDR of the proposed multipath routing model compared to the four multipath routing protocols. The delivered packets were recorded for different numbers of deployed nodes. With the increase in the number of deployed nodes, the percentage of delivered packets decreased due to the higher communication overhead. However, the proposed model proved to have higher efficiency than other models even with the increase in the number of deployed nodes. This is due to the reduction of overhead achieved by gathering packets and transmitting over the optimum routes.
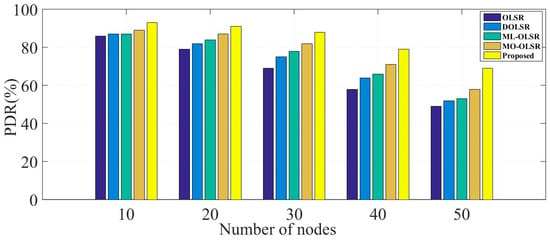
Figure 7.
Percentage of packet delivery for different numbers of nodes.
Figure 8 presents the node deployment of the 30-node scenario, while Figure 9 presents the average number of MPRs for the proposed model and considered algorithms. The recorded measures were carried out for the five considered cases. As the density of devices increased, i.e., number of network nodes per area increased, the average number of MPRs increased. However, the average number of MPRs of the cases of the proposed model was reduced compared to the four other algorithms, which indicates shorter paths and, thus, less overhead and lower latencies.
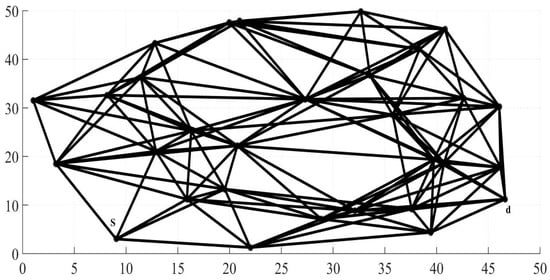
Figure 8.
Node deployment of 30-node scenario (s: source node, d: destination node).
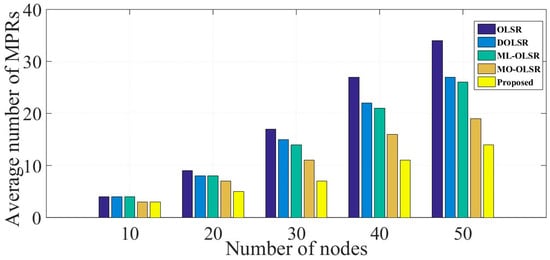
Figure 9.
Average number of MPRs for the considered scenarios.
The proposed model reduced the number of intermediate nodes by an average of 17% for the low-density network, e.g., cases 1 and 2. However, it had a higher efficiency in high-density networks, e.g., cases 4 and 5, by reducing MPRs by nearly 34%.
Figure 10 provides the average percentage of consumed energy of the proposed multipath routing compared to the four other algorithms. The measures were recorded for different numbers of deployed devices. The energy consumption increased with the increase in number of end devices due to the traffic overhead that requires retransmission due to packet loss. However, the proposed model selects the optimum route path, which reduced the energy cost.
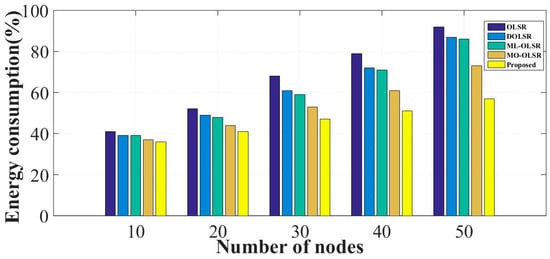
Figure 10.
The percentage of consumed energy for different numbers of nodes.
Figure 11 presents the average delay in delivering packets for the proposed and the considered algorithms. The delay was recorded for different numbers of deployed network nodes to investigate the effect of the network density on packet delays. This indicates the robustness of the routing algorithm against network density. The results indicate that the proposed model outperformed the other four models regarding packet delay. This is due to the optimized selection of intermediate paths and parallel routes, which reduces the overall path and the required time for packet delivery.
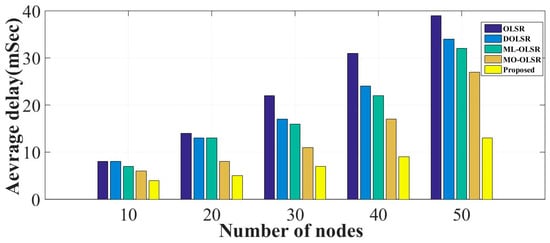
Figure 11.
The average delay of packets for different numbers of nodes.
The last considered metric was the overhead of the routing algorithm, which maps to the amount of data and processing power required to route packets through a network. Managing routing overhead is crucial to maintain efficient network operation and minimize any negative impact on network performance. Figure 12 presents the results of routing overhead for the proposed and the considered models. The proposed model reduced the overhead by considerable values. It significantly reduced overhead for dense networks, e.g., case 5, by 52% compared to 31% for low-density networks.
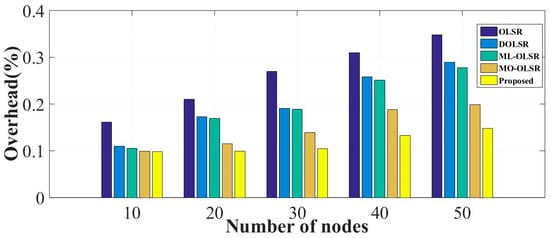
Figure 12.
Routing overhead for different numbers of nodes.
The time complexity of the proposed and traditional routing schemes is calculated as shown in Table 2.

Table 2.
Comparative analysis of the complexity.
n is the total available routes, while k is the selected routes from n (k <= n). Since k is considerably less than n, the time complexity is significantly lower than that of the other traditional routing schemes. Hence, the proposed method can be applied efficiently to improve the network reliability, availability, scalability, energy usage, and latency, through the optimized construction of parallel routes.
6. Conclusions
The analysis of multipath routing methods has shown that their use in IoT networks allows data transfer between network nodes at speeds significantly higher than the transmission speed of single-path routing. The number of routes in high-density IoT networks can be large enough to solve the multipath routing problem; therefore, such networks use independent routes. Selecting a group of routes with different parameters requires solving the problem of traffic distribution and can lead to different results, including a decrease in the equivalent transfer rate. Ensuring its increase requires a method that provides a rational choice of both the routes and the coefficients of traffic distribution over these routes. This work provided a method for choosing the optimum routes from a given number of available routes to achieve maximum data transfer. The proposed model uses dynamic programming to solve the proposed model. Moreover, the proposed method increased the efficiency of utilizing network resources. The introduced route selection scheme improved the transmission rate by 40%, compared to random selection and equal-probability traffic distribution. Also, it outperformed the OLSR, DOLSR, ML-OLSR, and MO-LSR algorithms in terms of energy usage, packet delivery delay, packet delivery ratio, and routing overhead.
Author Contributions
Conceptualization, A.P., A.A.A. and A.A.A.E.-L.; methodology, S.B., A.A.A.E.-L., A.P. and A.A.A.; software, S.A.C., A.P. and A.M.; validation, S.A.C., A.A.A. and A.K.; formal analysis, A.P., S.B., A.A.A. and A.A.A.E.-L.; investigation, S.A.C., A.K. and A.M.; resources, A.A.A.E.-L. and A.K.; data curation, A.A.A., A.A.A.E.-L. and A.P.; writing—original draft preparation, A.P., S.B., A.A.A.E.-L., A.A.A. and A.M.; writing—review and editing, A.K., S.A.C., A.A.A.E.-L. and A.A.A.; visualization, A.A.A., A.M. and A.A.A.E.-L.; supervision, A.K., A.A.A.E.-L. and A.A.A.; project administration, A.A.A.; funding acquisition, S.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
The studies at St. Petersburg State University of Telecommunications by Prof. M.A. Bonch-Bruevich were supported by the Ministry of Science and High Education of the Russian Federation through the grant 075-15-2022-1137. Also, this work was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R239), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to “the studies at St. Petersburg State University of Telecommunications” by M.A. Bonch-Bruevich which were supported by the Ministry of Science and High Education of the Russian Federation under the grant 075-15-2022-1137. The authors also would like to thank Prince Sultan University for their support. We are also grateful to the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R239), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia, for supporting this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maddikunta, P.K.R.; Pham, Q.-V.; Nguyen, D.C.; Thien, H.-T.; Aouedi, O.; Yenduri, G.; Bhattacharya, S.; Gadekallu, T.R. Incentive Techniques for the Internet of Things: A Survey. J. Netw. Comput. Appl. 2022, 206, 103464. [Google Scholar] [CrossRef]
- Sinha, B.B.; Dhanalakshmi, R. Recent Advancements and Challenges of Internet of Things in Smart Agriculture: A Survey. Future Gener. Comput. Syst. 2022, 126, 169–184. [Google Scholar] [CrossRef]
- Al-Bahri, M.; Ateya, A.; Muthanna, A.; Algarni, D.A.; Soliman, F.N. Digital Object Architecture for IoT Networks. Intell. Autom. Soft Comput. 2023, 35, 97–110. [Google Scholar] [CrossRef]
- Shen, X.; Liao, W.; Yin, Q. A Novel Wireless Resource Management for the 6G-Enabled High-Density Internet of Things. IEEE Wirel. Commun. 2022, 29, 32–39. [Google Scholar] [CrossRef]
- Marochkina, A.; Paramonov, A.; Tatarnikova, T.M. Ultra-Dense Internet of Things Model Network. In Communications in Computer and Information Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 111–122. ISBN 9783030971090. [Google Scholar]
- Paramonov, A.; Bushelenkov, S.; Tselykh, A.; Muthanna, A.; Koucheryavy, A. Model of the Internet of Things Access Network Based on a Lattice Structure. In Advances in Cybersecurity, Cybercrimes, and Smart Emerging Technologies; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; pp. 315–322. ISBN 9783031211003. [Google Scholar]
- Bushelenkov, S.; Paramonov, A.; Muthanna, A.; El-Latif, A.A.A.; Koucheryavy, A.; Alfarraj, O.; Pławiak, P.; Ateya, A.A. Multi-Story Building Model for Efficient IoT Network Design. Mathematics 2023, 11, 1403. [Google Scholar] [CrossRef]
- Mir, M.; Yaghoobi, M.; Khairabadi, M. A New Approach to Energy-Aware Routing in the Internet of Things Using Improved Grasshopper Metaheuristic Algorithm with Chaos Theory and Fuzzy Logic. Multimed. Tools Appl. 2023, 82, 5133–5159. [Google Scholar] [CrossRef]
- Srinidhi, N.N.; Dilip Kumar, S.M.; Venugopal, K.R. Network Optimizations in the Internet of Things: A Review. Eng. Sci. Technol. Int. J. 2019, 22, 1–21. [Google Scholar] [CrossRef]
- Choudhary, S.; Sugumaran, S.; Belazi, A.; El-Latif, A.A.A. Linearly Decreasing Inertia Weight PSO and Improved Weight Factor-Based Clustering Algorithm for Wireless Sensor Networks. J. Ambient Intell. Humaniz. Comput. 2023, 14, 6661–6679. [Google Scholar] [CrossRef]
- Paramonov, A.; Tonkikh, E.; Koucheryavy, A.; Tatarnikova, T.M. High Density Internet of Things Network Analysis. In Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 307–316. ISBN 9783030657253. [Google Scholar]
- Marietta, J.; Chandra Mohan, B. A Review on Routing in Internet of Things. Wirel. Pers. Commun. 2020, 111, 209–233. [Google Scholar] [CrossRef]
- Ateya, A.A.; Muthanna, A.; Gudkova, I.; Gaidamaka, Y.; Algarni, A.D. Latency and Energy-Efficient Multi-Hop Routing Protocol for Unmanned Aerial Vehicle Networks. Int. J. Distrib. Sens. Netw. 2019, 15, 155014771986639. [Google Scholar] [CrossRef]
- Yao, J.; Wang, Y.; Li, Q.; Mao, H.; El-Latif, A.A.A.; Chen, N. An Efficient Routing Protocol for Quantum Key Distribution Networks. Entropy 2022, 24, 911. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xu, L.D. A Review of Internet of Things—Resource Allocation. IEEE Internet Things J. 2021, 8, 8657–8666. [Google Scholar] [CrossRef]
- Avdhesh Yadav, S.; Poongoodi, T. A Novel Optimized Routing Technique to Mitigate Hot-spot Problem (NORTH) for Wireless Sensor Network-based Internet of Things. Int. J. Commun. Syst. 2022, 35, e5314. [Google Scholar] [CrossRef]
- Lakhlef, I.E.; Djamaa, B.; Senouci, M.R. A Comprehensive Study of Multicast Routing Protocols in the Internet of Things. In Artificial Intelligence and Its Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 325–335. ISBN 9783030963101. [Google Scholar]
- Ateya, A.A.; Sayed, M.S.; Abdalla, M.I. Multilevel Hierarchical Clustering Protocol for Wireless Sensor Networks. In Proceedings of the 2014 International Conference on Engineering and Technology (ICET), Cairo, Egypt, 19–20 April 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Ma, Z.; Xiao, M.; Xiao, Y.; Pang, Z.; Poor, H.V.; Vucetic, B. High-Reliability and Low-Latency Wireless Communication for Internet of Things: Challenges, Fundamentals, and Enabling Technologies. IEEE Internet Things J. 2019, 6, 7946–7970. [Google Scholar] [CrossRef]
- Dhanare, R.; Nagwanshi, K.K.; Varma, S. A Study to Enhance the Route Optimization Algorithm for the Internet of Vehicle. Wirel. Commun. Mob. Comput. 2022, 2022, 1453187. [Google Scholar] [CrossRef]
- Jamshed, M.A.; Ali, K.; Abbasi, Q.H.; Imran, M.A.; Ur-Rehman, M. Challenges, Applications, and Future of Wireless Sensors in Internet of Things: A Review. IEEE Sens. J. 2022, 22, 5482–5494. [Google Scholar] [CrossRef]
- Qi, H.; Li, Z.; Qi, J.; Wang, X.; Gani, A.; Whaiduzzaman, M. An Improved Sierpinski Fractal Based Network Architecture for Edge Computing Datacenters. In Proceedings of the 2019 IEEE International Conferences on Ubiquitous Computing & Communications (IUCC) and Data Science and Computational Intelligence (DSCI) and Smart Computing, Networking and Services (SmartCNS), Shenyang, China, 15 May 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Ramkumar, J.; Vadivel, R. Multi-Adaptive Routing Protocol for Internet of Things Based Ad-Hoc Networks. Wirel. Pers. Commun. 2021, 120, 887–909. [Google Scholar] [CrossRef]
- Mao, B.; Kawamoto, Y.; Kato, N. AI-Based Joint Optimization of QoS and Security for 6G Energy Harvesting Internet of Things. IEEE Internet Things J. 2020, 7, 7032–7042. [Google Scholar] [CrossRef]
- Lvovich, I.; Preobrazhenskiy, A.; Lvovich, Y. Modeling of Integrated Internet of Things System on the Base of Semi-Markov Processes. In Advances in Automation IV; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; pp. 157–165. ISBN 9783031223105. [Google Scholar]
- Artem, V.; Ateya, A.A.; Muthanna, A.; Koucheryavy, A. Novel AI-Based Scheme for Traffic Detection and Recognition in 5G Based Networks. In Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 243–255. ISBN 9783030308582. [Google Scholar]
- Zheng, Y.; Jiang, Y.; Dong, L.; Wang, Y.; Li, Z.; Zhang, H. A Mobility and Load Aware OLSR Routing Protocol for UAV Mobile Ad-Hoc Networks. In Proceedings of the 2014 International Conference on Information and Communications Technologies (ICT 2014), Surabaya, Indonesia, 14–16 November 2016; Institution of Engineering and Technology: Hertfordshire, UK, 2014. [Google Scholar]
- Wheeb, A.H.; Nordin, R.; Samah, A.A.; Kanellopoulos, D. Performance Evaluation of Standard and Modified OLSR Protocols for Uncoordinated UAV Ad-Hoc Networks in Search and Rescue Environments. Electronics 2023, 12, 1334. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).