On the Chromatic Number of Some (P₃ ∪ P₂)-Free Graphs

Abstract

Let G be a graph. We denote the chromatic (clique) number of G by $\chi \left(G\right)\left(\omega \right(G\left)\right)$. In this paper, we prove that (i) $\chi \left(G\right)\le 2\omega \left(G\right)$ if G is ($P_3\cup P_2$, kite)-free, (ii) $\chi \left(G\right)\le {\omega }^2\left(G\right)$ if G is ($P_3\cup P_2$, hammer)-free, (iii) $\chi \left(G\right)\le \frac{3{\omega }^2\left(G\right)+\omega \left(G\right)}{2}$ if G is ($P_3\cup P_2,C_5$)-free. Furthermore, we also discuss the chromatic number of ($P_3\cup P_2,K_4$)-Free Graphs.

1. Introduction

All graphs considered in this paper are finite and simple. We use $P_k$ and $C_k$ to denote a path and a cycle on k vertices, respectively, and follow [1] for undefined notations and terminology. Let G be a graph, and X be a subset of $V\left(G\right)$. We use $G\left[X\right]$ to denote the subgraph of G induced by X, and call X a clique (independent set) if $G\left[X\right]$ is a complete graph (has no edge). The clique number $\omega \left(G\right)$ of G is the maximum size taken over all cliques of G. Let $\delta \left(G\right)$ denote the minimum degree of G.

For $v\in V\left(G\right)$, let $N_G\left(v\right)$ be the set of vertices adjacent to v, $d_G\left(v\right)=\left|N_G\left(v\right)\right|$, $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$, $M_G\left(v\right)=V\left(G\right)\setminus N_G\left[v\right]$. For $X\subseteq V\left(G\right)$, let $N_G\left(X\right)=\{u\in V\left(G\right)\setminus X|u$ has a neighbor in $X\}$ and $M_G\left(X\right)=V\left(G\right)\setminus (X\cup N_G\left(X\right))$. If it does not cause any confusion, we will omit the subscript G and simply write $N\left(v\right),d\left(v\right),N\left[v\right],M\left(v\right),N\left(X\right)$ and $M\left(X\right)$.

For positive integer i, let $N_G^i\left(X\right):=\{u\in V\left(G\right)\setminus X|min\left\{d_G(u,v)\right\}=iforv\in X$}, where $d_G(u,v)$ is the distance between u and v in G. Moreover, let $N_G^{\ge i}\left(X\right):={\cup }_{j=i}^{\infty }{N}_G^i\left(X\right)$. Notice that $N_G^1\left(X\right)=N_G\left(X\right)$ is the neighborhood of X in G. We write $N_G^i\left(H\right)$ for $N_G^i\left(V\left(H\right)\right)$.

Let G and H be two vertex disjoint graphs. Join$G+H$ is the graph with $V(G+H)=V\left(G\right)\cup V\left(H\right)$ and $E(G+H)=E\left(G\right)\cup E\left(H\right)\cup \left\{xy\right|x\in V\left(G\right),y\in V\left(H\right)$}. Union$G\cup H$ is the graph with $V(G\cup H)=V\left(G\right)\cup \left(H\right)$ and $E(G\cup H)=E\left(G\right)\cup E\left(H\right)$. The union of k copies of the same graph G will be denoted by $kG$. We say that G induces H if G has an induced subgraph isomorphic to H, and say that G is H-free otherwise. Analogously, for a family $\mathcal{H}$ of graphs, we say that G is $\mathcal{H}$-free if G induces no member of $\mathcal{H}$. The complement of a graph G will be denoted by $\overline{G}$.

Let k be a positive integer, and let $\left[k\right]=\{1,2,\dots ,k\}$. A k-coloring of G is a mapping $c:V\left(G\right)\mapsto \left[k\right]$, such that $c\left(u\right)\ne c\left(v\right)$ whenever $u\sim v$ in G. The chromatic number$\chi \left(G\right)$ of G is the minimum integer k, such that G admits a k-coloring. It is well known that $\chi \left(G\right)\ge \omega \left(G\right)$. A perfect graph is one such that $\chi \left(H\right)=\omega \left(H\right)$ for all of its induced subgraphs H. A family $\mathcal{G}$ of graphs is said to be $\chi$-bounded if there is a function f such that $\chi \left(G\right)\le f\left(\omega \right(G\left)\right)$ for every $G\in \mathcal{G}$, and if such a function does exist for $\mathcal{G}$, then f is said to be a χ-binding function of $\mathcal{G}$.

Let G be a graph, $v\in V\left(G\right)$, and let X and Y be two subsets of $V\left(G\right)$. We say that v is complete to X if v is adjacent to all vertices of X, and say that v is anticomplete to X if v is not adjacent to any vertex of X. We say that X is complete (respectively, anticomplete) to Y if each vertex of X is complete (resp. anticomplete) to Y. Particularly, we say that X is almost complete to Y if at most one vertex of X is not complete to Y. For $u,v\in V\left(G\right)$, we simply write $u\sim v$ if $uv\in E\left(G\right)$, and write $u\nsim v$ if $uv\notin E\left(G\right)$.

A hole of G is an induced cycle of length at least 4, and a k-hole is a hole of length k. A k-hole is called an odd hole if k is odd, and is called an even hole otherwise. An antihole is the complement of some hole. An odd (respectively, even) antihole is defined analogously. The famous Strong Perfect Graph Theorem states that

Theorem 1

([2]). A graph is perfect if and only if it induces neither an odd hole nor an odd antihole.

Erdös [3] proved that for any positive integers $k,l\ge 3$, there exists a graph G with $\chi \left(G\right)\ge k$ and no cycles of length less than l. This result motivates us to study the chromatic number of F-free graphs, where F is a forest (a disjoint union of trees). Gyárfás [4] and Sumner [5] independently conjectured that if F is a forest, then F-free graphs are $\chi$-bounded.

The class of $2K_2$-free graphs has attracted a great deal of interest in recent years. It is known that for every $2K_2$-free graph G, $\chi \left(G\right)\le \left(\genfrac{}{}{0pt}{}{\omega +1}{2}\right)$ [6]. Up to now, the best known $\chi$-binding function for $2K_2$-free graphs is $f\left(\omega \right)=\left(\genfrac{}{}{0pt}{}{\omega +1}{2}\right)-2\lfloor \frac{\omega }{3}\rfloor$ [7]. We refer the interested readers to [6,8,9,10] for results of $2K_2$-free graphs, and to [11,12,13] for more results and problems about the $\chi$-bounded problem. In particular, Brause et al. [8] proved that the class of $(2K_2,3K_1)$-free graphs does not admit a linear $\chi$-binding function. In 2022, Brause et al. [14] gave a more general theorem.

Theorem 2

(Lemma 1 of [1]). Let $\mathcal{H}$ be a set of graphs and ℓ be an integer such that $\overline{H}$ has girth at most ℓ for each $H\in \mathcal{H}$. If the class of $\mathcal{H}$-free graphs is χ-bounded, then the class of $\mathcal{H}$-free graphs does not admit a linear χ-binding function.

Many scholars began to show interest in $(P_3\cup P_2)$-free graphs as $(P_3\cup P_2)$-free graphs is a superclass of $2K_2$-free graphs. The best known $\chi$-binding function for $(P_3\cup P_2)$-free graphs is $f\left(\omega \right)=\frac{1}{6}\omega (\omega +1)(\omega +2)$ [15]. In [16,17,18,19,20,21], the authors proved that the class of ($P_3\cup P_2,H$)-free graphs has a linear $\chi$-binding function when $H\in \{$ diamond, house, gem, paraglider, $HVN$, $W_4$}. Recently, Wu and Xu [22] proved that $\chi \left(G\right)\le \frac{1}{2}{\omega }^2\left(G\right)+\frac{3}{2}\omega \left(G\right)+1$ if G is ($P_3\cup P_2$, crown)-free. (see Figure 1 for the illustration of $P_3\cup P_2$ and some forbidden configurations.)

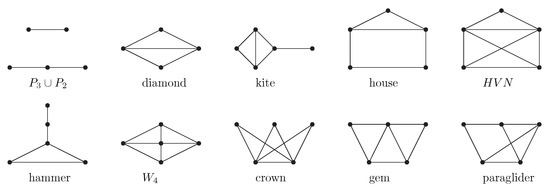
Figure 1. Illustration of $P_3\cup P_2$ and some forbidden configurations.

In this paper, we prove that

Theorem 3.

$\chi \left(G\right)\le 2\omega \left(G\right)$ if G is ($P_3\cup P_2$, kite)-free.

Let G be a graph on n-vertices $\{v_1,v_2,\cdots ,v_n\}$ and let $H_1,H_2,\cdots ,H_n$ be n vertex-disjoint graphs. An expansion $G(H_1,H_2,\cdots ,H_n)$ of G is a graph obtained from G by

(i) Replacing each $v_i$ of G by $H_i$, $i=1,2,\cdots ,n$;

(ii) Joining every vertex in $H_i$ with every vertex in $H_j$, whenever $v_i$ and $v_j$ are adjacent in G.

In addition, $G\cong K_n$ and $H_i\cong H$, denoted by $K_n\left(H\right)=G(H,H,\cdots ,H)$.

Let H be the Mycielski–Gröstzsch graph (see Figure 2). Then, $\omega \left(H\right)=2$ and $\chi \left(H\right)=4$. It is clear that $K_k\left(H\right)$ is ($P_3\cup P_2$, kite)-free, and $\chi \left(K_k\left(H\right)\right)=2\omega \left(K_k\left(H\right)\right)=2·2k=4k$. Let F be the complement of Schläfli graph (see https://houseofgraphs.org/graphs/19273) (accessed on 1 September 2023). Then, $\omega \left(F\right)=3$ and $\chi \left(F\right)=6$. Obviously, $K_{k-1}\left(H\right)+F$ is ($P_3\cup P_2$, kite)-free. Hence, $\omega (K_{k-1}\left(H\right)+F)=2k+1$ and $\chi (K_{k-1}\left(H\right)+F)=4k+2$. This implies that our bound is optimal when $\omega \left(G\right)\ge 2$.

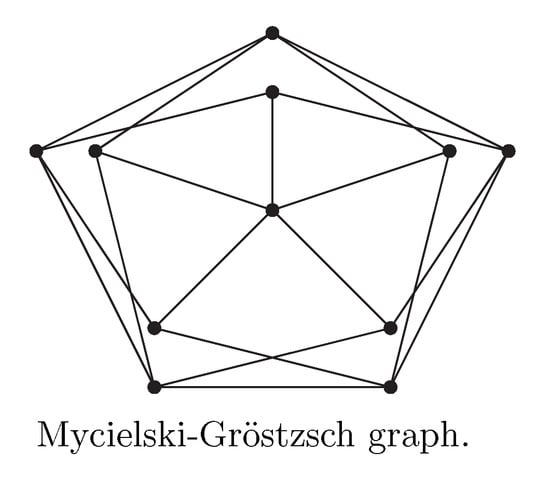
Figure 2. Mycielski–Gröstzsch graph.

By Theorem 2, we have that the class of ($P_3\cup P_2$, hammer)-free graphs has no linear $\chi$-binding functions. In this paper, we prove that

Theorem 4.

$\chi \left(G\right)\le {\omega }^2\left(G\right)$ if G is ($P_3\cup P_2$, hammer)-free.

Notice that H is also ($P_3\cup P_2$, hammer)-free. Therefore, the $\chi$-binding function $f={\omega }^2$ for ($P_3\cup P_2$, hammer)-free graphs is tight when $\omega =2$.

In [23], Choudum and Karthick proved that $\chi \left(G\right)\le \lceil \frac{5\omega \left(G\right)}{4}\rceil$ if G is $(P_3\cup P_2,C_4)$-free. By Theorem 2, we have that the class of $(P_3\cup P_2,C_5)$-free graphs does not admit a linear $\chi$-binding function. In this paper, we prove that

Theorem 5.

$\chi \left(G\right)\le \frac{3{\omega }^2\left(G\right)+\omega \left(G\right)}{2}$ if G is ($P_3\cup P_2,C_5$)-free.

In [24], Wang and Zhang proved that $\chi \left(G\right)\le 3$ if G is a $(P_3\cup P_2,K_3)$-free graph. In this paper, we also prove that

Theorem 6.

$\chi \left(G\right)\le 9$ if G is ($P_3\cup P_2,K_4$)-free.

Notice that $H^{\prime }$ is a $(P_3\cup P_2)$-free graph with $\omega \left(H^{\prime }\right)=3$ and $\chi \left(H^{\prime }\right)=6$. In reality, as mentioned above, $\chi \left(G\right)\le 6$ if G is $(P_3\cup P_2,H,K_4)$-free, where $H\in \{$ diamond, paraglider, gem, house, $W_4$, kite}. So, we may ask a question as follows.

Problem 1.

Is it true that $\chi \left(G\right)\le 6$ if G is ($P_3\cup P_2,K_4$)-free?

We will prove Theorem 3 in Section 2, prove Theorem 4 in Section 3, prove Theorem 5 in Section 4, and prove Theorem 6 in Section 5.

2. (${\mathit{P}}_{\mathbf{3}}\cup {\mathit{P}}_{\mathbf{2}}$, Kite)-Free Graphs

In this section, we consider ($P_3\cup P_2$, kite)-free graphs. We may always assume that G is a ($P_3\cup P_2$, kite)-free graph, such that $\chi \left(G^{\prime }\right)\le 2\omega \left(G^{\prime }\right)$ for every induced subgraph $G^{\prime }$ of G different from G, and $\chi \left(G\right)>2\omega \left(G\right)$. The following lemmas will be used in our proof.

Lemma 1

(Lemma 2.1 of [16]). Let u and v be two nonadjacent vertices in G. Then, $N\left(u\right)⊈N\left(v\right)$ and $N\left(v\right)⊈N\left(u\right)$.

Proof. 

Suppose to its contrary that $N\left(u\right)\subseteq N\left(v\right)$ by symmetry. By assumption, $\chi (G-u)\le 2\omega (G-u)$. Since we can color u by the color of v, it follows that $\chi \left(G\right)\le 2\omega (G-u)\le 2\omega \left(G\right)$, a contradiction. □

Lemma 2

([24]). If G is a $(P_3\cup P_2,C_3)$-free graph, then $\chi \left(G\right)\le 4$.

Lemma 3

(1.8 of [25]). Let G be a ($K_1\cup K_3$)-free graph. If G contains a $K_3$, then $\chi \left(G\right)\le 2\omega \left(G\right)$.

We will complete the proof of Theorem 3 by the following three propositions.

Proposition 1.

G is $(P_2\cup K_3)$-free.

Proof. 

Suppose not. Let Q be an induced $P_2\cup K_3$ in G with $V\left(Q\right)=\{u_1,u_2,v_1,v_2,v_3\}$ such that $v_1{v}_2{v}_3{v}_1$ is a triangle. We will prove that

$$N\left(u_1\right)\setminus N\left(u_2\right) \mathrm{and} N\left(u_2\right)\setminus N\left(u_1\right) \mathrm{are} \mathrm{both} \mathrm{independent}.$$

(1)

Suppose $N\left(u_1\right)\setminus N\left(u_2\right)$ has two adjacent vertices $x_1$ and $x_2$. If $|\{v_1,v_2,v_3\}\setminus N\left(x_1\right)| \ge 2$, we may by symmetry assume that $x_1\nsim v_1$ and $x_1\nsim v_2$, then $\{v_1,v_2,u_1,u_2,x_1\}$ induces a $P_3\cup P_2$, a contradiction. So, $|N\left(x_1\right)\cap \{v_1,v_2,v_3\}| \ge 2$. By symmetry, $|N\left(x_2\right)\cap \{v_1,v_2,v_3\}| \ge 2$. Therefore, there must exist a vertex in $\{v_1,v_2,v_3\}$, which is complete to $\{x_1,x_2\}$, say $v_1$. Now, $\{u_1,u_2,x_1,x_2,v_1\}$ induces a kite, a contradiction. So, $N\left(u_1\right)\setminus N\left(u_2\right)$ is independent and, by symmetry, $N\left(u_2\right)\setminus N\left(u_1\right)$ is independent. This proves (1).

Let $M=G\left[M\left(\{u_1,u_2\}\right)\right]$. Since G is $(P_3\cup P_2)$-free, we have that $G\left[M\right]$ is $P_3$-free. Choose a maximum clique in $G\left[M\right]$, say $C_1$. Without loss of generality, we may assume that $\{v_1,v_2,v_3\}\subseteq C_1$. Let $D=\{v\in N\left(u_1\right)\cap N\left(u_2\right)|v$, which is complete to $N\left(u_1\right)\cap N\left(u_2\right)\setminus \left\{v\right\}\}$, and $C=N\left(u_1\right)\cap N\left(u_2\right)\setminus D$. So, D is a clique, and for each vertex y in C, y is not complete to $C\setminus \left\{y\right\}$.

Suppose there exists a vertex $y_1\in C$ such that $y_1$ is anticomplete to $C_1$. Since $y_1$ is not complete to $C\setminus \left\{y_1\right\}$, it follows that C has a vertex $y_2$, such that $y_2\nsim y_1$. If $y_2$ is anticomplete to $C_1$, then $\{y_1,u_1,y_2,v_1,v_2\}$ induces a $P_3\cup P_2$, a contradiction. So, $y_2$ has a neighbor in $C_1$, say $v_1$. Then, $\{y_1,u_1,u_2,y_2,v_1\}$ induces a kite, a contradiction. So,

$$C\subseteq N\left(C_1\right).$$

(2)

Next, we prove that

$$C \mathrm{is} \mathrm{complete} \mathrm{to} C_1.$$

(3)

Suppose the contrary. We may assume that there exists a vertex $y_3$ in C, such that $y_3\nsim v_1$. By (2), $y_3\in N\left(C_1\right)$. If $y_3\sim v_2$ and $y_3\sim v_3$, then $\{u_1,y_3,v_1,v_2,v_3\}$ induces a kite, a contradiction. So, $|N\left(y_3\right)\cap C_1| =1$ and, by symmetry, $y_3\sim v_2$. Similarly, for each vertex $y\in C$, if y is not complete to $C_1$, then $|N\left(y\right)\cap C_1| =1$.

By the definition of C, we have that there exists a vertex $y_4$ in C such that $y_3\nsim y_4$. Suppose $y_4$ is not complete to $C_1$. Then, $|N\left(y_4\right)\cap C_1| =1$. If $y_4\sim v_2$, then $\{y_3,u_1,y_4,v_1,v_3\}$ induces a $P_3\cup P_2$, a contradiction. If $y_4\nsim v_2$, then $\{u_1,u_2,y_3,y_4,v_2\}$ induces a kite, a contradiction. So, $y_4$ is complete to $C_1$. Now, $\{u_1,u_2,y_3,y_4,v_1\}$ induces a kite, a contradiction. This proves (3).

Let ${\omega }_1=\omega \left(G\left[C\right]\right)$. By (3) and $C_1$ is a maximum clique in $G\left[M\right]$, we have that $\omega \left(G\left[M\right]\right)\le \omega \left(G\right)-{\omega }_1$. So, $\chi \left(G[M\cup \{u_1,u_2\}]\right)\le \omega \left(G\right)-{\omega }_1$. It is clear that D is complete to C. Since $\omega \left(G[N\left(u_1\right)\cap N\left(u_2\right)]\right)\le \omega \left(G\right)-2$, we have that $\omega \left(G\left[D\right]\right)\le \omega \left(G\right)-2-{\omega }_1$.

Note that $V\left(G\right)=\{u_1,u_2\}\cup N\left(\{u_1,u_2\}\right)\cup M$ and $N\left(\{u_1,u_2\}\right)=(N\left(u_1\right)\setminus N\left(u_2\right))\cup (N\left(u_2\right)\setminus N\left(u_1\right))\cup (N\left(u_1\right)\cap N\left(u_2\right))$. By (1), $\chi \left(G\right)\le \chi \left(G\left[C\right]\right)+\chi \left(G\left[D\right]\right)+2+\chi \left(G[M\cup \{u_1,u_2\}]\right)\le f\left({\omega }_1\right)+2+2\omega \left(G\right)-2{\omega }_1-2\le 2\omega \left(G\right)+2{\omega }_1-2{\omega }_1=2\omega \left(G\right)$, a contradiction.

This proves Proposition 1. □

Proposition 2.

G is hammer-free.

Proof. 

Suppose not. Let Q be an induced hammer in G with $V\left(Q\right)=\{v_1,v_2,v_3,v_4,v_5\}$ such that $v_1{v}_2{v}_3{v}_1$ is a triangle, $v_4\sim v_3$ and $d_Q\left(v_5\right)=1$. Notice that $\{v_1,v_2,v_4,v_5\}$ induces a $2K_2$. For a subset $S\subseteq \{1,2,4,5\}$, we define $N_S=\left\{v\right|v\in N(Q\setminus \left\{v_3\right\}),$ and $v_i\sim v$ if and only if $i\in S\}$. Let $N=N\left(\{v_1,v_2,v_4,v_5\}\right)$ and $M=M\left(\{v_1,v_2\}\right)$. By Proposition 1, we have that G is $(P_2\cup K_3)$-free.

If $N_{\{1,2\}}\ne \varnothing$, let $v_1^{\prime }\in N_{\{1,2\}}$, then $\{v_1,v_2,v_1^{\prime },v_4,v_5\}$ induces a $P_2\cup K_3$, a contradiction. So, $N_{\{1,2\}}=\varnothing$. Similarly, $N_{\{3,4\}}=\varnothing$. Since G is $(P_3\cup P_2)$-free, we have that $N_S=\varnothing$ if $\left|S\right|=1$. Therefore, $N=N_{\{1,4\}}\cup N_{\{1,5\}}\cup N_{\{2,4\}}\cup N_{\{2,5\}}\cup N_{\{1,2,4\}}\cup N_{\{1,2,5\}}\cup N_{\{1,4,5\}}\cup N_{\{2,4,5\}}\cup N_{\{1,2,4,5\}}$. Moreover, since G is $(P_3\cup P_2,P_2\cup K_3)$-free, we have that $G\left[M\right]$ is $(P_3,K_3)$-free, which implies that each component of $G\left[M\right]$ is a vertex or an edge.

If $N_{\{1,4\}}$ has two adjacent vertices $x_1$ and $x_2$, then $\{v_1,v_4,x_1,x_2,v_5\}$ induces a kite, a contradiction. So, $N_S$ is independent if $S\subseteq \{1,2,4,5\}$ and $\left|S\right|=2$. Similarly, $N_S$ is independent if $S\subseteq \{1,2,4,5\}$ and $\left|S\right|=3$. Let $J_2=N_{\{1,4\}}\cup N_{\{1,5\}}\cup N_{\{2,4\}}\cup N_{\{2,5\}}$ and $J_3=N_{\{1,2,4\}}\cup N_{\{1,2,5\}}\cup N_{\{1,4,5\}}\cup N_{\{2,4,5\}}$. We will prove that

$$J_2 \mathrm{is} \mathrm{anticomplete} \mathrm{to} J_3.$$

(4)

Suppose not. Without loss of generality, there exists a vertex $y_1\in J_2$ such that $y_1\sim v_3$. If $y_1\in N_{\{1,4\}}\cup N_{\{2,4\}}$, then $\{v_1,y_1,v_3,v_4,v_5\}$ or $\{v_2,y_1,v_3,v_4,v_5\}$ induces a kite, a contradiction. So, $y_1\in N_{\{1,5\}}\cup N_{\{2,5\}}$. But now, $\{v_1,v_2,y_1,v_3,v_5\}$ induces a kite, a contradiction. So, $J_2$ is anticomplete to $J_3$. This proves (4).

By (4), we have that $\chi \left(G\left[N\right]\right)\le \chi \left(G\left[J_2\right]\right)+\chi \left(G\left[J_3\right]\right)\le 4$. If $v_3$ is not complete to $N_{\{1,2,4,5\}}$, let $y_2\in N_{\{1,2,4,5\}}$ such that $v_3\nsim y_2$, then $\{y_2,v_1,v_2,v_3,v_5\}$ induces a kite, a contradiction. So, $V\left(Q\right)$ is complete to $N_{\{1,2,4,5\}}$. In particular, $\{v_1,v_2,v_3\}$ is complete to $N_{\{1,2,4,5\}}$, and thus $\omega \left(G\left[N_{\{1,2,4,5\}}\right]\right)\le \omega \left(G\right)-3$.

Suppose $\omega \left(G\right)=3$. Then, $N_{\{1,2,4,5\}}=\varnothing$, which implies that $\chi \left(G\right)\le \chi \left(G\left[N\right]\right)+\chi \left(G[M\cup \{v_1,v_2,v_4,v_5\}]\right)\le 4+2=6=2\omega \left(G\right)$, a contradiction. So, $\omega \left(G\right)\ge 4$. Now, $\chi \left(G\right)\le \chi \left(G\left[N\right]\right)+\chi \left(G[M\cup \{v_1,v_2,v_4,v_5\}]\right)\le f(\omega \left(G\right)-3)+4+2\le 2(\omega \left(G\right)-3)+6=2\omega \left(G\right)$, a contradiction.

This proves Proposition 2. □

Proposition 3.

G is $(K_1\cup K_3)$-free.

Proof. 

Suppose not. Let Q be an induced $K_1\cup K_3$ in G with $V\left(Q\right)=\{u,v_1,v_2,v_3\}$, such that $v_1{v}_2{v}_3{v}_1$ is a triangle. By Lemma 1, there exists a vertex $u^{\prime }\in V\left(G\right)$, such that $u^{\prime }\sim u$ and $u^{\prime }\nsim v_1$. By Proposition 1 and 2, G is ($P_2\cup K_3$, hammer)-free.

If $u^{\prime }$ is anticomplete to $\{v_2,v_3\}$, then $\{u,u^{\prime },v_1,v_2,v_3\}$ induces a $P_2\cup K_3$, a contradiction. If $u^{\prime }$ is complete to $\{v_2,v_3\}$, then $\{u,u^{\prime },v_1,v_2,v_3\}$ induces a kite, a contradiction. So, $|N\left(u^{\prime }\right)\cap \{v_2,v_3\}| =1$. But now, $\{u,u^{\prime },v_1,v_2,v_3\}$ induces a hammer, a contradiction. This proves Proposition 3. □

Proof of Theorem 3.

By Lemma 2, we may assume that $\omega \left(G\right)\ge 3$. Now, by Lemma 3 and Proposition 3, we have that $\chi \left(G\right)\le 2\omega \left(G\right)$, a contradiction. This completes the proof of Theorem 3. □

Actually, by the proof above, we have the following proposition.

Proposition 4.

$\chi \left(F\right)\le 2\omega \left(F\right)$ if F is a $(P_3\cup P_2,K_1\cup K_3)$-free graph.

3. (${\mathit{P}}_{\mathbf{3}}\cup {\mathit{P}}_{\mathbf{2}}$, Hammer)-Free Graphs

In this section, we consider ($P_3\cup P_2$, hammer)-free graphs. We may always assume that G is a ($P_3\cup P_2$, hammer)-free graph such that $\chi \left(G^{\prime }\right)\le {\omega }^2\left(G^{\prime }\right)$ for every induced subgraph $G^{\prime }$ of G different from G, and $\chi \left(G\right)>{\omega }^2\left(G\right)$. By Lemma 2, we may assume that $\omega \left(G\right)\ge 3$.

We will complete the proof of Theorem 3 by the following Proposition.

Proposition 5.

G is $(P_2\cup K_3)$-free.

Proof. 

Suppose not. Let Q be an induced $P_2\cup K_3$ in G with $V\left(Q\right)=\{u_1,u_2,v_1,v_2,v_3\}$ such that $v_1{v}_2{v}_3{v}_1$ is a triangle. We will prove that

$$N\left(u_1\right)=N\left(u_2\right).$$

(5)

Suppose not. Without loss of generality, let $u^{\prime }\in N\left(u_1\right)\setminus N\left(u_2\right)$. If $|\{v_1,v_2,v_3\}\setminus N\left(u^{\prime }\right)| \ge 2$, let $u^{\prime }\nsim v_1$ and $u^{\prime }\nsim v_2$, then $\{u_1,u_2,u^{\prime },v_1,v_2\}$ induces a $P_3\cup P_2$, a contradiction. So, $|N\left(u^{\prime }\right)\cap \{v_1,v_2,v_3\}| \ge 2$, let $u^{\prime }\sim v_1$ and $u^{\prime }\sim v_2$, then $\{u_1,u_2,u^{\prime },v_1,v_2\}$ induces a hammer, a contradiction. Therefore, $N\left(u_1\right)=N\left(u_2\right)$. This proves (5).

Let $N=N\left(\{u_1,u_2\}\right)$ and $M=M\left(\{u_1,u_2\}\right)$. By (5), we have that $\{u_1,u_2\}$ is complete to N, which implies that $\omega \left(G\right[N\left]\right)\le \omega \left(G\right)-2$. Since G is $(P_3\cup P_2)$-free, it follows that $G\left[M\right]$ is $P_3$-free, and thus $\chi \left(G\right[M\left]\right)\le \omega \left(G\right)$. Now, $\chi \left(G\right)\le \chi \left(G\left[N\right]\right)+\chi \left(G[M\cup \{u_1,u_2\}]\right)\le f(\omega \left(G\right)-2)+\omega \left(G\right)\le {(\omega \left(G\right)-2)}^2+\omega \left(G\right)\le {\omega }^2\left(G\right)$ as $\omega \left(G\right)\ge 3$, a contradiction.

This proves Proposition 5. □

Proof of Theorem 4.

By Proposition 5, we have that G is $(P_2\cup K_3)$-free. Let $C=\{v_1,v_2,\cdots ,v_{\omega }\}$ be a maximum clique in G. We divide $V\left(G\right)\setminus N\left[v_1\right]$ as follows:

$$A_2=\{v\in V\left(G\right)\setminus N\left[v_1\right]|v\dotplus v_2\},$$

$$A_i=\{v\in V\left(G\right)\setminus N\left[v_1\right]|v\dotplus v_i,v\notin {\cup }_{j=2}^{i-1}{A}_j,3\le i\le \omega \}$$

For $2\le i\le \omega$, since $A_i$ is anticomplete to $\{v_1,v_i\}$, we have that $G\left[A_i\right]$ is $P_3$-free. Consequently, $G\left[A_i\right]$ is $K_3$-free as G is $(P_2\cup K_3)$-free, which implies that each component of $G\left[A_i\right]$ is a vertex or an edge. So, $\chi \left(G\left[{\cup }_{i=2}^{\omega }{A}_i\right]\right)\le 2(\omega \left(G\right)-1)$.

Let $B=V\left(G\right)\setminus ({\cup }_{i=2}^{\omega }{A}_i\cup N\left[v_1\right])$. By the definition of $A_i$, we have that B is complete to $C\setminus \left\{v_1\right\}$. So, B is independent. Now, $\chi \left(G\right)\le \chi \left(G\left[N\right]\right)+\chi \left(G\left[{\cup }_{i=2}^{\omega }{A}_i\right]\right)+\chi \left(G\left[B\right]\right)\le f(\omega \left(G\right)-1)+2(\omega \left(G\right)-1)+1\le {(\omega \left(G\right)-1)}^2+2\omega \left(G\right)-1={\omega }^2\left(G\right)$, a contradiction.

This proves Theorem 4. □

Actually, by the proof above, we have the following proposition.

Proposition 6.

$\chi \left(F\right)\le {\omega }^2\left(F\right)$ if F is a $(P_3\cup P_2,P_2\cup K_3)$-free graph.

4. (${\mathit{P}}_{\mathbf{3}}\cup {\mathit{P}}_{\mathbf{2}},{\mathit{C}}_{\mathbf{5}}$)-Free Graphs

In this section, we consider ($P_3\cup P_2,C_5$)-free graphs. Let $f\left(x\right)=\frac{3x^2+x}{2}$. We may always assume that G is a ($P_3\cup P_2,C_5$)-free graph, such that $\chi \left(G^{\prime }\right)\le f\left(\omega \left(G^{\prime }\right)\right)$ for every induced subgraph $G^{\prime }$ of G different from G, and $\chi \left(G\right)>f\left(\omega \right(G\left)\right)$. By Lemma 2, we may assume that $\omega \left(G\right)\ge 3$.

Proof of Theorem 5.

Let $v\in V\left(G\right)$, $\omega \left(G\right)=\omega$ and $A_i=\{u\in N\left(v\right)|\omega \left(G\left[M_{N^{\ge 2}\left(v\right)}\left(u\right)\right]\right)=i\}$, where $i=0,1,2,\cdots ,\omega$. Let $A^{\prime }={\cup }_{j=3}^{\omega }{A}_j$. We will prove that

$$A^{\prime } \mathrm{is} \mathrm{a} \mathrm{clique}.$$

(6)

Suppose $A^{\prime }$ has two nonadjacent vertices, $v_1$ and $v_2$. Let $H_i$ be a component of $G\left[M_{N^{\ge 2}\left(v\right)}\left(v_i\right)\right]$ with $\omega \left(H_i\right)=\omega \left(G\left[M_{N^{\ge 2}\left(v\right)}\left(v_i\right)\right]\right)$, for $i\in \{1,2\}$. By the definition of $A^{\prime }$, we have that $\omega \left(H_1\right)\ge 3$ and $\omega \left(H_2\right)\ge 3$. For $i\in \{1,2\}$, let $Q_i$ be a triangle in $H_i$ with $V\left(Q_i\right)=\{x_i,y_i,z_i\}$.

If $|\{x_2,y_2,z_2\}\setminus N\left(v_1\right)| \ge 2$, let $v_1\nsim x_2$ and $v_1\nsim y_2$, then $\{v_1,v,v_2,x_2,y_2\}$ induces a $P_3\cup P_2$, a contradiction. So, $|N\left(v_1\right)\cap \{x_2,y_2,z_2\}| \ge 2$ and, by symmetry, we may assume that $v_1\sim x_2$ and $v_1\sim y_2$. Similarly, we may suppose that $v_2\sim x_1$ and $v_2\sim y_1$. To forbid an induced $P_3\cup P_2$ on $\{v,v_1,x_2,x_1,y_1\}$, we have that $x_2\sim x_1$ or $x_2\sim y_1$. But now, $\{v,v_1,x_2,x_1,v_2\}$ or $\{v,v_1,x_2,y_1,v_2\}$ induces a $C_5$, a contradiction. So, $A^{\prime }$ is a clique. This proves (6).

Suppose $A_0\cup A_1\cup A_2=\varnothing$. Then, $N\left(v\right)=A^{\prime }$ and $|A^{\prime }| \le \omega -1$. Let $v^{\prime }\in A^{\prime }$. Then, $G[M\left(v^{\prime }\right)\cap N^{\ge 2}\left(v\right)]$ is $P_3$-free as G is $(P_3\cup P_2)$-free, and $\omega \left(G[N\left(v^{\prime }\right)\cap N^{\ge 2}\left(v\right)]\right)\le \omega -1$. So, $\chi \left(G\right)\le \chi \left(G\left[N\left(v\right)\right]\right)+\chi \left(G[M\left(v^{\prime }\right)\cap N^{\ge 2}\left(v\right)]\right)+\chi \left(G[N\left(v^{\prime }\right)\cap N^{\ge 2}\left(v\right)]\right)\le \omega -1+\omega +f(\omega -1)=f(\omega -1)+2\omega -1\le f\left(\omega \right)$, a contradiction.

Therefore, we suppose $A_0\cup A_1\cup A_2\ne \varnothing$. Let C be a maximum clique in $G[A_0\cup A_1\cup A_2]$ with $C=\{t_1,t_2,\cdots ,t_{{\omega }_0}\}$. Let $I_i=C\cap A_i$ for $i\in \{0,1,2\}$. $D=\{u\in N^2\left(v\right)|u$ is complete to C}. Let $B_0=\varnothing$ and $B_i=M_{N^2\left(v\right)\setminus D}\left(t_i\right)\setminus {\cup }_{j=0}^{i-1}{B}_j$.

For $i\in \{1,2,\cdots ,{\omega }_0\}$, if $i\in I_0$, then $B_i=\varnothing$ as $A_0$ is complete to $N^2\left(v\right)$. If $i\in I_1$, then $B_i$ is independent by the definition of $A_1$. That is to say, if $i\in I_0\cup I_2$, then $\chi \left(G\left[B_i\right]\right)\le 1$. Suppose $i\in I_3$. Since G is $(P_3\cup P_2)$-free and $v{t}_i$ is an edge, it follows that $G\left[B_i\right]$ is $P_3$-free, and thus $G\left[B_i\right]$ is a union of cliques. By the definition of $A_2$, we have that $\chi \left(G\left[B_i\right]\right)\le 2$. Therefore, $\chi \left(G[N^2\left(v\right)\setminus D]\right)\le 2{\omega }_0$.

Since $G\left[N^{\ge 3}\left(v\right)\right]$ is $P_3$-free, we have that $\chi \left(G\left[N^{\ge 3}\left(v\right)\right]\right)\le \omega$. By (6), we see that $\chi \left(G[A^{\prime }\cup N^{\ge 3}\left(v\right)]\right)\le \omega$. Now, $\chi \left(G\right)\le \chi \left(G\left[N\left(v\right)\right]\right)+\chi \left(G\left[N^2\left(v\right)\right]\right)+\chi \left(G\left[N^{\ge 3}\left(v\right)\right]\right)\le \chi \left(G[A_0\cup A_1\cup A_2]\right)+\chi \left(G\left[A^{\prime }\right]\right)+\chi \left(G\left[D\right]\right)+\chi \left(G[N^2\left(v\right)\setminus D]\right)+\chi \left(G\left[N^{\ge 3}\left(v\right)\right]\right)\le f\left({\omega }_0\right)+f(\omega -{\omega }_0)+2{\omega }_0+\omega \le f\left({\omega }_0\right)+f(\omega -{\omega }_0)+3\omega -2\le f\left(1\right)+f(\omega -1)+3\omega -2\le f\left(\omega \right)$, a contradiction.

This proves Theorem 5. □

5. (${\mathit{P}}_{\mathbf{3}}\cup {\mathit{P}}_{\mathbf{2}},{\mathit{K}}_{\mathbf{4}}$)-Free Graphs

In this section, we consider ($P_3\cup P_2,K_4$)-free graphs. By Lemma 2, we may assume that G contains a triangle. Let G be a ($P_3\cup P_2,K_4$)-free graph; we will complete the proof of Theorem 6 by the two following propositions.

Proposition 7.

If G contains an induced $2K_3$, then $\chi \left(G\right)\le 6$.

Proof. 

Let Q be an induced $2K_3$ in G with $V\left(Q\right)=\{v_1,v_2,v_3,u_1,u_2,u_3\}$ such that $C=v_1{v}_2{v}_3{v}_1$ is a triangle. For a subset $S\subseteq \{1,2,3\}$, we define $N_S=\left\{v\right|v\in N\left(C\right),$ and $v_i\sim v$ if and only if $i\in S\}$. Note that $N\left(C\right)=N_{\left\{1\right\}}\cup N_{\left\{2\right\}}\cup N_{\left\{3\right\}}\cup N_{\{1,2\}}\cup N_{\{1,3\}}\cup N_{\{2,3\}}$, as G is $K_4$-free.

Suppose $N_{\left\{1\right\}}\ne \varnothing$. Let $v^{\prime }\in N_{\left\{1\right\}}$. If $|\{u_1,u_2,u_3\}\setminus N\left(v^{\prime }\right)| \ge 2$, let $u_1\nsim v^{\prime }$ and $u_2\nsim v^{\prime }$, then $\{v_1,v_2,v^{\prime },u_1,u_2\}$ induces a $P_3\cup P_2$, a contradiction. So, $|N\left(v^{\prime }\right)\cap \{u_1,u_2,u_3\}| \ge 2$, which implies that $|N\left(v^{\prime }\right)\cap \{u_1,u_2,u_3\}| =2$, as G is $K_4$-free. By symmetry, we may assume that $v^{\prime }\sim u_1$, $v^{\prime }\sim u_2$ and $v^{\prime }\nsim u_3$. Now, $\{v^{\prime },u_2,u_3,v_2,v_3\}$ induces a $P_3\cup P_2$, a contradiction. Therefore, $N_{\left\{1\right\}}=\varnothing$ and, by symmetry, $N_{\left\{2\right\}}=N_{\left\{3\right\}}=\varnothing$.

Since G is $K_4$-free, it follows that $N_{\{1,2\}}$, $N_{\{1,3\}}$ and $N_{\{2,3\}}$ are all independent. Moreover, $M\left(C\right)$ is $P_3$-free, as G is $(P_3\cup P_2)$-free, and thus $\chi \left(G\right[M\left(C\right)\left]\right)\le 3$, as G is $K_4$-free. Therefore, $\chi \left(G\right)\le \chi \left(G\right[N\left(C\right)\left]\right)+\chi \left(G\right[M\left(C\right)\left]\right)\le 3+3=6$. This proves Proposition 7. □

Proposition 8.

If G is $2K_3$-free and contains an induced $P_2\cup K_3$, then $\chi \left(G\right)\le 6$.

Proof. 

Let Q be an induced $P_2\cup K_3$ in G with $V\left(Q\right)=\{v_1,v_2,v_3,u_1,u_2\}$, such that $C=v_1{v}_2{v}_3{v}_1$ is a triangle. For a subset $S\subseteq \{1,2,3\}$, we define $N_S=\left\{v\right|v\in N\left(\left\{C\right\}\right),$ and $v_i\sim v$ if and only if $i\in S\}$. Note that $N\left(C\right)=N_{\left\{1\right\}}\cup N_{\left\{2\right\}}\cup N_{\left\{3\right\}}\cup N_{\{1,2\}}\cup N_{\{1,3\}}\cup N_{\{2,3\}}$ as G is $K_4$-free.

Let $v^{\prime }\in N_{\left\{1\right\}}$. If $v^{\prime }$ is anticomplete to $\{u_1,u_2\}$, then $\{v^{\prime },v_1,v_2,u_1,u_2\}$ induces a $P_3\cup P_2$, a contradiction. If $v^{\prime }$ is adjacent to exactly one element of $\{u_1,u_2\}$, say $u_1$, then $\{u_1,u_2,v^{\prime },v_2,v_3\}$ induces a $P_3\cup P_2$, a contradiction. So, $v^{\prime }$ is complete to $\{u_1,u_2\}$, and thus $N_{\left\{1\right\}}$ is complete to $\{u_1,u_2\}$. By symmetry, $N_{\left\{1\right\}}\cup N_{\left\{2\right\}}\cup N_{\left\{3\right\}}$ is complete to $\{u_1,u_2\}$. Since G is $K_4$-free, we have that $N_{\left\{1\right\}}\cup N_{\left\{2\right\}}\cup N_{\left\{3\right\}}$ is independent.

Since G is $K_4$-free, it follows that $N_{\{1,2\}}$, $N_{\{1,3\}}$ and $N_{\{2,3\}}$ are all independent. Moreover, $M\left(C\right)$ is $(P_3,K_3)$-free as G is $(P_3\cup P_2,2K_3)$-free, and thus $\chi \left(G\right[M\left(C\right)\left]\right)\le 2$. Therefore, $\chi \left(G\right)\le \chi \left(G\right[N\left(C\right)\left]\right)+\chi \left(G\right[M\left(C\right)\left]\right)\le 1+3+2=6$. This proves Proposition 8. □

Proof of Theorem 6.

By Propositions 7 and 8, we may assume that G is $(P_2\cup K_3)$-free. By Proposition 6, we have that $\chi \left(G\right)\le {\omega }^2\left(G\right)\le 9$. This proves Theorem 6. □