Robust Design Problem for Multi-Source Multi-Sink Flow Networks Based on Genetic Algorithm Approach

Abstract

Robust design problems in flow networks involve determining the optimal capacity assignments that enable the network to operate effectively even in the case of events’ occurrence such as arcs or nodes’ failures. Multi-source multi-sink flow networks (MMSFNs) are frequent in many real-life systems such as computer and telecommunication, logistics and supply-chain, and urban traffic. Although numerous studies on the design of MMSFNs have been conducted, the robust design problem for multi-source multi-sink stochastic-flow networks (MMSFNs) remains unexplored. To contribute to this field, this study addresses the robust design problem for MMSFNs using an approach of two steps. First, the problem is mathematically formulated as an optimization problem and second, a sub-optimal solution is proposed based on a genetic algorithm (GA) involving two components. The first component, an outer genetic algorithm, is employed to search the optimal capacity assigned to the network components with minimum sum. The second component, an inner genetic algorithm, is used to find the optimal flow vectors that maximize the system’s reliability. Through extensive experimentation on three different networks with different topologies, the proposed solution has been found to be efficient.

1. Introduction

Multi-source multi-sink stochastic-flow networks (MMSFNs) play a vital role in real-life systems, such as telecommunication, computer, logistics, supply-chain, and transportation networks. The optimization of such networks has been a popular topic for applied research for the last few years. The main concept behind these kinds of networks is related to optimizing both the network capacity and reliability under several constraints such as budget. As an example, Hassan [1] presented a strategy to maximize the reliability of the capacity vector for MMSFNs, considering an assignment budget. The strategy was divided into two parts: the first part searches for the preferable components that can be specified in the network with minimum cost, while the second part searches for the flow arc with maximum reliability of the capacity arc for the assigned components. Hassan [2] solved the problem of system reliability optimization for MMSFNs, subject to transmission budget constraints, by utilizing genetic algorithms to achieve maximum system reliability through obtaining the best optimal set of lower boundary points. Forghani-elahabad and Kagan [3] presented an algorithm to calculate the exact value of reliability in terms of minimal number of paths in MMSFNs. Network reliability is defined as the probability that a gathering of sinks is fed by a gathering of sources [4]. It refers to the ability of a network to fulfil its purpose within the specified timeframe, despite environmental factors, as determined by the connection between a source and a target [5].

Hamid et al. [6] employed a genetic algorithm (GA) to assign optimal capacities with minimum total capacities and maximum reliability. The authors presented a GA to optimize the reliability of MMSFN systems while solving flow allocation problems [7]. Liu et al. [8] used the GA to find the optimal allocation pattern (vector and node) by the implementation of the equations in the algorithm. The formulas sum up the flow quantity in each minimal pass when the node or arc belongs to this minimal pass. Chen [9] introduced an algorithm to achieve the optimal double-resource assignment for the robust design problem in multi-state computer networks. Atzori and Raccis [10] used a genetic algorithm to assign capacity for multicast services.

From the previous selected studies, it can be noticed that the concept of robustness was not considered when solving the MMSFN problem. For this reason, the current study will concentrate on solving these kinds of problems under constraints and robustness considerations.

Robust Design is defined as a powerful mechanism for improving the reliability of a system at a low cost in a short time [11,12]. It is a process used to find the best configuration for a product design in order to fulfil the end-user’s needs while considering feasibility requirements [13,14]. Robust Design (RD) is defined as an engineering approach that concentrates on the development/improvement of new/existing products (physical products or services), processes, and specific equipment. The robustness of a design refers to the insensitivity to different disturbances and variations coming from the surrounding environment [15]. Robust design, based on the concept of building quality into products or processes, is considered one of the most important systems engineering design concepts for improving quality and the optimization process. In this direction, Cho and Shin [16] presented new robust design empirical and optimization models for time-oriented data by developing a set of methods following three separate phases: modeling, estimation, and optimization.

The robust design problem in a capacitated flow network aims to achieve the minimum capacity allocated to each arc so that the network continues surviving even under the arc’s failure and external disturbances that may affect its operation [17]. Hassan and Abdou [16] conducted a study to evaluate the MMSFNs’ reliability under time constraints. The studies by [18,19] solved the robust design problem for single and two-commodity flow networks with node failure by using a genetic algorithm. Chen and Lin [20] proposed a solution to find feasible flows that meet flow requirements while minimizing the maximum occurring cost among all demand realizations. López-Prado [21] defined the robustness not only in terms of the algorithm’s ability to supply “good” solutions to problem instances of different sizes and numerical characteristics but also in terms of its ability to keep working well even when constraints are added or removed. A successful robust design should ensure a compromise between feasibility and optimality.

Reliability evaluation is the process of determining whether an existing system has achieved a particular level of operational reliability. For example, the reliability evaluation of electric power systems is a fundamental and vital problem in the planning, design, and operation of power systems. The reliability assessment in a conventional power system is the probability that it implements its functions properly, without any failure within a stipulated period of time, when it is subject to normal operating conditions [22]. In transport networks, reliability is a useful tool to represent its operational goodness [23]. Network reliability is important to measure the degree of stability and quality of infrastructure assembly of a network [24].

In order to carefully cope with the problems usually faced during the design phase of a network, this study’s main contributions are the formulation of the robust design problem for MMSFNs and its sub-optimal solution using efficient mathematical tools and proposing suitable algorithms. The solution of the problem is built around the concept of robustness defined as the ability of a network to operate even under uncertainties and failures. In addition, an approach based on genetic algorithms (GAs) is developed to solve the problem in MMSFNs by minimizing the sum of arcs capacities and searching for the best set of flow vectors that check the conditions and achieve maximum reliability. The proposed approach is illustrated through three networks having different topologies to show its efficiency. To the best of the authors’ knowledge, this study is the first that considers the concept of robustness in the design problem of MMSFNs.

The remaining parts of this paper are organized as follows: in Section 2, materials and methods including the structural analysis, problem formulation, the proposed approach for solving the problem, and the whole algorithm are presented in Section 2. The results and discussion are provided in Section 3. Finally, Section 4 concludes the paper.

2. Materials and Methods

2.1. Notations

• Network notations:

np	No. of paths
nc	No. of arcs
v	No. of nodes
σ	No. of sources
θ	No. of sinks
A	The set of arcs {a_b│1 ≤ b ≤ nc}
S	The set of source node {s_1,s_2,…,s_σ}
T	The set of sink node {t_1,t_2,…,t_θ}
MP	Minimal path
MPi, j, k	The kth minimal path from source i to sink j
m	No. of resources.
sdw,j	The demand for resource w at sink node tj
DD	The demand DD = {sdw,jǀ1 ≤ w ≤ m, 1≤ j ≤ θ}
srw,i	The maximum quantity of resource w that source node si can supply
RR	The resource RR = {srw,iǀ1≤ w ≤ m, 1 ≤ i ≤ σ}
Mi	Maximum capacity of an arc i
F	Flow vector defined as F = (f_1,1,1,1,f_1,1,2,1 …, f_(i,j,k_(i,j,) 1), …, f_(i,j,k_(i,j),m), …,f_(σ,θ,k_(σ,θ),m)), where f_(i,j,k,w) represents the flow quantity of resource w on MP_(i,j,k)
NF	Length of the flow vector, NF = np × m
RS	The system reliability

• Parameters of the outer GA:

NP1	Number of chromosomes
NG1	Number of genes equals to nc
MG1	The maximum number of generations
Cr1	The crossover rate
Mu1	The mutation rate

• Parameters of the inner GA:

NP2	Number of chromosomes
NG2	Number of genes equals to NF
MG2	The maximum number of generations
Cr2	The crossover rate
Mu2	The mutation rate
X	Capacity vector, X = (x_1,x_2,…,x_neq)
RX	The reliability of the capacity vectors

2.2. Assumptions

• The flow conservation law must apply to the flow network.
• The arcs have capacities that are statistically independent.
• The capacity of an arc is an integer-valued random variable, which takes values 0 < 1 < 2 <…< Me according to a given distribution.
• The flow along a path does not exceed its maximum capacity of that path.

2.3. The Robust Design Problem for MMSFNs: Definitions

The analysis of a network structure is important to assign the optimal capacity to network edges to guarantee that the network will continue surviving even under edges’ failures. In the following subsections, the progressive steps for getting a robust design for MMSFNs as well as the main concepts used during the design will be presented.

• Coverage set

Suppose that ${\mathsf{\Gamma }}_i=\{{MP}_{i,j,k}|{a_i\in MP}_{i,j,k}\}\mathrm{and}{\mathsf{\Gamma }}_j=\{{MP}_{i,j,l}|{a_j\in MP}_{i,j,l}\}$, the arc $a_j$ belongs to the coverage set $Q_i$ of $a_i$ if and only if ${\mathsf{\Gamma }}_j\subseteq {\mathsf{\Gamma }}_i$, [15].

• Structural impact

The structural impact (${\mathbb{S}}_i$) for $a_i$ is given by:

$${\mathbb{S}}_i=\frac{‖Q_i‖}{nc}$$

(1)

where${ Q}_i=\{{a_j|\mathsf{\Gamma }}_j\subseteq {\mathsf{\Gamma }}_i\}$. The edge $a_i$ has the strongest impact if ${\mathbb{S}}_i$ = 1.

• Critical edge

The arc $a_i$ is said to be critical if ${\mathbb{S}}_i$ = 1. The network reliability $R_s$ is zero if and only if $a_i$ has zero capacity [15].

• The capacity assignment

In a single-source single-sink network, the maximum capacity M_i of $a_i$ ranges from 0 to the demand value. However, in MMSFNs, there are multiple demands requested by the sinks. As a result, the following expression is proposed here to set $M_i$ values.

Let ${\mathcal{E}}_i=\sum \{{\mathrm{s}\mathrm{d}}_{\mathrm{w},\mathrm{j}}|a_i\in {MP}_{i,j}\}$, then $0\le M_i\le {\mathcal{E}}_i+\delta$, $\delta \in \left[0,\mathcal{N}\right],\mathcal{N}$ is a positive integer.

If $a_i$ is a critical edge, then $M_i$ should not be less than ${\mathcal{E}}_i$.

• Probabilities for each edge

The probability for the current capacity $\gamma$ ($0\le \gamma \le M_i$) for $a_i$, $\mathrm{Pr}\{\mathsf{\gamma }\}$:

$$\mathrm{P}\mathrm{r}\left\{\mathsf{\gamma }\right\}=\left(\genfrac{}{}{0pt}{}{M_i}{\gamma }\right){\mathrm{r}}_{\mathrm{i}}^{\mathsf{\gamma }}{\left(1-r_i\right)}^{M_i-\mathsf{\gamma }}$$

(2)

where $r_i$ is the probability (availability) of $a_i$ [15].

2.4. MMSFN Problem Formulation

The problem is divided into two subproblems, as detailed in the next subsections. The first subproblem is to determine the optimal capacities to be assigned to the network’s arcs. The second one is to find the optimal feasible solutions for the flow vector to evaluate the system’s reliability.

2.4.1. First Subproblem

Let us consider $M=(M_1,M_2,\dots ,M_{nc})$ as assigned capacities to the set of arcs $(a_1,a_2,\dots ,a_{nc})$. The mathematical formulation of the subproblem is provided as follows:

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} \mathcal{S}$$

(3)

$$\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} R_S$$

(4)

where $\mathcal{S}={\sum }_i^{nc}{M}_i$ refers to the sum of assigned capacities and R_s is the corresponding system reliability.

2.4.2. Second Subproblem

Searching the flow vectors that succeed to achieve Equations (5)–(7) (discussed in, [1,2,7,8]).

$$\sum _{\mathrm{i}=1}^{\mathsf{\sigma }}\sum _{\mathrm{k}=1}^{{\mathrm{k}}_{\mathrm{i},\mathrm{j}}}{\mathrm{f}}_{\mathrm{i},\mathrm{j},\mathrm{k},\mathrm{w}}={\mathrm{s}\mathrm{d}}_{\mathrm{w},\mathrm{j}},\mathrm{w}=1,\dots ,\mathrm{m};\mathrm{j}=1,\dots ,\mathsf{\theta }$$

(5)

$$\sum _{\mathrm{j}=1}^{\mathsf{\theta }}\sum _{\mathrm{k}=1}^{{\mathrm{k}}_{\mathrm{i},\mathrm{j}}}{\mathrm{f}}_{\mathrm{i},\mathrm{j},\mathrm{k},\mathrm{w}}\le {\mathrm{s}\mathrm{r}}_{\mathrm{w},\mathrm{i}},\mathrm{w}=1,\dots ,\mathrm{m};\mathrm{i}=1,\dots ,\mathsf{\sigma }$$

(6)

$${\mathrm{x}}_{\mathrm{l}}\le {\mathrm{M}}_{\mathrm{l}}\hspace{1em}\hspace{1em}\mathrm{l}=1,\dots ,\mathrm{n}\mathrm{c}$$

(7)

where,

$$x_l=\sum _{\mathrm{i}=1}^{\mathsf{\sigma }}\sum _{\mathrm{j}=1}^{\mathsf{\theta }}\sum _{\mathrm{k}=1}^{{\mathrm{k}}_{\mathrm{i},\mathrm{j}}}\sum _{\mathrm{w}=1}^{\mathrm{m}}\left\{{\mathrm{f}}_{\mathrm{i},\mathrm{j},\mathrm{k},\mathrm{w}}|{\mathrm{a}}_l\mathsf{ϵ}{\mathrm{M}\mathrm{P}}_{\mathrm{i},\mathrm{j},\mathrm{k}}\right\}$$

(8)

The reliability of the capacity vector is given by:

$$R_X=\prod _{\mathrm{l}=1}^{\mathrm{n}\mathrm{c}}\mathrm{P}\mathrm{r}\{\mathrm{x}\ge x_l\}$$

(9)

2.5. The Proposed Approach

The proposed approach to solve the design problem is based on a two genetic algorithms (GAs) approach. The first GA (outer) is used to assign the optimal capacities to the arcs and the second GA (inner) is employed to search for the flow vectors that satisfy the conditions in (3)–(5) while maximizing the network reliability. The proposed approach (as required in a GA solution) should include the representation of chromosomes, initial population generation, fitness function, crossover process, and mutation process. Interested readers can refer to [18,25] for details about the GA and its structure, components, and hyperparameters.

2.5.1. The Outer GA

Representation

The representation chromosome is used to characterize each chromosome in the GA. The chromosome M is exemplified by a series of length (nc), where (nc) refers to the number of arcs $(M_{1,}{M}_{2,}\dots ,M_{nc}$).

Initial Population

The initial population is the first step in the genetic algorithm (GA) and consists of a set of random potential solutions. Each solution is symbolized by a chromosome. Typically, this initial population is generated randomly to produce a range of possible solutions [26]. Although random initialization may allow diversification of solutions over the search space, other initialization methods such as pre-defined known solutions can be used.

Fitness Function

The fitness function is the heart of a genetic algorithm. This function makes it possible to evaluate a given individual solution and determine how well it satisfies the optimization criterion that the algorithm is developed for. The sum of the assigned capacities ($\mathcal{S}$) for the ith individual is selected to be the fitness function of this candidate solution, i.e., $fit\left(\mathrm{ɨ}\right)=\mathcal{S}$. To normalize the fitness function for each individual i, the calculated value is divided by the total sum of all fitnesses ($\sum _{i}fit\left(\mathrm{ɨ}\right)$) in the population. The following Algorithm 1 outlines how to calculate the fitness for the ith solution in the population:

Algorithm 1: Fitness evaluation

$fit\left(\mathrm{ɨ}\right)=\mathcal{S}$  $for \mathrm{ɨ}=1:NP1$   $Normalize\_fit\left(\mathrm{ɨ}\right)=fit\left(\mathrm{ɨ}\right)/\sum _{i}fit\left(\mathrm{ɨ}\right)$  $End for$

Selection

The selection process is one of the important steps in genetic algorithms, used to choose individuals based on their fitness value. Chromosomes with higher fitness values are more likely to be selected for reproduction, while those with lower values have a lower chance of being selected. In other words, the probability of a chromosome being chosen for reproduction is proportional to its fitness value [27].

This study employs the roulette wheel selection method, a widely adopted technique in genetic algorithms to identify promising individuals for the crossover and mutation process (Algorithm 2). In the roulette wheel selection, like all other selection methods, each prospective solution is assigned a solution through the fitness function. This measure of physical fitness determines the likelihood of an individual’s selection. Solutions with superior fitness have a higher probability of being selected, while inferior solutions may still have the opportunity to endure through the selection process. This characteristic may incorporate certain elements that could prove advantageous in subsequent recombination processes. In this study, the roulette wheel mechanism employed for parent selection relies on the cumulative sum of the respective individual’s fitness values.

Algorithm 2: Roulette wheel algorithm

Begin $for j=1 to NP1$  $for i=j to NP1$  $CSum\left(j\right)=CSum\left(j\right)+Normalize\_fit\left(i\right)$     //CSum stands for the commutative sum  $End for i$ $End for j$ Generate number random $\mathrm{ƙ}ϵ\left[0,1\right]$ $for j=1 to NP1$  $if \mathrm{ƙ}>CSum\left(j\right)$  $parent 1=j-1$  $end if$ $end for j$ Generate number random $\mathrm{ƙ}ϵ\left[0,1\right]$ $for j=1 to NP1$  $if \mathrm{ƙ}>CSum\left(j\right)$  $parent 2=j-1$  $end if$ $end for j$ $End$

Crossover

Crossover is a genetic operator that combines two chromosomes to produce a new chromosome. The idea behind crossover is that the new chromosome may inherit the best characteristics from each of the parent chromosomes.

In this study, a one-point crossover operator that randomly chooses one crossover point is used. The process involves copying everything before this point from the first parent and everything after the crossover points from the second parent, as follows [28].

$$M_C^{}=\left[M_{p1}^{}\right(j){]}_{j=1}^{\alpha }+[M_{p2}^{}\left(j\right){]}_{j=\alpha +1}^{nc}{M}_D^{}=\left[M_{p2}^{}\right(j){]}_{j=1}^{\alpha }+[M_{p1}^{}\left(j\right){]}_{j=\alpha +1}^{nc}$$

(10)

where $M_C^{}$ and $M_D^{}$ are the children and $M_{p1}^{}$ and $M_{p2}^{}$ parents selected based on Mc1 value and $\alpha$ is the random cut-point.

Mutation

Mutation represents the final mechanism of evolution, wherein one or multiple genes undergo genetic variation and are subsequently transmitted to offspring for potential adaptation. The genetic algorithm (GA) typically employs a low mutation rate to maintain its functionality since high rates of mutation may lead to a less efficient and more rudimentary random search process (Algorithm 3). The introduction of the mutation operator in the algorithm adds an additional level of randomness, thereby preserving the diversity of the population. The utilization of the genetic algorithm (GA) technique is fruitful in circumventing the emergence of analogous solutions and escalating the likelihood of evading local solutions [29].

Algorithm 3: Genetic algorithm

Generate a random number rm $\in$ [0,1] if rm $\le Mu1$ then  {   for i = 1 to nc, do    $M_D^{}\left(i\right)=\beta , \beta \in \{0,1,\dots ,M_i\}$ .  End for }

2.5.2. The Inner GA

The inner GA is used to locate the optimal set of lower boundary points that maximize the system reliability. The flowing formulation represents the problem of searching for the optimal lower boundaries to maximize the system reliability.

$$\begin{gathered} \mathrm{Find}\mathrm{the}\mathrm{optimal}\mathrm{set}\mathrm{of}\mathrm{X} \\ \mathrm{s}.\mathrm{t}. \\ {R}_S\mathrm{is}\mathrm{maximized} \end{gathered}$$

The equations needed to solve flow vectors searching problem are given in Section 2.4.2.

Representation

The chromosome F is represented by a series of length (NF), where (NF) refers to the number resulting from multiplying a number to the minimal path (np) and the number of resources (m) $(f_{\mathrm{1,1},\mathrm{1,1}},f_{\mathrm{1,1},\mathrm{2,1}}$, …, $f_{i,j,k_{i,j,}1}$, …, $f_{i,j,k_{i,j},m}$, …,$f_{\sigma ,\theta ,k_{\sigma ,\theta },m}$).

Fitness Function

The following Algorithm 4 shows how to calculate the fitness for each solution (i) in the population, where $X^i$ corresponds to $F^i$, and each $F^i$ satisfies Equations (5)–(7) presented in Section 2.4.2.

Algorithm 4: Fitness function

Begin Calculate the fitness value for $X^i{=R}_{X^i}$ $for all elements in the current population$  The $Normalized fitness for each element i=$       $the fitness value for X^i/Sum of all fitness$  $End for$  End

Selection

We used the roulette wheel mechanism in this work to select two parents (Algorithm 5).

Algorithm 5: Roulette wheel algorithm

Begin $for j=1 to NP2$  $for i=j to NP2$ $CSum\left(j\right)=CSum\left(j\right)+Normalize\_fit\left(i\right)$  $End for i$ $End for j$ Generate number random $\mathrm{ƙ} ϵ \left[0,1\right]$ $for j=1 to NP2$  $if \mathrm{ƙ}>CSum\left(j\right)$  $parent 1=j-1$  $end if$ $end for j$ Generate number random $\mathrm{ƙ} ϵ \left[0,1\right]$ $for j=1 to NP2$  $if \mathrm{ƙ}>CSum\left(j\right)$  $parent 2=j-1$  $end if$ $end for j$ $End$

Crossover

One-point crossover is used to generate new offspring for F as follows.

$$F_C^{}=\left[F_{p1}^{}\right(j){]}_{j=1}^{\alpha }+[F_{p2}^{}\left(j\right){]}_{j=\alpha +1}^{NF}{F}_D^{}=\left[F_{p2}^{}\right(j){]}_{j=1}^{\alpha }+[F_{p1}^{}\left(j\right){]}_{j=\alpha +1}^{NF}$$

(11)

where $F_C^{}$ and $F_D^{}$ are the new vectors generated by pairing up $F_{p1}^{}$ and $F_{p2}^{}$ based on Mc2 value and $\alpha$ is the random cut-point.

Mutation

A proposed a mutation mechanism to improve the flow vector F based on Mu2 is provided as follows (Algorithm 6):

Algorithm 6: Mutation mechanism

Generate a random number rm $\in$ [0,1] if rm $\le Mu2$ then  {   for i = 1 to NF, do    $F_C^{}\left(i\right)=\beta , \beta \in \{0,1,I,Minc\}$, $Minc$ the maximum value can be assigned to F(i), [2].  End for }

Evaluating Rs

If $X^1,X^2,\dots ,X^{NP2}$ represent the generated set of capacity vectors that correspond to the flow vectors, then by removing the non-minimal ones in $X^1,X^2,\dots ,X^{NP2}$, we obtain all lower boundary points if the network is cyclic (as discussed in, [30]). Next, if $X^1,X^2,\dots ,X^l$ are all lower boundary points, then the system reliability $R_S$ is calculated by Equation (12).

$$R_S=pr \bigcup _{i=1}^l\left\{Z|Z \ge X^i\right\}$$

(12)

$pr\left\{Z\right\}=pr\left\{z_1\right\}.pr\left\{z_2\right\}.\dots .pr\left\{z_{neq}\right\}$. Then, we use the recursive sum of disjoint products (RSDP) procedure presented in [31].

$$\begin{gathered} \mathrm{when} {\mathrm{T}\mathrm{M}}_1=\mathrm{p}\mathrm{r}\left\{\mathrm{Z}\ge {\mathrm{X}}^1\right\} \\ \mathrm{and} {\mathrm{T}\mathrm{M}}_{\mathrm{i}}=\mathrm{p}\mathrm{r}\left\{\mathrm{Z}\ge {\mathrm{X}}^{\mathrm{i}}\right\}-\mathrm{p}\mathrm{r}\left\{{\bigcup }_{\mathrm{j}=1}^{\mathrm{i}-1}\left\{\mathrm{Z}\ge {\mathrm{X}}^{\mathrm{j},\mathrm{i}}\right\},\hspace{1em}\hspace{1em}\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{i}\ge 2\right. \end{gathered}$$

$$Rs=pr \bigcup _{i=1}^l\left\{Z|Z \ge X^i\right\}=\sum _{i=1}^l{TM}_i$$

(13)

If $Z=\left(z_1,z_2,\dots ,z_e,\dots ,z_{neq}\right)$

$$pr(Z)=\prod _{e=1}^{neq}pr\left(z_e\right)$$

(14)

2.6. The Whole Algorithm of the Proposed Approach

Algorithm 7 shows the whole algorithm of the proposed approach.

Algorithm 7: The whole algorithm of the proposed approach

Start Input the network information, such as minimal path, demand, resources, MG1, NP1, NG1, Cr1, Mu1, MG2, NP2, NG2, Cr2, Mu2. Start outer GAGenerate the initial population randomly with size $NP1$. Evaluate the initial population. While $\mathcal{g}\le MG1$, do While $\mathrm{Ᵽ}\le NP1$, do                 Select two chromosomes.         Generate new offspring after applying crossover and mutation.              $\mathrm{Ᵽ}=\mathrm{Ᵽ}+1$ end do Evaluate the current population. Save the best solution to M. $\mathcal{g}=\mathcal{g}+1$ end do Report the best solution found. Start inner GA     Generate the initial population randomly with size $NP2$.     Evaluate the initial population.     While $\mathcal{g}\le MG2$, do While $\mathrm{Ᵽ}\le NP2$, do     Select two chromosomes.      Generate new offspring after applying crossover and mutation.         $\mathrm{Ᵽ}=\mathrm{Ᵽ}+1$        end do  Evaluate the current population.    Save the best solution to F.  $\mathcal{g}=\mathcal{g}+1$  end do  Report the optimal lowers found.  End inner GA Calculate the system reliability Rs.  End outer GA End

3. Results and Discussion

In the following subsections, the presented approach has been applied to three networks. The valid values of the GA parameters were as follows, MG1 = 100, NP1 = 20, Cr1 = 0.95, Mu1 = 0.05, MG2 = 100, NP2 = 10, 15, and 20. The value of Cr2 = 0.95, and that of Mu2 = 0.05. The proposed approach was implemented in MATLAB 2017a environment with hardware specification that comprises a core i7 Intel processor with 8 GB of RAM.

3.1. Case1: Network with Three Sources and Two Sinks

This network consists of 10 arcs as shown in Figure 1; it has 7 MPs; MP_1,1,1 = {a₁, a₇}, MP_1,1,2 = {a₂, a₉}, MP_1,2,1 = {a₁, a₈}, MP_2,1,1 = {a₃, a₉}, MP_2,2,1 = {a₄, a₁₀}, MP_3,1,1 = {a₅, a₉} and MP_3,2,1 = {a₆, a₁₀}. Where nc = NG1 = 10, NF = NG2 = 21, Resources: R = (r_1,1, r_1,2, r_1,3, r_2,1, r_2,2, r_2,3, r_3,1, r_3,2, r_3,3) = (5, 2, 3, 5, 3, 2, 2, 2, 3). Demand: D = (d_1,1, d_1,2, d_2,1, d_2,2, d_3,1, d_3,2) = (3, 1, 2, 2, 1, 3). Table 1 shows the best minimum $\mathcal{S}$ achieves maximum $R_s$ when NP2 = 10, 15, and 20, and Table 2 clarifies F and $R_X$.

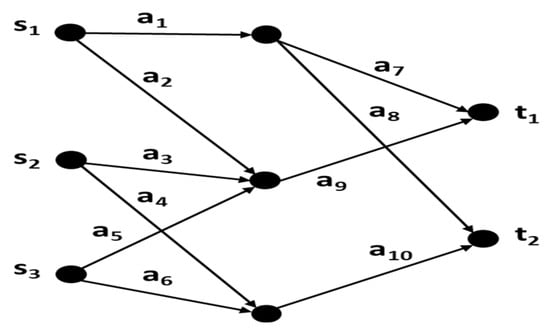
Figure 1. Network with three sources and two sinks.

Table 1. Case1: The best solution found while varying NP2 and its corresponding M, S, and R_s.

NP2	M										$\mathcal{S}$	${\mathit{R}}_{\mathit{S}}$
10	[4	2	4	2	5	4	3	3	5	4]	36	0.973585
15	[4	4	3	4	1	1	5	5	5	4]	36	0.968533
20	[5	3	3	3	3	1	4	5	4	5]	36	0.968419

Table 2. Case1: F and its corresponding R_X for different NP2 (10, 15, and 20).

F																					${\mathit{R}}_{\mathit{X}}$
1	0	0	0	0	1	0	1	1	1	1	0	1	0	1	1	1	0	0	1	1	0.8749
0	1	0	1	0	0	0	1	1	1	1	0	1	0	1	1	0	1	0	1	1	0.8749
1	0	0	1	1	0	0	1	1	1	1	0	0	0	1	0	0	1	1	1	1	0.8745
1	0	0	0	0	0	1	1	1	1	1	1	0	1	1	1	1	0	0	0	1	0.8407
0	0	1	1	1	0	0	1	1	1	1	0	1	0	1	1	0	0	0	1	1	0.8222
1	1	0	1	0	0	0	1	1	0	1	1	0	1	1	1	0	0	1	0	1	0.7904
1	0	0	1	0	0	0	1	1	0	1	0	0	0	1	1	1	1	1	1	1	0.7904
1	1	0	1	1	0	1	0	1	1	0	0	0	1	1	0	0	1	0	1	1	0.7899
1	1	0	1	0	1	0	1	1	0	1	0	0	0	1	1	0	0	1	1	1	0.7594
1	1	0	1	0	0	0	1	1	0	0	0	0	1	1	1	1	1	1	0	1	0.7413
1	1	0	1	0	1	0	1	1	1	0	0	1	1	1	0	1	0	0	0	1	0.9012
1	1	0	0	0	0	0	1	1	1	1	1	1	1	1	1	0	0	0	0	1	0.9012
1	0	0	0	1	0	1	1	1	1	1	1	0	1	1	1	0	0	0	0	1	0.8855
1	0	1	1	0	0	0	1	1	1	1	0	1	1	1	0	1	0	0	0	1	0.8855
1	0	0	1	1	1	1	1	1	1	1	0	0	1	1	0	0	0	0	0	1	0.8832
1	0	1	1	1	0	0	1	1	1	1	0	1	1	1	0	0	0	0	0	1	0.8832
0	0	1	1	1	0	1	1	1	1	1	0	0	1	1	1	0	0	0	0	1	0.8832
0	1	0	1	0	1	1	1	1	1	1	0	0	1	1	1	0	0	0	0	1	0.8120
1	0	1	1	1	0	0	1	1	1	0	0	1	1	1	0	1	0	0	0	1	0.8102
1	0	0	1	1	0	0	1	1	0	1	1	1	1	1	1	0	0	0	0	1	0.8082
1	0	0	1	1	1	0	1	1	1	1	0	1	1	1	0	0	0	0	0	1	0.7976
1	0	0	1	0	1	1	1	1	1	1	0	0	1	1	0	1	0	0	0	1	0.7976
1	1	0	1	1	0	0	1	1	1	0	1	1	1	1	0	0	0	0	0	1	0.7976
1	1	0	0	1	0	0	1	1	1	0	1	1	1	1	1	0	0	0	0	1	0.7958
1	1	0	1	0	0	0	1	1	1	0	1	1	1	1	0	1	0	0	0	1	0.7299
1	0	1	1	1	0	1	1	1	1	1	0	0	1	1	0	0	0	0	0	1	0.8760
1	1	0	0	1	0	1	1	1	1	0	0	0	1	1	1	0	1	0	0	1	0.8760
1	1	0	0	1	0	1	1	1	1	0	1	0	1	1	1	0	0	0	0	1	0.8760
1	1	0	0	0	0	1	1	1	1	0	0	0	1	1	1	1	1	0	0	1	0.8313
1	1	0	1	1	0	1	1	1	1	0	0	0	1	1	0	0	1	0	0	1	0.8313
1	1	1	1	0	0	0	1	1	0	1	0	1	1	1	1	0	0	0	0	1	0.8313
1	1	0	1	1	0	0	1	1	1	0	0	1	1	1	0	0	1	0	0	1	0.8301
0	1	1	1	0	0	0	1	1	1	1	0	1	1	1	1	0	0	0	0	1	0.8301
1	0	1	0	1	0	1	1	1	1	1	0	0	1	1	1	0	0	0	0	1	0.8301
1	0	1	1	1	0	0	1	1	1	0	0	1	1	1	0	1	0	0	0	1	0.8292
1	1	0	1	0	1	1	1	1	1	1	0	0	1	1	0	0	0	0	0	1	0.8292
1	1	0	1	1	0	0	1	1	1	0	1	1	1	1	0	0	0	0	0	1	0.8222
1	1	0	1	0	0	0	1	1	1	0	0	1	1	1	0	1	1	0	0	1	0.8222
0	1	1	1	1	0	0	1	1	1	0	0	1	1	1	1	0	0	0	0	1	0.8222
1	1	0	1	0	1	1	1	1	0	1	0	0	1	1	1	0	0	0	0	1	0.8222
1	1	1	0	1	0	0	1	1	1	0	0	1	1	1	1	0	0	0	0	1	0.8210
1	1	1	0	1	0	0	1	1	1	0	0	1	1	1	1	0	0	0	0	1	0.8210
1	1	0	1	0	0	1	1	1	0	0	0	0	1	1	1	1	1	0	0	1	0.8200
1	1	0	0	0	1	1	1	1	1	1	0	0	1	1	1	0	0	0	0	1	0.7834
1	0	1	1	0	0	0	1	1	1	1	0	1	1	1	0	1	0	0	0	1	0.7834

3.2. Case2: Network with Two Sources and Two Sinks

This network consists of 14 arcs as shown in Figure 2, it has 11 MPs; MP_1,1,1 = {a₁, a₅}, MP_1,1,2 = {a₁, a₆, a₉}, MP_1,1,3 = {a₂, a₇, a₉}, MP_1,2,1 = {a₁, a₆, a₁₄}, MP_1,2,2 = {a₂, a₇, a₁₄}, MP_2,1,1 = {a₃, a₇, a₉}, MP_2,1,2 = {a₄, a₈, a₁₃, a₉}, MP_2,2,1 = {a₃, a₇, a₁₄}, MP_2,2,2 = {a₄, a₈, a₁₃, a₁₄}, MP_2,2,3 = {a₄, a₈, a₁₀}, and MP_2,2,4 = {a₄, a₁₁, a₁₂}. Where nc = NG1 = 14, NF = NG2=22, Resources: R = (r_1,1, r_1,2, r_2,1, r_2,2) = (15, 17, 10, 13). Demand: D = (d_1,1, d_1,2, d_2,1, d_2,2) = (7, 8, 5, 8). Table 3 shows the best minimum $\mathcal{S}$ achieves maximum $R_s$ when NP2 = 10, 15, and 20, and Table 4 clarifies F and $R_X$.

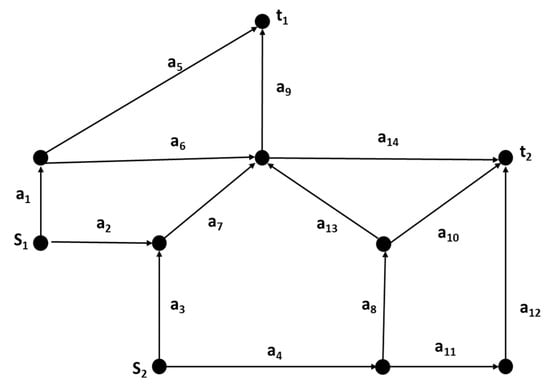
Figure 2. Network with two sources and two sinks.

Table 3. Case2: The best solution found while varying NP2 and its corresponding M, S, and R_s.

NP2	M														$\mathcal{S}$	${\mathit{R}}_{\mathit{S}}$
10	[15	16	4	17	4	18	9	11	14	9	9	19	10	14]	169	0.996641
15	[8	19	17	11	19	10	15	5	20	13	13	8	8	15]	181	0.989280
20	[19	6	18	18	15	7	11	16	13	19	9	4	17	17]	189	0.999984

Table 4. Case2: F and its corresponding R_X for different NP2 (10, 15, and 20).

F																						${\mathit{R}}_{\mathit{X}}$
2	0	1	0	0	2	2	0	1	2	2	1	2	2	0	1	2	2	1	1	2	2	0.9916
1	2	2	2	1	1	2	2	2	1	1	0	2	0	2	0	0	2	1	2	1	1	0.9645
1	1	2	1	1	1	1	1	1	2	1	0	2	2	2	1	2	0	1	2	1	2	0.8583
2	0	1	2	2	1	2	1	2	2	2	0	0	2	0	0	2	2	1	1	1	2	0.8530
2	1	1	0	2	2	1	0	1	2	0	1	2	1	0	1	2	2	2	2	2	1	0.7601
2	1	2	1	1	0	2	1	2	1	1	2	1	1	0	1	2	2	0	2	2	1	0.7536
2	2	2	2	2	0	1	2	2	2	0	1	1	0	0	2	2	1	1	0	2	1	0.6973
0	2	2	2	1	0	2	2	1	2	2	0	2	1	0	2	2	2	1	0	2	0	0.6722
2	1	2	2	0	2	1	1	2	2	2	0	1	0	0	1	2	2	2	2	1	0	0.6591
0	2	2	1	2	0	2	1	1	1	2	0	1	2	1	0	2	2	0	2	2	2	0.6070
1	0	2	0	2	2	2	2	2	1	1	2	1	1	1	1	1	0	0	2	2	2	0.9234
1	1	1	2	2	1	1	2	1	2	2	1	1	0	2	2	2	0	0	2	2	0	0.9210
0	1	2	1	2	1	2	1	1	2	2	1	1	1	1	2	2	0	0	1	2	2	0.9206
1	0	2	0	1	2	2	2	2	0	1	2	2	1	2	2	0	0	0	2	2	2	0.8997
1	1	0	0	2	2	2	0	2	2	2	2	2	0	2	1	0	1	0	2	2	2	0.8997
2	0	0	0	2	2	2	1	2	2	1	2	2	1	1	2	1	1	0	0	2	2	0.8997
2	0	1	1	0	2	1	2	2	2	2	2	2	0	2	2	2	0	0	0	1	2	0.8996
1	0	1	0	2	2	2	2	2	2	1	2	2	1	2	1	0	1	0	0	2	2	0.8943
2	1	0	0	1	0	2	2	2	2	2	2	2	2	1	2	1	0	0	0	2	2	0.8370
1	2	2	0	2	2	1	1	2	1	2	1	0	0	2	2	0	2	1	1	2	1	0.8333
2	2	1	0	1	1	1	2	1	2	2	1	1	1	1	2	2	0	1	0	2	2	0.8331
2	2	1	1	2	0	2	0	2	1	2	0	0	2	2	2	0	2	0	1	2	2	0.8331
1	1	2	2	2	1	2	0	2	2	0	1	2	0	2	2	1	2	0	0	1	2	0.8330
1	0	2	2	2	1	1	0	2	2	1	2	1	0	2	1	1	2	0	1	2	2	0.8263
1	1	2	1	2	2	1	2	1	1	2	1	0	0	2	1	2	2	1	0	1	2	0.5717
1	0	2	2	2	1	1	2	2	0	1	1	1	1	0	2	2	2	2	1	1	1	0.9992
1	1	2	1	2	0	0	2	2	1	1	1	1	2	2	2	2	0	1	2	1	1	0.9957
2	1	2	1	1	1	0	1	1	2	0	0	2	2	1	2	2	1	2	2	2	0	0.9957
2	0	2	0	1	1	2	2	1	2	2	2	0	2	1	1	2	1	1	1	1	1	0.9941
1	1	2	0	2	1	0	2	2	0	2	2	0	1	0	1	2	2	2	2	2	1	0.9906
2	2	0	1	2	1	2	2	0	1	1	0	2	1	2	0	1	2	2	1	1	2	0.9584
2	2	2	2	1	0	0	1	2	2	0	0	2	1	2	2	0	2	2	1	2	0	0.9566
2	2	0	2	2	0	2	2	1	1	1	1	2	0	2	2	0	0	2	2	1	1	0.9526
1	1	2	0	1	1	1	2	1	2	1	2	2	1	0	2	2	1	2	0	2	1	0.9522
1	1	2	0	2	2	2	2	0	2	1	2	1	0	2	0	0	2	2	0	2	2	0.9522
2	1	1	0	0	0	1	2	2	1	2	2	2	2	2	2	1	1	1	0	1	2	0.9229
2	1	2	1	1	1	0	2	2	0	0	2	2	0	2	2	2	1	1	2	1	1	0.9176
2	0	1	1	1	1	0	2	1	1	1	1	2	2	1	2	2	2	2	1	2	0	0.8803
0	2	2	0	2	2	2	2	1	1	1	0	2	1	2	0	2	1	1	2	0	2	0.7910
1	0	1	0	2	1	1	2	0	1	1	2	2	2	2	1	2	2	2	2	1	0	0.7149
1	1	0	2	2	0	1	2	2	1	2	0	2	2	2	2	1	0	0	2	2	1	0.7109
2	1	0	0	1	1	2	2	1	0	2	1	2	2	1	2	2	1	1	1	1	2	0.7105
1	2	2	1	1	1	2	2	2	2	1	1	2	0	0	2	2	0	1	0	1	2	0.7098
2	1	1	1	0	1	2	2	2	2	2	0	2	2	2	2	0	2	0	0	2	0	0.7095
2	0	2	1	2	0	2	2	2	1	1	2	0	2	0	1	0	2	2	2	2	0	0.6072

3.3. Case3: Network with Two Sources and Three Sinks

This network consists of 11 arcs as shown in Figure 3, it has 13 MPs; MP_1,1,1 = {a₁, a₇}, MP_1,1,2 = {a₂, a₅, a₇}, MP_1,2,1 = {a₁, a₈}, MP_1,2,2 = {a₂, a₉}, MP_1,2,3 = {a₂, a₅, a₈}, MP_1,3,1 = {a₂, a₁₀}, MP_2,1,1 = {a₃, a₅, a₇}, MP_2,1,2 = {a₄, a₆, a₅, a₇}, MP_2,2,1 = {a₃, a₉}, MP_2,2,2 = {a₄, a₆, a₉}, MP_2,3,1 = {a₃, a₁₁}, MP_2,3,2 = {a₄, a₆, a₁₀}, and MP_2,3,3 ={a₄, a₁₁}. Where nc = NG1 = 11, NF = NG2 = 26, Resources: R = (r_1,1, r_1,2, r_2,1, r_2,2) = (10, 19, 14, 19). Demand: D = (d_1,1, d_1,2, d_1,3, d_2,1, d_2,2, d_2,3) = (3, 2, 2, 2, 3, 3). Table 5 shows the best minimum $\mathcal{S}$ achieves maximum $R_s$ when NP2 = 10, 15, and 20, and Table 6 clarifies F and$R_X$.

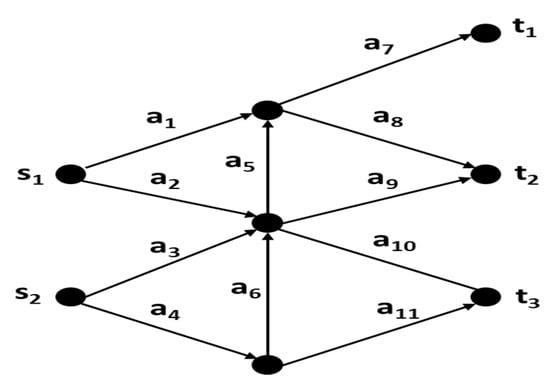
Figure 3. Network with two sources and three sinks.

Table 5. Case3: The best solution found while varying NP2 and its corresponding M, S, and R_s.

NP2	M											$\mathcal{S}$	${\mathit{R}}_{\mathit{S}}$
10	[8	12	14	4	15	13	7	2	14	12	10]	111	0.995669
15	[12	6	12	14	5	9	12	6	12	14	9]	111	0.999923
20	[15	12	12	15	9	4	10	11	14	4	5]	111	0.999403

Table 6. Case3: F and its corresponding R_X for different NP2 (10, 15, and 20).

F																										${\mathit{R}}_{\mathit{X}}$
0	1	1	1	0	1	1	0	0	1	1	0	1	0	1	0	1	1	0	0	0	1	0	1	1	1	0.9595
1	1	1	0	0	0	1	1	1	1	1	1	0	1	1	0	0	1	0	0	0	1	0	0	1	1	0.9595
1	0	1	1	1	0	1	1	0	1	1	1	0	1	1	0	0	1	0	0	1	1	0	1	0	0	0.9573
1	0	1	1	0	0	1	1	0	1	1	1	1	0	0	1	1	0	0	1	0	1	1	0	0	1	0.9573
1	1	1	1	0	1	0	1	1	0	1	1	0	0	1	0	0	1	1	0	0	1	1	1	0	0	0.9573
1	0	1	1	0	1	1	0	1	0	1	1	1	1	0	0	0	1	0	1	1	1	0	0	0	1	0.9212
1	0	1	1	0	1	0	1	1	0	0	1	1	0	0	1	0	1	1	0	1	1	1	1	0	0	0.8851
1	0	1	0	0	0	0	0	1	1	1	1	1	1	0	1	1	1	0	1	1	1	0	1	0	0	0.8851
0	0	1	1	0	1	1	0	1	0	1	1	1	0	1	1	0	1	0	1	1	1	0	1	0	0	0.8851
1	1	0	1	0	0	0	1	1	1	0	1	1	0	1	0	1	1	0	0	1	1	0	0	1	1	0.8851
1	1	0	0	1	0	0	0	0	1	1	1	1	0	1	1	1	1	0	1	1	1	0	1	0	0	0.9999
1	1	0	1	0	1	1	1	0	0	0	1	1	0	1	0	1	0	0	1	0	1	1	1	1	0	0.9998
1	1	1	0	1	1	0	0	0	0	1	1	1	1	0	0	0	1	1	1	0	1	1	0	0	1	0.9962
0	0	1	1	0	1	1	0	0	0	0	1	1	1	1	0	0	1	1	1	1	1	1	1	0	0	0.9962
1	1	0	0	0	0	0	0	0	1	0	1	1	1	1	0	1	1	1	1	0	1	1	0	1	1	0.9962
0	1	1	1	0	0	1	1	1	0	0	1	1	0	1	0	0	1	0	1	1	0	1	1	0	1	0.9962
1	0	1	1	1	0	0	1	0	1	0	1	1	0	0	1	1	0	0	1	1	1	1	1	0	0	0.9962
1	0	1	1	1	1	0	0	0	0	1	0	0	1	1	0	1	1	0	1	0	1	0	1	1	1	0.9960
1	0	1	1	1	1	1	1	0	0	0	0	0	0	1	1	0	0	0	1	1	1	0	1	1	1	0.9039
1	0	1	1	1	0	0	1	0	1	0	1	1	0	0	1	1	1	0	0	1	1	1	0	0	1	0.9038
0	1	1	0	0	0	0	1	0	1	1	1	1	0	1	1	1	0	1	1	0	1	1	1	0	0	0.9038
1	0	1	1	1	1	0	0	0	1	0	1	0	0	1	1	0	1	1	0	0	0	1	1	1	1	0.8988
1	0	1	1	0	1	0	0	0	0	1	0	0	1	1	0	1	1	1	1	0	1	1	1	0	1	0.8988
1	1	0	0	0	1	0	1	0	1	1	0	1	0	1	1	1	0	1	0	1	1	0	1	0	1	0.8988
0	1	1	0	1	1	0	1	1	0	0	0	1	0	1	1	0	1	0	0	0	1	1	1	1	1	0.8007
0	1	1	1	1	1	0	1	0	0	0	1	1	0	1	0	1	0	0	1	1	1	0	0	1	1	0.9994
1	1	1	0	1	1	1	0	0	0	0	1	1	0	0	1	0	1	0	1	1	0	0	1	1	1	0.9994
1	0	0	1	1	1	0	1	0	1	0	0	1	1	1	0	0	0	1	0	0	1	1	1	1	1	0.9988
1	1	1	0	1	0	0	1	0	0	0	1	1	0	0	1	1	1	0	1	0	1	1	0	1	1	0.9988
1	0	1	1	0	1	1	0	0	1	1	0	1	1	0	0	0	0	1	1	0	1	1	1	0	1	0.9988
1	0	1	1	1	0	0	1	0	0	1	0	1	0	0	1	1	1	0	1	1	1	0	1	0	1	0.9988
1	1	1	1	1	0	0	1	0	0	1	0	1	0	0	0	1	1	0	1	0	1	0	1	1	1	0.9988
0	0	1	1	0	0	0	1	1	1	1	0	1	1	1	0	0	1	1	0	0	1	0	1	1	1	0.9982
1	0	0	1	1	1	0	1	0	1	1	0	1	0	1	1	1	0	0	0	0	1	1	1	0	1	0.9606
1	0	1	1	1	1	0	1	1	0	1	1	1	0	0	1	0	0	0	1	0	0	1	1	0	1	0.9600
1	1	1	0	0	0	1	1	0	0	1	0	1	0	0	1	1	1	0	1	1	1	0	1	0	1	0.9600
1	0	1	1	0	0	1	1	0	0	1	1	0	1	1	0	1	1	0	1	0	1	0	1	1	0	0.9600
1	0	0	1	0	0	0	1	1	1	1	1	1	0	1	1	1	0	0	1	1	1	0	0	0	1	0.9600
0	1	1	0	0	0	1	1	1	1	0	1	1	1	1	0	0	0	0	1	0	1	1	0	1	1	0.9600
1	0	1	1	1	1	0	1	1	0	1	0	0	1	1	0	0	0	0	1	1	1	0	1	0	1	0.9600
0	1	1	0	1	1	0	0	0	1	0	1	1	1	1	0	1	0	0	1	1	0	0	1	1	1	0.9227
1	1	0	0	1	1	0	0	1	0	1	0	1	1	1	0	0	1	0	1	0	1	1	1	0	1	0.9227
1	0	1	1	0	0	1	1	0	1	0	1	1	1	0	0	1	1	0	0	0	1	1	1	1	0	0.9227
1	0	1	1	1	1	0	1	0	0	0	0	1	0	0	1	0	1	1	0	1	1	1	1	0	1	0.9227
0	1	1	0	1	1	0	0	1	1	1	0	1	0	1	1	0	1	0	0	0	1	0	1	1	1	0.9227

The main goal of the Robust Design Problem (RDP) for MMSFN is to find the optimal set of capacities assigned to arcs, ensuring network survival even under arc failures, i.e., ${\mathit{R}}_{\mathit{S}}>0$. Initially, we studied a network with three sources and two sinks. The best values for $\mathcal{S}$ and ${\mathit{R}}_{\mathit{S}}$ were 36 and 0.973585, respectively, with NP2(NF) = 10. Next, in a network with two sources and two sinks, the best values for $\mathcal{S}$ and ${\mathit{R}}_{\mathit{S}}$ were found to be, respectively, 169 and 0.996641 with NP2(NF) = 10. Finally, in a network with two sources and three sinks, the best values for $\mathcal{S}$ and ${\mathit{R}}_{\mathit{S}}$ were 111 and 0.999923, respectively, with NP2(NF) = 15. The NP2 for the inner GA (corresponding to NF, number of flow vectors) was selected to be 10, 15, and 20 for all studied cases to find the optimal or near-optimal value for the system reliability with NG2 equal to 100. The number of flow vectors for MMFNs cannot be anticipated. Therefore, we searched for the optimal flows that maximize the system reliability. According to [1,2,7], the obtained maximum value for NF number does not exceed 20 as summarized in Table 7. Furthermore, we follow up the reliability values of capacity vectors ${\mathit{R}}_{\mathit{X}}$ for each example, [1], o identify the best flow strategy with maximum ${\mathit{R}}_{\mathit{X}}$.

Table 7. The number of NF found by [1,2,7].

Approach	Problem	$\mathbf{Maximum} \mathbf{No}. \mathbf{of} \mathbf{N}\mathbf{F}$
[1]	Maximizing reliability of the capacity vector by searching the single optimal flow vector with minimum assignment cost	1
[2]	Optimal system reliability under transmission budget	10
[7]	Optimal system reliability evaluation under DD	9
Proposed approach	Optimal system reliability under maximum capacities (Robust Design Problem)	20

4. Conclusions

This paper presented a structural analysis of MMSFN to discuss and formulate the Robust Design Problem for this type of SFN. Additionally, it successfully solves the RDP for MMSFN using a two-stage GA approach. We divided the problem into two subproblems: first, searching for the optimal capacity assigned to network components with a minimum sum, and second, searching for the optimal lower vectors to achieve the maximum system reliability value. The proposed GA-based approach was applied to a group of networks, and it yielded satisfactory results. No comparisons were made as the RDP for MMSFNs has not been discussed previously.