Multi-Keyword Searchable Identity-Based Proxy Re-Encryption from Lattices

Abstract

To protect the privacy of cloud data, encryption before uploading provides a solution. However, searching for target data in ciphertext takes effort. Therefore, searchable encryption has become an important research topic. On the other hand, since the advancement of quantum computers will lead to the crisis of cracking traditional encryption algorithms, it is necessary to design encryption schemes that can resist quantum attacks. Therefore, we propose a multi-keyword searchable identity-based proxy re-encryption scheme from lattices. In addition to resisting quantum attacks, the proposed scheme uses several cryptographic techniques to improve encryption efficiency. First, identity-based encryption is used to reduce the computation and transmission costs caused by certificates. Second, the proposed scheme uses proxy re-encryption to achieve the purpose of outsourced computing, allowing the proxy server to reduce the computation and transmission costs of the users. Third, the proposed multi-keyword searchable encryption can provide AND and OR operators to increase the flexibility of searchability. Moreover, the access structure of the proposed scheme is not based on a linear secret sharing scheme (LSSS), avoiding the errors caused by an LSSS-based structure in decryption or search results. Finally, we also give formal security proof of the proposed scheme under the decisional learning with errors assumption.

1. Introduction

Encrypting data before uploading to the cloud has become a standard method to protect data privacy. With the advancement of technology, cloud services have become a part of people’s daily lives. Sharing data through the cloud server can reduce the storage cost of the user end, but at the same time, there will be concerns about data leakage. Therefore, to protect the data’s confidentiality, users may encrypt it before uploading it to the cloud server. Based on the convenience of key management, most people use the public key cryptography system to encrypt data. To confirm the correctness of a user’s public key, a certificate of the user’s public key is often required as proof. However, since the management and verification of certificates will lead to more computation and transmission costs, many certificate-less public key cryptosystems have been proposed.

Functional encryption is a type of certificate-less public key encryption. For example, identity-based encryption (IBE), attribute-based encryption (ABE), and subset-predicate encryption (SPE) are functional encryption methods. In 1984, Shamir proposed the first IBE scheme [1]. In his scheme, the data owner can use the receivers’ identities as the encryption keys, thereby saving the management and verification of certificates. In 2005, Sahai and Waters proposed a fuzzy IBE scheme [2]. Since a fuzzy identity can be regarded as an attribute, the scheme of Sahai and Waters is considered the first ABE scheme. In ABE schemes, the data owner can use attributes to encrypt data, so there is no need to use certificates. The concept of SPE was first introduced by Katz et al. [3] in 2017. In SPE schemes, the data owner can select an attribute set to encrypt data, and the receivers can decrypt it if and only if their attributes are subsets of the attribute set of the encrypted data.

Proxy re-encryption (PRE) is used to reduce file-sharing costs. To change the recipient of the ciphertext from Alice to Bob, one may decrypt the ciphertext with Alice’s private key and then encrypt it with Bob’s public key. However, this method is inefficient, and how to directly convert the ciphertext becomes an issue. Therefore, the purpose of PRE is to directly convert the ciphertext without decrypting it. The first PRE scheme was proposed by Blaze et al. in 1998 [4]. In their scheme, a semi-trusted proxy is allowed to transform the ciphertext for Alice into the ciphertext for Bob without changing the content of the message, thereby reducing the computation and transmission costs of sharing files. On the other hand, PRE can be used in combination with functional encryption. For example, the first identity-based PRE scheme was proposed by Green and Ateniese [5] in 2007; the first attribute-based PRE scheme was proposed by Liang et al. in 2009 [6].

Searchable encryption (SE) solves the problem that files cannot be searched after encryption. Although encryption can protect data privacy, searching for encrypted data takes effort. To solve this problem, Song et al. [7] proposed the first SE scheme in 2000, whereas encrypted files are searchable. In 2004, Boneh et al. proposed the first SE scheme with keyword search [8]. In Boneh et al.’s scheme, users can choose a keyword to search for files. In 2007, Hwang and Lee [9] proposed SE that supports multi-keyword search, increasing the flexibility of searchability.

On the other hand, due to the rapid development of quantum computers, some traditional encryption schemes are facing a crisis of being cracked. Due to the special properties of quantum bits, quantum computers can perform parallel operations on large amounts of data. Therefore, quantum computers can use their parallel computing capabilities to solve some traditional hard problems on classical computers. In 1994, Shor proposed a quantum algorithm [10] that can find the prime factors of a large integer. In addition, the discrete logarithm problem, which is generally considered as difficult as the prime factorization problem, is also considered to be at risk of being solved by quantum algorithms. Therefore, encryption schemes based on such mathematical problems suffer from the risk of being cracked.

Lattice-based cryptography has been extensively researched and validated for security on both classical and quantum algorithms. To resist quantum attacks, the National Institute of Standards and Technology (NIST) launched a post-quantum cryptography standards competition. In July 2022, the competition winner was Kyber [11], a lattice-based public-key encryption algorithm. The competition result shows that lattice-based schemes are generally considered to be effective against quantum attacks. Lattice-based cryptography is considered quantum-resistant because it is based on mathematical problems that are difficult for quantum computers to solve. Quantum computers cannot solve the shortest vector problem exponentially faster than classical computers, which means that quantum attacks would not be able to break the encryption schemes based on that problem. The Learning with Errors (LWE) problem is also considered intractable for quantum computers. In addition, no known quantum algorithm can break the Decisional Learning with Errors (D-LWE) problem, which has applications in many fields.

Many lattice-based public-key cryptosystems have been proposed. In 1996, Ajtai [12] proposed a one-way hash function based on the shortest vector problem. In 1997, Goldreich et al., proposed the first public-key cryptosystem based on the closest vector problem. Hoffstein et al. [13] proposed a public key encryption scheme called the Number Theory Research Unit (NTRU) in 1998. Although the security of NTRU is not formally proven, its computation cost is lower than previous schemes. In 2005, Regev [14] proposed the LWE problem, which is at least as hard as the worst case of the shortest independent vectors problem. Since then, most of the lattice-based public-key cryptosystems published after 2005 were based on the LWE problem due to the low computational cost required. Even the Kyber algorithm [11], the winner of the NIST post-quantum competition, is based on the LWE problem.

One of the advantages of the lattice encryption algorithm is that it can provide functional encryption. In 2008, Gentry et al., published an IBE scheme based on LWE. In 2013, Boneh proposed the first lattice-based ABE scheme [15]. In 2014, Singh et al. proposed the first identity-based PRE [16]. In 2019, Liu et al. [17] proposed an ABE protocol for searchable keywords. In 2022, Wang et al. [18] proposed a searchable SPE scheme.

Outsourcing computation reduces the computation and transmission costs of the data sender. In 2019 Zhang et al. [19] proposed a lattice-based SE support outsourcing computation. In their scheme, DO will generate oriented keys and send them to PS. With those keys, PS can prove that DO has authorized it to assist in encryption. With the assistance of PS, DO can save some computation and transmission costs.

Some lattice-based SE schemes [17,20,21,22] use linear secret sharing scheme (LSSS) as the access structure, but using LSSS under the LWE problem may cause problems. Because the Gaussian elimination method used to solve the LSSS problem will generate coefficients that cannot be guaranteed to be small enough, the decryption or search results after running LSSS may be wrong. Therefore, LSSS-based schemes under the LWE problem cannot be realized in practice. To avoid this problem, the proposed scheme uses a tree-based access structure.

1.1. Problem Statements

In summary, to improve the efficiency of cloud services, an encrypted file-sharing scheme should meet the following features:

• The encryption should resist quantum attacks.
• The encrypted file should be searchable. Moreover, the scheme should support multi-keyword to increase the flexibility of searchability.
• To reduce the file-sharing costs of the data owner, the scheme should support PRE.
• The encryption should avoid the cost of using certificates.

Unfortunately, no known scheme can achieve these features simultaneously. Therefore, we propose a scheme to satisfy these features simultaneously.

1.2. Contributions

We proposed a multi-keyword searchable identity-based proxy re-encryption scheme from lattices. To highlight the contributions, the features comparison between the proposed scheme and other schemes is shown in Table 2. The proposed scheme is the first to offer the following properties simultaneously:

• To resist quantum attacks, the security of the proposed scheme is based on the LWE problem from lattices.
• The flexibility of searchability is increased through the proposed multi-keyword search that supports AND and OR operations. The access structure is tree-based rather than LSSS-based, avoiding possible errors in the decryption and search phases.
• KGC only needs to assist users in generating private keys during the registration phase. The burden on the KGC is reduced since it does not involve other phases. Moreover, the risk of KGC being attacked by adversaries through the network can be reduced.
• The proposed scheme supports PRE to reduce file-sharing costs of the data owner. The concept of outsourcing computation is added to the scheme design. As the number of data users increases, the costs required for the data owner remain the same, and the proxy server will handle the increased workload.
• Users’ access rights are verified in both the search phase and the decryption phase to prevent adversaries from illegally accessing files.
• The proposed scheme is identity-based, which avoids the cost of using certificates.

2. Preliminaries

The definitions of lattice, trapdoors, and hardness assumptions are shown here. Furthermore, the access structure, system model, and security model of the proposed scheme are presented here.

2.1. Lattices

Definition 1.

An n-dimensional lattice $\Lambda$ is defined as a set of linear combinations of m linearly independent vectors ${\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_m\in {\mathbb{Z}}^n$.

$$\Lambda =\left\{{\sum }_{i=1}^m{x}_i{\mathbf{a}}_i|x_i\in \mathbb{Z}\right\},$$

where $\{{\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_m\}$ is a basis of $\Lambda$, and the rank of $\Lambda$ is m.

Definition 2.

Given a prime number q, a basis $\mathbf{A}=\{{\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_m\}\in {\mathbb{Z}}_q^{n\times m}$, and a vector $\mathbf{u}\in {\mathbb{Z}}_q^n$.

Three types of lattices are defined as follows:

$$\begin{array}{c}{\Lambda }_q\left(\mathbf{A}\right):=\left\{\mathbf{v}\in {\mathbb{Z}}^m|{\mathbf{A}}^{\top }\mathbf{s}=\mathbf{v}\mathrm{mod}q,\mathbf{s}\in {\mathbb{Z}}^n\right\}\hfill \\ {\Lambda }_q^{\mathbf{u}}\left(\mathbf{A}\right):=\left\{\mathbf{v}\in {\mathbb{Z}}^m|\mathbf{Av}=\mathbf{u}\mathrm{mod}q\right\}\hfill \\ {\Lambda }_q^{\perp }\left(\mathbf{A}\right):=\left\{\mathbf{v}\in {\mathbb{Z}}^m|\mathbf{Av}=0\mathrm{mod}q\right\}\hfill \end{array}$$

2.2. Discrete Gaussians

Definition 3.

Given a Gaussian parameter $\alpha \in {\mathbb{R}}^{+}$, a vector $\mathbf{c}\in {\mathbb{R}}^m$, and $\mathit{L}\in {\mathbb{Z}}^m$.

• The discrete Gaussian distribution over $\mathit{L}$ is

  $$\forall x\in L,{\mathcal{D}}_{L,\alpha ,c}\left(x\right)=\frac{{\rho }_{\alpha ,c}\left(x\right)}{{\rho }_{\alpha ,c}\left(L\right)}.$$
• The sum of all ${\rho }_{\alpha ,\mathbf{c}}\left(x\right)$ is

  $${\rho }_{\alpha ,c}\left(L\right)={\sum }_{x\in L}{\rho }_{\alpha ,c}\left(x\right).$$
• The Gaussian function on ${\mathbb{R}}^m$ is

  $${\rho }_{\alpha ,c}\left(x\right)=\exp (-\pi \frac{{\parallel x-c\parallel }^2}{{\alpha }^2}).$$

2.3. Inhomogeneous Short Integer Solution (ISIS)

Definition 4 (ISIS problem).

Given a prime q, a random matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$, a target vector $\mathbf{t}\in {\mathbb{Z}}_q^n$, and a parameter $\beta \in \mathbb{R}$, the goal is to find a non-zero vector $\mathbf{x}\in {\mathbb{Z}}_q^m$ such that $\mathbf{Ax}=\mathbf{t}\mathrm{mod}q$ and $∥\mathbf{x}∥\le \beta$.

The ISIS problem is a variant of the Shortest Vector Problem (SVP) in lattices, which is known to be computationally hard. It falls within the class of NP-hard problems and is believed to be resistant to efficient classical and quantum algorithms. Lattice-based schemes often design public and private keys based on the ISIS problem. $\mathbf{A}$ and $\mathbf{t}$ are often used as public parameters or public keys, while $\mathbf{x}$ is often used as a private key.

2.4. Decisional Learning with Errors (D-LWE)

Given a prime q, a Gaussian distribution $\chi$ over ${\mathbb{Z}}_q$, and a positive integer n. Assume that there is a non-specified oracle $\mathcal{O}$, which could be a truly uniform random sampler ${\mathcal{O}}_{\mathsf{\$}}$ or a noisy pseudo-random sampler ${\mathcal{O}}_s$. ${\mathcal{O}}_s$ and ${\mathcal{O}}_{\mathsf{\$}}$ are defined as follows:

• ${\mathcal{O}}_s:$ The noisy pseudo-random sampler ${\mathcal{O}}_s$ outputs pseudo-random samples $({\mathbf{u}}_i,v_i)=({\mathbf{u}}_i,{\mathbf{u}}_i^{\top }s+e_i)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$, where $e_i$ is sampled from $\chi$, $s\in {\mathbb{Z}}_q^n$ is a consistent secret vector, and ${\mathbf{u}}_i\in {\mathbb{Z}}_q^n$ is a uniformly random vector.
• ${\mathcal{O}}_{\mathsf{\$}}:$ The truly random sampler ${\mathcal{O}}_{\mathsf{\$}}$ outputs uniformly random samples in ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$.

Definition 5 (D-LWE problem).

Given a polynomial number of samples from $\mathcal{O}$. Decide whether $\mathcal{O}$ is ${\mathcal{O}}_s$ or ${\mathcal{O}}_{\mathsf{\$}}$.

Definition 6.

The advantage of an adversary $\mathcal{A}$ to break the D-LWE problem is defined as

$$Ad{v}_{D-LWE}\left(A\right)=\left|Pr[{\mathcal{A}}^{{\mathcal{O}}_s}=1]-Pr[{\mathcal{A}}^{{\mathcal{O}}_{\mathsf{\$}}}=1]\right|$$

Definition 7 (D-LWE Assumption).

If no polynomial-time algorithm has a non-negligible advantage in solving the D-LWE problem, then the D-LWE assumption holds.

The D-LWE problem is widely regarded as a hard problem in lattice-based cryptography. Many lattice-based cryptographic schemes, such as encryption, signatures, and key exchange protocols, rely on the hardness of D-LWE for their security. As long as solving the D-LWE problem is difficult, the security of those schemes will be guaranteed.

2.5. Trapdoor Functions

There are two types of trapdoor functions.Type 2 trapdoor functions are smaller, faster, and better than Type 1 trapdoor functions. The type 2 trapdoor functions are based on the one-way function proposed by Regev [23], and their security is constructed on the hardness of the learning with errors problem (LWE). In 2012, Micciancio and Peikert [24] proposed an efficient trapdoor generation function. Then, Genise and Micciancio [25] gave improved algorithms in 2018. Therefore, the proposed scheme applies the trapdoor generation functions [24,25] and introduces them here.

Given a prime q and two positive integers $n,m$. To obtain a trapdoor of a lattice, a gadget vector $\mathbf{g}$ is defined as $\mathbf{g}={\left[124\cdots 2^{k-1}\right]}^{\top }\in {\mathbb{Z}}_q^{1\times k}$, where $k=\lceil {log}_{2}q\rceil$. Moreover, a gadget matrix $\mathbf{G}$ is defined as

$$\mathbf{G}={\mathbf{I}}_n\otimes {\mathbf{g}}^{\top }=\left[\begin{array}{cccc}{\mathbf{g}}^{\top }& \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{0}& {\mathbf{g}}^{\top }& \cdots & \mathbf{0}\\ ⋮& \mathbf{0}& \ddots & ⋮\\ \mathbf{0}& \cdots & \mathbf{0}& {\mathbf{g}}^{\top }\end{array}\right]\in {\mathbb{Z}}_q^{n\times w},\mathrm{where}w=nk.$$

Definition 8.

$(\mathbf{A},\mathbf{R})\leftarrow \mathit{G}\mathit{e}\mathit{n}\mathit{T}\mathit{r}\mathit{a}\mathit{p}({\mathbf{A}}_0,\mathbf{H})$

• Given a matrix ${\mathbf{A}}_0\in {\mathbb{Z}}_q^{n\times m^{\prime }}$ and an invertible matrix $\mathbf{H}\in {\mathbb{Z}}_q^{n\times n}$. Output a matrix $\mathbf{A}=\left[{\mathbf{A}}_0|-{\mathbf{A}}_0\mathbf{R}+\mathbf{HG}\right]\in {\mathbb{Z}}_q^{n\times m}$ and a trapdoor $\mathbf{R}\in {\mathbb{Z}}_q^{m^{\prime }\times w}$ of $\mathbf{A}$, where $m=m^{\prime }+w$. Moreover, the trapdoor’s quality guaranteed that $s\left(\mathbf{R}\right)\le \sqrt{m}·\omega \left(\sqrt{logq}\right)$, where the function $s\left(\right)$ extracts the Euclidean length of the input, and the little-omega notation $\omega \left(\right)$ is an asymptotic notation.

Definition 9.

$\mathbf{x}\leftarrow \mathit{S}\mathit{a}\mathit{m}\mathit{p}\mathit{l}\mathit{e}\mathit{D}(\mathbf{A}=\left[{\mathbf{A}}_{\mathbf{0}}|-{\mathbf{A}}_{\mathbf{0}}\mathbf{R}+\mathbf{HG}\right],\mathbf{H},\mathbf{R},\mathbf{t},\sigma )$

• Given a matrix $\mathbf{A}=\left[{\mathbf{A}}_0|-{\mathbf{A}}_0\mathbf{R}+\mathbf{HG}\right]\in {\mathbb{Z}}_q^{n\times m}$, a trapdoor $\mathbf{R}\in {\mathbb{Z}}^{m^{\prime }\times w}$ of $\mathbf{A}$, an invertible matrix $\mathbf{H}\in {\mathbb{Z}}_q^{n\times n}$, a target $\mathbf{t}\in {\mathbb{Z}}_q^n$, and a Gaussian parameter σ. Output a vector $\mathbf{x}$ such that $\mathbf{Ax}=\mathbf{t}\in {\mathbb{Z}}_q^n$.

The details of how to generate $\mathbf{x}$ with a gadget matrix $\mathbf{G}$ is described as follows:

• Randomly choose a perturbation vector $\mathbf{p}\in {\mathbb{Z}}_q^m$ with $\sigma$, and divide $\mathbf{p}$ into two parts ${\mathbf{p}}_1\in {\mathbb{Z}}_q^{m^{\prime }}\mathrm{and}{\mathbf{p}}_2\in {\mathbb{Z}}_q^w$:

  $$\mathbf{p}=\left[\begin{array}{c}{\mathbf{p}}_1\\ {\mathbf{p}}_2\end{array}\right].$$
• Compute

  $${\mathbf{y}}_1={\mathbf{A}}_{\mathbf{0}}({\mathbf{p}}_1-\mathbf{R}{\mathbf{p}}_2)\in {\mathbb{Z}}_q^n$$

  $${\mathbf{y}}_2=\mathbf{G}{\mathbf{p}}_2\in {\mathbb{Z}}_q^n,$$

  $$\mathbf{v}={\mathbf{H}}^{-1}(\mathbf{t}-{\mathbf{y}}_1)-{\mathbf{y}}_2={\mathbf{H}}^{-1}(\mathbf{t}-\mathbf{Ap})\in {\mathbb{Z}}_q^n.$$
• Choose a vector $\mathbf{z}\in {\mathbb{Z}}_q^w$ from ${\Lambda }_q^{\mathbf{v}}\left(\mathbf{G}\right)$, and compute

  $$\mathbf{x}=\mathbf{p}+\left[\begin{array}{c}\mathbf{R}\\ {\mathbf{I}}_w\end{array}\right]\mathbf{z}.$$
• Output $\mathbf{x}$.

Definition 10.

${\mathbf{R}}^{\prime }\leftarrow \mathit{D}\mathit{e}\mathit{l}\mathit{T}\mathit{r}\mathit{a}\mathit{p}({\mathbf{A}}^{\prime }=\left[\mathbf{A}\right|{\mathbf{A}}_1],\mathbf{R},{\mathbf{H}}^{\prime },\sigma )$

• Given a matrix ${\mathbf{A}}^{\prime }=\left[\mathbf{A}\right|{\mathbf{A}}_1]\in {\mathbb{Z}}_q^{n\times m}\times {\mathbb{Z}}_q^{n\times w}$ (${\mathbf{A}}_1$ is an arbitrary matrix), a trapdoor $\mathbf{R}\in {\mathbb{Z}}^{m^{\prime }\times w}$ of $\mathbf{A}$, an invertible matrix ${\mathbf{H}}^{\prime }\in {\mathbb{Z}}_q^{n\times n}$, and a Gaussian parameter σ. Output a trapdoor ${\mathbf{R}}^{\prime }$ of ${\mathbf{A}}^{{}^{\prime }}$.

$\mathit{D}\mathit{e}\mathit{l}\mathit{T}\mathit{r}\mathit{a}\mathit{p}$ will call $\mathit{S}\mathit{a}\mathit{m}\mathit{p}\mathit{l}\mathit{e}\mathit{D}$ repeatedly until getting a trapdoor ${\mathbf{R}}^{\prime }$ containing d linearly independent vectors $[{\mathbf{y}}_1,\dots ,{\mathbf{y}}_d]$ such that $\mathbf{A}{\mathbf{R}}^{\prime }={\mathbf{H}}^{\prime }\mathbf{G}-{\mathbf{A}}_1$.

2.6. Tree-Based Access Structure

In the proposed scheme, the data owner will choose a set of keywords $KW$ while encrypting data, and a data user may determine a keyword-search policy $\tau$ while generating a search token. Moreover, the cloud server will send the encrypted data to the data user if $KW$ satisfies $\tau$. The access structure in the proposed scheme is a tree-based access structure supporting OR and AND gates.

Figure 1 shows an example of the tree-based access structure applied in the proposed scheme. In the example, the keyword-search policy $\tau =(k_1\cup k_3\cup k_5)\cap (k_6\cap k_7)$, where $k_i$ denotes the i-th keyword in the system. Here is how to generate ${\mathbf{T}}_{\tau ,k_i}\in {\{-1,0,1\}}^{n\times n}$, which will be used in the proposed scheme. First, the data user will set the value of the root node as an identity matrix ${\mathbf{I}}_n$. Second, since the root node has two child nodes and requires an AND gate, the data user will compute two invertible matrices ${\overline{\mathbf{T}}}_1,{\overline{\mathbf{T}}}_2\in {\{-1,0,1\}}^{n\times n}$ such that ${\overline{\mathbf{T}}}_1+{\overline{\mathbf{T}}}_2={\mathbf{I}}_n$. Third, since ${\overline{\mathbf{T}}}_1$ has three child nodes and requires an OR gate, the data user will set ${\mathbf{T}}_{\tau ,k_1}={\mathbf{T}}_{\tau ,k_3}={\mathbf{T}}_{\tau ,k_5}={\overline{\mathbf{T}}}_1$. Fourth, since ${\overline{\mathbf{T}}}_2$ has two child nodes and requires an AND gate, the data user will compute two invertible matrices ${\mathbf{T}}_{\tau ,k_6},{\mathbf{T}}_{\tau ,k_7}\in {\{-1,0,1\}}^{n\times n}$ such that ${\mathbf{T}}_{\tau ,k_6}+{\mathbf{T}}_{\tau ,k_7}={\overline{\mathbf{T}}}_2$. Finally, each ${\mathbf{T}}_{\tau ,k_i}$ belonging to $k_i$ will be used to generate a search token in the proposed scheme. If a keyword set $KW=\{k_1^{\prime },k_2^{\prime },\dots ,k_o^{\prime }\}$ can exactly satisfy $\tau$, then ${\sum }_{i=1}^o{\mathbf{T}}_{\tau ,k_i^{\prime }}={\mathbf{I}}_n$. For example, in Figure 1, both $\{k_1,k_6,k_7\}$ and $\{k_3,k_6,k_7\}$ can exactly satisfy $\tau$, then ${\mathbf{T}}_{\tau ,k_1}+{\mathbf{T}}_{\tau ,k_6}+{\mathbf{T}}_{\tau ,k_7}={\mathbf{T}}_{\tau ,k_3}+{\mathbf{T}}_{\tau ,k_6}+{\mathbf{T}}_{\tau ,k_7}={\mathbf{I}}_n$.

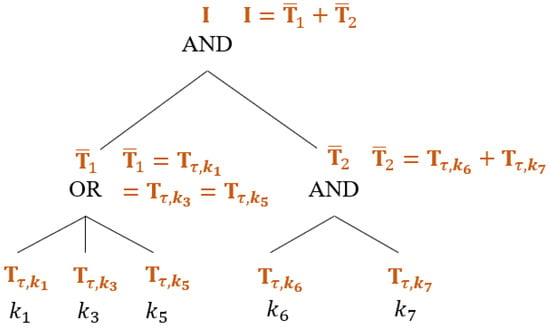
Figure 1. Example of a Tree-Based Keyword-Search Policy $\tau$.

2.7. System Model

Figure 2 shows the system model of the proposed scheme. It includes five system roles, and their behaviors are defined as follows.

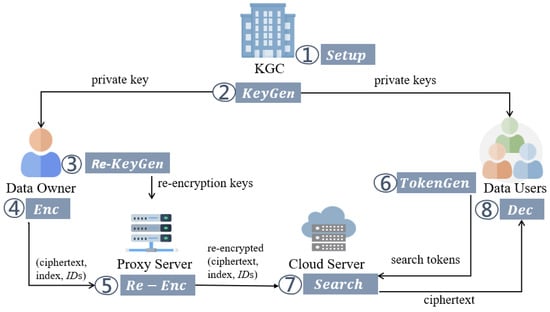
Figure 2. The System Model.

• Key Generation Center (KGC): KGC is fully trusted and is responsible for system setup and key distribution.
• Data Owner (DO): DO can pre-generate re-encryption keys and send them to PS before the encryption phase. Then, in the encryption phase, DO computes the ciphertext, index, and $ID$s (a set of DUs’ identities). Then, DO sends (ciphertext, index, $ID$s) to PS.
• Proxy Server (PS): PS is fully trusted and responsible for re-encryption. After receiving the re-encryption keys, ciphertext, index, and $ID$s from DO, PS re-encrypts the ciphertext and index. Finally, PS sends the re-encrypted results to CS.
• Cloud Server (CS): CS is honest-but-curious and responsible for data storage and search.
• Data User (DU): DU can send a search request with a search token to CS to download matching ciphertexts.

The proposed scheme consists of the following polynomial-time algorithms.

• $(MSK,PP)\leftarrow \mathit{Setup}\left(\lambda \right)$: Taking a security parameter $\lambda$ as input, KGC outputs the public parameters $PP$ and the master secret key $MSK$.
• $\left({SK}_{ID}\right)\leftarrow \mathit{KeyGen}(PP,MSK,ID)$: With a user’s identity $ID$ and $MSK$ as inputs, KGC computes the private key ${SK}_{ID}$ of the user.
• $\left(R{K}_{I{D}_x\leftarrow I{D}_y}\right)\leftarrow$Re-KeyGen($PP,I{D}_x,I{D}_y,S{K}_{I{D}_x}$): Taking DU’s identity $I{D}_y$, and ${SK}_{I{D}_x}$ as inputs, the user $I{D}_x$ computes the re-encryption key $R{K}_{I{D}_x\to I{D}_y}$.
• $(C_{I{D}_x},I_{I{D}_x})\leftarrow$Enc($PP,I{D}_x,\mu ,K{W}_{ID})$: Taking an identity $I{D}_x$, a one-bit message $\mu$, and a keyword set $K{W}_{I{D}_x}$ as inputs, DO outputs the ciphertext $C_{I{D}_x}$ and the index $I_{I{D}_x}$.
• $(C_{I{D}_y},I{D}_y)\leftarrow$Re-Enc($PP,(C_{I{D}_x},I{D}_x),I{D}_y,R{K}_{I{D}_x\to I{D}_y},$): Given the ciphertext $C_{I{D}_x}$, the index $I_{I{D}_x}$, DO’s identity $I{D}_x$, DU’s identity $I{D}_y$, and a re-encryption key $R{K}_{I{D}_x\to I{D}_y}$ as inputs, PS computes the re-encrypted ciphertext $C_{I{D}_y}$ and re-encrypted index $I_{I{D}_y}$.
• $(TK,ID)\leftarrow$TokenGen($PP,ID,{SK}_{ID},\tau$): Taking a keyword-search policy $\tau$, $ID$, and ${SK}_{ID}$ as inputs, DU can compute the search token $TK$.
• $(C_{ID}$ or $\perp )\leftarrow \mathit{Search}(PP,TK,ID,(C_{ID},I_{ID}))$: Given $TK$, $ID$, and $(C_{ID},I_{ID})$ as inputs, CS checks whether $TK$ matches $I_{ID}$. If the result matches, CS sends $C_{ID}$ to DU. Otherwise, CS sends ⊥ to DU.
• $\left(\mu \right)\leftarrow$ Dec($PP,ID,{SK}_{ID},C_{ID}$): With $C_{ID}$ and $S{K}_{ID}$, DU decrypts $C_{ID}$ and gets the plaintext $\mu$.

2.8. Security Model

Based on the security requirements of cloud services, the proposed scheme achieves indistinguishability under chosen plaintext attacks (IND-CPA) and indistinguishability under chosen keyword attacks (IND-CKA). The security model is defined as the following IND-CPA and IND-CKA games. Assume that $\mathcal{A}$ is a polynomial-time adversary, and the simulator $\mathcal{S}$ simulates the games.

2.8.1. Ciphertext Security

The IND-CPA game is defined as follows:

• $\mathbf{Init}$: $\mathcal{A}$ gives a target identity $I{D}^{*}$ to $\mathcal{S}$. $\mathcal{S}$ receives a polynomial number of samples from the D-LWE oracle.
• $\mathbf{Setup}$ $\mathcal{S}$ initializes the system and sends public parameters $PP$ to $\mathcal{A}$.
• $\mathbf{Phase}\mathbf{1}$ $\mathcal{A}$ can adaptively issue the following queries multiple times:

  –

  $H_0$ query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$. $\mathcal{S}$ sends $H_0\left(ID\right)$ to $\mathcal{A}$.

  –

  $H_1$ query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$. $\mathcal{S}$ sends $H_1\left(ID\right)$ to $\mathcal{A}$.

  –

  KeyGen query $\mathcal{A}$ gives an identity $ID$. If $ID=I{D}^{*}$, $\mathcal{S}$ aborts it. Otherwise, $\mathcal{S}$ sends $S{K}_{ID}$ to $\mathcal{A}$.

  –

  Re-KeyGen query $\mathcal{A}$ gives DO’s identity $I{D}_x$ and DU’s identity $I{D}_y$. If $I{D}_x=I{D}^{*}$, $\mathcal{S}$ aborts it. Otherwise, $\mathcal{S}$ sends $R{K}_{I{D}_x\to I{D}_y}$ to $\mathcal{A}$.

• $\mathbf{Challenge}$: $\mathcal{A}$ submits two messages (${\mu }_0,{\mu }_1$) to $\mathcal{S}$. $\mathcal{S}$ randomly chooses $b\in \{0,1\}$. Then, $\mathcal{S}$ computes the ciphertext $C_{I{D}^{*}}$ related to ${\mu }_b$. Finally, $\mathcal{S}$ sends $C_{I{D}^{*}}$ to $\mathcal{A}$.
• $\mathbf{Phase}\mathbf{2}$: $\mathcal{A}$ may do more queries as in $\mathbf{Phase}\mathbf{1}$.
• $\mathbf{Guess}$: Finally, $\mathcal{A}$ answers a bit $b^{\prime }$. If $b=b^{\prime }$, $\mathcal{A}$ wins the IND-CPA game.

Definition 11.

The advantage of $\mathcal{A}$ to win the IND-CPA game is defined as

$$Ad{v}^{IND-CPA}\left(\mathcal{A}\right)=\left|Pr\left[b^{\prime }=b\right]-\frac{1}{2}\right|$$

Definition 12.

If no polynomial-time adversary wins the IND-CPA game with a non-negligible advantage, then the proposed scheme is IND-CPA secure.

2.8.2. Keyword-Search Security

The IND-CKA game is defined as follows:

• $\mathbf{Init}$: $\mathcal{A}$ gives a target identity $I{D}^{*}$ and two target keywords $(k_0^{\prime },k_1^{\prime })$ to $\mathcal{S}$. $\mathcal{S}$ randomly chooses $b\in \{0,1\}$ and will use $k_b^{\prime }$ for the challenge. Furthermore, $\mathcal{S}$ receives a polynomial number of samples from the D-LWE oracle.
• $\mathbf{Setup}$ $\mathcal{S}$ initializes the system and sends public parameters $PP$ to $\mathcal{A}$.
• $\mathbf{Phase}\mathbf{1}$ $\mathcal{A}$ can adaptively issue the following queries multiple times:

  –

  $H_0$ query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$. $\mathcal{S}$ sends $H_0\left(ID\right)$ to $\mathcal{A}$.

  –

  $H_1$ query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$. $\mathcal{S}$ sends $H_1\left(ID\right)$ to $\mathcal{A}$.

  –

  KeyGen query $\mathcal{A}$ gives an identity $ID$. If $ID=I{D}^{*}$, $\mathcal{S}$ aborts it. Otherwise, $\mathcal{S}$ sends $S{K}_{ID}$ to $\mathcal{A}$.

  –

  Re-KeyGen query $\mathcal{A}$ gives DO’s identity $I{D}_x$ and DU’s indetiy $I{D}_y$. If $I{D}_x=I{D}^{*}$, $\mathcal{S}$ aborts it. Otherwise, $\mathcal{S}$ sends $R{K}_{I{D}_x\to I{D}_y}$ to $\mathcal{A}$.

  –

  TokenGen query $\mathcal{A}$ gives an identity $ID$ and a keyword-search policy $\tau$. If ($ID=I{D}^{*}$ and ($\tau$ contains $k_0^{\prime }$ or $k_1^{\prime }$)), $\mathcal{S}$ aborts it. Otherwise, $\mathcal{S}$ sends $(TK,ID)$ to $\mathcal{A}$.

• $\mathbf{Challenge}$: $\mathcal{A}$ submits a signal to start the $\mathbf{Challenge}$. $\mathcal{S}$ computes the index $I_{I{D}^{*}}$ related to $k_b^{\prime }$. Finally, $\mathcal{S}$ sends $I_{I{D}^{*}}$ to $\mathcal{A}$.
• $\mathbf{Phase}\mathbf{2}$: $\mathcal{A}$ may do more queries as in $\mathbf{Phase}\mathbf{1}$.
• $\mathbf{Guess}$: Finally, $\mathcal{A}$ answers a bit $b^{\prime }$. If $b=b^{\prime }$, $\mathcal{A}$ wins the IND-CKA game.

Definition 13.

The advantage of $\mathcal{A}$ to win the IND-CKA game is defined as

$$Ad{v}^{IND-CKA}\left(\mathcal{A}\right)=\left|Pr\left[b^{\prime }=b\right]-\frac{1}{2}\right|$$

Definition 14.

If no polynomial-time adversary wins the IND-CKA game with a non-negligible advantage, then the proposed scheme is IND-CKA secure.

3. Related Works

This section introduces a traditional SE scheme and some lattice-based schemes in recent years. The features comparison between the proposed scheme and those schemes will be shown in Section 6.

3.1. Huang et al.’s [26] Traditional Multi-Keyword Attribute-Based SE Scheme

Huang et al. [26] proposed a traditional multi-keyword attribute-based SE scheme in 2022. Their scheme supports AND and NOT operators in keyword search queries. Moreover, user access rights are verified during the decryption and keyword-search phases. However, since the scheme is based on discrete logarithm hard problems, it cannot resist quantum attacks. Since Huang et al.’s scheme uses traditional encryption, their scheme will not be compared in computation and transmission costs.

3.2. Wang et al.’s [27] Public Key SE Scheme from Lattices

In 2020, Wang et al. [27] introduced a public key SE scheme, which supports conjunctive keyword search (multi-keyword but only AND operators). Their multi-user scheme uses a user’s identity’s hash value as its public key. Therefore, their scheme is IBE. However, their scheme does not detail the decryption phase.

3.3. Attribute-Based SE Schemes from Lattices

Four attribute-based SE schemes are introduced here. Their access structures are all LSSS, which may cause errors in decryption.

3.3.1. Liu et al.’s [17] Scheme

In 2019, Liu et al. [17] proposed an attribute-based SE scheme. Since their method verifies user access rights only in the decryption phase, anyone can search the ciphertext without authentication in the keyword-search phase. Although there are multi-keywords in Liu et al.’s Encryption, the search token contains only one keyword. Liu et al.’s method requires KGC to be online to help users generate search tokens. Moreover, the access structure is LSSS, which may cause errors in decryption.

3.3.2. Varri et al.’s [20] Scheme

In 2021, Varri et al. [20] proposed an attribute-based SE scheme supporting multi-keyword searches. Although their method verifies user access rights in the keyword-search phase, all users use the same decryption key in the decryption phase. Although there are multi-keywords in their Encryption, the search token contains only one keyword. Therefore, the scheme does not support multi-keyword. Moreover, Varri et al.’s method also requires KGC to be online to generate search tokens. Furthermore, the access structure is LSSS, which may cause errors in decryption.

3.3.3. Chen’s [21] Scheme

In 2021, Chen [21] proposed an attribute-based SE scheme supporting dynamic membership management. His scheme is based on Wang’s scheme [28]. His method verifies user access rights in both the decryption and the keyword-search phases. Moreover, his search algorithm verifies $\zeta$ times to ensure that the user is valid. However, the access structure is LSSS, which may cause errors in decryption. Moreover, the data user needs to know the access structure of the data before generating a search token. The algorithms of his scheme are shown as follows:

3.3.4. Wang’s [22] Scheme

In 2022, Wang [22] proposed an attribute-based multi-keyword SE scheme supporting dynamic membership management. Her scheme is based on Chen’s scheme [21]. Therefore, her scheme shares many similar features with Chen’s scheme, and the access structure is LSSS, which may cause errors in decryption. Moreover, the keywords are only protected by the hash function, which may be attacked by offline dictionary attacks.

3.4. Zhang et al.’s [19] Identity-Based SE Scheme from Lattices

In 2019, Zhang et al. [19] introduced an identity-based SE scheme, which reduces data owners’ computation and transmission costs with a proxy mechanism. Users can generate search tokens by themselves so that KGC can be offline. However, their scheme does not detail the decryption phase. Moreover, DU needs to know which proxy PS sent the data when generating a search token. Furthermore, CS needs a special public key of PS when testing the search.

3.5. Wang et al.’s [18] Lattice-Based SE Schemes Supporting SPE

In 2022, Wang et al. [18] proposed a SE scheme supporting SPE. Their scheme verifies user access rights during the decryption and keyword-search phases. Moreover, users can generate search tokens in Wang et al.’s method. Although their method supports multi-keywords, only OR operations are supported.

3.6. Lattice-Based SE Schemes Supporting PRE

Two lattice-based SE schemes supporting PRE are introduced here. Both schemes do not support functional encryption.

3.6.1. Zhang et al.’s [29] Scheme

In 2021, Zhang et al. [29] introduced an SE scheme providing proxy re-encryption. In their scheme, although users can generate search tokens by themselves, KGC must be online to help users generate re-encryption keys. Moreover, their scheme does not detail the decryption phase.

3.6.2. Hou et al.’s [30] Scheme

In 2022, Hou et al. [30] proposed a multi-keyword SE scheme with proxy re-encryption. Their scheme supports semantic aware search in keyword search queries. However, like Zhang et al.’s method, Hou et al.’s scheme does not detail the decryption phase and requires KGC to be online to generate re-encryption keys.

4. Construction

This section presents the proposed multi-keyword searchable identity-based proxy re-encryption scheme from lattices. The system model is defined in Section 2.7.

4.1. Algorithms

Table 1 shows the notations of the proposed scheme. Figure 3 presents the data flow of the proposed scheme. To make the figure simple and easy to understand, Figure 3 only shows the case of one DU. In actual situations, there may be multiple DUs, and DO should provide a re-encryption key to PS for each DU. Then, PS will compute a re-encrypted ciphertext and a re-encrypted index for each DU.

Table 1. Notations.

Notation	Meaning
$PP$	Public parameters
$\lambda$	A security parameter
$\chi$	A Gaussian distribution
$\sigma$	A Gaussian parameter
q	A modulo prime number
n	The dimension of a vector space
m	The number of vectors of a basis
l	The number of keywords
w	A key generated by DelTrap has w bits
	more than the original private key
$KW$	A keyword set
$k_i$	The i-th keyword
${\mathbf{A}}_0$	A random matrix
${\mathbf{A}}^{\top }$	The transpose of a matrix $\mathbf{A}$
$\mathbf{H}$	An invertible matrix
$\mathbf{u}$	A random vector
$H_0$, $H_1$, $H_2$	Hash functions
$\mathbf{R}$	A trapdoor of ${\Lambda }_q^{\perp }\left(\mathbf{A}\right)$
$ID$	A user’s identity
$ID$s	A set of users’ identities
${SK}_{ID}$	The private key of $ID$
$\mu$	One-bit message
$TK$	A Search token
$\tau$	A keyword-search policy
${\mathbf{T}}_{\tau ,k_i}$	An invertible matrix belongs to $k_i$ and is related to $\tau$
f	A flag used to determine search results

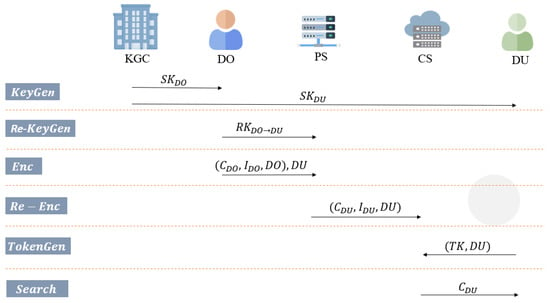
Figure 3. Data Flow of The Proposed Scheme.

The proposed scheme includes eight algorithms as follows (Appendix A).

• $(MSK,PP)\leftarrow \mathit{Setup}\left(\lambda \right)$
  Taking a security parameter $\lambda$, KGC sets up the system by the following steps:
  • Select a Gaussian distribution $\chi$, a Gaussian parameter $\sigma$, a prime q, four integers n, $m^{\prime }$, l, and w, a keyword set $KW={\left\{k_i\right\}}_{1\le i\le l}$, a random matrix ${\mathbf{A}}_0\in {\mathbb{Z}}_q^{n\times m^{\prime }}$, an invertible matrix $\mathbf{H}\in {\mathbb{Z}}_q^{n\times n}$, a random vector $\mathbf{u}\in {\mathbb{Z}}_q^n$. Let $m=m^{\prime }+w$.
  • Select three hash functions $H_0:{\{0,1\}}^{*}\to {\mathbb{Z}}_q^{n\times w}$, $H_1:{\{0,1\}}^{*}\to {\mathbb{Z}}_q^{n\times n}$, and $H_2:{\{0,1\}}^{*}\to {\mathbb{Z}}_q^{n\times n}$, where the output of $H_1$ or $H_2$ is an invertible matrix.
  • Generate a matrix $\mathbf{A}=\left[{\mathbf{A}}_0\right|-{\mathbf{A}}_0\mathbf{R}+\mathbf{H}\mathbf{G}]\in {\mathbb{Z}}_q^{n\times m}$ and a corresponding trapdoor $\mathbf{R}\in {\mathbb{Z}}_q^{m^{\prime }\times w}$ of ${\Lambda }_q^{\perp }\left(\mathbf{A}\right)$ by invoking $\mathit{GenTrap}({\mathbf{A}}_0,\mathbf{H})$ defined in Section 2.5, where $\mathbf{G}\in {\mathbb{Z}}_q^{n\times w}$ is a gadget matrix defined in Section 2.5.
  • Publish the public parameters $PP=(\chi ,\sigma ,q,n,m,l,w,KW={\left\{k_i\right\}}_{1\le i\le l},\mathbf{A},H_0,H_1,H_2,\mathbf{u})$ and keep the master secret key $MSK=\mathbf{R}$.
  In $\mathit{GenTrap}$ algorithm, $\mathbf{G}$ is a special matrix that is public. $\mathbf{H}$ can be an identity matrix and be public. Due to the difficulty of solving the ISIS problem defined in Section 2.3, even given $\mathbf{A}$, ${\mathbf{A}}_0$, $\mathbf{H}$, and $\mathbf{G}$, it is hard to find $\mathbf{R}$. Therefore, only the trapdoor $\mathbf{R}$ needs to be kept secret.
• $\left({SK}_{ID}\right)\leftarrow \mathit{KeyGen}(PP,MSK,ID)$
  With a user’s $ID$ and $MSK$ as inputs, KGC runs $\mathit{KeyGen}$ to compute the user’s private key ${\mathit{SK}}_{ID}$ by the following steps:
  • Compute ${\mathbf{A}}_{ID}=H_0\left(ID\right)\in {\mathbb{Z}}_q^{n\times w}$.
  • Set ${\mathbf{A}}_{ID}^{\prime }=\left[\mathbf{A}\right|{\mathbf{A}}_{ID}]$.
  • Compute ${\mathbf{H}}_{ID}=H_1\left(ID\right)\in {\mathbb{Z}}_q^{n\times n}$.
  • Run DelTrap(${\mathbf{A}}_{ID}^{\prime },\mathbf{R},{\mathbf{H}}_{ID},\sigma$) defined in Section 2.5 to generate ${\mathbf{R}}_{ID}\in {\mathbb{Z}}^{m\times w}$ such that $\mathbf{A}{\mathbf{R}}_{ID}={\mathbf{H}}_{ID}\mathbf{G}-{\mathbf{A}}_{ID}$, where ${\mathbf{R}}_{ID}$ is a trapdoor of ${\Lambda }_q^{\perp }\left(\left[\mathbf{A}\right|{\mathbf{A}}_{ID}]\right)$.
  • Run SampleD (${\mathbf{R}}_{ID},{\mathbf{A}}_{ID}^{\prime },{\mathbf{H}}_{ID},\mathbf{u},\sigma$) to generate ${\mathbf{x}}_{ID}$ so that ${\mathbf{A}}_{ID}^{\prime }{\mathbf{x}}_{ID}=\mathbf{u}$.
  • Set ${\mathit{SK}}_{ID}=\{{\mathbf{R}}_{ID},{\mathbf{x}}_{ID}\}$. and send it to the user.
  ${\mathbf{A}}_{ID}^{{}^{\prime }}$ will be treated as the public key associated with the user $ID$. However, because the number of bits of the matrix ${\mathbf{A}}_{ID}^{{}^{\prime }}$ is relatively high, directly storing ${\mathbf{A}}_{ID}^{{}^{\prime }}$ will consume a large storage space. Therefore, users only need to store the ID, and when users need to use A, they use the hash function to compute it. Anyone who knows the user ID can compute the corresponding $A_{ID}^{{}^{\prime }}$. Similarly, users do not store ${\mathbf{H}}_{ID}$ directly, thereby reducing storage requirements. On the other hand, the determinants $|{\mathbf{R}}_{ID}|$ and $|{\mathbf{x}}_{ID}|$ should be small. Otherwise, it will affect the correctness of the proposed scheme. Since $|{\mathbf{R}}_{ID}|$ and $|{\mathbf{x}}_{ID}|$ need to be small, the difficulty for an adversary to compute an effective private key is equivalent to solving the ISIS problem.
• $\left(R{K}_{I{D}_x\to I{D}_y}\right)\leftarrow \mathit{Re}-\mathit{KeyGen}(PP,I{D}_x,I{D}_y,S{K}_{I{D}_x}$)
  With ${SK}_{I{D}_x}$, the user $I{D}_x$ can compute the re-encryption key $R{K}_{I{D}_x\to I{D}_y}$ by the following steps:
  • Compute ${\mathbf{A}}_{I{D}_x}=H_0\left(I{D}_x\right)\in {\mathbb{Z}}_q^{n\times w}$.
  • Set ${\mathbf{A}}_{I{D}_x}^{\prime }=\left[\mathbf{A}\right|{\mathbf{A}}_{I{D}_x}]\in {\mathbb{Z}}_q^{n\times (m+w)}$.
  • Compute ${\mathbf{A}}_{I{D}_y}=H_0\left(I{D}_y\right)\in {\mathbb{Z}}_q^{n\times w}$.
  • Set ${\mathbf{A}}_{I{D}_y}^{\prime }=\left[\mathbf{A}\right|{\mathbf{A}}_{I{D}_y}]\in {\mathbb{Z}}_q^{n\times (m+w)}$.
  • Compute ${\mathbf{H}}_{I{D}_x}=H_1\left(I{D}_x\right)\in {\mathbb{Z}}_q^{n\times n}$.
  • Perform SampleD(${\mathbf{R}}_{I{D}_x},{\mathbf{A}}_{I{D}_x}^{\prime },{\mathbf{H}}_{I{D}_x},{\mathbf{A}}_{I{D}_y}^{\prime },\sigma$) defined in Section 2.5 to get ${\mathbf{R}}_{I{D}_x\to I{D}_y}$ such that ${\mathbf{A}}_{I{D}_x}^{\prime }{\mathbf{R}}_{I{D}_x\to I{D}_y}={\mathbf{A}}_{I{D}_y}^{\prime }$.
  • Set $R{K}_{I{D}_x\to I{D}_y}={\mathbf{R}}_{I{D}_x\to I{D}_y}^{\top }$.
  The concept of re-encryption is to compute a matrix ${\mathbf{R}}_{I{D}_x\to I{D}_y}$ so that the matrix ${\mathbf{A}}_{I{D}_x}^{{}^{\prime }}$ multiplied by ${\mathbf{R}}_{I{D}_x\to I{D}_y}$ will be equal to the matrix ${\mathbf{A}}_{I{D}_y}^{{}^{\prime }}$. Moreover, the determinant $|{\mathbf{R}}_{I{D}_x\to I{D}_y}^{\top }|$ should be small, so it can be ignored in the search results or the decryption results. Otherwise, it will affect the correctness of those results. Since $|{\mathbf{R}}_{I{D}_x\to I{D}_y}^{\top }|$ needs to be small, the difficulty for an adversary to compute an effective re-encryption key is equivalent to solving the ISIS problem.
• $(C_{I{D}_x},I_{I{D}_x})\leftarrow$ Enc($PP,I{D}_x,\mu ,K{W}_{ID}$)
  Taking a one-bit message $\mu \in \{0,1\}$ and a keyword set $K{W}_{I{D}_x}\subseteq KW={\left\{k_i\right\}}_{1\le i\le l}$, DO encrypts $\mu$ with its $I{D}_x$ by the following steps:
  • Compute ${\mathbf{A}}_{I{D}_x}=H_0\left(I{D}_x\right)\in {\mathbb{Z}}_q^{n\times w}$.
  • Set ${\mathbf{A}}_{I{D}_x}^{\prime }=\left[\mathbf{A}\right|{\mathbf{A}}_{I{D}_x}]\in {\mathbb{Z}}_q^{n\times (m+w)}$.
  • Sample noises $e_1,e_3\in \chi$ and $e_2,e_{4,1},e_{4,2},⁦,e_{4,l}\in {\chi }^{m+w}$.
  • Choose two secret vectors $\mathbf{s},\mathbf{v}\in {\mathbb{Z}}_q^n$.
  • Compute $C_1^{I{D}_x}={\mathbf{u}}^{\top }\mathbf{s}+\mu ⌊\frac{q}{2}⌋+e_1\in {\mathbb{Z}}_q$.
  • Compute $C_2^{I{D}_x}={\mathbf{A}}_{I{D}_x}^{{}^{\prime }\top }\mathbf{s}+e_2\in {\mathbb{Z}}_q^{m+w}$.
  • Set the ciphertext $C_{I{D}_x}=\{C_1^{I{D}_x},C_2^{I{D}_x}\}$.
  • Compute $I_1^{I{D}_x}={\mathbf{u}}^{\top }\mathbf{v}+e_3\in {\mathbb{Z}}_q$.
  • For $i=1$ to l,

    (a)

    if the keyword $k_i\notin K{W}_{I{D}_x}$,

    • generate a random matrix $I_{2,k_i}^{I{D}_x}\in {\mathbb{Z}}_q^{m+w}$.

    (b)

    if $k_i\in K{W}_{I{D}_x}$, perform the following steps:

    • Compute ${\mathbf{H}}_{k_i}=H_2\left(k_i\right)\in {\mathbb{Z}}_q^{n\times n}$.
    • Compute $I_{2,k_i}^{I{D}_x}={\mathbf{A}}_{I{D}_x}^{{}^{\prime }\top }{\mathbf{H}}_{k_i}^{\top }\mathbf{v}+e_{4,i}\in {\mathbb{Z}}_q^{m+w}$.

  • Set the index $I_{I{D}_x}=\{I_1^{I{D}_x},{\left\{I_{2,k_i}^{I{D}_x}\right\}}_{1\le i\le l}\}$.
  • Choose DUs’ identities $ID$s.
  • Send ($(C_{I{D}_x}$, $I_{I{D}_x}$, $I{D}_x$), $ID$s) to PS.
  To reduce the computation and transmission costs of DO by outsourced computing, DO encrypts the message with its public key. Then, DO sends the ciphertext, index, and DUs’ IDs to PS. When the number of DUs increases, DO only needs to increase the list of receivers without any other cost. Therefore, when the number of DUs is large, the proposed scheme can effectively reduce the burden on DO.
• $(C_{I{D}_y},I_{I{D}_y},I{D}_y)\leftarrow$ Re-Enc($PP,(C_{I{D}_x},I_{I{D}_x},I{D}_x),I{D}_y,R{K}_{I{D}_x\to I{D}_y},$)
  Given the ciphertext $C_{I{D}_x}$, the index $I_{I{D}_x}$, DO’s identity $I{D}_x$, DU’s identity $I{D}_y\in ID\mathrm{s}$, and a re-encryption key $R{K}_{I{D}_x\to I{D}_y}$, PS can transfer $(C_{I{D}_x},I_{I{D}_x})$ to $(C_{I{D}_y},I_{I{D}_y})$ by the following steps:
  • Sample noises $e_2^{\prime },e_{4,1}^{\prime },e_{4,2}^{\prime },⁦,e_{4,l}^{\prime }\in {\chi }^{m+w}$.
  • Set $C_1^{I{D}_y}=C_1^{I{D}_x}$.
  • Compute $C_2^{I{D}_y}=R{K}_{I{D}_x\to I{D}_y}{C}_2^{I{D}_x}+e_2^{\prime }$.
  • Set $C_{I{D}_y}=\{C_1^{I{D}_y},C_2^{I{D}_y}\}$.
  • Set $I_1^{I{D}_y}=I_1^{I{D}_x}$.
  • For $i=1$ to l, compute $I_{2,k_i}^{I{D}_y}=R{K}_{I{D}_x\to I{D}_y}{I}_{2,k_i}^{I{D}_x}+e_{4,i}^{\prime }$.
  • Set $I_{I{D}_y}=\{I_1^{I{D}_y},{\left\{I_{2,k_i}^{I{D}_y}\right\}}_{1\le i\le l}\}$.
  • Upload ($C_{I{D}_y},I_{I{D}_y},I{D}_y$) to CS.
  PS computes an independent re-encrypted ciphertext and re-encrypted index for each DU. Moreover, the difficulty for an adversary to compute the re-encryption key from the ciphertext (or index) and the re-encrypted ciphertext (or re-encrypted index) is equivalent to solving the LWE problem.
• $(TK,ID)\leftarrow$ TokenGen($PP,ID,{SK}_{ID},\tau$)
  Taking a keyword-search policy $\tau$ and the private key ${SK}_{ID}$, the user $ID$ can compute the search token $TK$ by the following steps:
  • Compute ${\mathbf{A}}_{ID}=H_0\left(ID\right)\in {\mathbb{Z}}_q^{n\times w}$.
  • Set ${\mathbf{A}}_{ID}^{\prime }=\left[\mathbf{A}\right|{\mathbf{A}}_{ID}]\in {\mathbb{Z}}_q^{n\times (m+w)}$.
  • Compute ${\mathbf{H}}_{ID}=H_1\left(ID\right)\in {\mathbb{Z}}_q^{n\times n}$.
  • According to $\tau$, generate invertible matrices ${\{{\mathbf{T}}_{\tau ,k_i}\in {\{-1,0,1\}}^{n\times n}\}}_{k_i\in \tau }$. The detail of how to generate ${\left\{{\mathbf{T}}_{\tau ,k_i}\right\}}_{k_i\in \tau }$ is described in Section 2.6.
  • For $i=1$ to l,

    (a)

    if $k_i\in \tau$, then perform the following steps:

    • Compute ${\mathbf{H}}_{k_i}=H_2\left(k_i\right)\in {\mathbb{Z}}_q^{n\times n}$.
    • Compute the inverse matrix ${\mathbf{H}}_{k_i}^{-1}$ of ${\mathbf{H}}_{k_i}$, such that ${\mathbf{H}}_{k_i}^{-1}·{\mathbf{H}}_{k_i}={\mathbf{I}}_n$, where ${\mathbf{I}}_n$ is an identity matrix.
    • Perform SampleD(${\mathbf{R}}_{ID},{\mathbf{A}}_{ID}^{\prime },{\mathbf{H}}_{ID},{\mathbf{H}}_{k_i}^{-1}{\mathbf{T}}_{\tau ,k_i}^{\top }\mathbf{u},\sigma$) to get ${\mathbf{w}}_{k_i}$ such that ${\mathbf{A}}_{ID}^{\prime }{\mathbf{w}}_{k_i}={\mathbf{H}}_{k_i}^{-1}{\mathbf{T}}_{\tau ,k_i}^{\top }\mathbf{u}$.

  • Set the search token $TK=(\tau ,{\left\{{\mathbf{w}}_{k_i}\right\}}_{k_i\in \tau })$.
  • Send $(TK,ID)$ to CS.
  In the proposed scheme, DU can generate tokens since it has a trapdoor specific to its public key ${\mathbf{A}}_{ID}^{{}^{\prime }}$. Therefore, KGC does not need to stay online to assist in generating tokens. On the other hand, through the method mentioned in Section 2.6, if a keyword set $\{k_1^{\prime },k_2^{\prime },\dots ,k_o^{\prime }\}$ can exactly satisfy the keyword-search policy $\tau$, then ${\sum }_{i=1}^o{\mathbf{T}}_{\tau ,k_i^{\prime }}={\mathbf{I}}_n$. Therefore, TK generated by the TokenGen algorithm will make the following equation hold: ${\sum }_{i=1}^o{\mathbf{w}}_{k_i^{\prime }}^{\top }{\mathbf{A}}_{ID}^{\prime \top }{\mathbf{H}}_{k_i^{\prime }}^{\top }={\sum }_{i=1}^o{\left({\mathbf{A}}_{ID}^{\prime }{\mathbf{w}}_{k_i^{\prime }}\right)}^{\top }{\mathbf{H}}_{k_i^{\prime }}^{\top }={\sum }_{i=1}^o{\mathbf{u}}^{\top }{\mathbf{T}}_{\tau ,k_i^{\prime }}{\mathbf{H}}_{k_i^{\prime }}^{-1^{\top }}{\mathbf{H}}_{k_i^{\prime }}^{\top }={\sum }_{i=1}^o{\mathbf{u}}^{\top }{\mathbf{T}}_{\tau ,k_i^{\prime }}={\mathbf{u}}^{\top }$.
• $(C_{ID}$ or $\perp )\leftarrow \mathit{Search}(PP,TK,ID,(C_{ID},I_{ID}))$
  Given $TK$, $ID$, and $(C_{ID},I_{ID})$, CS checks whether $TK$ matches $I_{ID}$ by the following steps:
  • According to the keyword-search policy $\tau$, for any keyword set $\{k_1^{\prime },k_2^{\prime },\dots ,k_o^{\prime }\}$ exactly satisfying $\tau$, CS performs the following steps:

    (a)

    Set $\mathbf{z}=\mathbf{0}$.

    (b)

    for $i=1$ to l,

    • if $k_i\in \{k_1^{\prime },k_2^{\prime },\dots ,k_o^{\prime }\}$,
      • compute $\mathbf{z}=\mathbf{z}+{\mathbf{w}}_{k_i}^{\top }{I}_{2,k_i}^{ID}$.

    (c)

    Compute $f=|\mathbf{z}-I_1^{ID}|$.

    (d)

    If $f<\frac{q}{4}$, send $C_{ID}$ to DU.

  • Return ⊥ to DU, if there are no matching search results.
  By choosing appropriate parameter values, the size of the error term should be between $-q/4$ and $q/4$. Therefore, if the search token matches the index, the search result f should be less than $q/4$.
• $\left(\mu \right)\leftarrow$ Dec($PP,{SK}_{ID},C_{ID}$)
  With the ciphertext $C_{ID}$ and private key $S{K}_{ID}$, the user ID can decrypt $C_{ID}$ by the following steps:
  • Compute ${\mu }^{\prime }=|C_1^{ID}-{\mathbf{x}}_{ID}^{\top }{C}_2^{ID}|$.
  • If ${\mu }^{\prime }<\frac{q}{4}$, return $\mu =0$; otherwise return $\mu =1$.
  By choosing appropriate parameter values, the size of the error term should be between $-q/4$ and $q/4$. Therefore, if the decrypted result ${\mu }^{{}^{\prime }}$ is less than $q/4$, the plaintext should be 0. Note that while DU may compute ${\mathbf{x}}_{ID}$ with the trapdoor ${\mathbf{R}}_{ID}$, we recommend DU to store ${\mathbf{x}}_{ID}$. Because computing it requires a  SampleD operation, storing ${\mathbf{x}}_{ID}$ can reduce the computation cost for decryption.

4.2. Correctness

• Correctness in Search
  Suppose ${\sum }_{i=1}^o{\mathbf{T}}_{\tau ,k_i^{\prime }}={\mathbf{I}}_n$, which means that the keyword set $\{k_1^{\prime },k_2^{\prime },\dots ,k_o^{\prime }\}$ can exactly satisfy the keyword-search policy $\tau$. Note that ${\mathbf{I}}_n$ is an identity matrix.
  $\begin{array}{cc}\hfill f& =|\mathbf{z}-I_1^{ID}|\hfill \\ & =|\sum _{i=1}^o{\mathbf{w}}_{k_i^{\prime }}^{\top }{I}_{2,k_i^{\prime }}^{ID}-I_1^{ID}|\hfill \\ & =|\sum _{i=1}^o({\mathbf{w}}_{k_i^{\prime }}^{\top }{\mathbf{A}}_{ID}^{\prime \top }{\mathbf{H}}_{k_i^{\prime }}^{\top }\mathbf{v}+{\mathbf{w}}_{k_i^{\prime }}^{\top }{e}_{4,i^{\prime }})-({\mathbf{u}}^{\top }\mathbf{v}+e_3)|\hfill \\ & =|\sum _{i=1}^o{\mathbf{u}}^{\top }{\mathbf{T}}_{\tau ,k_i^{\prime }}{\mathbf{H}}_{k_i^{\prime }}^{-1^{\top }}{\mathbf{H}}_{k_i^{\prime }}^{\top }\mathbf{v}+\sum _{i=1}^o{\mathbf{w}}_{k_i^{\prime }}^{\top }{e}_{4,i^{\prime }}-{\mathbf{u}}^{\top }\mathbf{v}-e_3|\hfill \\ & =|\sum _{i=1}^o{\mathbf{u}}^{\top }{\mathbf{T}}_{\tau ,k_i^{\prime }}\mathbf{v}+\sum _{i=1}^o{\mathbf{w}}_{k_i^{\prime }}^{\top }{e}_{4,i^{\prime }}-{\mathbf{u}}^{\top }\mathbf{v}-e_3|\hfill \\ & =|{\mathbf{u}}^{\top }\mathbf{v}+\sum _{i=1}^o{\mathbf{w}}_{k_i^{\prime }}^{\top }{e}_{4,i^{\prime }}-{\mathbf{u}}^{\top }\mathbf{v}-e_3|\hfill \\ & =|\underset{\mathrm{error}\mathrm{term}}{\underbrace{{\sum }_{i=1}^o{\mathbf{w}}_{k_i^{\prime }}^{\top }{e}_{4,i^{\prime }}-e_3}}|\hfill \end{array}$
  For the correctness of the search result, the absolute value of the error term must be less than $q/4$.
• Correctness in Decryption
  $\begin{array}{cc}\hfill {\mu }^{{}^{\prime }}& =|C_1^{ID}-{\mathbf{x}}^{\top }{C}_2^{ID}|\hfill \\ & =|({\mathbf{u}}^{\top }\mathbf{s}+\mu ⌊\frac{q}{2}⌋+e_1)-({\mathbf{x}}^{\top }{\mathbf{A}}_{ID}^{\prime \top }\mathbf{s}+{\mathbf{x}}^{\top }{e}_2)|\hfill \\ & =|{\mathbf{u}}^{\top }\mathbf{s}+\mu ⌊\frac{q}{2}⌋+e_1-{\mathbf{u}}^{\top }\mathbf{s}-{\mathbf{x}}^{\top }{e}_2|\hfill \\ & =|\mu \lfloor \frac{q}{2}\rfloor +\underset{\mathrm{error}\mathrm{term}}{\underbrace{e_1-{\mathbf{x}}^{\top }{e}_2}}|\hfill \end{array}$
  For the correctness of the decryption result, the absolute value of the error term must be less than $q/4$.

5. Security Proofs

The proposed scheme is IND-CPA secure in ciphertext security and IND-CKA secure in keyword-search security based on the D-LWE assumption defined in Section 2.4. Proof by contradiction is used to prove that the proposed scheme achieves IND-CPA security and IND-CKA security. This section presents the details of security proofs.

5.1. Ciphertext Security

Theorem 1.

The proposed scheme is IND-CPA secure in ciphertext security based on the D-LWE assumption.

Proof. 

If there exists an adversary $\mathcal{A}$ that can win the IND-CPA game defined in Section 2.8.1 with a non-negligible advantage in polynomial time, then the simulator $\mathcal{S}$ can break the D-LWE assumption with $\mathcal{A}$ by simulating the following game.

• $\mathbf{Init}$: $\mathcal{A}$ gives a target identity $I{D}^{*}$ to $\mathcal{S}$. $\mathcal{S}$ chooses two integers $(m^{\prime },w)$ and sets $m=m^{\prime }+w$. Then $\mathcal{S}$ receives $(1+m+w)$ samples $({\mathbf{u}}_0,v_0),({\mathbf{u}}_1,v_1),({\mathbf{u}}_2,v_2),\dots ,({\mathbf{u}}_{m+w},v_{m+w})$ from the D-LWE oracle $\mathcal{O}$, where each $({\mathbf{u}}_i,v_i)\in ({\mathbb{Z}}_q^n\times {\mathbb{Z}}_q)$.
• $\mathbf{Setup}$:

  –

  $\mathcal{S}$ chooses $\lambda$ and runs $\mathit{Setup}\left(\lambda \right)$ algorithm to generate the following parameters and hash functions $(\chi ,\sigma ,q,n,l,KW={\left\{k_i\right\}}_{1\le i\le l},H_0,H_1,H_2)$.

  –

  $\mathcal{S}$ sets $\mathbf{u}={\mathbf{u}}_0$, ${\mathbf{A}}_0=[{\mathbf{u}}_1|{\mathbf{u}}_2|\dots |{\mathbf{u}}_{m^{\prime }}]\in {\mathbb{Z}}_q^{n\times m^{\prime }}$, and ${\mathbf{A}}_1=[{\mathbf{u}}_{m^{\prime }+1}|{\mathbf{u}}_{m^{\prime }+2}|\dots |{\mathbf{u}}_m]\in {\mathbb{Z}}_q^{n\times w}$. Note that $m=m^{\prime }+w$.

  –

  $\mathcal{S}$ computes an invertible matrix $\mathbf{H}$ and a small matrix $\mathbf{R}$ such that ${\mathbf{A}}_1=-{\mathbf{A}}_0\mathbf{R}+\mathbf{H}\mathbf{G}$, where $\mathbf{G}\in {\mathbb{Z}}_q^{n\times w}$ is a gadget matrix defined in Section 2.5.

  –

  $\mathcal{S}$ sets $MSK=\mathbf{R},\mathbf{A}=\left[{\mathbf{A}}_0\right|{\mathbf{A}}_1]$, and $PP=(\chi ,\sigma ,q,n,m,l,w,KW,H_2,\mathbf{A},\mathbf{u})$.

  –

  Finally, $\mathcal{S}$ sends $PP$ to $\mathcal{A}$.

• $\mathbf{Phase}\mathbf{1}$: $\mathcal{A}$ may adaptively issue the following queries.

  –

  $H_0$ query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$.

  *

  If $ID\ne I{D}^{*}$, $\mathcal{S}$ computes ${\mathbf{A}}_{ID}=H_0\left(ID\right)\in {\mathbb{Z}}_q^{n\times w}$ and sends it to $\mathcal{A}$.

  *

  If $ID=I{D}^{*}$, $\mathcal{S}$ sets ${\mathbf{A}}_{I{D}^{*}}=[{\mathbf{u}}_{m+1}|{\mathbf{u}}_{m+2}|\dots |{\mathbf{u}}_{m+w}]\in {\mathbb{Z}}_q^{n\times w}$ and sends ${\mathbf{A}}_{I{D}^{*}}$ to $\mathcal{A}$.

  –

  $H_1$ query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$.

  *

  If $ID\ne I{D}^{*}$, $\mathcal{S}$ computes ${\mathbf{H}}_{ID}=H_1\left(ID\right)\in {\mathbb{Z}}_q^{n\times n}$ and sends it to $\mathcal{A}$.

  *

  If $ID=I{D}^{*}$,

  ·

  if ${\mathbf{H}}_{I{D}^{*}}$ exists, $\mathcal{S}$ returns ${\mathbf{H}}_{I{D}^{*}}$ to $\mathcal{A}$.

  ·

  else, $\mathcal{S}$ computes an invertible matrix ${\mathbf{H}}_{I{D}^{*}}$ and a small matrix ${\mathbf{R}}_{I{D}^{*}}$ such that $\mathbf{A}{\mathbf{R}}_{I{D}^{*}}={\mathbf{H}}_{I{D}^{*}}\mathbf{G}-{\mathbf{A}}_{I{D}^{*}}$. $\mathcal{S}$ stores ${\mathbf{H}}_{I{D}^{*}}$ and sends it to $\mathcal{A}$.

  –

  KeyGen query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$.

  *

  If $ID\ne I{D}^{*}$,

  ·

  if $S{K}_{ID}$ exists, $\mathcal{S}$ returns $S{K}_{ID}$ to $\mathcal{A}$.

  ·

  else, $\mathcal{S}$ runs $\mathbf{KeyGen}(PP,MSK,ID)$ to generate $S{K}_{ID}$. $\mathcal{S}$ stores $S{K}_{ID}$ and sends it to $\mathcal{A}$.

  *

  If $I{D}_x=I{D}^{*}$, $\mathcal{S}$ aborts it.

  –

  Re-KeyGen query: $\mathcal{A}$ gives DO’s identity $I{D}_x$ and DU’s indetiy $I{D}_y$ to $\mathcal{S}$.

  *

  If $I{D}_x\ne I{D}^{*}$, $\mathcal{S}$ runs Re-KeyGen($PP,I{D}_x,I{D}_y,S{K}_{I{D}_x}$) to generate $R{K}_{I{D}_x\to I{D}_y}$ and sends it to $\mathcal{A}$.

  *

  If $I{D}_x=I{D}^{*}$, $\mathcal{S}$ aborts it.

• $\mathbf{Challenge}$: $\mathcal{A}$ submits two different messages ${\mu }_0,{\mu }_1\in \{0,1\}$ to $\mathcal{S}$. $\mathcal{S}$ performs the following steps:

  –

  $\mathcal{S}$ randomly chooses $b\in \{0,1\}$.

  –

  $\mathcal{S}$ computes $C_1^{I{D}^{*}}=v_0+{\mu }_b⌊\frac{q}{2}⌋\in {\mathbb{Z}}_q$.

  –

  $\mathcal{S}$ sets $C_2^{I{D}^{*}}={[v_1,v_2,\dots ,v_{m+w}]}^{\top }\in {\mathbb{Z}}_q^{m+w}$.

  –

  $\mathcal{S}$ sets the ciphertext $C_{I{D}^{*}}=\{C_1^{I{D}^{*}},C_2^{I{D}^{*}}\}$ and sends it to $\mathcal{A}$.

• $\mathbf{Phase}\mathbf{2}$: $\mathcal{A}$ may do more queries as in $\mathbf{Phase}\mathbf{1}$.
• $\mathbf{Guess}$: $\mathcal{A}$ answers a bit $b^{\prime }$ to $\mathcal{S}$. If $b=b^{\prime }$, $\mathcal{S}$ answers the D-LWE assumption that the samples are from the noisy pseudo-random sampler ${\mathcal{O}}_s$. Otherwise, $\mathcal{S}$ answers that the samples are from the truly random sampler ${\mathcal{O}}_{\mathsf{\$}}$.

If the samples from the D-LWE assumption are generated from ${\mathcal{O}}_s$, the ciphertext $C_{I{D}^{*}}$ will be:

$\begin{array}{cc}\hfill C_1^{I{D}^{*}}& =v_0+{\mu }_b⌊\frac{q}{2}⌋\hfill \\ & ={\mathbf{u}}_0^{\top }\mathbf{s}+{\mu }_b\lfloor \frac{q}{2}\rfloor +e_0\hfill \\ & ={\mathbf{u}}^{\top }\mathbf{s}+{\mu }_b\lfloor \frac{q}{2}\rfloor +e_0\hfill \end{array}$

$\begin{array}{cc}\hfill C_2^{I{D}^{*}}& ={[v_1,v_2,\dots ,v_{m+w}]}^{\top }\hfill \\ & =[[{\mathbf{u}}_1,\dots ,{\mathbf{u}}_{m^{\prime }}]|[{\mathbf{u}}_{m^{\prime }+1},\dots ,{\mathbf{u}}_m]\left|[{\mathbf{u}}_{m+1},\dots ,{\mathbf{u}}_{m+w}]\right]{}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & =\left[\left[{\mathbf{A}}_0\right|{\mathbf{A}}_1]\right|{\mathbf{A}}_{I{D}^{*}}]{}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & ={\left[\mathbf{A}\right|{\mathbf{A}}_{I{D}^{*}}]}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & ={\left[{\mathbf{A}}_{I{D}^{*}}^{\prime }\right]}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \end{array}$

Therefore, the ciphertext simulated by $\mathcal{S}$ will conform to the format of the proposed scheme. If $\mathcal{A}$ has a non-negligible advantage $ϵ$ to win the IND-CPA game defined in Section 2.8.1, the probability that $\mathcal{A}$ can correctly guess b is $(\frac{1}{2}+ϵ)$.

Otherwise, if the samples are from ${\mathcal{O}}_{\mathsf{\$}}$, then the ciphertext $C_{I{D}^{*}}$ is uniformly random. In this case, the probability that $\mathcal{A}$ can correctly guess b is $\frac{1}{2}$.

Thus, the advantage for $\mathcal{S}$ to break the D-LWE assumption is

$$\left|Pr[{\mathcal{A}}^{{\mathcal{O}}_s}=1]-Pr[{\mathcal{A}}^{{\mathcal{O}}_{\mathsf{\$}}}=1]\right|=\left|(\frac{1}{2}+ϵ)-\frac{1}{2}\right|=ϵ$$

Therefore, if $\mathcal{A}$ has an advantage $ϵ$ to win the IND-CPA game, then $\mathcal{S}$ has an advantage $ϵ$ to break the D-LWE assumption in polynomial time. Since the D-LWE assumption is a hard problem, the proposed scheme achieves IND-CPA security.  □

5.2. Keyword-Search Security

Theorem 2.

The proposed scheme is IND-CKA secure in keyword-search security based on the D-LWE assumption.

Proof. 

If there exists an adversary $\mathcal{A}$ that can win the IND-CKA game defined in Section 2.8.2 with a non-negligible advantage in polynomial time, then the simulator $\mathcal{S}$ can break the D-LWE assumption with $\mathcal{A}$ by simulating the following game.

• $\mathbf{Init}$: $\mathcal{A}$ gives a target identity $I{D}^{*}$ and two target keywords $(k_0^{\prime },k_1^{\prime })$ to $\mathcal{S}$.

  –

  $\mathcal{S}$ randomly chooses $b\in \{0,1\}$ and will use $k_b^{\prime }$ for the challenge.

  –

  $\mathcal{S}$ chooses two integers $(m^{\prime },w)$ and sets $m=m^{\prime }+w$. Then $\mathcal{S}$ receives $(1+m+w)$ samples $({\mathbf{u}}_0,v_0),({\mathbf{u}}_1,v_1),({\mathbf{u}}_2,v_2),\dots ,({\mathbf{u}}_{m+w},v_{m+w})$ from the D-LWE oracle $\mathcal{O}$, where each $({\mathbf{u}}_i,v_i)\in ({\mathbb{Z}}_q^n\times {\mathbb{Z}}_q)$.

• $\mathbf{Setup}$:

  –

  $\mathcal{S}$ chooses $\lambda$ and runs $\mathbf{Setup}\left(\lambda \right)$ algorithm to generate the following parameters and hash functions $(\chi ,\sigma ,q,n,l,KW={\left\{k_i\right\}}_{1\le i\le l},H_0,H_1,H_2)$.

  –

  $\mathcal{S}$ sets $\mathbf{u}={\mathbf{u}}_0$, ${\mathbf{B}}_0=[{\mathbf{u}}_1|{\mathbf{u}}_2|\dots |{\mathbf{u}}_{m^{\prime }}]\in {\mathbb{Z}}_q^{n\times m^{\prime }}$, and ${\mathbf{B}}_1=[{\mathbf{u}}_{m^{\prime }+1}|{\mathbf{u}}_{m^{\prime }+2}|\dots |{\mathbf{u}}_m]\in {\mathbb{Z}}_q^{n\times w}$. Note that $m=m^{\prime }+w$.

  –

  $\mathcal{S}$ computes ${\mathbf{H}}_{k_b^{\prime }}=H_2\left(k_b^{\prime }\right)\in {\mathbb{Z}}_q^{n\times n}$ and its inverse matrix ${\mathbf{H}}_{k_b^{\prime }}^{-1}$. Then $\mathcal{S}$ stores ${\mathbf{H}}_{k_b^{\prime }}^{-1}$.

  –

  $\mathcal{S}$ computes the following matrices:

  *

  ${\mathbf{A}}_0={\mathbf{H}}_{k_b^{\prime }}^{-1}{\mathbf{B}}_0$,

  *

  ${\mathbf{A}}_1={\mathbf{H}}_{k_b^{\prime }}^{-1}{\mathbf{B}}_1$.

  Note that ${\mathbf{B}}_0={\mathbf{H}}_{k_b^{\prime }}{\mathbf{A}}_0$, and ${\mathbf{B}}_1={\mathbf{H}}_{k_b^{\prime }}{\mathbf{A}}_1$.

  –

  $\mathcal{S}$ computes an invertible matrix $\mathbf{H}$ and a small matrix $\mathbf{R}$ such that ${\mathbf{A}}_1=-{\mathbf{A}}_0\mathbf{R}+\mathbf{H}\mathbf{G}$, where $\mathbf{G}\in {\mathbb{Z}}_q^{n\times w}$ is a gadget matrix defined in Section 2.5.

  –

  $\mathcal{S}$ sets $MSK=\mathbf{R},\mathbf{A}=\left[{\mathbf{A}}_0\right|{\mathbf{A}}_1]$, and $PP=(\chi ,\sigma ,q,n,m,l,w,KW,H_2,\mathbf{A},\mathbf{u})$.

  –

  Finally, $\mathcal{S}$ sends $PP$ to $\mathcal{A}$.

• $\mathbf{Phase}\mathbf{1}$: $\mathcal{A}$ may adaptively issue the following queries.

  –

  $H_0$ query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$.

  *

  If $ID\ne I{D}^{*}$, $\mathcal{S}$ computes ${\mathbf{A}}_{ID}=H_0\left(ID\right)\in {\mathbb{Z}}_q^{n\times w}$ and sends it to $\mathcal{A}$.

  *

  If $ID=I{D}^{*}$, $\mathcal{S}$ sets ${\mathbf{B}}_{I{D}^{*}}=[{\mathbf{u}}_{m+1}|{\mathbf{u}}_{m+2}|\dots |{\mathbf{u}}_{m+w}]\in {\mathbb{Z}}_q^{n\times w}$. Then, $\mathcal{S}$ computes ${\mathbf{A}}_{I{D}^{*}}={\mathbf{H}}_{k_b^{\prime }}^{-1}{\mathbf{B}}_{I{D}^{*}}$ and sends ${\mathbf{A}}_{I{D}^{*}}$ to $\mathcal{A}$.

  –

  $H_1$ query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$.

  *

  If $ID\ne I{D}^{*}$, $\mathcal{S}$ computes ${\mathbf{H}}_{ID}=H_1\left(ID\right)\in {\mathbb{Z}}_q^{n\times n}$ and sends it to $\mathcal{A}$.

  *

  If $ID=I{D}^{*}$,

  ·

  if ${\mathbf{H}}_{I{D}^{*}}$ exists, $\mathcal{S}$ returns ${\mathbf{H}}_{I{D}^{*}}$ to $\mathcal{A}$.

  ·

  else, $\mathcal{S}$ computes an invertible matrix ${\mathbf{H}}_{I{D}^{*}}$ and a small matrix ${\mathbf{R}}_{I{D}^{*}}$ such that $\mathbf{A}{\mathbf{R}}_{I{D}^{*}}={\mathbf{H}}_{I{D}^{*}}\mathbf{G}-{\mathbf{A}}_{I{D}^{*}}$. $\mathcal{S}$ sets $S{K}_{I{D}^{*}}={\mathbf{R}}_{I{D}^{*}}$ and stores it. Finally, $\mathcal{S}$ stores ${\mathbf{H}}_{I{D}^{*}}$ and sends it to $\mathcal{A}$.

  –

  KeyGen query: $\mathcal{A}$ gives an identity $ID$ to $\mathcal{S}$.

  *

  If $ID\ne I{D}^{*}$,

  ·

  if $S{K}_{ID}$ exists, $\mathcal{S}$ returns $S{K}_{ID}$ to $\mathcal{A}$.

  ·

  else, $\mathcal{S}$ runs $\mathbf{KeyGen}(PP,MSK,ID)$ to generate $S{K}_{ID}$. $\mathcal{S}$ stores $S{K}_{ID}$ and sends it to $\mathcal{A}$.

  *

  If $I{D}_x=I{D}^{*}$, $\mathcal{S}$ aborts it.

  –

  Re-KeyGen query: $\mathcal{A}$ gives DO’s identity $I{D}_x$ and DU’s indetiy $I{D}_y$ to $\mathcal{S}$.

  *

  If $I{D}_x\ne I{D}^{*}$, $\mathcal{S}$ runs Re-KeyGen($PP,I{D}_x,I{D}_y,S{K}_{I{D}_x}$) to generate $R{K}_{I{D}_x\to I{D}_y}$ and sends it to $\mathcal{A}$.

  *

  If $I{D}_x=I{D}^{*}$, $\mathcal{S}$ aborts it.

  –

  TokenGen query: $\mathcal{A}$ gives an identity $ID$ and a keyword-search policy $\tau$ to $\mathcal{S}$.

  *

  If ($ID=I{D}^{*}$ and ($\tau$ contains $k_0^{\prime }$ or $k_1^{\prime }$)), $\mathcal{S}$ aborts it.

  *

  Else, $\mathcal{S}$ runs $\mathbf{TokenGen}(PP,ID,{SK}_{ID},\tau )$ to generate $TK$. Then $\mathcal{S}$ sends $(TK,ID)$ to $\mathcal{A}$.

• $\mathbf{Challenge}$: $\mathcal{A}$ submits a signal to start the $\mathbf{Challenge}$ phase. $\mathcal{S}$ performs the following steps:

  –

  $\mathcal{S}$ sets $I_1^{I{D}^{*}}=v_0\in {\mathbb{Z}}_q$.

  –

  $\mathcal{S}$ sets $I_{2,k_b^{\prime }}^{I{D}^{*}}={[v_1,v_2,\dots ,v_{m+w}]}^{\top }\in {\mathbb{Z}}_q^{m+w}$.

  –

  $\mathcal{S}$ sets the index $I_{I{D}^{*}}=\{I_1^{I{D}^{*}},I_{2,k_b^{\prime }}^{I{D}^{*}}\}$ and sends it to $\mathcal{A}$.

• $\mathbf{Phase}\mathbf{2}$: $\mathcal{A}$ may do more queries as in $\mathbf{Phase}\mathbf{1}$.
• $\mathbf{Guess}$: $\mathcal{A}$ answers a bit $b^{\prime }$ to $\mathcal{S}$. If $b=b^{\prime }$, $\mathcal{S}$ answers the D-LWE assumption that the samples are from the noisy pseudo-random sampler ${\mathcal{O}}_s$. Otherwise, $\mathcal{S}$ answers that the samples are from the truly random sampler ${\mathcal{O}}_{\mathsf{\$}}$.

If the samples from the D-LWE assumption are generated from ${\mathcal{O}}_s$, the index $I_{I{D}^{*}}$ will be:

$\begin{array}{cc}\hfill I_1^{I{D}^{*}}& =v_0\hfill \\ & ={\mathbf{u}}_0^{\top }\mathbf{s}+e_0\hfill \\ & ={\mathbf{u}}^{\top }\mathbf{s}+e_0\hfill \end{array}$

$\begin{array}{cc}\hfill I_{2,k_b^{\prime }}^{I{D}^{*}}& ={[v_1,v_2,\dots ,v_{m+w}]}^{\top }\hfill \\ & =[[{\mathbf{u}}_1,\dots ,{\mathbf{u}}_{m^{\prime }}]|[{\mathbf{u}}_{m^{\prime }+1},\dots ,{\mathbf{u}}_m]\left|[{\mathbf{u}}_{m+1},\dots ,{\mathbf{u}}_{m+w}]\right]{}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & =[{\mathbf{B}}_0|{\mathbf{B}}_1\left|{\mathbf{B}}_{I{D}^{*}}\right]{}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & =[\left({\mathbf{H}}_{k_b^{\prime }}{\mathbf{A}}_0\right)|\left({\mathbf{H}}_{k_b^{\prime }}{\mathbf{A}}_1\right){\left|\left({\mathbf{H}}_{k_b^{\prime }}{\mathbf{A}}_{I{D}^{*}}\right)\right]}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & =({\mathbf{H}}_{k_b^{\prime }}[{\mathbf{A}}_0|{\mathbf{A}}_1|{\mathbf{A}}_{I{D}^{*}}{\left]\right)}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & =[{\mathbf{A}}_0|{\mathbf{A}}_1{\left|{\mathbf{A}}_{I{D}^{*}}\right]}^{\top }{\mathbf{H}}_{k_b^{\prime }}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & ={\left[\mathbf{A}\right|{\mathbf{A}}_{I{D}^{*}}]}^{\top }{\mathbf{H}}_{k_b^{\prime }}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \\ & ={\left[{\mathbf{A}}_{I{D}^{*}}^{\prime }\right]}^{\top }{\mathbf{H}}_{k_b^{\prime }}^{\top }\mathbf{s}+{[e_1,e_2,\dots ,e_{m+w}]}^{\top }\hfill \end{array}$

Therefore, the index simulated by $\mathcal{S}$ will conform to the format of the proposed scheme. If $\mathcal{A}$ has a non-negligible advantage $ϵ$ to win the IND-CKA game defined in Section 2.8.2, the probability that $\mathcal{A}$ can correctly guess b is $(\frac{1}{2}+ϵ)$.

Otherwise, if the samples are from ${\mathcal{O}}_{\mathsf{\$}}$, then the index $I_{I{D}^{*}}$ is uniformly random. In this case, the probability that $\mathcal{A}$ can correctly guess b is $\frac{1}{2}$.

Thus, the advantage for $\mathcal{S}$ to break the D-LWE assumption is

$$\left|Pr[{\mathcal{A}}^{{\mathcal{O}}_s}=1]-Pr[{\mathcal{A}}^{{\mathcal{O}}_{\mathsf{\$}}}=1]\right|=\left|(\frac{1}{2}+ϵ)-\frac{1}{2}\right|=ϵ$$

Therefore, if $\mathcal{A}$ has an advantage $ϵ$ to win the IND-CKA game, then $\mathcal{S}$ has an advantage $ϵ$ to break the D-LWE assumption in polynomial time. Since the D-LWE assumption is a hard problem, the proposed scheme achieves IND-CKA security.  □

6. Comparison

Table 2 shows the features comparison between the proposed scheme and the schemes introduced in Section 3. Moreover, this section presents a performance comparison of the proposed scheme with other lattice-based searchable encryption schemes. Because some schemes use one-bit plaintext or one recipient to illustrate their schemes, it is not easy to make a completely fair comparison. For fairness, the plaintext in all schemes is set as a one-bit message, and the number of receivers is 1. Moreover, values that do not specify the meaning of parameters in all schemes will be set to m. The notations used for comparison are shown in Table 3.

Table 2. Features Comparison.

	Quantum Resistant	Multi- Keyword	Offline KGC	Proxy Re-Encryption	Authentication		Not LSSS-Based	Functional Encryption
					Decryption	Search
[26]	✗	✓	✓	✗	✓	✓	✓	ABE
[27]	✓	✓	✓	✗	✗	✓	✓	IBE
[17]	✓	✗	✗	✗	✓	✗	✗	ABE
[20]	✓	✗	✗	✗	✗	✓	✗	ABE
[21]	✓	✗	✓	✗	✓	✓	✗	ABE
[22]	✓	✓	✓	✗	✓	✓	✗	ABE
[19]	✓	✗	✓	✗	✗	✓	✓	IBE
[18]	✓	✗	✓	✗	✓	✓	✓	SPE
[29]	✓	✗	✗	✓	✗	✓	✓	✗
[30]	✓	✓	✗	✓	✗	✓	✓	✗
Ours	✓	✓	✓	✓	✓	✓	✓	IBE

KGC denotes the key generation center. ABE denotes attribute-based encryption. IBE denotes identity-based encryption. SPE denotes subset predicate encryption.

Table 3. Notations for Comparison.

	Meaning
n	The dimension of a vector space
m	The number of vectors of a basis
q	A modulo prime number
N	$N=(n+1)logq$
s	The number of attributes used in ABE
$s^{\prime }$	The number of bits of a set used in SPE
$\beta$	The number of random values to generate secret shares in LSSS
l	The number of keywords
w	A key generated by DelTrap has w bits more than the original private key
$\zeta$	A security parameter

6.1. Transmission Cost

We compare the ciphertext size, index size, and token size with other lattice-based schemes. The transmission cost of the schemes are shown in Table 4.

• Ciphertext size: Since the proposed scheme uses DelTrap to achieve ID-based features, the ciphertext size requires $(m+w+1)logq$ bits. On the other hand, all users use the same key for decryption in [20], so its ciphertext size can be shorter than other schemes. Moreover, [19,27,29,30] do not provide or detail the decryption phase.
• Index size: The proposed scheme supports multi-keyword search, which requires a multiple of l more index sizes. Therefore, the index size of the proposed scheme is $\left(l\right(m+w)+1)logq$.
• Token size: The proposed scheme supports multi-keyword search, which requires a multiple of l more token sizes. Therefore, the token size of the proposed scheme is $l(m+w)logq$.

To compare, one can consider comparing single-keyword searches. One can set $l=1$ and $w=m$. Then, in the proposed scheme, the ciphertext size is $(2m+1)logq$, the index size is $(2m+1)logq$, and the token size is $2mlogq$. In this case, the proposed scheme is only slightly worse than [19,29] in the part of the token size. Therefore, the proposed scheme has a good performance in transmission cost.

Table 4. Comparison of Transmission Cost.

	Ciphertext Size	Index Size	Token Size
Wang et al. [27]	✗	$(lm+3m)logq$	$m^{2}logq$
Liu et al. [17]	$(2ms+1)logq$	$(2lm+l)logq$	$2mlogq$
Varri et al. [20]	$(2m+n)logq$	$(2lm+ns)logq$	$2mlogq$
Chen [21]	$(ms+1)logq$	$(ms+\zeta )logq$	$\left(ms\zeta \right)logq$
Wang [22]	$(ms+1)logq$	$(ms+\zeta )logq$	$(ms\zeta +l)logq$
Zhang et al. [19]	✗	$(1+2m)logq$	$mlogq$
Wang et al. [18]	$(1+m+s^{\prime }m)logq$	$(m+s^{\prime }m+\zeta )logq$	$2\zeta mlogq$
Zhang et al. [29]	✗	$(2n+2)logq$	$mlogq$
Hou et al. [30]	✗	${\left(N\right)}^2(logq)$	${\left(N\right)}^2(logq)$
Ours	$(m+w+1)logq$	$\left(l\right(m+w)+1)logq$	$l(m+w)logq$

✗ indicates that the scheme does not provide or detail the part.

Table 4. Comparison of Transmission Cost.

	Ciphertext Size	Index Size	Token Size
Wang et al. [27]	✗	$(lm+3m)logq$	$m^{2}logq$
Liu et al. [17]	$(2ms+1)logq$	$(2lm+l)logq$	$2mlogq$
Varri et al. [20]	$(2m+n)logq$	$(2lm+ns)logq$	$2mlogq$
Chen [21]	$(ms+1)logq$	$(ms+\zeta )logq$	$\left(ms\zeta \right)logq$
Wang [22]	$(ms+1)logq$	$(ms+\zeta )logq$	$(ms\zeta +l)logq$
Zhang et al. [19]	✗	$(1+2m)logq$	$mlogq$
Wang et al. [18]	$(1+m+s^{\prime }m)logq$	$(m+s^{\prime }m+\zeta )logq$	$2\zeta mlogq$
Zhang et al. [29]	✗	$(2n+2)logq$	$mlogq$
Hou et al. [30]	✗	${\left(N\right)}^2(logq)$	${\left(N\right)}^2(logq)$
Ours	$(m+w+1)logq$	$\left(l\right(m+w)+1)logq$	$l(m+w)logq$

✗ indicates that the scheme does not provide or detail the part.

6.2. Computation Cost

We compare the costs of “Encryption plus Index”, Decryption, TokenGen, and Search with other lattice-based schemes. The details of computation cost are shown in Table 5 and Table 6. For fairness, we compare the amount of $T_{mul}$ required for matrix multiplication in each scheme, where $T_{mul}$ denotes the computation cost of a multiplication operation in ${\mathbb{Z}}_q$. $T_{inv}$ denotes the cost of computing an inverse matrix. $T_H$ and $T_{fla}$ denote the cost of running a hash function and a Flatten operation, respectively. $T_{bd},T_{sd},T_{sp}$, and $T_{sl}$ denote the costs of running algorithms BasisDel, SampleD, SamplePre, and SampleLeft, respectively. $T_{de{c}_{FHE}}$ denotes the decryption cost of fully homomorphic encryption. $T_{lsss}$ denotes the cost of computing an integer coefficient set in LSSS.

Table 5. Comparison of Computation Cost—Part 1.

	Encryption + Index	Decryption
[27]	$l{T}_H+((l+2)mn+m)T_{mul}$	✗
[17]	$l{T}_H+n(l+2lm+2ms+1)T_{mul}$	$T_{lsss}+s(3+4m)T_{mul}$
[20]	$l{T}_H+(s\beta +m^2+2lmn+n)T_{mul}$	$(2mn+2m)T_{mul}$
[21]	$\zeta T_H+(s\beta +1+n)+\zeta (1+n)+(s+2mns)T_{mul}$	$mns{T}_{mul}$
[22]	$\zeta T_H+(s\beta +1+n)+\zeta (1+n)+(s+2mns)T_{mul}$	$mns{T}_{mul}$
[19]	$2T_H+T_{sp}+T_{inv}+(2n{m}^2+mn)T_{mul}$	✗
[18]	$(s^{\prime }mn+\zeta n+mn+n)T_{mul}$	$2m{T}_{mul}$
[29]	$T_H+(n^2+mn+4n)T_{mul}$	✗
[30]	$T_{fla}+(N^3+N{m}^2)T_{mul}$	✗
Ours	$(l+1)T_H+(n(l+1)(m+w)+2n)T_{mul}$	$(m+w)T_{mul}$

✗ indicates that the scheme does not provide or detail the part.

Table 6. Comparison of Computation Cost—Part 2.

	TokenGen (Trapdoor)	Search (Test)
[27]	$l{T}_H+m{T}_{sp}$	$(l+2)m^2{T}_{mul}$
[17]	$Tsl$	$2lm{T}_{mul}$
[20]	$T_{sl}$	$T_{lsss}+l\left(s(2mn+2)\right)+2m)T_{mul}$
[21]	$\zeta T_H+\zeta T_{sp}+T_{lsss}+\zeta s{T}_{mul}$	$\zeta mns{T}_{mul}$
[22]	$\zeta T_H+\zeta T_{sp}+T_{lsss}+(s\beta +\zeta s)T_{mul}$	$2T_{lsss}+\zeta (2s+mns+1)T_{mul}$
[19]	$T_H+T_{bd}+T_{sp}$	$T_H+\left(2mn\right)T_{mul}$
[18]	$2\zeta m{T}_{mul}$	$2\zeta m{T}_{mul}$
[29]	$T_H+T_{sp}$	$2(n+m^2+m)T_{mul}$
[30]	$T_{fla}+(N^3+N{m}^2)T_{mul}$	$T_{de{c}_{FHE}}$
Ours	$(l+2)T_H+l{T}_{inv}+l{T}_{sd}+2n^2{T}_{mul}$	$l(m+w)T_{mul}$

To compare, one can consider comparing single-keyword searches. One can set $l=1$ and $w=m$. Then, in the proposed scheme, the Encryption cost is $2T_H+(4mn+2n)T_{mul}$, the Decryption cost is $2m{T}_{mul}$, the TokenGen cost is $3T_H+T_{inv}+T_{sd}+2n^2{T}_{mul}$, and the Search cost is $2m{T}_{mul}$. In this case, the proposed scheme has good performance in Decryption and Search costs but a higher cost in Encryption and TokenGen costs.

6.3. Summary

Compared with other schemes, the proposed scheme has good performance in transmission cost. Although the proposed scheme has a slightly higher computation cost than other schemes in the case of a single-keyword search, the proposed scheme is the first to simultaneously support multi-keyword search, identity-based encryption, proxy re-encryption, and offline KGC. Furthermore, it verifies the user’s access rights during the decryption phase and the search phase. In addition, as the number of DUs increases, the costs required for DO remain the same, and PS will handle the increased workload.

On the other hand, the type-2 trapdoor has smaller n and m than the type-1 trapdoor. Our scheme uses the type-2 trapdoor, but other schemes [19,21,22,29] use the type-1 trapdoor $\mathit{BasisDel}$, which does not increase dimension when generating new basis. If they use the type-1 trapdoor, then the comparison results will change. Therefore, the efficiency of the proposed scheme will be relatively better in reality.

7. Conclusions

In this research, a multi-keyword searchable identity-based proxy re-encryption scheme from lattices has been proposed. First, based on the D-LWE assumption, the proposed scheme can resist quantum attacks. Second, it provides multi-keyword searchability with AND and OR operators, increasing the flexibility of keyword searches. Third, KGC in the proposed scheme can be offline, avoiding the risk of being attacked by adversaries through the network. Fourth, the proposed scheme supports PRE to reduce file-sharing costs of the data owner. The costs of the data owner will remain the same as the number of data users increases. Fifth, to prevent illegal access to files, the user’s access rights are verified in both the search and decryption phases. Finally, the proposed scheme is identity-based, avoiding the cost of using certificates.

Compared with other schemes, the proposed scheme has good performance in transmission cost. Although the proposed scheme has a slightly higher computation cost than other schemes in the case of a single-keyword search, the proposed scheme supports multi-keyword search, increasing the flexibility of keyword searches. In addition, the cost of the data owner does not increase with the number of data users. In the future, we will try to reduce the transmission and computation costs of the proposed scheme. Furthermore, future research will be designing a new multi-keyword mechanism that supports threshold operations.