Fast Generalized Sliding Sinusoidal Transforms
Abstract
:1. Introduction
- A generalized solution of a second-order linear nonhomogeneous difference equation is obtained using the unilateral z-transform.
- Based on the generalized solution, eight generalized sliding sinusoidal transforms are proposed.
- Fast algorithms have been proposed for computing generalized sliding sinusoidal transforms. The algorithms are based on the derived recursive equations and fast-pruned DSTs.
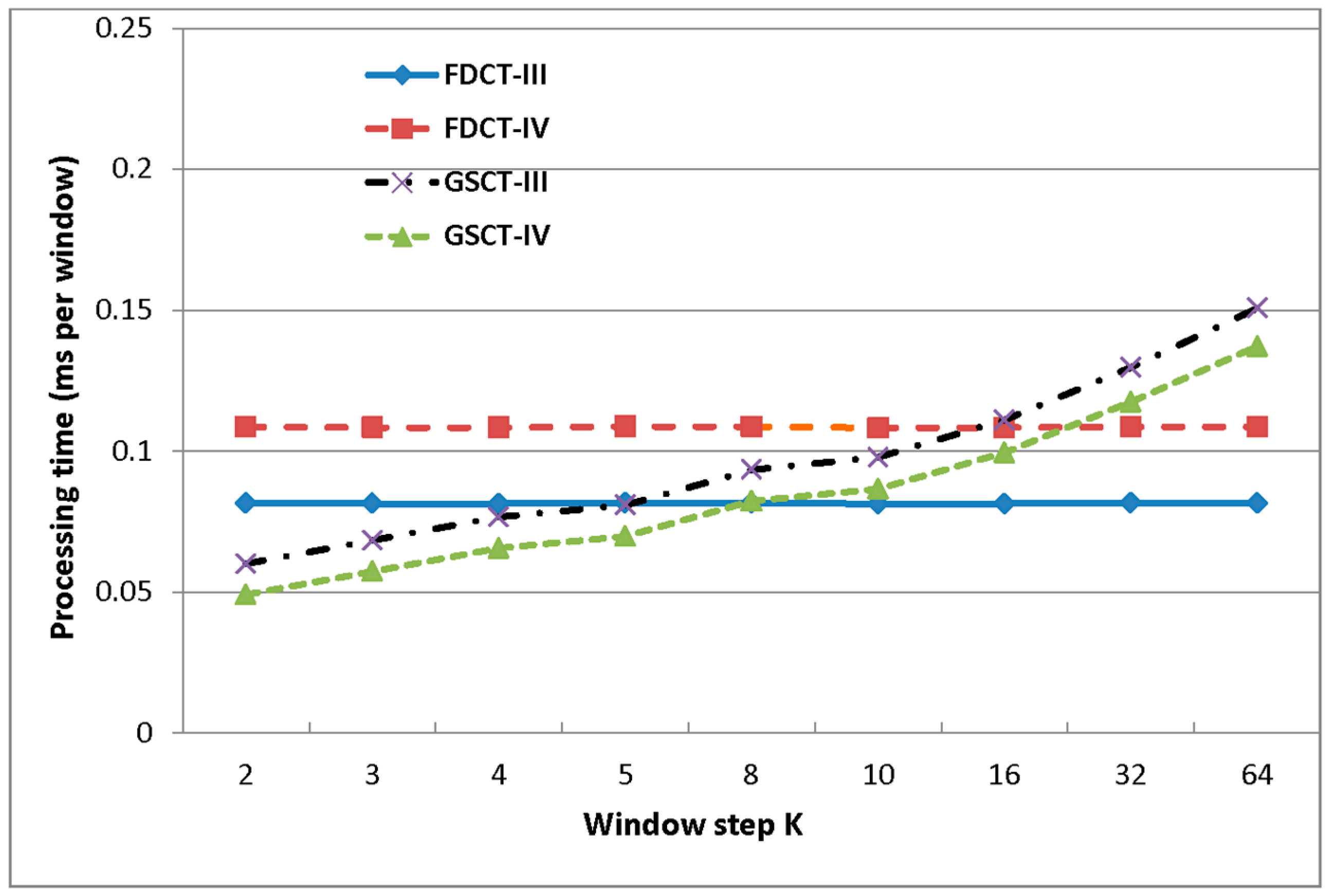
- The performance of the proposed algorithms in terms of computational complexity and execution time is compared with those of recursive sliding and fast sinusoidal algorithms.
2. Generalized Sliding Discrete Sinusoidal Transforms
2.1. Sliding Discrete Sinusoidal Transforms
2.2. Generalized Solution of Second-Order Linear Nonhomogeneous Difference Equation
2.3. Recursive Equations for Generalized Sliding Sinusoidal Transforms
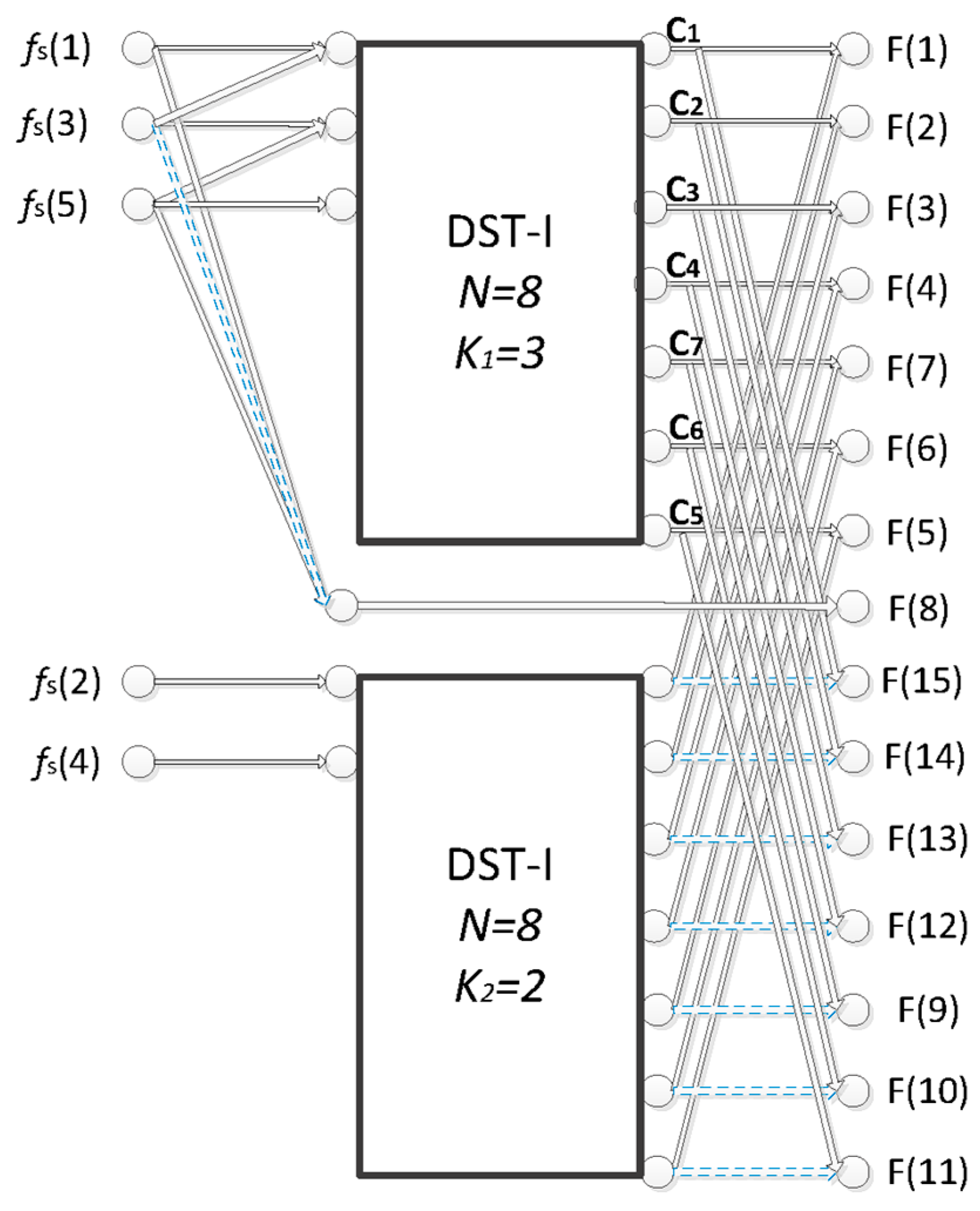
3. Fast Algorithms for Computing Generalized Sliding Sinusoidal Transforms
3.1. Fast-Pruned Discrete Sine Transforms
3.2. Fast Generalized Sliding Sinusoidal Transforms
3.3. Analysis of Computational Complexity
4. Results
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Jain, A.K. A fast Karhunen-Loeve transform for a class of random processes. IEEE Trans. Commun. 1976, 24, 1023–1029. [Google Scholar] [CrossRef]
- Jain, A.K. A sinusoidal family of unitary transforms. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 356–365. [Google Scholar] [CrossRef]
- Rose, K.; Heiman, A.; Dinstein, I. DCT/DST alternate-transform image coding. IEEE Trans. Commun. 1990, 38, 94–101. [Google Scholar] [CrossRef]
- Lee, J.; Un, C. Performance of transform-domain LMS adaptive digital filters. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 499–510. [Google Scholar] [CrossRef]
- Kober, V. Robust and efficient algorithm of image enhancement. IEEE Trans. Consum. Electron. 2006, 52, 655–659. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L. Interpolation using the fast discrete sine transform. Signal Process. 1992, 26, 131–137. [Google Scholar] [CrossRef]
- Kim, M.; Lee, Y.-L. Discrete sine transform-based interpolation filter for video compression. Symmetry 2017, 9, 257. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Sharma, R.R.; Kumar, M.; Pachori, R.B. Joint time-frequency domain-based CAD disease sensing system using ECG signals. IEEE Sensors J. 2019, 19, 3912–3920. [Google Scholar] [CrossRef]
- Portnoff, M. Short-time Fourier analysis of sampled speech. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 364–373. [Google Scholar] [CrossRef]
- Shi, J.; Zheng, J.; Liu, X.; Xiang, W.; Zhang, Q. Novel short-time fractional Fourier transform: Theory, implementation, and applications. IEEE Trans. Signal Process. 2020, 68, 3280–3295. [Google Scholar] [CrossRef]
- Wang, X.; Huang, G.; Zhou, Z.; Tian, W.; Yao, J.; Gao, J. Radar emitter recognition based on the energy cumulant of short-time Fourier transform and reinforced deep belief network. Sensors 2018, 18, 3103. [Google Scholar] [CrossRef]
- Wang, Y.; Veluvolu, K.C. Time-frequency analysis of non-stationary biological signals with sparse linear regression based Fourier linear combiner. Sensors 2017, 17, 1386. [Google Scholar] [CrossRef]
- Thalmayer, A.; Zeising, S.; Fischer, G.; Kirchner, J. A robust and real-time capable envelope-based algorithm for heart sound classification: Validation under different physiological conditions. Sensors 2020, 20, 972. [Google Scholar] [CrossRef]
- Priyadarshini, M.S.; Krishna, D.; Kumar, K.V.; Amaresh, K.; Goud, B.S.; Bajaj, M.; Altameem, T.; El-Shafai, W.; Fouda, M.M. Significance of harmonic filters by computation of short-time Fourier transform-based time–frequency representation of supply voltage. Energies 2023, 16, 2194. [Google Scholar] [CrossRef]
- Park, C.; Ko, S. The hopping discrete Fourier transform. IEEE Signal Process. Mag. 2014, 31, 135–139. [Google Scholar] [CrossRef]
- Kober, V. Fast recursive computation of sliding DHT with arbitrary step. Sensors 2020, 20, 5556. [Google Scholar] [CrossRef]
- Kober, V. Fast hopping discrete sine transform. IEEE Access 2021, 9, 94293–94298. [Google Scholar] [CrossRef]
- Xi, J.; Chiraro, J.F. Computing running DCT’s and DST’s based on their second-order shift properties. IEEE Trans. Circuits Syst. I 2000, 47, 779–783. [Google Scholar] [CrossRef]
- Kober, V. Fast algorithms for the computation of sliding discrete sinusoidal transforms. IEEE Trans. Signal Process. 2004, 52, 1704–1710. [Google Scholar] [CrossRef]
- Kober, V. Recursive algorithms for computing sliding DCT with arbitrary step. IEEE Sensors 2021, 21, 11507–11513. [Google Scholar] [CrossRef]
- Qian, L.; Luo, S.; He, S.; Chen, G. Recursive algorithms for direct computation of generalized sliding discrete cosine transforms. In Proceedings of the 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; pp. 3017–3020. [Google Scholar] [CrossRef]
- Wang, Z. Fast algorithms for the discrete W transform and for the discrete Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 803–816. [Google Scholar] [CrossRef]
- Yip, P.; Rao, K.R. Fast decimation-in-time algorithms for a family of discrete sine and cosine transforms. Circuits Syst. Signal Process. 1984, 3, 387–408. [Google Scholar] [CrossRef]
- Hou, H.S. A fast recursive algorithm for computing the discrete cosine transform. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1455–1461. [Google Scholar] [CrossRef]
- Wang, Z. Fast discrete sine transform algorithms. Signal Process. 1990, 19, 91–102. [Google Scholar] [CrossRef]
- Britanak, V. On the discrete cosine computation. Signal Process. 1994, 40, 183–194. [Google Scholar] [CrossRef]
- Britanak, V. A unified discrete cosine and sine transform computation. Signal Process. 1995, 43, 333–339. [Google Scholar] [CrossRef]


| Transforms | ||
|---|---|---|
| SCT-I | ||
| SCT-II | ||
| SCT-III | ||
| SCT-IV | ||
| SST-I | ||
| SST-II | ||
| SST-III | ||
| SST-IV |
| Transforms | ||
|---|---|---|
| GSCT-I, GSCT-II GSST-I, GSST-II | ||
| GSCT-III GSCT-IV | ||
| GSST-III GSST-IV |
| Transforms | Components | |
|---|---|---|
| SCT-I | even | |
| odd | ||
| SCT-II | even | |
| odd | ||
| SCT-III | even | |
| odd | ||
| SCT-IV | even | |
| odd | ||
| SST-I | even | |
| odd | ||
| SST-II | even | |
| odd | ||
| SST-III | even | |
| odd | ||
| SST-IV | even | |
| odd | ||
| Transforms | ||
|---|---|---|
| GSCT-I | ||
| GSST-I | ||
| GSCT-II GSST-II | ||
| GSCT-III GSST-III | ||
| GSCT-IV GSST-IV |
| Step K | GSCT-I | GSST-I | GSCT-II GSST-II | GSCT-III GSST-III | GSCT-IV GSST-IV |
|---|---|---|---|---|---|
| 2 | 1039 | 769 | 781 | 1543 | 1288 |
| 3 | 1176 | 899 | 917 | 1804 | 1549 |
| 4 | 1312 | 1028 | 1052 | 2065 | 1810 |
| 5 | 1386 | 1095 | 1125 | 2198 | 1943 |
| 8 | 1604 | 1292 | 1340 | 2597 | 2342 |
| 10 | 1689 | 1363 | 1423 | 2735 | 2480 |
| 16 | 1936 | 1568 | 1664 | 3149 | 2894 |
| 32 | 2352 | 1872 | 2064 | 3741 | 3486 |
| 64 | 2962 | 2240 | 2624 | 4413 | 4158 |
| Step K | GSCT-I | GSST-I | GSCT-II GSST-II | GSCT-III GSST-III | GSCT-IV GSST-IV |
|---|---|---|---|---|---|
| 2 | 1027 | 508 | 765 | 1284 | 1024 |
| 3 | 1093 | 570 | 828 | 1414 | 1152 |
| 4 | 1159 | 632 | 891 | 1544 | 1280 |
| 5 | 1193 | 662 | 922 | 1610 | 1344 |
| 8 | 1295 | 752 | 1015 | 1808 | 1536 |
| 10 | 1331 | 780 | 1045 | 1876 | 1600 |
| 16 | 1439 | 864 | 1135 | 2080 | 1792 |
| 32 | 1599 | 960 | 1247 | 2368 | 2048 |
| 64 | 1791 | 1024 | 1343 | 2688 | 2304 |
| Step K | DCT-I | DCT-II | DCT-III | DCT-IV |
|---|---|---|---|---|
| 2 | 2295 | 1275 | 2304 | 2304 |
| 3 | 3315 | 1785 | 3328 | 3328 |
| 4 | 4335 | 2295 | 4352 | 4352 |
| 5 | 5355 | 2805 | 5376 | 5376 |
| 8 | 8415 | 4335 | 8448 | 8448 |
| 10 | 10,455 | 5355 | 10,496 | 10,496 |
| 16 | 16,575 | 8415 | 16,640 | 16,640 |
| 32 | 32,895 | 16,575 | 33,024 | 33,024 |
| 64 | 65,535 | 32,895 | 65,792 | 65,792 |
| Step K | DCT-I | DCT-II | DCT-III | DCT-IV |
|---|---|---|---|---|
| 2 | 2304 | 1288 | 2304 | 2304 |
| 3 | 3328 | 1804 | 3328 | 3328 |
| 4 | 4352 | 2320 | 4352 | 4352 |
| 5 | 5376 | 2836 | 5376 | 5376 |
| 8 | 8448 | 4384 | 8448 | 8448 |
| 10 | 10,496 | 5416 | 10,496 | 10,496 |
| 16 | 16,640 | 8512 | 16,640 | 16,640 |
| 32 | 33,024 | 16,768 | 33,024 | 33,024 |
| 64 | 65,792 | 33,280 | 65,792 | 65,792 |
| Operations | FDCT-I [25] | FDST-I [26] | FDCT-II [27] FDST-II [26] | FDCT-III [28] FDST-III [26] | FDCT-IV [25] | FDST-IV [26] |
|---|---|---|---|---|---|---|
| ADD | 2716 | 2554 | 2818 | 2818 | 3456 | 3072 |
| MUL | 917 | 769 | 1025 | 1025 | 1664 | 1280 |
| N | GSCT-I | GSST-I | GSCT-II GSST-II | GSCT-III GSST-III | GSCT-IV GSST-IV |
|---|---|---|---|---|---|
| 32 | 368 | 224 | 320 | 461 | 430 |
| 64 | 592 | 416 | 512 | 845 | 782 |
| 128 | 1040 | 800 | 896 | 1613 | 1486 |
| 256 | 1936 | 1568 | 1664 | 3149 | 2894 |
| 512 | 3728 | 3104 | 3200 | 6221 | 5710 |
| 1024 | 7312 | 6176 | 6272 | 12,365 | 11,342 |
| 2048 | 14,480 | 12,320 | 12,416 | 24,653 | 22,606 |
| N | GSCT-I | GSST-I | GSCT-II GSST-II | GSCT-III GSST-III | GSCT-IV GSST-IV |
|---|---|---|---|---|---|
| 32 | 207 | 80 | 127 | 288 | 224 |
| 64 | 383 | 192 | 271 | 544 | 448 |
| 128 | 738 | 416 | 559 | 1056 | 896 |
| 256 | 1439 | 864 | 1135 | 2080 | 1792 |
| 512 | 2847 | 1760 | 2287 | 4128 | 3584 |
| 1024 | 5643 | 3552 | 4591 | 8224 | 7168 |
| 2048 | 11,295 | 7136 | 9199 | 16,416 | 14,336 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kober, V. Fast Generalized Sliding Sinusoidal Transforms. Mathematics 2023, 11, 3829. https://doi.org/10.3390/math11183829
Kober V. Fast Generalized Sliding Sinusoidal Transforms. Mathematics. 2023; 11(18):3829. https://doi.org/10.3390/math11183829
Chicago/Turabian StyleKober, Vitaly. 2023. "Fast Generalized Sliding Sinusoidal Transforms" Mathematics 11, no. 18: 3829. https://doi.org/10.3390/math11183829
APA StyleKober, V. (2023). Fast Generalized Sliding Sinusoidal Transforms. Mathematics, 11(18), 3829. https://doi.org/10.3390/math11183829







