Stability and Convergence Analysis of Multi-Symplectic Variational Integrator for Nonlinear Schrödinger Equation

Abstract

Stability and convergence analyses of the multi-symplectic variational integrator for the nonlinear Schr$\ddot{\mathrm{o}}$dinger equation are discussed in this paper. The variational integrator is proved to be unconditionally linearly stable using the von Neumann method. A priori error bound for the scheme is given from the Sobolev inequality and the discrete conservation laws. Subsequently, the variational integrator is derived to converge at $O(\Delta x^2+\Delta t^2)$ in the discrete $L^2$ norm using the energy method. The numerical experimental results match our theoretical derivation.

1. Introduction

The nonlinear Schr$\ddot{\mathrm{o}}$dinger equation (NLSE) is an important partial differential equation that is used to describe the motion state of microscopic particles. It is the underlying equation of quantum mechanics. Partial differential equations have a wide range of applications, which can be found in reference [1]. The NLS equation has wide applications in several fields such as nonlinear optics [2,3,4], underwater acoustics [5], water waves [6,7,8], plasma physics [9], quantum condensates [10,11] and bimolecular dynamics [12]. The NLS equation is also called the Gross–Pitaevskii equation (GPE) when simulating the dynamics of the Bose–Einstein condensate [13,14]. Reference [15] gives a detailed summary on the mathematical theory and numerical methods for the GPE.

In this paper, the following form of the nonlinear Schr$\ddot{\mathrm{o}}$dinger equation is to be studied:

$$i{\psi }_t+\alpha (t){\psi }_{xx}+V(x)\psi +\beta (t){|\psi |}^2\psi =0,$$

(1)

with the initial condition $\psi (x,0)={\psi }_0(x),x\in \mathbb{R}$, where $i=\sqrt{-1}$ and variable coefficients $\alpha (t)$, $V(x)$, and $\beta (t)$ are bounded real functions. Moreover, $\alpha (t)$ is related to the second-order dispersion coefficient, $V(x)$ represents a potential, and $\beta (t)$ describes the strength of the local interactions between particles [12]. The solution $\psi (x,t)$ is a complex-valued wave function, and its modulus ${|\psi (x,t)|}^2$ is a physically meaningful and measurable quantity, which states the probability density for a particle to be located at pointed x and at time t [12,16].

The nonlinear Schr$\ddot{\mathrm{o}}$dinger Equation (1) can be written in the form of a Euler–Lagrangian equation as follows:

$$\frac{\partial L}{\partial \psi }=\frac{d}{dt}\frac{\partial L}{\partial {\psi }_t}+\frac{d}{dx}\frac{\partial L}{\partial {\psi }_x},$$

(2)

where $L(\psi ,{\psi }_t,{\psi }_x)$ is a Lagrangian function. The exact solution of Equation (1) not only preserves the multi-symplectic geometric structures, whose corresponding multi-symplectic form formula is given in Proposition 1, but it also satisfies the global conservation laws, which are listed in Proposition 2.

Proposition 1.

As per [17,18], if ψ is a solution of the Euler–Lagrangian equation, and V and W are first variations of ψ, then for any subset U of the space of independent variables, the following multi-symplectic form formula holds:

$${\int }_{\partial U}{(j^1\psi )}^{\ast }(l_{j^{1}V}{l}_{j^{1}W}{\mathsf{\Omega }}_L)=0,$$

(3)

where $j^1\psi$ is the first jet of ψ, ∗ is a pullback operator, and ${\mathsf{\Omega }}_L$ is the Lagrangian multi-symplectic form.

Proposition 2.

As per [19], suppose that the wave function ψ is the solution of Equation (1); then, ψ satisfies the following three global conservation laws:

(1) Mass conservation

$$M={\int }_{\mathbb{R}}{|\psi (x,t)|}^{2}dx={\int }_{\mathbb{R}}{|\psi (x,0)|}^{2}dx,t>0.$$

(4)

(2) Energy conservation

If $\alpha (t)$ and $\beta (t)$ are independent of t, that is to say, $\alpha (t)\equiv \alpha$ and $\beta (t)\equiv \beta$, then

$$\begin{array}{cc}\hfill E& ={\int }_{\mathbb{R}}(\alpha |{\psi }_x{(x,t)|}^2-{V(x)|\psi (x,t)|}^2-\frac{\beta }{2}{|\psi (x,t)|}^4)dx\hfill \\ \hfill & ={\int }_{\mathbb{R}}(\alpha |{\psi }_x{(x,0)|}^2-{V(x)|\psi (x,0)|}^2-\frac{\beta }{2}{|\psi (x,0)|}^4)dx,t>0.\hfill \end{array}$$

(5)

(3) Momentum conservation

$$\begin{array}{cc}\hfill N& ={\int }_{\mathbb{R}}(\mathcal{R}(\psi (x,t))\mathcal{I}({\psi }_x(x,t))-\mathcal{R}({\psi }_x(x,t))\mathcal{I}(\psi (x,t)))dx\hfill \\ & ={\int }_{\mathbb{R}}(\mathcal{R}(\psi (x,0))\mathcal{I}({\psi }_x(x,0))-\mathcal{R}({\psi }_x(x,0))\mathcal{I}(\psi (x,0)))dx,t>0,\hfill \end{array}$$

(6)

where $\mathcal{R}$ and $\mathcal{I}$ represent the real part and the imaginary part, respectively.

Up to now, a large number of accurate and efficient numerical methods, which can conserve mass, energy and momentum, have been proposed to solve different types of nonlinear Schr$\ddot{\mathrm{o}}$dinger equations. Besides visually observing the effect of the proposed scheme from the numerical results, for example, drawing three-dimensional diagrams, mass or energy change plots or error graphs of the solved problem, some studies analyze theoretical properties of the proposed methods with a certain emphasis, such as on mass or energy conservation, solvability, stability or error bounds. For the cubic nonlinear Schr$\ddot{\mathrm{o}}$dinger equation with a wave operator, the reference [20] gives the linearized finite element method and derives its conservation property of energy and the optimal error estimates in the $L^2$ norm. For solving the damped nonlinear Schr$\ddot{\mathrm{o}}$dinger equation, the leap-frog finite element method is given in [9]. Meanwhile, the total discrete mass conservation, energy conservation and the bound in the $L^{\infty }$ norm and optimal $L^2$ error estimate of this scheme are presented. Many numerical methods, such as the classical explicit method, the hopscotch method, the implicit–explicit method and so on, are proposed in [21] to solve the nonlinear Schr$\ddot{\mathrm{o}}$dinger equation. In reference [22], a compact difference scheme with fourth-order precision in time is derived to obtain the numerical solution of the nonlinear Schr$\ddot{\mathrm{o}}$dinger equation. The authors obtained the conclusion that the proposed scheme has higher accuracy than the Crank–Nicholson scheme using numerical experiments. To obtain the numerical solution of the coupled nonlinear Schr$\ddot{\mathrm{o}}$dinger equation, the scheme in [23] is established using the Galerkin finite element method in space and the Crank–Nicolson difference method in time. The conservation laws, unique solvability and error estimates for the scheme are analyzed at the same time. The time-splitting Fourier spectral method is used to solve the coupled Schr$\ddot{\mathrm{o}}$dinger–Boussinesq equation in [24], and it is proven to be effective and accurate by numerical results. Xu et al. use the Fourier pseudo-spectral method to calculate the numerical solution of the space fractional nonlinear Schr$\ddot{\mathrm{o}}$dinger equation. They prove the solution’s existence and the conservation and convergence of the scheme in [25]. For a numerical solution of the Equation (1) to be discussed in this paper, a temporal two-mesh compact difference method was proposed in [12]. The convergence of the scheme was derived, and the corresponding numerical results indicate that the solution reduces the Central Processing Unit(CPU) time without loss of accuracy compared with the standard nonlinear implicit compact difference scheme. The cubic B-spline Galerkin method is given in [26], and the stability of the scheme is analyzed.

In [27], the exponential cubic B-spline differential quadrature method is used to solve NLSE numerically. The method adopts a leave-one-out cross validation strategy to improve accuracy and efficiency. A two-grid finite element scheme is proposed for NLSE in [28]. The optimal order error estimates of the scheme in $L^p$ and $H^1$ norm are derived without any time-step size. The convergence of symmetric discretization models for the nonlinear Schr$\ddot{\mathrm{o}}$dinger equation in dark solitons’ motion is discussed in [29]. The author in [30] shows us the application of the nonlinear Schr$\ddot{\mathrm{o}}$dinger equation to gravity-capillary waves on deep water with constant vorticity. There are other valid schemes for solving Equation (1), such as multi-grid methods [31], the two-grid finite volume method [32,33], the virtual element method [34] and so on.

The work in this paper is a continuation of earlier research [19]. In the article [19], the multi-symplectic variational integrator was developed for Schr$\ddot{\mathrm{o}}$dinger equations. Numerical methods, which are based on the Lagrangian viewpoint and variational principle [35,36], have long-time numerical simulations and maintain the internal properties and conservation laws of Hamiltonian equations. However, the stability of the schemes is judged from numerical experiments. There is no theoretical conclusions of stability for the multi-symplectic variational integrators. That is the main work and novelty in this paper. The stability conditions and global convergence errors are proved. Multi-symplectic variational integrators for nonlinear Schr$\ddot{\mathrm{o}}$dinger equations are proved to be unconditionally linearly stable by using the Von-Neumann method. Based on the Sobolev inequality and energy method, the global convergence errors of the scheme in solving linear equations are analyzed. The numerical results show that conclusions are also appropriate for nonlinear cases.

The paper is composed of the following parts: In Section 2, we give the multi-symplectic variational integrator for nonlinear Schr$\ddot{\mathrm{o}}$dinger equation with variable coefficients from the Lagrangian viewpoint and variational principle. In Section 3, we prove the proposed variational integrator is unconditionally linearly stable using the von Neumann method. In Section 4, a priori error bound for the scheme is derived from the Sobolev inequality, the discrete mass conservation law and the discrete energy conservation law. Then, based on the energy method, the convergence order of the variational integrator is $O(\Delta x^2+\Delta t^2)$ in the discrete $L^2$ norm, where $\Delta x$ is the mesh step and $\Delta t$ is the time step. Numerical experiments are carried out in Section 5.

2. Multi-Symplectic Variational Integrator for Nonlinear Schr$\ddot{\mathrm{o}}$dinger Equation with Variable Coefficients

The nonlinear Schr$\ddot{\mathrm{o}}$dinger equation with variable coefficients (1) can be rewritten into the form of a Euler–Lagrange Equation (2) with a Lagrangian function:

$$L(\psi ,{\psi }_t,{\psi }_x)=-\frac{1}{2}\alpha (t){\psi }_x\overline{{\psi }_x}+\frac{1}{4}i(\psi \overline{{\psi }_t}-\overline{\psi }{\psi }_t)+\frac{1}{4}\beta (t){(\psi \overline{\psi })}^2+\frac{1}{2}V(x)\psi \overline{\psi },$$

(7)

where $\overline{\psi }$ is the conjugation of $\psi$.

Supposing the regular quadrangular mesh in the base space is given, with mesh lengths $\Delta x$ and $\Delta t$, we note the value of field $\psi$ as ${\psi }_j^k=\psi (j\Delta x,k\Delta t)$. The discrete Lagrangian $L_d$ of the Lagrangian function is discretized by a finite difference method as follows:

$$\begin{array}{cc}\hfill L_d({\psi }_j^k,{\psi }_{j+1}^k,{\psi }_{j+1}^{k+1},{\psi }_j^{k+1})& =\Delta x\Delta t(-\frac{1}{2}{\alpha }_{k+\frac{1}{2}}\frac{{\psi }_{j+1}^{k+\frac{1}{2}}-{\psi }_j^{k+\frac{1}{2}}}{\Delta x}\frac{{\overline{\psi }}_{j+1}^{k+\frac{1}{2}}-{\overline{\psi }}_j^{k+\frac{1}{2}}}{\Delta x}\hfill \\ \hfill & +\frac{i}{4}({\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}\frac{{\overline{\psi }}_{j+\frac{1}{2}}^{k+1}-{\overline{\psi }}_{j+\frac{1}{2}}^k}{\Delta t}-{\overline{\psi }}_{j+\frac{1}{2}}^{k+\frac{1}{2}}\frac{{\psi }_{j+\frac{1}{2}}^{k+1}-{\psi }_{j+\frac{1}{2}}^k}{\Delta t})\hfill \\ \hfill & +\frac{1}{4}{\beta }_{k+\frac{1}{2}}{({\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{\overline{\psi }}_{j+\frac{1}{2}}^{k+\frac{1}{2}})}^2+\frac{1}{2}{V}_{j+\frac{1}{2}}{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{\overline{\psi }}_{j+\frac{1}{2}}^{k+\frac{1}{2}}),\hfill \end{array}$$

(8)

where ${\psi }_j^{k+\frac{1}{2}}=\frac{{\psi }_j^k+{\psi }_j^{k+1}}{2},{\psi }_{j+\frac{1}{2}}^k=\frac{{\psi }_j^k+{\psi }_{j+1}^k}{2},{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}=\frac{{\psi }_j^k+{\psi }_{j+1}^k+{\psi }_{j+1}^{k+1}+{\psi }_j^{k+1}}{4}$. In the same way, the detailed definitions of the discrete Lagrangian $L_d({\psi }_{j-1}^k,{\psi }_j^k,{\psi }_j^{k+1},{\psi }_{j-1}^{k+1})$, $L_d({\psi }_{j-1}^{k-1},{\psi }_j^{k-1},{\psi }_j^k,{\psi }_{j-1}^k)$ and $L_d({\psi }_j^{k-1},{\psi }_{j+1}^{k-1},{\psi }_{j+1}^k,{\psi }_j^k)$ on the other three squares adjacent to ${\psi }_j^k$ can be found in reference [19]. Based on the theories in [17,18,37], the following discrete Euler–Lagrange equation is obtained:

$$\begin{array}{c}{D}_1{L}_d({\psi }_j^k,{\psi }_{j+1}^k,{\psi }_{j+1}^{k+1},{\psi }_j^{k+1})+D_2{L}_d({\psi }_{j-1}^k,{\psi }_j^k,{\psi }_j^{k+1},{\psi }_{j-1}^{k+1})\hfill \\ +D_3{L}_d({\psi }_{j-1}^{k-1},{\psi }_j^{k-1},{\psi }_j^k,{\psi }_{j-1}^k)+D_4{L}_d({\psi }_j^{k-1},{\psi }_{j+1}^{k-1},{\psi }_{j+1}^k,{\psi }_j^k)=0,\hfill \end{array}$$

(9)

where $D_i$ means the derivative with respect to the i-th variable.

To obtain the numerical solution of the nonlinear Schr$\ddot{\mathrm{o}}$dinger Equation (1), based on the discrete Euler–Lagrange Equation (9), the following scheme is derived,

$$\begin{array}{c}\frac{i}{2}(\frac{{\psi }_{j+\frac{1}{2}}^{k+1}-{\psi }_{j+\frac{1}{2}}^{k-1}}{2\Delta t}+\frac{{\psi }_{j-\frac{1}{2}}^{k+1}-{\psi }_{j-\frac{1}{2}}^{k-1}}{2\Delta t})\hfill \\ +\frac{{\alpha }_{k+\frac{1}{2}}}{2}\frac{{\psi }_{j+1}^{k+\frac{1}{2}}-2{\psi }_j^{k+\frac{1}{2}}+{\psi }_{j-1}^{k+\frac{1}{2}}}{{(\Delta x)}^2}+\frac{{\alpha }_{k-\frac{1}{2}}}{2}\frac{{\psi }_{j+1}^{k-\frac{1}{2}}-2{\psi }_j^{k-\frac{1}{2}}+{\psi }_{j-1}^{k-\frac{1}{2}}}{{(\Delta x)}^2}\hfill \\ +\frac{1}{4}(V_{j+\frac{1}{2}}{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}+V_{j-\frac{1}{2}}{\psi }_{j-\frac{1}{2}}^{k+\frac{1}{2}}+V_{j-\frac{1}{2}}{\psi }_{j-\frac{1}{2}}^{k-\frac{1}{2}}+V_{j+\frac{1}{2}}{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}})\hfill \\ +\frac{1}{4}({\beta }_{k+\frac{1}{2}}|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}+{\beta }_{k+\frac{1}{2}}|{\psi }_{j-\frac{1}{2}}^{k+\frac{1}{2}}{|}^2{\psi }_{j-\frac{1}{2}}^{k+\frac{1}{2}}+{\beta }_{k-\frac{1}{2}}|{\psi }_{j-\frac{1}{2}}^{k-\frac{1}{2}}{|}^2{\psi }_{j-\frac{1}{2}}^{k-\frac{1}{2}}+{\beta }_{k-\frac{1}{2}}|{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}}{|}^2{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}})\hfill \\ =0.\hfill \end{array}$$

(10)

The numerical template for scheme (10) is shown in Figure 1. Since it is derived from the discrete variational principle, the scheme (10) is naturally multi-symplectic [35,37]. In addition, the multi-symplectic variational integrator (10) has the advantage of preserving the discrete multi-symplectic structure. In terms of how to verify it, reference [19] can give us an answer. In the rest of this paper, we prove the stability using the von Neumann method in Section 3 and prove the convergence accuracy using the energy method in Section 4 for the multi-symplectic variational integrator (10).

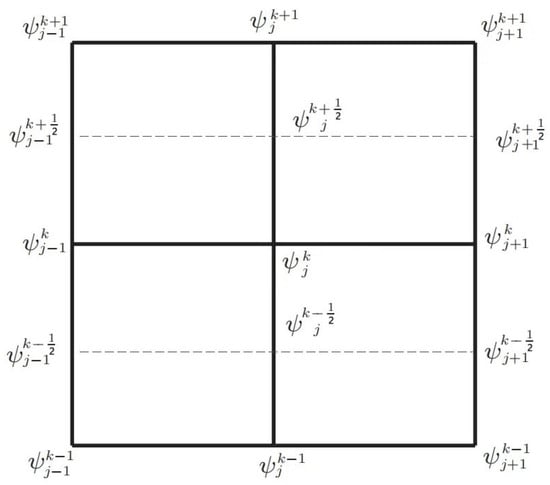
Figure 1. The numerical template for scheme (10).

Before deriving the stability and convergence of the scheme (10), it is necessary to give a lemma, which is about the solvability of the scheme (10).

Lemma 1

([38,39]). With the initial condition $\psi (x,0)={\psi }_0(x)\in C^4(x,0)$, the multi-symplectic variational integrator (10) is solvable.

3. Stability of the Multi-Symplectic Variational Integrator

In view of the complexity of proving the stability of the nonlinear Schr$\ddot{\mathrm{o}}$dinger equation with variable coefficients, using the von Neumann method, the stability of the multi-symplectic variational integrator (10) for solving the following nonlinear Schr$\ddot{\mathrm{o}}$dinger equation is investigated, where $\alpha (t)\equiv \alpha ,V(x)\equiv V,\beta (t)\equiv \beta$

$$i{\psi }_t+\alpha {\psi }_{xx}+V\psi +\beta {|\psi |}^2\psi =0.$$

(11)

We have the following.

Theorem 1.

The multi-symplectic variational integrator (10) is unconditionally linearly stable when solving the Schrödinger Equation (11).

Proof. 

Applying the multi-symplectic numerical scheme (10) to Equation (11), we have

$$\begin{array}{cc}\hfill & \frac{i}{2}(\frac{{\psi }_{j+\frac{1}{2}}^{k+1}-{\psi }_{j+\frac{1}{2}}^{k-1}}{2\Delta t}+\frac{{\psi }_{j-\frac{1}{2}}^{k+1}-{\psi }_{j-\frac{1}{2}}^{k-1}}{2\Delta t})\hfill \\ \hfill & +\frac{\alpha }{2}(\frac{{\psi }_{j+1}^{k+\frac{1}{2}}-2{\psi }_j^{k+\frac{1}{2}}+{\psi }_{j-1}^{k+\frac{1}{2}}}{{(\Delta x)}^2}+\frac{{\psi }_{j+1}^{k-\frac{1}{2}}-2{\psi }_j^{k-\frac{1}{2}}+{\psi }_{j-1}^{k-\frac{1}{2}}}{{(\Delta x)}^2})\hfill \\ \hfill & +\frac{1}{4}V({\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}+{\psi }_{j-\frac{1}{2}}^{k+\frac{1}{2}}+{\psi }_{j-\frac{1}{2}}^{k-\frac{1}{2}}+{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}})\hfill \\ \hfill & +\frac{1}{4}\beta (|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}+|{\psi }_{j-\frac{1}{2}}^{k+\frac{1}{2}}{|}^2{\psi }_{j-\frac{1}{2}}^{k+\frac{1}{2}}+|{\psi }_{j-\frac{1}{2}}^{k-\frac{1}{2}}{|}^2{\psi }_{j-\frac{1}{2}}^{k-\frac{1}{2}}+|{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}}{|}^2{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}})\hfill \\ \hfill & =0.\hfill \end{array}$$

(12)

Then, the frozen coefficient method is used for the linear stability analysis. In other words, we consider the coefficient of the nonlinear term as a constant (i.e., $|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2=|{\psi }_{j-\frac{1}{2}}^{k+\frac{1}{2}}{|}^2=|{\psi }_{j-\frac{1}{2}}^{k-\frac{1}{2}}{|}^2=|{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}}{|}^2\triangleq {|{\psi }_j^k|}^2$ in the Formula (12)). So, the Formula (12) has been organized and rewritten as follows:

$$\begin{array}{cc}\hfill & (\frac{i}{4\Delta t}+\frac{\alpha }{4{(\Delta x)}^2}+\frac{V}{16}+\frac{\beta |{\psi }_j^k{|}^2}{4}){\psi }_{j-1}^{k+1}+(\frac{i}{2\Delta t}-\frac{\alpha }{2{(\Delta x)}^2}+\frac{V}{8}+\frac{\beta |{\psi }_j^k{|}^2}{2}){\psi }_j^{k+1}\hfill \\ \hfill & +(\frac{i}{4\Delta t}+\frac{\alpha }{4{(\Delta x)}^2}+\frac{V}{16}+\frac{\beta |{\psi }_j^k{|}^2}{4}){\psi }_{j+1}^{k+1}\hfill \\ \hfill =& (\frac{i}{4\Delta t}-\frac{\alpha }{4{(\Delta x)}^2}-\frac{V}{16}-\frac{\beta |{\psi }_j^k{|}^2}{4}){\psi }_{j-1}^{k-1}+(\frac{i}{2\Delta t}+\frac{\alpha }{2{(\Delta x)}^2}-\frac{V}{8}-\frac{\beta |{\psi }_j^k{|}^2}{2}){\psi }_j^{k-1}\hfill \\ \hfill & +(\frac{i}{4\Delta t}-\frac{\alpha }{4{(\Delta x)}^2}-\frac{V}{16}-\frac{\beta |{\psi }_j^k{|}^2}{4}){\psi }_{j+1}^{k-1}+(-\frac{\alpha }{2{(\Delta x)}^2}-\frac{V}{8}-\frac{\beta |{\psi }_j^k{|}^2}{2}){\psi }_{j-1}^k\hfill \\ \hfill & +(\frac{\alpha }{{(\Delta x)}^2}-\frac{V}{4}-\beta |{\psi }_j^k{|}^2){\psi }_j^k+(-\frac{\alpha }{2{(\Delta x)}^2}-\frac{V}{8}-\frac{\beta |{\psi }_j^k{|}^2}{2}){\psi }_{j+1}^k.\hfill \end{array}$$

(13)

Taking product (13) with $\Delta t$, and letting $r=\frac{\Delta t}{{(\Delta x)}^2}$, we have

$$\begin{array}{cc}\hfill & (\frac{i}{4}+\frac{r\alpha }{4}+\frac{V}{16}\Delta t+\frac{\beta |{\psi }_j^k{|}^2}{4}\Delta t){\psi }_{j-1}^{k+1}+(\frac{i}{2}-\frac{r\alpha }{2}+\frac{V}{8}\Delta t+\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t){\psi }_j^{k+1}\hfill \\ \hfill & +(\frac{i}{4}+\frac{r\alpha }{4}+\frac{V}{16}\Delta t+\frac{\beta |{\psi }_j^k{|}^2}{4}\Delta t){\psi }_{j+1}^{k+1}\hfill \\ \hfill =& (\frac{i}{4}-\frac{r\alpha }{4}-\frac{V}{16}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{4}\Delta t){\psi }_{j-1}^{k-1}+(\frac{i}{2}+\frac{r\alpha }{2}-\frac{V}{8}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t){\psi }_j^{k-1}\hfill \\ \hfill & +(\frac{i}{4}-\frac{r\alpha }{4}-\frac{V}{16}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{4}\Delta t){\psi }_{j+1}^{k-1}+(-\frac{r\alpha }{2}-\frac{V}{8}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t){\psi }_{j-1}^k\hfill \\ \hfill & +(r\alpha -\frac{V}{4}\Delta t-\beta |{\psi }_j^k{|}^2\Delta t){\psi }_j^k+(-\frac{r\alpha }{2}-\frac{V}{8}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t){\psi }_{j+1}^k.\hfill \end{array}$$

(14)

Let $u_j^{k+1}={\psi }_j^k$; then, the expression (14) can be expressed as

$$\left\{\begin{array}{c}(\frac{i}{4}+\frac{r\alpha }{4}+\frac{V}{16}\Delta t+\frac{\beta |{\psi }_j^k{|}^2}{4}\Delta t)({\psi }_{j-1}^{k+1}+{\psi }_{j+1}^{k+1})+(\frac{i}{2}-\frac{r\alpha }{2}+\frac{V}{8}\Delta t+\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t){\psi }_j^{k+1}\hfill \\ =(\frac{i}{4}-\frac{r\alpha }{4}-\frac{V}{16}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{4}\Delta t)(u_{j-1}^k+u_{j+1}^k)+(\frac{i}{2}+\frac{r\alpha }{2}-\frac{V}{8}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t)u_j^k+\hfill \\ (-\frac{r\alpha }{2}-\frac{V}{8}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t)({\psi }_{j-1}^k+{\psi }_{j+1}^k)+(r\alpha -\frac{V}{4}\Delta t-\beta |{\psi }_j^k{|}^2\Delta t){\psi }_j^k,\hfill \\ u_j^{k+1}={\psi }_j^k.\hfill \end{array}\right.$$

Let $w_j^k$ = $\left(\begin{array}{c}{\psi }_j^k\\ u_j^k\end{array}\right)$; then, the above equation group can be rewritten as

$$\begin{array}{c}\hspace{1em}\hspace{1em}\left(\begin{array}{cc}\frac{i}{2}-\frac{r\alpha }{2}+\frac{V}{8}\Delta t+\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t& 0\\ 0& 1\end{array}\right)w_j^{k+1}+\left(\begin{array}{cc}\frac{i}{4}+\frac{r\alpha }{4}+\frac{V}{16}\Delta t+\frac{\beta |{\psi }_j^k{|}^2}{4}\Delta t& 0\\ 0& 0\end{array}\right)(w_{j-1}^{k+1}+w_{j+1}^{k+1})\hfill \\ =\left(\begin{array}{cc}r\alpha -\frac{V}{4}\Delta t-\beta {|{\psi }_j^k|}^2\Delta t& \frac{i}{2}+\frac{r\alpha }{2}-\frac{V}{8}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t\\ 1& 0\end{array}\right)w_j^k\hfill \\ +\left(\begin{array}{cc}-\frac{r\alpha }{2}-\frac{V}{8}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{2}\Delta t& \frac{i}{4}-\frac{r\alpha }{4}-\frac{V}{16}\Delta t-\frac{\beta |{\psi }_j^k{|}^2}{4}\Delta t\\ 0& 0\end{array}\right)(w_{j-1}^k+w_{j+1}^k).\hfill \end{array}$$

Using $w_j^k=\left(\begin{array}{c}{p}^k\\ q^k\end{array}\right)e^{imj\Delta x},m\in \mathbb{N}$ in the above formula, we have

$$\begin{array}{c}\left(\begin{array}{cc}i{cos}^2\frac{m\Delta x}{2}+(\frac{V}{4}\Delta t+\beta |{\psi }_j^k{|}^2\Delta t)co{s}^2\frac{m\Delta x}{2}-r\alpha {sin}^2\frac{m\Delta x}{2}& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}{p}^{k+1}\\ q^{k+1}\end{array}\right)=\hfill \\ \left(\begin{array}{cc}-(\frac{V}{2}\Delta t+2\beta |{\psi }_j^k{|}^2\Delta t)co{s}^2\frac{m\Delta x}{2}+2r\alpha {sin}^2\frac{m\Delta x}{2}& i{cos}^2\frac{m\Delta x}{2}-(\frac{V}{4}\Delta t+\beta |{\psi }_j^k{|}^2\Delta t)co{s}^2\frac{m\Delta x}{2}+r\alpha {sin}^2\frac{m\Delta x}{2}\\ 1& 0\end{array}\right)\left(\begin{array}{c}{p}^k\\ q^k\end{array}\right).\hfill \end{array}$$

In the above formula, making $a=(\frac{V}{4}\Delta t+\beta |{\psi }_j^k{|}^2\Delta t)co{s}^2\frac{m\Delta x}{2}-r\alpha {sin}^2\frac{m\Delta x}{2}$, the above formula can be simply denoted as

$$\left(\begin{array}{cc}i{cos}^2\frac{m\Delta x}{2}+a& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}{p}^{k+1}\\ q^{k+1}\end{array}\right)=\left(\begin{array}{cc}-2a& i{cos}^2\frac{m\Delta x}{2}-a\\ 1& 0\end{array}\right)\left(\begin{array}{c}{p}^k\\ q^k\end{array}\right).$$

Then, the amplification matrix of the numerical scheme (12) is obtained

$$G=\left(\begin{array}{cc}\frac{-2a}{i{cos}^2\frac{m\Delta x}{2}+a}& \frac{i{cos}^2\frac{m\Delta x}{2}-a}{i{cos}^2\frac{m\Delta x}{2}+a}\\ 1& 0\end{array}\right).$$

Assume that the two eigenvalues of G are ${\lambda }_1,{\lambda }_2$. When $|{\lambda }_1|\le 1$ and $|{\lambda }_1|\le 1$, the scheme (12) is stable. By calculating, we have

$${\lambda }_1=-1, {\lambda }_2=\frac{i{cos}^2(\frac{m\Delta x}{2})-a}{i{cos}^2(\frac{m\Delta x}{2})+a}.$$

Obviously,

$$|{\lambda }_1|=|{\lambda }_2|=1$$

. Hence, numerical format (12) is unconditionally stable when solving the constant nonlinear Schr$\ddot{\mathrm{o}}$dinger Equation (11). □

Therefore, the proof is completed.

4. Convergence Analysis of the Multi-Symplectic Variational Integrator

In this section, we focus on deriving the convergence order of the multi-symplectic variational integrator (10). Here, a few notations are given: ${\delta }_x{\psi }_j^k=\frac{{\psi }_{j+1}^k-{\psi }_j^k}{\Delta x}$, $||{\psi }^k|{|}_{\frac{1}{2}}^2=\Delta x{\sum }_j|{\psi }_{j+\frac{1}{2}}^k{|}^2$, ${\delta }_{2t}{\psi }_j^k=\frac{{\psi }_j^{k+1}-{\psi }_j^{k-1}}{2\Delta t}$.

The expression for the discrete mass for the variational integrator (10) is written as follows:

$$M^{k+\frac{1}{2}}=\Delta x\sum _j|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2.$$

(15)

The expression for the discrete energy for the variational integrator (10) is given:

$$E^{k+\frac{1}{2}}=\Delta x\sum _j(\alpha |{\delta }_x{\psi }_j^{k+\frac{1}{2}}{|}^2-V_{j+\frac{1}{2}}|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2-\frac{\beta }{2}|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^4).$$

(16)

And the discrete momentum expression corresponding to the variational integrator (10) is:

$$N^{k+\frac{1}{2}}=\Delta x\sum _j\left(\mathcal{R}({\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}})\mathcal{I}({\delta }_x{\psi }_j^{k+\frac{1}{2}})-\mathcal{R}({\delta }_x{\psi }_j^{k+\frac{1}{2}})\mathcal{I}({\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}})\right).$$

(17)

The multi-symplectic variational integrator (10) preserves the discrete mass conservation law and the discrete energy conservation law [40] when $\alpha (t)\equiv \alpha$, $\beta (t)\equiv \beta$.

Lemma 2

([40]). The variational integrator (10) possesses the discrete mass conservation law:

$$\begin{array}{cc}{M}^{k+\frac{1}{2}}-M^{k-\frac{1}{2}}=& \frac{\beta }{4}\Delta t\Delta x\sum _j\left(|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2-|{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}}{|}^2\right)\left({\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}-{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}}\right)\left({\overline{\psi }}_{j+\frac{1}{2}}^{k+\frac{1}{2}}+{\overline{\psi }}_{j+\frac{1}{2}}^{k-\frac{1}{2}}\right)\hfill \\ & -\frac{\beta }{4}\Delta t\Delta x\sum _j{\left(|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2-|{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}}{|}^2\right)}^2.\hfill \end{array}$$

(18)

In particular, when $\beta =0$, the equality holds: $M^{k+\frac{1}{2}}=M^{k-\frac{1}{2}}=\cdots =M^{\frac{1}{2}}$.

Lemma 3

([40]). The variational integrator (10) possesses the discrete energy conservation law:

$$\begin{array}{cc}\hfill E^{k+\frac{1}{2}}-E^{k-\frac{1}{2}}=& \frac{\beta }{2}\Delta x\sum _j\left(|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2-|{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}}{|}^2\right)|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}-{\psi }_{j+\frac{1}{2}}^{k-\frac{1}{2}}{|}^2.\hfill \end{array}$$

(19)

Particularly, supposing that $\beta =0$, the equality holds: $E^{k+\frac{1}{2}}=E^{k-\frac{1}{2}}=\cdots =E^{\frac{1}{2}}$.

Given the special case of the conservation laws in the above two lemmas, the multi-symplectic variational integrator (10) with $\beta =0$ is considered.

Next, relying on the Sobolev inequality and the discrete conservation laws, the priori error estimate for the scheme (10) with $\beta =0$ is derived.

Theorem 2.

The numerical solution of the multi-symplectic variational integrator (10) with $\beta =0$ is bounded under the $L^2$ norm and the $L^{\infty }$ norm, which are

$$||{\psi }^{k+\frac{1}{2}}|{|}_{\frac{1}{2}}\le C_1,||{\psi }^{k+\frac{1}{2}}|{|}_{\infty }\le C_2,$$

(20)

where $C_1,C_2$ are the positive constants.

Proof. 

Obviously, $M^{\frac{1}{2}}=\frac{M^1+M^2}{2}$, where $M^1$ is the discrete mass corresponding to the initial value ${\psi }_0$. For the feature of the multi-symplectic variational integrator (10) with $\beta =0$, we let ${\psi }_1={\psi }_0$ in practice, which means $M^1=M^2$. So, $M^{\frac{1}{2}}$ is bounded. That is to say, there is a positive constant $C_1$ satisfying $M^{\frac{1}{2}}\le C_1$. Based on the equality (18), we have $M^{k+\frac{1}{2}}\le C_1$, which represents $||{\psi }^{k+\frac{1}{2}}|{|}_{\frac{1}{2}}\le C_1$.

In the same manner, $E^{k+\frac{1}{2}}=E^{k-\frac{1}{2}}=\cdots =E^{\frac{1}{2}}$ is bounded. Because $E^{k+\frac{1}{2}}=\Delta x{\sum }_j(\alpha |{\delta }_x{\psi }_j^{k+\frac{1}{2}}{|}^2-V_{j+\frac{1}{2}}|{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}{|}^2)$ and $V(x)$ are bounded real functions, the inequality $\Delta x{\sum }_j{|{\delta }_x{\psi }_j^{k+\frac{1}{2}}|}^2\le C$ is obtained, where C is a positive constant. Based on the discrete version of the Sobolev inequality [15,41],

$$\begin{array}{cc}\hfill & ||{\psi }^{k+\frac{1}{2}}|{|}_{\infty }^2\le ||{\psi }^{k+\frac{1}{2}}|{|}_{\frac{1}{2}}·||{\delta }_x{\psi }_j^{k+\frac{1}{2}}||\le C_1·C\triangleq C_2.\hfill \end{array}$$

□

Therefore, the proof is completed.

Theorem 3.

Supposing the exact solution of the equation $i{\psi }_t+\alpha {\psi }_{xx}+V(x)\psi =0$ satisfies $\psi (x,t)\in C^4(x,t)$, the numerical solution of the multi-symplectic variational integrator (10) with $\beta =0$ converges to $O(\Delta x^2+\Delta t^2)$.

Proof. 

Firstly, the local truncation error ${\eta }^{k+\frac{1}{2}}$ of the multi-symplectic variational integrator (10) with $\beta =0$ when solving equation $i{\psi }_t+\alpha {\psi }_{xx}+V(x)\psi =0$ is denoted as

$$\begin{array}{cc}\hfill {\eta }_{j+\frac{1}{2}}^{k+\frac{1}{2}}=& \frac{i}{2}\left({\delta }_{2t}\psi (x_{j-\frac{1}{2}},t_k)+{\delta }_{2t}\psi (x_{j-\frac{1}{2}},t_k)\right)+\frac{\alpha }{2}\left({\delta }_x^2\psi (x_j,t_{k-\frac{1}{2}})+{\delta }_x^2\psi (x_j,t_{k+\frac{1}{2}})\right)\hfill \\ \hfill & +\frac{1}{4}[V(x_{j+\frac{1}{2}})\psi (x_{j+\frac{1}{2}},t_{k+\frac{1}{2}})+V(x_{j-\frac{1}{2}})\psi (x_{j-\frac{1}{2}},t_{k+\frac{1}{2}})\hfill \\ & +V(x_{j-\frac{1}{2}})\psi (x_{j-\frac{1}{2}},t_{k-\frac{1}{2}})+V(x_{j+\frac{1}{2}})\psi (x_{j+\frac{1}{2}},t_{k-\frac{1}{2}})].\hfill \end{array}$$

(21)

Using the Taylor expansion, we have ${\eta }_{j+\frac{1}{2}}^{k+\frac{1}{2}}=O(\Delta x^2+\Delta t^2)$. Thus, we obtain

$$\begin{array}{c}\hfill ||{\eta }^{k+\frac{1}{2}}|{|}_{\frac{1}{2}}\le C(\Delta x^2+\Delta t^2),\end{array}$$

(22)

where C is a positive constant.

Assume that ${\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}$ is the solution from the multi-symplectic variational integrator (10) with $\beta =0$. And we define the error function $e^{k+\frac{1}{2}}$ as $e_{j+\frac{1}{2}}^{k+\frac{1}{2}}=\psi (x_{j+\frac{1}{2}},t_{k+\frac{1}{2}})-{\psi }_{j+\frac{1}{2}}^{k+\frac{1}{2}}$.

In order to obtain the error function, subtract the scheme (10) with $\beta =0$ from (21). The result is as follows:

$$\begin{array}{c}\frac{i}{2}(\frac{e_{j+\frac{1}{2}}^{k+1}-e_{j+\frac{1}{2}}^{k-1}}{2\Delta t}+\frac{e_{j-\frac{1}{2}}^{k+1}-e_{j-\frac{1}{2}}^{k-1}}{2\Delta t})\hfill \\ =-\frac{\alpha }{2}\left(\frac{e_{j+1}^{k+\frac{1}{2}}-2e_j^{k+\frac{1}{2}}+e_{j-1}^{k+\frac{1}{2}}}{{(\Delta x)}^2}+\frac{e_{j+1}^{k-\frac{1}{2}}-2e_j^{k-\frac{1}{2}}+e_{j-1}^{k-\frac{1}{2}}}{{(\Delta x)}^2}\right)\hfill \\ -\frac{1}{4}(V_{j+\frac{1}{2}}{e}_{j+\frac{1}{2}}^{k+\frac{1}{2}}+V_{j-\frac{1}{2}}{e}_{j-\frac{1}{2}}^{k+\frac{1}{2}}+V_{j-\frac{1}{2}}{e}_{j-\frac{1}{2}}^{k-\frac{1}{2}}+V_{j+\frac{1}{2}}{e}_{j+\frac{1}{2}}^{k-\frac{1}{2}})+{\eta }_{j+\frac{1}{2}}^{k+\frac{1}{2}}.\hfill \end{array}$$

(23)

Let both sides of (23) be multiplied by $2({\overline{e}}_j^{k+\frac{1}{2}}+{\overline{e}}_j^{k-\frac{1}{2}})={\overline{e}}_j^{k+1}+2{\overline{e}}_j^k+{\overline{e}}_j^{k-1}$. Then, sum up for j and take the imaginary part. The item on the left is computed first.

$$\begin{array}{cc}\hfill & \mathcal{I}\{\frac{i\Delta x}{2}\sum _j(\frac{e_{j+\frac{1}{2}}^{k+1}-e_{j+\frac{1}{2}}^{k-1}}{2\Delta t}+\frac{e_{j-\frac{1}{2}}^{k+1}-e_{j-\frac{1}{2}}^{k-1}}{2\Delta t})({\overline{e}}_j^{k+1}+2{\overline{e}}_j^k+{\overline{e}}_j^{k-1})\}\hfill \\ \hfill =& \mathcal{I}\{\frac{i\Delta x}{4\Delta t}\sum _j[(e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_j^{k+1}+e_{j-\frac{1}{2}}^{k+1}{\overline{e}}_j^{k+1})-(e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_j^{k-1}+e_{j-\frac{1}{2}}^{k-1}{\overline{e}}_j^{k-1})+2(e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_j^k+e_{j-\frac{1}{2}}^{k+1}{\overline{e}}_j^k)\hfill \\ \hfill & -2(e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_j^k+e_{j-\frac{1}{2}}^{k-1}{\overline{e}}_j^k)+(e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_j^{k-1}+e_{j-\frac{1}{2}}^{k+1}{\overline{e}}_j^{k-1})-(e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_j^{k+1}+e_{j-\frac{1}{2}}^{k-1}{\overline{e}}_j^{k+1})]\}.\hfill \end{array}$$

(24)

For such terms shaped like $e_{j-\frac{1}{2}}^{k+1}{\overline{e}}_j^{k+1}$ in (24), replace j with $j+1$. So, (24) can be written as the following form

$$\begin{array}{cc}& \mathcal{I}\{\frac{i\Delta x}{4\Delta t}\sum _j[(e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_j^{k+1}+{\psi }_{j+\frac{1}{2}}^{k+1}{\overline{e}}_{j+1}^{k+1})-(e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_j^{k-1}+e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_{j+1}^{k-1})+2(e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_j^k+e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_{j+1}^k)\hfill \\ & -2(e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_j^k+e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_{j+1}^k)+(e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_j^{k-1}+e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_{j+1}^{k-1})-(e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_j^{k+1}+e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_{j+1}^{k+1})]\}.\hfill \end{array}$$

(25)

Then, the following formula is obtained

$$\begin{array}{cc}\hfill & \mathcal{I}\left\{\frac{i\Delta x}{2\Delta t}\sum _j(e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_{j+\frac{1}{2}}^{k+1}-e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_{j+\frac{1}{2}}^{k-1}+2e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_{j+\frac{1}{2}}^k-2e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_{j+\frac{1}{2}}^k+e_{j+\frac{1}{2}}^{k+1}{\overline{e}}_{j+\frac{1}{2}}^{k-1}-e_{j+\frac{1}{2}}^{k-1}{\overline{e}}_{j+\frac{1}{2}}^{k+1})\right\}.\hfill \end{array}$$

(26)

The result is obtained after simplifying the above Formula (26):

$$\begin{array}{cc}\hfill & \frac{2}{\Delta t}(||e^{k+\frac{1}{2}}{||}_{\frac{1}{2}}^2-||e^{k-\frac{1}{2}}|{|}_{\frac{1}{2}}^2).\hfill \end{array}$$

(27)

Similar to the calculation process (24)–(26), for the first term on the right side of Equation (23), the result is

$$\begin{array}{cc}\hfill & \mathcal{I}\{-\Delta x\sum _j[\frac{\alpha (e_{j+1}^{k+\frac{1}{2}}-2e_j^{k+\frac{1}{2}}+e_{j-1}^{k+\frac{1}{2}}+e_{j+1}^{k-\frac{1}{2}}-2e_j^{k-\frac{1}{2}}+e_{j-1}^{k-\frac{1}{2}})}{2{(\Delta x)}^2}]·2[{\overline{e}}_j^{k+\frac{1}{2}}+{\overline{e}}_j^{k-\frac{1}{2}}]\}\hfill \\ \hfill =& 0.\hfill \end{array}$$

(28)

For the second term on the right side of Equation (23), we have

$$\begin{array}{cc}\hfill & \mathcal{I}\left\{-\frac{\Delta x}{4}\sum _j\left(V_{j+\frac{1}{2}}{e}_{j+\frac{1}{2}}^{k+\frac{1}{2}}+V_{j-\frac{1}{2}}{e}_{j-\frac{1}{2}}^{k+\frac{1}{2}}+V_{j-\frac{1}{2}}{e}_{j-\frac{1}{2}}^{k-\frac{1}{2}}+V_{j+\frac{1}{2}}{e}_{j+\frac{1}{2}}^{k-\frac{1}{2}}\right)·2\left({\overline{e}}_j^{k+\frac{1}{2}}+{\overline{e}}_j^{k-\frac{1}{2}}\right)\right\}\hfill \\ \hfill =& 0.\hfill \end{array}$$

(29)

For the third term on the right side of Equation (23), based on the inequality (22), its range is estimated:

$$\begin{array}{cc}\hfill & \mathcal{I}\{{\eta }_{j+\frac{1}{2}}^{k+\frac{1}{2}},2({\overline{e}}_j^{k+\frac{1}{2}}+{\overline{e}}_j^{k-\frac{1}{2}})\}\hfill \\ \hfill & \le C^{\prime }[{(\Delta x^2+\Delta t^2)}^2+(||e^{k+\frac{1}{2}}{||}_{\frac{1}{2}}^2+||e^{k-\frac{1}{2}}|{|}_{\frac{1}{2}}^2)],\hfill \end{array}$$

(30)

where $C^{\prime }$ is a positive constant. Combining Formulas (27)–(30), the following conclusion is obtained:

$$\begin{array}{c}\hfill ||e^{k+\frac{1}{2}}{||}_{\frac{1}{2}}^2-||e^{k-\frac{1}{2}}|{|}_{\frac{1}{2}}^2\le C_3\Delta t[{(\Delta x^2+\Delta t^2)}^2+(||e^{k+\frac{1}{2}}{||}_{\frac{1}{2}}^2+||e^{k-\frac{1}{2}}|{|}_{\frac{1}{2}}^2)],\end{array}$$

(31)

where $C_3=\frac{C^{\prime }}{2}$. Adding up the inequality (31) for k, the following inequality is obtained

$$\begin{array}{c}\hfill ||e^{k+\frac{1}{2}}{||}_{\frac{1}{2}}^2-||e^{\frac{1}{2}}|{|}_{\frac{1}{2}}^2\le C_3[t{(\Delta x^2+\Delta t^2)}^2+\Delta t\sum _{l=0}^k(||e^{l+\frac{1}{2}}{||}_{\frac{1}{2}}^2)].\end{array}$$

(32)

Applying the discrete Gronwall inequality [41,42] and $||e^{\frac{1}{2}}|{|}_{\frac{1}{2}}=0$ to (32), the final result is

$$\begin{array}{c}\hfill ||e^{k+\frac{1}{2}}{||}_{\frac{1}{2}}\le C_3(\Delta x^2+\Delta t^2).\end{array}$$

(33)

In other words, the convergence order of the multi-symplectic variational integrator (10) with $\beta =0$ is $O(\Delta x^2+\Delta t^2)$.

The proof process is completed. □

Here is a note for Theorem 3.

Remark 1.

Although the theoretical result presents that the multi-symplectic variational integrator (10) with $\beta =0$ converges to $O(\Delta x^2+\Delta t^2)$, the numerical results in Section 5 show that the conclusion also holds true for $\beta \ne 0$.

5. Numerical Examples

In this section, the multi-symplectic variational integrator (10) is used to solve specific questions.

Example 1.

Taking the following periodic solitary-wave solution into account,

$$\begin{array}{c}\hfill i{\psi }_t+\alpha (t){\psi }_{xx}+\beta (t){|\psi |}^2\psi =0,\end{array}$$

(34)

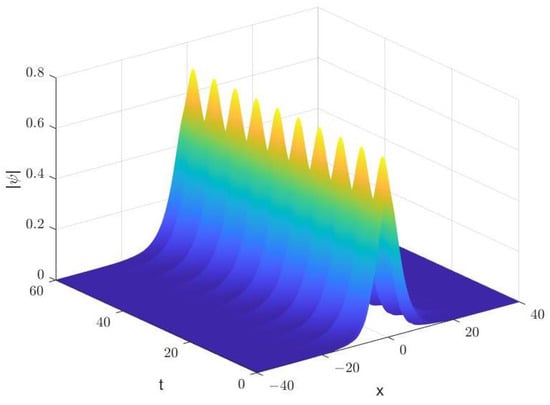
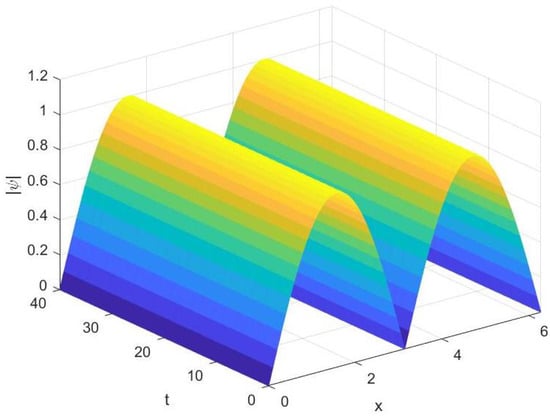
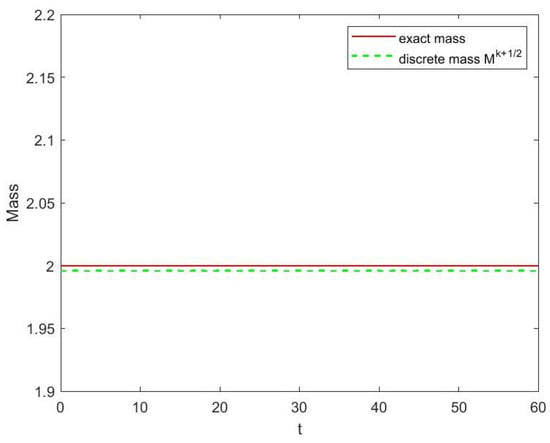
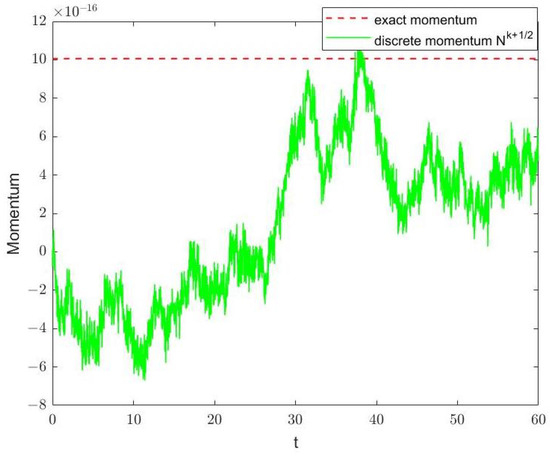
with $\alpha (t)=\frac{1}{2}cos(t),\beta (t)=\frac{cos(t)}{sin(t)+3}$. And $\psi (x,t)=\frac{1}{\sqrt{sin(t)+3}}sech(\frac{x}{sin(t)+3})exp(\frac{i(x^2-1)}{2(sin(t)+3)})$ is the analytical solution to the Equation (34). The numerical solution is given in Figure 2, and the evolutions of mass and momentum are shown separately in Figure 3 and Figure 4 with $\Delta x=0.1,\Delta t=0.02$ during the time from $t=0$ to $t=60$. Observing the three pictures, there is a conclusion that the variational integrator (10) can simulate the numerical solution stably for a long time and maintain the conservation laws precisely.

Figure 2. Numerical periodic waveform of Equation (34) by scheme (10).

Figure 3. Evolution of mass $M^{\frac{1}{2}}$ of Equation (34).

Figure 4. Evolution of momentum $N^{\frac{1}{2}}$ of Equation (34).

With fixed $\Delta t=0.001$, the following Table 1 shows that the variational integrator (10) converges at a second order in the spatial direction.

Table 1. Errors and convergence orders of scheme (10) for Equation (34) at time $t=1$.

$\mathbf{\Delta }\mathit{x}$	${\mathit{L}}^{\mathbf{\infty }}$ Error	Order	${\mathit{L}}^2$ Error	Order
0.2	1.3696 × 10${}^{-2}$	−	6.4490 × 10${}^{-2}$	−
0.1	3.2897 × 10${}^{-3}$	2.0577	1.7133 × 10${}^{-2}$	1.9123
0.05	7.8179 × 10${}^{-4}$	2.0731	3.9849 × 10${}^{-3}$	2.1042
0.025	1.7273 × 10${}^{-4}$	2.1783	9.3160 × 10${}^{-4}$	2.0968

The $L^{\infty }$ error, $L^2$ error and convergence order in Table 1 and Table 2 are obtained from the following formula:

$$L^{\infty } \mathit{error}={max}_j|{\psi }_j^k-\psi (x_j,t_k)|,$$

$$L^2 \mathit{error}=\sqrt{\Delta x{\sum }_j{|{\psi }_j^k-\psi (x_j,t_k)|}^2},$$

$$\mathit{convergence} \mathit{order}=\frac{ln(error(\Delta x_1))/(error(\Delta x_2))}{ln(\Delta x_1)/(\Delta x_2)}.$$

Table 2. Errors and convergence orders of scheme (10) for Equation (34) at time $t=1$.

$\mathbf{\Delta }\mathit{t}$	${\mathit{L}}^{\mathbf{\infty }}$ Error	Order	${\mathit{L}}^2$ Error	Order
0.2	3.7257 × 10${}^{-2}$	−	1.1961 × 10${}^{-1}$	−
0.1	9.7965 × 10${}^{-3}$	1.9272	3.8205 × 10${}^{-2}$	1.6465
0.05	2.3969 × 10${}^{-3}$	2.0311	1.1173 × 10${}^{-2}$	1.7737
0.025	5.7507 × 10${}^{-4}$	2.0594	2.9607 × 10${}^{-3}$	1.9160

With fixed $\Delta x=0.01$, the following Table 2 tells us the variational integrator (10) converges at a second order in time.

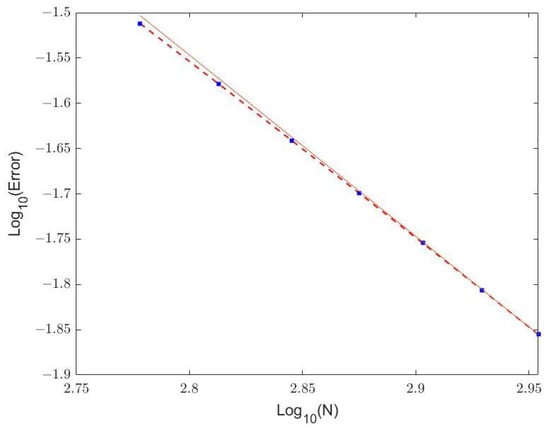
The log-log picture of the $L^2$ error of the multi-symplectic variational integrator (10) for Equation (34) is presented in Figure 5. The solid line in Figure 5 represents a straight line with a slope of −2. Take different N, which corresponds to a space step $\Delta x=\frac{80}{N}$, and the discrete dots represents the logarithm of the ${\mathit{L}}^{\mathbf{2}}$ error of Equation (34) at this space step. The slope of the discrete dots is close to −2. This figure again verifies that the scheme (10) has second-order convergence in the spatial direction.

Figure 5. Log–log plot of $L^2$ error of Equation (34).

Example 2.

The following nonlinear Schrödinger equation with external potential [43] is explored by the variational integrator (10).

$$\begin{array}{c}\hfill \left\{\begin{array}{c}i{\psi }_t+\alpha (t){\psi }_{xx}+V(x)\psi +\beta (t){|\psi |}^2\psi =0,0<x<2\pi ,t>0,\hfill \\ \psi (0,t)=\psi (2\pi ,t)=0,t\ge 0,\hfill \end{array}\right.\end{array}$$

(35)

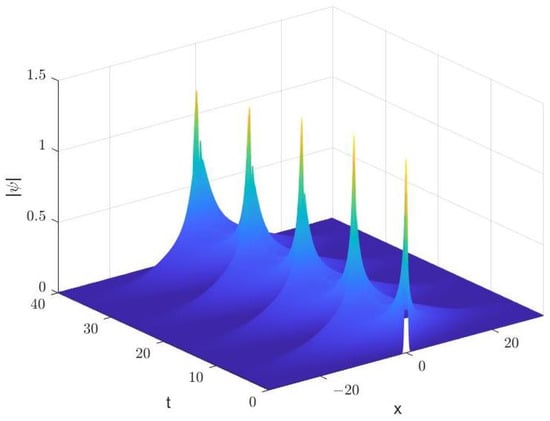
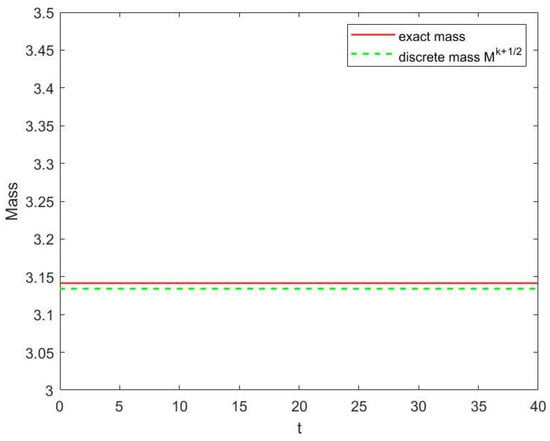
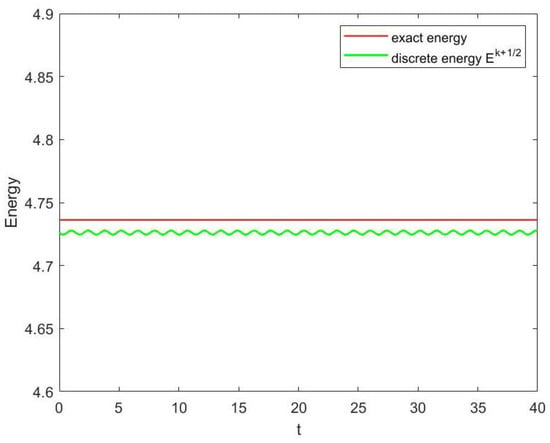
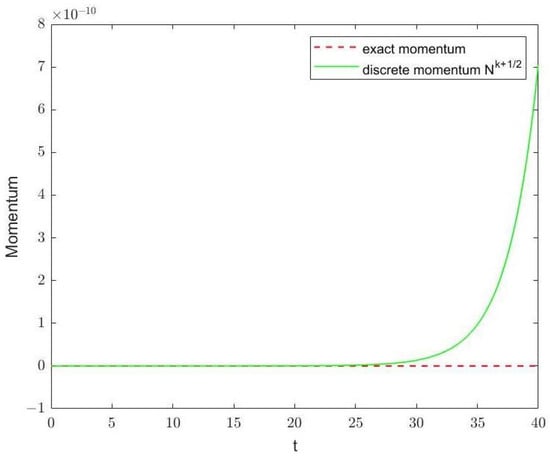
where $\alpha (t)=\frac{1}{2}$, $V(x)={cos}^2(x)$, $\beta (t)=1$. Its exact solution is $\psi (x,t)=sin(x)exp(-3it/2)$. Taking $\Delta x=\pi /32,\Delta t=0.01$, the waveform variation of Equation (35) from $t=0$ to $t=40$ is shown in Figure 6. During this time period, the evolution diagram of mass, energy and momentum are presented separately in Figure 7, Figure 8 and Figure 9. One can observe that the numerical waveform displays well. The characteristics of mass, energy, and momentum conservation laws are preserved well by (10).

Figure 6. Numerical periodic waveform of Equation (35) by scheme (10).

Figure 7. Evolution of mass $M^{\frac{1}{2}}$ of Equation (35).

Figure 8. Evolution of energy $E^{\frac{1}{2}}$ of Equation (35).

Figure 9. Evolution of momentum $N^{\frac{1}{2}}$ of Equation (35).

With fixed $\Delta t=0.0001$, the following Table 3 shows that the variational integrator (10) converges at a second order in the spatial direction.

Table 3. Errors and convergence orders of scheme (10) for Equation (35) at time $t=1$.

$\mathbf{\Delta }\mathit{x}$	${\mathit{L}}^{\mathbf{\infty }}$ Error	Order	${\mathit{L}}^2$ Error	Order
$\pi$/4	5.1709 × 10${}^{-2}$	−	9.3577 × 10${}^{-2}$	−
$\pi$/8	1.3624 × 10${}^{-2}$	1.9243	2.6002 × 10${}^{-2}$	1.8475
$\pi$/16	3.2335 × 10${}^{-3}$	2.0750	6.6999 × 10${}^{-3}$	1.9564
$\pi$/32	8.2855 × 10${}^{-4}$	1.9644	1.7040 × 10${}^{-3}$	1.9752

With fixed $\Delta x=\pi /4096$, the following Table 4 shows that the variational integrator (10) converges at a second order in time direction.

Table 4. Errors and convergence orders of scheme (10) for Equation (35) at time $t=1$.

$\mathbf{\Delta }\mathit{t}$	${\mathit{L}}^{\mathbf{\infty }}$ Error	Order	${\mathit{L}}^2$ Error	Order
1/2	2.3859 × 10${}^{-1}$	−	4.0465 × 10${}^{-1}$	−
1/4	5.2724 × 10${}^{-2}$	2.1780	9.6632 × 10${}^{-2}$	2.0661
1/8	1.2813 × 10${}^{-2}$	2.0409	2.3913 × 10${}^{-2}$	2.0147
1/16	3.1921 × 10${}^{-3}$	2.0050	5.9685 × 10${}^{-3}$	2.0024

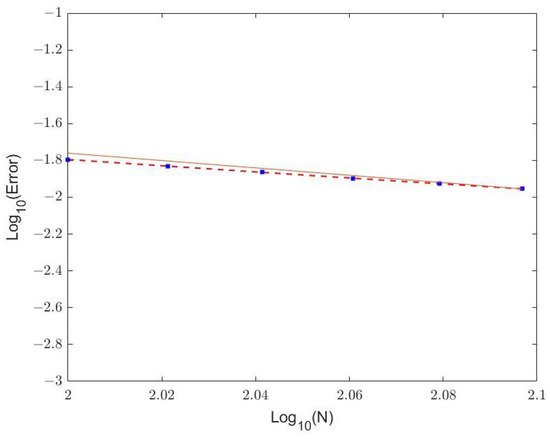
The log-log picture of the $L^2$ error of the multi-symplectic variational integrator (10) for Equation (35) is shown in Figure 10. The solid line in Figure 10 represents a straight line with a slope of −2. Take different N, which corresponds to a space step $\Delta x=\frac{2\pi }{N}$, and the discrete dots represents the logarithm of the ${\mathit{L}}^{\mathbf{2}}$ error of Equation (35) at this space step. The slope of the discrete dots is close to −2. So this figure again verifies that the scheme (10) has second-order convergence in the spatial direction.

Figure 10. Log-log plot of $L^2$ error of Equation (35).

Example 3.

The following NLSE [44] in the interval $[-32,32]$ with external potential is considered,

$$\begin{array}{c}\hfill i{\psi }_t+\alpha (t){\psi }_{xx}+V(x)\psi +\beta (t){|\psi |}^2\psi =0,\end{array}$$

(36)

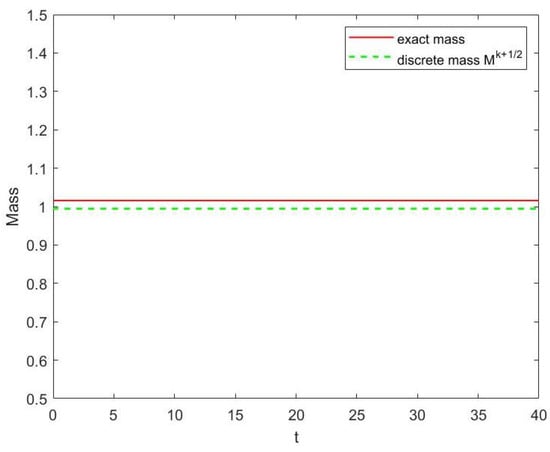
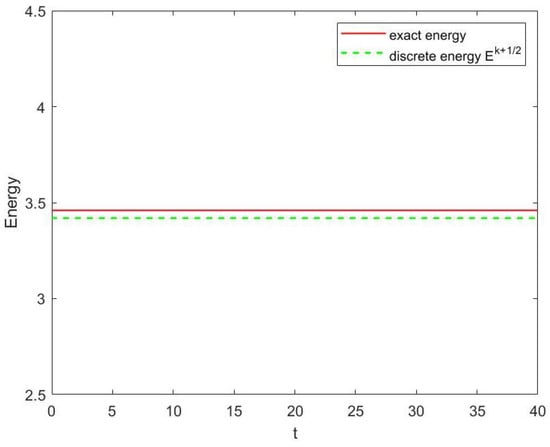
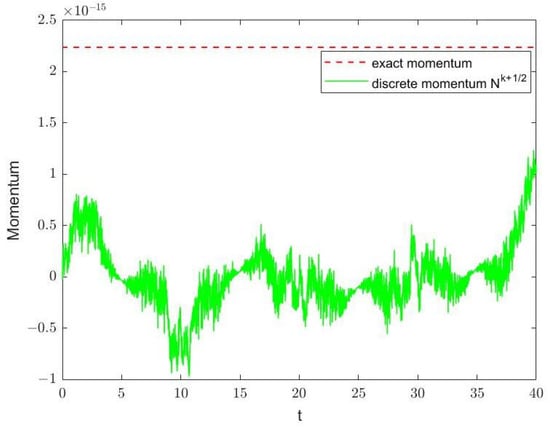
with $\alpha (t)=\frac{1}{2},V(x)=-\frac{1}{2}k{x}^2,k=0.1$, and $\beta (t)=-1$. The initial condition is ${\psi }_0=\frac{1}{{(\pi {\sigma }^2)}^{1/4}}exp(-\frac{x^2}{2{\sigma }^2})$, where $\sigma =0.3$ determines effective width of the initial distribution [43]. The numerical solution of the Equation (36) is shown in Figure 11 with $\Delta x=1/16,\Delta t=0.01$ from $t=0$ to $t=40$. Figure 12, Figure 13 and Figure 14 show the evolution of mass, energy and momentum separately. One can observe the multi-symplectic variational integrator (10) displays the long-time stability and good numerical behaviors of structural preserving properties.

Figure 11. Numerical periodic waveform of Equation (36) by scheme (10).

Figure 12. Evolution of mass $M^{\frac{1}{2}}$ of Equation (36).

Figure 13. Evolution of energy $E^{\frac{1}{2}}$ of Equation (36).

Figure 14. Evolution of momentum $N^{\frac{1}{2}}$ of Equation (36).

6. Conclusions

In this article, the stability conditions and global convergence errors of the multi-symplectic variational integrator for the nonlinear Schr$\ddot{\mathrm{o}}$dinger equation are derived. The von Neumann method is used to reach the conclusion that the multi-symplectic variational integrator is unconditionally linearly stable for solving the variable coefficients Schr$\ddot{\mathrm{o}}$dinger equation. Based on the Sobolev inequality and the discrete conservation laws, the a priori error estimate for the scheme is given. Using the energy method, the scheme in the linear case is proven to maintain the convergence order of $O(\Delta x^2+\Delta t^2)$ in the discrete $L^2$ norm. Via numerical experiments, it is found that this conclusion is applicable to nonlinear situations. The theoretical results of stability and convergence error are the main work in this paper. They are crucial and extend our previous work.

Since the numerical scheme in this paper is derived from a discrete variational principle, the construction of the scheme is somewhat complicated and nonintuitive. This also makes it challenging to establish stability and convergence theories in nonlinear cases. These are the limitations of the method.