Free Vibration Analysis of Trapezoidal Bi-Stable Laminates Supported at the Elastic Midpoint of the Median Line

Abstract

This study investigates the natural vibration of trapezoidal bi-stable laminates (TBL) with elastic supports at the midpoints of the median lines. Configuration of the midplane of the TBL is expressed by a polynomial with 17 parameters. Then, the first order shear deformation theory, curing temperature, and nonlinear strain displacement relations combining energy principles are applied to obtain the bi-stable shapes numerically. Three translational springs and two rotational springs are added at the midpoint of the median line in the trapezoidal bi-stable laminate to acquire elastic point supports. And, by varying the stiffness of the springs, arbitrary elastic point support boundary conditions can be achieved. Chebyshev polynomials are applied to characterize the mode shape function of the TBL. The vibration mode functions of the TBL are mapped to a square area under the new coordinate system by using the coordinate mapping method. Furthermore, the effects of geometry, layup sequence, and spring stiffness on the natural vibrations of the TBL are analyzed, which provides a reference for research in this field. The innovation and highlights lie in the following: (1) the natural frequencies and modes of trapezoidal bi-stable plates are solved; (2) arbitrary elastic support is achieved by a set of artificial springs; (3) the influences of spring stiffness, layer sequence, and trapezoidal base angle on the natural vibration of a trapezoidal bi-stable plate are studied.

1. Introduction

A bi-stable composite material structure is a novel kind of advanced structure that exhibits two distinct stable states and is deformable. Due to their unique multifunctional characteristics, bi-stable materials have received extensive attention, research, and application in fields such as aerospace, defense, automotive electronics, and green energy. As deformable structures, bi-stable laminated structures have two stable configurations and can undergo a snap-through transition between the two stable configurations under external loads. Moreover, they can maintain their stable configurations without the need for external forces or energy supplies. Therefore, bi-stable laminate structures have increasingly received widespread attention from researchers.

In 1981, Hyer [1] first discovered the bi-stable characteristics of asymmetrically laminated composite plates and conducted theoretical and experimental studies on bi-stable plates. Subsequently, Hyer [2] predicted the shapes of bi-stable plates with asymmetric cross-ply lamination. Using the minimum total potential energy principle, the Rayleigh–Ritz method was employed to solve for the stable configurations of bi-stable plates. The results showed that two cylindrical shapes were stable, while the saddle shape was unstable. Jun [3] introduced additional terms in the six-parameter displacement field to consider the influence of in-plane shear strains on the deformation of asymmetrically laid bi-stable laminated plates. They also studied the stable configurations for different ply orientations. Furthermore, some researchers have further investigated bi-stable plates by assuming displacement fields with different parameters. Diaconu [4] developed a displacement field with a higher order polynomial and combined Hamilton’s principle to study the static configurations and dynamic snap-through behavior of bi-stable plates under external loading. The accuracy of their model in practical applications was verified by comparing the results with finite element analysis. Emam [5] employed a simplified four-parameter displacement field in their Rayleigh–Ritz model and compared it with experimental and finite element results, demonstrating good agreement between them. Wu [6] studied the nonlinear dynamics of cross-ply bi-stable laminates (BL) subjected to external excitation by establishing a 17-parameter displacement field. As the accuracy of prediction increased, the numerical computations became more complex.

In the current research stage, most studies on bi-stable laminates have been limited to square or rectangular plates, with fewer studies focusing on bi-stable laminates of other shapes. The geometric shape of a trapezoidal bi-stable laminate is more versatile compared to square plates, as it can be modified by changing angles and aspect ratios. By fixing the dimensions of the TBL’s base and height, the shape of the trapezoidal plate can be achieved by varying the sizes of the two base angles. This approach offers significant potential for practical engineering applications such as deformable structural elements in morphing aircraft and spacecraft [7]. Orris [8] analyzed the vibrations of asymmetric trapezoidal plates with all edges simply supported. The Galerkin approach was employed to represent the deflection surface. Numerical values of the first seven to eight natural frequencies for various geometric shapes of asymmetric trapezoids were provided in tabular form. Node patterns for several typical configurations were also presented. Kumar [9] investigated the deformation behavior of bi-stable shapes obtained from triangular asymmetric composite laminate plates. They simulated the snap-through transition between bi-stable shapes under transverse point loads. Medina [10] established a criterion for the geometric parameters of electrostatically actuated curved axisymmetric circular plates in bi-stable behavior. They employed Berger’s approximate von-Kármán nonlinear plate theory and combined it with single-degree-of-freedom reduction order modeling. They derived a simple semi-analytical bi-stability criterion to obtain the critical deflection and the geometric parameters of the plate in the form of implicit algebraic equations. The criterion was then validated using the arc-length method and direct numerical solution. Quintana [11] proposed a general variational formulation for determining the free vibration of trapezoidal and triangular symmetric laminated plates. Murat [12] presented a convolution method for free vibration analysis of trapezoidal plates. Frequency parameters for symmetric cross-ply and angle plies trapezoidal plates were obtained. Zamani [13] researched the free vibration of moderately thick symmetric laminated trapezoidal plates under different boundary conditions. Sang [14] proposed an efficient method to analyze the free vibration of asymmetric trapezoidal membranes. Umut [15] investigated the frequency optimization problem of symmetric laminated general quadrilateral and trapezoidal thin plates. Rezaiee-Pajand [16] developed a hybrid interpolation formula for nonlinear analysis of plates and shells. Using the equivalent single layer (ESL) theory and mixed format rules, a formula for analyzing functional gradient (FG) sandwich structures was presented. Rezaiee-Pajand [17] used isoparametric six-node triangular elements for geometric nonlinear analysis of functionally graded shells.

A literature review indicates that most of the studies on bi-stable plates with classical boundary conditions are limited to the square and the rectangle. There is relatively little research on the trapezoidal bi-stable plates. As a structural element, the trapezoidal plate still plays an important part in engineering fields. Most of the research on plates and shells in the literature is about classical boundary conditions (CBC). However, in the majority of practical applications, these boundary conditions are not accurate. It is essential to study the dynamic characteristics of bi-stable structures under elastic support boundary conditions [18,19,20,21,22,23,24,25,26,27]. Also, both asymmetric and antisymmetric stacking sequences are the most common laminates; they should receive more attention and research.

Therefore, this study is an effort to research the static stable configurations and natural vibrations of TBLs under elastic support at the midpoint of the central line, in which artificial springs will be used to achieve elastic boundary conditions by adjusting the stiffness of the boundary springs. The research on these issues will greatly contribute to the development and application of bi-stable laminated plates, further deepening theoretical understanding about them.

2. Formulation

As shown in Figure 1, there is a four-layer, fiber-reinforced, composite trapezoidal bi-stable laminate. A Cartesian coordinate is constructed at the midplane of the TBL, as depicted in Figure 1a. The asymmetric and antisymmetric stacking sequences are considered, respectively, as shown in Figure 1b,c. The boundary conditions are defined as four-sided free edges with elastic supports at the midpoints of the median lines, which is simulated using five artificial springs, where $k_u$, $k_v$, and $k_w$ represent three translational springs, while $k_{{\varphi }_x}$ and $k_{{\varphi }_y}$ mean two rotational springs. Assuming the laminate has a base length of b, height L, and thickness h, the angles α and β represent the angles between the two legs of the laminate and the perpendicular baseline, respectively. By changing the size of α and β, bi-stable plates of different shapes can be obtained, such as trapezoidal plates, square plates, and triangular plates.

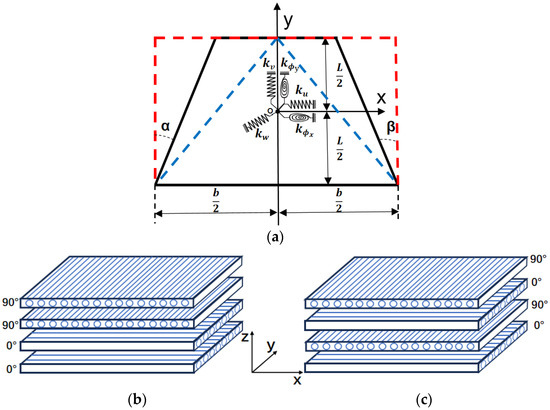
Figure 1. (a) Bi-stable laminates with elastic support at the midpoint of the median line; (b) bi-stable laminates of asymmetric cross-ply; (c) bi-stable laminates of antisymmetric cross-ply.

To describe the stable configurations and dynamic behavior of bi-stable laminated plates, a 17-parameter higher-order polynomial [28] is employed here:

$$u_0=a_{0}x+a_{1}x{y}^2+a_2{x}^3+a_{3}x{y}^4+a_4{x}^3{y}^2+a_5{x}^5,$$

(1)

$$v_0=b_{0}y+b_{1}y{x}^2+b_2{y}^3+b_{3}y{x}^4+b_4{y}^3{x}^2+b_5{y}^5,$$

(2)

$$w_0=\frac{1}{2}\left(q_0{x}^2+q_1{y}^2+q_2{y}^2{x}^2+q_3{x}^4+q_4{y}^4\right),$$

(3)

where $u_0$, $v_0$ and $w_0$ are the displacements of the TBL in the xoy plane; $a_i$, $b_j$ and $q_k$ are undetermined coefficients. The higher-order displacement field can describe its configuration more accurately because it can show the change of local curvature and edge effects.

In light of the FSDT, the displacement at any point can be given by

$$u=u_0+z{\varphi }_x,$$

(4)

$$v=v_0+z{\varphi }_y,$$

(5)

$$w=w_0,$$

(6)

where ${\varphi }_x$ and ${\varphi }_y$ represent the rotations of the midplane normal of the TBL around the y-axis and x-axis [29].

$${\varphi }_x=-\frac{\partial w_0}{\partial x},{\varphi }_y=-\frac{\partial w_0}{\partial y}.$$

(7)

The principal bending curvatures and twisting curvature of the TBL are given as follows:

$$k_x=-\frac{{\partial }^{2}w}{\partial x^2}=-q_0-q_2{y}^2-6q_3{x}^2,$$

(8)

$$k_y=-\frac{{\partial }^{2}w}{\partial y^2}=-q_1-q_2{x}^2-6q_4{y}^2,$$

(9)

$$k_{xy}=-2\frac{{\partial }^{2}w}{\partial x\partial y}=-4q_{2}xy,$$

(10)

where $k_{xy}$ is the twisting curvature; $k_x$ and $k_y$ are curvatures in the x and y directions. To solve the stable equilibrium configuration of the TBL, the nonlinear von Kármán strain –displacement relationship is employed. The relationship between the surface strain components and the displacement in the bi-stable plate are expressed as

$${\left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\gamma }_{xy}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\right\}}^{\left(k\right)}={\left\{\begin{array}{c}{\epsilon }_{xx}^{\left(0\right)}\\ {\epsilon }_{yy}^{\left(0\right)}\\ {\gamma }_{xy}^{\left(0\right)}\\ {\gamma }_{yz}^{\left(0\right)}\\ {\gamma }_{xz}^{\left(0\right)}\end{array}\right\}}^{\left(k\right)}+z{\left\{\begin{array}{c}{\epsilon }_{xx}^{\left(1\right)}\\ {\epsilon }_{yy}^{\left(1\right)}\\ {\gamma }_{xy}^{\left(1\right)}\\ {\gamma }_{yz}^{\left(1\right)}\\ {\gamma }_{xz}^{\left(1\right)}\end{array}\right\}}^{\left(k\right)}$$

(11)

where

$${\left\{\begin{array}{c}{\epsilon }_{xx}^{\left(0\right)}\\ {\epsilon }_{yy}^{\left(0\right)}\\ {\gamma }_{xy}^{\left(0\right)}\end{array}\right\}}^{\left(k\right)}={\left\{\begin{array}{c}\frac{\partial u_0}{\partial x}+\frac{1}{2}{\left(\frac{\partial w_0}{\partial x}\right)}^2\\ \frac{\partial v_0}{\partial y}+\frac{1}{2}{\left(\frac{\partial w_0}{\partial y}\right)}^2\\ \frac{\partial u_0}{\partial y}+\frac{\partial v_0}{\partial x}+\frac{\partial w_0}{\partial x}\frac{\partial w_0}{\partial y}\end{array}\right\}}^{\left(k\right)},{\left\{\begin{array}{c}{\gamma }_{yz}^{\left(0\right)}\\ {\gamma }_{xz}^{\left(0\right)}\end{array}\right\}}^{\left(k\right)}={\left\{\begin{array}{c}\frac{\partial w_0}{\partial y}+{\varphi }_y\\ \frac{\partial w_0}{\partial x}+{\varphi }_x\end{array}\right\}}^{\left(k\right)}$$

(12)

$${\left\{\begin{array}{c}{\epsilon }_{xx}^{\left(1\right)}\\ {\epsilon }_{yy}^{\left(1\right)}\\ {\gamma }_{xy}^{\left(1\right)}\end{array}\right\}}^{\left(k\right)}={\left\{\begin{array}{c}\frac{\partial {\varphi }_x}{\partial x}\\ \frac{\partial {\varphi }_y}{\partial y}\\ \frac{\partial {\varphi }_x}{\partial y}+\frac{\partial {\varphi }_y}{\partial x}\end{array}\right\}}^{\left(k\right)},{\left\{\begin{array}{c}{\gamma }_{yz}^{\left(1\right)}\\ {\gamma }_{xz}^{\left(1\right)}\end{array}\right\}}^{\left(k\right)}={\left\{\begin{array}{c}0\\ 0\end{array}\right\}}^{\left(k\right)}.$$

(13)

Concerning the curing temperature, the constitutive relationship is given in the following form:

$${\left\{\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\tau }_{xy}\\ {\tau }_{yz}\\ {\tau }_{xz}\end{array}\right\}}^{\left(k\right)}={\left\{\begin{array}{ccccc}{\bar{S}}_{11}& {\bar{S}}_{12}& {\bar{S}}_{16}& 0& 0\\ {\bar{S}}_{12}& {\bar{S}}_{22}& {\bar{S}}_{26}& 0& 0\\ {\bar{S}}_{16}& {\bar{S}}_{26}& {\bar{S}}_{66}& 0& 0\\ 0& 0& 0& {\bar{S}}_{44}& {\bar{S}}_{45}\\ 0& 0& 0& {\bar{S}}_{45}& {\bar{S}}_{44}\end{array}\right\}}^{\left(k\right)}{\left\{\left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\gamma }_{xy}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\right\}-\left\{\begin{array}{c}{\alpha }_{xx}\\ {\alpha }_{yy}\\ 2{\alpha }_{xy}\\ 0\\ 0\end{array}\right\}\Delta T\right\}}^{\left(k\right)},$$

(14)

where $\Delta T$ is the curing temperature; ${\alpha }_{xy}$, ${\alpha }_{xx}$, and ${\alpha }_{yy}$ are the thermal expansion coefficients after the coordinate transformation:

$$2{\alpha }_{xy}=2({\alpha }_1-{\alpha }_2)\cos \theta \sin \theta ,$$

(15)

$${\alpha }_{xx}={\alpha }_1{\cos }^2\theta +{\alpha }_2{\sin }^2\theta ,$$

(16)

$${\alpha }_{yy}={\alpha }_1{\sin }^2\theta +{\alpha }_2{\cos }^2\theta .$$

(17)

${\bar{S}}_{ij}$ is the conversion stiffness coefficient for the bi-stable plate, which can be rewritten as:

$${\bar{S}}_{11}=S_{11}{\cos }^4\theta +2(2S_{66}+S_{12}){\cos }^2\theta {\sin }^2\theta +S_{22}{\sin }^4\theta ,$$

(18)

$${\bar{S}}_{22}=S_{11}{\sin }^4\theta +2(2S_{66}+S_{12}){\cos }^2\theta {\sin }^2\theta +S_{22}{\cos }^4\theta ,$$

(19)

$${\bar{S}}_{12}=(S_{11}-4S_{66}+S_{22}){\cos }^2\theta {\sin }^2\theta +S_{12}({\sin }^4\theta +{\cos }^4\theta ),$$

(20)

$${\bar{S}}_{16}=(S_{11}-2S_{66}-S_{12}){\cos }^3\theta \sin \theta +(S_{12}+2S_{66}-S_{22})\cos \theta {\sin }^3\theta ,$$

(21)

$${\bar{S}}_{26}=(S_{11}-2S_{66}-S_{12})\cos \theta {\sin }^3\theta +(S_{12}+2S_{66}-S_{22}){\cos }^3\theta \sin \theta ,$$

(22)

$${\bar{S}}_{66}=(S_{11}+S_{22}-2S_{66}-2S_{12}){\cos }^2\theta {\sin }^2\theta +S_{66}({\sin }^4\theta +{\cos }^4\theta ),$$

(23)

$${\bar{S}}_{44}=S_{44}{\cos }^2\theta +S_{55}{\sin }^2\theta ,$$

(24)

$${\bar{S}}_{55}=S_{55}{\cos }^2\theta +S_{44}{\sin }^2\theta ,$$

(25)

$${\bar{S}}_{45}=(S_{55}-S_{44})\sin \theta \cos \theta ,$$

(26)

where $\theta$ is the fiber laying angle of the orthogonal laying bi-stable composite laminates, and $S_{ij}$ can be given by

$$S_{11}=\frac{E_1}{1-v_{12}{v}_{21}},S_{12}=\frac{v_{12}{E}_2}{1-v_{12}{v}_{21}},S_{22}=\frac{E_2}{1-v_{12}{v}_{21}},S_{66}=G_{12},S_{55}=G_{13},S_{44}=G_{23};$$

(27)

$${\left\{\begin{array}{c}{\sigma }_{xx}^T\\ {\sigma }_{yy}^T\\ {\tau }_{xy}^T\\ {\tau }_{yz}^T\\ {\tau }_{xz}^T\end{array}\right\}}^{\left(k\right)}={\left\{\begin{array}{ccccc}{\bar{S}}_{11}& {\bar{S}}_{12}& {\bar{S}}_{16}& 0& 0\\ {\bar{S}}_{12}& {\bar{S}}_{22}& {\bar{S}}_{26}& 0& 0\\ {\bar{S}}_{16}& {\bar{S}}_{26}& {\bar{S}}_{66}& 0& 0\\ 0& 0& 0& {\bar{S}}_{44}& {\bar{S}}_{45}\\ 0& 0& 0& {\bar{S}}_{45}& {\bar{S}}_{44}\end{array}\right\}}^{\left(k\right)}{\left\{\left\{\begin{array}{c}{\alpha }_{xx}\\ {\alpha }_{yy}\\ 2{\alpha }_{xy}\\ 0\\ 0\end{array}\right\}\Delta T\right\}}^{\left(k\right)},$$

(28)

where ${\sigma }_{xx}^T$, ${\sigma }_{yy}^T$, ${\tau }_{xy}^T$, ${\tau }_{yz}^T$, and ${\tau }_{xz}^T$ are the influence of the curing temperature upon the laminate.

The total potential energy of the TBL is

$$U_P=\frac{1}{2}\sum _{k=1}^N{\int }_{-\frac{L}{2}}^{\frac{L}{2}}{\int }_{L_0}^{L_1}{\int }_{Z_k}^{Z_{k+1}}\left[({\sigma }_{xx}-{\sigma }_{xx}^T){\epsilon }_{xx}+({\sigma }_{yy}-{\sigma }_{yy}^T){\epsilon }_{yy}+({\tau }_{xy}-{\tau }_{xy}^T){\gamma }_{xy}+({\tau }_{yz}-{\tau }_{yz}^T){\gamma }_{yz}+({\tau }_{xz}-{\tau }_{xz}^T){\gamma }_{xz}\right]\mathrm{d}z\mathrm{d}x\mathrm{d}y$$

(29)

where

$$L_1=-\tan \beta \cdot y-\frac{\tan \beta \cdot L}{2}+\frac{b}{2},$$

(30)

$$L_0=\tan \alpha \cdot y+\frac{\tan \alpha \cdot L}{2}-\frac{b}{2}.$$

(31)

To obtain the two stable structures of the bi-stable laminate, we can use the minimum total potential energy principle:

$$\delta U_P=\sum _{i=0}^5\left(\frac{\partial U_P}{\partial a_i}\right)\delta a_i+\sum _{j=0}^5\left(\frac{\partial U_P}{\partial b_j}\right)\delta b_j+\sum _{k=0}^4\left(\frac{\partial U_P}{\partial q_k}\right)\delta q_k\equiv 0$$

(32)

and

$$f_i=\frac{\partial U_P}{\partial a_i},(i=0-5),$$

(33)

$$f_j=\frac{\partial U_P}{\partial b_j},(j=0-5),$$

(34)

$$f_k=\frac{\partial U_P}{\partial q_k},(k=0-4).$$

(35)

Subsequently, the stability solutions of the TBL are determined by evaluating the positive definiteness of the Jacobian matrix. The Jacobian matrix can be represented as

$$J=\frac{\partial (f_1,\cdots ,f_{17})}{\partial (a_0,\cdots ,a_5,b_0,\cdots ,b_5,q_0,\cdots ,q_4)}.$$

(36)

2.1. Natural Vibration Frequency

The kinetic energy of the TBL is

$$T_P=\frac{\rho }{2}\sum _{k=1}^N{\int }_{-\frac{L}{2}}^{\frac{L}{2}}{\int }_{L_0}^{L_1}{\int }_{Z_k}^{Z_{k+1}}\left[{\dot{u}}^2+{\dot{v}}^2+{\dot{w}}^2\right]dzdxdy,$$

(37)

where $\rho$ is the density of the TBL.

The elastic potential energy at the support point of the TBL can be calculated by

$$U_{ES}=\frac{1}{2}\left[k_u{u}_0^2+k_v{v}_0^2+k_w{w}_0^2+k_{{\varphi }_x}{\varphi }_x^2+k_{{\varphi }_y}{\varphi }_y^2)\right].$$

(38)

Thus, the total energy is as

$${\prod =U_P+U_{ES}-T}_P.$$

(39)

Assume that

$$u=\widehat{U}(x,y)e^{\left(i\omega t\right)},$$

(40)

$$v=\widehat{V}(x,y)e^{\left(i\omega t\right)},$$

(41)

$$w=\widehat{W}(x,y)e^{\left(i\omega t\right)},$$

(42)

$${\varphi }_x={\widehat{\Phi }}_x(x,y)e^{\left(i\omega t\right)},$$

(43)

$${\varphi }_y={\widehat{\Phi }}_y(x,y)e^{\left(i\omega t\right)},$$

(44)

where $\omega$ is natural frequency, $\widehat{U}(x,y)$, $\widehat{V}(x,y)$, $\widehat{W}(x,y)$, ${\widehat{\Phi }}_x(x,y)$, and ${\widehat{\Phi }}_y(x,y)$ are the shape functions. And

$$\widehat{U}(\varsigma ,\eta )=\sum _{f=1}^F\sum _{g=1}^G{U}_{fg}{T}_{uf}\left(\varsigma \right)T_{ug}\left(\eta \right),$$

(45)

$$\widehat{V}(\varsigma ,\eta )=\sum _{f=1}^F\sum _{g=1}^G{V}_{fg}{T}_{vf}\left(\varsigma \right)T_{vg}\left(\eta \right),$$

(46)

$$\widehat{W}(\varsigma ,\eta )=\sum _{f=1}^F\sum _{g=1}^G{W}_{fg}{T}_{wf}\left(\varsigma \right)T_{wg}\left(\eta \right),$$

(47)

$${\widehat{\Phi }}_x(\varsigma ,\eta )=\sum _{f=1}^F\sum _{g=1}^G{{\Phi }_x}_{fg}{T}_{{\varphi }_{x}f}\left(\varsigma \right)T_{{\varphi }_{x}g}\left(\eta \right),$$

(48)

$${\widehat{\Phi }}_y(\varsigma ,\eta )=\sum _{f=1}^F\sum _{g=1}^G{{\Phi }_y}_{fg}{T}_{{\varphi }_{y}f}\left(\varsigma \right)T_{{\varphi }_{y}g}\left(\eta \right),$$

(49)

where $U_{fg}$, $V_{fg}$, $W_{fg}$, ${{\Phi }_x}_{fg}$, and ${{\Phi }_y}_{fg}$ are undetermined coefficients; $T_{\delta f}$ and $T_{\delta g}$ ($\delta =u,v,w,{\Phi }_x,{\Phi }_y$) are expressed as

$$T_{\delta f}\left(\varsigma \right)=f_{\delta }\left(\varsigma \right)p_f\left(\varsigma \right),$$

(50)

$$T_{\delta g}\left(\eta \right)=g_{\delta }\left(\eta \right)p_g\left(\eta \right).$$

(51)

Because Chebyshev polynomials have good orthogonality and convergence, therefore, we select them to compute the mode shapes and frequencies of the system. For the free boundary conditions, we have [30]:

$$\begin{array}{c}{p}_1\left(\varsigma \right)=1,p_2\left(\varsigma \right)=\varsigma ,\\ p_f\left(\varsigma \right)=2\varsigma p_{f-1}\left(\varsigma \right)-p_{f-2}\left(\varsigma \right),(F\ge f\ge 3),\end{array}$$

(52)

$$\begin{gathered} p_1\left(\eta \right)=1,p_2\left(\eta \right)=\eta , \\ {p}_g\left(\eta \right)=2\eta p_{g-1}\left(\eta \right)-p_{g-2}\left(\eta \right),(G\ge g\ge 3), \end{gathered}$$

(53)

where $\xi =2x/L_x$ and $\eta =2y/L_y$, applying the Rayleigh–Ritz method, yields

$$\begin{gathered} \frac{\partial \prod }{\partial U_{fg}}=0,\frac{\partial \prod }{\partial V_{fg}}=0, \\ \frac{\partial \prod }{\partial W_{fg}}=0,\frac{\partial \prod }{\partial {{\Phi }_x}_{fg}}=0,\frac{\partial \prod }{\partial {{\Phi }_y}_{fg}}=0, \end{gathered}$$

(54)

and

$$(\mathbf{K}-{\omega }^2\mathbf{M})\mathbf{X}=0,$$

(55)

where M and K are mass and stiffness matrix, respectively. X is the coefficient vector that can be expressed as

$$\mathbf{X}={\left[U_{11},\cdots ,U_{FG},V_{11},\cdots ,V_{FG},W_{11},\cdots ,W_{FG},{\Phi }_{x11},\cdots ,{\Phi }_{xFG},{\Phi }_{y11},\cdots ,{\Phi }_{yFG}\right]}^T.$$

(56)

Thus, the generalized eigenvalues can be calculated by Equation (55), and the mode shape function of the TBL yields by substituting the eigenvector $\mathbf{X}$ into Equations (45)–(49).

2.2. Coordinate Mapping

Traditional numerical methods can only compute the modes of square laminated plates and cannot generate mode shapes for complex shapes such as trapezoidal plates. To address this limitation, the original trapezoidal shape in a physical coordinate system is mapped onto a square in the ξ-η coordinate system [31]; see Figure 2.

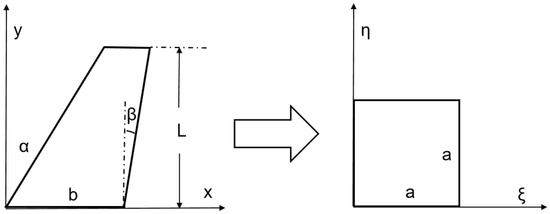
Figure 2. Original coordinates and transformation coordinates.

Assuming the image before mapping is $H(x,y)$ and the image after mapping is $H’(\bar{x},\bar{y})$, the following transformation relationship exists between the images before and after mapping:

$$\bar{x}=f(x,y),\bar{y}=g(x,y),$$

(57)

$$H(x,y)=H’(\bar{x},\bar{y}).$$

(58)

One can obtain

$$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}{f}^{-1}(\bar{x},\bar{y})\\ g^{-1}(\bar{x},\bar{y})\end{array}\right),$$

(59)

$$H’(\bar{x},\bar{y})=H\left(f^{-1}\right(\bar{x},\bar{y}),g^{-1}(\bar{x},\bar{y}\left)\right).$$

(60)

For a corresponding integer point position on the mapped image $(\bar{x},\bar{y})$, the position on the original image $(x,y)$ is a non-integer point. Interpolation is used using the input image values at the surrounding integer point positions to obtain the pixel value at that point; see Figure 3. After the coordinate transformation and interpolation steps, the transformed coordinates are obtained.

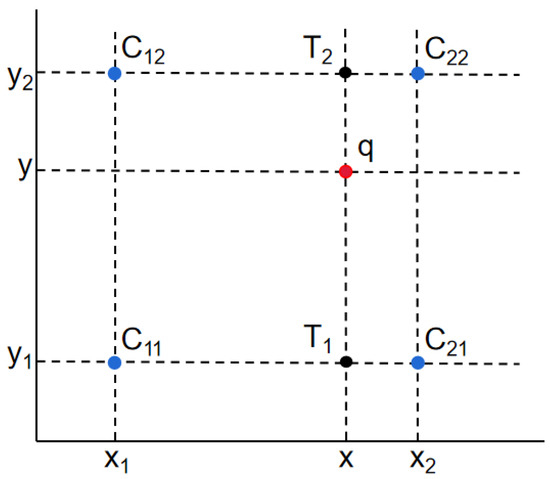
Figure 3. Transformation of original coordinates to transformed coordinates.

Interpolate in the x direction:

$$f\left(T_1\right)\approx \frac{x_2-x}{x_2-x_1}f\left(C_{11}\right)+\frac{x-x_1}{x_2-x_1}f\left(C_{21}\right),$$

(61)

where $T_1=(x,y_1)$, $C_{11}=(x_1,y_1)$, $C_{21}=(x_2,y_1)$;

$$f\left(T_2\right)\approx \frac{x_2-x}{x_2-x_1}f\left(C_{12}\right)+\frac{x-x_1}{x_2-x_1}f\left(C_{22}\right),$$

(62)

where $T_2=(x,y_2)$, $C_{12}=(x_1,y_2)$, $C_{22}=(x_2,y_2)$.

Interpolate in the y direction:

$$f\left(q\right)\approx \frac{y_2-y}{y_2-y_1}f\left(T_1\right)+\frac{y-y_1}{y_2-y_1}f\left(T_2\right),$$

(63)

where $q=(x,y)$.

In summary:

$$\begin{gathered} f(x,y)\approx \frac{(x_2-x)(y_2-y)}{(x_2-x_1)(y_2-y_1)}f\left(C_{11}\right)+\frac{(x-x_1)(y_2-y)}{(x_2-x_1)(y_2-y_1)}f\left(C_{21}\right) \\ +\frac{(x_2-x)(y-y_1)}{(x_2-x_1)(y_2-y_1)}f\left(C_{12}\right)+\frac{(x-x_1)(y-y_1)}{(x_2-x_1)(y_2-y_1)}f\left(C_{22}\right). \end{gathered}$$

(64)

3. Results and Discussions

3.1. Convergence and Validation

Consider a square bi-stable laminated plate with a bottom side length of 0.2 m, height L of 0.2 m, and angles α and β equal to 0°. The selected material parameters are:

$$\begin{gathered} E_1=138\mathrm{Gpa},E_2=8\mathrm{Gpa},V_{13}=0.29,V_{12}=0.29,V_{23}=0.31,G_{12}=4.5\mathrm{Gpa},G_{13}=4.5\mathrm{Gpa}, \\ {G}_{23}=3.24\mathrm{Gpa},{\alpha }_1=-0.5\times 10^{-6}1/\mathrm{K},{\alpha }_2=28\times 10^{-6}1/\mathrm{K}. \end{gathered}$$

Table 1 presents the first five frequencies of the bi-stable plate for the translational and rotational stiffness of 10¹⁰ N/m. It can be observed that the results have converged when the Chebyshev polynomials are taken up to the 11th order.

Table 1. Verification of natural frequency convergence of bi-stable plate.

M = N	Mode
	1	2	3	4	5
7	51.4039	75.1301	88.6148	94.8560	261.9735
8	50.9004	74.3799	79.0144	81.3500	217.7540
9	50.8660	73.4639	75.6499	76.2188	202.6985
10	50.8023	68.5561	71.5913	73.7912	193.1800
11	50.8037	69.0348	73.3088	74.5869	195.4104

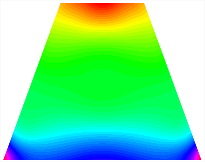
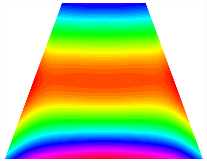
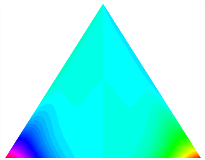
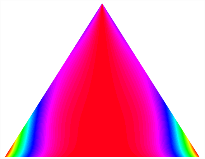
To verify the accuracy of this current method for calculating the stable configurations of the TBL, the stable configurations are compared with finite element results. The TBL has the base length b = 1 m, height L = 0.5 m, and the thickness $h=0.001 \mathrm{m}$. Figure 4 and Figure 5 show the comparison for the asymmetric TBL ($\alpha =\beta =30^{\circ }$) and the triangular bi-stable plate ($\alpha =\beta =45^{\circ }$), respectively. As shown in the figure, configuration 1 of the TBL is bent in the x direction, and configuration 2 is bent in the y direction. In the finite element software ABAQUS, the element type of trapezoidal bi-stable plate is SR4, and the number of elements is 168. The element type used for the triangular bi-stable plate is S3, and the number of elements is 226. The results show a good agreement between them.

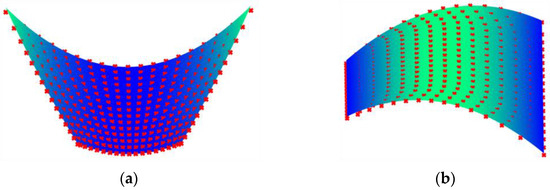
Figure 4. Trapezoidal laminates stable configuration, Marker ×—ABAQUS, continuous surfaces—present results: (a) stable configuration 1, (b) stable configuration 2.

Figure 5. Triangular laminated plates stable configurations, Marker ×—ABAQUS, continuous surfaces—present result: (a) stable configuration 1, (b) stable configuration state 2.

To further validate the accuracy and reliability of the current computational results, a comparison is performed for the first five order frequencies of the TBL obtained in this work and those mentioned in the existing literature [32]. In this comparison, the height is set to 0.2 m; $\alpha =0^{°},\beta =30^{°}$; the thickness $\mathrm{h}=0.5\times 10^{-3} \mathrm{m}$; and all spring stiffness values were set to k = 10¹⁰ N/m. The comparison results are presented in Table 2 and Table 3.

Table 2. Natural frequency of a TBL in stable state 1 with 0/80.

a/b	Method			Mode
		1	2	3	4	5
0.45	Present	8.1579	10.8591	13.9958	26.1037	56.5930
	Chen [32]	8.3471	10.9428	14.1820	26.0593	55.8160
0.65	Present	16.0010	18.6011	26.4764	70.7064	93.0424
	Chen [32]	15.8652	17.9806	25.9661	69.9717	91.4801
0.85	Present	21.0628	26.0702	38.1500	132.0828	135.4804
	Chen [32]	20.9375	27.9960	38.7974	134.0326	135.7221
1.05	Present	25.0950	35.3496	51.4138	162.2723	171.0691
	Chen [32]	24.8289	34.9399	51.2750	156.3854	176.3461
1.25	Present	28.0829	40.1271	62.1167	165.6647	178.2889
	Chen [32]	28.0305	39.4152	60.4244	162.6378	173.2389

Table 3. Natural frequency of a TBL in stable state 2 with 0/80.

a/b	Method			Mode
		1	2	3	4	5
0.45	Present	11.0705	33.8813	34.6891	48.7076	94.7213
	Chen [32]	11.1398	33.7664	35.3448	47.5304	91.4922
0.65	Present	15.3583	35.5024	37.6994	62.0993	129.3215
	Chen [32]	15.4329	34.7729	37.0834	61.3297	130.9006
0.85	Present	19.2595	34.5391	39.8866	79.8755	158.4627
	Chen [32]	18.7706	33.7920	39.0935	79.8245	154.1188
1.05	Present	21.6567	34.1345	41.7767	115.6784	165.9730
	Chen [32]	21.4174	33.8188	41.8840	111.4960	166.4675
1.25	Present	23.7366	31.7038	45.5477	148.8743	175.2377
	Chen [32]	23.5543	30.2057	44.3604	149.0339	175.7441

Table 4 calculates the first four orders’ natural frequencies of the homogeneous material square plate supported by four corner points; Poisson’s ratio $v=0.3$; dimensionless frequency $\bar{\omega }=\omega a^2\sqrt{\rho h/D}$. The results are compared with those in the literature and are in agreement with those in the literature.

Table 4. The first four natural frequencies of a square plate supported by four corner points.

Method		Mode
	1	2	3	4
Present	7.1187	15.8610	15.8610	19.8416
Kerstens [33]	7.15	15.64	15.64	19.49
Rao [34]	7.11089	15.77	15.77	19.596

Table 5 displays the first five orders’ frequencies and mode shapes of the square bi-stable plate clamped at the midpoint of the centerline, which are obtained and compared with the finite element results. The square bi-stable plate has a bottom length $b=0.3 \mathrm{m}$, height $L=0.3 \mathrm{m}$, $\alpha =0^{°}$, $\beta =0^{°}$, and thickness $h=0.001 \mathrm{m}$. The comparison results show good agreement.

Table 5. The first five natural frequencies and modal shapes of a square plate.

Method			Mode
	1	2	3	4	5
Present	30.9143	37.1701	53.9814	97.1963	129.7531
ABAQUS	30.4743	37.1490	53.9875	96.5702	125.8631
Error	1.42%	0.05%	0.01%	0.64%	2.99%
Present
ABAQUS

3.2. Analysis of Numerical Results

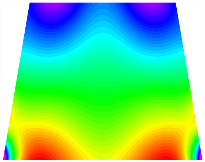
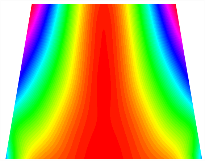
First, this section considers both asymmetric and antisymmetric cross-ply and investigates the effect of spring stiffness on the first four frequencies of the TBL. The trapezoidal bi-stable plate has a bottom length $b=1 \mathrm{m}$, $\alpha =15^{°}$, $\beta =15^{°}$, height $L=0.5 \mathrm{m}$, and thickness $h=0.001 \mathrm{m}$. Figure 6 shows the frequency curve of the TBL against the horizontal displacement of constrained spring stiffness. At this point, due to the different stable configurations of the TBL, the natural vibrations of each are studied.

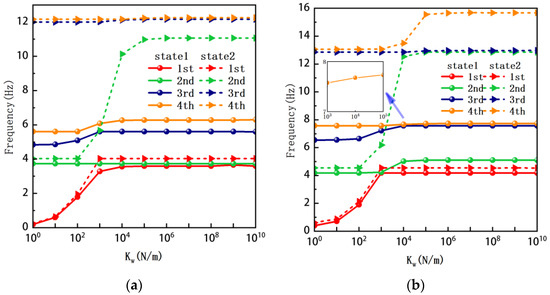
Figure 6. Natural frequency of trapezoidal bi-stable plate (a) [0/0/90/90], (b) [0/90/0/90].

Figure 6a shows the natural frequencies of the two stable configurations for an asymmetric TBL. It can be observed that as the stiffness of the lateral displacement-constraint springs increases, the second frequency of stable configuration 1 remains relatively constant, while that for stable configuration 2 undergoes the largest variation. The first natural frequencies of both stable configurations exhibit a similar trend. It is worth noting that the third and fourth natural frequencies of stable configuration 2 are close in magnitude, while they show a similar variation trend for stable configuration 1. Overall, when the stiffness of the lateral displacement-constraint springs increases to 10⁵ N/m, the first four natural frequencies of the TBL remain essentially unchanged.

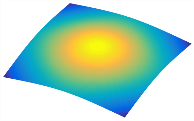
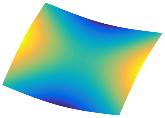
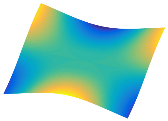
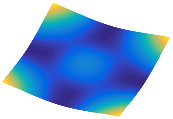
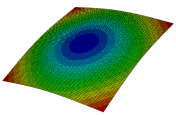
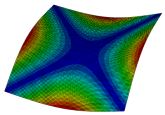
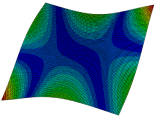
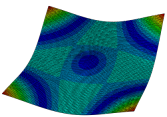
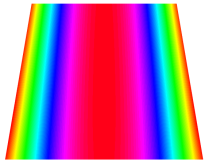
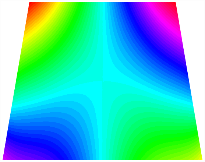
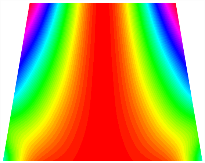
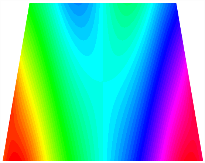
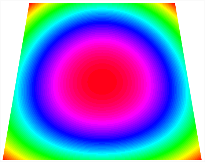
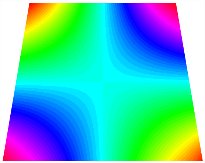
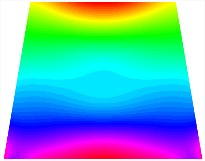
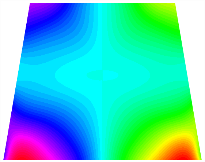
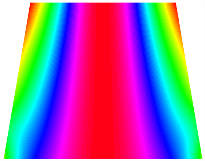
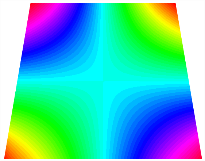
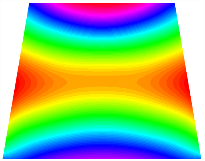
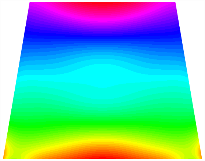
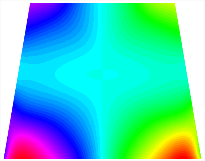
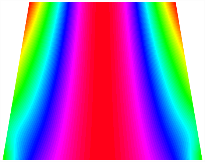
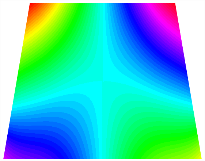
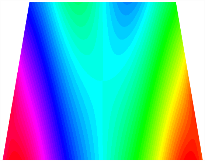
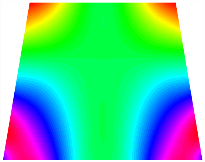
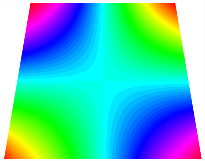
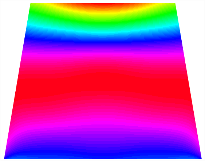
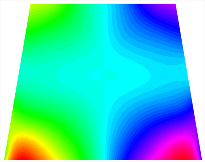
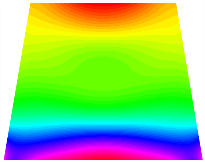
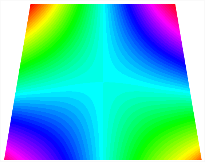
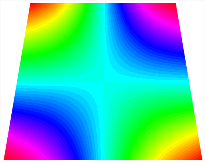
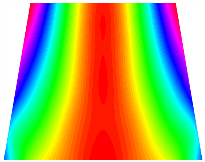
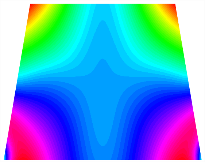
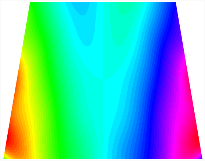
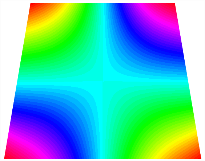
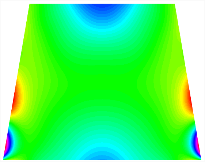
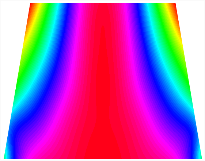
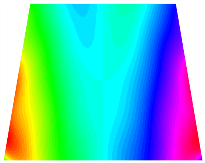
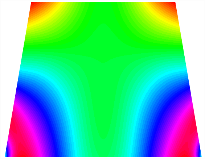
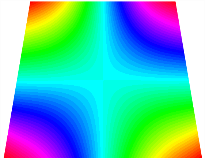
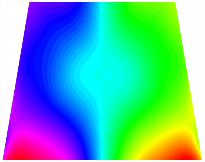
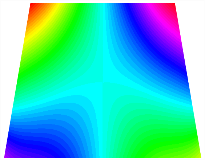
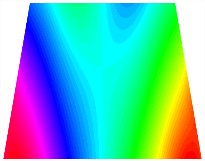
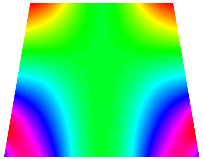
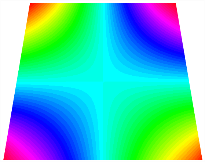
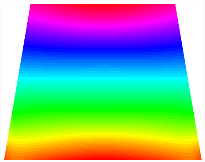
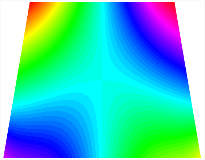
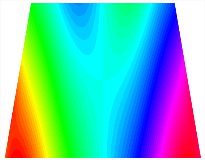
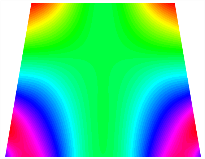
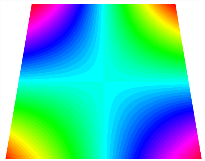
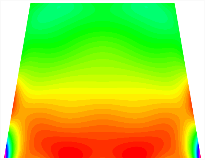
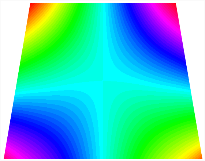
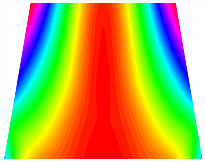
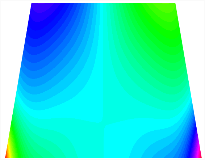
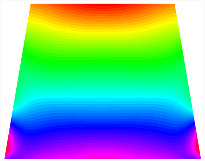
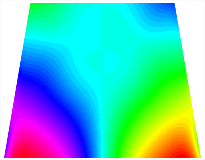
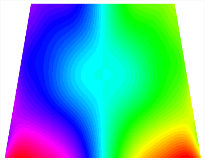
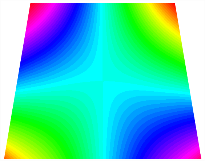
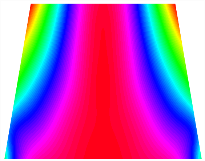
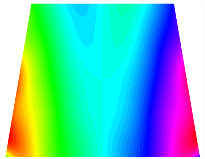
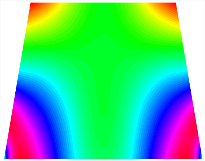
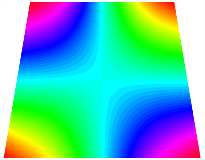
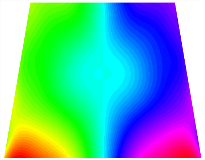
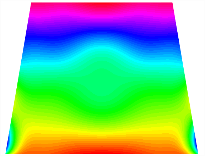
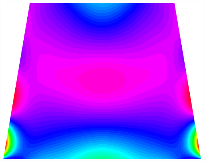
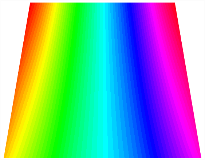
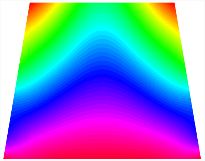
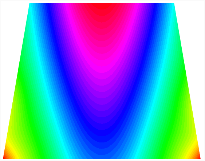
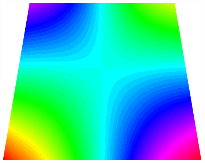
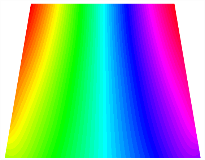
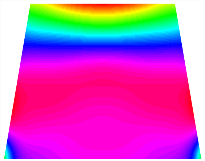
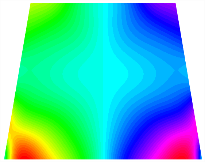
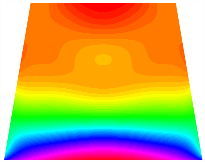
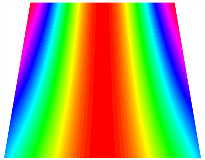
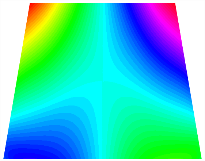
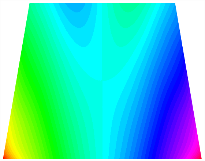
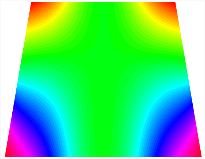
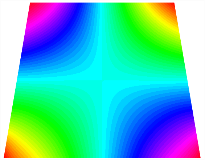
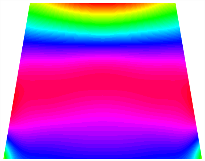
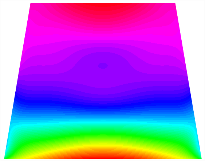
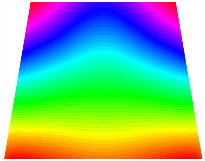
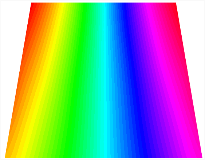
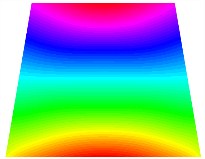
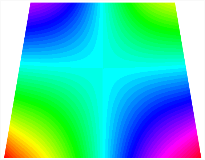
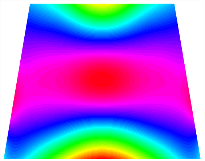
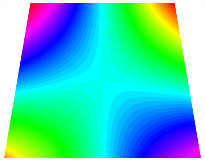
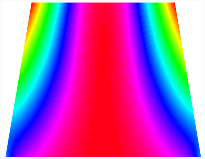
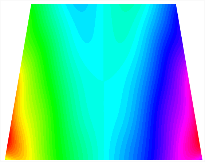
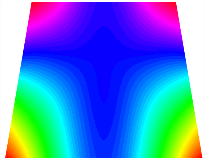
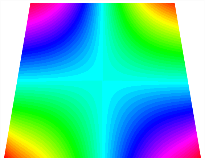
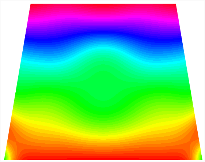
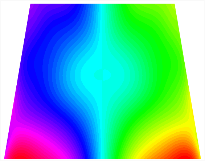
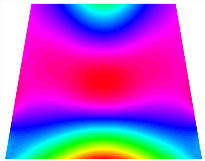
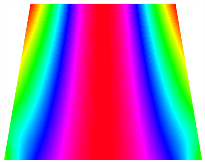
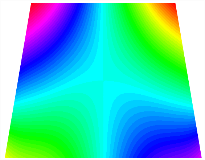
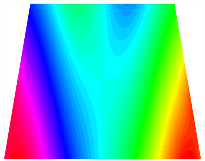
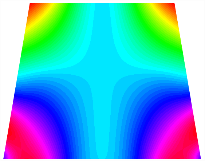
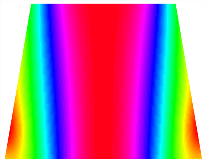
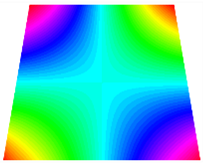
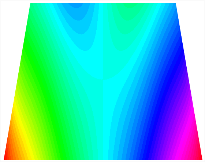
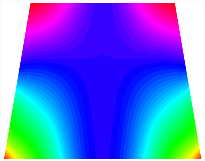
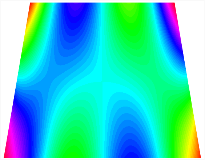
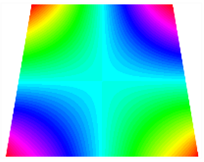
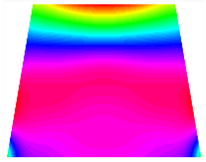
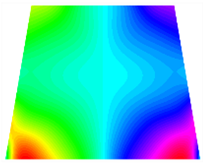
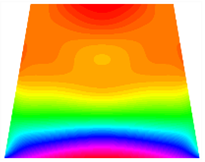
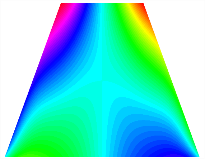
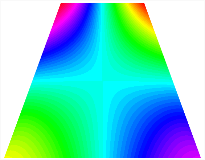
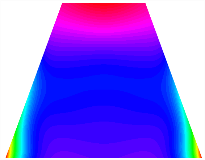
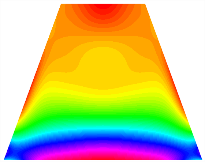
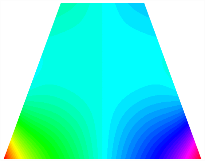
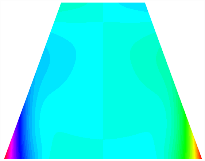
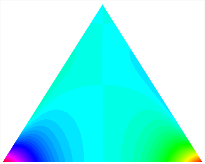
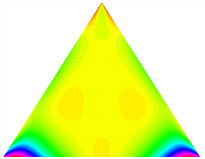
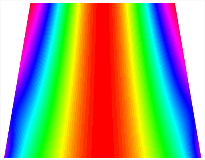
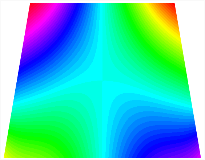
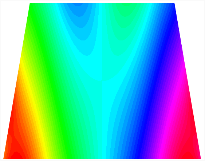
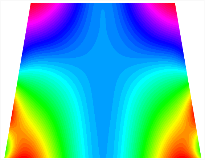
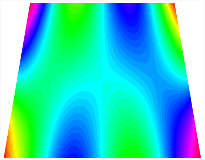
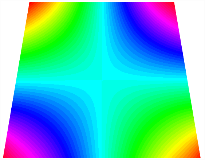
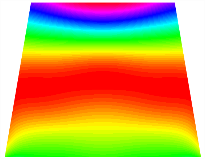
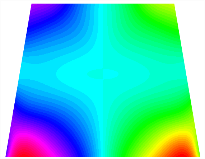
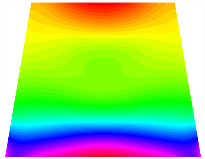
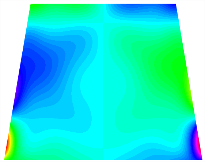
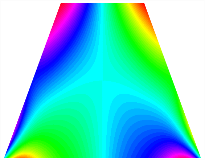
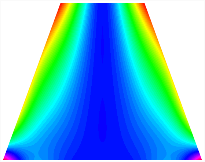
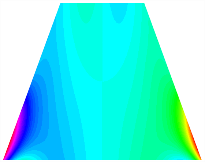
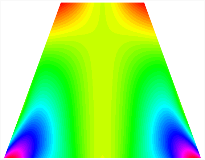
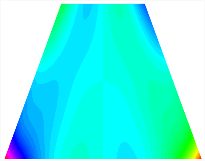
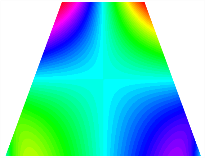
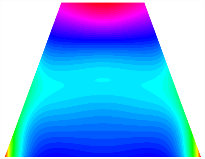
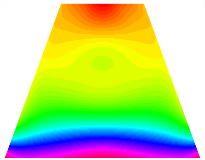
Figure 6b shows the natural frequencies of TBL with antisymmetric cross-ply. As can be seen from the figure, the fourth natural frequency of stable configuration 1 and the third natural frequency of stable configuration 2 remain largely unchanged. Furthermore, it is observed that for both configurations of the TBL, the natural frequencies of stable configuration 2 are always greater than those of stable configuration 1. This trend is because stable configuration 2 undergoes bending along the waist of the trapezoid, while stable configuration 1 undergoes bending along the two base edges. Additionally, it is found that for trapezoidal bi-stable structures of the same size, the natural frequencies are generally higher for antisymmetric placement compared to asymmetric placement. Table 6 and Table 7 present the first four mode shapes of the TBL for in-plane displacement-constraint spring stiffness values of 10¹ N/m, 10³ N/m, and 10⁵ N/m, respectively.

Table 6. The modal shapes of trapezoidal bi-stable plate with 0/0/90/90 with different K_w.

Kw		Mode
		1	2	3	4
101 (N/m)	State1
	State2
103 (N/m)	State1
	State2
105 (N/m)	State1
	State2

Table 7. The modal shapes of trapezoidal bi-stable plate with 0/90/0/90 and different Kw.

Kw		Mode
		1	2	3	4
101 (N/m)	State1
	State2
103 (N/m)	State1
	State2
105 (N/m)	State1
	State2

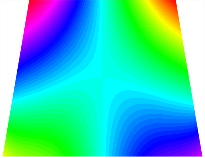
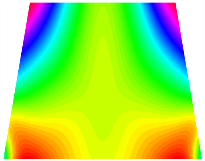
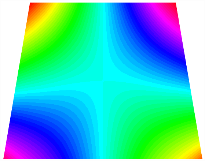
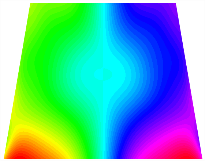
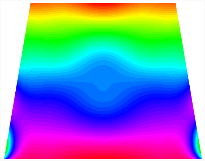
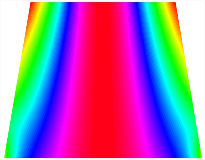
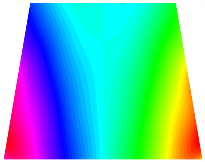
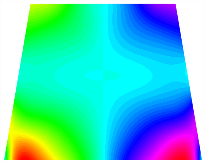
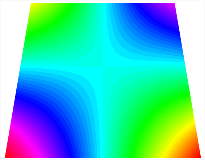
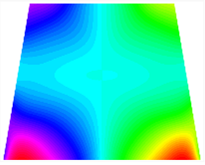
Figure 7 plots the frequency curves of the TBL with respect to the stiffness of the in-plane displacement-constraint spring. Figure 7a illustrates the natural frequencies of the TBL for the asymmetric form. It is shown that as the stiffness of the in-plane constraint springs increases, the first and second natural frequencies of stable configuration 1 become very close in magnitude and exhibit consistent variation patterns. When the spring stiffness increases to 10³ N/m, both the first and second natural frequencies remain unchanged. Furthermore, when the spring stiffness increases to 10⁴ N/m, the third natural frequency of stable configuration 2 approaches infinity and becomes very near in approach to the fourth natural frequency. Figure 7b presents the frequencies of the TBL with antisymmetric cross-ply. Clearly, when the spring stiffness increases to 10³ N/m, the third natural frequency of stable configuration 1 becomes near to the fourth natural frequency, and the second natural frequency of stable configuration 2 is close in magnitude and exhibits a similar variation pattern to the third natural frequency. Table 8 and Table 9 present the first four mode shapes of the TBL for in-plane displacement-constraint spring stiffness values of 10¹ N/m, 10³ N/m, and 10⁵ N/m, respectively.

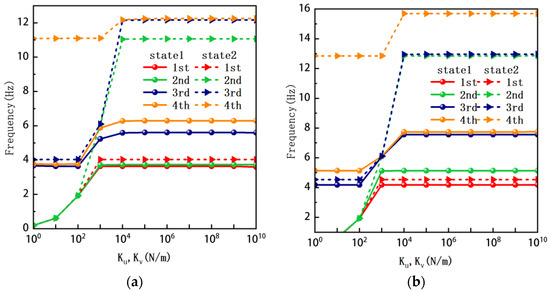
Figure 7. Natural frequency of trapezoidal bi-stable plate (a) [0/0/90/90], (b) [0/90/0/90].

Table 8. The modal shapes of trapezoidal bi-stable plate with 0/0/90/90 with different K_u and K_v.

Ku, Kv		Mode
		1	2	3	4
101 (N/m)	State1
	State2
103 (N/m)	State1
	State2
105 (N/m)	State1
	State2

Table 9. The modal shapes of trapezoidal bi-stable plate with 0/90/0/90 with different Ku and Kv.

Ku, Kv		Mode
		1	2	3	4
101 (N/m)	State1
	State2
103 (N/m)	State1
	State2
105 (N/m)	State1
	State2

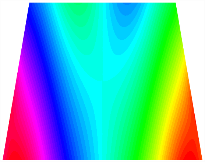
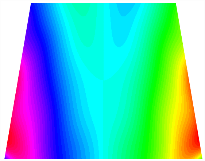
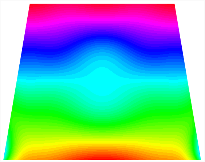
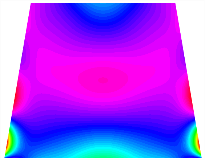
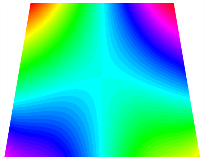
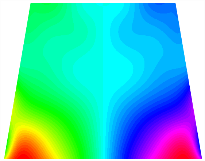
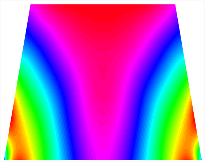
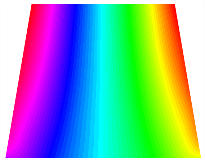
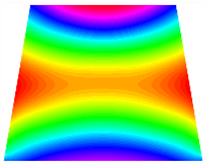
In Figure 8, the curves represent the variation of the natural frequencies of the TBL with the rotational displacement-constrained spring stiffness for both ply sequences. Figure 8a shows the frequencies of the two stable configurations of the asymmetrical TBL. From this figure, it is clearly seen that as the spring stiffness increases to 10² N/m, the first and second natural frequencies of stable configuration 1 are close in magnitude and follow a similar trend. When the spring stiffness increases to 10⁴ N/m, the third and fourth natural frequencies of stable configuration 2 are close in magnitude and follow a similar trend. Figure 8b represents the frequencies of the two stable configurations of the TBL when it is antisymmetric cross-ply. It can be observed that when the spring stiffness increases to 10⁴ N/m, the second and third natural frequencies of stable configuration 2 are close in magnitude and follow a similar trend. Furthermore, the fourth natural frequency of stable configuration 2 remains largely unchanged. Table 10 and Table 11 present the first four mode shapes of the TBL when it is subjected to rotational displacement-constraint spring stiffness values of 10¹ N/m, 10³ N/m, and 10⁵ N/m, respectively.

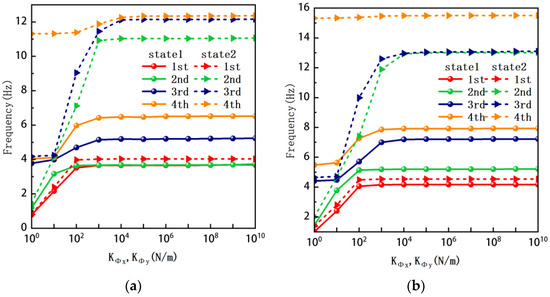
Figure 8. Natural frequency of trapezoidal bi-stable plate (a) [0/0/90/90], (b) [0/90/0/90].

Table 10. The modal shapes of trapezoidal bi-stable plate with 0/0/90/90 with different K_ΦX and K_Φy.

KΦX, KΦy		Mode
		1	2	3	4
101 (N/m)	State1
	State2
103 (N/m)	State1
	State2
105 (N/m)	State1
	State2

Table 11. The modal shapes of trapezoidal bi-stable plate with 0/90/0/90 with different K_ΦX and K_Φy.

KΦX, KΦy		Mode
		1	2	3	4
101 (N/m)	State1
	State2
103 (N/m)	State1
	State2
105 (N/m)	State1
	State2

The TBL exhibits inconsistent natural frequencies for its two stable configurations, and the natural frequencies of stable configuration 2 are always greater than those of the first one. These patterns occur because the two stable configurations of the TBL are asymmetric with respect to the midpoint of the median line, and the initial curvatures of the two configurations are also unequal. It is also noteworthy that, for both laying schemes, the trapezoidal bi-stable plate exhibits higher natural frequencies when the antisymmetric laying scheme is employed, compared to the asymmetric laying scheme. Additionally, under both ply schemes, the first natural frequency of the TBL in both stable configurations remains approximately the same, and its variation pattern is consistent with the increase in spring stiffness.

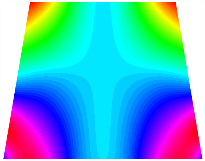
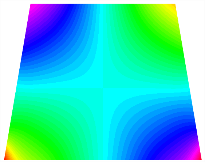
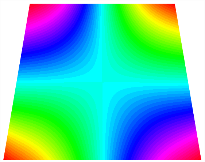
Figure 9 illustrates the influence of the bottom angle on the natural frequency of the asymmetric TBL under the three types of elastic boundary conditions listed in Table 12. From Figure 9, it is illustrated that the natural frequencies of state 2 for the three different bottom angles of the TBL are all greater than that of state 1. Under the E1 boundary condition, the natural frequency of each order of the asymmetric trapezoidal bi-stable plate increases with the decrease of the bottom angle. And the influence of the bottom angle on the natural frequencies increases with the order of the modes. Under the E2 and E3 boundary conditions, as the bottom angle decreases, the first-, second-, and fifth-order natural frequencies of the TBL are basically unchanged, while the third- and fourth-order frequencies increase significantly.

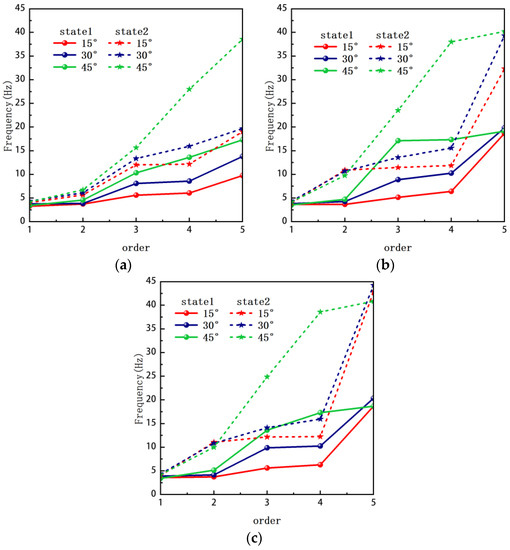
Figure 9. Natural frequency of bi-stable plate with different boundary conditions: (a) E1, (b) E2, (c) E3.

Table 12. Spring stiffness under three boundary conditions.

Boundary Condition	${\mathit{k}}_{\mathit{u}}$	${\mathit{k}}_{\mathit{v}}$	${\mathit{k}}_{\mathit{w}}$	${\mathit{k}}_{{\mathit{\varphi }}_{\mathit{x}}}$	${\mathit{k}}_{{\mathit{\varphi }}_{\mathit{y}}}$
E1 ($w_0\ne 0,u_0=0,v_0=0,{\varphi }_x=0,{\varphi }_y=0$)	1010	1010	103	1010	1010
E2 (${\varphi }_x\ne 0,{\varphi }_y\ne 0,u_0=0,v_0=0,w_0=0$)	1010	1010	1010	103	103
E3 (${\varphi }_x=0,{\varphi }_y=0,u_0=0,v_0=0,w_0=0$)	1010	1010	1010	1010	1010

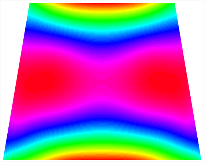
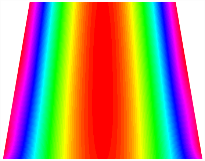
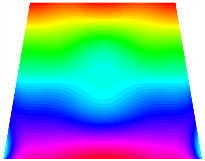
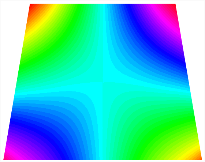
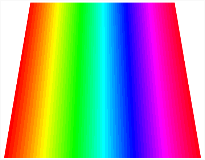
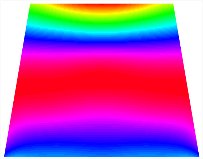
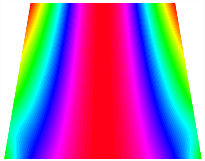
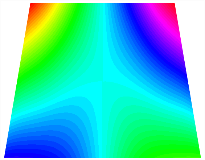
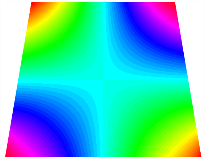
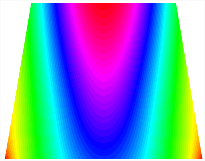
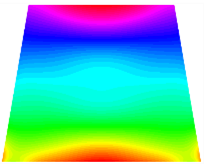
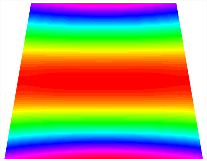
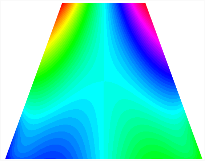
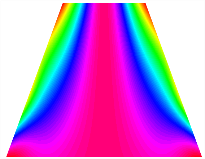
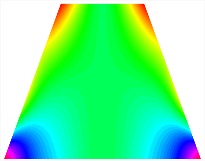
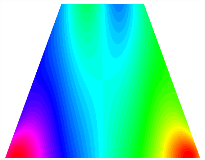
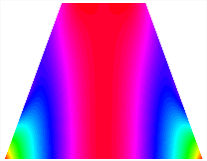
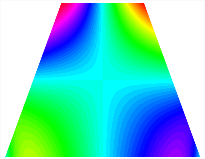
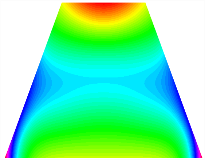
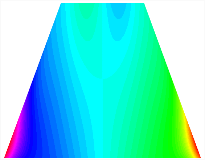
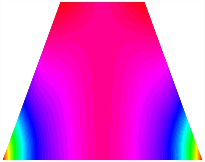
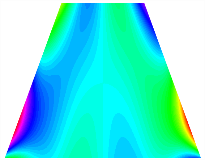
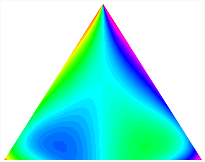
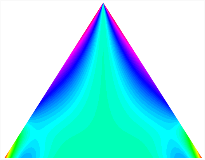
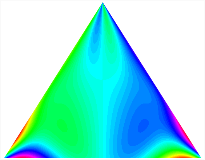
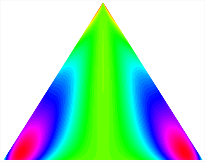
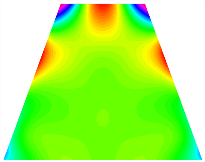
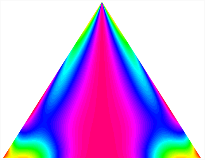
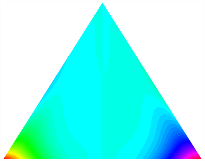
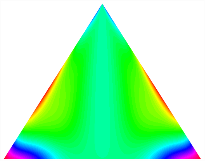
Table 13, Table 14 and Table 15 present the first five modes of vibration for the three different bottom angles of the asymmetric bi-stable plate under the E1, E2, and E3 boundary conditions, respectively. From the mode shapes shown in Table 13, Table 14 and Table 15, it is evident that as the bottom angle of the TBL decreases, its vibration gradually concentrates in the two bottom angles and their adjacent sides.

Table 13. The modal shapes of bi-stable plate with 0/0/90/90 (E1).

A, β		Mode
		1	2	3	4	5
15°	State1
	State2
30°	State1
	State2
45°	State1
	State2

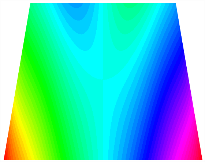
Table 14. The modal shapes of bi-stable plate with 0/0/90/90 (E2).

α, β		Mode
		1	2	3	4	5
15°	State1
	State2
30°	State1
	State2
45°	State1
	State2

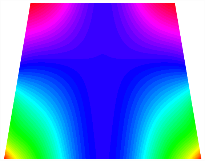
Table 15. The modal shapes of bi-stable plate with 0/0/90/90 (E3).

α, β		Mode
		1	2	3	4	5
15°	State1
	State2
30°	State1
	State2
45°	State1
	State2

4. Conclusions

In this work, the energy principle is employed to study the natural vibration of trapezoidal bi-stable laminated plates with elastic supports at the midpoint of the median line. A polynomial with a set of 17 parameters is selected as configuration functions. Five artificial springs are introduced at the midpoint of the median line of the laminated plate to simulate the elastic boundary. The computed results of this study are compared with finite element analysis and the existing literature, confirming the effectiveness of the current method. On this basis, the effects of geometry, layup sequence, and spring stiffness on the natural vibration characteristics of TBLs are analyzed. The results show the following:

• For trapezoidal bi-stable plates, the natural frequency of configuration 2 is always greater than that of configuration 1 due to the different curvatures of the two initial stable configurations.
• As the bottom angle decreases, the natural frequencies of each order at different elastic boundaries show an increasing trend. The vibration of the bi-stable plate gradually concentrates on the two bottom angles and their adjacent sides.
• The natural frequency of antisymmetric bi-stable laminates is usually greater than that of the asymmetric. When the spring stiffness increases to 10⁵ N/m, the natural frequencies of each order have reached the maximum value and tend to remain unchanged.