Optimal Melanoma Treatment Protocols for a Bilinear Control Model

Abstract

In this research, for a given time interval, which is the general period of melanoma treatment, a bilinear control model is considered, given by a system of differential equations, which describes the interaction between drug-sensitive and drug-resistant cancer cells both during drug therapy and in the absence of it. This model also contains a control function responsible for the transition from the stage of such therapy to the stage of its absence and vice versa. To find the optimal moments of switching between these stages, the problem of minimizing the cancer cells load both during the entire period of melanoma treatment and at its final moment is stated. Such a minimization problem has a nonconvex control set, which can lead to the absence of an optimal solution to the stated minimization problem in the classes of admissible modes traditional for applications. To avoid this problem, the control set is imposed to be convex. As a result, a relaxed minimization problem arises, in which the optimal solution exists. An analytical study of this minimization problem is carried out using the Pontryagin maximum principle. The corresponding optimal solution is found in the form of synthesis and may contain a singular arc. It shows that there are values of the parameters of the bilinear control model, its initial conditions, and the time interval for which the original minimization problem does not have an optimal solution, because it has a sliding mode. Then for such values it is possible to find an approximate optimal solution to the original minimization problem in the class of piecewise constant controls with a predetermined number of switchings. This research presents the results of the analysis of the connection between such an approximate solution of the original minimization problem and the optimal solution of the relaxed minimization problem based on numerical calculations performed in the Maple environment for the specific values of the parameters of the bilinear control model, its initial conditions, and the time interval.

1. Introduction

Melanoma is one of the most aggressive types of cancer. The increase in the number of patients with melanoma has been growing over the past 30 years, regardless of their geography, wealth, or age. With all localizations of melanoma (which can also grow in the retina, intestines, and throat), after the first detection by a doctor, about 30% die within 5 years. Mortality in the first year of treatment reaches 15% of those who seek help [1,2].

Melanoma is a malignant disease of the upper layer of the skin, the epidermis. The constant renewal of epidermal cells occurs due to keratinocytes formed in the lower layer of the epidermis. Along with keratinocytes, melanocytes are also formed in the lower layer of the epidermis, giving color to the skin. Melanocytes can accumulate in the epidermis in the form of small spots. In some melanocytes, under the influence of internal and external factors, signal transduction mechanisms that affect cell apoptosis can be disrupted [2]. This is the main reason for the unrestricted growth of melanoma. As a result, the process of endless division of melanocytes can begin and a small spot of melanocytes can turn into a malignant tumor of constantly dividing cells, spreading superficially in the form of a flat mass [2]. The linear growth of a tumor can reach 0.25 mm per day and, depending on the organ on which it grows, it can reach a length of more than 10 cm. According to various estimates, the specific growth rate of a population of dividing cells ranges from 0.003 to 0.100 per day [2,3,4].

Modern methods of treating patients with melanoma include the use of surgery, radiation, chemotherapy, immune and targeted methods, or their combination [5]. However, the practical results of treatment remain unsatisfactory due to the high recurrence rate and short survival after treatment. One reason that the diagnosis of melanoma is not associated with a favorable prognosis is that the expected outcomes of treatment often remain unsatisfactory due to late treatment seeking. About 25% of patients seek help in stage IV disease with multiple metastases.

There are other reasons for a negative prognosis for melanoma patients that relate to the methods of treatment for melanoma. Usually, chemotherapy is the first choice after surgery [2,6]. However, chemotherapy is also not always effective, as tumor cells gradually become resistant to drugs during their exposure [7,8,9,10]. At this stage of cancer, two types of cancer cells are distinguished—susceptible, which respond to treatment and die, and resistant cancer cells, which begin to quickly divide [11]. For this class of cancer cells, chemotherapy often plays the role of food—resistant cells begin to divide even faster with chemotherapy and do not die at all. Resistant cells quickly begin to dominate in the tumor [12]. Several studies have shown that phenotypic switching between susceptible and resistant types provides another pathway for acquired resistance during therapy. Once resistant cells begin to predominate, the treatment is ineffective because it no longer prevents tumor growth.

There is a dilemma—how to conduct the right treatment? If a patient rejects chemotherapy, then all cancer cells will continue to grow, and the patient will die. If chemotherapy is given, resistant cells start increasing in size, and the patient also dies.

The goal of successful cancer therapy is to control tumor growth in each patient by allowing a significant number of susceptible cells to survive, either by imposing treatment interruptions or by modulating the dose of the active drug. There is a hope that mathematical models of the dynamics and treatment of melanoma will help to choose the optimal treatment protocol. Mathematical models of cancer are commonly developed on the basis of ordinary differential equations or partial differential equations [9,10,13,14,15,16,17]. There are several articles that use optimal control theory to control drug dosage in various models of melanoma [18,19,20]. The most popular model is natural competition between susceptible and resistant cancer cells [7]. The developed probabilistic approach for estimating the time to reach a certain tumor size can be used in adaptive therapy [12] to determine the optimal time for treatment switching points, taking into account the specific characteristics of the patient.

In general, mathematical models of various cancers (not just melanoma) are presented in books [21,22,23,24] and related references within them. Finding the most effective protocols for the treatment of these cancers based on such models and using the optimal control theory is also given in books [25,26] and the relevant references within them.

The problems of optimal control of chemotherapy and drug resistance of cancer cells are presented in [25]. The same authors also discuss the uncertainty of model parameters and the effectiveness of some anticancer drugs. In all the above books and references in them, the control is the rate of drug delivery, so the search for optimal cancer treatments is reduced to finding the optimal concentrations of the anti-cancer drug as a function of time.

In clinical practices, chemotherapy involves the alternate administration of one or several drugs. The course of treatment can last from several days to several weeks and even months and be repeated several times during the total treatment time [7,8]. It has been noticed that if, for example, the drug is administered for 3–7 days, and then the patient rests for 3–7 days, and then the entire protocol is repeated, then such a plan does not lead to recovery or a sharp improvement in the patient’s condition. In our study, we consider differences in the responses of drug-sensitive and drug-resistant cancer cells to chemotherapy. Since drug-resistant cancer cells perceive the drug as food during chemotherapy, it is believed that there may be such a treatment schedule in which the intervals of taking the medication and the intervals of the break are not equal but can be optimized.

The novelty of our study lies in the fact that instead of searching for the optimal concentration of a chemotherapeutic drug, we use the optimal control theory and determine the optimal treatment protocol based on the frequent alternation of “drug in” and “no drug” intervals, minimizing the overall oncological burden on the patient. The corresponding optimal control problem is stated and solved in this paper.

For such an optimal control problem, the interaction between drug-sensitive and drug-resistant cancer cells during the “drug in” and “no drug” periods is described by systems of linear differential equations. When two models are combined, a bilinear control system arises with a scalar control that takes only two values—0 and 1 (the value 0 corresponds to the “no drug” intake, and the value 1 implies the “drug in” period.) Adding the objective function to be minimized, which has the meaning of the weighted sum of the cancer load over the total treatment period of the disease and the cancer load at the end of this time period, we obtain the desired optimal control problem. Due to the features of the control set, the minimization problem under consideration may not have an optimal solution in classes of admissible modes traditional for applications (which we will see later). The way out in such a situation is to consider the so-called relaxed minimization problem. Due to the fact that we are considering a control bilinear system, using the Pontryagin maximum principle allows us to analytically obtain a complete solution to such a minimization problem. Analysis of this solution shows that for some initial conditions and given total treatment period of the disease, the so-called singular control is possible, when the optimal control takes some intermediate value from the interval $(0,1)$. This means that the original minimization problem does not have an optimal solution. However, the optimal solution can be approximated arbitrarily accurately on the interval where the singular arc is realized by strongly oscillating piecewise constant controls taking values 0 and 1. In turn, this fact means that in the original minimization problem, the set, where the control system is located under the action of a singular control in the relaxed minimization problem, acts as a sliding mode. All this is analytically demonstrated in this paper. It is understood that piecewise constant controls with a very large number of switchings would be difficult to apply to the treatment protocols. Therefore, within the framework of the considered control system, at the moment of hitting the set, where the sliding mode is implemented, we propose to replace the optimal control portion with strong oscillation of values between 0 and 1 by the portion of this control with a fixed (predetermined) number of switchings between the same values. Such switchings and their lengths are found numerically. In the paper, we discuss some aspects of such a replacement. Additionally, we present the results of numerical calculations for the values of parameters of the bilinear control system, its initial conditions and the total treatment period of the disease, which are taken from sources where similar systems for the “drug in” and “no drug” periods of cancer treatment diseases are considered. Finally, we discuss our results in detail.

This paper is organized as follows. Section 2 and Section 3 detail a bilinear control system that describes the behavior of drug-susceptible and drug-resistant cancer cells over a given period of time in the treatment of melanoma. For this system, Section 3 states the problem of minimizing the cancer load, both during the entire time period of the treatment of the disease, and at its final moment. After that, the section discusses the possibility of the absence of an optimal solution in this minimization problem, as well as a way to overcome this difficulty. As a result, a relaxed minimization problem arises. A detailed analysis of the new optimal control problem based on the Pontryagin maximum principle (its various aspects) is presented in Section 4, Section 5, Section 6 and Section 7. Section 8 gives a complete description of the optimal solution in the relaxed minimization problem. In turn, Section 9 discusses the optimal solution of the already original minimization problem. The results of numerical calculations and their detailed analysis are presented in Section 10. Finally, Section 11 contains our conclusions.

2. Mathematical Model of Melanoma Treatment

Let us consider a setting where cells are assumed to mix well and dynamics are deterministic, which can be described by ordinary differential equations. The preliminary modeling uses systems of ordinary differential equations to describe the evolutionary co-dynamics of susceptible $x\left(t\right)$ and resistant $y\left(t\right)$ melanoma cells:

$$\mathrm{no} \mathrm{treatment}\left\{\begin{array}{cc}\hfill x^{\prime }\left(t\right)& =l_x^{\mathrm{off}}(1-p)x\left(t\right)-d_x^{\mathrm{off}}x\left(t\right),\hfill \\ \hfill y^{\prime }\left(t\right)& =l_x^{\mathrm{off}}px\left(t\right)+(l_y^{\mathrm{off}}-d_y^{\mathrm{off}})y\left(t\right),\hfill \end{array}\right.$$

(1)

$$\mathrm{in} \mathrm{treatment}\left\{\begin{array}{cc}\hfill x^{\prime }\left(t\right)& =l_x^{\mathrm{on}}(1-p)x\left(t\right)-d_x^{\mathrm{on}}x\left(t\right),\hfill \\ \hfill y^{\prime }\left(t\right)& =l_x^{\mathrm{on}}px\left(t\right)+(l_y^{\mathrm{on}}-d_y^{\mathrm{on}})y\left(t\right).\hfill \end{array}\right.$$

(2)

In equations of systems (1) and (2), susceptible cells divide at rates $l_x^{\mathrm{off}}$ and $l_x^{\mathrm{on}}$ in the absence and in the presence of treatment, respectively. They produce resistant mutants with probability p per cell division. In treatment, susceptible cells die at a higher rate $d_x^{\mathrm{on}}$ compared to their death rate $d_x^{\mathrm{off}}$ in the absence of treatment; their net growth rate in treatment is negative. Resistant cells grow faster in the presence of treatment ($l_y^{\mathrm{on}}>l_y^{\mathrm{off}}$), and they die at rates $d_y^{\mathrm{on}}$ and $d_y^{\mathrm{off}}$ in the two regimes.

Let us denote the net growth rate $\gamma$ of each cell type with the superscript ‘on’ for the treatment phase, or the superscript ‘off’ for the off-treatment phase. Given that in practical applications p is very small, we can neglect it and write:

$${\gamma }_x^{\mathrm{off}}=l_x^{\mathrm{off}}-d_x^{\mathrm{off}},{\gamma }_y^{\mathrm{off}}=l_y^{\mathrm{off}}-d_y^{\mathrm{off}},{\gamma }_x^{\mathrm{on}}=l_x^{\mathrm{on}}-d_x^{\mathrm{on}},{\gamma }_y^{\mathrm{on}}=l_y^{\mathrm{on}}-d_y^{\mathrm{on}}.$$

(3)

We will assume the following inequalities:

$${\gamma }_x^{\mathrm{off}}>0,{\gamma }_x^{\mathrm{on}}<0,{\gamma }_y^{\mathrm{off}}<0,{\gamma }_y^{\mathrm{on}}>0.$$

Indeed, in [27,28] the value $p=4·{10}^{-8}$ is used, and in [29] this value is equal ${10}^{-4}$.

3. Statement of the Minimization Problem and Its Discussion

Let us have a process of melanoma treatment, which consists in alternating between the period of treatment:

$$\left\{\begin{array}{cc}\hfill x^{\prime }\left(t\right)& ={\gamma }_x^{\mathrm{on}}x\left(t\right),\hfill \\ \hfill y^{\prime }\left(t\right)& ={\gamma }_y^{\mathrm{on}}y\left(t\right),\hfill \end{array}\right.$$

(4)

and the period of no treatment:

$$\left\{\begin{array}{cc}\hfill x^{\prime }\left(t\right)& ={\gamma }_x^{\mathrm{off}}x\left(t\right),\hfill \\ \hfill y^{\prime }\left(t\right)& ={\gamma }_y^{\mathrm{off}}y\left(t\right),\hfill \end{array}\right.$$

(5)

where ${\gamma }_x^{\mathrm{on}}$, ${\gamma }_y^{\mathrm{on}}$ and ${\gamma }_x^{\mathrm{off}}$, ${\gamma }_y^{\mathrm{off}}$ are given constants that satisfy the inequalities:

$${\gamma }_x^{\mathrm{on}}<0,{\gamma }_y^{\mathrm{on}}>0,{\gamma }_x^{\mathrm{off}}>0,{\gamma }_y^{\mathrm{off}}<0.$$

(6)

System (4) has a unique equilibrium $(0,0)$ in the region $\left\{(x,y):x\ge 0,y\ge 0\right\}$. Writing this system in a vector form:

$${\left(\begin{array}{c}x\\ y\end{array}\right)}^{\prime }=\left(\begin{array}{cc}{\gamma }_x^{\mathrm{on}}& 0\\ 0& {\gamma }_y^{\mathrm{on}}\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right),$$

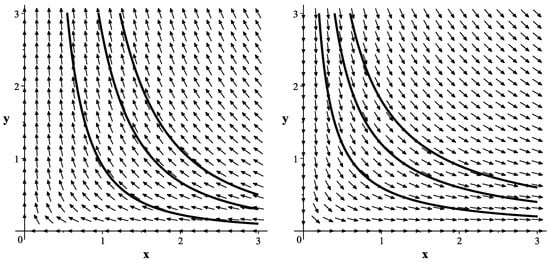
we see that its matrix has two real eigenvalues ${\lambda }_1={\gamma }_x^{\mathrm{on}}<0$ and ${\lambda }_2={\gamma }_y^{\mathrm{on}}>0$ corresponding to the respective eigenvectors $u_1=(1,0)$ and $u_2=(0,1)$. Therefore, the equilibrium is a saddle. Trajectories $\left(x\right(t),y(t\left)\right)$ of system (4) are schematically shown in Figure 1 (left).

Figure 1. Phase portrait of system (4) (left) and phase portrait of system (5) (right).

System (5) also has a single equilibrium $(0,0)$ in the same region. Representing this system in a vector form again:

$${\left(\begin{array}{c}x\\ y\end{array}\right)}^{\prime }=\left(\begin{array}{cc}{\gamma }_x^{\mathrm{off}}& 0\\ 0& {\gamma }_y^{\mathrm{off}}\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right),$$

we conclude that its matrix has two real eigenvalues ${\mu }_1={\gamma }_x^{\mathrm{off}}>0$ and ${\mu }_2={\gamma }_y^{\mathrm{off}}<0$ corresponding to the same eigenvectors. Then, the equilibrium is also a saddle. Trajectories $\left(x\right(t),y(t\left)\right)$ of system (5) are schematically presented in Figure 1 (right).

Let us introduce a value $v\in [0,1]$ and use it to connect the constants ${\gamma }_x^{\mathrm{on}}$, ${\gamma }_y^{\mathrm{on}}$ and ${\gamma }_x^{\mathrm{off}}$, ${\gamma }_y^{\mathrm{off}}$ by the following formulas:

$$\begin{array}{cc}\hfill {\gamma }_x^{\mathrm{off}}(1-v)+{\gamma }_x^{\mathrm{on}}v& ={\gamma }_x^{\mathrm{off}}+v\left({\gamma }_x^{\mathrm{on}}-{\gamma }_x^{\mathrm{off}}\right),\hfill \\ \hfill {\gamma }_y^{\mathrm{off}}(1-v)+{\gamma }_y^{\mathrm{on}}v& ={\gamma }_y^{\mathrm{off}}+v\left({\gamma }_y^{\mathrm{on}}-{\gamma }_y^{\mathrm{off}}\right).\hfill \end{array}$$

(7)

It is easy to see that there is no treatment for $v=0$ and in equalities (7) we have constants ${\gamma }_x^{\mathrm{off}}$, ${\gamma }_y^{\mathrm{off}}$. For $v=1$, treatment, on the contrary, is carried out, and from equalities (7) we obtain constants ${\gamma }_x^{\mathrm{on}}$, ${\gamma }_y^{\mathrm{on}}$. To simplify the subsequent arguments in (7), we define the following constants:

$$a={\gamma }_x^{\mathrm{off}}>0,b={\gamma }_x^{\mathrm{on}}-{\gamma }_x^{\mathrm{off}}<0,c={\gamma }_y^{\mathrm{off}}<0,d={\gamma }_y^{\mathrm{on}}-{\gamma }_y^{\mathrm{off}}>0.$$

(8)

Due to the inequalities (6), it can be seen that

$$a+b={\gamma }_x^{\mathrm{on}}<0,c+d={\gamma }_y^{\mathrm{on}}>0.$$

(9)

Using Formula (7) and involving in them the constants a, b, c and d satisfying inequalities (8) and (9), we combine systems (4) and (5) into the following bilinear control system:

$$\left\{\begin{array}{cc}\hfill x^{\prime }\left(t\right)& =(a+bv(t\left)\right)x\left(t\right),\hfill \\ \hfill y^{\prime }\left(t\right)& =(c+dv(t\left)\right)y\left(t\right),\hfill \\ \hfill x\left(0\right)& =x_0,y\left(0\right)=y_0;x_0,y_0>0.\hfill \end{array}\right.$$

(10)

Here $x_0$, $y_0$ are initial conditions, and $v\left(t\right)$ is a control function subject to the inclusion:

$$v\left(t\right)\in V=\{0;1\},$$

(11)

where V is a control set.

We will consider system (10) on a given time interval $[0,T]$, which is the total period of treatment of the disease. By the set of admissible controls ${\mathsf{\Lambda }}_T$ we mean all possible Lebesgue measurable functions $v\left(t\right)$ that satisfy the inclusion (11) for almost all $t\in [0,T]$.

The validity of the following lemma is easily established.

Lemma 1. 

For any admissible control $v\left(t\right)$, the components of the solution $\left(x\right(t),y(t\left)\right)$ of system (10) are absolutely continuous functions that are defined on the interval $[0,T]$ and are subject to inequalities:

$$0<x\left(t\right)<x_{max}=x_0{e}^{aT},0<y\left(t\right)<y_{max}=y_0{e}^{dT},t\in [0,T].$$

(12)

Proof of Lemma 1. 

The equations of the system (10) are linear differential equations, and therefore [30] the solution $\left(x\right(t),y(t\left)\right)$ of this system is defined on the entire interval $[0,T]$. Integrating each equation of the system (10) with the corresponding initial condition, we find the formulas:

$$x\left(t\right)=x_0{e}^{\underset{0}{\overset{t}{\int }}(a+bv\left(\xi \right))d\xi },y\left(t\right)=y_0{e}^{\underset{0}{\overset{t}{\int }}(c+dv\left(\xi \right))d\xi },t\in [0,T],$$

(13)

from which the positivity of the solution components $x\left(t\right)$ and $y\left(t\right)$ on the entire interval $[0,T]$ immediately follows (the left constraints in (12)). Using in Formula (13) the necessary inequalities from (8) and inclusion (11), we obtain the required right constraints in (12). The statement is proven. □

Remark 1. 

Lemma 1 implies the positive invariance of the control system (10) in the region

$$\mathsf{\Omega }=\left\{(x,y):x>0,y>0\right\}.$$

Let us establish other properties of system (10). To do this, we rewrite it in vector form:

$${\left(\begin{array}{c}x\\ y\end{array}\right)}^{\prime }=\left(\begin{array}{c}ax\\ cy\end{array}\right)+v\left(\begin{array}{c}bx\\ dy\end{array}\right).$$

For $v=0$ and $v=1$ we have the corresponding vectors:

$$q_0=\left(\begin{array}{c}ax\\ cy\end{array}\right),q_1=\left(\begin{array}{c}(a+b)x\\ (c+d)y\end{array}\right).$$

Let us study the linear dependence or independence of these vectors in the region $\mathsf{\Omega }$. To do this, we calculate the determinant $det[q_0,q_1]$, composed of vectors $q_0$ and $q_1$. As a result, we have the formula:

$$det[q_0,q_1]=(ad-bc)xy,(x,y)\in \mathsf{\Omega }.$$

If $ad-bc\ne 0$, then the vectors $q_0$ and $q_1$ are linearly independent in the region $\mathsf{\Omega }$. If $ad-bc=0$, then they are linearly dependent in $\mathsf{\Omega }$ and system (10) will be rewritten in the form:

$$\left\{\begin{array}{cc}\hfill x^{\prime }\left(t\right)& =b(\kappa +v(t\left)\right)x\left(t\right),\hfill \\ \hfill y^{\prime }\left(t\right)& =d(\kappa +v(t\left)\right)y\left(t\right),\hfill \\ \hfill x\left(0\right)& =x_0,y\left(0\right)=y_0;x_0,y_0>0.\hfill \end{array}\right.$$

(14)

where $a/b=c/d=\kappa <0$. System (14) is easily integrated. As a result, we obtain the formula:

$$y=y_0{\left(\frac{x}{x_0}\right)}^{\frac{d}{b}}.$$

(15)

This means that the dynamics of system (10) is determined by the first differential equation in (14) and carried out on the curve (15). Control system (10) degenerates. Therefore, we will not consider such a case further.

Thus, in what follows, we assume that the following inequality holds:

$$ad-bc={\gamma }_x^{\mathrm{off}}\left({\gamma }_y^{\mathrm{on}}-{\gamma }_y^{\mathrm{off}}\right)-{\gamma }_y^{\mathrm{off}}\left({\gamma }_x^{\mathrm{on}}-{\gamma }_x^{\mathrm{off}}\right)\ne 0.$$

(16)

For control system (10) on the set of admissible controls ${\mathsf{\Lambda }}_T$, we introduce an objective function:

$$J\left(v\right)=(x\left(T\right)+y\left(T\right))+\beta \underset{0}{\overset{T}{\int }}(x\left(t\right)+y\left(t\right))dt,$$

(17)

where $\beta$ is a positive weight coefficient. The medical meaning of the objective function (17) is the cancer load both during the total treatment period $[0,T]$ and in its final moment T. We consider the problem of minimizing the objective function (17):

$$J\left(v\right)\to \underset{v(·)\in {\mathsf{\Lambda }}_T}{min}.$$

(18)

The control set V is not convex. In turn, this leads to non-convexity of the set of admissible velocities:

$$Q(x,y)=\left\{\left(\begin{array}{c}(a+bv)x\\ (c+dv)y\end{array}\right),\mathrm{any}v\in V\right\}$$

for each point $(x,y)\in \mathsf{\Omega }$. This fact may lead to the absence of an optimal solution in the minimization problem (18). We will verify its correctness later. To overcome this problem, we will further apply the traditional approach, which consists in considering a relaxed minimization problem [31]). Such a problem is constructed as follows. First, the convex hull of the set of admissible velocities $Q(x,y)$ is taken. Due to the linearity of the components $(a+bv)x$ and $(c+dv)y$ in variables x, y and v, this action is equivalent to taking the convex hull of the control set V. As a result, the two-point set V turns into the segment $U=[0,1]$. Then, instead of the set of admissible controls ${\mathsf{\Lambda }}_T$, we consider the set of admissible controls ${\mathsf{\Psi }}_T$. It consists of all possible Lebesgue measurable functions $v\left(t\right)$ that satisfy the inclusion $v\left(t\right)\in U$ for almost all $t\in [0,T]$. Here, U is a new control set.

Remark 2. 

Lemma 1 remains valid for the control system (10), which is now considered on the set of admissible controls ${\mathsf{\Psi }}_T$.

Then, for the original minimization problem (18), the relaxed minimization problem consists in minimizing the objective function (17) for the control system (10) on the set of admissible controls ${\mathsf{\Psi }}_T$:

$$J\left(v\right)\to \underset{v(·)\in {\mathsf{\Psi }}_T}{min}.$$

(19)

System (10) is linear in control $v\left(t\right)$, which takes values in the convex set U, and constraints (12) are valid for it. Therefore, due to Theorem 4 from Chapter 4 [32]), in the relaxed minimization problem (19) there exists an optimal solution consisting of an optimal control $v_{*}\left(t\right)$ and the corresponding optimal solution $(x_{*}\left(t\right),y_{*}\left(t\right))$ for system (10).

4. Pontryagin Maximum Principle for the Relaxed Minimization Problem

To analyze the optimal solution of the relaxed minimization problem (19), we apply the Pontryagin maximum principle [33]). First, we write down the corresponding Hamiltonian:

$$H(x,y,v,{\psi }_1,{\psi }_2)=(a+bv)x{\psi }_1+(c+dv)y{\psi }_2-\beta (x+y),$$

where ${\psi }_1$ and ${\psi }_2$ are adjoint variables. Then we calculate the required partial derivatives of this Hamiltonian:

$$\begin{array}{cc}& H_x^{\prime }(x,y,v,{\psi }_1,{\psi }_2)=(a+bv){\psi }_1-\beta ,\hfill \\ & H_y^{\prime }(x,y,v,{\psi }_1,{\psi }_2)=(c+dv){\psi }_2-\beta ,\hfill \\ & H_v^{\prime }(x,y,v,{\psi }_1,{\psi }_2)=bx{\psi }_1+dy{\psi }_2.\hfill \end{array}$$

Then, according to the Pontryagin maximum principle, for the optimal control $v_{*}\left(t\right)$ and the corresponding optimal solution $(x_{*}\left(t\right),y_{*}\left(t\right))$ for system (10) there exists an adjoint function ${\psi }_{*}\left(t\right)=({\psi }_1^{*}\left(t\right),{\psi }_2^{*}\left(t\right))$, such that

• it is an absolutely continuous solution of the adjoint system:

  $$\left\{\begin{array}{cc}\hfill {{\psi }_1^{*}}^{\prime }\left(t\right)& =-H_x^{\prime }(x_{*}\left(t\right),y_{*}\left(t\right),v_{*}\left(t\right),{\psi }_1^{*}\left(t\right),{\psi }_2^{*}\left(t\right))\hfill \\ \hfill & =-(a+b{v}_{*}\left(t\right)){\psi }_1^{*}\left(t\right)+\beta ,\hfill \\ \hfill {{\psi }_2^{*}}^{\prime }\left(t\right)& =-H_y^{\prime }(x_{*}\left(t\right),y_{*}\left(t\right),v_{*}\left(t\right),{\psi }_1^{*}\left(t\right),{\psi }_2^{*}\left(t\right))\hfill \\ \hfill & =-(c+d{v}_{*}\left(t\right)){\psi }_2^{*}\left(t\right)+\beta ,\hfill \\ \hfill {\psi }_1^{*}\left(T\right)& =-J_{x\left(T\right)}^{\prime }=-1,{\psi }_2^{*}\left(T\right)=-J_{y\left(T\right)}^{\prime }=-1;\hfill \end{array}\right.$$

  (20)
• control $v_{*}\left(t\right)$ maximizes the Hamiltonian $H(x_{*}\left(t\right),y_{*}\left(t\right),v,{\psi }_1^{*}\left(t\right),{\psi }_2^{*}\left(t\right))$ in the variable $v\in [0,1]$ for almost all $t\in [0,T]$, and therefore it satisfies the following relationship:

  $$v_{*}\left(t\right)=\left\{\begin{array}{cc}1\hfill & ,\mathrm{if}L\left(t\right)>0,\hfill \\ \mathrm{any}v\in [0,1]\hfill & ,\mathrm{if}L\left(t\right)=0,\hfill \\ 0\hfill & ,\mathrm{if}L\left(t\right)<0,\hfill \end{array}\right.$$

  (21)

where a function

$$L\left(t\right)=H_v^{\prime }(x_{*}\left(t\right),y_{*}\left(t\right),v_{*}\left(t\right),{\psi }_1^{*}\left(t\right),{\psi }_2^{*}\left(t\right))=b{x}_{*}\left(t\right){\psi }_1^{*}\left(t\right)+d{y}_{*}\left(t\right){\psi }_2^{*}\left(t\right)$$

(22)

is the switching function. Its behavior determines the type of control $v_{*}\left(t\right)$ in accordance with the Formula (21).

Let us analyze relationships (20)–(22). Their analysis will show what the function $L\left(t\right)$ can be, and hence the optimal control $v_{*}\left(t\right)$ corresponding to it. Since the switching function $L\left(t\right)$ is an absolutely continuous function, it can vanish either in separate points or on intervals. Thus, the control $v_{*}\left(t\right)$ can have a bang-bang form and switch between the values 0 and 1. This will happen if, when passing through the value of $t_{★}$, in which the function $L\left(t\right)$ decreases to zero, the sign of this function changes. This value $t_{★}$ is the switching of the optimal control $v_{*}\left(t\right)$. In addition to sections of bang-bang form, control $v_{*}\left(t\right)$ may also contain singular sections in which a singular regimen takes place [26,34]. This happens when the corresponding switching function $L\left(t\right)$ vanishes identically on some subintervals of the interval $[0,T]$. The following arguments are devoted to a detailed study of the possible existence of a singular regimen for the optimal control $v_{*}\left(t\right)$.

5. Useful Transformations and Formulas

Let us first simplify the adjoint system (20) and the switching function $L\left(t\right)$ given by Formula (22). To do this, we introduce new adjoint variables of the form:

$${\varphi }_1^{*}\left(t\right)=x_{*}\left(t\right){\psi }_1^{*}\left(t\right),{\varphi }_2^{*}\left(t\right)=y_{*}\left(t\right){\psi }_2^{*}\left(t\right).$$

(23)

Then, using the equations of systems (10) and (20), as well as the initial conditions from (20), we obtain a new adjoint system:

$$\left\{\begin{array}{cc}\hfill {{\varphi }_1^{*}}^{\prime }\left(t\right)& =\beta x_{*}\left(t\right),\hfill \\ \hfill {{\varphi }_2^{*}}^{\prime }\left(t\right)& =\beta y_{*}\left(t\right),\hfill \\ \hfill {\varphi }_1^{*}\left(T\right)& =-x_{*}\left(T\right),{\varphi }_2^{*}\left(T\right)=-y_{*}\left(T\right).\hfill \end{array}\right.$$

(24)

At the same time, due to Formula (23), the switching function $L\left(t\right)$ is rewritten as

$$L\left(t\right)=b{\varphi }_1^{*}\left(t\right)+d{\varphi }_2^{*}\left(t\right).$$

(25)

Now using the equations of systems (10) and (24), as well as Formula (25), we find expressions for the first derivative $L^{\prime }\left(t\right)$ and the second derivative $L^{″}\left(t\right)$ of the switching function $L\left(t\right)$. As a result, we have formulas:

$$\begin{array}{ccc}\hfill L^{\prime }\left(t\right)& =& \beta (b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill L^{″}\left(t\right)& =& \beta (b(a+b{v}_{*}\left(t\right))x_{*}\left(t\right)+d(c+d{v}_{*}\left(t\right))y_{*}\left(t\right)).\hfill \end{array}$$

(27)

Let us determine the sign of the second derivative $L^{″}\left(t\right)$ of the function $L\left(t\right)$ on the intervals where the control $v_{*}\left(t\right)$ takes the value 0 or 1. The following lemma is true.

Lemma 2. 

If on the interval $\Delta \subset [0,T]$ the optimal control $v_{*}\left(t\right)$ has the value 0 (which means that $L\left(t\right)<0$), then $L^{″}\left(t\right)<0$. If on this interval the control $v_{*}\left(t\right)$ takes the value 1 (this implies that $L\left(t\right)>0$), then $L^{″}\left(t\right)>0$.

Proof of Lemma 2. 

The proof immediately follows from Formula (27), inequalities (8) and (9), and Lemma 1. Indeed, for $v_{*}\left(t\right)=0$ we have:

$$L^{″}\left(t\right)=\beta (ab{x}_{*}\left(t\right)+cd{y}_{*}\left(t\right))<0,$$

and for $v_{*}\left(t\right)=1$ we obtain:

$$L^{″}\left(t\right)=\beta (b(a+b)x_{*}\left(t\right)+d(c+d)y_{*}\left(t\right))>0.$$

The statement is proven. □

The following lemma also holds.

Lemma 3. 

There is no situation when moments $t_1$ and $t_2$, $t_1<t_2$ are defined on the interval $[0,T]$, which are zeros of the switching function $L\left(t\right)$, that on the interval $(t_1,t_2)$ this function takes either positive or negative values.

Proof of Lemma 3. 

For the sake of definiteness, we consider the situation when the interval $(t_1,t_2)\subset [0,T]$ on which the function $L\left(t\right)$ is positive is defined and the equalities $L\left(t_1\right)=0$ and $L\left(t_2\right)=0$ hold. Then, by the Weierstrass theorem, there is a value $t_0\in (t_1,t_2)$ at which this function reaches its maximum. This means that relationships $L^{\prime }\left(t_0\right)=0$ and $L^{″}\left(t_0\right)\le 0$ are valid, and the second of them contradicts Lemma 2. Therefore, the considered situation does not hold. The statement is proven. □

Lemma 3 can be weakened. Namely, the following lemma is true.

Lemma 4. 

There is no situation when moments $t_1$ and $t_2$, $t_1<t_2$ are defined on the interval $[0,T]$, where the moment $t_1$ is the zero of the switching function $L\left(t\right)$, but the moment $t_2$ is not. At the same time, the value of the function $L\left(t\right)$ in this moment, as well as on the entire interval $(t_1,t_2)$, can be either positive or negative and the inequality $L\left(t_2\right)L^{\prime }\left(t_2\right)<0$ holds.

Proof of Lemma 4. 

As in the proof of Lemma 3, for the sake of definiteness, we consider the situation when the interval $(t_1,t_2)\subset [0,T]$ on which the function $L\left(t\right)$ is positive is defined and the equality $L\left(t_1\right)=0$ and the inequalities $L\left(t_2\right)>0$, $L^{\prime }\left(t_2\right)<0$ hold. Let us define on the interval $[t_1,t_2]$ the auxiliary function $\tilde{L}\left(t\right)=L\left(t\right)-L\left(t_2\right)$. Then, the following relationships:

$$\tilde{L}\left(t_1\right)=L\left(t_1\right)-L\left(t_2\right)=-L\left(t_2\right)<0,\tilde{L}\left(t_2\right)=0,{\tilde{L}}^{\prime }\left(t_2\right)<0$$

are valid for it. The last two relationships imply that there is an interval adjacent to $t_2$ on which $\tilde{L}\left(t\right)>0$. Since $\tilde{L}\left(t_1\right)<0$, the interval $(t_1^{\prime },t_2)$ is defined on which $\tilde{L}\left(t\right)>0$ and $\tilde{L}\left(t_1^{\prime }\right)=0$. Using Lemma 3 for the function $\tilde{L}\left(t\right)$ we see that the considered situation does not hold as well. The statement is proven. □

The Formulas (26) and (27) imply that the first derivative $L^{\prime }\left(t\right)$ and the second derivative $L^{″}\left(t\right)$ of the switching function $L\left(t\right)$ depend on the components $x_{*}\left(t\right)$ and $y_{*}\left(t\right)$ of the optimal solution $(x_{*}\left(t\right),y_{*}\left(t\right))$. Therefore, by integrating the equations of the system (24) with the appropriate initial conditions and substituting the resulting expressions for the functions ${\varphi }_1^{*}\left(t\right)$ and ${\varphi }_2^{*}\left(t\right)$ into the Formula (25), we find the relationship for the function $L\left(t\right)$ also through the components $x_{*}\left(t\right)$ and $y_{*}\left(t\right)$:

$$L\left(t\right)=-(b{x}_{*}\left(T\right)+d{y}_{*}\left(T\right))-\beta \underset{t}{\overset{T}{\int }}(b{x}_{*}\left(s\right)+d{y}_{*}\left(s\right))ds,t\in [0,T].$$

(28)

6. Singular Regimen

Let there be an interval $\Delta \subset [0,T]$ on which the switching function $L\left(t\right)$ is identically equal to zero. Then the first derivative $L^{\prime }\left(t\right)$ and the second derivative $L^{″}\left(t\right)$ of this function vanish everywhere on this interval:

$$L^{\prime }\left(t\right)=0,L^{″}\left(t\right)=0.$$

(29)

From the first formula in (29), as well as from expression (26), we find the equality:

$$y_{*}\left(t\right)=-\frac{b}{d}{x}_{*}\left(t\right),t\in \Delta .$$

(30)

It defines a special ray

$$\mathsf{\Pi }=\left\{{(x,y)}^{\top }:x>0,y>0,y=-\frac{b}{d}x\right\}$$

on which the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is located when the control $v_{*}\left(t\right)$ has a singular regimen. Substituting equality (30) into the second formula in (29) leads to the relationship:

$$L^{″}\left(t\right)=\beta b((a-c)+(b-d)v_{*}\left(t\right))x_{*}\left(t\right)=0,$$

(31)

from which, by Lemma 1, we find the formula for the optimal control $v_{*}\left(t\right)$ on a singular regimen:

$$v_{\mathrm{sing}}=-\frac{a-c}{b-d}.$$

It is easy to verify that $v_{\mathrm{sing}}\in (0,1)$. Additionally, from (31) we conclude that the relationship:

$$\frac{\partial }{\partial v}{L}^{″}\left(t\right)=\beta b(b-d)x_{*}\left(t\right)>0$$

is valid for all $t\in \Delta$. It implies that the necessary condition for the optimality of the singular regimen (the Kelly condition) is satisfied [34]), and, moreover, in a strengthened form. This means that the optimal control $v_{*}\left(t\right)$ can have a singular regimen, which is concatenated with non-singular (bang-bang) sections on which this control takes values $\{0;1\}$ [26]).

7. Behavior of the Optimal Trajectory

Let us study the behavior of the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$. It is easy to see that

(a) 

for $v_{*}\left(t\right)=0$, the equations of system (10) are written in the form:

$$\left\{\begin{array}{cc}\hfill x_{*}^{\prime }\left(t\right)& =a{x}_{*}\left(t\right),\hfill \\ \hfill y_{*}^{\prime }\left(t\right)& =c{y}_{*}\left(t\right).\hfill \end{array}\right.$$

(32)

It follows that with increasing time t, the coordinate x increases, and the coordinate y, on the contrary, decreases. Schematically, the behavior of the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is shown in Figure 1 (right);

(b) 

for $v_{*}\left(t\right)=1$, the equations of system (10) are reduced to the form:

$$\left\{\begin{array}{cc}\hfill x_{*}^{\prime }\left(t\right)& =(a+b)x_{*}\left(t\right),\hfill \\ \hfill y_{*}^{\prime }\left(t\right)& =(c+d)y_{*}\left(t\right).\hfill \end{array}\right.$$

(33)

This implies that with increasing time t, the coordinate x decreases, and the coordinate y, on the contrary, increases. The behavior of the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is schematically presented in Figure 1 (left);

(c) 

for $v_{*}\left(t\right)=v_{\mathrm{sing}}$, the equations of system (10) are written as follows

$$\left\{\begin{array}{cc}\hfill x_{*}^{\prime }\left(t\right)& =-(ad-bc)/(b-d)x_{*}\left(t\right),\hfill \\ \hfill y_{*}^{\prime }\left(t\right)& =-(ad-bc)/(b-d)y_{*}\left(t\right).\hfill \end{array}\right.$$

(34)

The expression $(ad-bc)$ can take both positive and negative values. Therefore, the coordinates x and y either increase or decrease simultaneously with increasing time t. Due to the inequality (16), system (34) has a unique equilibrium $(0,0)$ in the region $\left\{(x,y):x\ge 0,y\ge 0\right\}$. Giving this system in a vector form:

$${\left(\begin{array}{c}x\\ y\end{array}\right)}^{\prime }=\left(\begin{array}{cc}-(ad-bc)/(b-d)& 0\\ 0& -(ad-bc)/(b-d)\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right),$$

it is easy to see that its matrix has two coinciding real eigenvalues

$${\nu }_1={\nu }_2=-(ad-bc)/(b-d)\ne 0.$$

Therefore, the equilibrium is a dicritical node. For $ad-bc<0$ it is stable, but for $ad-bc>0$ it is unstable. Schematically, trajectories $\left(x\right(t),y(t\left)\right)$ of the system (34) are shown in Figure 2.

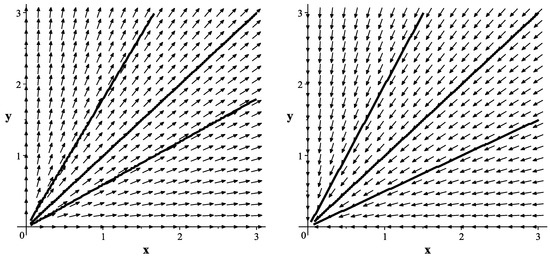Figure 2. Phase portrait of system (34) when $ad-bc>0$ (left) and $ad-bc<0$ (right).

8. Solving the Relaxed Minimization Problem

Let us now find the possible types of optimal control $v_{*}\left(t\right)$.

From the initial conditions of the adjoint system (24) and Formula (25) we obtain equality

$$L\left(T\right)=-(b{x}_{*}\left(T\right)+d{y}_{*}\left(T\right)),$$

(35)

and from the Formula (26) the equality follows

$$L^{\prime }\left(T\right)=\beta (b{x}_{*}\left(T\right)+d{y}_{*}\left(T\right)).$$

(36)

Then the following cases take place.

Case A. Let $b{x}_{*}\left(T\right)+d{y}_{*}\left(T\right)>0$, or $y_{*}\left(T\right)>-(b/d)x_{*}\left(T\right)$ (point $(x_{*}\left(T\right),y_{*}\left(T\right))$ is located above the special ray $\mathsf{\Pi }$). Then, by (35) and (36), $L\left(T\right)<0$ and $L^{\prime }\left(T\right)>0$. Therefore, there is an interval adjacent to T, on which $L\left(t\right)<0$. It follows from Lemma 4 that the switching function $L\left(t\right)$ takes negative values for all $t\in [0,T]$. Due to Formula (21), this means that the optimal control $v_{*}\left(t\right)$ is a constant function that has the value 0 on the entire interval $[0,T]$. In addition, from Lemma 2 it follows that the derivative $L^{\prime }\left(t\right)$ is a decreasing function up to the positive value of $L^{\prime }\left(T\right)$, and therefore $L^{\prime }\left(t\right)>0$ for all $t\in [0,T]$. Hence, $b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)>0$ on the entire interval $[0,T]$. Therefore, the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is above the special ray $\mathsf{\Pi }$ for all $t\in [0,T]$.

Case B. Let $b{x}_{*}\left(T\right)+d{y}_{*}\left(T\right)<0$, or $y_{*}\left(T\right)<-(b/d)x_{*}\left(T\right)$ (point $(x_{*}\left(T\right),y_{*}\left(T\right))$ is below the special ray $\mathsf{\Pi }$). Then, due to (35) and (36), $L\left(T\right)>0$ and $L^{\prime }\left(T\right)<0$. Therefore, an interval is defined adjacent to T, on which $L\left(t\right)>0$. Lemma 4 implies that the switching function $L\left(t\right)$ has positive values for all $t\in [0,T]$. By the Formula (21), this means that the optimal control $v_{*}\left(t\right)$ is a constant function that takes the value 1 on the entire interval $[0,T]$. Moreover, Lemma 2 implies that the derivative $L^{\prime }\left(t\right)$ is an increasing function up to the negative value of $L^{\prime }\left(T\right)$, and therefore $L^{\prime }\left(t\right)<0$ for all $t\in [0,T]$. Hence, $b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)<0$ on the entire interval $[0,T]$. This means that the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ lies below the special ray $\mathsf{\Pi }$ for all $t\in [0,T]$.

Case C. Let $b{x}_{*}\left(T\right)+d{y}_{*}\left(T\right)=0$, or $y_{*}\left(T\right)=-(b/d)x_{*}\left(T\right)$ (point $(x_{*}\left(T\right),y_{*}\left(T\right))$ is located on the special ray $\mathsf{\Pi }$). Then, in according with (35) and (36), $L\left(T\right)=0$ and $L^{\prime }\left(T\right)=0$. Subsequent arguments depend on the value $L^{″}\left(T\right)$. The following three subcases are possible.

Subcase C1. If $L^{″}\left(T\right)>0$, then there exists an interval adjacent to T, on which $L\left(t\right)>0$. Lemma 3 implies that the switching function $L\left(t\right)$ is positive for all $t\in [0,T)$. Due to the Formula (21), this means that the optimal control $v_{*}\left(t\right)$ is a constant function that has the value 1 on the entire interval $[0,T]$. Moreover, Lemma 2 implies that the derivative $L^{\prime }\left(t\right)$ is an increasing function up to zero value of $L^{\prime }\left(T\right)$, and therefore $L^{\prime }\left(t\right)<0$ for all $t\in [0,T)$. Hence, $b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)<0$ for $t\in [0,T)$. This means that the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is below the special ray $\mathsf{\Pi }$ for these values of t.

Subcase C2. If $L^{″}\left(T\right)<0$, then an interval is defined adjacent to T, on which $L\left(t\right)<0$. It follows from Lemma 3 that the switching function $L\left(t\right)$ is negative for all $t\in [0,T)$. According to the Formula (21), this means that the optimal control $v_{*}\left(t\right)$ is a constant function that takes the value 0 on the entire interval $[0,T]$. In addition, Lemma 2 implies that the derivative $L^{\prime }\left(t\right)$ is a decreasing function up to zero value of $L^{\prime }\left(T\right)$, and therefore $L^{\prime }\left(t\right)>0$ for all $t\in [0,T)$. Hence, $b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)>0$ for $t\in [0,T)$. This means that the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is above the special ray $\mathsf{\Pi }$ for these values of t.

Subcase C3. If $L^{″}\left(T\right)=0$, then there is an interval $\Delta$ adjacent to T, on which the optimal control $v_{*}\left(t\right)$ has a singular regimen. Everywhere on this interval $v_{*}\left(t\right)=v_{\mathrm{sing}}$ and equalities (29) hold. It follows from the first equality in (29) and Formula (26) that the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ moves along a special ray $\mathsf{\Pi }$, being on the interval $\Delta$. In this case, the interval $\Delta$ may coincide with the interval $(0,T)$. Then the initial point $(x_0,y_0)$ is located on the ray $\mathsf{\Pi }$, and on the entire interval $[0,T]$ the optimal control $v_{*}\left(t\right)$ is a constant function that takes the value $v_{\mathrm{sing}}$. In addition, the interval $\Delta =({\tau }_{*},T)$ may be contained within the interval $(0,T)$, when ${\tau }_{*}>0$. In this case, there are equalities $L\left({\tau }_{*}\right)=0$ and $L^{\prime }\left({\tau }_{*}\right)=0$. The optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ described either in Subcase C1 or in Subcase C2 will fall on the special ray $\mathsf{\Pi }$ at the moment ${\tau }_{*}$. Thus, the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ moves on the interval $[0,{\tau }_{*})$ either from the region above the ray $\mathsf{\Pi }$ with control $v_{*}\left(t\right)=0$, or from the region below this ray with control $v_{*}\left(t\right)=1$, to the ray $\mathsf{\Pi }$, and ends up on it at the moment ${\tau }_{*}$. Further, on the interval $({\tau }_{*},T]$, the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ moves along the special ray $\mathsf{\Pi }$ with control $v_{*}\left(t\right)=v_{\mathrm{sing}}$. Therefore, the following formulas are valid for the optimal control $v_{*}\left(t\right)$:

$$v_{*}\left(t\right)=\left\{\begin{array}{cc}0\hfill & ,\mathrm{if}0\le t\le {\tau }_{*},\hfill \\ v_{\mathrm{sing}}\hfill & ,\mathrm{if}{\tau }_{*}<t\le T,\hfill \end{array}\right.v_{*}\left(t\right)=\left\{\begin{array}{cc}1\hfill & ,\mathrm{if}0\le t\le {\tau }_{*},\hfill \\ v_{\mathrm{sing}}\hfill & ,\mathrm{if}{\tau }_{*}<t\le T.\hfill \end{array}\right.$$

(37)

Let us find formulas for the moment ${\tau }_{*}$, when the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is on the special ray $\mathsf{\Pi }$, depending on whether the initial point $(x_0,y_0)$ is located above or below this ray.

Firstly, we consider the situation, when point $(x_0,y_0)$ is above the ray $\mathsf{\Pi }$:

$$b{x}_0+d{y}_0>0,$$

(38)

and the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ moves under the action of the optimal control $v_{*}\left(t\right)=0$ towards this ray. Let us integrate the equations of the system (10) with this control. As a result, we obtain the formulas:

$$x_{*}\left(t\right)=x_0{e}^{at},y_{*}\left(t\right)=y_0{e}^{ct}.$$

(39)

Since we are looking for the moment ${\tau }_{*}$ when the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is on the special ray $\mathsf{\Pi }$, we will substitute the Formula (39) into the definition (30) of this ray. We have the expression:

$$b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)=b{x}_0{e}^{at}+d{y}_0{e}^{ct}.$$

Let us consider the function:

$$f\left(t\right)=b{x}_0{e}^{at}+d{y}_0{e}^{ct}.$$

(40)

We show that it has the unique value ${\tau }_{*}>0$, such that the equality $f\left({\tau }_{*}\right)=0$ holds. Indeed, inequality (38) implies $f\left(0\right)>0$, and Formula (40) with the inequalities (8) leads us to the relationship:

$$\underset{t\to +\infty }{lim}f\left(t\right)=-\infty .$$

In addition, turning again to inequalities (8), it is easy to verify by calculating the derivative of the function $f\left(t\right)$:

$$f^{\prime }\left(t\right)=ab{x}_0{e}^{at}+cd{y}_0{e}^{ct}<0,$$

that this function decreases for all $t\ge 0$. Let us find the formula for the moment ${\tau }_{*}$ from the expression:

$$b{x}_0{e}^{a{\tau }_{*}}+d{y}_0{e}^{c{\tau }_{*}}=0.$$

As a result, we have the relationship:

$${\tau }_{*}=\frac{1}{a-c}ln\left(-\frac{d{y}_0}{b{x}_0}\right).$$

(41)

It also follows from the arguments above that the inequality $b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)>0$ is satisfied for all $t\in [0,{\tau }_{*})$. In addition, due to Formula (30) taken on the interval $[{\tau }_{*},T]$, the expression (28) is rewritten in the form:

$$L\left(t\right)=-\beta \underset{t}{\overset{{\tau }_{*}}{\int }}(b{x}_{*}\left(s\right)+d{y}_{*}\left(s\right))ds,t\in [0,{\tau }_{*}].$$

(42)

This relationship immediately implies that $L\left(t\right)<0$ for all $t\in [0,{\tau }_{*})$.

Secondly, we study the situation, when point $(x_0,y_0)$ is below the ray $\mathsf{\Pi }$:

$$b{x}_0+d{y}_0<0,$$

(43)

and the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ moves under the action of the optimal control $v_{*}\left(t\right)=1$ towards this ray. Let us integrate the equations of the system (10) with this control. As a result, we obtain the formulas:

$$x_{*}\left(t\right)=x_0{e}^{(a+b)t},y_{*}\left(t\right)=y_0{e}^{(c+d)t}.$$

(44)

Since we are looking for the moment ${\tau }_{*}$ when the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is on the special ray $\mathsf{\Pi }$, we will substitute the Formula (44) into the definition (30) of this ray. We have the expression:

$$b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)=b{x}_0{e}^{(a+b)t}+d{y}_0{e}^{(c+d)t}.$$

Let us consider the function:

$$g\left(t\right)=b{x}_0{e}^{(a+b)t}+d{y}_0{e}^{(c+d)t}.$$

(45)

We show that it has the unique value ${\tau }_{*}>0$, such that the equality $g\left({\tau }_{*}\right)=0$ holds. Indeed, inequality (43) implies $g\left(0\right)<0$, and Formula (45) with the inequalities (8) and (9) leads us to the relationship:

$$\underset{t\to +\infty }{lim}g\left(t\right)=+\infty .$$

Moreover, turning again to inequalities (8) and (9), it is easy to verify by calculating the derivative of the function $g\left(t\right)$:

$$g^{\prime }\left(t\right)=b(a+b)x_0{e}^{(a+b)t}+d(c+d)y_0{e}^{(c+d)t}>0,$$

that this function increases for all $t\ge 0$. Let us find the formula for the moment ${\tau }_{*}$ from the expression:

$$b{x}_0{e}^{(a+b){\tau }_{*}}+d{y}_0{e}^{(c+d){\tau }_{*}}=0.$$

As a result, we have the relationship:

$${\tau }_{*}=\frac{1}{(a+b)-(c+d)}ln\left(-\frac{d{y}_0}{b{x}_0}\right).$$

(46)

These arguments lead to the inequality $b{x}_{*}\left(t\right)+d{y}_{*}\left(t\right)<0$ that is true for all $t\in [0,{\tau }_{*})$. Moreover, by virtue of the Formula (30) taking place on the interval $[{\tau }_{*},T]$, the expression (28) is transformed into the Formula (42), from which it immediately follows that $L\left(t\right)>0$ for all $t\in [0,{\tau }_{*})$.

Finally, we have the final conclusion related to the optimal solution of the relaxed minimization problem (19).

Theorem 1. 

The following statements are valid.

(a) 

Let the initial point $(x_0,y_0)$ be located above the special ray Π. Then the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ with the control $v_{*}\left(t\right)=0$ moves towards the ray Π. If at the final moment T it turns out to be either above it or on it, then the optimal control $v_{*}\left(t\right)$ has the value 0 on the entire interval $[0,T]$. If the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ reaches the ray Π at the moment ${\tau }_{*}<T$, then the control $v_{*}\left(t\right)$ is switched and further on the interval $({\tau }_{*},T]$ this trajectory moves along the ray with control $v_{*}\left(t\right)=v_{\mathrm{sing}}$.

(b) 

Let the initial point $(x_0,y_0)$ be below the special ray Π. Then the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ with the control $v_{*}\left(t\right)=1$ also moves towards the ray Π. If at the final moment T it is either below it or on it, then the optimal control $v_{*}\left(t\right)$ has the value 1 on the entire interval $[0,T]$. If the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ reaches the ray Π at the moment ${\tau }_{*}<T$, then the control $v_{*}\left(t\right)$ is switched and further on the interval $({\tau }_{*},T]$ this trajectory moves along the ray with control $v_{*}\left(t\right)=v_{\mathrm{sing}}$.

(c) 

Let the initial point $(x_0,y_0)$ lie on a special ray Π. Then, on the entire interval $[0,T]$, the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ moves along the ray Π with the control $v_{*}\left(t\right)=v_{\mathrm{sing}}$.

Remark 3. 

Previously, we justified the existence of the optimal solution in the relaxed minimization problem (19). To analyze this solution, we applied the Pontryagin maximum principle, which is only a necessary condition for optimality. As a result, we obtained the two-point boundary value problem of the maximum principle consisting of systems (10), (24) and Formulas (21) and (25), which we further studied in detail and presented the corresponding results in Theorem 1. Since the solution to such a boundary value problem turned out to be unique, it means that it is the optimal solution to the relaxed minimization problem (19). Thus, Theorem 1 gives the complete description of the optimal solution to the problem (19).

Below there are figures demonstrating the possible behaviors of the optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ and the corresponding optimal control $v_{*}\left(t\right)$.

Figure 3 considers the situation when

$$\begin{array}{cccc}a=0.5\hfill & b=-0.9\hfill & c=-0.5\hfill & d=0.7\hfill \\ x_0=1.0\hfill & y_0=3.5\hfill & \beta =1.0\hfill & T=10\hfill \end{array}$$

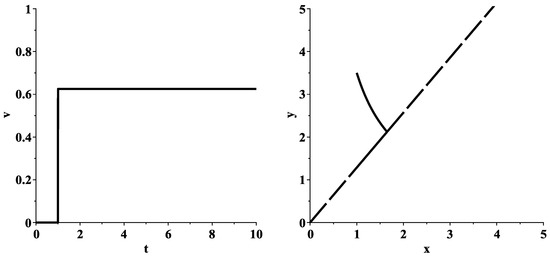
Figure 3. Graph of the optimal control $v_{*}\left(t\right)$ (left), behavior of the corresponding optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ (right). In the left picture, the special ray $\mathsf{\Pi }$ is shown as a longdash line. The initial point $(x_0,y_0)$ is located above this ray.

It is easy to see that the inequalities (8), (9) and (38), as well as the inequality $ad-bc<0$, are satisfied for the specified values of the parameters and initial conditions. In addition, according to Formula (41), the value ${\tau }_{*}=1.001485<T$. Therefore, the optimal control $v_{*}\left(t\right)$ is determined by the left formula in (37), where $v_{\mathrm{sing}}=0.625$. The behavior of the corresponding optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is given in Figure 3 (right). The objective function (17) takes the smallest value $J_{*}=J\left(v_{*}\right)=32.1622675$.

Figure 4 demonstrates the situation when

$$\begin{array}{cccc}a=0.5\hfill & b=-0.7\hfill & c=-0.5\hfill & d=0.9\hfill \\ x_0=2.8\hfill & y_0=0.2\hfill & \beta =1.0\hfill & T=15\hfill \end{array}$$

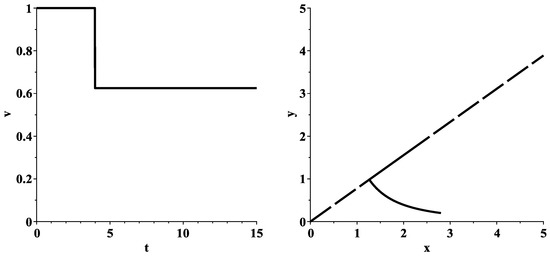
Figure 4. Graph of the optimal control $v_{*}\left(t\right)$ (left), behavior of the corresponding optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ (right). In the left picture, the special ray $\mathsf{\Pi }$ is represented by a longdash line. The initial point $(x_0,y_0)$ is located below this ray.

It can be seen that the inequalities (8), (9) and (43), as well as the inequality $ad-bc>0$, take place for the specified values of the parameters and initial conditions. Moreover, due to Formula (46), the value ${\tau }_{*}=3.979572<T$. Therefore, the optimal control $v_{*}\left(t\right)$ is defined by the right formula in (37), where the value $v_{\mathrm{sing}}$ is the same. The behavior of the corresponding optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is presented in Figure 4 (right). The objective function (17) reaches the smallest value $J_{*}=J\left(v_{*}\right)=49.7317181$.

9. Solving the Original Minimization Problem

Theorem 1 shows that the optimal solution of the relaxed minimization problem (19) can be one of the following three types and will be related to the optimal solution of the original minimization problem (18) as follows.

Case A. The initial point $(x_0,y_0)$ is located above or below the special ray $\mathsf{\Pi }$ ($b{x}_0+d{y}_0\ne 0$), and the time of movement along the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ from it to this ray ${\tau }_{*}\ge T$. Such a movement is carried out with the help of the constant control $v_{*}\left(t\right)$, which takes the value 0 or 1. Since the values $\{0;1\}$ are admissible in the original minimization problem (18), the optimal solution of the relaxed minimization problem (19) simultaneously serves as the optimal solution of the original minimization problem (18).

Case B. The initial point $(x_0,y_0)$ is above or below the special ray $\mathsf{\Pi }$ ($b{x}_0+d{y}_0\ne 0$), and the time of movement along the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ from it to this ray ${\tau }_{*}<T$. Such a movement is carried out due to the control $v_{*}\left(t\right)$, which takes the value 0 or 1 on the interval $[0,{\tau }_{*}]$. In this case, as already noted, the values $\{0;1\}$ are admissible in the original minimization problem (18). Then, the control $v_{*}\left(t\right)$ is switched, and then, on the interval $({\tau }_{*},T]$, the movement along the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ occurs along a special ray $\mathsf{\Pi }$ with the help of the control $v_{*}\left(t\right)=v_{\mathrm{sing}}\in (0,1)$ that is no longer admissible in the original minimization problem (18). Thus, the original minimization problem (18) does not have the optimal solution.

Case C. The initial point $(x_0,y_0)$ lies on a special ray $\mathsf{\Pi }$ ($b{x}_0+d{y}_0=0$). On the entire interval $[0,T]$, the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ moves along the special ray $\mathsf{\Pi }$ under the action of the control $v_{*}\left(t\right)=v_{\mathrm{sing}}\in (0,1)$, which, as already noted, is not admissible in the original minimization problem (18). Hence, the original minimization problem (18) again has no optimal solution.

Let us now show that in Cases B and C in the original minimization problem (18) the special ray $\mathsf{\Pi }$ acts as a sliding mode [35,36]). This means that there is such a family of strongly oscillating piecewise constant controls $\left\{v_{\rho }\left(t\right)\right\}$ that take values $\{0;1\}$ such that the corresponding family of trajectories $\left\{(x_{\rho }\left(t\right),y_{\rho }\left(t\right))\right\}$ uniformly converges to (or “is pressed against”) this ray as $\rho \to +0$. Here, $\rho >0$ is a scalar parameter. Moreover, the family of values $\left\{J\left(v_{\rho }\right)\right\}$ of the objective function (17) corresponding to such a family of trajectories, as $\rho \to +0$, will tend to the value $J_{*}=J\left(v_{*}\right)$ that is its smallest value in the corresponding relaxed minimization problem (19).

For definiteness, we will study the situation in Case B, when the initial point $(x_0,y_0)$ is located above the special ray $\mathsf{\Pi }$ ($b{x}_0+d{y}_0>0$) and ${\tau }_{*}<T$. Situations when the initial point $(x_0,y_0)$ is below the ray $\mathsf{\Pi }$ ($b{x}_0+d{y}_0<0$) at ${\tau }_{*}<T$ or is located on it ($b{x}_0+d{y}_0=0$) are considered similarly.

So, Theorem 1 shows that on the time interval $[0,{\tau }_{*}]$ the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$, due to the control $v_{*}\left(t\right)=0$, moves to the special ray $\mathsf{\Pi }$, on which it turns out at $t={\tau }_{*}$. Hence, we have the point $(x_{†},y_{†})$ such that, by virtue of (30), the following equalities hold:

$$x_{†}=x_{*}\left({\tau }_{*}\right),y_{†}=y_{*}\left({\tau }_{*}\right),b{x}_{†}+d{y}_{†}=0.$$

(47)

Now let us assume that on the interval $[0,{\tau }_{*}]$ the control $v_{\rho }\left(t\right)$ that we are constructing takes the value 0, which ensures that the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ coincides with the trajectory $(x_{\rho }\left(t\right),y_{\rho }\left(t\right))$ corresponding to the control $v_{\rho }\left(t\right)$.

In what follows, we assume that the parameter $\rho$ is arbitrarily small and consider the tube around the trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$:

$$\Gamma =\left\{(x,y):{(x-x_{*}\left(t\right))}^2+{(y-y_{*}\left(t\right))}^2\le {\rho }^2,t\in [{\tau }_{*},T]\right\}.$$

It is easy to see that the tube $\Gamma$ has lower and upper boundaries, which are located on the corresponding straight lines:

$$bx+dy=-\rho \sqrt{b^2+d^2},bx+dy=\rho \sqrt{b^2+d^2}.$$

(48)

Now, when $t>{\tau }_{*}$, we take the value 0 for the control $v_{\rho }\left(t\right)$ and then integrate the system (32) with the initial conditions:

$$x_{\rho }\left({\tau }_{*}\right)=x_{†},y_{\rho }\left({\tau }_{*}\right)=y_{†}.$$

As a result, we obtain the formulas:

$$x_{\rho }\left(t\right)=x_{†}{e}^{a(t-{\tau }_{*})},y_{\rho }\left(t\right)=y_{†}{e}^{c(t-{\tau }_{*})},$$

(49)

that define the curve coming out of the point $(x_{†},y_{†})$ on the ray $\mathsf{\Pi }$. Let us show that this curve intersects the lower boundary of the tube $\Gamma$. To do this, when $t\ge {\tau }_{*}$, we consider the function:

$$F\left(t\right)=b{x}_{†}{e}^{a(t-{\tau }_{*})}+d{y}_{†}{e}^{c(t-{\tau }_{*})}+\rho \sqrt{b^2+d^2},$$

that is obtained as the substitution of the Formula (49) into the equation of the lower boundary of the tube $\Gamma$ in (48). It is easy to see that, due to the definition of the point $(x_{†},y_{†})$ in (47) and inequalities (8), the following relationships hold:

$$F\left({\tau }_{*}\right)=\rho \sqrt{b^2+d^2}>0,\underset{t\to +\infty }{lim}F\left(t\right)=-\infty .$$

Moreover, by virtue of Lemma 1 and inequalities (8), the derivative of the function $F\left(t\right)$:

$$F^{\prime }\left(t\right)=ab{x}_{†}{e}^{a(t-{\tau }_{*})}+cd{y}_{†}{e}^{c(t-{\tau }_{*})}<0,$$

which implies that this function is decreasing. Therefore, there is the value ${\theta }_1>{\tau }_{*}$ for which $F\left({\theta }_1\right)=0$, either given the definition of the function $F\left(t\right)$:

$$b{x}_{†}{e}^{a({\theta }_1-{\tau }_{*})}+d{y}_{†}{e}^{c({\theta }_1-{\tau }_{*})}=-\rho \sqrt{b^2+d^2},$$

or due to the Formula (49):

$$b{x}_{\rho }\left({\theta }_1\right)+d{y}_{\rho }\left({\theta }_1\right)=-\rho \sqrt{b^2+d^2}.$$

(50)

This means that at time $t={\theta }_1$ the trajectory $(x_{\rho }\left(t\right),y_{\rho }\left(t\right))$ intersects the lower boundary of the tube $\Gamma$ at the point $(x_{{\theta }_1},y_{{\theta }_1})$, where

$$x_{{\theta }_1}=x_{\rho }\left({\theta }_1\right),y_{{\theta }_1}=y_{\rho }\left({\theta }_1\right),$$

(51)

and everywhere on the interval $[{\tau }_{*},{\theta }_1)$ such a trajectory is inside this tube.

Now, when $t>{\theta }_1$, we choose the value 1 for the control $v_{\rho }\left(t\right)$ (we make a switch for this control) and then integrate system (33) with the initial conditions (51). As a consequence of this, we obtain the formulas:

$$x_{\rho }\left(t\right)=x_{{\theta }_1}{e}^{(a+b)(t-{\theta }_1)},y_{\rho }\left(t\right)=y_{{\theta }_1}{e}^{(c+d)(t-{\theta }_1)},$$

(52)

that define a curve starting from the point $(x_{{\theta }_1},y_{{\theta }_1})$ on the lower boundary of the tube $\Gamma$. Let us make sure that this curve intersects the upper boundary of the tube $\Gamma$. To do this, when $t\ge {\theta }_1$, we introduce the function:

$$G\left(t\right)=b{x}_{{\theta }_1}{e}^{(a+b)(t-{\theta }_1)}+d{y}_{{\theta }_1}{e}^{(c+d)(t-{\theta }_1)}-\rho \sqrt{b^2+d^2},$$

that is the result of substituting Formula (52) into the equation for the upper boundary of the tube $\Gamma$ in (48). It can be seen that, by virtue of the definition of the point $(x_{{\theta }_1},y_{{\theta }_1})$ in (50), (51) and inequalities (8), (9), the following relationships are true:

$$G\left({\theta }_1\right)=-2\rho \sqrt{b^2+d^2}<0,\underset{t\to +\infty }{lim}G\left(t\right)=+\infty .$$

Moreover, due to Lemma 1 and inequalities (8), (9), the derivative of the function $G\left(t\right)$:

$$G^{\prime }\left(t\right)=b(a+b)x_{{\theta }_1}{e}^{(a+b)(t-{\theta }_1)}+d(c+d)y_{{\theta }_1}{e}^{(c+d)(t-{\theta }_1)}>0,$$

which means that this function is increasing. Therefore, the value ${\theta }_2>{\theta }_1$ is defined for which $G\left({\theta }_2\right)=0$, either due to the definition of the function $G\left(t\right)$:

$$b{x}_{{\theta }_1}{e}^{(a+b)({\theta }_2-{\theta }_1)}+d{y}_{{\theta }_1}{e}^{(c+d)({\theta }_2-{\theta }_1)}=\rho \sqrt{b^2+d^2},$$

or due to the Formula (52):

$$b{x}_{\rho }\left({\theta }_2\right)+d{y}_{\rho }\left({\theta }_2\right)=\rho \sqrt{b^2+d^2}.$$

(53)

This implies that at time $t={\theta }_2$ the trajectory $(x_{\rho }\left(t\right),y_{\rho }\left(t\right))$ intersects the upper boundary of the tube $\Gamma$ at the point $(x_{{\theta }_2},y_{{\theta }_2})$, where

$$x_{{\theta }_2}=x_{\rho }\left({\theta }_2\right),y_{{\theta }_2}=y_{\rho }\left({\theta }_2\right),$$

(54)

and everywhere on the interval $({\theta }_1,{\theta }_2)$ such a trajectory lies inside this tube.

Now let us take the last step of this kind. Namely, when $t>{\theta }_2$, we again take the value 0 for the control $v_{\rho }\left(t\right)$ (we perform switching for this control) and then we integrate system (32) with the initial conditions (54). As a result, we find the formulas:

$$x_{\rho }\left(t\right)=x_{{\theta }_2}{e}^{a(t-{\theta }_2)},y_{\rho }\left(t\right)=y_{{\theta }_2}{e}^{c(t-{\theta }_2)},$$

(55)

that define the curve starting from the point $(x_{{\theta }_2},y_{{\theta }_2})$ on the upper boundary of the tube $\Gamma$. Let us demonstrate that this curve intersects the lower boundary of the tube $\Gamma$. To do this, when $t\ge {\theta }_2$, we will study the function:

$$H\left(t\right)=b{x}_{{\theta }_2}{e}^{a(t-{\theta }_2)}+d{y}_{{\theta }_2}{e}^{c(t-{\theta }_2)}+\rho \sqrt{b^2+d^2},$$

that is formed as a result of substituting Formula (55) into the equation of the lower boundary of the tube $\Gamma$ in (48). We see that due to the definition of the point $(x_{{\theta }_2},y_{{\theta }_2})$ in (53), (54) and inequalities (8), the following relationships are valid:

$$H\left({\theta }_2\right)=2\rho \sqrt{b^2+d^2}>0,\underset{t\to +\infty }{lim}H\left(t\right)=-\infty .$$

In addition, Lemma 1 and inequalities (8) show that the derivative of the function $H\left(t\right)$:

$$H^{\prime }\left(t\right)=ab{x}_{{\theta }_2}{e}^{a(t-{\theta }_2)}+cd{y}_{{\theta }_2}{e}^{c(t-{\theta }_2)}<0,$$

which leads to the conclusion that this function is decreasing. This means that there is the value ${\theta }_3>{\theta }_2$ for which equality $H\left({\theta }_3\right)=0$ is satisfied, either due to the definition of the function $H\left(t\right)$:

$$b{x}_{{\theta }_2}{e}^{a({\theta }_3-{\theta }_2)}+d{y}_{{\theta }_2}{e}^{c({\theta }_3-{\theta }_2)}=-\rho \sqrt{b^2+d^2},$$

or due to the formulas (55):

$$b{x}_{\rho }\left({\theta }_3\right)+d{y}_{\rho }\left({\theta }_3\right)=-\rho \sqrt{b^2+d^2}.$$

Therefore, at time $t={\theta }_3$ the trajectory $(x_{\rho }\left(t\right),y_{\rho }\left(t\right))$ intersects the lower boundary of the tube $\Gamma$ at the point $(x_{{\theta }_3},y_{{\theta }_3})$, where

$$x_{{\theta }_3}=x_{\rho }\left({\theta }_3\right),y_{{\theta }_3}=y_{\rho }\left({\theta }_3\right),$$

and everywhere on the interval $({\theta }_2,{\theta }_3)$ such a trajectory is located inside this tube.

This process can be continued and using induction (the base of the induction has already been described above) we can obtain the trajectory $(x_{\rho }\left(t\right),y_{\rho }\left(t\right))$ whose points $(x_{\rho }\left({\theta }_{2k-1}\right),y_{\rho }\left({\theta }_{2k-1}\right))$, $k\ge 1$ are on the lower boundary of the tube $\Gamma$, and whose points $(x_{\rho }\left({\theta }_{2k}\right),y_{\rho }\left({\theta }_{2k}\right))$, $k\ge 1$ lie on the upper boundary of this tube. Moreover, for all $t\ge {\tau }_{*}$, such a trajectory is located in the tube $\Gamma$. Here the sequence of moments $\left\{{\theta }_m\right\}$, $m\ge 1$ when the trajectory $(x_{\rho }\left(t\right),y_{\rho }\left(t\right))$ is on the boundaries of the tube $\Gamma$ is increasing:

$${\tau }_{*}<{\theta }_1<{\theta }_2<{\theta }_3<\dots .$$

The corresponding control $v_{\rho }\left(t\right)$ has the form:

$$v_{\rho }\left(t\right)=\left\{\begin{array}{cc}0\hfill & ,\mathrm{if}0\le t\le {\theta }_1,\hfill \\ 1\hfill & ,\mathrm{if}{\theta }_1<t\le {\theta }_2,\hfill \\ 0\hfill & ,\mathrm{if}{\theta }_2<t\le {\theta }_3,\hfill \\ \hfill & \cdots \cdots \cdots \hfill \end{array}\right.$$

It remains for us to show that for the given value of the parameter $\rho$ there is a natural number $m_0$ such that ${\theta }_{m_0-1}\le T<{\theta }_{m_0}$. This means that the control $v_{\rho }\left(t\right)$ we have constructed is defined on the entire interval $[0,T]$. In turn, for this it suffices to establish the existence of such a value $w>0$ that ${\theta }_{m+1}-{\theta }_m\ge w$ for all $m\ge 1$.

Indeed, let us first consider the moments of switching ${\theta }_{2k-1}$ and ${\theta }_{2k}$, $k\ge 1$ and the function $G\left(t\right)$ corresponding to them (in previous arguments, such switchings were ${\theta }_1$ and ${\theta }_2$). We write the Lagrange formula for this function:

$$G\left({\theta }_{2k}\right)-G\left({\theta }_{2k-1}\right)=G^{\prime }\left(\xi \right)({\theta }_{2k}-{\theta }_{2k-1}),\xi \in ({\theta }_{2k-1},{\theta }_{2k}),$$

(56)

where the derivative $G^{\prime }\left(\xi \right)$ is written as

$$G^{\prime }\left(\xi \right)=b(a+b)x_{{\theta }_{2k-1}}{e}^{(a+b)(\xi -{\theta }_{2k-1})}+d(c+d)y_{{\theta }_{2k-1}}{e}^{(c+d)(\xi -{\theta }_{2k-1})}.$$

Let us estimate the modulus of this derivative from above. As a result, due to inequalities (8), (9) and (12), we obtain the relationship:

$$|G^{\prime }\left(\xi \right)|\le L_G,$$

where

$$L_G=\left|b\right|(a+b)x_{max}+d|c+d|y_{max}{e}^{(c+d)(T-{\tau }_{*})}.$$

Then, passing in the expression (56) to the modulo estimate and using the equalities obtained earlier:

$$G\left({\theta }_{2k-1}\right)=-2\rho \sqrt{b^2+d^2},G\left({\theta }_{2k}\right)=0,$$

we have the inequality:

$$2\rho \sqrt{b^2+d^2}\le L_G({\theta }_{2k}-{\theta }_{2k-1}),$$

or

$${\theta }_{2k}-{\theta }_{2k-1}\ge \frac{2\rho \sqrt{b^2+d^2}}{L_G}.$$

(57)

Now consider in a similar way the moments of switching ${\theta }_{2k}$ and ${\theta }_{2k+1}$, $k\ge 1$, and the function $H\left(t\right)$ corresponding to them (in previous arguments, such switchings were ${\theta }_2$ and ${\theta }_3$). Let us write again the Lagrange formula for this function:

$$H\left({\theta }_{2k+1}\right)-H\left({\theta }_{2k}\right)=H^{\prime }\left(\eta \right)({\theta }_{2k+1}-{\theta }_{2k}),\eta \in ({\theta }_{2k},{\theta }_{2k+1}),$$

(58)

where the derivative $H^{\prime }\left(\eta \right)$ resembles

$$H^{\prime }\left(\eta \right)=ab{x}_{{\theta }_{2k}}{e}^{a(\eta -{\theta }_{2k})}+cd{y}_{{\theta }_{2k}}{e}^{c(\eta -{\theta }_{2k})}.$$

Let us estimate the modulus of this derivative from above. As a consequence of this, by virtue of inequalities (8) and (12), we find the relationship:

$$|H^{\prime }\left(\eta \right)|\le L_H,$$

where

$$L_H=a\left|b\right|x_{max}{e}^{a(T-{\tau }_{*})}+\left|c\right|d{y}_{max}.$$

Then, passing in expression (58) to the modulo estimate and using the equalities established earlier:

$$H\left({\theta }_{2k}\right)=2\rho \sqrt{b^2+d^2},H\left({\theta }_{2k+1}\right)=0,$$

we obtain an inequality:

$$2\rho \sqrt{b^2+d^2}\le L_H({\theta }_{2k+1}-{\theta }_{2k}),$$

or

$${\theta }_{2k+1}-{\theta }_{2k}\ge \frac{2\rho \sqrt{b^2+d^2}}{L_H}.$$

(59)

Let us introduce the constant $L=max\{L_G;L_H\}$. Then, combining the inequalities (57) and (59), we arrive at the required inequality:

$${\theta }_{m+1}-{\theta }_m\ge \frac{2\rho \sqrt{b^2+d^2}}{L}=\omega ,m\ge 1.$$

(60)

Using the inequality (60), we define the desired constraints for the value $m_0$ as

$$(m_0-1)\omega \le T-{\tau }_{*}<m_0\omega ,$$

or

$$\left[\frac{T-{\tau }_{*}}{\omega }\right]+1<m_0<\left[\frac{T-{\tau }_{*}}{\omega }\right]+2,$$

where $\left[\kappa \right]$ is the integer part of the positive number $\kappa$.

Finally, let us estimate the difference between the values of the objective function (17) taken on the controls $v_{\rho }\left(t\right)$ and $v_{*}\left(t\right)$. We have the equality:

$$\begin{array}{cc}\hfill J\left(v_{\rho }\right)-J\left(v_{*}\right)& =(x_{\rho }\left(T\right)-x_{*}\left(T\right))+(y_{\rho }\left(T\right)-y_{*}\left(T\right))\hfill \\ & +\beta \underset{{\tau }_{*}}{\overset{T}{\int }}\left[(x_{\rho }\left(t\right)-x_{*}\left(t\right))+(y_{\rho }\left(t\right)-y_{*}\left(t\right))\right]dt.\hfill \end{array}$$

Passing in this expression to the modulo estimate and using the Cauchy-Schwarz inequality, as well as the fact that the trajectory $(x_{\rho }\left(t\right),y_{\rho }\left(t\right))$ lies in the tube $\Gamma$ on the interval $[{\tau }_{*},T]$, we achieve the inequality:

$$|J\left(v_{\rho }\right)-J\left(v_{*}\right)|\le \sqrt{2}\rho (1+\beta (T-{\tau }_{*})).$$

(61)

By now specifying an arbitrarily small number $ϵ>0$ and requiring that the following inequality hold

$$\sqrt{2}\rho (1+\beta (T-{\tau }_{*}))<ϵ,$$

(62)

we complete the justification of the result discussed at the beginning of this section. Namely, by tending the value $ϵ$ to zero, due to inequalities (61) and (62), we tend the parameter $\rho$ also to zero and simultaneously increase the number $m_0$. Then the trajectory $(x_{\rho }\left(t\right),y_{\rho }\left(t\right))$ “is pressed against” the special ray $\mathsf{\Pi }$, and the value of the objective function $J\left(v_{\rho }\right)$ is arbitrarily close to the value $J_{*}=J\left(v_{*}\right)$. Thus, we come to the conclusion that the special ray $\mathsf{\Pi }$ in the considered situation is a sliding mode.

10. Results of Numerical Calculations and Their Discussion

In this section, we will discuss how the results of the previous section can be used to find effective treatment protocols for melanoma when a sliding mode occurs. It is clear that it makes no sense to use a very large number of switchings in treatment protocols. Therefore, we will consider a situation with a given small number of switchings ${\theta }_1\le {\theta }_2\le \cdots \le {\theta }_n$, which will act as variables and whose values will be determined as a result of solving some minimization problem. Let us describe it.

First, on the interval $[0,T]$, we define the piecewise constant control $v^{\theta }\left(t\right)$ that takes values $\{0;1\}$ and has n switchings as follows. If $b{x}_0+d{y}_0>0$, then it resembles

$$v^{\theta }\left(t\right)=\left\{\begin{array}{cc}0\hfill & ,\mathrm{if}0\le t\le {\tau }_{*},\hfill \\ 0\hfill & ,\mathrm{if}{\tau }_{*}<t\le {\theta }_1,\hfill \\ 1\hfill & ,\mathrm{if}{\theta }_1<t\le {\theta }_2,\hfill \\ 0\hfill & ,\mathrm{if}{\theta }_2<t\le {\theta }_3,\hfill \\ 1\hfill & ,\mathrm{if}{\theta }_3<t\le {\theta }_4,\hfill \\ \hfill & \cdots \cdots \cdots \hfill \end{array}\right.$$

If $b{x}_0+d{y}_0\le 0$, then it is determined by the formula:

$$v^{\theta }\left(t\right)=\left\{\begin{array}{cc}1\hfill & ,\mathrm{if}0\le t\le {\tau }_{*},\hfill \\ 1\hfill & ,\mathrm{if}{\tau }_{*}<t\le {\theta }_1,\hfill \\ 0\hfill & ,\mathrm{if}{\theta }_1<t\le {\theta }_2,\hfill \\ 1\hfill & ,\mathrm{if}{\theta }_2<t\le {\theta }_3,\hfill \\ 0\hfill & ,\mathrm{if}{\theta }_3<t\le {\theta }_4,\hfill \\ \hfill & \cdots \cdots \cdots \hfill \end{array}\right.$$

(63)

Then we substitute this control into system (10) and integrate it. The resulting solution is substituted into the objective function (17). As a consequence of this, we obtain the function $\tilde{J}({\theta }_1,{\theta }_2,\dots ,{\theta }_n)$ of a finite number of variables ${\theta }_i$, $i=1,\dots ,n$ which we will then minimize on the set:

$${\Gamma }_{\theta }=\left\{({\theta }_1,{\theta }_2,\dots ,{\theta }_n):{\tau }_{*}\le {\theta }_1\le {\theta }_2\le \cdots \le {\theta }_n\le T\right\}.$$

The results of the corresponding numerical calculations in the Maple environment are presented below.

Remark 4. 

Similar finite-dimensional minimization problems were previously considered in the study of control models of the spread of Ebola epidemics and HIV treatment [37,38,39,40,41,42].

Remark 5. 

We note that system (10) is linear in phase variables. Additionally, the right-hand sides of its equations depend linearly on the parameters a, b, c and d. Therefore, due to the scaling of this system in terms of phase variables and time, we can consider phase variables, parameters a, b, c, d and time t in ranges convenient for numerical calculations.

Now we consider the following values of the parameters a, b, c, d and initial conditions $x_0$, $y_0$ of system (10), as well as the final moment T of the interval $[0,T]$:

$$\begin{array}{cccc}a=0.0016,\hfill & b=-0.003,\hfill & c=-0.014,\hfill & d=0.03,\hfill \\ x_0={10}^5,\hfill & y_0={10}^3,\hfill & T=200.\hfill \end{array}$$

These values of the quantities a, b, c and d satisfy the inequality (16) and were found by Formula (8), based on the following values of the parameters of systems (4) and (5):

$${\gamma }_x^{\mathrm{on}}=-0.0014,{\gamma }_x^{\mathrm{off}}=0.0016,{\gamma }_y^{\mathrm{on}}=0.016,{\gamma }_y^{\mathrm{off}}=-0.014.$$

It is easy to see that they satisfy restrictions (6).

In turn, to determine these quantities according to Formula (3), the following values were used:

$$\begin{array}{cccc}{l}_x^{\mathrm{on}}=0.006,\hfill & l_x^{\mathrm{off}}=0.008,\hfill & l_y^{\mathrm{on}}=0.04,\hfill & l_y^{\mathrm{off}}=0.02,\hfill \\ d_x^{\mathrm{on}}=0.0074,\hfill & d_x^{\mathrm{off}}=0.0064,\hfill & d_y^{\mathrm{on}}=0.024,\hfill & d_y^{\mathrm{off}}=0.034,\hfill \end{array}$$

which were taken based on similar values from [27].

After that, in system (10), due to Remark 5, the scale of parameters a, b, c, d, initial conditions $x_0$, $y_0$, and final moment T was changed. Namely, the time scale was changed first as

$$0\le t\le 200\to 0\le t\le 2.$$

This made it possible to change the scale for the parameters a, b, c and d:

$$\begin{array}{cc}a=0.0016\to a=0.16,\hfill & b=-0.003\to b=-0.3,\hfill \\ c=-0.014\to c=-1.4,\hfill & d=0.03\to d=3.0,\hfill \end{array}$$

after which, the scales of the initial conditions $x_0$ and $y_0$ were also changed as

$$x_0={10}^5\to x_0=1,y_0={10}^3\to y_0=1,$$

which is equivalent to changing the scales of the variables x and y. As a result of these actions, the values $x_{max}$ and $y_{max}$ from the Formula (12) took on values:

$$x_{max}=1.37713,y_{max}=403.42879,$$

which led to the need to once again correct the initial conditions $x_0$ and $y_0$ to the values:

$$x_0=1.0\to x_0=20.0,y_0=1.0\to y_0=0.1,$$

and the values $x_{max}$ and $y_{max}$ have become the values of the same order.

As a result, we have the following values of the quantities a, b, c, d, $x_0$, $y_0$ and T:

$$\begin{array}{cccc}a=0.16,\hfill & b=-0.3,\hfill & c=-1.4,\hfill & d=3.0,\hfill \\ x_0=20.0,\hfill & y_0=0.1,\hfill & T=2.0,\hfill \end{array}$$

(64)

which will be used in numerical calculations. Moreover, we will put the weight coefficient $\beta =1.0$.

Figure 5 shows the graph of the optimal control $v_{*}\left(t\right)$ and the behavior of the corresponding optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ in the relaxed minimization problem (19) for the values of the parameters, initial conditions and final moment T presented in (64). It is easy to see that the inequalities (8), (9) and (43), as well as the inequality $ad-bc>0$, are satisfied. In addition, according to Formula (46), the value ${\tau }_{*}=1.72168<T$. Therefore, the optimal control $v_{*}\left(t\right)$ is determined by the right formula in (37), where $v_{\mathrm{sing}}=0.473$. The behavior of the corresponding optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ is given in Figure 5 (right). The objective function (17) takes the smallest value $J_{*}=J\left(v_{*}\right)=53.71712$.

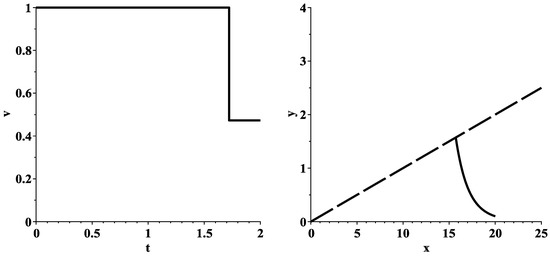
Figure 5. Graph of the optimal control $v_{*}\left(t\right)$ (left), behavior of the corresponding optimal trajectory $(x_{*}\left(t\right),y_{*}\left(t\right))$ (right) in the relaxed minimization problem (19). In the left picture, the special ray $\mathsf{\Pi }$ is represented by a longdash line. The initial point $(x_0,y_0)$ is located below this ray.

Figure 6 presents the graph of the optimal control $v_{*}^{\theta }\left(t\right)$ and the behavior of the corresponding optimal trajectory $(x_{*}^{\theta }\left(t\right),y_{*}^{\theta }\left(t\right))$ in the problem of minimizing the function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3)$ on the set ${\Gamma }_{\theta }$, which for $n=3$ is given as

$${\Gamma }_{\theta }=\left\{({\theta }_1,{\theta }_2,{\theta }_3):{\tau }_{*}\le {\theta }_1\le {\theta }_2\le {\theta }_3\le T\right\}.$$

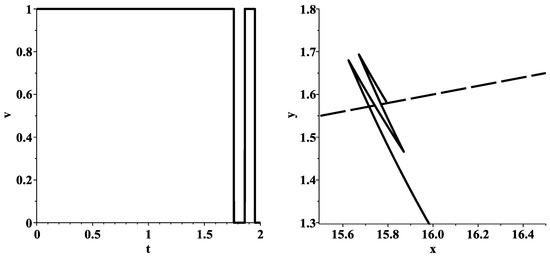
Figure 6. Graph of the optimal control $v_{*}^{\theta }\left(t\right)$ (left), behavior of the corresponding optimal trajectory $(x_{*}^{\theta }\left(t\right),y_{*}^{\theta }\left(t\right))$ (right) in the problem of minimizing the function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3)$. In the left picture, the special ray $\mathsf{\Pi }$ is represented by a longdash line. The initial point $(x_0,y_0)$ is located below this ray.

The switchings ${\theta }_1^{*}$, ${\theta }_2^{*}$, ${\theta }_3^{*}$ of the optimal control $v_{*}^{\theta }\left(t\right)$, which is determined by formula (63), take the following values:

$${\theta }_1^{*}=1.76343,{\theta }_2^{*}=1.86084,{\theta }_3^{*}=1.95129.$$

The function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3)$ has the smallest value ${\tilde{J}}_{*}^3=\tilde{J}({\theta }_1^{*},{\theta }_2^{*},{\theta }_3^{*})=53.71752$.

As noted at the beginning of this section, the minimization problem for the function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3)$ is some approximation of the original minimization problem (18). It follows from the numerical calculations that this approximation is quite acceptable. Indeed, the distinction between the smallest value $J_{*}$ of the objective function (17) in the relaxed minimization problem (19) and the smallest value ${\tilde{J}}_{*}^3$ of the function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3)$ occurs only in the fourth decimal place of the fractional part of the difference $|J_{*}-{\tilde{J}}_{*}^3|$.

Figure 7 gives the graph of the optimal control $v_{*}^{\theta }\left(t\right)$ and the behavior of the corresponding optimal trajectory $(x_{*}^{\theta }\left(t\right),y_{*}^{\theta }\left(t\right))$ in the problem of minimizing the function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5)$ on the set ${\Gamma }_{\theta }$, which for $n=5$ is defined as follows

$${\Gamma }_{\theta }=\left\{({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5):{\tau }_{*}\le {\theta }_1\le {\theta }_2\le {\theta }_3\le {\theta }_4\le {\theta }_5\le T\right\}.$$

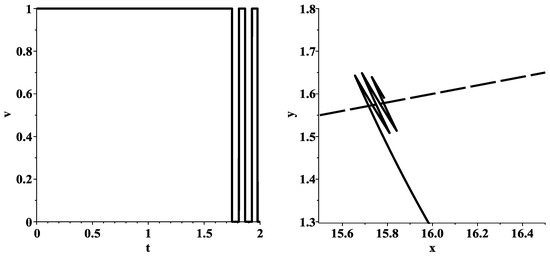
Figure 7. Graph of the optimal control $v_{*}^{\theta }\left(t\right)$ (left), behavior of the corresponding optimal trajectory $(x_{*}^{\theta }\left(t\right),y_{*}^{\theta }\left(t\right))$ (right) in the problem of minimizing the function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5)$. In the left picture, the special ray $\mathsf{\Pi }$ is represented by a longdash line. The initial point $(x_0,y_0)$ is located below this ray.

The switchings ${\theta }_1^{*}$, ${\theta }_2^{*}$, ${\theta }_3^{*}$, ${\theta }_4^{*}$, ${\theta }_5^{*}$ of the optimal control $v_{*}^{\theta }\left(t\right)$, which is determined by Formula (63), take the following values:

$${\theta }_1^{*}=1.74952,{\theta }_2^{*}=1.81075,{\theta }_3^{*}=1.86641,{\theta }_4^{*}=1.92764,{\theta }_5^{*}=1.97773.$$

The function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5)$ has the smallest value ${\tilde{J}}_{*}^5=\tilde{J}({\theta }_1^{*},{\theta }_2^{*},{\theta }_3^{*},{\theta }_4^{*},{\theta }_5^{*})=53.71730$.

It is easy to see that an increase in the number of switchings from three to five leads to an improvement in the result. Indeed, the value ${\tilde{J}}_{*}^5$ of the function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5)$ is less than the value ${\tilde{J}}_{*}^3$ of the function $\tilde{J}({\theta }_1,{\theta }_2,{\theta }_3)$, but greater than the value $J_{*}$ of the objective function $J\left(v\right)$.

It is also clear why the numerical calculations for $n=3$ and $n=5$ gave such good results. This is due to the fact that most of the time (interval $[0,{\tau }_{*}]$ with length $1.72$) we move along the trajectory $(x_{*}^{\theta }\left(t\right),y_{*}^{\theta }\left(t\right))$ that is simultaneously optimal in the relaxed minimization problem (19), and a smaller part of the time (interval $[{\tau }_{*},T]$ with length $0.28$) is not.

We also use the full finite-dimensional optimization in the studied example. To do this, we first consider the situation $n=3$. Let us introduce two piecewise constant controls $u^{\nu }\left(t\right)$ and $w^{\mu }\left(t\right)$ as follows

$$\begin{array}{cc}& u^{\nu }\left(t\right)=\left\{\begin{array}{cc}1\hfill & ,\mathrm{if}0\le t\le {\nu }_1,\hfill \\ 0\hfill & ,\mathrm{if}{\nu }_1<t\le {\nu }_2,\hfill \\ 1\hfill & ,\mathrm{if}{\nu }_2<t\le {\nu }_3,\hfill \\ 0\hfill & ,\mathrm{if}{\nu }_3<t\le T;\hfill \end{array}\right.\hfill \\ & w^{\mu }\left(t\right)=\left\{\begin{array}{cc}0\hfill & ,\mathrm{if}0\le t\le {\mu }_1,\hfill \\ 1\hfill & ,\mathrm{if}{\mu }_1<t\le {\mu }_2,\hfill \\ 0\hfill & ,\mathrm{if}{\mu }_2<t\le {\mu }_3,\hfill \\ 1\hfill & ,\mathrm{if}{\mu }_3<t\le {\mu }_4,\hfill \\ 0\hfill & ,\mathrm{if}{\mu }_4<t\le T.\hfill \end{array}\right.\hfill \end{array}$$

The difference between the controls $u^{\nu }\left(t\right)$, $w^{\mu }\left(t\right)$ and the control $v^{\theta }\left(t\right)$ is that the switchings ${\nu }_i$, $i=1,2,3$ and ${\mu }_i$, $i=1,2,3,4$ of these controls are on the entire interval $[0,T]$, and not on its part $[{\tau }_{*},T]$.

Now we substitute these controls into system (10) and then integrate it. The resulting solution is substituted into the objective function (17). As a result, we obtain the functions $\tilde{I}({\nu }_1,{\nu }_2,{\nu }_3)$ and $\tilde{K}({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4)$ of a finite number of the respective variables ${\nu }_i$, $i=1,2,3$ and ${\mu }_i$, $i=1,2,3,4$, which we then numerically minimize in a similar way on the corresponding sets:

$$\begin{array}{cc}\hfill {\Sigma }_{\nu }& =\left\{({\nu }_1,{\nu }_2,{\nu }_3):0\le {\nu }_1\le {\nu }_2\le {\nu }_3\le T\right\},\hfill \\ \hfill {\mathsf{\Lambda }}_{\mu }& =\left\{({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4):0\le {\mu }_1\le {\mu }_2\le {\mu }_3\le {\mu }_4\le T\right\}.\hfill \end{array}$$

As a result of numerical minimization of the function $\tilde{I}({\nu }_1,{\nu }_2,{\nu }_3)$ on the set ${\Sigma }_{\nu }$, we have the following switchings of the corresponding optimal control $u_{*}^{\nu }\left(t\right)$:

$${\nu }_1^{*}={\theta }_1^{*},{\nu }_2^{*}={\theta }_2^{*},{\nu }_3^{*}={\theta }_3^{*},$$

and the smallest value ${\tilde{I}}_{*}^3$ of the function $\tilde{I}({\nu }_1,{\nu }_2,{\nu }_3)$ coincides with ${\tilde{J}}_{*}^3$.

When minimizing the function $\tilde{K}({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4)$ numerically on the set ${\mathsf{\Lambda }}_{\mu }$, the following switchings of the corresponding optimal control $w_{*}^{\mu }\left(t\right)$ are found:

$${\mu }_1^{*}=0,{\mu }_2^{*}={\theta }_1^{*},{\mu }_3^{*}={\theta }_2^{*},{\mu }_4^{*}={\theta }_3^{*},$$

and the smallest value ${\tilde{K}}_{*}^4$ of the function $\tilde{K}({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4)$ is also equal to ${\tilde{J}}_{*}^3$.

We note that similar phenomena also occur for the situation $n=5$.

These results for $n=3$ and $n=5$ demonstrate the optimality of the corresponding solutions discussed at the beginning of this section on a wider set of piecewise constant controls with a predetermined number of switchings.

11. Conclusions

The paper considers a bilinear control system that models the interaction between drug-sensitive and drug-resistant cancer cells over a given time interval, which is the general period of melanoma treatment. This system also contains a control function responsible for switching between the period of taking drugs in the treatment of illness and the period of rest, and vice versa. To determine an effective protocol for switching between these periods, the task was to minimize the cancer load both during the entire period of melanoma treatment and at the end of the time interval. A feature of such a problem is that it may not have an optimal solution due to the nonconvexity of the control set. This shortcoming was eliminated by taking the convex hull of this set and then considering a relaxed minimization problem for the original controlled bilinear system. Then, a detailed analytical analysis of such a minimization problem was carried out, and it turned out that only two situations are possible for the corresponding optimal solution: either the optimal solution of the relaxed minimization problem coincides with the optimal solution of the original minimization problem, or the optimal solution of the relaxed minimization problem contains a singular arc corresponding to the sliding mode in the original minimization problem. The last situation is the most interesting, since it is implemented with the help of optimal controls containing strongly oscillating piecewise constant sections, which, obviously, have no medical meaning.

From a medical point of view, if the optimal solution contains singular arc, this means that in certain cases (for some patients) the treatment must take a singular form, so the optimal solution will not just “jump” between off and on treatment, but could be in the state somewhere in between. Thus, it was found that the optimal control would take not only the values 0 and 1 but can take a singular form and take the values $0.7$, or $0.5$, or $0.9$, etc., and that it may be optimal for the patient to “stay” on that special ray. What would that mean? Remember that the dosage of the drug for the stated problem is not modulated and is not a control function.

Naturally, such optimal control could not be associated with a reasonable treatment protocol within the framework of the proposed model. The doctor treating the patient relies in her decisions on the results of medical examinations and tests. So, she would like to have an optimal treatment schedule from which she could presumably be able to tell how many “treat-not treat” switches the patient can tolerate. Based on this, it was further proposed to replace optimal controls with strongly oscillating piecewise constant portions by piecewise constant controls with a given number of switchings, which are variable and whose optimal values are found as a result of solving some minimization problem. We have written a computer program in Maple that approximates the patient’s “movement” along special ray $\mathsf{\Pi }$ with a piecewise constant function (transition from 0 to 1 or vice versa) in the order depending on the patient’s health. The results obtained are quite stunning—if the cancer patient approaches this special ray at time ${\tau }_{*}<T$, (T is the duration of treatment) and depending on which side (left or right) (it depends on whether the patient has more melanoma-resistant or more susceptible cells), the clinician can choose the optimal length of “on” and “off” periods and their alternation in accordance with our optimal treatment protocol that minimizes the overall cancer load.

Numerical calculations have shown that such a replacement is quite acceptable and its efficiency increases, but not too much, with an increase in the given number of switchings. These calculations were carried out for the specific values of the parameters of the bilinear control model, its initial conditions, and the time interval.

Moreover, we note that the problem investigated in the paper can be used for educational purposes in an advanced/graduate course of optimal control theory and its applications. On the one hand, the problem is “simple” from the point of view of its complete analytical study, and on the other hand, since the singular arc in the relaxed optimal control problem acts as a sliding mode in the original optimal control problem. Note that all results are unique and substantiated analytically.