Dynamics and Embedded Solitons of Stochastic Quadratic and Cubic Nonlinear Susceptibilities with Multiplicative White Noise in the Itô Sense
Abstract
1. Introduction
2. Dynamics of (1) and (2)
2.1. Mathematical Derivation
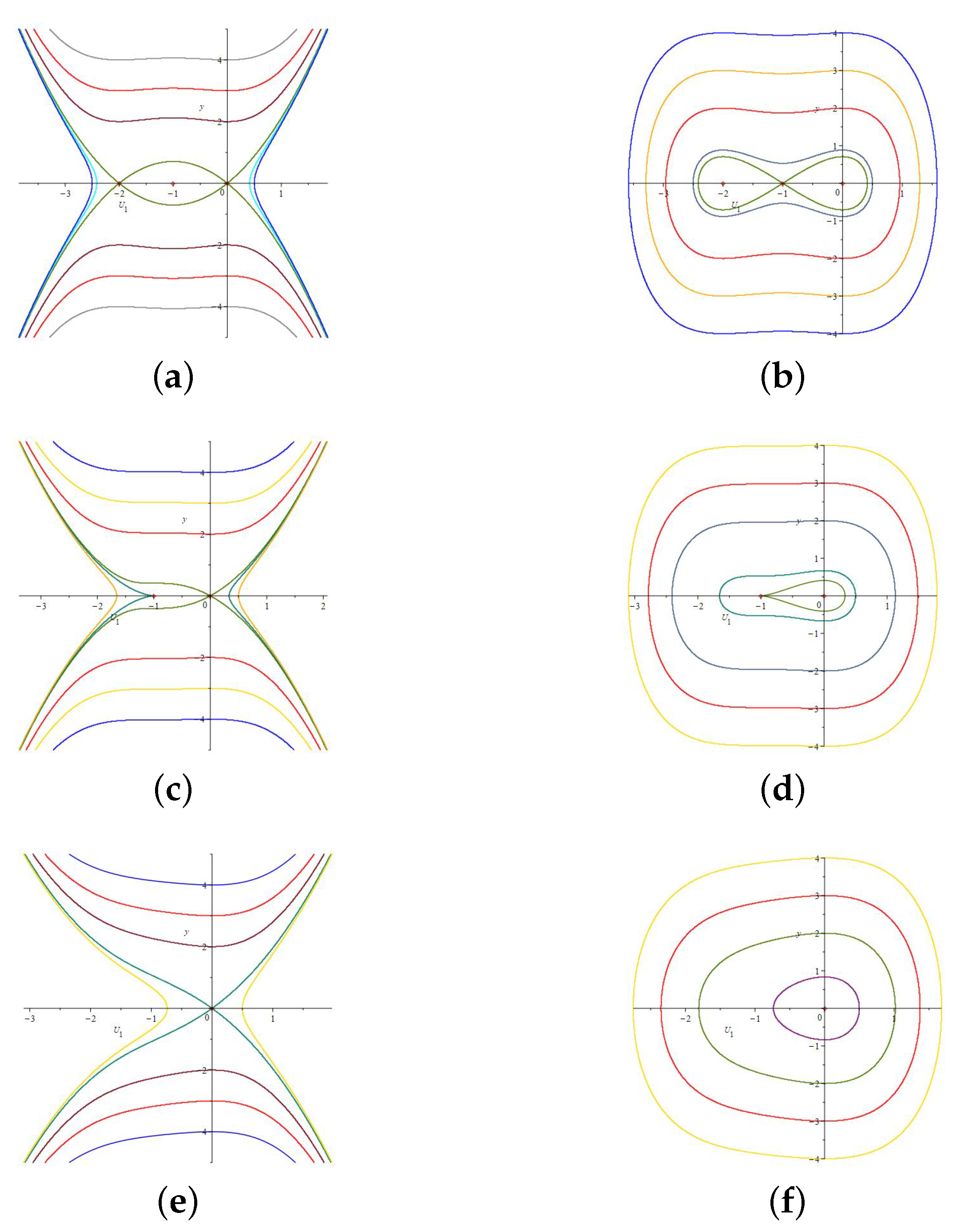
2.2. Phase Portraits of System (9)
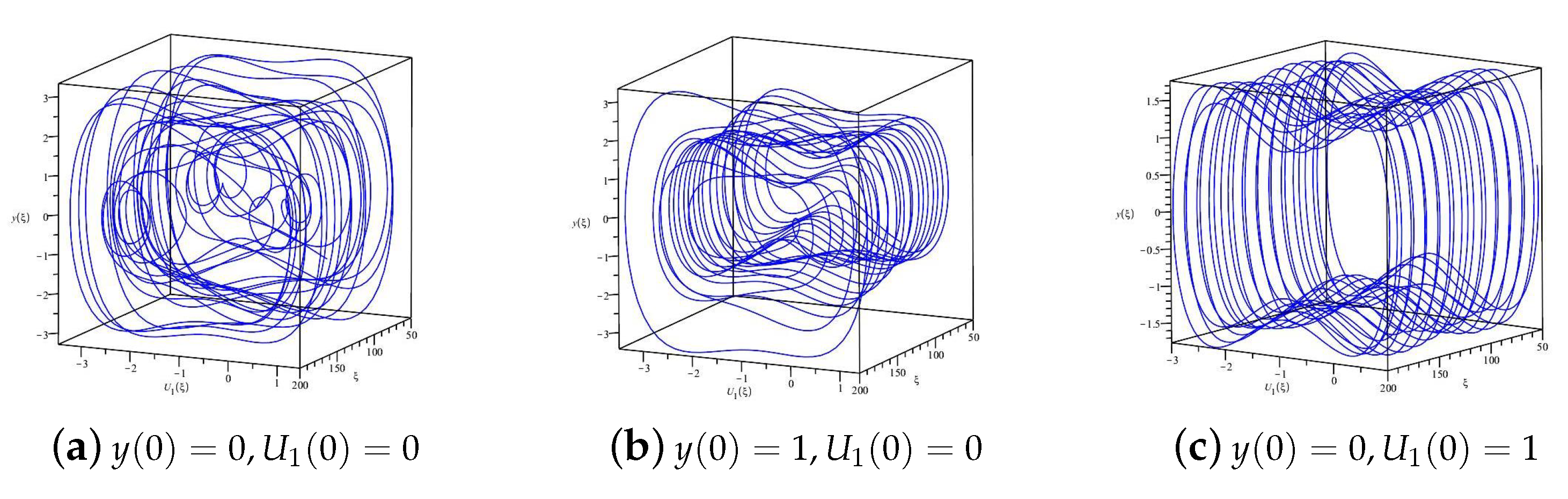
2.3. Chaotic Behaviors of (2)
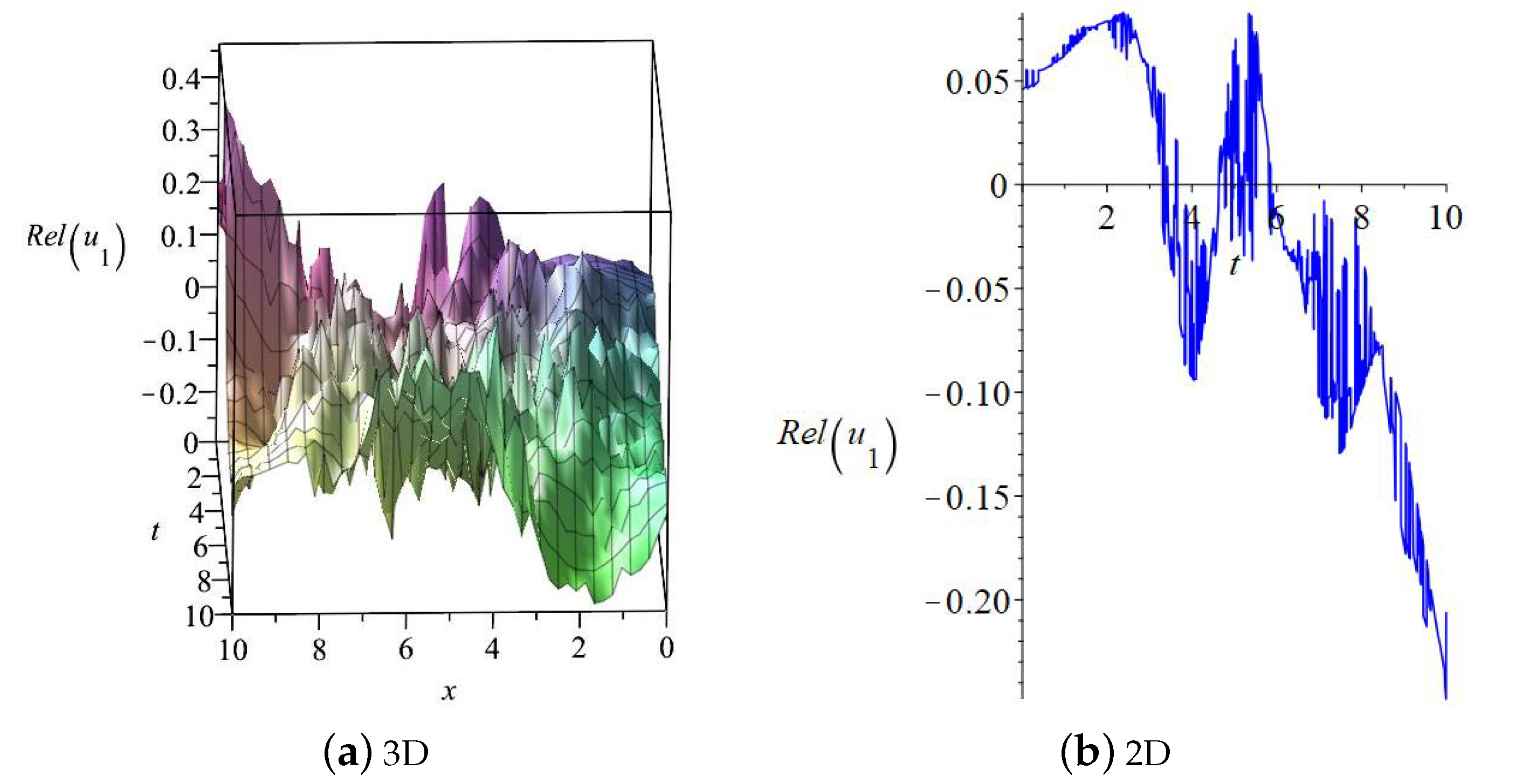
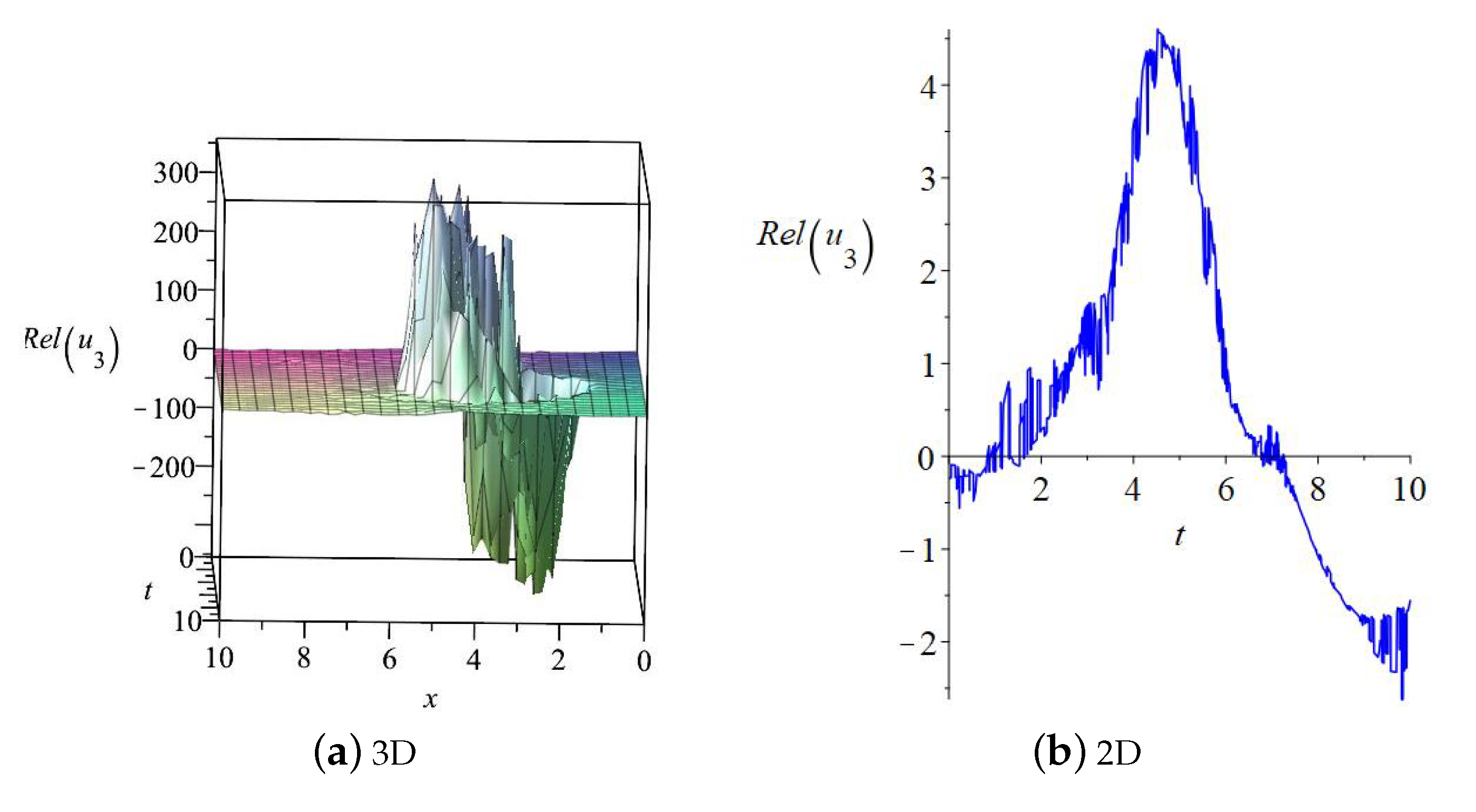
3. Embedded Solitons of System (1)
3.1.
3.2.
4. Discuss
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fujioka, J.; Espinosa-Cerón, A.; Rodriguez, R. A survey of embedded solitons. Rev. Mex. Fis. 2006, 52, 6–14. [Google Scholar]
- Yang, J.; Malomed, B.A.; Kaup, D.J.; Champneys, A.R. Embedded solitons: A new type of solitary wave. Math. Comput. Simul. 2001, 56, 585–600. [Google Scholar] [CrossRef]
- Tan, Y.; Yang, J.K.; Pelinovsky, D.E. Semi-stability of embedded solitons in the general fifth-order KdV equation. Wave Motion 2002, 36, 241–255. [Google Scholar] [CrossRef]
- Sonmezoglu, A.; Ekici, M.; Arnous, A.H.; Zhou, Q.; Triki, H.; Moshokoa, S.P.; Ullah, M.Z.; Biswas, A.; Belic, M. Embedded solitons with χ(2) and χ(3) nonlinear susceptibilities by extended trial equation method. Optik 2018, 154, 1–9. [Google Scholar] [CrossRef]
- Susanto, H.; Malomed, B.A. Embedded solitons in second-harmonic-generating lattices. Chaos Solitons Fractals 2021, 142, 110534. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact solutions of equation for description of embedded solitons. Optik 2022, 268, 169801. [Google Scholar] [CrossRef]
- Smith, T.B.; Choudhury, S.R. Regular and embedded solitons in a generalized pochammer PDE. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2637–2641. [Google Scholar] [CrossRef]
- Animasaun, I.I.; Shah, N.A.; Wakif, A.; Mahanthesh, B.; Sivaraj, R.; Koriko, O.K. Ratio of Momentum Diffusivity to Thermal Diffusivity; Chapman and Hall/CRC: New York, NY, USA, 2022. [Google Scholar]
- Zayed, E.M.E.; Alngar, M.E.M.; Shohib Reham, M.A. Cubic-quartic embedded solitons with χ(2) and χ(3) nonlinear susceptibilities having multiplicative white noise via Itô Calculus. Chaos Solitons Fractals 2023, 168, 113186. [Google Scholar] [CrossRef]
- Chen, Z.M.; Zeng, J.H. Two-dimensional optical gap solitons and vortices in a coherent atomic ensemble loaded on optical lattices. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105911. [Google Scholar] [CrossRef]
- Palmero, F.; Molina, M.I.; Guevas-Maraver, J.; Kevrekidis, P.G. Discrete embedded solitary waves and breathers in one-dimensional nonlinear lattices. Phys. Lett. A 2022, 425, 127880. [Google Scholar] [CrossRef]
- Han, T.Y.; Li, Z.; Zhang, K. Exact solutions of the stochastic fractional long-short wave interaction system with multiplicative noise in generalized elastic medium. Results Phys. 2023, 44, 106174. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A.; Alngar, M.E.M. Dispersive optical solitons in magneto-optic waveguides with stochastic generalized Schrödinger-Hirota equation having multiplicative white noise. Optik 2022, 271, 170069. [Google Scholar] [CrossRef]
- He, T.; Wang, Y.Y. Dark-multi-soliton and soliton molecule solutions of stochastic nonlinear Schrödinger equation in the white noise space. Appl. Math. Lett. 2021, 121, 107405. [Google Scholar] [CrossRef]
- Li, W.; Tian, B. Stochastic solitons in a two-layer fluid system. Chin. J. Phys. 2023, 81, 155–161. [Google Scholar] [CrossRef]
- Li, Z.; Huang, C.; Wang, B.J. Phase portrait, bifurcation, chaotic pattern and optical soliton solutions of the Fokas-Lenells equation with cubic-quartic dispersion in optical fibers. Phys. Lett. A 2023, 465, 128714. [Google Scholar] [CrossRef]
- Li, Z.; Huang, C. Bifurcation, phase portrait, chaotic pattern and optical soliton solutions of the conformable Fokas-Lenells model in optical fibers. Chaos Solitons Fractals 2023, 169, 113237. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M.; Shohib, R.M.A.; Biswas, A.; Yıldırım, Y.; Moraru, L.; Mereuta, E.; Alshehri, H.M. Embedded solitons with χ(2) and χ(3) nonlinear susceptibilities having multiplicative white noise in the Itô Calculus. Chaos Solitons Fractals 2022, 162, 112494. [Google Scholar] [CrossRef]
- Rao, R.; Lin, Z.; Ai, X.; Wu, J. Synchronization of epidemic systems with Neumann boundary value under delayed impulse. Mathematics 2022, 10, 2064. [Google Scholar] [CrossRef]
- Li, G.D.; Zhang, Y.; Guan, Y.J.; Li, W.J. Stability analysis of multi-point boundary conditions for fractional differential equation with non-instantaneous integral impulse. Math. Biosci. Eng. 2023, 20, 7020–7041. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L. Practical exponential stability of impulsive stochastic food chain system with time-varying delays. Mathematics 2023, 11, 147. [Google Scholar] [CrossRef]
- Li, K.; Li, R.; Cao, L.; Feng, Y.; Onasanya, B.O. Periodically intermittent control of Memristor-based hyper-chaotic bao-like system. Mathematics 2023, 11, 1264. [Google Scholar] [CrossRef]
- Xia, M.; Liu, L.; Fang, J.; Zhang, Y. Stability analysis for a class of stochastic differential equations with impulses. Mathematics 2023, 11, 1541. [Google Scholar] [CrossRef]
- Xue, Y.; Han, J.; Tu, Z.; Chen, X. Stability analysis and design of cooperative control for linear delta operator system. AIMS Math. 2023, 8, 12671–12693. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, L.; Tang, J.; Rao, Y.; Fan, H.; Zhu, J. Hybrid impulsive pinning control for mean square synchronization of uncertain multi-link complex networks with stochastic characteristics and hybrid delays. Mathematics 2023, 11, 1697. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Jiao, F.; Mai, H.; Chen, H.; Lin, R. Generalized Halanay inequalities and relative application to time-delay dynamical systems. Mathematics 2023, 11, 1940. [Google Scholar] [CrossRef]
- Ma, Z.; Yuan, S.; Meng, K.; Mei, S. Mean-square stability of uncertain delayed stochastic systems driven by G-Brownian motion. Mathematics 2023, 11, 2405. [Google Scholar] [CrossRef]
- Wang, C.; Song, Y.; Zhang, F.; Zhao, Y. Exponential stability of a class of neutral inertial neural networks with multi-proportional delays and leakage delays. Mathematics 2023, 11, 2596. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, X.; Cheng, X.; Du, B.; Zhao, Y. Positive periodic solution for neutral-type integral differential equation arising in epidemic model. Mathematics 2023, 11, 2701. [Google Scholar] [CrossRef]
- Li, J.B.; Dai, H.H. On the Study of Singular Nonlinear Traveling Wave Solutions: Dynamical System Approach; Science Press: Beijing, China, 2007. [Google Scholar]



| Results | Our Results | Results of Ref. [18] | |
|---|---|---|---|
| Type of Solutions | |||
| Exponential function solutions | , , | ||
| Trigonometric function solutions | , , | Solutions (19), (31)∼(34), | |
| Solutions (50), (51), (58), (59), | |||
| Rational function solutions | Solutions (37), (38) | ||
| Hyperbolic function solutions | , , | Solutions (18), (25)∼(30), | |
| Solutions (48), (49), (56), (57), | |||
| , , | |||
| Jacobi elliptic function solutions | , | ||
| , | |||
| Implicit function solutions | Solutions (16)∼(23) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Peng, C. Dynamics and Embedded Solitons of Stochastic Quadratic and Cubic Nonlinear Susceptibilities with Multiplicative White Noise in the Itô Sense. Mathematics 2023, 11, 3185. https://doi.org/10.3390/math11143185
Li Z, Peng C. Dynamics and Embedded Solitons of Stochastic Quadratic and Cubic Nonlinear Susceptibilities with Multiplicative White Noise in the Itô Sense. Mathematics. 2023; 11(14):3185. https://doi.org/10.3390/math11143185
Chicago/Turabian StyleLi, Zhao, and Chen Peng. 2023. "Dynamics and Embedded Solitons of Stochastic Quadratic and Cubic Nonlinear Susceptibilities with Multiplicative White Noise in the Itô Sense" Mathematics 11, no. 14: 3185. https://doi.org/10.3390/math11143185
APA StyleLi, Z., & Peng, C. (2023). Dynamics and Embedded Solitons of Stochastic Quadratic and Cubic Nonlinear Susceptibilities with Multiplicative White Noise in the Itô Sense. Mathematics, 11(14), 3185. https://doi.org/10.3390/math11143185






