Control Factors for the Equilibrium Composition of Microbial Communities in Open Systems: Theory and Experiments
Abstract
1. Introduction
2. The Rule of Coexistence of Microbial Populations in Continuous Cultures
Coexistence, Interaction Coefficients, and the New Criterion of Interactions between Populations
3. Sensitivity Coefficients
3.1. An Invariant for Sensitivity Coefficients
- (1)
- The value of for each regulator j, in the general case, will be a fractional number both greater and less than zero, which can change from equilibrium to a new equilibrium when input levels of regulators are varied;
- (2)
- Although all values are variable and non-integer, summation of them always produces the same natural number—deduction of the total number of species in the equilibrium mixture from the total number of regulators;
- (3)
- It allows us to assess the level of our understanding of the completeness of relationships in a mixture of species: Violation of Formula (12) requires the search for additional regulators and/or new species.
3.2. The Generalization Taking into Account the “Non-Factor” Species Interaction
- (1)
- Matrix (9) of population interactions in the community through factors coincides with . Formula (20) can be rewritten as
- (2)
- If there are no “non-factor” interactions in the community (), Theorem 2 gives the result of Theorem 1.
- (3)
- If the factors do not affect the dynamics of the community (), the sum of sensitivity coefficients is equal to the number of factors, n, suggesting that the community does not affect the factors either; thus, the community and the factors do not interact. For the community, the factors taken into account are imaginary and fictitious.
- (4)
- If the effects of “non-factor” interactions and factors in the community are proportional to each other ( at some ), Formula (21) has the following form: . Then, the condition is satisfied. One can only assume that the range of K is the same in the general case as well.
3.3. An Invariant for the Theorem of Quantization in the Case of Distribution of Cells by Growth Rate and Age
4. Experiments with Monocultures
4.1. Interaction Coefficients and Verification of Models
4.2. Experimental Testing of the Method of Searching for Density-Dependent Growth Control Factors in Microbial Populations Based on the Quantization Theorem
5. Discussion: Coexistence of Microbial Populations and Regulating Factors
6. Results and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| List of Symbols | |
| DDGCF | Density-dependent growth control factor |
| RF | Regulating factor |
| SGR (h−1) | Specific growth rate |
| FBL | Feedback level |
| (h−1) | Specific growth rate (SGR) or corresponding vector SGRs |
| ks, k (mg·L−1) | Michaelis–Menten constant |
| (L·mg−1·h−1) | SGR sensitivity to unit change in the level of factor R |
| D (h−1) | Specific dilution rate [the ratio of the flow rate (L h−1) to the culture vessel volume (l)] |
| D−1, h | Time necessary for the culture to be completely renewed |
| (h−2) | Coefficient of the action of the jth population on the ith, or growth acceleration |
| B (L·mg−1·h−1) | Specific growth acceleration (per unit SGR and per unit biomass perturbation) |
| (mg·L−1) | Substrate concentration in the medium and substrate input concentration |
| ; (mg∙ L−1) | jth RF concentration in the medium and jth RF input concentration |
| (mg·L−1·h−1) | The rate of change in the density of the ith population and concentration of the jth RF |
| The vector of species abundance in the community. The number of species is denoted by m and the species index by i. | |
| The vector of RFs. The number of factors is denoted by n and the factor index by j. | |
| (mg·mg−1) | The amount of the jth RF taken up or released by unit increase in the abundance of the ith population (dimensionless) |
| Matrix of the RFs amount taken up or released by unit increase in the abundance of the populations | |
| (mg·mg−1) | Yield coefficient (the amount of biomass increase per 1 mg substrate) |
| (dimensionless) | A change in steady-state concentration of the substrate or the jth RF in response to unit change in input RF, RF autostabilization coefficient, or sensitivity coefficient |
| “·” | Wherever necessary, matrix multiplication, the dot product, in particular. If the operation is obvious, this symbol is omitted. |
| “*” | Component-wise multiplication of vectors |
References
- Calcott, P.H. Continuous culture: Where it came from and where it is now. In Continuous Cultures of Cells; Calcott, P.H., Ed.; CRC Press Taylor & Francis Group: Dayton, OH, USA, 2019; Volume 1, pp. 10–34. [Google Scholar]
- Lelekov, A.S.; Trenkenshu, R.P. Two-Component Model of Microalgae Growth in the Turbidostat. Mat. Biol. Bioinf. 2021, 16, 101–114. [Google Scholar] [CrossRef]
- Gitelson, I.I.; Kovrov, B.G.; Lisovsky, G.M.; Okladnikov, Y.N.; Rerberg, M.S.; Sidko, F.Y.; Terskov, I.A. Experimental ecological systems including the human. In Problemy Kosmicheskoi Biologii (Problems of Space Biology); Nichiporovich, A.A., Ed.; Nauka: Moscow, Russia, 1975; Volume 28, p. 312. [Google Scholar]
- Lotka, A.J. Elements of Physical Biology; Williams and Wilkins: Baltimore, MA, USA, 1925. [Google Scholar]
- Volterra, V. Fluctuations in the abundance of a species considered mathematically. Nature 1926, 188, 558–560. [Google Scholar] [CrossRef]
- Hardin, G. The competitive exclusion principle. Science 1960, 131, 1292–1297. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Wang, X.; Wang, L.; Song, H. Competitive Exclusion in Delayed Chemostat Models with Differential Removal Rates. SIAM J. Appl. Mat. 2014, 74, 634–648. [Google Scholar] [CrossRef]
- Hutchinson, G.E. The paradox of the plankton. Am. Nat. 1961, 95, 137–145. [Google Scholar] [CrossRef]
- MacArthur, R.; Levins, S. Competition, habitat selection, and character displacement in a patchy environment. Proc. Natl. Acad. Sci. USA 1964, 51, 1207–1210. [Google Scholar] [CrossRef] [PubMed]
- MacArthur, R. Selection for life tables in periodic environments. Am. Nat. 1968, 102, 381–383. [Google Scholar] [CrossRef]
- Stewart, F.M.; Levin, B.R. Partitioning of resources and the outcome of interspecific competition: A model and some general considerations. Am. Nat. 1973, 107, 171–198. [Google Scholar] [CrossRef]
- Armstrong, R.A.; McGehee, R. Coexistence of two competitors on one resource. J. Theor. Biol. 1976, 56, 449–502. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, R.A.; McGehee, R. Coexistence of species competing for shared resources. Theor. Pop. Biol. 1976, 9, 317–328. [Google Scholar] [CrossRef] [PubMed]
- Mixed Dilution Cultures of Microorganisms; Pechurkin, N., Ed.; Nauka: Novosibirsk, Russia, 1981. (In Russian) [Google Scholar]
- Tilman, D. Resource competition and community structure. Princeton Univ Press, Princeton Vet LEM (1999). From chemical to population ecology: Infochemical use in an evolutionary context. J. Chem. Ecol. 1982, 25, 31–51. [Google Scholar]
- Shmida, A.; Ellner, S. Coexistence of plants with similar niches. Vegetatio 1984, 58, 29–55. [Google Scholar] [CrossRef]
- Hanski, I.; Woiwod, I.P. Spatial synchrony in the dynamics of moth and aphid populations. J. Anim. Ecol. 1993, 62, 656–668. [Google Scholar] [CrossRef]
- Neuhauser, C.P.; Pacala, S.W. An explicitly spatial version 1 of the Lotka-Volterra model with interspecific competition. Ann. Appl. Probab. 1999, 9, 1226–1259. [Google Scholar] [CrossRef]
- Chesson, P. Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 2000, 31, 343–366. [Google Scholar] [CrossRef]
- Szabo, P.; Meszena, G. Limiting similarity revisited. Oikos 2006, 112, 612–619. [Google Scholar] [CrossRef]
- Münkemüller, T.; Bugmann, H.; Johst, K. Hutchinson revisited: Patterns of density regulation and the coexistence of strong competitors. J. Theor. Biol. 2009, 259, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, H.L.; Hungate, B.A.; Chapin, F.I.S., III; D’Antonio, C.M. Soil heterogeneity and plant competition in an annual grassland. Ecology 1997, 78, 2076–2090. [Google Scholar] [CrossRef]
- Levin, S.A. Community equilibria and stability: An extension of the competitive exclusion principle. Am. Nat. 1970, 104, 413–423. [Google Scholar] [CrossRef]
- MacArthur, R. Species packing and competitive equilibrium for many species. Theor. Pop. Biol. 1970, 1, 1–11. [Google Scholar] [CrossRef]
- Odum, E.P. Fundamentals of Ecology; W. Saunders: Philadelphia, PA, USA, 1971. [Google Scholar]
- Degermendzhi, A. Coexistence of microbal populations and autostabilization of regularing factors in continuous culture: Theory and experiments. Aquat. Ecol. 2010, 44, 541–560. [Google Scholar] [CrossRef]
- Degermendzhi, A.G.; Abakumov, A.I. The Principle of Competitive Exception in a Two-Species Community with One Metabolic Regulation Factor. Dokl. Biochem. Biophys. 2018, 480, 149–151. [Google Scholar] [CrossRef] [PubMed]
- Degermendzhi, A.G.; Adamovich, V.A.; Pozdyaev, V.N. On the cybernetics of bacterial communities: Observation, experiments and theory. Cyber. Syst. 1989, 20, 501–541. [Google Scholar] [CrossRef]
- Lee, I.H.; Fredrickson, A.G.; Tsuchiya, H.M. Dynamics of mixed cultures of Lactobacillus plantarum and Propionibacterium shermanii. Biotechnol. Bioeng. 1976, 78, 513–526. [Google Scholar] [CrossRef]
- Cappenberg, T.E.A. A study of mixed continuous cultures of sulfate-reducing and methane-producing bacteria. Microb. Ecol. 1975, 2, 60–72. [Google Scholar] [CrossRef]
- Chao, C.-C.; Reilley, P.J. Symbiotic growth of Acetobacter suboxydans and Saccharomyces carlsbergensis in a chemostat. Biotechnol. Bioeng. 1972, 14, 75–92. [Google Scholar] [CrossRef]
- Osman, A.; Bull, A.T.; Slater, J.H. Growth of mixed microbial populations on orcinol in continuous culture. In Proceedings of the 5th International Fermentation Symposium and 4th International Specialized Symposium Yeasts, Berlin, Germany; 1976; p. 124. [Google Scholar]
- Tilman, D. Ecological competition between algae: Experimental confirmation of resource-based competition theory. Science 1976, 192, 463–465. [Google Scholar]
- Daughton, C.G.; Hsieh, D.P.H. Paration utilization by bacterial symbionts in a chemostat. Appl. Environ. Microbiol. 1977, 34, 175–184. [Google Scholar] [CrossRef]
- Wilkinson, T.G.; Topiwala, H.H.; Hamer, G. Interactions in a mixed population growing on methane in continuous culture. Biotechnol. Bioeng. 1974, 16, 41–60. [Google Scholar] [CrossRef]
- Trilli, A.; Pirt, S.J. Permissive and non-permissive conditions for the stable association of Klebsiella aerogenes and Pseudomonas aeruginosa in a chemostat. J. Appl. Chem. Biotechnol. 1976, 26, 328–329. [Google Scholar]
- Megee, R.D.; Drake, J.F.; Fredrickson, A.G.; Tsuchiya, N.M. Studies in intermicrobial symbiosis Saccharomyces cerevisiae and Lactobacillus casei. Can. J. Microbiol. 1972, 18, 1733–1742. [Google Scholar] [CrossRef] [PubMed]
- Degermendzhi, A.G. On the problem of coexistence of interacting continuous populations. In Mixed Continuous Cultures of Microorganisms; Pechurkin, N., Ed.; Nauka: Novosibirsk, Russia, 1981; pp. 26–106. (In Russian) [Google Scholar]
- Tagughi, H.; Yoshida, T.; Nakatani, K. Studies on a model mixed culture for simulation of a bulking phenomenon. J. Ferment. Technol. 1978, 56, 158–168. [Google Scholar]
- Lenski, R.E. Coexistence of Two Competitors on One Resource and One Inhibitor: A Chemostat Model Based on Bacteria and Antibiotics. J. Theoret. Biol. 1986, 122, 83–93. [Google Scholar] [CrossRef]
- Volova, T.G. Hydrogen-Based Biosynthesis; Nova Science Publishers, Inc.: New York, NY, USA, 2009; p. 287. [Google Scholar]
- Andriychuk, M. (Ed.) Matrix Theory—Classics and Advances; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Fredrickson, A.G. Behavior of mixed cultures of microorganisms. Annu. Rev. Microbiol. 1977, 31, 63–87. [Google Scholar] [CrossRef] [PubMed]
- Fredrickson, A.G.; Stephanopoulos, G. Microbial competition. Science 1981, 213, 972–979. [Google Scholar] [CrossRef]
- Smith, I.S. The nature of the stimulation of the growth of Streptococcus lactis by yeast extract. J. Dairy Res. 1975, 42, 123–138. [Google Scholar] [CrossRef] [PubMed]
- Slyter, L.L.; Weaver, I.M. Tetrahydrofolate and other growth requirements of certain strains of Ruminococcus flavefaciens. Appl. Env. Microbiol. 1977, 33, 363–369. [Google Scholar] [CrossRef] [PubMed]
- Smith, H.L.; Waltman, P. The Theory of Chemostat: Dynamics of Microbial Competition; Cambridge University Press: Cambridge, UK, 2008; 332p. [Google Scholar]
- Ji, J.; Wan, H. Competitive Exclusion and Coexistence in a Stoichiometric Chemostat Model. J. Dyn. Differ. Equ. 2022, 5, 1–33. [Google Scholar] [CrossRef]
- Xu, C.; Yuan, S.; Zhang, T. Competitive Exclusion in a General Multi-species Chemostat Model with Stochastic Perturbations. Bul. Mathemat. Biol. 2021, 83, 1–17. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, D.; Wolkowicz, G.S.K. Global asymptotic behavior of a multi-species stochastic chemostat model with discrete delays. J. Dyn. Differ. Equ. 2020, 32, 849–872. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, D.; O’Regan, D. The periodic solutions of a stochastic chemostat model with periodic washout rate. Commun. Nonlin. Sci. Numer. Simul. 2016, 37, 1–13. [Google Scholar] [CrossRef]
- Baltzis, B.C.; Fredrickson, A.G. Competition of two microbial populations for a single resource in a chemostat when one of them exhibits wall attachment. Biotechnol. Bioeng. 2004, 25, 2419–2439. [Google Scholar] [CrossRef]
- Gall, L.S. Significance of microbial interactions in control of microbial ecosystems. Biotechnol. Bioeng. 2004, 12, 333–340. [Google Scholar] [CrossRef] [PubMed]
- Lenbury, Y.; Siengsanan, M. Coexistence of competing microbial species in a chemostat where one population feeds on another. Acta Biotech. 2004, 13, 13–20. [Google Scholar] [CrossRef]
- Meyer, J.S.; Tsuchiya, H.M.; Fredrickson, A.G. Dynamics of mixed populations having complementary metabolism. Biotechnol. Bioeng. 2004, 17, 1065–1081. [Google Scholar] [CrossRef]
- Yoon, H.; Klinzing, G.; Blanch, H.W. Competition for mixed substrates by microbial populations. Biotechnol Bioeng. 2004, 19, 1193–1210. [Google Scholar] [CrossRef]
- Straight, J.V.; Ramkrishna, D. Cybernetic modeling and regulation of metabolic pathways. Biotechnol. Prog. 1994, 10, 574–587. [Google Scholar] [CrossRef]
- Gaebler, H.J.; Eber, H.J. Thermodynamic Inhibition in Chemostat Models with an Application to Bioreduction of Uranium. Bull. Mat. Biol. 2020, 82, 76. [Google Scholar] [CrossRef]
- Degermendzhi, A.G.; Bartsev, S.I.; Gubanov, V.G.; Erokhin, D.V.; Shevirnogov, A.P. Forecast of biosphere dynamics using small-scale models. In Global Climatology and Ecodynamics: Anthropogenic Changes to Planet Earth; Cracknell., A.P., Krapivin, V.F., Varotsos, C.A., Eds.; Springer Praxis Books/Environmental Sciences: Berlin/Heidelberg, Germany, 2008; pp. 241–300. [Google Scholar]
- Kirsta, Y.B. System-analytical modelling—Part II: Wheat biotime run and yield formation. Agroclimatic potential, the Le Chatelier principle, and changes in agroclimatic potential and climate in Russia and the U.S. Ecol. Modell. 2006, 191, 331–345. [Google Scholar] [CrossRef]
- Zhu, Y.-G.; Zhu, D.; Rillig, M.C.; Yang, Y.; Chu, H.; Chen, Q.-L.; Penuelas, J.; Cui, H.-L.; Gillings, M. Ecosystem Microbiome Science. mLife 2023, 2, 2–10. [Google Scholar] [CrossRef]
- Wade, M.J.; Harmand, J.; Benyahia, B.; Bouchez, T.; Chaillou, S.; Cloez, B.; Godon, J.-J.; Boudjemaa, B.M.; Rapaport, A.; Sari, T.; et al. Perspectives in mathematical modelling for microbial ecology. Ecol. Model. 2016, 321, 64–74. [Google Scholar] [CrossRef]
- Guzmán-Palomino, A.; Aguilera-Vázquez, L.; Hernández-Escoto, H.; García-Vite, P.M. Sensitivity, Equilibria, and Lyapunov Stability Analysis in Droop’s Nonlinear Differential Equation System for Batch Operation Mode of Microalgae Culture Systems. Mathematics 2021, 9, 2192. [Google Scholar] [CrossRef]
- Theorell, A.; Stelling, J. Assumptions on decision making and environment can yield multiple steady states in microbial community models. BMC Bioinform. 2023, 24, 262. [Google Scholar] [CrossRef] [PubMed]
- Clenet, M.; Massol, F.; Najim, J. Equilibrium and surviving species in a large Lotka–Volterra system of differential equations. J. Math. Biol. 2023, 87, 13. [Google Scholar] [CrossRef]
- Bernard, O.; Mairet, F.; Chachuat, B. Modelling of microalgae culture systems with applications to control and optimization. Adv. Biochem. Eng. Biotechnol. 2016, 2016, 59–87. [Google Scholar] [CrossRef]
- Chen, M.; Zheng, Q.; Wu, R.; Chen, L. Hopf bifurcation in delayed nutrient-microorganism model with network structure. J. Biol. Dyn. 2022, 16, 1–13. [Google Scholar] [CrossRef] [PubMed]
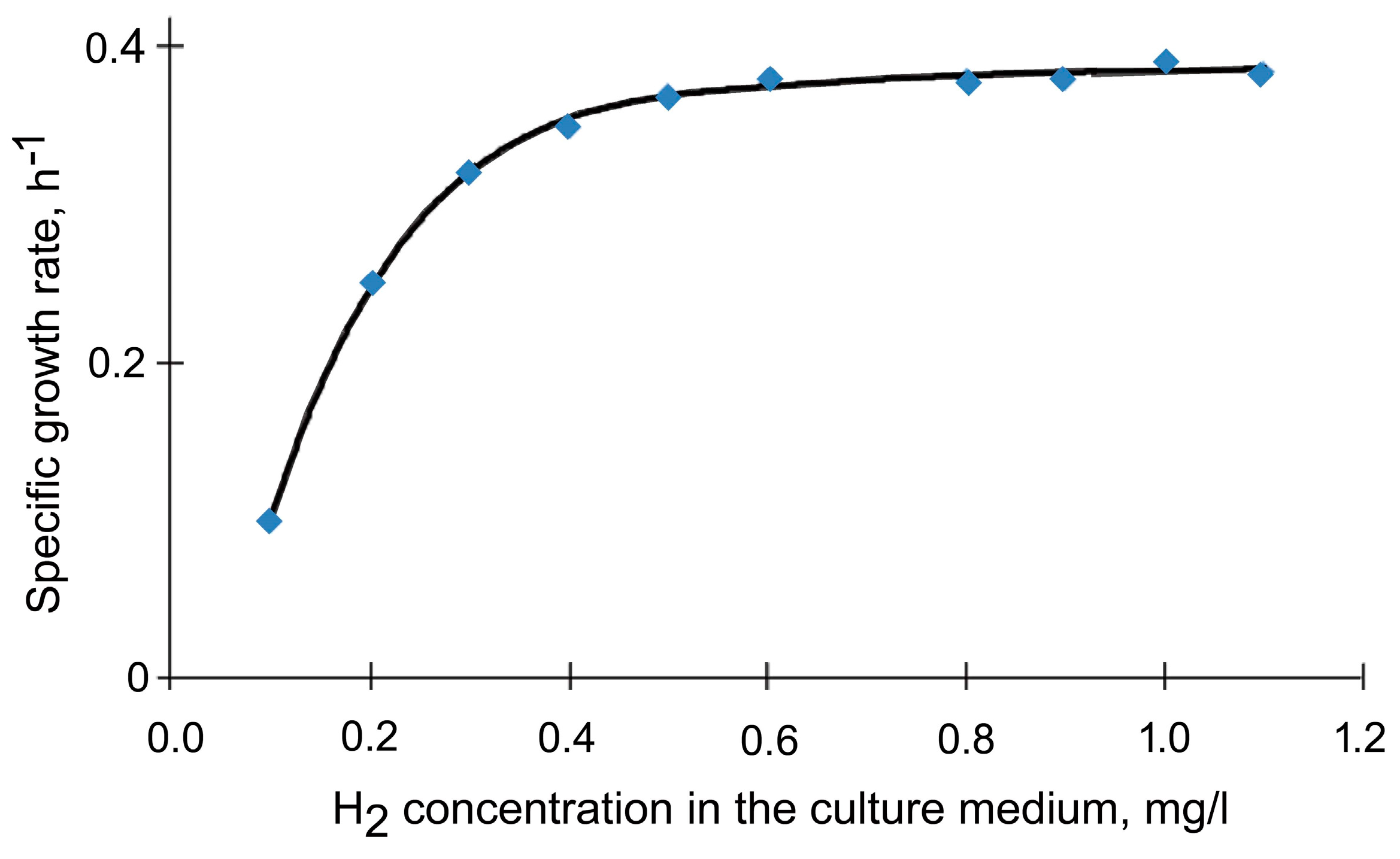
 , mg/L) and biomass (
, mg/L) and biomass ( , g/L) in Seliberia carboxydohydrogena Z1062 vs. chemostat culture (flow rate 0.15 h−1) as dependent on hydrogen fed into the fermenter (vol.%) [41].
, g/L) in Seliberia carboxydohydrogena Z1062 vs. chemostat culture (flow rate 0.15 h−1) as dependent on hydrogen fed into the fermenter (vol.%) [41].
 , mg/L) and biomass (
, mg/L) and biomass ( , g/L) in Seliberia carboxydohydrogena Z1062 vs. chemostat culture (flow rate 0.15 h−1) as dependent on hydrogen fed into the fermenter (vol.%) [41].
, g/L) in Seliberia carboxydohydrogena Z1062 vs. chemostat culture (flow rate 0.15 h−1) as dependent on hydrogen fed into the fermenter (vol.%) [41].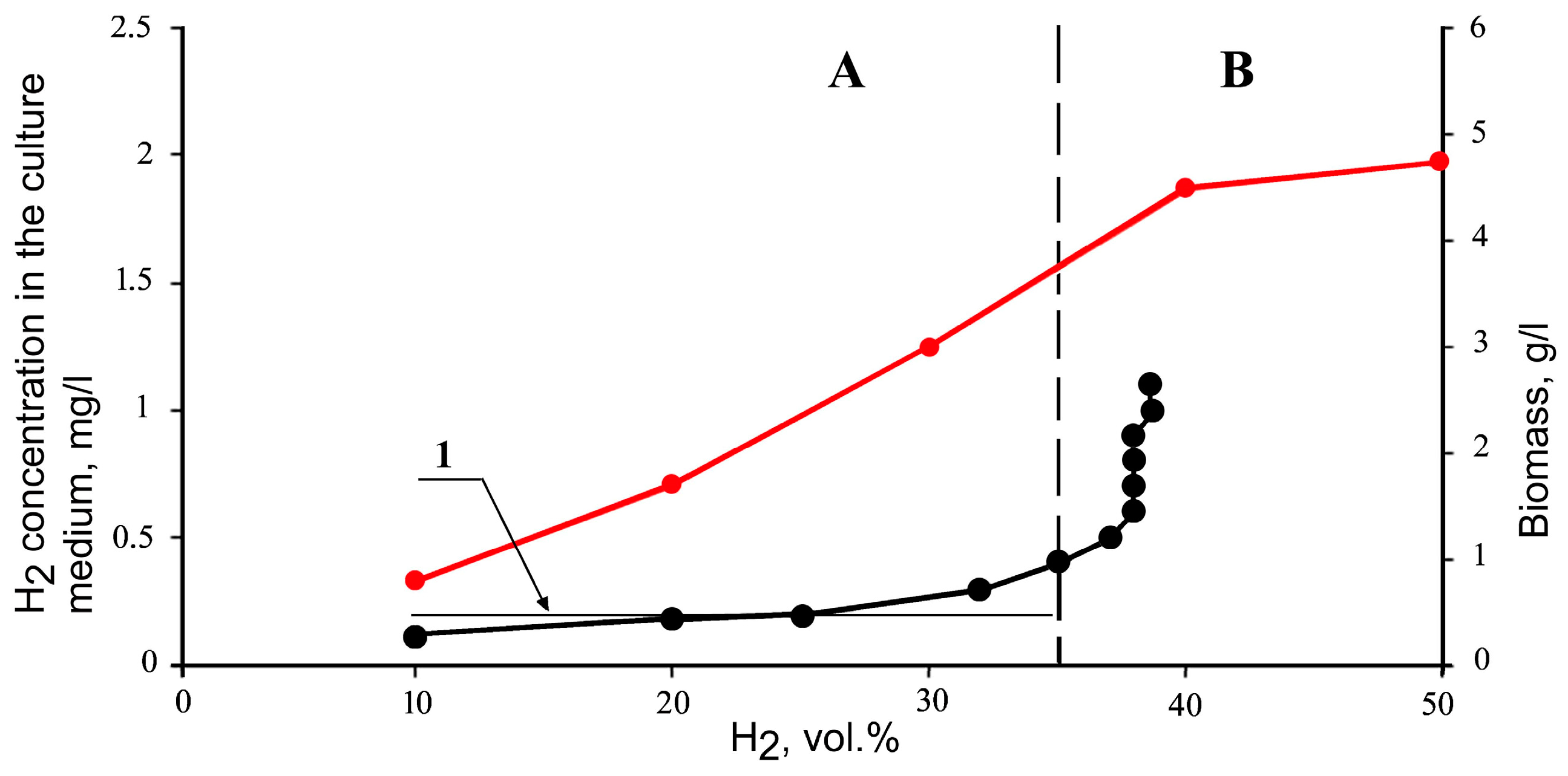
| St. No. | Medium Factors (RFs) | Coexisting Species | Interaction Diagram | Ref. |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| 1 | S, glucose, P, lactate | X1—Lactobacillus plantarum x2—Proptonibacterium shermanii | 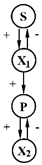 | [29] |
| 2 | S, lactate P, acetate | X1—Desulfovibrio desulfuricans X2—Methanobacterium sp. | [30] | |
| 3 | S, manitol P, fructose | X1—Acetobacter suboyxdans X2—Saccharomyces carlsbergensis | [31] | |
| 4 | S, 5-methyl-recorcin (orcin) P1, unknown product P2, unknown product | X1—Pseudomonas sp. x2—Gram-positive bacilli x3—Gram-positive bacilli | 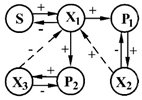 | [32] |
| 5 | S1—PO4 ions S2—SiO2 ions | Diatoms X1—Cyclotello x2—Asterionella | 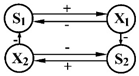 | [33] |
| 6 | S—parathion (organophosphorus insecticide) P1—paranitrophenol P2—diethyl phosphate | X1—Ps. stutzeri x2—Ps. aeruginosa | 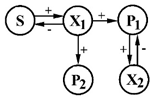 | [34] |
| 7 | S—oxygen P1—methanol P2—organic matter P3—organic matter | X1—Pseudomonas sp. x2—Hyphomicrobium X3—Flavobacterium sp. X4—Acinetobacter sp. | 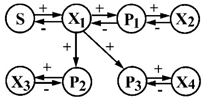 | [35] |
| 8 | S1—n—oxibenzoate S2—glucose | X1—Klebsiella aerogenes X2—Pseudomonas aeruginosa | 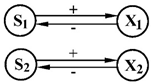 | [36] |
| 9 | S—glucose P—riboflavin | X1—Saccharomyces cerevisiqe X2—Lactobacillus casei | 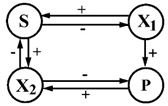 | [37] |
| 10 | S—glucose P—vitamin | X1—Candida mycoderma X2—C. tropicalis | [38] | |
| 11 | S—glucose P—unidentified compound | X1—Flavobacterium breve (F-39) X2—Fl. ferrugineum (B-21) | 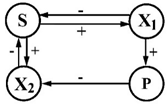 | [39] |
| 12 | S1—glucose S2—xylose | x1—Candida mycoderma X2—C. tropicalis |  | [38] |
| 13 | S1—glucose S2—galactose | X1—Candida mycoderma X2—C. tropicalis | [38] | |
| 14 | S1—glucose S2—arabinose | X1—Candida scottii X2—C. tropicalis | 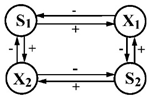 | [38] |
| 15 | S—glucose P—H+ | Saccharomyces cerevisiae: X1—haploid X2—diploid |  | [38] |
| 16 | S—substrate P—inhibitor | Bacteria: X1—inhibitor-insensitive strain X2—sensitive strain | [40] |
| State Number | Sinput, g/L | Sst, mg/L | pHinput | pHst | Xst, mg/L | αS, g/g | αH, 10−3 M/g |
|---|---|---|---|---|---|---|---|
| Flow rate 0.1 h−1 | |||||||
| 1 | 1 | 13 ± 2 | 2.79 | 2.60 | 375 ± 20 | 2.63 ± 0.15 | 2.37 ± 0.33 |
| 2 | 1 | 16 ± 4 | 4.12 | 3.10 | 400 ± 10 | 2.45 ±0.13 | 1.79 ± 0.07 |
| 3 | 1 | 20 ± 6 | 3.15 | 2.79 | 390 ± 25 | 2.54 + 0.16 | 2.37 ± 0.13 |
| 4 | 2 | 16 ± 1 | 3.14 | 2.62 | 840 ± 10 | 2.36 ± 0.12 | 1.99 ± 0.10 |
| 5 | 0.5 | 7 ± 2 | 3.15 | 2.89 | 205 ± 10 | 2.40 ± 0.10 | 2.83 ± 0.34 |
| 6 | 1 | 12 ± 1 | 2.46 | 2.32 | 410 ± 10 | 2.40 ± 0.13 | 3.19 ± 0.43 |
| 7 | 1.5 | 19 ± 4 | 2.37 | 2.22 | 590 ± 10 | 2.51 ± 0.13 | 3.02 ± 0.41 |
| 8 | 1 | 10 ± 2 | 2.38 | 2.28 | 415 ± 10 | 2.38 ± 0.12 | 2.59 ± 0.38 |
| 9 | 1 | 16 ± 4 | 2.32 | 2.21 | 410 ± 10 | 2.41 ± 0.13 | 3.38 ± 0.54 |
| 10 | 2 | 21 ± 4 | 2.37 | 2.15 | ≥920 | ≤2.15 | ≤2.93 |
| 11 | 2 | 30 ± 5 | 2.23 | 2.09 | 945 ± 15 | 2.08 ± 0.11 | 2.36 ± 0.33 |
| 12 | 2 | 21 ± 6 | 2.18 | 2.02 | 1070 ± 20 | 1.85 ± 0.10 | 2.75 ± 0.42 |
| 13 | 2 | 25 ± 6 | 2.14 | 2.00 | 980 ± 15 | 2.02 ± 0.10 | 2.70 ± 0.45 |
| 14 | 2.5 | 48 ± 6 | 2.14 | 1.90 | 1290 ± 20 | 1.90 ± 0.10 | 2.80 ± 0.58 |
| Flow rate 0.055 h−1 | |||||||
| 15 | 2.5 | 58 ± 5 | 2.24 | 2.10 | 1130 ± 30 | 2.16 ± 0.06 | 1.93 ± 0.21 |
| 16 | 2.5 | 91 ± 10 | 2.14 | 2.05 | 1020 ± 25 | 2.36 ± 0.07 | 1.67 ± 0.26 |
| 17 | 2 | 40 ± 5 | 2.14 | 2.07 | 710 ± 30 | 2.30 ±0.10 | 1.79 ± 0.37 |
| Steady State | Sinput, g/L | pHinput | SC for Glucose | SC for pH |
|---|---|---|---|---|
| 1–5 | 1 | 3.15 | 0.00 ± 0.01 | 1.10 ± 0.10 |
| 6–9 | 1 | 2.38 | 0.02 ± 0.02 | 1.06 ± 0.07 |
| 7, 10, 11 | 2 | 2.37 | 0.00 ± 0.01 | 0.65 ± 0.10 |
| 12–14 | 2 | 2.14 | 0.05 ± 0.02 | 0.71 ± 0.13 |
| 13–17 | 2.5 | 2.14 | 0.10 ± 0.03 | 0.65 ± 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Degermendzhi, A.; Abakumov, A. Control Factors for the Equilibrium Composition of Microbial Communities in Open Systems: Theory and Experiments. Mathematics 2023, 11, 3183. https://doi.org/10.3390/math11143183
Degermendzhi A, Abakumov A. Control Factors for the Equilibrium Composition of Microbial Communities in Open Systems: Theory and Experiments. Mathematics. 2023; 11(14):3183. https://doi.org/10.3390/math11143183
Chicago/Turabian StyleDegermendzhi, Andrey, and Alexander Abakumov. 2023. "Control Factors for the Equilibrium Composition of Microbial Communities in Open Systems: Theory and Experiments" Mathematics 11, no. 14: 3183. https://doi.org/10.3390/math11143183
APA StyleDegermendzhi, A., & Abakumov, A. (2023). Control Factors for the Equilibrium Composition of Microbial Communities in Open Systems: Theory and Experiments. Mathematics, 11(14), 3183. https://doi.org/10.3390/math11143183






