Survival Analysis of the PRC Model from Adaptive Progressively Hybrid Type-II Censoring and Its Engineering Applications

Abstract

A new two-parameter statistical model, obtained by compounding the generalized-exponential and exponential distributions, called the PRC lifetime model, is explored in this paper. This model can be easily linked to other well-known six-lifetime models; namely the exponential, log-logistic, Burr, Pareto and generalized Pareto models. Adaptive progressively hybrid Type-II censored strategy, used to increase the efficiency of statistical inferential results and save the total duration of a test, has become widely used in various sectors such as medicine, biology, engineering, etc. Via maximum likelihood and Bayes inferential methodologies, given the presence of such censored data, the challenge of estimating the unknown parameters and some reliability time features, such as reliability and failure rate functions, of the PRC model is examined. The Markov-Chain Monte Carlo sampler, when the model parameters are assumed to have independent gamma density priors, is utilized to produce the Bayes’ infer under the symmetric (squared-error) loss of all unknown subjects. Asymptotic confidence intervals as well as the highest posterior density intervals of the unknown parameters and the unknown reliability indices are also created. An extensive Monte Carlo simulation is implemented to investigate the accuracy of the acquired point and interval estimators. Four various optimality criteria, to select the best progressive censored design, are used. To demonstrate the applicability and feasibility of the proposed model in a real-world scenario, two data sets from the engineering sector; one based on industrial devices and the other on aircraft windshield, are analyzed. Numerical evaluations showed that the PRC model furnishes a superior fit compared to seven other models in the literature, including: alpha-power exponential, log-logistic, Nadarajah–Haghighi, generalized-exponential, Weibull, gamma and exponential lifetime distributions. The findings demonstrate that, in order to obtain the necessary estimators, the Bayes’ paradigm via Metropolis–Hastings sampler is recommended compared to its competitive likelihood approach.

1. Introduction

Compounding of several discrete and lifetime distributions is a common strategy for producing new distributions in lifetime modelling. Via compounding the generalized exponential and exponential distributions, Popović et al. [1] introduced a new two-parameter lifetime model, called the generalized exponential distribution. They also derived various mathematical and reliability properties of this model.

Henceforth, due to the fact that several extended exponential models have been proposed in the literature, we will call this model PRC, which is an abbreviation of its authors’ names. Suppose Y, a random variable of lifetime of a test item(s), follows $\mathrm{PRC}\left(\mathit{\sigma }\right)$, where $\mathit{\sigma }={(\mu ,\gamma )}^{\top }$. Then, the probability density function (PDF) $f(·)$ and cumulative distribution function (CDF) $F(·)$ of Y, are given by

$$f(y;\mathit{\sigma })=\frac{\mu e^{-\mu y}}{\gamma (1-e^{-\mu y})}{\left[1-{\gamma }^{-1}log(1-e^{-\mu y})\right]}^{-2},y>0,\mu ,\gamma >0,$$

(1)

and

$$F(y;\mathit{\sigma })={\left[1-{\gamma }^{-1}log(1-e^{-\mu y})\right]}^{-1},$$

(2)

respectively. Usually, a reliability practitioner uses two reliability time indices, namely: reliability function (RF) $R(·)$ and hazard rate function (HRF) $h(·)$, from any lifespan model as key aspects for assessing capability.

Thus, besides $\mu$ and $\gamma$, we investigate both $R(·)$ and $h(·)$ of the PRC model as unknown time parameters, for $t>0$, are given by

$$R(t;\mathit{\sigma })=1-{\left[1-{\gamma }^{-1}log(1-e^{-\mu t})\right]}^{-1},t>0,$$

(3)

and

$$h(t;\mathit{\sigma })=\frac{\mu e^{-\mu t}}{(1-e^{-\mu t})(-log(1-e^{-\mu t}))}{\left[1-{\gamma }^{-1}log(1-e^{-\mu t})\right]}^{-1},$$

(4)

respectively. Figure 1 depicts the PDF and HRF shapes of the $\mathrm{PRC}\left(\mathit{\sigma }\right)$ distribution based on several options of its parameters. It exhibits that the density (1) function has a unimodal, decreasing, or increasing shape, while the failure rate (4) function has a bathtub-shaped or decreasing shape.

Figure 1. The PDF (left) and HRF (right) shapes of the PRC model.

From (1), Popović et al. [1] showed also that the PRC distribution could be investigated as a new extended model of five widely known distributions in the literature, namely: log-logistic, generalized Pareto, Pareto, Burr and exponential models. Taking $Y^{★}\left(\mu \right)=log\left(1-e^{-\mu Y}\right)$, the PRC model can be easily linked to:

• Exponential distribution with scale parameter one if setting $X=log\left[1-{\gamma }^{-1}{Y}^{★}\left(\mu \right)\right]$.
• Log-logistic distribution with shape $\beta (=1)$ parameter and scale $\lambda (=\mu )$ parameter if setting $X=Y^{★}\left(\mu \right)$.
• Burr distribution with shape $({\beta }_1,{\beta }_2)=(2,1)$ parameters if setting $X=\sqrt{-{\gamma }^{-1}{Y}^{★}\left(\mu \right)}$.
• Pareto distribution with shape $\beta (=1)$ parameter if setting $X=1-{\gamma }^{-1}{Y}^{★}\left(\mu \right)$.
• Generalized Pareto distribution without location parameter, shape $\beta (=1)$ parameter and scale $\lambda (=\mu )$ parameter if setting $X=-Y^{★}\left(\mu \right)$.

In the reliability sector, as a result of time constraints or a lack of money, life-testing investigations typically conclude before all of the items fail. The observations resulting from these circumstances are known as the censored sample.

The adaptive progressive hybrid Type-II (AT2-PH) censored method, proposed by Ng et al. [2], has received a lot of attention from numerous authors since it allows for the construction of quite effective statistical analyses. According to this mechanism, on a test at time zero, n independent experimental items units are considered. The threshold point $T>0$, the progressive censoring design $\mathbf{R}=(R_1,R_2,\dots ,R_m)$, and the number of failures $m(<$$n)$ are predetermined. Specifically, the fixed values of some of progressive stages $R_i$ for $i=1,2,\dots ,m,$ may be reassigned consequently during the experiment. It should be mentioned here that T is an ideal full test time due to the fact that it allows the testing to pass the preassigned time T. At the moment of the first failure (say $Y_{1:m:n}$) recorded, $R_1$ surviving items are randomly selected and extracted from the staying $n-1$ items. Again, at the moment of the second failure $Y_{2:m:n}$ recorded, $R_2$ items of the staying $n-R_1-2$ items are randomly selected and withdrawn out of the test and so on. If $Y_{m:m:n}<T$, the test proceeds using the same ${R_i}^{\prime }s$ and stops at $Y_{m:m:n}$. This situation is similar to the same traditional Type-II progressive (T2-P) censored strategy. Otherwise, if $T<Y_{m:m:n}$ such as $Y_{d:m:n}<T<Y_{d+1:m:n}$, we reset the removal scenario by setting $R_i=0$ for $i=d+1,\cdots ,m-1$, where d is the number of failed items recorded before time T. Then, the test ends at mth failure occur and all staying surviving subjects, i.e., $R_m=n-m-{\sum }_{i=1}^d{R}_i$ are removed. However, let $\mathbf{y}=\{(Y_{1:m:n},R_1),\dots ,(Y_{d:m:n},R_d),(Y_{d+1:m:n},0),\dots ,(Y_{m:m:n},R_m)\}$ be an AT2-PH censored sample from a continuous population, with PDF $f(·)$ and CDF $F(·)$, hence, the joint PDF for the AT2-PH failure times of size m can be expressed as

$$L\left(\mathit{\sigma }\right|\mathbf{y})=\mathcal{K}{\prod }_{i=1}^{m}f(y_i;\mathit{\sigma }){\prod }_{i=1}^d{\left[R(y_i;\mathit{\sigma })\right]}^{R_i}{\left[R(y_m;\mathit{\sigma })\right]}^{R_m^{*}},$$

(5)

where $\mathcal{K}$ is a constant. The most significant benefit of this technique is that it allows us to obtain the effective number of failures m while also ensuring that the overall test duration does not deviate too much from the pre-specified period T. Various investigations based on AT2-PH have been conducted; readers can refer for example to Nassar et al. [3], Panahi and Moradi [4], Elshahhat and Nassar [5], Panahi and Asadi [6], Alotaibi et al. [7], Alotaibi et al. [8], Ateya et al. [9] and references cited therein.

The originality of this work stems from the fact that, in the presence of incomplete sampling, it is the first time since the PRC distribution’s establishment that two maximum likelihood and Bayesian methods for its parameters of life have been compared. The impetus for this work stems from the relevance of the suggested censoring mechanism in boosting the efficacy of statistical inference when compared to Type-I (time) and Type-II (failure) censoring mechanisms. However, we are motivated to perform this work for two reasons: (i) the HRF of the PRC distribution exhibits a bathtub-shaped or decreasing shape, which is a preferable occurrence in many practical domains; (ii) the usefulness of AT2-PH censoring plan is that it provides flexibility in terminating experiments at a predetermined time and lowering total test length while retaining the desirable qualities of progressive design in practical reliability investigations. As far as we know, there is no treatment of inferred aspects of the RRC distribution, especially in reliability practice. The goal of this work, using AT2-PH censoring plan, is to address this gap by proving that the PRC lifespan model may be employed as a survival model. Thus, the present study has five objectives, which can be viewed as:

• The issue of estimating the model parameters ($\mu ,\gamma$) as well as the reliability indices ($R\left(t\right)$,$h\left(t\right)$) of the PRC distribution using maximum likelihood and Bayes estimation techniques from adaptive progressively hybrid Type-II censoring is addressed.
• Via independent gamma conjugate density priors, the Bayes estimates against the squared-error loss (SEL) of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ are evaluated through the Monte Carlo Markov-chain (MCMC) techniques.
• Approximate confidence interval (ACI) and highest posterior density (HPD) interval estimates of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ are also obtained.
• As anticipated, the analytical solutions of $\alpha$ or $\mu$ developed by the proposed estimation approaches cannot be represented in closed expressions, so in $\mathsf{R}$ programming software, ‘$\mathsf{maxLik}$’ (by Henningsen and Toomet [10]) and ‘$\mathsf{coda}$’ (by Plummer et al. [11]) packages are recommended to evaluate the offered estimates.
• Determine the most efficient progressively designed solution that delivers a substantial amount of information on the model parameter(s) of interest, depending on four distinct optimality criteria.
• Through a series of numerical comparisons, we assess the efficiency of the offered estimate in terms of root-mean-squared error, average relative absolute bias, average interval length and coverage probability simulated values.
• Two real-world engineering-data-sets-based applications demonstrate the PRC distribution’s capacity to fit various data types and adapt the offered methodologies to actual practical circumstances.

The remaining sections of the paper are: Non-Bayesian and Bayesian estimations are provided in Section 2 and Section 3, respectively. In Section 4, Monte Carlo outcomes are presented. Engineering applications are examined in Section 5. In Section 6, criteria for specifying the best progressive censoring are depicted. Lastly, the study concludes in Section 7.

2. Likelihood Estimation

The likelihood estimation method is used to evaluate the parameters of a probability distribution by maximizing the likelihood (or log-likelihood) function in order to make the observed data most probable for the statistical model. In general, the Expectation-Maximization (EM) approach is used to discover the local maximum likelihood parameters of a statistical model when latent variables are present or data are missing or incomplete; see Zhang et al. [12]. For brevity, the main advantages of the EM algorithm are: (i) it is guaranteed that the likelihood will increase on each iteration; (ii) the E-Step and M-Step are both easy for many problems; and (iii) the M-Step solution is often found in closed form. Unfortunately, the main drawbacks of the EM algorithm are: (i) its convergence is very slow; (ii) it achieves convergence to the local optima only; and (iii) it requires both forward and backward probabilities.

However, the likelihood methodology is considered in this section to provide the point ML and ACI estimates of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$. Suppose $\mathbf{y}$, is an AT2-PH censored sample taken from the PRC population whose PDF (1) and CDF (2) are given. Substituting (1) and (2) into (5), where $y_i$ is used, for instance, in place of $y_{i:m:n}$, the likelihood Function (5) becomes

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill L\left(\mathit{\sigma }\right|\mathbf{y})& \propto {\left({\gamma }^{-1}\mu e^{-\mu \overline{y}}\right)}^m{\left(1-{\xi }^{-1}(y_m;\mu ,\gamma )\right)}^{R_m}\hfill \\ & \times \prod _{i=1}^d{\left(1-{\xi }^{-1}(y_i;\mu ,\gamma )\right)}^{R_i}\prod _{i=1}^m{(1-e^{-\mu y_i})}^{-1}{\xi }^{-2}(y_i;\mu ,\gamma ),\hfill \end{array}\end{array}$$

(6)

where $\xi (y_i;\mu ,\gamma )=1-{\gamma }^{-1}log\left(1-e^{-\mu y_i}\right)$ for $i=1,2,\dots ,m$.

As a result, the natural logarithm of (6), symbolized by $\ell (·)\propto logL(·)$, is

$$\begin{array}{cc}\hfill \ell \left(\left.\mathit{\sigma }\right|\mathbf{y}\right)& \propto mlog\left({\gamma }^{-1}\mu e^{-\mu \overline{y}}\right)-\sum _{i=1}^{m}log(1-e^{-\mu y_i})-2\sum _{i=1}^{m}log\xi (y_i;\mu ,\gamma )\hfill \\ \hfill & +\sum _{i=1}^d{R}_{i}log\left(1-{\xi }^{-1}(y_i;\mu ,\gamma )\right)+R_{m}log\left(1-{\xi }^{-1}(y_m;\mu ,\gamma )\right).\hfill \end{array}$$

(7)

Consequently the MLEs $(\widehat{\mu },\widehat{\gamma })$ of $(\mu ,\gamma )$, from (7), can be derived directly by solution of the following normal formulas

$$\begin{array}{cc}\hfill \frac{\partial \ell }{\partial \mu }=m({\mu }^{-1}-\overline{y})& -{\sum }_{i=1}^m{y}_i{e}^{-\mu y_i}{(1-e^{-\mu y_i})}^{-1}-2{\sum }_{i=1}^m{\xi }^{\circ }(y_i;\mu ,\gamma ){\xi }^{-1}(y_i;\mu ,\gamma )\hfill \\ \hfill & +{\sum }_{i=1}^d{R}_i{\xi }^{\circ }(y_i;\mu ,\gamma ){\xi }^{-2}(y_i;\mu ,\gamma ){(1-{\xi }^{-1}(y_i;\mu ,\gamma ))}^{-1}\hfill \\ \hfill & +R_m{\xi }^{\circ }(y_m;\mu ,\gamma ){\xi }^{-2}(y_m;\mu ,\gamma ){(1-{\xi }^{-1}(y_m;\mu ,\gamma ))}^{-1}\hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill \frac{\partial \ell }{\partial \gamma }& =-m{\gamma }^{-1}-2{\sum }_{i=1}^m{\xi }^{•}(y_i;\mu ,\gamma ){\xi }^{-1}(y_i;\mu ,\gamma )\hfill \\ \hfill & +{\sum }_{i=1}^d{R}_i{\xi }^{•}(y_i;\mu ,\gamma ){\xi }^{-2}(y_i;\mu ,\gamma ){(1-{\xi }^{-1}(y_i;\mu ,\gamma ))}^{-1}\hfill \\ \hfill & +R_m{\xi }^{•}(y_m;\mu ,\gamma ){\xi }^{-2}(y_m;\mu ,\gamma ){(1-{\xi }^{-1}(y_m;\mu ,\gamma ))}^{-1},\hfill \end{array}$$

(9)

where ${\xi }^{\circ }(y_i;\mu ,\gamma )=-{\gamma }^{-1}{y}_i{e}^{-\mu y_i}{\left(1-e^{-\mu y_i}\right)}^{-1}$ and ${\xi }^{•}(y_i;\mu ,\gamma )={\gamma }^{-2}log\left(1-e^{-\mu y_i}\right)$.

It is obvious, from (8) and (9), that there are no closed-form expressions for the offered MLEs $\widehat{\mu }$ or $\widehat{\gamma }$. Given an AT2-PH censored sample, we recommend employing the Newton–Raphson technique by installing the ‘$\mathsf{maxLik}$’ package in $\mathsf{R}$ 4.2.2 software ($\mathsf{R}$ Foundation for Statistical Computing, Vienna, Austria) to evaluate the acquired $\widehat{\mu }$ and $\widehat{\gamma }$.

Once the values of $\widehat{\mu }$ and $\widehat{\gamma }$ obtained, via replacing $(\mu ,\gamma )$ by $(\widehat{\mu },\widehat{\gamma })$, we obtain the MLEs of $R\left(t\right)$ (3) and $h\left(t\right)$ (4), at a distinct $t>0$, respectively, as follows:

$$\widehat{R}\left(t\right)=1-{\left[1-{\widehat{\gamma }}^{-1}log(1-e^{-\widehat{\mu }t})\right]}^{-1},$$

and

$$\widehat{h}\left(t\right)=\frac{\widehat{\mu }{e}^{-\widehat{\mu }t}}{(1-e^{-\widehat{\mu }t})(-log(1-e^{-\widehat{\mu }t}))}{\left[1-{\widehat{\gamma }}^{-1}log(1-e^{-\widehat{\mu }t})\right]}^{-1}.$$

To build the $100(1-\alpha )\%$ ACIs of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$, the asymptotic behavior of each MLE is used. Following a large sample theory, the asymptotic distribution of the MLEs $(\widehat{\mu },\widehat{\gamma })$ is the normal distribution with mean $\left(\mathit{\sigma }\right)$ and 2 × 2 variance/covariance ${\mathbf{I}}^{-1}\left(\mathit{\sigma }\right)$ matrix. Following Lawless [13], using the observed Fisher information, we utilize ${\mathbf{I}}^{-1}\left(\widehat{\mathit{\sigma }}\right)$ to estimate ${\mathbf{I}}^{-1}\left(\mathit{\sigma }\right)$ as

$$\begin{array}{c}\hfill {\mathbf{I}}^{-1}\left(\widehat{\mathit{\sigma }}\right)={\left[\begin{array}{cc}-{\mathcal{I}}_{11}& -{\mathcal{I}}_{12}\\ -{\mathcal{I}}_{21}& -{\mathcal{I}}_{22}\end{array}\right]}_{\left(\mu ,\gamma \right)=\left(\widehat{\mu },\widehat{\gamma }\right)}^{-1}=\left[\begin{array}{cc}{\widehat{\nu }}_{11}& {\widehat{\nu }}_{12}\\ {\widehat{\nu }}_{21}& {\widehat{\nu }}_{22}\end{array}\right],\end{array}$$

(10)

where, in Appendix A, the Fisher elements ${\mathcal{I}}_{ij}$ for $i,j=1,2$ of (10) are reported.

Hence, the $100(1-\alpha )\%$ ACIs of $\mu$ and $\gamma$ can be obtained as follows:

$$\widehat{\mu }\mp z_{\frac{\alpha }{2}}\sqrt{{\widehat{\nu }}_{11}}\mathrm{and}\widehat{\gamma }\mp z_{\frac{\alpha }{2}}\sqrt{{\widehat{\nu }}_{22}},$$

(11)

respectively, where $z_{\frac{\alpha }{2}}$ is the $\left(\frac{\alpha }{2}\right)$th percentile of standard normal distribution.

Additionally, to create the $100(1-\alpha )\%$ ACIs of $R\left(t\right)$ and $h\left(t\right)$, the variances ${\widehat{\nu }}_R$ and ${\widehat{\nu }}_h$ of the MLEs $\widehat{R}\left(t\right)$ and $\widehat{h}\left(t\right)$ of $R\left(t\right)$ and $h\left(t\right)$, respectively, must be derived first. To achieve this aim, the delta technique, which is a generic strategy for estimating confidence intervals for any unknown parametric function, is considered. Following Greene [14], we estimate ${\widehat{\nu }}_R$ and ${\widehat{\nu }}_h$ of $\widehat{R}\left(t\right)$ and $\widehat{h}\left(t\right)$ as

$${\widehat{\nu }}_R\approx {\left[{\mathcal{M}}_R^{\top }{\mathbf{I}}^{-1}\left(\mathit{\sigma }\right){\mathcal{M}}_R\right]}_{(\widehat{\mu },\widehat{\gamma })}\mathrm{and}{\widehat{\nu }}_h\approx {\left[{\mathcal{M}}_h^{\top }{\mathbf{I}}^{-1}\left(\mathit{\sigma }\right){\mathcal{M}}_h\right]}_{(\widehat{\mu },\widehat{\gamma })},$$

respectively, where ${\mathcal{M}}_R=\left(\frac{\partial R}{\partial \mu }\frac{\partial R}{\partial \gamma }\right)$ and ${\mathcal{M}}_h=\left(\frac{\partial h}{\partial \mu }\frac{\partial h}{\partial \gamma }\right)$.

As a result, the respective ACIs of $R\left(t\right)$ and $h\left(t\right)$ at a confidence level $100(1-\alpha )$ are obtained, respectively, by

$$\widehat{R}\left(t\right)\mp z_{\frac{\alpha }{2}}\sqrt{{\widehat{\nu }}_R}\mathrm{and}\widehat{h}\left(t\right)\mp z_{\frac{\alpha }{2}}\sqrt{{\widehat{\nu }}_h}.$$

3. Bayes’ Estimation

The Bayes’ paradigm of statistical analysis has received substantial attention in recent decades as an efficient and useful alternative to the conventional ML approach. This section deals with deriving the Bayes estimators of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ in addition to their HPD intervals. To achieve this goal, we assume that the PRC parameters $\mu$ and $\gamma$ are stochastically independent and have gamma PDFs $Gamma({\theta }_1,{\beta }_1)$ and $Gamma({\theta }_2,{\beta }_2)$, respectively.

Thus, the joint prior PDF (say $\omega (·)$) of $\mu$ and $\gamma$ is

$$\omega (\mu ,\gamma )\propto {\mu }^{{\theta }_1-1}{\gamma }^{{\theta }_2-1}{e}^{-({\beta }_1\mu +{\beta }_2\gamma )},\mu ,\gamma >0,$$

(12)

where ${\theta }_j,{\beta }_j>0,j=1,2$ are the hyperparameters.

Loss functions play an important part in the Bayesian framework because they may be used to detect the overestimation and underestimating of a research of interest. We thus consider the most important loss, called the SEL function (say $l(·)$), which is given by

$$l\left(\tau ,\tilde{\tau }\right)={\left(\tilde{\tau }-\tau \right)}^2,$$

(13)

where $\tilde{\tau }$ denotes the symmetric Bayes estimates of $\tau$. Using (13), the Bayes estimator $\tilde{\tau }$ is provided directly by the posterior mean of $\tau$.

3.1. Posterior Distribution

Substituting (6) with (12) into the continuous Bayes’ theorem, the posterior PDF (say $\mathsf{\Omega }(·)$) of $\mu$ and $\gamma$ can be written as

$$\begin{array}{cc}\hfill \mathsf{\Omega }\left(\left.\mathit{\sigma }\right|\mathbf{y}\right)& ={\mathcal{G}}^{-1}{\mu }^{m+{\theta }_1-1}{e}^{-\mu \left({\beta }_1+\overline{y}\right)}{\gamma }^{{\theta }_2-m-1}{e}^{-{\beta }_2\gamma }{\left(1-{\xi }^{-1}(y_m;\mu ,\gamma )\right)}^{R_m}\hfill \\ \hfill & \times \prod _{i=1}^d{\left(1-{\xi }^{-1}(y_i;\mu ,\gamma )\right)}^{R_i}\prod _{i=1}^m{(1-e^{-\mu y_i})}^{-1}{\xi }^{-2}(y_i;\mu ,\gamma ),\hfill \end{array}$$

where $\mathcal{G}={\int }_0^{\infty }{\int }_0^{\infty }L\left(\mathit{\sigma }\right|\mathbf{y})\times \omega (\mu ,\gamma )\mathrm{d}\mu \mathrm{d}\gamma .$

It is obvious, from (14), that the Bayes estimators $\tilde{\mu }$ and $\tilde{\gamma }$ of $\mu$ and $\gamma$, respectively, cannot be formulated in closed form. As a result, the Bayes estimate may be approximated using the MCMC approach. To adopt this technique, the respective full conditional distributions of $\mu$ and $\gamma$ take the following forms

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_1\left(\left.\mu \right|\gamma ,\mathbf{y}\right)\propto {\mu }^{m+{\theta }_1-1}{e}^{-\mu \left({\beta }_1+\overline{y}\right)}{\left(1-{\xi }^{-1}(y_m;\mu ,\gamma )\right)}^{R_m}\prod _{i=1}^d{\left(1-{\xi }^{-1}(y_i;\mu ,\gamma )\right)}^{R_i}\prod _{i=1}^m{(1-e^{-\mu y_i})}^{-1}{\xi }^{-2}(y_i;\mu ,\gamma ),\end{array}$$

(14)

and

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_2\left(\left.\gamma \right|\mu ,\mathbf{y}\right)\propto {\gamma }^{{\theta }_2-m-1}{e}^{-{\beta }_2\gamma }{\left(1-{\xi }^{-1}(y_m;\mu ,\gamma )\right)}^{R_m}\prod _{i=1}^d{\left(1-{\xi }^{-1}(y_i;\mu ,\gamma )\right)}^{R_i}\prod _{i=1}^m{\xi }^{-2}(y_i;\mu ,\gamma ).\end{array}$$

(15)

As a result, the full conditional PDFs of $\mu$ and $\gamma$ cannot be reduced to any known density. So, acquiring samples straightforward of $\mu$ and $\gamma$ from (14) and (15), respectively, is unattainable. Plotting a random AT2-PH censored sample taken from the PRC$(0.5,0.2)$ population, when $(n,m,T)=(80,40,5)$ and $\mathbf{R}$ is uniform censoring, Figure 2 indicates that the full conditional PDFs of $\mu$ and $\gamma$ are similar to the normal density. Subsequently, we consider the normal PDF as the proposal model to derive the Bayes estimates as well as to derive the HPD intervals of $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$; see Gelman et al. [15] and Lynch [16] for further details.

Figure 2. Plots of the conditional PDFs of $\mu$ (left) and $\gamma$ (right).

3.2. Metropolis–Hastings Algorithm

To offer the Bayes point and HPD interval estimates, we propose to employ the following Metropolis–Hastings steps:

Step 1: 

Set the starting points of $(\mu ,\gamma )$ say $({\mu }^{\left(0\right)},{\gamma }^{\left(0\right)})=(\widehat{\mu },\widehat{\gamma })$.

Step 2: 

Set $k=1$.

Step 3: 

Obtain ${\mu }^{*}$ and ${\gamma }^{*}$ from (14) and (15) using the normal distributions $N(\widehat{\mu },{\widehat{\nu }}_{11})$ and $N(\widehat{\gamma },{\widehat{\nu }}_{22})$, respectively.

Step 4: 

Obtain ${\mathsf{\Psi }}_i,i=1,2$ as

$${\mathsf{\Psi }}_1=\frac{{\mathsf{\Omega }}_1\left(\left.{\mu }^{*}\right|{\gamma }^{(k-1)},\mathbf{y}\right)}{{\mathsf{\Omega }}_1\left(\left.{\mu }^{(k-1)}\right|{\gamma }^{(k-1)},\mathbf{y}\right)}\mathrm{and}{\mathsf{\Psi }}_2=\frac{{\mathsf{\Omega }}_2\left(\left.{\gamma }^{*}\right|{\mu }^{\left(k\right)},\mathbf{y}\right)}{{\mathsf{\Omega }}_2\left(\left.{\gamma }^{(k-1)}\right|{\mu }^{\left(k\right)},\mathbf{y}\right)},$$

Step 5: 

Obtain $u_i,i=1,2$ from a uniform $U(0,1)$ distribution.

Step 6: 

If $u_1⩽min\{1,{\mathsf{\Psi }}_1\}$, set ${\mu }^{\left(k\right)}={\mu }^{*}$; else, set ${\mu }^{\left(k\right)}={\mu }^{(k-1)}$.

Step 7: 

If $u_2⩽min\{1,{\mathsf{\Psi }}_2\}$, set ${\gamma }^{\left(k\right)}={\gamma }^{*}$; else, set ${\gamma }^{\left(k\right)}={\gamma }^{(k-1)}$.

Step 8: 

Obtain $R^{\left(k\right)}\left(t\right)$ and $h^{\left(k\right)}\left(t\right)$ for $t>0$, respectively, as

$$R^{\left(k\right)}\left(t\right)=1-{\left[1-{{\gamma }^{\left(k\right)}}^{-1}log(1-e^{-{\mu }^{\left(k\right)}t})\right]}^{-1},$$

and

$$h^{\left(k\right)}\left(t\right)=\frac{{\mu }^{\left(k\right)}{e}^{-{\mu }^{\left(k\right)}t}}{(1-e^{-{\mu }^{\left(k\right)}t})(-log(1-e^{-{\mu }^{\left(k\right)}t}))}{\left[1-{{\gamma }^{\left(k\right)}}^{-1}log(1-e^{-{\mu }^{\left(k\right)}t})\right]}^{-1}.$$

Step 9: 

Set $k=k+1$.

Step 10: 

Repeat Steps 2–8 $\mathcal{B}$ times and ignore the first ${\mathcal{B}}^{•}$ draws as ‘burn-in’ to obtain

$$\left[{\mu }^{({\mathcal{B}}^{•}+1)},{\gamma }^{({\mathcal{B}}^{•}+1)},R^{({\mathcal{B}}^{•}+1)}\left(t\right),h^{({\mathcal{B}}^{•}+1)}\left(t\right)\right],\dots ,\left[{\mu }^{\left(\mathcal{B}\right)},{\gamma }^{\left(\mathcal{B}\right)},R^{\left(\mathcal{B}\right)}\left(t\right),h^{\left(\mathcal{B}\right)}\left(t\right)\right].$$

Step 11: 

Get the Bayes estimates of $\mu$, $\gamma$, $R\left(t\right)$, or $h\left(t\right)$ (say $\tau$) as

$$\begin{array}{c}\hfill \tilde{\tau }=\frac{1}{\mathcal{B}-{\mathcal{B}}^{•}}{\sum }_{k={\mathcal{B}}^{•}+1}^M{\tau }^{\left(k\right)},\end{array}$$

Step 12: 

Create the $100(1-\alpha )\%$ HPD interval of $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$ (say $\tau$) as:

(a)

Sort the MCMC draws of ${\tau }^{\left(k\right)}$ for $k={\mathcal{B}}^{•}+1,{\mathcal{B}}^{•}+2,\dots ,{\mathcal{B}}^{•}$ as

$$\begin{array}{c}\hfill {\tau }_{({\mathcal{B}}^{•}+1)},{\tau }_{({\mathcal{B}}^{•}+2)},\dots ,{\tau }_{\left(\mathcal{B}\right)}.\end{array}$$

(b)

Obtain the $100(1-\alpha )\%$ two-sided HPD interval of $\tau$ as

$$\begin{array}{c}\hfill \left({\tau }_{\left(k^{*}\right)},{\tau }_{\left(k^{*}+\left(1-\alpha \right)\left(\mathcal{B}-{\mathcal{B}}^{•}\right)\right)}\right),\end{array}$$

where $k^{*}={\mathcal{B}}^{•}+1,{\mathcal{B}}^{•}+2,\dots ,M$ is chosen such that

$${\tau }_{\left(k^{*}+\left[\left(1-\alpha \right)\left(\mathcal{B}-{\mathcal{B}}^{•}\right)\right]\right)}-{\tau }_{\left(k^{*}\right)}=\underset{1⩽k⩽\alpha \left(\mathcal{B}-{\mathcal{B}}^{•}\right)}{min}\left({\tau }_{\left(k+\left[\left(1-\gamma \right)\left(\mathcal{B}-{\mathcal{B}}^{•}\right)\right]\right)}-{\tau }_{\left(k\right)}\right).$$

where the largest integer less than or equal to e is denoted by $\left[e\right]$, Chen and Shao [17].

4. Numerical Comparisons

To assess the validity of the obtained point and interval estimations of the PRC’s parameters and reliability features such as RF $R\left(t\right)$ and HRF $h\left(t\right)$, for $t>0$, presented in the preceding sections, based on various scenarios, this section demonstrates extensive Monte Carlo simulations.

4.1. Simulation Scenarios

This subsection exhibits several censoring designs, in turn, to examine the behavior of acquired estimators, based on the proposed censored data. To do this, based on various choices of T (threshold point), n (total number of items on the test), m (size of censored sample) and $\mathbf{R}$ (progressive design), we replicate 1000 AT2-PH samples from different sets of $\mathrm{PRC}(\mu ,\gamma )$, namely; Set-A:$\mathrm{PRC}$ (0.2, 0.5) and Set-B:$\mathrm{PRC}$ (1.5, 1). Fixing $t=0.1$, the plausible values of $\left(R\right(t),h(t\left)\right)$ are taken as (0.8869, 0.2854) and (0.6634, 1.5825) using Set-A and -B, respectively. Taking $T(=2,5)$ and $n(=40,80)$, we obtain m as a failure percentage (FP%) for each n such as $\frac{m}{n}\times 100\%$ (=50, 80)%. Clearly, the test is terminated when FP% achieves the pre-specified 50% (or 80%). Further, three different scenarios of progressive patterns $\mathbf{R}$ are used, namely:

$$\begin{array}{cc}& \mathrm{Scheme}\text{-}1:\mathbf{R}=\left(n-m,0^{*}(m-1)\right),\hfill \\ & \mathrm{Scheme}\text{-}2:\mathbf{R}=\left(0^{*}\left(0.5m-1\right),n-m,0^{*}\left(0.5m\right)\right),\hfill \\ & \mathrm{and}\hfill \\ & \mathrm{Scheme}\text{-}3:\mathbf{R}=\left(0^{*}(m-1),n-m\right),\hfill \end{array}$$

where $0^{*}(m-1)$ represents 0 is repeated $m-1$ times.

Specifically, to obtain a AT2-PH censored sample of size m from the PRC model, after assigning T, n and $\mathbf{R}$, do the following procedure:

Step 1: 

Set the specified actual values of $\mathrm{PRC}(\mu ,\gamma )$.

Step 2: 

Obtain an ordinary T2-P censored sample as:

(a)

Simulate $\kappa$ independent items (say ${\kappa }_1,{\kappa }_2,\dots ,{\kappa }_m$) from uniform $U(0,1)$ distribution.

(b)

Set ${\varrho }_i={\kappa }_i^{{\left(i+{\sum }_{l=m-i+1}^m{R}_l\right)}^{-1}},$ for $i=1,2,\dots ,m.$

(c)

Set $U_i=1-{\varrho }_m{\varrho }_{m-1}\dots {\varrho }_{m-i+1}$ for $i=1,2,\dots ,m$.

(d)

Collect a T2-P censored sample (with size m) from $\mathrm{PRC}(\mu ,\gamma )$ distribution by setting

$$Y_i=-{\mu }^{-1}log\left(1-e^{\gamma (1-u_i^{-1})}\right),i=1,2,\dots ,m.$$

Step 3: 

Determine d at predetermined T.

Step 4: 

Discard the remaining sample $(Y_{d+2},\dots ,Y_m)$ when $T<Y_m$.

Step 5: 

Use the truncated $f(y;\mu ,\gamma ){\left[1-F(y_{d+1};\mu ,\gamma )\right]}^{-1}$ distribution to obtain $(Y_{d+2},\dots ,Y_m)$ order statistics with size $n-d-{\sum }_{l=1}^d{R}_l-1$.

To do the required computations of the acquired Bayes point (or interval) estimates, according to Kundu [18], we assign different priors to the values of the hyperparameters $({\theta }_1,{\theta }_2,{\beta }_1,{\beta }_2)$ as follows:

• For Set-A: Pr.1:(1,2.5,5,5) and Pr.2:(2,5,10,10);
• For Set-B: Pr.1:(7.5,5,5,5) and Pr.2:(15,10,10,10).

Following the Bayes’ MCMC technique described in Section 3, to remove of the affection for the starting choice, the first 2000 (from the total 12,000 MCMC iterations) are removed. One the target 1000 AT2-PH samples collected, by installing ‘$\mathsf{maxLik}$’ and ‘$\mathsf{coda}$’ packages (by Henningsen and Toomet [10] and Plummer et al. [11], respectively) in $\mathsf{R}$ 4.2.2 software, the maximum likelihood and Bayes MCMC estimates (in addition to their 95% ACI and HPD interval estimates) of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ are evaluated.

Though MCMC is a powerful technique for evaluating complex models and posterior distributions in statistical programming, it needs thorough verification and adjustment to assure its validity and efficiency. Before proceeding, in Bayes’ history, various plotting tools for visualizing the convergence of MCMC drawn from the posterior density of the parameters of a studied model are suggested. There are two MCMC diagnostics, namely:

(i)

Brooks–Gelman–Rubin (BGR): It measures a chain’s convergence by comparing the variances within and between chains.

(ii)

Trace (with thinning): It shows the sampled values per chain and node throughout iterations.

The thinning procedure entails selecting separate points from the sample at each predetermined phase in order to produce an independent sample; see for example Riabiz et al. [19]. Here, we take each 5th point (for instance) for thinning procedure. For instance, from both given sets A and B, we draw 12,000 samples from the joint posterior PDF of $\mu$ and $\gamma$ using Scheme-1, Pr.1, $(n,m)=(40,20)$ and $T=2$ (as an example); see Figure 3. It highlights that the MCMC draws displayed in each chain are sufficiently mixed, and the length of the draws removed at the start of each chain (burn) is sufficient to reduce autocorrelation. It also shows there are no differences among the variances within and between chains. As a result, the acquired estimations are reliable.

Figure 3. Trace (with Gaussian kernel) and BGR plots of $\mu$ and $\gamma$ in Monte Carlo simulation.

Practically, the average estimates (Av.Es) for the theoretical point estimators of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ (say $\rho$) derived from frequentist (or Bayes) approach are given by

$${\overline{\check{\rho }}}_q=\frac{1}{1000}\sum _{i=1}^{1000}{\check{\rho }}_q^{\left(i\right)},$$

where ${\check{\rho }}^{\left(i\right)}$ is the computed estimate of $\rho$ at ith sample, ${\rho }_1=\mu$, ${\rho }_2=\gamma$, ${\rho }_3=R\left(t\right)$ and ${\rho }_4=h\left(t\right)$.

Comparing the acquired point estimates of $\rho$ is carried out based on their root mean squared-errors (RMSEs) and average relative absolute biases (ARABs) as

$$\mathrm{RMSE}\left({\check{\rho }}_q\right)=\sqrt{\frac{1}{1000}\sum _{i=1}^{1000}{\left({\check{\rho }}^{\left(i\right)}-\rho \right)}^2},$$

and

$$\mathrm{ARAB}\left({\check{\rho }}_q\right)=\frac{1}{1000}\sum _{i=1}^{1000}\frac{1}{{\rho }_q}\left|{\check{\rho }}_q^{\left(i\right)}-{\rho }_q\right|,$$

respectively.

On the other hand, the acquired 95% ACI and HPD interval estimates obtained of $\rho$ are compared based on their average confidence lengths (ACLs) and coverage percentages (CPs) as

$${\mathrm{ACL}}_{(1-\alpha )\%}\left(\rho \right)=\frac{1}{1000}\sum _{i=1}^{1000}\left({\mathcal{U}}_{{\check{\rho }}_q^{\left(i\right)}}-{\mathcal{L}}_{{\check{\rho }}_q^{\left(i\right)}}\right),$$

and

$${\mathrm{CP}}_{(1-\alpha )\%}\left(\rho \right)=\frac{1}{1000}\sum _{i=1}^{1000}{{\mathbf{J}}^{•}}_{\left({\mathcal{L}}_{{\check{\rho }}_q^{\left(i\right)}};{\mathcal{U}}_{{\check{\rho }}_q^{\left(i\right)}}\right)}\left(\rho \right),$$

respectively, where ${\mathbf{J}}^{•}(·)$ refers the indicator operator and $\left(\mathcal{L}\right(·),\mathcal{U}(·\left)\right)$ refers the (lower-limit, upper-limit) of the interval estimator.

4.2. Simulation Results

A heatmap (or heat-map) is a popular tool for data visualization. It is described as a visual representation of data in which individual values in a matrix are shown by colors. So, via a heatmap tool, this subsection presents the simulated RMSE, ARAB, ACL and CP values of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ in Figure 4, Figure 5, Figure 6 and Figure 7. To better distinguish the methods, in Figure 4, Figure 5, Figure 6 and Figure 7, the proposed estimation methods are defined on the ‘$\mathsf{x}\text{-}\mathsf{axis}$’ line while the proposed censored test (referred by “T-n[FP%]-Scheme”) is defined on the ‘$\mathsf{y}\text{-}\mathsf{axis}$’ line. For each elegant heatmap, the values of the RMSE, ARAB, ACL, or CP are specified using colors from yellow (lowest values) to red (highest values). In each heat-map, for distinguishing, using Pr.1 (as an example), the Bayes estimator using Pr.1 is symbolized by “BE-Pr.1” and the HPD estimator is symbolized by “HPD-Pr.1”. In the Supplementary Materials, the numerical outcomes of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ are provided.

Figure 4. Heatmap for the inferred results of $\mu$.

Figure 5. Heatmap for the inferred results of $\gamma$.

Figure 6. Heatmap for the inferred results of $R\left(t\right)$.

Figure 7. Heatmap for the inferred results of $h\left(t\right)$.

From Figure 4, Figure 5, Figure 6 and Figure 7, for the smallest RMSE, ARAB and ACL values as well as the largest values of CP, we draw several comments on the behavior of $\sigma$, $R\left(t\right)$ and $h\left(t\right)$ as follows:

• All acquired estimates of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ show superior behavior and provide more efficient results.
• As n (or m) grows, for $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$, the offered Bayesian and classical estimates perform well. A similar pattern is also noted when the total number of the removal items, i.e., ${\sum }_{l=1}^m{R}_l$, decreases.
• As $T_i,i=1,2$ increases, it can be noted that

  (i)

  For Set-A: The RMSE, ARAB and ACL values developed from the maximum likelihood (or Bayes’) approach of $\mu$ decrease while those of $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ increase.

  (ii)

  For Set-B: The RMSE, ARAB and ACL values developed from the maximum likelihood (or Bayes’) approach of $\mu$ and $\gamma$ decrease while those of $R\left(t\right)$ and $h\left(t\right)$ increase.

  (iii)

  The opposite result of (i)–(ii) is observed when comparing the acquired ACI (or HPD interval) estimators in relation to their CPs.

• As $\mu$ and $\gamma$ increase, it is clear that

  (i)

  For Set-A (or Set-B): The RMSE and ARAB values created from the maximum likelihood (or Bayes’) estimates of $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$ increase.

  (ii)

  For Set-A (or Set-B): The ACL values created from the asymptotic (or HPD interval) estimates of $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$ increase. The opposite pattern is also recorded if acquired ACI (or HPD interval) estimators are compared in terms of their CPs.

• Comparing the proposed schemes 1, 2 and 3, it is observed that

  (i)

  For Set-A: The offered estimates of $\mu$, $\gamma$ and $R\left(t\right)$ perform satisfactorily via Scheme-1 ‘left-censoring’ whereas those of $h\left(t\right)$ perform satisfactorily via Scheme-3 ‘right-censoring’ than others.

  (ii)

  For Set-B: The offered estimates of $\mu$ and $h\left(t\right)$ perform satisfactorily via Scheme-3 ‘right-censoring’ whereas those of $\gamma$ and $R\left(t\right)$ perform satisfactorily via Scheme-1 ‘left-censoring’ than others.

• From Set-A (or Set-B), since Pr.2’s variance is smaller than Pr.1’s variance, the Bayes’ evaluations employing Prior-2 produce more reliable estimations than others for all unknown parameters.
• Due to the fact that the offered Bayes’ estimates involved more priority information compared to the competitive frequentist estimates, the Bayes estimates of $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$ showed better behavior compared to others.
• As a consequence, in the case of data created using an adaptive Type-II gradually hybrid technique, the Bayes M-H methodology is advised for assessing the PRC parameters or its reliability time features.

5. Engineering Applications

In this section, we will give two real data sets from the engineering sector to analyze the capacity to adapt the research objectives to actual situations and to demonstrate the flexibility and superiority of the suggested lifespan model.

5.1. Industrial Devices Data Analysis

This application provides an analysis of the lifetimes of fifty industrial devices put on life test at time zero, given by Aarset [20] and reanalyzed by Elshahhat and Nassar [5]; see Table 1. The main feature of this type of data is that it presents a bathtub-shaped failure rate.

Table 1. Failure times of 50 industrial devices.

0.1	0.2	1	1	1	1	1	2	3	6
7	11	12	18	18	18	18	18	21	32
36	40	45	45	47	50	55	60	63	63
67	67	67	67	72	75	79	82	82	83
84	84	84	85	85	85	85	85	86	86

Just before going any further, we shall fit the PRC model to the complete industrial devices data set along with seven other statistical models in the literature as its competitors, namely: (1) alpha-power exponential ($\mathrm{APE}(\mu ,\gamma )$) by Mahdavi and Kundu [21]; (2) log-logistic ($\mathrm{LoL}(\mu ,\gamma )$) by Johnson et al. [22]; (3) Nadarajah–Haghighi $\mathrm{NH}(\mu ,\gamma )$ by Nadarajah and Haghighi [23]; (4) generalized exponential $\mathrm{GE}(\mu ,\gamma )$ by Gupta and Kundu [24]; (5) Weibull $\mathrm{W}(\mu ,\gamma )$ by Weibull [25]; (6) gamma $\mathrm{G}(\mu ,\gamma )$ by Johnson et al. [22]; and (7) exponential ($\mathrm{E}\left(\mu \right)$) by Johnson et al. [22] distributions.

To highlight the best model, besides the Kolmogorov–Smirnov (K–S) distance (along its p-value), several measures of fit are taken into account, namely: negative log-likelihood (NL), Akaike (A), Bayesian (B), consistent Akaike (CA), Hannan–Quinn (HQ), Anderson–Darling (A–D) and Cramér–von Mises (CvM). By installing the ‘$\mathsf{AdequacyModel}$’ package, by Marinho et al. [26] in $\mathsf{R}$ 4.2.2 software, all suggested criteria are evaluated through the ML approach. So, Table 2 displays the MLEs (along with their standard–errors (St.Es)) of $\mu$ and $\gamma$, as well as the fitted results of the PRC model and other competing models. It shows that the PRC model fits the industrial devices data adequately and that the PRC model is the best compared to other distributions because it provides the lowest value of all proposed statistics and the highest p-value.

Table 2. Results of fit of the PRC and its competitive models from industrial devices data.

Model	MLE(St.E)		NL	A	B	CA	K–S (p-Value)
				HQ	A–D	CvM
	$\mathit{\mu }$	$\mathit{\gamma }$
PRC	0.0384 (0.0059)	0.2160 (0.0881)	234.7804	473.561	477.385	473.816	0.1484 (0.2209)
				475.017	2.13398	0.32793
APE	6.5479 (17.940)	0.0307 (0.0117)	241.1075	486.215	490.039	486.470	0.1587 (0.1609)
				487.671	2.56896	0.41510
LoL	1.0880 (0.1334)	29.937 (6.7031)	251.0748	506.150	509.974	506.405	0.2408 (0.0061)
				507.606	4.03382	0.69540
NH	2.2030 (0.5870)	0.0074 (0.0024)	238.3326	480.665	484.489	480.921	0.1738 (0.0976)
				482.122	2.55577	0.41148
GE	0.7804 (0.1351)	0.0187 (0.0036)	239.9734	483.947	487.771	484.202	0.2045 (0.0305)
				485.403	2.94197	0.48371
W	0.9487 (0.1195)	44.793 (6.9216)	240.9797	485.959	489.783	486.215	0.1937 (0.0469)
				487.416	3.00024	0.49469
G	0.7991 (0.1375)	0.0175 (0.0041)	240.1683	484.337	488.161	484.592	0.2024 (0.0333)
				485.793	2.96249	0.48758
E	0.0219 (0.0031)	-	241.068	484.135	486.047	484.219	0.1915 (0.0512)
				484.864	2.95454	0.48605

Additionally, based on the full industrial devices data set, the superiority of the PRC model is examined via various graphical plot tools, namely: (a) probability–probability (PP); (b) estimated PDFs; and (c) estimated/empirical RFs; see Figure 8. It supports the same findings provided in Table 2. To show the existence and uniqueness characteristics of the acquired ML estimates of the PRC parameters $\mu$ and $\gamma$, based on the full industrial devices data set, the contour plot of the natural logarithm of the likelihood function for different options of $\mu$ and $\gamma$ is shown in Figure 8d. It shows that the MLEs $\widehat{\mu }$ and $\widehat{\gamma }$ exist and are unique.

Figure 8. The PP (a), Fitted PDF (b) Fitted RF (c), Contour of log-likelihood (d,e) scaled–TTT transform from industrial devices data.

Henceforward, to run any additional calculations based on the industrial devices data, we propose considering these values as suitable starting points. We recommend using the acquired estimates $\widehat{\mu }\approx 0.0384$ and $\widehat{\gamma }\approx 0.2160$ as starting points for any future computations based on the data from industrial devices. Moreover, Figure 8e demonstrates the estimated/empirical scaled–TTT transform of the PRC lifetime distribution and indicates that the PRC failure rate model provides a bathtub-shaped failure rate.

Now, to evaluate the offered estimators in the presence of industrial devices data, various AT2-PH samples of size $m=25$, using different choices of T and $\mathbf{R}$, are created and listed in Table 3. For each artificial sample, the maximum likelihood and Bayes’ MCMC estimates (with their St.Es) in addition to the associated 95% two-sided ACI/HPD-interval estimates (with their lengths) of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ (at $t=1$) are obtained; see Table 4.

Table 3. Various AT2-PH samples from industrial devices data.

Sample	$\mathbf{T}\left(\mathbf{d}\right)$	R	${\mathit{R}}_{\mathit{m}}$	Censored Data
S[1]	0.5 (2)	$(5^5,0\ast 20)$	15	0.1, 0.2, 1, 1, 1, 1, 2, 3, 6, 7, 11, 12, 18, 18, 18, 21, 32, 36, 40, 45, 45, 47, 50, 55, 60
S[2]	15 (13)	$(0\ast 10,5^5,0\ast 10)$	10	0.1, 0.2, 1, 1, 1, 1, 1, 2, 3, 6, 7, 11, 12, 18, 18, 18, 21, 32, 36, 40, 47, 50, 55, 60, 63
S[3]	60 (24)	$(0\ast 20,5^5)$	5	0.1, 0.2, 1, 1, 1, 1, 1, 2, 3, 6, 7, 11, 12, 18, 18, 18, 18, 18, 21, 32, 36, 40, 45, 50, 67

Table 4. Estimates of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ from industrial devices data.

Sample	Par.	MLE		MCMC		ACI			HPD
		Est.	St.E	Est.	St.E	Lower	Upper	Length	Lower	Upper	Length
S[1]	$\mu$	0.0237	0.0073	0.0094	0.0380	0.0286	0.0233	0.0034	0.0167	0.0300	0.0133
	$\gamma$	0.4577	0.2020	0.0618	0.8536	0.7918	0.4575	0.0050	0.4474	0.4671	0.0197
	$R\left(1\right)$	0.8913	0.0370	0.8187	0.9638	0.1451	0.8919	0.0039	0.8843	0.8994	0.0150
	$h\left(1\right)$	0.0286	0.0084	0.0122	0.0451	0.0329	0.0283	0.0020	0.0243	0.0322	0.0079
S[2]	$\mu$	0.0275	0.0079	0.0121	0.0429	0.0308	0.0271	0.0036	0.0202	0.0343	0.0141
	$\gamma$	0.4059	0.1680	0.0766	0.7352	0.6586	0.4055	0.0050	0.3956	0.4152	0.0196
	$R\left(1\right)$	0.8989	0.0327	0.8349	0.9629	0.1280	0.8994	0.0035	0.8928	0.9064	0.0136
	$h\left(1\right)$	0.0276	0.0078	0.0124	0.0429	0.0304	0.0274	0.0019	0.0238	0.0311	0.0073
S[3]	$\mu$	0.0208	0.0072	0.0067	0.0349	0.0282	0.0204	0.0033	0.0141	0.0268	0.0128
	$\gamma$	0.4573	0.1957	0.0737	0.8409	0.7672	0.4570	0.0050	0.4471	0.4666	0.0195
	$R\left(1\right)$	0.8946	0.0342	0.8277	0.9616	0.1339	0.8953	0.0040	0.8877	0.9032	0.0155
	$h\left(1\right)$	0.0269	0.0073	0.0125	0.0412	0.0287	0.0265	0.0021	0.0227	0.0306	0.0079

Since no a priori information about the PRC parameters $\mu$ and $\gamma$ is available, the Bayes’ evaluations are developed based on 50,000 MCMC iterations, the first 10,000 of which are considered as ‘burn-in’. It can be shown that the point and interval estimates obtained using the MCMC method are quite close to those created using the maximum likelihood approach. Remaining 40,000 draws of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ are used to evaluate several properties of each unknown parameter including: mean, mode, (1st, 2nd, 3rd) quartiles denoted by ${\mathcal{Q}}_i,i=1,2,3$, standard deviation (St.D) and skewness (Skew.); see Table 5. It appears that the findings of central tendency are relatively near to one other.

Table 5. Characteristics of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ from industrial devices data.

Sample	Par.	Mean	Mode	${\mathcal{Q}}_1$	${\mathcal{Q}}_2$	${\mathcal{Q}}_3$	St.D	Skew.
S[1]	$\mu$	0.02335	0.02296	0.02102	0.02330	0.02562	0.00340	0.09963
	$\gamma$	0.45752	0.45071	0.45416	0.45752	0.46089	0.00500	$-0.01970$
	$R\left(1\right)$	0.89190	0.89021	0.88926	0.89183	0.89443	0.00384	0.12186
	$h\left(1\right)$	0.02834	0.02787	0.02698	0.02834	0.02972	0.00202	$-0.02828$
S[2]	$\mu$	0.02708	0.02514	0.02461	0.02702	0.02954	0.00361	0.07485
	$\gamma$	0.40554	0.40020	0.40211	0.40551	0.40894	0.00501	0.02838
	$R\left(1\right)$	0.89944	0.90230	0.89707	0.89939	0.90177	0.00347	0.09654
	$h\left(1\right)$	0.02738	0.02611	0.02612	0.02739	0.02865	0.00187	$-0.02191$
S[3]	$\mu$	0.02042	0.01820	0.01815	0.02034	0.02265	0.00328	0.10599
	$\gamma$	0.45699	0.45523	0.45358	0.45696	0.46039	0.00501	0.02319
	$R\left(1\right)$	0.89533	0.89355	0.89260	0.89525	0.89797	0.00398	0.14052
	$h\left(1\right)$	0.02655	0.02551	0.02517	0.02655	0.02795	0.00203	$-0.04074$

Trace and MCMC frequencies (with Gaussian kernel) plots, based on the staying 40,000 MCMC variates of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$, are shown in Figure 9. In each MCMC plot, to distinguish, the Bayes estimate (or sample mean) and HPD interval limits are displayed with horizontal solid and dashed lines, respectively. It reveals that the MCMC process converges successfully and that deleting the first 10,000 samples as burn-in is an adequate size to remove the influence of the starting values. It is also evident from the estimates that the acquired estimates of $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$ are fairly symmetric.

Figure 9. Density (left) and Trace (right) plots of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ from industrial devices data.

5.2. Aircraft Windshield Data Analysis

A big aircraft’s windscreen is a sophisticated piece of equipment made up of multiple layers of material, including a highly tough outer skin with a heated layer just behind it. These objects’ failures are not structural failures and do not cause aircraft damage, but they do require that the windscreen be repaired. This application provides an analysis of the remaining 65 service times of windshields that had not failed at the time of observation. This application provides an analysis of 63 observations of windshields’ service times for a particular windshield model; see Murthy et al. [27]. In Table 6, aircraft windshield service times (AWSTs) are displayed.

Table 6. Aircraft windshield service times.

0.046	0.140	0.150	0.248	0.280	0.313	0.389	0.487	0.622	0.900
0.952	0.996	1.003	1.010	1.085	1.092	1.152	1.183	1.244	1.249
1.262	1.436	1.492	1.580	1.719	1.794	1.915	1.920	1.963	1.978
2.053	2.065	2.117	2.137	2.141	2.163	2.183	2.240	2.341	2.435
2.464	2.543	2.592	2.600	2.670	2.717	2.819	2.820	2.878	2.950
3.003	3.102	3.304	3.483	3.500	3.622	3.665	3.695	4.015	4.628
4.806	4.881	5.140

As described in Section 5.1, just like our comparison of the PRC model and its competitive (including: APE, LoL, NH, GE, W, G and E) distributions, here we shall calculate the suggested measures of model selection (including: NL, A, B, CA, HQ, A–D, CvM and K–S (p-value)) based on the complete AWST data; see Table 7. It demonstrates that the PRC model gives the lowest values with regard to the NL, A, B, CA, HQ, A–D, CvM and K–S statistics, except for the highest p-value among all fitted lifetime models. As a result, from the AWST data, the PRC model is the best choice. Further, Figure 10 displays the PP, estimated PDFs, estimated/empirical RFs, contour plot of the log-likelihood function and estimated/empirical scaled–TTT transform plots. As we anticipated, Figure 10a–c supports the same facts provided by Table 7. Figure 8d shows that the acquired ML estimates $\widehat{\mu }\approx 1.2648$ and $\widehat{\gamma }\approx 0.0829$ existed and are unique. These offered estimates can be easily utilized as starting points for any forthcoming assessments in presence of the complete AWST data. Furthermore, Figure 8e indicates that the AWST data have an increasing failure rate, which is one of the common PRC failure rates.

Table 7. Results of fit of the PRC and its competitive models from AWST data.

Model	MLE(St.E)		NL	A	B	CA	K–S (p-Value)
				HQ	A–D	CvM
	$\mathit{\mu }$	$\mathit{\gamma }$
PRC	1.2649 (0.1551)	0.0830 (0.0329)	99.6012	203.202	207.489	203.402	0.0652 (0.9356)
				204.888	0.22701	0.03013
APE	21.339 (14.195)	0.8551 (0.0972)	100.430	204.860	209.146	205.060	0.1167 (0.3315)
				206.546	0.60220	0.09895
LoL	2.1352 (0.2312)	1.8015 (0.1809)	108.742	221.485	225.771	221.685	0.1199 (0.3012)
				223.170	1.97884	0.32711
NH	7.3061 (2.9223)	0.0447 (0.0192)	100.886	205.773	210.059	205.973	0.1483 (0.1127)
				207.458	0.44358	0.07303
GE	1.8978 (0.3402)	0.6921 (0.0942)	103.547	211.093	215.380	211.293	0.1438 (0.1340)
				212.779	1.23153	0.20347
W	1.6327 (0.1686)	2.3124 (0.1866)	100.318	204.636	208.922	204.836	0.1078 (0.4270)
				206.322	0.62980	0.10395
G	1.9085 (0.3148)	0.9152 (0.1725)	102.833	209.665	213.951	209.865	0.1387 (0.1613)
				211.351	1.11174	0.18364
E	0.4796 (0.0604)	-	109.299	220.597	222.740	220.663	0.2078 (0.0073)
				221.440	1.12643	0.18614

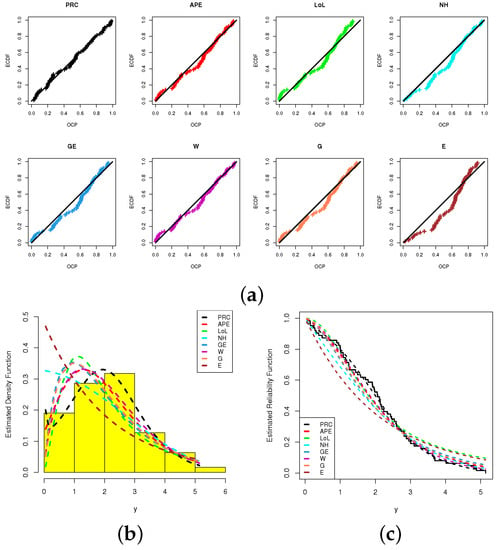
Figure 10. The PP (a), Fitted PDF (b) Fitted RF (c), Contour of log-likelihood (d), (e) scaled–TTT transform from AWST data.

To obtain the acquired estimates of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$, using $m=33$ along with different selects of T and $\mathbf{R}$, three artificial AT2-PH samples are collected from the AWST data and provided in Table 8. Using S[i] for $i=1,2,3$, the frequentist and Bayes estimates (with their St.Es) as well as the 95% ACI and HPD-interval estimates (with their lengths) of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ (at $t=0.1$) are calculated; see Table 9. Recall that the acquired Bayes point and HPD interval estimates, based on 50,000 MCMC iterations (when the first 10,000 iterations are taken as ‘burn-in’), are carried out using non-informative priors. As a result, Table 9 shows that the point (or interval) estimates of $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$ obtained by considered maximum likelihood and Bayes’ estimation methodologies are high similar to each other. This finding is due to the fact that the MCMC calculations are implemented based on improper gamma densities. Again, using S[i] for $i=1,2,3$ created from AWST data, the same properties reported in Table 5 are re-computed and presented in Table 10. The results of the central tendency, reported in Table 10, appear to be quite close to one another and support the same findings listed in Table 5.

Table 8. Various AT2-PH samples from AWST data.

Sample	$\mathit{T}\left(\mathit{d}\right)$	R	${\mathit{R}}_{\mathit{m}}$	Censored Data
S[1]	0.1 (1)	$({10}^3,0\ast 30)$	20	0.046, 0.140, 0.150, 0.248, 0.280, 0.313, 0.389, 0.487, 0.622, 0.900, 0.952,
				0.996, 1.003, 1.010, 1.092, 1.152, 1.183, 1.244, 1.262, 1.436, 1.492, 1.580,
				1.719, 1.915, 1.920, 1.978, 2.053, 2.065, 2.117, 2.137, 2.141, 2.163, 2.240
S[2]	1.2 (17)	$(0\ast 15,{10}^3,0\ast 15)$	10	0.046, 0.140, 0.150, 0.248, 0.280, 0.313, 0.389, 0.487, 0.622, 0.900, 0.952,
				0.996, 1.003, 1.010, 1.085, 1.092, 1.183, 1.244, 1.249, 1.262, 1.436, 1.580,
				1.719, 1.794, 1.978, 2.053, 2.141, 2.163, 2.341, 2.435, 2.543, 2.592, 2.600
S[3]	2.2 (33)	$(0\ast 30,{10}^3)$	0	0.046, 0.140, 0.150, 0.248, 0.280, 0.313, 0.389, 0.487, 0.622, 0.900, 0.952,
				0.996, 1.003, 1.010, 1.085, 1.092, 1.152, 1.183, 1.244, 1.249, 1.262, 1.436,
				1.492, 1.580, 1.719, 1.794, 1.915, 1.920, 1.963, 1.978, 2.053, 2.065, 2.117

Table 9. Estimates of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ from AWST data.

Sample	Par.	MLE		MCMC		ACI			HPD
		Est.	St.E	Est.	St.E	Lower	Upper	Length	Lower	Upper	Length
S[1]	$\mu$	1.2865	0.2411	0.8139	1.7590	0.9450	1.2862	0.0050	1.2763	1.2958	0.0195
	$\gamma$	0.0912	0.0454	0.0022	0.1801	0.1780	0.0907	0.0049	0.0812	0.1005	0.0192
	$R\left(0.1\right)$	0.9587	0.0169	0.9255	0.9919	0.0664	0.9589	0.0021	0.9546	0.9630	0.0084
	$h\left(0.1\right)$	0.1832	0.0649	0.0560	0.3104	0.2544	0.1822	0.0095	0.1638	0.2009	0.0371
S[2]	$\mu$	1.3342	0.2374	0.8690	1.7995	0.9305	1.3340	0.0050	1.3241	1.3435	0.0195
	$\gamma$	0.0805	0.0381	0.0057	0.1552	0.1495	0.0799	0.0049	0.0705	0.0896	0.0191
	$R\left(0.1\right)$	0.9628	0.0146	0.9341	0.9914	0.0573	0.9630	0.0022	0.9587	0.9672	0.0085
	$h\left(0.1\right)$	0.1673	0.0570	0.0556	0.2790	0.2234	0.1662	0.0098	0.1477	0.1860	0.0383
S[3]	$\mu$	1.2450	0.2497	0.7556	1.7345	0.9789	1.2448	0.0050	1.2349	1.2543	0.0195
	$\gamma$	0.0856	0.0434	0.0006	0.1706	0.1700	0.0851	0.0049	0.0757	0.0948	0.0191
	$R\left(0.1\right)$	0.9616	0.0159	0.9305	0.9928	0.0623	0.9618	0.0021	0.9576	0.9659	0.0082
	$h\left(0.1\right)$	0.1680	0.0593	0.0518	0.2843	0.2325	0.1670	0.0093	0.1493	0.1854	0.0361

Table 10. Characteristics of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ from AWST data.

Sample	Par.	Mean	Mode	${\mathcal{Q}}_1$	${\mathcal{Q}}_2$	${\mathcal{Q}}_3$	St.D	Skew.
S[1]	$\mu$	1.28618	1.28810	1.28279	1.28617	1.28952	0.00496	0.01673
	$\gamma$	0.09065	0.08297	0.08730	0.09065	0.09397	0.00491	0.02521
	$R\left(0.1\right)$	0.95890	0.96222	0.95745	0.95889	0.96035	0.00213	$-0.01195$
	$h\left(0.1\right)$	0.18215	0.16752	0.17572	0.18216	0.18858	0.00947	0.01234
S[2]	$\mu$	1.33396	1.32170	1.33057	1.33395	1.33730	0.00496	0.01546
	$\gamma$	0.07992	0.06919	0.07660	0.07992	0.08321	0.00487	0.02718
	$R\left(0.1\right)$	0.96301	0.96475	0.96154	0.96301	0.96449	0.00217	$-0.01377$
	$h\left(0.1\right)$	0.16621	0.14393	0.15958	0.16622	0.17282	0.00976	0.01415
S[3]	$\mu$	1.24477	1.23251	1.24137	1.24476	1.24811	0.00496	0.01716
	$\gamma$	0.08510	0.07435	0.08177	0.08509	0.08839	0.00487	0.02597
	$R\left(0.1\right)$	0.96185	0.96356	0.96043	0.96185	0.96328	0.00210	$-0.01292$
	$h\left(0.1\right)$	0.16700	0.14588	0.16075	0.16700	0.17322	0.00921	0.01331

Based on S[i], $i=1,2,3$ created from AWST data, Figure 11 displays both trace and MCMC frequencies plots of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ based on their staying 40,000 MCMC iterations. It indicates that the simulated MCMC draws of $\mu$, $\gamma$, $R\left(t\right)$ or $h\left(t\right)$ are mixed sufficiently and behave fairly symmetrically. Also, the facts displayed in Figure 11 support the same facts displayed in Table 10.

Figure 11. Density (left) and Trace (right) plots of $\mu$, $\gamma$, $R\left(t\right)$ and $h\left(t\right)$ from AWST data.

6. Optimal Progressive Designs

In the area of reliability, the investigator can choose the best effective censoring technique from a set of all accessible progressive patterns in order to provide the most information on the parameter(s) under research as feasible; see for additional details Ng et al. [28]. Depending on unit capacity, experimental facilities and budgetary restrictions, when n, m and $T_i,i=1,2$ are predetermined, the ideal censoring design $\mathbf{R}=(R_1,R_2,\dots ,R_m)$ is obtained. However, different criteria have been established in the literature, and several results on the optimal censoring fashions have also been suggested; see for example Pradhan and Kundu [29]; Sen et al. [30]; Ashour et al. [31]; Elshahhat and Abu El Azm [32] and references cited therein. Table 11 lists several metrics to help us determine the best censoring strategy.

Table 11. Criteria for optimum censoring.

Criterion	Goal
${\mathcal{O}}_1$	$\mathrm{Minimize}det\left({\mathbf{I}}^{-1}\left(\widehat{\mu },\widehat{\gamma }\right)\right)$
${\mathcal{O}}_2$	$\mathrm{Minimize}\mathrm{trace}\left({\mathbf{I}}^{-1}\left(\widehat{\mu },\widehat{\gamma }\right)\right)$
${\mathcal{O}}_3$	$\mathrm{Maximize}\mathrm{trace}\left({\mathbf{I}}^{}\left(\widehat{\mu },\widehat{\gamma }\right)\right)$
${\mathcal{O}}_4$	$\mathrm{Minimize}\widehat{var}(log\left({\widehat{\mathcal{Q}}}_{\zeta }\right))$

From Table 11, it is clear that the proposed optimum ${\mathcal{Q}}_1$, ${\mathcal{Q}}_2$ and ${\mathcal{Q}}_4$, criteria aim to minimize the determinant, trace and the variance of the logarithmic-ML estimate of the $\zeta$th quantile of the estimated variance–covariance ${\mathbf{I}}^{-1}\left(\widehat{\mu },\widehat{\gamma }\right)$ matrix, while criterion ${\mathcal{Q}}_3$ aims to maximize the observed Fisher information ${\mathbf{I}}^{}\left(\widehat{\mu },\widehat{\gamma }\right)$ matrix. Obviously, the best progressive pattern must correspond to the highest value of ${\mathcal{Q}}_3$ and the lowest value of other criteria ${\mathcal{Q}}_i$ for $i=1,2,4$.

Subsequently, from (2), the logarithm of the quantile of the PRC lifetime distribution ${\mathcal{Q}}_{\zeta }$ is

$$log\left({\widehat{\mathcal{Q}}}_{\zeta }\right)={\left.log\left(\mu \right)+log\left[log\left(1-e^{\gamma (1-{\zeta }^{-1})}\right)\right]\right|}_{(\widehat{\mu },\widehat{\gamma })},0<\zeta <1.$$

(16)

Again, performing the delta method, the approximated variance (say $\widehat{var}(·)$) of $log\left({\widehat{\mathcal{Q}}}_{\zeta }\right)$ is given by

$$\widehat{var}\left(log\left({\widehat{\mathcal{Q}}}_{\zeta }\right)\right)={\left.{\Sigma }_{log\left({\mathcal{Q}}_{\zeta }\right)}^{\top }{\mathbf{I}}^{-1}\left(\vartheta \right){\Sigma }_{log\left({\mathcal{Q}}_{\zeta }\right)}\right|}_{(\widehat{\mu },\widehat{\gamma })},$$

where

$${\Sigma }_{log\left({\widehat{\mathcal{Q}}}_{\zeta }\right)}^{\top }={\left.\left[\frac{\partial }{\partial \mu }log\left({\mathcal{Q}}_{\zeta }\right)\phantom{\partial log\left({\mathcal{Q}}_{\zeta }\right)},\frac{\partial }{\partial \gamma }log\left({\mathcal{Q}}_{\zeta }\right)\right]\right|}_{(\widehat{\mu },\widehat{\gamma })}.$$

6.1. Optimum for Industrial Devices

In this part, using the three created samples S[i] for $i=1,2,3$, which are reported in Table 3, we shall evaluate the optimum criteria in Table 11 in turn to suggest the best progressive censoring plans from the industrial devices data. However, based on the acquired MLEs $\widehat{\mu }$ and $\widehat{\gamma }$ obtained from industrial devices data, the optimum criteria ${\mathcal{Q}}_i$ for $i=1,2,3,4$ are evaluated; see Table 12.

Table 12. Optimum progressive plans from industrial devices data.

Sample	${\mathcal{O}}_1$	${\mathcal{O}}_2$	${\mathcal{O}}_3$	${\mathcal{O}}_4$
$\zeta \to$				0.3	0.6	0.9
S[1]	8.72 × ${10}^{-7}$	0.04085	46,849.38	50.0820	126.346	750.602
S[2]	7.71 × ${10}^{-7}$	0.02829	36,712.71	38.7364	102.774	558.193
S[3]	7.49 × ${10}^{-7}$	0.03836	51,235.33	54.2833	186.183	1316.36

As a result, Table 12 shows that:

• According to ${\mathcal{O}}_i,i=1,3,4$; the progressive design used in S[3] is the optimum censoring than others.
• According to ${\mathcal{O}}_2$; the progressive design used in S[2] is the optimum censoring than others.

6.2. Optimum for Aircraft Windshield

In this part, based on the generated samples S[i] for $i=1,2,3$ reported from the aircraft windshield data, we shall suggest the optimal progressive censored plan. However, from Table 8 and Table 11, the optimum criteria are evaluated; see Table 13.

Table 13. Optimum progressive plans from AWST data.

Sample	${\mathcal{O}}_1$	${\mathcal{O}}_2$	${\mathcal{O}}_3$	${\mathcal{O}}_4$
$\zeta \to$				0.3	0.6	0.9
S[1]	2.89 × ${10}^{-5}$	0.06018	2082.76	0.03295	0.04128	0.14746
S[2]	2.46 × ${10}^{-5}$	0.06425	2613.76	0.03097	0.04583	0.18699
S[3]	2.17 × ${10}^{-5}$	0.05780	2658.20	0.02940	0.04119	0.13977

Table 13 shows, according to all optimum criteria ${\mathcal{O}}_i,i=1,2,3,4$, the progressive design used in sample S[3] is the best compared to others. Additionally, Table 12 and Table 13 support the same recommended censoring mechanisms as set out in Section 4.

Ultimately, we found that the suggested infer techniques, which use both industrial devices and aircraft windshield data sets, give a good illustration of the unknown parameters along with the reliability properties of the PRC lifetime model when an adaptive progressive hybrid Type-II censored sample is created.

7. Concluding Remarks

A new two-parameter lifetime distribution called the PRC lifetime model obtained by compounding the generalized-exponential and exponential distributions, which allows a bathtub-shaped or decreasing failure rate shape, has been explored in the presence of incomplete data collected from an adaptive progressively hybrid Type-II censored mechanism. In this study, using the proposed censoring plan, we took into account both maximum likelihood (non-Bayesian) and Bayesian estimations of the parameter, reliability and hazard functions of the PRC distribution. The asymptotic confidence intervals of each unknown quantity using the asymptotic distribution of the frequentist estimates have been obtained. The Newton–Raphson technique, via ‘$\mathsf{maxLik}$’ package, has been utilized in turn to evaluate the point and interval estimates developed by the likelihood method. Squared-error loss as well as independent gamma prior functions have been considered to create the Bayes estimates in addition to their HPD interval estimates. The Metropolis–Hastings approximation technique, via ‘$\mathsf{coda}$’ package, has also been utilized to approximate the Bayes estimates and also to construct the associated HPD intervals. Four accuracy metrics in the proposed Monte Carlo simulation experiments, namely: root-mean-squared error, average absolute relative bias, average interval length and coverage probability, have been used to evaluate the effectiveness of the suggested estimation approaches. Using four optimality metrics, the optimum progressive censored designs have been proposed. Two applications using the lifetimes of industrial devices and the remaining service times of windshields have been analyzed to exemplify the offered methodologies. The main results of the applications examined demonstrate that the suggested PRC lifespan model may be employed as an appropriate model when compared to the other seven competing models. As a future study, it may be useful to extend the proposed estimation methodologies to accelerated tests, competing risks, or other censoring designs. We hope that the approaches provided in this paper will be valuable to statisticians, reliability practitioners, clinicians and anyone else who needs to perform this kind of life test.