Further Studies on the Dynamics of a Lotka–Volterra Competitor–Competitor–Mutualist System with Time-Varying Delays

Abstract

In this paper, a Lotka–Volterra (L-V) competitor–competitor–mutualist system with time-varying delays is studied. Some dynamical behaviors of the considered system are investigated. Firstly, we obtain the boundedness, permanence and periodic solution of the system using the comparison principle of differential equations and inequality estimation method. Then, the global attractiveness of the system is analyzed by multiple Lyapunov functionals. Meanwhile, the existence and global attractivity of positive periodic solutions is derived. In the third section, in order to validate the practicability and feasibility of the obtained theoretical results, we conducted numerical simulations using MATLAB function ddesd. Finally, the fourth section is where conclusions are drawn.

1. Introduction

Population dynamics systems often use mathematical models to describe the interactions and relationships between populations and their environment. These models can involve differential equations, integral equations, or difference equations, depending on the specific variables being considered and the level of complexity of the system. The goal of these models is typically to better understand how populations change over time in response to various factors such as resource availability, disease, predation, competition and cooperation [1].

In recent years, various kinds of delay differential equations have been increasingly used in the modeling of complex systems such as ecosystems [2,3], population dynamical systems [4,5], infectious diseases systems [6], neural networks systems [7,8], enterprise clusters systems [9,10] and so on. These equations take into account time delays in the system’s response to its own behavior or external stimuli, which can result in interesting and often unexpected dynamics [11]. For example, in the predator–prey model [5], time delays can play an important role in the dynamics of the system. Time delays can arise due to various factors, such as the time it takes for prey to reproduce or for predators to consume their prey. In addition, when considering the predator–prey model without time delays [12], the dynamics of the system are simpler. In this case, the population sizes of predator and prey species can be modeled using a set of coupled differential equations, which can be solved analytically or numerically to determine the long-term behavior of the system.

On the other hand, the survival of species in a population dynamical system is one of the most important problem, and permanence analysis is an important tool in studying the long-term behavior of population dynamical systems. For example, in the predator model, which describes the interaction between predator and prey populations, permanence analysis is necessary to understand the conditions under which the populations will persist or go extinct over time. Hence, in an ecological system, the permanence analysis is important because the extinction of one or more populations may have significant ecological and economic consequences. Overall, permanence analysis plays a critical role in understanding the dynamics of ecological systems, and it is essential for making informed decisions about conservation and management efforts.

As is well known, the L-V model, also known as the predator–prey model, is a mathematical model that describes the dynamics of two interacting species in an ecosystem. The model was developed independently by Alfred Lotka [13] and Vito Volterra [14] in the early 20th century. The L-V model has been applied to many different ecosystems, including ocean fisheries, terrestrial ecosystems, and even economic systems.

Recently, Lu et al. [15] considered the following L-V cooperative systems with discrete delays:

$$\begin{array}{c}{\dot{y}}_1\left(\theta \right)=y_1\left(\theta \right)[s_1-c_1{y}_1\left(\theta \right)-d_{11}{y}_1(\theta -{\iota }_{11})+b_{12}{y}_2(\theta -{\iota }_{12})],\hfill \\ {\dot{y}}_2\left(\theta \right)=y_2\left(\theta \right)[s_2-c_2{y}_2\left(\theta \right)+b_{21}{y}_1(\theta -{\iota }_{21})-d_{22}{y}_2(\theta -{\iota }_{22})],\hfill \end{array}$$

(1)

and derived the conditions for permanence of system (1). Li et al. [16] investigated the following delayed L-V competitive system with feedback controls

$$\begin{array}{c}{\displaystyle {\dot{z}}_1\left(t\right)=d_1{z}_1\left(t\right)[1-z_1\left(t\right)-\frac{b_1{z}_2}{1+a_1{z}_1^2}],}\hfill \\ {\displaystyle {\dot{z}}_2\left(t\right)=d_2{z}_2\left(t\right)[1-z_2\left(t\right)-\frac{b_2{z}_1}{1+a_2{z}_2^2}],}\hfill \end{array}$$

(2)

and the conditions for the stability of equilibriums, coexistence and exclusion of species are obtained.

However, pure competition, as described by the L-V model, can lead to species exclusion or coexistence with reduced carrying capacity for both species. In addition, while pure competition can drive natural selection, it does not necessarily promote the coexistence of multiple species. In fact, the L-V model, which describes pure competition between two species, predicts that one species will eventually outcompete and exclude the other. Therefore, other factors such as resource partitioning, niche differentiation, and mutualism are necessary to facilitate the coexistence of multiple species in an ecosystem [17]. Based on the above analysis, when modeling ecosystems or populations, it is important to consider the various interactions that occur between species, including competition for resources, cooperation in certain behaviors or activities, and predator–prey relationships. These interactions can significantly affect the dynamics of the system and its stability over time.

In recent years, some L-V type mathematical models on the various interactions have been proposed in the study of delay differential equations [18,19,20,21,22,23,24,25] and several research results have been obtained. For example, in [19], the authors considered the following L-V type predator–prey-competition system with delays

$$\begin{array}{cc}\hfill {\dot{z}}_1\left(\mu \right)=& {\displaystyle z_1\left(\mu \right)[s_1\left(\mu \right)-a_{11}^1\left(\mu \right)z_1(\mu -\theta )-a_{11}^2\left(\mu \right)z_1(\mu -2\theta )}\hfill \\ & {\displaystyle -a_{12}\left(\mu \right)z_2(\mu -2\theta )-a_{13}\left(\mu \right)z_3(\mu -2\theta )],}\hfill \\ \hfill {\dot{z}}_2\left(\mu \right)=& {\displaystyle z_2\left(\mu \right)[-s_2\left(\mu \right)+a_{21}\left(\mu \right)z_1(\mu -2\theta )-a_{22}^1\left(\mu \right)z_2(\mu -\theta )}\hfill \\ & {\displaystyle -a_{22}^2\left(\mu \right)z_2(\mu -2\theta )-a_{23}\left(\mu \right)z_3(\mu -2\theta )],}\hfill \\ \hfill {\dot{z}}_3\left(\mu \right)=& {\displaystyle z_3\left(\mu \right)[-s_3\left(\mu \right)+a_{31}\left(\mu \right)z_1(\mu -2\theta )-a_{32}\left(\mu \right)z_2(\mu -2\theta )}\hfill \\ & {\displaystyle -a_{33}^1\left(\mu \right)z_3(\mu -\theta )-a_{33}^2\left(\mu \right)z_3(\theta -2\theta )].}\hfill \end{array}$$

(3)

and obtained some conditions on the global attractivity, extinction, and permanence of system (3).

On the other hand, competition–mutualism is a type of ecological interaction where two or more species both compete and mutually benefit from each other, and it is common in nature. A classic example is the relationship between hermit crabs and sea anemones, where the crabs provide protection for the anemones while the anemones offer a home for the crabs. Another example is when two different plant species compete for nutrients from the same tree, but they also provide shade for each other. These interactions are the result of natural selection over time, and which plays a very important role in maintaining the ecosystem and helps us to better protect the balance of the ecosystem.

In [21], the authors considered the following competitor–competitor–mutualist L-V systems with time-varying delays

$$\begin{array}{cc}\hfill {\dot{z}}_1\left(t\right)=& {\displaystyle z_1\left(t\right)(r_1\left(t\right)-a_{11}\left(t\right)z_1(t-{\tau }_{11}\left(t\right))}\hfill \\ & {\displaystyle -a_{12}\left(t\right)z_2(t-{\tau }_{12}\left(t\right))+a_{13}\left(t\right)z_3(t-{\tau }_{13}\left(t\right))),}\hfill \\ \hfill {\dot{z}}_2\left(t\right)=& {\displaystyle x_2\left(t\right)(r_2\left(t\right)-a_{21}\left(t\right)z_1(t-{\tau }_{21}\left(t\right))}\hfill \\ & {\displaystyle -a_{22}\left(t\right)z_2(t-{\tau }_{22}\left(t\right))+a_{23}\left(t\right)z_3(t-{\tau }_{23}\left(t\right))),}\hfill \\ \hfill {\dot{z}}_3\left(t\right)=& {\displaystyle z_3\left(t\right)(r_3\left(t\right)+a_{31}\left(t\right)z_1(t-{\tau }_{31}\left(t\right))}\hfill \\ & {\displaystyle +a_{32}\left(t\right)z_2(t-{\tau }_{32}\left(t\right))-a_{33}\left(t\right)z_3(t-{\tau }_{33}\left(t\right))),}\hfill \end{array}$$

(4)

where $z_1\left(t\right)$, $z_2\left(t\right)$ denote the densities of competing species at time t and $z_3\left(t\right)$ denotes the density of cooperating species at time t; $a_{ii}\left(t\right)(i=1,2,3)$ denote the intra-patch restriction density of species $z_1\left(t\right)$, $z_2\left(t\right)$ and $z_3\left(t\right)$ at time t; $a_{12}\left(t\right)$ and $a_{21}\left(t\right)$ denote the competition coefficients of competing species $z_1\left(t\right)$ and $z_2\left(t\right)$ at time t; $a_{13}\left(t\right),a_{23}\left(t\right),a_{31}\left(t\right)$ and $a_{32}\left(t\right)$ denote the cooperation coefficients of species $z_1\left(t\right)$, $z_2\left(t\right)$ and $z_3\left(t\right)$ at time t. The authors have derived some conditions on the existence of periodic solutions by Krasnosselsii’s fixed point theorem. As for the special case of the model, when ${\tau }_{ii}\left(t\right)=0(i=1,2,3)$, they also derived the global attractivity of positive periodic solution of system (4) by means of the construction of Lyapunov functionals.

Based on the studies cited above and as supplements and extensions of the results in [21], in this paper we further study system (4).

Our main purpose is to study the general case ${\tau }_{ii}\left(t\right)\ne 0(i=1,2,3)$ of system (4), and establish several sufficient conditions on the periodic solution, permanence and global attractivity for system (4) by using the inequality analysis, comparison method, and construction of the multiple Lyapunov functional.

Throughout this paper, we denote that

$$\mathcal{J}\triangleq \{1,2,3\},z\left(t\right)={(z_1\left(t\right),z_2\left(t\right),z_3\left(t\right))}^{\mathrm{T}},y\left(t\right)={(y_1\left(t\right),y_2\left(t\right),y_3\left(t\right))}^{\mathrm{T}},$$

and we define

$$\begin{array}{c}{\mathcal{B}}^l={\displaystyle \underset{s\in [0,+\infty )}{inf}}\mathcal{B}\left(s\right),{\mathcal{B}}^u={\displaystyle \underset{s\in [0,+\infty )}{sup}}\mathcal{B}\left(s\right),\end{array}$$

where $\mathcal{B}\left(s\right)$ is any bounded continuous function defined on $[0,+\infty )$.

For system (4), we introduce the following assumptions.

($H_1$)  

${\tau }_{ij}\left(t\right)>0,(i,j\in \mathcal{J}),r_i\left(t\right)>0(i\in \mathcal{J})$ and $a_{ij}\left(t\right)>0(i,j\in \mathcal{J})$ are all continuous bounded functions on $[0,+\infty )$ with ${\tau }_{ij}^{\prime }\left(t\right)<1$.

($H_2$)  

${\tau }_{ij}\left(t\right)>0,(i,j\in \mathcal{J}),r_i\left(t\right)>0(i\in \mathcal{J})$ and $a_{ij}\left(t\right)>0(i,j\in \mathcal{J})$ are all continuous bounded and $\mathsf{\Omega }$-periodic functions on $[0,+\infty )$ with ${\tau }_{ij}^{\prime }\left(t\right)<1$.

The initial conditions for system (4) are given as follows:

$$x_i\left(t\right)={\varpi }_i\left(t\right),t\in [-\tau ,0],i\in \mathcal{J},$$

where ${\varpi }_i\left(t\right)$$(i\in \mathcal{J})$ are satisfying ${\varpi }_i\left(0\right)>0$ and continuous non-negative functions defined on $[-\tau ,0]$ with $\tau ={max}_{(i,j\in \mathcal{J})}\left\{{sup}_{t\in [0,+\infty )}{\tau }_{ij}\left(t\right)\right\}$.

We need the following lemma in this paper.

Lemma 1 

([18]). If for any $\Gamma \in {\mathcal{C}}_{+}^n[-\sigma ,0]$, there exist constants $A>0$ and $B>0$ such that

$$0<B\le \underset{t\to \infty }{lim\; inf}{z}_i(t,0,\Gamma )\le \underset{t\to \infty }{lim\; sup}{z}_i(t,0,\Gamma )\le A,i=1,2,3,$$

then periodic differential equation $\dot{z}\left(t\right)=H(t,z_t)$ with solution $z(t,0,\Gamma )$ admits at least one positive $\mathsf{\Omega }$-periodic solution. Where $H(t,x_t)$ is a $3$-dimensional continuous functional and $z\left(t\right)\in R^n$, $z(t,0,\Gamma )=(z_1(t,0,\Gamma ),z_2(t,0,\Gamma ),z_3(t,0,\Gamma ))$ is a solution of $\dot{z}\left(t\right)=H(t,z_t)$ with initial condition $z_0=\Gamma$.

The organization of this paper is as follows. In Section 2, we will present the main results of this paper. In Section 3, an example is given to illustrate the feasibility of our results. In Section 4, we will discuss what we study in this paper and what we found in this paper.

2. Main Results

Theorem 1. 

Assume that $\left(H_1\right)$ holds and let $z\left(t\right)$ denote any positive solution of system (4),

(i) 

if ${lim}_{t\to \infty }sup{z}_3\left(t\right)<\infty$, then

$$0<\underset{\begin{array}{c}t\to \infty \end{array}}{lim}inf{z}_3\left(t\right),0<\underset{\begin{array}{c}t\to \infty \end{array}}{lim}\underset{i=1,2}{inf}{z}_i\left(t\right)\le \underset{\begin{array}{c}t\to \infty \end{array}}{lim}\underset{i=1,2}{sup}{z}_i\left(t\right)<\infty ;$$

(ii) 

if there exists a $M_3^{*}>0$ such that for any positive solution $z\left(t\right)$ of system (4),

$$\underset{t\to \infty }{lim}sup{z}_3\left(t\right)\le M_3^{*},$$

(iii) 

$R_i>0(i=1,2)$, where $R_i(i=1,2)$ will defined in the proof,

then system (4) is permanent.

Proof. 

Since ${lim}_{t\to \infty }sup{z}_3\left(t\right)<\infty$, then $M_3>0$ and $t_0>0$ exist, such that $0<z_3\left(t\right)\le M_3$ for $t\ge t_0$. According to the first equation of system (4), we have

$$\begin{array}{cc}\hfill {\dot{z}}_1\left(t\right)\le & z_1\left(t\right)[r_1^u+a_{13}^u{M}_3-a_{11}^l{z}_1(t-{\tau }_{11}\left(t\right))]\hfill \\ \hfill \le & z_1\left(t\right)(r_1^u+a_{13}^u{M}_3),\hfill \end{array}$$

(5)

for $t\ge t_0+{\tau }_{12}^u+{\tau }_{13}^u$. When $t\ge t_0+{\sum }_{i=1}^3{\tau }_{1i}^u=t_1$, integrating (5) from $t-{\tau }_{11}\left(t\right)$ to t, one has

$$\begin{array}{cc}\hfill z_1(t-{\tau }_{11}\left(t\right))& \ge z_1\left(t\right)exp\{-(r_1^u+a_{13}^u{M}_3){\tau }_{11}\left(t\right)\}\hfill \\ & \ge z_1\left(t\right)exp\{-(r_1^u+a_{13}^u{M}_3){\tau }_{11}^u\}.\hfill \end{array}$$

(6)

Hence, from (6) we further have

$${\dot{z}}_1\left(t\right)\le z_1\left(t\right)[(r_1^u+a_{13}^u{M}_3)-a_{11}^{l}exp\{-(r_1^u+a_{13}^u{M}_3){\tau }_{11}^u\}{z}_1\left(t\right)].$$

Let $a=r_1^u+a_{13}^u{M}_3,b=a_{11}^l,\overline{N}=bexp\{-a{\tau }_{11}^u\},y_1\left(t\right)=z_1\left(t\right)exp\{-at\}$, then,

$${\dot{z}}_1\left(t\right)exp\{-at\}\le a{z}_1\left(t\right)exp\{-at\}-bexp\{-a{\tau }_{11}^u\}{z}_1^2\left(t\right)exp\{-2at\}exp\left\{at\right\},$$

for $t\ge t_1$. Thus,

$$\frac{d{y}_1\left(t\right)}{dt}\le -\overline{N}{y}_1^2\left(t\right)exp\left\{at\right\},\frac{d\left(\frac{1}{y_1\left(t\right)}\right)}{dt}\ge \overline{N}exp\left\{at\right\}.$$

(7)

Integrating from $t_1$ to $t\ge t_1$ on both sides of (7), one has

$$\frac{1}{y_1\left(t\right)}\ge \frac{1}{a}[\overline{N}exp\left\{at\right\}-\overline{N}exp\left\{a{t}_0\right\}]+\frac{1}{y_1\left(t_0\right)}=\frac{1}{a}\overline{N}exp\left\{at\right\}+\frac{1}{y_1\left(t_0\right)}-\frac{\overline{N}}{a}exp\left\{a{t}_0\right\}.$$

which leads to

$$y_1\left(t\right)\le \frac{exp\left\{at\right\}}{\frac{1}{a}\overline{N}exp\left\{at\right\}+\frac{1}{y_1\left(t_0\right)exp\left\{-a{t}_0\right\}}-\frac{\overline{N}}{a}exp\left\{a{t}_0\right\}}.$$

On the other hand, one can see that $\phi \left(\mu \right)=\frac{\mu }{\alpha \mu +\beta }$ is a rigorous monotone increasing function for sufficient larger $\mu$ with positive constant $\alpha$, $\beta$, then,

$$z_1\left(t\right)\le \frac{1}{a_{11}^l}(r_1^u+a_{13}^u{M}_3)exp\left\{(r_1^u+a_{13}^u{M}_3){\tau }_{11}^u\right\}=:M_1,$$

(8)

for $t\ge t_2\ge t_1$. Next, according to the second equation of system (4) for $t\ge t_0+{\tau }_{21}^u+{\tau }_{23}^u$, we have

$${\dot{z}}_2\left(t\right)\le z_2\left(t\right)(r_2^u+a_{23}^u{M}_3).$$

(9)

Similarly with the above discussion, for $t\ge t_0+{\sum }_{i=1}^3{\tau }_{2i}^u=t_3$, we can prove that

$$z_2\left(t\right)\le \frac{1}{a_{22}^l}(r_2^u+a_{23}^u{M}_3)exp\left\{(r_2^u+a_{23}^u{M}_3){\tau }_{22}^u\right\}=:M_2$$

(10)

Next, we seek the positive constants $m_1,m_2,m_3$. It follows from the third equation of system (4) for $t\ge t_2+{\tau }_{33}^u$, we have

$${\dot{z}}_3\left(t\right)\ge z_3\left(t\right)[r_3^l-a_{33}^u{M}_3].$$

(11)

Integrating (11) from $t-{\tau }_{33}\left(t\right)$ to t, one has,

$$z_3\left(t\right)\ge z_3(t-{\tau }_{33}\left(t\right))exp\left\{(r_3^l-a_{33}^u{M}_3){\tau }_{33}^{*}\right\},$$

(12)

where, take ${\tau }_{33}^{*}={\tau }_{33}^u$, if $r_3^l-a_{33}^u{M}_3<0$; take ${\tau }_{33}^{*}={\tau }_{33}^l$, if $r_3^l-a_{33}^u{M}_3>0$.

Thus, we have

$$z_3^{\prime }\left(t\right)\ge z_3\left(t\right)[r_3^l-a_{33}^{u}exp\{-(r_3^l-a_{33}^u{M}_3){\tau }_{33}^{*}\}{z}_3\left(t\right)].$$

(13)

Therefore, there exist $t_4\ge t_3+{\tau }_{33}^u$, one has

$$z_3\left(t\right)\ge \frac{r_3^l}{a_{33}^u}exp\left\{(r_3^l-a_{33}^u{M}_3){\tau }_{33}^{*}\right\}=:m_3.$$

(14)

for $t\ge t_4$. It follows from the first and second equation of system (4) for $t\ge t_4+{\tau }_{ii}^u(i=1,2)$, and we further have

$${\dot{z}}_i\left(t\right)\ge z_i\left(t\right)[R_i-a_{ii}^u{z}_i(t-{\tau }_{ii}\left(t\right))].$$

(15)

where $R_1=r_1^l+m_3-a_{12}^u{M}_2,R_2=r_2^l+m_3-a_{21}^u{M}_1$.

Integrating (15) from $t-{\tau }_{ii}\left(t\right)(i=1,2)$ to t, one has

$$z_i\left(t\right)\ge z_i(t-{\tau }_{ii}\left(t\right))exp\left\{(R_i-a_{ii}^u{M}_i){\tau }_{ii}^{*}\right\},$$

where, for i = 1, 2 take ${\tau }_{ii}^{*}={\tau }_{ii}^u$, if $R_i-a_{ii}^u{M}_i<0$; take ${\tau }_{ii}^{*}={\tau }_{ii}^l$, if $R_i-a_{ii}^u{M}_i>0$.

Thus, we have

$${\dot{z}}_i\left(t\right)\ge z_i\left(t\right)[R_i-a_{ii}^{u}exp\{-(R_3-a_{ii}^u{M}_i){\tau }_{ii}^{*}\}{z}_i\left(t\right)],i=1,2.$$

Therefore, there exist $t_5\ge t_4+max\{{\tau }_{11}^u,{\tau }_{22}^u\}$, one has

$$z_i\left(t\right)\ge \frac{R_i}{a_{ii}^u}exp\left\{(R_i-a_{ii}^u{M}_i){\tau }_{ii}^{*}\right\}=:m_i,i=1,2.$$

(16)

for $t\ge t_5$. □

From Theorem 1, we have the following result.

Corollary 1. 

Let $z\left(t\right)$ denote any positive solution of system (4), suppose that $\left({\mathrm{H}}_1\right)$ hold and following conditions hold:

(1) 

If

$$\underset{t\to \infty }{lim\; sup}{z}_3\left(t\right)<+\infty ,$$

then

$$\underset{t\to \infty }{lim}sup{z}_i\left(t\right)<+\infty ,i=1,2.$$

(2) 

If there exist a real number $M_3>0$ such that for any positive solution $z\left(t\right)$ of system (4),

$$\underset{t\to \infty }{lim\; sup}{z}_3\left(t\right)\le M_3.$$

Then, system (4) is ultimately bounded.

By Lemma 1 and Theorem 1, we can obtain the following result for system (4).

Corollary 2. 

If (H2) holds and let $z\left(t\right)$ denote any positive solution of system (4),

(i) 

If ${lim}_{t\to \infty }sup{z}_3\left(t\right)<\infty$, then

$$0<\underset{\begin{array}{c}t\to \infty \end{array}}{lim}inf{z}_3\left(t\right),0<\underset{\begin{array}{c}t\to \infty \end{array}}{lim}\underset{i=1,2}{inf}{z}_i\left(t\right)\le \underset{\begin{array}{c}t\to \infty \end{array}}{lim}\underset{i=1,2}{sup}{z}_i\left(t\right)<\infty ;$$

(ii) 

If there exists a $M_3^{*}>0$ such that for any positive solution $z\left(t\right)$ of system (4),

$$\underset{t\to \infty }{lim}sup{z}_3\left(t\right)\le M_3^{*},$$

(iii) 

$R_i^{*}>0(i=1,2)$,

then system (4) is permanent and has a Ω-periodic solution.

Theorem 2. 

If the conditions of Corollary 1 hold and $\mathcal{A}>0$, then system (4) is globally attractive. Where $\mathcal{A}={min}_{i\in \mathcal{J}}\left\{{lim}_{t\to \infty }{inf}_{i\in \mathcal{J}}{\mathcal{A}}_i\right\}$, $0<{\lambda }_i<\infty (i\in \mathcal{J})$, and

$$\begin{array}{cc}\hfill {\mathcal{A}}_i\left(t\right)=& {\lambda }_i{a}_{ii}\left(t\right)-\sum _{j=1,j\ne i}^3{\lambda }_j\frac{a_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{1-{\dot{\tau }}_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}\hfill \\ & -{\lambda }_i{\int }_t^{{\psi }_{ii}^{-1}\left(t\right)}{a}_{ii}\left(u\right)\mathrm{du}[r_i\left(t\right)+\sum _{j=1}^3{a}_{ij}\left(t\right)M_j]\hfill \\ & -\sum _{j=1}^3{\lambda }_j{M}_j\frac{a_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{1-{\dot{\tau }}_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{\int }_{{\psi }_{ji}\left(t\right)}^{{\psi }_{ji}^{-1}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{a}_{jj}\left(u\right)\mathrm{du},i\in \mathcal{J}.\hfill \end{array}$$

(17)

Proof. 

Let $z\left(t\right)$ and $y\left(t\right)$ are any positive solutions of system (4), then from the ultimately boundedness of the solutions, there exist real numbers $T_0^M>0$ and $M_i>0(i\in \mathcal{J})$ such that $0<z_i\left(t\right),y_i\left(t\right)\le M_i(i\in \mathcal{J}).$ First consider the Lyapunov function

$$V_1\left(t\right)=\sum _{i=1}^3{\lambda }_i{V}_{i1}\left(t\right),$$

(18)

where

$$V_{i1}\left(t\right)=\mid ln{z}_i\left(t\right)-ln{y}_i\left(t\right)\mid ,(i\in \mathcal{J}).$$

Computing the Dini derivative of $V_1(t)$, we obtain

$$\begin{array}{cc}\hfill D^{+}{V}_1(t)=& {\lambda }_{1}sign(z_1(t)-y_1(t))[-\sum _{j=1}^2{a}_{1j}(t)(z_j(t-{\tau }_{1j}(t))-y_j(t-{\tau }_{1j}(t)))\hfill \\ & +a_{13}(t)(z_3(t-{\tau }_{13}(t))-y_3(t-{\tau }_{13}(t))]\hfill \\ & +{\lambda }_{2}sign(z_2(t)-y_2(t))[-\sum _{j=1}^2{a}_{2j}(t)(z_j(t-{\tau }_{2j}(t))-y_j(t-{\tau }_{2j}(t)))\hfill \\ & +a_{23}(t)(z_3(t-{\tau }_{23}(t))-y_3(t-{\tau }_{23}(t))]\hfill \\ & +{\lambda }_{3}sign(z_3(t)-y_3(t))[\sum _{j=1}^2{a}_{3j}(t)(z_j(t-{\tau }_{3j}(t))-y_j(t-{\tau }_{3j}(t)))\hfill \\ & -a_{33}(t)(z_3(t-{\tau }_{33}(t))-y_3(t-{\tau }_{33}(t))]\hfill \\ \hfill =& {\lambda }_{1}sign(z_1(t)-y_1(t))[-a_{11}(t)(z_1(t)-y_1(t))+a_{11}(t){\int }_{t-{\tau }_{11}(t)}^t({\dot{z}}_1(s)-{\dot{y}}_1(s))ds\hfill \\ & -a_{12}(t)(z_2(t-{\tau }_{12}(t))-y_2(t-{\tau }_{12}(t))+a_{13}(t)(z_3(t-{\tau }_{13}(t))-y_3(t-{\tau }_{13}(t))]\hfill \\ & +{\lambda }_{2}sign(z_2(t)-y_2(t))[-a_{21}(t)(z_1(t-{\tau }_{21}(t))-y_1(t-{\tau }_{21}(t)))\hfill \\ & -a_{22}(t)(z_2(t)-y_2(t))+a_{22}(t){\int }_{t-{\tau }_{22}(t)}^t({\dot{z}}_2(s)-{\dot{y}}_2(s))ds\hfill \\ & +a_{23}(t)(z_3(t-{\tau }_{23}(t))-y_3(t-{\tau }_{23}(t))]\hfill \\ & +{\lambda }_{3}sign(z_3(t)-y_3(t))[a_{31}(t)(z_1(t-{\tau }_{31}(t))-y_1(t-{\tau }_{31}(t))\hfill \\ & +a_{32}(t)(z_2(t-{\tau }_{32}(t))-y_2(t-{\tau }_{32}(t))\hfill \\ & -a_{33}(t)(z_3(t)-y_3(t))+a_{33}(t){\int }_{t-{\tau }_{33}(t)}^t({\dot{z}}_3(s)-{\dot{y}}_3(s))ds]\hfill \\ \hfill =& {\lambda }_{1}sign(z_1(t)-y_1(t))[-a_{11}(t)(z_1(t)-y_1(t))\hfill \\ & +a_{11}(t){\int }_{t-{\tau }_{11}(t)}^t(z_1(s)[r_1(s)-a_{11}(s)z_1(s-{\tau }_{11}(s))\hfill \\ & -a_{12}(s)z_2(s-{\tau }_{12}(s))+a_{13}(s)z_3(s-{\tau }_{13}(s))]\hfill \\ & -y_1(s)[r_1(s)-a_{11}(s)y_1(s-{\tau }_{11}(s))-a_{12}(s)y_2(s-{\tau }_{12}(s))\hfill \\ & +a_{13}(s)y_3(s-{\tau }_{13}(s))])ds-a_{12}(t)(z_2(t-{\tau }_{12}(t))-y_2(t-{\tau }_{12}(t))\hfill \\ & +a_{13}(t)(z_3(t-{\tau }_{13}(t))-y_3(t-{\tau }_{13}(t))]\hfill \\ & +{\lambda }_{2}sign(z_2(t)-y_2(t))[-a_{21}(t)(z_1(t-{\tau }_{21}(t))-y_1(t-{\tau }_{21}(t)))\hfill \\ & -a_{22}(t)(z_2(t)-y_2(t))+a_{22}(t){\int }_{t-{\tau }_{22}(t)}^t(z_2(s)[r_2(s)-a_{21}(s)z_1(s-{\tau }_{21}(s))\hfill \\ & -a_{22}(s)z_2(s-{\tau }_{22}(s))+a_{23}(s)z_3(s-{\tau }_{23}(s))]\hfill \\ & -y_2(s)[r_2(s)-a_{21}(s)y_1(s-{\tau }_{21}(s))-a_{22}(s)y_2(s-{\tau }_{22}(s))\hfill \\ & +a_{23}(s)y_3(s-{\tau }_{23}(s))])ds+a_{23}(s)(z_3(s-{\tau }_{23}(s))-y_3(s-{\tau }_{23}(s))]\hfill \\ & +{\lambda }_{3}sign(z_3(t)-y_3(t))[a_{31}(t)(z_1(t-{\tau }_{31}(t))-y_1(t-{\tau }_{31}(t))\hfill \\ & +a_{32}(t)(z_2(t-{\tau }_{32}(t))-y_2(t-{\tau }_{32}(t))-a_{33}(t)(z_3(t)-y_3(t))\hfill \\ & +a_{33}(t){\int }_{t-{\tau }_{33}(t)}^t(z_3(s)[r_3(s)+a_{31}(s)z_1(s-{\tau }_{31}(s))+a_{32}(s)z_2(s-{\tau }_{32}(s))\hfill \\ & -a_{33}(s)z_3(s-{\tau }_{33}(s))]-y_3(s)[r_3(s)+a_{31}(s)y_1(s-{\tau }_{31}(s))\hfill \\ & +a_{32}(s)y_2(t-{\tau }_{32}(s))-a_{33}(s)y_3(s-{\tau }_{33}(s))])ds]\hfill \end{array}$$

$$\begin{array}{cc}\hfill =& {\lambda }_{1}sign(z_1(t)-y_1(t))[-a_{11}(t)(z_1(t)-y_1(t))\hfill \\ & +a_{11}(t){\int }_{t-{\tau }_{11}(t)}^t((z_1(s)-y_1(s))[r_1(s)-a_{11}(s)y_1(s-{\tau }_{11}(s))\hfill \\ & -a_{12}(s)y_2(s-{\tau }_{12}(s))+a_{13}(s)y_3(s-{\tau }_{13}(s))]\hfill \\ & +x_1(s)[-a_{11}(s)(z_1(s-{\tau }_{11}(s))-y_1(s-{\tau }_{11}(s)))\hfill \\ & -a_{12}(s)(z_2(s-{\tau }_{12}(s))-y_2(s-{\tau }_{12}(s)))\hfill \\ & +a_{13}(s)(z_3(s-{\tau }_{13}(s))-y_3(s-{\tau }_{13}(s)))])ds\hfill \end{array}$$

$$\begin{array}{cc}& -a_{12}(t)(z_2(t-{\tau }_{12}(t))-y_2(t-{\tau }_{12}(t))\hfill \\ & +a_{13}(t)(z_3(t-{\tau }_{13}(t))-y_3(t-{\tau }_{13}(t))]\hfill \\ & +{\lambda }_{2}sign(z_2(t)-y_2(t))[-a_{21}(t)(z_1(t-{\tau }_{21}(t))-y_1(t-{\tau }_{21}(t)))\hfill \\ & -a_{22}(t)(z_2(t)-y_2(t))+a_{22}(t){\int }_{t-{\tau }_{22}(t)}^t((z_2(s)-y_2(s))[r_2(s)-a_{21}(s)y_1(s-{\tau }_{21}(s))\hfill \\ & -a_{22}(s)y_2(s-{\tau }_{22}(s))+a_{23}(s)y_3(s-{\tau }_{23}(s))]\hfill \\ & +z_2(s)[-a_{21}(s)(z_1(s-{\tau }_{21}(s))-y_1(s-{\tau }_{21}(s)))\hfill \\ & -a_{22}(s)(z_2(s-{\tau }_{22}(s))-y_2(s-{\tau }_{22}(s)))\hfill \\ & +a_{23}(s)(z_3(s-{\tau }_{23}(s))-y_3(s-{\tau }_{23}(s))])ds]\hfill \\ & +{\lambda }_{3}sign(z_3(t)-y_3(t))[a_{31}(t)(z_1(t-{\tau }_{31}(t))-y_1(t-{\tau }_{31}(t))\hfill \\ & +a_{32}(t)(z_2(t-{\tau }_{32}(t))-y_2(t-{\tau }_{32}(t)))\hfill \\ & -a_{33}(t)(z_3(t)-y_3(t))+a_{33}(t){\int }_{t-{\tau }_{33}(t)}^t((z_3(s)-y_3(s))[r_3(s)+a_{31}(s)z_1(s-{\tau }_{31}(s))\hfill \\ & +a_{32}(s)z_2(s-{\tau }_{32}(s))-a_{33}(s)z_3(s-{\tau }_{33}(s))]\hfill \\ & +z_3(s)[a_{31}(s)(z_1(s-{\tau }_{31}(s))-y_1(s-{\tau }_{31}(s)))\hfill \\ & +a_{32}(s)(z_2(s-{\tau }_{32}(s))-y_2(s-{\tau }_{32}(s)))\hfill \\ & -a_{33}(s)(z_3(s-{\tau }_{33}(s))-y_3(s-{\tau }_{33}(s))])ds]\hfill \\ \hfill \le & -{\lambda }_1{a}_{11}(t)\mid z_1(t)-y_1(t)\mid +{\lambda }_1{a}_{11}(t){\int }_{t-{\tau }_{11}(t)}^t(\mid z_1(s)-y_1(s)\mid [r_1(s)+a_{11}(s)y_1(s-{\tau }_{11}(s))\hfill \\ & +a_{12}(s)y_2(s-{\tau }_{12}(s))+a_{13}(s)y_3(s-{\tau }_{13}(s))]\hfill \\ & +z_1(s)[a_{11}(s)\mid x_1(s-{\tau }_{11}(s))-y_1(s-{\tau }_{11}(s))\mid \hfill \\ & +a_{12}(s)\mid z_2(s-{\tau }_{12}(s))-y_2(s-{\tau }_{12}(s))\mid \hfill \\ & +a_{13}(s)\mid z_3(s-{\tau }_{13}(s))-y_3(s-{\tau }_{13}(s))\mid ])ds\hfill \\ & +{\lambda }_1{a}_{12}(t)\mid z_2(t-{\tau }_{12}(t))-y_2(t-{\tau }_{12}(t)\mid \hfill \\ & +{\lambda }_1{a}_{13}(t)\mid z_3(t-{\tau }_{13}(t))-y_3(t-{\tau }_{13}(t)\mid +{\lambda }_1{a}_{21}(t)\mid z_1(t-{\tau }_{21}(t))-y_1(t-{\tau }_{21}(t))\mid \hfill \\ & -{\lambda }_2{a}_{22}(t)\mid z_2(t)-y_2(t)\mid +{\lambda }_2{a}_{22}(t){\int }_{t-{\tau }_{22}(t)}^t(\mid z_2(s)-y_2(s)\mid [r_2(s)+a_{21}(s)y_1(s-{\tau }_{21}(s))\hfill \\ & +a_{22}(s)y_2(s-{\tau }_{22}(s))+a_{23}(s)y_3(s-{\tau }_{23}(s))]\hfill \\ & +z_2(s)[a_{21}(s)\mid z_1(s-{\tau }_{21}(s))-y_1(s-{\tau }_{21}(s))\mid \hfill \\ & +a_{22}(s)\mid z_2(s-{\tau }_{22}(s))-y_2(s-{\tau }_{22}(s))\mid \hfill \\ & +a_{23}(s)\mid z_3(s-{\tau }_{23}(s))-y_3(s-{\tau }_{23}(s))\mid ])ds\hfill \\ & +{\lambda }_3{a}_{31}(t)\mid z_1(t-{\tau }_{31}(t))-y_1(t-{\tau }_{31}(t)\mid \hfill \\ & +{\lambda }_3{a}_{32}(t)\mid z_2(t-{\tau }_{32}(t))-y_2(t-{\tau }_{32}(t))\mid \hfill \\ & -{\lambda }_3{a}_{33}(t)\mid z_3(t)-y_3(t)\mid +{\lambda }_3{a}_{33}(t){\int }_{t-{\tau }_{33}(t)}^t(\mid z_3(s)-y_3(s)\mid [r_3(s)+a_{31}(s)z_1(s-{\tau }_{31}(s))\hfill \end{array}$$

$$\begin{array}{cc}& +a_{32}\left(s\right)z_2(s-{\tau }_{32}\left(s\right))+a_{33}\left(s\right)z_3(s-{\tau }_{33}\left(s\right))]\hfill \\ & +z_3\left(s\right)[a_{31}\left(s\right)\mid z_1(s-{\tau }_{31}\left(s\right))-y_1(s-{\tau }_{31}\left(s\right))\mid \hfill \\ & +a_{32}\left(s\right)\mid z_2(s-{\tau }_{32}\left(s\right))-y_2(s-{\tau }_{32}\left(s\right))\mid \hfill \\ & +a_{33}\left(s\right)\mid z_3(s-{\tau }_{33}\left(s\right))-y_3(s-{\tau }_{33}\left(s\right)\mid ])ds\hfill \end{array}$$

(19)

Define

$$V_2\left(t\right)={\lambda }_1{V}_{12}\left(t\right)+{\lambda }_2{V}_{22}\left(t\right)+{\lambda }_3{V}_{32}\left(t\right)$$

(20)

where

$$\begin{array}{cc}\hfill V_{12}=& {\int }_{t-{\tau }_{12}\left(t\right)}^t\frac{a_{12}\left({\psi }_{12}^{-1}\left(s\right)\right)}{1-{\dot{\tau }}_{12}\left({\psi }_{12}^{-1}\left(s\right)\right)}\mid z_2\left(s\right)-y_2\left(s\right)\mid ds+{\int }_{t-{\tau }_{13}\left(t\right)}^t\frac{a_{13}\left({\psi }_{13}^{-1}\left(s\right)\right)}{1-{\dot{\tau }}_{13}\left({\psi }_{13}^{-1}\left(s\right)\right)}\mid z_3\left(s\right)-y_3\left(s\right)\mid ds\hfill \\ & +{\int }_t^{{\psi }_{11}^{-1}\left(t\right)}{\int }_{{\psi }_{11}\left(u\right)}^t{a}_{11}\left(u\right)(\mid z_1\left(s\right)-y_1\left(s\right)\mid [r_1\left(s\right)+a_{11}\left(s\right)y_1(s-{\tau }_{11}\left(s\right))\hfill \\ & +a_{12}\left(s\right)y_2(s-{\tau }_{12}\left(s\right))+a_{13}\left(s\right)y_3(s-{\tau }_{13}\left(s\right))]\hfill \\ & +z_1\left(s\right)[a_{11}\left(s\right)\mid z_1(s-{\tau }_{11}\left(s\right))-y_1(s-{\tau }_{11}\left(s\right)\mid \hfill \\ & +a_{12}\left(s\right)\mid z_2(s-{\tau }_{12}\left(s\right))-y_2(s-{\tau }_{12}\left(s\right))\mid \hfill \\ & +a_{13}\left(s\right)\mid z_3(s-{\tau }_{13}\left(s\right))-y_3(s-{\tau }_{13}\left(s\right))])dsdu,\hfill \\ & \begin{array}{cc}\hfill V_{22}=& {\int }_{t-{\tau }_{21}\left(t\right)}^t\frac{a_{21}\left({\psi }_{21}^{-1}\left(s\right)\right)}{1-{\dot{\tau }}_{21}\left({\psi }_{21}^{-1}\left(s\right)\right)}\mid z_2\left(s\right)-y_2\left(s\right)\mid ds\hfill \\ & +{\int }_{t-{\tau }_{23}\left(t\right)}^t\frac{a_{23}\left({\psi }_{23}^{-1}\left(s\right)\right)}{1-{\dot{\tau }}_{23}\left({\psi }_{23}^{-1}\left(s\right)\right)}\mid z_3\left(s\right)-y_3\left(s\right)\mid ds\hfill \\ & +{\int }_t^{{\psi }_{22}^{-1}\left(t\right)}{\int }_{{\psi }_{22}\left(u\right)}^t{a}_{22}\left(u\right)(\mid z_2\left(s\right)-y_2\left(s\right)\mid [r_2\left(s\right)\hfill \\ & +a_{21}\left(s\right)y_1(s-{\tau }_{21}\left(s\right))+a_{22}\left(s\right)y_2(s-{\tau }_{22}\left(s\right))+a_{23}\left(s\right)y_3(s-{\tau }_{23}\left(s\right))]\hfill \\ & +x_2\left(s\right)[a_{21}\left(s\right)\mid z_1(s-{\tau }_{21}\left(s\right))-y_1(s-{\tau }_{21}\left(s\right)\mid \hfill \\ & +a_{22}\left(s\right)\mid z_2(s-{\tau }_{22}\left(s\right))-y_2(s-{\tau }_{22}\left(s\right))\mid \hfill \\ & +a_{23}\left(s\right)\mid z_3(s-{\tau }_{23}\left(s\right))-y_3(s-{\tau }_{23}\left(s\right))])dsdu,\hfill \end{array}\hfill \\ & \begin{array}{cc}\hfill V_{32}=& {\int }_{t-{\tau }_{31}\left(t\right)}^t\frac{a_{31}\left({\psi }_{31}^{-1}\left(s\right)\right)}{1-{\dot{\tau }}_{31}\left({\psi }_{31}^{-1}\left(s\right)\right)}\mid z_1\left(s\right)-y_1\left(s\right)\mid ds\hfill \\ & +{\int }_{t-{\tau }_{32}\left(t\right)}^t\frac{a_{33}\left({\psi }_{32}^{-1}\left(s\right)\right)}{1-{\dot{\tau }}_{32}\left({\psi }_{32}^{-1}\left(s\right)\right)}\mid z_2\left(s\right)-y_2\left(s\right)\mid ds\hfill \\ & +{\int }_t^{{\psi }_{33}^{-1}\left(t\right)}{\int }_{{\psi }_{33}\left(u\right)}^t{a}_{33}\left(u\right)(\mid z_3\left(s\right)-y_3\left(s\right)\mid [r_3\left(s\right)\hfill \\ & +a_{31}\left(s\right)y_1(s-{\tau }_{31}\left(s\right))+a_{32}\left(s\right)y_2(s-{\tau }_{32}\left(s\right))+a_{33}\left(s\right)y_3(s-{\tau }_{33}\left(s\right))]\hfill \\ & +x_3\left(s\right)[a_{31}\left(s\right)\mid z_1(s-{\tau }_{31}\left(s\right))-y_1(s-{\tau }_{31}\left(s\right)\mid \hfill \\ & +a_{32}\left(s\right)\mid z_2(s-{\tau }_{32}\left(s\right))-y_2(s-{\tau }_{32}\left(s\right))\mid \hfill \\ & +a_{33}\left(s\right)\mid z_3(s-{\tau }_{33}\left(s\right))-y_3(s-{\tau }_{33}\left(s\right))])dsdu.\hfill \end{array}\hfill \end{array}$$

From (19) and (20), we have

$$\begin{array}{cc}\hfill D^{+}(V_1\left(t\right)+V_2\left(t\right))\le & -a_{ii}\left(t\right)\mid z_i\left(t\right)-y_i\left(t\right)\mid \hfill \\ & +\sum _{j=1,j\ne i}^3\frac{a_{ij}\left({\psi }_{ij}^{-1}\left(t\right)\right)}{1-{\dot{\tau }}_{ij}\left({\psi }_{ij}^{-1}\left(t\right)\right)}\mid z_j\left(t\right)-y_j\left(t\right)\mid \hfill \\ & +{\int }_t^{{\psi }_{ii}^{-1}\left(t\right)}{a}_{ii}\left(u\right)du[r_i\left(t\right)+a_{ii}\left(t\right)y_i(t-{\tau }_{ii}\left(t\right)\hfill \\ & +\sum _{j=1,j\ne i}^3{a}_{ij}\left(t\right)y_j(t-{\tau }_{ij}\left(t\right))\mid z_i\left(t\right)-y_i\left(t\right)\mid \hfill \\ & +{\int }_t^{{\psi }_{ii}^{-1}\left(t\right)}{a}_{ii}\left(u\right)du{z}_i\left(t\right)[a_{ii}\left(t\right)\mid z_i(t-{\tau }_{ii}\left(t\right))-y_j(t-{\tau }_{ii}\left(t\right))\mid \hfill \\ & +\sum _{j=1,j\ne i}^3{a}_{ij}\left(t\right)\mid z_j(t-{\tau }_{ij}\left(t\right))-y_j(t-{\tau }_{ij}\left(t\right))\mid ],(i\in \mathcal{J}).\hfill \end{array}$$

(21)

Let

$$V_3\left(t\right)={\lambda }_1{V}_{13}\left(t\right)+{\lambda }_2{V}_{23}\left(t\right)+{\lambda }_3{V}_{33}\left(t\right),$$

(22)

where

$$V_{i3}\left(t\right)=\sum _{j=1}^3{M}_i{\int }_{t-{\tau }_{ij}\left(t\right)}^t{\int }_{{\psi }_{ij}^{-1}\left(s\right)}^{{\psi }_{ij}^{-1}\left({\psi }_{ij}^{-1}\left(s\right)\right)}{a}_{ii}\left(u\right)\frac{a_{ij}\left({\psi }_{ij}^{-1}\left(s\right)\right)}{1-{\dot{\tau }}_{ij}\left({\psi }_{ij}^{-1}\left(s\right)\right)}\mid z_j\left(s\right)-y_j\left(s\right)\mid duds,i\in \mathcal{J}.$$

(23)

Finally, define a Lyapunov functional

$$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)+V_3\left(t\right).$$

Then,

$$\begin{array}{cc}\hfill D^{+}V\left(t\right)\le & \sum _{i=1}^3[-a_{ii}\left(t\right)\mid z_i\left(t\right)-y_i\left(t\right)\mid \hfill \\ & +\sum _{j=1,j\ne i}^3\frac{a_{ij}\left({\psi }_{ij}^{-1}\left(t\right)\right)}{1-{\dot{\tau }}_{ij}\left({\psi }_{ij}^{-1}\left(t\right)\right)}\mid z_j\left(t\right)-y_j\left(t\right)\mid \hfill \\ & +{\int }_t^{{\psi }_{ii}^{-1}\left(t\right)}{a}_{ii}\left(u\right)du[r_i\left(t\right)+\sum _{j=1}^3{a}_{ij}\left(t\right)M_j]\hfill \\ & +M_i\sum _{j=1}^3{\int }_{{\psi }_{ij}^{-1}\left(t\right)}^{{\psi }_{ij}^{-1}\left({\psi }_{ij}^{-1}\left(t\right)\right)}{a}_{ii}\left(u\right)du\frac{a_{ij}\left({\psi }_{ij}^{-1}\left(t\right)\right)}{1-{\dot{\tau }}_{ij}\left({\psi }_{ij}^{-1}\left(t\right)\right)}\mid z_j\left(t\right)-y_j\left(t\right)\mid ]\hfill \\ \hfill \le & -\sum _{i=1}^3{\mathcal{A}}_i\left(t\right)\mid z_i\left(t\right)-y_i\left(t\right)\mid \hfill \\ \hfill \le & -\mathcal{A}\sum _{i=1}^3\mid z_i\left(t\right)-y_i\left(t\right)\mid .\hfill \end{array}$$

(24)

Integrating from $T_0$ to t on both sides of (24) produces

$$V\left(t\right)+\mathcal{A}\sum _{i=1}^3{\int }_{T_0}^t\left(z_i\left(s\right)-y_i\left(s\right)\right)ds\le V\left(T_0\right)<\infty .$$

(25)

Hence, we have

$${\int }_{T_0}^t\sum _{i=1}^3\mid z_i\left(s\right)-y_i\left(s\right)\mid ds<\frac{V\left(T_0\right)}{\mathcal{A}}<\infty .$$

(26)

From (26) and the boundedness of the solutions, we can find that $\mid z_i\left(t\right)-y_i\left(t\right)\mid (i\in \mathcal{J})$ and their derivatives remain bounded on $[T_0,\infty )$. As a consequence, $\mid z_i\left(t\right)-y_i\left(t\right)\mid (i\in \mathcal{J})$ is uniformly continuous on $[T_0,\infty )$. By Barbalat’s theorem, it follows that

$$\underset{t\to \infty }{lim}(z_i\left(t\right)-y_i\left(t\right))=0,i\in \mathcal{J}.$$

□

Corollary 3. 

If the conditions of Corollary 2 hold and $\mathcal{B}>0$, then system (4) has a globally attractive positive Ω-periodic solution. Where $\mathcal{B}={min}_{i\in \mathcal{J}}\left\{{lim}_{t\to \infty }{inf}_{i\in \mathcal{J}}{\mathcal{B}}_i\left(t\right)\right\}$, $0<{\nu }_i<\infty (i\in \mathcal{J})$ and

$$\begin{array}{cc}\hfill {\mathcal{B}}_i\left(t\right)=& {\nu }_i{a}_{ii}\left(t\right)-\sum _{j=1,j\ne i}^3{\nu }_j\frac{a_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{1-{\dot{\tau }}_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}\hfill \\ & -{\nu }_i{\int }_t^{{\psi }_{ii}^{-1}\left(t\right)}{a}_{ii}\left(u\right)\mathrm{du}[r_i\left(t\right)+\sum _{j=1}^3{a}_{ij}\left(t\right)M_j^{*}]\hfill \end{array}$$

$$\begin{array}{cc}& -\sum _{j=1}^3{\nu }_j{M}_j^{*}\frac{a_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{1-{\dot{\tau }}_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{\int }_{{\psi }_{ji}\left(t\right)}^{{\psi }_{ji}^{-1}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{a}_{jj}\left(u\right)\mathrm{du},i\in \mathcal{J}.\hfill \end{array}$$

(27)

Remark 1. 

In system (4), if ${\tau }_{ii}\left(t\right)=0(i=1,2,3)$, then condition (27) reduced to the following condition of Theorem 3.1 in [21]

$${\mathcal{D}}_i\left(t\right)={\nu }_i{a}_{ii}\left(t\right)-\sum _{j=1,j\ne i}^3{\nu }_j\frac{a_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}{1-{\dot{\tau }}_{ji}\left({\psi }_{ji}^{-1}\left(t\right)\right)}>0,i\in \mathcal{J}.$$

Therefore, the established results in this paper can be seen as the extensions, supplements and improvements of the results obtained in the studies by Lv et al. [21].

3. Numerical Example

We consider the following system:

$$\begin{array}{cc}\hfill {\dot{z}}_1\left(t\right)=& z_1\left(t\right)[(0.5+0.1sint)-(2.5+0.2cost)z_1(t-(0.1+0.01cost))\hfill \\ & -(0.43+0.1cost)z_2(t-(0.101+0.01cost))\hfill \\ & +(0.51+0.1sint)z_3(t-(0.101+0.01cost)],\hfill \\ \hfill {\dot{z}}_2\left(t\right)=& z_2\left(t\right)[(0.55+0.1cost)-(0.43+0.1cost)z_1(t-(0.105+0.01cost))\hfill \\ & -(2.55-0.2sint)z_2(t-(0.106+0.01cost))\hfill \\ & +(0.52+0.1cost)z_3(t-(0.101+0.01cost)],\hfill \\ \hfill {\dot{z}}_3\left(t\right)=& z_3\left(t\right)[(0.45+0.1sint)+(0.525+0.1cost)z_1(t-(0.102+0.01cost))\hfill \\ & +(0.54-0.1sint)z_2(t-(0.105+0.01cost))\hfill \\ & -(2.35+0.1cost)z_3(t-(0.11+0.01cost)].\hfill \end{array}$$

(28)

Let $M_3^{*}=0.5$, then we have

$$\begin{array}{c}{M}_1^{*}\approx 0.47,M_2^{*}\approx 0.49,m_3^{*}\approx 0.12,m_1^{*}\approx 0.08,m_2^{*}\approx 0.11,R_1^{*}\approx 0.2603,R_2^{*}\approx 0.3209,\hfill \\ \underset{t\to \infty }{lim\; inf}{\mathcal{B}}_1\left(t\right)\approx 2.44,\underset{t\to \infty }{lim\; inf}{\mathcal{B}}_2\left(t\right)\approx 2.61,\underset{t\to \infty }{lim\; inf}{\mathcal{B}}_3\left(t\right)\approx 1.72.\hfill \end{array}$$

Thus, the assumptions of Corollary 3 are satisfied. Then, system (28) is permanent and has a global attractive positive periodic solution. The corresponding numerical simulation is given in Figure 1 by using the MATLAB function ddesd.

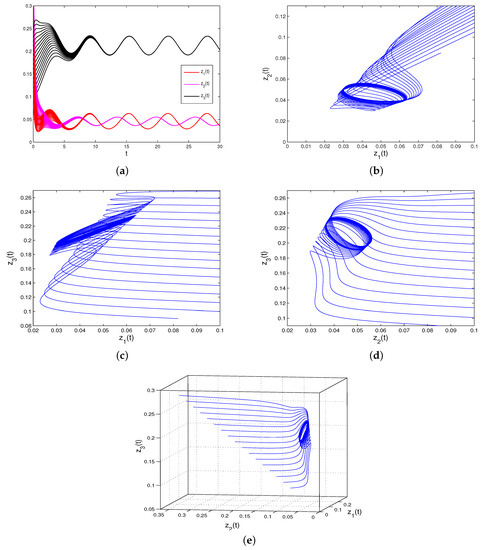
Figure 1. Dynamical behaviors of system (28). Here, we take different initial values. (a) Permanence, periodicity and global attractivity of $z_1\left(t\right),z_2\left(t\right)$ and $z_3\left(t\right)$. (b) Permanence, periodicity and global attractivity of $z_1\left(t\right)$ and $z_2\left(t\right)$. (c) Permanence, periodicity and global attractivity of $z_1\left(t\right)$ and $z_3\left(t\right)$. (d) Permanence, periodicity and global attractivity of $z_2\left(t\right)$ and $z_3\left(t\right)$. (e) Permanence, periodicity and global attractivity of $z_1\left(t\right),z_2\left(t\right)$ and $z_3\left(t\right)$.

From the numerical simulations, we find that system (28) is permanent and has a global attractive positive periodic solution.

Remark 2. 

Obviously, in system (28), the assumptions of Theorem 3.1 in [21] do not hold. If ${\tau }_{ii}\left(t\right)=0(i=1,2,3)$, then the assumptions of Theorem 3.1 in [21] are satisfied, and the assumptions of Corollary 3 are also satisfied. Therefore, it can be seen that our obtained results are more general than the results in [21].

4. Conclusions

The Lotka–Volterra competitor–competitor–mutualist system is a mathematical model that describes the interactions between two competing species and a mutualistic species. The model assumes that the two competing species compete for a common resource, while the mutualistic species benefits from the presence of both competitors. In this paper, a Lotka–Volterra competitor–competitor–mutualist system with varying time delay is analyzed, and the permanence, global attractivity and periodic solution of the system are studied. By means of the multiple Lyapunov functional, comparison principle and inequality estimation method, we obtained a set of easily verifiable new sufficient conditions on the aforementioned results. Therefore, the results in this paper can be seen as the supplements and extensions of the results in [21] and other relative known results.

Although our study provides a thorough analysis of the dynamical behavior of system (4) in the general case, however, there are several important avenues for future research such as the extensions and improvements of the considered model and obtained results in this paper to more general cases.