Abstract
A -container of a graph G is a set of k disjoint paths between any pair of nodes whose union covers all nodes of G. The spanning connectivity of G, , is the largest k, such that there exists a -container between any pair of nodes of G for all . If , then G is super spanning connected. Spanning connectivity is an important property to measure the fault tolerance of an interconnection network. The divide-and-swap cube is a newly proposed hypercube variant, which reduces the network cost from to compared with the hypercube and other hypercube variants. The folded divide-and-swap cube is proposed based on to reduce the diameter of . Both and possess many better properties than hypercubes. In this paper, we investigate the super spanning connectivity of where and . We show that , which means there exists an m-DPC(node-disjoint path cover) between any pair of nodes in for all .
Keywords:
folded divide-and-swap cube; node-disjoint path cover; interconnection network; Hamiltonian; super spanning connectivity MSC:
05C85; 68W15
1. Introduction
In a parallel computer system, the interconnection network determines the performance of the system. Generally, an interconnection network is denoted by , where is the edge set and is the node set. We say that two nodes and are adjacent if . A path P is a sequence of n nodes in G, denoted by where with . If the endpoints and are the same, then P is a cycle. A Hamiltonian path consists of all the nodes in G. A Hamiltonian cycle traverses all nodes of G exactly once. G is Hamiltonian connected if and only if there exists a Hamiltonian path connecting any two nodes of G, and G is Hamiltonian if there exists a Hamiltonian cycle in G. Two paths between a and b are node-disjoint if they do not have common nodes except a and b.
Let be the connectivity of G. From Menger’s theorem, there exist k node-disjoint paths between any pair of nodes a and b in G if . The node-disjoint path problem has been studied for many networks, such as alternating group networks [1], balanced hypercubes [2], DCell networks [3], and so on. A set of k node-disjoint paths between a and b is called a k-container, denoted by . is called a spanning k-container, denoted by -container, if it covers all nodes of G. A -container is also known as a one-to-one disjoint path cover (DPC for short) of G. A disjoint path cover problem of G is to find node-disjoint paths between any two distinct nodes whose union covers all nodes of G [4]. If any two nodes have a -container between them, then G is said to be -connected. Obviously, if G is Hamiltonian-connected, it is -connected, and if G is Hamiltonian, then it is -connected. The spanning connectivity of a graph G, denoted by , is the largest k such that G is -connected for all . If , then G is super spanning connected.
It is important to study the node-disjoint path problem between any pair of distinct nodes [5,6]. Disjoint paths between nodes can be used to accelerate data transmission by allocating data to different communication paths [7]. Other advantages of adopting such a node-disjoint routing scheme are the improved robustness to node failures, as well as the improved load balancing capability [8,9]. Software testing is another well-known application of multiple disjoint path covers [10]. Node-disjoint path cover or spanning connectivity is an important property to measure the fault tolerance of a network, which has been studied for many networks, such as hypercube-like networks [11], alternating group graphs [12], multi-dimensional toris [13], DCell networks [14], WK-recursive networks [15], generalized Petersen graphs [16], split-star networks [17], and so on.
The n-dimensional divide-and-swap cube, denoted by (), was proposed by Kim et al. in [18] as a hypercube variant. Compared with a hypercube, reduces the network cost from to . Moreover, possesses many other attractive properties. The diameter upper bound of is and the degree is . is Hamiltonian and Hamiltonian-connected. In [19], Ning has shown that the connectivity and edge connectivity are both , and the super connectivity and super edge connectivity are both . In [20], Zhou et al. studied the -structure connectivity and -substructure connectivity for . In [21], Zhou et al. showed that the component connectivity and the diagnosability for , . In [22], Zhao et al. investigated the generalized connectivity for . The n-dimensional folded divide-and-swap cube, (), was also proposed in [18]. is constructed based on by adding one edge to each node of . Obviously, the connectivity of is [23]. In addition, the diameter upper bound of is and the network cost is . is also Hamiltonian and Hamiltonian-connected. is appropriate as a candidate topology for a data center network. In [24], Chang et al. constructed the dual-CIST for . In [23], Zhao and Chang investigated the connectivity, super connectivity and generalized 3-connectivity of . We can see that and have many better properties than the hypercube.
In this work, we investigated the super spanning connectivity of with and . We show that there exists an m-DPC between any pair of nodes in for all . The remainder of the paper is structured as follows. We formally define and In Section 2, and then provide two basic properties of . The proof of super spanning connectivity of is given in Section 3. Finally, we summarize the paper.
2. Preliminaries
In this section, we give the formal definition of and . Each node u in is denoted by an n-bit binary string, where and for . is defined as follows.
Definition 1
([18]). For and , has nodes, each of which is represented by an n-bit binary string, where and for . For each k with , , and . If , then and is empty. If node v satisfies one of the following conditions, then .
- (1)
- , where is the complement of . Here, is called an -edge.
- (2)
- Here, is called an -edge.
and are shown in Figure 1. For any integer n with and , is built based on by adding an edge to each node of .
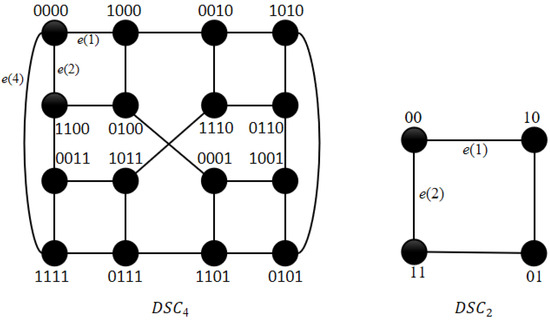
Figure 1.
and .
Definition 2
([18]). , , where and . An edge in is called an -edge.
can be divided into , each of which is represented by or , with . We call a module of . Let be any node in . We have is the local address in the module and is the module address. Then, a module can also be represented by . For example, node 0100 is in (or with decimal representation) and node 1111 is in (or with decimal representation) in (see Figure 2).
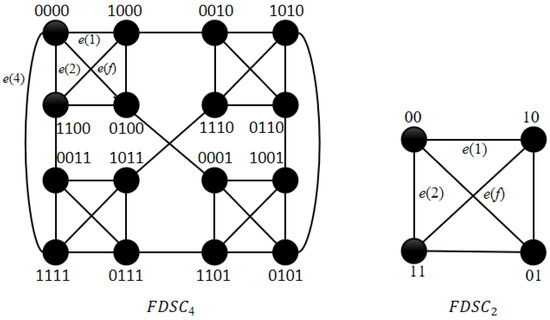
Figure 2.
and .
Property 1
([18]). For modules and with , if , then there are two edges, and , between and ; otherwise, there exists only one edge, , between and .
For example, modules and are connected by two edges and in , where and . Modules and are connected by one edge, in , where and . If , then is in . By Definition 1, , , and are all -edges with . An -edge of node u is denoted by , which is an external edge of u. Obviously, each module has only one node with . Let and . Since each node in the same module has the same module address and the different local address, then each node in S is connected to a different module of and is connected to in module . Since is connected to node , then and are both connected to module . Let . According to Property 1, we have the following property.
Property 2.
Let be the h modules of each of which has h nodes. Let be the node with in with . Then each node in is connected to a different with with an -edge. Let . Then both u and v are connected to with an -edge.
If the local addresses of two nodes u and v are complemented, and are connected to the same module of .
3. The Super Spanning Connectivity of
In this section, we will give some terminologies of and . We list some symbols in Table 1. Throughout this paper, let .

Table 1.
Acronyms and Notation.
Lemma 1
([18]). is Hamiltonian-connected for and .
Lemma 2
([18]). is Hamiltonian for and .
Based on the definition of , we have two lemmas below.
Lemma 3.
is Hamiltonian-connected for and .
Lemma 4
([18]). is Hamiltonian for and .
By Lemmas 3 and 4, we have Lemma 5.
Lemma 5.
For any integer n with and , there is a 1-DPC and a 2-DPC between any pair of nodes μ and ν.
Lemma 6.
Given and its h modules where and , let where and , which consists of r modules and the -edges between them. If u and v are two nodes in different modules of T with , then there exists a Hamiltonian path between u and v, which covers all the nodes of T.
Proof.
We present the cases as follows.
Case 1. .
Suppose and . Since , by Property 2, we can find a node and a node such that . Since and are both Hamiltonian-connected, there exists a Hamiltonian path in and a Hamiltonian path in . Combining the paths constructed above, we obtain the required Hamiltonian path .
Case 2. .
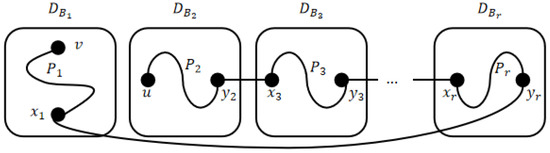
Suppose and . For each module with , we can find two nodes and such that is connected to in and is connected to in . For module , we can find two nodes, and , such that is connected to in . Hence, we can construct the required Hamiltonian path, (see Figure 3). □

Figure 3.
Illustration for Case 2 of Lemma 6.
Lemma 7.
Given and its h modules , where and , let , where and , which consists of r modules and the -edges between them. If u and v are two nodes in the same module of T with , then there exists a Hamiltonian path between u and v, which covers all the nodes of T.
Proof.
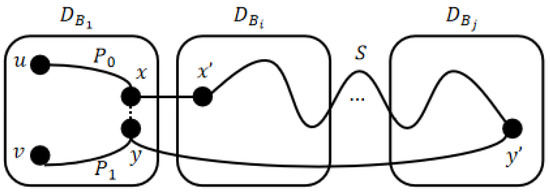
Suppose . Since and , by Property 2, we can build a Hamiltonian path in such that x and y are connected to different modules of T and . Suppose x is connected to in and y is connected to in , where . By Lemma 6, there is a Hamiltonian path , which covers all the nodes of . Combining the paths constructed above, we obtain the required Hamiltonian path, (see Figure 4). □

Figure 4.
Illustration for Lemma 7.
Lemma 8.
Let μ be any node in . We can find a node set with such that there exists a one-to-many node disjoint path cover between μ and T in and the node labels in are not complementary with each other.
Proof.
For , since is Hamiltonian connected, it is easy to construct a one-to-many node disjoint path cover between and in where is not complementary with . For , W.L.O.G., suppose is in . Let where . It is obvious the node labels are not complementary with each other in . Since is a complete graph with four nodes, then there is a one-to-many node disjoint path cover between and in . Suppose is connected to x in with . We can find at least one node , of which the label is not complementary with those in , where . By Lemma 6, there exists a Hamiltonian path between x and y, which covers all the nodes of . Hence, is the required node set for . □
Lemma 9.
Let μ be any node in for and . We can find a node set with , such that there exists a one-to-many node disjoint path cover between μ and T in and the node labels are not complementary with each other in .
Proof.
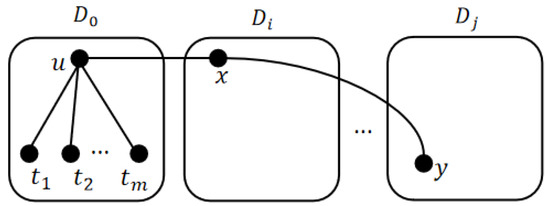
To prove this lemma, we proceed by induction on d. According to Lemma 8, this lemma holds for and . Suppose that this lemma holds for for , we will prove that this lemma holds for .
For , it is easy to find a node set to meet the condition this lemma holds. For , W.L.O.G., suppose is in . According to the hypothesis, there is a one-to-many node disjoint path cover between and in where . Suppose that is connected to x in with . Let y be any vertex in where and y is not complementary with each node in . By Lemma 6, we can construct a path between x and y covering all the nodes of . Hence, is the required node set for (see Figure 5). □

Figure 5.
Illustration for Lemma 9.
Lemma 10.
Let μ and ν be any two nodes in for integer and . There exists an m-DPC between μ and ν in where .
Proof.

By Lemma 5, there exists an m-DPC between and in for . For and , is a complete graph. Obviously, there exists a 3-DPC between any two distinct nodes in . For , we need to prove there exists an m-DPC between and for . We consider the following three cases.
Case 1. , where .
Suppose that , . Since is a complete graph, there exists an m-DPC between and in with .
Case 1.1. and are connected to the same with .
Suppose that is connected to x and is connected to y in . By Lemma 7, there exists a -Hamiltonian path covering all the nodes of . Hence, there exists a -DPC between and where .
Case 1.2. is connected to and is connected to with .
Suppose that is connected to x in and is connected to y in . By Lemma 6, there exists a -Hamiltonian path covering all the nodes of . Hence, there exists a -DPC between and where .
Case 2. and and and are connected with two -edges where .
We can suppose , , and . Let . furthermore let and with . Since and are complete graphs, there exists a one-to-many disjoint path cover between and U in , and a one-to-many disjoint path cover between and V in .
Case 2.1. and are connected to and , respectively.
For , we can have , and are connected to and , respectively. Then we construct the 3-DPC as follows: , , and .
For , we can have , and are connected to and , respectively. Then we construct the 4-DPC as follows: , , , and .
Case 2.2. and are connected to and , respectively.
By Lemma 6, there is a path which covers all the nodes of . For , we can have . Then we construct the 3-DPC as follows: , , and .
For , we can have , and are connected to and , respectively. Then we construct the 4-DPC as follows: , , , and .
Case 2.3. and are connected to and , respectively.
For , we can have , is connected to . By Lemma 6, there is a path which covers all the nodes of . Then we construct the 3-DPC as follows: , , and .
For , we can have , is connected to , and are connected to and , respectively. Then we construct the 4-DPC as follows: , , , and .
Case 2.4. and are connected to and respectively.
The proof of this case is similar to Case 2.3.
Case 2.5. .
For , we can have , and are connected to and , respectively. Then we construct the 3-DPC as follows: , , and .
For , we can have , and are connected to and , and are connected to and , respectively. Then we construct the 4-DPC as follows: , , , and .
Case 2.6. and are connected to and , respectively.
For , we can have and are connected to and , respectively. Then we construct the 3-DPC as follows: , , and .
For , we can have and are connected to and , and are connected to and , respectively. Then we construct the 4-DPC as follows: , , , and .
Case 3. and and and are connected with one -edge where .
We can suppose and . When , we list the 3-DPC and 4-DPC between and in Table 2. Similarly, there is a 3-DPC and a 4-DPC between every two nodes and .

Table 2.
The 3-DPC and 4-DPC between and .
Hence, there exists an m-DPC between and for in for integer and . □
Lemma 11.
Let μ and ν be any two nodes in for any integer and . There exists an m-DPC between μ and ν in with .
Proof.
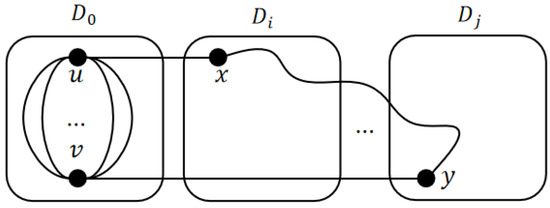
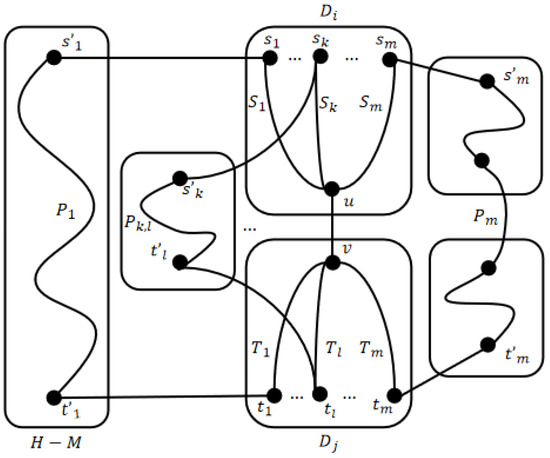
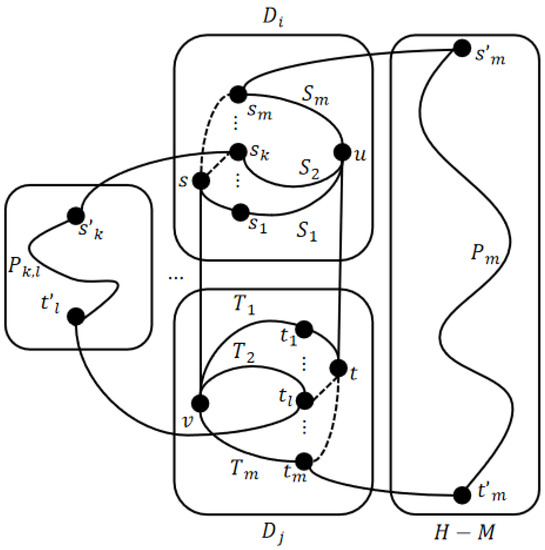
To prove this lemma, we proceed by induction on d. The base case is given in Lemma 10 for . Suppose this lemma holds for when , we will prove that this lemma holds for with . By Lemma 5, there exists an m-DPC between and in for , so we need to prove this lemma holds for . Considering the locations of and in , we have the cases as follows.
Case 1. , with .
W.L.O.G., suppose and are in . According to the hypothesis, there exists an m-DPC between and in where .
Case 1.1. and are connected to different modules of .
Suppose that is connected to and is connected to , where . By Lemma 6, there exists a Hamiltonian path covering all nodes of . Hence, there exists a -DPC between and in where (see Figure 6).

Figure 6.
Illustration for Case 1.1 of Lemma 11.
Case 1.2. and are connected to the same module of .
Suppose that and are connected to with . By Lemma 7, there exists a Hamiltonian path covering all nodes of . Hence, there exists a -DPC between and in where .
Case 2. and with .
Let .
Case 2.1. and are connected to H.
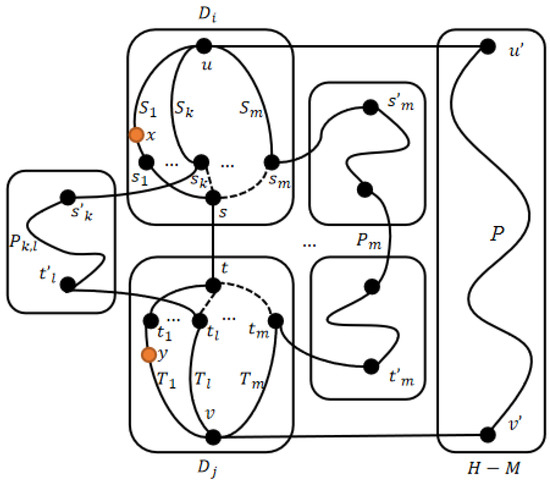
By Property 1, we can find two nodes and such that . According to the hypothesis, there exists an m-DPC between and s in and an m-DPC between and t in where . Let and be the neighbor set of s and t in the m-DPC. By Property 1, and have at most two edges between them. Let be another edge between and if it exists. Suppose that x is in path and y is in path . We can construct a path between and whether or not x, y exist. Then, for each k with , (resp. ) is connected to a different module in H. We can find node pairs between and to build paths which covers 1 or 2 module(s) of H. Let M be the module set consisting of modules covered by the paths between and . Then . By Lemmas 6 and 7, there exists a path which covers all the modules of . Hence, there exists a -DPC between and where (see Figure 7).

Figure 7.
Illustration for Case 2.1 of Lemma 11.
Case 2.2. is connected to and is connected to H.
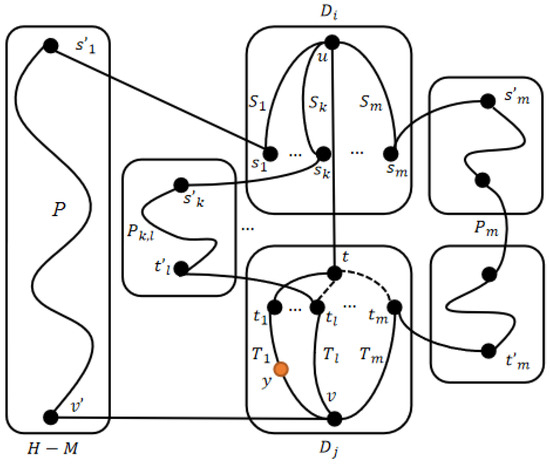
Let and . According to the hypothesis, there exists an m-DPC between and t in where . We have be the neighbor set of t in the m-DPC. By Lemma 9, we can find a vertex set such that there exists a one-to-many node disjoint path cover between and S in and the vertex labels are not complementary with each other in . Hence, each with is connected to a different module of H. Let be connected to if exists. Suppose that y is in path . We can construct a path between and whether or not y exists. For and , we can construct paths between them, the union of which covers module set M. Then . By Lemmas 6 and 7, there exists a path which covers all the modules of . Hence, there exists a -DPC between and where (see Figure 8).

Figure 8.
Illustration for Case 2.2 of Lemma 11.
Case 2.3. is connected to and is connected to H.
This case is similar to Case 2.2.
Case 2.4. (, ).
By Lemma 9, we can find a vertex set such that there exists a one-to-many node-disjoint path cover between and S in and the vertex labels are not complementary with each other in . Similarly, we can find a vertex set such that there exists a one-to-many node disjoint path cover between and T in , and the vertex labels are not complementary with each other in . We can construct paths between and the union of which covers module set M. By Lemmas 6 and 7, there exists a path , which covers all the modules of . Including path , we get a -DPC between and (see Figure 9).

Figure 9.
Illustration for Case 2.4 of Lemma 11.
Case 2.5. , and .
According to the hypothesis, there exists an m-DPC between and s in and an m-DPC between and t in where . Let and be the neighbor set of s and t in the m-DPC. We have two paths, and , between and . Then, for each k with , (resp. ) is connected to a different module in H. We can find node pairs between and to build paths whose union covers module set M. Then . By Lemma 6 and Lemma 7, there exists a path which covers all the modules of . Hence, there exists a -DPC between and where (see Figure 10).

Figure 10.
Illustration for Case 2.5 of Lemma 11.
Hence, there exists an m-DPC between and in where . □
For all , is -connected, then is super spanning connected. We have Theorem 1.
Theorem 1.
for and .
With Theorem 1, we show that there exist m disjoint paths between any pair of nodes for all . Since each node of has neighbors, the result is optimal.
4. Conclusions
and are newly proposed hypercube variants, which reduce the network cost from to compared with the hypercube and other hypercube variants. Both and possess many superior properties than hypercubes. In this work, we investigated the super spanning connectivity of . We show that , which means there exists an m-DPC between any pair of nodes in for all . Since the degree of is , then is the maximal integer of node-disjoint paths that can be built in . In future work, the one-to-many node-disjoint path cover problem of could be considered. In addition, the diagnosability [25,26,27] of is another research topic that could be considered.
Author Contributions
Conceptualization, L.Y.; methodology, Y.H.; investigation, J.J.; writing—original draft preparation, L.Y. and J.J.; writing—review and editing, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Research Project of Suzhou Industrial Park Institute of Services Outsourcing (No. SISO-ZD202202).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, S.; Xiao, W.; Parhami, B. Construction of vertex-disjoint paths in alternating group networks. J. Supercomput. 2010, 54, 206–228. [Google Scholar] [CrossRef]
- Cheng, D.; Hao, R.; Feng, Y. Two node-disjoint paths in balanced hypercubes. Appl. Math. Comput. 2014, 242, 127–142. [Google Scholar] [CrossRef]
- Wang, X.; Fan, J.; Lin, C.-K.; Jia, X. Vertex-disjoint paths in dcell networks. J. Parallel Distrib. Comput. 2016, 96, 38–44. [Google Scholar] [CrossRef]
- Lai, P.-L.; Hsu, H.-C. On the two-equal-disjoint path cover problem of crossed cubes. In Proceedings of the 9th Joint Conference on Information Sciences, JCIS, Kaohsiung, Taiwan, 8–11 October 2006; pp. 603–606. [Google Scholar]
- Gomes, T.; Craveirinha, J.; Jorge, L. An effective algorithm for obtaining the minimal cost pair of disjoint paths with dual arc costs. Comput. Oper. Res. 2009, 36, 1670–1682. [Google Scholar] [CrossRef]
- Liu, C.; Yarvis, M.; Conner, W.S.; Guo, X. Guaranteed on-demand discovery of node-disjoint paths in Ad Hoc networks. Comput. Commun. 2007, 30, 2917–2930. [Google Scholar] [CrossRef]
- Day, K.; Al-Ayyoub, A.E. Fault diameter of k-ary n-cube networks. IEEE Trans. Parallel Distrib. Syst. 1997, 8, 903–907. [Google Scholar] [CrossRef]
- Shih, Y.-K.; Kao, S.-S. One-to-one disjoint path covers on k-ary n-cubes. Theoret. Comput. Sci. 2011, 412, 4513–4530. [Google Scholar] [CrossRef]
- Lai, P.-L.; Hsub, H.-C. The two-equal-disjoint path cover problem of Matching Composition Network. Inform. Process. Lett. 2008, 107, 18–23. [Google Scholar] [CrossRef]
- Ntafos, S.C.; Hakimi, S.L. On path cover problems in digraphs and applications to program testing. IEEE Trans. Softw. Eng. 1979, 5, 520–529. [Google Scholar] [CrossRef]
- Lin, C.K.; Tan, J.J.; Hsu, D.F.; Hsu, L.H. On the spanning connectively and spanning laceability of hypercube-like networks. Theor. Comput. Sci. 2007, 381, 218–229. [Google Scholar] [CrossRef]
- You, L.; Fan, J.; Han, Y.; Jia, X. One-to-one disjoint path covers on alternating group graphs. Theoret. Comput. Sci. 2015, 562, 146–164. [Google Scholar] [CrossRef]
- Li, J.; Liu, D.; Yang, Y.; Yuan, J. One-to-one disjoint path covers on multi-dimensional tori. Int. J. Comput. Math. 2015, 92, 1114–1123. [Google Scholar] [CrossRef]
- Wang, X.; Fan, J.; Jia, X.; Lin, C.-K. An efficient algorithm to construct disjoint path covers of DCell networks. Theoret. Comput. Sci. 2016, 609, 197–210. [Google Scholar] [CrossRef]
- You, L.; Fan, J.; Han, Y. Super spanning connectivity on WK-recursive networks. Theor. Comput. Sci. 2018, 713, 42–55. [Google Scholar] [CrossRef]
- Wang, J.-J.; Hsu, L.-H. On the spanning connectivity of the generalized Petersen graphs P(n, 3). Discret. Math. 2018, 341, 672–690. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Cheng, E. Super spanning connectivity of split-star networks. Inf. Process. Lett. 2021, 166, 106037. [Google Scholar] [CrossRef]
- Kim, J.S.; Kim, D.Y.; Qiu, K.; Lee, H.O. The divide-and-swap cube: A new hypercube variant with small network cost. J. Supercomput. 2019, 75, 3621–3639. [Google Scholar] [CrossRef]
- Ning, W. Connectivity and super connectivity of the divide-and-swap cube. Theor. Comput. Sci. 2020, 842, 1–5. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, S.; Liu, J.; Liu, X. Structure and substructure connectivity of divide-and-swap cube. Theor. Comput. Sci. 2021, 880, 20–36. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, S.; Liu, X.; Yu, Z. Reliability of divide-and-swap cube based on r-component connectivity and diagnosability. J. Interconnect. Netw. 2022, 22, 2142021. [Google Scholar] [CrossRef]
- Zhao, S.; Chang, J. Reliability assessment of the divide-and-swap cube in terms of generalized connectivity. Theor. Comput. Sci. 2023, 943, 1–15. [Google Scholar] [CrossRef]
- Zhao, S.-L.; Chang, J.-M. Connectivity, super connectivity and generalized 3-connectivity of folded divide-and-swap cubes. Inf. Process. Lett. 2023, 182, 106377. [Google Scholar] [CrossRef]
- Chang, Y.-H.; Pai, K.-J.; Hsu, C.-C.; Yang, J.-S.; Chang, J.-M. Constructing dual-CISTs of folded divide-and-swap cubes. Theor. Comput. Sci. 2021, 856, 75–87. [Google Scholar] [CrossRef]
- Li, X.; Fan, J.; Lin, C.-K.; Jia, X. Diagnosability Evaluation of the Data Center Network DCell. Comput. J. 2018, 61, 129–143. [Google Scholar] [CrossRef]
- Gu, M.; Hao, R.; Jiang, L. Fault-tolerance and diagnosability of hierarchical star networks. Int. J. Comput. Math. Comput. Syst. Theory 2018, 3, 106–121. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, S.; Liu, X.; Yu, Z. Extra (component) connectivity and diagnosability of bubble sort networks. Theor. Comput. Sci. 2023, 940, 180–189. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).