Complementary Gamma Zero-Truncated Poisson Distribution and Its Application
Abstract
:1. Introduction
2. The Complementary Gamma Zero-Truncated Poisson Distribution
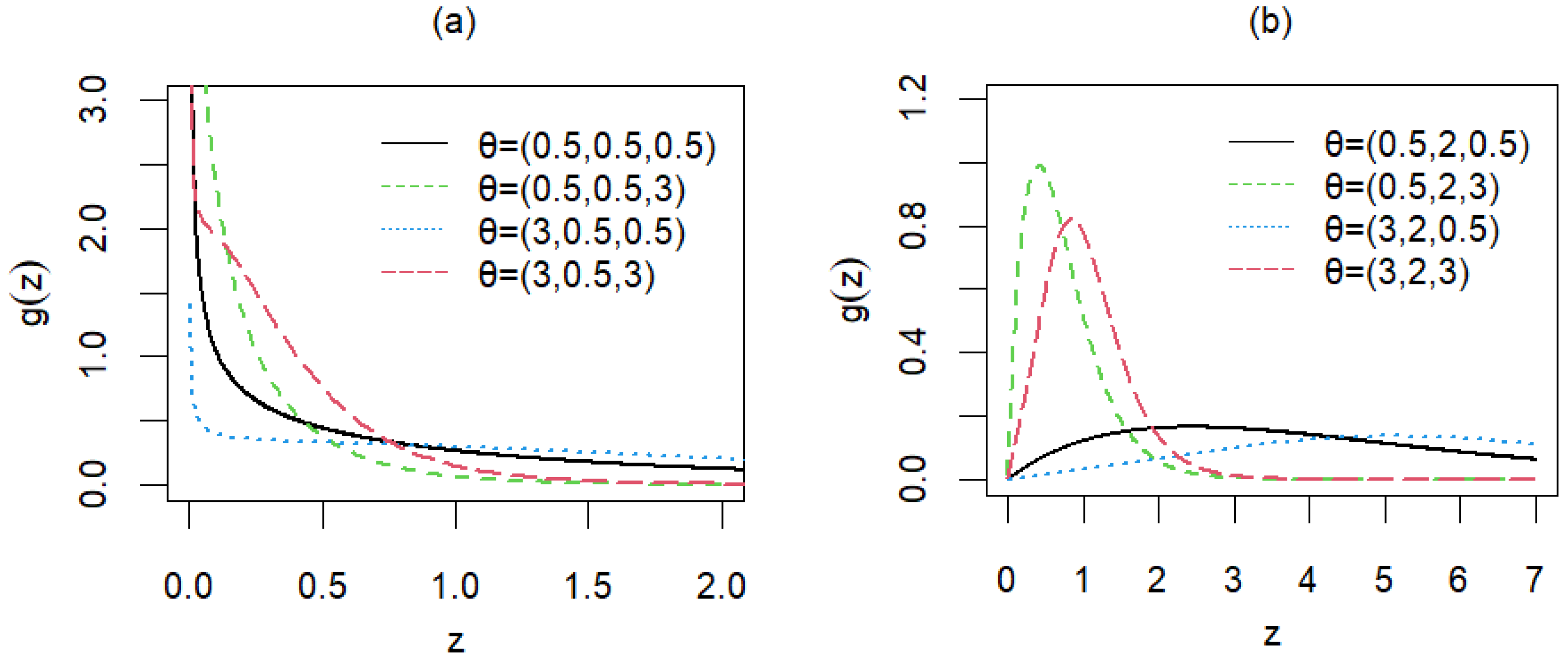
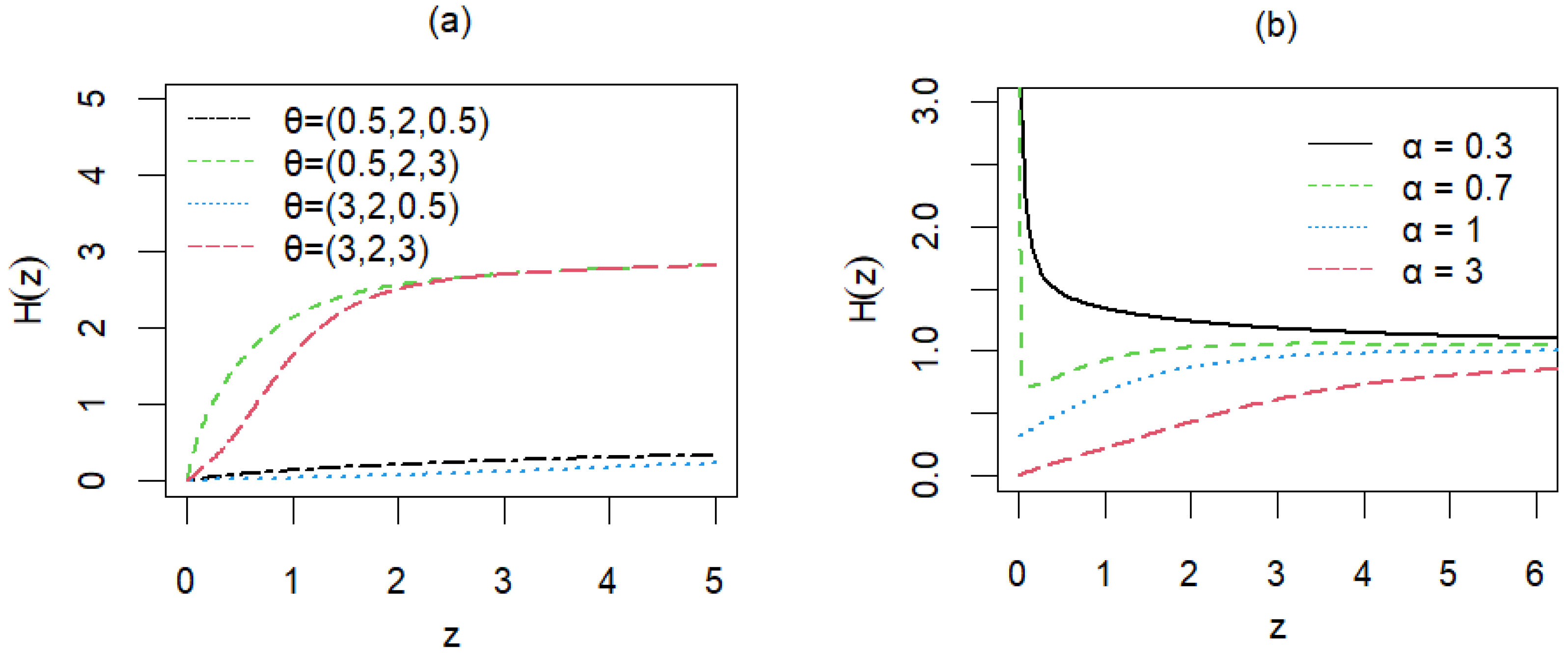
3. Properties of the Distribution
3.1. Cumulative Distribution Function, Quantile and Moment
3.2. Survival Function and Hazard Function
4. Parameter Estimation
4.1. Method of Maximum Likelihood
- (a)
- and where and are integer numbers.
- (b)
- for and which implies that no pole of any , coincide with any pole of any ,.
- (c)
- .
- (a)
- Let , If and are known, then is the uniquely exist root of if .
- (b)
- Let . If and are known, then there exists at least one solution of .
4.2. Variance–Covariance Matrix of the MLEs
4.3. Asymptotic Confidence Interval
5. Simulation Study
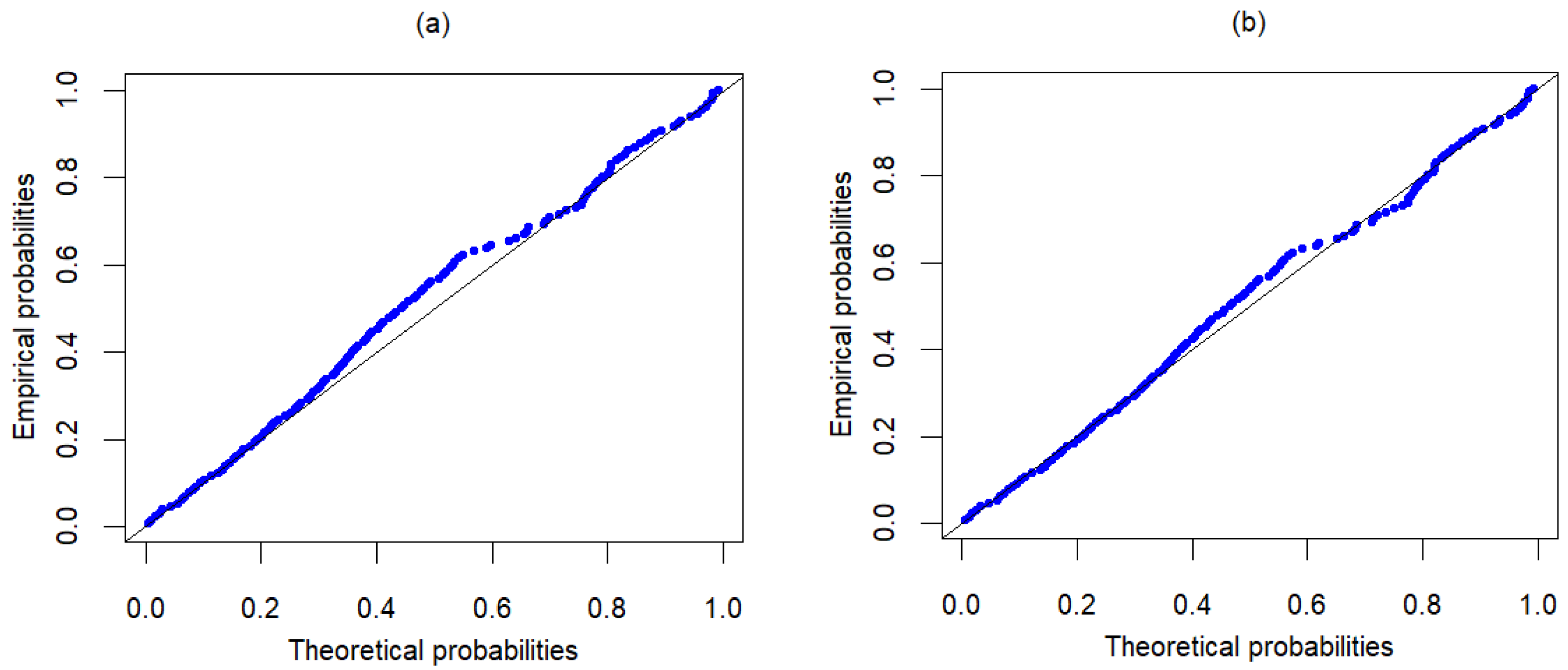
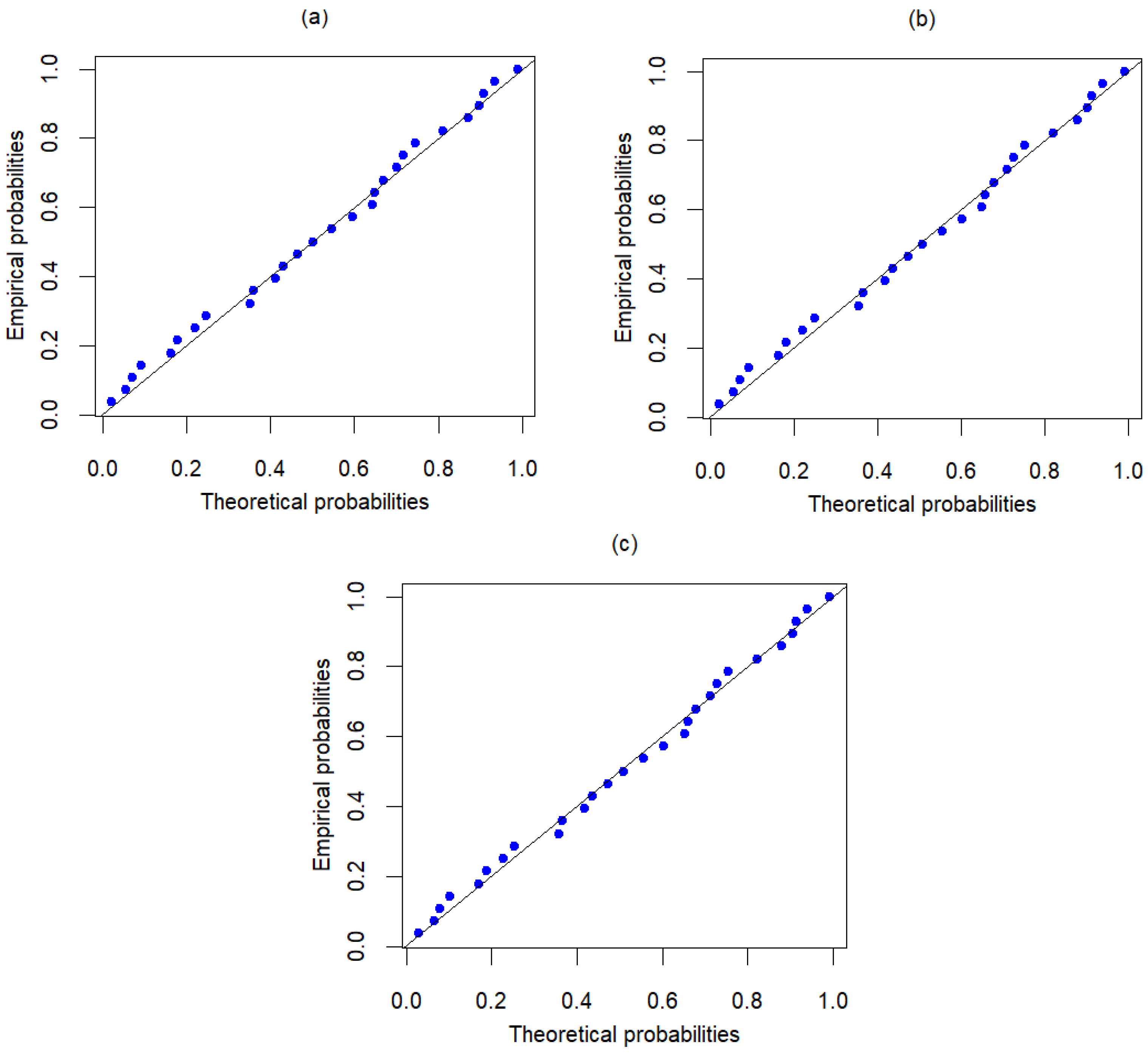
6. Application on Real Data
6.1. The Number of Successive Failures
6.2. March Precipitation
6.3. Breaking Stress of Carbon Fibers
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adamidis, K.; Loukas, S. A Lifetime Distribution with Decreasing Failure Rate. Stat. Probab. Lett. 1998, 39, 35–42. [Google Scholar] [CrossRef]
- Louzada, F.; Roman, M.; Cancho, V.G. The Complementary Exponential Geometric Distribution: Model, Properties, and a Comparison with Its Counterpart. Comput. Stat. Data Anal. 2011, 55, 2516–2524. [Google Scholar] [CrossRef]
- Barreto-Souza, W.; de Morais, A.L.; Cordeiro, G.M. The Weibull-Geometric Distribution. J. Stat. Comput. Simul. 2011, 81, 645–657. [Google Scholar] [CrossRef] [Green Version]
- Tojeiro, C.; Louzada, F.; Roman, M.; Borges, P. The Complementary Weibull Geometric Distribution. J. Stat. Comput. Simul. 2014, 84, 1345–1362. [Google Scholar] [CrossRef]
- Zakerzadeh, H.; Mahmoudi, E. A New Two Parameter Lifetime Distribution: Model and Properties. arXiv 2012, arXiv:1204.4248. [Google Scholar]
- Gui, W.; Zhang, H.; Guo, L. The Complementary Lindley-Geometric Distribution and Its Application in Lifetime Analysis. Sankhya B 2017, 79, 316–335. [Google Scholar] [CrossRef]
- Kuş, C. A New Lifetime Distribution. Comput. Stat. Data Anal. 2007, 51, 4497–4509. [Google Scholar] [CrossRef]
- Hemmati, F.; Khorram, E.; Rezakhah, S. A New Three-Parameter Ageing Distribution. J. Stat. Plan. Inference 2011, 141, 2266–2275. [Google Scholar] [CrossRef]
- Lu, W.; Shi, D. A New Compounding Life Distribution: The Weibull–Poisson Distribution. J. Appl. Stat. 2012, 39, 21–38. [Google Scholar] [CrossRef]
- Ismail, E. The Complementary Compound Truncated Poisson-Weibull Distribution for Pricing Catastrophic Bonds for Extreme Earthquakes. Br. J. Econ. Manag. Trade 2016, 14, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Alkarni, S.; Oraby, A. A Compound Class of Poisson and Lifetime Distributions. J. Stat. Appl. Probab. 2012, 1, 45–51. [Google Scholar] [CrossRef]
- Gui, W.; Zhang, S.; Lu, X. The Lindley-Poisson Distribution in Lifetime Analysis and Its Properties. Hacet. J. Math. Stat. 2014, 43, 1063–1077. [Google Scholar] [CrossRef]
- Cancho, V.G.; Louzada-Neto, F.; Barriga, G.D.C. The Poisson-Exponential Lifetime Distribution. Comput. Stat. Data Anal. 2011, 55, 677–686. [Google Scholar] [CrossRef]
- Stewart, J. Calculus, 8th ed.; Cengage Learning: Florence, Italy, 2015; pp. 567–576. [Google Scholar]
- Glaser, R.E. Bathtub and Related Failure Rate Characterizations. J. Am. Stat. Assoc. 1980, 75, 667–672. [Google Scholar] [CrossRef]
- Rajshreemishra, K.R. Research scholar in the department of SOMAAS, Jiwaji University Gwalior. A Note on Natural Transformation & Meijer’s G-Function. Int. J. Math. Comput. Res. 2022, 10, 2630–2632. [Google Scholar] [CrossRef]
- Proschan, F. Theoretical Explanation of Observed Decreasing Failure Rate. Technometrics 1963, 5, 375–383. [Google Scholar] [CrossRef]
- Hinkley, D. On Quick Choice of Power Transformation. J. R. Stat. Soc. Ser. C. Appl. Stat. 1977, 26, 67–69. [Google Scholar] [CrossRef]
- Nichols, M.D.; Padgett, W.J. A Bootstrap Control Chart for Weibull Percentiles. Qual. Reliab. Eng. Int. 2006, 22, 141–151. [Google Scholar] [CrossRef]

| Distribution | n | Estimator | Mean Estimate | Min | Max | MSE |
|---|---|---|---|---|---|---|
| CGZTP (1,2,1) | 50 | 1.7122 | 0.0001 | 17.6696 | 5.3198 | |
| 1.9225 | 0.1245 | 4.3819 | 0.4782 | |||
| 1.0064 | 0.4106 | 1.9742 | 0.0519 | |||
| 100 | 1.6464 | 0.0002 | 15.5108 | 4.5325 | ||
| 1.8901 | 0.2544 | 3.9272 | 0.3659 | |||
| 0.9864 | 0.5593 | 1.6377 | 0.0272 | |||
| 1000 | 1.0225 | 0.0005 | 7.3604 | 0.3992 | ||
| 2.0003 | 0.5176 | 2.5456 | 0.0523 | |||
| 0.9965 | 0.6622 | 1.1687 | 0.0025 | |||
| CGZTP (3,1,0.5) | 50 | 2.2571 | 0.0020 | 12.5656 | 4.4487 | |
| 1.4061 | 0.1748 | 3.1618 | 0.5402 | |||
| 0.5503 | 0.2714 | 1.1914 | 0.0193 | |||
| 100 | 2.4622 | 0.0027 | 10.0311 | 3.4684 | ||
| 1.2759 | 0.2918 | 2.7858 | 0.3293 | |||
| 0.5294 | 0.3194 | 0.8996 | 0.0092 | |||
| 1000 | 2.9382 | 0.7820 | 7.2618 | 0.8841 | ||
| 1.0504 | 0.3924 | 1.7449 | 0.0597 | |||
| 0.5049 | 0.3728 | 0.6275 | 0.0015 | |||
| CGZTP (3,0.5,0.5) | 50 | 2.3268 | 0.0015 | 14.3020 | 4.5848 | |
| 0.715 | 0.0946 | 1.8241 | 0.1518 | |||
| 0.5386 | 0.2916 | 1.0680 | 0.0165 | |||
| 100 | 2.5139 | 0.0002 | 12.7619 | 3.679 | ||
| 0.6553 | 0.0989 | 1.4855 | 0.0981 | |||
| 0.5265 | 0.3043 | 0.8963 | 0.0086 | |||
| 1000 | 2.853 | 0.5444 | 7.7735 | 0.7855 | ||
| 0.5561 | 0.1756 | 0.9525 | 0.0159 | |||
| 0.5098 | 0.3992 | 0.6041 | 0.0010 |
| CP | AL | |||
|---|---|---|---|---|
| 50 | 0.9130 | 1.4147 | ||
| 100 | 0.9090 | 1.0495 | ||
| 1000 | 0.9530 | 0.3411 | ||
| 50 | 0.8920 | 2.6400 | ||
| 100 | 0.9130 | 1.9795 | ||
| 1000 | 0.9550 | 0.6626 | ||
| 50 | 0.9800 | 6.0251 | ||
| 100 | 0.9610 | 4.5462 | ||
| 1000 | 0.9520 | 1.3820 | ||
| 50 | 0.9840 | 6.2418 | ||
| 100 | 0.9580 | 5.2028 | ||
| 1000 | 0.9560 | 1.7814 | ||
| 50 | 0.9670 | 0.5587 | ||
| 100 | 0.9640 | 0.3832 | ||
| 1000 | 0.9470 | 0.1144 | ||
| 50 | 0.9710 | 1.0991 | ||
| 100 | 0.9630 | 0.7861 | ||
| 1000 | 0.9530 | 0.2311 | ||
| Minimum | Maximum | Median | Mean | Skewness | SD | |
|---|---|---|---|---|---|---|
| 213 | 1.00 | 603.00 | 57.00 | 93.14 | 1.6665 | 106.7636 |
| Distribution | Estimates | K-S | p-Value | AIC |
|---|---|---|---|---|
| CGZTP | 0.0561 | 0.5136 | 2364.206 | |
| Gamma | 0.0574 | 0.4826 | 2360.642 |
| Minimum | Maximum | Median | Mean | Skewness | SD | |
|---|---|---|---|---|---|---|
| 30 | 0.320 | 4.750 | 1.470 | 1.675 | 1.1447 | 1.0006 |
| Distribution | Estimates | K-S | p-Value | AIC |
|---|---|---|---|---|
| CGZTP | 0.05480 | 0.9999906 | 82.221 | |
| Gamma | 0.05552 | 0.9999868 | 80.197 | |
| WP | 0.05709 | 0.9999734 | 82.506 |
| Minimum | Maximum | Median | Mean | Skewness | SD | |
|---|---|---|---|---|---|---|
| 100 | 0.390 | 5.560 | 2.700 | 2.621 | 0.3738 | 1.0139 |
| Distribution | Estimates | K-S | p-Value | AIC |
|---|---|---|---|---|
| CGZTP | 0.0788 | 0.5639 | 289.334 | |
| Gamma | 0.0933 | 0.3484 | 290.467 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niyomdecha, A.; Srisuradetchai, P. Complementary Gamma Zero-Truncated Poisson Distribution and Its Application. Mathematics 2023, 11, 2584. https://doi.org/10.3390/math11112584
Niyomdecha A, Srisuradetchai P. Complementary Gamma Zero-Truncated Poisson Distribution and Its Application. Mathematics. 2023; 11(11):2584. https://doi.org/10.3390/math11112584
Chicago/Turabian StyleNiyomdecha, Ausaina, and Patchanok Srisuradetchai. 2023. "Complementary Gamma Zero-Truncated Poisson Distribution and Its Application" Mathematics 11, no. 11: 2584. https://doi.org/10.3390/math11112584







