Traveling Wave Optical Solutions for the Generalized Fractional Kundu–Mukherjee–Naskar (gFKMN) Model
Abstract
:1. Introduction
2. Mathematical Analysis of the Model
3. Expansion Methods
4. Solving Equation (1)
4.1. Solutions via First Exponential Expansion
4.2. Solutions via Second Exponential Expansion
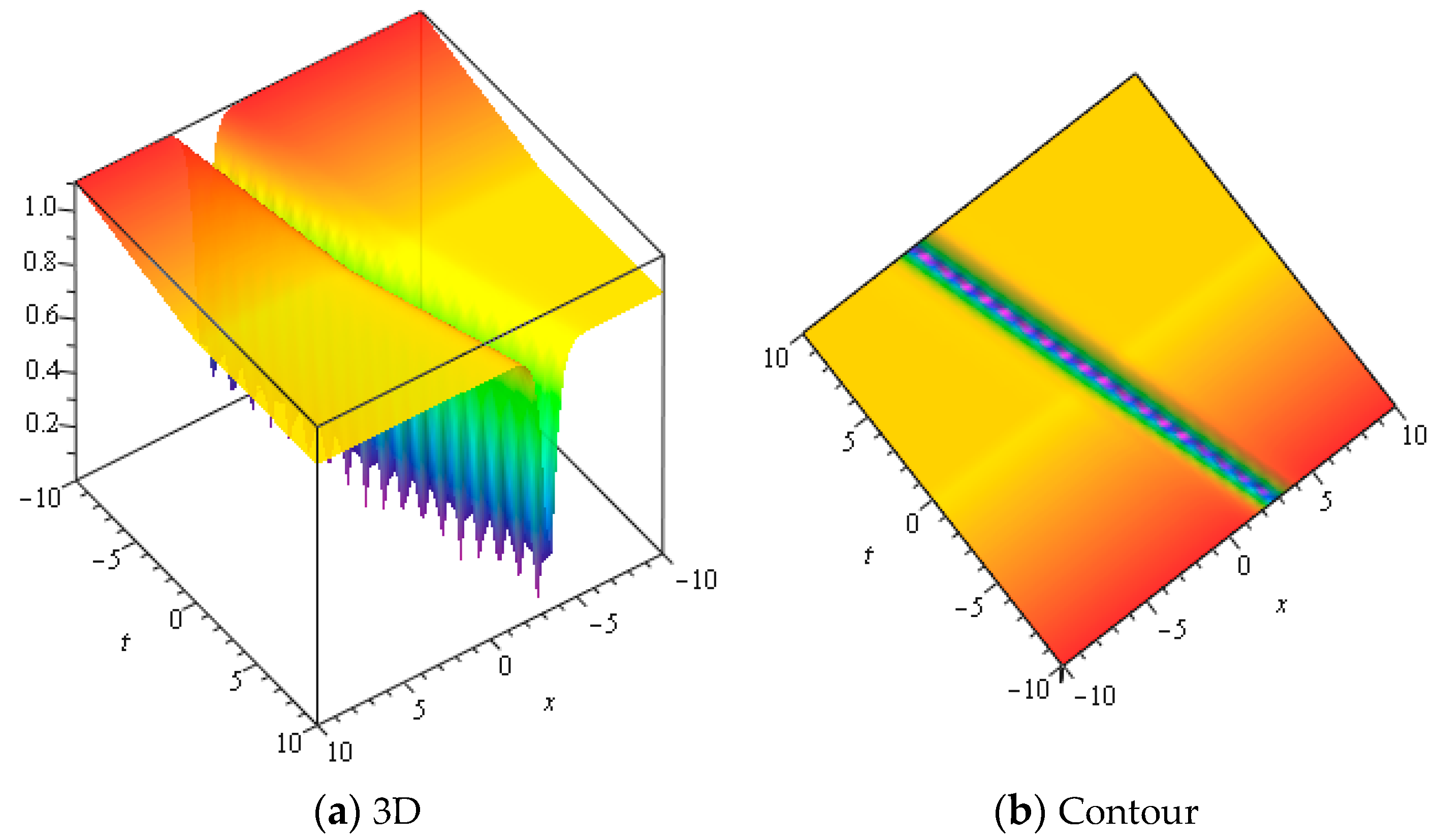
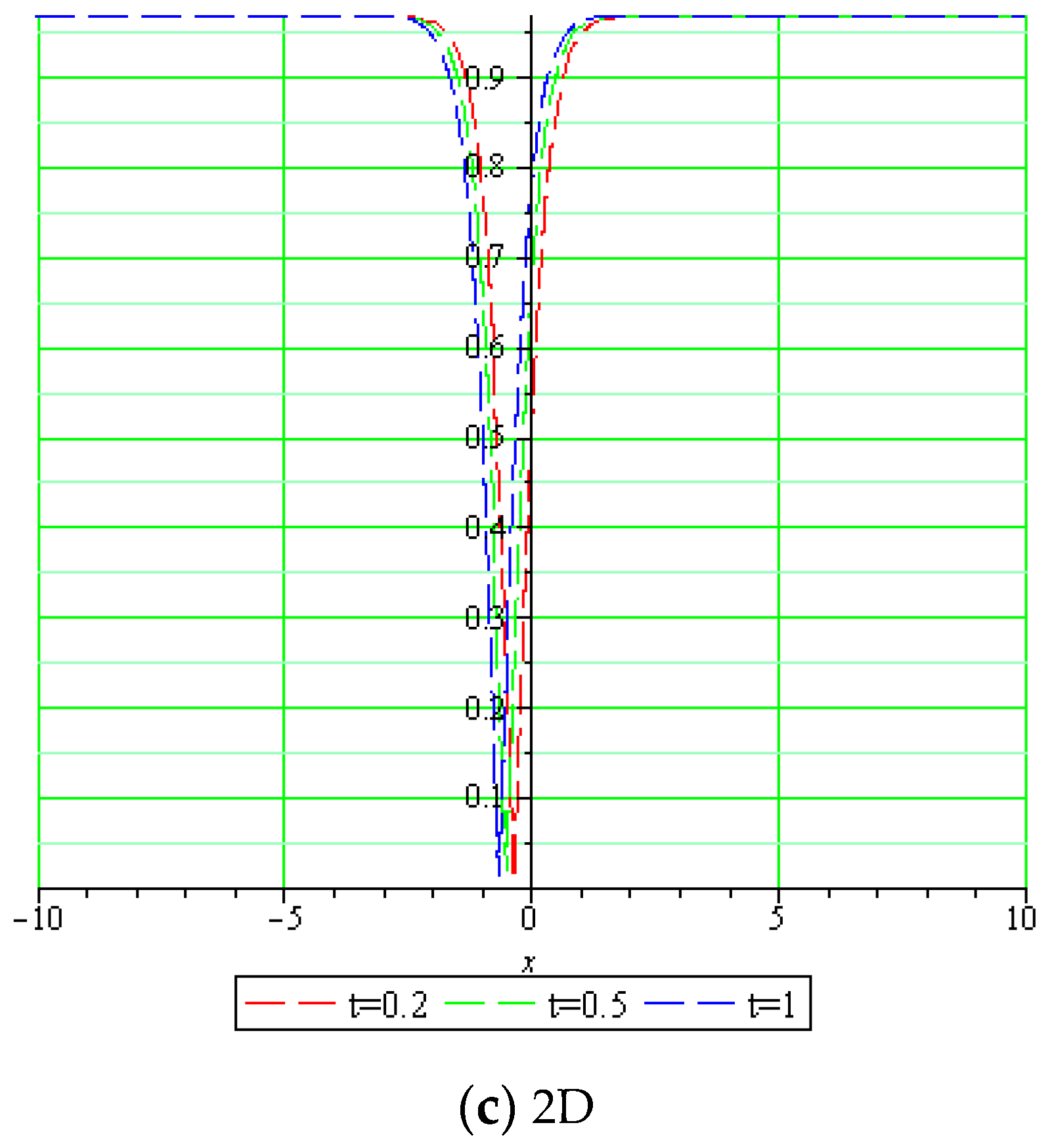
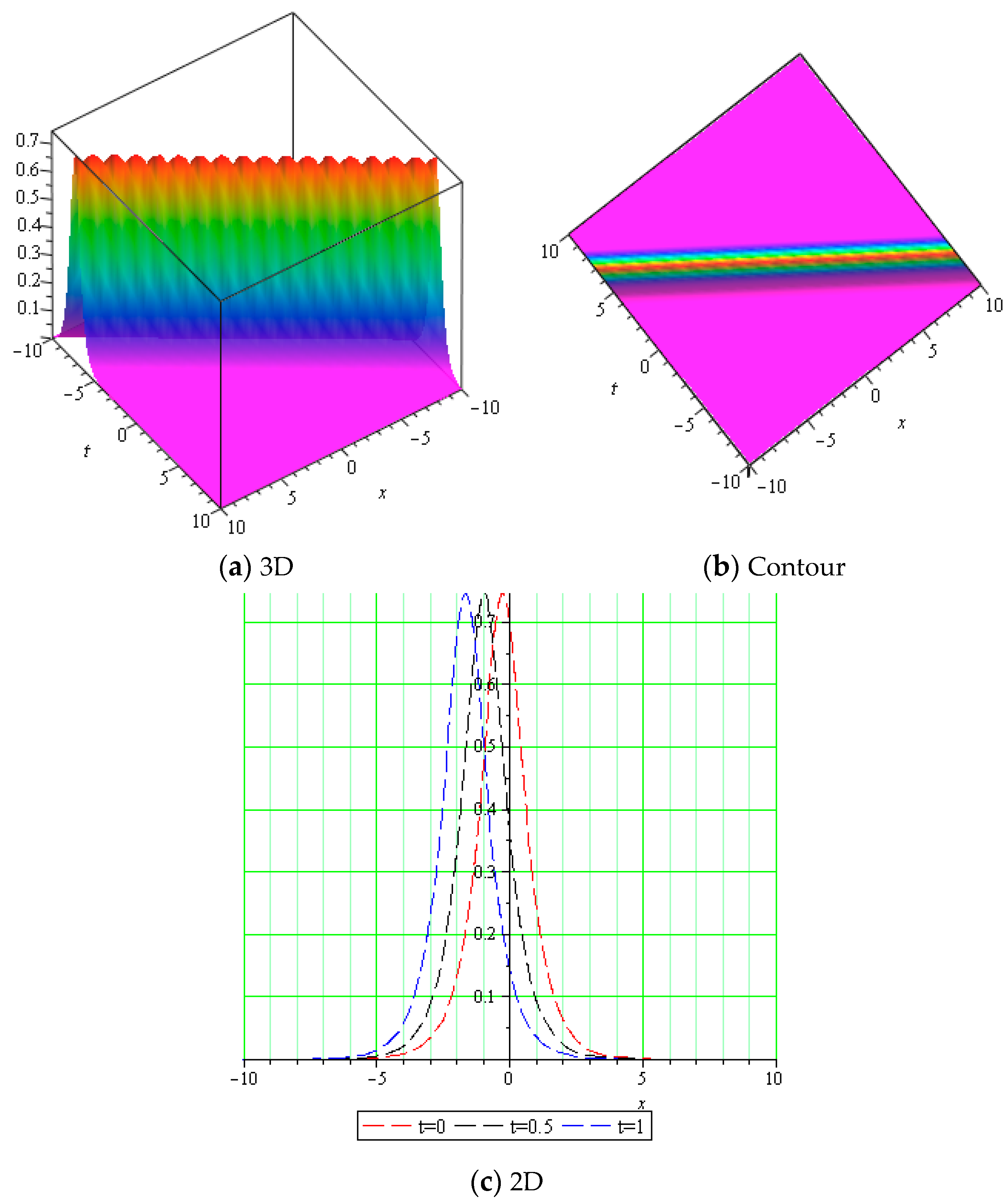
5. Physical Explanation
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raza, N.; Osman, M.S.; Abdel-Aty, A.H.; Abdel-Khalek, S.; Besbes, H.R. Optical solitons of space-time fractional Fokas-Lenells equation with two versatile integration architectures. Adv. Differ. Equ. 2020, 2020, 517. [Google Scholar] [CrossRef]
- Ghanbari, B. On novel nondifferentiable exact solutions to local fractional Gardner’s equation using an effective technique. Math. Methods Appl. Sci. 2021, 44, 4673–4685. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New Complex Hyperbolic Structures to the Lonngren-Wave Equation by Using Sine-Gordon Expansion Method. Appl. Math. Nonlinear Sci. 2019, 4, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Jiong, S. Auxiliary equation method for solving nonlinear partial differential equations. Phys. Lett. A 2003, 309, 387–396. [Google Scholar] [CrossRef]
- Akinyemi, L.; Mirzazadeh, M.; Amin Badri, S.; Hosseini, K. Dynamical solitons for the perturbated Biswas-Milovic equation with Kudryashov’s law of refractive index using the first integral method. J. Mod. Opt. 2022, 69, 172–182. [Google Scholar] [CrossRef]
- Hashemi, M.S.; İnç, M.; Bayram, M. Symmetry properties and exact solutions of the time fractional Kolmogo-rov-Petrovskii-Piskunov equation. Rev. Mex. Fis. 2019, 65, 529–535. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, K.; Ansari, R. New exact solutions of nonlinear conformable time-fractional Boussinesq equations using the modified Kudryashov method. Waves Random Complex Media 2017, 27, 628–636. [Google Scholar] [CrossRef]
- Khater, M.M.; Lu, D.; Attia, R.A. Dispersive long wave of nonlinear fractional Wu-Zhang system via a modified auxiliary equation method. AIP Adv. 2019, 9, 25003. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.; Kaplan, M. New analytical solutions of (2+1)-dimensional conformable time fractional Zoomeron equation via two distinct techniques. Chin. J. Phys. 2018, 56, 2173–2185. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, W.; Xia, Y.; Bai, Y. A Unified Analysis of Exact Traveling Wave Solutions for the Fractional-Order and Integer-Order Biswas–Milovic Equation: Via Bifurcation Theory of Dynamical System. Qual. Theory Dyn. Syst. 2020, 19, 11. [Google Scholar] [CrossRef]
- Younas, U.; Ren, J.; Akinyemi, L.; Rezazadeh, H. On the multiple explicit exact solutions to the double-chain DNA dynamical system. Math. Methods Appl. Sci. 2023, 46, 6309–6323. [Google Scholar] [CrossRef]
- Naeem, M.; Rezazadeh, H.; Khammash, A.A.; Shah, R.; Zaland, S. Analysis of the Fuzzy Fractional-Order Solitary Wave Solutions for the KdV Equation in the Sense of Caputo-Fabrizio Derivative. J. Math. 2022, 2022, 3688916. [Google Scholar] [CrossRef]
- Kumar, D.; Yildirim, A.; Kaabar, M.K.A.; Rezazadeh, H.; Samei, M.E. Exploration of some novel solutions to a coupled Schrödinger–KdV equations in the interactions of capillary-gravity waves. Math. Sci. 2022, 1–13. [Google Scholar] [CrossRef]
- Rao, R.; Lin, Z.; Ai, X.; Wu, J. Synchronization of Epidemic Systems with Neumann Boundary Value under Delayed Impulse. Mathematics 2022, 10, 2064. [Google Scholar] [CrossRef]
- Kudryashov, N.A. General solution of traveling wave reduction for the Kundu–Mukherjee–Naskar model. Optik 2019, 186, 22–27. [Google Scholar] [CrossRef]
- Cimpoiasu, R.; Rezazadeh, H.; Florian, D.A.; Ahmad, H.; Nonlaopon, K.; Altanji, M. Symmetry reductions and invariant-group solutions for a two-dimensional Kundu–Mukherjee–Naskar model. Results Phys. 2021, 28, 104583. [Google Scholar] [CrossRef]
- Jhangeer, A.; Seadawy, A.R.; Ali, F.; Ahmed, A. New complex waves of perturbed Shrödinger equation with Kerr law nonlinearity and Kundu-Mukherjee-Naskar equation. Results Phys. 2020, 16, 102816. [Google Scholar] [CrossRef]
- Yıldırım, Y. Optical solitons to Kundu–Mukherjee–Naskar model with trial equation approach. Optik 2019, 183, 1061–1065. [Google Scholar] [CrossRef]
- Bashar, H.; Arafat, S.Y.; Islam, S.R.; Rahman, M. Extraction of some optical solutions to the (2+1)-dimensional Kundu–Mukherjee–Naskar equation by two efficient approaches. Partial Differ. Equ. Appl. Math. 2022, 6, 100404. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Kaabar, M.K. A Generalized Definition of the Fractional Derivative with Applications. Math. Probl. Eng. 2021, 2021, 9444803. [Google Scholar] [CrossRef]
- Martínez, F.; Kaabar, M.K.A. A Novel Theoretical Investigation of the Abu-Shady–Kaabar Fractional Derivative as a Modeling Tool for Science and Engineering. Comput. Math. Methods Med. 2022, 2022, 4119082. [Google Scholar] [CrossRef]
- Günerhan, H.; Khodadad, F.S.; Rezazadeh, H.; Khater, M.M. Exact optical solutions of the (2+1) dimensions Kundu–Mukherjee–Naskar model via the new extended direct algebraic method. Int. J. Mod. Phys. B 2020, 34, 2050225. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Afzal, I.; Ali, K. Dark and singular optical solitons for Kundu–Mukherjee–Naskar model. Int. J. Mod. Phys. B 2020, 34, 2050074. [Google Scholar] [CrossRef]
- Talarposhti, R.A.; Jalili, P.; Rezazadeh, H.; Jalili, B.; Ganji, D.D.; Adel, W.; Bekir, A. Optical soliton solutions to the (2+ 1)-dimensional Kundu–Mukherjee–Naskar equation. Int. J. Mod. Phys. B 2020, 34, 2050102. [Google Scholar] [CrossRef]
- Onder, I.; Secer, A.; Ozisik, M.; Bayram, M. On the optical soliton solutions of Kundu–Mukherjee–Naskar equation via two different analytical methods. Optik 2022, 257, 168761. [Google Scholar] [CrossRef]
- Zafar, A.; Raheel, M.; Ali, K.K.; Inc, M.; Qaisar, A. Optical solitons to the Kundu–Mukherjee–Naskar equation in (2+1)-dimensional form via two analytical techniques. J. Laser Appl. 2022, 34, 022024. [Google Scholar] [CrossRef]
- Kumar, D.; Paul, G.C.; Biswas, T.; Seadawy, A.R.; Baowali, R.; Kamal, M.; Rezazadeh, H. Optical solutions to the Kundu-Mukherjee-Naskar equation: Mathematical and graphical analysis with oblique wave propagation. Phys. Scr. 2020, 96, 025218. [Google Scholar] [CrossRef]
- Ekici, M.; Sonmezoglu, A.; Biswas, A.; Belic, M.R. Optical solitons in (2+1)–Dimensions with Kundu–Mukherjee–Naskar equation by extended trial function scheme. Chin. J. Phys. 2019, 57, 72–77. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Bulut, H. The new extended rational sgeem for construction of optical solitons to the (2+1)–dimensional kundu–mukherjee–naskar model. Appl. Math. Nonlinear Sci. 2019, 4, 513–522. [Google Scholar] [CrossRef] [Green Version]
- He, J.H. Variational principle and periodic solution of the Kundu–Mukherjee–Naskar equation. Results Phys. 2020, 17, 103031. [Google Scholar] [CrossRef]
- Wang, K.-J.; Zhu, H.-W. Periodic wave solution of the Kundu-Mukherjee-Naskar equation in birefringent fibers via the Hamiltonian-based algorithm. EPL Europhysics Lett. 2020, 139, 35002. [Google Scholar] [CrossRef]
- Khater, M.M. Extended Exp (-(ξ))-Expansion Method for Solving the Generalized Hirota-Satsuma Coupled KdV System. Glob. J. Sci. Front. Res. 2015, 15, 1–15. [Google Scholar]
- Harun-Or-Roshid, M.; Rahman, A. The exp (−Φ(η))-expansion method with application in the (1+1)-dimensional classical Boussinesq equations. Results Phys. 2014, 4, 150–155. [Google Scholar] [CrossRef] [Green Version]
- Islam, R.; Alam, M.N.; Hossain, A.K.M.K.S.; Roshid, H.O.; Akbar, M.A. Traveling wave solutions of nonlinear evolution equations via Exp (−Φ(η))-expansion method. Glob. J. Sci. Front. Res. 2013, 13, 63–71. [Google Scholar]
- Akbulut, A.; Kaplan, M.; Tascan, F. The investigation of exact solutions of nonlinear partial differential equations by using exp (− Φ (ξ)) method. Optik 2017, 132, 382–387. [Google Scholar] [CrossRef]
- Rahman, N.; Akter, S.; Roshid, H.O.; Alam, M.N. Traveling wave solutions of the (1+ 1)-dimensional compound KdVB equation by exp (−Φ(η))-expansion method. Glob. J. Sci. Front. Res. 2014, 13, 7–13. [Google Scholar]
- Akbar, M.A.; Ali, N.H.M. Solitary wave solutions of the fourth order Boussinesq equation through the exp (–Φ(η))-expansion method. Springer Plus 2014, 3, 344. [Google Scholar] [CrossRef] [Green Version]
- Hafez, M.G.; Akbar, M.A. An exponential expansion method and its application to the strain wave equation in microstructured solids. Ain Shams Eng. J. 2015, 6, 683–690. [Google Scholar] [CrossRef] [Green Version]
- Hafez, M.G.; Kauser, M.A.; Akter, M.T. Some New Exact Traveling Wave Solutions for the Zhiber-Shabat Equation. Br. J. Math. Comput. Sci. 2014, 4, 2582–2593. [Google Scholar] [CrossRef]
- Hafez, M.; Alam, M.; Akbar, M. Traveling wave solutions for some important coupled nonlinear physical models via the coupled Higgs equation and the Maccari system. J. King Saud Univ.-Sci. 2015, 27, 105–112. [Google Scholar] [CrossRef] [Green Version]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y. Traveling Wave Optical Solutions for the Generalized Fractional Kundu–Mukherjee–Naskar (gFKMN) Model. Mathematics 2023, 11, 2583. https://doi.org/10.3390/math11112583
Tang Y. Traveling Wave Optical Solutions for the Generalized Fractional Kundu–Mukherjee–Naskar (gFKMN) Model. Mathematics. 2023; 11(11):2583. https://doi.org/10.3390/math11112583
Chicago/Turabian StyleTang, Yong. 2023. "Traveling Wave Optical Solutions for the Generalized Fractional Kundu–Mukherjee–Naskar (gFKMN) Model" Mathematics 11, no. 11: 2583. https://doi.org/10.3390/math11112583




