Abstract
It is well known in quantum mechanics that the theory of quantum transitions is based on the convergence of the series of time-dependent perturbation theory. This series converges in atomic and nuclear physics. However, in molecular and chemical physics, this series converges only in the Born–Oppenheimer adiabatic approximation and due to the application of the Franck–Condon principle, and it diverges as a result of going beyond the adiabatic approximation and the Franck–Condon principle. This divergence (singularity) is associated with the incommensurability of the masses of light electrons and heavy nuclei which jointly participate in the full-fledged movement in the transient state of molecular “quantum” transitions. In a new physical theory—quantum–classical mechanics (Egorov, V.V. Heliyon Physics 2019, 5, e02579)—this singularity is damped by introducing chaos into the transient state. This transient chaos is introduced by replacing the infinitely small imaginary additive in the energy denominator of the spectral representation of the total Green’s function of the system with a finite value and is called dozy chaos. In this article, resonance at the nanoscale (nano-resonance) between electron and nuclear reorganization motions in the quantum–classical (dozy-chaos) mechanics of elementary electron transfers in condensed media and their applications to polymethine dyes and J-aggregates in solutions are reviewed. Nano-resonance explains the resonant character of the transformation of the shape of the optical absorption band in a series of polymethine dyes in which the length of the polymethine chain changes, as well as the nature of the red-shifted absorption band of the J-aggregates of polymethine dyes (J-band), which is narrow and intense. The process of dye aggregation in an aqueous solution with an increase in its concentration by the formation of J-aggregates is considered a structural tuning of the “polymethine dye + environment” system into resonance with light absorption. For J-aggregates in Langmuir films, the asymmetry of the luminescence and absorption bands, as well as the small value of their Stokes shifts, are explained. The parasitic transformation of the resonant shape of the optical absorption band of a polymethine dye in solution during the transition from one-photon to two-photon absorption is also explained, and the conditions for the restoration of this nano-resonance shape are predicted.
Keywords:
dozy-chaos mechanics; charge transfer; condensed matter; optical band shapes; polymethine dyes; J-aggregates; Egorov nano-resonance MSC:
81-08; 81-10; 81-11; 81P40; 81P99; 81Q50; 81Q99; 81V55; 81V70; 81V80; 81V99 78-10; 78-11; 78A99
1. Introduction
It is well known that classical mechanics cannot describe, for example, a hydrogen atom. Therefore, more than a hundred years ago, the need arose to create a new mechanics, namely quantum mechanics. However, quantum mechanics, like classical mechanics, has a wide but still limited area of applicability. For example, one of the main branches of quantum mechanics, the theory of quantum transitions, is, strictly speaking, inapplicable to molecular and chemical physics [1,2,3,4,5,6,7,8].
In other words, from general physical considerations, one should expect that “quantum” transitions in molecules and condensed matter are not at all what quantum transitions are in atoms, and “quantum” transitions in molecular and chemical physics are not at all what quantum transitions are in atomic physics. In the latter cases, the dynamics of the transition are insignificant and can be neglected, while in the former cases, these dynamics play a fundamentally important role in the physics of the transition, and its correct accounting is a fundamental physical problem [5]. Such molecular “quantum” transitions, in which the dynamics of the transitions cannot be neglected, we call extended transitions. For example, extended transitions take place in an extended polymethine chain—the main optical chromophore of polymethine dyes (see below, Section 4).
The dynamics of extended transitions are determined by the dynamics of the electronic and nuclear subsystems of the molecular system. It turns out that the interaction of these two subsystems in the transition dynamics can lead to some resonance in their motions, despite the strong difference in the masses of the light electronic subsystem and the very heavy nuclear subsystem. Since the region of space of the molecular system, in which such a resonant transition is localized, is on the order of a nanometer, we call this resonant transition a nano-resonance. According to a recent ACS article [9], this nano-resonance is also called Egorov resonance (a dynamic electron–nuclear-reorganization resonance, see below, Section 3). This dynamic electron–nuclear-reorganization resonance or Egorov nano-resonance is one of the main theoretical foundations of nanophotonics and modern photochemistry.
Apparently, the first to realize the aforementioned inapplicability of quantum mechanics to molecular and chemical physics were Max Born and Robert Oppenheimer [10], who, with their adiabatic approximation (see [11,12,13,14]), proposed to separate the motion of light electrons from the motion of heavy nuclei in a stationary state, thus avoiding consideration of the problem of their joint full-fledged motion. The proposal of the Franck–Condon principle [15,16,17,18] made it possible to avoid considering the problem of the joint full-fledged motion of electrons and nuclei also in the process of the “quantum” transition itself [5]. As a result, the whole problem of the dynamics of the “quantum” electron–nuclear or electronic–vibrational transition was ignored. Good agreement between this theoretical picture and the experimental data on the optical spectra of molecules [19,20,21] played a false role in this respect.
However, as soon as we pose, in theory, the question of considering the full-fledged joint motion of electrons and nuclei in the process of transitions, we immediately get a singularity in the transition rates [5]. The presence of this singularity in the dynamics of transitions is associated with the incommensurability of the masses of a light electron and the heavy nuclei with which it interacts during the transition [5].
The presence of such a singular point can be easily shown using the simplest problem from quantum mechanics, namely the problem of a one-dimensional potential box, in which we consider one of the walls to be movable (Figure 1a). Such a box is a primitive albeit convenient model for understanding transitions in a molecule in which, along with an electronic transition, the equilibrium positions of oscillating nuclei are shifted, or in other words, the nuclear subsystem is reorganized. The movable wall of the box simulates this reorganization of the nuclei. A standard potential box with a rigid, fixed wall is, in this case, a primitive model of the atom.
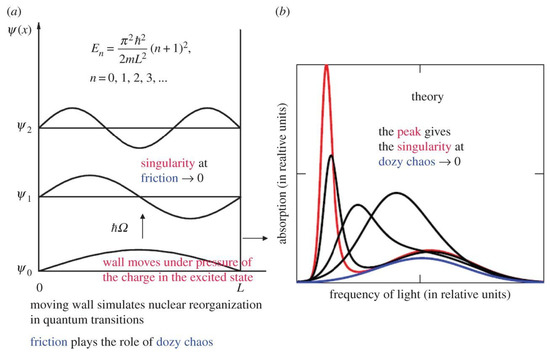
Figure 1.
The simplest demonstration of singularity in the rate of molecular “quantum” transitions [5,6,7,8]. (a) The physical picture of quantum transitions in a potential box with a moving wall simulates the presence of a singularity in molecular “quantum” transitions when the wall moves without friction [5,6,7,8]. The case of a wall moving with friction corresponds to quantum–classical (dozy-chaos) mechanics [5,22,23,24], in which dozy chaos plays the role of friction. (b) Shapes of optical absorption bands obtained from dozy-chaos mechanics, as a function of dozy-chaos intensity [5,6,7,8]. The band with the most pronounced peak (J-band) corresponds to the weakest dozy chaos. (Original citation)—Reproduced by permission of The Royal Society of Chemistry.
In order to avoid a singularity in the rate of the transition, we must introduce friction at the base of the wall moving during the transition. A similar procedure should be carried out in exact theory. In the optical version of the new theory, we have, as a result, a set of shapes of optical absorption bands (Figure 1b). With a decrease in friction, which in the exact theory is called transient or dozy chaos [5,25,26], such a transformation of the band shape occurs that when chaos tends to zero, we obtain a band shape tending to singular band shape (Figure 1b).
Now let’s take a quick look at the formal part of the problem. By definition, in atomic and nuclear physics, quantum transitions are quantum jumps, or in other words, the dynamics of the transient state are insignificant there and can certainly be neglected [5]. In this case, the rates of transitions in atoms and nuclei are determined only by the characteristics of the initial and final states. The fact that the dynamics of the transient state in atomic and nuclear physics are insignificant leads to the convergence of the series of time-dependent perturbation theory, on which the theory of quantum transitions in quantum mechanics is based. We have a completely different physical picture for molecular and chemical physics. “Quantum” transitions there are formed both from electronic transitions and from the accompanying structural reorganization of the nuclear subsystem. As a result of electronic transitions, the electron charge density is redistributed in space. As a result of the reorganization of the nuclear subsystem, there is a shift in the equilibrium positions of oscillating nuclei, which, due to the presence of the interaction of their charges with the charges of electrons, are forced to adapt to the new distribution of the electronic charge in space. Thus, in contrast to atomic and nuclear quantum transitions, in “quantum” transitions in molecular and condensed matter it is necessary to take into account the dynamics of the strong Coulomb interaction between light electrons and very heavy nuclei. In other words, in molecules and condensed matter, there is a transient state of dynamics in “quantum” transitions, and it can be significant in calculating the transition rates there. The first theoretical work that took into account the interaction of light electrons and very heavy nuclei was the theory of molecules by Born and Oppenheimer [10]. This theory is based on the adiabatic approximation. The Born–Oppenheimer adiabatic approximation [10,11,12,13,14] makes it possible in principle to calculate the structure of molecules by “turning off” the light electron subsystem from the dynamics of the joint motion of electrons and nuclei. The role of light, and therefore adiabatically fast, electrons is reduced only to the creation of an electric potential for oscillating nuclei. If now, when considering “quantum” transitions, we assume that the initial and final states are adiabatic, then, similarly to atomic and nuclear physics, the series of time-dependent perturbation theory in molecular and chemical physics will converge. This fact forms the formal basis of the well-known Franck–Condon principle [15,16,17,18] in molecular spectroscopy [19,20,21]. In other words, the convergence of the series of time-dependent perturbation theory here is due to the neglect of the electron-nuclear dynamics in the transient state. Accounting for these dynamics in the framework of quantum mechanics leads, due to the incommensurability of the masses of light electrons and heavy nuclei, to the divergence of the series of time-dependent perturbation theory, and, accordingly, to a singularity in the rates of “quantum” transitions in molecular and chemical physics [5]. Using the example of solving the simplest problem in chemical physics, namely, the problem of elementary electron transfers in condensed media, it is shown that this singularity can be damped by introducing chaos into the dynamics of the joint motion of electrons and nuclei in the transient state [5]. However, the introduction of damping chaos, which we call dozy chaos, takes the theory beyond quantum mechanics and leads us to a new physical theory, namely dozy-chaos mechanics. In this new mechanics, the electron-nuclear transient state is chaotic, while the initial and final states are quantum in the adiabatic approximation. At the same time, due to chaos in the transient state, the electron-nuclear(-vibrational) spectrum of energy there turns out to be continuous, which is a characteristic feature of classical mechanics. Therefore, the new mechanics, along with dozy-chaos mechanics, can be called quantum–classical mechanics (QCM). The efficient performance of QCM has been demonstrated by the successful theoretical interpretation of a large number of experiments, in particular, by applying the Egorov nano-resonance discussed above to explaining the shape of the optical bands in polymethine dyes and their J-aggregates [1,4,5,6,7,8,9,22,23,24,25,26]. The application of QCM to the optical spectra of polymethine dyes in the case of two-photon absorption makes it possible, in particular, to comprehend experimental data in the field of photodynamic therapy and bioimaging (see [1,4,9] and references therein). Prospects for further developments in QCM and their possible applications to various problems are discussed in [1,2,3,4,5,25,26,27].
2. Quantum–Classical Mechanics in Brief
The exact theory is constructed for the simplest case of the dynamics of the relationship between the electron and nuclear motions, namely in the case of elementary electron transfers in condensed matter [5]. It was in the case of this problem that the Egorov nano-resonance was discovered [22,23,24]: the region of space of the molecular system, in which such a resonant transition is localized, is determined by the distance between the donor and acceptor, when it is on the order of a nanometer.
The Hamiltonian for this problem has the form [5,11,22,23,24,25,26]
where the first term corresponds to the kinetic energy of the electron with an effective mass , the last term corresponds to the kinetic and potential energy of vibrations of the nuclei of the medium in the harmonic approximation, are the real normal phonon coordinates, are the phonon frequencies, and are the potential wells of the electron donor 1 and acceptor 2 separated by distance , the term corresponds to the electron–phonon interaction, is the phonon index.
The considered below energy (Section 3)
is the energy of reorganization of the medium nuclei associated with the localization of an electron on the donor or acceptor. The quantities are the shifts of the normal phonon coordinates associated with this presence of an electron in the medium.
As shown in my pioneering works [22,23,24], an attempt to take into account the transient state dynamics with the Green’s function method in quantum mechanics with Hamiltonian (1) leads to a significant singularity in the rates of “quantum” transitions.
This singularity is eliminated by replacing the infinitesimally small with a finite quantity [5,6,7,8,22,23,24,25,26] in the Green’s function
where are the eigenfunctions of the Hamiltonian (1); are all electronic and nuclear coordinates; are the eigenvalues of , and is the total energy of the system. The aforementioned replacement of with a finite quantity in Equation (3), or in similar Green’s functions of more complex molecular and/or condensed matter systems, lies at the foundation of a new theory—dozy-chaos or quantum–classical mechanics [5] (cf. Section 1).
Comparison of theory with experiment shows that (, see below, Section 5) [1,6,7,8,9,22,23,24,25,26]. Therefore, the energy is not the width of the electron-vibrational energy levels in the transient state, but it is a measure of dynamic or dozy chaos in this state [25,26] and therefore can be called dozy-chaos energy [25,26] (see Figure 1). Transient or dozy chaos consists of chaotic motions of the electronic charge and nuclear reorganization, and also of a fluctuating electromagnetic field (dozy-chaos radiation) that provides interaction between electrons and nuclei [27,28].
The prime cause of the dozy chaos is the light and mobile (in comparison with very heavy nuclei) electron—the dynamics of which, like that of the entire molecular system, is no longer described by quantum mechanics [5]. These chaotic dynamics are described by new, dozy-chaos mechanics [5] (cf. Section 1).
In the name of the new theory, dozy-chaos mechanics, the word “mechanics” reflects its genesis: dozy-chaos mechanics comes from the well-known theory of many-phonon transitions [11], which is a quantum mechanics of condensed matter [3].
Due to chaos, the energy spectrum of the entire system in a transient state is continuous. In other words, the “electron + nuclei” system, which is quantum in the initial and final states (in the Born–Oppenheimer adiabatic approximation [10,11,12,13,14]), becomes classical in nature in the transient state. Therefore, dozy-chaos mechanics can also be called quantum–classical mechanics [5] (cf. Section 1).
Apparently, the root cause of the emergence of dozy chaos lies in the interaction of the actual electron, its charge and spin, with the induction field of optical phonons [3]. However, the clarification of this important issue in theory can be obtained only on the basis of taking into account relativistic effects in it, that is, by generalizing quantum–classical mechanics and creating quantum–classical electrodynamics, similarly to what has already been done in the history of physics when creating quantum electrodynamics [29,30,31] after the creation of quantum mechanics [32,33].
There is an obvious analogy in the history of the discovery of quanta and the discovery of dozy chaos [27]. When creating quantum–classical mechanics, the elimination of the singularity in the rates of molecular “quantum” transitions (arising from quantum mechanics) by introducing chaos into the transient state is similar to the elimination of the singularity in the absorption spectrum of an absolutely black body (arising from classical physics), which gave rise to the creation of the most quantum mechanics [3,5]. However, in the case of quantum mechanics, the then introduced elementary quantum of action, Planck’s constant [34], is a universal physical constant, while in the case of quantum–classical mechanics, the dozy-chaos energy introduced by us is not a universal physical constant and its value depends on a specific physical system.
3. Nano-Resonance
The Egorov nano-resonance (see Section 1) is defined as follows
where
is the characteristic time of electron motion in a donor–acceptor system, is the electron binding energy at the donor 1, the value of is on the order of a nanometer (see below, Section 4, Section 9, Section 11, and Section 13); and
is the characteristic time of the nuclear environment reorganization movement, where the reorganization energy is given by Equation (2). The Egorov nano-resonance is the simplest dynamic expression of quantum order in quantum–classical mechanics. For the simplest dynamic expression of classical disorder in quantum–classical mechanics, see Section 12 below.
4. Nano-Resonance in Polymethine Dyes
Experimentally, the Egorov nano-resonance manifests itself, for example, in polymethine dyes, as shown in Figure 2. In Equation (5) for the nano-resonance, the quantity is also equal to the length of the polymethine chain—the main optical chromophore of polymethine dyes [5,6,7,8,22,23,24,25,26], and the quantity is also equal to the electron energy of the ground state of the dye [5,6,7,8,22,23,24,25,26]. Figure 2 shows the Brooker series [35] of the optical absorption band shapes, which reveals its resonance character. The optical band with corresponds to the nano-resonance or is near to it. The Egorov nano-resonance (Enr) is a bright nano-phenomenon since, for example, for the Brooker series (Figure 2), this resonance is near L (Enr) = 2 (3 + 2) 0.14 nm = 1.4 nm.

Figure 2.
Shapes of optical absorption bands and Egorov nano-resonance (n = 3) in a series of polymethine dyes with varying lengths of polymethine chain L = 2 (n + 2) d, where d are certain roughly equal bond lengths (0.14 nm) in the chain (thiapolymethinecyanine in methanol at room temperature; is the extinction coefficient) [7,8]. (a) Experimental data [35,36] and (b) theoretical modeling [24,37] based on quantum–classical mechanics [5]. (Original citation)—Reproduced by permission of The Royal Society of Chemistry.
The “polymethine dye + environment” system discussed above (Figure 2) is a striking example of applications of the quantum–classical mechanics [5,6,7,8,22,23,24,25,26]: extended quantum–classical transitions in the main optical chromophore of a dye monomer—the polymethine chain—can be approximated by elementary electron-charge transfers. This follows from the concept of the ideal polymethine state (IPS) developed by Dähne [38], according to which a clearly extended -electron charge density strongly alternates along the quasi-linear polymethine chain and is alternatively redistributed during optical excitation [39] (see Figure 3). All polymethine dyes, which are discussed in this article, belong to IPS.

Figure 3.
Alternation of positive (1) and negative (2) charges on carbon atoms along an ideal polymethine chain (IPS) in the ground state [8,38,39]. The distance between nitrogen atoms (N) is the length of the polymethine chain . (Original citation)—Reproduced by permission of The Royal Society of Chemistry.
Extended quantum–classical transitions in the polymethine chain can be approximated by elementary electron-charge transfers since the electron transition moment in the IPS first excited state is focused along the chain [39], and therefore, the distance can be considered as its length (see the caption to Figure 3). The charge structure of the quasi-linear polymethine chain alternating on a scale of rather small distances (Figure 3) makes it possible to almost completely neglect the tunneling effects in the electron-charge transfers within the chain and accordingly to take the tunneling factor in the quantum–classical mechanics of elementary electron-charge transfers close to unity [6,7,8,22,23,24,25,26] (see below, Section 5, Equations (24) and (25), ). In addition, the rather large length of the quasi-linear polymethine chain provides a favorable opportunity for a significant simplification of the structure of the electron-phonon interaction, namely, this fact allows one to neglect the intramolecular vibrations of the polymethine chain itself in the total electron-phonon interaction and to consider only the electron-charge transfers coupling with the nuclear environment vibrations [6,7,8,22,23,24,25,26]. Quantum–chemical calculations [9,40] for thiacyanine [40] and thiapyrylocyanine [9] perfectly confirm such a physical picture in the nano-resonance domain (Equations (4)–(6)) (see also comments in [1], Section 4 there).
5. Analytical Results in the Quantum–Classical Mechanics of Elementary Electron Transfers
In this section, we present the analytical results for absorption band shapes (Equations (7)–(27), is frequency of light) and associated optical extinction coefficient (Equation (28)) [5,6,7,8,11,22,23,24,25,26] shown in Figure 1 and Figure 2 above and many other figures (see sections below). In the framework of the Einstein model of nuclear vibrations () this result is as follows [5,23,24]:
where , is the absolute temperature,
Here, we use the notation
and where we finally have
The factor becomes
where
and
In Equations (12) and (13), is the heat energy associated with the energy of the absorbed photon by the law of energy conservation:
where is the electron binding energy at the acceptor 2. The heat energy fits luminescence [2,6,11] (see below, Equation (31)). The wavelength indicated in figures corresponds to the frequency by the standard formula ( and are the speed of light in vacuum and the refractive index). The time scales from Equation (13) regulate the electron-transfer dynamics. They are considered in [2,5,7,24,25,26,41]. The time scales included in the nano-resonance (Equations (4)–(6)) are the part of Equation (13).
The result for (Equations (7)–(27)) does not change when the sign of the dozy-chaos energy is changed. This symmetry is due to the presence of chaos (dozy-chaos) in the dynamics of the transient “electron-nuclear(-vibrational)” state, in which, due to chaos, motion and energy pass both from the electron to the nuclei, and vice versa, from the nuclei to the electron. The physical meaning of all the constituent elements in Equations (7)–(27) and the associated cause of the optical absorption spectra in theory is discussed in [5,7].
Next, let us pay attention to the fact that not discrete optical spectra, but continuous optical bands, are observed in the experiment, and how this fact is explained in theory. In the standard quantum–mechanical theory [11], which does not take into account the dynamics of “quantum” transitions, within the framework of the Einstein model of nuclear vibrations , the optical absorption spectrum is a set of equidistant absorption lines separated from one another by the phonon frequency (see Figure 2 in [11]). The reason the lines of Figure 2 [11] broaden and merge into a continuous band is the dispersion of the phonon frequencies [11]. It is noteworthy that in quantum–classical mechanics [5], which takes into account the dynamics of the transition, due to the chaotic transient state and its classical nature (, see Section 2), the theoretical optical absorption spectrum is already continuous in the framework of the Einstein model of nuclear vibrations (Equations (7)–(27)).
The optical transition-rate constant and the extinction coefficient are related by the following formula [11]:
where is the totality of electron charge transferred in an elementary act, and is the Avogadro constant.
6. Passage to the Standard Quantum–Mechanical Theory and the Formal Origin of Finite Gamma Values
The standard result in the theory of many-phonon transitions [11] is effected from Equations (7)–(27) by ( according to Equation (12)) in Equation (10) for (see Figure 3 in [5]) and by () in Equation (24) for (see Equation (162) in [5]) [5,23]:
where and . The Gaussian (Marcus, see below) formula
is the well-known, simplest result in the theory of many-phonon transitions for (see [11,12]) and is associated with the works of Marcus on his electron-transfer model [42,43,44,45,46,47] and with the previous works by Huang and Rhys [48], Pekar [49,50,51], Lax [52], Krivoglaz and Pekar [53] and Krivoglaz [54]. Usually, the aforementioned Gaussian formula is called the Marcus formula, and the energy is called the Marcus reorganization energy. In contrast to Equations (7)–(27), where the dynamics of the transient state are properly taken into account, in Equation (29) and the Marcus formula the dynamics of the transient state are completely neglected.
In connection with passage to the standard quantum–mechanical theory by limiting transitions and , we offer two remarks. As mentioned above (Section 2), to eliminate the singularity in the rates of “quantum” transitions, the infinitely small value of in the Green’s function (3) is replaced by its finite value. The formal admissibility of this procedure is due to the following circumstance. Usually, the quantity specifies the rule for bypassing singular points in contour integration. However, in our theory of charge transfers [5,23], some mathematical technique [5,23] manages to perform an exact summation over the intermediate states that are associated with . This “releases from former duties” and lets it gain a new status. The author’s mathematical technique [5,23] is a substantial development of the generating polynomial (generating function) technique of Krivoglaz and Pekar [53,54], and the Krivoglaz–Pekar technique [53,54] in its turn is analogous to computing thermodynamic quantities by the Darwin–Fowler technique [5,11], known from statistical physics.
The second remark is related to a statement, striking at first glance, in the derivation of Equation (29) and the Marcus formula when two opposite limits (zero and infinity) are taken for that parameter . The result (7)–(27) of quantum–classical mechanics, in none of the limiting cases of , zero or infinity, does not pass into any result of quantum mechanics. With , we get infinity for the transition rate, and with , we get zero for it. (This situation is easy to understand from a qualitative examination of quantum–classical transitions in a potential box with a movable wall, the movement of which simulates the reorganization of the positions of the nuclei in space during electronic transitions, see Figure 1a; the graphs in Figure 1b explain this situation as well). Therefore, a natural question arises about the possibility of passing the result (7)–(27) to the well-known result in the standard theory of many-phonon transitions (standard quantum–mechanical theory) [11], from which quantum–classical mechanics “follows”. The tendency of to infinity in the dynamic parameter in the exponent and at the same time the “opposite” tendency of to zero in the pre-exponential allows us to obtain this standard result (Equation (29) and the Marcus formula). This seemingly “contradictory” fact points to the fundamental novelty of the “chaotic” result from quantum–classical mechanics with respect to the “regular” result from quantum mechanics: the former takes into account chaos in the dynamics of the transient state, while the latter ignores chaos and the dynamics of the transient state itself.
7. Entanglement of Homogeneous and Inhomogeneous Effects in Quantum–Classical Mechanics
The half-width of the Gaussian absorption band (Equation (29) and the Marcus formula)
is determined by the reorganization energy and temperature T. Thus, even within the standard theory [11,12], the effects of homogeneous and inhomogeneous broadening in the optical band—associated with the individual properties of the “donor–acceptor + medium” system and the properties of an ensemble of these systems, and expressed in and T, correspondingly—cannot be separated. Quantum–classical mechanics introduce another “homogeneous effect” associated with the dozy-chaos energy , which greatly entangles homogeneous and inhomogeneous effects in the shape of an optical band, which, in turn, results in a strong complication in the result for it (cf. Equation (29) and the Marcus formula and Equations (7)–(27)). As follows from the tricky result given by Equations (7)–(27)), quantum–classical mechanics afford a great multiplicity of optical band shapes (see, e.g., Figure 1), whereas the standard quantum theory of spectral line broadening gives only the two band shapes, Lorentzian and Gaussian, corresponding to homogeneous and inhomogeneous broadening, respectively. These two differences are explained in an open quantum system: by the quantum system joined to an outer classical bath. Unlike standard quantum theory, in quantum–classical mechanics this bath is quantum and introduced into the not open quantum “donor–acceptor + medium” system (see Equation (1), the bath term ). However, the quantum bath becomes the classical one in the transient, dozy-chaos state (see Equation (3), where ).
8. Introduction to History of Researching the Nature of the J-Band of J-Aggregates
The well-known J-aggregates have a narrow, intense and red-shifted absorption band and are widely used in practice (see, e.g., [25,26] and references therein). The J-band (after Jelley) was discovered by Jelley [55,56] and Scheibe [57,58] independently in 1936. The optical absorption J-band appears along with the absorption band of the polymethine dye (M-band) with a significant increase in its concentration in an aqueous solution (see below, Section 9). The J-band is much narrower and more intense than the M-band, and is shifted, relative to the M-band, towards the red region of the spectrum. The first explanation of the nature of the J-band was associated with the creation of molecular aggregates, subsequently called J-aggregates, in which single molecules, similar to a molecular crystal (see, e.g., [59]), are bound by exciton interactions. This explanation of the nature of the J-band by the exciton mechanism was given by Franck and Teller in 1938 [60] and subsequently became widespread and developed (see, for example, recent reviews [61,62]), including an explanation of the J-band shape. One of the main drawbacks of the existing explanation of the J-band shape [63,64,65,66,67], based on the Frenkel exciton mechanism [68,69], is the fundamental impossibility of explaining the shape of the band of polymethine dye monomers composing J-aggregates by the exciton mechanism. In other words, a theory that claims to explain some property of a complex physical system (the shape of the optical band of J-aggregates), but is unable to explain the analogous property of a simpler, constituent, physical element (the shape of the optical band of polymethine dye monomers), cannot be regarded as satisfactory. A detailed critique of the explanation of the nature of the J-band and its shape, based on the exciton mechanism, is provided in reviews [25,26].
First of all, it should be noted that experimental data on the resonant nature of the dependence of the shape and intensity of the optical absorption band of polymethine dye monomers on the length of the polymethine chain in the Brooker series [35] (see also, for example, [7,24,36,62]), the main optical chromophore of polymethine monomers (Section 4), indicate a mechanism completely different to the exciton mechanism for the formation of a narrow and intense J-band of J-aggregates, namely these data point to the resonant nature of the J band. We refer to this resonance as the Egorov nano-resonance (Section 3 and Section 4). There are a number of other experiments, for example, on the dependence of the band shape of polymethine monomers on the polarity of the solvent [7,40,70], in which the Egorov nano-resonance clearly manifests itself. Therefore, it is natural to explain by this nano-resonance also the nature of the J-band of J-aggregates: the resonant effect, which is associated with the extended nature of the alternating -electron charge in the polymethine chain, strongly interacting with the environment, is simply significantly enhanced by J-aggregation [24] (see explanation in Section 9 below).
Since the J-band is an a priori collective optical excitation, the hypothesis of the plasmonic nature of optical excitations in a molecular J-aggregate was recently considered in [71], where this hypothesis was evaluated by a numerical quantum–chemical method. In this case, the plasmon resonance was described not at the macroscopic physical level, as is usually done, but at the microscopic level. This quantitative assessment showed that the electronic excitations within the characteristic J-band with a shift towards the red region have a less pronounced plasmon character compared to that for a monomer. Thus, although the J-band is associated with collective excitation, it was shown that it does not have a plasmonic character [71], and as a result, the plasmon hypothesis of the J-band turned out to be uncompetitive with respect to the mechanism of J-band formation by the Egorov nano-resonance in quantum–classical mechanics.
9. J-Aggregation as a Structural Tuning into the Egorov Nano-Resonance
Figure 4 demonstrates the efficient performance of quantum–classical mechanics in explaining the shape of optical absorption bands for various aggregates of polymethine dyes [7,37]. One of these aggregates is the J-aggregate, and the nature of the J-band is explained by Egorov nano-resonance (Section 8).

Figure 4.
Optical absorption band shapes in thiapolymethinecyanines [36]. (a) Experimental data on monomers (M), dimers (D), H-, H*- and J-aggregates [36]. (b) Appropriate theoretical fit to these data [7,72]. The fitting parameters for the theoretical band shapes for the monomer, dimer, H-aggregate and H*-aggregate are given in [7,37]. The narrow, intense and red-shifted absorption J-band is computed from Equations (7)–(28), where the “J-aggregate + environment” system parameters are , , , nm, LJ (Enr) = (6 + 2) 0.14 nm = 1.12 nm, , eV, eV, eV, eV, and . Regarding the narrow and blue-shifted H*-band, see in [7,37,73].
The Egorov nano-resonance (Enr) for J-aggregates (EJ-nano-resonance) (Figure 4) is a bright nano-phenomenon, as in the case of polymethine-dye monomers (Figure 2); this resonance is near LJ (Enr) = (6 + 2) 0.14 nm = 1.12 nm (see the captions to Figure 4 and Figure 5).
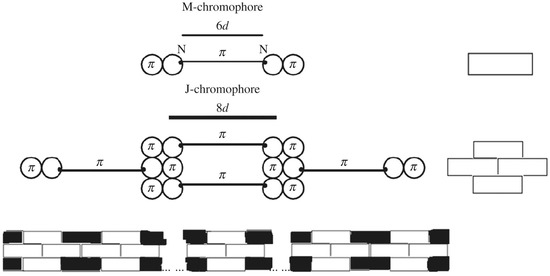
Figure 5.
Scheme of polymethine dye chromophore elongation as a result of J-aggregation. The J-chromophore consists of four identical molecules forming a brickwork-like structure [7,36,74,75] in which the -electron system of the polymethine chain joins with the -electron system of the benzene rings of two neighboring monomers ( is a some unit bond length). The fourth molecule is “neutral” with respect to the formation of a common -electron system and acts as a stabilizer of the J-chromophore structure [6,7,22,23,24,25,26]. The J-aggregate is a thin and long “rod” composed of J-chromophores [6,7,22,23,24,25,26].
The nature of EJ-nano-resonance is determined by a coherence impact of the environmental nuclear dynamics in weak dozy chaos into the electron transition dynamics in the J-chromophore [7,22,23,24,25,26]. The J-chromophore (Figure 5) has a brickwork-type structure consisting of four polymethine dye molecules [7,22,23,24,25,26]. This structure is formed as a result of stacking the -system of a quasi-linear polymethine chain and the -systems of adjacent planar benzene rings (see Figure 5 and details below) [22,23]. The currently fashionable idea of -stacking [76] was first put forward by Hunter and Sanders in 1990 [77], and in relation to the structure of J-aggregates it was put forward by Egorov in 2001 [22,23]. At present, the nature of -stacking is being actively studied by computational methods of quantum chemistry [78,79,80,81,82,83].
The J-chromophores form long, thin “rods” that we call J-aggregates (Figure 5, bottom) [7,22,23,24,25,26]. Such a structure of J-aggregates in the form of J-chromophores arranged in a straight line minimizes the potential parasitic exciton effects on the shape of the J-band [7,22,23,24,25,26] (on the exciton mechanism see above, Section 8).
With J-aggregation, two important effects can be distinguished in the structural tuning of the polymethine system to the Egorov nano-resonance. The first effect is to increase the length of the monomer’s quasi-linear -electron chromophore, which is somewhat shorter than that required to satisfy the nano-resonance condition (Equations (4)–(6)): in the Brooker series, the corresponding monomer band is situated left of the Egorov nano-resonance (Figure 2, ). This elongation of the -electron system is achieved by staking the -electron system of the polymethine chain of one monomer with the -electron systems of the benzene rings of two adjacent monomers in a J-chromophore of J-aggregates (see Figure 5). A monomer that is mirror-symmetrical to a monomer whose -electron system of the polymethine chain is extended by staking with the -electron system of benzene rings is assumed to be neutral with respect to this elongation of the -electron system, and its role is reduced only to the structural stabilization of this chromophore block of four molecules [6,7,22,23,24,25,26]. Thus, the fulfillment of the nano-resonance condition (Equations (4)–(6)) as a result of the elongation of the -system of the polymethine chain—the monomer chromophore—due to J-aggregation is the first physical reason that leads to a narrow and intense J-band.
The second effect during J-aggregation is associated with a change in the spatial structure of the -electron system from one-dimensional to two-dimensional due to the above-discussed staking of two benzene rings to a polymethine chain. This leads to an increase in the interaction of the optical chromophore -system with the environment (to an increase in the reorganization energy , see Equation (2)), which, in turn, leads to a weakening of chaos in the transient state (to a decrease in the dozy-chaos energy ), and hence to a higher degree of self-organization in quantum–classical transitions. This is the second physical reason that leads to a narrow and intense J-band. It can be said that as a result of this second effect in J-aggregation, the nano-resonance state turns out to be much more “powerful” compared to that which would result from a simple elongation of the polymethine chain in the dye monomer in the Brooker series (Figure 2) [6,7,22,23,24,25,26].
Figure 6A (at the top) shows the well-known experimental data of Hertz on the concentration equilibrium of monomers and J-aggregates of benzimidazolocarbocyanine in an aqueous solution [74]. As the dye concentration increases, the intensity of the optical absorption band of J-aggregates (the intensity of the J-band) increases, while the intensity of the band of the dye monomers (the intensity of the M-band) decreases. This effect is due to the formation of J-aggregates from monomers. Due to an increase in the size of the optical chromophore in J-aggregates, as well as due to the increased interaction of the optical chromophore with the environment during J-aggregation, which leads to a decrease in the dozy-chaos energy (see above), the J-band is shifted to the red region of the spectrum with respect to the M-band (see Figure 1a, where is the potential box width, and see Figure 1b, which shows the shift of the peak of the absorption band to the red region of the spectrum with decreasing the dozy-chaos energy ). The presence of a clearly defined isosbestic point at the intersection of optical curves in concentration equilibria indicates the formation of J-aggregates with only one type of optical chromophore. Figure 6B (at the top) shows the relationship between the concentration of J-aggregates and the concentration of dye monomers in concentration equilibria for various degrees of J-aggregation. Based on the law of mass action, one can estimate the number of dye monomer molecules included in the optical chromophores of J-aggregates. This number turns out to be four [74] (cf. Figure 5).

Figure 6.
At the (top): Hertz experimental data on the optical absorption of monomers (M) and J-aggregates (J) of benzimidazolocarbocyanine, which are in concentration equilibrium in an aqueous NaOH solution () at 25 °C [36,74]. (A) Dye concentration is measured in micromole/liter: 0.5 (1), 1.0 (2), 5.0 (3), 10 (4), 100 (5), and 400 (6). (B) Molar concentrations of the dye monomers () and J-aggregates ( ) are taken from (A). The number of molecules in the J-chromophore (Figure 5) is calculated from the law of mass action and is equal to 4. At the (bottom): Theoretical band shapes fitted to Hertz’s experimental data (see at the (top)) [22,23,24]. (A) Absorption M-bands and J-bands are calculated from Equations (7)–(28) with . The relative dye concentrations in the intermediate states are: 1% (1), 9% (2), 53% (3), 66% (4), 82% (5), and 99% (6). (B) Molar concentrations of the dye monomers ( ) and J-aggregates ( ) are derived from the absolute concentrations reported by Herz (see the caption at the (top)) and relative concentrations obtained by our theoretical fitting. The number of molecules in the J-chromophore (Figure 5) is calculated from the law of mass action and is equal to 4 (cf. (B) at the (top)). The fitting parameters for the “J-aggregate + environment” and “monomer + environment” systems are and , , nm, ; eV, eV and eV, eV and eV, eV and eV; the total charges transferred along chromophores = 1.12 nm and = 0.84 nm of J-aggregate and monomer are and , where permittivity [75] (contribution from -electrons and the solvent). Reprinted from [22], Copyright 2001, with permission from Elsevier.
Figure 6A (bottom) shows the results of fitting the theoretical shape of the optical absorption band (7)–(28) (with the replacement of the Gamow factor in formula (25) by the number 1, see rationale in Section 4), obtained on basis of quantum–classical mechanics [5,22,23,24,25,26], to Hertz’s experimental data on concentration -equilibrium [36,74]. It turns out that the number of molecules that form the J-chromophore is four, as in Hertz (cf. Figure 5). In addition, Figure 6B (bottom) shows that the experimental data at high concentrations have a lower accuracy compared to Figure 6B (top). The reason for this is the high probability of the formation of not only J-aggregates, but also colloidal particles, at high dye concentrations in an aqueous solution [22,23,24,25,26].
In ref. [40], a strong detuning of the Egorov nano-resonance explains the experimental data of Harrison et al. regarding the change in the shape of the J-band of THIAMS dye [61,84] (see Table 3 in [40]]) as a result of large increase in dye concentration [84]. In [40] the nano-resonance, parameters are obtained by fitting theoretical Equations (7)–(27) to the experimental data. These theoretical equations based on quantum–classical mechanics successfully generate the Harrison absorption band shapes (Figure 7). According to [40], inclusions of additional dye monomers into the J-aggregate chromophore (Figure 5) occurs due to increase in dye concentration, and for such modified J-chromophore, this leads to the rise of reorganization energy E from the value E = 0.2 eV, corresponding to the nano-resonance, to the non-resonant value E = 0.4 eV (see the caption to Figure 7). In the so-modified “J-band”, its D-wing appears to be even slightly more intense compared to its L-peak (on D-wing and L-peak see in [23,40]). Thus, the new “J-band” is characterized by a broadening and a hypsochromic shift compared to the resonant J-band (Figure 7).

Figure 7.
Change in theoretical spectra of J-aggregate with deflection from the nano-resonance condition (Equations (4)–(6)) [40]. The black line describes a J-band, consisting of L-peak and D-wing, with the following parameters: , , , , and ; the red line describes a “J-band” with the following parameters: , , , , and [40]. Presented theoretical spectra generate changes in the sharp J-band of THIAMS dye (Table 3 in [40]) in aqueous solution at 0.80% w/w dye into a wide “J-band” at 3.53% w/w dye [84]. Reprinted (adapted) with permission from Petrenko A, Stein M. [40]. Copyright 2015, American Chemical Society.
10. On Ad Hoc and By-Product Theoretical Approaches
Usually, the theory of the optical spectra of polymethine dyes and their aggregates is built in physics (e.g., [25,26] and references there) and chemistry (e.g., [67,71,85] and references there) as an ad hoc theory. Because of the specific structure of the polymethine chain (Section 4), polymethine dyes are apt operands for the quantum–classical mechanics of elementary electron-charge transfers. Therefore, our theory of the optical spectra of polymethine dyes and their aggregates is not an ad hoc theory, but it is a by-product of quantum–classical mechanics. This is similar to how theoretical atomic and nuclear physics were created in the last century as a by-product of quantum mechanics.
11. Direct and Reverse Processes
According to the standard theory overlooking the transient dynamics, the luminescence spectra are obtained from the absorption spectra by changing the sign in the heat energy [6,11], i.e., in Equations (12), (13) and (27)
On the right in Figure 8 are the shapes of optical absorption bands depending on the dozy-chaos energy , which are shown in Figure 1b. On the left in Figure 8, the same band shapes are given after a sign change according to Equation (31) in Equations (12), (13) and (27), that is, for luminescence.

Figure 8.
Symmetric picture of absorption (see Figure 1b) [7,8] and luminescence spectra obtained by changing the sign in the heat energy (Equation (31)) in theoretical absorption spectra (Equations (7)–(27)) [6] according to standard quantum mechanics of condensed matter [11].
Figure 9 shows a comparison of our theory with the experiment for J-aggregates in Langmuir films [86], which involve a polymethine dye molecule, as shown in Figure 10. The change of sign only in the value of according to Equation (31) leads, as we see, to the mutual symmetry of the theoretical luminescence and absorption spectra (Figure 8 and Figure 9b), while the experiment [86] shows their shape asymmetry.

Figure 9.
Comparison of theory with experiment for J-aggregates in Langmuir films. (a) Absorption and fluorescence J-bands of a C18S4 monolayer obtained in a Langmuir film [86]. The characteristics of photoluminescence (PL) spectrum: a peak at 590 nm, a FWHM = 18 nm and a Stokes shift of 1 nm [86]. (b) Theoretical absorption and fluorescence J-bands [6], fitted to the experimental data [86] (see (a)). The absorption J-band is computed from Equations (7)–(27), where the “J-aggregate + environment” system parameters are ( is the electron mass); ; ; ; ; ( lengthening the optical chromophore shown in Figure 10 due to the J-aggregation [6,7,22,23,24,25,26,40] (see Figure 5), [7,8,22,23,24,25,26,40,75], LJ (Enr) = (6 + 2) 0.14 nm = 1.12 nm), then we obtain from the Egorov nano-resonance (4) (in Equation (12) parameter ); ; and . The fluorescence J-band is symmetric to the absorption J-band and obtained from the latter by changing the sign in the heat energy and increasing the energy gap by 0.785 eV in order for the Stokes shift to be zero (cf. Figure 8).

Figure 10.
Structure of the dye C18S4 [6] investigated experimentally in [86]. The length of the main optical chromophore, the polymethine chain [38], is defined as the distance between nitrogen atoms and with , where designates roughly equal the C−C bond lengths of methine groups (cf. Figure 3), [7,8,22,23,24,25,26,40,75].
According to quantum–classical mechanics, which takes into account the dynamics of the transient state, in addition to changing the sign in the heat energy , it is also necessary to change the sign before the length of the optical chromophore , or equivalently, before the electron-charge-transfer distance [2,3,4,6], i.e., in Equations (5), (12), (13), and (25), we make the change
After such a sign change in both and , the luminescence and absorption spectra and their shape asymmetry, which was observed in the experiment [86], are well reproduced by our theory (Figure 11) [6].
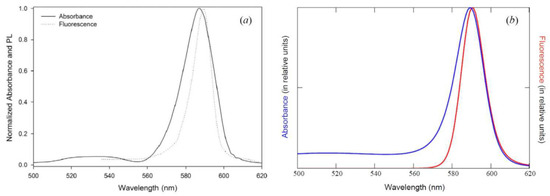
Figure 11.
Comparison of theory with experiment for J-aggregates in Langmuir films. (a) Experimental absorption and fluorescence J-bands [86] shown in Figure 9a. (b) Theoretical absorption and fluorescence J-bands [6], fitted to the experimental data [86] (see (a)). The fluorescence J-band is asymmetric to the absorption J-band and obtained from the latter by changing the sign both in the heat energy Δ and in the J-chromophore length , and increasing the energy gap by 0.785 eV in order for the Stokes shift to be 1 nm (cf. Figure 9b). The rest of the fitting parameters are the same as those in Figure 9b.
In the transition from the theoretical optical absorption spectra to the luminescence spectra, as shown above, the mutual asymmetry of the shape of the luminescence and absorption J-bands is associated with a change in sign in the length of the chromophore . However, this sign change in has practically no effect on the peak position of the luminescence J-band: the position of the J-peak, other things being equal, is determined by the change in sign in the heat energy and by the value of the dozy-chaos energy . It can be seen from Figure 1b and Figure 8 that, as the value of decreases, the mutually symmetrical J-peaks of luminescence and absorption approach each other, which leads to a decrease in their Stokes shift. However, this decrease in the Stokes shift is not enough to explain the very small value of the Stokes shift (1 nm) observed in the experiment for J-aggregates in Langmuir films [86]. Therefore, in addition to this mechanism, which follows from quantum–classical mechanics, there must be one more additional mechanism that, together with our quantum–classical mechanism, leads to very small values of the Stokes shift for the J-band [6].
Due to the very large extent of the actual -electron system of polymethine dyes and their J-aggregates, it is natural to assume that this second mechanism is associated with a strong loosening of the excited -electron state of J-aggregates immediately before the act of photon emission [6]. Such spontaneous and strong loosening leads to a strong decrease in the binding energy of the excited -electron state, and, as a consequence, to a very small Stokes shift. Apparently, this loosening effect is universal [6]; however, for molecular systems in which the optical electronic system is not extended, but compact, the loosening effect manifests itself weakly. For a detailed theoretical study of the loosening effect, in quantum–classical mechanics it is necessary to take into account relativistic effects [6]. In other words, along with the further development of quantum–classical mechanics [5,23,24], it is necessary to construct quantum–classical electrodynamics, which is a kind of generalization quantum–classical mechanics, just as standard quantum electrodynamics [29,30,31] is a generalization of quantum mechanics [32,33].
12. Nano-Resonance as Antiadiabatic Invariant in the Dynamics of a Transient State and Its “Antisymmetric Twin”
Homogeneous effects (Section 7) in quantum–classical mechanics of elementary electron transfers in condensed matter (Section 2) are associated with three characteristic times
(cf. Equation (13)), from which two physically significant resonances can be composed [24]:
The former resonance is the Egorov nano-resonance (cf. Equations (4)–(6)), whereas the latter resonance is the antisymmetric twin of the nano-resonance [2,24,25,26]: these resonances are formed between the extended electron movements and, correspondingly, ordered and disordered (chaotic) fundamental ingredients of the environmental nuclear reorganization movements. The resonances given by Equations (33) and (34) are the dynamic invariants for the transient dozy-chaos state. These simplest dynamic resonance-invariants—antiadiabatic invariants—can be regarded as alternatives to the Born–Oppenheimer adiabatic invariants—potential energy surfaces. In refs. [24,25,26,41], these antiadiabatic dynamical invariants are studied on the basis of the Heisenberg uncertainty relation.
On the other hand, because the Egorov nano-resonance is the simplest dynamic expression of quantum order in quantum–classical mechanics (Section 3), the antisymmetric twin of the nano-resonance can be considered as the simplest dynamic expression of classical disorder in quantum–classical mechanics. Finally, we note that the nano-resonance is a new physical phenomenon that has no analogs in physics and chemistry, while the antisymmetric twin of the nano-resonance is an analog of the classical “reaction coordinate” in chemistry [25,26].
13. Nano-Resonance in Two-Photon Absorption
Here, I will consider the problem to be solved within the framework of quantum–classical mechanics in the near future.
The primary task is to generalize quantum–classical mechanics to the case of nonlinear optics [1,9]. Figure 12 shows the experimental shapes of optical bands for one-photon and two-photon absorption of some polymethine dye in a solvent—chloroform. In the case of one-photon absorption, the band is rather narrow and intense, and therefore it can be assumed that it corresponds to the Egorov nano-resonance. When going to two-photon absorption, the shape of the band sharply deteriorates, which is associated with a strong violation of the conditions of this resonance [1].

Figure 12.
Nondegenerate 2PA spectra for a solution of selenopyrylium-terminated polymethine dye Se-3C dissolved in chloroform. Different pump wavelengths were used to observe the full ND-2PA spectra. Solid circles are degenerate 2PA (D-2PA) cross sections derived from femtosecond-pulsed Z-scan measurements. 1 GM is defined as 1 × 10–50 cm4 s photon–1. Experimental uncertainties in the values were estimated to be ±10%. The linear absorption spectra are shown as reference. Reproduced from Hales et al. [87] with permission from the American Association for the Advancement of Science (AAAS).
In Figure 13, both of these experimental band shapes are simulated [1,9] within the framework of what we have so far—in the case of one-photon absorption, quantum–classical mechanics.

Figure 13.
Transformation of the theoretical spectra of a model polymethine dye with different deviations from the nano-resonance condition θ = 1/2 (see Equations (4)–(6), in Equation (12) parameter θ = 1/2) [1,9]. The optical band that is near the nano-resonance band (black curve) corresponds to θ = 0.44, the optical band that is far beyond the nano-resonance band (red curve) corresponds to θ = 0.88. Both bands are computed from Equations (7)–(27), where the “dye + environment” system parameters are ( is the electron mass); ; ; ; ; ; ; ; ; ; and . A mathcad program file validating these results is available at http://dx.doi.org/10.17632/c4h9rm5xk6.1 (accessed on 19 June 2020). Reprinted from [1], Copyright 2021, with permission from Elsevier.
Figure 14 shows the same two band shapes, but for photon energies on the abscissa axis [1]. Under resonance conditions with one-photon absorption
(see Equations (4)–(6) and (12)), it is clear that the most probable absorption of photons occurs at the peak of the band, while the less probable one occurs in its wing (Figure 14, the black curve) [1]. In the transition from resonant one-photon absorption
(see Equation (27)) to two-photon absorption
the primary region of photon absorption moves from the low-energy peak of the band to its high-energy wing (Figure 14, the red curve) [1]. In order to retune the “polymethine dye + environment” system to the Egorov nano-resonance under two-photon absorption conditions (Equation (37)) it is required to reduce either the solvent reorganization energy or the polymethine chain length in the experimental conditions (see Equation (35)) [1].

Figure 14.
The theoretical spectra in Figure 13 are shown in photon-energy coordinates for convenience of discussion [1]. Additionally, for convenience, it is assumed that the energy gap . A mathcad program file validating these results is available at http://dx.doi.org/10.17632/c4h9rm5xk6.1 (accessed on 19 June 2020). Reprinted from [1], Copyright 2021, with permission from Elsevier.
Figure 15 and Figure 16 illustrate, by examining the dependence of the absorption band shape on the reorganization energy , how the “polymethine dye + environment” system can be retuned to the Egorov nano-resonance after its parasitic two-photon detuning. In Figure 15a and Figure 16a, the value of varies as long as the dozy-chaos energy is constant, while in Figure 15b and Figure 16b, the value of varies as long as the dimensionless parameter is constant. It follows from these results that the nano-resonance in two-photon absorption is restored as a result of a decrease in the reorganization energy (i.e., by replacing a polar solvent with a non-polar one) [1]. In this case, it shifts with respect to nano-resonance in single-photon absorption to the red and even to the infrared regions of the spectrum [1].

Figure 15.
Transformation of the theoretical band shape for the two-photon absorption (Figure 14, red curve) with varying the reorganization energy [1]. (a) ; (blue), (red), (green), (magic). (b) ; (blue), (red), (green), (magic). The magic band shape corresponds to the restored Egorov nano-resonance. Mathcad program files validating these results are available at http://dx.doi.org/10.17632/psdhby5hhg.1 (accessed on 3 December 2020). Reprinted from [1], Copyright 2021, with permission from Elsevier.

Figure 16.
The same as in Figure 15, except for the wavelengths on the abscissa axis [1]. Mathcad program files validating these results are available at http://dx.doi.org/10.17632/psdhby5hhg.1 (accessed on 3 December 2020). Reprinted from [1], Copyright 2021, with permission from Elsevier.
On a qualitative physical level, the shift of nano-resonance to the red region of the spectrum as a result of its recovery from parasitic two-photon detuning is easily explained using a potential box with a moving wall (Figure 1a). With a decrease in the reorganization energy , which can be interpreted as a decrease in the “mass of the wall”, the mobility of the wall increases, which leads to an increase in the rate of decrease in the energy gap between the excited and ground states (cf. as in the situation with a decrease in the dozy-chaos energy , Figure 1b). As a result, we effectively get a decrease in the energy gap and the discussed “red shift”. Another explanation for this “red shift” at a qualitative physical level can be found in [8] (see Figure 3 and Figure 4 therein).
The peak of the restored Egorov nano-resonance in the case of constancy of the dimensionless parameter (Figure 15b) turns out to be significantly narrower than the peak of the restored nano-resonance in the case of constancy of the dozy-chaos energy (Figure 15a). It follows that the self-organization of quantum–classical transitions for the spectra in Figure 15b () is much higher than their self-organization for the spectra in Figure 15a (). Therefore, we call the parameter the parameter of organization or self-organization of quantum–classical transitions [1].
Note that if we construct the model spectra of two-photon absorption in Figure 15, plotting along the abscissa axis not the photon energy, as in Figure 15, but the photon wavelength, as in Figure 16, then the inferiority of the restored nano-resonance in the case of becomes even stronger (cf. the half-width of the “resonant” two-photon band in Figure 16a (magic) and the half-width of the original resonant one-photon band (black)). Thus, the constancy of the organization parameter will follow from the discovery in the experiment of a full-fledged restored Egorov nano-resonance (Figure 16b (magic)) [1]. For more accurate clarifications about the restored nano-resonance, it is necessary to generalize existing quantum–classical mechanics to nonlinear optics [1,9].
14. Conclusions
We call such “quantum” transitions extended transitions [23] in which the self-organization of the dynamics of the interaction of the electronic and nuclear subsystems in the process of transitions is essential. In ordinary optical spectroscopy, such self-organization is insignificant because of the strong chaos (dozy chaos) in the transition dynamics, which leads to the independence of the transition rates from these dynamics. Formally, this is expressed in the use of the Born–Oppenheimer adiabatic approximation for the initial and final states and the Franck–Condon principle when calculating the rate constants of transitions.
A striking, and the simplest, example of self-organization of the electron-nuclear dynamics of extended “quantum” transitions is the resonance between the extended motion of the electronic subsystem and the movement of reorganization of the nuclear subsystem of its environment during elementary electron transfers between the donor and acceptor. This resonance was discovered within the framework of a new physical theory—quantum–classical mechanics [1,2,3,4,5,6,7,8,9,22,23,24,25,26,27,28], which was created by the author with the aim of damping the singularity that exists within the framework of quantum mechanics in electron-nuclear motion in the transient state of “quantum” transitions. Since this resonance was discovered by the author and manifests itself on a spatial nanoscale, it is called Egorov nano-resonance [1,9].
A striking example of the applications of quantum–classical mechanics of elementary electron transfers in condensed media is the theoretical explanation of the optical spectra (shapes of optical bands) of polymethine dyes and their various aggregates in solutions [1,2,3,4,5,6,7,8,9,22,23,24,25,26,28,40]. The outstanding results here are an explanation of the resonant nature of the transformation of the optical band shape in the series of polymethine dye, in which the length of the polymethine chain changes (Figure 2), as well as an explanation of the resonant nature of the well-known optical, narrow and intense, J-band of J-aggregates (Figure 4 and Figure 6), on the basis of Egorov nano-resonance.
On the basis of the Egorov nano-resonance, it is also possible to explain the Harrison detuning of the J-band (Figure 7) [40,84], the shapes of the optical absorption and luminescence bands in Langmuir films (Figure 11) [6,86], as well as the detuning of the resonance absorption band during the transition from one-photon to two-photon absorption in selenopyrylium-terminated polymethine dye Se-3C dissolved in chloroform (Figure 12, Figure 13 and Figure 14) [1,9,87]. The conditions for the restoration of the Egorov nano-resonance after its parasitic two-photon detuning are found on the basis of studying the dependence of the shape of the two-photon absorption band on the reorganization energy of the nuclear environment (Figure 15 and Figure 16) [1]. The latter results are also proposed to be considered as a stimulus for the generalization of quantum–classical mechanics to the case of nonlinear optics [1,9]. This generalization makes it possible to approach the theoretical study of nonlinear optical processes not only in polymethine dyes but also in other applied and more complex organic systems [1].
Funding
This work was supported by the Ministry of Science and Higher Education within the State assignment Federal Scientific Research Center “Crystallography and Photonics” Russian Academy of Sciences.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data on which this article is based are available as an online resource with digital object identifier (doi) 10.5061/dryad.t0r3p [37] and at the Egorov, Vladimir (2018), Mendeley Data, V2, https://doi.org/10.17632/h4g2yctmvg.2 (accessed on 9 March 2019) [6].
Conflicts of Interest
The author declares no conflict of interest.
References
- Egorov, V.V.; Thomas, S. Quantum-classical mechanics: On the problem of a two-photon resonance band shape in polymethine dyes. Nano-Struct. Nano-Objects 2021, 25, 100650. [Google Scholar] [CrossRef]
- Egorov, V.V. Dynamic symmetry in dozy-chaos mechanics. Symmetry 2020, 12, 1856. [Google Scholar] [CrossRef]
- Egorov, V.V. Dozy-chaos mechanics for a broad audience. Challenges 2020, 11, 16. [Google Scholar] [CrossRef]
- Egorov, V.V. Quantum-classical electron as an organizing principle in nature. Int. J. Sci. Technol. Soc. 2020, 8, 93–103. [Google Scholar] [CrossRef]
- Egorov, V.V. Quantum-classical mechanics as an alternative to quantum mechanics in molecular and chemical physics. Heliyon Phys. 2019, 5, e02579. [Google Scholar] [CrossRef] [PubMed]
- Egorov, V.V. Quantum-classical mechanics: Luminescence spectra in polymethine dyes and J-aggregates. Nature of the small Stokes shift. Results Phys. 2019, 13, 102252. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the optical band shapes in polymethine dyes and H-aggregates: Dozy chaos and excitons. Comparison with dimers, H*- and J-aggregates. R. Soc. Open Sci. 2017, 4, 160550. [Google Scholar] [CrossRef] [PubMed]
- Egorov, V.V. Optical lineshapes for dimers of polymethine dyes: Dozy-chaos theory of quantum transitions and Frenkel exciton effect. RSC Adv. 2013, 3, 4598–4609. [Google Scholar] [CrossRef]
- Petrenko, A.; Stein, M. Toward a molecular reorganization energy-based analysis of third-order nonlinear optical properties of polymethine dyes and J-aggregates. J. Phys. Chem. A 2019, 123, 9321–9327. [Google Scholar] [CrossRef]
- Born, M.; Oppenheimer, J.R. Quantum theory of the molecules. Ann. Phys. 1927, 84, 457–484. [Google Scholar] [CrossRef]
- Perlin, Y.E. Modern methods in the theory of many-phonon processes. Sov. Phys. Uspekhi 1964, 6, 542–565. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, M.D.; Lukashin, A.V. Electron-vibrational interactions in polyatomic molecules. Sov. Phys. Uspekhi 1975, 18, 391–409. [Google Scholar] [CrossRef]
- Bersuker, I.B.; Polinger, V.Z. Vibronic Interactions in Molecules and Crystals; Springer: New York, NY, USA, 1989. [Google Scholar]
- Stanke, M. Adiabatic, Born-Oppenheimer, and non-adiabatic approaches. In Handbook of Computational Chemistry; Leszczynski, J., Kaczmarek-Kedziera, A., Puzyn, T., Papadopoulos, M.G., Reis, H., Shukla, M.K., Eds.; Springer: Cham, Switzerland, 2017; pp. 173–223. [Google Scholar]
- Franck, J.; Dymond, E.G. Elementary processes of photochemical reactions. Trans. Faraday Soc. 1925, 21, 536–542. [Google Scholar] [CrossRef]
- Condon, E.U. A theory of intensity distribution in band systems. Phys. Rev. 1926, 28, 1182–1201. [Google Scholar] [CrossRef]
- Condon, E.U. Nuclear motions associated with electron transitions in diatomic molecules. Phys. Rev. 1928, 32, 858–872. [Google Scholar] [CrossRef]
- Condon, E.U. The Franck-Condon principle and related topics. Am. J. Phys. 1947, 15, 365–374. [Google Scholar] [CrossRef]
- Herzberg, G.; Spinks, J.W.T. Molecular Spectra and Molecular Structure. 1. Spectra of Diatomic Molecules; Prentice-Hall: New York, NY, USA, 1939. [Google Scholar]
- Herzberg, G. Molecular Spectra and Molecular Structure. 2. Infrared and Raman Spectra; D. Van Nostrand: Princeton, NJ, USA, 1945. [Google Scholar]
- Herzberg, G. Molecular Spectra and Molecular Structure. 3. Electronic Spectra and Electronic Structure of Polyatomic Molecules; Van Nostrand Reinhold: New York, NY, USA; London, UK, 1966. [Google Scholar]
- Egorov, V.V. Electron-transfer approach to the nature of the optical lineshape for molecular J-aggregates. Chem. Phys. Lett. 2001, 336, 284–291. [Google Scholar] [CrossRef]
- Egorov, V.V. On electrodynamics of extended multiphonon transitions and nature of the J-band. Chem. Phys. 2001, 269, 251–283. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the optical transition in polymethine dyes and J-aggregates. J. Chem. Phys. 2002, 116, 3090–3103. [Google Scholar] [CrossRef]
- Egorov, V.V.; Alfimov, M.V. Theory of the J-band: From the Frenkel exciton to charge transfer. Phys. Uspekhi 2007, 50, 985–1029. [Google Scholar] [CrossRef]
- Egorov, V.V. Theory of the J-band: From the Frenkel exciton to charge transfer. Phys. Procedia 2009, 2, 223–326. [Google Scholar] [CrossRef][Green Version]
- Egorov, V.V. Discovery of Dozy Chaos and Discovery of Quanta: Analogy Being in Science and Perhaps in Human Progress. In Chaos and Complex Systems, Proceedings of the 4th International Interdisciplinary Chaos Symposium, Antalya, Turkey, 29 April–2 May 2012; Stavrinides, S.G., Banerjee, S., Caglar, H., Ozer, M., Eds.; Springer: Berlin, Germany, 2013; pp. 41–46. [Google Scholar] [CrossRef]
- Egorov, V.V. Dozy Chaos in Chemistry: Simplicity in Complexity. In Chaos and Complex Systems, Proceedings of the 4th International Interdisciplinary Chaos Symposium, Antalya, Turkey, 29 April–2 May 2012; Stavrinides, S.G., Banerjee, S., Caglar, H., Ozer, M., Eds.; Springer: Berlin, Germany, 2013; pp. 219–224. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the emission and absorption of radiation. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1927, 114, 243–265. [Google Scholar] [CrossRef]
- Fermi, E. Quantum theory of radiation. Rev. Mod. Phys. 1932, 4, 87–132. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Davydov, A.S. Quantum Mechanics; Pergamon Press: Oxford, UK, 1976. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Non-Relativistic Theory, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Planck, M. On the law of distribution of energy in the normal spectrum. Ann. Phys. 1901, 309, 553–563. [Google Scholar] [CrossRef]
- Brooker, L.G.S.; Sprague, R.H.; Smith, C.P.; Lewis, G.L. Color and constitution. I. Halochromism of anhydronium bases related to the cyanine dyes. J. Am. Chem. Soc. 1940, 62, 1116–1125. [Google Scholar] [CrossRef]
- James, T.H. (Ed.) The Theory of the Photographic Process; Macmillan: New York, NY, USA, 1977. [Google Scholar]
- Egorov, V.V. Dryad Digital Repository. Data from: R. Soc. Open Sci. 2017, 4, 160550. [Google Scholar] [CrossRef]
- Dähne, S. Color and constitution: One hundred years of research. Science 1978, 199, 1163–1167. [Google Scholar] [CrossRef]
- Kachkovskii, A.D. The nature of electronic transitions in linear conjugated systems. Russ. Chem. Rev. 1997, 66, 647–664. [Google Scholar] [CrossRef]
- Petrenko, A.; Stein, M. Molecular Reorganization energy as a key determinant of J-band formation in J-aggregates of polymethine dyes. J. Phys. Chem. A 2015, 119, 6773–6780. [Google Scholar] [CrossRef] [PubMed]
- Egorov, V.V. Dynamic pumping of elementary charge transfer by environmental dissipative reorganization. Russ. J. Electrochem. 2003, 39, 86–96. [Google Scholar] [CrossRef]
- Marcus, R.A. On the theory of oxidation-reduction reactions involving electron transfer. I. J. Chem. Phys. 1956, 24, 966–978. [Google Scholar] [CrossRef]
- Marcus, R.A. Electrostatic free energy and other properties of states having nonequilibrium polarization. J. Chem. Phys. 1956, 24, 979–989. [Google Scholar] [CrossRef]
- Marcus, R.A. On the theory of oxidation-reduction reactions involving electron transfer. II. Applications to data on the rates of isotopic exchange reactions. J. Chem. Phys. 1957, 26, 867–871. [Google Scholar] [CrossRef]
- Marcus, R.A. On the theory of oxidation-reduction reactions involving electron transfer. III. Applications to data on the rates of organic redox reactions. J. Chem. Phys. 1957, 26, 872–877. [Google Scholar] [CrossRef]
- Marcus, R.A.; Sutin, N. Electron transfers in chemistry and biology. Biochim. Biophys. Acta 1985, 811, 265–322. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599–610. [Google Scholar] [CrossRef]
- Huang, K.; Rhys, A. Theory of light absorption and non-radiative transitions in F-centres. Proc. R. Soc. A 1950, 204, 406–423. [Google Scholar]
- Pekar, S.I. Theory of F-centers. Zh. Eksp. Teor. Fiz. 1950, 20, 510–522. (In Russian) [Google Scholar]
- Pekar, S.I. To the theory of luminescence and light absorption by impurities in dielectrics. Zh. Eksp. Teor. Fiz. 1952, 22, 641–657. (In Russian) [Google Scholar]
- Pekar, S.I. On the effect of lattice deformations by electrons on optical and electrical properties of crystals. Uspekhi Fiz. Nauk 1953, 50, 197–252. (In Russian) [Google Scholar] [CrossRef]
- Lax, M. The Franck-Condon principle and its application to crystals. J. Chem. Phys. 1952, 20, 1752–1760. [Google Scholar] [CrossRef]
- Krivoglaz, M.A.; Pekar, S.I. The shape of the spectra of the impurity light absorption and luminescence in dielectrics. Tr. Inst. Fiz. Akad. Nauk UKR SSR 1953, 4, 37–70. (In Russian) [Google Scholar]
- Krivoglaz, M.A. The theory of thermal transitions. Zh. Eksp. Teor. Fiz. 1953, 25, 191–207. (In Russian) [Google Scholar]
- Jelley, E.E. Spectral absorption and fluorescence of dyes in the molecular state. Nature 1936, 138, 1009–1010. [Google Scholar] [CrossRef]
- Jelley, E.E. Molecular, nematic and crystal states of 1:1′-diethyl-ψ-cyanine chloride. Nature 1937, 139, 631–632. [Google Scholar] [CrossRef]
- Scheibe, G. Variability of the absorption spectra of some sensitizing dyes and its cause. Angew. Chem. 1936, 49, 563. [Google Scholar]
- Scheibe, G. On the variability of the absorption spectra in solutions and the secondary bonds as its cause. Angew. Chem. 1937, 50, 212–219. [Google Scholar] [CrossRef]
- Davydov, A.S. Theory of Molecular Excitons; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Franck, J.; Teller, E. Migration and photochemical action of excitation energy in crystals. J. Chem. Phys. 1938, 6, 861–872. [Google Scholar] [CrossRef]
- Würthner, F.; Kaiser, T.E.; Saha-Möller, C.R. J-aggregates: From serendipitous discovery to supra-molecular engineering of functional dye materials. Angew. Chem. Int. Ed. 2011, 50, 3376–3410. [Google Scholar] [CrossRef] [PubMed]
- Bricks, J.L.; Slominskii, Y.L.; Panas, I.D.; Demchenko, A.P. Fluorescent J-aggregates of cyanine dyes: Basic research and applications review. Methods Appl. Fluoresc. 2018, 6, 012001. [Google Scholar] [CrossRef]
- Knapp, E.W. Lineshapes of molecular aggregates, exchange narrowing and intersite correlation. Chem. Phys. 1984, 85, 73–82. [Google Scholar] [CrossRef]
- Makhov, D.V.; Egorov, V.V.; Bagatur’yants, A.A.; Alfimov, M.V. Numerical calculations of optical lineshapes for disordered molecular aggregates. Chem. Phys. Lett. 1995, 246, 371–380. [Google Scholar] [CrossRef]
- Makhov, D.V.; Egorov, V.V.; Bagatur’yants, A.A.; Alfimov, M.V. Efficient approach to the numerical calculation of optical line shapes for molecular aggregates. J. Chem. Phys. 1999, 110, 3196–3199. [Google Scholar] [CrossRef]
- Eisfeld, A.; Briggs, J.S. The J-band of organic dyes: Lineshape and coherence length. Chem. Phys. 2002, 281, 61–70. [Google Scholar] [CrossRef]
- Spano, F.C. The spectral signatures of Frenkel polarons in H- and J-aggregates. Acc. Chem. Res. 2010, 43, 429–439. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, J. On the transformation of light into heat in solids. I. Phys. Rev. 1931, 37, 17–44. [Google Scholar] [CrossRef]
- Frenkel, J. On the transformation of light into heat in solids. II. Phys. Rev. 1931, 37, 1276–1294. [Google Scholar] [CrossRef]
- Kachkovski, O.; Tolmachov, O.; Slominskii, Y.; Kudinova, M.; Derevyanko, N.; Zhukova, O. Electronic properties of polymethine systems 7: Soliton symmetry breaking and spectral features of dyes with a long polymethine chain. Dyes Pigment. 2005, 64, 207–216. [Google Scholar] [CrossRef]
- Guerrini, M.; Calzolari, A.; Varsano, D.; Corni, S. Quantifying the plasmonic character of optical excitations in a molecular J-aggregate. J. Chem. Theory Comput. 2019, 15, 3197–3203. [Google Scholar] [CrossRef] [PubMed]
- Egorov, V.V. Optical line shapes for polymethine dyes and their aggregates: Novel theory of quantum transitions and its correlation with experiment. J. Lumin. 2011, 131, 543–547. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the narrow optical band in H*-aggregates: Dozy-chaos-exciton coupling. AIP Adv. 2014, 4, 077111. [Google Scholar] [CrossRef]
- Herz, A.H. Aggregation of sensitizing dyes in solution and their adsorption onto silver halides. Adv. Colloid Interface Sci. 1977, 8, 237–298. [Google Scholar] [CrossRef]
- Kuhn, H.; Kuhn, C. Chromophore coupling effects. In J-Aggregates; Kobayashi, T., Ed.; World Scientific: Singapore, 1996; pp. 1–40. [Google Scholar]
- Zhao, Y.S.; Fu, H.; Peng, A.; Ma, Y.; Liao, Q.; Yao, J. Construction and optoelectronic properties of organic one-dimensional nanostructures. Acc. Chem. Res. 2010, 43, 409–418. [Google Scholar] [CrossRef]
- Hunter, C.A.; Sanders, J.K.M. The nature of π-π interactions. J. Am. Chem. Soc. 1990, 112, 5525–5534. [Google Scholar] [CrossRef]
- McGaughey, G.B.; Gagné, M.; Rappé, A.K. π-stacking interactions. J. Biol. Chem. 1998, 273, 15458–15463. [Google Scholar] [CrossRef] [PubMed]
- Bloom, J.W.G.; Wheeler, S.E. Taking the aromaticity out of aromatic interactions. Angew. Chem. 2011, 123, 7993–7995. [Google Scholar] [CrossRef]
- Martinez, C.R.; Iverson, B.L. Rethinking the term “π-stacking”. Chem. Sci. 2012, 3, 2191–2201. [Google Scholar] [CrossRef]
- Wheeler, S.E.; Bloom, J.W.G. Toward a more complete understanding of noncovalent interactions involving aromatic rings. J. Phys. Chem. A 2014, 118, 6133–6147. [Google Scholar] [CrossRef]
- Avakyan, V.G.; Shapiro, B.I.; Alfimov, M.V. Dimers, tetramers, and octamers of mono- and trimethyne thiacarbocyanine dyes. Structure, formation energy, and absorption band shifts. Dyes Pigment. 2014, 109, 21–33. [Google Scholar] [CrossRef]
- Wheeler, S.E. Unraveling the origin of substituents effects in π-stacking interactions. In Noncovalent Forces, Challenges and Advances in Computational Chemistry and Physics 19; Scheiner, S., Ed.; Springer International Publishing: Cham, Switzerland, 2015; Chapter 14; pp. 421–442. [Google Scholar]
- Harrison, W.J.; Mateer, D.L.; Tiddy, G.J.T. Liquid-crystalline J-Aggregates formed by aqueous ionic cyanine dyes. J. Phys. Chem. 1996, 100, 2310–2321. [Google Scholar] [CrossRef]
- Masunov, A.E.; Anderson, D.; Freidzon, A.Y.; Bagatur’yants, A.A. Symmetry-breaking in cationic polymethine dyes: Part 2. Shape of electronic absorption bands explained by the thermal fluctuations of the solvent reaction field. J. Phys. Chem. A 2015, 119, 6807–6815. [Google Scholar] [CrossRef] [PubMed]
- Aviv, H.; Tischler, Y.R. Synthesis and characterization of a J-aggregating TDBC derivative in solution and in Langmuir-Blodgett films. J. Lumin. 2015, 158, 376–383. [Google Scholar] [CrossRef]
- Hales, J.M.; Matichak, J.; Barlow, S.; Ohiro, S.; Yesudas, K.; Bredas, J.-L.; Perry, J.W.; Marder, S.R. Design of polymethine dyes with large third-order optical nonlinearities and loss figures of merit. Science 2010, 327, 1485–1488. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).