Yetter–Drinfeld Modules for Group-Cograded Hopf Quasigroups

Abstract

Let H be a crossed group-cograded Hopf quasigroup. We first introduce the notion of p-Yetter–Drinfeld quasimodule over H. If the antipode of H is bijective, we show that the category $YDQ\left(H\right)$ of Yetter–Drinfeld quasimodules over H is a crossed category, and the subcategory $YD\left(H\right)$ of Yetter–Drinfeld modules is a braided crossed category.

1. Introduction

In order to understand the structure and relevant properties of the algebraic 7-sphere, Klim and Majid in [1] proposed the notion of Hopf quasigroups. They are non-associative generalizations of Hopf algebras; however, there are certain conditions about antipode that can compensate for their lack of associativity. Hopf quasigroups are no longer associative algebras, so their compatibility conditions are quite different from those of Hopf algebras.

Turaev introduced the notion of braided crossed categories, which is based on a group G, and showed that such a category gives rise to a 3-dimensional homotopy quantum field theory with target space $K(G,1)$. In fact, braided crossed categories are braided monoidal categories in Freyd–Yetter categories of crossed G-sets (see [2]), and play a key role in the construction of these homotopy invariants.

Zunino introduced a kind of Yetter–Drinfeld module over crossed group coalgebra in [3], and constructed a braided crossed category for this kind of Yetter–Drinfeld module. This idea was generalized to multiplier Hopf T-coalgebras by Yang in [4]. It is natural to ask the question: Does this method also hold for some other algebraic structures?

Motivated by this question, the main purpose of this paper is to construct a braided crossed category by p-Yetter–Drinfeld modules over crossed group-cograded Hopf quasigroups.

This paper is organized as follows: In Section 2, we recall some notions, such as braided crossed categories, Turaev’s left index notation, and Hopf quasigroups. These are the most important building blocks on which this article is founded.

In Section 3, we introduce crossed group-cograded Hopf quasigroups and then provide some examples of this algebraic structure. Moreover, we give a method to construct crossed group-cograded Hopf quasigroups, which relies on a fixed crossed group-cograded Hopf quasigroup. At the end of this section, we show that a group-cograded Hopf quasigroup with the group G is indeed a Hopf quasigroup in the Turaev category.

In Section 4, we first give the definition of p-Yetter–Drinfeld quasimodules over a crossed group-cograded Hopf quasigroup H. We then show the category $YDQ\left(H\right)$ of Yetter–Drinfeld quasimodules over H is a crossed category, and the subcategory $YD\left(H\right)$ of Yetter–Drinfeld modules is a braided crossed category.

2. Preliminaries

2.1. Crossed Categories and Turaev Category

Recall the following definitions from [5,6,7]. Let G be a group. A category C over G is called a crossed category if it satisfies the following:

(1)

C is a monoidal category;

(2)

C is a disjoint union of a family of subcategories ${\left(C_{\alpha }\right)}_{\alpha \in G}$, and for any $U\in C_{\alpha },V\in C_{\beta },U\otimes V\in C_{\alpha \beta }$. The subcategory $C_{\alpha }$ is called the $\alpha th$ component of C;

(3)

Consider a group homomorphism $\varphi :G\to Aut\left(C\right),\beta \to {\varphi }_{\beta }$, and assume that ${\varphi }_{\beta }\left(C_{\alpha }\right)=C_{\beta \alpha {\beta }^{-1}}$, where $Aut\left(C\right)$ is the group of invertible strict tensor functors from C to itself, for all $\alpha ,\beta \in G$. The functors ${\varphi }_{\beta }$ are called conjugation isomorphisms.

We will use Turaev’s left index notation from [7,8] for functors ${\varphi }_{\beta }$: Given $\beta \in G$ and an object $V\in C$, the functor ${\varphi }_{\beta }$ will be denoted by ${}^{\beta }(·)$ or ${}^V(·)$ and ${}^{{\beta }^{-1}}(·)$ will be denoted by ${}^{\overline{V}}(·)$. Since ${}^V(·)$ is a functor, for any object $U\in \mathcal{C}$ and any composition of morphism $g\circ f$ in C, we obtain ${}^{V}i{d}_U=i{d}_{{}^{V}U}$ and ${}^V(g\circ f)={}^{V}g\circ {}^{V}f$. Since the conjugation $\phi :G\to Aut\left(C\right)$ is a group homomorphism, for any $V,W\in C$, we have ${}^{V\otimes W}(·)={}^V\left({}^W(·)\right)$ and ${}^1(·)={}^V{(}^{\overline{V}}(·))={}^{\overline{V}}\left({}^V(·)\right)=i{d}_C$. Since for any $V\in C$, the functor ${}^V(·)$ is strict, we have ${}^V(g\otimes f)={}^{V}g\otimes {}^{V}f$ for any morphism f and g in C, and ${}^V\left(1\right)=1$.

Recall that a braiding of a crossed category C is a family of isomorphisms ${(C=C_{U,V})}_{U,V\in C}$, where $C_{U,V}:U\otimes V\to {}^{U}V\otimes U$ satisfies the following conditions:

(1)

For any arrow $f\in C_p(U,U^{\prime })$ and $g\in C(V,V^{\prime })$,

$$\begin{array}{c}\hfill (\left({}^{p}g\right)\otimes f)C_{U,V}=C_{U^{\prime },V^{\prime }}(f\otimes g);\end{array}$$

(1)

(2)

For all $U,V,W\in C$, we have

$$\begin{array}{ccc}\hfill C_{U\otimes V,W}& =& a_{{}^{U\otimes V}W,U,V}(C_{U,{}^{V}W}\otimes i{d}_V)a_{U,{}^{V}W,V}^{-1}({\iota }_U\otimes C_{V,W})a_{U,V,W},\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill C_{U,V\otimes W}& =& a_{{}^{U}V,{}^{U}W,U}^{-1}({\iota }_{{}^{U}V}\otimes C_{U,W})a_{{}^{U}V,U,W}(C_{U,V}\otimes {\iota }_W)a_{U,V,W}^{-1},\hfill \end{array}$$

(3)

where a is the natural isomorphisms in the tensor category C.

(3)

For all $U,V\in C$ and $q\in G$,

$$\begin{array}{c}\hfill {\varphi }_q\left(C_{U,V}\right)=C_{{\varphi }_q\left(U\right),{\varphi }_q\left(V\right)}.\end{array}$$

(4)

A crossed category endowed with a braiding is called a braided crossed category. For more details, see [9].

A Turaev category as a special symmetric monoidal category is introduced by Caenepeel from [10]. We recall the notion of Turaev category $T_R$: Let R be a commutative ring. A Turaev R-module is a couple $\underline{M}=(X,M)$, where X is a set, and $M={\left(M_x\right)}_{x\in X}$ is a family of R-modules indexed by X. A morphisms between two T-modules $(X,M)$ and $(Y,N)$ is a couple $\underline{\varphi }=(f,\varphi )$, where $f:Y\to X$ is a function, and $\varphi ={({\varphi }_y:M_{f_y}\to N_y)}_{y\in Y}$ is a family of linear maps indexed by Y. The composition of $\underline{\varphi }:\underline{M}\to \underline{N}$ and $\underline{\psi }:\underline{N}\to \underline{P}=(Z,P)$ is defined as follows:

$$\begin{array}{ccc}& & \underline{\psi }\underline{\varphi }=(fg,{\left({\psi }_z{\varphi }_{g\left(z\right)}\right)}_{z\in Z}).\hfill \end{array}$$

The category of Turaev R-modules is called the Turaev category and denoted by $T_R$.

2.2. Hopf Quasigroups

Throughout this article, all spaces we consider are over a fixed field k.

Recall from [1] that a Hopf quasigroup H is a unital (not necessarily associative) algebra $(H,{\mu }_H,{\eta }_H)$ and a counital and coassociative coalgebra $(H,{\delta }_H,{ϵ}_H)$ with the morphisms ${\delta }_H$ and ${ϵ}_H$ are algebra morphisms. There exists a linear map $S:H\to H$ such that

$$\begin{array}{c}\hfill \mu (id\otimes \mu )(S\otimes id\otimes id)(\Delta \otimes id)=ϵ\otimes id=\mu (id\otimes \mu )(id\otimes S\otimes id)(\Delta \otimes id),\end{array}$$

(5)

$$\begin{array}{c}\hfill \mu (\mu \otimes id)(id\otimes id\otimes S)(id\otimes \Delta )=id\otimes ϵ=\mu (\mu \otimes id)(id\otimes S\otimes id)(id\otimes \Delta ).\end{array}$$

(6)

In this paper, we use Sweelder notation for the coproduct: $\Delta \left(h\right)={\displaystyle \sum _h}{h}_{\left(1\right)}\otimes h_{\left(2\right)}$, for any $h\in H$. As in [11], in the following, we write $\Delta \left(h\right)=h_{\left(1\right)}\otimes h_{\left(2\right)}$ for simplicity. Using this notation, we can rewrite the conditions (5) and (6) of a Hopf quasigroup as

$$\begin{array}{c}\hfill S\left(h_{\left(1\right)}\right)\left(h_{\left(2\right)}g\right)=ϵ\left(h\right)g=h_{\left(1\right)}\left(S\left(h_{\left(2\right)}\right)g\right),\end{array}$$

(7)

$$\begin{array}{c}\hfill \left(g{h}_{\left(1\right)}\right)S\left(h_{\left(2\right)}\right)=gϵ\left(h\right)=\left(gS\left(h_{\left(1\right)}\right)\right)h_{\left(2\right)},\end{array}$$

(8)

for all $h,g\in H$.

If the antipode S of H is bijective, then for all $h,g\in H$, we have

$$\begin{array}{ccc}& & S^{-1}\left(h_2\right)\left(h_{1}g\right)=ϵ\left(h\right)g=h_2\left(S^{-1}\left(h_1\right)g\right),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & \left(g{S}^{-1}\left(h_2\right)\right)h_1=gϵ\left(h\right)=g\left(h_2{S}^{-1}\left(h_1\right)\right).\hfill \end{array}$$

(10)

A morphism between Hopf quasigroups H and B is a map $f:H\to B$ which is both an algebra and a coalgebra morphism. A Hopf quasigroup is associative if, and only if, it is a Hopf algebra. For more details, see [1,11].

3. Crossed Group-Cograded Hopf Quasigroup

In this section, we first introduce the notion of crossed group-cograded Hopf quasigroups, generalizing crossed Hopf group-coalgebra introduced in [7]. Then we prove that a group-cograded Hopf quasigroup is indeed a Hopf quasigroup in the Turaev category, and provide a method to construct crossed group-cograded Hopf quasigroups.

Definition 1.

Let G be a group. $(H={⨁}_{p\in G}{H}_p,\Delta ,ϵ)$ is called a group-cograded Hopf quasigroup over k, where each $H_p$ is a unital k-algebra with multiplication ${\mu }_p$ and unit ${\eta }_p$, comultiplication Δ is a family of homomorphisms ${({\Delta }_{p,q}:H_{pq}\to H_p\otimes H_q)}_{p,q\in G}$, and counit ϵ is a homomorphism defined by $ϵ:H_e\to k$, such that the following conditions:

(1) 

$H_p{H}_q=0$ whenever $p,q\in G$ and $p\ne q$, and ${\eta }_p\left(1_k\right)=1_p$;

(2) 

Δ is coassociative, in the sense that for any $p,q,r\in G$,

$$\begin{array}{c}\hfill ({\Delta }_{p,q}\otimes i{d}_{H_r}){\Delta }_{pq,r}=(i{d}_{H_p}\otimes {\Delta }_{q,r}){\Delta }_{p,qr},\end{array}$$

(11)

and for all $p,q\in G$ the ${\Delta }_{p,q}$ is an algebra homomorphism and ${\Delta }_{p,q}\left(H_{pq}\right)\subseteq H_p\otimes H_q$.

(3) 

ϵ is counitary in the sense that for any $p\in G$,

$$\begin{array}{c}\hfill (i{d}_{H_p}\otimes ϵ){\Delta }_{p,e}=(ϵ\otimes i{d}_{H_p}){\Delta }_{e,p}=i{d}_{H_p},\end{array}$$

(12)

and ϵ is an algebra homomorphism and $ϵ\left(1_e\right)=1_k$;

(4) 

endowed H with algebra anti-homomorphisms $S={(S_p:H_p\to H_{p^{-1}})}_{p\in G}$, then for any $p\in G$,

$$\begin{array}{ccc}\hfill ϵ\otimes i{d}_{H_p}& =& {\mu }_p(i{d}_{H_p}\otimes {\mu }_p)(S_{p^{-1}}\otimes i{d}_{H_p}\otimes i{d}_{H_p})({\Delta }_{p^{-1},p}\otimes i{d}_{H_p})\hfill \\ & =& {\mu }_p(i{d}_{H_p}\otimes {\mu }_p)(i{d}_{H_p}\otimes S_{p^{-1}}\otimes i{d}_{H_p})({\Delta }_{p,p^{-1}}\otimes i{d}_{H_p}),\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill i{d}_{H_p}\otimes ϵ& =& {\mu }_p({\mu }_p\otimes i{d}_{H_p})(i{d}_{H_p}\otimes i{d}_{H_p}\otimes S_{p^{-1}})(i{d}_{H_p}\otimes {\Delta }_{p,p^{-1}})\hfill \\ & =& {\mu }_p({\mu }_p\otimes i{d}_{H_p})(i{d}_{H_p}\otimes S_{p^{-1}}\otimes i{d}_{H_p})(i{d}_{H_p}\otimes {\Delta }_{p^{-1},p}).\hfill \end{array}$$

(14)

We extend the Sweedler notation for a comultiplication in the following way: For any $p,q\in G,h_{pq}\in H_{pq}$,

$$\begin{array}{c}\hfill {\Delta }_{p,q}\left(h_{pq}\right)=h_{(1,p)}\otimes h_{(2,q)}.\end{array}$$

Then, we can rewrite the conditions (13) and (14) as: for all $p\in G$ and $h_e\in H_e,g\in H_p$,

$$\begin{array}{c}\hfill S_{p^{-1}}\left(h_{(1,p^{-1})}\right)\left(h_{(2,p)}g\right)=ϵ\left(h_e\right)g=h_{(1,p)}\left(S_{p^{-1}}\left(h_{(2,p^{-1})}\right)g\right),\end{array}$$

(15)

$$\begin{array}{c}\hfill \left(g{h}_{(1,p)}\right)S_{p^{-1}}\left(h_{(1,p^{-1})}\right)=gϵ\left(h_e\right)=\left(g{S}_{p^{-1}}\left(h_{(1,p^{-1})}\right)\right)h_{(2,p)}.\end{array}$$

(16)

As in the Hopf group-coalgebra (or group-cograded Hopf algebra) case, we show group-cograded Hopf quasigroups are Hopf quasigroups in a special category as follows.

Proposition 1.

If $H={⨁}_{p\in G}{H}_p$ is a group-cograded Hopf quasigroup, then $(G,H)$ is a Hopf quasigroup in the Turaev category $T_k$.

Proof. 

As H is a group-cograded Hopf quasigroup and G is a group with the multiplication m, we can give $\underline{H}=(G,H)$ a unital algebra structure $(\underline{H},\underline{\mu },\underline{\eta })$ by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underline{k}& \stackrel{\underline{\eta }}{⟶}\underline{H}\hfill \\ \hfill (\ast )& \stackrel{\alpha }{⟵}G\hfill \\ \hfill k& \stackrel{{\eta }_p}{⟶}{H}_p,\hfill \end{array}\mathrm{and}\begin{array}{cc}\hfill \underline{H}\otimes \underline{H}& \stackrel{\underline{\mu }}{⟶}\underline{H}\hfill \\ \hfill G\times G& \stackrel{\delta }{⟵}G\hfill \\ \hfill H_p\otimes H_p& \stackrel{{\mu }_p}{⟶}{H}_p,\hfill \end{array}\end{array}$$

such that

$$\begin{array}{c}\hfill \begin{array}{ccccc}\hfill \underline{H}& \stackrel{\underline{id}\otimes \underline{\eta }}{⟶}\hfill & \hfill \underline{H}\otimes \underline{H}& \stackrel{\underline{\mu }}{⟶}\hfill & \hfill \underline{H}\\ \hfill G& \stackrel{(1,\alpha )}{⟵}\hfill & \hfill G\times G& \stackrel{\delta }{⟵}\hfill & \hfill G\\ \hfill H_p& \stackrel{id\otimes {\eta }_p}{⟶}\hfill & \hfill H_p\otimes H_p& \stackrel{{\eta }_p}{⟶}\hfill & \hfill H_p,\end{array}\mathrm{and}\begin{array}{ccccc}\hfill \underline{H}& \stackrel{\underline{\eta }\otimes \underline{\mathrm{id}}}{⟶}\hfill & \hfill \underline{H}\otimes \underline{H}& \stackrel{\underline{\mu }}{⟶}\hfill & \hfill \underline{H}\\ \hfill G& \stackrel{(\alpha ,1)}{⟵}\hfill & \hfill G\times G& \stackrel{\delta }{⟵}\hfill & \hfill G\\ \hfill H_p& \stackrel{{\eta }_p\otimes \mathrm{id}}{⟶}\hfill & \hfill H_p\otimes H_p& \stackrel{{\eta }_p}{⟶}\hfill & \hfill H_p.\end{array}\end{array}$$

We can also give $(G,H)$ a coalgebra structure $(\underline{H},\underline{\Delta },\underline{ϵ})$ by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underline{H}& \stackrel{\underline{ϵ}}{⟶}\underline{k}\hfill \\ \hfill G& \stackrel{i}{⟵}(\ast )\hfill \\ \hfill H_1=H_{i\left(e\right)}& \stackrel{ϵ}{⟶}k,\hfill \end{array}\mathrm{and}\begin{array}{cc}\hfill \underline{H}& \stackrel{\underline{\Delta }}{⟶}\underline{H}\otimes \underline{H}\hfill \\ \hfill G& \stackrel{m}{⟵}G\times G\hfill \\ \hfill H_{\mathrm{gh}}=H_{m(g\times h)}& \stackrel{{\Delta }_{g,h}}{⟶}{H}_g\otimes H_h,\hfill \end{array}\end{array}$$

such that $(\underline{\Delta },\underline{ϵ})$ are algebra maps.

Let $s:G\to G,s\left(g\right)=g^{-1}$, then we can consider a map $\underline{S}=(s,S)$ in the Turaev category as the antipode of $\underline{H}$, where S is the antipode of the group-cograded Hopf quasigroup H. Next, we will only check that $\underline{S}$ satisfy the condition (7), the condition (8) is similar. Indeed,

$$\begin{array}{c}\hfill \begin{array}{ccccccccc}\hfill \underline{H}\otimes \underline{H}& \stackrel{\underline{\Delta }\otimes \underline{id}}{⟶}\hfill & \hfill \underline{H}\otimes \underline{H}\otimes \underline{H}& \stackrel{\underline{S}\otimes \underline{id}\otimes \underline{id}}{⟶}\hfill & \hfill \underline{H}\otimes \underline{H}\otimes \underline{H}& \stackrel{\underline{id}\otimes \underline{\mu }}{⟶}\hfill & \hfill \underline{H}\otimes \underline{H}& \stackrel{\underline{\mu }}{⟶}\hfill & \hfill \underline{H}\\ \hfill G\times G& \stackrel{(m,1)}{⟵}\hfill & \hfill G\times G\times G& \stackrel{(s,1,1)}{⟵}\hfill & \hfill G\times G\times G& \stackrel{(1,\delta )}{⟵}\hfill & \hfill G\times G& \stackrel{\delta }{⟵}\hfill & \hfill G\\ \hfill H_e\otimes H_p& \stackrel{\Delta \otimes id}{⟶}\hfill & \hfill H_{p^{-1}}\otimes H_p\otimes H_p& \stackrel{S_{p^{-1}}\otimes id\otimes id}{⟶}\hfill & \hfill H_p\otimes H_p\otimes H_p& \stackrel{id\otimes {\mu }_p}{⟶}\hfill & \hfill H_p\otimes H_p& \stackrel{{\mu }_p}{⟶}\hfill & \hfill H_p,\end{array}\end{array}$$

and

$$\begin{array}{ccc}\hfill \underline{H}\otimes \underline{H}& \stackrel{\underline{ϵ}\otimes \underline{id}}{⟶}& \underline{k}\otimes \underline{H}\hfill \\ \hfill G\times G& \stackrel{i\otimes 1}{⟵}& (\ast )\times G\hfill \\ \hfill H_{i\left(e\right)}\otimes H& \stackrel{ϵ\otimes id}{⟶}& k\otimes H.\hfill \end{array}$$

Since H is a group-cograded Hopf quasigroup, we have $(\underline{\Delta }\otimes \underline{id})(\underline{S}\otimes \underline{id}\otimes \underline{id})(\underline{id}\otimes \underline{\mu })\underline{\mu }=\underline{ϵ}\otimes \underline{id}$. Thus, the left hand of Equation (7) holds, and the right hand is similar. □

Definition 2.

A group-cograded Hopf quasigroup $(H={⨁}_{p\in G}{H}_p,\Delta ,ϵ,S)$ is said to be a crossed group-cograded Hopf quasigroup provided it is endowed with a crossing $\pi :G\to Aut\left(H\right)$ such that

(1) 

each ${\pi }_p$ satisfies ${\pi }_p\left(H_q\right)=H_{pq{p}^{-1}}$, and preserves the counit, the antipode, and the comultiplication, i.e., for all $p,q,r\in G$,

$$\begin{array}{ccc}& & ϵ{\pi }_p{|}_{H_e}=ϵ,\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & {\pi }_p{S}_q=S_{pq{p}^{-1}}{\pi }_p,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}& & ({\pi }_p\otimes {\pi }_p){\Delta }_{q,r}={\Delta }_{pq{p}^{-1},pr{p}^{-1}}{\pi }_p,\hfill \end{array}$$

(19)

(2) 

π is multiplicative in the sense that for all $p,q\in G$, ${\pi }_{pq}={\pi }_p{\pi }_q$.

If all of its subalgebras ${\left(H_p\right)}_{p\in G}$ are associative, then H is a crossed Hopf group-coalgebra introduced in [7]. In the following, we give two examples of crossed group-cograded Hopf quasigroups; both examples are derived from an action of G on a Hopf quasigroup over k by Hopf quasigroup endomorphisms.

Example 1.

Let $(H,\Delta ,ϵ,S)$ be a Hopf quasigroup. Set $H^G=(H_p{)}_{p\in G}$ and G is the homomorphism group of H, where for each $p\in G$, the algebra $H_p$ is a copy of H. Fix an identification isomorphism of algebras $i_p:H\to H_p$. For $p,q\in G$, we define a comultiplication ${\Delta }_{p,q}:H_{pq}\to H_p\otimes H_q$ by

$$\begin{array}{ccc}& & {\Delta }_{p,q}\left(i_{pq}\left(h\right)\right)=\sum _{\left(h\right)}{i}_p\left(h_{\left(1\right)}\right)\otimes i_q\left(h_{\left(2\right)}\right),\hfill \end{array}$$

where $h\in H$. The counit $ϵ:H_e\to k$ is defined by $ϵ\left(i_e\left(h\right)\right)=ϵ\left(h\right)\in k$ for $h\in H$. For $p\in G$, the antipode $S_p:H_p\to H_{p^{-1}}$ is given by

$$\begin{array}{ccc}& & S_p\left(i_p\left(h\right)\right)=i_{p^{-1}}\left(S\left(h\right)\right),\hfill \end{array}$$

where $h\in H$. For $p,q\in G$, the homomorphism ${\pi }_p:H_q\to H_{pq{p}^{-1}}$ is defined by ${\pi }_p\left(i_q\left(h\right)\right)=i_{pq{p}^{-1}}\left(p\left(h\right)\right)$. It is easy to check that $H^G$ is a crossed group-cograded Hopf quasigroup.

Using the mirror reflection technique introduced in Turaev [7], we can give a construction of crossed group-cograded Hopf quasigroups from a fixed crossed group-cograded Hopf quasigroup as follows.

Theorem 1.

Let $(H={⨁}_{p\in G}{H}_p,\Delta ,ϵ,S,\pi )$ be a crossed group-cograded Hopf quasigroup, then we can define its mirror $(\tilde{H}={⨁}_{p\in G}{\tilde{H}}_p,\tilde{\Delta },\widetilde{ϵ},\tilde{S},\tilde{\pi })$ in the following way:

(1) 

as an algebra, ${\tilde{H}}_p=H_{p^{-1}}$, for all $p\in G$;

(2) 

define the comultiplication ${\tilde{\Delta }}_{p,q}:{\tilde{H}}_{pq}\to {\tilde{H}}_p\otimes {\tilde{H}}_q$ by: for $h_{q^{-1}{p}^{-1}}\in {\tilde{H}}_{pq}$,

$$\begin{array}{ccc}\hfill {\tilde{\Delta }}_{p,q}\left(h_{q^{-1}{p}^{-1}}\right)& =& ({\pi }_q\otimes i{d}_{H_{q^{-1}}}){\Delta }_{q^{-1}{p}^{-1}q,q^{-1}}\left(h_{q^{-1}{p}^{-1}}\right);\hfill \end{array}$$

(20)

(3) 

the counit $\widetilde{ϵ}$ of $\tilde{H}$ is the original counit ϵ;

(4) 

the antipode ${\tilde{S}}_p={\pi }_p{S}_{p^{-1}}:{\tilde{H}}_p=H_{p^{-1}}\to H_p={\tilde{H}}_{p^{-1}}$;

(5) 

for all $p\in G$, define the cross action ${\tilde{\pi }}_p={\pi }_p$.

Then $(\tilde{H}={⨁}_{p\in G}{\tilde{H}}_p,\tilde{\Delta },\widetilde{ϵ},\tilde{S},\tilde{\pi })$ is also a crossed group-cograded Hopf quasigroup.

Proof. 

It is easy to check that $\tilde{\Delta }$ is coassociative, and $ϵ$ is a counit of $\tilde{H}$. By the definition of $\tilde{H}$, $h_{r^{-1}{q}^{-1}{p}^{-1}}\in {\tilde{H}}_{pqr}$, for all $p,q,r\in G$, naturally holds.

We will only prove Equation (13) of $\tilde{H}$ holds; the Equation (14) of $\tilde{H}$ is similar. Indeed,

$$\begin{array}{ccc}& & {\mu }_{p^{-1}}(i{d}_{{\tilde{H}}_p}\otimes {\mu }_{p^{-1}})({\tilde{S}}_{p^{-1}}\otimes i{d}_{{\tilde{H}}_p}\otimes i{d}_{{\tilde{H}}_p})({\tilde{\Delta }}_{p^{-1},p}\otimes i{d}_{{\tilde{H}}_p})\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})({\pi }_{p^{-1}}{S}_p\otimes i{d}_{H_{p^{-1}}}\otimes i{d}_{H_{p^{-1}}})\left(({\pi }_p\otimes i{d}_{H_{p^{-1}}}){\Delta }_{p,p^{-1}}\otimes i{d}_{H_{p^{-1}}}\right)\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})\left(({\pi }_{p^{-1}}{S}_p{\pi }_p\otimes i{d}_{H_{p^{-1}}}){\Delta }_{p,p^{-1}}\otimes i{d}_{H_{p^{-1}}}\right)\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})\left((S_p\otimes i{d}_{H_{p^{-1}}}){\Delta }_{p,p^{-1}}\otimes i{d}_{H_{p^{-1}}}\right)\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})(S_p\otimes i{d}_{H_{p^{-1}}}\otimes i{d}_{H_{p^{-1}}})({\Delta }_{p,p^{-1}}\otimes i{d}_{H_{p^{-1}}})\hfill \\ & =& ϵ\otimes i{d}_{{\tilde{H}}_p},\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\mu }_{p^{-1}}(i{d}_{{\tilde{H}}_p}\otimes {\mu }_{p^{-1}})(i{d}_{{\tilde{H}}_p}\otimes {\tilde{S}}_{p^{-1}}\otimes i{d}_{{\tilde{H}}_p})({\tilde{\Delta }}_{p,p^{-1}}\otimes i{d}_{{\tilde{H}}_p})\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})(i{d}_{H_{p^{-1}}}\otimes {\pi }_{p^{-1}}{S}_{p^{-1}}\otimes i{d}_{H_{p^{-1}}})\left(({\pi }_{p^{-1}}\otimes i{d}_{H_p}){\Delta }_{p{p}^{-1}{p}^{-1},p}\otimes i{d}_{H_{p^{-1}}}\right)\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})\left(({\pi }_{p^{-1}}\otimes S_{p^{-1}pp}{\pi }_{p^{-1}}){\Delta }_{p^{-1},p}\otimes i{d}_{H_{p^{-1}}}\right)\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})\left((i{d}_{H_{p^{-1}}}\otimes S_p)({\pi }_{p^{-1}}\otimes {\pi }_{p^{-1}}){\Delta }_{p^{-1},p}\otimes i{d}_{H_{p^{-1}}}\right)\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})\left((i{d}_{H_{p^{-1}}}\otimes S_p){\Delta }_{p^{-1},p}{\pi }_{p^{-1}}\otimes i{d}_{H_{p^{-1}}}\right)\hfill \\ & =& {\mu }_{p^{-1}}(i{d}_{H_{p^{-1}}}\otimes {\mu }_{p^{-1}})(i{d}_{H_{p^{-1}}}\otimes S_p\otimes i{d}_{H_{p^{-1}}})({\Delta }_{p^{-1},p}\otimes i{d}_{H_{p^{-1}}})({\pi }_{p^{-1}}\otimes i{d}_{H_{p^{-1}}})\hfill \\ & =& (ϵ\otimes i{d}_{H_{p^{-1}}})({\pi }_{p^{-1}}\otimes i{d}_{H_{p^{-1}}})\hfill \\ & =& ϵ\otimes i{d}_{{\tilde{H}}_p},\hfill \end{array}$$

so the Equation (13) of $\tilde{H}$ holds.

It is obvious that $\tilde{\pi }=\pi$ is multiplicative, and each ${\pi }_p$ preserves the counit, so if each ${\pi }_p$ preserves the antipode and comultiplication, the mirror $\tilde{H}$ of H is also a crossed group-cograded Hopf quasigroup. Indeed, for all $p,q\in G$,

$$\begin{array}{c}\hfill {\tilde{S}}_{pq{p}^{-1}}{\pi }_p={\pi }_{pq{p}^{-1}}{S}_{pq{p}^{-1}}{\pi }_p={\pi }_{pq{p}^{-1}}{\pi }_p{S}_q={\pi }_{pq}{S}_q={\pi }_p{\pi }_q{S}_q={\pi }_p{\tilde{S}}_q,\end{array}$$

thus ${\pi }_p$ preserves the antipode. We finally consider comultiplication, for all $p,q,r\in G$,

$$\begin{array}{ccc}\hfill ({\pi }_p\otimes {\pi }_p){\tilde{\Delta }}_{q,r}& =& ({\pi }_p\otimes {\pi }_p)({\pi }_r\otimes i{d}_{H_{r^{-1}}}){\Delta }_{r^{-1}{q}^{-1}r,r^{-1}}\hfill \\ & =& ({\pi }_{pr}\otimes {\pi }_p){\Delta }_{r^{-1}{q}^{-1}r,r^{-1}},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tilde{\Delta }}_{pq{p}^{-1},pr{p}^{-1}}{\pi }_p& =& ({\pi }_{pr{p}^{-1}}\otimes i{d}_{H_{p{r}^{-1}{p}^{-1}}}){\Delta }_{p{r}^{-1}{q}^{-1}r{p}^{-1},p{r}^{-1}{p}^{-1}}{\pi }_p\hfill \\ & =& ({\pi }_{pr{p}^{-1}}\otimes i{d}_{H_{p{r}^{-1}{p}^{-1}}})({\pi }_p\otimes {\pi }_p){\Delta }_{r^{-1}{q}^{-1}r,r^{-1}}\hfill \\ & =& ({\pi }_{pr}\otimes {\pi }_p){\Delta }_{r^{-1}{q}^{-1}r,r^{-1}},\hfill \end{array}$$

hence ${\pi }_p$ preserves comultiplication. Then we conclude $\tilde{H}$ is a crossed group-cograded Hopf quasigroup. □

Remark 1.

Let H be a crossed group-cograded Hopf quasigroup. If $\tilde{H}$ is the mirror of H, then the mirror of $\tilde{H}$ is $\tilde{\tilde{H}}$ = H.

Example 2.

Let $H^G$ be a crossed group-cograded Hopf quasigroup introduced in Example 1.

Set ${\tilde{H}}^G$ to be the same family of algebras ${(H_p=H)}_{p\in G}$ with the same counit, the same action π of G, the comultiplication ${\tilde{\Delta }}_{p,q}:H_{pq}\to H_p\otimes H_q$, and the antipode ${\tilde{S}}_p:H_p\to H_{p^{-1}}$ defined by

$$\begin{array}{ccc}& & {\tilde{\Delta }}_{p,q}\left(i_{pq}\left(h\right)\right)=\sum _{\left(h\right)}{i}_p\left(q\left(h_{\left(1\right)}\right)\right)\otimes i_q\left(h_{\left(2\right)}\right),\hfill \\ & & {\tilde{S}}_p\left(i_p\left(h\right)\right)=i_{p^{-1}}\left(p\left(S\left(h\right)\right)\right)=i_{p^{-1}}\left(S\left(p\left(h\right)\right)\right),\hfill \end{array}$$

where $h\in H$. By Theorem 1, ${\tilde{H}}^G$ becomes a crossed group-cograded Hopf quasigroup.

Note that the crossed group-cograded Hopf quasigroups $H^G$ and ${\tilde{H}}^G$, which are defined in Examples 1 and 2, respectively, are mirrors of each other.

4. Construction of Braided Crossed Categories

Let $H={⨁}_{r\in G}{H}_r$ be a crossed group-cograded Hopf quasigroup with a bijective antipode S. We introduce the definition of p-Yetter–Drinfeld quasimodules over H, then show the category $YDQ\left(H\right)$ of Yetter–Drinfeld quasimodules is a crossed category, and the subcategory $YD\left(H\right)$ of Yetter–Drinfeld modules over H is a braided crossed category.

Recall the definition of left H-quasimodule in [11]; we give the following definition.

Definition 3.

Let V be a vector space, $(V,\phi )$ is called a left $H_p$-quasimodule if there exists an action $\phi :H_p\otimes V\to V,h_p\otimes v\to h_p·v$ satisfying

$$\begin{array}{ccc}\hfill \phi ({\eta }_p\otimes i{d}_V)& =& i{d}_V,\hfill \\ \hfill \phi (S_{p^{-1}}\otimes \phi )({\Delta }_{p^{-1},p}\otimes i{d}_V)& =& ϵ\otimes i{d}_V\hfill \end{array}$$

(21)

$$\begin{array}{ccc}& =& \phi (i{d}_{H_p}\otimes \phi )(i{d}_{H_p}\otimes S_{p^{-1}}\otimes i{d}_V)({\Delta }_{p,p^{-1}}\otimes i{d}_V).\hfill \end{array}$$

(22)

Using Sweelder notation, for all $h\in H_e,v\in V$, (21) and (22) is equivalent to

$$\begin{array}{ccc}\hfill 1_p·v& =& v,\hfill \\ \hfill S_{p^{-1}}\left(h_{(1,p^{-1})}\right)·(h_{(2,p)}·v)& =& ϵ\left(h\right)v\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& =& h_{(1,p)}·\left(S_{p^{-1}}\left(h_{2,p^{-1}}\right)·v\right).\hfill \end{array}$$

(24)

Moreover, if the condition (22) is instead by $h·(g·v)=\left(hg\right)·v$, where $h,g\in H_p$, then the left $H_p$-quasimodule is a left $H_p$-module.

Definition 4.

Let V be a vector space and p a fixed element in group G. A couple $(V,{\rho }^V={\left({\rho }_r^V\right)}_{r\in G})$ is said to be a left-right p-Yetter–Drinfeld quasimodule, where V is a unital $H_p$-quasimodule, and for any $r\in G,{\rho }_r^V:V\to V\otimes H_r$ is a k-linear morphism, denoted by Sweedler notation ${\rho }_r^V\left(v\right)={\displaystyle \sum _v}{v}_{\left(0\right)}\otimes v_{(1,r)}$ (write ${\rho }_r^V\left(v\right)=v_{\left(0\right)}\otimes v_{(1,r)}$ for short) such that the following conditions are satisfied:

(1) 

V is coassociative in the sense that, for any $r_1,r_2\in G$, we have

$$\begin{array}{c}\hfill ({\rho }_{r_1}^V\otimes i{d}_{H_{r_2}}){\rho }_{r_2}^V=(i{d}_V\otimes {\Delta }_{r_1,r_2}){\rho }_{r_1{r}_2}^V;\end{array}$$

(2) 

V is counitary, in the sense that

$$\begin{array}{c}\hfill (i{d}_V\otimes ϵ){\rho }_e^V=i{d}_V;\end{array}$$

(3) 

V is crossed, in the sense that for all $v\in V$, $r\in G$ and $h,g\in H_{\left(r\right)}$,

$$\begin{array}{cc}& h_{(1,p)}·v_{\left(0\right)}\otimes h_{(2,r)}{v}_{(1,r)}={(h_{(2,p)}·v)}_{\left(0\right)}\otimes {(h_{(2,p)}·v)}_{(1,r)}{\pi }_{p^{-1}}\left(h_{(1,pr{p}^{-1})}\right),\end{array}$$

(25)

$$\begin{array}{cc}& v_{\left(0\right)}\otimes v_{(1,r)}\left(hg\right)=v_{\left(0\right)}\otimes \left(v_{(1,r)}h\right)g,\end{array}$$

(26)

$$\begin{array}{cc}& v_{\left(0\right)}\otimes \left(h{v}_{(1,r)}\right)g=v_{\left(0\right)}\otimes h\left(v_{(1,r)}g\right).\end{array}$$

(27)

Remark 2.

The conditions (26) and (27) follow the definition of a Yetter–Drinfeld quasimodule in Alonso’s paper.

Given two p-Yetter–Drinfeld quasimodules $(V,\rho {}^V)$ and $(W,{\rho }^W)$, a morphism of these two p-Yetter–Drinfeld quasimodules $f:(V,{\rho }^V)\to (W,{\rho }^W)$ is an $H_p$-linear map $f:V\to W$ and satisfies the following diagram: for any $r\in G$,

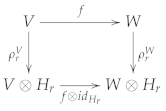that is, for all $v\in V$,

$$\begin{array}{c}\hfill f{\left(v\right)}_{\left(0\right)}\otimes f{\left(v\right)}_{(1,r)}=f\left(v_{\left(0\right)}\right)\otimes v_{(1,r)}.\end{array}$$

Then we have the category $YDQ{\left(H\right)}_p$ of p-Yetter–Drinfeld quasimodules; the composition of morphisms of p-Yetter–Drinfeld quasimodules is the standard composition of the underlying linear maps. Moreover, if we assume that V is a left $H_p$-module, then we say that is a left-right p-Yetter–Drinfeld module. Obviously, left-right p-Yetter–Drinfeld modules with the obvious morphisms is a subcategory of $YDQ{\left(H\right)}_p$, denoted by $YD{\left(H\right)}_p$.

Proposition 2.

The Equation (25) is equivalent to

$$\begin{array}{c}\hfill {(h_p·v)}_{\left(0\right)}\otimes {(h_p·v)}_{(1,r)}=h_{(2,p)}·v_{\left(0\right)}\otimes \left(h_{(3,r)}{v}_{(1,r)}\right)S^{-1}{\pi }_{p^{-1}}\left(h_{(1,p{r}^{-1}{p}^{-1})}\right),\end{array}$$

(28)

for all $h_p\in H_p$ and $v\in V$.

Proof. 

Suppose the condition (25) holds, then we have

$$\begin{array}{ccc}& & h_{(2,p)}·v_{\left(0\right)}\otimes \left(h_{(3,r)}{v}_{(1,r)}\right)S^{-1}{\pi }_{p^{-1}}\left(h_{(1,p{r}^{-1}{p}^{-1})}\right)\hfill \\ & =& {(h_{(3,p)}·v)}_{\left(0\right)}\otimes \left({(h_{(3,p)}·v)}_{(1,r)}{\pi }_{p^{-1}}\left(h_{(2,pr{p}^{-1})}\right)\right)S^{-1}{\pi }_{p^{-1}}\left(h_{(1,p{r}^{-1}{p}^{-1})}\right)\hfill \\ & =& {(h_{(3,p)}·v)}_{\left(0\right)}\otimes {(h_{(3,p)}·v)}_{(1,r)}\left({\pi }_{p^{-1}}\left(h_{(2,pr{p}^{-1})}{S}^{-1}\left(h_{(1,p{r}^{-1}{p}^{-1})}\right)\right)\right)\hfill \\ & =& {(h_{(2,p)}·v)}_{\left(0\right)}\otimes {(h_{(2,p)}·v)}_{(1,r)}{\pi }_{p^{-1}}ϵ\left(h_e\right)\hfill \\ & =& {(h_{(2,p)}·v)}_{\left(0\right)}\otimes {(h_{(2,p)}·v)}_{(1,r)}ϵ\left(h_e\right)\hfill \\ & =& {(h_p·v)}_{\left(0\right)}\otimes {(h_p·v)}_{(1,r)}\hfill \end{array}$$

where the first equality follows by (25), the others rely on the properties of the crossed group-cograded Hopf quasigroup.

Conversely, if the Equation (28) holds, then

$$\begin{array}{ccc}& & {(h_{(2,p)}·v)}_{\left(0\right)}\otimes {(h_{(2,p)}·v)}_{(1,r)}{\pi }_{p^{-1}}\left(h_{(1,pr{p}^{-1})}\right)\hfill \\ & =& h_{(3,p)}·v_{\left(0\right)}\otimes \left(h_{(4,r)}{v}_{(1,r)}\right)S^{-1}{\pi }_{p^{-1}}\left(h_{(2,pr{p}^{-1})}\right){\pi }_{p^{-1}}\left(h_{(1,pr{p}^{-1})}\right)\hfill \\ & =& h_{(3,p)}·v_{\left(0\right)}\otimes \left(h_{(4,r)}{v}_{(1,r)}\right){\pi }_{p^{-1}}\left(S^{-1}\left(h_{(2,pr{p}^{-1})}\right)h_{(1,pr{p}^{-1})}\right)\hfill \\ & =& h_{(1,p)}·v_{\left(0\right)}\otimes \left(h_{(2,r)}{v}_{(1,r)}\right){\pi }_{p^{-1}}ϵ\left(h_e\right)\hfill \\ & =& h_{(1,p)}·v_{\left(0\right)}\otimes h_{(2,r)}{v}_{(1,r)}\hfill \end{array}$$

where the first equality follows by (28), the rest follows by the properties of the crossed group-cograded Hopf quasigroup. □

Remark 3.

According to the Equation (27), the condition (28) is equivalent to

$$\begin{array}{c}\hfill {(h_p·v)}_{\left(0\right)}\otimes {(h_p·v)}_{(1,r)}=h_{(2,p)}·v_{\left(0\right)}\otimes h_{(3,r)}\left(v_{(1,r)}{S}^{-1}{\pi }_{p^{-1}}\left(h_{(1,p{r}^{-1}{p}^{-1})}\right)\right).\end{array}$$

(29)

Proposition 3.

If $(V,{\rho }^V)\in YDQ{\left(H\right)}_p$ and $(W,{\rho }^W)\in YDQ{\left(H\right)}_q$, then $V\otimes W\in YDQ{\left(H\right)}_{pq}$ with the module and comodule structures, as follows:

$$\begin{array}{ccc}\hfill h_{pq}·(v\otimes w)& =& h_{(1,p)}·v\otimes h_{(2,q)}·w,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\rho }_r^{V\otimes W}(v\otimes w)& =& v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes w_{(1,r)}{\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right),\hfill \end{array}$$

(31)

where $v\in V,w\in W$ and $h_{pq}\in H_{pq}$.

Proof. 

We first check that $V\otimes W$ is a left $H_{pq}$-quasimodule, and the unital property is obvious. We only check the left hand side of Equation (22); the right hand is similar. For all $v\in V,w\in W$,

$$\begin{array}{ccc}& & h_{(1,pq)}·\left(S^{-1}\left(h_{(2,{\left(pq\right)}^{-1})}\right)·(v\otimes w)\right)\hfill \\ & =& h_{(1,pq)}·\left(S^{-1}\left(h_{(2,p^{-1})}\right)·v\otimes S^{-1}\left(h_{(2,q^{-1})}\right)·w\right)\hfill \\ & =& \left(h_{(1,p)}·\left(S^{-1}\left(h_{(2,p^{-1})}\right)·v\right)\right)\otimes \left(h_{(2,q)}·\left(S^{-1}\left(h_{(2,q^{-1})}\right)·w\right)\right)\hfill \\ & =& \left(ϵ\left(h_{(1,e)}\right)·v\right)\otimes \left(ϵ\left(h_{(2,e)}\right)·w\right)\hfill \\ & =& ϵ\left(h_e\right)·(v\otimes w)\hfill \end{array}$$

where the first and second equalities rely on (30), the third equality follows by (22). Then $V\otimes W$ is a left $H_{pq}$-quasimodule.

In the following equations, we check that the coassociative condition holds:

$$\begin{array}{ccc}& & (i{d}_{V\otimes W}\otimes {\Delta }_{r_1,r_2}){\rho }_{r_1{r}_2}(v\otimes w)\hfill \\ & =& (i{d}_{V\otimes W}\otimes {\Delta }_{r_1,r_2})\left(v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes w_{(1,r_1{r}_2)}{\pi }_{q^{-1}}\left(v_{(1,q{r}_1{r}_2{q}^{-1})}\right)\right)\hfill \\ & =& v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes w_{(1,r_1)}{\pi }_{q^{-1}}{v}_{(1,q{r}_1{q}^{-1})}\otimes w_{(2,r_2)}{\pi }_{q^{-1}}\left(v_{(2,q{r}_2{q}^{-1})}\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}& & ({\rho }_{r_1}\otimes i{d}_{r_2}){\rho }_{r_2}(v\otimes w)\hfill \\ & =& ({\rho }_{r_1}\otimes i{d}_{r_2})(v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes w_{(1,r_2)}{\pi }_{q^{-1}}\left(v_{1,q{r}_2{q}^{-1}}\right))\hfill \\ & =& v_{\left(0\right)\left(0\right)}\otimes w_{\left(0\right)\left(0\right)}\otimes w_{\left(0\right)(1,r_1)}{\pi }_{q^{-1}}\left(v_{\left(0\right)(1,q{r}_1{q}^{-1})}\right)\otimes w_{(1,r_2)}{\pi }_{q^{-1}}\left(v_{1,q{r}_2{q}^{-1}}\right)\hfill \\ & =& v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes w_{(1,r_1)}{\pi }_{q^{-1}}\left(v_{(1,q{r}_1{q}^{-1})}\right)\otimes w_{(2,r_2)}{\pi }_{q^{-1}}\left(v_{(2,q{r}_2{q}^{-1})}\right).\hfill \end{array}$$

This shows that $(i{d}_{V\otimes W}\otimes {\Delta }_{r_1,r_2}){\rho }_{r_1{r}_2}=({\rho }_{r_1}\otimes i{d}_{r_2}){\rho }_{r_2}$.

The counitary condition is easy to show. Then we check the crossed condition, as follows:

$$\begin{array}{ccc}& & h_{(1,pq)}·{(v\otimes w)}_{\left(0\right)}\otimes h_{(2,r)}{(v\otimes w)}_{(1,r)}\hfill \\ & \stackrel{\mathrm{(31)}}{=}& h_{(1,pq)}·(v_{\left(0\right)}\otimes w_{\left(0\right)})\otimes h_{(2,r)}\left(w_{(1,r)}{\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)\right)\hfill \\ & \stackrel{\mathrm{(26)}}{=}& h_{(1,pq)}·(v_{\left(0\right)}\otimes w_{\left(0\right)})\otimes \left(h_{(2,r)}{w}_{(1,r)}\right){\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)\hfill \\ & \stackrel{\mathrm{(30)}}{=}& h_{(1,p)}·v_{\left(0\right)}\otimes h_{(2,q)}·w_{\left(0\right)}\otimes \left(h_{(3,r)}{w}_{(1,r)}\right){\pi }_{q^{-1}}\left(v_{1,qr{q}^{-1}}\right)\hfill \\ & \stackrel{\mathrm{(25)}}{=}& h_{(1,p)}·v_{\left(0\right)}\otimes {(h_{(3,q)}·w)}_{\left(0\right)}\otimes {(h_{(3,q)}·w)}_{(1,r)}{\pi }_{q^{-1}}\left(h_{(2,qr{q}^{-1})}\right){\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)\hfill \\ & =& h_{(1,p)}·v_{\left(0\right)}\otimes {(h_{(3,q)}·w)}_{\left(0\right)}\otimes {(h_{(3,q)}·w)}_{(1,r)}{\pi }_{q^{-1}}\left(h_{(2,qr{q}^{-1})}{v}_{(1,qr{q}^{-1})}\right)\hfill \\ & \stackrel{\mathrm{(25)}}{=}& {(h_{(2,p)}·v)}_{\left(0\right)}\otimes {(h_{(3,q)}·w)}_{\left(0\right)}\hfill \\ & & \otimes {(h_{(3,q)}·w)}_{(1,r)}{\pi }_{q^{-1}}\left({(h_{(2,q)}·v)}_{(1,qr{q}^{-1})}{\pi }_{p^{-1}}\left(h_{(1,pqr{q}^{-1}{p}^{-1})}\right)\right)\hfill \\ & =& {(h_{(2,p)}·v)}_{\left(0\right)}\otimes {(h_{(3,q)}·w)}_{\left(0\right)}\hfill \\ & & \otimes {(h_{(3,q)}·w)}_{(1,r)}{\pi }_{q^{-1}}\left({(h_{(2,q)}·v)}_{(1,qr{q}^{-1})}\right){\pi }_{q^{-1}{p}^{-1}}\left(h_{(1,pqr{q}^{-1}{p}^{-1})}\right)\hfill \\ & \stackrel{\mathrm{(31)}}{=}& {(h_{(2,p)}·v\otimes h_{(3,q)}·w)}_{\left(0\right)}\otimes {(h_{(2,p)}·v\otimes h_{(3,q)}·w)}_{(1,r)}{\pi }_{q^{-1}{p}^{-1}}\left(h_{(1,pqr{q}^{-1}{p}^{-1})}\right)\hfill \\ & \stackrel{\mathrm{(30)}}{=}& h_{(2,pq)}·{(v\otimes w)}_{\left(0\right)}\otimes {\left(h_{(2,pq)}·(v\otimes w)\right)}_{(1,r)}{\pi }_{q^{-1}{p}^{-1}}\left(h_{(1,pqr{q}^{-1}{p}^{-1})}\right).\hfill \end{array}$$

Finally, we check the Equation (26), and the Equation (27) is similar.

$$\begin{array}{ccc}\hfill {(v\otimes w)}_{\left(0\right)}\otimes {(v\otimes w)}_{(1,r)}\left(hg\right)& =& v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes \left(w_{(1,r)}{\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)\right)\left(hg\right)\hfill \\ & =& v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes w_{(1,r)}\left({\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)\left(hg\right)\right)\hfill \\ & =& v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes w_{(1,r)}\left(\left({\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)h\right)g\right)\hfill \\ & =& v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes \left(w_{(1,r)}\left({\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)h\right)\right)g\hfill \\ & =& v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes \left(\left(w_{(1,r)}{\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)\right)h\right)g\hfill \\ & =& {(v\otimes w)}_{\left(0\right)}\otimes \left({(v\otimes w)}_{(1,r)}h\right)g.\hfill \end{array}$$

Hence $V\otimes W\in YDQ{\left(H\right)}_{pq}$. □

Following Turaev’s left index notation, let $V\in YDQ{\left(H\right)}_p$, the object ${}^{q}V$ have the same underlying vector space as V. Given $v\in V$, we denote ${}^{q}v$ the corresponding element in ${}^{q}V$.

Proposition 4.

Let $(V,{\rho }^V)\in YDQ{\left(H\right)}_p$ and $q\in G$. Set ${}^{q}V=V$ as a vector space with structures

$$\begin{array}{ccc}& & h_{qp{q}^{-1}}·{}^{q}v={}^q({\pi }_{q^{-1}}\left(h_{qp{q}^{-1}}\right)·v)\hfill \end{array}$$

(32)

$$\begin{array}{ccc}& & {\rho }_r^{{}^{q}V}{(}^{q}v)={}^q\left(v_{\left(0\right)}\right)\otimes {\pi }_q\left(v_{(1,q^{-1}rq)}\right)\hfill \end{array}$$

(33)

for any $v\in V$ and $h_{qp{q}^{-1}}\in H_{qp{q}^{-1}}$. Then ${}^{q}V\in YDQ{\left(H\right)}_{qp{q}^{-1}}$.

Proof. 

We first check that ${}^{q}V$ is a left $H_{qp{q}^{-1}}$-quasimodule. The condition (21) is easy to check. Next, we prove the condition (22).

$$\begin{array}{ccc}\hfill h_{(1,qp{q}^{-1})}·(S^{-1}\left(h_{(2,q{p}^{-1}{q}^{-1})}\right)·{}^{q}v)& =& h_{(1,qp{q}^{-1})}·\left({}^q\left({\pi }_{q^{-1}}\left(S^{-1}\left(h_{(2,q{p}^{-1}{q}^{-1})}\right)\right)·v\right)\right)\hfill \\ & =& {}^q\left({\pi }_{q^{-1}}\left(h_{(1,qp{q}^{-1})}\right)·\left({\pi }_{q^{-1}}\left(S^{-1}\left(h_{(2,q{p}^{-1}{q}^{-1})}\right)\right)·v\right)\right)\hfill \\ & =& {}^q\left(ϵ\left({\pi }_{q^{-1}}\left(h_e\right)\right)·v\right)\hfill \\ & =& ϵ\left({\pi }_{q^{-1}}\left(h_e\right)\right)·{}^{q}v\hfill \\ & =& ϵ\left(h_e\right){}^{q}v.\hfill \end{array}$$

The proof of the other side is similar to the above, so ${}^{q}V$ is a left $H_{qp{q}^{-1}}$-quasimodule, and the coassociative and counitary are also satisfied.

In the following, we show that the crossing condition holds:

$$\begin{array}{ccc}& & {(h_{qp{q}^{-1}}·{}^{q}v)}_{\left(0\right)}\otimes {(h_{qp{q}^{-1}}·{}^{q}v)}_{(1,r)}\hfill \\ & \stackrel{\mathrm{(32)}}{=}& {\left({}^q\left({\pi }_{q^{-1}}\left(h_{qp{q}^{-1}}\right)·v\right)\right)}_{\left(0\right)}\otimes {\left({}^q\left({\pi }_{q^{-1}}\left(h_{qp{q}^{-1}}\right)·v\right)\right)}_{(1,r)}\hfill \\ & \stackrel{\mathrm{(33)}}{=}& {}^q\left({\left({\pi }_{q^{-1}}\left(h_{qp{q}^{-1}}\right)·v\right)}_{\left(0\right)}\right)\otimes {\pi }_q\left({\left({\pi }_{q^{-1}}\left(h_{qp{q}^{-1}}\right)\right)}_{(1,r)}\right)\hfill \\ & \stackrel{\mathrm{(28)}}{=}& {}^q\left({\pi }_{q^{-1}}{\left(h_{qp{q}^{-1}}\right)}_{(2,p)}·v_{\left(0\right)}\right)\hfill \\ & & \otimes {\pi }_q\left(\left({\pi }_{q^{-1}}{\left(h_{qp{q}^{-1}}\right)}_{(3,q^{-1}rq)}{v}_{(1,q^{-1}rq)}\right)S^{-1}{\pi }_{p^{-1}}\left({\pi }_{q^{-1}}{\left(h_{qp{q}^{-1}}\right)}_{(1,p{q}^{-1}{r}^{-1}q{p}^{-1})}\right)\right)\hfill \\ & =& {}^q\left({\pi }_{q^{-1}}\left(h_{(2,qp{q}^{-1})}\right)·v_{\left(0\right)}\right)\hfill \\ & & \otimes {\pi }_q\left(\left({\pi }_{q^{-1}}\left(h_{(3,r)}\right)v_{(1,q^{-1}rq)}\right)S^{-1}{\pi }_{p^{-1}}\left({\pi }_{q^{-1}}\left(h_{(1,qp{q}^{-1}{r}^{-1}q{p}^{-1}{q}^{-1})}\right)\right)\right)\hfill \\ & =& {}^q\left({\pi }_{q^{-1}}\left(h_{(2,qp{q}^{-1})}\right)·v_{\left(0\right)}\right)\otimes \left(h_{(3,r)}{\pi }_q\left(v_{(1,q^{-1}rq)}\right)\right)S^{-1}{\pi }_{qp{q}^{-1}}\left(h_{(1,qp{q}^{-1}{r}^{-1}q{p}^{-1}{q}^{-1})}\right)\hfill \\ & \stackrel{\mathrm{(32)}}{=}& h_{(2,qp{q}^{-1})}·{}^q\left(v_{\left(0\right)}\right)\otimes \left(h_{(3,r)}{\pi }_q\left(v_{(1,q^{-1}rq)}\right)\right)S^{-1}{\pi }_{qp{q}^{-1}}\left(h_{(1,qp{q}^{-1}{r}^{-1}q{p}^{-1}{q}^{-1})}\right)\hfill \\ & \stackrel{\mathrm{(33)}}{=}& h_{(2,qp{q}^{-1})}·{\left({}^{q}v\right)}_{\left(0\right)}\otimes \left(h_{(3,r)}{\left({}^{q}v\right)}_{(1,r)}\right)S^{-1}{\pi }_{qp{q}^{-1}}\left(h_{(1,qp{q}^{-1}{r}^{-1}q{p}^{-1}{q}^{-1})}\right).\hfill \end{array}$$

Finally, we will check that the quasimodule coassociative conditions hold. We just compute the Equation (26); the Equation (27) is similar. For all ${}^{q}v\in {}^{q}V,h,g\in H_r$,

$$\begin{array}{ccc}\hfill {\left({}^{q}v\right)}_{\left(0\right)}\otimes {\left({}^{q}v\right)}_{(1,r)}\left(hg\right)& =& {}^q\left(v_{\left(0\right)}\right)\otimes {\pi }_q\left(v_{(1,q^{-1}rq)}\right)\left(hg\right)\hfill \\ & =& {}^q\left(v_{\left(0\right)}\right)\otimes \left({\pi }_q\left(v_{(1,q^{-1}rq)}\right)h\right)g\hfill \\ & =& {\left({}^{q}v\right)}_{\left(0\right)}\otimes \left({\left({}^{q}v\right)}_{(1,r)}h\right)g,\hfill \end{array}$$

where the first and third equalities rely on (33); the second one follows by (26). This completes the proof. □

Proposition 5.

Let $(V,{\rho }^V)\in YDQ{\left(H\right)}_p$ and $(W,{\rho }^W)\in YDQ{\left(H\right)}_q$. Then ${}^{st}V={}^s{(}^{t}V)$ is an object in $YDQ{\left(H\right)}_{stp{t}^{-1}{s}^{-1}}$, and ${}^s(V\otimes W)={}^{s}V\otimes {}^{s}W$ is an object in $YDQ{\left(H\right)}_{spq{s}^{-1}}$.

Proof. 

We first check that ${}^{st}V={}^s{(}^{t}V)$ is an object in $YDQ{\left(H\right)}_{stp{t}^{-1}{s}^{-1}}$. It is obvious that both ${}^{st}V$ and ${}^s{(}^{t}V)$ are in the category $YDQ{\left(H\right)}_{stp{t}^{-1}{s}^{-1}}$. Then we show that the action and coaction of these two $stp{t}^{-1}{s}^{-1}$-Yetter–Drinfeld quasimodules are exactly equivalent.

As ${}^{st}V$ is a $stp{t}^{-1}{s}^{-1}$-Yetter–Drinfeld quasimodule with the structures

$$\begin{array}{ccc}\hfill h_{stp{t}^{-1}{s}^{-1}}·{}^{st}v& =& {}^{st}\left({\pi }_{t^{-1}{s}^{-1}}\left(h_{stp{t}^{-1}{s}^{-1}}\right)·v\right),\hfill \\ \hfill {\rho }_r^{{}^{st}V}\left({}^{st}v\right)& =& {}^{st}\left(v_{\left(0\right)}\right)\otimes {\pi }_{st}\left(v_{(1,t^{-1}{s}^{-1}rst)}\right).\hfill \end{array}$$

Then, we show ${}^s{(}^{t}V)$ is a $stp{t}^{-1}{s}^{-1}$-Yetter–Drinfeld quasimodule with the same structures of ${}^{st}V$. Indeed, the action of ${}^s{(}^{t}V)$ is

$$\begin{array}{ccc}\hfill h_{stp{t}^{-1}{s}^{-1}}·{}^s\left({}^{t}v\right)& =& {}^s\left({\pi }_{s^{-1}}\left(h_{stp{t}^{-1}{s}^{-1}}\right)·{}^{t}v\right)\hfill \\ & =& {}^s\left({}^t\left({\pi }_{t^{-1}}{\pi }_{s^{-1}}\left(h_{stp{t}^{-1}{s}^{-1}}\right)·v\right)\right)\hfill \\ & =& {}^s{}^t\left({\pi }_{t^{-1}{s}^{-1}}\left(h_{stp{t}^{-1}{s}^{-1}}\right)·v\right).\hfill \end{array}$$

Hence ${}^s{(}^{t}V)$ has the same cation with ${}^{st}V$.

And the coaction of ${}^s{(}^{t}V)$ is

$$\begin{array}{ccc}\hfill {\rho }^{{}^s{(}^{t}V)}\left({}^s{(}^{t}v)\right)& =& {}^s\left({\left({}^{t}v\right)}_{\left(0\right)}\right)\otimes {\pi }_s\left({\left({}^{t}v\right)}_{(1,s^{-1}rs)}\right)\hfill \\ & =& {}^s\left({}^t\left(v_{\left(0\right)}\right)\right)\otimes {\pi }_s\left({\pi }_t\left(v_{(1,t^{-1}{s}^{-1}rst)}\right)\right)\hfill \\ & =& {}^{st}\left(v_{\left(0\right)}\right)\otimes {\pi }_{st}\left(v_{(1,t^{-1}{s}^{-1}rst)}\right).\hfill \end{array}$$

Hence, ${}^{st}V={}^s{(}^{t}V)$ as an object in $YDQ{\left(H\right)}_{stp{t}^{-1}{s}^{-1}}$.

As ${}^s(V\otimes W)$ is a $spq{s}^{-1}$-Yetter–Drinfeld quasimodule with the structures

$$\begin{array}{ccc}\hfill h_{spq{s}^{-1}}·{}^s(v\otimes w)& =& {}^s\left({\pi }_{s^{-1}}\left(h_{spq{s}^{-1}}\right)·(v\otimes w)\right)\hfill \\ & =& {}^s({\pi }_{s^{-1}}\left(h_{(1,sp{s}^{-1})}\right)·v\otimes {\pi }_{s^{-1}}\left(h_{(2,sq{s}^{-1})}\right)·w),\hfill \\ \hfill {\rho }_r^{{}^s(V\otimes W)}\left({}^s(v\otimes w)\right)& =& {}^s\left({(v\otimes w)}_{\left(0\right)}\right)\otimes {\pi }_s\left({(v\otimes w)}_{(1,s^{-1}rs)}\right)\hfill \\ & =& {}^s(v_{\left(0\right)}\otimes w_{\left(0\right)})\otimes {\pi }_s\left(w_{(1,s^{-1}rs)}{\pi }_{q^{-1}}\left(v_{(1,q{s}^{-1}rs{q}^{-1})}\right)\right)\hfill \\ & =& {}^s(v_{\left(0\right)}\otimes w_{\left(0\right)})\otimes {\pi }_s\left(w_{(1,s^{-1}rs)}\right){\pi }_{s{q}^{-1}}\left(v_{(1,q{s}^{-1}rs{q}^{-1})}\right).\hfill \end{array}$$

Then we show ${}^{s}V\otimes {}^{s}W$ is a $spq{s}^{-1}$-Yetter–Drinfeld quasimodule with the same structures of ${}^s(V\otimes W)$. Indeed, the action of ${}^{s}V\otimes {}^{s}W$ is

$$\begin{array}{ccc}\hfill h_{spq{s}^{-1}}·({}^{s}v\otimes {}^{s}w)& =& h_{(1,sp{s}^{-1})}·{}^{s}v\otimes h_{(2,sq{s}^{-1})}·{}^{s}w\hfill \\ & =& {}^s({\pi }_{s^{-1}}\left(h_{(1,sp{s}^{-1})}\right)·v)\otimes {}^s({\pi }_{s^{-1}}\left(h_{(2,sq{s}^{-1})}\right)·w)\hfill \\ & =& {}^s({\pi }_{s^{-1}}\left(h_{(1,sp{s}^{-1})}\right)·v\otimes {\pi }_{s^{-1}}\left(h_{(2,sq{s}^{-1})}\right)·w)\hfill \end{array}$$

Hence ${}^{s}V\otimes {}^{s}W$ has the same cation with ${}^s(V\otimes W)$.

And the coaction of ${}^{s}V\otimes {}^{s}W$ is

$$\begin{array}{ccc}\hfill {\rho }_r^{{}^{s}V\otimes {}^{s}W}({}^{s}v\otimes {}^{s}w)& =& {\left({}^{s}v\right)}_{\left(0\right)}\otimes {\left({}^{s}w\right)}_{\left(0\right)}\otimes {\left({}^{s}w\right)}_{(1,r)}{\pi }_{s{q}^{-1}{s}^{-1}}\left({\left({}^{s}v\right)}_{(1,sq{s}^{-1}rs{q}^{-1}{s}^{-1})}\right)\hfill \\ & =& {\left({}^{s}v\right)}_{\left(0\right)}\otimes {}^s\left(w_{\left(0\right)}\right)\otimes {\pi }_s\left(w_{(1,s^{-1}rs)}\right){\pi }_{s{q}^{-1}{s}^{-1}}\left({\pi }_s\left(v_{(1,q{s}^{-1}rs{q}^{-1})}\right)\right)\hfill \\ & =& {}^s\left(v_{\left(0\right)}\right)\otimes {}^s\left(w_{\left(0\right)}\right)\otimes {\pi }_s\left(w_{(1,s^{-1}rs)}\right){\pi }_{s{q}^{-1}}\left(v_{(1,q{s}^{-1}rs{q}^{-1})}\right)\hfill \\ & =& {}^s(v_{\left(0\right)}\otimes w_{\left(0\right)})\otimes {\pi }_s\left(w_{(1,s^{-1}rs)}\right){\pi }_{s{q}^{-1}}\left(v_{(1,q{s}^{-1}rs{q}^{-1})}\right).\hfill \end{array}$$

Thus, ${}^s(V\otimes W)={}^{s}V\otimes {}^{s}W$ as an object in $YDQ{\left(H\right)}_{spq{s}^{-1}}$. □

For a crossed group-cograded Hopf quasigroup H, we define $YDQ\left(H\right)$ as the disjoint union of all $YDQ{\left(H\right)}_p$ with $p\in G$. If we endow $YDQ\left(H\right)$ with tensor product as in Proposition 3, then we obtain the following result.

Theorem 2.

The Yetter–Drinfeld quasimodules category $YDQ\left(H\right)$ is a crossed category.

Proof. 

By Proposition 4, we can give a group homomorphism $\varphi :G\to Aut\left(YDQ\right(H\left)\right)$, $p⟼{\varphi }_p$ by

$$\begin{array}{c}\hfill {\varphi }_p:YDQ{\left(H\right)}_q\to YDQ{\left(H\right)}_{pq{p}^{-1}},{\varphi }_p\left(W\right)={}^{p}W,\end{array}$$

where the functor ${\varphi }_p$ acts as follows: given a morphism $f:(V,{\rho }^V)\to (W,{\rho }^W)$, for any $v\in V$, we set ${(}^{p}f){(}^{p}v)={}^p\left(f\left(v\right)\right)$.

Then it is easy to prove $YDQ\left(H\right)$ is a crossed category. □

Following the ideas by $\acute{\mathrm{A}}$lonso in [12], we will consider $YD{\left(H\right)}_p$ the category of left-right p-Yetter–Drinfeld modules over H, which is a subcategory of $YDQ{\left(H\right)}_p$.

Proposition 6.

Let $(V,{\rho }^V)\in YD{\left(H\right)}_p$ and $(W,{\rho }^W)\in YD{\left(H\right)}_q$. Set ${}^{V}W={}^{p}W$ as an object in $YD{\left(H\right)}_{pq{p}^{-1}}$. Define the map

$$\begin{array}{ccc}& & C_{V,W}:V\otimes W\to {}^{V}W\otimes V\hfill \\ & & C_{V,W}(v\otimes w)={}^p\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)\otimes v_{\left(0\right)}\hfill \end{array}$$

(34)

Then $C_{V,W}$ is H-linear, H-colinear and satisfies the conditions:

$$\begin{array}{ccc}& & C_{V\otimes W,X}=(C_{V{,}^{W}X}\otimes i{d}_W)(i{d}_V\otimes C_{W,X})\hfill \end{array}$$

(35)

$$\begin{array}{ccc}& & C_{V,W\otimes X}=(i{d}_{{}^{V}W}\otimes C_{V,X})(C_{V,W}\otimes i{d}_X)\hfill \end{array}$$

(36)

for $X\in YD{\left(H\right)}_s$. Moreover, $C_{{}^{s}V{,}^{s}W}={}^s(·)C_{V,W}$.

Proof. 

We first show that $C_{V,W}$ is H-linear. First, compute

$$\begin{array}{ccc}& & C_{V,W}\left(h_{pq}·(v\otimes w)\right)\hfill \\ & \stackrel{\mathrm{(30)}}{=}& C_{V,W}(h_{(1,p)}·v\otimes h_{(2,q)}·w)\hfill \\ & \stackrel{\mathrm{(34)}}{=}& {}^p\left(S_{q^{-1}}\left({(h_{(1,p)}·v)}_{(1,q^{-1})}\right)·(h_{(2,q)}·w)\right)\otimes {(h_{(1,p)}·v)}_{\left(0\right)}\hfill \\ & \stackrel{\mathrm{(28)}}{=}& {}^p\left(S_{q^{-1}}\left(h_{(3,q^{-1})}{v}_{(1,q^{-1})}{S}^{-1}{\pi }_{p^{-1}}\left(h_{(1,pq{p}^{-1})}\right)\right)·(h_{(4,q)}·w)\right)\otimes \left(h_{(2,p)}·v_{\left(0\right)}\right)\hfill \\ & =& {}^p\left(\left({\pi }_{p^{-1}}\left(h_{(1,pq{p}^{-1})}\right)S_{q^{-1}}\left(v_{(1,q^{-1})}\right)S^{-1}\left(h_{3,q^{-1}}\right)\right)·(h_{(4,q)}·w)\right)\otimes \left(h_{(2,p)}·v_{\left(0\right)}\right)\hfill \\ & =& {}^p\left(\left({\pi }_{p^{-1}}\left(h_{(1,pq{p}^{-1})}\right)S_{q^{-1}}\left(v_{(1,q^{-1})}\right)\right)·\left(S^{-1}\left(h_{(3,q^{-1})}\right)h_{(4,q)}·w\right)\right)\otimes \left(h_{(2,p)}·v_{\left(0\right)}\right)\hfill \\ & =& {}^p\left({\pi }_{p^{-1}}\left(h_{(1,pq{p}^{-1})}\right)\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)\right)\otimes \left(h_{(2,p)}·v_{\left(0\right)}\right)\hfill \\ & \stackrel{\mathrm{(32)}}{=}& \left(h_{(1,pq{p}^{-1})}·{}^p\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)\right)\otimes \left(h_{(2,p)}·v_{\left(0\right)}\right)\hfill \\ & \stackrel{\mathrm{(30)}}{=}& h_{pq}·\left({}^p\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)\otimes v_{\left(0\right)}\right)\hfill \\ & \stackrel{\mathrm{(34)}}{=}& h_{pq}·C_{V,W}(v\otimes w),\hfill \end{array}$$

so we have $C_{V,W}\left(h_{pq}·(v\otimes w)\right)=h_{pq}·C_{V,W}(v\otimes w)$, that is, $C_{V,W}$ is H-linear.

Secondly, we prove that $C_{V,W}$ is H-colinear. In fact,

$$\begin{array}{ccc}& & {\rho }_r^{{}^{V}W\otimes V}{C}_{V,W}(v\otimes w)\hfill \\ & =& {\rho }_r^{{}^{V}W\otimes V}\left({}^p\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)\otimes v_{\left(0\right)}\right)\hfill \\ & \stackrel{\mathrm{(31)}}{=}& {}^p{\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)}_{\left(0\right)}\otimes v_{\left(0\right)\left(0\right)}\otimes v_{\left(0\right)(1,r)}{\pi }_{p^{-1}}\left({}^p{\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)}_{(1,pr{p}^{-1})}\right)\hfill \\ & \stackrel{\mathrm{(33)}}{=}& {}^p\left({\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)}_{\left(0\right)}\right)\otimes v_{\left(0\right)\left(0\right)}\hfill \\ & & \otimes v_{\left(0\right)(1,r)}{\pi }_{p^{-1}}\left({\pi }_p{\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)}_{(1,p^{-1}pr{p}^{-1}p)}\right)\hfill \\ & =& {}^p\left({\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)}_{\left(0\right)}\right)\otimes v_{\left(0\right)\left(0\right)}\otimes v_{\left(0\right)(1,r)}{\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)}_{(1,r)}\hfill \\ & \stackrel{\mathrm{(28)}}{=}& {}^p\left(S_{q^{-1}}{\left(v_{(1,q^{-1})}\right)}_{(2,q)}·w_{\left(0\right)}\right)\otimes v_{\left(0\right)\left(0\right)}\hfill \\ & & \otimes v_{\left(0\right)(1,r)}\left(S_{q^{-1}}{\left(v_{(1,q^{-1})}\right)}_{(3,r)}{w}_{(1,r)}\right)S^{-1}{\pi }_{q^{-1}}\left(S_{q^{-1}}{\left(v_{(1,q^{-1})}\right)}_{(1,q{r}^{-1}{q}^{-1})}\right)\hfill \\ & =& {}^p\left(S_{q^{-1}}\left(v_{(3,q^{-1})}\right)·w_{\left(0\right)}\right)\otimes v_{\left(0\right)}\otimes v_{(1,r)}\left(S_r\left(v_{(2,r)}\right)w_{(1,r)}\right){\pi }_{q^{-1}}\left(v_{(4,q{r}^{-1}{q}^{-1})}\right)\hfill \\ & =& {}^p\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w_{\left(0\right)}\right)\otimes v_{\left(0\right)}\otimes w_{(1,r)}){\pi }_{q^{-1}}\left(v_{(2,q{r}^{-1}{q}^{-1})}\right)\hfill \\ & =& C_{V,W}(v_{\left(0\right)}\otimes w_{\left(0\right)})\otimes w_{(1,r)}{\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)\hfill \\ & =& (C_{V,W}\otimes id)\left(v_{\left(0\right)}\otimes w_{\left(0\right)}\otimes w_{(1,r)}{\pi }_{q^{-1}}\left(v_{(1,qr{q}^{-1})}\right)\right)\hfill \\ & =& (C_{V,W}\otimes id){\rho }_r^{V\otimes W}(v\otimes w).\hfill \end{array}$$

Thirdly, we can find $C_{V,W}$ satisfies the conditions (35) and (36). However, here we only check the first condition, and the other is similar.

$$\begin{array}{ccc}& & (C_{V{,}^{W}X}\otimes i{d}_W)(i{d}_V\otimes C_{W,X})(v\otimes w\otimes x)\hfill \\ & \stackrel{\mathrm{(34)}}{=}& (C_{V{,}^{W}X}\otimes i{d}_W)(v\otimes {}^q(S_{s^{-1}}\left(w_{(1,s^{-1})}\right)·x)\otimes w_{\left(0\right)})\hfill \\ & =& C_{V{,}^{W}X}\left(v\otimes {}^q\left(S_{s^{-1}}\left(w_{(1,s^{-1})}\right)·x\right)\right)\otimes w_{\left(0\right)}\hfill \\ & \stackrel{\mathrm{(34)}}{=}& {}^p\left(S_{q{s}^{-1}{q}^{-1}}\left(v_{(1,q{s}^{-1}{q}^{-1})}\right)·{}^q\left(S_{s^{-1}}\left(w_{1,s^{-1}}\right)·x\right)\right)\otimes v_{\left(0\right)}\otimes w_{\left(0\right)}\hfill \\ & \stackrel{\mathrm{(30)}}{=}& {}^{pq}\left({\pi }_{q^{-1}}\left(S_{q{s}^{-1}{q}^{-1}}\left(v_{(1,q{s}^{-1}{q}^{-1})}\right)\right)·\left(S_{s^{-1}}\left(w_{1,s^{-1}}\right)·x\right)\right)\otimes v_{\left(0\right)}\otimes w_{\left(0\right)}\hfill \\ & =& {}^{pq}\left({\pi }_{q^{-1}}\left(S_{q{s}^{-1}{q}^{-1}}\left(v_{(1,q{s}^{-1}{q}^{-1})}\right)\right)S_{s^{-1}}\left(w_{1,s^{-1}}\right)·x\right)\otimes v_{\left(0\right)}\otimes w_{\left(0\right)}\hfill \\ & =& {}^{pq}\left(S_{s^{-1}}{\pi }_{q^{-1}}\left(v_{(1,q{s}^{-1}{q}^{-1})}\right)S_{s^{-1}}\left(w_{1,s^{-1}}\right)·x\right)\otimes v_{\left(0\right)}\otimes w_{\left(0\right)}\hfill \\ & =& {}^{pq}\left(S_{s^{-1}}\left(w_{(1,s^{-1})}{\pi }_{q^{-1}}\left(v_{(1,q{s}^{-1}{q}^{-1})}\right)\right)·x\right)\otimes v_{\left(0\right)}\otimes w_{\left(0\right)}\hfill \\ & \stackrel{\mathrm{(31)}}{=}& {}^{pq}\left(S_{s^{-1}}{(v\otimes w)}_{(1,s^{-1})}·x\right)\otimes {(v\otimes w)}_{\left(0\right)}\hfill \\ & =& C_{V\otimes W,X}(v\otimes w,x).\hfill \end{array}$$

Finally, we check the condition $C_{{}^{s}V{,}^{s}W}={}^s(·)C_{V,W}$. Indeed,

$$\begin{array}{ccc}\hfill C_{{}^{s}V,{}^{s}W}{(}^{s}v\otimes {}^{s}w)& =& {}^{sp{s}^{-1}}\left(S_{sq{s}^{-1}}\left({\left({}^{s}v\right)}_{(1,sq{s}^{-1}})\right)·{}^{s}w\right)\otimes {\left({}^{s}v\right)}_{\left(0\right)}\hfill \\ & \stackrel{\mathrm{(31)}}{=}& {}^{sp{s}^{-1}}\left(S_{sq{s}^{-1}}\left({\pi }_s\left(v_{(1,s^{-1}s{q}^{-1}{s}^{-1}s)}\right)\right)·{}^{s}w\right)\otimes {}^s\left(v_{\left(0\right)}\right)\hfill \\ & =& {}^{sp{s}^{-1}}\left({\pi }_s{S}_{q^{-1}}\left(v_{(1,q^{-1})}\right)·{}^{s}w\right)\otimes {}^s\left(v_{\left(0\right)}\right)\hfill \\ & \stackrel{\mathrm{(30)}}{=}& {}^{sp{s}^{-1}}\left({}^s\left({\pi }_{s^{-1}}\left({\pi }_s{S}_{q^{-1}}\left(v_{(1,q^{-1})}\right)\right)·w\right)\right)\otimes {}^s\left(v_{\left(0\right)}\right)\hfill \\ & =& {}^{sp{s}^{-1}}\left({}^s\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)\right)\otimes {}^s\left(v_{\left(0\right)}\right)\hfill \\ & =& {}^{sp}\left(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w\right)\otimes {}^s\left(v_{\left(0\right)}\right)\hfill \\ & =& {}^s(·)\left({}^p(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·w)\otimes v_{\left(0\right)}\right)\hfill \\ & \stackrel{\mathrm{(34)}}{=}& {}^s(·)C_{V,W}(v\otimes w).\hfill \end{array}$$

This completes the proof. □

Similar to [12], we can give the braided $C_{V,W}$ an inverse in the following way.

Proposition 7.

Let $(V,{\rho }^V)\in YD{\left(H\right)}_p$ and $(W,{\rho }^W)\in YD{\left(H\right)}_q$. Then this can give the braided $C_{V,W}$ an inverse $C_{V,W}^{-1}$, which is defined by

$$\begin{array}{ccc}\hfill C_{V,W}^{-1}:{}^{V}W\otimes V& \to & V\otimes W,\hfill \\ \hfill C_{V,W}^{-1}\left({}^{p}w\otimes v\right)& =& v_{\left(0\right)}\otimes v_{(1,q)}·w,\hfill \end{array}$$

where $p,q\in G$.

Proof. 

For any $v\in V,w\in W$, we have

$$\begin{array}{ccc}\hfill C_{V,W}^{-1}{C}_{V,W}(v\otimes w)& =& C_{V,W}^{-1}({}^p\left(S_{q^{-1}}(v_{(1,q^{-1})}·w)\right)\otimes v_{\left(0\right)})\hfill \\ & =& v_{\left(0\right)}\otimes v_{(1,q)}·(\left(S_{q^{-1}}\left(v_{(2,q^{-1})}\right)\right)·w)\hfill \\ & =& v_{\left(0\right)}\otimes \left(v_{(1,q)}{S}_{q^{-1}}\left(v_{(2,q^{-1})}\right)\right)·w\hfill \\ & =& v_{\left(0\right)}\otimes ϵ\left(v_e\right)·w\hfill \\ & =& v\otimes w.\hfill \end{array}$$

Conversely, for any ${}^{p}w\in {}^{V}W,v\in V$,

$$\begin{array}{ccc}\hfill C_{V,W}{C}_{V,W}^{-1}({}^{p}w\otimes v)& =& C_{V,W}(v_{\left(0\right)}\otimes v_{(1,q)}·w)\hfill \\ & =& {}^p(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·(v_{(2,q)}·w))\otimes v_{\left(0\right)}\hfill \\ & =& {}^p(S_{q^{-1}}\left(v_{(1,q^{-1})}\right)·v_{(2,q)})·w)\otimes v_{\left(0\right)}\hfill \\ & =& {}^{p}w\otimes v.\hfill \end{array}$$

Since $C_{V,W}$ is an isomorphism with inverse $C_{V,W}^{-1}$. □

As a consequence of the above results, we obtain another main result of this paper.

Theorem 3.

Denote $YD\left(H\right)$ as the disjoint union of all $YD{\left(H\right)}_p$ with $p\in G$, where H is a crossed group-cograded Hopf quasigroup. Then $YD\left(H\right)$ is a braided crossed category over group G.

Proof. 

As $YD\left(H\right)$ is a subcategory of the category $YDQ\left(H\right)$, so it is a crossed category. Then we only need prove $YD\left(H\right)$ is braided.

The braiding in $YD\left(H\right)$ can be given by Proposition 6, and the braiding is invertible; its inverse is the family $C_{V,W}^{-1}$, which is defined in Proposition 7. Hence, it is obvious that $YD\left(H\right)$ is a braided crossed category. □

Example 3.

Let us consider the crossed group-cograded Hopf quasigroup $H^G$ in Example 1. Moreover, G is the isomorphism group of Hopf quasigroup H. If V is a Yetter–Drinfeld module of H, then we can endow V with a p-Yetter–Drinfeld module structure of $H^G$, as follows:

(1) 

The left $H_p$-module structure of V is a copy of the left H-module structure of V, because $i_p$ is an identification isomorphism of algebras;

(2) 

Define a new coaction ${\rho }_r^{\prime }:V\to V\otimes H_r$ by ${\rho }_r^{\prime }=(i{d}_V\otimes i_r)\rho$.

Then we can show that V is a p-Yetter–Drinfeld module over $H^G$, and it is easy to check that $YD\left(H^G\right)$ is a braided crossed category; the braided structure is given by $C_{V,W}:V\otimes W\to {}^{V}W\otimes V,C_{V,W}(v\otimes W)={}^p\left(S_{q^{-1}}\left(i_{q^{-1}}\left(v_{\left(1\right)}\right)\right)·w\right)\otimes v_{\left(0\right)}$.

5. Conclusions

For a group-cograded Hopf quasigroup $H={⨁}_{p\in G}{H}_p$, we first discovered that H with the group G is a Hopf quasigroup in the Turaev category $T_k$. Moreover, if $H={⨁}_{p\in G}{H}_p$ is a crossed group-cograded Hopf quasigroup, then the mirror ${\tilde{H}}_p$ is also a crossed group-cograded Hopf quasigroup. Following Alonso’s idea, we prove that the category $YDQ\left(H\right)$ of Yetter–Drinfeld quasimodules is a crossed category. Furthermore, the subcategory $YD\left(H\right)$ is a braided crossed category, which is relevant to the construction of some homotopy invariants. A possible topic for further research is a braid structure of the category $YDQ\left(H\right)$.