Vasicek Quantile and Mean Regression Models for Bounded Data: New Formulation, Mathematical Derivations, and Numerical Applications

Abstract

The Vasicek distribution is a two-parameter probability model with bounded support on the open unit interval. This distribution allows for different and flexible shapes and plays an important role in many statistical applications, especially for modeling default rates in the field of finance. Although its probability density function resembles some well-known distributions, such as the beta and Kumaraswamy models, the Vasicek distribution has not been considered to analyze data on the unit interval, especially when we have, in addition to a response variable, one or more covariates. In this paper, we propose to estimate quantiles or means, conditional on covariates, assuming that the response variable is Vasicek distributed. Through appropriate link functions, two Vasicek regression models for data on the unit interval are formulated: one considers a quantile parameterization and another one its original parameterization. Monte Carlo simulations are provided to assess the statistical properties of the maximum likelihood estimators, as well as the coverage probability. An R package developed by the authors, named vasicekreg, makes available the results of the present investigation. Applications with two real data sets are conducted for illustrative purposes: in one of them, the unit Vasicek quantile regression outperforms the models based on the Johnson-SB, Kumaraswamy, unit-logistic, and unit-Weibull distributions, whereas in the second one, the unit Vasicek mean regression outperforms the fits obtained by the beta and simplex distributions. Our investigation suggests that unit Vasicek quantile and mean regressions can be of practical usage as alternatives to some well-known models for analyzing data on the unit interval.

1. Introduction

Modeling of bounded data has been extensively discussed in the literature to infer some statistical indicators such as mortality rates, recovery rates, as well as economic and risk measures. In diverse areas of knowledge, researchers are faced with continuous variables expressed as indices, proportions, rates, and ratios, among others. When there is an interest in explaining the relationship between these variables and some covariates, it is necessary to use a regression model that, in general, offers a summary of the mean of the response variable conditioned to the covariates. However, since the mean is clearly affected by extreme values in the data, inference from mean regression models is also affected by this situation.

When the response variable is skew-distributed, using a robust modeling is more suitable than a mean regression. Some works related to skew distributions are presented in [1,2,3]. For this reason, the quantile regression [4] can be proposed as an alternative modeling.

If the interest is in evaluating the effect of covariates on different quantiles of the distribution of the response variable, including the median, the quantile regression models are also appropriate. For a parametric analysis, the model is constructed considering a distribution supported in the same range as the response variable.

Parametric quantile regression models for variables bounded on the unit interval, that is, on (0, 1), have often appeared recently. These models are formulated by first parameterizing the baseline distribution in terms of a quantile. Then, a regression-based functional form through a link function is introduced. For example, models based on the arcsecant hyperbolic Weibull [5], Lambert-uniform [6], unit-Birnbaum–Saunders [7,8,9,10], unit-Burr-XII [11], exponentiated arcsecant hyperbolic normal [12], unit-Chen [13], log-extended exponential-geometric [14], Johnson-t [15], power Johnson SB [16], L-logistic [17], unit-Weibull [18,19,20], generalized Johnson SB [21], and Kumaraswamy [22] distributions have been postulated. These formulations have been proposed to model the conditional quantiles of a bounded response variable and are well known in the literature [23].

Although many other quantile regression models to adjust the limited data are already available, it is clear that none of them are a panacea for the diverse problems that a practitioner confronts. In this sense, it is important to propose and evaluate new alternatives. For example, the Vasicek (VASI) distribution, proposed in [24], is an alternative probability distribution bounded on the (0, 1) interval. This distribution has two parameters, which are defined on such as interval, where one of them is equal to the model mean. Hence, unlike other models whose parameters do not allow an interpretation direct, the VASI distribution has this advantage since the mean is one of its parameters. This also permits us to consider the distribution mean in the presence of covariates. The VASI distribution is typically employed to model economic data on the (0, 1) interval. The probability density function (PDF) of such a distribution can take different forms, such as U-shaped, J-shaped, or uniform [25]. Note that the literature on the VASI distribution is rather scarce.

Based on the above, the objective of our investigation is to introduce an alternative to the parametric quantile regression models for skewed distributed response variables restricted to the (0, 1) interval by considering the VASI distribution. Then, we extend the range of applications of this distribution.

This paper is organized as follows. Section 2 introduces the VASI distribution parameterized either in terms of its quantile or its mean. Directions regarding the maximum likelihood (ML) estimation method in both quantile and mean parameterizations are presented in Section 3. In this section, diagnostics based on residuals are also considered. In Section 4, we provide two Monte Carlo simulation analyses to assess some statistical properties of the ML estimators, such as bias and mean squared error, in a regression-based functional form through the logit link function. The potential and competitiveness of the proposed models are shown in Section 5 through two applications involving real-world data. Section 6 presents some final considerations about the proposed model. Finally, in Appendix A, we characterize other distributions that appear in this paper.

2. The Vasicek Distribution

In this section, we introduce the VASI distribution parameterized either in terms of its quantile or its mean. A random variable Y with bounded support on the $(0,1)$ interval is VASI distributed [24] if its PDF, cumulative distribution function (CDF), and quantile function (QF) are written, respectively, as    

$$\begin{array}{ccc}\hfill f(y;\alpha ,\theta )& =& \hfill \sqrt{\frac{1-\theta }{\theta }}exp\left\{\frac{1}{2}\left[{\mathrm{\Phi }}^{-1}{\left(y\right)}^2-{\left(\frac{{\mathrm{\Phi }}^{-1}\left(y\right)\sqrt{1-\theta }-{\mathrm{\Phi }}^{-1}\left(\alpha \right)}{\sqrt{\theta }}\right)}^2\right]\right\},\hfill \\ \hfill F(y;\alpha ,\theta )& =& \mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(y\right)\sqrt{1-\theta }-{\mathrm{\Phi }}^{-1}\left(\alpha \right)}{\sqrt{\theta }}\right),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill Q(\tau ;\alpha ,\theta )& =& F^{-1}(\tau ;\alpha ,\theta )=\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(\alpha \right)+{\mathrm{\Phi }}^{-1}\left(\tau \right)\sqrt{\theta }}{\sqrt{1-\theta }}\right)\hfill \end{array}$$

(2)

where $0<\left(y,\alpha ,\theta ,\tau \right)<1$, whereas $\mathrm{\Phi }$ and ${\mathrm{\Phi }}^{-1}$ denote, respectively, the standard normal CDF and QF.

Note that $\theta$ is the shape parameter of the VASI distribution, and its mean and variance are, respectively, $\mathrm{E}\left(Y\right)=\alpha$ and $\mathrm{Var}\left(Y\right)={\mathrm{\Phi }}_2\left({\mathrm{\Phi }}^{-1}\left(\alpha \right),{\mathrm{\Phi }}^{-1}\left(\alpha \right),\theta \right)-{\alpha }^2$, where ${\mathrm{\Phi }}_2$ is the bivariate standard normal PDF with correlation $\theta$ [26] (p. 900) calculated from the double integral stated as

$${\mathrm{\Phi }}_2(a,b,c)=\frac{1}{2\pi \sqrt{1-c^2}}{\int }_{-\infty }^a{\int }_{-\infty }^{b}exp\left(-\frac{x^2-2cxy+y^2}{2(1-c^2)}\right)\mathrm{d}y\mathrm{d}x.$$

As presented in [27], the PDF defined in (1) is unimodal with mode computed from $\mathrm{\Phi }[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\sqrt{1-\theta }/(1-2\theta )]$, when $\theta <0.5$; monotone, when $\theta =0.5$; and U-shaped, when $\theta >0.5$. Figure 1 shows the PDF defined in (1) for different values of $\theta$ and $\alpha$. Observe that the distribution possesses a symmetry property, that is, $F(y;\alpha ,\theta )=1-F(1-y;\alpha ,\theta )$.

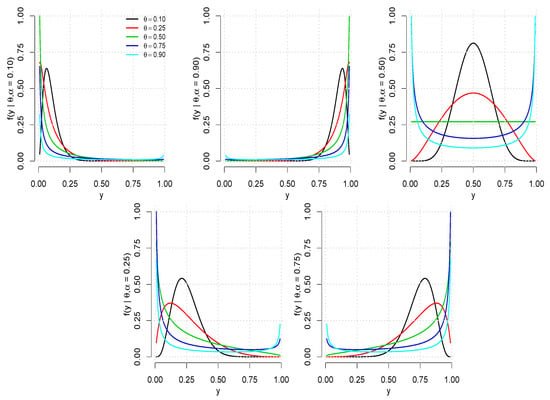
Figure 1. Plots of the PDF stated in (1) for different combinations of $\theta$ and $\alpha$.

Note that we can assess the effect of covariates on the mean of the distribution of Y through some appropriate link function. Moreover, from the QF formulated in (2), we can re-parameterize $\alpha$ in terms of the $\tau$-th quantile, for $\tau \in (0,1)$, considering a one-to-one transformation $(\alpha ,\theta )\to (\mu ,\theta )$, as

$$\alpha =h^{-1}\left(\mu \right)=\mathrm{\Phi }\left({\mathrm{\Phi }}^{-1}\left(\mu \right)\sqrt{1-\theta }-{\mathrm{\Phi }}^{-1}\left(\tau \right)\sqrt{\theta }\right),$$

(3)

where $\mu$ is, for a fixed and known value $\tau$, the $\tau$-th quantile of the distribution of Y. Figure 2 shows the PDF stated in (1) re-parameterized and assuming different values for $\mu$, $\theta$, and $\tau$. We consider the first decile ($\tau =0.10$), the first quartile ($\tau =0.25$), the median ($\tau =0.50$), the third quartile ($\tau =0.75$), and the ninth decile ($\tau =0.90$) for $\tau$. The dotted vertical lines in Figure 2 indicate where the parameter $\alpha$ is located according to the values of $\tau$. Observe that $F\left(y;\mu ,\theta ,\tau \right)=1-F\left(1-y;\mu ,\theta ,\tau \right)$.

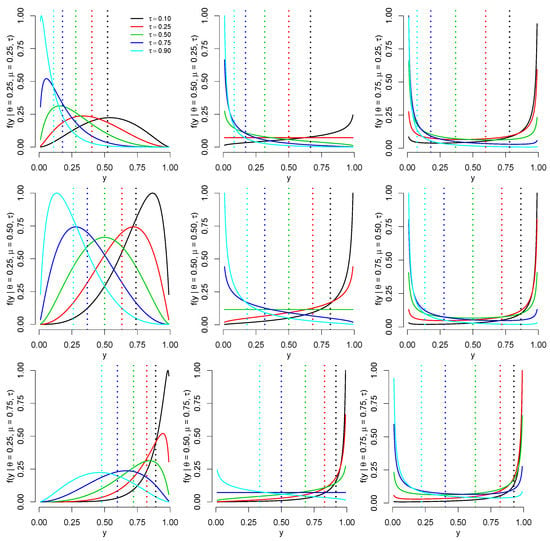
Figure 2. Plots of the PDF stated in (1) with quantile parameterization for different combinations of $\theta$, $\mu$, and $\tau$.

In summary, assuming that Y is VASI distributed, we can fit its regression models for estimating both the mean and quantile of the response variable, for a fixed $\tau$-level. Its desirable properties may distinguish it from some other distributions proposed in the literature for data on the $(0,1)$ interval.

3. Maximum Likelihood Estimation and Residuals Analysis

In this section, we describe the ML estimation considering the parameterizations $(\alpha ,\theta )$, $(\mu ,\theta )$, $\left(\alpha \right(x),\theta (z\left)\right)$, and $\left(\mu \right(x),\theta (z\left)\right)$, where $x$ and $z$ are values of the covariate vectors. Some directions on residuals analysis are also provided here.

Let $Y={(Y_1,\dots ,Y_n)}^{\top }$ be a random sample of size n from a VASI distribution with unknown parameters $\alpha$ and $\theta$ and consider that $y={(y_1,\dots ,y_n)}^{\top }$ are its observed values. Based on the PDF stated in (1), the corresponding log-likelihood function is proportional to

$$\ell \left(\alpha ,\theta ;\mathit{y}\right)\propto \frac{n}{2}log\left(\frac{1-\theta }{\theta }\right)-\frac{1}{2\theta }\sum _{i=1}^n{\left[{\mathrm{\Phi }}^{-1}\left(y_i\right)\sqrt{1-\theta }-{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]}^2.$$

(4)

The ML estimates of $\alpha$ and $\theta$ are obtained maximizing the log-likelihood function stated in (4) by solving the score equations $U_{\alpha }=\partial \ell \left(\alpha ,\theta ;\mathit{y}\right)/\partial \alpha =0$ and $U_{\theta }=\partial \ell \left(\alpha ,\theta ;\mathbf{y}\right)/\partial \theta =0$ written, respectively, as

$$\begin{array}{ccc}\hfill U_{\alpha }& =& \hfill \frac{1}{\varphi \left[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]\theta }\sum _{i=1}^n\left[{\mathrm{\Phi }}^{-1}\left(y_i\right)\sqrt{1-\theta }-{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right],\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill U_{\theta }& =& \frac{n}{\theta \left(\theta -1\right)}+\frac{1}{2\theta \sqrt{1-\theta }}\sum _{i=1}^n\left[{\mathrm{\Phi }}^{-1}\left(y_i\right)\sqrt{1-\theta }-{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]{\mathrm{\Phi }}^{-1}\left(y_i\right)+\hfill \\ & & \frac{1}{2{\theta }^2}\sum _{i=1}^n{\left[{\mathrm{\Phi }}^{-1}\left(y_i\right)\sqrt{1-\theta }-{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]}^2,\hfill \end{array}$$

(6)

where $\varphi$ denotes the standard normal PDF.

By solving the equation $U_{\theta }=0$, obtained from (6), in $\alpha$, we have

$$\widehat{\alpha }=\mathrm{\Phi }\left[\frac{\sqrt{1-\widehat{\theta }}}{n}\sum _{i=1}^n{\mathrm{\Phi }}^{-1}\left(y_i\right)\right]=\xi \left(\widehat{\theta }\right),$$

while $\widehat{\theta }$ is calculated numerically considering $\alpha =\xi \left(\theta \right)$ in the formula stated (6). The estimated asymptotic standard errors (SEs) of $\widehat{\alpha }$ and $\widehat{\theta }$ are computed by the corresponding inverse Hessian matrix. Such a matrix is obtained by the second-order derivative of the expression given in (4) with respect to $\alpha$ and $\theta$. Note that

$$\begin{array}{ccc}\hfill \frac{\mathrm{d}}{\mathrm{d}\alpha }{\mathrm{\Phi }}^{-1}\left(\alpha \right)& =& \frac{1}{\varphi \left[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]},\hfill \\ \hfill \frac{\mathrm{d}}{\mathrm{d}\alpha }\varphi \left[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]& =& \hfill -\frac{{\mathrm{\Phi }}^{-1}\left(\alpha \right)}{\sqrt{2\pi }\varphi \left[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]}exp\left\{-\frac{1}{2}{\left[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]}^2\right\}=-{\mathrm{\Phi }}^{-1}\left(\alpha \right),\hfill \\ \hfill \frac{{\mathrm{d}}^2}{\mathrm{d}{\alpha }^2}{\mathrm{\Phi }}^{-1}\left(\alpha \right)& =& -\frac{\mathrm{d}}{\mathrm{d}\alpha }\varphi \left[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]\frac{1}{{\left\{\varphi \left[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]\right\}}^2}=\frac{{\mathrm{\Phi }}^{-1}\left(\alpha \right)}{{\left\{\varphi \left[{\mathrm{\Phi }}^{-1}\left(\alpha \right)\right]\right\}}^2}.\hfill \end{array}$$

Now, by considering the re-parameterization given in (3), the log-likelihood function is proportional to

$$\begin{array}{c}\hfill \ell \left(\mu ,\theta ;\mathit{y},\tau \right)\propto \frac{n}{2}log\left(\frac{1-\theta }{\theta }\right)-\frac{1}{2\theta }\sum _{i=1}^n{\left\{\sqrt{1-\theta }\left[{\mathrm{\Phi }}^{-1}\left(y_i\right)-{\mathrm{\Phi }}^{-1}\left(\mu \right)\right]+\sqrt{\theta }{\mathrm{\Phi }}^{-1}\left(\tau \right)\right\}}^2,\end{array}$$

such that

$$U_{\mu }={\left.U_{\alpha }\right|}_{\alpha =g^{-1}\left(\mu \right)}\frac{\partial }{\partial \mu }\mathrm{\Phi }\left[{\mathrm{\Phi }}^{-1}\left(\mu \right)\sqrt{1-\theta }-\sqrt{\theta }{\mathrm{\Phi }}^{-1}\left(\tau \right)\right]$$

and

$$U_{\theta }=U_{\theta }\frac{\partial }{\partial \theta }\mathrm{\Phi }\left[{\mathrm{\Phi }}^{-1}\left(\mu \right)\sqrt{1-\theta }-\sqrt{\theta }{\mathrm{\Phi }}^{-1}\left(\tau \right)\right]$$

are the score equations for $\mu$ and $\theta$, respectively.

Note that, concomitant with $y_i$, for $i\in \{1,\dots ,n\}$, we can also observe covariate vectors $x_i$ and $z_i$. Then, we are interested in evaluating the effects of these covariates on $(\alpha ,\theta )$ or $(\mu ,\theta )$. For ML estimation, we have the observations $y_1,\dots ,y_n$ from n VASI distributed independent random variables $Y_1,\dots ,Y_n$. Now, assume the equations expressed as

$$g_1\left({\omega }_i\right)={\eta }_i={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_p{x}_{ip}$$

and

$$g_2\left({\theta }_i\right)={\zeta }_i={\delta }_0+{\delta }_1{z}_{i1}+\cdots +{\delta }_p{z}_{iq},$$

which link both ${\eta }_i$ and ${\zeta }_i$ with a linear combination of the values of the covariates $x_i={(1,x_{i1},\dots ,x_{ip})}^{\top }$ and $z_i={(1,z_{i1},\dots ,z_{iq})}^{\top }$, respectively. Note that ${\omega }_i$ can be the mean or the $\tau$-th quantile of Y. We assume that $g_1$ and $g_2$ are strictly monotonic, twice differentiable functions that map the mean ${\alpha }_i$ or the $\tau$-th quantile ${\mu }_i$ and ${\theta }_i$ to the real line. Suitable choices of $g_1$ and $g_2$ are the inverse CDF of the logistic (logit link), standard normal (probit link), minimum extreme value (complementary log–log link), maximum extreme value (log–log link), and Cauchy (Cauchit link) distributions. It is important to note that $x$ and $z$ can be identical or they could be subsets of each other.

To obtain the parameter estimates, we need the first-order and second-order partial derivatives of the logarithm of the likelihood function. For the response i, $y_i$ namely, with $i\in \{1,\dots ,n\}$ and, as mentioned, $\omega$ being the mean or the $\tau$-th quantile of Y, the log-likelihood function is given by ${\ell }_i={\ell }_i\left(\mathrm{\Theta }\right)=log\left[f\left(y_i;\mathrm{\Theta },x_i,z_i,\tau \right)\right]$, such that the score equations are stated as

$$\frac{\partial {\ell }_i}{\partial {\beta }_j}=\frac{\partial {\ell }_i}{\partial {\omega }_i}\frac{\partial {\omega }_i}{\partial {\eta }_i}\frac{\partial {\eta }_i}{\partial {\beta }_j},\frac{\partial {\ell }_i}{\partial {\delta }_j}=\frac{\partial {\ell }_i}{\partial {\theta }_i}\frac{\partial {\theta }_i}{\partial {\zeta }_i}\frac{\partial {\zeta }_i}{\partial {\delta }_j},j\in \{1,\dots ,p\},$$

where $\mathrm{\Theta }={({\mathbf{\beta }}^{\top },{\mathbf{\delta }}^{\top })}^{\top }$, $\mathbf{\beta }={({\beta }_0,\dots ,{\beta }_p)}^{\top }$ is a $(p+1)\times 1$ parameter vector associated with an $n\times (p+1)$ covariate matrix $X$ and $\mathbf{\delta }={({\delta }_0,\dots ,{\delta }_q)}^{\top }$ is a $(q+1)\times 1$ parameter vector associated with an $n\times (q+1)$ covariate matrix $Z$. Considering the full log-likelihood function, we have the score vectors for $\mathrm{\Theta }$, written, respectively, as

$$\frac{\partial \ell }{\partial \mathbf{\beta }}=X^{\top }\mathrm{diag}\left(W_{\omega }\right){\dot{\ell }}_{\omega },\frac{\partial \ell }{\partial \mathbf{\delta }}=Z^{\top }\mathrm{diag}\left(W_{\delta }\right){\dot{\ell }}_{\delta },$$

with “diag” denoting an $n\times n$ diagonal matrix and

$$W_{\omega }=\left[\frac{\partial {\omega }_1}{\partial {\eta }_1},\cdots ,\frac{\partial {\omega }_n}{\partial {\eta }_n}\right],{\dot{\ell }}_{\omega }={\left[\frac{\partial \ell }{\partial {\omega }_1},\cdots ,\frac{\partial \ell }{\partial {\omega }_n}\right]}^{\top },W_{\delta }=\left[\frac{\partial {\theta }_1}{\partial {\zeta }_1},\cdots ,\frac{\partial {\theta }_n}{\partial {\zeta }_n}\right],{\dot{\ell }}_{\delta }={\left[\frac{\partial \ell }{\partial {\theta }_1},\cdots ,\frac{\partial \ell }{\partial {\theta }_n}\right]}^{\top }.$$

For the Hessian matrix, we have the expressions stated as

$$\begin{array}{ccc}\hfill \frac{{\partial }^2\ell }{\partial \mathbf{\beta }\partial {\mathbf{\beta }}^{\top }}& =& X^{\top }\mathrm{diag}\left({\ddot{\ell }}_{\omega \omega }\right)\mathrm{diag}\left(W_{\omega }^2\right)X,\hfill \\ \frac{{\partial }^2\ell }{\partial \mathbf{\delta }\partial {\mathbf{\delta }}^{\top }}\hfill & =& Z^{\top }\mathrm{diag}\left({\ddot{\ell }}_{\delta \delta }\right)\mathrm{diag}\left(W_{\delta }^2\right)Z,\hfill \\ \hfill \frac{{\partial }^2\ell }{\partial \mathbf{\beta }\partial {\mathbf{\delta }}^{\top }}& =& \hfill X^{\top }\mathrm{diag}\left({\ddot{\ell }}_{\mu \delta }\right)\mathrm{diag}\left(W_{\mu }\right)\mathrm{diag}\left(W_{\delta }\right)Z,\hfill \end{array}$$

where

$${\ddot{\ell }}_{\omega \omega }=\left[\frac{{\partial }^2\ell }{\partial {\omega }_1\partial {\omega }_1},\cdots ,\frac{{\partial }^2\ell }{\partial {\omega }_n\partial {\omega }_n}\right],{\ddot{\ell }}_{\delta \delta }=\left[\frac{{\partial }^2\ell }{\partial {\delta }_1\partial {\delta }_1},\cdots ,\frac{{\partial }^2\ell }{\partial {\delta }_n\partial {\delta }_n}\right],{\ddot{\ell }}_{\omega \delta }=\left[\frac{{\partial }^2\ell }{\partial {\omega }_1\partial {\delta }_1},\cdots ,\frac{{\partial }^2\ell \left(\mathrm{\Theta }\right)}{\partial {\omega }_n\partial {\delta }_n}\right].$$

The ML estimates ${({\widehat{\beta }}_0,\cdots ,{\widehat{\beta }}_p)}^{\top }$ and ${({\widehat{\delta }}_0,\cdots ,{\widehat{\delta }}_q)}^{\top }$ can be obtained, for instance, through general-purpose optimization algorithms such as Nelder–Mead, quasi-Newton, and conjugate-gradient, available in the optim function of R [28]. As an alternative, to model $(\alpha ,\theta )$ or $(\mu ,\theta )$, conditional on covariates, we create two generalized additive model for location, scale, and shape (GAMLSS) frameworks that can be used directly in the gamlss function of the gamlss package [29,30,31] of R. An advantage of having a GAMLSS structure is that all the parameters of the distribution can be modeled as linear, nonlinear, or smooth functions of covariates. In addition, we have available all the resources for the statistical modeling process within the gamlss package of R as model selection and diagnostics.

Considering some regularity conditions ([32] pp. 118–119), note that

$$\widehat{\mathrm{\Theta }}\dot{\sim }{\mathrm{N}}_{p+1}(\mathrm{\Theta },{\left(\mathcal{I}\left(\mathrm{\Theta }\right)\right)}^{-1}),$$

(7)

with $\mathcal{I}\left(\mathrm{\Theta }\right)$ being the expected information matrix that can be obtained as

$$\mathcal{I}\left(\mathrm{\Theta }\right)=\mathrm{E}\left[-\frac{{\partial }^2\ell \left(\mathrm{\Theta }\right)}{\partial \mathrm{\Theta }\partial {\mathrm{\Theta }}^{\top }}\right].$$

(8)

Observe that approximate confidence intervals may be reached employing the expression given in (7), while, for obtaining the information matrix defined in (8), we can utilize the observed information matrix defined by

$$\mathcal{J}\left(\mathrm{\Theta }\right)=-\frac{{\partial }^2\ell \left(\mathrm{\Theta }\right)}{\partial \mathrm{\Theta }\partial {\mathrm{\Theta }}^{\top }},$$

(9)

whose elements established in (9) may be calculated from the results above presented, evaluated at $\mathrm{\Theta }=\widehat{\mathrm{\Theta }}$.

To test the hypotheses ${\mathrm{H}}_0:\mathrm{\Theta }={\mathrm{\Theta }}_0$ versus ${\mathrm{H}}_1:\mathrm{\Theta }\ne {\mathrm{\Theta }}_0$, with $\mathrm{\Theta }={({\mathbf{\beta }}^{\top },{\mathbf{\delta }}^{\top })}^{\top }$, as mentioned, we may employ the Wald and likelihood ratio tests. The Wald [33] and likelihood ratio statistics considering the observed information matrix [34] are, respectively, stated as

$$\begin{array}{ccc}\hfill W& =& \hfill {(\widehat{\mathrm{\Theta }}-{\mathrm{\Theta }}_0)}^{\top }\mathcal{J}((\widehat{\mathrm{\Theta }})(\widehat{\mathrm{\Theta }}-{\mathrm{\Theta }}_0),\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill L& =& \hfill -2\left(\ell \left({\mathrm{\Theta }}_0\right)-\ell (\widehat{\mathrm{\Theta }})\right).\hfill \end{array}$$

(11)

As $n\to \infty$, these statistics converge to a random variable with ${\chi }^2$ distribution and r degrees of freedom (DF), ${\chi }_r^2$ namely, with r being the number of parameters under ${\mathrm{H}}_0$, which is rejected, at a significance level $\varrho$, if the statistic computed according to (10) or (11) is greater than ${\chi }_{r,1-\varrho }^2$, which represents the $100(1-\varrho )$th ${\chi }_r^2$ quantile.

Diagnostics and goodness-of-fit are important because they reveal the strengths and weaknesses of a proposed model. As pointed out in [35]: “Goodness-of-fit is concerned with assessing the validity of models involving statistical distributions, an essential and sometimes forgotten aspect of the modeling exercise. One can only speculate on how many wrong decisions are made due to the use of an incorrect model”. Within the gamlss package, we may utilize the fitted normalized quantile residual [36] defined as

$${\widehat{r}}_i={\mathrm{\Phi }}^{-1}\left(F(y_i;{\widehat{\omega }}_i,{\widehat{\theta }}_i)\right),i\in \{1,\dots ,n\}.$$

(12)

If the model is correctly specified, the residual ${\widehat{r}}_i$ stated in (12) has an approximate standard normal distribution. Alternatively, defining ${\widehat{r}}_i=-log(1-F(y_i;{\widehat{\omega }}_i,{\widehat{\theta }}_i))$, we have the estimated Cox–Snell residual [37]. An important property of the Cox–Snell residual is that, if the model selected fits the data, ${\widehat{r}}_i$ follows the standard exponential distribution.

Note that, from a gamlss object, we can use these residuals to construct theoretical quantile versus empirical quantile (QQ) plots with simulated envelopes [38]. The main advantage of this simulation technique is its ease of interpretation without imposing any assumption on the residual distribution [39].

4. Simulation Studies

In this section, we report the results of two Monte Carlo simulation analyses employed to state the bias and root mean-squared error (RMSE) of the ML estimators of the VASI quantile regression coefficients. In addition, we provide the coverage probability (CP) of the 95% confidence interval (CP_95%) using the asymptotic normality of such ML estimators.

Here, we assume $\tau \in \{0.10,0.25,0.50,0.75,0.90\}$; sample sizes $n\in \{20,50,80,110,140$, $170,200\}$; and $\theta \in \{0.25,0.50,0.75\}$, inserted on two regression frameworks formulated as: (i) $\mathrm{logit}\left({\mu }_i\right)={\delta }_0+{\delta }_1{z}_{i1}$ for ${\delta }_0=1.0$, ${\delta }_1=2.0$ and $z_{i1}\sim \mathrm{N}(\mu =0,\sigma =1)$; and (ii) $\mathrm{logit}\left({\mu }_i\right)={\delta }_0+{\delta }_1{z}_{i1}+{\delta }_2{z}_{i2}$ for ${\delta }_0=1.0$, ${\delta }_1=1.0$, ${\delta }_2=0.5$, $z_{i1}\sim \mathrm{Bernoulli}(p=0.5)$ and $z_{i2}\sim \mathrm{N}(\mu =0,\sigma =1)$. For each $(\tau ,n,\theta )$ and both regressions, with the covariates being kept constant in the simulations, $M=10,000$ replicates were generated using the SAS Data-Step, while the estimates were calculated with the quasi-Newton method of PROC SAS/NLMIXED [40]. Response values, for $(\tau ,n,\theta )$ and the covariates, are obtained from the QF given by

$$y_i=\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left({\alpha }_i\right)+{\mathrm{\Phi }}^{-1}\left(u_i\right)\sqrt{\theta }}{\sqrt{1-\theta }}\right),$$

(13)

where $u_i\sim \mathrm{U}(0,1)$ and ${\alpha }_i=h^{-1}\left({\mu }_i\right)=\mathrm{\Phi }[{\mathrm{\Phi }}^{-1}\left({\mu }_i\right)\sqrt{1-\theta }-{\mathrm{\Phi }}^{-1}\left(\tau \right)\sqrt{\theta }]$.

The bias, RMSE, and CP were calculated, respectively, as

$$\mathrm{Bias}\left(\widehat{\varsigma }\right)=\frac{1}{M}\sum _{i=1}^M({\widehat{\varsigma }}_i-\varsigma ),\mathrm{RMSE}\left(\widehat{\varsigma }\right)={\left(\frac{1}{M}\sum _{i=1}^M{\left({\widehat{\varsigma }}_i-\varsigma \right)}^2\right)}^{1/2},$$

and ${\mathrm{CP}}_{95\%}\left(\widehat{\varsigma }\right)=(1/M){\sum }_{i=1}^M𝟙[{\widehat{\varsigma }}_i\pm 1.96\times \widehat{\mathrm{SE}}\left({\widehat{\varsigma }}_i\right)]$, where $\varsigma =\theta$, ${\delta }_0$, ${\delta }_1$, or ${\delta }_2$; $𝟙$ is the indicator function; and $\widehat{\mathrm{SE}}\left({\widehat{\varsigma }}_i\right)$ is the corresponding estimated SE.

Table 1, Table 2 and Table 3 and Table 4, Table 5 and Table 6 present the results for the first and second regression models, respectively. Such tables report a small bias when estimating $\theta$ and $\mathbf{\delta }$ for all settings considered in this study. In addition, the estimated RMSE is small and quickly approaches zero as n, the sample size, increases. Larger values of the bias and RMSE are detected as the quantiles are distant from $\tau =0.5$, either from the left or right, that is, the values $\tau \in \{0.1,0.25,0.75,0.9\}$. Moreover, for all scenarios, the CPs tend towards the nominal confidence coefficient, that is, 95%, as n increases from $n=20$ to $n=200$, with $n\in \{20,50,80,110,140,170,200\}$. The Monte Carlo simulation results for the mean and the same regression structures give us evidence that the coefficients are also well estimated according to the bias, RMSE, and CP, that is, once again, the bias and RMSE decrease as the sample size increases, whereas the CPs approach the confidence coefficient considered, that is, $95\%$, as expected. These results are not shown here and can be obtained from the authors upon request.

Table 1. Empirical bias, RMSE, and $95\%$ CP (true values: ${\delta }_0=1.00$, ${\delta }_1=2.00$, and $\theta =0.25$) with simulated data.

		Bias			RMSE			CP95%
τ	n	δ0	δ1	θ	δ0	δ1	θ	δ0	δ1	θ
0.10	20	$0.0897$	$0.0210$	$-0.0227$	$0.3373$	$0.2856$	$0.0623$	$89.88$	$91.88$	$85.16$
	50	$0.0361$	$0.0087$	$-0.0085$	$0.2068$	$0.1852$	$0.0382$	$93.54$	$93.56$	$91.40$
	80	$0.0218$	$0.0047$	$-0.0050$	$0.1653$	$0.1361$	$0.0299$	$93.94$	$93.72$	$92.84$
	110	$0.0153$	$0.0033$	$-0.0036$	$0.1406$	$0.1154$	$0.0252$	$94.10$	$93.90$	$93.62$
	140	$0.0131$	$0.0024$	$-0.0029$	$0.1244$	$0.1014$	$0.0222$	$94.26$	$94.38$	$94.02$
	170	$0.0101$	$0.0018$	$-0.0022$	$0.1117$	$0.0921$	$0.0202$	$94.66$	$94.80$	$94.38$
	200	$0.0090$	$0.0025$	$-0.0019$	$0.1027$	$0.0854$	$0.0184$	$94.64$	$94.66$	$94.66$
0.25	20	$0.0483$	$0.0132$	$-0.0228$	$0.2697$	$0.2829$	$0.0624$	$91.34$	$91.78$	$85.14$
	50	$0.0209$	$0.0063$	$-0.0086$	$0.1682$	$0.1845$	$0.0384$	$94.18$	$93.54$	$91.32$
	80	$0.0129$	$0.0035$	$-0.0051$	$0.1353$	$0.1357$	$0.0301$	$94.20$	$93.74$	$92.80$
	110	$0.0088$	$0.0025$	$-0.0037$	$0.1154$	$0.1150$	$0.0254$	$94.38$	$93.98$	$93.44$
	140	$0.0079$	$0.0017$	$-0.0030$	$0.1026$	$0.1011$	$0.0224$	$94.74$	$94.28$	$94.02$
	170	$0.0061$	$0.0013$	$-0.0023$	$0.0918$	$0.0918$	$0.0204$	$94.66$	$94.84$	$94.38$
	200	$0.0056$	$0.0021$	$-0.0020$	$0.0848$	$0.0852$	$0.0186$	$94.66$	$94.64$	$94.58$
0.50	20	$0.0030$	$0.0059$	$-0.0228$	$0.2371$	$0.2813$	$0.0625$	$93.00$	$91.68$	$85.08$
	50	$0.0042$	$0.0042$	$-0.0086$	$0.1498$	$0.1841$	$0.0385$	$94.72$	$93.62$	$91.42$
	80	$0.0029$	$0.0024$	$-0.0051$	$0.1208$	$0.1354$	$0.0302$	$94.56$	$93.84$	$92.68$
	110	$0.0016$	$0.0017$	$-0.0037$	$0.1032$	$0.1148$	$0.0255$	$94.74$	$94.06$	$93.52$
	140	$0.0021$	$0.0011$	$-0.0030$	$0.0922$	$0.1008$	$0.0224$	$95.18$	$94.36$	$93.92$
	170	$0.0017$	$0.0009$	$-0.0023$	$0.0824$	$0.0916$	$0.0205$	$94.94$	$94.78$	$94.10$
	200	$0.0017$	$0.0017$	$-0.0020$	$0.0765$	$0.0851$	$0.0186$	$94.94$	$94.72$	$94.68$
0.75	20	$-0.0410$	$0.0002$	$-0.0226$	$0.2643$	$0.2811$	$0.0624$	$91.52$	$91.68$	$85.28$
	50	$-0.0120$	$0.0026$	$-0.0085$	$0.1660$	$0.1841$	$0.0385$	$94.38$	$93.48$	$91.20$
	80	$-0.0069$	$0.0017$	$-0.0051$	$0.1332$	$0.1354$	$0.0302$	$94.78$	$93.84$	$92.54$
	110	$-0.0055$	$0.0012$	$-0.0037$	$0.1135$	$0.1147$	$0.0255$	$94.56$	$94.24$	$93.44$
	140	$-0.0036$	$0.0007$	$-0.0030$	$0.1013$	$0.1008$	$0.0224$	$95.04$	$94.38$	$93.90$
	170	$-0.0028$	$0.0007$	$-0.0023$	$0.0909$	$0.0915$	$0.0204$	$95.12$	$94.72$	$94.12$
	200	$-0.0021$	$0.0015$	$-0.0020$	$0.0841$	$0.0850$	$0.0186$	$94.78$	$94.78$	$94.60$
0.90	20	$-0.0790$	$-0.0037$	$-0.0224$	$0.3272$	$0.2818$	$0.0621$	$89.80$	$91.82$	$85.34$
	50	$-0.0260$	$0.0016$	$-0.0085$	$0.2033$	$0.1846$	$0.0383$	$93.78$	$93.26$	$91.24$
	80	$-0.0154$	$0.0014$	$-0.0051$	$0.1622$	$0.1355$	$0.0300$	$94.36$	$93.86$	$92.56$
	110	$-0.0116$	$0.0010$	$-0.0036$	$0.1380$	$0.1148$	$0.0254$	$94.20$	$94.32$	$93.20$
	140	$-0.0085$	$0.0005$	$-0.0030$	$0.1226$	$0.1009$	$0.0223$	$94.20$	$94.40$	$94.06$
	170	$-0.0066$	$0.0005$	$-0.0023$	$0.1105$	$0.0915$	$0.0204$	$94.80$	$94.72$	$94.08$
	200	$-0.0055$	$0.0013$	$-0.0020$	$0.1017$	$0.0851$	$0.0186$	$94.82$	$95.00$	$94.64$

Table 2. Empirical bias, RMSE, and $95\%$ CP (true values: ${\delta }_0=1.00$, ${\delta }_1=2.00$, and $\theta =0.50$) with simulated data.

		Bias			RMSE			CP95%
τ	n	δ0	δ1	θ	δ0	δ1	θ	δ0	δ1	θ
0.10	20	$0.1632$	$0.0498$	$-0.0381$	$0.5939$	$0.5017$	$0.0911$	$90.32$	$91.80$	$87.54$
	50	$0.0658$	$0.0207$	$-0.0143$	$0.3606$	$0.3223$	$0.0529$	$93.88$	$93.60$	$92.34$
	80	$0.0396$	$0.0114$	$-0.0084$	$0.2872$	$0.2362$	$0.0408$	$94.14$	$93.76$	$93.66$
	110	$0.0280$	$0.0082$	$-0.0061$	$0.2441$	$0.2003$	$0.0342$	$94.29$	$94.01$	$93.97$
	140	$0.0239$	$0.0059$	$-0.0049$	$0.2160$	$0.1759$	$0.0301$	$94.35$	$94.29$	$94.41$
	170	$0.0183$	$0.0046$	$-0.0038$	$0.1938$	$0.1597$	$0.0273$	$94.77$	$94.79$	$94.67$
	200	$0.0163$	$0.0055$	$-0.0033$	$0.1784$	$0.1482$	$0.0248$	$94.70$	$94.64$	$94.87$
0.25	20	$0.0876$	$0.0350$	$-0.0379$	$0.4727$	$0.4952$	$0.0914$	$91.84$	$91.74$	$87.56$
	50	$0.0382$	$0.0163$	$-0.0142$	$0.2926$	$0.3208$	$0.0532$	$94.22$	$93.36$	$92.48$
	80	$0.0234$	$0.0092$	$-0.0084$	$0.2349$	$0.2355$	$0.0410$	$94.38$	$93.58$	$93.34$
	110	$0.0161$	$0.0066$	$-0.0061$	$0.2002$	$0.1995$	$0.0345$	$94.40$	$94.06$	$93.84$
	140	$0.0144$	$0.0048$	$-0.0049$	$0.1780$	$0.1753$	$0.0303$	$94.76$	$94.28$	$94.40$
	170	$0.0111$	$0.0038$	$-0.0038$	$0.1592$	$0.1592$	$0.0275$	$94.70$	$94.84$	$94.70$
	200	$0.0101$	$0.0048$	$-0.0032$	$0.1472$	$0.1477$	$0.0250$	$94.62$	$94.74$	$94.70$
0.50	20	$0.0080$	$0.0214$	$-0.0379$	$0.4137$	$0.4911$	$0.0915$	$93.06$	$91.64$	$87.60$
	50	$0.0090$	$0.0123$	$-0.0142$	$0.2603$	$0.3199$	$0.0533$	$94.92$	$93.30$	$92.64$
	80	$0.0059$	$0.0072$	$-0.0085$	$0.2096$	$0.2350$	$0.0412$	$94.62$	$93.88$	$93.44$
	110	$0.0035$	$0.0052$	$-0.0061$	$0.1789$	$0.1991$	$0.0346$	$94.78$	$94.24$	$93.74$
	140	$0.0042$	$0.0037$	$-0.0049$	$0.1599$	$0.1748$	$0.0303$	$95.26$	$94.36$	$94.44$
	170	$0.0033$	$0.0030$	$-0.0038$	$0.1429$	$0.1588$	$0.0276$	$95.00$	$94.78$	$94.68$
	200	$0.0034$	$0.0041$	$-0.0033$	$0.1325$	$0.1474$	$0.0251$	$94.96$	$94.84$	$94.84$
0.75	20	$-0.0679$	$0.0124$	$-0.0378$	$0.4600$	$0.4900$	$0.0914$	$91.62$	$91.66$	$87.72$
	50	$-0.0189$	$0.0098$	$-0.0141$	$0.2882$	$0.3199$	$0.0533$	$94.44$	$93.28$	$92.58$
	80	$-0.0109$	$0.0062$	$-0.0084$	$0.2309$	$0.2348$	$0.0412$	$94.84$	$93.98$	$93.44$
	110	$-0.0087$	$0.0044$	$-0.0061$	$0.1968$	$0.1990$	$0.0346$	$94.60$	$94.48$	$93.74$
	140	$-0.0056$	$0.0031$	$-0.0049$	$0.1757$	$0.1747$	$0.0303$	$95.08$	$94.30$	$94.34$
	170	$-0.0043$	$0.0026$	$-0.0038$	$0.1576$	$0.1587$	$0.0275$	$95.10$	$94.66$	$94.60$
	200	$-0.0032$	$0.0038$	$-0.0033$	$0.1457$	$0.1473$	$0.0251$	$94.78$	$94.84$	$94.88$
0.90	20	$-0.1326$	$0.0082$	$-0.0374$	$0.5692$	$0.4912$	$0.0910$	$89.94$	$91.68$	$87.84$
	50	$-0.0426$	$0.0090$	$-0.0140$	$0.3530$	$0.3207$	$0.0530$	$93.96$	$93.10$	$92.58$
	80	$-0.0253$	$0.0062$	$-0.0084$	$0.2813$	$0.2351$	$0.0410$	$94.38$	$93.98$	$93.36$
	110	$-0.0190$	$0.0044$	$-0.0060$	$0.2392$	$0.1992$	$0.0344$	$94.24$	$94.32$	$93.88$
	140	$-0.0140$	$0.0030$	$-0.0048$	$0.2127$	$0.1749$	$0.0302$	$94.32$	$94.44$	$94.26$
	170	$-0.0108$	$0.0027$	$-0.0038$	$0.1916$	$0.1587$	$0.0274$	$94.86$	$94.70$	$94.52$
	200	$-0.0089$	$0.0038$	$-0.0033$	$0.1763$	$0.1474$	$0.0250$	$94.78$	$95.02$	$94.80$

Table 3. Empirical bias, RMSE, and $95\%$ CP (true values: ${\delta }_0=1.00$, ${\delta }_1=2.00$, and $\theta =0.75$) with simulated data.

		Bias			RMSE			CP95%
τ	n	δ0	δ1	θ	δ0	δ1	θ	δ0	δ1	θ
0.10	20	$0.3389$	$-0.0624$	$-0.0548$	$1.0520$	$0.8201$	$0.0901$	$90.03$	$91.58$	$89.31$
	50	$0.1364$	$-0.1039$	$-0.0287$	$0.6283$	$0.5316$	$0.0495$	$93.43$	$92.54$	$91.61$
	80	$0.0863$	$-0.1028$	$-0.0226$	$0.5013$	$0.4020$	$0.0378$	$92.86$	$91.49$	$91.62$
	110	$0.0792$	$-0.1130$	$-0.0214$	$0.4327$	$0.3528$	$0.0336$	$93.45$	$90.92$	$91.34$
	140	$0.0775$	$-0.1020$	$-0.0198$	$0.3766$	$0.3145$	$0.0306$	$92.86$	$89.44$	$89.60$
	170	$0.0642$	$-0.1081$	$-0.0179$	$0.3309$	$0.2995$	$0.0274$	$94.08$	$89.10$	$89.57$
	200	$0.0685$	$-0.1129$	$-0.0166$	$0.3096$	$0.2849$	$0.0249$	$93.95$	$87.90$	$90.39$
0.25	20	$0.1600$	$0.0259$	$-0.0418$	$0.8327$	$0.8425$	$0.0816$	$92.49$	$91.78$	$91.34$
	50	$0.0615$	$-0.0166$	$-0.0179$	$0.5087$	$0.5411$	$0.0438$	$94.29$	$93.27$	$93.71$
	80	$0.0396$	$-0.0205$	$-0.0124$	$0.4073$	$0.4021$	$0.0331$	$94.39$	$93.17$	$94.07$
	110	$0.0287$	$-0.0266$	$-0.0104$	$0.3446$	$0.3363$	$0.0279$	$94.50$	$93.82$	$94.07$
	140	$0.0244$	$-0.0301$	$-0.0092$	$0.3050$	$0.2967$	$0.0243$	$95.25$	$94.09$	$94.09$
	170	$0.0144$	$-0.0312$	$-0.0083$	$0.2717$	$0.2721$	$0.0220$	$95.06$	$94.38$	$94.69$
	200	$0.0089$	$-0.0284$	$-0.0077$	$0.2517$	$0.2524$	$0.0201$	$94.49$	$94.45$	$94.66$
0.50	20	$0.0165$	$0.0530$	$-0.0372$	$0.7268$	$0.8619$	$0.0799$	$93.60$	$91.61$	$91.44$
	50	$0.0124$	$0.0229$	$-0.0141$	$0.4513$	$0.5546$	$0.0426$	$95.06$	$93.03$	$94.06$
	80	$0.0065$	$0.0104$	$-0.0087$	$0.3622$	$0.4062$	$0.0323$	$94.81$	$93.89$	$94.10$
	110	$0.0018$	$0.0043$	$-0.0065$	$0.3088$	$0.3422$	$0.0268$	$94.90$	$94.47$	$94.50$
	140	$0.0028$	$0.0019$	$-0.0053$	$0.2755$	$0.3020$	$0.0233$	$95.50$	$94.36$	$94.66$
	170	$0.0020$	$0.0016$	$-0.0044$	$0.2475$	$0.2749$	$0.0212$	$95.04$	$94.56$	$95.00$
	200	$0.0026$	$0.0024$	$-0.0038$	$0.2296$	$0.2550$	$0.0192$	$95.02$	$94.80$	$95.28$
0.75	20	$-0.1108$	$0.0548$	$-0.0358$	$0.8099$	$0.8653$	$0.0794$	$92.13$	$91.49$	$91.33$
	50	$-0.0285$	$0.0315$	$-0.0130$	$0.5028$	$0.5590$	$0.0424$	$94.56$	$93.06$	$93.96$
	80	$-0.0169$	$0.0191$	$-0.0077$	$0.4015$	$0.4083$	$0.0320$	$94.80$	$93.89$	$93.97$
	110	$-0.0141$	$0.0138$	$-0.0056$	$0.3418$	$0.3460$	$0.0266$	$94.71$	$94.41$	$94.49$
	140	$-0.0093$	$0.0100$	$-0.0045$	$0.3048$	$0.3037$	$0.0232$	$95.15$	$94.34$	$94.60$
	170	$-0.0071$	$0.0081$	$-0.0035$	$0.2734$	$0.2756$	$0.0210$	$95.12$	$94.59$	$95.04$
	200	$-0.0052$	$0.0095$	$-0.0030$	$0.2527$	$0.2561$	$0.0191$	$94.79$	$94.83$	$95.13$
0.90	20	$-0.2196$	$0.0570$	$-0.0353$	$1.0056$	$0.8707$	$0.0791$	$90.56$	$91.60$	$91.38$
	50	$-0.0670$	$0.0343$	$-0.0127$	$0.6171$	$0.5615$	$0.0423$	$94.00$	$93.00$	$93.94$
	80	$-0.0397$	$0.0218$	$-0.0076$	$0.4900$	$0.4101$	$0.0319$	$94.54$	$93.90$	$94.02$
	110	$-0.0301$	$0.0157$	$-0.0054$	$0.4161$	$0.3468$	$0.0265$	$94.28$	$94.42$	$94.22$
	140	$-0.0219$	$0.0116$	$-0.0043$	$0.3697$	$0.3041$	$0.0232$	$94.50$	$94.34$	$94.54$
	170	$-0.0170$	$0.0098$	$-0.0034$	$0.3327$	$0.2757$	$0.0209$	$94.88$	$94.62$	$95.00$
	200	$-0.0139$	$0.0111$	$-0.0029$	$0.3062$	$0.2560$	$0.0190$	$94.96$	$95.10$	$95.14$

Table 4. Empirical bias, RMSE, and $95\%$ CP (true values: ${\delta }_0=1.00$, ${\delta }_1=1.00$, ${\delta }_2=0.50$, and $\theta =0.25$) with simulated data.

		Bias				RMSE				CP95%
τ	n	δ0	δ1	δ2	θ	δ0	δ1	δ2	θ	δ0	δ1	δ2	θ
0.10	20	$0.1236$	$0.0166$	$0.0169$	$-0.0328$	$0.4493$	$0.4989$	$0.3022$	$0.0667$	$89.44$	$91.02$	$91.14$	$81.10$
	50	$0.0480$	$0.0075$	$0.0009$	$-0.0122$	$0.2612$	$0.3027$	$0.1438$	$0.0396$	$92.98$	$93.78$	$93.54$	$89.34$
	80	$0.0299$	$0.0035$	$0.0017$	$-0.0074$	$0.2114$	$0.2402$	$0.1119$	$0.0308$	$93.44$	$93.92$	$93.94$	$91.56$
	110	$0.0199$	$0.0047$	$0.0012$	$-0.0054$	$0.1745$	$0.2038$	$0.0958$	$0.0258$	$94.20$	$94.42$	$94.26$	$92.94$
	140	$0.0157$	$0.0058$	$0.0014$	$-0.0043$	$0.1501$	$0.1781$	$0.0820$	$0.0227$	$94.40$	$94.40$	$94.38$	$93.30$
	170	$0.0121$	$0.0055$	$0.0009$	$-0.0034$	$0.1308$	$0.1615$	$0.0750$	$0.0206$	$94.60$	$94.64$	$94.82$	$93.66$
	200	$0.0110$	$0.0043$	$0.0013$	$-0.0030$	$0.1209$	$0.1486$	$0.0703$	$0.0187$	$94.54$	$94.54$	$94.92$	$94.42$
0.25	20	$0.0680$	$0.0086$	$0.0129$	$-0.0329$	$0.3985$	$0.4942$	$0.2995$	$0.0667$	$90.90$	$91.08$	$91.42$	$81.14$
	50	$0.0279$	$0.0044$	$-0.0006$	$-0.0122$	$0.2336$	$0.3014$	$0.1432$	$0.0396$	$93.46$	$93.82$	$93.58$	$89.34$
	80	$0.0177$	$0.0017$	$0.0008$	$-0.0074$	$0.1907$	$0.2396$	$0.1115$	$0.0308$	$93.92$	$93.92$	$93.88$	$91.54$
	110	$0.0111$	$0.0034$	$0.0006$	$-0.0054$	$0.1576$	$0.2032$	$0.0956$	$0.0258$	$94.32$	$94.34$	$94.30$	$92.96$
	140	$0.0086$	$0.0047$	$0.0008$	$-0.0043$	$0.1353$	$0.1777$	$0.0818$	$0.0227$	$94.78$	$94.52$	$94.44$	$93.28$
	170	$0.0065$	$0.0047$	$0.0005$	$-0.0034$	$0.1168$	$0.1611$	$0.0749$	$0.0206$	$94.90$	$94.58$	$94.74$	$93.64$
	200	$0.0062$	$0.0036$	$0.0009$	$-0.0030$	$0.1080$	$0.1483$	$0.0702$	$0.0187$	$94.74$	$94.52$	$94.92$	$94.48$
0.50	20	$0.0077$	$0.0008$	$0.0088$	$-0.0329$	$0.3749$	$0.4900$	$0.2970$	$0.0667$	$91.48$	$91.06$	$91.42$	$81.22$
	50	$0.0060$	$0.0014$	$-0.0021$	$-0.0122$	$0.2213$	$0.3004$	$0.1428$	$0.0396$	$93.84$	$93.80$	$93.68$	$89.38$
	80	$0.0045$	$-0.0001$	$-0.0001$	$-0.0074$	$0.1812$	$0.2391$	$0.1113$	$0.0308$	$93.64$	$93.90$	$93.84$	$91.44$
	110	$0.0016$	$0.0021$	$-0.0001$	$-0.0054$	$0.1505$	$0.2028$	$0.0955$	$0.0258$	$94.20$	$94.34$	$94.16$	$93.02$
	140	$0.0009$	$0.0037$	$0.0003$	$-0.0043$	$0.1290$	$0.1774$	$0.0817$	$0.0227$	$94.92$	$94.58$	$94.46$	$93.34$
	170	$0.0005$	$0.0039$	$0.0002$	$-0.0034$	$0.1109$	$0.1609$	$0.0749$	$0.0206$	$94.94$	$94.62$	$94.84$	$93.68$
	200	$0.0009$	$0.0029$	$0.0006$	$-0.0030$	$0.1024$	$0.1482$	$0.0701$	$0.0187$	$94.94$	$94.56$	$94.90$	$94.52$
0.75	20	$-0.0513$	$-0.0059$	$0.0053$	$-0.0329$	$0.3901$	$0.4870$	$0.2950$	$0.0667$	$90.66$	$91.12$	$91.34$	$81.14$
	50	$-0.0154$	$-0.0012$	$-0.0033$	$-0.0122$	$0.2308$	$0.2998$	$0.1425$	$0.0396$	$93.50$	$93.90$	$93.54$	$89.28$
	80	$-0.0085$	$-0.0016$	$-0.0008$	$-0.0074$	$0.1877$	$0.2389$	$0.1112$	$0.0308$	$94.12$	$93.88$	$93.92$	$91.36$
	110	$-0.0078$	$0.0010$	$-0.0006$	$-0.0054$	$0.1568$	$0.2026$	$0.0955$	$0.0258$	$94.30$	$94.50$	$94.14$	$92.94$
	140	$-0.0066$	$0.0028$	$-0.0001$	$-0.0043$	$0.1350$	$0.1772$	$0.0817$	$0.0227$	$94.70$	$94.60$	$94.50$	$93.34$
	170	$-0.0055$	$0.0032$	$-0.0002$	$-0.0034$	$0.1166$	$0.1608$	$0.0749$	$0.0206$	$94.70$	$94.54$	$94.80$	$93.62$
	200	$-0.0043$	$0.0023$	$0.0003$	$-0.0030$	$0.1072$	$0.1482$	$0.0702$	$0.0187$	$94.96$	$94.50$	$94.98$	$94.58$
0.90	20	$-0.1034$	$-0.0110$	$0.0025$	$-0.0329$	$0.4329$	$0.4850$	$0.2938$	$0.0668$	$89.26$	$91.16$	$91.18$	$81.18$
	50	$-0.0342$	$-0.0032$	$-0.0043$	$-0.0122$	$0.2559$	$0.2996$	$0.1425$	$0.0396$	$92.90$	$93.88$	$93.48$	$89.28$
	80	$-0.0200$	$-0.0028$	$-0.0014$	$-0.0074$	$0.2060$	$0.2390$	$0.1113$	$0.0308$	$93.50$	$93.84$	$93.98$	$91.38$
	110	$-0.0161$	$0.0001$	$-0.0011$	$-0.0054$	$0.1729$	$0.2026$	$0.0955$	$0.0258$	$93.94$	$94.56$	$94.14$	$92.92$
	140	$-0.0132$	$0.0021$	$-0.0005$	$-0.0043$	$0.1496$	$0.1772$	$0.0818$	$0.0227$	$94.38$	$94.62$	$94.48$	$93.36$
	170	$-0.0107$	$0.0026$	$-0.0005$	$-0.0034$	$0.1304$	$0.1609$	$0.0750$	$0.0206$	$94.26$	$94.52$	$94.66$	$93.64$
	200	$-0.0088$	$0.0019$	$0.0001$	$-0.0029$	$0.1194$	$0.1483$	$0.0702$	$0.0187$	$94.74$	$94.38$	$95.04$	$94.62$

Table 5. Empirical bias, RMSE, and $95\%$ CP (true values: ${\delta }_0=1.00$, ${\delta }_1=1.00$, ${\delta }_2=0.50$, and $\theta =0.50$) with simulated data.

		Bias				RMSE				CP95%
τ	n	δ0	δ1	δ2	θ	δ0	δ1	δ2	θ	δ0	δ1	δ2	θ
0.10	20	$0.2321$	$0.0301$	$0.0366$	$-0.0528$	$0.8048$	$0.8884$	$0.5378$	$0.1004$	$90.32$	$91.40$	$91.32$	$84.53$
	50	$0.0887$	$0.0149$	$0.0030$	$-0.0192$	$0.4578$	$0.5297$	$0.2520$	$0.0555$	$93.32$	$93.86$	$93.78$	$90.98$
	80	$0.0552$	$0.0071$	$0.0040$	$-0.0116$	$0.3693$	$0.4189$	$0.1952$	$0.0423$	$93.70$	$94.08$	$94.00$	$92.46$
	110	$0.0368$	$0.0092$	$0.0030$	$-0.0084$	$0.3038$	$0.3546$	$0.1669$	$0.0352$	$94.38$	$94.44$	$94.40$	$93.40$
	140	$0.0289$	$0.0110$	$0.0030$	$-0.0067$	$0.2611$	$0.3097$	$0.1426$	$0.0308$	$94.54$	$94.52$	$94.44$	$93.82$
	170	$0.0224$	$0.0104$	$0.0021$	$-0.0053$	$0.2273$	$0.2806$	$0.1303$	$0.0278$	$94.76$	$94.64$	$94.86$	$94.34$
	200	$0.0202$	$0.0081$	$0.0026$	$-0.0046$	$0.2100$	$0.2581$	$0.1220$	$0.0253$	$94.70$	$94.52$	$94.96$	$94.74$
0.25	20	$0.1309$	$0.0157$	$0.0291$	$-0.0527$	$0.7083$	$0.8733$	$0.5293$	$0.1004$	$91.64$	$91.34$	$91.34$	$84.44$
	50	$0.0525$	$0.0094$	$0.0002$	$-0.0192$	$0.4084$	$0.5258$	$0.2503$	$0.0555$	$93.70$	$93.98$	$93.72$	$91.00$
	80	$0.0334$	$0.0038$	$0.0023$	$-0.0116$	$0.3324$	$0.4170$	$0.1943$	$0.0423$	$94.02$	$94.08$	$93.94$	$92.52$
	110	$0.0211$	$0.0069$	$0.0018$	$-0.0084$	$0.2742$	$0.3532$	$0.1663$	$0.0352$	$94.46$	$94.36$	$94.38$	$93.36$
	140	$0.0163$	$0.0091$	$0.0021$	$-0.0067$	$0.2350$	$0.3086$	$0.1422$	$0.0308$	$94.78$	$94.58$	$94.40$	$93.80$
	170	$0.0123$	$0.0089$	$0.0015$	$-0.0053$	$0.2028$	$0.2797$	$0.1301$	$0.0278$	$94.96$	$94.68$	$94.82$	$94.30$
	200	$0.0116$	$0.0069$	$0.0021$	$-0.0046$	$0.1875$	$0.2575$	$0.1218$	$0.0253$	$94.88$	$94.56$	$94.90$	$94.80$
0.50	20	$0.0235$	$0.0024$	$0.0221$	$-0.0528$	$0.6615$	$0.8605$	$0.5219$	$0.1004$	$92.16$	$91.34$	$91.30$	$84.38$
	50	$0.0141$	$0.0041$	$-0.0023$	$-0.0192$	$0.3858$	$0.5227$	$0.2489$	$0.0555$	$94.04$	$93.98$	$93.80$	$90.96$
	80	$0.0101$	$0.0007$	$0.0007$	$-0.0116$	$0.3152$	$0.4156$	$0.1937$	$0.0423$	$93.90$	$94.00$	$93.96$	$92.52$
	110	$0.0043$	$0.0045$	$0.0007$	$-0.0084$	$0.2614$	$0.3521$	$0.1659$	$0.0352$	$94.28$	$94.38$	$94.30$	$93.36$
	140	$0.0029$	$0.0072$	$0.0011$	$-0.0067$	$0.2240$	$0.3078$	$0.1419$	$0.0308$	$94.96$	$94.60$	$94.56$	$93.86$
	170	$0.0017$	$0.0075$	$0.0008$	$-0.0053$	$0.1924$	$0.2792$	$0.1300$	$0.0278$	$94.96$	$94.66$	$94.86$	$94.30$
	200	$0.0023$	$0.0057$	$0.0015$	$-0.0046$	$0.1776$	$0.2571$	$0.1217$	$0.0253$	$95.00$	$94.56$	$94.94$	$94.82$
0.75	20	$-0.0798$	$-0.0076$	$0.0166$	$-0.0528$	$0.6849$	$0.8515$	$0.5167$	$0.1005$	$90.96$	$91.40$	$91.30$	$84.42$
	50	$-0.0229$	$-0.0001$	$-0.0044$	$-0.0192$	$0.4016$	$0.5209$	$0.2481$	$0.0555$	$93.68$	$93.96$	$93.70$	$91.06$
	80	$-0.0124$	$-0.0017$	$-0.0005$	$-0.0116$	$0.3261$	$0.4149$	$0.1933$	$0.0423$	$94.18$	$93.94$	$94.10$	$92.52$
	110	$-0.0119$	$0.0026$	$-0.0002$	$-0.0084$	$0.2722$	$0.3515$	$0.1657$	$0.0352$	$94.36$	$94.48$	$94.20$	$93.38$
	140	$-0.0101$	$0.0057$	$0.0004$	$-0.0067$	$0.2341$	$0.3074$	$0.1418$	$0.0308$	$94.76$	$94.68$	$94.58$	$93.86$
	170	$-0.0085$	$0.0063$	$0.0002$	$-0.0053$	$0.2022$	$0.2789$	$0.1300$	$0.0278$	$94.70$	$94.56$	$94.80$	$94.30$
	200	$-0.0065$	$0.0047$	$0.0010$	$-0.0046$	$0.1858$	$0.2570$	$0.1217$	$0.0252$	$94.98$	$94.54$	$95.00$	$94.76$
0.90	20	$-0.1701$	$-0.0138$	$0.0129$	$-0.0528$	$0.7586$	$0.8466$	$0.5137$	$0.1005$	$89.64$	$91.48$	$91.30$	$84.52$
	50	$-0.0551$	$-0.0029$	$-0.0057$	$-0.0192$	$0.4449$	$0.5202$	$0.2479$	$0.0555$	$93.16$	$94.02$	$93.70$	$91.08$
	80	$-0.0319$	$-0.0033$	$-0.0013$	$-0.0116$	$0.3577$	$0.4148$	$0.1933$	$0.0423$	$93.58$	$93.98$	$94.12$	$92.42$
	110	$-0.0259$	$0.0013$	$-0.0009$	$-0.0084$	$0.3000$	$0.3514$	$0.1657$	$0.0352$	$94.02$	$94.64$	$94.28$	$93.42$
	140	$-0.0214$	$0.0047$	$-0.0001$	$-0.0067$	$0.2593$	$0.3073$	$0.1419$	$0.0308$	$94.48$	$94.64$	$94.58$	$93.86$
	170	$-0.0174$	$0.0055$	$-0.0002$	$-0.0053$	$0.2261$	$0.2790$	$0.1302$	$0.0278$	$94.26$	$94.56$	$94.66$	$94.38$
	200	$-0.0143$	$0.0041$	$0.0006$	$-0.0046$	$0.2069$	$0.2571$	$0.1219$	$0.0252$	$94.80$	$94.40$	$95.04$	$94.80$

Table 6. Empirical bias, RMSE, and $95\%$ CP (true values: ${\delta }_0=1.00$, ${\delta }_1=1.00$, ${\delta }_2=0.50$, and $\theta =0.75$) with simulated data.

		Bias				RMSE				CP95%
τ	n	δ0	δ1	δ2	θ	δ0	δ1	δ2	θ	δ0	δ1	δ2	θ
0.10	20	$0.5589$	$-0.0299$	$0.0406$	$-0.0676$	$1.5145$	$1.5813$	$0.9422$	$0.1010$	$91.22$	$91.87$	$91.65$	$85.88$
	50	$0.2687$	$-0.0555$	$-0.0201$	$-0.0347$	$0.8187$	$0.9035$	$0.4341$	$0.0537$	$93.20$	$94.52$	$93.80$	$89.33$
	80	$0.1991$	$-0.0373$	$-0.0260$	$-0.0276$	$0.6558$	$0.6952$	$0.3317$	$0.0416$	$93.07$	$94.50$	$93.82$	$89.55$
	110	$0.1848$	$-0.0319$	$-0.0285$	$-0.0253$	$0.5474$	$0.5877$	$0.2916$	$0.0362$	$93.11$	$94.93$	$93.40$	$87.85$
	140	$0.1681$	$-0.0421$	$-0.0259$	$-0.0231$	$0.4713$	$0.5131$	$0.2539$	$0.0326$	$94.03$	$95.76$	$93.50$	$87.67$
	170	$0.1363$	$-0.0290$	$-0.0256$	$-0.0216$	$0.3935$	$0.4508$	$0.2241$	$0.0301$	$94.22$	$97.11$	$95.31$	$86.28$
	200	$0.1349$	$-0.0166$	$-0.0213$	$-0.0215$	$0.3682$	$0.4068$	$0.2050$	$0.0284$	$93.78$	$96.41$	$95.45$	$85.89$
0.25	20	$0.2759$	$0.0103$	$0.0545$	$-0.0537$	$1.3020$	$1.5745$	$0.9434$	$0.0921$	$93.08$	$92.02$	$92.13$	$88.39$
	50	$0.1102$	$0.0043$	$-0.0066$	$-0.0216$	$0.7261$	$0.9258$	$0.4359$	$0.0462$	$94.05$	$94.07$	$94.09$	$92.99$
	80	$0.0721$	$-0.0058$	$-0.0015$	$-0.0147$	$0.5838$	$0.7325$	$0.3361$	$0.0344$	$94.33$	$93.83$	$94.51$	$93.68$
	110	$0.0480$	$0.0050$	$-0.0054$	$-0.0118$	$0.4750$	$0.6154$	$0.2878$	$0.0285$	$94.85$	$94.28$	$94.47$	$93.65$
	140	$0.0409$	$0.0030$	$-0.0061$	$-0.0100$	$0.4093$	$0.5379$	$0.2415$	$0.0248$	$95.05$	$94.41$	$95.02$	$94.18$
	170	$0.0323$	$0.0024$	$-0.0075$	$-0.0085$	$0.3526$	$0.4799$	$0.2213$	$0.0222$	$94.99$	$95.14$	$95.21$	$94.59$
	200	$0.0298$	$-0.0029$	$-0.0053$	$-0.0079$	$0.3285$	$0.4425$	$0.2085$	$0.0202$	$94.48$	$95.10$	$95.30$	$94.81$
0.50	20	$0.0663$	$0.0057$	$0.0547$	$-0.0492$	$1.2038$	$1.5467$	$0.9390$	$0.0900$	$93.42$	$92.05$	$92.37$	$88.73$
	50	$0.0340$	$0.0079$	$-0.0049$	$-0.0175$	$0.6795$	$0.9147$	$0.4369$	$0.0449$	$94.72$	$94.37$	$94.23$	$93.30$
	80	$0.0232$	$0.0004$	$0.0004$	$-0.0108$	$0.5526$	$0.7250$	$0.3388$	$0.0332$	$94.25$	$94.25$	$94.35$	$93.80$
	110	$0.0115$	$0.0064$	$-0.0000$	$-0.0080$	$0.4558$	$0.6124$	$0.2883$	$0.0273$	$94.44$	$94.48$	$94.44$	$94.00$
	140	$0.0063$	$0.0116$	$0.0022$	$-0.0064$	$0.3903$	$0.5348$	$0.2473$	$0.0237$	$95.09$	$94.61$	$94.63$	$94.57$
	170	$0.0044$	$0.0115$	$0.0012$	$-0.0052$	$0.3343$	$0.4843$	$0.2265$	$0.0213$	$95.02$	$94.72$	$94.85$	$94.91$
	200	$0.0046$	$0.0098$	$0.0015$	$-0.0045$	$0.3087$	$0.4471$	$0.2112$	$0.0193$	$95.02$	$94.52$	$95.05$	$95.26$
0.75	20	$-0.1173$	$-0.0036$	$0.0504$	$-0.0487$	$1.2419$	$1.5266$	$0.9314$	$0.0898$	$92.06$	$92.28$	$92.50$	$88.70$
	50	$-0.0301$	$0.0056$	$-0.0034$	$-0.0170$	$0.7061$	$0.9127$	$0.4372$	$0.0447$	$94.23$	$94.33$	$94.17$	$93.21$
	80	$-0.0154$	$0.0005$	$0.0019$	$-0.0102$	$0.5709$	$0.7250$	$0.3387$	$0.0332$	$94.37$	$94.25$	$94.41$	$93.69$
	110	$-0.0161$	$0.0070$	$0.0021$	$-0.0073$	$0.4750$	$0.6124$	$0.2890$	$0.0273$	$94.65$	$94.63$	$94.41$	$93.87$
	140	$-0.0142$	$0.0123$	$0.0025$	$-0.0058$	$0.4074$	$0.5350$	$0.2472$	$0.0237$	$94.93$	$94.77$	$94.79$	$94.49$
	170	$-0.0122$	$0.0132$	$0.0017$	$-0.0046$	$0.3517$	$0.4853$	$0.2263$	$0.0213$	$94.84$	$94.64$	$94.90$	$94.80$
	200	$-0.0092$	$0.0100$	$0.0027$	$-0.0040$	$0.3230$	$0.4468$	$0.2117$	$0.0193$	$95.16$	$94.60$	$95.08$	$95.20$
0.90	20	$-0.2778$	$-0.0053$	$0.0474$	$-0.0487$	$1.3766$	$1.5197$	$0.9277$	$0.0898$	$90.62$	$92.62$	$92.68$	$88.56$
	50	$-0.0841$	$0.0027$	$-0.0043$	$-0.0169$	$0.7831$	$0.9122$	$0.4368$	$0.0447$	$93.66$	$94.34$	$94.12$	$93.12$
	80	$-0.0476$	$-0.0014$	$0.0014$	$-0.0101$	$0.6264$	$0.7251$	$0.3386$	$0.0332$	$93.82$	$94.26$	$94.42$	$93.66$
	110	$-0.0393$	$0.0057$	$0.0015$	$-0.0072$	$0.5235$	$0.6127$	$0.2890$	$0.0273$	$94.32$	$94.78$	$94.46$	$93.86$
	140	$-0.0325$	$0.0111$	$0.0020$	$-0.0057$	$0.4515$	$0.5350$	$0.2472$	$0.0237$	$94.56$	$94.72$	$94.82$	$94.52$
	170	$-0.0266$	$0.0124$	$0.0015$	$-0.0046$	$0.3933$	$0.4853$	$0.2265$	$0.0213$	$94.40$	$94.70$	$94.84$	$94.78$
	200	$-0.0218$	$0.0094$	$0.0025$	$-0.0039$	$0.3597$	$0.4469$	$0.2119$	$0.0193$	$94.94$	$94.48$	$95.22$	$95.18$

Observe that the empirical results based on the Monte Carlo simulations for large samples are coherent with the asymptotic theoretical results presented at the end of Section 3 and just before the diagnostic analysis.

5. Applications

In the next subsections, we present two real applications in order to show the potentiality of the proposed quantile and mean regression models, taking the VASI distribution as a baseline. For comparison purposes, in addition to the VASI quantile regression model, we also consider the Johnson SB (JOSB), Kumaraswamy (KUMA), unit-logistic (ULOG), and unit-Weibull (UWEI) quantile regression models, whose PDF, CDF, and QF are defined in Appendix A. The VASI mean regression model is compared with the beta and simplex regression models. Note that this section does not seek to provide all analyses for link function and variable selection, regression diagnostics, or parameter interpretation. Indeed, we are suggesting here the use of the VASI regression model as an alternative to other models available in the literature and not as a full regression analysis.

5.1. The VASI Quantile Regression Model

This application considers a real data set first reported in [41], which was also analyzed in [7]. This data set contains 298 observations about the body fat proportion of patients in a public hospital located in Curitiba, Paraná, Brazil. The fat proportion at android, arms, gynecoid, legs, and body are related to five response variables, and the data set is formed by two continuous and two categorical covariates. Note that the continuous covariates refer to the age (in years) and body mass index (bmi) (in kg/m²) of the individuals, while the categorical covariates are related to gender (female or male) and ipaq (sedentary (S), insufficiently active (I), or active (A)). Observe that the ipaq is a questionnaire that permits the estimation of weekly time spent on physical activities of moderate and strong intensity, in different aspects of daily life, such as transportation, leisure, housework, and work, as well as the time spent in passive activities [42].

The sample contains information from 150 women and 148 men. Patients have a mean age of 46 years old and a standard deviation of 19.88 years old, while the average BMI is 24.72 kg/m² with a standard deviation of 3.15 kg/m². The ipaq questionnaire classified individuals as follows: 76 individuals as insufficiently active, 60 sedentary, and 162 active. According to [41], the data set has one outlier, which consists of the individual #158 with the following characteristics: female, 49 years old, with BMI = 29.3 kg/m² and fat proportion in the arms equal to 0.196; in other words, this patient has a high BMI but low fat proportion in the arms.

For the response variable “proportion of fat in the arms”, we assume that ${\mu }_i$ is modeled as

$$\mathrm{logit}\left({\mu }_i\right)={\delta }_0+{\delta }_1{x}_{i1}+{\delta }_2{x}_{i2}+{\delta }_3{x}_{i3}+{\delta }_4{x}_{i4}+{\delta }_5{x}_{i5},i\in \{1,\dots ,298\},$$

(14)

where

• $x_{i1}$ is the (age_i − 46.00) with 46.00 being the average age;
• $x_{i2}$ is the (BMI_i − 24.72) with 24.72 being the average BMI;
• $x_{i3}$ is an indicator covariate, in which $x_{i3}=0$ for female or $x_{i3}=1$ for male;
• $x_{i4}$ is an indicator covariate, in which $x_{i4}=0$ for ipaq = S or $x_{i4}=1$ for ipaq = I;
• $x_{i5}$ is an indicator covariate, in which $x_{i5}=0$ for ipaq = S or $x_{i5}=1$ for ipaq = A.

Table 7 presents the values of the ML estimates and their corresponding SEs for the indicated models. The ${\widehat{\delta }}_0$ is the estimate for a female with age of 46 years old, BMI = 24.72 kg/m², and ipaq = S. The parameter estimates for ${\delta }_1$ and ${\delta }_2$ indicate that the arm fat proportion is larger for older individuals with larger BMI. In contrast, the estimates for ${\delta }_3$, ${\delta }_4$, and ${\delta }_5$ have a negative influence on the arm fat proportion, indicating that this proportion is smaller for insufficiently active and active men, respectively. Consequently, the fat proportion is larger for women and sedentary individuals. As expected, $\widehat{\theta }$ does not vary with the quantiles, since it does not depend on covariates. From the variation in the parameters for different values of $\tau$, we can conclude that the estimated arm fat proportion depends on the quantiles. This conditional quantile variation rate, expressed by the estimated regression coefficients, is illustrated in Figure 3. We can also see that, from a statistical point of view, all covariates are significant at 5%, since they do not contemplate the value of zero in their respective confidence intervals.

Table 7. ML estimates and SEs for the body fat proportion data.

		ML Estimate					SE
		$\mathit{\tau }$ Levels					$\mathit{\tau }$ Levels
Distribution	Parameter	0.10	0.25	0.50	0.75	0.90	0.10	0.25	0.50	0.75	0.90
VASI	${\delta }_0$	$-0.8467$	$-0.6696$	$-0.4757$	$-0.2842$	$-0.1132$	$0.0481$	$0.0455$	$0.0441$	$0.0442$	$0.0456$
	${\delta }_1$	$0.0047$	$0.0046$	$0.0045$	$0.0044$	$0.0044$	$0.0012$	$0.0012$	$0.0011$	$0.0011$	$0.0011$
	${\delta }_2$	$0.0924$	$0.0907$	$0.0891$	$0.0878$	$0.0869$	$0.0069$	$0.0067$	$0.0066$	$0.0065$	$0.0064$
	${\delta }_3$	$-0.9579$	$-0.9386$	$-0.9203$	$-0.9052$	$-0.8944$	$0.0380$	$0.0372$	$0.0364$	$0.0357$	$0.0352$
	${\delta }_4$	$-0.1205$	$-0.1188$	$-0.1172$	$-0.1161$	$-0.1154$	$0.0539$	$0.0529$	$0.0519$	$0.0512$	$0.0506$
	${\delta }_5$	$-0.2657$	$-0.2606$	$-0.2557$	$-0.2517$	$-0.2488$	$0.0520$	$0.0509$	$0.0500$	$0.0492$	$0.0487$
	$\theta$	$0.0302$	$0.0301$	$0.0301$	$0.0300$	$0.0299$	$0.0024$	$0.0024$	$0.0024$	$0.0024$	$0.0024$
ULOG	${\delta }_0$	$-0.8528$	$-0.6641$	$-0.4753$	$-0.2866$	$-0.0979$	$0.0468$	$0.0441$	$0.0432$	$0.0443$	$0.0471$
	${\delta }_1$	$0.0047$	$0.0047$	$0.0047$	$0.0047$	$0.0047$	$0.0011$	$0.0011$	$0.0011$	$0.0011$	$0.0011$
	${\delta }_2$	$0.0888$	$0.0888$	$0.0888$	$0.0888$	$0.0888$	$0.0066$	$0.0066$	$0.0066$	$0.0066$	$0.0066$
	${\delta }_3$	$-0.9324$	$-0.9324$	$-0.9324$	$-0.9324$	$-0.9324$	$0.0359$	$0.0359$	$0.0359$	$0.0359$	$0.0359$
	${\delta }_4$	$-0.1223$	$-0.1223$	$-0.1223$	$-0.1223$	$-0.1223$	$0.0513$	$0.0513$	$0.0513$	$0.0513$	$0.0513$
	${\delta }_5$	$-0.2385$	$-0.2385$	$-0.2385$	$-0.2385$	$-0.2385$	$0.0486$	$0.0486$	$0.0486$	$0.0486$	$0.0486$
	$\theta$	$5.8208$	$5.8208$	$5.8208$	$5.8208$	$5.8208$	$0.2824$	$0.2824$	$0.2824$	$0.2824$	$0.2824$
JOSB	${\delta }_0$	$-0.8661$	$-0.6784$	$-0.4699$	$-0.2614$	$-0.0738$	$0.0494$	$0.0474$	$0.0467$	$0.0474$	$0.0494$
	${\delta }_1$	$0.0047$	$0.0047$	$0.0047$	$0.0047$	$0.0047$	$0.0012$	$0.0012$	$0.0012$	$0.0012$	$0.0012$
	${\delta }_2$	$0.0916$	$0.0916$	$0.0916$	$0.0916$	$0.0916$	$0.0068$	$0.0068$	$0.0068$	$0.0068$	$0.0068$
	${\delta }_3$	$-0.9379$	$-0.9379$	$-0.9379$	$-0.9379$	$-0.9379$	$0.0373$	$0.0373$	$0.0373$	$0.0373$	$0.0373$
	${\delta }_4$	$-0.1174$	$-0.1174$	$-0.1174$	$-0.1174$	$-0.1174$	$0.0546$	$0.0546$	$0.0546$	$0.0546$	$0.0546$
	${\delta }_5$	$-0.2635$	$-0.2635$	$-0.2635$	$-0.2635$	$-0.2635$	$0.0524$	$0.0524$	$0.0524$	$0.0524$	$0.0524$
	$\theta$	$3.2351$	$3.2351$	$3.2351$	$3.2351$	$3.2351$	$0.1325$	$0.1325$	$0.1325$	$0.1325$	$0.1325$
KUMA	${\delta }_0$	$-1.1035$	$-0.8088$	$-0.5298$	$-0.2908$	$-0.1018$	$0.0515$	$0.0484$	$0.0486$	$0.0516$	$0.0559$
	${\delta }_1$	$0.0036$	$0.0038$	$0.0042$	$0.0045$	$0.0048$	$0.0009$	$0.0010$	$0.0010$	$0.0011$	$0.0011$
	${\delta }_2$	$0.0729$	$0.0772$	$0.0823$	$0.0874$	$0.0921$	$0.0055$	$0.0058$	$0.0061$	$0.0064$	$0.0068$
	${\delta }_3$	$-0.7302$	$-0.7715$	$-0.8201$	$-0.8699$	$-0.9150$	$0.0328$	$0.0345$	$0.0367$	$0.0391$	$0.0414$
	${\delta }_4$	$-0.0724$	$-0.0744$	$-0.0763$	$-0.0776$	$-0.0783$	$0.0475$	$0.0503$	$0.0537$	$0.0572$	$0.0604$
	${\delta }_5$	$-0.1963$	$-0.2057$	$-0.2163$	$-0.2267$	$-0.2359$	$0.0467$	$0.0496$	$0.0530$	$0.0565$	$0.0597$
	$\theta$	$4.7048$	$4.7148$	$4.7237$	$4.7307$	$4.7360$	$0.2103$	$0.2103$	$0.2101$	$0.2100$	$0.2099$
UWEI	${\delta }_0$	$-0.8251$	$-0.6813$	$-0.4940$	$-0.2697$	$-0.0288$	$0.0464$	$0.0440$	$0.0423$	$0.0422$	$0.0441$
	${\delta }_1$	$0.0058$	$0.0055$	$0.0051$	$0.0047$	$0.0044$	$0.0014$	$0.0014$	$0.0013$	$0.0012$	$0.0011$
	${\delta }_2$	$0.0859$	$0.0820$	$0.0773$	$0.0722$	$0.0674$	$0.0073$	$0.0069$	$0.0065$	$0.0060$	$0.0056$
	${\delta }_3$	$-0.9658$	$-0.9193$	$-0.8632$	$-0.8028$	$-0.7460$	$0.0426$	$0.0402$	$0.0374$	$0.0346$	$0.0321$
	${\delta }_4$	$-0.1312$	$-0.1266$	$-0.1210$	$-0.1149$	$-0.1089$	$0.0551$	$0.0527$	$0.0498$	$0.0467$	$0.0437$
	${\delta }_5$	$-0.3551$	$-0.3389$	$-0.3192$	$-0.2978$	$-0.2774$	$0.0554$	$0.0529$	$0.0499$	$0.0466$	$0.0434$
	$\theta$	$5.9760$	$5.9797$	$5.9849$	$5.9918$	$6.0001$	$0.2430$	$0.2429$	$0.2428$	$0.2427$	$0.2427$

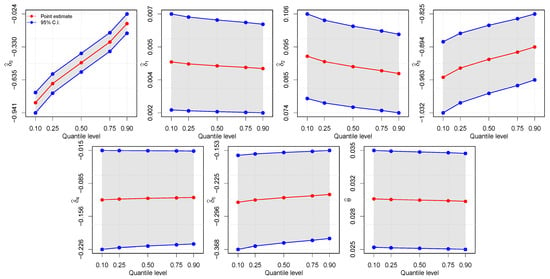
Figure 3. Estimated quantile process plot for ${\delta }_i$, with $i\in \{0,1,2,3,4,5\}$ and $\theta$.

To support this inference, the model’s appropriateness should be stated. With this aim, we provide the QQ plots with envelopes considering the Cox–Snell and quantile residuals in Figure 4, from which we can conclude that the model presented a good fit, since all the observations are inside the simulated envelopes. Furthermore, Table 8 reports the values of the Akaike information criterion (AIC) employed to compare diverse models. We can conclude by this criterion that the quantile regression model considering the VASI distribution was the one that presented the best fit, as it had the smallest value. Note that, when the quantile level increases, the value of the AIC decreases. The largest estimated log-likelihood values have been obtained at $\tau =0.90$, that is, the left skew distribution of the response variable has been captured successfully by this quantile level.

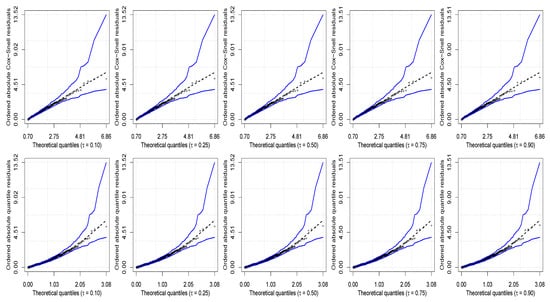
Figure 4. QQ plots with simulated envelopes of Cox–Snell (first row) and normalized quantile (second row) residuals for the listed $\tau$ quantile with fat proportion in the arms.

Table 8. The Akaike information criterion for the body fat proportion data.

	$\mathit{\tau }$ Levels
Model	0.10	0.25	0.50	0.75	0.90
VASI	$-894.6886$	$-895.7425$	$-896.9891$	$-898.2973$	$-899.5114$
ULOG	$-888.4015$	$-888.4015$	$-888.4015$	$-888.4015$	$-888.4015$
JOSB	$-883.9673$	$-883.9673$	$-883.9673$	$-883.9673$	$-883.9673$
KUMA	$-839.6604$	$-842.2240$	$-845.0303$	$-847.6574$	$-849.8131$
UWEI	$-838.1505$	$-839.3637$	$-840.9321$	$-842.7567$	$-844.6025$

ML estimates for the model parameters may be calculated using the vasicekreg package by means of the following R codes:

library(gamlss)

library(vasicekreg)

data(bodyfat, package = “vasicekreg”)

fit <- lapply(c(0.10, 0.25, 0.50, 0.75, 0.90), function(Tau)

{

   tau <<- Tau;

   gamlss(arms ~ age +  sex2 + ipaq1 + ipaq2, data = bodyfat, trace = FALSE,

       family = VASIQ(mu.link = “logit”, sigma.link = “logit”))

})

sapply(fit, coef)

Probit, complement log–log, and cauchit link functions could also be used through the argument mu.link and sigma may be employed depending on covariates through the argument sigma.formula. The vasicekreg package is available online at https://cloud.r-project.org/web/packages/vasicekreg/index.html (accessed on 24 March 2022) and through it we can also consider, beyond quantile regression, mean regression and all the functionality of the gamlss package. For the other fitted models, the corresponding ML estimates were calculated with the unitquantreg package, which is under development and available online at https://github.com/AndrMenezes/unitquantreg (accessed on 24 March 2022).

5.2. The VASI Mean Regression Model

From Section 2, we observe that E$\left(Y\right)=\alpha$, with Y VASI distributed. Hence, we can easily assess the effect of covariates on the mean of the response variable. Thus, in addition to the quantile regression model, we also propose a regression model considering the mean of the VASI distribution. As an alternative to the VASI regression model for the mean, the beta [43] and simplex [44] regression models are also considered.

In what follows, we illustrate the potential of the VASI mean regression model considering a political data set extracted from the baquantreg package of R [45]. The response corresponds to the proportion of votes in the 2014 presidential election in Brazil, obtained by the elected president, Dilma Rousseff, in the Minas Gerais and Piaui states. First, for each state, we considered the Human Development Index (HDI) in 2010, centered at the mean, as covariate and a regression structure given by

$$\mathrm{logit}\left({\alpha }_i\right)={\delta }_0+{\delta }_1{\mathrm{HDI}}_i^{+},\mathrm{for}i\in \{1,\dots ,1065\},$$

(15)

where $n=843\left(222\right)$ for Minas Gerais (Piaui) and ${\mathrm{HDI}}_i^{+}=({\mathrm{HDI}}_i-0.6479)$.

Table 9 reports the ML estimates, estimated SEs, and the values of AIC for the three fitted models. The estimate of ${\delta }_0$ indicates that the logit of the vote proportion for the state of Minas Gerais is $0.6012$ and for the state of Piaui is $0.7885$ when HDI is $0.6479$. Furthermore, since ${\widehat{\delta }}_1$ is obtained as a negative value, there is an opposite linear relation between the vote proportion response and HDI covariate for both Brazilian states. Hence, we can conclude that, when HDI increases, a smaller proportion of votes has been received in both Brazilian states. This fact is more accentuated in the state of Minas Gerais since this value is smaller. The AIC values indicate that the VASI mean regression model is the best when compared to the beta and simplex models.

Table 9. ML estimates (with SEs in parentheses) and AIC values for the vote data.

		Distribution
State	Parameter	VASI	Beta	Simplex
Minas Gerais	$\theta$	$-2.3233$	$-1.1733$	$0.0759$
		$\left(0.0487\right)$	$\left(0.0293\right)$	$\left(0.0244\right)$
	${\delta }_0$	$0.4104$	$0.4079$	$0.4101$
		$\left(0.0180\right)$	$\left(0.0181\right)$	$\left(0.0178\right)$
	${\delta }_1$	$-5.7168$	$-5.6945$	$-5.8076$
		$\left(0.3359\right)$	$\left(0.3403\right)$	$\left(0.3251\right)$
	AIC	$-1252.4860$	$-1248.1210$	$-1250.7680$
Piauí	$\theta$	$-2.9806$	$-1.7376$	$0.0987$
		$\left(0.0949\right)$	$\left(0.0543\right)$	$\left(0.0475\right)$
	${\delta }_0$	$1.3165$	$1.3099$	$1.3468$
		$\left(0.0562\right)$	$\left(0.0544\right)$	$\left(0.0597\right)$
	${\delta }_1$	$-2.9229$	$-3.0062$	$-2.5073$
		$\left(0.6604\right)$	$\left(0.6511\right)$	$\left(0.6691\right)$
	AIC	$-646.7614$	$-646.3025$	$-643.6276$

We also consider a second mean regression structure, where “state” is a covariate, and we insert covariates into the parameter $\theta$, as 

$$\begin{array}{ccc}\hfill \mathrm{logit}\left({\alpha }_i\right)& =& \hfill {\delta }_0+{\delta }_1{\mathrm{state}}_i+{\delta }_2{\mathrm{HDI}}_i^{+},\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \mathrm{logit}\left({\theta }_i\right)& =& \hfill {\beta }_0+{\beta }_1{\mathrm{state}}_i,i\in \{1,\dots ,1065\}.\hfill \end{array}$$

(17)

Table 10 reports the ML estimates, estimated SEs, and the AIC values. The estimate of ${\delta }_0$ indicates that the logit of the proportion of votes is $0.5984$ for the reference state (Minas Gerais) and HDI is centered at its mean value. The estimate of ${\delta }_1$ indicates the variation that occurs in the proportion of votes from the reference state when there is a change of one unit in the HDI. From ${\widehat{\delta }}_2$, we can conclude that the proportion of votes is smaller for larger HDI values. The parameter estimate ${\widehat{\beta }}_0$ indicates the logit of the shape parameter of the distribution for the reference state. The parameter estimate ${\widehat{\beta }}_1$ indicates the variation that occurs in the logit of the shape parameter of the distribution for the reference state. Based on the AIC values, we can conclude that the VASI regression model considering the mean is the best fit to the data, when compared to the beta and simplex models.

Table 10. ML estimates (with SEs in parentheses) and AIC values for the vote data.

	Distribution
Parameter	VASI	Beta	Simplex
${\delta }_0$	$0.3986$ $\left(0.0178\right)$	$0.3954$ $\left(0.0178\right)$	$0.3985$ $\left(0.0178\right)$
${\delta }_1$	$0.7499$ $\left(0.0433\right)$	$0.7617$ $\left(0.0423\right)$	$0.7224$ $\left(0.0461\right)$
${\delta }_2$	$-5.1550$ $\left(0.3038\right)$	$-5.1200$ $\left(0.3032\right)$	$-5.2187$ $\left(0.3057\right)$
${\beta }_0$	$-2.3173$ $\left(0.0489\right)$	$-1.1689$ $\left(0.0294\right)$	$0.0778$ $\left(0.0244\right)$
${\beta }_1$	$0.6194$ $\left(0.1080\right)$	$-0.5481$ $\left(0.0625\right)$	$0.0556$ $\left(0.0542\right)$
AIC	$-1887.1730$	$-1882.9680$	$-1877.7550$

The results displayed in Table 10 can be obtained from R codes as follows:

vasi <- gamlss(percvotes ~ state + hdi, sigma.formula = ~ state,

               data = votesmgpi, family = VASIM(), trace =  FALSE)

beta <- gamlss(percvotes ~ state + hdi, sigma.formula = ~ state,

               data = votesmgpi, family = BE(), trace = FALSE)

simp <- gamlss(percvotes ~ state + hdi, sigma.formula = ~ state,

               data = votesmgpi, family = SIMPLEX(), trace = FALSE)

GAIC(vasi, beta, simp)

    DF    AIC

vasi  5 -1887.173

beta  5 -1882.968

simp  5 -1877.755

Once a VASI model is fitted, it is important to assess its adequacy by examining the residuals. Through the plot function, applied to objects vasi, beta, or simp, we have available four plots for checking the normalized quantile residuals. The four plots are residuals against the fitted values of the parameter $\alpha$, residuals against an index, a kernel density estimate of the residuals, and the QQ plot of the residuals.

6. Concluding Remarks

There are various alternative classes of regression models for proportions and rates. Despite having great flexibility and taking different forms, the Vasicek distribution has been neglected in the analysis of data in the unit interval, both in the presence and in the absence of covariates. In this paper, two regression models considering the Vasicek distribution for response variables restricted to the unit interval were presented. The first one was formulated considering a re-parameterization in the parameter $\alpha$ of the Vasicek distribution. The second one was proposed stating the original parameterization in terms of the distribution mean.

In both models proposed, the covariates were related to the quantile or mean of the response variable by the logit link function. Through a Monte Carlo simulation study, we found that, for both models, the parameters are well estimated in terms of bias and root mean squared error. It was also possible to observe that the coverage probabilities tend towards the nominal confidence coefficient as the sample size increases.

The Vasicek quantile regression model was applied to a real-world data set, in which the response variable was the fat proportion measured in the arms. When compared with another four models existing in the literature, that is, those based on the Johnson SB, Kumaraswamy, and unit-Weibull distributions, the model that best fitted the data was the Vasicek quantile regression, according to the values of the Akaike information criterion.

The Vasicek regression model considering the mean of the response variable was applied to a politics data set and compared with the beta and simplex regression models. The model was built considering covariates in the parameter representing the mean and also in the shape parameter of the distribution. By the criteria considered, the Vasicek regression model offered the best fit to the data. In the end, the results revealed that the Vasicek distribution has great potential for analyzing data restricted to the unit interval in the presence of covariates. The analysis using both regression models (quantile and mean) was facilitated by means of a package made available in the R software, which was implemented by the authors of this paper.