Risk Evaluation: Brief Review and Innovation Model Based on Fuzzy Logic and MCDM

Abstract

The risk assessment of engineering systems represents an important part of the quality of service and dependability. The existing methods for risk evaluation use crisp sets for rating partial indicators’ proposition and their cumulative products as an overall indicator. In this paper, existing FMEA and FMECA methods have been improved using the fuzzy expert system for calculating the risk priority number. The application of fuzzy logic allows the use of linguistic descriptions for risk analysis. In this way, the state of the system in terms of risks and consequences is better described. The settings of the fuzzy systems are based on the application of two multi-criteria decision-making methods. The AHP method was used to define the mutual relationship of the impact of partial indicators (occurrence, severity, and detectability) on risk. In this way, subjectivity in risk assessment is reduced. In the composition of the fuzzy model, the TOPSIS method is introduced to reduce the dissipation of results, which contributes to the accuracy of the outcome. This contributes to the accuracy of the results. The results were verified through a case study of a complex engineering system—bucket-wheel excavators. The risk was observed from the aspect of the danger of damage and the danger of downtime. The initial information for weak points of ES is defined according to historical damage events and statistics of downtime. Expert knowledge was used for weak points grading in the model. Additional model verification was performed using similar methods, using the same input data. The innovative model, presented in the paper, shows that it is possible to correct different weights of risk indicators. The obtained results show less dispersion compared with other existing methods. Weak points with increased risk have been located, and an algorithm has been proposed for risk-based maintenance application and implementation.

1. Introduction

One of the fundamental tasks in the asset management of engineering systems (hereinafter ES) is to develop a risk calculation and prediction model. Assessment of risk level is a significant overall indicator of ES state, an indicator of remaining capabilities of ES, and guideline for risk-based maintenance methodology [1,2,3]. According to standard ISO 31000:2018 [4], risk is defined as the “effect of uncertainty on objectives”. An effect is a deviation from the expected [4]. It can be positive, negative, or both, and can address, create, or result in opportunities and threats. Objectives can have different aspects and categories and can be applied at different levels [4]. Additional important terms in risk are sources, events, consequences, and likelihood [4,5]. Risk management coordinates and controls risk activities with the organizations. Generally, it includes risk assessment, risk treatment, risk acceptance, and risk communications [4,5,6].

According to the same standard, risk assessment is the overall process of risk identification, risk analysis, and risk evaluation [4]. Risk identification has the purpose to find, recognize, and describe risks that might help or prevent an organization from achieving its objectives [4]. The basic questions that are asked when identifying risk are what, where, when why, and how something could happen. It involves the process of finding and categorizing risk elements. Elements can include source or danger, event, consequence, and probability [4]. Risk analysis is a systematic process to understand the risk nature and its characteristics. It involves a detailed consideration of uncertainties, risk sources, consequences, likelihood, events, scenarios, controls, and their effectiveness [4]. The multiple causes and consequences of an event can affect different objectives. Analysis techniques can be qualitative, quantitative, or a combination. It depends on the circumstances and intended use. Highly uncertain events and events with severe consequences can be difficult to quantify. Risk analysis provides input to risk evaluation, to decisions on whether risk needs to be treated and how, and on the most appropriate risk treatment strategy and methods [4]. The purpose of risk evaluation is to support decisions. Risk evaluation involves comparing the results of the risk analysis with the established risk criteria to determine where additional action is required [4,5]. This can lead to a decision to: do nothing further; consider risk treatment options; undertake further analysis to better understand the risk; maintain existing controls; reconsider objectives [4,5].

The most important activity in risk assessment is establishing the level of risk [7]. ES risk assessment is most often performed based on two methods: FMEA (Failure Mode and Effects Analysis) and FMECA (Failure Mode Effects and Criticality Analysis). The methods are defined by the international standard ISO/IEC 31010 [4]. They are based on the risk priority number (hereinafter RPN) concept. RPN is calculated according to the potential causes of failure. It is the evaluation of partial indicators Occurrence (O), Severity (S), and Detectability (D). The probability of occurrence is the possibility that failure will occur [8]. Criticality/severity is a serious measure of the possible consequences of a failure [8]. Detectability is the probability that control could eliminate or locate the defect on time [8]. The RPN number is obtained by multiplying the values of the risk indicators, which are obtained by expert grades on a scale from 1 to 10 (sometimes from 1 to 5). A higher RPN number represents a higher seriousness or risk [9]. For both methods, FMEA and FMECA, the calculation principle is the same. The FMEA method uses data recorded on maintenance analysis sheets and is directed towards reliability. With the FMECA method, there is a difference in the approach that is aimed at the preventive analysis of the problem.

This approach (with cumulative multiplying) to risk assessment was criticized by numerous authors [10,11,12,13,14,15,16,17]. All the mentioned authors record the disadvantages of using the RPN concept. The disadvantages can be reduced to:

• The same RPN results can be observed from different input combinations of partial indicators’ values (S, O, and D). Consider two cases as an example. In the first case, one indicator was ranked as very high, and the other two are at a low level (9 × 2 × 1 = 18). In the second case, all indicators are at the low level (3 × 3 × 2 = 18). Both results are the same. In that case, the high value of the partial indicator (9) will not be recognized as a potential risk event and corrective actions might not be performed;
• The RPN calculation model is sensitive. A small change in one partial indicator can greatly affect other factors and vice versa;
• The same importance is given to all risk indicators. The different impact of partial indicators on risk level is not considered;
• Estimates of partial indicators are subjective. An outcome can be predicted.

The risk assessment model needs a change in the way of partial indicators (hereinafter PI) evaluation and calculation. In that sense, in this article, a new approach in RPN calculation is proposed, which is based on the application of fuzzy logic and two MCDM (Multi-Criteria Decision Making) methods. Fuzzy logic is used in situations where uncertainty and ambiguity dominate and when it is necessary to reduce the impact of subjectivity. Using the fuzzy approach creates the possibility of applying specific linguistic descriptions in the PI evaluation process. Furthermore, the fuzzy proposition of PI loses the linear structure of RPN cumulative multiplication.

According to different authors [18,19,20], the main classification of MCDM is on discrete multi-attribute decision-making (MADM) methods and continuous multi-objective decision-making (MODM) methods. MADM methods are classified as utility methods (SAW/WSM, SMART, SPW/WPM, AHP, ANP, and MACBETH), outranking methods (ELEC-TREE, PROMETHEE, NAIADE, REGIME, ORESTE, COPRAS, and ARAS), compromise methods (TOPSIS, VIKOR, and CP), and other (DEMATEL, FLAG, and SMAA). MODM methods are DEA, LP, NP, MOP, GP, MOORA, and MULTIMOORA. The AHP method is often used to determine the weight of criteria. For the evaluation of potential alternatives, TOPSIS, EDAS, MABAC, COP-RAS, and MAIRCA are most often used.

The MCDM methods that are implemented in the fuzzy model are AHP (Analytical Hierarchy Process) and TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution). The application of the AHP method introduces the rank of PI significance to the comprehensive RPN. The TOPSIS method in the fuzzy composition reduces the subjectivity of the initial expert assessments. All this brings quality to the expert model.

The AHP method is in a group of discrete MADM methods for utilization and criteria ranking. The application is simple, at the level of expert assessments based on experience, it is suitable for the problem that is analysed in the paper. The mutual ranking of partial indicators is the initial part of the model, and in that way, their influence on the overall risk is determined. The method is based on a pair-wise comparison of all the parameters. The output values of the method are in the range from 0 to 1, where the sum is 1. This is suitable for the following steps in the model. An important advantage in selecting this method is the ability to check the consistency of the decision maker. Inconsistency is easily noticed and the growing problems in the following steps of the model are prevented.

The TOPSIS method enables the definition of preferences in the criteria. It is based on the mutual analysis of the data achieved by the alternatives according to the criteria, taking into account the orientation. The model relies on a presented data comparison with the best from the group. The best result is the one that is closest to the ideal, which is important in terms of such as risk.

In general, the consequences of risk in ES can be observed from several aspects:

• Risk to structural stability—design errors, insufficient maintenance, or ES management errors can cause catastrophic damage with total damage [21,22,23,24,25];
• Risk of interruption of the production process—downtime of ES causes losses in planned production [26,27];
• Risk to the work environment—ES users may be exposed to various adverse health effects. First of all, influence means noise and vibration [28]; electromagnetic emission and radiation [29]; extreme temperatures and other climatic factors [30]; dust [31]; chemical and other hazardous substances [32]; open flame [33]; rotating and other parts with high inertia [22]; height works [34]; and others;
• Environmental risks—there are distinguished direct and indirect impacts. Direct effects on soil degradation and pollution, contamination of surface and groundwater, air pollution, and other similar impacts. Indirect impacts are consumption of electricity and/or heat energy obtained from conventional sources, consumption of various resources and materials for the production of ES, etc.

The paper considers two risk segments. The first is the risk to the structural stability of the machine, i.e., the risk of damage. The second risk is the interruption of the production process, i.e., the risk of downtime. These two risks are dominant in ES. The remaining two are indirectly expressed and are not analysed in this paper.

A bucket-wheel excavator operating on an open-cast coal mine was chosen to present and verify the new risk assessment model. These are machines that carry great risk in their operation. The investment is large, and the operating costs are high. The price of machines correlates with weight. For machines around 3000 tons, it amounts to over EUR 25 million. The operation and maintenance are complex and induce high costs. In the continuous system of operation, they are 24 h/day, under the pressure of achieving performance, the indirect costs of unplanned downtime are high.

Verification of the results is performed by comparative analysis with other existing methods. The same input data is used. Checking the influence of the weights of the partial indicators is performed on models that do not have an integrated AHP method. The dispersion of the results is checked on models that have MAX–MIN or MIN–MAX composition instead of the innovative approach in this paper with the proposed TOPSIS method in composition. The level of result dispersion is an important segment in risk evaluation. The obtained results should indicate the priorities in maintaining the ES, which introduces the concept of risk-based maintenance.

This paper is structured in the following way: (i) literature overview with critical opinion according to current risk assessment models; (ii) risk theory and weak points analyses of ES; (iii) development of innovative risk assessment model, describing the algorithm; (iv) case study, verification of the model; (v) comparison with appropriate risk assessment models. Model (iii) is based on fuzzy expert concepts, with two-step expertise judgment and specific composition. In this way, greater objectivity of ex-pert judgment and accuracy of final risk mark were obtained.

2. Literature Review

Risk analysis using existing methods allows the assessment of ES at different stages of the lifetime (engineering and design, production, maintenance, etc.) in the event of the occurrence of various problems (downtime, failure, potential accidents, etc.) [35]. The following is a review of the literature focused on the FMEA and FMECA methods, implementing fuzzy sets and MCDM methods in risk management, etc.

FMEA method is a widely used quality improvement tool to identify potential failure modes and to rate the reliability of a product or a process [36]. The FMECA method is aimed at a preventive approach to problem analysis. It is based on the optimization of design, production processes, and maintenance through re-engineering to improve the situation and eliminate all known and potential problems [35]. Risk in the field of mining machinery has not been sufficiently analysed in the professional literature. There are several papers published in this field [27,35,37]. Kumar and Srivastava in the paper [37] define quality maintenance of technical systems through reliability. The authors note a more comprehensive approach to maintenance in the form of TPQM (Total Planned Quality Maintenance), which includes preventive, predictive, and planned maintenance activities. Functional analysis of the excavator, its assemblies, and sub-assemblies was performed. The methodology is based on FMECA, FMEA, and CBM (Condition Based Maintenance) that predict failure or deterioration of excavator components [37]. The same authors [35] present the possibility of applying the FMEA and FMECA methods for the analysis of the causes and consequences of excavator procedures. Both methods on 5 different excavators of the same category were used for the case study. For locations with located risk, RPN was calculated, and causes, consequences, preventive and corrective measures were defined. They then recalculated the performance of the RPN in case all the recommendations obtained from the previous analysis were followed. The new RPN value is significantly reduced compared with the initial one. Pantelic, Bosnjak, et al. [27] use the S-FMECA model as one of the basic analytical tools for the creation of maintenance concepts. The data were obtained based on monitoring the operation of the machine in the time interval. Equations for numerical calculation are set for O and S, while D is based on a linguistic description. Based on the analysis, they located the highest risk of downtime from the mechanical aspect on the crawler of the excavator and the return drum of the conveyor three. From the electrical aspect, the highest risk of downtime is due to the failure of the high-voltage power cable.

Existing risk assessment methods based on the RPN concept within the FMEA and FMECA methods have many shortcomings that have been previously presented. For these reasons, in the recent literature, clear efforts, which were conducted to overcome the shortcomings of this method, can be seen.

2.1. Implementing the Fuzzy Theory to RPN

The authors Wang et al. [38] applied the fuzzy sets for the safety analysis of complex ES. They propose the structural decomposition of complex ES into hierarchical levels. For failure description, they used fuzzy logic and evidential reasoning to determine the functionality of the system. Bowles and Pelaez [39] described and applied the model with the implementation of the fuzzy logic approach in the FMEA method. The linguistic terms were used to describe risk partial indicators: occurrence, severity, and detectability. Based on expert knowledge of the ES, they formed an if-then base of fuzzy rules for correlation between partial indicators. Since the base of if-then fuzzy rules can be quite extensive, a few papers that give measures to reduce the volume of fuzzy rule bases can be found in the literature. Pillay and Wang [10] have suggested indicators grading based on linguistic description instead of grading from 1 to 10. The model consists of two parts. The first process is failure screening with a formal risk assessment (relative ranking). The second process is hazard assessment that uses linguistic variables. By combining the existing 125 rules, their number was reduced to 35. Gargama and Chaturvedi [40] suggested a fuzzy FMEA model for analysing the risk of failure based on the degree of identity and fuzzy rule base that was reduced from the initial 125 to 14 rules. The proposed model includes the normalization of fuzzy numbers. Wang et al. [13] believe that it is not appropriate to apply a shortening of the fuzzy rules base. They propose the implementation of a fuzzy weighted geometric mean for the assessment of risk level. Braglia et al. [11] suggested using the normalized RPN values in the risk function, where normalized RPN values represent a value of RPN/1000. Łapczyńska and Burduk [41] apply the fuzzy FMEA (fFMEA) method in the automotive industry where quality control is conducted. Rafie and Namin [36] also use the combined FMEA method to assess land sinking due to the construction of subways in urban areas. Partial indicators O, S, and D are obtained through fuzzy and neuro systems. Petrović et al. [17] presented a model for the risk assessment of machine failure in mining. The proposed model is based on the application of fuzzy logic and implementing the MIN–MAX fuzzy composition. The partial indicators of RPN are given in the linguistic form. The mentioned authors also applied traditional risk calculation according to the RPN concept, after which they conclude all advantages of the proposed new model. For risk management purposes in the mechanization of underground mines, Balaraju, Raj and Murthy [42] used the fuzzy-FMEA method. In total, 16 potential risks of failure of subsystems (highest risk of the electrical subsystem) have been located. The authors also performed a comparative analysis with traditional RPN calculations. Das et al. [43] analyse the problem of scheduling and routing ships to reduce overall costs and transport interruptions. The analysis was conducted according to risks where imprecise cost parameters were treated as a triangular fuzzy set. The modified genetic algorithm (MGA) method was developed. The results show better quality than others heuristic algorithms. A modified fuzzy risk assessment model has also been used in the field of infrastructure analysis [44]. The same approach was suggested by Xu et al. [45] in the working analysis of engine systems and by Sadiq and Husain [46] in environmental risk analysis of drilling time loss during a drilling operation. Kushwaha et al. [47] suggest an integrated framework based on IF techniques to reduce the subjectivity and hesitation of experts from the FMEA team. In the first part of the model, the IF-FMEA approach was used. The expert knowledge according to a linguistic scale of risk indicators (O, S, and D) was applied. Critical causes were identified based on fuzzy RPN results. In the second part, IF-TOPSIS was implemented. Both parts are compared in the fuzzy approach. The case study was conducted on the example of the sugar industry in India. The adopted fuzzy logic model was used by Guimara and Lapa [48] to improve risk assessment in the inlet water system of a reserved steam boiler of a nuclear power plant.

2.2. Implementing the MCDM and Other Methods to RPN

Zammori and Gabbrielli [49] have introduced an approach called an analytic network process (ANP/RPN), which represents a modified version of FMECA, considering the possible interactions between the main causes of failure in the evaluation of the criticality of failure. Liu et al. [50] applied the VIKOR method to analyse the ranking of the failure mode according to the FMEA method. In this approach, linguistic variables were used to estimate the rating and weight for risk factors S, O, and D. The extended VIKOR method was used to determine the priority of the risks of the failures. The risk assessment model based on the combination of fuzzy-TOPSIS methods was used by the authors Khodadadi-Karimvand and Shirouyehzad [51]. The TOPSIS method was used to rank the indicators, while the fuzzy logic background was used for the calculation. The case study was performed on the example of drilling operations for gas and oil wells. MCDM methods for risk analysis have been applied in the field of finance and investment in mutual funds [52]. In the first step of the model, the DEA method is used to analyse the efficiency of assets, while the MABAC method is used to rank the risk and return parameters. In the second step, the entropy method is used, where weights are calculated. A case study was conducted in India.

Bevilacqua et al. [53] developed a risk assessment methodology based on a combination of FMECA and Monte Carlo simulations. In this paper, a new method of computing RPN is proposed, where the sum of weighted values of six indicators (safety, machine importance for the process, maintenance costs, frequency of failure, downtime, and machine operating conditions) was multiplied with the seventh indicator (difficult access to the machine) to obtain the RPN value. Rhee and Ishii [54] proposed a similar methodology. They presented an FMEA model that, with the help of Monte Carlo simulation, enables the estimation of the risk level from the aspect of costs over the lifetime of the system. An, Mikhaylov and Jung [55] analyse the problems in an airline, i.e., risk in network revenue management. A model based on the criterion of minimum regret is proposed. A heuristic-based approach on a genetic algorithm to define the booking limits has been developed to minimize regret. Chin et al. [56] developed a risk model using a grouped ER approach involving risk assessment. Factors using belief structures synthesize individual belief structures into group trust structures and rank expected risk results using the minimax regret approach (MRA). Risk analysis in energy is a popular topic and is of great importance, especially when it comes to the security of supply and safety through the use of nuclear, thermal, or renewable sources [57,58,59].

To reduce subjectivity, different authors have introduced linguistic variables for risk description in general and the fuzzy inference model for the composition of risk parameters. However, it has not been observed that motivation has been found for the development of the model that reduces the dissipation of results in phenomena such as risk.

3. Materials and Methods

The improved risk assessment model retains the traditional structure of partial indicators S, O, and D but with an innovative system of their evaluation and synthesis. The risk assessment model is based on the application of the fuzzy theory in combination with the MCDM. The goal of the innovative model is to reduce the subjectivity of the expert model by introducing PI ranking; to reduce the dispersion of outcomes, i.e., to increase the accuracy of the final risk assessment; to define a risk assessment algorithm. The model algorithm is presented in Figure 1.

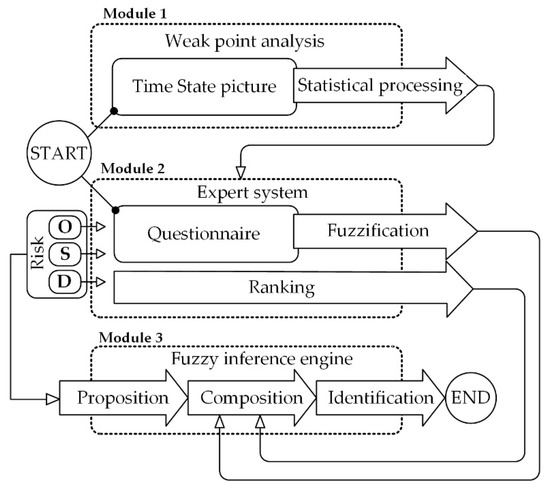
Figure 1. Structural algorithm of the model.

The model consists of three parts (Figure 1):

• Module 1, deep analyses of an engineering system (ES), with the aim of statistical processing of recorded data on behaviour primarily based on damages that have occurred, time state picture, reliability, and availability. Output from module 1 is a weak point list (hereinafter WP) on ES for which further risk evaluation is done;
• Module 2, experts’ judgment of PI and their mutual ranking. Output from Module 2 is a PI assessment for each WP in fuzzy number form and rank of PI impact on risk;
• Module 3 is a model of the fuzzy logical conclusion, which uses TOPSIS preferences in defining the outcome of fuzzy composition where fuzzy relationships are previously weighted based on AHP rank. Output from Module 3 is a risk assessment for each WP.

The theoretical explanation of certain specific parts of the model is provided below.

3.1. Fuzzy Proposition

To present estimates that contain linguistic values, the fuzzy proposition procedure is used. The fuzzy proposition is the process of perceiving reality in such a way that it can be presented in an analytical form, i.e., in numerical form. Fuzzy proposition belongs to the domain of artificial intelligence.

Five linguistic variables are introduced for each PI and risk as an overall indicator, which is defined in the coordinate system of the membership function (µ) and the class as the representative of the unit of indicator measure (j = 1 to 10) [60,61,62]. Linguistic variables are presented as fuzzy sets. Fuzzy sets are in a trapezoidal shape. This shape is applied for the linguistic variables for which there is no clear and precise difference between the fuzzy terms [17,63]. The linguistic variable (LV) is in the following form:

$$LV=\left\{\mu (j=1), \mu (j=1), \dots , \mu (j=10)\right\}$$

(1)

All the linguistic variables are defined in the following way, which is also presented in Figure 2.

$$\begin{array}{l}‘A’=\left\{0\left(1\right), \dots , 0\left(8\right), 1\left(9\right), 1\left(10\right)\right\};\\ ‘B’=\left\{0\left(1\right), \dots , 0\left(5\right), 0.33\left(6\right), 1\left(7\right), 1\left(8\right), 0\left(9\right), 0\left(10\right)\right\};\\ ‘C’=\left\{0\left(1\right), \dots , 0.5\left(4\right), 1\left(5\right), 1\left(6\right), 0.5\left(7\right), 0\left(8\right), 0\left(9\right), 0\left(10\right)\right\};\\ ‘D’=\left\{0\left(1\right), 0\left(2\right), 1\left(3\right), 1\left(4\right), 0.33\left(5\right), 0\left(6\right), \dots , 0\left(10\right)\right\};\\ ‘E’=\left\{1\left(1\right), 1\left(2\right), 0\left(3\right), \dots , 0\left(10\right)\right\};\end{array}$$

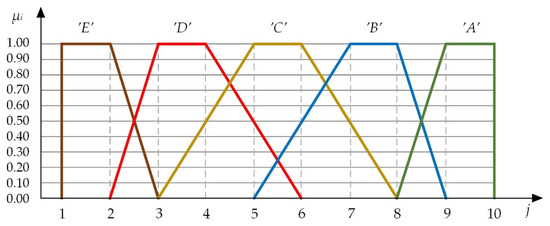
Figure 2. Dependence of linguistic variables and membership function, the general form.

The partial indicators are described according to the linguistic variable. The linguistic description helps experts in assigning grades. The descriptions are given in Table 1.

Table 1. The linguistic descriptions of partial indicators grade.

Grade	Keyword	Risk of Damage	Risk of Downtime
Occurrence
AO1, AO2	Extremely	Damage is expected	The same working and downtime
BO1, BO2	Probably	High probability of damage	Failures are frequent and repeated
CO1, CO2	Moderate	Damage is possible	Occasionally there is a failure
DO1, DO2	Rarely	Low probability of damage	Failures are not frequent
EO1, EO2	Slightly	There is no danger of damage	Failures are very rare
Severity
AS1, AS2	Extremely	ES stability endangered	Long delay, great repairs needed
BS1, BS2	Serious	Great ES disturbance	Serious defect, frequent downtime
CS1, CS2	Moderate	Potential uncertainty present	The failure can be repaired
DS1, DS2	Light	Slight disturbance	Minor ES failure, short downtime
ES1, ES2	Very low	The ES is not endangered	Working without downtime
Detectability
AD1, AD2	Impossible	Damage detection is not possible	Failure cannot be prevented
BD1, BD2	Slightly	Damage detection is complex	Low failure recognition capability
CD1, CD2	Moderate	There is a chance to locate the problem	There is a chance to locate the failure
DD1, DD2	Possible	The risky damage is easily located	A failure is visible
ED1, ED2	Obviously	Damages can be prevented	The downtime is predictable

3.2. AHP Method—PI Ranking

Multi-criteria decision-making (hereinafter MCDM) methods are used for evaluation or selection among multiple alternatives. Analysis of the parameters that by their nature are not mutually comparable is possible with these methods in which basis is a simple mathematical tool [64]. Among the other MCDM methods, AHP is the most used method [65]. This method decomposes the problem into elementary components, which then can be compared in pairs. Input data in this model can be in the form of either quantitative or qualitative. Inconsistency checks of the decision maker in assigning values of the relative importance could be calculated, which is an additional advantage of this method [66].

The first step in this method is the mutual comparison of two alternatives in each interaction. For that purpose, the Saaty scale of relative importance is used (Table 2) [67,68].

Table 2. AHP scale.

The Level of Importance	Numerical Value	Reciprocal Value
Extreme importance	9	1/9 (0.111)
Very strong to extreme importance	8	1/8 (0.125)
Very strong importance	7	1/7 (0.143)
Strong to very strong importance	6	1/6 (0.167)
Strong importance	5	1/5 (0.200)
Moderate to strong importance	4	1/4 (0.250)
Moderate importance	3	1/3 (0.333)
Equal to moderate importance	2	1/2 (0.500)
Equal importance	1	1 (1.000)

The result of the pair-wise comparison of the elements is the priority vector (w_i) [68]. The numerical value of the priority vector is used to form matrix M(m × n) (2) in which n is the number of considered criteria and a_ij is the relative comparison measure of w_i/w_j while i, j = 1, …, n. [69,70,71].

$$M=\left[\begin{array}{cccc}{w}_1/w_1& w_1/w_2& \dots & w_1/w_j\\ w_2/w_1& w_2/w_2& \dots & w_2/w_j\\ \dots & \dots & \dots & \dots \\ w_i/w_1& w_i/w_2& \dots & w_i/w_j\end{array}\right]=\left[\begin{array}{cccc}1& a_{12}& \dots & a_{1j}\\ a_{21}& 1& \dots & a_{2j}\\ \dots & \dots & \dots & \dots \\ a_{i1}& a_{i2}& \dots & 1\end{array}\right]$$

(2)

By calculating the matrix, the result of the AHP method was obtained for alternatives ranking according to given parameters and sub-parameters. The output value is defined as a weight coefficient of different PI (W_O, W_S, W_D). The final step in the AHP method is the consistency check [72]. This is achieved by calculating the value consistency index (CI) and the random consistency index (CR). To fulfil a condition of consistency, the value (CR) must be less than 0.1. In other cases (CR > 0.1), it is necessary to determine the reasons for inconsistency (usually to repeat the pair-wise comparisons) [64,70]. For calculation values of (CI) and (CR), Equations (3) and (4) are used:

$$CI=\frac{({\lambda }_{\max }-n)}{(n-1)},$$

(3)

where λ_max is the weighted mean of coefficient λ_i calculated by Equation (5); n is the number of compared elements [60].

$${\lambda }_{\max }=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\lambda }_i}$$

(4)

$${\lambda }_i=\frac{{\displaystyle \sum _{j=1}^n(a_{ij}\cdot W_i)}}{W_i}$$

(5)

Follows,

$$CR=\frac{CI}{RI},$$

(6)

where RI is the random index which depends on the number of compared elements (n) and it is shown in Table 3 [60].

Table 3. The random index values depending on number of elements (n).

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RI	0.0	0.0	0.58	0.89	1.12	1.24	1.32	1.41	1.45	1.49	1.51	1.48	1.56	1.57	1.59

3.3. Composition—TOPSIS Method

Fuzzy composition (product) is a procedure of synthesising two or more fuzzy relations into one overall. Fuzzy relations in this case represent PI provided in the form of fuzzy numbers. Fuzzy composition is in general a screening model. The product may or may not have a commutation property [63]. In that sense, the order of product members may but may not be defined. Depending on the desired function of the goal, the result (outcome) of the composition is defined. Basically, “IF-THEN” logical operators are used, i.e., derived application models MAX–MIN and MIN–MAX [38,60,73,74]. The MAX–MIN composition is called a pessimistic composition [60]. In this composition, the best possible solution is found from the set of the worst combinations of outcomes. The opposite is the MIN–MAX composition, called optimistic. From the best possible outcomes, the worst is found [60]. In the first, the goal function is oriented towards phenomena such as safety or dependability, while the second is used for risk-oriented phenomena [60]. The paper introduces an innovative composition model where the TOPSIS method is used. The goal is a concentration of screening model.

The basic principle of the method is to compare the considered alternatives with the best within the defined parameter. The TOPSIS method is based on the choice of the alternative that has the shortest “distance” from the ideal solution, i.e., the longest to the anti-ideal solution [75]. The ideal positive solution is formed of all the best values that can be obtained from the considered criteria. In contrast, the negative ideal solution is formed from all the lowest values [76].

The TOPSIS method starts with the forming of a matrix M (7) consisting of m alternatives and n criteria [69]:

$$M_{m\times n}=\left[\begin{array}{llllll}{x}_{11}\hfill & x_{12}\hfill & \cdots \hfill & x_{1j}\hfill & \cdots \hfill & x_{1n}\hfill \\ x_{21}\hfill & x_{22}\hfill & \cdots \hfill & x_{2j}\hfill & \cdots \hfill & x_{2n}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{i1}\hfill & x_{i2}\hfill & \cdots \hfill & x_{ij}\hfill & \cdots \hfill & x_{in}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill \\ x_{m1}\hfill & x_{m2}\hfill & \cdots \hfill & x_{mj}\hfill & \cdots \hfill & x_{mn}\hfill \end{array}\right]$$

(7)

where x_ij (for i = 1, 2… m; j = 1, 2… n) represents the value of i-th alternative toward j-th criterion.

In the next step, the matrix (8) is normalized (r_ij) and then (9) multiplied (p_ij) by the weight coefficients of the parameters obtained by the AHP method (W_i = W_O, W_S, W_D).

$$r_{ij}=\frac{x_{ij}}{\sqrt{{\displaystyle \sum _{i=1}^m{x}_{ij}^2}}}i=1,\dots , m;j=1,\dots , n$$

(8)

$$p_{ij}=W_i\cdot r_{ij},i=1,\dots , m;j=1,\dots , n;$$

(9)

Follows creation an ideal (A⁺) and anti-ideal (A⁻) solution, Equations (10) and (11). Only different values from zero are taken into account in the composition [77]. The next step is calculating the distance of each alternative from the ideal solution (Si ⁺, Si ⁻) through Equations (12) and (13) [76,78]:

$$A^{+}=\left(\begin{array}{c}MAX\\ i\ne 0\end{array}{p}_{ij}|j\in J^{\prime }\right),\left(\begin{array}{c}MIN\\ i\ne 0\end{array}{p}_{ij}|j\in J^{″}\right)=\left\{p_1,p_2,\dots ,p_j\dots ,p_n\right\}$$

(10)

$$A^{-}=\left(\begin{array}{c}MIN\\ i\ne 0\end{array}{p}_{ij}|j\in J^{\prime }\right),\left(\begin{array}{c}MAX\\ i\ne 0\end{array}{p}_{ij}|j\in J^{″}\right)=\left\{p_1,p_2,\dots ,p_j\dots ,p_n\right\}$$

(11)

where J′ and J″ are associated with beneficial and non-beneficial attributes.

$$S{i}^{+}=\sqrt{{\displaystyle \sum _{j=1}^n{(p_{ij}-p_j{}^{+})}^2}}$$

(12)

$$S{i}^{-}=\sqrt{{\displaystyle \sum _{j=1}^n{(p_{ij}-p_j{}^{-})}^2}}$$

(13)

The final step in composition is to calculate the relative closeness of the alternative to the ideal solution,

$${\mu }_i=\frac{S_i{}^{-}}{S_i{}^{-}+S_i{}^{+}},\hspace{1em}0\le {\mu }_i\le 1$$

(14)

The rank value of µ_i arranged in descending order (from highest to lowest value) corresponds to the rank of alternatives A_i (from the best to the worst) [69,76,78]. The output shape of risk assessment after TOPSIS fuzzy composition:

$$R=\mu \left(j=1\right),\mu \left(j=2\right),\dots ,\mu \left(j=10\right)$$

(15)

3.4. Identification

The identification process aims to map form (15) into a form where the dependence is given according to the fuzzy sets ‘A’…‘E’.

$$RPN=\mu \left(‘A’\right),\mu \left(‘B’\right),\dots ,\mu \left(‘E’\right)$$

(16)

The identification method that is used in the paper is the best fit [60]. This approach maps the membership functions to classes (14) in the membership function of the fuzzy sets (1). The relative distance d between the membership functions of the result (14) and the fuzzy number defined by the linguistic variable ‘A’, …, ‘E’ [60] is calculated. The following form applies to each linguistic variables’ ‘A’, …, ‘E’:

$$d_{‘A’(R,‘A’)}=\sqrt{{{\displaystyle \sum {}_{j=1}^{j=10}\left({\mu }_R^j-{\mu }_{‘A’}^j\right)}}^2}\dots d_{‘E’(R,‘E’)}=\sqrt{{{\displaystyle \sum {}_{j=1}^{j=10}\left({\mu }_R^j-{\mu }_{‘E’}^j\right)}}^2}$$

(17)

where: μ_R(j) is output from (14) and μ_{‘A’(j)…‘E’(j)} is according to (1).

In the next step, among the values d_{‘A’…‘E’}, the minimum value is selected d_min. The nearer RPN is to the certain linguistic variable, the lower d_min is. Gap d_min is equal to zero if RPN is just the same as the certain expression in terms of the membership functions [63]. For that purpose, RPN should not at all be evaluated to other expressions due to the exclusiveness of these expressions.

Based on the ratio d_min/d_{‘A’,…‘E’} finally gets the membership function that appears in the Equation for RPN (16):

$${\mu }_{RPN(‘A’)}=\frac{d_{\min }}{d_{‘A’}\cdot \left(\frac{d_{\min }}{d_{‘A’}}+\dots +\frac{d_{\min }}{d_{‘E’}}\right)}\dots {\mu }_{RPN(‘E’)}=\frac{d_{\min }}{d_{‘E’}\cdot \left(\frac{d_{\min }}{d_{‘A’}}+\dots +\frac{d_{\min }}{d_{‘E’}}\right)}$$

(18)

The values of µ_RPN in the model are calculated for all grades ‘A’ to ‘E’, which is the input value for the process of defuzzification and determination of the dissipation measure.

Each μ_{RPN (‘A’, …, ‘E’)} represents the extent to which RPN belongs to the defined risk fuzzy sets expressions (1). It can be noted that if RPN completely belongs to a certain expression, then μ_{RPN(‘A’, …, ‘E’)} is equal to 1 and the others are equal to 0 [63]. Thus, μ_{RPN (‘A’, …, ‘E’)} could be viewed as a degree of confidence that RPN belongs to the certain risk expressions defined to the procedure of proposition (Section 3.1).

Depending on the input parameters and the identification process, the risk value can be interpreted as ‘A’—very high risk, ‘B’—high risk, ‘C’—average risk, ‘D’—low risk, and ‘E’—very low risk.

3.5. Defuzzification

The fuzzy number is converted into a real number by the process of defuzzification. The output values of the identification procedure are arranged according to the grades (µ_i = ‘A’, ‘B’, ‘C’, ‘D’, and ‘E’). These values are combined into a final assessment that becomes comparative. The method of defuzzification that is used in this paper is the centre of mass (Z_n) method [13,39,79]. The grade ‘A’ is assigned a value of C_i = 5. The remaining grades fall until grade ‘E’, which gets a value of C_i = 1 [80]. The value (Z_n) is obtained according to the Equation (19):

$$Z_n=\frac{{\displaystyle \sum {}_{i=1}^j{\mu }_i\cdot C_i}}{{\displaystyle \sum {}_{i=1}^j{\mu }_i}}$$

(19)

A standard deviation is used to determine the scatter around the value obtained [81]. The Equation for the standard deviation has the form (20):

$$S_n=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^{i=N}{\left({\mu }_i-{\mu }_{sr}\right)}^2}}{N-1}}$$

(20)

Considering the calculation from Equations (19) and (20), the risk assessment can be expressed in the form:

$$RPN=Z_n, S_n$$

(21)

where Z_n = 1… 5 and S_n = 0… 1.

4. Results of the Case Study: Bucket-Wheel Excavator

The bucket-wheel excavator SRs2000, operating on the open-cast lignite mine, was used as the subject of analysis in the case study. The selection of this excavator was made based on the complexity of the ES, the availability of data, and a large number of the same excavators worldwide. The total number of excavators of this type in the world is 57. In general, a bucket-wheel excavator (BWE) is, together with a belt conveyor and spreader, part of continuous ES. From the aspect of reliability, these machines are in a connection in series. The downtime of one of the machines induces a downtime of the entire ES. BWEs are the initial and most responsible segment. It is designed to work in changing operating and climatic conditions. It is a complex ES composed of a large number of partial subsystems.

4.1. Module 1—Weak Point Analysis

An analysis of the background of serious failures (damages) and excavator downtimes was performed [23,24,25]. From the aspect of accident risk, four weak points are located that are characteristic for this type of excavator (Figure 3):

Figure 3. Weak points according to damage risk.

• First point (P1.1)—rope wheel in the hoisting system. If the initial cracks in the rope wheel are not noticed in time, the rope may break, and the excavator may collapse. The causes are most often a bad technical solution (fabrication of segments by bending and welding) or excessive wear of the grooves;
• Second point (P1.2)—bucket-wheel head. Problems that occurred were: fracture of the rotor wheel shaft, damage to the small diaphragm assembly, longitudinal cracks on the hollow shaft, fracture of 10 of the 12 screws on the diaphragm, damage to the support, etc. These problems can cause catastrophic damage to the excavator. Similar problems occurred at several excavators of the open-cast mines in Serbia;
• Third point (P1.3)—support to A mast. The structural disadvantage of this excavator was due to water retention in the A-mast. The water caused corrosion and was frozen in the winter. There was a crack in the mast under the tension link;
• Fourth point (P1.4)—slewing platform. Deformation (bulging of the plate) of the vertical mast/cylinder of the upper slewing platform was observed on several excavators of this type in Serbia and the surrounding area. A turntable is a central, carrying part of the excavator. It carries a bucket-wheel boom, a central pillar, and a counterweight boom. The cracking of a vertical mast can cause catastrophic damage or collapse of the excavator.

Weak points according to the risk of failure are defined based on statistical processing of data on machine failures. Downtimes induce high costs. Indirect costs are then often higher than direct ones. Analyses show that the indirect cost per hour of bucket-wheel excavator downtime can be up to EUR 15,000 [26,27].

Based on the insight into the data on the recorded sheets of malfunctions/failures, statistical processing was performed. All failures are qualified in categories. The analysis showed that 77.68% of interventions were caused at six weak points. Due to the complexity of the number of statistics data, only the percentage distribution is shown in Figure 4. The highest percentage of interventions are on bucket-wheel elements at 24.31%, followed by the conveyor drive system at 19.79%, crawler dive system at 14.51%, slewing drive system at 8.61%, digging drive system at 7.80%, and hoisting drive system at 2.66%. The number of interventions does not always have to correlate with the severity of the failure and the downtime. These six weak points are adopted as a starting point for further analysis of the risk of downtime.

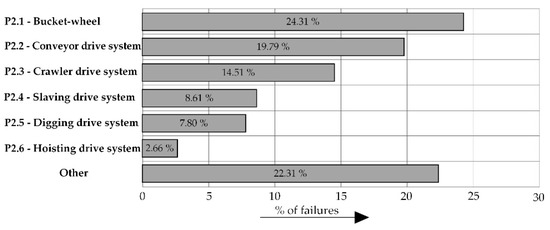
Figure 4. Distribution of failures.

4.2. Module 2 Expert System

The expert system contains a collection of initial information about O, S, and D using expertise judgments. The expert system is presented through the assessment phase and the ranking phase. Expert opinions were obtained from engineers and supervisory and technical staff dealing with the maintenance of the considered machines. Due to the complexity of the calculation, a detailed overview of the module is provided for the first located point of risk of damage P1.1 (rope wheel in the hoisting system) for which the risk performance is calculated. For the remaining weak points of the risk of damage and the risk of downtime in the analysis, only the input data and the result are presented.

4.2.1. Input Data—Questionnaire

For each of the defined subjects of analysis, it is necessary to perform an expert evaluation. Five experts assigned grades for each segment of the analysis. For each of the partial risk indicators (O, S, and D), values were assigned based on the ratings (‘A’, ‘B’, ‘C’, ‘D’, and ‘E’, where the rating with the highest risk is ‘A’, while the lowest risk is ‘E’). Grades were assigned based on the linguistic description provided in Section 3.1. The sum of assigned grades according to the partial indicator must be 100%. Table 4 shows the values of the assigned grades for P1.1. The last part of the table shows the mean values of the grades that represent the input to the next part of the model.

Table 4. Results of a questionnaire for P1.1.

Expert No.	PI	‘A’	‘B’	‘C’	‘D’	‘E’
1.	O				0.9	0.1
	S	0.8	0.2
	D			0.6	0.4
2.	O			0.3	0.7
	S	0.5	0.5
	D				0.3	0.7
3.	O				0.7	0.3
	S	0.4	0.6
	D				0.8	0.2
4.	O			0.5	0.5
	S		0.8	0.2
	D				1.0
5.	O				0.6	0.4
	S	0.4	0.6
	D			0.6	0.4
Average	O	0	0	0.16	0.68	0.16
	S	0.42	0.54	0.04	0	0
	D	0	0	0.24	0.58	0.18

It can be seen from Table 4 that for the O indicator, the first expert assigned 90% for grade ‘D’ and 10% for grade ‘E’. For indicator S, he assigned 80% for grade ‘A’ and 20% for ‘B’, while according to indicator D, he assigned 60% and 40% to grades ‘C’ and ‘D’, respectively. Below, an example of calculating the average grade according to the O indicator is given. Grades ‘A’ and ‘B’ were not awarded by an expert. Two experts gave a grade of ‘C’, all five a grade of ‘D’, and three a grade of ‘E’. The average grades are:

$$\begin{gathered} ‘C’=\frac{\left(0+0.3+0+0.5+0\right)}{5}=0.16 \\ ‘D’=\frac{\left(0.9+0.7+0.7+0.5+0.6\right)}{5}=0.68 \\ ‘E’=\frac{\left(0.1+0+0.3+0+0.4\right)}{5}=0.16 \end{gathered}$$

The average grades for P1.1 for indicators O, S, and D have the following form:

$$\begin{gathered} O_{P1.1}=\left(0/‘A’, 0/‘B’, 0.16/‘C’, 0.68/‘D’, 0.16/‘E’\right) \\ {S}_{P1.1}=\left(0.42/‘A’, 0.54/‘B’, 0.04/‘C’, 0/‘D’, 0/‘E’\right) \\ {D}_{P1.1}=\left(0/‘A’, 0/‘B’, 0.24/‘C’, 0.58/‘D’, 0.18/‘E’\right) \end{gathered}$$

For the remaining P1.2–P2.6 analyses, only calculated mean grades are displayed. An overview of the input data to the partial models is provided in Table 5.

Table 5. Input data for all segments of the analysis.

WP	PI	‘A’	‘B’	‘C’	‘D’	‘E’	WP	PI	‘A’	‘B’	‘C’	‘D’	‘E’
P1.1	O	0	0	0.16	0.68	0.16	P2.2	O	0.22	0.62	0.16	0	0
	S	0.42	0.54	0.04	0	0		S	0	0.26	0.34	0.40	0
	D	0	0	0.24	0.58	0.18		D	0	0	0.06	0.54	0.40
P1.2	O	0	0.36	0.64	0	0	P2.3	O	0	0.06	0.34	0.46	0.14
	S	0.18	0.78	0.04	0	0		S	0	0.20	0.28	0.32	0.20
	D	0	0	0.28	0.66	0.06		D	0.54	0.46	0	0	0
P1.3	O	0	0	0.02	0.58	0.40	P2.4	O	0.64	0.36	0	0	0
	S	0.18	0.62	0.20	0	0		S	0	0.82	0.18	0	0
	D	0	0	0.10	0.54	0.36		D	0	0	0.22	0.66	0.12
P1.4	O	0	0	0.12	0.70	0.18	P2.5	O	0.62	0.38	0	0	0
	S	0.68	0.30	0.02	0	0		S	0	0.54	0.46	0	0
	D	0.04	0.40	0.40	0.16	0		D	0.38	0.38	0.24	0	0
P2.1	O	0.36	0.62	0.02	0	0	P2.6	O	0	0	0.28	0.72	0
	S	0	0	0.44	0.34	0.22		S	0	0	0.50	0.50	0
	D	0	0	0	0.20	0.80		D	0	0.44	0.38	0.26	0

4.2.2. Fuzzification

The input data in Table 5 are multiplied by the intersection points of the fuzzy sets defined in Section 3.1. Each fuzzy set ‘A’, …, ‘E’ has its values on the j-scale (1). By multiplying, the assigned expert grades are mapped on the j-scale. Table 6 provides example P1.1 for the partial indicator O.

Table 6. Fuzzification P1.1 according to partial indicator O.

	j = 1	j = 2	j = 3	j = 4	j = 5	j = 6	j = 7	j = 8	j = 9	j = 10
‘A’	0 × 0	0 × 0	0 × 0	0 × 0	0 × 0	0 × 0	0 × 0	0 × 0	0 × 1	0 × 1
‘B’	0 × 0	0 × 0	0 × 0	0 × 0	0 × 0	0 × 0.5	0 × 1	0 × 1	0 × 0	0 × 0
‘C’	0.16 × 0	0.16 × 0	0.16 × 0	0.16 × 0.5	0.16 × 1	0.16 × 1	0.16 × 0.5	0.16 × 0	0.16 × 0	0.16 × 0
‘D’	0.68 × 0	0.68 × 0	0.68 × 1	0.68 × 1	0.5 × 1	0.68 × 0	0.68 × 0	0.68 × 0	0.68 × 0	0.68 × 0
‘E’	0.16 × 1	0.16 × 1	0.16 × 0	0.16 × 0	0.16 × 0	0.16 × 0	0.16 × 0	0.16 × 0	0.16 × 0	0.16 × 0
Σ	0.16	0.16	0.68	0.76	0.66	0.16	0.08	0	0	0

The fuzzification form of the expert assessment on the j-scale for P1.1 in relation to the indicator O has the form:

$$O_{P1.1}=\left(0.16/1, 0.16/2, 0.68/3, 0.76/4, 0.66/5, 0.16/6, 0.08/7, 0/8, 0/9, 0/10\right)$$

According to the same principle, grades for indicators S and D are obtained:

$$\begin{gathered} S_{P1.1}=\left(0/1, 0/2, 0/3, 0.02/4, 0.04/5, 0.22/6, 0.56/7, 0.54/8, 0.42/9, 0.42/10\right) \\ {D}_{P1.1}=\left(0.18/1, 0.18/2, 0.58/3, 0.70/4, 0.43/5, 0.24/6, 0.12/7, 0/8, 0/9, 0/10\right) \end{gathered}$$

To analyse each weak point in the model, the same principle is applied to map the assigned expert grades on the scale.

4.2.3. AHP Ranking

In this section, experts’ judgment is used for priority vector evaluation among PI on risk. Experts have offered combinations of O:S:D ratios in the form of 3:2:1, 3:1:1, …, 1:1:1, …, 1:1:3, 1:2:3. The most common expert answer given for each analysed weak point is adopted in the further calculation. An example of calculating the PI weight for a weak point P1.1 is shown in Table 7. A matrix (2) with basic setting is shown in the table. By calculating the matrix, the solutions shown in the last column of the table are obtained (W_i). The consistency check of the decision maker using Equations (3)–(6) obtained a CR value that is less than 10%, which satisfies the condition.

Table 7. The ranking of partial indicator according to P1.1.

Parameters	O	S	D	Wi
O	1.00	0.33	0.50	0.163
S	3.00	1.00	2.00	0.540
D	2.00	0.50	1.00	0.297
λmax	3.00921
n	3
RI	0.58
CI	0.0046
CR	0.00794

An assessment of the impact of each of the PI on risk was obtained in the following form:

$$W_O=0.163; W_S=0.540; W_D=0.297$$

While W_O + W_S + W_D = 1.

Based on the obtained values of weight coefficient, it is concluded that at P1.1, the influence of severity on risk, is dominant to the extent of 54%. This outcome of the ranking was expected because the failure in this position leads to the violation of the static stability of the machine.

According to the same principle, the weight coefficient of the mentioned indicators for other weak points was assessed. The values of weight coefficient (W_i) and consistency check (CR) are shown in Table 8.

Table 8. The ranking of partial indicator according to all segments.

AHP	P1.1	P1.2	P1.3	P1.4	P2.1	P2.2	P2.3	P2.4	P2.5	P2.6
WO	0.163	0.500	0.144	0.144	0.163	0.333	0.200	0.163	0.540	0.163
WS	0.540	0.250	0.428	0.428	0.540	0.333	0.400	0.540	0.297	0.540
WD	0.297	0.250	0.428	0.428	0.297	0.333	0.400	0.297	0.163	0.297
λmax	3.0092	3.0	3.0	3.0	3.0092	3.0	3.0	3.0092	3.0092	3.0092
CI	0.0046	0.0	0.0	0.0	0.0046	0.0	0.0	0.0046	0.0046	0.0046
CR	0.0079	0.0	0.0	0.0	0.0079	0.0	0.0	0.0079	0.0079	0.0079

4.3. Module 3—Fuzzy Inference Engine

4.3.1. Composition

Weighted grades of PI are synthesized by using fuzzy-TOPSIS composition. In the first step of the TOPSIS composition, the average values of PI defined in Table 4 are mapped to the membership functions of the fuzzy set. Fuzzy sets are in a trapezoidal shape. The obtained values represent the input parameters for the TOPSIS composition and are shown in Table 9.

Table 9. Input data for model composition.

Parameters		O	S	D
Weight Coefficient		0.163	0.540	0.297
Grades (ji)	1	0.16000	0.00000	0.18000
	2	0.16000	0.00000	0.18000
	3	0.68000	0.00000	0.58000
	4	0.76000	0.02000	0.70000
	5	0.38667	0.04000	0.43333
	6	0.16000	0.22000	0.24000
	7	0.08000	0.56000	0.12000
	8	0.00000	0.54000	0.00000
	9	0.00000	0.42000	0.00000
	10	0.00000	0.42000	0.00000

In the next step, the values from the previous table are normalized using Equation (8). The normalized values of the matrix are shown in Table 10. In the third step, the values of the weight coefficient (W_i) obtained by the AHP method are introduced. According to Equation (9), the normalized values (r_ij) are multiplied by the weight coefficients from Table 8. The results (p_ij) of this step are also shown in Table 10.

Table 10. Normalized and weighted decision matrix of parameters.

	rij (Equation (8))			pij (Equation (9))
j	O	S	D	O	S	D
1	0.14183	0.00000	0.16778	0.02312	0.00000	0.04980
2	0.14183	0.00000	0.16778	0.02312	0.00000	0.04980
3	0.60276	0.00000	0.54062	0.09826	0.00000	0.16048
4	0.67367	0.01992	0.65248	0.10982	0.01076	0.19368
5	0.34275	0.03983	0.40391	0.05587	0.02152	0.11990
6	0.14183	0.21908	0.22371	0.02312	0.11834	0.06640
7	0.07091	0.55766	0.11185	0.01156	0.30122	0.03320
8	0.00000	0.53775	0.00000	0.00000	0.29046	0.00000
9	0.00000	0.41825	0.00000	0.00000	0.22591	0.00000
10	0.00000	0.41825	0.00000	0.00000	0.22591	0.00000

By using Equations (10) and (11), the values of ideal (A⁺) and anti-ideal (A⁻) solutions from the weighted normalized matrix (p_ij) are found. In the following account, only combinations other than zero are taken. The next step involves defining the distance (Si⁺, Si) of each parameter relative to the ideal (A⁺) and anti-ideal (A⁻) using Equations (12) and (13). The output value of the TOPSIS method is the synthesis coefficient µ_i calculated according to Equation (14). The values of (A⁺, A⁻), (S_i⁺, S_i⁻) and (µ_i) are presented in Table 11 and Table 12, respectively.

Table 11. Determined positive and negative ideal solutions.

	O	S	D
A+	0.10982	0.30122	0.19368
A−	0.01156	0.01076	0.03320

Table 12. Sum of alternative distance from positive and negative ideal solution and results of risk (R).

j	Si+	Si−	µi
1	0.34489	0.02291	0.06229
2	0.34489	0.02291	0.06229
3	0.30326	0.15437	0.33733
4	0.29046	0.18817	0.39314
5	0.29426	0.09796	0.24975
6	0.23909	0.11318	0.32129
7	0.18817	0.29046	0.60686
8	0.22291	0.28190	0.55843
9	0.23504	0.21801	0.48121
10	0.23504	0.21801	0.48121

Output value R (µ_i) from TOPSIS composition according to j-scale has the following form:

$$R({\mu }_{P1.1})=\left\{\begin{array}{l}0.0623\left(1\right), 0.0623\left(2\right), 0.3373\left(3\right), 0.3931\left(4\right), 0.2497\left(5\right),\\ 0.3213\left(6\right), 0.6069\left(7\right), 0.5584\left(8\right), 0.4812\left(9\right), 0.4812\left(10\right)\end{array}\right\}$$

The results are also shown graphically in Figure 5.

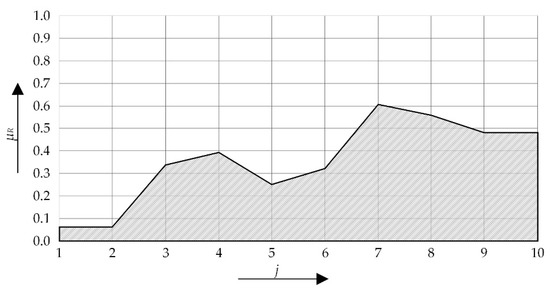
Figure 5. Output values from the model composition.

4.3.2. Identification

Identification best-fit method is used to obtain the final grades (‘A’, ‘B’, ‘C’, ‘D’, and ‘E’). According to Equation (15) an example is provided for the grade ‘A’ and has the following form:

$$d_{1(P1.1,‘A’)}=\sqrt{{(0-0.06229)}^2+{(0-0.06229)}^2+\dots +{(0-0.55843)}^2+{(1-0.48121)}^2+{(1-0.48121)}^2}=1.28846$$

where: μ_A(P1.1) according to μ_i from Table 12 and μ_A according to (6).

For other fuzzy sets:

$$\begin{array}{l}{d}_{2(P1.1, ‘B’)}=1.07298,d_{3(P1.1, ‘C’)}=1.39387,\\ d_{4(P1.1, ‘D’)}=1.43827,d_{5(P1.1, ‘E’)}=1.82641.\end{array}$$

For d_min = d₂ according to Equation (16):

$$\mu { }_{‘A’}=\frac{1.07298}{\left(1.28846\cdot \left(\frac{1.07298}{1.28846}+\frac{1.07298}{1.07298}+\frac{1.07298}{1.39387}+\frac{1.07298}{1.43827}+\frac{1.07298}{1.82641}\right)\right)}=0.21157$$

Other values are: μ_‘B’ = 0.25406, μ_‘C’ = 0.19557, μ_‘D’ = 0.18954, and μ_‘E’ = 0.14926.

The grade for P1.1 of the machine is recorded in the form:

$$RPN\left(P1.1\right)=\left(0.21157/‘A’, 0.25406/‘B’, 0.19557/‘C’, 0.18954/‘D’, 0.14926/‘E’\right)$$

The grades are designated as: ‘A’—very high risk, ‘B’—high risk, ‘C’—average risk, ‘D’—low risk, and ‘E’—very low risk. For P1.1, very high risk is 21.16% and high risk is in the rating level of 25.41%. The low risk according to grades ‘A’ and ‘B’ are in ratings 18.95% and 14.93%. The distribution of grades (‘A’, …, ‘E’) of risk with the center of gravity after the identification process for P1.1 is presented in Figure 6. The calculated values for the remaining machine segments are shown in Table 13.

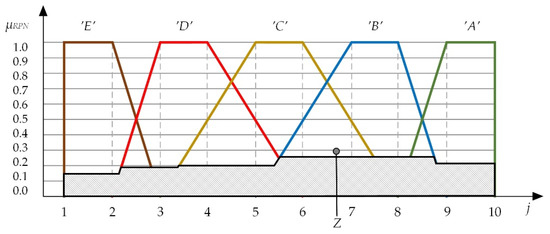
Figure 6. Output values of Identification with a marked centre of gravity.

Table 13. Identification results for all segments of the analysis.

	P1.1	P1.2	P1.3	P1.4	P2.1	P2.2	P2.3	P2.4	P2.5	P2.6
‘A’	0.21157	0.16424	0.15335	0.21917	0.17496	0.16706	0.19867	0.15686	0.24737	0.15495
‘B’	0.25406	0.23007	0.22492	0.23749	0.18280	0.22104	0.22752	0.32015	0.24718	0.16274
‘C’	0.19557	0.25404	0.20949	0.21864	0.21731	0.20919	0.21441	0.19996	0.18005	0.26790
‘D’	0.18954	0.18905	0.22683	0.17728	0.20488	0.21960	0.19785	0.17648	0.16224	0.25946
‘E’	0.14926	0.16260	0.18540	0.14742	0.22005	0.18312	0.16156	0.14655	0.16317	0.15495

4.3.3. Defuzzification and Standard Deviation

The last part of the analysis involves the synthesis of the obtained results into one final grade. Defuzzification is performed using the centre of mass point method defined in Section 3.5. For P1.1 by applying Equation (19) the result is:

$$Z_{P1.1}=\frac{{\displaystyle \sum {}_{i=1}^{i=5}}{\mu }_i\cdot C_i}{{\displaystyle \sum {}_{i=1}^{i=5}{\mu }_i}}=\frac{0.21157\cdot 5+0.25406\cdot 4+0.19557\cdot 3+0.18954\cdot 2+0.14926\cdot 1}{0.21157+0.25406+0.19557+0.18954+0.14926}=3.189$$

Standard deviation is calculated according to the Equation (20):

$$\begin{array}{l}{S}_{P1.1}=\sqrt{\frac{{\displaystyle \sum {}_{i=1}^{i=N}{\left({\mu }_i\cdot {\mu }_{sr}\right)}^2}}{N-1}}\\ =\sqrt{\frac{{\left(0.21157-0.2\right)}^2+{\left(0.25406-0.2\right)}^2+{\left(0.19557-0.2\right)}^2+{\left(0.18954-0.2\right)}^2+{\left(0.14926-0.2\right)}^2}{5-1}}\\ =0.03795\end{array}$$

According to Equation (21), final value of calculated risk for P1.1 is presented in the form:

$$RP{N}_{P1.1}=3.189, 0.03795$$

Other RPN results are shown in Table 14.

Table 14. Results of risk performance and standard deviations for all segments of the analysis.

RPN	P1.1	P1.2	P1.3	P1.4	P2.1	P2.2	P2.3	P2.4	P2.5	P2.6
Zi	3.1892	3.0443	2.9340	3.2037	2.8877	2.9696	3.1039	3.1643	3.2533	2.9033
Si	0.03795	0.04069	0.03090	0.03674	0.02030	0.02388	0.02475	0.07019	0.04373	0.05829

5. Discussion

The analysis conducted in this paper was performed with two aspects of the risk of damage for items P1.1–P1.4 and the risk of interruption of production for items P2.1–P.2.6. Based on the applied innovative fuzzy–AHP–TOPSIS model, further considerations can be conducted in three directions: the concept of the created model, the results of the conducted case study, and guidelines in risk-based maintenance.

5.1. Discussion According to Innovation Model

Previous analysis in different areas of risk indicates that the MIN–MAX composition is used, which reduces the dissipation of results compared with MAX–MIN [82]. In this paper, the composition was developed by applying the TOPSIS method (M1). The goal was to find out if this method further reduces dissipation and shifts the centre of gravity. The same input data was used for the models: AHP-fuzzy with MIN–MAX composition (M2), fuzzy with MIN–MAX composition (M3), AHP-fuzzy with MAX–MIN composition (M4), and fuzzy with MAX–MIN composition (M5). The results are shown in Table 15.

Table 15. Results of different method applications.

RPN		P1.1	P1.2	P1.3	P1.4	P2.1	P2.2	P2.3	P2.4	P2.5	P2.6
M1	Zi	3.189	3.044	2.934	3.204	2.888	2.969	3.104	3.164	3.253	2.903
	Si	0.0379	0.0407	0.0309	0.0367	0.0203	0.0239	0.0247	0.0702	0.0437	0.0583
M2	Zi	3.150	3.015	2.874	3.288	2.753	2.939	3.131	3.236	3.208	2.891
	Si	0.0400	0.0417	0.0315	0.0632	0.0456	0.0473	0.0251	0.1077	0.0460	0.0630
M3	Zi	3.017	3.008	2.874	3.142	2.836	2.939	3.112	3.153	3.193	2.841
	Si	0.0301	0.0406	0.0315	0.0314	0.0282	0.0473	0.0248	0.0703	0.0438	0.0779
M4	Zi	3.085	3.062	2.934	3.219	2.854	2.954	3.088	3.094	3.215	2.907
	Si	0.0697	0.1187	0.0748	0.0903	0.0589	0.0637	0.0539	0.0684	0.0572	0.0794
M5	Zi	2.961	3.030	2.854	3.113	2.914	2.954	3.044	3.153	3.206	2.907
	Si	0.0741	0.1382	0.0632	0.0679	0.0649	0.0637	0.0566	0.0780	0.0645	0.0794

The dissipation measure in the M1 method is the lowest in five cases. In four cases it is approximately equal to M3, while in one case dissipation is the lowest in method M3. The differences in the degree of dissipation are also shown graphically in Figure 7. The radius of the circle around the results indicates the measure of dissipation around the results.

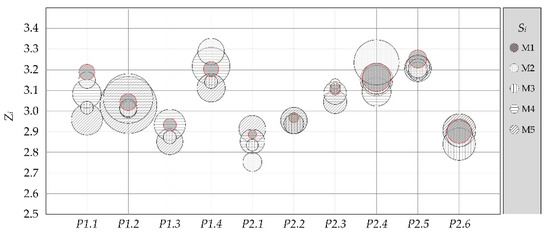
Figure 7. Difference in dissipation.

5.2. Discussion According to the Case Study Results

The results of the case study are shown in Table 14 and graphically in Figure 8. On the abscissa of the diagram the weak points of both considered risks (P1.1, …, P2.6) are presented. The output values of identification according to µ_RPN from 0 to 1 for each of the grades (‘A’, …, ‘E’) are marked on the primary ordinate (left). The secondary ordinate (right) indicates the output value from defuzzification (Z_i) in the range of 2.70–3.30. This rating is marked with dots as the centre of gravity. For easier tracking of the difference in results between weak points, they are linked with a red line.

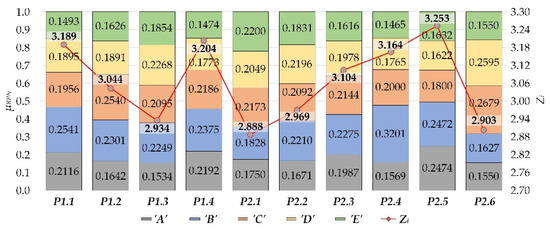
Figure 8. Partial evaluations of the analysed WP and final RPN values.

The highest risk of damage is on the weak point P1.4—a slewing platform with a value of 3.204 on a scale from 1 to 5. This rating mostly belongs to the linguistic rating ‘D’, with a slight tendency towards the rating ‘C’. The second weak point with the highest risk of damage is P1.1—rope wheel in the hoisting system with a risk value of 3.189. It is followed by P1.2—bucket-wheel head with 3.044, while the lowest risk is with P1.3—support to A mast with a rating of 2.934. The distribution of affiliation to linguistic assessments is shown in Figure 7.

The highest risk of downtime is on P2.5—digging drive system with a value of 3.253. The second weak point with the highest risk is P2.4—slewing drive system where the grade is 3.164. The distribution of the remaining grades and affiliation to the linguistic descriptions is shown in Figure 7.

Statistics related to data to the risk of downtime are shown in Figure 4. The highest number of downtimes is at P2.1—bucket-wheel elements with 24.31%. The risk at this place is the lowest with a value of 2.888. There are several reasons for this result: downtimes that can be easily detected visually; replacement time planning is possible; the element is made up of several parts whose failure or damage will not, in any case, lead to machine downtime; etc. The second position where a larger number of interventions was statistically observed is the P2.2—conveyor drive system with a share of 19.79%. The risk at P2.2 is also low with a grade of 2.969. The reasons are similar. Detection is simple and the severity of the consequences does not jeopardize prolonged operation downtime of the machine.

5.3. Risk-Based Maintenance

The concept of ES maintenance may be different. “Work to failure” is the least favourable [83,84]. Such a concept is obsolete. Today, concepts strive for predictive and proactive maintenance. Additional progress can be made by implementing the risk-based maintenance concept. This reduces the possibility of damages and unplanned downtimes.

From the aspect of damage risk, attention should be paid to P1.4—slaving platform. Checking the condition of the steel structure of the slewing platform is performed from the aspect of deformations, cracks, or other defects. This includes modern diagnostic methods such as acoustic testing, tensometric testing, etc. The central vertical mast carries the bucket-wheel boom, its weight, and the counterweight. At the same time, it suffers from all dynamic loads during operation. From the aspect of the seriousness of the consequences, the risk is extremely high. The second weak point with the highest risk P1.1—rope wheel in the hoisting system requires testing of all ropes (magnetic testing), pulleys, drives (vibration and stress measurements), as well as safety brakes. Controls should be time defined to detect potential initial deformations in time.

The statistical number of interventions and the risk of downtime analysis conducted in the model are not in agreement. Most frequent failures are on P2.1—bucket-wheel elements. It can be said that the probability of occurrence is high, the severity of the consequences is small, and the possibility of detection is also good. For example, with P2.1, teeth often break out. The total number of teeth on the bucket wheel is large. The excavator is continues to work without any problems until a large number of teeth are damaged or broken. Then, the replacement is made, or the time is used when the excavator is at a standstill for some other reason. Other elements of P2.1 cause similar problems that are not of high risk.

Risk-based maintenance must be directed towards a weak point with high risk. The digging drive system (P2.5) is the initial drive in the digging process. It initiates the slewing movement of the working element and is exposed to different working and climatic conditions. Defects can be serious and require workshop repairs. The time that the machine is at a standstill is great and the costs are high. Improvements must focus on detecting dangers and reducing the severity of consequences. The application of modern diagnostic methods is required, such as monitoring the temperature of assemblies, mechanical damages, vibrations, the level of lubrication of rotating parts, etc. If conditions allow, monitoring should be online, i.e., monitoring of important elements from the aspect of risk should be carried out. For all elements and assemblies that would require workshop repair, it is necessary to prepare spare parts and aggregates on time. Maintenance would be carried out according to the system of aggregate/assembly replacement. A spare aggregate/assembly would always be available, the repair of the current one would be performed later, and it would then become a replacement. Similar problems occur with other drives with a higher risk of downtime (P2.4, P2.3). The risk-based maintenance setting should be used in these cases as well.

6. Conclusions

The paper presents an innovative model of EC risk assessment. So far, the two most used methods are FMEA and FMECA. The shortcomings of the model were noticed by several authors, and they are: increased subjectivity, the unambiguous influence of PI, obtaining the same RPN values by combining different PI, the sensitivity of the model, etc. This paper presents an innovative model that eliminates these shortcomings.

The existing RPN calculation method has been improved by introducing an innovative fuzzy expert model in combination with MCDM methods. The basis is a fuzzy model that allows the entry of linguistic estimates according to a defined algorithm.

The AHP method was used to define the relationship between influential partial risk indicators. In this way, the model gained flexibility and adaptability. Its objectivity through two-stage expert input has also been increased. The influence of O, S, and D on RPN may or may not always be the same. For some ESs, the severity or probability of occurrence is more important, while in other cases it is the possibility of risk detection. To create a comprehensive approach to risk performance, it is necessary to consider the PI weight coefficients.

The TOPSIS method was used in the fuzzy composition to define fuzzy rules and fuzzy outcomes to increase the accuracy of the output. For phenomena such as risks, the value of the results should be concentrated. Dissipation around the results should be kept to a minimum. With that goal, the TOPSIS method is applied in this paper. The TOPSIS method was used in the composition instead of IF-THEN, i.e., derived MAX–MIN and MIN–MAX compositions. The rate of dissipation in the innovative model is lower than in others.

According to the presented results, in relation to the other models, the innovative model has less dispersion on average at 29.9%. With detailed observation, M1 has less dispersion of M2 at 20.5%, M3 at 5.8%, M4 at 45.9%, and M5 at 47.3%.

The case study was conducted on a bucket-wheel excavator as a complex ES. The risk was analysed from two aspects: the risk of damage and the risk of downtime. From the aspect of risk of damage, the highest value is on the slewing platform, then on the rope wheel in the hoisting system, support to A mast, and on the bucket-wheel head. In terms of downtime risk, the highest value is on the digging drive system, then on the slewing drive system. The number of interventions does not agree with this distribution, which is understandable considering the seriousness and detectability of the considered weak points.

The model was developed in conceptual and mathematical terms and verification was conducted on an appropriate example. The model can be a useful tool for different ES-s in industry. Based on the located points, the concept of preventive maintenance can be applied or the concept of risk-based maintenance can be as well. Furthermore, further research should focus on the application of equipment maintenance management. Risk assessments need to be reconciled with the implications of quality of service and dependability of ES. Questions need to be answered regarding when and how to manage operations and maintenance depending on risk assessment.