Construction of Full Order-of-Addition Generalization Simplex-Centroid Designs by the Directed Graph Approach

Abstract

The order-of-addition generalization simplex-centroid designs play a key role in mixture experiments, for example, the mixture experiments with process variables. The paper formally combines order-of-addition (OofA) with mixture components in the same experiment. This paper proposes a new algorithm which generates full OofA mth-degree generalization simplex-centroid designs for q components by a class of the direction graphs, and a series of examples also confirms the value of the proposed algorithm.

1. Introduction

In a mixture experiment, two or more ingredients are blended together in varying proportions to produce a response. It is typically assumed that the response depends only on the proportions of the ingredients in the mixture and not on the amount of the mixture. In a q ingredient mixture in which $x_i$ represents the proportion of the ith ingredient present in the mixture, these proportions are non-negative and sum to unity. The mixture ingredients take values in the experimental region in which the $(q-1)$-dimensional simplex $S^{q-1}$ is given by

$$S^{q-1}=\left\{(x_1,x_2,\dots ,x_q)\in {[0,1]}^q|\sum _{i=1}^q{x}_i=1,0\le x_i\le 1,i=1,\dots ,q\right\}.$$

When $q=2$, the simplex is a straight line; when $q=3$, the simplex is an equilateral triangle; and when $q=4$, the simplex is a tetrahedron. Ref. [1] proposed a simplex-lattice design and the associated canonical form of a polynomial model. Corresponding to the points in a $\{q,m\}-$ lattice, the proportions used for each of the q components have $m+1$ equally spaced values from 0 to 1, that is, $x_i=0,1/m,2/m,\dots ,1$, and all possible mixtures with these proportions for each component are used. Ref. [2] proposed a simplex-centroid design and its associated model. The simplex-centroid design consists of $2^q-1$ points, that is, the q permutations of $(1,0,0,\cdots ,0)$, the $\left(\genfrac{}{}{0pt}{}{q}{2}\right)$ permutations of $(\frac{1}{2},\frac{1}{2},0,\cdots ,0)$, the $\left(\genfrac{}{}{0pt}{}{q}{3}\right)$ permutations of $(\frac{1}{3},\frac{1}{3},\frac{1}{3},0,\cdots ,0)$,…, and finally the overall centroid point $(\frac{1}{q},\frac{1}{q},\cdots ,\frac{1}{q})$. By [3], the corresponding model to be fitted to data at the points of a simplex-centroid design is

$$y=\sum _{i=1}^q{\beta }_i{x}_i+\sum _{i<j}{\beta }_{ij}{x}_i{x}_j+\sum _{i<j<k}{\beta }_{ijk}{x}_i{x}_j{x}_k+\cdots +{\beta }_{123\dots q}{x}_1{x}_2{x}_3\dots x_q+\epsilon .$$

(1)

The number of terms in model (1) show a one-to-one correspondence between the number of points in the design and the number of terms in the model. However, the higher-order term is invalid for the q components in some mixture experiments [3]. An mth-degree generalization simplex-centroid design is used. An mth-degree generalization simplex-centroid design consists of $\left(\genfrac{}{}{0pt}{}{q}{1}\right)+\left(\genfrac{}{}{0pt}{}{q}{2}\right)+\cdots +\left(\genfrac{}{}{0pt}{}{q}{m}\right)$ points, that is, the q permutations of $(1,0,0,\dots ,0)$, the $\left(\genfrac{}{}{0pt}{}{q}{2}\right)$ permutations of $(\frac{1}{2},\frac{1}{2},0,\dots ,0)$, the $\left(\genfrac{}{}{0pt}{}{q}{3}\right)$ permutations of $(\frac{1}{3},\frac{1}{3},\frac{1}{3},0,\dots ,0)$,…, etc., and finally the $\left(\genfrac{}{}{0pt}{}{q}{m}\right)$ permutations of $(\underset{m}{\underbrace{\frac{1}{m},\dots ,\frac{1}{m}}},0,\dots ,0)$. The corresponding model to be fitted to data at the points of this design is written as

$$\eta =\sum _{i=1}^q{\beta }_i{x}_i+\sum _{i<j}{\beta }_{ij}{x}_i{x}_j+\sum _{i<j<k}{\beta }_{ijk}{x}_i{x}_j{x}_k+\cdots +\sum _{i_1<i_2<\cdots <i_m}{\beta }_{i_1{i}_2\cdots i_m}{x}_{i_1}{x}_{i_2}\cdots x_{i_m}+\epsilon$$

(2)

where the terms up to the mth degree are included. The order-of-addition generalization simplex-centroid designs play a significant role in mixture experiments. The mixture experiments with process variables are a classic example. Recently, Ref. [4] investigated I-optimal mixture designs, which minimize the average prediction variance over the experimental region. Ref. [5] obtained optimum designs when the experimental region is an ellipsoidal subspace of the entire factor space which does not cover the vertex points of the simplex. Ref. [6] studied the equivalence theorem of D-optimal equal allocation design for multiresponse mixture experiments.

The order-of-addition (OofA) mixture experiments have wide applications in biochemistry, food science, engineering and pharmaceutical science. For instance, Ref. [7] introduced the famous experiment of a lady tasting tea which is perhaps the first OofA mixture experiment in the literature. Ref. [8] studied an experiment for extracting anthocyanins from cranberries. They found that “The order of addition of the lead acetate (before or after the pH adjustment) had a definite influence on the reaction. Higher recoveries were obtained by adjusting the pH after lead acetate addition.” In the algorithmic construction of “maximum-likelihood phylogentic trees” from DNA sequences, the likelihood of the fitted tree relies on the order of adding different taxa into the computer program [9,10]. Ref. [11] investigated the order of mixing of feed rations and the time spent blending using two types of mixers. In an experiment analyzing protein function within an in vitro transport system [12], the sequence of actions for two components and the proportions of two components were found to be significant for the response. In another drug combination experiment on oral cancer [13], the authors showed that the sequence of adding three drugs (nortezomib, camptothecin and doxorubicin) and the ingredients of three drugs played a vital role in ensuring the efficacy of treatments.

The OofA experiments have recently become popular in the field of design of experiments. Ref. [14] proposed a model which assumes that an OofA affects the response via pair-wise order (PWO) effects. Alternatives to model-based criteria are balanced- based criteria, and for those it is natural to consider orthogonal arrays (OAs). Ref. [15] proposed order-of-addition orthogonal arrays (OofA-OAs) which have the same correlation structures as the full designs, for the case of $q=4,5,6,7$. Ref. [16] considered a variety of commonly used design criteria including D-, A- and $M.S.$-optimal criteria and proposed a systematic method to construct a class of robust optimal fractional OofA designs. Ref. [17] constructed systematically optimal fractional OofA designs via block designs. Ref. [18] have reviewed the PWO model and its relevant optimality theorems. Ref. [19] extended the modeling of OofA experiments by taking into account the higher-order interactions between PWO factors. Ref. [20] systematically constructed a class of minimal-point PWO designs. Ref. [21] recently proposed component orthogonal arrays (COAs) and developed a position effect model which extends the PWO model for characterizing mixing order effects. Ref. [22] constructed COAs with any number of components. Ref. [23] proposed a new method of finding COAs of broader run sizes and tabulated some COAs with four, five and six components. Ref. [24] systematically constructed OofA-OAs and considered a class of D-, A-, $M.S.$- and ${\chi }^2$-optimal designs under the predominant PWO model.

The majority of papers on including the order of addition of mixture experiments either ignore the order of addition, randomize the mixing order or choose a constant mixing order. This paper is not only concerned with the mixture proportions but their addition order as well. Ref. [25] proposed an original algorithm for full OofA generalization simplex-centroid design construction. For a full OofA mth-degree generalization simplex-centroid design, the number of rows N in the design matrix $\mathbf{D}$ is

$$N=q+\left(\genfrac{}{}{0pt}{}{q}{2}\right)2!+\left(\genfrac{}{}{0pt}{}{m}{3}\right)3!+\cdots +\left(\genfrac{}{}{0pt}{}{q}{m}\right)m!.$$

Therefore, N increases dramatically with increases in q and m. For example, if $q=8$ and $m=6$, there will be N = 28,960. For large runs, the previous algorithm will be invalid. To solve this problem, we give a new method which generates full OofA generalization simplex-centroid designs by an iterating algorithm.

In this paper, we aim to systematically construct full OofA mth-degree generalization simplex-centroid designs for q components. In Section 2, we discuss the full OofA generalization simplex-centroid design and its properties. Section 3 gives an algorithm which constructs the full OofA generalization simplex-centroid designs. A final conclusion is given in the last section. The full OofA generalization simplex-centroid design with $q=4$, $m=2,3,4$ is displayed in Appendix A.

2. The Full OofA Generalization Simplex-Centroid Design and Its Properties

A full OofA design under the pair-wise order (PWO) model is defined below [14]. Suppose there are q components $1,2,\dots ,q$ which can be ordered in $q!$ ways. Any ordering $a=a_1{a}_2\cdots a_q$ which is a permutation of $1,\dots ,q$ is a treatment. Let ${\mathcal{O}}_q$ denote the full OofA design in which the $q!$ rows are $q!$ treatments of the q components. For $a\in {\mathcal{O}}_q$, let $\tau \left(a\right)$ be the treatment mean of a, that is, the expectation of any observation arising from treatment a. As usual, it is assumed that the observations have equal variance and are uncorrelated. Let $\mathcal{P}$ be the set of all pairs $(j,k)$ where $1\le j<k\le q$. Let $jk$ denote the pair $(j,k)$. By [14], the PWO indicator for all $jk\in \mathcal{P}$ is defined as

$$\begin{array}{c}\hfill {\lambda }_{jk}\left(a\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}j\mathrm{precedes}k\mathrm{in}a,\hfill \\ -1,\hfill & \mathrm{if}k\mathrm{precedes}j\mathrm{in}a.\hfill \end{array}\right.\end{array}$$

(3)

Therefore, if $a=213$, then ${\lambda }_{12}\left(a\right)=-1$ as 2 precedes 1 in a, $z_{13}\left(a\right)=1$ as 1 precedes 3 in a and $z_{23}\left(a\right)=1$ as 2 precedes 3 in a. The PWO model is

$$\tau \left(a\right)={\beta }_0+\sum _{jk\in \mathcal{P}}{\lambda }_{jk}\left(a\right){\beta }_{jk}$$

(4)

A $q!$-dimensional vector ${\lambda }_{ij}={({\lambda }_{ij}\left(a_1\right),{\lambda }_{ij}\left(a_2\right),\dots ,{\lambda }_{ij}\left(a_{q!}\right))}^{\mathrm{T}}$ relating to the components i and j is called to a PWO factor. For q components, there are $\left(\genfrac{}{}{0pt}{}{q}{2}\right)$ PWO factors. The column-juxtaposed matrix $({\lambda }_{12},{\lambda }_{13},\dots ,{\lambda }_{(q-1)q})$ is referred to as the full PWO design.

In OofA mixture design, by [25], the modified PWO variables are defined as

$$\begin{array}{c}\hfill z_{jk}(x,a)=\left\{\begin{array}{cc}1,\hfill & x_j,x_k\ne 0\mathrm{and}j\mathrm{precedes}k\mathrm{in}a,\hfill \\ 0,\hfill & x_j=0\mathrm{or}{x}_k=0,\hfill \\ -1,\hfill & x_j,x_k\ne 0\mathrm{and}k\mathrm{precedes}j\mathrm{in}a.\hfill \end{array}\right.\end{array}$$

(5)

These modified PWO variables describe the ordering of the nonzero mixture components. For example, if $x=(\frac{1}{3},\frac{2}{3},0)$ and $a=123$, then $z_{12}(x,a)=1$ but $z_{13}(x,a)=z_{23}(x,a)=0$. A $q!$-dimensional vector $z_{ij}={(z_{ij}(x,a_1),z_{ij}(x,a_2),\dots ,z_{ij}(x,a_{q!}))}^{\mathrm{T}}$ relating to the components i and j is called a modified PWO factor. For q components, there are $\left(\genfrac{}{}{0pt}{}{q}{2}\right)$ modified PWO factors. The column-juxtaposed matrix $(z_{12},z_{13},\dots ,z_{(q-1)q})$ is referred to as the full modified PWO design.

In an OofA mixture design, the full OofA mth-degree generalization simplex-centroid design is defined as follows.

Definition 1.

Let x be a point in the mth-degree generalization simplex-centroid design, k is the number of nonzero components of x. Replicate $k!$ times and associate each replicate with a unique ordering a of the k nonzero components of x. For each replicate, represent its ordering a using a row vector z of $\left(\genfrac{}{}{0pt}{}{q}{2}\right)$ modified PWO variables $z_{jk}(x,a)$ for each $jk\in \mathcal{P}$. Then, stack the rows x and z into the matrixes X and Z, respectively. Then, a $\left(q+\left(\genfrac{}{}{0pt}{}{q}{2}\right)2!+\left(\genfrac{}{}{0pt}{}{q}{3}\right)3!+\cdots +\left(\genfrac{}{}{0pt}{}{q}{m}\right)m!\right)\times \left(q+\left(\genfrac{}{}{0pt}{}{q}{2}\right)\right)$ matrix $\mathbf{D}=(\mathbf{X},\mathbf{Z})$ is known as a full OofA mth-degree generalization simplex-centroid design.

The full OofA generalization simplex-centroid designs play an important role in mixture experiments for choosing optimal fractional OofA generalization simplex-centroid designs. The full OofA generalization simplex-centroid designs with $q=2$, $m=2$ and $q=3$, $m=3$ are listed in Table 1 and Table 2, respectively.

Table 1. The full OofA generalization simplex-centroid design with $q=2$, $m=2$.

${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{z}}_{12}(\mathit{x},\mathit{a})$
1	0	0
0	1	0
$\frac{1}{2}$	$\frac{1}{2}$	1
$\frac{1}{2}$	$\frac{1}{2}$	$-1$

Table 2. The full OofA generalization simplex-centroid design with $q=3$, $m=3$.

${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{z}}_{12}(\mathit{x},\mathit{a})$	${\mathit{z}}_{13}(\mathit{x},\mathit{a})$	${\mathit{z}}_{23}(\mathit{x},\mathit{a})$
1	0	0	0	0	0
0	1	0	0	0	0
0	0	1	0	0	0
$\frac{1}{2}$	$\frac{1}{2}$	0	1	0	0
$\frac{1}{2}$	$\frac{1}{2}$	0	$-1$	0	0
$\frac{1}{2}$	0	$\frac{1}{2}$	0	1	0
$\frac{1}{2}$	0	$\frac{1}{2}$	0	$-1$	0
0	$\frac{1}{2}$	$\frac{1}{2}$	0	0	1
0	$\frac{1}{2}$	$\frac{1}{2}$	0	0	$-1$
$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$	1	1	1
$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$	1	1	$-1$
$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$	1	$-1$	$-1$
$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$	$-1$	1	1
$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$	$-1$	$-1$	1
$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$	$-1$	$-1$	$-1$

By Table 2, we obtain

$$\mathbf{X}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ \frac{1}{2}& \frac{1}{2}& 0\\ \frac{1}{2}& \frac{1}{2}& 0\\ \frac{1}{2}& 0& \frac{1}{2}\\ \frac{1}{2}& 0& \frac{1}{2}\\ 0& \frac{1}{2}& \frac{1}{2}\\ 0& \frac{1}{2}& \frac{1}{2}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right),\mathbf{Z}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ -1& 0& 0\\ 0& 1& 0\\ 0& -1& 0\\ 0& 0& 1\\ 0& 0& -1\\ 1& 1& 1\\ 1& 1& -1\\ 1& -1& -1\\ -1& 1& 1\\ -1& -1& 1\\ -1& -1& -1\end{array}\right).$$

Then,

$$\mathbf{D}=\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ \frac{1}{2}& \frac{1}{2}& 0& 1& 0& 0\\ \frac{1}{2}& \frac{1}{2}& 0& -1& 0& 0\\ \frac{1}{2}& 0& \frac{1}{2}& 0& 1& 0\\ \frac{1}{2}& 0& \frac{1}{2}& 0& -1& 0\\ 0& \frac{1}{2}& \frac{1}{2}& 0& 0& 1\\ 0& \frac{1}{2}& \frac{1}{2}& 0& 0& -1\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}& 1& 1& 1\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}& 1& 1& -1\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}& 1& -1& -1\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}& -1& 1& 1\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}& -1& -1& 1\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}& -1& -1& -1\end{array}\right).$$

To construct full OofA generalization simplex-centroid designs, we first give some properties of full OofA generalization simplex-centroid designs. Definition 2 plays a key role in the construction of full OofA generalization simplex-centroid designs.

Definition 2.

A directed graph is set of vertices and a collection of directed edges that each connect an ordered pair of vertices. In a directed graph, points from the first vertex in the pair and points to the second vertex in the pair are called a directed edge.

By Definition 2, we have the following theorem.

Theorem 1.

In q components OofA mixture design, we regard one of the q components $x_1,x_2,\dots ,x_q$ and a modified PWO variable as the vertex and directed edge of a directed graph, respectively. Then, the row of full OofA generalization simplex-centroid designs corresponds one-to-one to the directed graph, where all directed edges have to obey the triangle rule for vectors, where the modified PWO variable $z_{ij}(x,a)$ is zero, i.e., the directed edge is nonexistent between the vertex i and the vertex j.

Proof of Theorem 1.

Let S be the set of all rows of full OofA generalization simplex-centroid designs. Let T be the set all directed graphs and directed edges. By Definition 2, there is surjective mapping $\tau :S\to T$, and we obtain $\tau \left(S\right)=T$. $\forall s_1,s_2\in S,s_1\ne s_2$, $s_1$ and $s_2$ are two different rows in OofA generalization simplex-centroid designs. By Definition 2, $\tau \left(s_1\right)\ne \tau \left(s_2\right)$. Then, $\tau$ is injective.    □

The one-to-one correspondences between the rows of full OofA third-degree generalization simplex-centroid designs for three components and their directed graphs are listed below.

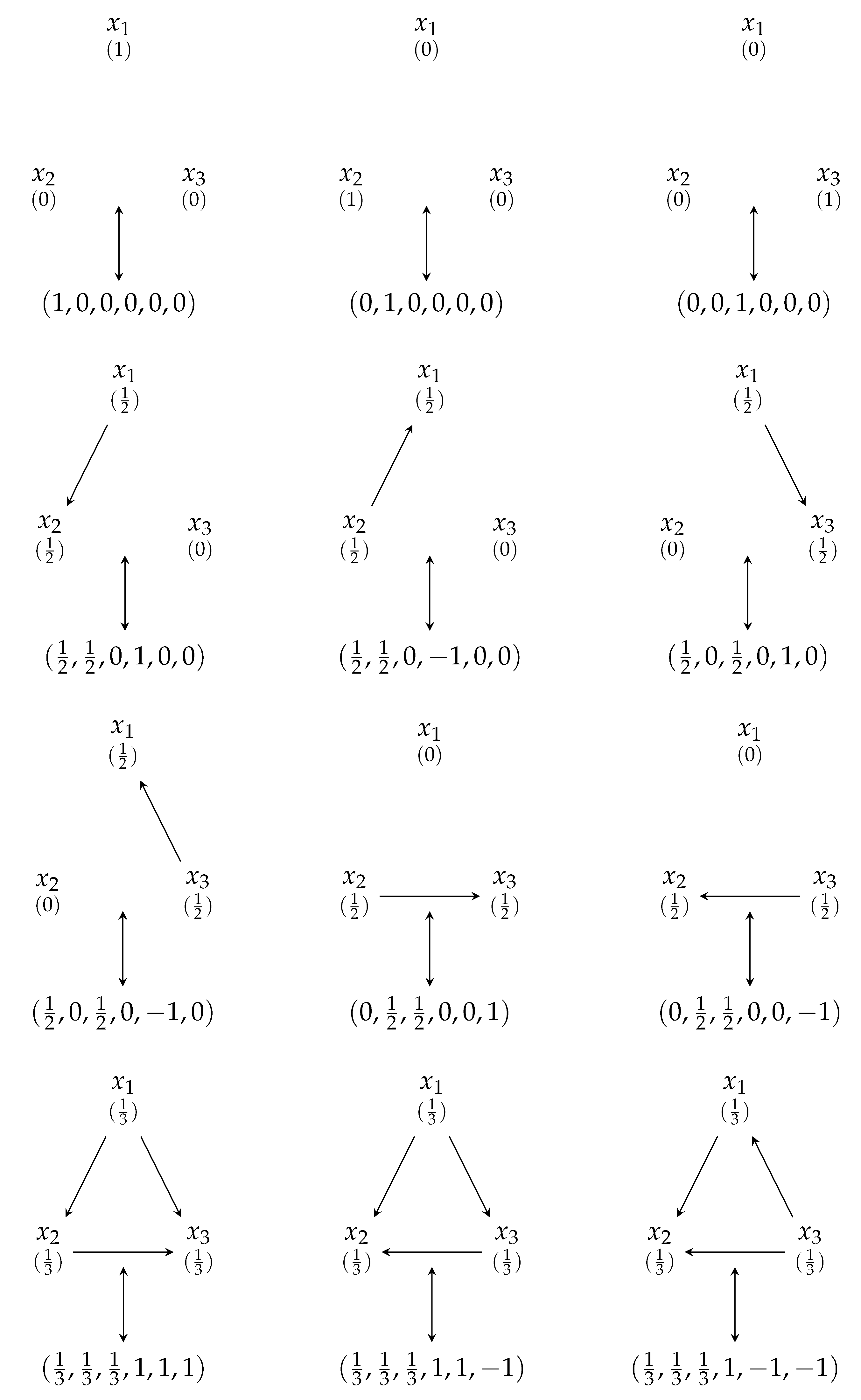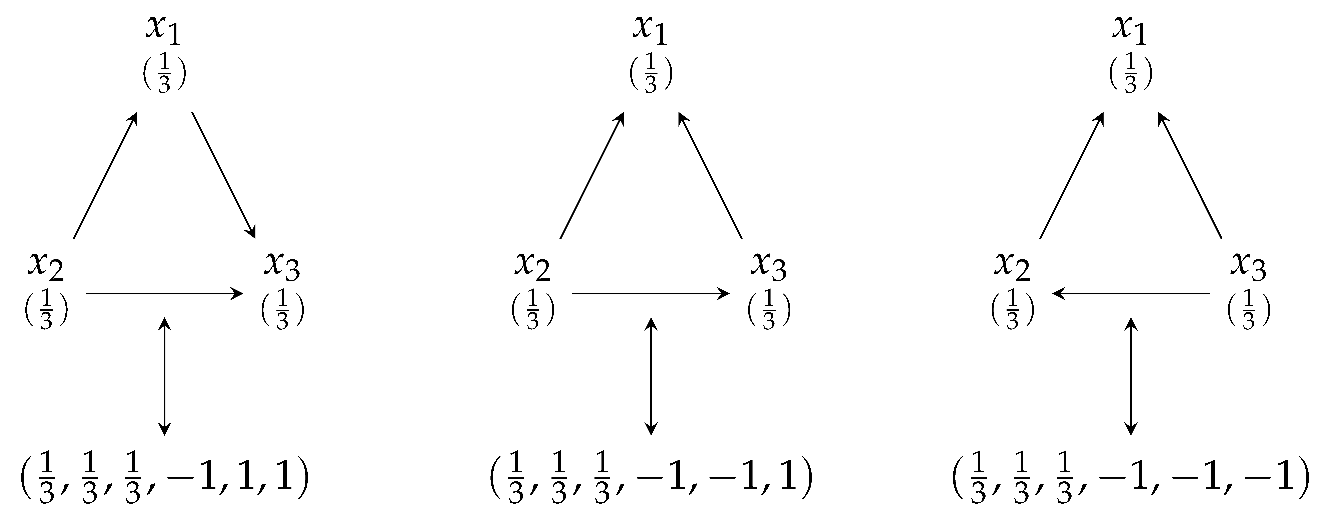$(·)$ denotes the component $x_i(1\le i\le q)$ which takes values. By Theorem 1, the full OofA third-degree generalization simplex-centroid design for three components does not have the combinations $(\frac{1}{3},\frac{1}{3},\frac{1}{3},1,-1,1)$ and $(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1,1,-1)$. The directed graphs corresponding to them do not satisfy the triangle rule for vectors. In the same way, we will obtain the one-to-one correspondence between the rows of full OofA mth-degree generalization simplex-centroid designs for q components and their directed graphs.

The numbers of rows N in the full OofA mth-degree generalization simplex-centroid designs for q components with $3\le q\le 10$, $1\le m\le 6$, $m\le q$ are listed in Table 3. Therefore, N increases dramatically as q and m increase. For example, if $q=9$ and $m=6$, there will be N = 79,209. Algorithm 1 will be invalid in [25]. To solve the problem, we give an iterating algorithm which generates full OofA generalization simplex-centroid designs.

Table 3. Number of rows N in the full OofA mth-degree generalization simplex-centroid designs for q components with $3\le q\le 10$, $1\le m\le 6$, $m\le q$.

Degree of Model, m	Number of Components
	$\mathit{q}=3$	4	5	6	7	8	9	10
1	3	4	5	6	7	8	9	10
2	9	16	25	36	49	64	81	100
3	15	40	85	156	259	400	585	820
4	∖	64	205	516	1099	2080	3609	5860
5	∖	∖	325	1236	3619	8800	18,729	36,100
6	∖	∖	∖	1956	8659	28,960	79,209	187,300

3. Algorithm for Obtaining Full OofA Generalization Simplex-Centroid Designs

In this section, we propose an iterative algorithm which generates a full OofA generalization simplex-centroid design for any q and m. Moreover, a series of examples also confirms the use of the proposed algorithm.

Let $d=(x_d,z_d)$ be one of the rows of a full OofA mth-degree generalization simplex-centroid design for q components, where $x_d$ and $z_d$ are the points in the mth-degree generalization simplex-centroid design and correspond to the modified PWO design, respectively. Then row-juxtaposed vector $(x_d,0,z_d,{\mathbf{0}}_{\mathbf{q}\times \mathbf{1}})$ must be one of the rows of the full OofA mth-degree generalization simplex-centroid design for $q+1$ components. The rest of the points are $(0,\dots ,\underset{q}{0},1)$, $(\frac{1}{2},0,\dots ,\underset{q}{0},\frac{1}{2})$, $(0,\frac{1}{2},0,\dots ,\underset{q}{0},\frac{1}{2})$, …, $(0,\dots ,0,\underset{q}{\frac{1}{2}},\frac{1}{2})$, …, $(\frac{1}{m},\dots ,\underset{m-1}{\frac{1}{m}},0,\dots ,\underset{q}{0},\frac{1}{m})$, …, $(0,\dots ,0,\underset{q-m+2}{\frac{1}{m}},\dots ,\frac{1}{m})$. By Theorem 1, there is one-to-one correspondence between the abovementioned points and their modified PWO designs by their directed graphs. Row-juxtaposing the abovementioned points and their modified PWO designs (i.e., stacking the point x and its PWO design z), we then obtain the full OofA mth-degree generalization simplex-centroid design for $q+1$ components. Hence, we have the following Algorithm 1.

Algorithm 1: Generate full OofA mth-degree generalization simplex-centroid design for q is an expected value.

Step 1. Regard the full OofA second-degree generalization simplex-centroid design for two components as an original design.

Step 2. If $d=(x_d,z_d)$ is one of the rows of the original design, then the row vector $(x_d,0,z_d,0,0)$ must be one of the rows of the full OofA second-degree generalization simplex-centroid design for 3 components. The rest of the points with a full OofA second-degree generalization simplex-centroid design for 3 components are $(0,0,1)$, $(0,\frac{1}{2},\frac{1}{2})$, $(\frac{1}{2},0,\frac{1}{2})$. Then, there is one-to-one correspondence between such points and PWO designs by their directed graphs. Row-juxtaposing such points and their modified PWO designs, we then obtain the full OofA second-degree generalization simplex-centroid design for 3 components.

Step 3. By step 2, we will obtain the full OofA mth-degree generalization simplex-centroid designs for $q+1$ components. Replicate the above step until q is an expected value.

The rows of the full OofA mth-degree generalization simplex-centroid design for q components must be the rows of the full OofA $(m+1)$th-degree generalization simplex-centroid design for q components. The rest of the points with full OofA $(m+1)$th-degree generalization simplex-centroid design for q components are $\left(\genfrac{}{}{0pt}{}{q}{m}\right)$ permutations of $(\underset{m}{\underbrace{\frac{1}{m},\dots ,\frac{1}{m}}},0,\dots ,0)$. By Theorem 1, there is one-to-one correspondence between such points and PWO designs by their directed graphs. Row-juxtaposing such points and their modified PWO designs, we then obtain the full OofA $(m+1)$th-degree generalization simplex-centroid design for q components. Then, we have the following Algorithm 2.   

Algorithm 2: Algorithm for finding the full OofA mth-degree generalization simplex-centroid designs for q components respectively.

Step 1. The rows of the full OofA mth-degree generalization simplex-centroid design for q components must be the rows of the full OofA $(m+1)$th-degree generalization simplex-centroid design for q components. The rest of the points with full OofA $(m+1)$th-degree generalization simplex-centroid design for q components are $\left(\genfrac{}{}{0pt}{}{q}{m}\right)$ permutations of $(\underset{m}{\underbrace{\frac{1}{m},\dots ,\frac{1}{m}}},0,\dots ,0)$. By Theorem 1, there is one-to-one correspondence between such points and PWO designs by their directed graphs. Row-juxtaposing above mentioned points and the corresponding PWO designs, we then obtain the full OofA $(m+1)$th-degree generalization simplex-centroid design for q components.

Step 2. By step 1, we will obtain the full OofA $(m+1)$th-degree generalization simplex-centroid designs for q components. Replicate the above step until m is an expected value.

Example 1.

Consider the construction of a full OofA third-degree generalization simplex-centroid design for 3 components. For the full OofA second-degree generalization simplex-centroid design for two components, the row vectors are $(1,0,0)$, $(0,1,0)$, $(\frac{1}{2},\frac{1}{2},1)$, $(\frac{1}{2},\frac{1}{2},-1)$. By Algorithm 1, the row vectors $(1,0,0,0,0,0)$, $(0,1,0,0,0,0)$, $(\frac{1}{2},\frac{1}{2},0,1,0,0)$, $(\frac{1}{2},\frac{1}{2},0,-1,0,0)$ are the rows of the full OofA second-degree generalization simplex-centroid design for three components. The rest of the points are $(0,0,1)$, $(0,\frac{1}{2},\frac{1}{2})$, $(\frac{1}{2},0,\frac{1}{2})$. By Theorem 1, there is one-to-one correspondence between such points and PWO designs by their directed graphs. Then, the row vectors $(0,0,1,0,0,0)$, $(0,\frac{1}{2},\frac{1}{2},0,0,1)$, $(0,\frac{1}{2},\frac{1}{2},0,0,-1)$, $(\frac{1}{2},0,\frac{1}{2},0,1,0)$, $(\frac{1}{2},0,\frac{1}{2},0,-1,0)$ are the rows of the full OofA second-degree generalization simplex-centroid design for three components. By Algorithm 2, the rows of the full OofA second-degree generalized simplex-centroid design for three components must be the rows of the full OofA third-degree generalized simplex-centroid design for three components. The remaining point is $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. By Theorem 1, there is one-to-one correspondence between such points and PWO designs by their directed graphs. Then, the row vectors $(\frac{1}{3},\frac{1}{3},\frac{1}{3},1,1,1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},1,1,-1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},1,-1,-1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1,1,1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1,-1,1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1,-1,-1)$ are the rows of the full OofA third-degree generalization simplex-centroid design with for three components. Hence, the rows of the full OofA thrid-degree generalization simplex-centroid design for three components are $(1,0,0,0,0,0)$, $(0,1,0,0,0,0)$, $(0,0,1,0,0,0)$, $(\frac{1}{2},\frac{1}{2},0,1,0,0)$, $(\frac{1}{2},\frac{1}{2},0,-1,0,0)$, $(0,\frac{1}{2},\frac{1}{2},0,0,1)$, $(0,\frac{1}{2},\frac{1}{2},0,0,-1)$, $(\frac{1}{2},0,\frac{1}{2},0,1,0)$, $(\frac{1}{2},0,\frac{1}{2},0,-1,0)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},1,1,1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},1,1,-1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},1,-1,-1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1,1,1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1,-1,1)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1,-1,-1)$.

4. Conclusions

An OofA mixture experiment is a kind of experiment in which the response is affected by the addition order of components or materials and the proportions of mixture experiments. The order-of-addition (OofA) experiment is critical when the addition order of experimental factors and the mixture components have definite influence on the response. An efficient OofA mixture experiment can help experimenters not only find an optimal order but also search for a optimal arrangement for mixture components. We proposed a new algorithm which generates full OofA mth-degree generalization simplex-centroid designs for q components and discussed the construction of full OofA generalization simplex-centroid designs for mixture experiments. There is one-to-one correspondence between the rows of the full OofA generalization simplex-centroid design and the specific direction graphs. Comparing our algorithms and Algorithm 1 in [25], Algorithm 1 in [25] is invalid for $q=9$ and $m=6$. However, our algorithms are still valid. The direction graph approach also extends to others of the field in OofA experiments. Using Algorithms 1 and 2, experimenters obtain full OofA generalization simplex-centroid designs for any q and m by computer searching. Finally, the full OofA generalization simplex-centroid designs with $q=4$, $m=2,3,4$ are tabulated in Appendix A.