Abstract
Previous research showed that employing results from meta-analyses of relevant previous fMRI studies can improve the performance of voxelwise Bayesian second-level fMRI analysis. In this process, prior distributions for Bayesian analysis can be determined by information acquired from the meta-analyses. However, only image-based meta-analysis, which is not widely accessible to fMRI researchers due to the lack of shared statistical images, was tested in the previous study, so the applicability of the prior determination method proposed by the previous study might be limited. In the present study, whether determining prior distributions based on coordinate-based meta-analysis, which is widely accessible to researchers, can also improve the performance of Bayesian analysis, was examined. Three different types of coordinate-based meta-analyses, BrainMap and Ginger ALE, and NeuroQuery, were tested as information sources for prior determination. Five different datasets addressing three task conditions, i.e., working memory, speech, and face processing, were analyzed via Bayesian analysis with a meta-analysis informed prior distribution, Bayesian analysis with a default Cauchy prior adjusted for multiple comparisons, and frequentist analysis with familywise error correction. The findings from the aforementioned analyses suggest that use of coordinate-based meta-analysis also significantly enhanced performance of Bayesian analysis as did image-based meta-analysis.
1. Introduction
In fMRI analysis, how to threshold a statistical image resulting from the analysis has been a significant issue. As fMRI analysis involves testing more than a hundred thousand voxels in a simultaneous manner, fMRI researchers have been concerned about how to address the potential inflation of false positives originating from multiple comparisons [1]. For instance, one recent study reported that multiple comparison correction methods implemented in widely used fMRI analysis tools, such as AFNI, SPM, and FSL, are likely to inflate false positives [2]. Following this study, researchers have retested the validity of the tools and attempted to address the aforementioned issue in various ways [3,4,5]. Hence, it would be necessary to consider and examine how to address potential issues and problems associated with multiple comparison correction and inflated false positives in fMRI analysis, which involves simultaneous multiple tests.
In addition to the aforementioned issue associated with inflated false positives and thresholding, the interpretation of resultant p-values could also be problematic in traditional frequentist fMRI analysis. Even if it is possible to control potential false positives through multiple comparison correction, it is still unclear whether resultant p-values can be used to examine whether a hypothesis of interest, instead of a null hypothesis, is supported by evidence [6]. Thus, the use of p-values could be epistemologically inappropriate for hypothesis testing [7]. For example, even if a t-test reports p < 0.01, the resultant p-value does not mean that the likelihood that a hypothesis of interest, i.e., there is a significant non-zero difference or effect, is the case is 99%. Instead, the p-value can only indicate whether a null hypothesis is likely to be rejected [6,8]. Even if the null hypothesis is highly likely to be rejected, such as fact does not directly support an alternative hypothesis. Given that researchers are primarily interested in whether evidence supports their alternative hypothesis regarding the presence of a significant effect, this epistemological issue, associated with traditional frequentist fMRI analysis, shall be carefully considered.
As a possible way to address the aforementioned issues associated with traditional frequentist fMRI analysis, several researchers have suggested the use of the Bayesian approach in fMRI analysis. At the epistemological level, the Bayesian approach is more suitable for directly testing a hypothesis of interest in lieu of a null hypothesis. Frequentist analysis employing p-values is primarily concerned about the extremity of the observed data given a hypothesis, P(D|H). However, Bayesian analysis is more interested in a posterior probability, which is about to what extent a hypothesis is likely to be the case given specific data, P(H|D) [6,7,9]. Furthermore, Bayesian statisticians argue that the Bayesian approach is not very susceptible to the inflated false positives associated with multiple comparisons, since it is not based on frequentist assumptions. For example, the Bayesian approach does not strongly rely on the Type I error paradigm, which is about false positives [10].
In fact, as an alternative approach in fMRI analysis with methodological and epistemological merits, the Bayesian approach has been implemented in analysis tools in the field. Some widely used analysis tools, such as SPM, have implemented the Bayesian approach possessing the aforementioned methodological merits [11]. A recent study demonstrated that the Bayesian analysis implemented in SPM 12 outperformed frequentist analysis in terms of consistency [12]. Moreover, researchers have also developed open source tools, such as BayesfMRI and BayesFactorFMRI, that are customized and specialized for the Bayesian analysis of fMRI data [13,14].
Although the Bayesian approach has methodological merits and has demonstrated improvements in the performance of fMRI analysis, as reported in the previous studies [12], several issues that can emerge while applying the approach in fMRI analysis should be carefully examined. First, in the previous studies, how to address the multiple comparison correction in Bayesian analysis was not clearly addressed. Although Bayesian statisticians are not very concerned about the issue of inflated false positives, as previously mentioned [10], due to the nature of fMRI analysis, which is involved in the simultaneous tests of numerous voxels, some have been concerned about whether the Bayesian approach is capable of resolving the problem of inflated false positives in a straightforward manner. As one possible solution, one recent study [15] has attempted to implement multiple comparison correction in voxelwise fMRI analysis by adjusting prior distributions based on the number of voxels to be tested [16,17].
Second, although the issue of multiple comparison was able to be addressed, whether the prior distributions to be used are reasonably and plausibly determined could also be problematic. As even slight changes in prior distributions may significantly alter the outcomes of Bayesian analysis [18,19], prior distributions should be carefully determined. The prior distributions employed in the previous study [20] were in fact default Cauchy prior distributions, which were not actually informed by the previous information. In fact, there have been concerns regarding the potential arbitrariness existing in default priors [21]. As a way to address the issue, the use of informative priors, priors determined based on results from relevant previous studies, can be considered. Researchers who applied the aforementioned approach to determine prior distributions have reported that the use of informative priors resulted in fewer biased outcomes and improved analysis performance [22,23,24]. In addition, in the case of voxelwise Bayesian fMRI analysis, when prior distributions were determined based on the results from the Bayesian image-based meta-analyses of relevant previous fMRI studies, the performance was significantly improved in terms of sensitivity and selectivity [20].
Although the concerns regarding Bayesian fMRI analysis, those associated with multiple comparison correction and the determination of prior distributions, can be addressed by determining prior distributions based on meta-analysis [15,20], a major practical issue may hinder the wide employment of the method in the field. In a previous study [20], the determination of informed prior distributions was performed with results from image-based fMRI meta-analyses that could not be easily performed in ordinary cases. To perform image-based meta-analysis, researchers must have access to statistical images produced by relevant previous studies conducted by other researchers. Although there are several open repositories to share such images (e.g., NeuroVault, OpenfMRI), it is difficult to acquire large scale image data for every research topic [20,25]. Of course, compared with coordinate-based meta-analysis, which is more accessible to researchers and has been widely employed in the field, image-based meta-analysis possesses methodological advantages [25,26]. For instance, image-based meta-analysis is performed with actual statistical images, instead of information of peak voxel coordinate information, so it does not estimate significant cluster information (e.g., size, shape), but meta-analyzes the real activity information reported in previous studies. As a result, image-based meta-analysis shows a better analysis performance compared with coordinate-based meta-analysis. Despite such superiority, the lack of accessible large scale statistical image data may prohibit researchers from feasibly performing image-based meta-analysis, and, thus, determining prior distributions based on such meta-analysis could also be difficult.
Hence, to address the aforementioned issue related to image-based meta-analysis and its application in prior determination, in the present study, the use of coordinate-based meta-analysis for prior determination was implemented and tested. First, based on the procedures that were used to determine informative priors based on image-based meta-analysis, how to design informative priors with a result from coordinate-based meta-analyses was considered. While developing the procedure for prior determination, two tools for large scale coordinate-based fMRI meta-analysis, Ginger ALE (activation likelihood estimation) [27,28,29] and NeuroQuery [30], were utilized. Second, after performing voxelwise Bayesian second-level fMRI analyses with prior distributions determined by coordinate-based meta-analyses, whether the use of coordinate-based meta-analyses, instead of image-based meta-analyses, in a prior determination resulted in a significant reduction of performance of Bayesian fMRI analysis was tested. In the present study, to what extent the analysis results overlapped with results from large scale fMRI meta-analyses was examined. Based on the performance evaluation results, the potential values, implications, and limitations of the prior determination procedure based on coordinate-based meta-analysis were discussed.
2. Experimental Procedure
2.1. Materials
Source code and data files to test the features introduced in the present study are available via GitHub (https://github.com/hyemin-han/Prior-Adjustment-CBM (accessed on 13 January 2022)).
2.1.1. Statistical Image Datasets for Analyses
To apply and test different prior determination methods, in the present study, a total of five different datasets containing statistical brain images that were created from first-level fMRI analyses addressing three different categories of task conditions were used. The employed datasets are available via open repositories (e.g., NeuroVault, SPM tutorial file repository; see Table 1 further details about how to obtain them). All datasets used in the analyses in the present study are available for free download under CC0 License (NeuroVault) or the GNU General Public License (SPM). First, three different datasets with statistical images were created from three fMRI experiments focusing on the working memory [31,32,33,34]. Second, one dataset containing statistical images was generated from an fMRI experiment that examined the neural correlates of speech processing [34]. Third, one dataset with statistical images files were created by an fMRI experiment that focused on the neural correlates of face processing [35]. Further details, including the bibliographic information, sample size, task condition, and repository link, regarding each dataset are presented in Table 1. All image files to be analyzed were acquired in the format of NIfTI.

Table 1.
List of datasets analyzed in the present study.
2.1.2. Meta-Analysis Results for Prior Determination and Performance Evaluation
In the present study, brain images reporting results from meta-analyses of previous fMRI studies were employed for prior determination and performance evaluation (see Table 2 for further details about the images). First, information required for prior determination, including the proportion of significant voxels within each image, mean and standard deviation of voxel values, was extracted from each image before performing Bayesian second-level fMRI analysis. Second, upon completion of Bayesian analysis, analysis result images were compared with meta-analysis result images for performance evaluation.

Table 2.
Meta-analyses used for prior determination and performance evaluation.
For these purposes, four different meta-analysis methods were employed. First, image-based Bayesian fMRI data meta-analysis was performed. Statistical images reporting results from previous fMRI studies were obtained from NeuroVault, and they were meta-analyzed with a tool for image-based Bayesian fMRI meta-analysis implemented in BayesFactorFMRI [14,25]. Bayesian image-based meta-analysis was applied only while examining the three working memory datasets, because statistical images reporting results from previous fMRI experiment relevant to two other topic, speech and face processing, were not sufficiently available on NeuroVault.
Second, coordinate-based meta-analysis was performed by employing Sleuth, a tool to search the BrainMap database, and Ginger ALE. The database containing coordinate information of significant activation foci that has been reported in previous fMRI studies, BrainMap, was explored with Sleuth [36]. By entering task condition or topic keywords, activation foci information was automatically crawled from relevant previous studies registered in BrainMap, and, then, was exported into text files. Then, the exported text files containing coordinate information were imported by Ginger ALE for coordinate-based meta-analysis [28,29,37]. Once all meta-analysis procedures were completed, one unthresholded statistical image reporting activation likelihood in analyzed voxels and one thresholded image were generated for each completed meta-analysis [27,38]. See Table 2 for further details about which search terms were used in Sleuth and which parameters were used in Ginger ALE (e.g., cluster forming threshold, cluster level threshold).
Third, large-scale fMRI meta-analysis was conducted with NeuroSynth, a web-based tool for automatized large-scale meta-analysis and synthesis of previous fMRI studies [39]. NeuroSynth (https://neurosynth.org/ (accessed on 13 January 2022)) performs meta-analysis with activation foci coordinate information that has been automatically extracted from previously published articles. Such information was associated with key terms (e.g., “working memory,” “speech,” “face”) for further analyses (see Table 2 for further details about key terms used in the present study). Once a key term was entered to NeuroSynth, it generated a statistical map reporting which voxels showed significant activity associated with the entered key term. In the present study, a result from an association test, which identifies voxels reporting significant activity within a specific key term condition controlled for baseline activity across all other conditions, was used. According to previous research, the association test based on large scale database is a possible way to examine brain regions specifically associated with a psychological functionality of interest while minimizing problems that can emerge from erroneous reverse inference [40,41]. The generated image was automatically thresholded with a false discovery rate corrected threshold p < 0.01. NeuroSynth images were used only for evaluation performance, not for prior determination, because unthresholded original statistical images were not available for download at NeuroSynth.
Fourth, images generated with NeuroQuery were also used for prior determination and performance evaluation. NeuroQuery is a web based tool to generate a statistical image that reports which voxels are most likely to show activity when a query is entered [30]. Unlike NeuroSynth, which primarily tests consistency of activation foci reported across different studies when a key term is given, NeuroQuery mainly intends to predict which brain regions are more likely to report activity when a topic query is given [42]. To generate NeuroQuery images, designated keyword queries were entered to the system (see Table 2 for further details about the used keywords). Generated NeuroQuery images reported the predicted likelihood of activity in each voxel within the provided keyword condition in terms of z statistics. Following the guidelines suggested by the developers, the generated z maps were thresholded at z ≥ 3 [30].
2.2. Basis of Voxelwise Second-Level fMRI Analysis
In the present study, the brain images reporting results from first-level (individual-level) fMRI analysis were analyzed at the second (group) level. As explained above, five datasets containing first-level analysis results across three task categories (i.e., working memory, speech, face) were acquired from open repositories for this purpose. For inputs, contrast images reporting differences in activity across two conditions (e.g., n-back vs. control) at the individual level were used. These input images were converted with a standard MNI space for further analyses.
Basically, the voxelwise second-level analysis was performed following the general rules of t-test. Let us assume that we are interested in comparing brain activity in a specific voxel between two conditions, Condition A and B. The current second-level fMRI analysis is carried out by performing a one-sample t-test examining whether brain activity value in a specific voxel is significantly higher (or lower) than zero. For each voxel, results from first-level (or individual-level) fMRI analyses are used as inputs. Each input value, a contrast value reported by a specific first-level fMRI analysis, represents the calculated difference in brain activity in Condition A versus Condition B in a specific subject. Then, with the input values, a one-sample t-test is performed following , where is the mean brain activity value, s is the standard deviation of brain activity values, and n is the number of subjects analyzed at the first level. With the result from the conducted t-test, it is possible to examine whether there is significant brain activity in a specific voxel of interest.
2.3. Voxelwise Bayesian Second-Level fMRI Analysis
In the present study, whether brain activity in a specific voxel of interest, which was examined following the theme of a t-test, was significant was examined through Bayesian approach. Voxelwise Bayesian second-level fMRI analysis, in the present study, was performed with customized R and Python scripts that were modified from BayesFactorFMRI [14]. Bayesian second-level analysis performed in the present study produced an output image that demonstrated the Bayes Factor value in each voxel. Bayes Factor (BFab) indicates to what extent evidence supports a specific hypothesis of interest (Ha) over another (Hb) [8,43]. To calculate Bayes Factor, we need to examine the posterior probability of each hypothesis by updating its prior probability through observing data. Let us assume that P(Ha) indicates the prior probability of Ha associated with our belief about whether Ha is the case before observing data. In the same way, the prior probability of Hb, P(Hb), can also be determined. Through observation, the posterior probability of each hypothesis is updated from its prior probability. The posterior probability of Ha, P(Ha|D), means the likelihood of Ha given data (D). In the same vein, the posterior probability of Hb, P(Hb|D), can also be defined. To calculate the posterior probabilities, the Bayesian updating process is performed following Bayes theorem as follows:
where P(D|H) is the likelihood to observe data (D) given a hypothesis (H) and P(D) is the marginal probability to normalize the constant of the numerator. Both P(D|H) and P(D) can be acquired by observing data.
When two posterior probabilities, P(Ha|D) and P(Hb|D), are acquired, Bayes Factor BFab can be calculated. We can start with considering the posterior odds, P(Ha|D)/P(Hb|D), which indicate the relative ratio of P(Ha|D) versus P(Hb|D). These odds shall be calculated as follows [6]:
In this equation, P(D|Ha)/P(D|Hb) indicates Bayes Factor, BFab, where P(Ha)/P(Hb) is the prior odds. We can utilize the value, BFab = P(D|Ha)/P(D|Hb), to examine to what extent evidence (D) supports Ha over Hb. If BFab exceeds 1, evidence is supposed to favorably support Ha in lieu of Hb. If BFab < 1, Hb is deemed to be more likely to be the case given evidence.
Bayesian statisticians have proposed some guidelines about how to interpret Bayes Factors in Bayesian inference [7,8,43]. For instance, when 1/3 < BFab < 3, evidence is deemed to be anecdotal so it would still be unclear whether evidence significantly supports one hypothesis over the other. When BFab ≥ 3, evidence positively supports Ha over Hb. In the same vein, BFab ≥ 10, ≥ 30, and ≥ 100 have been used as indicators for presence of strong, very strong, and extremely strong evidence supporting Ha over Hb, respectively. If BFab becomes smaller than 1/3, we can assume that evidence is more likely to support Hb over Ha. BFab ≤ 1/3, 1/10, 1/30, and 1/100 are deemed to indicate the presence of positive, strong, very strong, and extremely strong evidence supporting Hb over Ha, respectively.
Compared with p-values that have been widely used for frequentist inference, Bayes factors have significant epistemological merit in fMRI research. Let us assume that our hypothesis of interest, H1, is about whether there is a significant non-zero effect in a voxel when two conditions are compared. Then, H0, a null hypothesis, is about whether there is not a significant non-zero effect. If we conduct frequentist analysis, then a resultant p-value indicates more about P(D|H), whether observed data is likely to be the case given a hypothesis, rather than P(H|D), whether the hypothesis is likely to be the case given the data, in which we, fMRI researchers are primarily interested, in most cases, unless we intend to examine null effects. In fact, p-values do not inform us about whether H1, an alternative hypothesis, shall be accepted; instead, they are only related to whether H0, a null hypothesis, shall be rejected. Interpreting p-values is also challenging. Unlike Bayes factors, which are about to what extent evidence supporting a hypothesis of interest, p-values are about the extremity of the observed data given the hypothesis. As fMRI researchers are primarily interested in testing presence of a significant non-zero effect (H1) instead of its absence (H0), at the epistemological level, in terms of interpretation, Bayes factors would be more useful than p-values.
Given voxelwise Bayesian second-level fMRI analysis was performed in the present study, for each voxel, BF10, regarding to what extent evidence supporting presence of a significant effect (activity difference) in the voxel, was calculated with input images. Then, to identify voxels that reported significant activity, the resultant BF10 values were thresholded at BF10 ≥ 3, indicating presence of positive evidence supporting a non-zero effect in each voxel.
2.4. Prior Determination Based on Results from Meta-Analyses
Although Bayes factors have the aforementioned methodological merits, one fundamental issue should be considered and addressed while employing Bayesian inference in fMRI analysis. To estimate a posterior probability, P(H|D), and Bayes factor, BF, researchers need to determine a prior probability, P(H), which is updated with data, D. Given a change in P(H) significantly impacts the resultant P(H|D) [18,19,20], determination of P(H) is critical, and, thus, should not be arbitrary. As a possible way to address this issue, in the previous study that first employed multiple comparison correction in Bayesian second-level fMRI analysis [15], one of the most widely used noninformative prior distributions, the default Cauchy prior distribution, Cauchy (x0 = 0, σ = 0.707), was used [7,8,9]. The Cauchy distribution has been employed as a default prior distribution in the fields of psychology and neuroscience [9]. In fact, it has been utilized in statistical analysis tools for generic purposes in psychological research, such as JASP and BayesFactor R package [8]. The Cauchy distribution has several benefits, such as robustness in BF-based inference and less likelihood to produce false positives compared with other noninformative priors [9], so the distribution has been employed in the present study.
This default Cauchy prior is centered around x0 = 0, while having a scale, σ = 0.707 [8]. Here, x0 determines where the peak of the distribution shall be located. A scale parameter, σ, determines the width of the distribution and fattiness of tails. As σ increases, the distribution becomes more dispersed and has fatter tails. When multiple comparison correction was applied, the scale, σ, was computationally adjusted according to the number of voxels to be tested to control potential false positives. As the number of voxels to be tested increases, σ becomes smaller and the adjusted prior distributions has a steeper peak centered around x0 = 0. Then, the resultant BF becomes smaller, and the thresholding becomes more stringent. As reported, use of the adjusted default Cauchy prior distribution resulted in significant decrease in false positive rates in Bayesian second-level fMRI analysis [15].
In addition to the aforementioned use of the default Cauchy prior distribution after multiple comparison correction, a prior distribution was also determined by a priori information extracted from meta-analysis of relevant previous fMRI studies. In fact, in Bayesian analysis, a prior distribution is about the prior belief that one has before observing actual data [23]. Hence, determining such a prior distribution based on what has found in relevant previous studies is deemed to be philosophically appropriate and is reported to improve analysis performance in general [20,23,44].
As meta-analysis of fMRI is one possible way to examine the pattern of neural activity that can be commonly observable in the task condition of interest while possibly improving statistical power [45,46], information from such meta-analysis should be considered as one reliable and valid source to determine a prior distribution in Bayesian fMRI analysis. There was a previous study that implemented prior determination based on information from meta-analysis, i.e., contrast strength, noise strength (or standard deviation of signal strength in voxels), proportion of significant voxels [20]. This study reported that voxelwise Bayesian second-level fMRI analysis with a prior distribution determined by meta-analysis showed better performance compared with Bayesian analysis with an adjusted default Cauchy prior distribution as well as frequentist analysis.
However, the aforementioned previous study only tested image-based meta-analysis, which is less feasible to conduct compared with coordinate-based meta-analysis due to the lack of available open statistical fMRI images. Thus, in the present study, a prior distribution was determined with results from coordinate-based meta-analysis for the improvement of the applicability of the prior determination procedure in Bayesian fMRI analysis. As mentioned previously, three pieces of information, a contrast strength, a standard deviation of the voxel strength, and a proportion of significant voxels, acquired from meta-analysis, was used for prior determination [20]. First, the contrast strength (C) was defined in terms of the difference in the mean strength in significant voxels versus the mean strength in nonsignificant voxels. Second, the standard deviation of the voxel strength (N) was simply calculated in terms of the standard deviation of the values in all meta-analyzed voxels, including both significant and nonsignificant voxels. Third, the proportion of significant voxels (R) was determined in terms of the ratio of significant voxels to all meta-analyzed voxels. Based on the aforementioned information, an expected effect size value, X, which was used for determining a prior distribution, can be calculated as follows:
Once X value was calculated, then a Cauchy scale, σ, to determine the prior distribution was numerically calculated with the X value. In this process, σ should satisfy:
where P is a user-defined percentile value; in the previous study, P = 80%, 85%, 90%, and 95% were tested [20]. The P is a hyperparameter that was employed to let users change the overall shape of the adjusted Cauchy prior distribution. When X is constant, a higher P ends up with a smaller Cauchy distribution scale, σ, so the adjusted distribution becomes less dispersed and has a steeper peak at x0. The P value is supposed to be determined by users, so it allows them to customize the shape of the resulting adjusted prior distribution to be used with rationale. As explained in the original study that developed and tested the prior adjustment method [20], use of the P value would be a possible way to customize the shape of the adjusted prior distribution in a less arbitrary manner based on expectation about the overall strength of brain activity in voxels to be analyzed. Following the previous study, the same four P values were applied and tested in the present study. Once σ was calculated based on X, which was acquired with C, N, and R from meta-analysis, voxelwise Bayesian second-level fMRI analysis was performed with a Cauchy distribution, Cauchy (x0 = 0, σ).
2.5. Performance Evaluation
2.5.1. Overlap Index for Evaluation
To compare the performances of different analysis methods (i.e., voxelwise Bayesian second-level fMRI analysis based on an adjusted default Cauchy prior distribution, voxelwise Bayesian second-level fMRI analysis based on a prior distribution determined by meta-analysis, voxelwise frequentist analysis), the thresholded results were compared with results from relevant meta-analyses. As real data, not simulated data, was examined in the present study, it was practically difficult to assume true positives, so results from meta-analyses were used as proxies for true positives. As meta-analyses, particularly those based on large-scale database (i.e., BrainMap, NeuroSynth, NeuroQuery), are capable of demonstrating activation patterns that appear commonly across different studies, they might be practically accessible methods to acquire standards for evaluation although they cannot reveal exact true positives associated with task conditions of interest [47]. Hence, in the present study, following the present studies [47,48], to what extent a thresholded image that generated by each analysis method overlapped with a meta-analysis result image was examined for performance evaluation. As two images showed greater overlap, the tested analysis method was deemed to possess better performance.
The degree of overlap was quantified in terms of an overlap index. For each comparison between an fMRI analysis result image and meta-analysis result image, an overlap index, Iovl, was calculated as follows [47]:
where Vovl was the number of voxels that were significant in both the fMRI analysis result and meta-analysis result images, Vres was the number of significant voxels in the fMRI analysis result image, and Vmet was the number of significant voxels in the meta-analysis result image. Iovl was calculated with a customized R code.
In the present study, performance evaluation was conducted to examine whether voxelwise Bayesian second-level fMRI analysis with a prior distribution determined by meta-analysis showed better performance compared with the aforementioned two other analysis methods. In addition, while analyzing the three working memory datasets, whether use of coordinate-based meta-analysis for prior determination resulted in significant decrease in performance was also tested. Unfortunately, the comparison between application of coordinate-based meta-analysis versus that of image-based meta-analysis was conducted only for the three working memory datasets. Due to the lack of shared statistical images related to the speech and face processing task conditions, the aforementioned comparison could not be carried out in these two cases.
When performance evaluation was performed with the three working memory datasets, results from different types of meta-analyses—Bayesian image-based meta-analysis, coordinate-based meta-analysis with Ginger ALE, NeuroSynth, and NeuroQuery—were employed as standards. For performance evaluation of two other datasets, the result from Bayesian image-based meta-analysis was not used due to the aforementioned lack of available open statistical images.
Similar to the previous studies [15,20], the performance of Bayesian analysis in general was also compared with the performance of frequentist analysis. To conduct this additional analysis, all five datasets were analyzed with SPM 12 [49]. As voxelwise analysis was the main focus of the present study, while conducting frequentist analysis, thresholding was performed with p < 0.05 after familywise error correction at the voxel level. Furthermore, whether employing different P values (i.e., 80%, 85%, 90%, 95%) in prior distribution determination significantly altered performance outcomes was also examined.
2.5.2. Statistical Analysis of Performance Outcomes
For statistical analysis of performance outcomes, frequentist and Bayesian mixed-effects analyses were performed to examine whether the analysis type was significantly associated with Iovl. Frequentist mixed-effects analysis was performed with an R package, lmerTest. In addition to ordinary frequentist mixed-effects analysis, which reports p-values of tested predictors, Bayesian mixed-effect analysis was also performed with BayesFactor. Bayesian mixed-effects analysis is suitable for identifying the best regression model that predicts the dependent variable of interest in simple linear regression [50] as well as multilevel modeling [51]. By employing this method, whether the best regression model identified through Bayesian mixed-effects analysis included the analysis type as a predictor was examined. If the analysis type was included, it was deemed that the employment of different analysis methods was significantly associated with the difference in performance outcomes.
While conducting main statistical analyses, first, whether Bayesian analysis with a prior distribution based on meta-analysis performed significantly better than Bayesian analysis with a default prior distribution and frequentist analysis was tested. This test was conducted to examine whether the findings from the previous study that reported better performance of Bayesian analysis with a prior distribution determined by meta-analysis [20] were replicated in the present study. For this test, frequentist and Bayesian mixed-effects analyses were performed while setting Iovl as the dependent variable, the analysis method (Bayesian analysis with a prior distribution determined by meta-analysis vs. Bayesian analysis with a default prior distribution vs. frequentist analysis) as the fixed effect, and the analyzed dataset, task condition category, and type of meta-analysis result used for performance evaluation as random effects. As explained previously, whether the best regression model included the analysis type as a predictor and whether evidence significantly supported inclusion of the analysis type in the model were tested. Moreover, to conduct auxiliary analysis, the same mixed-effects analyses were performed while employing a different fixed effect, the analysis type further differentiated by four different P values used for prior distribution determination (Bayesian analysis with a prior distribution determined by meta-analysis with four different P values (80%, 85%, 90%, 95%) vs. Bayesian analysis with a default prior distribution vs. frequentist analysis).
Second, whether use of coordinate-based meta-analysis for prior determination in Bayesian fMRI analysis resulted in significant decrease in analysis performance was also examined. As image-based meta-analysis was conducted only with the three working memory datasets, only the results from the analyses of the three working memory datasets were analyzed. The same frequentist and Bayesian mixed-effects analyses were performed to answer the aforementioned question. In these analyses, Iovl was set as the dependent variable, the analysis type (Bayesian analysis with a prior distribution determined by meta-analysis vs. Bayesian analysis with a default prior vs. frequentist analysis) and the type of meta-analysis used for prior determination (coordinate-based meta-analysis vs. image-based meta-analysis) as the two fixed effects, and the analyzed dataset, and type of meta-analysis result used for performance evaluation as random effects.
3. Results
3.1. Voxelwise Second-Level fMRI Analyses
Figure 1 demonstrates the results of the voxelwise second-level fMRI analyses of one sample dataset, DeYoung et al. (2009)’s working memory dataset. The Bayesian analyses based on prior distributions determined by three different information sources, image-based Bayesian meta-analysis (Figure 1A), BrainMap and Ginger ALE (Figure 1B), and NeuroQuery (Figure 1C), resulted in similar activity patterns. However, compared with these cases, when Bayesian analysis with an adjusted default Cauchy prior (Figure 1D) or frequentist analysis with familywise error correction (Figure 1E) was performed, significantly fewer active voxels were reported.
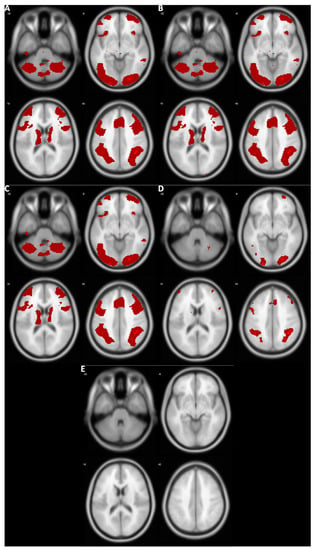
Figure 1.
Results from the analyses of DeYoung et al.’s (2009) working memory dataset. Red: Voxels survived thresholding. (A) Bayesian analysis with a prior distribution determined by image-based meta-analysis. (B) Bayesian analysis with a prior distribution determined by coordinate-based meta-analysis with BrainMap and Ginger ALE. (C) Bayesian analysis with a prior distribution determined by coordinate-based meta-analysis with NeuroQuery. (D) Bayesian analysis with an adjusted default Cauchy prior distribution. (E) Voxelwise frequentist analysis with familywise error correction.
The performance outcomes from all the voxelwise second-level analyses, in terms of Iovl, are presented in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. The results are presented for each dataset, each type of meta-analysis used for prior determination, and each analysis type. In Figure 2, Figure 3 and Figure 4, the results of the analyses of three working memory datasets, DeYoung et al. (2009), Henson et al. (2002), and Pinho et al. (2020), respectively, are presented. In these cases, three subplots report results from Bayesian analyses with prior distributions determined by image-based meta-analysis (Figure 2A, Figure 3A and Figure 4A), BrainMap and Ginger ALE (Figure 2B, Figure 3B and Figure 4B), and NeuroQuery (Figure 2C, Figure 3C and Figure 4C), respectively. In Figure 5A,B, the results from the analyses of Pinho et al.’s (2020) speech dataset are presented. The results of the analyses of Gordon et al.’s (2017) face dataset are demonstrated in Figure 6. In the analyses of these two datasets, two different information sources, BrainMap and Ginger ALE (Figure 6A), and NeuroQuery (Figure 6B), were employed for prior determination.
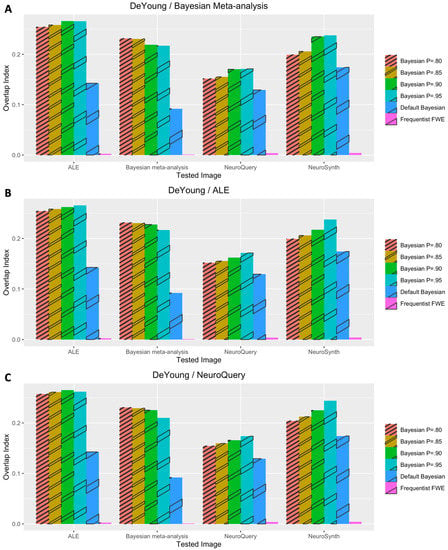
Figure 2.
Performance evaluation with DeYoung et al.’s (2009) dataset. (A) Analysis results when image-based meta-analysis was used for prior determination. (B) Analysis results when coordinate-based meta-analysis with BrainMap and Ginger ALE was used for prior determination. (C) Analysis results when coordinate-based meta-analysis with NeuroQuery was used for prior determination.
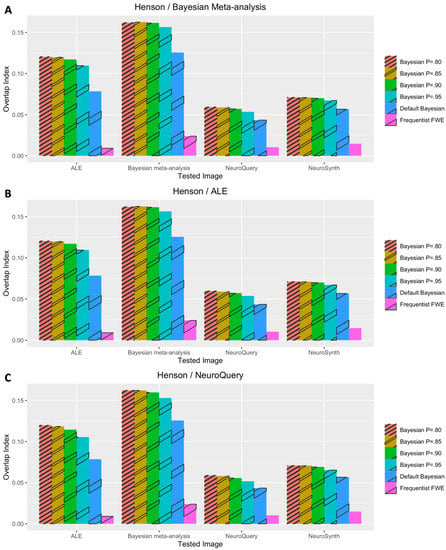
Figure 3.
Performance evaluation with Henson et al.’s (2002) dataset. (A) Analysis results when image-based meta-analysis was used for prior determination. (B) Analysis results when coordinate-based meta-analysis with BrainMap and Ginger ALE was used for prior determination. (C) Analysis results when coordinate-based meta-analysis with NeuroQuery was used for prior determination.
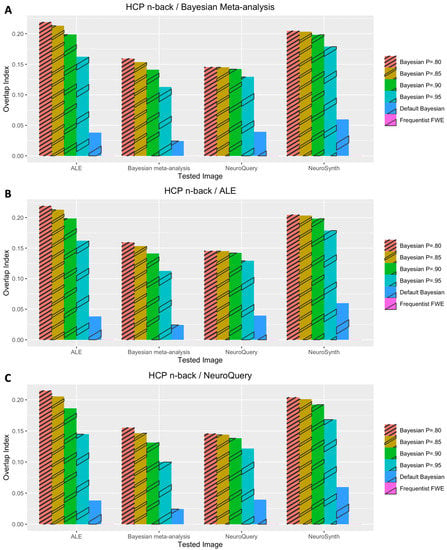
Figure 4.
Performance evaluation with Pinho et al.’s (2020) working memory dataset. (A) Analysis results when image-based meta-analysis was used for prior determination. (B) Analysis results when coordinate-based meta-analysis with BrainMap and Ginger ALE was used for prior determination. (C) Analysis results when coordinate-based meta-analysis with NeuroQuery was used for prior determination.
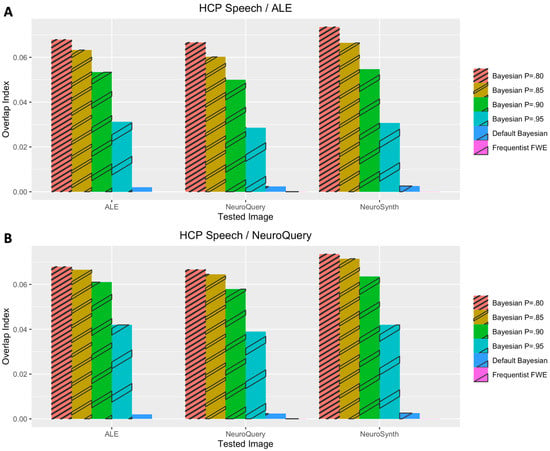
Figure 5.
Performance evaluation with Pinho et al.’s (2020) speech dataset. (A) Analysis results when coordinate-based meta-analysis with BrainMap and Ginger ALE was used for prior determination. (B) Analysis results when coordinate-based meta-analysis with NeuroQuery was used for prior determination.
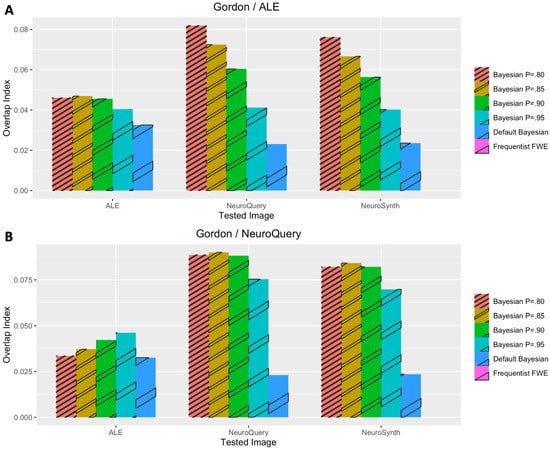
Figure 6.
Performance evaluation with Gordon et al.’s (2017) dataset. (A) Analysis results when coordinate-based meta-analysis with BrainMap and Ginger ALE was used for prior determination. (B) Analysis results when coordinate-based meta-analysis with NeuroQuery was used for prior determination.
In general, Iovls resulting from meta-analysis-informed Bayesian analyses were significantly higher than those resulting from Bayesian analyses with a default Cauchy prior distribution or frequentist analyses. The aforementioned higher Iovls of Bayesian analyses with prior distributions determined by meta-analyses were reported from the analyses of all datasets, regardless of which type of meta-analysis was used for prior determination.
3.2. Statistical Analyses of Performance Outcomes
First, whether meta-analysis informed Bayesian analysis outperformed Bayesian analysis with an adjusted default Cauchy prior distribution and frequentist analysis was examined in the present study. When these three analysis types were compared, Bayesian mixed-effects analysis indicated that the regression model including the analysis type as a predictor was the best model, BF = 2.68 × 1084. In addition, the inclusion of the analysis type was significantly substantiated by evidence, BF = 5.44 × 1064. The result from frequentist mixed-effects analysis reported that meta-analysis informed Bayesian analysis outperformed both Bayesian analysis with a default prior distribution, t (259.97) = −14.43, B = −0.07, se = 0.00, p < 0.001, Cohen’s d = −1.79, and frequentist analysis, t (260.32) = −27.35, B = −0.14, se = 0.01, p < 0.001, Cohen’s d = −3.39.
Furthermore, when the different P values used for prior determination were included in the analysis type predictor in the regression model, similar to the previous case, the model including the analysis type was indicated as the best model, BF = 8.38 × 1081. Inclusion of the analysis type was also supported by evidence, BF = 1.69 × 1062. When meta-analysis informed Bayesian analysis with P = 80% was set as the reference group, frequentist mixed-effects analysis indicated that it outperformed meta-analysis informed Bayesian analysis with P = 95%, t (257.00) = −2.45, B = −0.01, se = 0.00, p = 0.01, Cohen’s d = −0.31, Bayesian analysis with a default prior distribution, t (257.00) = −12.30, B = −0.07, se = 0.00, p < 0.001, Cohen’s d = −1.53, and frequentist analysis, (257.20) = −23.27, B = −0.15, se = 0.00, p < 0.001, Cohen’s d = −2.90. However, such differences were not found when it was compared with meta-analysis informed Bayesian analysis with different P values, 85%, t (257.00) = −0.16, B = −0.00, se = 0.00, p = 0.87, Cohen’s d = −0.02, and 90%, t (257.00) = −0.64, B = −0.00, se = 0.00, p = 0.52, Cohen’s d = −0.08.
Second, the performance of Bayesian analysis with a prior distribution determined by coordinate-based meta-analysis was also examined. In this process, only the working memory datasets were analyzed due to the availability of public statistical images for image-based meta-analysis. When the two candidate predictors, the analysis type (meta-analysis-informed Bayesian vs. Bayesian with a default prior distribution vs. frequentist) and the type of meta-analysis used for prior determination (image-based meta-analysis vs. coordinate-based meta-analysis with BrainMap and Ginger ALE vs. coordinate-based meta-analysis with NeuroQuery) were tested, the Bayesian mixed-effects model analysis indicated that the model with the fixed effect of the analysis type but without the fixed effect of the type of meta-analysis used for prior determination was the best model, BF = 2.40 × 1067. Similarly, the inclusion of the analysis type was substantiated by evidence, BF = 7.34 × 1058, while that of the meta-analysis type was not, BF = 0.06. When the best model without the type of meta-analysis used for prior determination was examined, compared with Bayesian analysis with meta-analysis-informed prior determination, both Bayesian analysis with a default prior distribution, t (202.00) = −13.67, B = −0.08, se = 0.01, p < 0.001, Cohen’s d = −1.92, and frequentist analysis reported worse performance, t (202.00) = −27.36, B = −0.16, se = 0.01, p < 0.001, Cohen’s d = −3.85.
A similar result was reported when the analysis type variable was modified to take into account four different P values within the meta-analysis-informed Bayesian analysis. Bayesian mixed-effects analysis reported that the best model (BF = 2.18 × 1064) included the type of analysis but not the type of meta-analysis used for prior determination. Although the inclusion of the analysis type in the best model was substantiated by evidence, BF = 6.7 × 1055, that of the type of meta-analysis employed for prior determination was not, BF = 0.05. When the best model was examined, Bayesian analysis with P = 80% outperformed Bayesian analysis with P = 95%, t (257.00) = −2.45, B = −0.01, se = 0.01, p = 0.02, Cohen’s d = −0.23, Bayesian analysis with a default prior distribution, t (257.00) = −12.30, B = −0.07, se = 0.01, p < 0.001, Cohen’s d = −1.60, and frequentist analysis, t (257.20) = −23.27, B = −0.15, se = 0.01, p < 0.001, Cohen’s d = −3.14. However, it did not show better performance compared with when P = 85%, t (257.00) = −0.16, B = −0.00, se = 0.01, p = 0.87, Cohen’s d = −0.01, or P = 90% was employed in Bayesian analysis, t (257.00) = −0.64, B = −0.00, se = 0.01, p = 0.52, Cohen’s d = −0.04.
4. Discussion
In the present study, how to utilize results from the coordinate-based meta-analyses of relevant previous fMRI studies for prior distribution determination in voxelwise Bayesian second-level fMRI analysis was examined. As Han (2021a) only tested prior determination based on image-based meta-analysis in a previous study, in the present study, how the employment of coordinate-based meta-analysis, which has been widely used in the field, influenced the performance of Bayesian fMRI analysis was investigated. In general, when the performance was compared with the performance of Bayesian analysis with a default prior distribution and that of frequentist analysis, the use of the newly invented prior determination method resulted in a significantly better performance in terms of overlaps with large-scale meta-analysis results, as reported in the previous study [20]. In the examination of the working memory datasets, the results showed that the Bayesian analysis based on coordinate-based meta-analysis did not result in a worse performance compared with that based on image-based meta-analysis. Finally, in the auxiliary analysis of the effects of different P values, Bayesian analysis with P = 80% showed a better performance than the Bayesian analysis with P = 95% and a default prior distribution, and frequentist analysis; however, Bayesian analysis with p = 85% or 90% did not show a significantly different performance.
The most noteworthy finding from the present study was that information from the coordinate-based meta-analysis of relevant previous fMRI studies can be used to determine a prior distribution in voxelwise Bayesian second-level fMRI analysis. The present study, which developed and tested the aforementioned novel method for prior determination, was motivated by a practical limitation in the previous study which employed image-based meta-analysis. Although image-based meta-analysis has been reported to produce less biased meta-analysis outcomes compared with coordinate-based meta-analysis [25,26], it requires researchers to collect statistical images reporting results from previous studies to be meta-analyzed. Of course, some statistical images are shared via online repositories, such as NeuroVault [52], as mentioned in the previous and present studies [20,25]. However, the number of available images did not appear to be sufficient to conduct a meta-analysis across diverse task conditions. Unlike image-based meta-analysis, coordinate-based meta-analysis to acquire information required for prior determination can be feasibly done even in a large scale through BrainMap and Ginger ALE [28,36,53] as well as a web-based tool, NeuroQuery [30]. Hence, demonstrating that Bayesian fMRI analysis based on coordinate-based meta-analyses is capable of producing reliable and valid analysis results would be a possible way to convince more fMRI researchers to use Bayesian fMRI analysis with a meta-analysis informed prior distribution in their studies.
Although coordinate-based meta-analysis has been reported to demonstrate a worse performance compared with image-based meta-analysis [25,26], there might be a reason why the use of coordinate-based meta-analysis in prior determination did not result in a worse analysis performance in the present study. One major limitation of coordinate-based meta-analysis would be that it utilizes coordinate information reported in published articles instead of real statistical images that contain significantly more information regarding actual experimental outcomes [25]. However, the methods for coordinate-based meta-analysis employed in the present study, BrainMap-Ginger ALE and NeuroQuery, were conducted with a large-scale coordinate information database [30,36,53,54]. Thus, the scale of the meta-analyzed datasets might be a possible factor that mitigates the aforementioned methodological limitation of coordinate-based meta-analysis. For instance, in the case of the working memory task condition, only six statistical images from previous studies were meta-analyzed with image-based meta-analysis [20]; however, Ginger ALE was performed with the coordinate information of 301 experiments extracted from BrainMap, and NeuroQuery result was based on information from 74 previous publications. Given both Ginger ALE and NeuroQuery were able to estimate activation patterns based on large-scale data, results from the coordinate-based meta-analyses might successfully approximate the common activation patterns that could be discovered via image-based meta-analysis. Hence, the use of coordinate-based meta-analysis for prior distribution determination might not significantly worsen the performance of voxelwise Bayesian second-level fMRI analysis in the present study.
Furthermore, in agreement with previous studies that compared Bayesian versus frequentist approaches in voxelwise second-level fMRI analysis [12,15,20], in the present study, Bayesian analysis outperformed frequentist analysis in general, regardless of which method was used to determine prior distributions. The reported superiority of voxelwise Bayesian analysis in the present study would support the point that Bayesian analysis can contribute to improvement of fMRI analysis in general. In addition, by examining how the use of coordinate-based meta-analysis for prior distribution impacted performance of Bayesian analysis, it would be possible to suggest that Bayesian analysis can be feasibly performed with information from coordinate-based meta-analysis, which is well accessible to fMRI researchers.
The results of the auxiliary examination of how the use of different p values in prior determination resulted in different performance outcomes in Bayesian fMRI analysis would also provide fMRI researchers with additional information. In determining a prior distribution based on meta-analysis, parameters other than P required in the process, C, N, and R, can be acquired from meta-analysis, so researchers do not need to determine them. However, as shown in the previous study [20], P should be determined by the researchers independent from the meta-analysis result. Although multiple P values, 80% to 95%, were tested in the previous study, performance outcomes were not compared across different P-value conditions. Results from the present study demonstrated that the use of P = 80% significantly outperformed that of 95%; however, use of P = 85% or 90% did not significantly influence the performance outcome. Given the results, fMRI researchers may consider employing P = 80% while determining a prior distribution if they do not have any prior information about which P value would be most appropriate within the context of their study.
However, there are several limitations that may warrant further investigations. First, although the use of coordinate-based meta-analysis was tested and validated in the present study, the method might not be applicable to diverse domains in fMRI research. The task conditions examined in the present study, i.e., working memory, speech, and face processing task conditions, are relatively well-defined compared with task conditions addressing higher order psychological functions. We may consider a case of “moral” psychology as an example. Moral functioning consists of multiple different psychological processes, such as moral intuition, moral reasoning, etc. [55]. Let us assume that we intend to analyze data collected from an experiment addressing a specific aspect of moral functioning. In this situation, the use of information from the meta-analysis of previous fMRI studies addressing morality could be problematic because the meta-analyzed previous studies might include experiments addressing diverse aspects of moral functioning, which do not be necessarily directly relevant to the main focus of the current experiment. Thus, it is more difficult to determine which keyword or topic should be used for the meta-analysis of a more complicated psychological functioning, so use of coordinate-based meta-analysis for prior determination could be challenging.
Second, although both image-based and coordinate-based meta-analyses were examined and compared in the present study, the comparison was completed only with the working memory datasets. As not many open statistical images files, which were required for image-based meta-analysis, were available for task conditions other than the working memory task condition, the comparison could not be conducted for the speech and face task conditions. This issue might limit the generalizability of the findings from the present study, particularly those about the performance of coordinate-based meta-analysis for prior determination, in other task conditions. Hence, further investigations should be conducted once more shared statistical images become available on open image repositories, such as NeuroVault [52].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and source codes used in this study are openly available via GitHub: https://github.com/hyemin-han/Prior-Adjustment-CBM (accessed on 13 December 2021).
Conflicts of Interest
The author declares no conflict of interest.
References
- Bennett, C.M.; Miller, M.B.; Wolford, G.L. Neural Correlates of Interspecies Perspective Taking in the Post-Mortem Atlantic Salmon: An Argument for Multiple Comparisons Correction. NeuroImage 2009, 47, S125. [Google Scholar] [CrossRef] [Green Version]
- Eklund, A.; Nichols, T.E.; Knutsson, H. Cluster Failure: Why FMRI Inferences for Spatial Extent Have Inflated False-Positive Rates. Proc. Natl. Acad. Sci. USA 2016, 113, 7900–7905. [Google Scholar] [CrossRef] [Green Version]
- Mueller, K.; Lepsien, J.; Möller, H.E.; Lohmann, G. Commentary: Cluster Failure: Why FMRI Inferences for Spatial Extent Have Inflated False-Positive Rates. Front. Hum. Neurosci. 2017, 11, 345. [Google Scholar] [CrossRef]
- Nichols, T.E.; Eklund, A.; Knutsson, H. A Defense of Using Resting-State FMRI as Null Data for Estimating False Positive Rates. Cogn. Neurosci. 2017, 8, 144–149. [Google Scholar] [CrossRef] [Green Version]
- Cox, R.W.; Chen, G.; Glen, D.R.; Reynolds, R.C.; Taylor, P.A. FMRI Clustering in AFNI: False-Positive Rates Redux. Brain Connect. 2017, 7, 152–171. [Google Scholar] [CrossRef]
- Wagenmakers, E.-J.; Marsman, M.; Jamil, T.; Ly, A.; Verhagen, J.; Love, J.; Selker, R.; Gronau, Q.F.; Šmíra, M.; Epskamp, S.; et al. Bayesian Inference for Psychology. Part I: Theoretical Advantages and Practical Ramifications. Psychon. Bull. Rev. 2018, 25, 35–57. [Google Scholar] [CrossRef]
- Han, H.; Park, J.; Thoma, S.J. Why Do We Need to Employ Bayesian Statistics and How Can We Employ It in Studies of Moral Education?: With Practical Guidelines to Use JASP for Educators and Researchers. J. Moral Educ. 2018, 47, 519–537. [Google Scholar] [CrossRef] [Green Version]
- Wagenmakers, E.-J.; Love, J.; Marsman, M.; Jamil, T.; Ly, A.; Verhagen, J.; Selker, R.; Gronau, Q.F.; Dropmann, D.; Boutin, B.; et al. Bayesian Inference for Psychology. Part II: Example Applications with JASP. Psychon. Bull. Rev. 2018, 25, 58–76. [Google Scholar] [CrossRef] [Green Version]
- Rouder, J.N.; Speckman, P.L.; Sun, D.; Morey, R.D.; Iverson, G. Bayesian t Tests for Accepting and Rejecting the Null Hypothesis. Psychon. Bull. Rev. 2009, 16, 225–237. [Google Scholar] [CrossRef]
- Gelman, A.; Hill, J.; Yajima, M. Why We (Usually) Don’t Have to Worry about Multiple Comparisons. J. Res. Educ. Eff. 2012, 5, 189–211. [Google Scholar] [CrossRef] [Green Version]
- Woolrich, M.W. Bayesian Inference in FMRI. NeuroImage 2012, 62, 801–810. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Park, J. Using SPM 12’s Second-Level Bayesian Inference Procedure for FMRI Analysis: Practical Guidelines for End Users. Front. Neuroinform. 2018, 12, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mejia, A.F.; Yue, Y.; Bolin, D.; Lindgren, F.; Lindquist, M.A. A Bayesian General Linear Modeling Approach to Cortical Surface FMRI Data Analysis. J. Am. Stat. Assoc. 2020, 115, 501–520. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, H. BayesFactorFMRI: Implementing Bayesian Second-Level FMRI Analysis with Multiple Comparison Correction and Bayesian Meta-Analysis of FMRI Images with Multiprocessing. J. Open Res. Softw. 2021, 9, 1. [Google Scholar] [CrossRef]
- Han, H. Implementation of Bayesian Multiple Comparison Correction in the Second-Level Analysis of FMRI Data: With Pilot Analyses of Simulation and Real FMRI Datasets Based on Voxelwise Inference. Cogn. Neurosci. 2020, 11, 157–169. [Google Scholar] [CrossRef]
- de Jong, T. A Bayesian Approach to the Correction for Multiplicity; The Society for the Improvement of Psychological Science: Charlottesville, VA, USA, 2019. [Google Scholar] [CrossRef]
- Westfall, P.H.; Johnson, W.O.; Utts, J.M. A Bayesian Perspective on the Bonferroni Adjustment. Biometrika 1997, 84, 419–427. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.C.; Aitkin, M. Bayes Factors: Prior Sensitivity and Model Generalizability. J. Math. Psychol. 2008, 52, 362–375. [Google Scholar] [CrossRef]
- Sinharay, S.; Stern, H.S. On the Sensitivity of Bayes Factors to the Prior Distributions. Am. Stat. 2002, 56, 196–201. [Google Scholar] [CrossRef]
- Han, H. A Method to Adjust a Prior Distribution in Bayesian Second-Level FMRI Analysis. PeerJ 2021, 9, e10861. [Google Scholar] [CrossRef]
- Kruschke, J.K.; Liddell, T.M. Bayesian Data Analysis for Newcomers. Psychon. Bull. Rev. 2018, 25, 155–177. [Google Scholar] [CrossRef] [Green Version]
- van de Schoot, R.; Sijbrandij, M.; Depaoli, S.; Winter, S.D.; Olff, M.; van Loey, N.E. Bayesian PTSD-Trajectory Analysis with Informed Priors Based on a Systematic Literature Search and Expert Elicitation. Multivar. Behav. Res. 2018, 53, 267–291. [Google Scholar] [CrossRef] [Green Version]
- Avci, E. Using Informative Prior from Meta-Analysis in Bayesian Approach. J. Data Sci. 2017, 15, 575–588. [Google Scholar] [CrossRef]
- Zondervan-Zwijnenburg, M.; Peeters, M.; Depaoli, S.; van de Schoot, R. Where Do Priors Come From? Applying Guidelines to Construct Informative Priors in Small Sample Research. Res. Hum. Dev. 2017, 14, 305–320. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Park, J. Bayesian Meta-Analysis of FMRI Image Data. Cogn. Neurosci. 2019, 10, 66–76. [Google Scholar] [CrossRef] [PubMed]
- Salimi-Khorshidi, G.; Smith, S.M.; Keltner, J.R.; Wager, T.D.; Nichols, T.E. Meta-Analysis of Neuroimaging Data: A Comparison of Image-Based and Coordinate-Based Pooling of Studies. NeuroImage 2009, 45, 810–823. [Google Scholar] [CrossRef] [PubMed]
- Eickhoff, S.B.; Bzdok, D.; Laird, A.R.; Roski, C.; Caspers, S.; Zilles, K.; Fox, P.T. Co-Activation Patterns Distinguish Cortical Modules, Their Connectivity and Functional Differentiation. NeuroImage 2011, 57, 938–949. [Google Scholar] [CrossRef] [Green Version]
- Eickhoff, S.B.; Bzdok, D.; Laird, A.R.; Kurth, F.; Fox, P.T. Activation Likelihood Estimation Meta-Analysis Revisited. NeuroImage 2012, 59, 2349–2361. [Google Scholar] [CrossRef] [Green Version]
- Eickhoff, S.B.; Laird, A.R.; Grefkes, C.; Wang, L.E.; Zilles, K.; Fox, P.T. Coordinate-Based Activation Likelihood Estimation Meta-Analysis of Neuroimaging Data: A Random-Effects Approach Based on Empirical Estimates of Spatial Uncertainty. Hum. Brain Mapp. 2009, 30, 2907–2926. [Google Scholar] [CrossRef] [Green Version]
- Dockès, J.; Poldrack, R.A.; Primet, R.; Gözükan, H.; Yarkoni, T.; Suchanek, F.; Thirion, B.; Varoquaux, G. NeuroQuery, Comprehensive Meta-Analysis of Human Brain Mapping. eLife 2020, 9, e53385. [Google Scholar] [CrossRef]
- DeYoung, C.G.; Shamosh, N.A.; Green, A.E.; Braver, T.S.; Gray, J.R. Intellect as Distinct from Openness: Differences Revealed by FMRI of Working Memory. J. Personal. Soc. Psychol. 2009, 97, 883–892. [Google Scholar] [CrossRef] [Green Version]
- Henson, R.N.A.; Shallice, T.; Gorno-Tempini, M.L.; Dolan, R.J. Face Repetition Effects in Implicit and Explicit Memory Tests as Measured by FMRI. Cereb. Cortex 2002, 12, 178–186. [Google Scholar] [CrossRef]
- Kragel, P.A.; Kano, M.; van Oudenhove, L.; Ly, H.G.; Dupont, P.; Rubio, A.; Delon-Martin, C.; Bonaz, B.L.; Manuck, S.B.; Gianaros, P.J.; et al. Generalizable Representations of Pain, Cognitive Control, and Negative Emotion in Medial Frontal Cortex. Nat. Neurosci. 2018, 21, 283–289. [Google Scholar] [CrossRef]
- Pinho, A.L.; Amadon, A.; Gauthier, B.; Clairis, N.; Knops, A.; Genon, S.; Dohmatob, E.; Torre, J.J.; Ginisty, C.; Becuwe-Desmidt, S.; et al. Individual Brain Charting Dataset Extension, Second Release of High-Resolution FMRI Data for Cognitive Mapping. Sci. Data 2020, 7, 353. [Google Scholar] [CrossRef]
- Gordon, E.M.; Laumann, T.O.; Gilmore, A.W.; Newbold, D.J.; Greene, D.J.; Berg, J.J.; Ortega, M.; Hoyt-Drazen, C.; Gratton, C.; Sun, H.; et al. Precision Functional Mapping of Individual Human Brains. Neuron 2017, 95, 791–807.e7. [Google Scholar] [CrossRef] [Green Version]
- Laird, A.R.; Lancaster, J.L.; Fox, P.T. BrainMap: The Social Evolution of a Human Brain Mapping Database. Neuroinformatics 2005, 3, 65–78. [Google Scholar] [CrossRef]
- Turkeltaub, P.E.; Eickhoff, S.B.; Laird, A.R.; Fox, M.; Wiener, M.; Fox, P. Minimizing within-Experiment and within-Group Effects in Activation Likelihood Estimation Meta-Analyses. Hum. Brain Mapp. 2012, 33, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Laird, A.R.; Fox, P.M.; Price, C.J.; Glahn, D.C.; Uecker, A.M.; Lancaster, J.L.; Turkeltaub, P.E.; Kochunov, P.; Fox, P.T. ALE Meta-Analysis: Controlling the False Discovery Rate and Performing Statistical Contrasts. Hum. Brain Mapp. 2005, 25, 155–164. [Google Scholar] [CrossRef]
- Yarkoni, T.; Poldrack, R.A.; Nichols, T.E.; van Essen, D.C.; Wager, T.D. Large-Scale Automated Synthesis of Human Functional Neuroimaging Data. Nat. Methods 2011, 8, 665–670. [Google Scholar] [CrossRef] [Green Version]
- Poldrack, R.A. Inferring Mental States from Neuroimaging Data: From Reverse Inference to Large-Scale Decoding. Neuron 2011, 72, 692–697. [Google Scholar] [CrossRef] [Green Version]
- Glymour, C.; Hanson, C. Reverse Inference in Neuropsychology. Br. J. Philos. Sci. 2016, 67, 1139–1153. [Google Scholar] [CrossRef]
- Dockès, J.; Poldrack, R.A.; Primet, R.; Gözükan, H.; Yarkoni, T.; Suchanek, F.; Thirion, B.; Varoquaux, G. About NeuroQuery. Available online: https://neuroquery.org/about (accessed on 13 January 2022).
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Stefan, A.M.; Gronau, Q.F.; Schönbrodt, F.D.; Wagenmakers, E.-J. A Tutorial on Bayes Factor Design Analysis Using an Informed Prior. Behav. Res. Methods 2019, 51, 1042–1058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, H. Neural Correlates of Moral Sensitivity and Moral Judgment Associated with Brain Circuitries of Selfhood: A Meta-Analysis. J. Moral Educ. 2017, 46, 97–113. [Google Scholar] [CrossRef]
- Cremers, H.R.; Wager, T.D.; Yarkoni, T. The Relation between Statistical Power and Inference in FMRI. PLoS ONE 2017, 12, e0184923. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Glenn, A.L. Evaluating Methods of Correcting for Multiple Comparisons Implemented in SPM12 in Social Neuroscience FMRI Studies: An Example from Moral Psychology. Soc. Neurosci. 2018, 13, 257–267. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Glenn, A.L.; Dawson, K.J. Evaluating Alternative Correction Methods for Multiple Comparison in Functional Neuroimaging Research. Brain Sci. 2019, 9, 198. [Google Scholar] [CrossRef] [Green Version]
- Ashburner, J.; Barnes, G.; Chen, C.-C.; Daunizeau, J.; Flandin, G.; Friston, K.; Kiebel, S.; Kilner, J.; Litvak, V.; Moran, R.; et al. SPM 12 Manual; Wellcome Trust Centre for Neuroimaging: London, UK, 2016. [Google Scholar]
- Han, H.; Dawson, K.J. Improved Model Exploration for the Relationship between Moral Foundations and Moral Judgment Development Using Bayesian Model Averaging. J. Moral Educ. 2021, 1–5. [Google Scholar] [CrossRef]
- Han, H. Exploring the Association between Compliance with Measures to Prevent the Spread of COVID-19 and Big Five Traits with Bayesian Generalized Linear Model. Personal. Individ. Differ. 2021, 176, 110787. [Google Scholar] [CrossRef]
- Gorgolewski, K.J.; Varoquaux, G.; Rivera, G.; Schwarz, Y.; Ghosh, S.S.; Maumet, C.; Sochat, V.V.; Nichols, T.E.; Poldrack, R.A.; Poline, J.-B.; et al. NeuroVault.Org: A Web-Based Repository for Collecting and Sharing Unthresholded Statistical Maps of the Human Brain. Front. Neuroinform. 2015, 9, 8. [Google Scholar] [CrossRef] [Green Version]
- Laird, A.R.; Eickhoff, S.B.; Fox, P.M.; Uecker, A.M.; Ray, K.L.; Saenz, J.J.; McKay, D.R.; Bzdok, D.; Laird, R.W.; Robinson, J.L.; et al. The BrainMap Strategy for Standardization, Sharing, and Meta-Analysis of Neuroimaging Data. BMC Res. Notes 2011, 4, 349. [Google Scholar] [CrossRef] [Green Version]
- Poldrack, R.A. Can Cognitive Processes Be Inferred from Neuroimaging Data? Trends Cogn. Sci. 2006, 10, 59–63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ly, A.; Stefan, A.; van Doorn, J.; Dablander, F.; van den Bergh, D.; Sarafoglou, A.; Kucharský, S.; Derks, K.; Gronau, Q.F.; Raj, A.; et al. The Bayesian Methodology of Sir Harold Jeffreys as a Practical Alternative to the P Value Hypothesis Test. Comput. Brain Behav. 2020, 3, 153–161. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).