Hölder Space Theory for the Rotation Problem of a Two-Phase Drop

Abstract

We investigate a uniformly rotating finite mass consisting of two immiscible, viscous, incompressible self-gravitating fluids which is governed by an interface problem for the Navier–Stokes system with mass forces and the gradient of the Newton potential on the right-hand sides. The interface between the liquids is assumed to be closed. Surface tension acts on the interface and on the exterior free boundary. A study of this problem is performed in the Hölder spaces of functions. The global unique solvability of the problem is obtained under the smallness of the initial data, external forces and rotation speed, and the proximity of the given initial surfaces to some axisymmetric equilibrium figures. It is proved that if the second variation of the energy functional is positive and mass forces decrease exponentially, then small perturbations of the axisymmetric figures of equilibrium tend exponentially to zero as the time $t\to \infty$, and the motion of liquid mass passes into the rotation of the two-phase drop as a solid body.

1. Introduction

The paper deals with the stability of the problem of rotation of an isolated liquid mass about a fixed axis. Such problems were treated by many outstanding mathematicians. A review of the topic was presented in the book of Appell [1]. One can find there, for example, the results of Charrueau [2,3], who was one of the first to start studying the problem with a capillarity effect at the beginning of the 20th century.

A. M. Lyapunov [4,5] analyzed the stability of equilibrium figures for a rotating fluid mass without surface tension by analytical methods. He investigated the second variation of an energy functional considering small perturbations of the boundary of an equilibrium figure. The positiveness of this variation guarantees the stability of the figure because the energy potential possesses a minimum in this case.

The Lyapunov method was generalized for a rotating capillary fluid by one of the authors of this paper in [6,7]. We developed this technique for a finite mass of two-phase liquids. We studied the stability problem for two rotating incompressible capillary self-gravitating fluids with an unknown interface and a free surface to be close to the boundaries of two equilibrium figures inserted into each other. The existence of two-phase figures of equilibrium was obtained in [8]. We adapted the proof of the global maximal regularity of two-fluid problem without rotation ([9] Ch. 7, 12) to our case. A study of rotating two-phase drop was performed in the Sobolev–Slobodetskiǐ spaces by ourselves in [10,11], where an a priori exponential inequality was obtained for a generalized energy. At first, on this basis, the global solvability of a linearized problem was proved. Next, a solution to the non-linear problem was found as the sum of the solution of the linear homogeneous system and that of a problem with small non-linear terms. We use this technique also in the case of the Hölder spaces. We note that the problem in [10] governs the rotation without mass force and self-gravity of the drop. In the present paper, we take both these forces into account.

2. Setting of a Problem

We give a mathematical statement of the problem. We assume two immiscible viscous incompressible fluids of densities ${\rho }^{\pm }$ and viscosities ${\mu }^{\pm }$ to be situated in a domain ${\Omega }_t\subset {\mathbb{R}}^3$ which is separated by a variable closed interface ${\Gamma }_t^{+}$ and bounded by a free surface ${\Gamma }_t^{-}$, ${\Gamma }_t^{+}$ being the boundary of the domain ${\Omega }_t^{+}$ filled with a fluid of the density ${\rho }^{+}$. It is surrounded by another fluid of the density ${\rho }^{-}$ contained in the domain ${\Omega }_t^{-}={\Omega }_t\backslash \overline{{\Omega }_t^{+}}$ (see Figure 1). At the initial moment $t=0$, the boundaries ${\Gamma }_0^{\pm }$ are given. This two-layer fluid mass rotates about the vertical axis $x_3$. One should find the surfaces ${\Gamma }_t^{\pm }$, velocity vector field $\mathit{v}(x,t)$ and pressure function $p(x,t)$ which satisfy the interface problem for the Navier–Stokes equations:

$$\begin{array}{cc}\hfill & {\rho }^{\pm }\left({\mathcal{D}}_t\mathit{v}+(\mathit{v}·\nabla )\mathit{v}\right)-{\mu }^{\pm }{\nabla }^2\mathit{v}+\nabla p={\rho }^{\pm }(\mathit{f}+\varkappa \nabla U),\hfill \\ \hfill & \nabla ·\mathit{v}=0\mathrm{in}\cup {\Omega }_t^{\pm }={\Omega }_t^{+}\cup {\Omega }_t^{-},t>0,\hfill \\ \hfill & \mathit{v}(x,0)={\mathit{v}}_0\left(x\right),x\in \cup {\Omega }_0^{\pm },\hfill \\ \hfill & \left[\mathit{v}\right]{|}_{{\Gamma }_t^{+}}\equiv \underset{\begin{array}{c}x\to x_0\in {\Gamma }_t^{+},\\ x\in {\Omega }_t^{+}\end{array}}{lim}\mathit{v}(x,t)-\underset{\begin{array}{c}x\to x_0\in {\Gamma }_t^{+},\\ x\in {\Omega }_t^{-}\end{array}}{lim}\mathit{v}(x,t)=0,\hfill \\ \hfill & \left[\mathbb{T}(\mathit{v},p)\mathit{n}\right]{|}_{{\Gamma }_t^{+}}={\sigma }^{+}{H}^{+}\mathit{n}\mathrm{on}{\Gamma }_t^{+},\mathbb{T}(\mathit{v},p)\mathit{n}{|}_{{\Gamma }_t^{-}}={\sigma }^{-}{H}^{-}\mathit{n}\mathrm{on}{\Gamma }_t^{-},\hfill \\ \hfill & V_{\mathit{n}}=\mathit{v}·\mathit{n}\mathrm{on}{\Gamma }_t={\Gamma }_t^{+}\cup {\Gamma }_t^{-},\hfill \end{array}$$

(1)

where ${\mathcal{D}}_t=\partial /\partial t$, $\nabla =(\partial /\partial x_1,\partial /\partial x_2,\partial /\partial x_3)$, ${\nabla }^2\equiv \nabla ·\nabla$; $\mathit{f}$ is the vector of mass forces,

$$U(x,t)={\int }_{{\Omega }_t}\frac{{\rho }^{\pm }\mathrm{d}z}{|x-z|};$$

$\varkappa ⩾0$ is the gravitational constant; ${\mathit{v}}_0$ is initial velocity vector field; the stress tensor is

$$\mathbb{T}(\mathit{v},p)=-p\mathbb{I}+{\mu }^{\pm }\mathbb{S}\left(\mathit{v}\right),$$

where $\mathbb{I}$ is identity matrix, $\mathbb{S}\left(\mathit{v}\right)=(\nabla \mathit{v})+{(\nabla \mathit{v})}^T$ is the twice rate-of-strain tensor, the superscript T means the transposition, the step-functions of density and dynamical viscosity ${\rho }^{\pm },{\mu }^{\pm }>0$ are equal to ${\rho }^{-},{\mu }^{-}$ in ${\Omega }_t^{-}$ and ${\rho }^{+},{\mu }^{+}$ in ${\Omega }_t^{+}$, respectively; ${\sigma }^{\pm }>0$ are surface tension coefficients on ${\Gamma }_t^{\pm }$, $H^{\pm }$ are the doubled mean curvatures of the surfaces ${\Gamma }_t^{\pm }$ and $(H^{+}<0$ at the points where ${\Gamma }_t^{+}$ is convex toward ${\Omega }_t^{-}$), the vector $\mathit{n}$ is the outward normal to ${\Gamma }_t^{-}\cup {\Gamma }_t^{+}$ and $V_{\mathit{n}}$ is the speed of evolution of the surfaces ${\Gamma }_t^{\pm }$ in the direction of $\mathit{n}$. A Cartesian coordinate system $\left\{x\right\}$ is assumed to be introduced in ${\mathbb{R}}^3$. The centered dot · denotes the Cartesian scalar product.

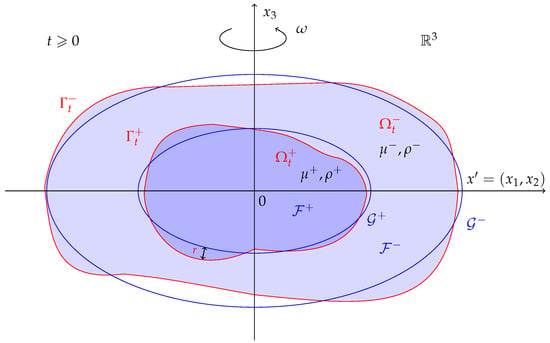
Figure 1. Two–phase drop.

The vectors and vector spaces are marked by boldface letters. We imply the summation from 1 to 3 by repeated indices, indicated in Latin letters.

The domains ${\Omega }_0^{+}$ and ${\Omega }_0$ are supposed to be close to equilibrium figures ${\mathcal{F}}^{+}$ and $\mathcal{F}$ of the same volumes:

$$|{\Omega }_0^{+}|=|{\mathcal{F}}^{+}|,|{\Omega }_0|=|\mathcal{F}|.$$

(2)

In view of the incompressibility of the fluids, equalities (2) hold for arbitrary $t>0$:

$$|{\Omega }_t^{+}|=|{\mathcal{F}}^{+}|,|{\Omega }_t|=|\mathcal{F}|.$$

(3)

Mass conservation follows from the constancy of the densities.

We set ${\mathcal{G}}^{+}=\partial {\mathcal{F}}^{+}$, ${\mathcal{G}}^{-}=\partial \mathcal{F}$ and ${\mathcal{F}}^{-}=\mathcal{F}\backslash \overline{{\mathcal{F}}^{+}}$ (see Figure 1).

If mass force $\mathit{f}$ is orthogonal to all the vectors of rigid motion, i.e.,

$${\int }_{{\Omega }_t}{\rho }^{\pm }\mathit{f}(x,t)\mathrm{d}x=0,{\int }_{{\Omega }_t}{\rho }^{\pm }\mathit{f}(x,t)·{\mathit{\eta }}_i\left(x\right)\mathrm{d}x=0,i=1,2,3,$$

(4)

a solution of system (1) also satisfies the additional conservation laws:

$$\begin{gathered} {\int }_{{\Omega }_t}{\rho }^{\pm }{x}_j\mathrm{d}x={\int }_{{\Omega }_0}{\rho }^{\pm }{x}_j\mathrm{d}x\equiv 0,j=1,2,3,(\mathrm{barycenter}\mathrm{conservation}), \\ {\int }_{{\Omega }_t}{\rho }^{\pm }\mathit{v}(x,t)\mathrm{d}x={\int }_{{\Omega }_0}{\rho }^{\pm }{\mathit{v}}_0\left(x\right)\mathrm{d}x\equiv 0(\mathrm{momentum}\mathrm{conservation}), \\ {\int }_{{\Omega }_t}{\rho }^{\pm }\mathit{v}(x,t)·{\mathit{\eta }}_i\left(x\right)\mathrm{d}x={\int }_{{\Omega }_0}{\rho }^{\pm }{\mathit{v}}_0\left(x\right)·{\mathit{\eta }}_i\left(x\right)\mathrm{d}x\equiv \omega {\int }_{\mathcal{F}}\overline{\rho }{\mathit{\eta }}_3\left(x\right)·{\mathit{\eta }}_i\left(x\right)\mathrm{d}x=\beta {\delta }_i^3, \\ i=1,2,3,(\mathrm{angular}\mathrm{momentum}\mathrm{conservation}), \end{gathered}$$

(5)

where ${\delta }_i^k$ is the Kronecker delta, ${\mathit{\eta }}_j\left(x\right)={\mathit{e}}_j\times \mathit{x},$ $j=1,2,3$, $\overline{\rho }$ is a density step-function: $\overline{\rho }={\rho }^{-}$ in ${\mathcal{F}}^{-}$, $\overline{\rho }={\rho }^{+}$ in ${\mathcal{F}}^{+}$, $\omega$ is the angular speed of the rotation and

$$\beta =\omega {\int }_{\mathcal{F}}\overline{\rho }\left(x\right){|x^{\prime }|}^2\mathrm{d}x\equiv \omega \mathcal{I}$$

is angular momentum of the rotating fluids. Under conditions (4) for $t⩾0$, it was shown in [8] that laws (5) are satisfied for all $t>0$ if they hold at $t=0$.

For the new pressure function $p-{\rho }^{\pm }\varkappa U$, system (1) transforms into the problem

$$\begin{gathered} {\rho }^{\pm }\left({\mathcal{D}}_t\mathit{v}+(\mathit{v}·\nabla )\mathit{v}\right)-{\mu }^{\pm }{\nabla }^2\mathit{v}+\nabla p={\rho }^{\pm }\mathit{f}, \\ \nabla ·\mathit{v}=0\mathrm{in}\cup {\Omega }_t^{\pm },t>0, \\ \mathit{v}(x,0)={\mathit{v}}_0\left(x\right)\mathrm{in}\cup {\Omega }_0^{\pm }={\Omega }_0^{+}\cup {\Omega }_0^{-}, \end{gathered}$$

(6)

$$\begin{array}{c}\left[\mathit{v}\right]{|}_{{\Gamma }_t^{+}}=0,\left[\mathbb{T}(\mathit{v},p)\mathit{n}\right]{|}_{{\Gamma }_t^{+}}=({\sigma }^{+}{H}^{+}+\left[{\rho }^{\pm }\right]{|}_{{\Gamma }_t^{+}}\varkappa U)\mathit{n}\mathrm{on}{\Gamma }_t^{+},\hfill \\ \mathbb{T}(\mathit{v},p)\mathit{n}{|}_{{\Gamma }_t^{-}}=({\sigma }^{-}{H}^{-}+{\rho }^{-}\varkappa U)\mathit{n}\mathrm{on}{\Gamma }_t^{-},\hfill \\ V_{\mathit{n}}=\mathit{v}·\mathit{n}\mathrm{on}{\Gamma }_t={\Gamma }_t^{+}\cup {\Gamma }_t^{-}.\hfill \end{array}$$

(7)

The uniform rotation of a two-phase drop about the $x_3$-axis with constant angular velocity $\omega =\beta /\mathcal{I}$ is governed by the homogeneous steady Navier–Stokes equations:

$$\overline{\rho }(\mathcal{V}·\nabla )\mathcal{V}-\overline{\mu }{\nabla }^2\mathcal{V}+\nabla \mathcal{P}=0,\nabla ·\mathcal{V}=0\mathrm{in}\cup {\mathcal{F}}^{\pm }$$

with the step-function of dynamical viscosity $\overline{\mu }\equiv {\mu }^{+}$ in ${\mathcal{F}}^{+}$ and $\overline{\mu }\equiv {\mu }^{-}$ in ${\mathcal{F}}^{-}$. The solution of this system is the couple of velocity vector field

$$\mathcal{V}\left(x\right)=\omega {\mathit{e}}_3\times \mathit{x}\equiv \omega {\mathit{\eta }}_3$$

and the function of pressure

$$\mathcal{P}\left(x\right)=\overline{\rho }\frac{{\omega }^2}{2}{|x^{\prime }|}^2+p_0^{\pm },$$

where $|x^{\prime }{|}^2=x_1^2+x_2^2$ and $\overline{\rho }$ and $p_0^{\pm }$ are step-functions in ${\mathcal{F}}^{\pm }$. In order to find the equations of the surfaces ${\mathcal{G}}^{\pm }$ of the domains ${\mathcal{F}}^{\pm }$, we substitute $\mathcal{V},\mathcal{P}$ into boundary conditions (7)

$$\begin{array}{c}{\sigma }^{-}{\mathcal{H}}^{-}\left(x\right)+{\rho }^{-}\frac{{\omega }^2}{2}|x^{\prime }{|}^2+{\rho }^{-}\varkappa \mathcal{U}+p_0^{-}=0,x\in {\mathcal{G}}^{-},\\ {\sigma }^{+}{\mathcal{H}}^{+}\left(x\right)+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}\frac{{\omega }^2}{2}{|x^{\prime }|}^2+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}\varkappa \mathcal{U}+\left[p_0^{\pm }\right]{|}_{{\mathcal{G}}^{+}}=0,x\in {\mathcal{G}}^{+},\end{array}$$

(8)

where ${\mathcal{H}}^{-}$ and ${\mathcal{H}}^{+}$ are twice the mean curvatures of ${\mathcal{G}}^{-}$ and ${\mathcal{G}}^{+}$, respectively, and

$$\mathcal{U}\left(x\right)={\int }_{\mathcal{F}}\frac{\overline{\rho }\mathrm{d}z}{|x-z|}.$$

In [8], the existence of the boundaries ${\mathcal{G}}^{\pm }$ satisfying Equation (8) was proved, provided that $\beta$ is small enough, and $\varkappa ,\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}>0$ (Proposition 3.3). It was noted there that ${\mathcal{G}}^{\pm }$ are flattened spheroids. If $\varkappa =0$, the condition $\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}>0$ is not necessary. We cite this proposition.

Proposition 1.

Let the angular momentum β be small enough, and $\varkappa >0$ and ${\rho }^{+}>{\rho }^{-}$. Then, for given volumes $|{\mathcal{F}}^{+}|$ and $|\mathcal{F}|$, there exists a unique equilibrium figure which is axially symmetric about the axis $x_3$ and symmetric about the plane $x_3=0$. The surfaces ${\mathcal{G}}^{\pm }$ are close to the spheres $S_{R_{\pm }}=\{|x|=R_{\pm }\}$, respectively, where $R_{+}$, $R_{-}$ are such that

$$\frac{4\pi }{3}{R}_{+}^3=|{\mathcal{F}}^{+}|,\frac{4\pi }{3}{R}_{-}^3=|\mathcal{F}|$$

and

$${\mathcal{G}}^{\pm }=\{x=z+{\varphi }^{\pm }\left(z\right)\frac{\mathit{z}}{|z|},z\in S_{R_{\pm }}\}.$$

Thus, we admit the axial symmetry of ${\mathcal{F}}^{\pm }$ and their symmetry about the plane $x_3=0$. Then

$${\int }_{\mathcal{F}}\overline{\rho }{x}_{i}dx=0,i=1,2,3,$$

(9)

$${\int }_{\mathcal{F}}\overline{\rho }{x}_3{x}_{j}dx=0,j=1,2.$$

Relation (9) corresponds to the first condition in (5). It means that mass center of the fluids is in the origin all the time. The other conservation laws in (5) take the form

$${\int }_{{\Omega }_t}{\rho }^{\pm }\mathit{v}(x,t)dx={\int }_{\mathcal{F}}\overline{\rho }\mathcal{V}\left(x\right)dx=0,$$

(10)

$${\int }_{{\Omega }_t}{\rho }^{\pm }\mathit{v}(x,t)·{\mathit{\eta }}_i\left(x\right)dx={\int }_{\mathcal{F}}\overline{\rho }\mathcal{V}\left(x\right)·{\mathit{\eta }}_i\left(x\right)dx={\delta }_i^3\beta ,i=1,2,3.$$

Let us consider the perturbations of the velocity and pressure

$${\mathit{v}}_r(x,t)=\mathit{v}(x,t)-\mathcal{V}\left(x\right),p_r(x,t)=p(x,t)-\mathcal{P}\left(x\right).$$

We introduce the new coordinates $\left\{y_i\right\}$ rotating about the $x_3$-axis with the angular velocity $\omega$ and the new unknown functions ($\tilde{\mathit{v}}$, $\tilde{p}$) by the formulas

$$x=\mathcal{Z}\left(\omega t\right)y,$$

$$\tilde{\mathit{v}}(y,t)={\mathcal{Z}}^{-1}\left(\omega t\right){\mathit{v}}_r(\mathcal{Z}\left(\omega t\right)y,t),\tilde{p}(y,t)=p_r(\mathcal{Z}\left(\omega t\right)y,t),$$

where

$$\mathcal{Z}\left(\theta \right)=\left(\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right).$$

We note that ${\nabla }_x=\mathcal{Z}{\nabla }_y,{\mathcal{Z}}^{-1}\left(\omega t\right)(\mathcal{V}·{\nabla }_x){\mathit{v}}_r=\omega \left({\mathit{\eta }}_3\left(x\right)·{\nabla }_x\right)\tilde{\mathit{v}}(y,t)=\omega \left(\mathcal{Z}{\mathit{\eta }}_3\left(y\right)·\mathcal{Z}{\nabla }_y\right)\tilde{\mathit{v}}=\omega \left({\mathit{\eta }}_3\left(y\right)·{\nabla }_y\right)\tilde{\mathit{v}}(y,t)=\omega \left(y_2\frac{\partial \tilde{\mathit{v}}}{\partial y_1}-y_1\frac{\partial \tilde{\mathit{v}}}{\partial y_2}\right)$ and ${\mathcal{D}}_t{\mathit{v}}_r{|}_{x=\mathcal{Z}y}={\mathcal{D}}_t{\mathit{v}}_r(\mathcal{Z}y,t)-(\mathcal{V}·\nabla ){\mathit{v}}_r.$ By substituting this in (6) and (7), acting by ${\mathcal{Z}}^{-1}$ and taking (8) into account in the boundary conditions, we obtain the following interface problem for the perturbations $\tilde{\mathit{v}}$ and $\tilde{p}$:

$$\begin{gathered} \begin{array}{c}{\rho }^{\pm }\left({\mathcal{D}}_t\tilde{\mathit{v}}+(\tilde{\mathit{v}}·\nabla )\tilde{\mathit{v}}+2\omega (e_3\times \tilde{\mathit{v}})\right)-{\mu }^{\pm }{\nabla }^2\tilde{\mathit{v}}+\nabla \tilde{p}={\rho }^{\pm }\tilde{\mathit{f}},\\ \nabla ·\tilde{\mathit{v}}=0\mathrm{in}\cup {\tilde{\Omega }}_t^{\pm }\equiv {\tilde{\Omega }}_t^{-}\cup {\tilde{\Omega }}_t^{+},t>0,\\ \tilde{\mathit{v}}(y,0)={\mathit{v}}_0\left(y\right)-\mathcal{V}\left(y\right)\equiv {\tilde{\mathit{v}}}_0\left(y\right),y\in \cup {\tilde{\Omega }}_0^{\pm },\\ -\tilde{p}\tilde{\mathit{n}}+{\mu }^{-}\mathbb{S}\left(\tilde{\mathit{v}}\right)\tilde{\mathit{n}}{|}_{{\tilde{\Gamma }}_t^{-}}=\left\{{\sigma }^{-}\left({\tilde{H}}^{-}\left(y\right)-{\mathcal{H}}^{-}\left(z\right)\right)+{\rho }^{-}{\omega }^2\left(|y^{\prime }{|}^2-{|z^{\prime }|}^2\right)/2 \\ +\varkappa {\rho }^{-}\left(\tilde{U}(y,t)-\mathcal{U}\left(z\right)\right)\right\}\tilde{\mathit{n}},\\ \left[\tilde{\mathit{v}}\right]{|}_{{\tilde{\Gamma }}_t^{+}}=0,\\ [-\tilde{p}\tilde{\mathit{n}}+{\mu }^{\pm }\mathbb{S}\left(\tilde{\mathit{v}}\right)\tilde{\mathit{n}}]{|}_{{\tilde{\Gamma }}_t^{+}}=\left\{{\sigma }^{+}\left({\tilde{H}}^{+}\left(y\right)-{\mathcal{H}}^{+}\left(z\right)\right)+\left[{\rho }^{\pm }\right]{\omega }^2\left(|y^{\prime }{|}^2-{|z^{\prime }|}^2\right)/2 \\ +\varkappa \left[{\rho }^{\pm }\right]{|}_{{\Gamma }_t^{+}}\left(\tilde{U}(y,t)-\mathcal{U}\left(z\right)\right)\right\}\tilde{\mathit{n}},\\ {\tilde{V}}_{\tilde{\mathit{n}}}=\tilde{\mathit{v}}·\tilde{\mathit{n}}\mathrm{on}{\tilde{\Gamma }}_t\equiv {\tilde{\Gamma }}_t^{-}\cup {\tilde{\Gamma }}_t^{+},\end{array} \end{gathered}$$

(11)

where ${\tilde{\Omega }}_t^{\pm }={\mathcal{Z}}^{-1}\left(\omega t\right){\Omega }_t^{\pm },$ ${\tilde{\Gamma }}_t^{\pm }={\mathcal{Z}}^{-1}\left(\omega t\right){\Gamma }_t^{\pm }$, $\tilde{\mathit{f}}(y,t)={\mathcal{Z}}^{-1}\left(\omega t\right)\mathit{f}(\mathcal{Z}\left(\omega t\right)y,t)$, $\tilde{\mathit{n}}$ is the outward normal to ${\tilde{\Gamma }}_t$, $\mathit{n}=\mathcal{Z}\tilde{\mathit{n}}$, $y^{\prime }=(y_1,y_2,0)$, etc. We note that the kinematic boundary condition $V_{\mathit{n}}=\mathit{v}·\mathit{n},$ conserves its form (see [10]).

Relations (3), (5) and (10) go over into

$$|{\tilde{\Omega }}_t^{+}|=|{\mathcal{F}}^{+}|,|{\tilde{\Omega }}_t|=|\mathcal{F}|,$$

(12)

$$\begin{gathered} \begin{array}{c}{\int }_{{\tilde{\Omega }}_t}{\rho }^{\pm }{y}_j\mathrm{d}y=0,j=1,2,3,(\mathrm{centroid}\mathrm{conservation}),\\ {\int }_{{\tilde{\Omega }}_t}{\rho }^{\pm }\tilde{\mathit{v}}(y,t)\mathrm{d}y=0(\mathrm{impulse}\mathrm{conservation}),\\ {\int }_{{\tilde{\Omega }}_t}{\rho }^{\pm }\tilde{\mathit{v}}(y,t)·{\mathit{\eta }}_i\left(y\right)\mathrm{d}y+\omega {\int }_{{\tilde{\Omega }}_t}{\rho }^{\pm }{\mathit{\eta }}_3·{\mathit{\eta }}_i\left(y\right)\mathrm{d}y=\omega {\int }_{\mathcal{F}}\overline{\rho }{\mathit{\eta }}_3·{\mathit{\eta }}_i\left(y\right)\mathrm{d}y=\beta {\delta }_i^3 \\ (\mathrm{angular}\mathrm{momentum}\mathrm{conservation}),\end{array} \end{gathered}$$

(13)

where ${\mathit{\eta }}_i\left(y\right)={\mathit{e}}_i\times \mathit{y},$ $i=1,2,3$.

We give the definition of the anisotropic Hölder spaces which we use below.

Let $\Omega$ be a domain in ${\mathbb{R}}^n$, $n\in \mathbb{N}$ and $\alpha \in (0,1)$. We set $Q_T=\Omega \times (0,T)$ for $T>0$. By $C^{\alpha ,\alpha /2}\left(Q_T\right)$, we denote the set of functions f in $Q_T$ having the norm

$${|f|}_{Q_T}^{(\alpha ,\alpha /2)}={|f|}_{Q_T}+{⟨f⟩}_{Q_T}^{(\alpha ,\alpha /2)},$$

where

$${|f|}_{Q_T}=\underset{t\in (0,T)}{sup}\underset{x\in \Omega }{sup}|f(x,t)|,{⟨f⟩}_{Q_T}^{(\alpha ,\alpha /2)}={⟨f⟩}_{x,Q_T}^{\left(\alpha \right)}+{⟨f⟩}_{t,Q_T}^{(\alpha /2)},$$

and

$$\begin{array}{ccc}\hfill {⟨f⟩}_{x,Q_T}^{\left(\alpha \right)}& =& \underset{t\in (0,T)}{sup}\underset{x,y\in \Omega }{sup}{|f(x,t)-f(y,t)||x-y|}^{-\alpha },\hfill \\ \hfill {⟨f⟩}_{t,Q_T}^{\left(\mu \right)}& =& \underset{x\in \Omega }{sup}\underset{t,\tau \in (0,T)}{sup}{|f(x,t)-f(x,\tau )||t-\tau |}^{-\mu },\mu \in (0,1).\hfill \end{array}$$

We introduce the following notation:

$$\begin{array}{ccc}\hfill {\mathcal{D}}_x^{\mathit{r}}& =& {\partial }^{|\mathit{r}|}/\partial x_1^{r_1}\cdots \partial x_n^{r_n},\mathit{r}=(r_1,\dots r_n),r_i⩾0,|\mathit{r}|=r_1+\cdots +r_n,\hfill \\ \hfill {\mathcal{D}}_t^s& =& {\partial }^s/\partial t^s,s\in \mathbb{N}\cup \left\{0\right\}.\hfill \end{array}$$

Let $k\in \mathbb{N}$. By definition, the space $C^{k+\alpha ,(k+\alpha )/2}\left(Q_T\right)$ consists of functions f with finite norm

$${|f|}_{Q_T}^{(k+\alpha ,\frac{k+\alpha }{2})}\equiv \sum _{|\mathit{r}|+2s⩽k}{|{\mathcal{D}}_x^{\mathit{r}}{\mathcal{D}}_t^{s}f|}_{Q_T}+{⟨f⟩}_{Q_T}^{(k+\alpha ,\frac{k+\alpha }{2})},$$

where

$${⟨f⟩}_{Q_T}^{(k+\alpha ,\frac{k+\alpha }{2})}=\sum _{|\mathit{r}|+2s=k}{⟨{\mathcal{D}}_x^{\mathit{r}}{\mathcal{D}}_t^{s}f⟩}_{Q_T}^{(\alpha ,\frac{\alpha }{2})}+\sum _{|\mathit{r}|+2s=k-1}{⟨{\mathcal{D}}_x^{\mathit{r}}{\mathcal{D}}_t^{s}f⟩}_{t,Q_T}^{\left(\frac{1+\alpha }{2}\right)}.$$

We define $C^{k+\alpha }(\Omega )$, $k\in \mathbb{N}\cup \left\{0\right\}$, as the space of functions $f\left(x\right)$, $x\in \Omega$, with the norm

$${|f|}_{\Omega }^{(k+\alpha )}\equiv \sum _{|\mathit{r}|⩽k}{|{\mathcal{D}}_x^{\mathit{r}}f|}_{\Omega }+{⟨f⟩}_{\Omega }^{(k+\alpha )}.$$

Here

$${⟨f⟩}_{\Omega }^{(k+\alpha )}=\sum _{|\mathit{r}|=k}{⟨{\mathcal{D}}_x^{\mathit{r}}f⟩}_{\Omega }^{\left(\alpha \right)}=\sum _{|\mathit{r}|=k}\underset{x,y\in \Omega }{sup}|{\mathcal{D}}_x^{\mathit{r}}f\left(x\right)-{\mathcal{D}}_y^{\mathit{r}}f\left(y\right){||x-y|}^{-\alpha }.$$

One also needs the following norm with $\alpha ,\gamma \in (0,1)$:

$${\mathbf{\left|}f\mathbf{\right|}}_{Q_T}^{(\gamma ,1+\alpha )}={\mathbf{⟨}f\mathbf{⟩}}_{Q_T}^{(\gamma ,1+\alpha )}+{⟨f⟩}_{t,Q_T}^{\left(\frac{1+\alpha -\gamma }{2}\right)}+{|f|}_{Q_T}$$

with

$${\mathbf{⟨}f\mathbf{⟩}}_{Q_T}^{(\gamma ,1+\alpha )}\equiv \underset{t,\tau \in (0,T)}{sup}\underset{x,y\in \Omega }{sup}\frac{|f(x,t)-f(y,t)-f(x,\tau )+f(y,\tau )|}{{|x-y|}^{\gamma }{|t-\tau |}^{(1+\alpha -\gamma )/2}}.$$

The estimate

$${\mathbf{⟨}f\mathbf{⟩}}_{Q_T}^{(\gamma ,1+\alpha )}⩽c_1{⟨f⟩}_{Q_T}^{(1+\alpha ,\frac{1+\alpha }{2})}$$

is known. By definition, $f\in C^{(\gamma ,1+\alpha )}\left(Q_T\right)$ if

$${\mathbf{\left|}f\mathbf{\right|}}_{Q_T}^{(\gamma ,1+\alpha )}<\infty .$$

Finally, if a function f has finite norm

$${|f|}_{Q_T}^{(\gamma ,\mu )}\equiv {⟨f⟩}_{x,Q_T}^{\left(\gamma \right)}+{|f|}_{t,Q_T}^{\left(\mu \right)},\gamma \in (0,1),\mu \in [0,1),$$

where

$${|f|}_{t,Q_T}^{\left(\mu \right)}=\left\{\begin{array}{cc}{|f|}_{Q_T}+{⟨f⟩}_{t,Q_T}^{\left(\mu \right)}\hfill & \mathrm{if}\mu >0,\hfill \\ {|f|}_{Q_T}\mathrm{if}\mu =0,\hfill \end{array}\right.$$

we consider that $f\in C^{\gamma ,\mu }\left(Q_T\right)$.

We consider that a vector-valued function belongs to a Hölder space if all of its components belong to this space and define its norm as the maximum of component norms. The same applies to a tensor-valued function.

We set

$${|f|}_{D_T}^{(k+\alpha ,\frac{k+\alpha }{2})}\equiv {|f|}_{Q_T^{-}}^{(k+\alpha ,\frac{k+\alpha }{2})}+{|f|}_{Q_T^{+}}^{(k+\alpha ,\frac{k+\alpha }{2})},D_T\equiv Q_T^{+}\cup Q_T^{-},$$

$${|f|}_{\cup {\Omega }^{\pm }}^{(k+\alpha )}\equiv {|f|}_{{\Omega }^{-}}^{(k+\alpha )}+{|f|}_{{\Omega }^{+}}^{(k+\alpha )}.$$

3. A Linearized Problem

We suppose the surfaces ${\tilde{\Gamma }}_t^{\pm }$ to be given by the relations

$${\tilde{\Gamma }}_t^{\pm }=\{y=z+\mathit{N}\left(z\right)r(z,t),z\in {\mathcal{G}}^{\pm }\},$$

(14)

where $\mathit{N}$ is the outward normal to ${\mathcal{G}}^{-}\cup {\mathcal{G}}^{+}$.

Let us map ${\tilde{\Omega }}_t^{\pm }$ into ${\mathcal{F}}^{\pm }$ by the inverse transformation to the Hanzawa transform

$$y=z+{\mathit{N}}^{*}\left(z\right)r^{*}(z,t)\equiv e_r(z,t),$$

(15)

where ${\mathit{N}}^{*}$, $r^{*}$ are some extensions of $\mathit{N}$ and r into $\mathcal{F}$, respectively.

In order to analyze problem (11) with initial data close to the regime of rotation as a rigid body (see Figure 1), we linearize it. To this end, we calculate the first variation with respect to r of the differences $H\left(y\right)-\mathcal{H}\left(z\right)$, $|y^{\prime }{|}^2-{|z^{\prime }|}^2$, $U(y,t)-\mathcal{U}\left(z\right)$. We use the following formulas for the first and second variations of a functional $R\left[r\right]$

$${\delta }_{0}R\left[r\right]=\frac{\mathrm{d}}{\mathrm{d}s}R\left[sr\right]{|}_{s=0},{\delta }_0^{2}R\left[r\right]=\frac{{\mathrm{d}}^2}{\mathrm{d}{s}^2}R\left[sr\right]{|}_{s=0}.$$

(16)

It is easily seen that ${\delta }_0\left(|y^{\prime }{|}^2-{|z^{\prime }|}^2\right)=\frac{\mathrm{d}}{\mathrm{d}s}\left(|{\mathit{z}}^{\prime }+{\mathit{N}}^{\prime }{sr|}^2-{|{\mathit{z}}^{\prime }|}^2\right){|}_{s=0}=2{\mathit{z}}^{\prime }·{\mathit{N}}^{\prime }r,{\mathit{N}}^{\prime }=(N_1,N_2,0).$ By [12], ${\delta }_0\left(H^{\pm }\left(y\right)-{\mathcal{H}}^{\pm }\left(z\right)\right)={\Delta }^{\pm }{r}^{\pm }+\left({\mathcal{H}}^{{\pm }^2}\left(z\right)-2{\mathcal{K}}^{\pm }\left(z\right)\right)r^{\pm },$ where the Laplace–Beltrami operators ${\Delta }^{\pm }$ act on ${\mathcal{G}}^{\pm }$. Moreover, as mentioned in [8],

$${\delta }_0\left(U(y,t)-\mathcal{U}\left(z\right)\right)=\frac{\partial \mathcal{U}}{\partial \mathit{N}}r+\mathcal{W}\left[r\right](z,t),$$

where

$$\mathcal{U}\left(z\right)={\int }_{\mathcal{F}}\frac{\overline{\rho }\mathrm{d}x}{|z-x|},\mathcal{W}\left[r\right](z,t)\equiv {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}\frac{r(x,t)}{|z-x|}\mathrm{d}{\mathcal{G}}_x+\left[{\rho }^{\pm }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}\frac{r(x,t)}{|z-x|}\mathrm{d}{\mathcal{G}}_x.$$

In new coordinates (15), the kinematic condition for $V_{\mathit{n}}\equiv {\mathcal{D}}_t{\mathit{y}·\mathit{n}|}_{\mathcal{G}}$ takes the form

$${\mathcal{D}}_{t}r\mathit{N}·\mathit{n}=\tilde{\mathit{v}}·\mathit{n}.$$

(17)

Thus, collecting the above relations, we obtain a linear problem corresponding to (11) with the unknown functions $\mathit{w}$ and $p_1$:

$$\begin{array}{c}\overline{\rho }\left({\mathcal{D}}_t\mathit{w}+2\omega (e_3\times \mathit{w})\right)-\overline{\mu }{\nabla }^2\mathit{w}+\nabla p_1=\overline{\rho }\mathit{f},\\ \nabla ·\mathit{w}=f\equiv \nabla ·\mathit{F}\mathrm{in}\cup {\mathcal{F}}^{\pm }\equiv {\mathcal{F}}^{-}\cup {\mathcal{F}}^{+},t>0,\\ \mathit{w}(z,0)={\mathit{v}}_0\left(z\right)-\mathcal{V}\left(z\right)\equiv {\mathit{w}}_0\left(z\right),z\in \cup {\mathcal{F}}^{\pm },\\ \left[\mathit{w}\right]{|}_{{\mathcal{G}}^{+}}=0,\left[\mathbb{T}(\mathit{w},p_1)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}+\mathit{N}{\mathcal{B}}_0^{+}\left(r\right)=\mathit{d}\mathrm{on}{\mathcal{G}}^{+},\\ \mathbb{T}(\mathit{w},p_1)\mathit{N}+\mathit{N}{\mathcal{B}}_0^{-}\left(r\right)=\mathit{d}\mathrm{on}{\mathcal{G}}^{-},\\ {\mathcal{D}}_{t}r-\mathit{w}·\mathit{N}=g\mathrm{on}\mathcal{G}\equiv {\mathcal{G}}^{-}\cup {\mathcal{G}}^{+},r(z,0)=r_0\left(z\right),z\in \mathcal{G},\end{array}$$

(18)

where the operators

$$\begin{array}{c}{\mathcal{B}}_0^{-}\left(r\right)=-{\sigma }^{-}{\Delta }^{-}r-b^{-}\left(z\right)r-{\rho }^{-}\varkappa \mathcal{W}\left[r\right],z\in {\mathcal{G}}^{-},\\ {\mathcal{B}}_0^{+}\left(r\right)=-{\sigma }^{+}{\Delta }^{+}r-b^{+}\left(z\right)r-\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}\varkappa \mathcal{W}\left[r\right],z\in {\mathcal{G}}^{+},\end{array}$$

(19)

with

$$\begin{array}{cc}\hfill b^{-}\left(z\right)& ={\sigma }^{-}({{\mathcal{H}}^{-}}^2-2{\mathcal{K}}^{-})+{\rho }^{-}{\omega }^2\mathit{N}·{\mathit{z}}^{\prime }+{\rho }^{-}\varkappa \partial \mathcal{U}/\partial \mathit{N},\hfill \\ \hfill b^{+}\left(z\right)& ={\sigma }^{+}({{\mathcal{H}}^{+}}^2-2{\mathcal{K}}^{+})+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\omega }^2\mathit{N}·{\mathit{z}}^{\prime }+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}\varkappa \partial \mathcal{U}/\partial \mathit{N},\hfill \end{array}$$

where ${\mathit{z}}^{\prime }=(z_1,z_2,0)$ and ${\mathcal{K}}^{\pm }$ are the Gaussian curvatures of ${\mathcal{G}}^{\pm }$, $\omega$ is the angular velocity, $r(x,t)$ is an unknown function equal to the deviation of the surfaces ${\Gamma }_t^{\pm }$ from ${\mathcal{G}}^{\pm }$ and $\mathit{f},f,\mathit{d},g,$ ${\mathit{w}}_0,r_0$ are given functions.

First, we study problem (18) with the homogeneous equations and boundary conditions:

$$\begin{array}{c}\overline{\rho }({\mathcal{D}}_t\mathit{w}+2\omega ({\mathit{e}}_3\times \mathit{w}))-\overline{\mu }{\nabla }^2\mathit{w}+\nabla p_1=0,\nabla ·\mathit{w}=0\mathrm{in}\cup {\mathcal{F}}^{\pm },t>0,\\ \mathit{w}{|}_{t=0}={\mathit{w}}_0\mathrm{in}\cup {\mathcal{F}}^{\pm },\\ \left[\mathit{w}\right]{|}_{{\mathcal{G}}^{+}}=0,\left[\mathbb{T}(\mathit{w},p_1)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}+\mathit{N}{\mathcal{B}}_0^{+}\left(r\right)=0\mathrm{on}{\mathcal{G}}^{+},\\ \mathbb{T}(\mathit{w},p_1)\mathit{N}{|}_{{\mathcal{G}}^{-}}+\mathit{N}{\mathcal{B}}_0^{-}\left(r\right)=0\mathrm{on}{\mathcal{G}}^{-},\\ {\mathcal{D}}_{t}r-\mathit{w}·\mathit{N}=0\mathrm{on}\mathcal{G},r{|}_{t=0}=r_0\mathrm{on}\mathcal{G}.\end{array}$$

(20)

We assume that the domains ${\mathcal{F}}^{\pm }$ are symmetric with respect to $z_1,z_2,z_3$ and that the initial data satisfy, due to assumptions (12), (13), orthogonality conditions

$$\begin{array}{c}{\int }_{{\mathcal{G}}^{\pm }}{r}_0\left(z\right)\mathrm{d}\mathcal{G}=0,\\ {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{r}_0\left(z\right)z_j\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}{r}_0\left(z\right)z_j\mathrm{d}\mathcal{G}=0,j=1,2,3,\end{array}$$

(21)

$$\begin{gathered} \begin{array}{c}\hspace{1em}\hspace{1em}\hspace{1em}{\int }_{\mathcal{F}}\overline{\rho }{\mathit{w}}_0\left(z\right)\mathrm{d}z=0,\\ {\int }_{\mathcal{F}}\overline{\rho }{\mathit{w}}_0\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}z+\omega \left({\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{r}_0\left(z\right){\mathit{\eta }}_3\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}\mathcal{G} \\ +\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}{r}_0\left(z\right){\mathit{\eta }}_3\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}\mathcal{G}\right)=0.\end{array} \end{gathered}$$

(22)

We put $Q_T^{\pm }={\mathcal{F}}^{\pm }\times (0,T)$, $G_T^{\pm }={\mathcal{G}}^{\pm }\times (0,T)$, $D_T=Q_T^{+}\cup Q_T^{-}$, $Q_T=Q_T^{+}\cup \overline{Q_T^{-}}$, $G_T=G_T^{+}\cup G_T^{-}$, $T\in (0,\infty ]$.

Proposition 2.

A solution of problem (20) under conditions (21), (22) at the initial instant satisfies (21) and (22) for all $t>0$.

This proposition is proved in the same way as Proposition 2.1 in [10] by virtue of Proposition 3.

In view of impulse conservation, the following statement is valid.

Corollary 1.

There holds the decomposition

$$\mathit{w}={\mathit{w}}^{\perp }+\sum _{i=1}^3{d}_i\left(r\right){\mathit{\eta }}_i,$$

(23)

where ${\mathit{w}}^{\perp }$ means a vector field orthogonal to all the vectors of rigid motion η; i.e.,

$${\int }_{\mathcal{F}}\overline{\rho }{\mathit{w}}^{\perp }·\mathit{\eta }\mathrm{d}z=0,$$

$\mathit{\eta }={\mathit{e}}_{i}or\mathit{\eta }\left(z\right)={\mathit{\eta }}_i\left(z\right),i=1,2,3,$ and

$$d_i\left(r\right)=-\frac{\omega }{S_i}\left({\rho }^{-}{\int }_{{\mathcal{G}}^{-}}r{\mathit{\eta }}_3·{\mathit{\eta }}_i\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}r{\mathit{\eta }}_3·{\mathit{\eta }}_i\mathrm{d}\mathcal{G}\right),S_i={\int }_{\mathcal{F}}\overline{\rho }{|{\mathit{\eta }}_i|}^2\mathrm{d}z.$$

Proposition 3.

The following relations hold:

$$\begin{array}{c}{\mathcal{B}}_0^{-}(\mathit{\eta }·\mathit{N})=-{\omega }^2{\rho }^{-}\mathit{\eta }·{\mathit{z}}^{\prime },z\in {\mathcal{G}}^{-},\\ {\mathcal{B}}_0^{+}(\mathit{\eta }·\mathit{N})=-{\omega }^2\left[\overline{\rho }\right]{|}_{{\mathcal{G}}_t^{+}}\mathit{\eta }·{\mathit{z}}^{\prime },z\in {\mathcal{G}}^{+},\end{array}$$

where η is an arbitrary vector of rigid motion.

This statement was proved in [11].

We cite the result obtained in ([9], § 5.3) about the solvability of the following linear problem for the Stokes system in an unbounded domain ${\Omega }^{-}\cup {\Omega }^{+}$, $\overline{{\Omega }^{+}}\cup {\Omega }^{-}={\mathbb{R}}^3$, with the closed interface $\Gamma =\partial {\Omega }^{+}$:

$$\begin{gathered} {\mathcal{D}}_t\mathit{v}-{\nu }^{\pm }{\nabla }^2\mathit{v}+\frac{1}{{\rho }^{\pm }}\nabla p=\mathit{f},\nabla ·\mathit{v}=g\mathrm{in}{D}_T\equiv \cup Q_T^{\pm }={\Omega }^{\pm }\times (0,T), \\ {\mathit{v}|}_{t=0}={\mathit{v}}_0\mathrm{in}{\Omega }^{-}\cup {\Omega }^{+},\mathit{v}\underset{|x|\to \infty }{⟶}0, \\ \begin{array}{c}\hfill {\left[\mathit{v}\right]|}_{\Gamma }=0,\left[{\Pi }_0\mathbb{T}\mathit{n}\right]{|}_{\Gamma }=\mathit{b}\left(\mathit{b}·\mathit{n}=0\right),\end{array} \\ {[\mathit{v}·\mathbb{T}\mathit{n}]|}_{\Gamma }-\sigma \mathit{n}·{\int }_0^t{\Delta }_{\Gamma }\mathit{v}\mathrm{d}{t}^{\prime }=b^{\prime }+\sigma {\int }_0^{t}B\mathrm{d}{t}^{\prime }\mathrm{on}{G}_T\equiv \Gamma \times (0,T), \end{gathered}$$

(24)

where f, g, b, b′, B, v₀ are given functions; n denotes the outward unit normal to Γ; II₀a = a − (n · a)n.

We assume first that there hold two representations:

$$g=\nabla ·\mathit{R}\mathrm{and}{\mathcal{D}}_t\mathit{R}-\mathit{f}\equiv \mathit{h}=\nabla ·\mathbb{M}=\sum _{k=1}^3\partial M_{ik}/\partial x_k,$$

(25)

and second, that compatibility conditions

$$\left[{\mathit{v}}_0\right]{|}_{\Gamma }=0,\nabla ·{\mathit{v}}_0\left(x\right)=g(x,0),x\in {\Omega }^{-}\cup {\Omega }^{+},$$

$$\left[{\mu }^{\pm }{\Pi }_0\mathbb{S}\left({\mathit{v}}_0\left(x\right)\right)\mathit{n}\right]{|}_{x\in \Gamma }=\mathit{b}(x,0),x\in \Gamma ,$$

(26)

$$\left[{\Pi }_0\left(\mathit{f}(x,0)-\frac{1}{{\rho }^{\pm }}\nabla p(x,0)+{\nu }^{\pm }{\nabla }^2{\mathit{v}}_0\left(x\right)\right)\right]{|}_{x\in \Gamma }=0$$

are satisfied. The last of relations (26) follows from the tangential part of the necessary condition of the continuity of velocity derivative ${\mathcal{D}}_t\mathit{v}$ at $t=0:\left[{\mathcal{D}}_t\mathit{v}\right]{|}_{\Gamma }=0$. The normal part of this equality $[{\mathcal{D}}_t\mathit{v}·\mathit{n}]{|}_{\Gamma ,t=0}=0$ holds if the initial pressure $p_0\equiv p(x,0)$ is a solution to the problem

$$\frac{1}{{\rho }^{\pm }}{\nabla }^2{p}_0\left(x\right)=\nabla ·\left(\mathit{f}(x,0)+{\nu }^{\pm }\nabla g(x,0)-{\mathcal{D}}_t\mathit{R}(x,0)\right)\mathrm{in}\cup {\Omega }^{\pm },$$

$$\left[p_0\right]{{|}_{\Gamma }=\left[2{\mu }^{\pm }\frac{\partial {\mathit{v}}_0}{\partial \mathit{n}}·\mathit{n}\right]{|}_{\Gamma }-b^{\prime }|}_{t=0}\equiv p_{00},$$

(27)

$$\left[\frac{1}{{\rho }^{\pm }}\frac{\partial p_0}{\partial \mathit{n}}\right]{|}_{\Gamma }=\left[\mathit{n}·\left(\mathit{f}(x,0)+{\nu }^{\pm }{\nabla }^2{\mathit{v}}_0\right)\right]{|}_{\Gamma }\equiv p_{01}\left(\frac{\partial \psi }{\partial \mathit{n}}\equiv \nabla \psi ·\mathit{n}\right).$$

(Here the first equation is understood in a weak sense.)

Theorem 1.

Let assumptions (25)–(27) be fulfilled. In addition, we assume for $\alpha ,\gamma \in (0,1)$ and $\gamma <\alpha$ when $\sigma >0$ and $T<\infty$ that $\Gamma \in C^{2+\alpha }$, $\mathit{f}\in {\mathit{C}}^{\alpha ,\frac{\alpha }{2}}\left(D_T\right)$, $g\in C^{1+\alpha ,\frac{1+\alpha }{2}}\left(D_T\right),$ $\mathit{R}\in {\mathit{C}}^{(\gamma ,1+\alpha )}\left(D_T\right),$ ${\mathcal{D}}_t\mathit{R}\in {\mathit{C}}^{\alpha ,\frac{\alpha }{2}}\left(D_T\right)$, $[\mathit{R}·\mathit{n}]{|}_{G_T}=0,{\mathit{v}}_0\in {\mathit{C}}^{2+\alpha }({\Omega }^{-}\cup {\Omega }^{+})$, $\mathit{b}\in {\mathit{C}}_{\mathit{n}}^{1+\alpha ,\frac{1+a}{2}}\left(G_T\right),$ $b^{\prime }\in C^{(\gamma ,1+\alpha )}\left(G_T\right),B\in C^{\alpha ,\alpha /2}\left(G_T\right)$, and the elements of the tensor $\mathbb{M}$ have finite semi-norms ${\mathbf{\left|}{M}_{ik}\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}$, ${⟨M_{ik}⟩}_{x,D_T}^{\left(\gamma \right)}$, $i,k=1,2,3.$ We suppose also that all given functions decrease quickly enough for $|x|\to \infty$(for example, in a power-law way). Then problem (24) has a solution $(\mathit{v},p)$ such that $\mathit{v}\in {\mathit{C}}^{2+\alpha ,1+\alpha /2}\left(D_T\right),\nabla p\in {\mathit{C}}^{\alpha ,\alpha /2}\left(D_T\right)$, $p\in C^{(\gamma ,1+\alpha )}\left(B_T\right)$ and the inequality

$$\begin{array}{cc}\hfill & {|\mathit{v}|}_{D_T}^{(2+\alpha ,1+\alpha /2)}+{|\nabla p|}_{D_T}^{(\alpha ,\alpha /2)}+{\mathbf{⟨}p\mathbf{⟩}}_{D_T}^{(\gamma ,1+\alpha )}+{|p|}_{t,B_T}^{\left(\frac{1+\alpha -\gamma }{2}\right)}\hfill \\ \hfill & ⩽c_{13}{\left(T\right)\{|\mathit{f}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+{|g|}_{D_T}^{(1+\alpha ,\frac{1+a}{2})}+|{\mathcal{D}}_t{\mathit{R}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}\mathit{R}\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}+{|\mathit{b}|}_{G_T}^{(1+\alpha ,\frac{1+\alpha }{2})}+{\mathbf{\left|}{b}^{\prime }\mathbf{\right|}}_{G_T}^{(\gamma ,1+\alpha )}\hfill \\ \hfill & +|b^{\prime }{|}_{G_T}+|{\nabla }_{\tau }{b}^{\prime }{|}_{G_T}^{(\alpha ,\frac{\alpha }{2})}+{\sigma |B|}_{G_T}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}\mathbb{M}\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}+{⟨\mathbb{M}⟩}_{x,D_T}^{\left(\gamma \right)}+{|{\mathit{v}}_0|}_{\cup {\Omega }^{\pm }}^{(2+\alpha )}\}\hfill \\ \hfill & \equiv c_{13}\left(T\right)F\left(T\right)\hfill \end{array}$$

(28)

holds, where ${\nabla }_{\tau }={\Pi }_0\nabla ,c_{13}\left(T\right)$ is a nondecreasing function of T, $B_T\equiv B_1\times (0,T)$ and $B_1$ is a ball containing the domain $\overline{{\Omega }^{+}}$. The velocity vector field $\mathit{v}$ is defined uniquely, and the pressure p is determined in the class of functions of weak power-law growth up to a smooth bounded time-dependent function.

A similar theorem for the bounded domain $D_T\equiv \cup {\mathcal{F}}^{\pm }\times (0,T),$ is also valid [9]. In order to prove such a theorem, one applies the estimates near the outer boundary ${\mathcal{G}}^{-}$ which were obtained in [13,14] for a single liquid.

Theorem 2

(Local Solvability of the Linear Problem). Let $\mathcal{G}\in C^{3+\alpha }$ and $r_0\in C^{3+\alpha }\left(\mathcal{G}\right)$ with $\alpha \in (0,1).$ We suppose that $\mathit{f}\in {\mathit{C}}^{\alpha ,\frac{\alpha }{2}}\left(D_T\right),$ $f\in C^{1+\alpha ,\frac{1+\alpha }{2}}\left(D_T\right),$ $f=\nabla ·\mathit{F},$ $\mathit{F}\in {\mathit{C}}^{(\gamma ,1+\alpha )}\left(D_T\right),$ ${\mathcal{D}}_t\mathit{F}\in {\mathit{C}}^{\alpha ,\alpha /2}\left(D_T\right),$ ${[\mathit{F}·\mathit{N}]|}_{{\mathcal{G}}^{+}}=0,$ ${\mathit{w}}_0\in {\mathit{C}}^{2+\alpha }\left(\cup {\mathcal{F}}^{\pm }\right),$ $\mathit{d}={\mathit{d}}_{\tau }+d\mathit{N},$ ${\mathit{d}}_{\tau }\in {\mathit{C}}^{1+\alpha ,\frac{1+a}{2}}\left(G_T\right),$ $\mathit{N}·{\mathit{d}}_{\tau }=0,$ $d\in C^{(\gamma ,1+\alpha )}\left(G_T\right),$ ${\nabla }_{\tau }d\in {\mathit{C}}^{\alpha ,\alpha /2}\left(G_T\right),$ $g\in C^{2+\alpha ,1+\frac{\alpha }{2}}\left(G_T\right),$ $G_T\equiv \mathcal{G}\times (0,T)$ and $\gamma \in (0,1),$ $\gamma <\alpha ,$ $T<\infty ,$ satisfy compatibility conditions

$$\begin{array}{cc}\hfill & \nabla ·{\mathit{w}}_0{=f|}_{t=0},\hfill \\ \hfill & \left[{\mathit{w}}_0\right]{|}_{{\mathcal{G}}^{+}}=0,\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{w}}_0\right)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}={\mathit{d}}_{\tau }{|}_{t=0},{\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{w}}_0\right)\mathit{N}{{|}_{{\mathcal{G}}^{-}}={\mathit{d}}_{\tau }|}_{t=0},\hfill \end{array}$$

$$\left[{\Pi }_{\mathcal{G}}\left(\mathit{f}(x,0)-\frac{1}{{\rho }^{\pm }}\nabla p_1(x,0)+\overline{\nu }{\nabla }^2{\mathit{w}}_0\left(x\right)\right)\right]{|}_{x\in {\mathcal{G}}^{+}}=0,$$

where ${\Pi }_{\mathcal{G}}\mathit{b}=\mathit{b}-(\mathit{N}·\mathit{b})\mathit{N}.$ Moreover, we assume $\mathit{f}$ and $\mathit{F}$ to satisfy the representation

$${\mathcal{D}}_t\mathit{F}-\mathit{f}\equiv \mathit{h}=\nabla ·\mathbb{M}=\sum _{k=1}^3\partial M_{ik}/\partial x_k,$$

where $M_{ik}$ have finite norm ${\mathbf{\left|}{M}_{ik}\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}$ and semi-norm ${⟨M_{ik}⟩}_{x,D_T}^{\left(\gamma \right)}$, $i,k=1,2,3.$ We also assume the initial pressure $p_0\equiv p_1(x,0)$ to be a solution (in a weak sense) to the problem

$$\begin{array}{cc}\hfill \frac{1}{\overline{\rho }}{\nabla }^2{p}_0\left(x\right)& =\nabla ·\left(\mathit{f}(x,0)+\overline{\nu }\nabla f(x,0)-{\mathcal{D}}_t\mathit{F}(x,0)-2\omega (e_3\times {\mathit{w}}_0)\right),x\in \cup {\mathcal{F}}^{\pm },\hfill \\ \hfill \left[p_0\right]{|}_{{\mathcal{G}}^{+}}& =\left[2\overline{\mu }\frac{\partial {\mathit{w}}_0}{\partial \mathit{N}}·\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}+{\mathcal{B}}_0^{+}\left(r_0\right){-d|}_{t=0}\equiv p_{00}^{+},\hfill \\ \hfill \left[\frac{1}{\overline{\rho }}\frac{\partial p_0}{\partial \mathit{N}}\right]{|}_{{\mathcal{G}}^{+}}& =\left[\mathit{N}·\left(\mathit{f}(x,0)+\overline{\nu }{\nabla }^2{\mathit{w}}_0\right)\right]{|}_{{\mathcal{G}}^{+}}\equiv p_{01}^{+}\left(\frac{\partial \psi }{\partial \mathit{N}}\equiv \nabla \psi ·\mathit{N}\right),\hfill \\ \hfill p_0{|}_{{\mathcal{G}}^{-}}& =2{\mu }^{-}\frac{\partial {\mathit{w}}_0}{\partial \mathit{N}}·\mathit{N}{|}_{{\mathcal{G}}^{-}}+{\mathcal{B}}_0^{-}\left(r_0\right){-d|}_{t=0}\equiv p_{00}^{-}.\hfill \end{array}$$

Then problem (18) has a unique solution $(\mathit{w},p_1,r)$ such that $\mathit{w}\in {\mathit{C}}^{2+\alpha ,1+\alpha /2}\left(D_T\right),$ $\nabla p_1\in {\mathit{C}}^{\alpha ,\alpha /2}\left(D_T\right)$, $p_1\in C^{(\gamma ,1+\alpha )}\left(D_T\right)$, $r(·,t)\in C^{3+\alpha }\left(\mathcal{G}\right)$ for any $t\in (0,T)$ and the inequality

$$\begin{array}{cc}\hfill & Y_{(0,T)}[\mathit{w},p_1,r]\equiv {|\mathit{w}|}_{D_T}^{(2+\alpha ,1+\frac{\alpha }{2})}+{|\nabla p_1|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}{p}_1\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}+{|r|}_{G_T}^{(3+\alpha ,\frac{3+\alpha }{2})}+{|{\mathcal{D}}_{t}r|}_{G_T}^{(2+\alpha ,1+\frac{\alpha }{2})}\hfill \\ \hfill & ⩽c_{13}{\left(T\right)\{|\mathit{f}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+{|f|}_{D_T}^{(1+\alpha ,\frac{1+a}{2})}+|{\mathcal{D}}_t{\mathit{F}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}\mathit{F}\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}+{|{\mathit{d}}_{\tau }|}_{G_T}^{(1+\alpha ,\frac{1+\alpha }{2})}+{\mathbf{\left|}d\mathbf{\right|}}_{G_T}^{(\gamma ,1+\alpha )}\hfill \\ \hfill & +|{\nabla }_{\tau }{d|}_{G_T}^{(\alpha ,\frac{\alpha }{2})}+{\sigma |B|}_{G_T}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}\mathbb{M}\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}+{⟨\mathbb{M}⟩}_{x,D_T}^{\left(\gamma \right)}+{|{\mathit{w}}_0|}_{\cup {\Omega }^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}+{|g|}_{G_T}^{(2+\alpha ,1+\alpha /2)}\}\hfill \\ \hfill & \equiv c_{13}\left(T\right)F\left(T\right)\hfill \end{array}$$

(29)

holds.

Proof. 

Let $r_1$ be a function satisfying the conditions

$$\begin{array}{cc}\hfill & r_1(y,0)=r_0\left(y\right),\hfill \\ \hfill & {\mathcal{D}}_t{r}_1(y,0)=g(y,0)+{\mathit{w}}_0\left(y\right)·\mathit{N}\left(y\right)\equiv r_0^{\prime }\left(y\right)\hfill \end{array}$$

and the estimate

$$\begin{array}{cc}\hfill {|r_1|}_{G_T}^{(3+\alpha ,3/2+\frac{\alpha }{2})}+{|{\mathcal{D}}_t{r}_1|}_{G_T}^{(2+\alpha ,1+\frac{\alpha }{2})}& ⩽c\left\{|r_0{|}_{\mathcal{G}}^{(3+\alpha )}+{|r_0^{\prime }|}_{\mathcal{G}}^{(2+\alpha )}\right\}.\hfill \end{array}$$

(30)

Such a $r_1$ exists. Indeed, we find this function as a solution of a hyperbolic equation with the initial data $r_1^{*}(y,0)=r_0^{*}\left(y\right)$ and ${\mathcal{D}}_t{r}_1^{*}={r^{\prime }}_0^{*}$, where $r_0^{*}$ and ${r^{\prime }}_0^{*}$ are extensions of the initial data into ${\mathbb{R}}^3$ with conservation of class. Then

$$|r_1{|}_{G_T}^{(3+\alpha ,\frac{3+\alpha }{2})}+{|{\mathcal{D}}_t{r}_1|}_{G_T}^{(2+\alpha ,1+\alpha /2)}⩽{|r_1^{*}|}_{Q_T}^{(3+\alpha ,3+\alpha )}+{|{\mathcal{D}}_t{r}_1^{*}|}_{Q_T}^{(2+\alpha ,2+\alpha )}⩽c\left\{|r_0{|}_{\mathcal{G}}^{(3+\alpha )}+{|r_0^{\prime }|}_{\mathcal{G}}^{(2+\alpha )}\right\}.$$

We can write

$$\begin{array}{cc}{\mathcal{B}}_0^{\pm }r(y,t)& ={\mathcal{B}}_0^{\pm }{r}_1(y,t)+{\int }_0^t{\mathcal{B}}_0^{\pm }{\mathcal{D}}_t\left(r(y,\tau )-r_1(y,\tau )\right)\mathrm{d}\tau \\ & ={\mathcal{B}}_0^{\pm }{r}_1(y,t)+{\int }_0^t{\mathcal{B}}_0^{\pm }\left(g(y,\tau )+\mathit{w}(y,\tau )·\mathit{N}\left(y\right)-{\mathcal{D}}_t{r}_1(y,\tau )\right)\mathrm{d}\tau .\end{array}$$

Hence, problem (18) can be transformed to the form:

$$\begin{array}{cc}& \overline{\rho }\left({\mathcal{D}}_t\mathit{w}+2\omega ({\mathit{e}}_3\times \mathit{w})\right)-\overline{\mu }{\nabla }^2\mathit{w}+\nabla p_1=\overline{\rho }\mathit{f},\nabla ·\mathit{w}=f\mathrm{in}{D}_T,\hfill \\ \hfill & \mathit{w}(y,0)={\mathit{w}}_0\left(y\right)\mathrm{in}\cup {\mathcal{F}}^{\pm },\hfill \\ \hfill & {\left[\mathit{w}\right]|}_{G_T^{+}}=0,\left[{\mu }^{\pm }{\Pi }_{\mathcal{G}}\mathbb{S}\left(\mathit{w}\right)\mathit{N}\right]{|}_{G_T^{+}}={\mathit{d}}_{\tau },{\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left(\mathit{w}\right)\mathit{N}{|}_{G_T^{-}}={\mathit{d}}_{\tau },\hfill \\ \hfill & \mathit{N}·\mathbb{T}(\mathit{w},p_1)\mathit{N}{|}_{G_T^{-}}-{\sigma }^{-}\mathit{N}·{\Delta }^{-}{\int }_0^t{\mathit{w}|}_{G_T^{-}}\mathrm{d}\tau =d^{\prime }+{\sigma }^{-}{\int }_0^t{B}^{\prime }\mathrm{d}\tau \hfill \\ \hfill & +{\rho }^{-}\varkappa {\int }_0^t\left(\mathcal{W}[\mathit{N}·\mathit{w}]+\frac{\partial \mathcal{U}}{\partial \mathit{N}}\mathit{N}·\mathit{w}\right)\mathrm{d}\tau +{\sigma }^{-}{\nabla }_{\mathcal{G}}\mathcal{H}·{\int }_0^t\mathit{w}\mathrm{d}\tau \hfill \\ \hfill & -{\sigma }^{-}{\omega }^2{\rho }^{-}\mathit{N}·{\mathit{y}}^{\prime }{\int }_0^t\mathit{w}·\mathit{N}\mathrm{d}\tau +2{\sigma }^{-}{\int }_0^t{\nabla }_{\mathcal{G}}\mathit{w}:{\nabla }_{\mathcal{G}}\mathit{N}\mathrm{d}\tau \mathrm{on}{G}_T^{-},\hfill \\ \hfill & [\mathit{N}·\mathbb{T}(\mathit{w},p_1)\mathit{N}]{|}_{G_T^{+}}-{\sigma }^{+}\mathit{N}·{\Delta }^{+}{\int }_0^t{\mathit{w}|}_{G_T^{+}}\mathrm{d}\tau =d^{\prime }+{\sigma }^{+}{\int }_0^t{B}^{\prime }\mathrm{d}\tau +{\sigma }^{+}{\nabla }_{\mathcal{G}}{\mathcal{H}}^{+}·{\int }_0^t\mathit{w}\mathrm{d}\tau \hfill \\ \hfill & +\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}\varkappa {\int }_0^t\left(\mathcal{W}[\mathit{N}·\mathit{w}]+\frac{\partial \mathcal{U}}{\partial \mathit{N}}\mathit{N}·\mathit{w}\right)\mathrm{d}\tau -{\sigma }^{+}{\omega }^2\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}\mathit{N}·{\mathit{y}}^{\prime }{\int }_0^t\mathit{w}·\mathit{N}\mathrm{d}\tau \hfill \\ \hfill & +2{\sigma }^{+}{\int }_0^t{\nabla }_{\mathcal{G}}\mathit{w}:{\nabla }_{\mathcal{G}}\mathit{N}\mathrm{d}\tau \mathrm{on}{G}_T^{+},\hfill \end{array}$$

(31)

where $d^{\prime }=d-{\mathcal{B}}_0^{\pm }{r}_1$, $B^{\prime }=-{\mathcal{B}}_0^{\pm }(g-{\mathcal{D}}_t{r}_1)$, ${\nabla }_{\mathcal{G}}={\Pi }_{\mathcal{G}}\nabla$ is the surface gradient on $\cup {\mathcal{G}}^{\pm }$; $\mathbb{S}:\mathbb{T}\equiv S_{ij}{T}_{ij}$. Here we have used (Lemma 10.7 in [15]) the relation

$${\Delta }^{\pm }\mathit{N}={\nabla }_{\mathcal{G}}{\mathcal{H}}^{\pm }-({\mathcal{H}}^{{\pm }^2}-2{\mathcal{K}}^{\pm })\mathit{N}.$$

We can apply Theorem 1, formulated for a bounded domain, to problem (31) in order to state the solvability of it, the additional terms $2\omega ({\mathit{e}}_3\times \mathit{w})$ and

$$\begin{array}{c}\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{\pm }}\varkappa {\int }_0^t\left(\mathcal{W}[\mathit{N}·\mathit{w}]+\frac{\partial \mathcal{U}}{\partial \mathit{N}}\mathit{N}·\mathit{w}\right)\mathrm{d}\tau +{\sigma }^{\pm }{\nabla }_{\mathcal{G}}\mathcal{H}·{\int }_0^t\mathit{w}\mathrm{d}\tau \hfill \\ -{\sigma }^{\pm }{\omega }^2\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{\pm }}\mathit{N}·{\mathit{y}}^{\prime }{\int }_0^t\mathit{w}·\mathit{N}{{|}_{{\mathcal{G}}^{\pm }}\mathrm{d}\tau +2{\sigma }^{\pm }{\int }_0^t{\nabla }_{\mathcal{G}}\mathit{w}(y,t):{\nabla }_{\mathcal{G}}\mathit{N}\left(y\right)|}_{{\mathcal{G}}^{\pm }}\mathrm{d}\tau \hfill \end{array}$$

being of lower order and having no essential influence on the final result. Indeed, let us evaluate, for example, the terms connected with self-gravity:

$$\begin{array}{cc}\hfill {|\mathcal{W}[\mathit{w}·\mathit{N}]|}_{G_T}^{(\alpha ,\alpha /2)}& ⩽{c|\mathit{w}·\mathit{N}|}_{G_T}^{(\alpha ,\alpha /2)}⩽{c|\mathit{w}|}_{G_T}^{(\alpha ,\alpha /2)}{|\mathit{N}|}_{\mathcal{G}}^{\left(\alpha \right)},\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill |\frac{\partial \mathcal{U}}{\partial \mathit{N}}\mathit{w}·\mathit{N}{|}_{G_T}^{(\alpha ,\alpha /2)}& ⩽{c|\mathcal{U}|}_{\mathcal{G}}^{(1+\alpha )}{|\mathit{w}·\mathit{N}|}_{G_T}^{(\alpha ,\alpha /2)}⩽c{|\mathit{w}|}_{G_T}^{(\alpha ,\alpha /2)}.\hfill \end{array}$$

(33)

The others terms can be treated in a similar way. Thus, inequality (28) together with (30), (32) and (33) implies estimate (29). □

Let us consider now homogeneous problem (20) with ${\mathit{w}}_0$ and $r_0$ satisfying orthogonality conditions (21) and (22). On the basis of decomposition (23), an $L_2$-estimate of $\mathit{w}$ and r with exponential weight was obtained in [11] (Proposition 2.3). We cite it here.

Proposition 4.

Assume that the form

$$R_0\left(r\right)={\int }_{\mathcal{G}}r{\mathcal{B}}_0^{\pm }r\mathrm{d}\mathcal{G}$$

(34)

is positive definite—i.e.,

$$c^{-1}{\parallel r\parallel }_{W_2^1\left(\mathcal{G}\right)}^2⩽R_0\left(r\right)⩽c{\parallel r\parallel }_{W_2^1\left(\mathcal{G}\right)}^2$$

(35)

for arbitrary $r\left(x\right)$ satisfying (21). Then a solution of (20)–(22) is subjected to the inequality

$$\parallel e^{{\beta }_{1}t}{\mathit{w}(·,t)\parallel }_{\mathcal{F}}^2+{\parallel e^{{\beta }_{1}t}r(·,t)\parallel }_{W_2^1\left(\mathcal{G}\right)}^2⩽c\left\{\parallel {\mathit{w}}_0{\parallel }_{\mathcal{F}}^2+{\parallel r_0\parallel }_{W_2^1\left(\mathcal{G}\right)}^2\right\},t>0,$$

(36)

where ${\beta }_1,$ $c>0$ are independent of $t.$

Remark 1.

Condition (35) coincides with the positiveness of the second variation of the expression for potential energy

$$G\left(r\right)={\sigma }^{+}|{\Gamma }_t^{+}|+{\sigma }^{-}|{\Gamma }_t^{-}|-\frac{{\omega }^2}{2}{\int }_{\cup {\Omega }_t^{\pm }}{\rho }^{\pm }{|x^{\prime }|}^2\mathrm{d}x-\frac{\varkappa }{2}{\int }_{\cup {\Omega }_t^{\pm }}{\rho }^{\pm }U\mathrm{d}x-p_0^{+}|{\Omega }_t^{+}|-p_0^{-}|{\Omega }_t^{-}|$$

for given volumes of ${\Omega }_t^{\pm }$. One can calculate it by (16) (see [6,8,11]). Taking into account Equation (8), we finally obtain

$$\begin{array}{cc}\hfill {\delta }_0^{2}G\left(r\right)=& {\int }_{{\mathcal{G}}^{-}}\left\{{\sigma }^{-}{|{\nabla }_{\mathcal{G}}r|}^2+\left({\sigma }^{-}(2\mathcal{K}-{\mathcal{H}}^2)-{\rho }^{-}{\omega }^2\mathit{N}·{\mathit{x}}^{\prime }\right)r^2\right\}\mathrm{d}\mathcal{G}\hfill \\ \hfill & +{\int }_{{\mathcal{G}}^{+}}\left\{{\sigma }^{+}{|{\nabla }_{\mathcal{G}}r|}^2+\left({\sigma }^{+}(2\mathcal{K}-{\mathcal{H}}^2)-\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\omega }^2\mathit{N}·{\mathit{x}}^{\prime }\right)r^2\right\}\mathrm{d}\mathcal{G}\hfill \\ \hfill & -\varkappa {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}\frac{\partial \mathcal{U}}{\partial \mathit{N}}{r}^2\mathrm{d}\mathcal{G}-\varkappa \left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}\frac{\partial \mathcal{U}}{\partial \mathit{N}}{r}^2\mathrm{d}\mathcal{G}\hfill \\ \hfill & -\varkappa {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}r\left(x\right)\mathcal{W}\left[r\right](x.t)\mathrm{d}{\mathcal{G}}_x-\varkappa \left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}r\left(x\right)\mathcal{W}\left[r\right](x.t)\mathrm{d}{\mathcal{G}}_x.\hfill \end{array}$$

If ${\delta }_0^{2}G\left(r\right)⩾0$ for the subspace of r satisfying orthogonality conditions (21), then the potential $G\left(r\right)$ is weakly lower semicontinuous. Since $G\left(r\right)$ is also coercive, it has a minimum which is clear to be realized at $r=0$. This means the stability of the figures $\mathcal{F}$ and ${\mathcal{F}}^{+}$ with the boundaries ${\mathcal{G}}^{\pm }$ defined by (8). We note that these relations serve as the Euler equations for $G\left(r\right)$. This is variational setting for stability problem of $\mathcal{F}$ and ${\mathcal{F}}^{+}$.

Theorem 3

(Global Existence for the Linear Homogeneous Problem). We assume that estimate (35) is valid for the functional $R_0\left(r\right)$ defined by (34) and that ${\mathit{w}}_0\in {\mathit{C}}^{2+\alpha }(\cup {\mathcal{F}}^{\pm })$, $r_0\in C^{3+\alpha }\left(\mathcal{G}\right)$, $\mathcal{G}\in C^{3+\alpha }$ with $\alpha \in (0,1)$ satisfy orthogonality conditions (21) and (22) and compatibility ones

$$\begin{array}{cc}\hfill & \nabla ·{\mathit{w}}_0=0\mathrm{in}\cup {\mathcal{F}}^{\pm },\hfill \\ \hfill & \left[{\mathit{w}}_0\right]{|}_{{\mathcal{G}}^{+}}=0,\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{w}}_0\right)\mathit{N}\right]{{|}_{{\mathcal{G}}^{+}}=0,{\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{w}}_0\right)\mathit{N}|}_{{\mathcal{G}}^{-}}=0,\hfill \end{array}$$

(37)

$$\left[{\Pi }_{\mathcal{G}}\left(-\frac{1}{\overline{\rho }}\nabla p_1(x,0)+\overline{\nu }{\nabla }^2{\mathit{w}}_0\left(x\right)\right)\right]{|}_{x\in {\mathcal{G}}^{+}}=0$$

with initial pressure function $p_1(x,0)\equiv p_0$ being a solution to the problem

$$\frac{1}{\overline{\rho }}{\nabla }^2{p}_0\left(x\right)=-2\omega \nabla ·(e_3\times {\mathit{w}}_0)\mathrm{in}\cup {\mathcal{F}}^{\pm },$$

$$\left[p_0\right]{{|}_{{\mathcal{G}}^{+}}=\left[2\overline{\mu }\frac{\partial {\mathit{w}}_0}{\partial \mathit{N}}·\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}+{\mathcal{B}}_0^{+}\left(r_0\right)\equiv p_{00}^{+},p_0|}_{{\mathcal{G}}^{-}}=2{\mu }^{-}\frac{\partial {\mathit{w}}_0}{\partial \mathit{N}}·\mathit{N}{|}_{{\mathcal{G}}^{-}}+{\mathcal{B}}_0^{-}\left(r_0\right)\equiv p_{00}^{-},$$

$$\left[\frac{1}{\overline{\rho }}\frac{\partial p_0}{\partial \mathit{N}}\right]{|}_{{\mathcal{G}}^{+}}=\left[\overline{\nu }{\nabla }^2{\mathit{w}}_0\right]{|}_{{\mathcal{G}}^{+}}\equiv p_{01}^{+}.$$

Then problem (20) has a unique solution $(\mathit{w},p_1,r)$ such that $\mathit{w}\in {\mathit{C}}^{2+\alpha ,1+\alpha /2}\left(D_{\infty }\right),$ $\nabla p_1\in {\mathit{C}}^{\alpha ,\alpha /2}\left(D_{\infty }\right)$, $p_1\in C^{(\gamma ,1+\alpha )}\left(B_{\infty }\right)$, $r(·,t)\in C^{3+\alpha }\left(\mathcal{G}\right)$ for any $t\in (0,\infty )$, and the inequality

$$\begin{array}{cc}\hfill |{\mathrm{e}}^{\beta t}{\mathit{w}|}_{D_{\infty }}^{(2+\alpha ,1+\alpha /2)}& +{|{\mathrm{e}}^{\beta t}\nabla p_1|}_{D_{\infty }}^{(\alpha ,\alpha /2)}+{\mathbf{\left|}{\mathrm{e}}^{\beta t}{p}_1\mathbf{\right|}}_{D_{\infty }}^{(\gamma ,1+\alpha )}+|{\mathrm{e}}^{\beta t}{r|}_{G_{\infty }}^{(3+\alpha ,\frac{3+\alpha }{2})}+{|{\mathrm{e}}^{\beta t}{\mathcal{D}}_{t}r|}_{G_{\infty }}^{(2+\alpha ,1+\alpha /2)}\hfill \\ \hfill & ⩽c_{14}\left\{|{\mathit{w}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right\}\hfill \end{array}$$

(38)

holds with a certain $\beta >0$.

In order to obtain bounds for the exponentially weighted Hölder norms of a solution, we apply a local-in-time estimate.

Proposition 5.

Let $T>2$. For a solution to problem (20)–(22), the inequality

$$\begin{array}{cc}\hfill & Y_{(t_0-1,t_0)}[\mathit{w},p_1,r]⩽c\left\{{\parallel \mathit{w}\parallel }_{Q_{t_0-2,t_0}}+{\parallel r\parallel }_{G_{t_0-2,t_0}}\right\}\hfill \end{array}$$

(39)

is valid, where $2<t_0⩽T,$ $D_{t_1,t_2}=\cup {\mathcal{F}}^{\pm }\times (t_1,t_2)$, $Q_{t_1,t_2}=\mathcal{F}\times (t_1,t_2)$, $\mathcal{F}=\overline{{\mathcal{F}}^{+}}\cup {\mathcal{F}}^{-}$, $G_{t_1,t_2}=\mathcal{G}\times (t_1,t_2)$.

Proof of Proposition 5. 

Let $t_0\in (2,T)$. We multiply (20) by the cutoff function ${\zeta }_{\lambda }\left(t\right)$, which is smooth and monotone, ${\zeta }_{\lambda }\left(t\right)=0$ if $t⩽t_0-2+\lambda /2$ and ${\zeta }_{\lambda }\left(t\right)=1$ if $t⩾t_0-2+\lambda ,$ where $\lambda \in (0,1].$ In addition, for ${\dot{\zeta }}_{\lambda }\left(t\right)\equiv \frac{\mathrm{d}{\zeta }_{\lambda }\left(t\right)}{\mathrm{d}t}$ and ${\ddot{\zeta }}_{\lambda }\left(t\right)$, the inequalities

$$\underset{t\in \mathbb{R}}{sup}|{\dot{\zeta }}_{\lambda }\left(t\right)|⩽c{\lambda }^{-1},\underset{t\in \mathbb{R}}{sup}|{\ddot{\zeta }}_{\lambda }\left(t\right)|⩽c{\lambda }^{-2},{⟨{\ddot{\zeta }}_{\lambda }\left(t\right)⟩}_{\mathbb{R}}^{\left(\vartheta \right)}⩽c{\lambda }^{-2-\vartheta },\forall \vartheta \in (0,1),$$

hold.

Then, for ${\mathit{w}}_{\lambda }=\mathit{w}{\zeta }_{\lambda }$, $p_{\lambda }=p_1{\zeta }_{\lambda }$, $r_{\lambda }=r{\zeta }_{\lambda },$ we obtain the system

$$\begin{array}{c}\overline{\rho }\left({\mathcal{D}}_t{\mathit{w}}_{\lambda }+2\omega \nabla ·({\mathit{e}}_3\times {\mathit{w}}_{\lambda })\right)-\overline{\mu }{\nabla }^2{\mathit{w}}_{\lambda }+\nabla p_{\lambda }=\overline{\rho }\mathit{w}{\dot{\zeta }}_{\lambda },\\ \nabla ·{\mathit{w}}_{\lambda }=0\mathrm{in}\cup {\mathcal{F}}^{\pm },t>0,\\ {\mathit{w}}_{\lambda }(y,0)=0\mathrm{in}\cup {\mathcal{F}}^{\pm },r_{\lambda }(y,0)=0\mathrm{on}\mathcal{G},\\ {\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{w}}_{\lambda }\right)\mathit{N}{|}_{{\mathcal{G}}^{-}}=0,\mathit{N}·\mathbb{T}({\mathit{w}}_{\lambda },p_{\lambda })\mathit{N}{|}_{{\mathcal{G}}^{-}}+{\mathcal{B}}_0\left(r_{\lambda }\right){|}_{{\mathcal{G}}^{-}}=0,\\ \left[{\mathit{w}}_{\lambda }\right]{{|}_{{\mathcal{G}}^{+}}=0,\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{w}}_{\lambda }\right)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}=0,[\mathit{N}·\mathbb{T}({\mathit{w}}_{\lambda },p_{\lambda })\mathit{N}]{|}_{{\mathcal{G}}^{+}}+{\mathcal{B}}_0\left(r_{\lambda }\right)|}_{{\mathcal{G}}^{+}}=0,\\ {\mathcal{D}}_t{r}_{\lambda }-{\mathit{w}}_{\lambda }·\mathit{N}=r{\dot{\zeta }}_{\lambda }\left(t\right)\mathrm{on}\mathcal{G}.\end{array}$$

(40)

From Theorem 2 applied to system (40), (21) and (22), it follows that estimate (29) is valid for ${\mathit{w}}_{\lambda },$ $p_{\lambda }$ and $r_{\lambda }$, which implies

$$\begin{array}{cc}\hfill \Psi \left(\lambda \right)& \equiv {|\mathit{w}|}_{D_{t_1+\lambda ,t_0}}^{(2+\alpha ,1+\alpha /2)}+{|\nabla p|}_{D_{t_1+\lambda ,t_0}}^{(\alpha ,\alpha /2)}+{\mathbf{\left|}p\mathbf{\right|}}_{D_{t_1+\lambda ,t_0}}^{(\gamma ,1+\alpha )}+{|r|}_{G_{t_1+\lambda ,t_0}}^{(3+\alpha ,3/2+\alpha /2)}+{|{\mathcal{D}}_{t}r|}_{G_{t_1+\lambda ,t_0}}^{(2+\alpha ,1+\alpha /2)}\hfill \\ \hfill & ⩽c_{13}\left(T\right)\left\{{|\mathit{w}{\dot{\zeta }}_{\lambda }|}_{D_{t_1+\lambda /2,t_0}}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}\mathbb{M}\mathbf{\right|}}_{D_{t_1+\lambda /2,t_0}}^{(\gamma ,1+\alpha )}+{⟨\mathbb{M}⟩}_{x,D_{t_1+\lambda /2,t_0}}^{\left(\gamma \right)}+{|r{\dot{\zeta }}_{\lambda }|}_{G_{t_1+\lambda /2,t_0}}^{(2+\alpha ,1+\alpha /2)}\right\},\hfill \end{array}$$

(41)

where $t_1=t_0-2$, and

$$\mathbb{M}(\xi ,t)=\nabla \underset{{\mathbb{R}}^3}{\int }\mathcal{E}(\xi ,y)\mathit{w}{\dot{\zeta }}_{\lambda }\mathrm{d}y$$

with $\mathcal{E}(x,y)=\frac{-1}{4\pi |x-y|}$; the vector $\mathit{w}$ is extended into the whole ${\mathbb{R}}^3$ and vanishes at infinity. By Lemmas 1, 2 which are given below, inequality (41) can be prolonged as follows:

$$\begin{array}{cc}\hfill \Psi \left(\lambda \right)& ⩽c\left(T\right){\lambda }^{-2-\alpha /2}\left\{{|\mathit{w}|}_{D_{t_1+\lambda /2,t_0}}^{(\alpha ,\frac{\alpha }{2})}+{|\mathit{w}|}_{t,D_{t_1+\lambda /2,t_0}}^{\left(\frac{1+\alpha -\gamma }{2}\right)}+{|r|}_{G_{t_1+\lambda /2,t_0}}^{(2+\alpha ,1+\alpha /2)}\right\}\hfill \\ \hfill & ⩽c{\lambda }^{-2-\alpha /2}\{{\theta }^{\gamma }{|\mathit{w}|}_{D_{t_1+\lambda /2,t_0}}^{(2+\alpha ,1+\frac{\alpha }{2})}+\theta {⟨r⟩}_{G_{t_1+\lambda /2,t_0}}^{(3+\alpha ,\frac{3+\alpha }{2})}+\underset{t_1}{\overset{t_0}{\int }}({\theta }^{-\frac{7}{2}}{\parallel \mathit{w}(·,\tau )\parallel }_{2,\Omega }\hfill \\ \hfill & \phantom{⩽c{\lambda }^{-2-\alpha /2}\{{\theta }^{\gamma }{|\mathit{w}|}_{D_{t_1+\lambda /2,t_0}}^{(2+\alpha ,1+\frac{\alpha }{2})}+\theta {⟨r⟩}_{G_{t_1+\lambda /2,t_0}}^{(3+\alpha ,\frac{3+\alpha }{2})}}+{\theta }^{-\alpha -\frac{11}{2}}{\parallel r(·,\tau )\parallel }_{2,\mathcal{G}}\left)\mathrm{d}\tau \right\}\hfill \end{array}$$

with $\theta <1$, which leads to

$$\Psi \left(\lambda \right)⩽c_1\theta {\lambda }^{-2-\alpha /2}\Psi (\lambda /2)+c_2{\theta }^{-m}{\lambda }^{-2-\alpha /2}K.$$

Here, $K={\parallel \mathit{w}\parallel }_{Q_{t_1,t_0}}+{\parallel r\parallel }_{G_{t_1,t_0}}$, $m=\alpha +11/2$.

Setting $\theta =\delta {\lambda }^{2+\alpha /2}<1$, we obtain

$${\lambda }^{(m+1)(2+\alpha /2)}\Psi \left(\lambda \right)⩽c_1\delta 2^{(m+1)(2+\alpha /2)}{(\lambda /2)}^{(m+1)(2+\alpha /2)}\Psi (\lambda /2)+c_2{\delta }^{-m}K.$$

This implies

$$\Psi \left(\lambda \right)⩽c_3\left(\delta \right){\lambda }^{-(m+1)(2+\alpha /2)}(K+2^{-1}K+2^{-2}K+...)⩽\frac{c_3{\lambda }^{-(m+1)(2+\alpha /2)}}{1-1/2}K,$$

provided that $c_1\delta 2^{(m+1)(2+\alpha /2)}<1/2.$ For $\lambda =1$, this inequality coincides with (39). □

In ([9] Ch. 5), the following lemma was established on the estimate of Newtonian potential gradient for the Hölder spaces over $D_T\equiv \left({\Omega }_0^{+}\cup ({\mathbb{R}}^3\backslash \overline{{\Omega }_0^{+}})\right)\times (0,T)$.

Lemma 1.

If $F\in C^{(0,\frac{1+\alpha -\gamma }{2})}\left(D_T\right)$ and vanishes at infinity; then, for the gradient of the Newtonian potential

$${\nabla }_{x}V(x,t)={\nabla }_x\underset{{\mathbb{R}}^3}{\int }\mathcal{E}(x,y)F(y,t)\mathrm{d}y,$$

the inequalities

$$\begin{array}{ccc}\hfill {|\nabla V|}_{D_T}^{(\gamma ,0)}& ⩽& {c|F|}_{D_T},\hfill \\ \hfill {|\nabla V|}_{D_T}^{(\gamma ,1+\alpha )}& ⩽& c\left({|F|}_{D_T}+{⟨F⟩}_{t,D_T}^{\left(\frac{1+\alpha -\gamma }{2}\right)}\right)\equiv c{|F|}_{D_T}^{(0,\frac{1+\alpha -\gamma }{2})}\hfill \end{array}$$

hold.

Interpolation inequalities are proved in a way similar to ([9] Ch. 6).

Lemma 2.

Let $v\in C^{0,\frac{1+\alpha }{2}}\left(D_{T_0}\right)$ with $T_0>{\theta }^2>0$. Then v satisfies the estimate

$${⟨v⟩}_{t,D_{T_0}}^{\left(\frac{1+\alpha -\gamma }{2}\right)}⩽2{\theta }^{\gamma }{⟨v⟩}_{t,D_{T_0}}^{\left(\frac{1+\alpha }{2}\right)}+c{\theta }^{\gamma -\alpha -\frac{9}{2}}\underset{0}{\overset{T_0}{\int }}{\parallel v(·,\tau )\parallel }_{2,\Omega }\mathrm{d}\tau .$$

Functions $u\in C^{2+\alpha ,1+\frac{\alpha }{2}}\left(D_{T_0}\right)$ and $r\in C^{3+\alpha ,\frac{3+\alpha }{2}}\left(D_{T_0}\right),0<\theta <min\left\{\mathrm{diam}\{\Omega \},T_0^{1/2}\right\},$ are subjected the inequalities

$$\begin{array}{ccc}\hfill {⟨u⟩}_{D_{T_0}}^{(\alpha ,\frac{\alpha }{2})}& ⩽& 2{\theta }^2{⟨u⟩}_{D_{T_0}}^{(2+\alpha ,1+\frac{\alpha }{2})}+c{\theta }^{-\alpha -\frac{7}{2}}\underset{0}{\overset{T_0}{\int }}{\parallel u(·,\tau )\parallel }_{2,\Omega }\mathrm{d}\tau ,\hfill \\ \hfill {|u|}_{D_{T_0}}& ⩽& c\left\{{\theta }^{2+\alpha }{⟨u⟩}_{D_{T_0}}^{(2+\alpha ,1+\frac{\alpha }{2})}+{\theta }^{-\frac{7}{2}}\underset{0}{\overset{T_0}{\int }}{\parallel u(·,\tau )\parallel }_{2,\Omega }\mathrm{d}\tau \right\},\hfill \\ \hfill {|r|}_{D_{T_0}}^{(2+\alpha ,1+\frac{\alpha }{2})}& ⩽& c\left\{\theta {⟨r⟩}_{D_{T_0}}^{(3+\alpha ,\frac{3+\alpha }{2})}+{\theta }^{-\alpha -\frac{11}{2}}\underset{0}{\overset{T_0}{\int }}{\parallel r(·,\tau )\parallel }_{2,\Omega }\mathrm{d}\tau \right\}.\hfill \end{array}$$

Proof of Theorem 3. 

By Theorem 2 and Proposition 5, one has

$$\begin{array}{c}\hfill e^{\beta (T-j)}{Y}_{(T-j-1,T-j)}[\mathit{w},p_1,r]⩽c{e}^{\beta (T-j)}\left\{{\parallel \mathit{w}\parallel }_{Q_{T-j-2,T-j}}+{\parallel r\parallel }_{G_{T-j-2,T-j}}\right\},\\ \hfill j=0,1,...,\left[T\right]-2.\end{array}$$

(42)

Summing (42) from $j=0$ to $j=\left[T\right]-2$, we obtain an inequality which implies

$$\sum _{j=0}^{j=\left[T\right]-2}{Y}_{(T-j-1,T-j)}[e^{\beta t}\mathit{w},e^{\beta t}{p}_1,e^{\beta t}r]⩽c{\int }_{T-\left[T\right]}^T{e}^{\beta t}\left({\parallel \mathit{w}(·,t)\parallel }_{\Omega }+{\parallel r(·,t)\parallel }_{\mathcal{G}}\right)\mathrm{d}t.$$

(43)

By choosing $\beta ⩽{\beta }_1$ in (43) from Proposion 4, we make use of an inequality equivalent to (36) and add the estimate

$$Y_{(0,2)}[\mathit{w},p_1,r]⩽c\left\{|{\mathit{w}}_0{|}_{\cup {\Omega }^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right\}.$$

Now taking supremum in $t\in (0,\infty )$, one arrives at (38). □

4. Global Solvability of the Nonlinear Problem

We separate the normal and tangent parts in the boundary conditions in (11) after transformation (15) and take (17) and (19) into account. Then this problem can be written in the form ([9], Ch. 12, [16]):

$$\begin{array}{c}\overline{\rho }\left({\mathcal{D}}_t\mathit{u}+2\omega ({\mathit{e}}_3\times \mathit{u})\right)-\overline{\mu }{\nabla }^2\mathit{u}+\nabla q=\overline{\rho }\widehat{\mathit{f}}+{\mathit{l}}_1(\mathit{u},q,r)\equiv {\mathit{f}}_1,\\ \nabla ·\mathit{u}=l_2(\mathit{u},r)\mathrm{in}\cup {\mathcal{F}}^{\pm },t>0,\\ \mathit{u}{|}_{t=0}={\mathit{u}}_0\mathrm{in}\cup {\mathcal{F}}^{\pm },r{|}_{t=0}=r_0\mathrm{on}\mathcal{G},\\ {\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left(\mathit{u}\right)\mathit{N}={\mathit{l}}_3^{-}(\mathit{u},r)\mathrm{on}{\mathcal{G}}^{-},\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left(\mathit{u}\right)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}={\mathit{l}}_3^{+}(\mathit{u},r)\mathrm{on}{\mathcal{G}}^{+},\\ -q+{\mu }^{-}\mathit{N}·\mathbb{S}\left(\mathit{u}\right)\mathit{N}+{\mathcal{B}}_0^{-}r=l_4^{-}(\mathit{u},r)+l_5^{-}\left(r\right)\mathrm{on}{\mathcal{G}}^{-},\\ \left[\mathit{u}\right]{|}_{{\mathcal{G}}^{+}}=0,[-q+\overline{\mu }\mathit{N}·\mathbb{S}\left(\mathit{u}\right)\mathit{N}]{|}_{{\mathcal{G}}^{+}}+{\mathcal{B}}_0^{+}r=l_4^{+}(\mathit{u},r)+l_5^{+}\left(r\right)\mathrm{on}{\mathcal{G}}^{+},\\ {\mathcal{D}}_{t}r-\mathit{u}·\mathit{N}=l_6(\mathit{u},r)\mathrm{on}\mathcal{G},\end{array}$$

(44)

where $\mathit{u}(z,t)=\tilde{\mathit{v}}\left(e_r(z,t),t\right)$, ${\mathit{u}}_0\left(z\right)=\tilde{\mathit{v}}\left(e_{r_0}(z,0),0\right)$, $q(z,t)=\tilde{p}\left(e_r(z,t),t\right)$, $\widehat{\mathit{f}}(z,t)=\tilde{\mathit{f}}\left(e_r(z,t),t\right)$,

$$\begin{array}{cc}\hfill & {\mathit{l}}_1(\mathit{u},q,r)=\overline{\mu }({\tilde{\nabla }}^2-{\nabla }^2)\mathit{u}+(\nabla -\tilde{\nabla })q+\overline{\rho }{\mathcal{D}}_t{r}^{*}({\mathbb{L}}^{-1}{\mathit{N}}^{*}·\nabla )\mathit{u}-\overline{\rho }({\mathbb{L}}^{-1}\mathit{u}·\nabla )\mathit{u},\hfill \\ \hfill & l_2(\mathit{u},r)=(\nabla -\tilde{\nabla })·\mathit{u}\equiv \nabla ·{\mathit{L}}_2(\mathit{u},r),\hfill \\ \hfill & {\mathit{l}}_3^{-}(\mathit{u},r)={\mu }^{-}{\Pi }_{\mathcal{G}}\left({\Pi }_{\mathcal{G}}\mathbb{S}\left(\mathit{u}\right)\mathit{N}-\tilde{\Pi }\tilde{\mathbb{S}}\left(\mathit{u}\right)\tilde{\mathit{n}}\left(e_r\right)\right),\hfill \\ \hfill & {\mathit{l}}_3^{+}(\mathit{u},r)=\left[\overline{\mu }{\Pi }_{\mathcal{G}}\left({\Pi }_{\mathcal{G}}\mathbb{S}\left(\mathit{u}\right)\mathit{N}-\tilde{\Pi }\tilde{\mathbb{S}}\left(\mathit{u}\right)\tilde{\mathit{n}}\left(e_r\right)\right)\right]{|}_{{\mathcal{G}}^{+}},\hfill \\ \hfill & l_4^{-}(\mathit{u},r)={\mu }^{-}\left(\mathit{N}·\mathbb{S}\left(\mathit{u}\right)\mathit{N}-\tilde{\mathit{n}}\left(e_r\right)·\tilde{\mathbb{S}}\left(\mathit{u}\right)\tilde{\mathit{n}}\left(e_r\right)\right),\hfill \\ \hfill & l_4^{+}(\mathit{u},r)=\left[\overline{\mu }\left(\mathit{N}·\mathbb{S}\left(\mathit{u}\right)\mathit{N}-\tilde{\mathit{n}}\left(e_r\right)·\tilde{\mathbb{S}}\left(\mathit{u}\right)\tilde{\mathit{n}}\left(e_r\right)\right)\right]{|}_{{\mathcal{G}}^{+}},\hfill \\ \hfill & l_5^{-}\left(r\right)={\sigma }^{-}{\int }_0^1(1-s)\frac{{\mathrm{d}}^2}{\mathrm{d}{s}^2}\left({\mathbb{L}}^{-T}(z,sr){\nabla }_{\mathcal{G}}·\frac{{\widehat{\mathbb{L}}}^T(z,sr)\mathit{N}}{|{\widehat{\mathbb{L}}}^T(z,sr)\mathit{N}|}\right)\mathrm{d}s+\frac{{\omega }^2}{2}{\rho }^{-}{|{\mathit{N}}^{\prime }|}^2{r}^2\hfill \\ \hfill & +\varkappa {\rho }^{-}{\int }_0^1(1-s)\frac{{\mathrm{d}}^2}{\mathrm{d}{s}^2}\tilde{U}(e_{sr}\left(z\right),t)\mathrm{d}s,\hfill \\ \hfill & l_5^{+}\left(r\right)={\sigma }^{+}{\int }_0^1(1-s)\frac{{\mathrm{d}}^2}{\mathrm{d}{s}^2}\left({\mathbb{L}}^{-T}(z,sr){\nabla }_{\mathcal{G}}·\frac{{\widehat{\mathbb{L}}}^T(z,sr)\mathit{N}}{|{\widehat{\mathbb{L}}}^T(z,sr)\mathit{N}|}\right)\mathrm{d}s+\frac{{\omega }^2}{2}\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{|{\mathit{N}}^{\prime }|}^2{r}^2\hfill \\ \hfill & +\varkappa \left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_0^1(1-s)\frac{{\mathrm{d}}^2}{\mathrm{d}{s}^2}\tilde{U}(e_{sr}\left(z\right),t)\mathrm{d}s,\hfill \\ \hfill & l_6(\mathit{u},r)=\left(\frac{{\widehat{\mathbb{L}}}^T\mathit{N}}{\mathit{N}·{\widehat{\mathbb{L}}}^T\mathit{N}}-\mathit{N}\right)·\mathit{u},\hfill \end{array}$$

(45)

$\mathbb{L}$ is the Jacobi matrix of transformation (15):

$$\mathbb{L}(z,r)\equiv \left\{L_{ij}\right\}={\left\{{\delta }_j^i+\frac{\partial \left(r^{*}(z,t)N_i^{*}\left(z\right)\right)}{\partial z_j}\right\}}_{i,j=1}^3,$$

• $\widehat{\mathbb{L}}\equiv L{\mathbb{L}}^{-1}$, $L\equiv \det \mathbb{L}$. In addition, $\tilde{\nabla }={\mathbb{L}}^{-T}\nabla$ is the transformed gradient ${\nabla }_x$;
• ${\mathbb{L}}^{-T}\equiv {\left({\mathbb{L}}^{-1}\right)}^T$; the superscript T means transposition;$\tilde{\mathit{n}}=\frac{{\widehat{\mathbb{L}}}^T(z,r)\mathit{N}}{|{\widehat{\mathbb{L}}}^T(z,r)\mathit{N}|};$
• $\tilde{\mathbb{S}}\left(\mathit{u}\right)=\tilde{\nabla }\mathit{u}+{\left(\tilde{\nabla }\mathit{u}\right)}^T$ is the transformed doubled rate-of-strain tensor;
• $\tilde{\Pi }\mathit{b}=\mathit{b}-\tilde{\mathit{n}}·\mathit{b}\tilde{\mathit{n}}$ and ${\Pi }_{\mathcal{G}}\mathit{b}=\mathit{b}-\mathit{N}·\mathit{b}\mathit{N}$ are the projections of a vector $\mathit{b}$ on the tangent planes to ${\tilde{\Gamma }}_t$ and $\mathcal{G}$; ${\nabla }_{\mathcal{G}}={\Pi }_{\mathcal{G}}\nabla$.

We observe that the operators ${\mathit{l}}_1$ and $l_2$ have divergence form:

$$\begin{array}{cc}\hfill {\mathit{l}}_1(\mathit{w},s)=& \overline{\rho }\partial {\mathit{L}}_{1j}(\mathit{w},s)/\partial {\xi }_j,\hfill \\ \hfill {\mathit{L}}_{1j}(\mathit{w},s,r)=& \overline{\nu }({\widehat{L}}_{ji}{\widehat{L}}_{mi}/L^2-{\delta }_j^m)\partial \mathit{w}/\partial {\xi }_m-{\mathbb{B}}^T{\mathit{e}}_{j}s/\overline{\rho }+\partial \mathit{U}(\mathit{w},s,r)/\partial {\xi }_j\hfill \\ \hfill =& \overline{\nu }(B_{ji}{\widehat{L}}_{mi}/L+B_{mj})\partial \mathit{w}/\partial {\xi }_m-{\mathbb{B}}^T{\mathit{e}}_{j}s/\overline{\rho }+\partial \mathit{U}(\mathit{w},s,r)/\partial {\xi }_j,\hfill \\ \hfill \mathit{U}(\xi ,t)=& {\int }_{\cup {\mathcal{F}}^{\pm }}\mathcal{E}(\xi ,\mathit{\eta })\{{\mathcal{D}}_t{r}^{*}({\mathbb{L}}^{-1}{\mathit{N}}^{*}·\nabla )\mathit{w}-({\mathbb{L}}^{-1}\mathit{w}·\nabla )\mathit{w}\hfill \\ \hfill & +\overline{\nu }\frac{{\widehat{L}}_{ki}}{L^2}\frac{\partial L}{\partial {\xi }_k}\frac{{\widehat{L}}_{mi}}{L}\frac{\partial \mathit{w}}{\partial {\xi }_m}-s\frac{{\mathbb{L}}^{-T}{\nabla }_{\mathit{\eta }}L}{\overline{\rho }L(\mathit{\eta },t)}\}d\mathit{\eta },\hfill \\ \hfill l_2\left(\mathit{w}\right)=& (\mathbb{I}-{\mathbb{L}}^{-T})\nabla ·\mathit{w}=\nabla ·{\mathit{L}}_2(\mathit{w},r),\hfill \\ \hfill {\mathit{L}}_2(\mathit{w},r)=& -\mathbb{B}\mathit{w}+\nabla V\left(\mathit{w}\right),\mathbb{B}\equiv {\mathbb{L}}^{-1}-\mathbb{I},\hfill \\ \hfill V(\xi ,t)\equiv & -\underset{\cup {\mathcal{F}}^{\pm }}{\int }\frac{\mathcal{E}(\xi ,\mathit{\eta })}{L^2(\mathit{\eta },t)}{\nabla }_{\mathit{\eta }}L·\widehat{\mathbb{L}}\mathit{w}(\mathit{\eta },t)d\mathit{\eta }=-\underset{\cup {\mathcal{F}}^{\pm }}{\int }\frac{\mathcal{E}(\xi ,\mathit{\eta })}{L(\mathit{\eta },t)}{\mathbb{L}}^{-T}{\nabla }_{\mathit{\eta }}L·\mathit{w}(\mathit{\eta },t)d\mathit{\eta }.\hfill \end{array}$$

(${\mathit{e}}_j$ is the unit vector in the direction of ${\xi }_j$, $\overline{\nu }=\overline{\mu }/\overline{\rho }$ and $\mathbb{I}$ is identity matrix). We have used the equality ${\widehat{\mathbb{L}}}^T\nabla ·\mathit{w}=\nabla ·\widehat{\mathbb{L}}\mathit{w}$ that follows from the identity

$$\frac{\partial {\widehat{L}}_{ij}}{\partial {\xi }_i}=0,$$

which is valid for the cofactors of the Jacobi matrix of any transformation.

Moreover, the expression $\overline{\rho }{\mathcal{D}}_t{l}_2\left(\mathit{u}\right)-\nabla ·{\mathit{f}}_1$ is also representable in divergence form:

$$\begin{array}{cc}\hfill \overline{\rho }{\mathcal{D}}_t{l}_2\left(\mathit{u}\right)-\nabla ·{\mathit{f}}_1=& \overline{\rho }\left({\mathcal{D}}_t{l}_2\left(\mathit{u}\right)-\nabla ·\widehat{\mathit{f}}\right)-\nabla ·{\mathit{l}}_1(\mathit{u},q)\hfill \\ \hfill =& \nabla ·[\overline{\rho }{\mathcal{D}}_t{\mathit{L}}_2(\mathit{u},r)-\overline{\rho }\widehat{\mathit{f}}-{\mathit{l}}_1(\mathit{u},q)]\hfill \\ \hfill =& -\nabla ·[\overline{\rho }\widehat{\mathit{f}}+\overline{\rho }\mathbb{B}{\mathcal{D}}_t\mathit{u}+\overline{\rho }\left({\mathcal{D}}_t\mathbb{B}\right)\mathit{u}+\overline{\rho }\nabla {\mathcal{D}}_{t}V\left(\mathit{u}\right)+{\mathit{l}}_1(\mathit{u},q)]\hfill \\ \hfill \equiv & -\nabla ·\left(\overline{\rho }{\mathbb{L}}^{-1}\widehat{\mathit{f}}+{\mathit{l}}_7(\mathit{u},q)\right)\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill {\mathit{l}}_7(\mathit{u},q)& =\overline{\rho }\mathbb{B}({\mathcal{D}}_t\mathit{u}-\widehat{\mathit{f}})+\overline{\rho }\left({\mathcal{D}}_t\mathbb{B}\right)\mathit{u}+\overline{\rho }\nabla {\mathcal{D}}_{t}V\left(\mathit{u}\right)+{\mathit{l}}_1(\mathit{u},q)\hfill \\ \hfill & =-\mathbb{B}\left(2\omega \overline{\rho }({\mathit{e}}_3\times \mathit{u})-\overline{\mu }{\nabla }^2\mathit{u}+\nabla q\right)+\overline{\rho }\left({\mathcal{D}}_t\mathbb{B}\right)\mathit{u}+{\mathbb{L}}^{-1}{\mathit{l}}_1(\mathit{u},q)\equiv \frac{\partial {\mathit{L}}_{7j}(\mathit{u},q)}{\partial {\xi }_j},\hfill \\ \hfill {\mathit{L}}_{7j}(\mathit{u},q)& =\overline{\mu }\mathbb{B}\frac{\partial \mathit{u}}{\partial {\xi }_j}-\mathbb{B}{\mathit{e}}_{j}q+\overline{\rho }{\mathbb{L}}^{-1}{\mathit{L}}_{1j}+\frac{\partial \mathit{W}}{\partial {\xi }_j},j=1,2,3,\hfill \\ \hfill \mathit{W}(\xi ,t)& =-\underset{\cup {\mathcal{F}}^{\pm }}{\int }\mathcal{E}(\xi ,\mathit{\eta })\left\{\frac{\partial \mathbb{B}}{\partial {\mathit{\eta }}_m}\left(\overline{\mu }\frac{\partial \mathit{u}}{\partial {\mathit{\eta }}_m}-{\mathit{e}}_{m}q+\overline{\rho }{\mathit{L}}_{1m}\right)+2\omega \overline{\rho }\mathbb{B}({\mathit{e}}_3\times \mathit{u})-\overline{\rho }\left({\mathcal{D}}_t\mathbb{B}\right)\mathit{u}\right\}\mathrm{d}\mathit{\eta }.\hfill \end{array}$$

(46)

We assume the fulfillment of restrictions (4). Then we can express conditions (12) and (13) in terms of r in the following way (see [17]):

$$\begin{gathered} \begin{array}{c}{\int }_{{\mathcal{G}}^{\pm }}{\phi }^{\pm }(z,r)\mathrm{d}\mathcal{G}=0(\mathrm{mass}\mathrm{conservation}),\\ {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{\psi }^{-}(z,r)\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}{\psi }^{+}(z,r)\mathrm{d}\mathcal{G}=0(\mathrm{barycenter}\mathrm{conservation})\\ {\int }_{\mathcal{F}}\overline{\rho }\mathit{u}(z,t)L(z,r)\mathrm{d}z=0(\mathrm{momentum}\mathrm{conservation}),\\ {\int }_{\mathcal{F}}\overline{\rho }\mathit{u}(z,t)·{\mathit{\eta }}_j\left(e_r(z,t)\right)L(z,r)\mathrm{d}z+\omega {\int }_{\mathcal{F}}\overline{\rho }{\mathit{\eta }}_3\left(e_r(z,t)\right)·{\mathit{\eta }}_j\left(e_r(z,t)\right)L(z,r)\mathrm{d}z \\ ={\int }_{\mathcal{F}}\overline{\rho }{\mathit{\eta }}_3\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}zj=1,2,3,\left(\mathrm{angular}\mathrm{momentum}\mathrm{conservation}\right),\end{array} \end{gathered}$$

(47)

where

$$\begin{array}{cc}\hfill {\phi }^{\pm }(z,r)& =r-\frac{r^2}{2}{\mathcal{H}}^{\pm }\left(z\right)+\frac{r^3}{3}{\mathcal{K}}^{\pm }\left(z\right),\hfill \\ \hfill {\mathit{\psi }}^{\pm }(z,r)& ={\phi }^{\pm }(z,r)\mathit{z}+\mathit{N}\left(z\right)\left(\frac{r^2}{2}-\frac{r^3}{3}{\mathcal{H}}^{\pm }\left(z\right)+\frac{r^4}{4}{\mathcal{K}}^{\pm }\left(z\right)\right).\hfill \end{array}$$

Proposition 6.

For arbitrary numbers $l^{\pm }$, vectors $\mathit{l},\mathit{m},\mathit{M}=(M_1,M_2,M_3)$, a function $f_0\in C^{1+\alpha }\left(\cup {\mathcal{F}}^{\pm }\right)$ and a vector field ${\mathit{b}}_0\in {\mathit{C}}^{1+\alpha }\left(\mathcal{G}\right)$, there exist $r\in C^{3+\alpha }\left(\mathcal{G}\right)$ and $\mathit{u}\in {\mathit{C}}^{2+\alpha }\left(\cup {\mathcal{F}}^{\pm }\right)$ satisfying the conditions

$$\begin{array}{c}{\int }_{{\mathcal{G}}^{-}}r\left(z\right)\mathrm{d}\mathcal{G}=l^{-},{\int }_{{\mathcal{G}}^{+}}r\left(z\right)\mathrm{d}\mathcal{G}=l^{+},\\ {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}r\left(z\right)\mathit{z}\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}r\left(z\right)\mathit{z}\mathrm{d}\mathcal{G}=\mathit{l},\end{array}$$

(48)

$$\begin{array}{c}{\int }_{\mathcal{F}}\overline{\rho }\mathit{u}\left(z\right)\mathrm{d}z=\mathit{m},\\ {\int }_{\mathcal{F}}\overline{\rho }\mathit{u}\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}z+\omega ({\rho }^{-}{\int }_{{\mathcal{G}}^{-}}r\left(z\right){\mathit{\eta }}_3\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}\mathcal{G}\\ +\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}r\left(z\right){\mathit{\eta }}_3\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}\mathcal{G})=M_j,j=1,2,3,\\ \nabla ·\mathit{u}=f_{0}in\cup {\mathcal{F}}^{\pm },{\mathit{b}}_0·{\mathit{n}}_0=0on{\mathcal{G}}^{\pm },\\ {\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left(\mathit{u}\right)\mathit{N}={\mathit{b}}_{0}on{\mathcal{G}}^{-},\left[\mathit{u}\right]{{|}_{{\mathcal{G}}^{+}}=0,\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left(\mathit{u}\right)\mathit{N}\right]|}_{{\mathcal{G}}^{+}}={\mathit{b}}_{0}on{\mathcal{G}}^{+}\end{array}$$

and the inequality

$${|r|}_{\mathcal{G}}^{(3+\alpha )}+{|\mathit{u}|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}⩽c\left(|l^{+}|+|l^{-}|+|\mathit{l}|+|\mathit{m}|+|\mathit{M}|+|f_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(1+\alpha )}+{|{\mathit{b}}_0|}_{\mathcal{G}}^{(1+\alpha )}\right).$$

(49)

Proof. 

Let

$$\begin{array}{c}r\left(z\right)=\frac{l^{-}\mathit{N}\left(z\right)·\mathit{z}}{3|\mathcal{F}|}+\frac{C^{-}}{|\mathcal{F}|}\mathit{l}·\mathit{N}\left(z\right),z\in {\mathcal{G}}^{-},\\ r\left(z\right)=\frac{l^{+}\mathit{N}\left(z\right)·\mathit{z}}{3|{\mathcal{F}}^{+}|}+\frac{C^{+}}{|{\mathcal{F}}^{+}|}\mathit{l}·\mathit{N}\left(z\right),z\in {\mathcal{G}}^{+}.\end{array}$$

(50)

Since $\mathit{l}$ is a constant vector, we have

$${\int }_{{\mathcal{G}}^{\pm }}\mathit{l}·\mathit{N}\left(z\right)\mathrm{d}\mathcal{G}=0.$$

In addition,

$${\int }_{{\mathcal{G}}^{-}}\mathit{N}·\mathit{z}\mathrm{d}\mathcal{G}={\int }_{\mathcal{F}}\nabla ·\mathit{z}\mathrm{d}z=3|\mathcal{F}|.$$

Thus, the relations in the first line in (48) is satisfied.

We take into account that

$$\begin{array}{cc}\hfill {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}& r\left(z\right)\mathit{z}\mathrm{d}\mathcal{G}=\frac{{\rho }^{-}{l}^{-}}{3|\mathcal{F}|}{\int }_{\mathcal{F}}\left(\nabla ·\left(z_1\mathit{z}\right),\nabla ·\left(z_2\mathit{z}\right),\nabla ·\left(z_3\mathit{z}\right)\right)\mathrm{d}z\hfill \\ \hfill & +\frac{{\rho }^{-}{C}^{-}}{|\mathcal{F}|}{\int }_{\mathcal{F}}\left(\nabla ·\left(z_1\mathit{l}\right),\nabla ·\left(z_2\mathit{l}\right),\nabla ·\left(z_3\mathit{l}\right)\right)\mathrm{d}z=\frac{4{\rho }^{-}{l}^{-}}{3|\mathcal{F}|}{\int }_{\mathcal{F}}\mathit{z}\mathrm{d}z+{\rho }^{-}{C}^{-}\mathit{l}.\hfill \end{array}$$

In view of barycenter conservation, the second line in relation (48) for (50) holds if ${\rho }^{-}{C}^{-}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{C}^{+}=1.$ Thus, we set

$$C^{+}=\frac{\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}}{{{\rho }^{-}}^2+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}^2},C^{-}=\frac{{\rho }^{-}}{{{\rho }^{-}}^2+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}^2}.$$

We find now a vector ${\mathit{u}}_1$ which satisfies the equations

$$\begin{array}{c}\nabla ·{\mathit{u}}_1=f_0\mathrm{in}\cup {\mathcal{F}}^{\pm },\\ \left[{\mathit{u}}_1\right]{{|}_{{\mathcal{G}}^{+}}=0,{\mathit{u}}_1·\mathit{N}|}_{{\mathcal{G}}^{-}}=f_1\mathrm{on}{\mathcal{G}}^{-},\end{array}$$

(51)

where

$$f_1\left(z\right)=\frac{\mathit{N}\left(z\right)·\mathit{z}}{3|\mathcal{F}|}{\int }_{\mathcal{F}}{f}_0\left(z\right)\mathrm{d}z+\frac{1}{|\mathcal{F}|}{\mathit{K}}^{-}·\mathit{N}\left(z\right),z\in {\mathcal{G}}^{-},$$

with some vector ${\mathit{K}}^{-}$ defined below. A solution of (51) can be found as ${\mathit{u}}_1=\nabla \Psi$ with $\Psi$ solving the problem

$$\begin{array}{c}{\nabla }^2\Psi =f_0\mathrm{in}\cup {\mathcal{F}}^{\pm },\\ [\Psi ]|{\mathcal{G}}^{+}=0,\left[\frac{\partial \Psi }{\partial \mathit{N}}\right]{|}_{{\mathcal{G}}^{+}}=0,\frac{\partial \Psi }{\partial \mathit{N}}{|}_{{\mathcal{G}}^{-}}=f_1\mathrm{on}{\mathcal{G}}^{-}.\end{array}$$

(52)

Since the compatibility condition

$${\int }_{{\mathcal{G}}^{-}}{f}_1\left(z\right)\mathrm{d}\mathcal{G}={\int }_{\mathcal{F}}{f}_0\left(z\right)\mathrm{d}z$$

holds, there exists $\Psi$ satisfying (52) and the inequality

$${|\Psi |}_{\cup {\mathcal{F}}^{\pm }}^{(3+\alpha )}⩽c\left(|f_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(1+\alpha )}+{|f_1|}_{\mathcal{G}}^{(2+\alpha )}\right)$$

(53)

(see [9], Ch. 9).

From the relation

$$\begin{array}{cc}\hfill & {\int }_{\mathcal{F}}\overline{\rho }(\nabla ·{\mathit{u}}_1)\mathit{z}\mathrm{d}z=-{\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_1\mathrm{d}z+{\rho }^{-}{\int }_{{\mathcal{G}}^{-}}({\mathit{u}}_1·\mathit{N})\mathit{z}\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}({\mathit{u}}_1·\mathit{N})\mathit{z}\mathrm{d}\mathcal{G},\end{array}$$

we deduce

$${\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_1\mathrm{d}z=-{\int }_{\mathcal{F}}\overline{\rho }{f}_0\mathit{z}\mathrm{d}z+{\rho }^{-}{\mathit{K}}^{-}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\mathit{K}}^{+}=\mathit{m},$$

provided that

$$\begin{array}{c}\hfill {\mathit{K}}^{-}=\frac{{\rho }^{-}}{{{\rho }^{-}}^2+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}^2}\left(\mathit{m}+{\int }_{\mathcal{F}}\overline{\rho }{f}_0\mathit{z}\mathrm{d}z\right),{\mathit{K}}^{+}=\frac{\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}}{{{\rho }^{-}}^2+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}^2}\left(\mathit{m}+{\int }_{\mathcal{F}}\overline{\rho }{f}_0\mathit{z}\mathrm{d}z\right).\end{array}$$

Note that ${\int }_{{\mathcal{G}}^{-}}({\mathit{u}}_1·\mathit{N})\mathit{z}\mathrm{d}\mathcal{G}={\int }_{{\mathcal{G}}^{-}}{f}_1\mathit{z}\mathrm{d}\mathcal{G}={\mathit{K}}^{-}.$ Due to (53), ${\mathit{u}}_1$ is subject to the inequality

$${|{\mathit{u}}_1|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}⩽c\left(|f_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(1+\alpha )}+|\mathit{m}|\right).$$

Next, we construct a vector field ${\mathit{u}}_2$ satisfying the relations

$$\begin{array}{cc}& {\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}_2\right)\mathit{N}={\mathit{b}}_0\left(z\right)-{\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}_1\right)\mathit{N}\equiv {\mathit{b}}^{\prime }\left(z\right),z\in {\mathcal{G}}^{-},\hfill \\ \hfill & \left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}_2\right)\mathit{N}\right]{{|}_{{\mathcal{G}}^{+}}={\mathit{b}}_0\left(z\right)-\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}_1\right)\mathit{N}\right]|}_{{\mathcal{G}}^{+}}\equiv {\mathit{b}}^{\prime }\left(z\right),z\in {\mathcal{G}}^{+}.\hfill \end{array}$$

Following [9] (Ch. 12), we put ${\mathit{u}}_2=$ rot $\Phi \left(z\right)$, where $\Phi \in {\mathit{C}}^{3+\alpha }\left(\cup {\mathcal{F}}^{\pm }\right)$,

$$\begin{array}{c}\Phi \left(z\right)=\frac{\partial \Phi \left(z\right)}{\partial \mathit{N}}=0,\frac{{\partial }^2\Phi \left(z\right)}{\partial {\mathit{N}}^2}={\mathit{b}}^{\prime }\left(z\right)\times \mathit{N},z\in {\mathcal{G}}^{-},\\ \Phi \left(z\right)=\frac{\partial \Phi \left(z\right)}{\partial \mathit{N}}=0,\left[\overline{\mu }\frac{{\partial }^2\Phi \left(z\right)}{\partial {\mathit{N}}^2}\right]{|}_{{\mathcal{G}}^{+}}={\mathit{b}}^{\prime }\left(z\right)\times \mathit{N},z\in {\mathcal{G}}^{+},\end{array}$$

and we require that

$${|\Phi |}_{{\mathcal{F}}^{\pm }}^{(3+\alpha )}⩽c{|{\mathit{b}}^{\prime }|}_{{\mathcal{G}}^{\pm }}^{(1+\alpha )}⩽c\left\{|{\mathit{b}}_0{|}_{{\mathcal{G}}^{\pm }}^{(1+\alpha )}+{|{\mathit{u}}_1|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}\right\}.$$

We define

$${\mathit{u}}_3\left(z\right)=\sum _{k=1}^3{\widehat{M}}_k\mathrm{rot}{\mathit{e}}_{i}A\left(z\right),$$

where $A\in C_0^{\infty }\left({\mathcal{F}}^{-}\right)$, ${\rho }^{-}{\int }_{{\mathcal{F}}^{-}}A\left(z\right)\mathrm{d}z=\frac{1}{2},$ and

$$\begin{array}{c}{\widehat{M}}_k=M_k-{\int }_{\mathcal{F}}\overline{\rho }({\mathit{u}}_1\left(z\right)+{\mathit{u}}_2\left(z\right))·{\mathit{\eta }}_k\left(z\right)\mathrm{d}z-\omega ({\rho }^{-}{\int }_{{\mathcal{G}}^{-}}r{\mathit{\eta }}_3·{\mathit{\eta }}_k\mathrm{d}\mathcal{G}\hfill \\ \hfill +\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}r{\mathit{\eta }}_3·{\mathit{\eta }}_k\mathrm{d}\mathcal{G}).\end{array}$$

Finally, we have ${\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_3\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}z={\widehat{M}}_j$ and

$$|{\mathit{u}}_3{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}⩽c|\widehat{\mathit{M}}|.$$

Now one can conclude that the function r defined by (50) and the vector $\mathit{u}={\mathit{u}}_1+{\mathit{u}}_2+{\mathit{u}}_3$ satisfy all the necessary requirements. □

We denote $D_T\equiv \cup {\mathcal{F}}^{\pm }\times (0,T),$ $Q_T\equiv \mathcal{F}\times (0,T),$ $G_T\equiv \cup {\mathcal{G}}^{\pm }\times (0,T).$

Theorem 4

(Local Solvability of the Nonlinear Problem). Let $\Gamma \in C^{3+\alpha }$, $\mathit{f},$ ${\mathcal{D}}_x\mathit{f}\in {\mathit{C}}^{\alpha ,\frac{1+\alpha -\gamma }{2}}\left(Q_{T_0}\right)$, ${\mathit{u}}_0\in {\mathit{C}}^{2+\alpha }(\cup {\mathcal{F}}^{\pm })$ for some $\alpha ,\gamma \in (0,1)$, $\gamma <\alpha$ and $T_0<\infty$. We assume that compatibility conditions are satisfied:

$$\begin{array}{c}\nabla ·{\mathit{u}}_0=l_2({\mathit{u}}_0,r_0)in\cup {\mathcal{F}}^{\pm },{\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}_0\right)\mathit{N}={\mathit{l}}_3^{-}({\mathit{u}}_0,r_0)on{\mathcal{G}}^{-},\\ \left[{\mathit{u}}_0\right]{|}_{{\mathcal{G}}^{+}}=0,\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}_0\right)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}={\mathit{l}}_3^{+}({\mathit{u}}_0,r_0)on{\mathcal{G}}^{+},\\ \left[{\Pi }_{\mathcal{G}}\left(\overline{\nu }{\nabla }^2{\mathit{u}}_0\left(x\right)-\frac{1}{\overline{\rho }}\nabla q_0+\frac{1}{\overline{\rho }}{\mathit{l}}_1({\mathit{u}}_0,q_0,r_0)\right)\right]{|}_{x\in {\mathcal{G}}^{+}}=0,\end{array}$$

where $q_0\equiv q(x,0)$ is the initial pressure function being a solution to the problem

$$\begin{array}{cc}\hfill \frac{1}{\overline{\rho }}{\nabla }^2{q}_0\left(x\right)-& \frac{1}{\overline{\rho }}\nabla ·{\mathit{l}}_1({\mathit{u}}_0,q_0,r_0)=\widehat{\mathit{f}}-2\omega \nabla ·({\mathit{e}}_3\times {\mathit{u}}_0)+\overline{\nu }{\nabla }^2{l}_2({\mathit{u}}_0,r_0)in\cup {\mathcal{F}}^{\pm },\hfill \\ \hfill [q_0{]|}_{{\mathcal{G}}^{+}}& =\left[2\overline{\mu }\frac{\partial {\mathit{u}}_0}{\partial \mathit{N}}·\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}+{\mathcal{B}}_0^{+}\left(r_0\right)-l_4({\mathit{u}}_0,r_0)-l_5\left(r_0\right),\hfill \\ \hfill \left[\frac{1}{\overline{\rho }}\frac{\partial q_0}{\partial \mathit{N}}\right]{|}_{{\mathcal{G}}^{+}}& -\mathit{N}·{\mathit{l}}_1({\mathit{u}}_0,q_0,r_0)=\left[\overline{\nu }\mathit{N}·{\nabla }^2{\mathit{u}}_0\right]{|}_{{\mathcal{G}}^{+}},\hfill \\ \hfill q_0{|}_{{\mathcal{G}}^{-}}& =2{\mu }^{-}\frac{\partial {\mathit{u}}_0}{\partial \mathit{N}}·\mathit{N}{|}_{{\mathcal{G}}^{-}}+{\mathcal{B}}_0^{-}\left(r_0\right)-l_4({\mathit{u}}_0,r_0)-l_5\left(r_0\right).\hfill \end{array}$$

Then there exists such a value $\epsilon \left(T_0\right)\ll 1$ that problem (44) with the data

$$\begin{array}{cc}\hfill & |{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}+{|\mathit{f}|}_{Q_{T_0}}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}+{|\nabla \mathit{f}|}_{Q_{T_0}}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}⩽\epsilon \hfill \end{array}$$

(54)

has a unique solution $(\mathit{u},q,r)$ on the interval $(0,T_0]$, and

$$Y_{(0,T_0)}(\mathit{u},q,r)⩽c\left(\epsilon \right)\left\{N({\mathit{u}}_0,r_0)+{|\mathit{f}|}_{Q_{T_0}}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}\right\},$$

(55)

$$N\left(\mathit{u}(·,T_0),r(·,T_0)\right)⩽\vartheta N({\mathit{u}}_0,r_0)+c{|\mathit{f}|}_{Q_{T_0}}^{(\alpha ,\frac{1+\alpha -\gamma }{2})},$$

(56)

where $\vartheta <1/2$,

$$Y_{(0,T)}(\mathit{u},q,r)\equiv {|\mathit{u}|}_{D_T}^{(2+\alpha ,1+\alpha /2)}+{|\nabla q|}_{D_T}^{(\alpha ,\alpha /2)}+{\mathbf{\left|}q\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}+{|r|}_{G_T}^{(3+\alpha ,\frac{3+\alpha }{2})}+{|{\mathcal{D}}_{t}r|}_{G_T}^{(2+\alpha ,1+\alpha /2)}$$

and

$$N(\mathit{w},\rho )\equiv {|\mathit{w}|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|\rho |}_{\mathcal{G}}^{(3+\alpha )}.$$

The proof of Theorem 4 is based on Theorem 2 and on the smallness of the nonlinear terms.

Proposition 7.

If

$${|r|}_{G_T}^{(2+\alpha ,1+\frac{\alpha }{2})}+|{\mathcal{D}}_t{r|}_{G_T}^{(2,1+\frac{\alpha -\gamma }{2})}+{|\mathit{u}|}_{D_T}^{(1+\alpha ,\frac{1+\alpha }{2})}⩽\delta ,$$

(57)

where δ is a certain small positive number and $\mathit{f},\nabla \mathit{f}\in {\mathit{C}}^{\alpha ,\frac{1+\alpha -\gamma }{2}}\left(Q_{T_0}\right)$ satisfy smallness condition (54), then nonlinear terms (45) and $\widehat{\mathit{f}}(z,t)\equiv \tilde{\mathit{f}}(e_r(z,t),t)$ are subject to the inequalities

$$\begin{array}{cc}\hfill Z_{(0,T)}& (\mathit{u},q,r)\equiv |{\mathit{l}}_1{(\mathit{u},r)|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+|l_2{(\mathit{u},r)|}_{D_T}^{(1+\alpha ,\frac{1+\alpha }{2})}+{|{\mathcal{D}}_t{\mathit{L}}_2(\mathit{u},r)|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}{\mathit{L}}_2(\mathit{u},r)\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}\hfill \\ \hfill & +|{\mathit{l}}_3{(\mathit{u},r)|}_{G_T}^{(1+\alpha ,\frac{1+\alpha }{2})}+{\mathbf{\left|}{l}_4(\mathit{u},r)\mathbf{\right|}}_{G_T}^{(\gamma ,1+\alpha )}+|l_4{(\mathit{u},r)|}_{G_T}+|{\nabla }_{\tau }{l}_4{(\mathit{u},r)|}_{G_T}^{(\alpha ,\frac{\alpha }{2})}+{|l_5\left(r\right)|}_{G_T}\hfill \\ \hfill & +{\mathbf{\left|}{l}_5\left(r\right)\mathbf{\right|}}_{G_T}^{(\gamma ,1+\alpha )}+|{\nabla }_{\tau }{l}_5{\left(r\right)|}_{G_T}^{(\alpha ,\frac{\alpha }{2})}+{|l_6(\mathit{u},r)|}_{G_T}^{(1+\alpha ,\frac{1+\alpha }{2})}+{\mathbf{\left|}\mathbb{M}\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}+{⟨\mathbb{M}⟩}_{x,D_T}^{\left(\gamma \right)}\hfill \\ \hfill & ⩽c_1\left\{\left(1+|{\mathcal{D}}_t{r}^{*}{|}_{D_T}^{(1,0)}\right){|\mathit{f}|}_{Q_T}^{(1,\frac{1+\alpha -\gamma }{2})}+Y_{(0,T)}^2(\mathit{u},q,r)\right\},\hfill \end{array}$$

(58)

where $\nabla ·\mathbb{M}=-\overline{\rho }{\mathbb{L}}^{-1}\widehat{\mathit{f}}-{\mathit{l}}_7$, and

$$\begin{array}{cc}\hfill |\widehat{\mathit{f}}{|}_{Q_T}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}& ⩽c\left\{{|\mathit{f}|}_{Q_T}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}+\left({|\nabla r|}_{G_T}+{|{\mathcal{D}}_t{r}^{*}|}_{Q_T}\right){|\nabla \mathit{f}|}_{Q_T}\right\}.\hfill \end{array}$$

If $(\mathit{u},r)$ and $({\mathit{u}}^{\prime },r^{\prime })$ satisfy (57), then

$$\begin{array}{cc}\hfill Z_{(0,T)}(\mathit{u}-{\mathit{u}}^{\prime },q-q^{\prime },r-r^{\prime })& ⩽c(\delta +\epsilon )Y_{(0,T)}(\mathit{u}-{\mathit{u}}^{\prime },q-q^{\prime },r-r^{\prime }),\hfill \\ \hfill |\widehat{\mathit{f}}-{\widehat{\mathit{f}}}^{\prime }{|}_{Q_T}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}& ⩽c\epsilon Y_{(0,T)}(\mathit{u}-{\mathit{u}}^{\prime },q-q^{\prime },r-r^{\prime }),\hfill \end{array}$$

(59)

where ${\widehat{\mathit{f}}}^{\prime }=\tilde{\mathit{f}}(e_{r^{\prime }}(z,t),t)$.

Proof. 

We estimate, for instance, the term ${\mathit{l}}_1$. In view of the form of $\mathbb{L}$, it is easily seen that the first summand in ${\mathit{l}}_1$ contains the second-order derivatives only multiplied by functions of $\nabla r(z,t)$. Thus, one can conclude

$$|\overline{\mu }({\tilde{\nabla }}^2-{\nabla }^2){\mathit{u}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}⩽c\left(|r^{*}{|}_{D_T}^{(1+\alpha ,\frac{\alpha }{2})}+{|\nabla r^{*}|}_{D_T}^{(1+\alpha ,\frac{\alpha }{2})}\right){|\mathit{u}|}_{D_T}^{(2+\alpha ,\frac{\alpha }{2})}⩽c{Y}_{(0,T)}^2(\mathit{u},q,r).$$

The term $(\nabla -\tilde{\nabla })q$ can be evaluated in a similar way. The third summand satisfies the inequality

$$\begin{array}{cc}\hfill |\overline{\rho }{\mathcal{D}}_t{r}^{*}({\mathbb{L}}^{-1}{\mathit{N}}^{*}·\nabla ){\mathit{u}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}& ⩽c|{\mathcal{D}}_t{r}^{*}{|}_{D_T}^{(\alpha ,0)}(1+|\nabla r^{*}{|}_{D_T}^{(\alpha ,0)}{)|\nabla \mathit{u}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}\hfill \\ \hfill & +|{\mathcal{D}}_t{r}^{*}{|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}(1+|\nabla r^{*}{|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}{)|\mathit{u}|}_{D_T}^{(1+\alpha ,0)}⩽c{Y}_{(0,T)}^2(\mathit{u},q,r).\hfill \end{array}$$

Additionally, the last one can be estimated as follows:

$$\begin{array}{cc}\hfill \overline{\rho }({\mathbb{L}}^{-1}\mathit{u}·\nabla ){\mathit{u}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}& ⩽c\left(\left(1+|r^{*}{|}_{D_T}^{(1+\alpha ,0)}\right){|\mathit{u}|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+|\nabla r^{*}{|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}{|\mathit{u}|}_{D_T}^{(\alpha ,0)}\right){|\mathit{u}|}_{D_T}^{(1+\alpha ,\frac{1+\alpha }{2})}\hfill \\ \hfill & ⩽{c|\mathit{u}|}_{D_T}^{(2+\alpha ,1+\frac{\alpha }{2})}{Y}_{(0,T)}(\mathit{u},q,r).\hfill \end{array}$$

Next,

$$\begin{array}{cc}\hfill |l_2(\mathit{u},r)|& {}_{D_T}^{(1+\alpha ,\frac{1+\alpha }{2})}+{|{\mathcal{D}}_t{\mathit{L}}_2(\mathit{u},r)|}_{D_T}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}{\mathit{L}}_2(\mathit{u},r)\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}\hfill \\ \hfill & ⩽c\left\{|r^{*}{|}_{D_T}^{(3+\alpha ,\frac{3+\alpha }{2})}{|\nabla \mathit{u}|}_{D_T}^{(1+\alpha ,\frac{1+\alpha }{2})}+\left(|{\mathcal{D}}_t{r}^{*}{|}_{D_T}^{(1+\alpha ,\frac{\alpha }{2})}+{|r^{*}|}_{D_T}^{(2+\alpha ,1+\frac{\alpha }{2})}\right){|\mathit{u}|}_{D_T}^{(2+\alpha ,1+\frac{\alpha }{2})}\right\}\hfill \\ \hfill & ⩽c{Y}_{(0,T)}(\mathit{u},q,r){|\mathit{u}|}_{D_T}^{(2+\alpha ,1+\frac{\alpha }{2})}.\hfill \end{array}$$

Now consider ${\mathit{l}}_7(\mathit{u},q,r)=\partial {\mathit{L}}_{7j}(\mathit{u},q,r)/\partial x_j$ and

$$\mathbb{M}(x,t)=-{\left\{{\mathit{L}}_{7j}\right\}}_{j=1}^3-\nabla \underset{{\mathbb{R}}^3}{\int }\overline{\rho }\mathcal{E}(x,y){\mathbb{L}}^{-1}\mathit{f}\mathrm{d}y,$$

where, by (46),

$$\begin{array}{cc}\hfill {\mathit{L}}_{7j}(\mathit{u},q)& =\overline{\mu }\mathbb{B}\frac{\partial \mathit{u}}{\partial {\xi }_j}-\mathbb{B}{\mathit{e}}_{j}q+\overline{\rho }{\mathbb{L}}^{-1}{\mathit{L}}_{1j}+\frac{\partial \mathit{W}}{\partial {\xi }_j},j=1,2,3,\hfill \\ \hfill \mathit{W}(\xi ,t)& =-\underset{\cup {\mathcal{F}}^{\pm }}{\int }\mathcal{E}(\xi ,\mathit{\eta })\left\{\frac{\partial \mathbb{B}}{\partial {\mathit{\eta }}_m}\left(\overline{\mu }\frac{\partial \mathit{u}}{\partial {\mathit{\eta }}_m}-{\mathit{e}}_{m}q+\overline{\rho }{\mathit{L}}_{1m}\right)+2\omega \overline{\rho }\mathbb{B}({\mathit{e}}_3\times \mathit{u})-\overline{\rho }\left({\mathcal{D}}_t\mathbb{B}\right)\mathit{u}\right\}\mathrm{d}\mathit{\eta }.\hfill \end{array}$$

In order to estimate $\mathbb{M}$, we apply Lemma 1. Then we have

$$\begin{array}{cc}\hfill \mathbf{\left|}\mathbb{M}\mathbf{\right|}& {}_{D_T}^{(\gamma ,1+\alpha )}+{⟨\mathbb{M}⟩}_{x,D_T}^{\left(\gamma \right)}⩽c\left\{\underset{j}{max}{\mathbf{\left|}{\mathit{L}}_{7j}\mathbf{\right|}}_{D_T}^{(\gamma ,1+\alpha )}+\underset{j}{max}{⟨{\mathit{L}}_{7j}⟩}_{x,D_T}^{\left(\gamma \right)}+{|\overline{\rho }{\mathbb{L}}^{-1}\mathit{f}|}_{D_T}^{(0,\frac{1+\alpha -\gamma }{2})}\right\}\hfill \\ \hfill ⩽& c\{\left(1+|\nabla r^{*}{|}_{D_T}^{(0,\frac{1+\alpha -\gamma }{2})}\right){|\mathit{f}|}_{D_T}^{(0,\frac{1+\alpha -\gamma }{2})}+{|\mathit{u}|}_{D_T}^{(0,\frac{1+\alpha -\gamma }{2})}\left(|{\mathcal{D}}_t{r}^{*}{|}_{D_T}^{(1+\alpha ,\frac{1+\alpha }{2})}+{|r^{*}|}_{D_T}^{(2+\alpha ,\frac{1+\alpha }{2})}\right)\hfill \\ \hfill & +\left(|r^{*}{|}_{D_T}^{(1,\frac{1+\alpha -\gamma }{2})}+{|\nabla \nabla r^{*}|}_{D_T}^{(0,\frac{1+\alpha -\gamma }{2})}\right)\left({|\mathit{u}|}_{D_T}^{(2+\alpha ,\frac{1+\alpha }{2})}+{|q|}_{D_T}^{(0,\frac{1+\alpha -\gamma }{2})}\right)\}\hfill \\ \hfill ⩽& c\left\{\left(1+|{\mathcal{D}}_t{r}^{*}{|}_{D_T}^{(1,0)}\right){|\widehat{\mathit{f}}|}_{D_T}^{(0,\frac{1+\alpha -\gamma }{2})}+Y_{(0,T)}^2(\mathit{u},q,r)\right\}.\hfill \end{array}$$

Moreover,

$$\begin{array}{cc}\hfill & {\mathbf{\left|}{l}_4(\mathit{u},r)\mathbf{\right|}}_{G_T}^{(\gamma ,1+\alpha )}+|{\nabla }_{\tau }{l}_4{(\mathit{u},r)|}_{G_T}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}{l}_5\left(r\right)\mathbf{\right|}}_{G_T}^{(\gamma ,1+\alpha )}+|{\nabla }_{\tau }{l}_5{\left(r\right)|}_{G_T}^{(\alpha ,\frac{\alpha }{2})}+{|l_6(\mathit{u},r)|}_{G_T}^{(1+\alpha ,\frac{1+\alpha }{2})}\hfill \\ \hfill & ⩽c\left\{{\mathbf{|}\nabla r\mathbf{|}}_{G_T}^{(\gamma ,1+\alpha )}{|\mathit{u}|}_{D_T}^{(2+\alpha ,1+\frac{\alpha }{2})}+{|\nabla r|}_{G_T}^{(1+\alpha ,\frac{1+\alpha }{2})}\left({\mathbf{|}\nabla \nabla r\mathbf{|}}_{G_T}^{(\gamma ,1+\alpha )}+{|r|}_{G_T}^{(3+\alpha ,\frac{3+\alpha }{2})}+{|\mathit{u}|}_{D_T}^{(1+\alpha ,\frac{1+\alpha }{2})}\right)\right\}.\hfill \end{array}$$

The estimation of the deviations of the potential U from $\mathcal{U}$ and the doubled mean curvature H from $\mathcal{H}$ can be found in [18] (Proposition 3.1).

The other nonlinear terms are estimated in a similar way.

Finally, we extend the function $\mathit{f}$ outside $\Omega$ with preservation of class and make use of the relation

$$\begin{array}{cc}\hfill & \mathit{f}\left(e_r(y,t),t\right)-\mathit{f}\left(e_r(y,t-\tau ),t\right)\hfill \\ \hfill & ={\int }_0^1\nabla \mathit{f}\left(e_r(y,t)-\lambda {\int }_0^{\tau }{\mathit{N}}^{*}\left(y\right){\mathcal{D}}_t{r}^{*}(y,t-{\tau }^{\prime })\mathrm{d}{\tau }^{\prime },t\right)\mathrm{d}\lambda {\int }_0^{\tau }{\mathit{N}}^{*}\left(y\right){\mathcal{D}}_t{r}^{*}(y,t-{\tau }^{\prime })\mathrm{d}{\tau }^{\prime }.\hfill \end{array}$$

Then we conclude that

$$\begin{array}{cc}\hfill |\widehat{\mathit{f}}{|}_{Q_T}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}& ⩽c\left\{{|\mathit{f}|}_{Q_T}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}+\left({|\nabla r|}_{G_T}+{|{\mathcal{D}}_{t}r|}_{G_T}\right){|\nabla \mathit{f}|}_{Q_T}\right\}.\hfill \end{array}$$

Collecting the previous estimates, we arrive at (58).

To prove inequality (59), one should apply the above estimate to

$\mathit{f}\left(e_r,t\right)-\mathit{f}\left(e_{r^{\prime }},t\right)={\int }_0^1\nabla \mathit{f}\left(e_{r^{\prime }}+\lambda \left({\mathit{N}}^{*}(y,t)(r-r^{\prime })\right),t\right)\mathrm{d}\lambda {\mathit{N}}^{*}(y,t)(r-r^{\prime }).$□

On the basis of Proposition 7, Theorem 4 can be proved by successive approximations similarly to [9] (Ch. 12).

Now we state the main result of the paper.

Theorem 5

(Global Solvability of the Nonlinear Problem). Let $\varkappa ⩾0,\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}>0$, and in addition, let all the hypotheses of Theorem 4 be satisfied. We assume also that smallness condition

$$|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}⩽\epsilon \ll 1,$$

(60)

and inequality (35), restrictions (47) at $t=0$ and (4) hold. Moreover, we assume that $\mathit{f}$ has small norms:

$$|e^{bt}{\mathit{f}|}_{Q_{\infty }}^{(1,\frac{1+\alpha -\gamma }{2})}⩽\epsilon ,b>0,|{\mathcal{D}}_x^{\mathit{i}}{\mathit{f}|}_{Q_{\infty }}^{(\alpha ,\frac{1+\alpha -\gamma }{2})}⩽\epsilon ,|\mathit{i}|=1,$$

(61)

where $Q_{\infty }=\mathcal{F}\times (0,\infty ),$ $T_0>2$ is an appropriate fixed number.

Then problem (44) has a unique solution defined for all $t>0$ and

$$\begin{gathered} |{\mathrm{e}}^{at}{\mathit{u}|}_{D_{\infty }}^{(2+\alpha ,1+\frac{\alpha }{2})}+|{\mathrm{e}}^{at}{\nabla q|}_{D_{\infty }}^{(\alpha ,\frac{\alpha }{2})}+{\mathbf{\left|}{\mathrm{e}}^{at}q\mathbf{\right|}}_{D_{\infty }}^{(\gamma ,1+\alpha )}+|{\mathrm{e}}^{at}{r|}_{G_{\infty }}^{(3+\alpha ,\frac{3+\alpha }{2})}+{|{\mathrm{e}}^{at}{\mathcal{D}}_{t}r|}_{G_{\infty }}^{(2+\alpha ,1+\frac{\alpha }{2})} \\ ⩽c_1\left(\epsilon \right)\left\{|{\mathrm{e}}^{at}{\mathit{f}|}_{Q_{\infty }}^{(1,\frac{1+\alpha -\gamma }{2})}+|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right\} \end{gathered}$$

(62)

with a certain $0<a<b;$ $c_1\left(\epsilon \right)$ is a bounded function of ε.

We note that a similar result in the case of $\varkappa =0$ can be proved without the restriction $\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}>0$.

Proof of Theorem 5. 

Conditions (47) may be written in the form

$$\begin{gathered} \begin{array}{c}{\int }_{{\mathcal{G}}^{\pm }}r\mathrm{d}\mathcal{G}={\int }_{{\mathcal{G}}^{\pm }}(r-\phi (z,r))\mathrm{d}\mathcal{G},\phi (z,r)={\phi }^{\pm }(z,r)\mathrm{on}{\mathcal{G}}^{\pm },\\ {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}r\mathit{z}\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}r\mathit{z}\mathrm{d}\mathcal{G}={\rho }^{-}{\int }_{{\mathcal{G}}^{-}}\left(r\mathit{z}-{\mathit{\psi }}^{-}(z,r)\right)\mathrm{d}\mathcal{G} \\ +\left[\overline{\rho }\right]|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}\left(r\mathit{z}-{\mathit{\psi }}^{+}(z,r)\right)\mathrm{d}\mathcal{G},\\ {\int }_{\mathcal{F}}\overline{\rho }\mathit{u}\mathrm{d}z={\int }_{\mathcal{F}}\overline{\rho }\mathit{u}\left(1-L(z,r)\right)\mathrm{d}z,\\ {\int }_{\mathcal{F}}\overline{\rho }\mathit{u}·{\mathit{\eta }}_j\left(z\right)\mathrm{d}z+\omega \left({\rho }^{-}{\int }_{{\mathcal{G}}_i}r{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}_i}r{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}\right)\\ =\omega \left({\rho }^{-}{\int }_{{\mathcal{G}}_i}r{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}_i}r{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}-{\int }_{{\tilde{\Omega }}_t}{\rho }^{\pm }{\mathit{\eta }}_3\left(y\right)·{\mathit{\eta }}_j\left(y\right)\mathrm{d}y\right)\\ +{\int }_{\mathcal{F}}\overline{\rho }\mathit{u}·{\mathit{\eta }}_j\left(z\right)\left(1-L(z,r)\right)\mathrm{d}z+{\int }_{\mathcal{F}}\overline{\rho }{\mathit{\eta }}_3\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}z,j=1,2,3.\end{array} \end{gathered}$$

(63)

By Proposition 44, we can find the functions ${\mathit{u}}_0^{″},r_0^{″}$ satisfying the relations

$$\begin{array}{c}{\int }_{{\mathcal{G}}^{\pm }}{r}_0^{″}\mathrm{d}\mathcal{G}={\int }_{{\mathcal{G}}^{\pm }}\left(r_0-\phi (z,r_0)\right)\mathrm{d}\mathcal{G}\equiv l^{\pm },\\ {\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{r}_0^{″}\mathit{z}\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}{r}_0^{″}\mathit{z}\mathrm{d}\mathcal{G}={\rho }^{-}{\int }_{{\mathcal{G}}^{-}}\left(r_0\mathit{z}-{\psi }^{-}(z,r_0)\right)\mathrm{d}\mathcal{G}\\ +\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}\left(r_0\mathit{z}-{\psi }^{+}(z,r_0)\right)\mathrm{d}\mathcal{G}\equiv \mathit{l},\\ {\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_0^{″}\mathrm{d}z={\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_0\left(1-L(z,r_0)\right)\mathrm{d}z\equiv m,\\ {\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_0^{″}·{\mathit{\eta }}_j\left(z\right)\mathrm{d}z+\omega \left({\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{r}_0^{\prime \prime }{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}{r}_0^{\prime \prime }{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}\right)\\ =\omega \left({\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{r}_0{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}_i}{r}_0{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}-{\int }_{{\tilde{\Omega }}_0}{\rho }^{\pm }{\mathit{\eta }}_3\left(y\right)·{\mathit{\eta }}_j\left(y\right)\mathrm{d}y\right)\\ +{\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_0·{\mathit{\eta }}_j\left(z\right)\left(1-L(z,r_0)\right)\mathrm{d}z+{\int }_{\mathcal{F}}\overline{\rho }{\mathit{\eta }}_3\left(z\right)·{\mathit{\eta }}_j\left(z\right)\mathrm{d}z,j=1,2,3,\\ \nabla ·{\mathit{u}}_0^{″}=l_2({\mathit{u}}_0,r_0)\mathrm{in}\cup {\mathcal{F}}^{\pm },\\ \left[{\mathit{u}}_0^{\prime \prime }\right]{|}_{{\mathcal{G}}^{+}}=0,\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}_0^{\prime \prime }\right)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}={\mathit{l}}_3^{+}({\mathit{u}}_0,r_0),{\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}_0^{\prime \prime }\right)\mathit{N}{|}_{{\mathcal{G}}^{-}}={\mathit{l}}_3^{-}({\mathit{u}}_0,r_0).\end{array}$$

(64)

We seek a solution to (44) in the form of the sum

$$\mathit{u}={\mathit{u}}^{\prime }+{\mathit{u}}^{″},q=q^{\prime }+q^{″},r=r^{\prime }+r^{″},$$

while defining $({\mathit{u}}^{\prime },q^{\prime },r^{\prime })$ as a solution to the linear problem

$$\begin{array}{c}\overline{\rho }\left({\mathcal{D}}_t{\mathit{u}}^{\prime }(z,t)+2\omega ({\mathit{e}}_3\times {\mathit{u}}^{\prime })\right)-\overline{\mu }{\nabla }^2{\mathit{u}}^{\prime }+\nabla q^{\prime }=0,\nabla ·{\mathit{u}}^{\prime }=0\mathrm{in}\cup {\mathcal{F}}^{\pm },\\ {\mathit{u}}^{\prime }(z,0)={\mathit{u}}_0^{\prime }\left(z\right),z\in \mathcal{F},r^{\prime }(z,0)=r_0^{\prime }\left(z\right),z\in \mathcal{G},\\ \left[{\mathit{u}}^{\prime }\right]{|}_{{\mathcal{G}}^{+}}=0,\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}^{\prime }\right)\mathit{N}\left(z\right)\right]{|}_{{\mathcal{G}}^{+}}=0,\\ \left[-q^{\prime }+{\mu }^{-}\mathit{N}·\mathbb{S}\left({\mathit{u}}^{\prime }\right)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}+{\mathcal{B}}_0^{+}{r}^{\prime }=0\mathrm{on}{\mathcal{G}}^{+},\\ {\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}^{\prime }\right)\mathit{N}{|}_{{\mathcal{G}}^{-}}=0,-q^{\prime }+{\mu }^{-}\mathit{N}·\mathbb{S}\left({\mathit{u}}^{\prime }\right)\mathit{N}+{\mathcal{B}}_0^{-}{r}^{\prime }=0\mathrm{on}{\mathcal{G}}^{-},\\ {\mathcal{D}}_t{r}^{\prime }-{\mathit{u}}^{\prime }·\mathit{N}=0\mathrm{on}\mathcal{G},\end{array}$$

(65)

where ${\mathit{u}}_0^{\prime }\equiv {\mathit{u}}_0-{\mathit{u}}_0^{″},$ $r_0^{\prime }\equiv r_0-r_0^{″}$ which satisfy (21), (22) and homogeneous compatibility conditions (37).

Finally, as $({\mathit{u}}^{″},q^{″},r^{″})$, we take a solution of the nonlinear system

$$\begin{array}{cc}\hfill & \overline{\rho }\left({\mathcal{D}}_t{\mathit{u}}^{\prime \prime }+2\omega ({\mathit{e}}_3\times {\mathit{u}}^{\prime \prime })\right)-\overline{\mu }{\nabla }^2{\mathit{u}}^{\prime \prime }+\nabla q^{\prime \prime }=\overline{\rho }\widehat{\mathit{f}}+{\mathit{l}}_1({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },q^{\prime }+q^{\prime \prime },r^{\prime }+r^{\prime \prime }),\hfill \\ \hfill & \nabla ·{\mathit{u}}^{\prime \prime }=l_2({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },r^{\prime }+r^{\prime \prime })\mathrm{in}\cup {\mathcal{F}}^{\pm },t>0,\hfill \\ \hfill & {\mathit{u}}^{\prime \prime }{|}_{t=0}={\mathit{u}}_0^{\prime \prime }\mathrm{in}\cup {\mathcal{F}}^{\pm },r^{\prime \prime }{|}_{t=0}=r_0^{\prime \prime }\mathrm{on}\mathcal{G},\hfill \\ \hfill & \left[{\mathit{u}}^{\prime \prime }\right]{|}_{{\mathcal{G}}^{+}}=0,\left[\overline{\mu }{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}^{\prime \prime }\right)\mathit{N}\right]{|}_{{\mathcal{G}}^{+}}={\mathit{l}}_3^{+}({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },r^{\prime }+r^{\prime \prime })\mathrm{on}{\mathcal{G}}^{+},\hfill \\ \hfill & [-q^{\prime \prime }+\overline{\mu }\mathit{N}·\mathbb{S}\left({\mathit{u}}^{\prime \prime }\right)\mathit{N}]{|}_{{\mathcal{G}}^{+}}+{\mathcal{B}}_0^{+}{r}^{\prime \prime }=l_4^{+}({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },r^{\prime }+r^{\prime \prime })+l_5^{+}(r^{\prime }+r^{\prime \prime })\mathrm{on}{\mathcal{G}}^{+},\hfill \\ \hfill & {\mu }^{-}{\Pi }_{\mathcal{G}}\mathbb{S}\left({\mathit{u}}^{\prime \prime }\right)\mathit{N}={\mathit{l}}_3^{-}({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },r^{\prime }+r^{\prime \prime })\mathrm{on}{\mathcal{G}}^{-},\hfill \\ \hfill & -q^{\prime \prime }+{\mu }^{-}\mathit{N}·\mathbb{S}\left({\mathit{u}}^{\prime \prime }\right)\mathit{N}+{\mathcal{B}}_0^{-}{r}^{\prime \prime }=l_4^{-}({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },r^{\prime }+r^{\prime \prime })+l_5^{-}(r^{\prime }+r^{\prime \prime })\mathrm{on}{\mathcal{G}}^{-},\hfill \\ \hfill & {\mathcal{D}}_t{r}^{\prime \prime }-{\mathit{u}}^{\prime \prime }·\mathit{N}=l_6({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },r^{\prime }+r^{\prime \prime })\mathrm{on}\mathcal{G}.\hfill \end{array}$$

(66)

Let us consider restrictions (64). If (60) holds, then the expressions

$$\begin{array}{cc}\hfill & l^{\pm }={\int }_{{\mathcal{G}}^{\pm }}\left(r_0-\phi (z,r_0)\right)\mathrm{d}\mathcal{G},\hfill \\ \hfill & \mathit{l}=\rho {\int }_{{\mathcal{G}}^{-}}\left(r_0\mathit{z}-{\psi }^{-}(z,r_0)\right)\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}(r_0\mathit{z}-{\psi }^{+}(z,r_0))\mathrm{d}\mathcal{G},\hfill \\ \hfill & \mathit{m}={\int }_{\mathcal{F}}\rho {\mathit{u}}_0\left(1-L(z,r_0)\right)\mathrm{d}z,\hfill \\ \hfill & M_j={\int }_{\mathcal{F}}\rho {\mathit{u}}_0·{\mathit{\eta }}_j\left(1-L(z,r_0)\right)\mathrm{d}z,j=1,2,3,\hfill \end{array}$$

and the functions $f_0=l_2({\mathit{u}}_0,r_0)$, ${\mathit{b}}_0\left(z\right)={\mathit{l}}_3^{\pm }({\mathit{u}}_0,r_0),z\in {\mathcal{G}}^{\pm }$ and satisfy the inequality

$$|l^{+}|+|l^{-}|+|\mathit{l}|+|\mathit{m}|+|\mathit{M}|+|f_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(1+\alpha )}+{|{\mathit{b}}_0|}_{\mathcal{G}}^{(1+\alpha )}⩽c\epsilon \left(|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right).$$

Hence, by (49),

$$\begin{array}{cc}\hfill & |{\mathit{u}}_0^{\prime \prime }{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0^{\prime \prime }|}_{\mathcal{G}}^{(3+\alpha )}⩽c\epsilon \left(|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right),\hfill \\ \hfill & |{\mathit{u}}_0^{\prime }{|}_{\mathcal{F}}^{(2+\alpha )}+{|r_0^{\prime }|}_{\mathcal{G}}^{(3+\alpha )}⩽c\left(|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right).\hfill \end{array}$$

(67)

Moreover, in view of (63) and (64), ${\mathit{u}}_0^{\prime }$ and $r_0^{\prime }$ are subjected to the necessary conditions

$${\int }_{{\mathcal{G}}^{\pm }}{r}_0^{\prime }\mathrm{d}\mathcal{G}={\int }_{{\mathcal{G}}^{\pm }}(r_0-r_0^{\prime \prime })\mathrm{d}\mathcal{G}={\int }_{{\mathcal{G}}^{\pm }}\phi (z,r_0)\mathrm{d}S=0,$$

$${\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{r}_0^{\prime }\mathit{z}\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}{r}_0^{\prime }\mathit{z}\mathrm{d}\mathcal{G}={\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{\psi }^{-}(z,r_0)\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}{\psi }^{+}\mathrm{d}\mathcal{G}=0,$$

$${\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_0^{\prime }\mathrm{d}\mathcal{G}=0,$$

$${\int }_{\mathcal{F}}\overline{\rho }{\mathit{u}}_0^{\prime }·{\mathit{\eta }}_j\mathrm{d}z+\omega \left({\rho }^{-}{\int }_{{\mathcal{G}}^{-}}{r}_0^{\prime }{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}\mathcal{G}+\left[\overline{\rho }\right]{|}_{{\mathcal{G}}^{+}}{\int }_{{\mathcal{G}}^{+}}{r}_0^{\prime }{\mathit{\eta }}_3·{\mathit{\eta }}_j\mathrm{d}S\right)=0.$$

Theorem 3 guarantees for the solution $({\mathit{u}}^{\prime },q^{\prime },r^{\prime })$ of problem (65), the inequality:

$$\begin{array}{c}\hfill N\left({\mathit{u}}^{\prime }(·,T),r^{\prime }(·,T)\right)\equiv |{\mathit{u}}^{\prime }{(·,T)|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r^{\prime }(·,T)|}_{\mathcal{G}}^{(3+\alpha )}⩽c_1{\mathrm{e}}^{-\beta T}\left\{|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right\}\end{array}$$

for any positive T. Let $T=T_0$ be so large that

$$c_1{e}^{-\beta T_0}⩽\theta /2\ll 1/2,\beta >0.$$

Next, problem (66) can be solved by iterations, similarly to [9] (Ch. 12), on the basis of Theorem 2 and estimate (58) of nonlinear terms (45):

$$Z_{0,T}({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },q^{\prime }+q^{\prime \prime },r^{\prime }+r^{\prime \prime })⩽c\left\{{|\mathit{f}|}_{Q_{T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}+Y_{0,T}^2({\mathit{u}}^{\prime }+{\mathit{u}}^{\prime \prime },q^{\prime }+q^{\prime \prime },r^{\prime }+r^{\prime \prime })\right\}.$$

We observe that smallness inequality (57) of the zero-approximation is guaranteed by (67) and (60). Thus, if $\epsilon$ is small enough, by inequalities (55) and (56), we obtain

$$Y_{0,T_0}({\mathit{u}}^{\prime \prime },q^{\prime \prime },r^{\prime \prime })⩽c_2\left(\epsilon \right)\left({|\mathit{f}|}_{Q_{T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}+|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right),$$

$$\begin{array}{cc}N\left(\mathit{u}(·,T_0),r(·,T_0)\right)& ⩽N\left({\mathit{u}}^{\prime }(·,T_0),r^{\prime }(·,T_0)\right)+N\left({\mathit{u}}^{\prime \prime }(·,T_0),r^{\prime \prime }(·,T_0)\right)\\ & ⩽(\theta /2+\vartheta )\left(|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right)+c{|\mathit{f}|}_{Q_{T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}.\end{array}$$

We set $\lambda \equiv \theta /2+\vartheta <1$, due to (60), (61), which implies

$$\begin{gathered} Y_{0,T_0}(\mathit{u},q,r)⩽c\left({|\mathit{f}|}_{Q_{T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}+|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right)⩽c\epsilon , \\ N\left(\mathit{u}(·,T_0),r(·,T_0)\right)⩽\lambda \left(|{\mathit{u}}_0{|}_{\cup {\mathcal{F}}^{\pm }}^{(2+\alpha )}+{|r_0|}_{\mathcal{G}}^{(3+\alpha )}\right)+c{|\mathit{f}|}_{Q_{T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}⩽C\epsilon . \end{gathered}$$

(68)

In view of inequalities (68), we can extend the solution $(\mathit{u},q,r)$ into the intervals $(T_0,2T_0),$ $...,(k{T}_0,(k+1)T_0),...$ up to the infinite interval $t>0$ by means of the repeated applications of the obtained local result and to complete the proof of Theorem 5 by analogy with [9] (Ch. 12).

Thus, let us suppose that the solution has already been found for $t⩽k{T}_0$. Then we can define it for $t\in (k{T}_0,(k+1)T_0]$ as a solution of the problem with the initial conditions $\mathit{u}(z,k{T}_0)\equiv {\mathit{u}}_k\left(z\right)$ and $r(z,k{T}_0)\equiv r_k\left(z\right)$.

We consider the case $k=1$. From (54) and (55), it follows that

$$N_1\equiv N({\mathit{u}}_1,r_1)⩽C\epsilon ;$$

hence, by replacing $\epsilon$ with $C^{-1}\epsilon$, we see that this problem is solvable in the time interval $(T_0,2T_0]$, and by (68), the estimates

$$Y_1(\mathit{u},q,r)⩽c\left\{N_1+{|\mathit{f}|}_{Q_{T_0,2T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}\right\},$$

$$N_2⩽\lambda N_1+c{|\mathit{f}|}_{Q_{T_0,2T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}⩽C\epsilon$$

are satisfied, where

$$N_k\equiv N({\mathit{u}}_k,r_k),Y_k(\mathit{u},q,r)\equiv Y_{k{T}_0,(k+1)T_0}(\mathit{u},q,r).$$

If the solution is found for $t⩽k{T}_0$ and the inequalities

$$\begin{array}{cc}\hfill & N_j⩽\lambda N_{j-1}+c{|\mathit{f}|}_{Q_{(j-1)T_0,j{T}_0}}^{(1,\frac{1+\alpha -\gamma }{2})},\lambda <1,\hfill \\ \hfill & Y_j⩽c\left\{N_j+{|\mathit{f}|}_{Q_{j{T}_0,(j+1)T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}\right\},j=1,...,k,\hfill \end{array}$$

(69)

are proved, then for ${\lambda }_0={\mathrm{e}}^{-b{T}_0}<\lambda$

$$\begin{array}{cc}{N}_j& ⩽...⩽{\lambda }^j{N}_0+c{\displaystyle \sum _{i=0}^{j-1}}{\lambda }^{j-1-i}{|\mathit{f}|}_{Q_{i{T}_0,(i+1)T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}\\ & ⩽{\lambda }^j{N}_0+c{\lambda }^{j-1}{|{\mathrm{e}}^{b{T}_0}\mathit{f}|}_{Q_{0,j{T}_0}}^{(1,\frac{1+\alpha -\gamma }{2})}{\displaystyle \sum _{i=0}^{j-1}}\frac{{\lambda }_0^i}{{\lambda }^i}⩽c{\lambda }^j\left(N_0+\frac{|{\mathrm{e}}^{b{T}_0}{\mathit{f}|}_{Q_{\infty }}^{(1,\frac{1+\alpha -\gamma }{2})}}{\lambda -{\lambda }_0}\right)⩽c{\lambda }^j\epsilon \end{array}$$

(70)

with the constants c independent of j. We have used inequalities (61) for $\mathit{f}$. Since ${\lambda }^j\to 0$ as $j\to \infty$, the right-hand side of (70) is less than $\epsilon$ for $j⩾j_0$, and the replacement of $\epsilon$ with $C^{-1}\epsilon$ can be done only a finite number of times.

Let ${\lambda }_1>\lambda$ (${\lambda }_1={\mathrm{e}}^{-a{T}_0}$, $a<b$). We multiply (70) by ${\lambda }_1^{-j}$ and sum it with respect to j. This gives us

$$\begin{array}{cc}\hfill \sum _{j=0}^k{\lambda }_1^{-j}{N}_j⩽& N_0+\sum _{j=1}^k\frac{{\lambda }^j}{{\lambda }_1^j}{N}_0+c\sum _{j=1}^k\frac{{\lambda }^j}{{\lambda }_1^j}\sum _{i=0}^{j-1}{|\mathit{f}|}_{Q_{i{T}_0,(i+1)T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}\hfill \\ \hfill ⩽& \frac{{\lambda }_1}{{\lambda }_1-\lambda }\left(N_0+\frac{c\lambda }{\lambda -{\lambda }_0}{|{\mathrm{e}}^{b{T}_0}\mathit{f}|}_{Q_{\infty }}^{(1,\frac{1+\alpha -\gamma }{2})}\right).\hfill \end{array}$$

Finally, the sum of (69) multiplied by ${\lambda }_1^{-j}$ leads us to

$$\begin{array}{cc}\hfill \sum _{j=0}^k{\lambda }_1^{-j}{Y}_j(\mathit{u},q,r)⩽& c\left\{\frac{{\lambda }_1}{{\lambda }_1-\lambda }\left(N_0+\frac{c\lambda }{\lambda -{\lambda }_0}{|{\mathrm{e}}^{b{T}_0}\mathit{f}|}_{Q_{\infty }}^{(1,\frac{1+\alpha -\gamma }{2})}\right)+\sum _{j=0}^k{\lambda }_1^{-j}{|\mathit{f}|}_{Q_{j{T}_0,(j+1)T_0}}^{(1,\frac{1+\alpha -\gamma }{2})}\right\}\hfill \\ \hfill ⩽& c\left\{N_0+\left(c+\frac{{\lambda }_1}{{\lambda }_1-{\lambda }_0}\right){|{\mathrm{e}}^{b{T}_0}\mathit{f}|}_{Q_{\infty }}^{(1,\frac{1+\alpha -\gamma }{2})}\right\}.\hfill \end{array}$$

The left-hand side in the last inequality can be replaced by ${max}_{j⩽k}{\lambda }_1^{-j}{Y}_j$. Thus, by passing to the limit there as $k\to \infty$, one arrives at an inequality equivalent to (62). □

5. Conclusions

We have studied a uniformly rotating finite mass consisting of two immiscible, viscous, incompressible, self-gravitating capillary fluids. We have assumed that the interface between the liquids is closed and unknown and the initial form of the drop is close to an axially symmetric two-layer equilibrium figure $\cup {\mathcal{F}}^{\pm }$. An analysis of the problem has been performed in the spaces of Hölder functions. The stability of a rotating two-phase drop with self-gravity has been proved for sufficiently small initial data, an angular velocity and exponentially decreasing mass forces. The proof was based on the analysis of small perturbations of equilibrium state $(\mathcal{V},\mathcal{P},0)$ of rotating two-layer liquids.

First, we have linearized the non-linear problem and obtained global maximal regularity for a linear homogeneous problem (Theorem 3). Next, we have found a solution to the non-linear problem as the sum of the solution of the linear homogeneous problem and that of a system with small non-linear terms. We have proved the global solvability of the last one on the basis of local existence theorem (Theorem 4) step by step.

The conclusion that can be drawn from the main theorem (Theorem 5) is as follows. Solution $(\mathit{u},q,r)$ of problem (44) tends exponentially to zero as $t\to \infty$. This means that velocity vector field $\mathit{v}\to \mathcal{V}$, pressure function $p\to \mathcal{P}$ and the boundaries of two-layer drop ${\Gamma }_t^{\pm }$ approach the surfaces ${\mathcal{G}}^{\pm }$ of the two-phase equilibrium figure $\mathcal{F}$. This regime describes the rotation of a fluid as a rigid body. Since the proof has been based on inequality (35), which coincides with the positiveness of the second variation of the energy functional, we conclude that it is a necessary condition for the stability of the two-phase figure of equilibrium $\cup {\mathcal{F}}^{\pm }$.