Design and Experimental Verification of a General Single-Switch N-Stage Z-Network High Gain Boost Converter

Abstract

A single-switch N-stage Z-network high-gain boost converter is proposed in this study, which can be applied in the field of chip etching for bias provision. The circuit topology, operation mode, voltage gain and the control strategy are analyzed. Thereafter, the steady-state performance of the circuit is analyzed with small signal stability modeling. A simulation model is built using Simulink and compared with the traditional quadratic circuit. Combined with the control strategy, the circuit can obtain better steady-state performance by controlling the number of working N-networks and adjusting the duty ratio in the case of high voltage, wide range of voltage output and dynamic voltage output. The simulation model and hardware prototype of the single-switch four-stage Z-network high-gain boost circuit are built and tested, which have verified the effectiveness of the proposed design.

1. Introduction

Dry etching is an important step in the chip manufacturing process. In the etching process, ion energy, ion angle and ion density play important roles in the etching rate, surface reaction and etching selectivity, respectively [1]. These ion characteristics are influenced by the voltage bias applied to the electrode where the silicon wafer is located [2]. The biasing sources directly or indirectly relate to a high-voltage DC power supply. So, how to generate the high-voltage DC power supply with simple structure, high efficiency and low cost deserves attention in the field of chip etching. The etching process [3,4,5,6,7,8] and biasing voltage are shown in Figure 1.

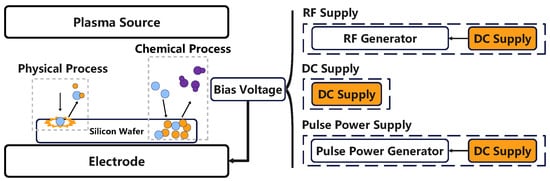
Figure 1. Etching process and bias voltage.

In order to achieve the above high-voltage DC, many methods can be used [9]. Step-up DC–DC converters are one of most popular methods to directly pump up DC voltage. They can be divided into isolated boost circuits and non-isolated boost circuits. The isolated boost circuit is suitable for a situation requiring an isolated power supply [10,11,12], but the disadvantages are the large volume of the transformer and electromagnetic interference. Non-isolated boost circuits have many different structures, and the traditional boost circuit is one of the most popular boost cirucits with a simple structure. However, it has the drawback of a limited voltage gain. The rise of the duty ratio will lead to higher operating temperature of the switch, causing damage and failure of the switch.

In order to solve this problem, many high-gain boost circuits have been proposed [13,14]. For example, the cascade boost circuit [15] or the interleaved boost converter [16] are composed of multistage boost circuits, and the total gain is the product of the gain of each stage. However, it is difficult to control the circuit with multiple switches, and the cost is high. Some scholars put forward the quadratic boost circuit with a single switch [17,18], but the voltage stress of the switch is high, leading to a higher demand for the switching. Based on this quadratic boost circuit, the introduction of coupled inductor [19,20,21,22], switched inductor [23,24,25] and switched capacitor [26,27] have shown improvement of device stress or boost gain, but the circuit structure is complex, which is not conducive to the expansion of use. Some scholars put forward the quadratic boost circuit using a voltage doubler and voltage-lift technique to increase the voltage gain [28,29,30,31], but the introduction of voltage-double cells makes component design more complicated. The voltage gain, switch stress and diode stress in different methods are shown in Table 1.

Table 1. The voltage gain, switch stress and diode stress in different Methods.

Method Type	Voltage Gain	Switch Stress	Diode Stress
Boost circuit	$\frac{1}{\left(1-D\right)}$	$V_{out}$	$V_{out}$
Quadratic boost circuit	$\frac{1}{{\left(1-D\right)}^2}$	$V_{out}$	$V_{out}$
Interlaced parallel converter	$\frac{1}{\left(1-D\right)}$	$V_{out}$	$V_{out}$
Quadratic boost circuit with switch-inductors	$\frac{\left(1+D\right)}{\left(1-D\right)}$	$V_{out}$	$V_{out}$
Quadratic boost circuit with switch-capacitors	$\frac{2}{\left(1-D\right)}$	$\frac{V_{out}}{2}$	$\frac{V_{out}}{2}$
Quadratic boost circuit with coupled inductors	$\frac{2\left(1+N\right)}{\left(1-D\right)}$	$\frac{V_{out}}{2\left(1+N\right)}$	$\frac{V_{out}}{2}$

In this paper, a single-switch N-stage Z-network high-gain boost circuit (SS-NS-ZN-HGBC) is proposed. Inspired by the idea of Z-source structure [32,33,34,35,36] and quasi-Z-source structure [37,38,39], N-stage Z-network is introduced to achieve a high voltage gain while avoiding complex structures compared with other methods mentioned. Voltage gain can be greatly increased by increasing the number of Z-networks, which can be obtained with a small duty ratio. In addition, only one switch is used for control in the SS-NS-ZN-HGBC. Therefore, the control circuit will be simplified, and the control accuracy will be improved.

2. Modeling and Control Design of SS-NS-ZN-HGBC

2.1. Structure of the SS-NS-ZN-HGBC

The structure of the SS-NS-ZN-HGBC is shown in Figure 2. There is only one switch, and each dashed line frame represents a basic Z-network, which includes an inductor, a capacitor and two diodes. The operations of the SS-NS-ZN-HGBC contain two stages as follows.

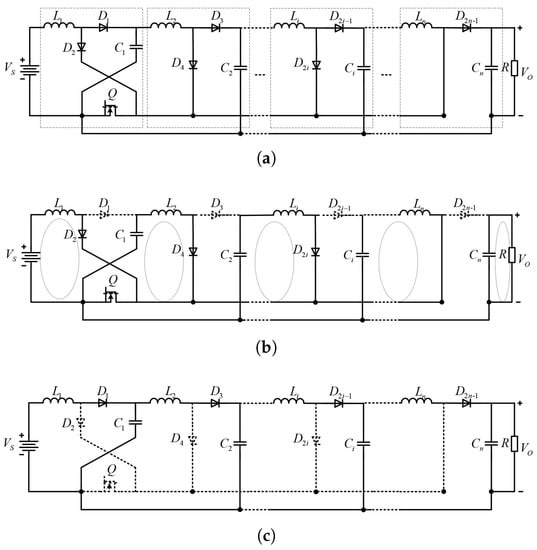
Figure 2. The structure and operational model of the SS-NS-ZN-HGBC: (a) the structure of the SS-NS-ZN-HGBC; (b) stage I; (c) stage II.

Stage I: When Q is turned on, diodes $D_2$, $D_4$, …, $D_{2n}$ are turned on, while diodes $D_1$, $D_3$, …, $D_{2n-1}$ are turned off. For the first Z-network, the input voltage $V_s$, inductor $L_1$ and diode $D_2$ are connected in series to form a closed loop, and $V_s$ provides power for this loop. For the other Z-networks, a capacitor from the upper Z-network $C_{i-1}$, inductor $L_i$ and diode $D_{2i}$ are connected in series to form a closed loop, and the capacitor provides power for the loop. In this case, the voltage of both ends of the inductor $v_{L_i}$ in the Z-network at all levels can be calculated.

$$\begin{array}{cc}\mathrm{For}{L}_1:v_{L_1}\hfill & =V_S\hfill \\ \mathrm{For}{L}_i:v_{L_i}\hfill & =V_{C_{i-1}}\left(1<i\le n\right)\hfill \end{array}$$

(1)

Stage II: When Q is turned off, diodes $D_2$, $D_4$, …, $D_{2i}$ are turned off, while diodes $D_1$, $D_3$, …, $D_{2i-1}$ are turned on. For the first Z-network, the input voltage $V_s$, inductor $L_1$, diode $D_1$ and capacitor $C_1$ are connected in turn to form a closed loop. For the other Z-networks, an inductor $L_i$, a diode $D_{2i-1}$, the capacitor $C_i$ in this Z-network and the capacitor from the upper Z-network $C_{i-1}$ are connected in turn to form a closed loop. In this case, the voltage of both ends of the inductor in the Z-network $v_{L_i}$ at all levels can be calculated.

$$\begin{array}{cc}\mathrm{For}{L}_1:v_{L_1}\hfill & =V_{C_1}-V_S\hfill \\ \mathrm{For}{L}_i:v_{L_i}\hfill & =V_{C_i}-V_{C_{i-1}}\left(1<i<n\right)\hfill \\ \mathrm{For}{L}_n:v_{L_n}\hfill & =V_{\mathrm{out}}-V_{C_{n-1}}\hfill \end{array}$$

(2)

For the inductor in the Z-network at all levels, in one period T, the voltage-second balance is used in (1) and (2).

$$\begin{array}{cc}\mathrm{For}{L}_1:V_S{t}_{\mathrm{up}}\hfill & =\left(V_{C_1}-V_S\right)t_{\mathrm{down}}\hfill \\ \mathrm{For}{L}_i:V_{C_{i-1}}{t}_{\mathrm{up}}\hfill & =\left(V_{C_i}-V_{C_{i-1}}\right)t_{\mathrm{down}}\left(1<i<n\right)\hfill \\ \mathrm{For}{L}_n:V_{C_{n-1}}{t}_{\mathrm{up}}\hfill & =\left(V_{\mathrm{out}}-V_{C_{n-1}}\right)t_{\mathrm{down}}\hfill \end{array}$$

(3)

The inductor has two working states, discontinuous current mode (DCM) and continuous current mode (CCM). In this paper, the inductors of the SS-NS-ZN-HGBC all work in CCM mode, so $t_{\mathrm{up}}$ and $t_{\mathrm{down}}$ are equal to the switch turning-on time $t_{\mathrm{on}}$ and switch turning-off time $t_{\mathrm{off}}$. The $\mathrm{on}$ and $t_{\mathrm{off}}$ can be expressed with (4), where D is the duty cycle of the switch and can be adjusted by the control circuit, and T is the total time of the switching cycle.

$$\begin{array}{ccc}{t}_{\mathrm{up}}\hfill & =t_{\mathrm{on}}\hfill & =TD\hfill \\ t_{\mathrm{down}}\hfill & =t_{\mathrm{off}}\hfill & =T(1-D)\hfill \end{array}$$

(4)

Substituting (4) into (3), the gain of the circuit M can be as follows,

$$M=\frac{V_{\mathrm{out}}}{V_{\mathrm{s}}}={\left(\frac{1}{1-D}\right)}^n$$

(5)

In addition, the voltage of each capacitor $v_{C_i}$ can be derived as below,

$$V_{C_i}={\left(\frac{V_s}{1-D}\right)}^i$$

(6)

2.2. Parameter Design of Circuit Components

2.2.1. Inductors Design

In the SS-NS-ZN-HGBC, inductance has an important impact on the output voltage. To obtain the voltage gain M in (5), we must ensure that each inductor $L_i$ operates in the CCM mode, which means that the inductance of all inductors must be greater than critical inductance $L_i^C$. Critical inductance is the minimum inductance to operate in the CCM mode. In CCM mode, the current through the inductor at any time must be greater than zero, so the minimum current is greater than zero.

$$I_{L_i}-\frac{\mathrm{\Delta }{i}_{L_i}}{2}>0$$

(7)

According to the formula, $v_L=L\frac{\mathrm{\Delta }{i}_L}{\mathrm{\Delta }t}$, and $\mathrm{\Delta }i$ is expressed in (8).

$$\mathrm{\Delta }{i}_L=\frac{v_L\mathrm{\Delta }t}{L}=\frac{T\left(1-D\right)}{L_i}\left(\frac{V_s}{{\left(1-D\right)}^i}-\frac{V_s}{{\left(1-D\right)}^{i-1}}\right)=\frac{T{V}_{s}D}{L_i{\left(1-D\right)}^{i-1}}$$

(8)

When the switch is turned on, the current through the inductor of each Z-network is shown in (9).

$$\begin{array}{cc}\mathrm{For}{C}_1:i_{C_1}\hfill & =I_{L_2}\hfill \\ \mathrm{For}{C}_i:i_{C_i}\hfill & =I_{L_{i+1}}\left(1<i<n\right)\hfill \\ \mathrm{For}{C}_n:i_{C_n}\hfill & =I_{\mathrm{out}}\hfill \end{array}$$

(9)

When the switch is turned off, the current through the inductor of each Z-network is shown in (10).

$$\begin{array}{cc}\mathrm{For}{C}_1:i_{C_1}\hfill & =I_s-I_{L_2}\hfill \\ \mathrm{For}{C}_i:i_{C_i}\hfill & =I_{L_i}-I_{L_{i+1}}\left(1<i<n\right)\hfill \\ \mathrm{For}{C}_n:i_{C_n}\hfill & =I_{L_n}-I_{\mathrm{out}}\hfill \end{array}$$

(10)

For the capacitor in the Z-network at all levels, in a period T, the ampere-second balance yields (1) and (2).

$$\begin{array}{cccc}\mathrm{For}{C}_1:I_{L_2}{t}_{\mathrm{on}}\hfill & =\hfill & \left(I_s-I_{L_2}\right)& t_{\mathrm{off}}\hfill \\ \mathrm{For}{C}_i:I_{L_{i+1}}{t}_{\mathrm{on}}\hfill & =\hfill & \left(I_{L_i}-I_{L_{i+1}}\right)& t_{\mathrm{off}}\left(1<i<n\right)\hfill \\ \mathrm{For}{C}_n:I_{\mathrm{out}}{t}_{\mathrm{on}}\hfill & =\hfill & \left(I_{L_n}-I_{\mathrm{out}}\right)& t_{\mathrm{off}}\hfill \end{array}$$

(11)

Therefore, the current flowing through the inductor can be calculated as follows,

$$I_{L_i}={\left(1-D\right)}^{i-1}{I}_s$$

(12)

In an ideal converter, the input power $P_{in}$ is equal to the output power $P_{out}$,

$$P_{in}=V_s{I}_s=P_{out}=\frac{{V_{out}}^2}{R}$$

(13)

Substituting (5) into (13), we can calculate $I_s$.

$$I_s=\frac{V_s}{{\left(1-D\right)}^{2n}R}$$

(14)

Substituting (14) into (12).

$$I_{L_i}=\frac{V_s}{{\left(1-D\right)}^{2n-i+1}R}$$

(15)

According to (15), $L_i^C$ should satisfy the following relation,

$$I_{L_i^C}-\frac{\mathrm{\Delta }{i}_{L_i^C}}{2}=0$$

(16)

According to (7), (8) and (16), critical inductance $L_i^C$ can be calculated as follows,

$$L_i^C=\frac{TDR{\left(1-D\right)}^{2\left(n-i+1\right)}}{2}$$

(17)

In addition, inductor $L_n$ decides whether the SS-NS-ZN-HGBC works in complete inductor supply mode (CISM). To work in CISM, the lowest current through $L_n$ should be greater than $I_{out}$.

$$I_{L_n}-\frac{\mathrm{\Delta }i}{2}>I_{out}$$

(18)

$L_{nk}$ is the minimum inductance to let the SS-NS-ZN-HGBC work in CISM.

$$\begin{array}{c}{\displaystyle I_{L_{nk}}-\frac{\mathrm{\Delta }{i}_{L_{nk}}}{2}=I_{out}}\hfill \\ {\displaystyle I_{L_{nk}}=\frac{TR{\left(1-D\right)}^2}{2}}\hfill \end{array}$$

(19)

Accoring to (17) and (19), each level of inductor parameters needs to meet the following conditions to work in CCM.

$$\begin{array}{cc}{\displaystyle L_i>L_i^C=\frac{TDR{\left(1-D\right)}^{2\left(n-i+1\right)}}{2}}\hfill & \left(0<i<n\right)\hfill \\ {\displaystyle L_n>max\left\{\frac{TR{\left(1-D\right)}^2}{2},\frac{TDR{\left(1-D\right)}^{2\left(n-i+1\right)}}{2}\right\}}\hfill & \left(i=n\right)\hfill \end{array}$$

(20)

2.2.2. Output Capacitor Design

When the circuit operates in CISM mode, the ripple voltage of the output voltage is only related to the magnitude of the drop in the output capacitor $C_n$ during the conduction of the switch.

$$C_n=\frac{DT{I}_{out}}{\mathrm{\Delta }{v}_{out}}=\frac{DT{V}_{out}}{R\mathrm{\Delta }{v}_{out}}$$

(21)

Term $r_v$ is introduced to represent the output voltage ripple rate and is expressed as follows.

$$r_v=\frac{\mathrm{\Delta }{v}_{out}}{V_{out}}$$

(22)

Substituting (22) into (21).

$$C_n=\frac{DT}{R\mathrm{\Delta }{r}_v}$$

(23)

The output capacitor $C_n$ is there determined by the output voltage ripple $r_v$.

2.2.3. Forward Voltage Drop of Diode and DC Resistance of Inductor

The M in (5) is the value in an ideal case. In practice, the diode has a forward voltage drop $v_D$ when it is turned on, and the inductor has parasitic resistance, which reduces the voltage output of the system. Considering these factors, the inductors are re-analyzed as follows.

$$\begin{array}{cc}\mathrm{For}{L}_1:\left(V_S-V_{D_2}-V_{R_{L_1}}\right)t_{\mathrm{on}}\hfill & =\left(V_{C_1}+V_{D_1}+V_{R_{L_1}}-V_S\right)t_{\mathrm{off}}\hfill \\ \mathrm{For}{L}_i:\left(V_{C_{i-1}}-V_{D_{2i}}-V_{R_{L_i}}\right)t_{\mathrm{on}}\hfill & =\left(V_{C_i}+V_{D_{2i-1}}+V_{R_{L_i}}-V_{C_{i-1}}\right)t_{\mathrm{off}}\left(1<i<n\right)\hfill \\ \mathrm{For}{L}_n:\left(V_{C_{n-1}}-V_{R_{L_n}}\right)t_{\mathrm{on}}\hfill & =\left(V_{\mathrm{out}}+V_{D_{2n-1}}+V_{R_{L_n}}-V_{C_{n-1}}\right)t_{\mathrm{off}}\hfill \end{array}$$

(24)

(24) can be expressed as,

$$\left\{\begin{array}{c}{\displaystyle V_{\mathrm{out}}=\frac{V_S-{\sum }_{i=1}^{n-2}\left(V_{R_{L_i}}+V_{D_{2i}}D+V_{D2i-1}\left(1-D\right)\right){\left(1-D\right)}^i}{{\left(1-D\right)}^n}-\frac{V_{R_{L_n}}}{1-D}-V_{D_{2n-1}}}\hfill \\ {\displaystyle V_{R_{L_i}}=I_{L_i}{R}_{L_i}=\frac{V_{\mathrm{out}}{R}_{L_i}}{R{\left(1-D\right)}^{n-i+1}}\left(i=1,2\cdots ,n\right)}\hfill \end{array}\right.$$

(25)

$V_{\mathrm{out}}$ can be calculated.

$$V_{\mathrm{out}}=\frac{\left(V_s-D{V}_{D_2}\right)-{\left(1-D\right)}^{n-1}{V}_{D_{2n-3}}-{\left(1-D\right)}^n{V}_{D_{2n-1}}-{\sum }_1^{n-2}{\left(1-D\right)}^i\left(V_{D_{2i-1}}+D{V}_{D_{2i+2}}\right)}{{\left(1-D\right)}^n+\frac{1}{R}{\sum }_1^n{R}_{L_i}{\left(1-D\right)}^{2i-2-n}}$$

(26)

For a better description, we set the voltage output without considering the forward voltage drop of the diode and the DC resistance of the inductor as $V_{\mathrm{iout}}$.

$$V_{\mathrm{iout}}=\frac{V_s}{{\left(1-D\right)}^n}$$

(27)

If the influence of DC resistance is not considered, (26) can be simplified as (28).

$$V_{\mathrm{out}}=V_{\mathrm{iout}}-\frac{{\sum }_{i=1}^n{\left(1-D\right)}^i{V}_{D_{2i-1}}+{\sum }_{i=1}^{n-1}D{\left(1-D\right)}^{i-1}{V}_{D_{2i}}}{{\left(1-D\right)}^n}$$

(28)

If the influence of forward voltage drop of the diode is not considered, (26) can be simplified as (29).

$${\displaystyle V_{\mathrm{out}}=\frac{V_{\mathrm{iout}}}{1+{\sum }_{i=1}^n\frac{R_{L_i}}{R}{\left(1-D\right)}^{2i-2-2n}}}$$

(29)

The influence of $V_{D_i}$ and $R_{L_i}$ on the output voltage $V_{\mathrm{out}}$ will vary with the total number of Z-networks n, the order of Z-network i and the duty cycle ratioD. We express the influence of these factors in $K_{D_i}$ and $K_{R_i}$ for $V_{D_i}$ and $V_{L_i}$, respectively.

$$\begin{array}{c}{K}_{D_i}={\left(1-D\right)}^{i-n}\left(i=1,\dots ,2n-1\right),K_{D_i}=D{\left(1-D\right)}^{i-1-n}\left(i=2,\dots ,2n-2\right)\\ K_{R_i}={\left(1-D\right)}^{2i-2-2n}\end{array}$$

(30)

Set D as a fixed value 0.35, and calculate $K_{D_i}$ and $K_{R_i}$ when $n=2,n=3,n=4,n=5$, respectively. As shown in Figure 3, no matter what the value of n, $K_{D_i}$ and $K_{R_i}$ decrease as i increases. It means that the value of $V_{D_1}$ and $R_{L_1}$ has the greatest influence on the output voltage. To obtain higher output voltage, their values should reduce as much as possible. In addition, $K_{D_i}$ and $K_{R_i}$ increase as n increases, especially $K_{R_i}$. It is an important reason why the actual voltage output of the high-order boost circuit is much less than the ideal voltage output.

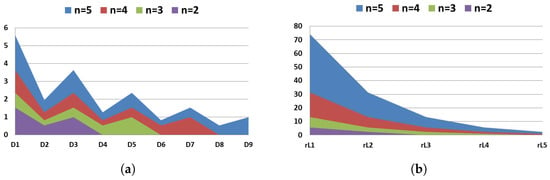
Figure 3. The value of $K_{D_i}$ and $K_{R_i}$ when $D=0.35$. (a) $K_{D_i}$; (b) $K_{R_i}$.

The diode’s forward voltage drop has an inevitable impact on the output voltage. In order to reduce this impact, increasing the input voltage, selecting a lower positive voltage drop diode and reducing the duty cycle reasonably can be useful. As for DC resistance of inductors, selecting inductors with lower DC resistance or decreasing the value of load R can be helpful.

2.3. Control Design of the SS-NS-ZN-HGBC

First, the transfer function of the circuit with small signal analysis is derived, and then the compensation circuit is designed by observing the Bode diagram of the transfer function. The design process is shown in Figure 4.

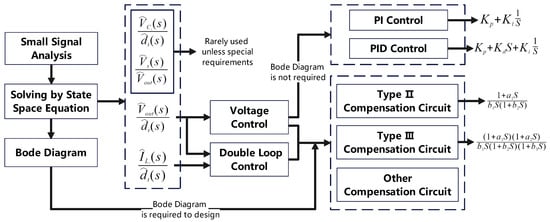
Figure 4. Control design flow chart.

2.3.1. Small Signal Analysis

Through analyzing the stability of the Bode diagram of the transfer function, the appropriate control loop can be designed.

$$\begin{array}{ccccc}t=[t_0,t_0+DT]:\hfill & {\displaystyle \frac{L_{i}d{i}_{L_i}}{dt}}\hfill & =v_{in},\hfill & {\displaystyle \frac{C_{i}d{v}_{C_i}}{dt}}\hfill & =-i_o\hfill \\ t=[t_0+DT,t_0+T]:\hfill & {\displaystyle \frac{L_{i}d{i}_{L_i}}{dt}}\hfill & =v_{in}-v_o,\hfill & {\displaystyle \frac{C_{i}d{v}_{C_i}}{dt}}\hfill & =i_{L_i}-i_o\hfill \end{array}$$

(31)

where $d_t$ is the duty ratio. Use the time average equivalence principle.

$$\begin{array}{cc}{\displaystyle \frac{L_{i}d{i}_{L_i}}{dt}}\hfill & {\displaystyle =\frac{v_{in}dT+\left(v_{in}-v_o\right)\left(1-d_t\right)T}{T}}\hfill \\ {\displaystyle \frac{C_{i}d{v}_{C_i}}{dt}}\hfill & {\displaystyle =\frac{\left(i_{L_i}-i_o\right)\left(1-d_t\right)T}{T}}\hfill \end{array}$$

(32)

Superimpose the disturbance on the voltage and current parameters of (32) as follows.

$$\begin{array}{cc}{i}_{L_i}\hfill & =I_{L_i}+{\widehat{i}}_{L_i}\hfill \\ i_o\hfill & =I_o+{\widehat{i}}_o\hfill \\ v_{in}\hfill & =V_{in}+{\widehat{v}}_{in}\hfill \\ v_o\hfill & =V_o+{\widehat{v}}_o\hfill \\ d_t\hfill & =D+{\widehat{d}}_t\hfill \end{array}$$

(33)

Therefore, (32) can be expressed as follows,

$$\begin{array}{cc}{\displaystyle \frac{L_{i}d\left(I_{L_i}+{\widehat{i}}_{L_i}\right)}{dt}}\hfill & =-V_o\left(1-D\right)+V_{in}-{\widehat{v}}_o\left(1-D-{\widehat{d}}_t\right)+{\widehat{v}}_{in}-{\widehat{v}}_o{\widehat{d}}_t\hfill \\ {\displaystyle \frac{C_{i}d\left(V_{C_i}+{\widehat{v}}_{C_i}\right)}{dt}}\hfill & =-I_o+I_{L_i}\left(1-D\right)-{\widehat{i}}_o+{\widehat{i}}_{L_i}\left(1-D\right)-I_{L_i}\left(1-D-{\widehat{d}}_t\right)-{\widehat{i}}_{L_i}{\widehat{d}}_t\hfill \end{array}$$

(34)

Separate the DC part and the small-signal part as follows, (34).

$$\begin{array}{cc}{\displaystyle \frac{L_{i}d{I}_{L_i}}{dt}}\hfill & =-V_o\left(1-D\right)+V_{in}\hfill \\ {\displaystyle \frac{L_{i}d{\widehat{i}}_{L_i}}{dt}}\hfill & =-{\widehat{v}}_o\left(1-D-{\widehat{d}}_t\right)+{\widehat{v}}_{in}-{\widehat{v}}_o{\widehat{d}}_t-V_o\left(1-D\right)\hfill \\ {\displaystyle \frac{C_{i}d{V}_{C_i}}{dt}}\hfill & {\displaystyle =-I_o+I_{L_i}\left(1-D\right)}\hfill \\ {\displaystyle \frac{C_{i}d{\widehat{V}}_{C_i}}{dt}}\hfill & =-{\widehat{i}}_o+{\widehat{i}}_{L_i}\left(1-D\right)-I_{L_i}{\widehat{d}}_t-{\widehat{i}}_{L_i}{\widehat{d}}_t\hfill \end{array}$$

(35)

To conduct steady-state analysis for the SS-NS-ZN-HGBC, the differential term of the DC part should be set as zero. In steady state, the relationship between different stages of voltage or current in N-stage can be calculated.

$$\begin{array}{cc}{V}_o\hfill & {\displaystyle =\frac{V_{in}}{1-D}}\hfill \\ I_{in}\hfill & {\displaystyle =\frac{I_o}{1-D}}\hfill \end{array}$$

(36)

In the SS-NS-ZN-HGBC, when i is different, the values of $v_{in}$, $v_o$ and $i_o$ are shown in Table 2.

Table 2. The $v_{in}$, $v_o$ and $i_o$ in the SS-NS-ZN-HGBC.

i	${\mathit{v}}_{\mathbf{in}}$	${\mathit{v}}_{\mathit{o}}$	${\mathit{i}}_{\mathit{o}}$
1	$v_s$	$v_{C_1}$	$i_{L_2}$
$1<i<n$	$v_{C_{i-1}}$	$v_{C_i}$	$i_{L_{i+1}}$
n	$v_{C_{n-1}}$	$v_{C_n}$	$\frac{v_{\mathrm{out}}}{R}$

Inserting the corresponding data in Table 2 into (35), we obtain

$$\begin{array}{cc}{\displaystyle \frac{L_{1}d{\widehat{i}}_{L_1}}{dt}}\hfill & =-{\widehat{v}}_{C_1}\left(1-D\right)+{\widehat{v}}_s+V_{C_1}{\widehat{d}}_t\hfill \\ {\displaystyle \frac{C_{1}d{\widehat{v}}_{C_1}}{dt}}\hfill & =-{\widehat{i}}_{L_2}+{\widehat{i}}_{L_1}\left(1-D\right)-I_{L_1}{\widehat{d}}_t\hfill \\ \hfill & ⋮\hfill \\ {\displaystyle \frac{L_{i}d{\widehat{i}}_{L_i}}{dt}}\hfill & =-{\widehat{v}}_{C_i}\left(1-D\right)+{\widehat{v}}_{C_{i-1}}+V_{C_i}{\widehat{d}}_t\hfill \\ {\displaystyle \frac{C_{i}d{\widehat{v}}_{C_i}}{dt}}\hfill & =-{\widehat{i}}_{L_{i+1}}+{\widehat{i}}_{L_i}\left(1-D\right)-I_{L_i}{\widehat{d}}_t\hfill \\ \hfill & ⋮\hfill \\ {\displaystyle \frac{L_{n}d{\widehat{i}}_{L_n}}{dt}}\hfill & =-{\widehat{v}}_{\mathrm{out}}\left(1-D\right)+{\widehat{v}}_{C_{n-1}}+V_{\mathrm{out}}{\widehat{d}}_t\hfill \\ {\displaystyle \frac{C_{n}d{\widehat{v}}_{\mathrm{out}}}{dt}}\hfill & {\displaystyle =-\frac{{\widehat{v}}_{\mathrm{out}}}{R}+{\widehat{i}}_{L_n}\left(1-D\right)-I_{L_n}{\widehat{d}}_t}\hfill \end{array}$$

(37)

Equation (37) is too complex, so the state space equation is introduced as follows,

$$\begin{array}{cc}\dot{x}& =Ax+Bu\\ y& =Cx+Du\end{array}$$

(38)

$$\begin{array}{c}\left(\begin{array}{c}\frac{d{\widehat{i}}_{L_1}}{dt}\\ \frac{d{\widehat{v}}_{C_1}}{dt}\\ ⋮\\ \frac{d{\widehat{i}}_{L_i}}{dt}\\ \frac{d{\widehat{v}}_{C_i}}{dt}\\ ⋮\\ \frac{d{\widehat{i}}_{L_n}}{dt}\\ \frac{d{\widehat{v}}_{C_n}}{dt}\end{array}\right)=\left(\begin{array}{ccccccccccccccc}0& \frac{D-1}{L_1}& 0& 0& 0& & & & & \cdots & & & & 0& \\ \frac{1-D}{C_1}& 0& \frac{-1}{C_1}& 0& 0& & & & & \cdots & & & & 0& \\ ⋮& ⋮& ⋮& ⋮& ⋮& & & & & \cdots & & & & ⋮& \\ 0& 0& 0& 0& 0& \cdots & \frac{1}{L_i}& 0& \frac{D-1}{L_i}& 0& & & \cdots & 0& \\ 0& 0& 0& 0& 0& \cdots & 0& \frac{1-D}{C_i}& 0& \frac{-1}{C_i}& & & \cdots & 0& \\ ⋮& ⋮& ⋮& ⋮& ⋮& \cdots & ⋮& ⋮& ⋮& ⋮& & & \cdots & ⋮& \\ 0& 0& 0& 0& 0& \cdots & 0& 0& 0& 0& \cdots & \frac{1}{L_n}& 0& \frac{D-1}{L_n}& \\ 0& 0& 0& 0& 0& \cdots & 0& 0& 0& 0& \cdots & 0& \frac{1-D}{C_n}& \frac{-1}{C_{n}R}& \end{array}\right)\left(\begin{array}{c}{\widehat{i}}_{L_1}\\ {\widehat{v}}_{C_1}\\ ⋮\\ {\widehat{i}}_{L_i}\\ {\widehat{v}}_{C_i}\\ ⋮\\ {\widehat{i}}_{L_n}\\ {\widehat{v}}_{C_n}\end{array}\right)+\left(\begin{array}{cc}\frac{Vs}{L_1\left(1-D\right)}& 1\\ \frac{-Vs}{R{C}_1{\left(1-D\right)}^{2n}}& 0\\ ⋮& ⋮\\ \frac{Vs}{L_i{\left(1-D\right)}^i}& 0\\ \frac{-Vs}{R{C}_i{\left(1-D\right)}^{2n-i+1}}& 0\\ ⋮& ⋮\\ \frac{Vs}{L_n{\left(1-D\right)}^n}& 0\\ \frac{-Vs}{R{C}_n{\left(1-D\right)}^{n+1}}& 0\end{array}\right)\left(\begin{array}{c}{\widehat{d}}_t\\ {\widehat{v}}_s\end{array}\right)\\ y=\left(0,0,\cdots ,1\right)x\end{array}$$

(39)

Perform Laplace transform on (38):

$$\left.\begin{array}{cc}X\left(s\right)& ={\left(sI-A\right)}^{-1}BU\left(s\right)\\ Y\left(s\right)& =CX\left(s\right)+DU\left(s\right)\end{array}\right\}$$

(40)

According to (40), the relationship between ${\widehat{d}}_t$ and ${\widehat{v}}_{C_i}$ or ${\widehat{i}}_{L_i}$ in a complex domain can be calculated.

$$\begin{array}{c}{\displaystyle W_{ux}\left(s\right)=\frac{X\left(s\right)}{U\left(s\right)}={\left(sI-A\right)}^{-1}BU\left(s\right)}\\ {\displaystyle \frac{{\widehat{v}}_{C_i}\left(s\right)}{{\widehat{d}}_t\left(s\right)}=W_{1\left(2i\right)}\left(s\right),\frac{{\widehat{i}}_{L_i}\left(s\right)}{{\widehat{d}}_t\left(s\right)}=W_{1\left(2i-1\right)}\left(s\right)}\end{array}$$

(41)

According to (40), the relationship between ${\widehat{v}}_{\mathrm{out}}$ and ${\widehat{d}}_t$ or ${\widehat{v}}_s$ in a complex domain can be calculated.

$$\begin{array}{c}{\displaystyle W_{uy}\left(s\right)=\frac{Y\left(s\right)}{U\left(s\right)}=C{\left(sI-A\right)}^{-1}BU\left(s\right)+D}\\ {\displaystyle \frac{{\widehat{v}}_{\mathrm{out}}\left(s\right)}{{\widehat{d}}_t\left(s\right)}=W_{1\left(2n\right)}\left(s\right),\frac{{\widehat{v}}_{\mathrm{out}}\left(s\right)}{{\widehat{v}}_s\left(s\right)}=W_{2\left(2n\right)}\left(s\right)}\end{array}$$

(42)

After calculation, the general form of $\frac{{\widehat{v}}_{\mathrm{out}}\left(s\right)}{{\widehat{d}}_t\left(s\right)}$ is shown below.

$$G\left(s\right)=\frac{{\widehat{v}}_{\mathrm{out}}\left(s\right)}{{\widehat{d}}_t\left(s\right)}=\frac{a_{2n-1}{S}^{2n-1}+a_{2n-2}{S}^{2n-2}+\cdots +a_{1}S+a_0}{b_{2n}{S}^{2n}+b_{2n-1}{S}^{2n-1}+\cdots +b_{1}S+b_0}$$

(43)

The coefficients $a_{2n-1},a_{2n},\cdots ,a_0$ and $b_{2n},b_{2n-1},\cdots ,b_0$ can be calculated in MATLAB. Bode diagrams, concerning two-stage, three-stage, four-stage and five-stage Z-network high-gain boost circuits are plotted by MATLAB as shown in Figure 5.

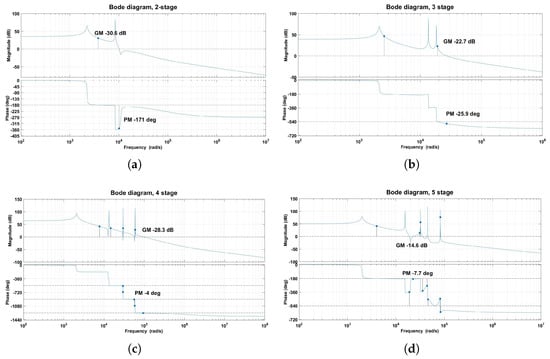
Figure 5. Bode diagram of the single-switch N-stage Z-network high-gain boost converter: (a) 2-stage, GM −30.6 dB, PM −171 deg; (b) 3-stage, GM −22.7 dB, PM −25.9 deg; (c) 4-stage, GM −28.3 dB, PM −4 deg; (d) 5-stage, GM −14.6 dB, PM −7.7 deg.

It can be seen from the figures that as the number of Z-networks increases, the number of resonance peaks in an amplitude frequency characteristic diagram will also increase, but these resonance peaks are relatively concentrated, which lead a sharp phase drop in the phase-frequency characteristic figure.

2.3.2. Feedback Compensation Design

The appropriate compensation circuit can make the system more stable and reliable. Common compensation circuits, such as PI correction, PID control, double loop control and so on, all have their own advantages.

Without considering the current control, PI control is simple and efficient. It can basically achieve more accurate output, which shows in Figure 6. It processes the input signals actual output voltage $V_{out}$ and ideal output voltage $V_R$, and then outputs the signal a, which adjusts the switching frequency of the switch transistor Q in order to minimize the difference between $V_{out}$ and $V_R$.

Figure 6. Control design of duty ratio adjustment circuit.

The relationship between the output $V_{k_1}$ of the error amplifier and its input is shown in (44), where A is the amplification coefficient.

$$V_{k_1}=A\left(V_{\mathrm{out}}-V_R\right)$$

(44)

The relationship between the output $V_k$ of PI regulator and its input is shown in (45), where $K_i$ and $K_p$ are the coefficients depending on the circuit structure.

$$V_{k_2}=K_p{V}_{k_1}+K_i\int V_{k_1}dt$$

(45)

The voltage comparator compares $V_{K_2}$ with a sawtooth wave to output a PWM wave with an adjusted duty cycle. Then, this PWM wave controls the on and off switch through the switch transistor drive circuit to change the output voltage.

We perform small-signal analysis and Laplace transform on it in as follows.

$${\widehat{v}}_{k_2}=A{K}_p{\widehat{v}}_{\mathrm{out}}+K_i\int {\widehat{v}}_{\mathrm{out}}dt$$

(46)

$${\widehat{v}}_{k_2}\left(s\right)=A{K}_p{\widehat{v}}_{\mathrm{out}}\left(s\right)+\frac{K_i{\widehat{v}}_{\mathrm{out}}\left(s\right)}{s}$$

(47)

The process of $V_{k_2}$ and sawtooth wave generating PWM through the comparator is expressed by $\frac{1}{V_d}$ in the transfer function, where $V_d$ is the peak value of the sawtooth wave. Therefore, the transfer function of this feedback compensation circuit $C\left(s\right)$ can be expressed as follows,

$$C\left(s\right)=\frac{A{K}_p+\frac{K_i}{s}}{V_d}$$

(48)

After the compensation, the amplitude of the resonance peak becomes smaller, the amplitude margin and phase margin are sufficient and the system is stable. PI control can meet the requirements of stable operation of the system. For better steady-state performance, other more complex control circuits can be introduced, such as a single zero two-pole compensation circuit and a peak current compensation circuit [40].

3. Steady-State Performance Analysis

3.1. Analysis of Voltage Stress and Current Stress

When the switch is turned off, the voltage stress can be calculated.

$$\begin{array}{cc}\mathrm{For}\mathrm{Switch}:\hfill & V_{S_{\mathrm{stress}}}=V_{\mathrm{out}}\hfill \\ \mathrm{For}{D}_1,D_3\dots \dots D_{2n-1}:\hfill & V_{D_{i\mathrm{stress}}}=V_{C_i}\hfill \\ \mathrm{For}{D}_2,D_4\dots \dots D_{2n-2}:\hfill & V_{D_{i\mathrm{stress}}}=V_{\mathrm{out}}-V_{C_i}\hfill \end{array}$$

(49)

When the switch is turned on, the current stress can be calculated.

$$\begin{array}{cc}\mathrm{For}\mathrm{Switch}:\hfill & I_{S_{\mathrm{stress}}}=\sum _{i=1}^n{I}_{L_i}\hfill \\ \mathrm{For}{D}_1,D_3\dots \dots D_{2n-1}:\hfill & I_{D_{\mathrm{stress}}}=I_{L_i}\hfill \\ \mathrm{For}{D}_2,D_4\dots \dots D_{2n-2}:\hfill & I_{D_{\mathrm{stress}}}=I_{L_i}\hfill \end{array}$$

(50)

Set D a fixed value of 0.35, and calculate $V_{D_{i\mathrm{stress}}}$ and $I_{D_{i\mathrm{stress}}}$ when $n=2,n=3,n=4,$$n=5$. As shown in Figure 7a, we set $V_s$ a fixed value of 10 V to observe that $V_{D_{i\mathrm{stress}}}$, $D_{2n-1}$ and $D_2$ have the first and second largest voltage stress, respectively. As shown in Figure 7b, we set $I_{out}$ a fixed value of 1 A to observe that $I_{D_{i\mathrm{stress}}}$, $D_1$ and $D_2$ have the largest current stress.

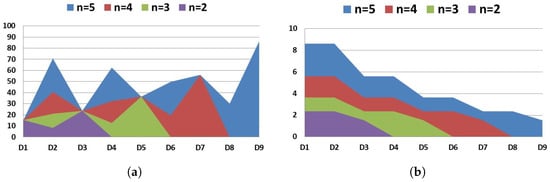
Figure 7. The value of $V_{D_{i\mathrm{stress}}}$ and $I_{D_{i\mathrm{stress}}}$ when $D=0.35$: (a) $V_{D_{i\mathrm{stress}}}-D_i$, $V_s=10$ V; (b) $I_{D_{i\mathrm{stress}}}-D_i$, $I_{\mathrm{out}}=1$ A.

3.2. Analysis of Efficiency

3.2.1. The Power Loss of Inductor

Calculate the power loss of inductors $P_{L_{i}loss}$.

$$P_{L_{i}loss}={I_{L_i}}^2{R}_{L_i}={\left(\frac{V_s}{{\left(1-D\right)}^{2n-i+1}R}\right)}^2{R}_{L_i}$$

(51)

Calculate total power loss of inductors $P_{Lloss}$.

$$P_{Lloss}=\sum _{i=1}^n{P}_{L_{i}loss}=\frac{{V_s}^2}{R^2}\sum _1^n{R}_{L_i}{\left(\frac{1}{1-D}\right)}^{4n-2i+2}$$

(52)

3.2.2. The Power Loss of Capacitor

According to (9), (10) and (15), the current flowing through the capacitor in stage I and stage II is $I_{C_{i}Stage1}$ and $I_{C_{i}Stage2}$ separately.

$$\begin{array}{c}{\displaystyle I_{C_{i}Stage1}=I_{L_{i+1}}=\frac{V_s}{{\left(1-D\right)}^{2n-i}R}}\hfill \\ {\displaystyle I_{C_{i}Stage2}=I_{L_i}-I_{L_{i+1}}=\frac{V_s}{{\left(1-D\right)}^{2n-i+1}R}-\frac{V_s}{{\left(1-D\right)}^{2n-i}R}}\hfill \end{array}$$

(53)

T is the period of the switching transistor, and the power loss of the capacitor $P_{C_{i}loss}$ can be calculated.

$$\begin{array}{cc}{P}_{C_{i}loss}\hfill & {\displaystyle =\frac{{\int }_0^{DT}{I_{C_{i}Stage1}}^2{R}_{C_i}+{\int }_{DT}^T{I_{C_{i}Stage2}}^2{R}_{C_i}}{T}}\hfill \\ \hfill & {\displaystyle =\frac{R_{C_i}{V_s}^{2}D}{R^2{\left(1-D\right)}^{4n-2i+1}}}\hfill \end{array}$$

(54)

Calculate the total power loss of capacitors $P_{Closs}$.

$$P_{C_{loss}}=\sum _{i=1}^n{P}_{C_{i}loss}=\frac{D{V_s}^2}{R^2}\sum _{i=1}^n{R}_{C_i}{\left(\frac{1}{1-D}\right)}^{4n-2i+1}$$

(55)

3.2.3. Diode Conduction Loss

$V_{D_i}$ is the forward voltage drop of diode $D_i$, and the current flowing through the diode can be approximated as the current of the inductor in (15). The diode conduction loss $P_{D_{i}loss}$ can be calculated.

$$\begin{array}{cc}\mathrm{For}{\mathrm{D}}_2,{\mathrm{D}}_4\dots \dots {\mathrm{D}}_{2\mathrm{n}-2}:\hfill & P_{D_{i}loss}=D{V}_{D_i}{I}_{D_i}=D{V}_{D_i}{I}_{L\frac{i}{2}}\hfill \\ \mathrm{For}{\mathrm{D}}_1,{\mathrm{D}}_3\dots \dots {\mathrm{D}}_{2\mathrm{n}-1}:\hfill & P_{D_{i}loss}=(1-D)V_{D_i}{I}_{D_i}=(1-D)V_{D_i}{I}_{L\frac{i+1}{2}}\hfill \end{array}$$

(56)

Assuming that the same diodes are used in the circuit, the total diode conduction loss $P_{Dloss}$ can be calculated.

$$\begin{array}{cc}{P}_{Dloss}\hfill & =\sum _{i=1}^{2n-1}{P}_{D_{i}loss}=D{V}_D\sum _{i=1}^{n-1}{I}_{L_i}+(1-D)V_D\sum _{i=1}^n{I}_{L_i}=V_D\sum _{i=1}^n{I}_{L_i}-D{V}_D{I}_{L_n}\hfill \\ \hfill & =\frac{V_D{V}_s}{R{\left(1-D\right)}^{n+1}}\left(-D+\sum _{i=1}^n\frac{1}{{\left(1-D\right)}^{n-i}}\right)\hfill \end{array}$$

(57)

3.2.4. Switch Conduction Loss

Here, $r_s$ is the resistance of the switch transistor, and $I_s$ is the current through it, so the switch transistor conduction loss $P_{Sloss}$ is shown in (58)

$$P_{SWloss}=D{R}_{sw}{I}_{sw}^2$$

(58)

Insert (50) into (58).

$$P_{SWloss}=D{R}_{sw}{\left(\sum _{i=1}^n{I}_{L_i}\right)}^2=D{R}_{sw}{\left(\sum _{i=1}^n\frac{V_s}{R{\left(1-D\right)}^{2n-i+1}}\right)}^2=\frac{D{R}_{sw}{V_s}^2}{R^2}\sum _{i=1}^n\frac{1}{{\left(1-D\right)}^{4n-2i+2}}$$

(59)

3.2.5. Efficiency Analysis

Calculate the output power $P_o$ as follows,

$$P_o=\frac{{V_{\mathrm{out}}}^2}{R}=\frac{{V_s}^2}{{\left(1-D\right)}^{2n}R}$$

(60)

Calculate the efficiency $\eta$ of the SS-NS-ZN-HGBC.

$$\eta =\frac{P_o}{P_o+P_{loss}}\times 100\%=\frac{P_o}{P_o+P_{Lloss}+P_{Closs}+P_{Dloss}+P_{Sloss}}\times 100\%$$

(61)

The ratio of power loss of different components to the total loss is shown in Figure 8.

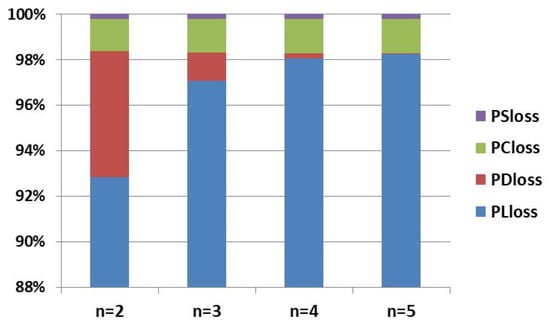
Figure 8. The proportion of each part loss to total loss in different n.

The power loss of inductor $P_{Lloss}$ accounts for the largest proportion of total loss, and the proportion will increase as n increases, while the proportion of diode conduction loss $P_{Dloss}$ decreases as the n increases. $P_{Closs}$ and $P_{Sloss}$ remain unchanged as the n increases.

4. Simulation Verification

4.1. Single-Switch Four-Stage Z-Network High Gain Boost Converter

A single-switch four-stage Z-network high-gain boost converter is taken as an example for simulation analysis, and its operational modes are shown in Figure 9.

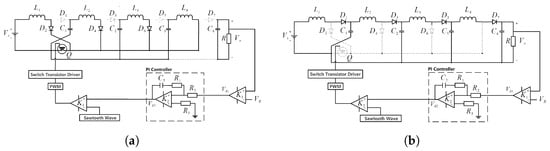
Figure 9. Stage of the single-switch four-stage Z-network high-gain boost converter: (a) stage I; (b) stage II.

According to (44), the gain of the circuit M can be calculated as follows,

$$M=\frac{V_{\mathrm{out}}}{V_{\mathrm{s}}}={\left(\frac{1}{1-D}\right)}^4$$

(62)

4.2. Simulation Studies and Result Analysis

According to Equations (20) and (21), the values of the circuit elements of a single-switch four-stage Z-network high-gain boost circuit can be calculated and are shown in Table 3.

Table 3. Circuit parameters and number of components.

Components	Critical Value	Parameters	Components	Parameters
Inductor $L_1$	72 $\mathsf{\mu }$H	100 $\mathsf{\mu }$H	Capacitor $C_1$	47 $\mathsf{\mu }$F
Inductor $L_2$	170 $\mathsf{\mu }$H	220 $\mathsf{\mu }$H	Capacitor $C_2$	22 $\mathsf{\mu }$F
Inductor $L_3$	403 $\mathsf{\mu }$H	1 mH	Capacitor $C_3$	2.2 $\mathsf{\mu }$F
Inductor $L_4$	2.7 mH	3.3 mH	Capacitor $C_4$	470 $\mathsf{\mu }$F
DC Voltage Source	/	12 V	Capacitor $C_5$	12 $\mathsf{\mu }$F
Resistor R	/	800 $\mathrm{\Omega }$	Resistor $R_1$	2 $\mathrm{\Omega }$
Resistor $R_2$	/	2500 $\mathrm{\Omega }$	Resistor $R_3$	1000 $\mathrm{\Omega }$

When the input voltage is 12 V, the duty cycle ratio is 0.35, and the switching frequency is 62,000 Hz, according to (62). The theoretical output voltage $V_{\mathrm{out}1}$ is 67.2 V. Considering the voltage drop of the diode and the resistance of the inductor, according to (62), the theoretical output voltage $V_{\mathrm{out}2}$ is 59.4 V.

PSIM is an electronic simulation software. We build and simulated a single-switch four-stage Z-network high-gain boost trcuit in PSIM, and the results are shown in Figure 10. The simulation result is consistent with the theoretical value.

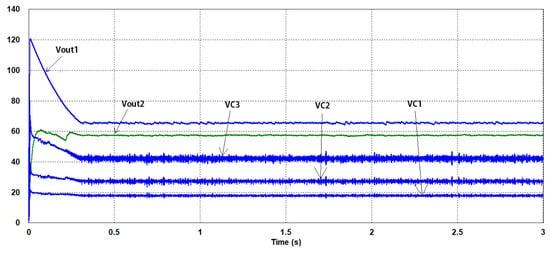
Figure 10. Capacitor voltage output in PSIM.

According to (49) and (50), $V_{D_7}$ and $V_{D_2}$ have larger voltage stresses compared with other diodes theoretically, and $D_2$ has the largest current stress. The current and voltage waves of $D_2$,$D_7$ and switch in PSIM are shown in Figure 11.

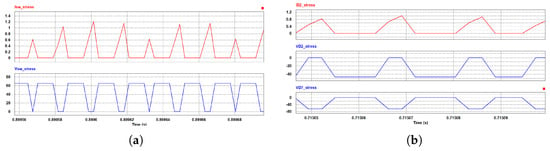
Figure 11. The voltage stress and current stress of important components: (a) the stress waveforms of switch Q; (b) the stress waveforms of $D_2$ and $D_7$.

5. Experimental Studies

To further verify the proposed method, an experimental prototype was built, and circuit parameters and the number of components are depicted in Table 4.

Table 4. Circuit parameters and number of components.

Components	Parameters	Components	Parameters
Inductor $L_1$	22 $\mathsf{\mu }$H	Diode $D_1$	1.05 V
Inductor $L_2$	33 $\mathsf{\mu }$H	Diode $D_2$	1.05 V
Inductor $L_3$	33 $\mathsf{\mu }$H	Diode $D_3$	1.05 V
Inductor $L_4$	33 $\mathsf{\mu }$H	Diode $D_4$	1.05 V
Capacitor $C_1$	1 $\mathsf{\mu }$F	Diode $D_5$	1.05 V
Capacitor $C_2$	10 $\mathsf{\mu }$F	Diode $D_6$	1.05 V
Capacitor $C_3$	15 $\mathsf{\mu }$F	Diode $D_7$	1.05 V
Capacitor $C_4$	220 $\mathsf{\mu }$F	Switch	IRFB4115PBF
Resistance R	1000 $\mathrm{\Omega }$	DC Voltage Source	4 V

The prototype consists of the SS-NS-ZN-HGBC, a PI control circuit, a DC power supply, a mobile charging power supply and a driver circuit. The control circuit is implemented in Arduino Uno. The experimental environment is shown in Figure 12.

Figure 12. Experimental environment.

The duty ratio D is 0.25, and the switching frequency f is 62,000 Hz. The Arduino Uno converts the input voltage (0–5 V) to the digital signal (0–255), and then outputs the PWM control signal after the PI control program proceeding. The $K_p$ and $K_i$ of the PI controller used in the experiment was 0.001 and 1.1, respectively. The experimental result waveforms are shown in Figure 13. The waveforms of the input voltage $V_{\mathrm{s}}$, output voltage $V_{\mathrm{out}}$ and drive signal PWM in open loop are shown in Figure 13a. As shown in Figure 13b, in the experimental results, $V_{\mathrm{out}}$ is close to the theoretical result of 12.64 V.

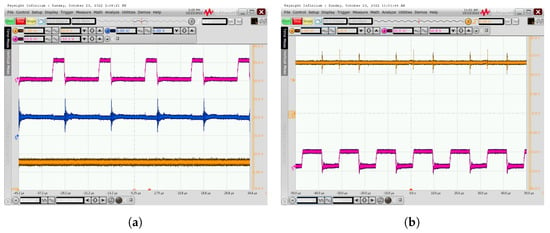
Figure 13. Experimental result waveforms: (a) PWM, $V_{\mathrm{s}}$, $V_{\mathrm{out}}$ in open loop; (b) output voltage with PI control.

Table 5 shows the output voltage $V_{\mathrm{out}}$ in different methods when input voltage $V_s$ is 4 V and the duty ratio D is 0.25. The voltage gain M of the quadratic boost circuit with coupled inductors $\left(M=\frac{2\left(1+N\right)}{\left(1-D\right)}\right)$ is related to its turns ratio N of the coupled inductors, which varies in different cases. This is not shown in Table 5.

Table 5. Circuit parameters and number of components.

Method	Voltage Gain	Output Voltage
Boost circuit	$\frac{1}{\left(1-D\right)}$	5.33
Quadratic boost circuit	$\frac{1}{{\left(1-D\right)}^2}$	7.11
Interlaced parallel converter	$\frac{1}{\left(1-D\right)}$	5.33
Quadratic boost circuit with switch-inductors	$\frac{\left(1+D\right)}{\left(1-D\right)}$	6.67
Quadratic boost circuit with switch-capacitors	$\frac{1}{\left(1-D\right)}$	10.67
SS-NS-ZN-HGBC ($n=4$)	$\frac{2}{{\left(1-D\right)}^4}$	12.64

Compared with other methods, the SS-NS-ZN-HGBC has a much higher output voltage with the same input voltage and duty ratio because of its high voltage gain. The experimental results are consistent with the simulation results and theoretical analysis, which verify the effectiveness of the proposed design.

6. Conclusions

This study has proposed a class of general single-switch N-stage Z-network high-gain converters. Small signal modeling and stability analysis have been conducted for the converter. Simulations and prototype experiments were carried out on a 4-stage Z-network boost converter as an example, with a closed-loop control system. The simulation and experimental results agree well with the theoretical analysis, which verifies the effectiveness of the design approach. Compared with other methods mentioned, the SS-NS-ZN-HGBC has a higher voltage gain with a small duty ratio and only one switch. Its structure is simple and easy to expand.

Therefore, the proposed SS-NS-ZN-HGBC can be used for various applications that require high DC voltages, e.g., the etching process in chip manufacturing, auxiliary power supplies for electrical vehicles, and medical X-ray equipment. However, although the SS-NS-ZN-HGBC has a very high voltage gain, its voltage stress is also relatively high. In future research, some auxiliary circuits can be designed to reduce the voltage stress of the switch and diodes for wide practical applications.