A New Mixture Differential Cryptanalysis on Round-Reduced AES

Abstract

AES is the most widely used secret-key cryptosystem in industry, and determining the security of AES is a central problem in cryptanalysis. The mixture differential property proposed in Eurocrypt 2017 is an essential property to setup state-of-the-art key recovery attacks on some round-reduced versions of AES. In this paper, we exploit mixture differential properties that are automatically deduced from a mixed integer linear programming (MILP)-based model to extend key recovery attacks on AES. Specifically, we modify the MILP model toolkit to produce all mixture trails explicitly and test a 5-round secret-key mixture differential distinguisher on small-scale AES experimentally. Moreover, we utilize this distinguisher to do a key recovery attack on 6-round AES-128 that outperforms previous work in the same fashion. We also for the first time utilize a 6-round AES secret-key distinguisher to set up a key recovery attack on 7-round AES-192. This work is a new yet simple cryptanalysis on AES by exploiting mixture differential properties.

1. Introduction

Block ciphers, as a category of private key cryptographic algorithms, are the workhorse of cryptography for ensuring confidentiality due to their high efficiency compared with public key cryptographic algorithms. The security of cryptographic algorithms is analyzed from both theoretical and practical points of view. Analysis from the theoretical point of view is referred to as cryptanalysis, where an attacker can only access plaintexts and ciphertexts of the target algorithm. Cryptanalysis aims to find out flaws in the cipher design, which can give a more accurate security evaluation of the target cipher. In this paper, we focus on cryptanalysis of the most widely used standard block cipher, AES [1], to try to find out special statistic properties reflected only in plaintexts and ciphertexts to recover the secret key from a theoretical point of view. In addition to theoretical cryptanalysis, analysis from a practical point of view (e.g., differential power analysis [2] or differential fault analysis [3]) analyzes the security of the implementation of the target cipher, which is beyond the scope of this paper.

A key recovery attack on AES comes in two steps: (1) finding out the property that can make a distinguisher and (2) designing the key recovery attack algorithm based on the found distinguisher to recover the secret key. Distinguishing a block cipher under a secret key from a random permutation is a devastating violation of security. Technically, the distinguishers are properties that hold on (even reduced round) block ciphers with a probability significantly different from that for random permutations. After a distinguisher is found, the divide-and-conquer framework can be used to setup a key recovery attack. However, the key recovery procedure is not always so obvious because the data/time/memory complexities of the whole process will probably exceed the complexities of brute-force methods that are standard measures to compare against. The state-of-the-art key recovery attacks on AES exploit a variety of statistical properties that can be used as a distinguisher, including the mixture differential properties revealed in [4] by an automatic searching method. Whether this kind of distinguisher can be used to setup key recovery attacks on AES remains unclear. In this paper, we answer this question by providing effective key recovery attacks based on the mixture differential distinguishers.

1.1. Related Work

A variety of properties of AES have been investigated to do key recovery attacks. The collision attack [5] revealed that there exist collisions between some partial byte-oriented functions induced by the AES structure, and thus a 4-round distinguisher can be constructed that in turn enables attacks on 7-round AES with any key length. Differential cryptanalysis [6] provides the basic concepts of many cryptanalysis methods, including the impossible differential cryptanalysis [7]. As for key recovery attacks on AES, the impossible differential cryptanalysis [8] put a 4-round impossible differential distinguisher in the middle to launch a 6-round key recovery attack. Meet-in-the-Middle (MITM) attack [9] utilized the 4-round property that, for a special plaintext set called $\delta$-set, the number of possible values for one byte in the ciphertext set after four-round encryption is very limited. With additional techniques such as data/time/memory trade-off and differential enumeration, key recovery attack complexities for 6-round AES-128 and up to 8-round AES-192 and AES-256 are modified from that in a previous MITM attack [10]. The Square attack was presented in the design of AES [11], and shows that for a $\delta$-set of plaintexts, the XOR sum of the intermediate states after three rounds of encryption is equal to zero. A “partial sum” technique has been introduced [12], which substantially reduces the work factor of the dedicated Square attack. The “partial sum” method in the Square attack can be improved by analyzing more information per $\delta$-set [13], and thus the time complexity can be significantly reduced.

In Eurocrypt 2017, Grassi et al. [14] discovered the first secret-key distinguisher for 5-round AES. In FSE/ToSC 2019, this property is further refined as “mixture-differential cryptanalysis” [15]. The main idea is, given that the 4-round ciphertexts from a chosen plaintext pair lie in a particular subspace, the probability is 1 that a specially constructed pair has the same property, while this is not the case for the random permutation. This 4-round property is modified to 5-round and a 6-round key recovery attack is launched by prepending one round before the distinguisher [16]. Note that this is the first time that a 5-round distinguisher can be used to set up key recovery attacks. The mixture differential property was used by Bar-On et al. [17,18] to launch key-recovery attacks on up to 7-round AES-192 and -256 with practical data and memory complexities. Meanwhile, the record for a 5-round key recovery attack, which cost $2^{16.5}$ encryption/decryption [19], is also highly related to such mixture differential structures.

The mixture differential property has been investigated from diverse perspectives to extend to more block ciphers [20] and to setup distinguishers with more rounds [16]. However, all these properties are deduced by scrutinizing structures of AES-like constructions manually. Not until recently has a Mixed Integer Linear Programming (MILP)-based method been proposed to search for mixture differential properties automatically [4]. With this method, given a description of an aligned block cipher, whether in SPN or Feistel structure, finding the mixture differential distinguishers is converted to an MILP problem that can be solved by off-the-shelf constraint programming problem solvers (e.g., Gurobi [21]), which is the paradigm for the automatic symmetric-key cryptanalysis that has been gaining popularity in recent years [22,23,24,25,26,27]. The automatically deduced mixture differential distinguishers for AES cover up to 6 rounds and have been used to perform distinguishing attacks. However, no key recovery attacks have been provided based on distinguishers on AES. Furthermore, no previous work has ever directly applied a 6-round distinguisher to perform key recovery attacks.

1.2. Our Contribution

In this paper, we answer the question of whether the automatically deduced mixture differential distinguishers can be used to do key recovery attacks. The contributions are summarized below.

• We verify the 5-round mixture differential distinguisher deduced from the MILP method experimentally on small-scale AES practically. With lookup-table-based implementation, the verification efficiency is improved about 20 times. Compared with the textbook implementation, the verification time with $2^{30}$ 5-round encryption is decreased from more than 20 min to about 1 min when running on 32 parallel threads with an AMD Ryzen Threadripper 3970X Processor. We also refined the MILP-based automatic tool for searching for mixture differential distinguishers to illustrate all trails to form the distinguisher.
• In the key recovery aspect, we give a 6-round key recovery attack on AES-128 by directly exploiting the automatically deduced 5-round secret key distinguisher with data/time complexity reduced to $2^{38}/2^{83.36}/2^{33}$. The previous best attack in the same fashion was by Grassi [16], with data/time/memory complexity being $2^{72.8}/2^{105}/2^{33}$. Our methods present a dramatic decrease in data and time complexity with the same memory complexity.
• Further, a novel 7-round key recovery attack on AES-192 that directly exploits a 6-round secret-key distinguisher is also presented. Though this attack has higher complexity than some previous ones, this is the first direct utilization of a 6-round secret-key distinguisher to do key recovery attacks on 7-round AES with complexity lower than a brute-force attack.

All our source codes are provided in the repository https://github.com/qiaokexin/mixture-differential-for-AES.git (accessed on 10 October 2022).

This paper is organized as follows. In Section 2, after a short description of AES, we introduce metrics for evaluating cryptanalysis methods and mixture differential distinguishers. In Section 3, we rewrite the automatic mixture differential searching model and verify the 5-round distinguisher on small-scale AES practically and also illustrate the 6-round mixture characteristics concretely for verification. In Section 4, key recovery attacks on 6-round AES-128 and 7-round AES-192 are given. The paper is summarized in Section 5.

2. Preliminary

We inherit some notations from [4,18].

2.1. A Brief Description of AES

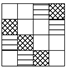
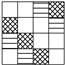
AES [1] block cipher takes in a 128-bit block organized as a $4\times 4$ matrix on $GF\left(2^8\right)$ and a 128-, 192- or 256-bit master key. Denote the three versions by AES-128, AES-192 and AES-256 respectively. The number of rounds for AES-128, AES-192 and AES-256 are 10, 12 and 14, respectively. The key schedules for generating subkeys in each round for the three versions are different in detail but follow the same framework. The encryption operations in each round for all versions are identical. The input state is denoted by $x_{-1}$. After XORing a whiten key $k_{-1}$, the state iterates on round functions 10, 12 and 14 times, respectively. The whitening key is the first 128 bits of the master key. The state before the i-th round is denoted by $x_i$. In the i-th round, the state goes through the following four steps (Figure 1):

Figure 1. AES round function.

• SubBytes ($\mathsf{SB}$): each byte of $x_i$ is substituted by another byte according to an invertible 8-bit $\mathsf{Sbox}$ to get state $x_i^{\prime }$. The substitution is determined by a table called Sbox, which is a permutation of 8-bit elements. The Sbox and inverse Sbox are given in Appendix A. An inverse Sbox is used in decryption, and this step is denoted by InvSubBytes.
• ShiftRows ($\mathsf{SR}$): the j-th ($j=0,\cdots ,3$) row of state $x_i^{\prime }$ is cyclicly shifted by j bytes to the left to get state $x_i^{″}$. Cyclic shifting to the right with the same offsets is applied in decryption, and this step is denoted by InvShiftRows.
• MixColumn ($\mathsf{MC}$): multiply each column of $x_i^{″}$ by a $4\times 4$ MDS (maximum distance separable) matrix over $GF\left(2^8\right)$. The MDS matrix and its inverse are

  $$M=\left(\begin{array}{cccc}2& 3& 1& 1\\ 1& 2& 3& 1\\ 1& 1& 2& 3\\ 3& 1& 1& 2\end{array}\right),\mathrm{and}{M}^{-1}=\left(\begin{array}{cccc}E& B& D& 9\\ 9& E& B& D\\ D& 9& E& B\\ B& D& 9& E\end{array}\right),$$

  where each element in the matrix is an element in $GF\left(2^8\right)$ defined by the irreducible polynomial $x^8+x^4+x^3+x+1$, and multiplication and addition are also performed in this field. Multiplication of $M^{-1}$ on each column is performed in decryption, and this step is denoted by InvMixColumn. The MDS property ensures that the number of non-zero bytes among the input column and output column is no less than 5, except for the all-zero case, i.e., the branch number being 5.
• AddRoundKey ($\mathsf{ARK}$): XORing a 128-bit subkey $k_i$ to the state to get $x_{i+1}$.

Note that in the last round, $\mathsf{MC}$ operation is omitted, and this is also the case for reduced versions in this paper. The key schedule algorithm processes the master key to generate the whiten key and all subkeys. As our attack does not utilize relations among subkeys, we do not show the key schedule here.

The indexes of each byte in a state are in column first order. Use $x_{r,I}$ to denote the bytes of state $x_r$ indicated by I, where I can be a single index or a set of indexes. Use $Col\left(j\right)$ to denote the j-th column of the state and $Col(j_0,\cdots ,j_{l-1})$ for multi-columns. We are interested in diagonals of states, denoted by $x_{i,{\mathsf{SR}}^{-1}\left(Col\left(J\right)\right)}$, and also inversive diagonals, denoted by $x_{i,\mathsf{SR}\left(Col\right(J\left)\right)}$, where J is a column index or consists of several column indexes. Use $\Delta \left(x\right)$ to denote the difference on specific state x. We use $x^{\left(0\right)},x^{\left(1\right)},x^{\left(2\right)},x^{\left(3\right)}$ to denote four states in a quadruple.

A straightforward decryption of AES is done by using the inverses of the steps InvSubBytes, InvShiftRows, InvMixColumns and AddRoundKey and reversing their order. However, an equivalent algorithm for decryption that performs InvSubBytes–InvShiftRows–InvMixColumns–AddRoundKey in each round and omits InvMixColumns in the last round has been anticipated in the AES design. So we can have a decryption algorithm that has the same structure as the encryption, with a change in the key schedule in that we need to apply the InvMixColumns operation to the round keys in the middle rounds. Considering that the distinguishers used in our key recovery attacks are independent of the details of the Sbox and the MixColumn matrix, we can get an equivalent distinguisher on the decryption direction by shifting the patterns on diagonal positions to the anti-diagonal positions due to the shift row differentiations. Therefore, our key recovery attack can be applicable to both encryption and decryption with the same complexities.

AES block cipher by itself is only suitable for encryption or decryption of one block, say a 128-bit string. When processing messages longer than a block, a mode of operation is needed to repeatedly apply AES. Common modes of operation include ECB, CBC, CFB, OFB, CTR, etc. As cryptanalyses on modes of operation are beyond the scope of this work, we do not present them in detail.

2.2. Metrics of Evaluation of Cryptanalysis Methods

Cryptanalysis tries to find non-randomness in the cipher design that can be reflected from plaintexts and ciphertexts without any side-channel information from the execution. Key recovery attacks are the most threatening cryptanalysis method. Technically, the key recovery procedure is a divide-and-conquer process. By appending or prepending extra rounds to the distinguisher, partial key bits involved in the added rounds can be recovered by utilizing the distinguisher property. Then, the non-involved key bits are exhaustively searched. The cost of a key recovery attack is estimated with respect to the following aspects: data complexity, time complexity and memory complexity. Data complexity is measured by the number of queries of encryption oracle by the attacker. Time complexity is measured by the computational cost executed by the attacker offline. The unit is usually the cost of one execution of the encryption algorithm. Memory complexity is the memory required to launch the attack. An effective key recovery attack should have complexities lower than those of a brute-force attack, which is the standard measure to compare against. A brute-force attack has data/time/memory complexity of $1/2^n/1$ (by enumerating all keys) or $1/1/2^n$ (by lookup from a precomputed table), where n is the number of key bits. More basics of cryptanalysis on block ciphers can be found in ([28], Chap. 4). The goal of cryptanalysts is to reduce the complexities of the attack, and one cryptanalysis method outperforms another if its complexity is lower.

2.3. Mixture Differentials

Mixture differential property reflects the byte-wise equality relation among a quadruple of states. There are a total of 15 sorted combinations of four bytes up to pair-wise equality:

$$\begin{array}{cc}& (a,b,b,b),(a,a,b,b),(a,b,a,a),(a,b,b,a),(a,b,c,c),(a,b,b,c),(a,a,b,a),\hfill \\ & (a,b,c,a),(a,a,a,a),(a,b,a,c),(a,b,a,b),(a,b,c,d),(a,a,b,c),(a,a,a,b),\hfill \\ & (a,b,c,b),\hfill \end{array}$$

where different letters indicate different values. We call them quadruple patterns. If the four bytes consist of two same pairs, we call this quadruple a mixture ([18], Def. 1). Quadruple patterns of mixtures include the following cases:

• copy pattern $(a,b,a,b)$, which means the second pair is a copy of the first pair. This pattern is denoted by “c” and shown graphically as .
• exchange pattern $(a,b,b,a)$, which means the second pair is acquired by exchange of the two values in the first pair. This pattern is denoted by “e” and shown graphically as .
• shift pattern $(a,a,b,b)$, which means the second pair is acquired by shifting an inactive pair, denoted by “s” and shown graphically as .
• inactive pattern $(a,a,a,a)$, which consists of four equal bytes. This pattern is denoted by “-” and shown graphically as .

Other quadruple patterns are denoted by “∗” and shown graphically as . Throughout this paper, mixture patterns or mixture differential patterns include these five quadruple patterns. Probability for a random quadruple to have a “c”, “e” or “s” pattern is $2^{-2w}$, and probability to have an inactive pattern is $2^{-3w}$, where w is width of the word.

For aligned block ciphers, the quadruple/mixture patterns on each byte (or nibble for nibble-wise block ciphers) constitute the quadruple/mixture pattern of the full state. In the iterative cryptographic primitives, certain mixture patterns can be deduced with some probability through the iteration. The mixture patterns for states in each round constitute a pattern trail. With fixed input and output mixture patterns, probability on all trails with significantly high probability can be summed up to make a mixture differential distinguisher with higher probability, which resembles the differential hull for classical differential cryptanalysis. If the probability is higher than that of a random permutation, this property can potentially be used for distinguishing attacks or key recovery attacks. We refine the formal definition and proposition for mixture differentials from [4].

Definition  1

((Refined) Mixture Differential). A mixture differential is a pair of quadruple patterns $({\mathbf{P}}_{in},{\mathbf{P}}_{out})$ such that given plaintext quadruples $(P^0,P^1,P^2,P^3)$ conforming ${\mathbf{P}}_{in}$, the ciphertext quadruples $(C^0,C^1,C^2,C^3)$ conform ${\mathbf{P}}_{out}$ with probability p.

We have the following proposition

Proposition 1.

To distinguish an aligned cryptographic permutation from a random one by mixture differentials defined in Definition 1, it is required that for cryptographic permutation, $p>2^{-w(3n_{-}+2(n_{\mathbf{c}}+n_{\mathbf{x}}+n_{\mathbf{s}}))}$ significantly, where w is the width of the word for the cryptographic permutation, and $n_{-},n_{\mathbf{c}},n_{\mathbf{x}},n_{\mathbf{s}}$ are the number of word-wise “-”, “$\mathbf{c}$”, “$\mathbf{x}$” and “$\mathbf{s}$” mixture patterns in the output pattern.

Figure 2 shows a mixture trail on 4-round AES with probability $2^{-32}$ that is utilized in Bar-On et al.’s work [17,18] (they actually consider a cluster of similar distinguishers). Note that for a random ${\mathbb{F}}_2^{128}\to {\mathbb{F}}_2^{128}$ permutation, the probability of having the output mixture pattern given the input mixture pattern is $2^{-64}$.

Figure 2. A 4-round AES mixture differential trail with probability $2^{-32}$. ($\mathsf{ARK}$ layer omitted as it does not influence pattern propagation).

3. Mixture Differential Distinguishers

Though mixture differential cryptanalysis has attracted a lot of attention since its proposed, it was not until recently that it was investigated by using an automatic tool to search for such distinguishers. In [4], an MILP-based automatic tool is developed to search for mixture distinguishers.

3.1. Search for Mixture Differential Distinguishers with MILP Model

The framework of the MILP model firstly uses binary variables to represent the equality between any two states among a quadruple; thus, the mixture pattern is encoded to a 6-bit string for each byte. Then, the mixture patterns propagate through each layer with probabilities that are also encoded as binary strings. The mixture pattern variables and probability variables affect each other by satisfying some linear inequalities. Noting that second-order property—whether the first pair difference equals the second pair difference on a byte—influences the probability of getting a certain mixture pattern; second-order equalities on each byte are also encoded to binary variables, and with some auxiliary variables, the effect on probability is expressed by linear inequalities as well. All 0-1 variables used in the model are summarized as follows.

• ${\mathtt{e}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},\mathtt{s}},\mathtt{ij}\in \mathtt{Ind}={\{}^{\prime }{\mathtt{01}}^{\prime }{,}^{\prime }{\mathtt{02}}^{\prime }{,}^{\prime }{\mathtt{03}}^{\prime }{,}^{\prime }{\mathtt{12}}^{\prime }{,}^{\prime }{\mathtt{13}}^{\prime }{,}^{\prime }{\mathtt{23}}^{\prime }\},\mathtt{s}\in [\mathtt{0},\mathtt{15}]$, mixture pattern encoding variables for the s-th byte in the input state to the r-th round, i.e., $x_{r-1,s}$. We have ${\mathtt{e}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=\mathtt{0}$ iff $x_{r-1,s}^{\left(i\right)}=x_{r-1,s}^{\left(j\right)}$.
• ${\mathtt{deA}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},\mathtt{ij}\in \mathtt{Ind},\mathtt{t}\in [\mathtt{0},\mathtt{3}]$, column-wise mixture pattern encoding variables for the t-th input column for $\mathsf{MC}$ operation in the r-th round. Note that an input column to $\mathsf{MC}$ layer is a diagonal of the input state, i.e., $x_{r-1,{\mathsf{SR}}^{-1}\left(Col\left(t\right)\right)}$. We have ${\mathtt{deA}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},\mathtt{t}}=0$ iff $x_{r-1,{\mathsf{SR}}^{-1}\left(Col\left(t\right)\right)}^{\left(i\right)}=x_{r-1,{\mathsf{SR}}^{-1}\left(Col\left(t\right)\right)}^{\left(j\right)}$.
• ${\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},\mathtt{s}},{\mathtt{A}}_{\mathtt{l}}^{\mathtt{r}-\mathtt{1},\mathtt{s}},\mathtt{s}\in [\mathtt{0},\mathtt{15}]$, probability encoding variables. By considering the first-order differential property, the probability to have some mixture pattern on $x_{r,s}$ is $2^{-w(2{\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}+{\mathtt{A}}_{\mathtt{l}}^{\mathtt{r}-\mathtt{1},\mathtt{s}})}$. For example, for a random input quadruple, the probability of an output byte conforming a “$\mathbf{c}$”, “$\mathbf{s}$” or “$\mathbf{e}$” pattern is $2^{-2w}({\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=1,{\mathtt{A}}_{\mathtt{l}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=0)$, and it is $2^{-3w}({\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=1,{\mathtt{A}}_{\mathtt{l}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=1)$ for a “-” pattern.
• ${\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}$ together with ${\mathtt{A}}_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}},\mathtt{s}\in [\mathtt{0},\mathtt{15}]$. The former indicates whether the second-order differential is 0 for $x_{r-1,s}^{\prime }$, i.e., ${\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=\mathtt{0}$ iff $x_{r-1,s}^{\prime \left(0\right)}\oplus x_{r-1,s}^{\prime \left(1\right)}=x_{r-1,s}^{\prime \left(2\right)}\oplus x_{r-1,s}^{\prime \left(3\right)}$. The latter describes that the assignment of ${\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}$ holds with probability $2^{-w{\mathtt{A}}_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}}$. If the s-th $\mathsf{Sbox}$ is active for both the first pair and the second pair in the quadruple, with probability $2^{-w}$ (${\mathtt{A}}_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=1$) we have ${\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=\mathtt{0}$, or we have ${\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=\mathtt{1}$ with probability 1 (${\mathtt{A}}_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=0$). If the s-th $\mathsf{Sbox}$ is inactive for both pairs, ${\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=\mathtt{0}$ with probability 1 (${\mathtt{A}}_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=0$). If the s-th $\mathsf{Sbox}$ is inactive for only one pair, we have ${\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=\mathtt{1}$ with probability 1 (${\mathtt{A}}_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}=0$).
• ${\mathtt{dop}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},\mathtt{t}\in [\mathtt{0},\mathtt{3}]$, indicates whether second-order differential is 0 on $x_{r-1,Col\left(t\right)}^{″}$. We have ${\mathtt{dop}}^{\mathtt{r}-\mathtt{1},\mathtt{t}}={\vee }_{\mathtt{s}\in {\mathtt{SR}}^{-\mathtt{1}}\left(\mathtt{Col}\left(\mathtt{t}\right)\right)}{\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}$.
• ${\mathtt{lab}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},\mathtt{t}\in [\mathtt{0},\mathtt{3}]$, a dummy variable used as a label. We have ${\mathtt{lab}}^{\mathtt{r}-\mathtt{1},\mathtt{t}}=0\iff {\mathtt{deA}}_{\mathsf{Ind}}=111111$.
• ${\mathtt{A}}_{\mathtt{minus}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}$, number of activity variables reduced considering second-order differential properties. The probability of the mixture pattern trail covering R rounds is estimated as $2^{-{\sum }_{\mathtt{r}=\mathtt{1}}^{\mathtt{R}}{\sum }_{\mathtt{s}=\mathtt{0}}^{\mathtt{15}}(\mathtt{2}{\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}+{\mathtt{A}}_{\mathtt{l}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}+{\mathtt{A}}_{\mathsf{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}---{\mathtt{A}}_{\mathtt{minus}}^{\mathtt{r}-\mathtt{1},\mathtt{s}})}$.

Now we are ready to impose constraints on these variables. The pseudo-code of how the MILP model is built is shown in Algorithm 1, and we refer the readers to [4] for the detailed mechanism of how the inequality templates are generated. For completeness and to enable the readers to reproduce the distinguishers (once produced, deduced distinguishers are easy to be verified experimentally or theoretically, as will be shown later), details of how linear inequalities concerning certain variables are generated by templates are provided in Appendix B. Note that the input pattern and output pattern can be left null and additional variables and constraints need to be added to describe how many activity variables are consumed to have an output pattern for random permutations, which is used as a threshold. By imposing that the objective function is smaller than the threshold, we get an optimization model to deduce input and output patterns to form a distinguisher.

With this model, by solving an optimization problem, the largest probability together with input and output mixture patterns are deduced. Furthermore, given the input and output mixture patterns, by solving an enumeration problem, one can enumerate all mixture pattern trails with the same high probability and sum up the probabilities to estimate the true probability of making a distinguisher.

Two distinguishers are impressive, which we will use in key recovery attacks. Table 1 shows the input and output pattern of the distinguishers, the probability for one trail, the number of trails with the same probability and the total probabilities on AES and on a random permutation. The input mixture patterns of the two distinguishers are the same, which are “inactive” patterns on $x_{0,{\mathsf{SR}}^{-1}\left(Col(0,1)\right)}$, “copy” patterns on $x_{0,{\mathsf{SR}}^{-1}\left(Col\left(2\right)\right)}$ and “exchange” patterns on $x_{0,{\mathsf{SR}}^{-1}\left(Col\left(3\right)\right)}$. Define this pattern to be ${\mathbf{D}}_{in}$. The 5-round distinguisher has “shift” patterns on $x_{4,\mathsf{SR}\left(Col\right(0\left)\right)}^{″}$. Denote it by ${\mathbf{D}}_{out}^{\left\{0\right\}}$. The probability to have ${\mathbf{D}}_{out}^{\left\{0\right\}}$ after 5 full rounds and ${\mathsf{MC}}^{-1}$ of AES is $15\times 2^{-8}=2^{-60.19}$, while it is $2^{-64}$ for random permutations. The 6-round distinguisher has “shift”-type mixture patterns on $x_{5,\mathsf{SR}\left(Col\right(0,1,2\left)\right)}^{″}$. Denote it by ${\mathbf{D}}_{out}^{\{0,1,2\}}$. The probability to have ${\mathbf{D}}_{out}^{\{0,1,2\}}$ after 6 full round and ${\mathsf{MC}}^{-1}$ of AES is $56\times 2^{-8\times 22}=2^{-170.19}$, while it is $2^{-192}$ for random permutations. Source codes for generating these two distinguishers are provided in the repository.

Table 1. Mixture distinguishers covering 5- and 6-round AES.

No.	Rd.	Mix. Pattern for ${\mathit{x}}_0$	Mix. Pattern for ${\mathit{x}}_{\mathbf{Rd}.-1}^{″}$	Single Prob.	#Trails Prob.	AES Prob.	Rand.
1	5			$2^{-64}$	15	$2^{-60.19}$	$2^{-64}$
2	6			$2^{-176}$	56	$2^{-170.19}$	$2^{-192}$

Algorithm 1 MILP model to get the probability of given mixture patterns

1: functionGenerateModel($R,{\mathbf{P}}_{in},{\mathbf{P}}_{out}$)   ▹ Number of rounds, input and output patterns 2:     Index set $\mathtt{Ind}={\{}^{\prime }{\mathtt{01}}^{\prime }{,}^{\prime }{\mathtt{02}}^{\prime }{,}^{\prime }{\mathtt{03}}^{\prime }{,}^{\prime }{\mathtt{12}}^{\prime }{,}^{\prime }{\mathtt{13}}^{\prime }{,}^{\prime }{\mathtt{23}}^{\prime }\}$ 3:     Initialize an MILP model $\mathcal{M}$ 4:     $\mathcal{M}.\mathit{var}\leftarrow {\mathtt{e}}_{\mathtt{ij}}^{\mathtt{0},\mathtt{s}},\mathtt{ij}\in \mathtt{Ind},\mathtt{s}\in [\mathtt{0},\mathtt{15}]$   ▹ mixture pattern encoding variables 5:     for $1\le r\le R$ do 6:         $\mathcal{M}.\mathit{var}\leftarrow {\mathtt{e}}_{\mathtt{ij}}^{\mathtt{r},\mathtt{l}},\mathtt{ij}\in \mathtt{Ind},\mathtt{l}\in [\mathtt{0},\mathtt{15}]$ 7:         $\mathcal{M}.\mathit{con}\leftarrow$ inequalities on ${\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r},\mathtt{l}}$ by Template 1 8:         for $0\le t\le 3$do    ▹ for each column 9:            Prepare input and output coding variables for the t-th column: ${\mathtt{var}}_{\mathtt{Ind}}=[{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{0}}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{1}}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{2}}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{3}}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r},{\mathtt{out}}_{\mathtt{0}}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r},{\mathtt{out}}_{\mathtt{1}}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r},{\mathtt{out}}_{\mathtt{2}}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r},{\mathtt{out}}_{\mathtt{3}}}]$ 10:            $\mathcal{M}.\mathit{con}\leftarrow$ inequalities on ${\mathtt{var}}_{\mathtt{ij}}$ by Template 2 for each $\mathtt{ij}\in \mathtt{Ind}$   ▹ branch number=5 11:            $\mathcal{M}.\mathit{var}\leftarrow {\mathtt{deA}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},\mathtt{ij}\in \mathtt{Ind}$   ▹ column-wise mixture pattern encoding variables 12:            $\mathcal{M}.\mathit{con}\leftarrow {\mathtt{deA}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},\mathtt{t}}={\mathtt{e}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{0}}}\vee {\mathtt{e}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{1}}}\vee {\mathtt{e}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{2}}}\vee {\mathtt{e}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{3}}},\mathtt{ij}\in \mathtt{Ind}$ 13:            $\mathcal{M}.\mathit{var}\leftarrow {\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},{\mathtt{out}}_{\mathtt{j}}},{\mathtt{A}}_{\mathtt{l}}^{\mathtt{r}-\mathtt{1},{\mathtt{out}}_{\mathtt{j}}},\mathtt{j}\in [\mathtt{0},\mathtt{3}]$   ▹ variables corresponding to probability    /* Constraints concerning first-order property */ 14:            for $0\le s\le 3$ do 15:                $\mathcal{M}.\mathit{con}\leftarrow$ inequalities on $[{\mathtt{deA}}_{\mathtt{Ind}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r},{\mathtt{out}}_{\mathtt{s}}},{\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},{\mathtt{out}}_{\mathtt{s}}},{\mathtt{A}}_{\mathtt{l}}^{\mathtt{r}-\mathtt{1},{\mathtt{out}}_{\mathtt{s}}}]$ by Template 3 16:            end for 17:         end for     /* Concerning second-order property effect*/ 18:         $\mathcal{M}.\mathit{var}\leftarrow {\Delta }_{\mathsf{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}},\mathtt{s}\in [\mathtt{0},\mathtt{15}]$   ▹ variables for second-order equality on each byte 19:         $\mathcal{M}.\mathit{var}\leftarrow A_{\mathsf{SB}}^{r-1,s},s\in [0,15]$   ▹ variables corresponding to probability 20:         for $0\le s\le 15$ do 21:            $\mathcal{M}.\mathit{con}\leftarrow$ inequalities on $[{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r}-\mathtt{1},\mathtt{s}},{\Delta }_{\mathsf{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}},{\mathtt{A}}_{\mathsf{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}]$ by Template 4 22:         end for 23:         for $0\le t\le 3$ do 24:            $\mathcal{M}.\mathit{var}\leftarrow {\mathtt{dop}}^{\mathtt{r}-\mathtt{1},\mathtt{t}}$   ▹ variables for column-wise second-order equality 25:            $\mathcal{M}.\mathit{con}\leftarrow {\mathtt{dop}}^{\mathtt{r}-\mathtt{1},\mathtt{t}}={\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{0}}}\vee {\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{1}}}\vee {\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{2}}}\vee {\Delta }_{\mathtt{SB}}^{\mathtt{r}-\mathtt{1},{\mathtt{in}}_{\mathtt{3}}}$ 26:            $\mathcal{M}.\mathit{var}\leftarrow {\mathtt{lab}}^{\mathtt{r}-\mathtt{1},\mathtt{t}}$   ▹ a variable to indicate if not ${\mathtt{deA}}_{\mathtt{Ind}}=111111$ 27:            $\mathcal{M}.\mathit{con}\leftarrow \mathtt{lab}=\mathtt{1}-{\wedge }_{\mathtt{ij}\in \mathtt{Ind}}{\mathtt{deA}}_{\mathtt{ij}}^{\mathtt{r}-\mathtt{1},\mathtt{t}}$ 28:            for $0\le s\le 3$ do 29:                $\mathcal{M}.\mathit{con}\to$ inequalities on $[{\mathtt{lab}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},{\mathtt{dop}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},{\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{r},\mathtt{4}\mathtt{t}+\mathtt{s}}]$ by Template 5 30:            end for 31:         end for 32:         for $0\le s\le 15$ do 33:            $\mathcal{M}.\mathit{var}\leftarrow {\mathtt{A}}_{\mathtt{minus}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}$   ▹ variables corresponding to probability 34:         end for 35:         for $0\le t\le 3$ do 36:            for $0\le s\le 3$ do 37:                $\mathcal{M}.\mathit{con}\leftarrow$ inequalities on $[{\mathtt{lab}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},{\mathtt{dop}}^{\mathtt{r}-\mathtt{1},\mathtt{t}},{\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},\mathtt{4}\mathtt{t}+\mathtt{s}},{\mathtt{A}}_{\mathtt{l}}^{\mathtt{4}\mathtt{t}+\mathtt{s}},{\mathtt{A}}_{\mathtt{minus}}^{\mathtt{r}-\mathtt{1},\mathtt{4}\mathtt{t}+\mathtt{s}}]$ by Template 6 38:            end for 39:         end for 40:     end for 41:     $\mathcal{M}.\mathit{con}\leftarrow {\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{0},\mathtt{s}}$ conforming input mixture pattern ${\mathbf{P}}_{in}$ 42:     $\mathcal{M}.\mathit{con}\leftarrow {\mathtt{e}}_{\mathtt{Ind}}^{\mathtt{R},\mathtt{s}}$ conforming input mixture pattern ${\mathbf{P}}_{out}$ 43:     $\mathcal{M}.\mathit{obj}\leftarrow min{\sum }_{\mathtt{r}=\mathtt{1}}^{\mathtt{R}}{\sum }_{\mathtt{s}=\mathtt{0}}^{\mathtt{15}}(\mathtt{2}{\mathtt{A}}_{\mathtt{h}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}+{\mathtt{A}}_{\mathtt{l}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}+{\mathtt{A}}_{\mathsf{SB}}^{\mathtt{r}-\mathtt{1},\mathtt{s}}-{\mathtt{A}}_{\mathtt{minus}}^{\mathtt{r}-\mathtt{1},\mathtt{s}})$ 44:     return $\mathcal{M}$ 45: end function

3.2. Verification of 5-Round Distinguishers

It is worth noting that the single 5-round mixture trail does not make a distinguisher, as it has the same probability as that of random permutations. Thus, to show the validity of the mixture differential distinguisher as a hull of mixture trails, we tested the validity of the 5-round distinguisher on the small-scale AES [29], which has the same structure as standard AES but with a 4-bit $\mathsf{Sbox}$. As the probability of the distinguisher is not relevant to the size of $\mathsf{Sbox}$ and details of $\mathsf{MC}$ matrix but reflects how the structure allows for trails with a certain number of active Sboxes to hold, the verification on small scale AES is strong evidence for the distinguisher to hold on standard AES. The small scale AES is implemented in a lookup-table-based implementation [11] that resembles the AES implementation in many cryptographic libraries such as OpenSSL [30]. Four precomputed tables are generated by applying $\mathsf{SB},\mathsf{SR},\mathsf{MC}$ for all possible input nibbles such that each table consists of sixteen 16-bit values. The cost of each round is 16 table lookups and XORing of the table elements and round keys.

The Sbox used in the small-scale AES is in Table 2.

Table 2. The Sbox for the small-scale AES.

x	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
$S\left(x\right)$	6	B	5	4	2	E	7	A	9	D	F	C	3	1	0	8

The operations in the i-th round can be expressed as

$$x_i=\left(\begin{array}{cccc}2& 3& 1& 1\\ 1& 2& 3& 1\\ 1& 1& 2& 3\\ 3& 1& 1& 2\end{array}\right)·\left(\begin{array}{cccc}S\left(x_{i-1,0}\right)& S\left(x_{i-1,4}\right)& S\left(x_{i-1,8}\right)& S\left(x_{i-1,12}\right)\\ S\left(x_{i-1,5}\right)& S\left(x_{i-1,9}\right)& S\left(x_{i-1,13}\right)& S\left(x_{i-1,1}\right)\\ S\left(x_{i-1,10}\right)& S\left(x_{i-1,14}\right)& S\left(x_{i-1,2}\right)& S\left(x_{i-1,6}\right)\\ S\left(x_{i-1,15}\right)& S\left(x_{i-1,3}\right)& S\left(x_{i-1,7}\right)& S\left(x_{i-1,11}\right)\end{array}\right)\oplus k_{i-1},$$

(1)

where the matrix elements are elements in $GF\left(2^4\right)$ defined by the primitive polynomial $x^4+x+1$. The lookup-table-based implementation calculates one column by looking up four tables and adding the results as well as the corresponding subkey column. For the first column,

$$\begin{array}{cc}\hfill x_{i,Col\left(0\right)}=& \left(\begin{array}{c}2\\ 1\\ 1\\ 3\end{array}\right)·S\left(x_{i-1,0}\right)\oplus \left(\begin{array}{c}3\\ 2\\ 1\\ 1\end{array}\right)·S\left(x_{i-1,5}\right)\oplus \left(\begin{array}{c}1\\ 3\\ 2\\ 1\end{array}\right)·S\left(x_{i-1,10}\right)\oplus \left(\begin{array}{c}1\\ 1\\ 3\\ 2\end{array}\right)·S\left(x_{i-1,15}\right)\hfill \\ \hfill & \oplus k_{i-1,Col\left(10\right)}.\hfill \end{array}$$

(2)

The four precomputed tables are the compositions of the dot multiplication by the column elements and the Sbox operation, i.e.,

$$T_0(·)=\left(\begin{array}{c}2\\ 1\\ 1\\ 3\end{array}\right)·S(·),T_1(·)=\left(\begin{array}{c}3\\ 2\\ 1\\ 1\end{array}\right)·S(·),T_2(·)=\left(\begin{array}{c}1\\ 3\\ 2\\ 1\end{array}\right)·S(·),T_3(·)=\left(\begin{array}{c}1\\ 1\\ 3\\ 2\end{array}\right)·S(·).$$

(3)

The input to the tables is 4-bit string and the output is 16-bit. So each table is a list with sixteen 16-bit elements. The four tables are shown in Table 3.

Table 3. Lookup tables for the small-scale AES.

x	0	1	2	3	4	5	6	7
$T_0\left(x\right)$	c66a	5bbe	a55f	844c	4226	fee1	e779	7aad
$T_1\left(x\right)$	ac66	e5bb	fa55	c844	6422	1fee	9e77	d7aa
$T_2\left(x\right)$	6ac6	be5b	5fa5	4c84	2642	e1fe	79e7	ad7a
$T_3\left(x\right)$	66ac	bbe5	55fa	44c8	2264	ee1f	779e	aad7
x	8	9	a	b	c	d	e	f
$T_0\left(x\right)$	1998	9dd4	dff2	bcc7	6335	2113	0	388b
$T_1\left(x\right)$	8199	49dd	2dff	7bcc	5633	3211	0	b388
$T_2\left(x\right)$	9819	d49d	f2df	c7bc	3563	1321	0	8b38
$T_3\left(x\right)$	9981	dd49	ff2d	cc7b	3356	1132	0	88b3

Then, $x_i$ can be calculated by

$$\begin{array}{cc}\hfill x_{i,Col\left(0\right)}& =T_0\left(x_{i-1,0}\right)\oplus T_1\left(x_{i-1,5}\right)\oplus T_2\left(x_{i-1,10}\right)\oplus T_3\left(x_{i-1,15}\right)\oplus k_{i-1,Col\left(0\right)},\hfill \\ \hfill x_{i,Col\left(1\right)}& =T_0\left(x_{i-1,4}\right)\oplus T_1\left(x_{i-1,9}\right)\oplus T_2\left(x_{i-1,14}\right)\oplus T_3\left(x_{i-1,3}\right)\oplus k_{i-1,Col\left(1\right)},\hfill \\ \hfill x_{i,Col\left(2\right)}& =T_0\left(x_{i-1,8}\right)\oplus T_1\left(x_{i-1,13}\right)\oplus T_2\left(x_{i-1,2}\right)\oplus T_3\left(x_{i-1,7}\right)\oplus k_{i-1,Col\left(2\right)},\hfill \\ \hfill x_{i,Col\left(3\right)}& =T_0\left(x_{i-1,12}\right)\oplus T_1\left(x_{i-1,1}\right)\oplus T_2\left(x_{i-1,6}\right)\oplus T_3\left(x_{i-1,11}\right)\oplus k_{i-1,Col\left(3\right)},\hfill \end{array}$$

(4)

with 16 table lookup operations.

This implementation is faster than the textbook implementation where each operation is implemented by its definition, as used in [16]. We verified the 5-round distinguisher on both this lookup-table-based implementation and the implementation provided in [16]. The expected probability for the 5-round distinguisher to hold on small scale AES is $2^{-4\times 8}\times 15=2^{-28.09}$. We test on 200 randomly generated master keys and use a 20-round version to simulate a random permutation. For each randomly generated master key, $2^{30}$ quadruples conforming input patterns are randomly generated. On average, the number of quadruples whose ciphertexts confirm the output pattern are 3.885 and 0.215 for 5-round small-scale AES and 20-round small-scale AES, respectively; thus, the probability of right quadruples is $2^{-28.04}$ for 5-round small scale AES and $2^{-32.22}$ for the 20-round version. This result verifies that the accumulated truncated mixture differential trails can make a distinguisher. The verification codes are included in our repository. The average running time with the textbook implementation is about 20 min, while it is about 1 min with a lookup-table-based implementation when run on an AMD Ryzen Threadripper 3970X Processor.

3.3. Illustration of 6-Round Distinguishers

Regarding 6-round distinguishers, the probability is too low to be verified experimentally even on a small variant of AES. Therefore, we demonstrate the mixture pattern trails of the 6-round distinguishers. Figure 3 shows one trail with probability $2^{-176}$. The probability lies on the $\mathsf{MC}$ layer to make specific mixture patterns in states $x_1,x_3$ and $x_4$, marked in yellow. The deduced patterns reflect equality among quadruples. It is worth noting that for state $x_0^{″}$ and state $x_2^{″}$, the differences of the first pair and the second pair are the same, so after the $\mathsf{MC}$ layer conditioned on that one pair has zero difference on specific bytes, the other pair has the same difference with probability 1. This is where the mixture differential distinguisher gains an advantage. However, after one more round of confusion, this property does not hold anymore, and probability is calculated independently on two pairs, as is the case for $x_3^{″}$ to $x_4$.

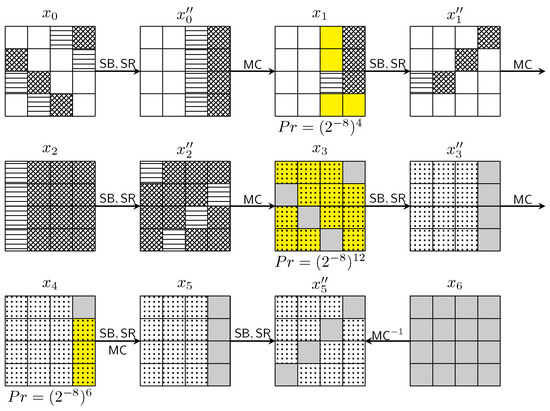
Figure 3. A 6-round AES mixture differential trail with probability $2^{-176}$.

There are a total of 56 trails with probability $2^{-176}$ with the same input and output pattern as in Figure 3. All trails are shown in abbreviated form in Table A4 in Appendix C.

4. Key Recovery Attacks

We utilize the 6-round mixture differential distinguisher with probability $2^{-170.19}$ to do a key recovery attack on 7-round AES-192 and use a 5-round distinguisher with probability $2^{-60.19}$ to do cryptanalysis on 6-round AES-128, all by appending one round after the distinguisher. As we do not prepend rounds before the distinguisher, we can acquire N quadruples conforming ${\mathbf{D}}_{in}$ trivially and concentrate on the guess-and-determine procedure on the ciphertext side.

4.1. Key Recovery on 6-Round AES-128

Suppose the plaintext quadruples in $x_{-1}$ conform ${\mathbf{D}}_{in}$, with probability $2^{-60.19}$ that the mixture pattern is $\mathbf{s}$ in position $x_{4,\mathsf{SR}\left(Col\right(0\left)\right)}^{″}$, i.e., the differences of both the first pair and second pair are zero on the first inversed diagonal. These conditions are used as filters to filter out wrong guesses of $k_5$. To use the MITM technique to reduce complexity, express the filter conditions by combinations of $\Delta \left(x_5\right)$ through ${\mathsf{MC}}^{-1}$ operation. Specifically, the filter conditions and corresponding key byte that needs to be guessed to deduce the target difference are

$$\begin{array}{cc}\hfill \Delta \left(x_{4,0}^{″}\right)=0\iff 0E_x·\Delta (& x_{5,0})\oplus 0B_x·\Delta \left(x_{5,1}\right)=0D_x·\Delta \left(x_{5,2}\right)\oplus {09}_x·\Delta \left(x_{5,3}\right),\hfill \\ \hfill & \uparrow \uparrow \uparrow \uparrow \hfill \\ \hfill & k_{5,0}{k}_{5,13}{k}_{5,10}{k}_{5,7}\hfill \\ \hfill \Delta \left(x_{4,7}^{″}\right)=0\iff 0B_x·\Delta (& x_{5,4})\oplus 0D_x·\Delta \left(x_{5,5}\right)={09}_x·\Delta \left(x_{5,6}\right)\oplus 0E_x·\Delta \left(x_{5,7}\right),\hfill \\ \hfill & \uparrow \uparrow \uparrow \uparrow \hfill \\ \hfill & k_{5,4}{k}_{5,1}{k}_{5,14}{k}_{5,11}\hfill \\ \hfill \Delta \left(x_{4,10}^{″}\right)=0\iff 0D_x·\Delta (& x_{5,8})\oplus {09}_x·\Delta \left(x_{5,9}\right)=0E_x·\Delta \left(x_{5,10}\right)+0B_x\Delta \left(x_{5,11}\right),\hfill \\ \hfill & \uparrow \uparrow \uparrow \uparrow \hfill \\ \hfill & k_{5,8}{k}_{5,5}{k}_{5,2}{k}_{5,15}\hfill \\ \hfill \Delta \left(x_{4,13}^{″}\right)=0\iff {09}_x·\Delta (& x_{5,12})\oplus 0E_x·\Delta \left(x_{5,13}\right)=0B_x·\Delta \left(x_{5,14}\right)\oplus 0D_x·\Delta \left(x_{5,15}\right).\hfill \\ \hfill & \uparrow \uparrow \uparrow \uparrow \hfill \\ \hfill & k_{5,12}{k}_{5,9}{k}_{5,6}{k}_{5,3}\hfill \end{array}$$

(5)

The four filter bytes together with four involved bytes for each are called four groups. In the key recovery procedure, initialize four counters of size $2^{32}$ for each group. To get $2^m$ right quadruple, we prepare $2^{60.09+m}$ quadruples conforming the input pattern. Then,

• For each quadruple, do the MITM procedure on four groups:

  (a)

  For the first group, guess $K_{5,\{0,13\}}$, compute the value $0E_x·\Delta \left(x_{5,0}\right)\oplus 0B_x·\Delta \left(x_{5,1}\right)$ on both the first pair and the second pair, and store the current guess in a hash table T indexed by this 16-bit value. After this step, each item of T contains on average one element.

  (b)

  Guess $k_{5,\{10,7\}}$ and compute the value $0D_x·\Delta \left(x_{5,2}\right)\oplus {09}_x·\Delta \left(x_{5,3}\right)$ on both the first pair and the second pair. Look up the table T by this 16-bit value and get the candidate for the combination $k_{5,\{0,13,10,7\}}$. Increase the counter for the first group. After this step, on average, $2^{16}$ candidates are suggested.

  (c)

  Repeat Step 1(a)–(b) for the other three groups.

• To have h-bit advantage of key exhaustive search on each group, combine the top $2^{32-h}$ candidates suggested by each counter to get $2^{128-4h}$ candidates of the full 128-bit key $k_5$. Check with plaintext–ciphertext pairs.

Time and memory complexity. The memory complexity of the attack is $4\times 2^{32}$ counters, and the hash table is sized $2^{16}$, which are negligible. For each quadruple, the first MITM step takes $2^{16}\times 8$ times $\mathsf{Sbox}$ lookups and $2^{16}$ hash table lookups. The second step has about the same cost. If each round of AES is estimated as 20 times $\mathsf{Sbox}$ lookups and each hash table lookup is estimated as one AES round, the time complexity for each group in Step 1 is $2\times 2^{16}\times (8\times \frac{1}{5\times 20}+\frac{1}{5})\approx 2^{15.16}$ 5-round AES encryptions. The total time complexity of the attack is $2^{60.19+m}\times 4\times 2^{15.16}+2^{128-4h}=2^{77.36+m}+2^{128-4h}$.

Success probability and data complexity. Step 1 of the attack goes on each group independently, so we only need to know whether the 32-bit right key will appear in the top $2^h$ positions for each group with high probability. Each quadruple recommends $2^{16}$ candidates on average. Each right quadruple hits the right key once and hits the wrong keys $2^{16}-1$ times. Each wrong quadruple hits the right key and wrong keys indiscriminately a total of $2^{16}$ times. The right key is hit about $2^m+2^{60.19+m-16}=2^{44.19+m}+2^m$ times, and each wrong key is, on average, hit $(2^m(2^{16}-1)+2^{60.19+m}(2^{16}-2^{-16}))/(2^{32}-1)\approx 2^{44.19+m}+2^{m-16}$ times. Thus, the signal/noise ratio, i.e., the ratio of the counter of the right key and the average counter of a wrong key, is $S_N=\frac{2^{44.19+m}+2^m}{2^{44.19+m}+2^{m-16}}\approx 1+2^{-44.19}$. We estimate the success probability by the formula $P_s=\mathsf{\Phi }\left(\frac{\sqrt{2^m{S}_N}-{\mathsf{\Phi }}^{-1}(1-2^{-h})}{\sqrt{S_N+1}}\right)$ [31], where $\mathsf{\Phi }$ is the cumulative distribution function of the standard normal distribution. By setting $m=6$ and $h=12$, the success probability is above 99% and the time complexity is $2^{83.36}$.

To have $2^6$ right quadruples, we need to build up $2^{66.19}$ quadruples conforming input pattern ${\mathbf{D}}_{in}$. We fix 90 bits of plaintexts and enumerate the remaining 38 bits. Among the 90 fixed bits, 64 are located in $x_{0,{\mathsf{SR}}^{-1}(0,1)}$. Choose six bytes from $x_{0,{\mathsf{SR}}^{-1}(2,3)}$ and fix 3-bit in each of these six bytes, and fix 4-bit in each of the remaining 2bytes. We could build ${\left(\frac{2^5(2^5-1)}{2}\right)}^6{\left(\frac{2^4(2^4-1)}{2}\right)}^2\approx 2^{67.53}$ quadruples, which is enough for the attack. The data complexity is no larger than $2^{38}$.

4.2. Key Recovery on 7-Round AES-192

The key recovery attack on 7-round AES-192 is quite similar to the previous one on 6-round AES-128, considering that they both append one round after a distinguisher and the distinguishers have the same input pattern. But there are more filter conditions on the output of the 6-round distinguisher. The filters can be divided into four groups, each involving four bytes in $k_6$. We show the guess-and-filter procedure in the first group, and the other three groups proceed in the same fashion.

In the first group, the filters are $\Delta \left(x_{5,0}^{″}\right)=0,\Delta \left(x_{5,1}^{″}\right)=0$ and $\Delta \left(x_{5,2}^{″}\right)=0$, holding on to both the first pair and the second pair. Equivalently, $\Delta \left(x_5^{″}\right)$ can be expressed by $\Delta x_6$ through the ${\mathsf{MC}}^{-1}$ layer. In the key recovery procedure, to apply the MITM technique, write the filter conditions in the first group as

$$\begin{array}{cc}\hfill \Delta \left(x_{5,0}^{″}\right)=0\iff 0E_x·\Delta (& x_{6,0})\oplus 0B_x·\Delta \left(x_{6,1}\right)=0D_x·\Delta \left(x_{6,2}\right)\oplus {09}_x·\Delta \left(x_{6,3}\right),\hfill \\ \hfill \Delta \left(x_{5,1}^{″}\right)=0\iff {09}_x·\Delta (& x_{6,0})\oplus 0E_x·\Delta \left(x_{6,1}\right)=0B_x·\Delta \left(x_{6,2}\right)\oplus 0D_x·\Delta \left(x_{6,3}\right),\hfill \\ \hfill \Delta \left(x_{5,2}^{″}\right)=0\iff 0D_x·\Delta (& x_{6,0})\oplus {09}_x·\Delta \left(x_{6,1}\right)=0E_x·\Delta \left(x_{6,2}\right)\oplus 0B_x·\Delta \left(x_{6,3}\right).\hfill \\ \hfill & \uparrow \uparrow \uparrow \uparrow \hfill \\ \hfill & k_{6,0}{k}_{6,13}{k}_{6,10}{k}_{6,7}\hfill \end{array}$$

(6)

Initialize four counters of size $2^{32}$ for each group. Suppose we have prepared $2^{170.19+m}$ plaintext quadruples conforming ${\mathbf{D}}_{in}$ to expect $2^m$ right quadruples. Then:

• For each quadruple, do the MITM procedure on four groups:

  (a)

  For the first group, guess $k_{6,\{0,13\}}$, compute the value $0E_x·\Delta \left(x_{6,0}\right)\oplus 0B_x·\Delta \left(x_{6,1}\right)$ on both the first pair and the second pair, and store the current guess in a hash table T indexed by this 16-bit value. After this step, each item of T contains, on average, one element.

  (b)

  Guess $k_{5,\{10,7\}}$ and compute the value $0D_x·\Delta \left(x_{6,2}\right)\oplus {09}_x·\Delta \left(x_{6,3}\right)$ on both the first pair and the second pair. Look up the table T by this 16-bit value and get the candidate for the combination $k_{6,\{0,13,10,7\}}$. Test if the last two equations in Equation (6) are satisfied under this candidate on both the first pair and the second pair. This test is a filter with probability $2^{-32}$. If so, increase the counter; otherwise, discard the key candidate.

  (c)

  Repeat Step 1(a–b) for the other three groups.

• To have h-bit advantage of key exhaustive search on each group, combine the top $2^{32-h}$ candidates indicated by each counter to form $2^{128-4h}$ full 128-bit key $k_6$ and combine with the other 64-bit keys that are independent of $k_6$. Check the $2^{192-4h}$ candidate keys with plaintext–ciphertext pairs.

Time and memory complexity. The memory complexity of the attack is $4\times 2^{32}$ counters, and it has a hash table of size $2^{16}$, which are negligible. For each quadruple, the first MITM step takes $2^{16}\times 8$ times $\mathsf{Sbox}$ lookups and $2^{16}$ hash table lookups. Step 1(b) takes an additional 16 $\mathsf{Sbox}$ lookups in each guess of $k_{5,\{10,7\}}$. The complexity of Step 1 is estimated as $2\times 2^{16}\times (8\times \frac{1}{6\times 20}+\frac{1}{6})+2^{16}\times \frac{16}{6\times 20}\approx 2^{15.26}$ 6-round AES encryptions. The total time complexity of the attack is $2^{170.19+m}\times 4\times 2^{15.26}+2^{192-4h}=2^{187.45+m}+2^{192-4h}$.

Success probability and data complexity. Each quadruple only suggests $2^{-16}$ 32-bit keys for each group on average. Each right quadruple will hit the right 32-bit key once. The wrong quadruples will hit all keys indiscriminately. Thus, the right key will be hit about $2^m+2^{170.19+m-16}/2^{32}\approx 2^{122.19+m}+2^m$ times. The wrong key will be hit $2^{122.19+m}$ times on average. The signal/noise ratio is no smaller than $S_N=1+2^{-122.19}$. By setting $m=1,h=2$, the success probability is about 69.95% with time complexity $2^{188.45}$.

To build up $2^{171.19}$ plaintext quadruples conforming the input pattern, we build structures such that in each structure, 64-bits of $x_{0,{\mathsf{SR}}^{-1}(0,1)}$ are fixed and the other bits are enumerated. Each structure can provide ${\left(\frac{2^8(2^8-1)}{2}\right)}^8\approx 2^{119.95}$ quadruples conforming the input pattern; therefore, $2^{52}$ structures are needed. The data complexity of the attack is $2^{52+64}=2^{116}$.

The comparison of our work and previous ones is shown in Table 4. Key recovery attacks are estimated from the data/time/memory complexities. From Table 4, it is obvious that for the 6-round key recovery attack on AES-128, our method outperforms the impossible differential attack [8], MITM attack [9] and the original mixture differential attack [17]. Especially considering the number of rounds of distinguishers used, denoted by $R_{\mathrm{Dist}}$ in the table, our result is the best one by utilizing a 5-round distinguisher to launch key recovery attacks. For 7-round AES-192, our result is the first one to setup a key recovery attack with a 6-round distinguisher.

Table 4. Comparison of attacks on 6- and 7-round AES. ($R_{\mathrm{Dist}}$ is the number of rounds of the distinguisher exploited to set up the attack. Our results are highlighted in bold).

Version	R	Method	Data (CP)	Time (ENC.)	Memory	${\mathit{R}}_{\mathbf{Dist}}$ (16-byte)	Ref.
AES-128	6	Partial Sum	$2^{32}$	$2^{42}$	$2^{40}$	4	[13]
		Integral	$2^{35}$	$2^{69.7}$	$2^{32}$	4	[11]
		Mixture Diff.	$2^{27.5}$	$2^{81}$	$2^{27.5}$	4	[17]
		Mixture Diff.	${\mathbf{2}}^{\mathbf{38}}$	${\mathbf{2}}^{\mathbf{83}.\mathbf{36}}$	${\mathbf{2}}^{\mathbf{33}}$	5	Ours
		Mixture Diff.	$2^{72.8}$	$2^{105}$	$2^{33}$	5	[16]
		MITM	$2^8$	$2^{106.2}$	$2^{106.2}$	—	[9]
		Imp. Differential	$2^{91.5}$	$2^{122}$	$2^{89}$	4	[8]
AES-192	7	MITM	$2^{97}$	$2^{99}$	$2^{98}$	—	[10]
		MITM	$2^{32}$	$2^{129.7}$	$2^{129.7}$	—	[9]
		Collision	$2^{32}$	$2^{146.3}$	$2^{80}$	4	[5]
		Square	$2^{36.2}$	$2^{155}$	$2^{36.2}$	4	[12]
		Mixture Diff.	$2^{26}$	$2^{146.3}$	$2^{40}$	4	[17]
		Mixture Diff.	${\mathbf{2}}^{\mathbf{116}}$	${\mathbf{2}}^{\mathbf{188}.\mathbf{45}}$	${\mathbf{2}}^{\mathbf{34}}$	6	Ours

5. Conclusions

In this paper, we exploited the secret-key mixture differential properties on round-reduced AES deduced from MILP models to present key recovery attacks on 6-round AES-128 and 7-round AES-192 by appending one round after the distinguishers. The complexity of our 6-round AES-128 key recovery attack with a 5-round distinguisher outperforms the previous one of the same fashion, as the data/time/memory complexities are significantly reduced from $2^{72.8}/2^{105}/2^{33}$ to $2^{38}/2^{83.36}/2^{33}$. Further, this is the first time that a 7-round key recovery attack has been possible by utilizing a 6-round distinguisher directly. Moreover, in the distinguisher verification part, the implementation of the small-scale AES used in our experiments is about 20 times more efficient than the previous one.

Future work can include finding out more properties to make a distinguisher on block ciphers as well as designing key recovery attacks with reduced data/time/memory complexity. For the AES block cipher, the current mixture differential property is byte-oriented. That is to say, the details of the Sbox and the mix column matrix are not taken into account when searching for the mixture differential properties. Methods to search for properties with higher probability on AES or that that can cover more rounds remain to be investigated. In the key recovery aspects, the current method is independent of the key schedule. There may exist useful relations among subkeys to further reduce the complexity of the key recovery attack. The key schedule effect will be taken into consideration in future work.