Abstract
Numerical investigation of a chemically reactive second grade fluid flow towards an exponentially stretching sheet into a porous medium induced by thermal and concentration slips boundary conditions is carried out. Further, nonlinear thermal radiations, Joule heating, MHD and thermophoretic impacts are also taken into account. The modified Fourier and Fick’s law is used to analyse the thermal and solutal energy features. The nonlinear systems of partial differential equations, as well as boundary conditions, are transformed into systems of nonlinear ordinary differential equations by imposing appropriate similarity variables. Then these transformed equations are solved using the BVP4C Matlab approach numerically. The graphs and tables of a number of emerging parameters are plotted and discussed. It is noticed that by the improvement of the second grade fluid parameter, the velocity profile is reduced. Moreover, the upsurge of Eckert numbers and thermal slip parameter enhance the temperature of the fluid in the flow domain.
Keywords:
second grade fluid; porous medium; nonlinear thermal radiation; joule heating; thermophoretic effect; exponentially stretching sheet MSC:
76-10; 70-10; 76D05; 76D10
1. Introduction
Magnetohydrodynamics (MHD) is a modern area of recent science involving the mechanics of fluids and electromagnetism. It is pertinent to mention that electrically conducting fluids are significant due to the electromagnetic forces produced in the fluid due to the applied magnetic field. This mechanism has numerous industrial applications, such as, steel-making processes, semiconductor crystal growth, electromagnetic pumps, dynamo simulation of planets, electromagnetic pumps and levitation of drop and so on. Boussinesq type approximation for second grade fluid was carried out by Passerini and Thater [1]. Ishak [2] deliberated the effect of the thermal radiation effect for the MHD flow of a viscous fluid towards an exponentially expanding sheet. Mukhopadhyay [3] scrutinized the mass and heat transportation for the MHD boundary layer flow into a thermally stratified medium towards an exponentially stretching sheet. Mukhopadhyay [4] deliberated the flow of mass and heat transfer of a viscous fluid flow under the impacts of thermal and velocity slips, suction or injection and thermal radiation impacts towards an exponentially expanding surface. Hayat et al. [5] analysed the MHD flow of viscous nanofluids through a porous medium on a permeable stretched surface. Hayat et al. [6] scrutinized the three-dimensional hydromagnetic flow of viscous fluid along a permeable medium. Thermal and velocity slips boundary conditions were induced by an exponentially expanding sheet. For more studies on MHD flow, the readers are referred to [7,8,9,10,11].
Joule heating is produced due to the interconnection between the motion of the charged particles, which produce the atomic ions and current and make up the body of the conductor. It is a consequence of the collision amongst the motion of the particles of the fluid. In that process, a proportion of the kinetic energy is converted into heat and, consequently, there is a body temperature boost. For example, electric heaters, electric stoves, electric fuses, soldering irons, electric cigarettes, food, cartridge heaters and thermistors processing accoutrements are real-word usages of Joule heating. The Joule heating phenomenon demonstrates a vigorous charm in enormous engineering and built-up desire. The central benefit of Joule heating is the transportation of electrical strength to diminish the reparations by abating the current. Shamshuddin et al. [12] constructed a mathematical model of an incompressible, steady, two-dimensional flow of a non-Newtonian fluid with the magnetic effect, Joule heating, Hall currents, thermal radiation, viscous dissipation and Power-law slip velocity conditions towards an exponentially stretched sheet. Hayat and Qasim [13] addressed the heat and mass communication in Maxwell fluid under the existence of magnetic, thermophoretic, Joule heating and thermal radiation effects past a stretching surface. Srinivasachraya and Jagadeeshuwar [14] discussed the influence of Joule heating, thermal slip, suction or injection and magnetic effects for the viscous fluid flow on a porous exponentially expanding surface with convective boundary conditions by a permeable medium. Murugesan and Kumar [15] explained the transmission of heat and mass in the MHD flow of thermo-solutal stratified nanofluids with heat source or sink, viscous dissipation, Joule heating and thermal radiation impacts towards an exponentially stretched sheet. Sharada and Skankar [16] inspected the effect of convective boundary conditions and particle slip in the mixed convective MHD flow of Williamson fluid under the effect of Joule heating towards an exponentially stretching surface. For more studies on Joule heating for the different fluid flows, the readers are referred to [17,18,19,20].
Several researchers have inspected the heat and mass transfer solutions of Newtonian or non-Newtonian fluids under the supposition of nonadherence force that is the fundamental percept of the Navier–Stokes principle. However, it has been experimentally noted that the supposition of boundary condition has no slip does not follow in various everyday examples and, therefore, it is perhaps fundamental to change the no-slip boundary condition to the partial slip boundary conditions. The nonadherence force of fluid towards a solid boundary is recognized by means of a velocity slip boundary condition. The temperature jump and solutal jump boundary conditions are characterized as incoherent with the transportation variable through the boundary and more precisely designates the nonequilibrium area near the surface. The applications of slip effect are polymer solutions, suspensions and emulsions every where there is perhaps a slip amongst the fluid and the boundary. Oyelakin et al. [21] elaborated the heat and mass transfer into an unsteady Casson nanofluid flow with the effect of the Dufour and Soret effect, heat generation, Brownian, thermal radian and thermophoresis effects over an expandable sheet. Baker et al. [22] described the flow and the heat transmission for the steady, laminar flow by means of partial slip, and convective boundary condition past a stretched surface. Sajid et al. [23] studied the impact of general slip boundary conditions for the viscous incompressible flows through a stretching surface. Andersson [24] elaborated the influence of flow of fluid, which has variable viscosity above a linearly stretched sheet. Hayat et al. [25] explored the mass and heat transportation of the second order fluid flow into a permeable medium by means of slip boundary conditions and magnetic field past a stretched sheet. For more study on slip boundary conditions for the different fluid flows, the readers are referred to [26,27,28,29]. Recently, Ashraf [30,31,32] and his co-authors discussed the combined effects of thermophoretic motion and magnetohydrodynamics on mixed convection flow numerically. The authors in [33,34] investigated the impact of Newtonian heating with the inclusion of variable heat source and sink over stretched surface, and unsteady second grade nanofluids flow subject to the mixed convection and thermal radiation. An optimal control problem for nonisothermal steady flows of low concentrated aqueous polymer solution was studied by Baranovskii [35].
The leading purpose of the present research is to constitute a mathematical formulation for MHD three-dimensional flow of a chemically reactive second grade fluid under the existence of thermal radiation and multiple slips impacts on an exponentially stretched surface. When studying the literature, it was found that no one has yet investigated second order fluid with modified Fourier and Fick’s law across a permeable medium through an exponentially expandable surface. The consequences of thermophoretic and Joule heating are also deliberated. Appropriate similarity transformations are used to change the system of nonlinear PDEs into the system of ODEs. The developed strong nonlinear system is evaluated and scrutinized by BVP4C built in Matlab technique. The deliberation of plots and analysis of numerical tables of physical quantities of interest are presented to highlight the physical phenomena that occurred in this study. The main motivation in the current work is the claim that as magnetic force parameter is increased, a decreasing effect in the speed of the fluid flow occurs due to the increasing effect of magnetic energy.
2. Mathematical Modelling
Here, we consider a steady laminar, the 3-D flow of incompressible second grade fluid. The flow of the fluid is produced by an exponentially stretching surface in a bidirectional manner. The sheet is in the xy-plane. Suppose and are the velocities of the stretching sheet in x and y direction individually. Heat transfer investigation is carried out under the influence thermophoretic and Joule heating effects. The is the sheet temperature, where is the ambient fluid temperature. The magnetic field effect is adjusted in the z-direction of strength . Further, is the fluid particles concentration, where is the ambient concentration of the fluid particles and is the concentration exponent coefficient (See Figure 1). With the help of theory of boundary layer assumption, mass, energy and concentration equations for the second grade fluid are as followed:
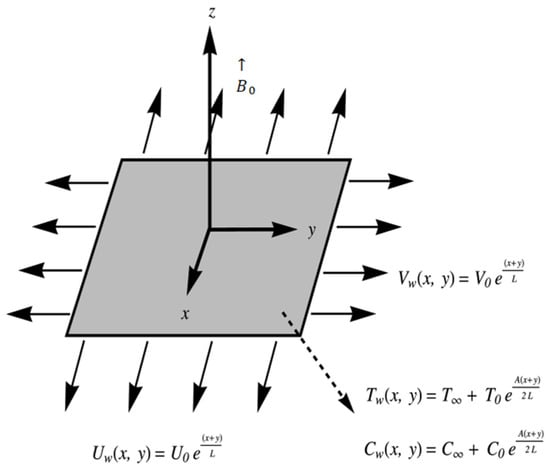
Figure 1.
Flow mechanism of problem.
Similarity transformations are as follows,
Here , , , , , , , , , , , , , , , , , , , , , , , , , , , and are kinematic viscosity, coordinates, velocity components, electric conductivity, density, magnetic field strength, medium porosity, medium permeability, second grade fluid coefficient, temperature of the fluid, thermal relaxation time, thermal conductivity, specific heat capacity, heat generation source coefficient, wall temperature, thermal radiation coefficient, time of relaxation of heat flux, diffusion coefficient, a constant, concentration of fluid, ambient concentration of fluid, mass time relaxation coefficient, thermophoretic effect coefficient, across x-axis wall velocity, across y-axis wall velocity, reference length, coefficient of temperature slip, coefficient of concentration slip and reference velocity, respectively.
Non-dimensional equations are as follows,
The interrelated boundary conditions are as follows,
Here (Second grade fluid parameter), (Porous medium parameter), (Magnetic field parameter), (Radiation parameter), (Temperature ratio parameter), (Prandtl number), (Temperature relaxation parameter), (Eckert number along x-axis), (Eckert number along y-axis). (Parameter of heat generation/absorption), (Parameter of chemical reaction), (Lewis number), (Concentration relaxation time parameter), (Parameter of thermophoretic velocity).
Physical Quantities
The physical quantities of interest are Skin friction, Sherwood and Nusselt numbers are very pivotal from the engineering perspective as follows,
Sherwood and Nusselt numbers are as follows,
where the Reynolds number demonstrates as .
3. Graphical Results and Discussion
The numerical study of three-dimensional flow of a second grade fluid with the chemical reaction and Cattaneo–Christov theory over an exponentially stretched sheet is investigated. The graphical analysis of the emerging parameters is presented. Figure 2a reveals the impression of second grade fluid parameter on velocity profile . The second grade fluid parameter gives an increase in the speed of the fluid along the x-axis. Additionally, the velocity sketch and the corresponding thickness of the momentum boundary layer increase. Therefore, from a boundary layer perspective, the thickness of the fluid rises with the stronger variations of . Figure 2b indicates the significance of the magnetic effect parameter on the fluid flow. There is a decreasing effect in the speed of the fluid when the values of magnetic fluid parameter are improved. The magnetic field parameter is influenced on the Lorentz force. Obviously, the Lorentz force is a mediator that generates a resistive in the fluid flow. A rise in magnetic field parameter reveals a boost in the Lorentz force that displays a decrease in the density and the corresponding momentum boundary layer thickness. Indeed, the existence of the transverse in Lorentz force results in a fallout in the retarding force to the velocity profile. Figure 2c shows the variation of the parameter of porous medium on the velocity sketch. A rise in the estimations of porosity parameter exhibits a reduction in the velocity profile. Consequently, for stronger variations of porosity parameter, a small drag occurs in the fluid and flow retardation and thereby is improved. An increase in the variations of , results in the density of the momentum boundary layer becoming thinner. Figure 3a depicts the alteration in the velocity profile due to an upshot of the second grade fluid parameter along the y-axis. Clearly velocity field and the density of thickness of the boundary layer diminish for the higher values of the second grade fluid parameter . Figure 3b clarifies the impacts of the magnetic field parameter on the velocity field . For stronger estimations of , the velocity boundary layer thickness improves. In effect, the existence of the transverse magnetic field generates a Lorentz force that reduces the velocity field .
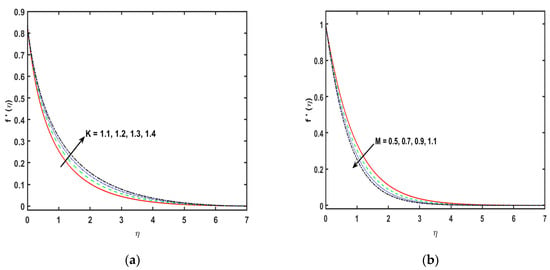
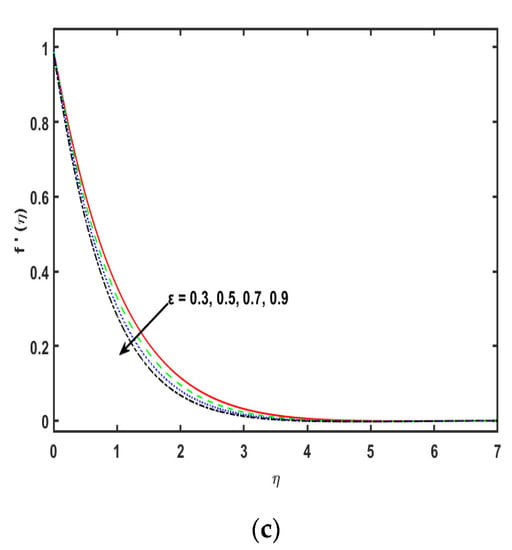
Figure 2.
(a–c): Variation in and against , respectively.
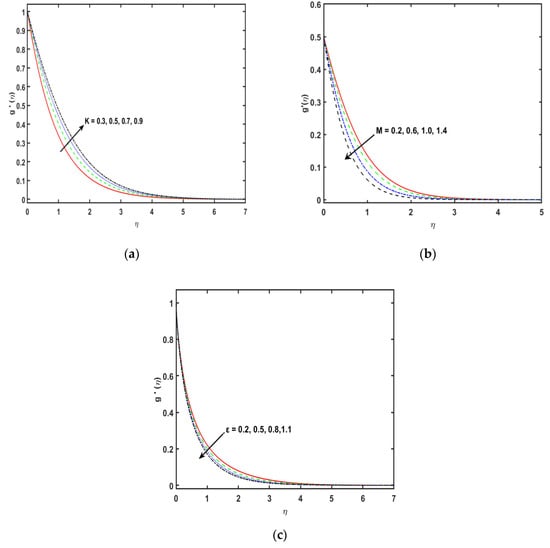
Figure 3.
(a–c): Variation in and against , respectively.
Figure 3c displays the change in the velocity profile along the y-axis for varying the porosity parameter . It has been recorded that the stronger estimations of porosity parameter demonstrate a decrease in the velocity profile, as the permeability of the medium is inversely proportional to the Darcian body force. Figure 4a is sketched to detect the effect of the thermal radiation parameter on the fluid temperature profile. So, it is perceived that the fluid temperature flow enhances for a stronger variation of the parameter . Physically, stronger values of the thermal radiation parameter are responsible for extra heat in working fluid that exhibits an increase in the temperature and the related boundary layer density. Therefore, the temperature of the fluid is increased for stronger values of thermal radiation parameter . The consequences of temperature ratio parameter on the plot of the fluid are exhibited in Figure 4b. It is distinguished that the temperature of the fluid flow increases for the higher values of temperature difference parameter . Physically, the thermal boundary layer thickness versus the profile are boosted by enhancing the temperature difference parameter . Effect of on the sketch is presented in Figure 4c. So, it is perceived that the temperature of the fluid diminishes for the stronger variations of the An enhancement in the values of , causes a boost in the rate of heat transmission. Therefore, it diminishes the density of the associated thickness boundary layer. This is because of the , which is the proportion of the momentum of the thermal diffusivities. Liquids with a smaller Prandtl number will retain the thicker thermal boundary layer designated as greater thermal conductivities. Consequently, the heat can diffuse from the sheet quicker than for higher fluids. Figure 4d indicates that there is an upshot of thermal relaxation time parameter on the sketch. It is noticed that the profile diminishes for stronger effects of thermal relaxation time parameter . In fact, the upset in the estimations of thermal relaxation time parameter offers the associated condition for temperature exchanges and deterioration of the boundary layer thickness. It is detected that the temperature profile diminishes due to relaxation time parameter ; consequently, the viscosity of the fluid will have a small increase. Figure 4e portrays the impact of Eckert number through exponentially stretching sheet along the x-axis on the temperature profile. It is detected that the plot improves for the greater variations of Eckert number . Physically, when there is a growth in the variations of Eckert number , the corresponding boundary layer thickness boosts because of the rate of heat transfer reduced at the exponentially expanding surface. Figure 4f indicates the salient feature of the Eckert number by virtue of the exponentially stretching sheet along the y-axis on the field. It is shown that the Eckert number increases the temperature profile . In effect, the stronger Eckert number leads to fractional heating, which eventually raises the temperature sketch. Figure 4g displays the significance of parameter of heat source/sink in the plot. It is noticed that for the stronger variations in heat generation or absorption, parameter increases the profile . Figure 4h indicates the consequences of the temperature slip parameter on the quantity . It is indicated that the plot boosts for the greater values of the temperature slip parameter . The plot discloses that the wall temperature and the related density increases as the estimations of thermal slip parameter is increased. Figure 5a explains the consequence of Schmidt number on the profile. It is found that by enhancing the values of , there is mitigation in the concentration profile . Essentially, is delineated as the ratio of the momentum to the mass diffusivities, consequently, by an increase in Schmidt number , mass diffusivity is mitigated, therefore, a boost in Schmidt number causes a decline in the concentration of the fluid. Figure 5b indicates the consequences of concentration relaxation time parameter on the profile. The concentration profile reduces cumulative . Therefore, the concentration boundary layer and the momentum become thinner. Figure 5c determines the consequence of the chemical reaction parameter on the field. For the stronger estimations of , the plot increases. The chemical reaction parameter inside the boundary layer has the tendency to enhance the concentration profile. This is by virtue of a decrease in the concentration boundary layer thickness. The salient feature of on the profile is presented in the Figure 5c. An enhancement in the thermophoretic parameter leads to a slight decrease through the boosting of the estimations of the thermophoretic parameter. Figure 5e illustrates the impacts of concentration slip parameter on the sketch. It is shown that for improving the concentration slip parameter, the concentration profile is reduced. Table 1 shows the numerical variations of and of and . It is perceived that the coefficient of the skin friction upsurges by increasing the estimations of and . Table 2 is about the Nusselt number for the stronger variations of and . The Nusselt number is enhanced for enhancing the values of and and is decreased for the stronger values of . Table 3 determines the numerical values of Sherwood number for and . The Sherwood number enhances for the stronger variations of and and is decreased for the stronger estimations of .
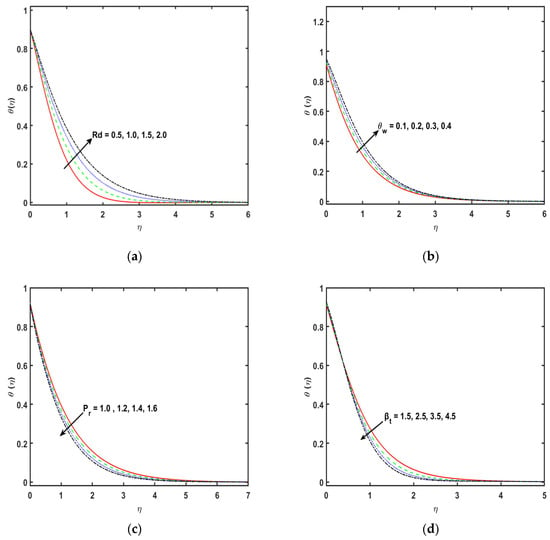
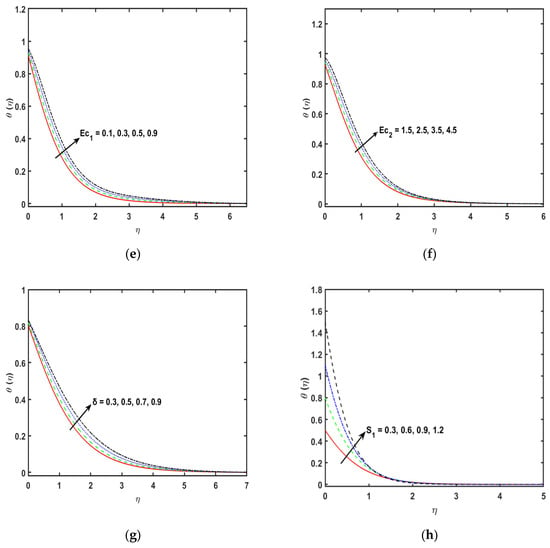
Figure 4.
(a–h): Variation in , , , , , , and , respectively.
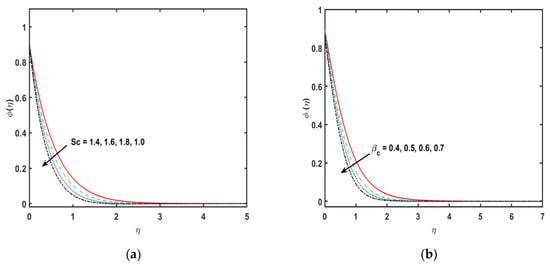
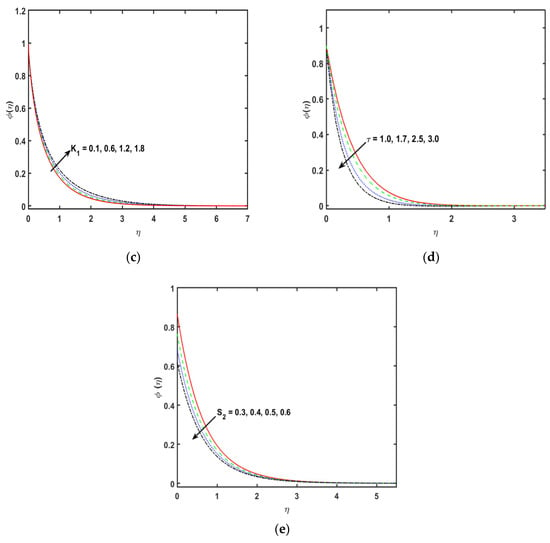
Figure 5.
(a–e): Variation in , , , and , respectively.

Table 1.
Numerical variations of skin friction coefficient against some parameters at , , , and .

Table 2.
Numerical variations of Nusselt number against some dominating parameters at , and .

Table 3.
Numerical variations of Sherwood number against some parameters at , , , and .
4. Concluding Remarks
In this article, the consequences of Cattaneo–Christov theory, thermophoretic effect, Joule heating, nonlinear thermal radiation, slip boundary conditions and magnetic effect on the flow of second order fluid flow by an exponentially stretched sheet are scrutinized. The flow model equations are transformed into a system of ODEs by using the similarity transformations. The acquired ordinary differential equations are solved numerically by BVP4C Matlab technique. The numerical results are attained for different dominating parameters. The leading results of the current article are as follows:
- The enhancement in the second order fluid parameter decreases the velocity profile.
- The variation in the magnetic effect parameter declines the velocity profile due to the resistive force.
- The growing values of porosity parameter boost the velocity sketch.
- The stronger variations of the radiation parameters and temperature difference parameter are prominent in the temperature profile.
- The growing in the estimations of and decline the profile.
- The result of Eckert numbers and thermal slip parameter enhance the temperature profile of the prescribed domain.
- Improving the value of the Schmidt number and thermophoretic parameter raise the concentration field.
- The higher values of and are prominent in the quantity .
Author Contributions
All authors have equal work. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number (IF2/PSAU/2022/01/22970)”.
Data Availability Statement
Data available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
List of Parameters
| Nusselt number | |
| Sharwood number | |
| Second grade fluid parameter | |
| Magnetic force parameter | |
| Porous medium parameter | |
| Thermal radiation parameter | |
| Temperature ratio parameter | |
| Pr | Prandtl number |
| Thermal relaxation parameter | |
| Eckert number | |
| Schmidt number | |
| Chemical reaction parameter |
References
- Passerini, A.; Thater, G. Boussinesq type approximation for second grade. Int. J. Non Linear Mech. 2005, 40, 821–831. [Google Scholar] [CrossRef]
- Ishak, A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. SainsMalaysiana 2011, 40, 391–395. [Google Scholar]
- Mukhopadhyay, S. MHD boundary layer flow and heat transfer over an exponentially stretching sheet embedded in a thermally stratified medium. Alex. Eng. J. 2013, 52, 259–265. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Slip effects on MHD boundary layer flow over an exponentially stretching sheet with suction/blowing and thermal radiation. Ain Shams Eng. J. 2013, 4, 485–491. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A.; Mansoor, R. MHD flow of nanofluids over an exponentially stretching sheet in a porous medium with convective boundary conditions. Chin. Phys. B 2014, 23, 054701. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Alsaedi, A.; Shahzad, S.A. Unsteady MHD flow over exponentially stretching sheet with slip conditions. Appl. Math. Mech. 2016, 37, 193–208. [Google Scholar] [CrossRef]
- Ahmad, R.; Mustafa, M.; Hayat, T.; Alsaedi, A. Numerical study of MHD nanofluid flow and heat transfer past a bidirectional exponentially stretching sheet. J. Magn. Magn. Mater. 2016, 407, 69–74. [Google Scholar] [CrossRef]
- Nayak, M.K.; Akbar, N.S.; Tripathi, D.; Khan, Z.H.; Pandey, V.S. MHD 3D free convective flow of nanofluid over an exponentially stretching sheet with chemical reaction. Adv. Powder Technol. 2017, 28, 2159–2166. [Google Scholar] [CrossRef]
- Senapati, M.; Swain, K.; Parida, S.K. Numerical analysis of three-dimensional MHD flow of Casson nano fluid past an exponentially stretching sheet. Karbala Int. J. Mod. Sci. 2020, 6, 13. [Google Scholar] [CrossRef]
- Reddy, N.N.; Rao, V.S.; Reddy, B.R. Chemical reaction impact on MHD natural convection flow through porous medium past an exponentially stretching sheet in presence of heat source/sink and viscous dissipation. Case Stud. Therm. Eng. 2021, 25, 100879. [Google Scholar] [CrossRef]
- Mandal, C.I.; Mukhopadhyay, S.; Vajravelu, K. Melting Heat Transfer of MHD Micropolar Fluid Flow Past An Exponentially Stretching Sheet with Slip and Thermal Radiation. Int. J. Appl. Comput. Math. 2021, 7, 31. [Google Scholar] [CrossRef]
- Shamshuddin; Khan, S.U.; Bég, O.A.; Bég, T.A. Hall current, viscous and Joule heating effects on steady radiative 2-D magneto-power-law polymer dynamics from an exponentially stretching sheet with power-law slip velocity: A numerical study. Therm. Sci. Eng. Prog. 2020, 20, 100732. [Google Scholar] [CrossRef]
- Hayat, T.; Qasim, M. Influence of thermal radiation and Joule heating on MHD flow of a Maxwell fluid in the presence of thermophoresis. Int. J. Heat Mass Transf. 2010, 53, 4780–4788. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Jagadeeshwar, P. Effect of Joule heating on the flow over an exponentially stretching sheet with convective thermal condition. Math. Sci. 2019, 13, 201–211. [Google Scholar] [CrossRef]
- Murugesan, T.; Kumar, M.D. Viscous dissipation and Joule heating effects on MHD flow of a Thermo-Solutal stratified nanofluid over an exponentially stretching sheet with radiation and heat generation/absorption. World Sci. News 2019, 129, 193–210. [Google Scholar]
- Sharada, K.; Shankar, B. Effect of partial slip and convective boundary condition on MHD mixed convection flow of Williamson fluid over an exponentially stretching sheet in the presence of joule heating. Glob. J. Pure Appl. Math. 2017, 13, 5965–5975. [Google Scholar]
- Yashkun, U.; Zaimi, K.; Ishak, A.; Pop, I.; Sidaoui, R. Hybrid nanofluid flow through an exponentially stretching/shrinking sheet with mixed convection and Joule heating. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 1930–1950. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Jagadeeshwar, P. MHD flow with Hall current and Joule heating effects over an exponentially stretching sheet. Nonlinear Eng. 2017, 6, 101–114. [Google Scholar] [CrossRef]
- Kumar, D.; Sinha, S.; Sharma, A.; Agrawal, P.; Dadheech, P.K. Numerical study of chemical reaction and heat transfer of MHD slip flow with Joule heating and Soret–Dufour effect over an exponentially stretching sheet. Heat Transf. 2021, 51, 1939–1963. [Google Scholar] [CrossRef]
- Agrawal, R.; Kaswan, P. Influence Of Thermal Radiation On Entropy Analysis Of Generalized Mhd Unsteady Viscous Fluid Flow On A Stretching Sheet With Joule Heating And Viscous Dissipation. Comput. Therm. Sci. Int. J. 2021, 13, 21–33. [Google Scholar] [CrossRef]
- Oyelakin, I.S.; Mondal, S.; Sibanda, P. Unsteady Casson nano fluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alex. Eng. J. 2016, 55, 1025–1035. [Google Scholar] [CrossRef]
- Bakar, N.; Zaimi WM KA, W.; Hamid, R.; Bidin, B.; Ishak, A. Boundary layer flow over a stretching sheet with a convective boundary condition and slip effect. World Appl. Sci. J. 2012, 17, 49–53. [Google Scholar]
- Sajid, M.; Ali, N.; Abbas, Z.; Javed, T. Stretching Flows with General Slip Boundary Condition. Int. J. Mod. Phys. B 2010, 24, 5939–5947. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, T.; Abbas, Z. Slip flow and heat transfer of a second grade fluid past a stretching sheet through a porous space. Int. J. Heat Mass Transf. 2008, 51, 4528–4534. [Google Scholar] [CrossRef]
- Afify, A.A. The influence of slip boundary condition on Casson nano fluid flow over a stretching sheet in the presence of viscous dissipation and chemical reaction. Math. Probl. Eng. 2017, 2017, 3804751. [Google Scholar] [CrossRef]
- Goud, B. Thermal Radiation Influences on MHD Stagnation Point Stream over a Stretching Sheet with Slip Boundary Conditions. Int. J. Thermofluid Sci. Technol. 2020, 7, 070201. [Google Scholar] [CrossRef]
- Khan, S.A.; Nie, Y.; Ali, B. Multiple slip effects on MHD unsteady viscoelastic nano-fluid flow over a permeable stretching sheet with radiation using the finite element method. SN Appl. Sci. 2020, 2, 66. [Google Scholar] [CrossRef]
- Wahab, H.A.; Hussain Shah, S.Z.; Ayub, A.; Sabir, Z.; Bilal, M.; Altamirano, G.C. Multiple characteristics of three-dimensional radiative Cross fluid with velocity slip and inclined magnetic field over a stretching sheet. Heat Transf. 2021, 50, 3325–3341. [Google Scholar] [CrossRef]
- Ahmad, U.; Ashraf, M.; Abbas, A.; Rashad, A.M.; Nabwey, H.A. Mixed convection flow along a curved surface in the presence of exothermic catalytic chemical reaction. Sci. Rep. 2021, 11, 12907. [Google Scholar] [CrossRef]
- Abbas, A.; Ashraf, M.; Chamkha, A.J. Combined effects of thermal radiation and thermophoretic motion on mixed convection boundary layer flow. Alex. Eng. J. 2021, 60, 3243–3252. [Google Scholar] [CrossRef]
- Ilyas, A.; Ashraf, M.; Rashad, A.M. Periodical Analysis of Convective Heat Transfer Along Electrical Conducting Cone Embedded in Porous Medium. Arab. J. Sci. Eng. 2021, 47, 8177–8188. [Google Scholar] [CrossRef]
- Ramzan, M.; Shaheen, N.; Chung, J.D.; Kadry, S.; Chu, Y.-M.; Howari, F. Impact of Newtonian heating and Fourier and Fick’s laws on a magnetohydrodynamic dusty Casson nanofluid flow with variable heat source/sink over a stretching cylinder. Sci. Rep. 2021, 11, 2357. [Google Scholar] [CrossRef] [PubMed]
- Abbas, S.Z.; Waqas, M.; Thaljaoui, A.; Zubair, M.; Riahi, A.; Chu, Y.M.; Khan, W.A. Modeling and analysis of unsteady second-grade nanofluid flow subject to mixed convection and thermal radiation. Soft Comput. 2022, 26, 1033–1042. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Optimal Boundary Control of the Boussinesq Approximation for Polymeric Fluids. J. Optim. Theory Appl. 2021, 189, 623–645. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).