Random Maximum 2 Satisfiability Logic in Discrete Hopfield Neural Network Incorporating Improved Election Algorithm
Abstract
1. Introduction
- To formulate a novel non-satisfiability logical rule by connecting Random 2 Satisfiability with Maximum 2 Satisfiability into one single formula called Random Maximum 2 Satisfiability. In this context, the logical outcome of the proposed logic is always False and allows the existence of redundant variable. Thus, the goal of the Random Maximum 2 Satisfiability to find the interpretation that maximize the number of satisfied clauses.
- To implement the proposed Random Maximum 2 Satisfiability into Discrete Hopfield Neural Network by finding the cost function of the sub-logical rule that is satisfiable. Each of the variables will be represented in terms of neurons and the synaptic weight of the neurons can be found by comparing cost function with the Lyapunov energy function.
- To propose Election Algorithm that consists of several operators such as positive advertisement, negative advertisement, and coalition to optimize the learning phase of the Discrete Hopfield Neural Network. In this context, the proposed EA will be utilized to find interpretation that maximize the number of the satisfied clause.
- To evaluate the performance of the proposed hybrid network in doing simulated datasets. The hybrid network consisting of Random Maximum 2 Satisfiability, Election Algorithm, and Hopfield Neural Network will be evaluated based on various performance metrics. Note that the performance of the hybrid network will be compared with other state of the art metaheuristics algorithm.
2. Related Works
2.1. Random Maximum 2 Satisfiability
2.2. Discrete Hopfield Neural Network
| Algorithm 1: The pseudocode of DHNN-RANMAX2SAT |
| Start |
| Create the initial parameters, , trial number, relaxation rate, tolerance value; |
| Initialize the neuron to each variable consisting of ; |
| while ; |
| Form initial states by using Equation (7); |
| [TRAINING PHASE] |
| Apply Equation (8) to define cost function ; |
| for do |
| Apply Equation (8) to check clauses satisfaction of clauses; |
| if |
| Satisfied; |
| Else |
| Unsatisfied; |
| end |
| Apply WA method to calculate synaptic weights; |
| Apply Equation (13) to compute the ; |
| [TESTING PHASE] |
| Compute final state by using local field computation, Equation (10); |
| for ; |
| End |
| Apply Equation (18) to compute the ; |
| Compute the final energy; |
| Assign global minimum energy or local minimum energy |
| if |
| Allocate Global minimum energy; |
| Else |
| Allocate Local minimum energy; |
| end |
| return Output the final neuron state; |
2.3. Genetic Algorithm
2.3.1. Initialization
2.3.2. Fitness Evaluation
2.3.3. Selection
2.3.4. Crossover
2.3.5. Mutation
| Algorithm 2: The pseudocode of GA in the training phase |
| Start |
| Create initial parameters including chromosomes population size consisting of , trial number; |
| while |
| Initialize random ; |
| [Selection] |
| for do |
| Apply Equation (21) to compute the fitness of each ; |
| Apply Equation (25) to compute ; |
| end |
| [Crossover] |
| for do |
| The states of the selected two exchanged at a random point; |
| End |
| [Mutation] |
| for do |
| Flipping states of at random location; |
| Evaluate the fitness of the based on Equation (21); |
| End |
| end while |
| return Output the final neuron state. |
2.4. Election Algorithm
2.4.1. Initializing Population and Forming Initial Parties
2.4.2. Positive Advertisement
2.4.3. Negative Advertisement
2.4.4. Coalition
2.4.5. Election Day
| Algorithm 3: The pseudocode of EA in the training phase |
| Start |
| Create the initial parameters that includes the population size consisting of , trial number; |
| while |
| Forming initial parties by using Equation (30); |
| for do |
| Apply Equation (31) to compute the similarity between the voters and the candidates |
| end |
| [Positive Advertisement] |
| For do |
| Apply Equation (32) to evaluate the number of voters; |
| Calculate the reasonable effect from the candidate by using Equation (33); |
| Update the neuron state according to Equation (26); |
| if ; |
| Assign as new ; |
| Else |
| Remain ; |
| end |
| [Negative Advertisement] |
| for do |
| Calculate the similarity between the voters from the other party and the candidate from Equation (36); |
| Compute the reasonable effect from the candidate and update the neuron state by using Equation (37); |
| if ; |
| Assign as new ; |
| else |
| Remain ; |
| end |
| [Coalition] |
| for do |
| Calculate the similarity between the voters from the other party and the candidate from Equation (36); |
| Compute the reasonable effect from the candidate and update the neuron state by using Equation (37); |
| If ; |
| Assign as new ; |
| Else |
| Remain ; |
| End |
| end while |
| return Output the final neuron state; |
3. Methodology
3.1. Performance Metrices
3.1.1. Root Mean Square Error (RMSE) and Mean Absolute Error (MAE)
3.1.2. Mean Absolute Percentage Error (MAPE)
3.1.3. Global Minimum Ratio
3.1.4. Jaccard Similarity Index ()
3.2. Baseline Methods
3.3. Experimental Design
4. Results and Discussion
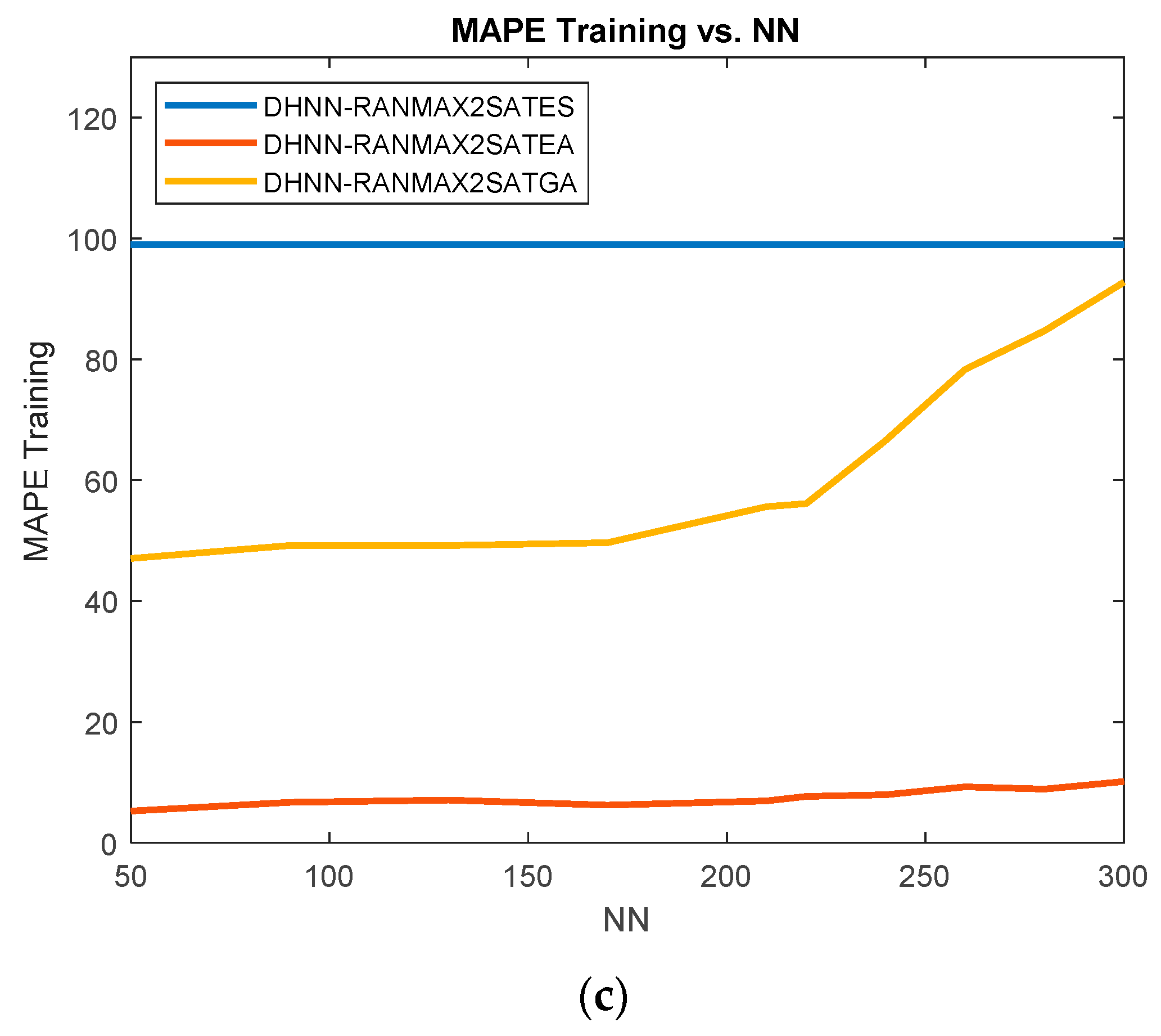
4.1. Training Error
- (i)
- Observe that, as the total number of neurons increases, the value of RMSE training, MAE training, and MAPE training increases for DHNN-RANMAX2SATES, DHNN-RANMAX2SAEA, and DHNN-RANMAX2SAGA. We can also observe that there is a drastic increase in phase 2 compared to phase 1 in the graphs. This is due to the non-systematic logical structure that consists of first order clauses in phase 2 having the chances of getting a satisfied interpretation being low compared to second order clauses in phase 1 which makes the graph increase. Therefore, overall, when the number of neurons increases, the number of satisfied interpretations decrease which makes the training errors increase due to the complexity of the logical structure [16].
- (ii)
- According to Figure 3, it is noticeable that the highest training error is shown at by DHNN-RANMAX2SATES compared to DHNN-RANMAX2SATEA and DHNN-RANMAX2SATGA. This is due to less stability of the neurons during the training phase and ES derives the wrong synaptic weight. Since ES is operated by a random search method, the complexity to get correct synaptic weight will increase as the number of neurons increases.
- (iii)
- Observe that as the number of neurons increases, DHNN-RANMAX2SATGA manages to achieve low training error compared to DHNN-RANMAX2SATES. Note that the operator of crossover with crossover rate of 1 in the Genetic Algorithm is able to change the fitness of the population frequently by using the fitness function [19]. Moreover, the mutation rate of 0.01 based on [19] is able to obtain the optimum fitness. Therefore, it is easy for the chromosomes to achieve an optimal cost function to retrieve the correct synaptic weight.
- (iv)
- However, based on the graph above, DHNN-RANMAX2SATEA outperformed DHNN-RANMAX2SATES and DHNN-RANMAX2SATGA as the number of neurons increased. Lower training error indicates the better accuracy of our model. This is due to proposed metaheuristic in which EA enhanced the training phase of DHNN. DHNN-RANMAX2SAEA is efficient in retrieving global minimum energy due to the global search and local search operators of EA [27]. This indicates that the optimization operators in EA enhanced the training phase of DHNN-RANMAX2SATEA. The highest rate of positive advertisement and negative advertisement chosen based on [27] that quickens the process of obtaining the candidate with maximum fitness. By diving the solution spaces during training phase, the synaptic weight management improved and the proposed model achieves the optimal training phase successfully.
4.2. Testing Error
- (i)
- According to Figure 4, the graphs show similar trends for DHNN-RANMAX2SATES, DHNN-RANMAX2SATEA, and DHNN-RANMAX2SATGA gives a constant graph for both phase 1 and phase 2 as the number of neurons increases. This is due to the logical structure becoming more complex as it contains a greater number of the neuron. In this case, as the number of neurons increases, the logical structure fails to retrieve more final states that lead to global minimum energy.
- (ii)
- Based on Figure 4, RMSE testing, MAE testing, and MAPE testing of DHNN-RANMAX2SATES increases at . ES is a searching algorithm. The training phase could be affected by the nature of ES which will continuously affect the testing phase, thus resulting in a high value of testing error. Wrong synaptic weights retrieved during the testing phase due to the inefficiency of synaptic weight management. The complexity of the network increases when resulting in a constant graph with maximum values of RMSE testing, MAE testing, and MAPE testing. Thus, the DHNN-RANMAX2SATES model starts retrieving the non-optimal states.
- (iii)
- According to the graphs, the accumulated errors are mostly 0 for DHNN-RANMAX2SATGA for RMSE testing, MAE testing, and MAPE testing. This is due to metaheuristics GA consisting of an optimization operator which can help to improve the solution. It can be deduced that GA barely gets trapped in the local minima solutions. The operators of GA always search for optimal solutions which correspond to the global minimum energy. Moreover, mutation operator in GA reduced the chances for the bit string to retrieve local minima solutions. Thus, this resulted in a zero value of RMSE testing, MAE testing, and MAPE testing as the number of neurons increases.
- (iv)
- Notice that the graphs of RMSE testing, MAE testing, and MAPE testing of DHNN-RANMAX2SATEA also show a constant graph that achieves zero testing error as the number of neurons increases. Lower errors of RMSE testing, MAE testing, and MAPE testing define the effectiveness of proposed model to generates more global minimum energy. This is due to the effective synaptic weight management during training phase of DHNN-RANMAX2SATEA. The presence of local search and global search operator in EA that divides the solution spaces during training phase is the main reason that improves the synaptic weight management during retrieval phase. This leads DHNN-RANMAX2SATEA to produce global minimum energy in the testing phase.
- (v)
- Generally, we can say that DHNN-RANMAX2SATEA and DHNN-RANMAX2SATGA outperformed DHNN-RANMAX2SATES in terms of RMSE testing, MAE testing, and MAPE testing. This indicates that ES failed to retrieve optimal synaptic weight during the training phase and consequently affected the testing phase, thus resulting in local minima solution. Meanwhile, GA and EA find more variation of the solution (more global solution). Therefore, DHNN-RANMAX2SATEA and DHNN-RANMAX2SATGA help the network to reduce generating local minimum energy by achieving zero for RMSE testing, MAE testing, and MAPE testing.
4.3. Energy Analysis (Global Minimum Ratio)
- (i)
- According to the graph, DHNN-RANMAX2SATES shows a decrease in the graph when with almost 0. At this stage, ES is only able to produce much less global minimum energy because most of the solutions are trapped at sub-optimal states. When the number of neurons increases in ES, the network becomes more complex. Thus, the local field is not able to generate the correct state of the neuron as the number of neuron increases. Hence, we can observe a constant graph at when .
- (ii)
- However, DHNN-RANMAX2SATGA manages to achieve almost 1 as the total number of neurons increases which indicates that most of the final neuron state in the solution space achieved global minimum energy [19]. The complexity of the searching technique has been reduced by implementing GA. The crossover stage improves the unsatisfied bit string with the highest fitness. The bit strings improved when it achieved the highest fitness as the number of generations increased. Therefore, GA produces many bit strings that achieved global minimum energy compared to the exhaustive search method.
- (iii)
- Therefore, DHNN-RANMAX2SATEA also manages to achieve almost 1 as the total number of neurons increases. This indicates that DHNN-RANMAX2SATEA manages to obtain stable final neuron states. The reason is due to the capability of DHNN-RANMAX2SATEA in achieving optimal training phase which results in an optimal testing phase where global minimum energy will be produced. Moreover, EA produces a bit string with less complexity by partitioning the solution space into 4 parties. The number of local solutions produced at the end of computation will be reduced by the effective relaxation method by choosing a relaxation rate of 3 [30].
- (iv)
- Generally, based on the outcomes of DHNN-RANMAX2SATES, DHNN-RANMAX2SATEA, and DHNN-RANMAX2SATGA is able to withstand the complexity up to 300 neurons. It was observed that more than 99% of final state of the neuron in DHNN-RANMAX2SATGA and DHNN-RANMAX2SATEA achieved the global minimum solution. However, it was observed that 0.1% of final state of the neuron in DHNN-RANMAX2SATES achieved the global minimum solution. Therefore, DHNN-RANMAX2SATGA and DHNN-RANMAX2SATEA outperformed DHNN-MAX2SATES as the number of neurons increased in terms of global minimum ratio.
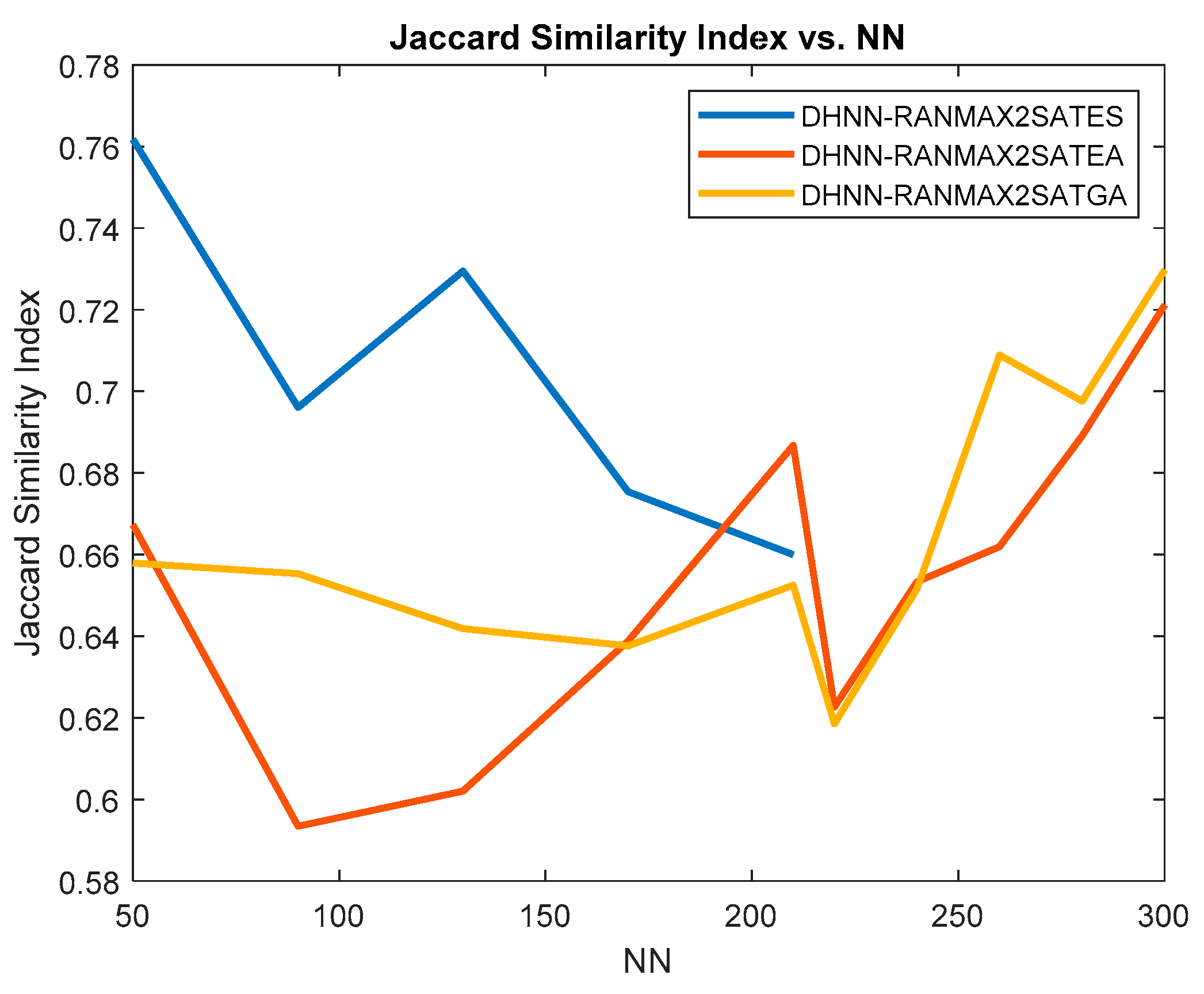
4.4. Similarity Analysis (Jaccard Similarity Index)
- (i)
- Based on Figure 6, DHNN-RANMAX2SATES shows the highest at . This indicates the major deviation and bias in the final states generated. The high value of indicates that the model achieves overfitting as the DHNN-RANMAX2SATES model failed to produce differences in the final states of the neuron. However, there is a decrease in trend from to . The is decreasing, showing that the final neuron state generated is varied as the neuron increased [15]. This is due to the fewer benchmark neurons generated during the retrieval phase by the proposed model.
- (ii)
- However, Jaccard has stopped getting any value when because all the solutions retrieved by the network are local solutions. This is because the nature of ES that operates based on trial and error could affect the minimization of the cost function. Since ES failed to produce optimal synaptic weight in training phase, it affects the final neuron states produced by the model at the end of computation.
- (iii)
- According to Figure 6, we can see that the fluctuation for DHNN-RANMAX2SATGA and DHNN-RANMAX2SATEA increased. This is due to the total number of neurons increases. This increases the chances for the neuron to be trapped at the local minima. A higher number of total clauses imply more training error during the training phase which causes less variation of the final solution than the benchmark solution. Thus, this causes the trend of for DHNN-RANMAX2SATGA and DHNN-RANMAX2SATEA to increase.
- (iv)
- However, DHNN-RANMAX2SATEA has the lowest index value for Jaccard when . In this case, the neuron retrieved from DHNN-RANMAX2SATEA has a lowest similarity with the benchmark state. The higher number of neuron variations produced by the network obtains lower value similarity index. This shows that the network produces less overfitting of the final states of the neuron.
4.5. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- (i)
- Initialization population and forming initial parties.
| 1 | 1 | −1 | −1 | 1 | 1 | 1 | 1 | 6 | |
| −1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| 1 | −1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| 1 | 1 | −1 | 1 | −1 | −1 | −1 | 1 | 5 |
| 1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| −1 | 1 | −1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| 1 | −1 | −1 | −1 | −1 | 1 | −1 | −1 | 4 | |
| 1 | −1 | −1 | −1 | −1 | 1 | −1 | 1 | 5 | |
| 1 | −1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 |
| 1 | 1 | 1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 4 | |
| 1 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 4 | |
| −1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| −1 | −1 | −1 | −1 | 1 | 1 | −1 | −1 | 4 |
| 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| −1 | −1 | −1 | −1 | −1 | 1 | −1 | −1 | 4 | |
| −1 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | 5 | |
| −1 | −1 | −1 | −1 | 1 | 1 | −1 | −1 | 4 | |
| −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 3 |
- (ii)
- Positive Advertisement
| 1 | 1 | −1 | −1 | 1 | 1 | 1 | 1 | 6 | |
| −1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| 1 | −1 | 1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | 1 | 1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | 1 | −1 | 1 | −1 | −1 | −1 | 1 | 5 |
| 1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| −1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | −1 | −1 | −1 | 1 | −1 | −1 | −1 | 4 | |
| 1 | −1 | −1 | −1 | −1 | 1 | −1 | 1 | 5 | |
| 1 | −1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 |
| 1 | 1 | 1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 5 | |
| 1 | 1 | 1 | −1 | −1 | 1 | 1 | 1 | 7 | |
| −1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| −1 | −1 | −1 | −1 | 1 | 1 | −1 | −1 | 4 |
| 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| −1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 5 | |
| −1 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | 5 | |
| −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 6 | |
| −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 3 |
- (iii)
- Negative Advertisement
| 1 | 1 | −1 | −1 | 1 | 1 | 1 | 1 | 6 | |
| −1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| 1 | −1 | 1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | 1 | 1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | 1 | −1 | 1 | −1 | −1 | −1 | 1 | 5 | |
| −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 6 |
| 1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| −1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | −1 | −1 | −1 | 1 | −1 | −1 | −1 | 4 | |
| 1 | −1 | −1 | −1 | −1 | 1 | −1 | 1 | 5 | |
| 1 | −1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| −1 | 1 | 1 | 1 | 1 | −1 | 1 | 1 | 7 |
| 1 | 1 | 1 | 1 | 1 | 1 | −1 | −1 | 5 | |
| 1 | 1 | −1 | −1 | 1 | −1 | 1 | −1 | 5 | |
| 1 | 1 | 1 | −1 | −1 | 1 | 1 | 1 | 7 | |
| −1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| −1 | −1 | −1 | −1 | 1 | 1 | −1 | −1 | 4 |
| 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| −1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 5 | |
| −1 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | 5 | |
| −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 6 | |
| −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 3 |
- (iv)
- Coalition
| −1 | −1 | 1 | 1 | −1 | −1 | −1 | −1 | 6 | |
| −1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 6 | |
| 1 | 1 | −1 | 1 | 1 | 1 | 1 | 1 | 5 | |
| 1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 5 | |
| 1 | 1 | −1 | −1 | 1 | 1 | 1 | 1 | 5 | |
| 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 6 | |
| 1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | 4 | |
| 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 6 | |
| −1 | −1 | −1 | −1 | −1 | −1 | 1 | 1 | 3 |
| 1 | 1 | −1 | −1 | 1 | 1 | 1 | 1 | 6 | |
| −1 | 1 | −1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| 1 | −1 | −1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| 1 | −1 | −1 | −1 | −1 | 1 | 1 | −1 | 5 | |
| 1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 3 | |
| −1 | 1 | 1 | 1 | 1 | −1 | 1 | 1 | 7 | |
| 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 4 | |
| 1 | 1 | −1 | −1 | −1 | −1 | −1 | −1 | 3 | |
| −1 | −1 | −1 | 1 | 1 | −1 | −1 | −1 | 5 | |
| −1 | 1 | 1 | −1 | 1 | 1 | −1 | 1 | 6 |
- (v)
- Election Day
References
- Liu, X.; Qu, X.; Ma, X. Improving flex-route transit services with modular autonomous vehicles. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102331. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing data supported traffic flow prediction via denoising schemes and ANN: A comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Chereda, H.; Bleckmann, A.; Menck, K.; Perera-Bel, J.; Stegmaier, P.; Auer, F.; Kramer, F.; Leha, A.; Beißbarth, T. Explaining decisions of graph convolutional neural networks: Patient-specific molecular subnetworks responsible for metastasis prediction in breast cancer. Genome Med. 2021, 13, 42. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y. Prediction of temperature distribution on piston crown surface of dual-fuel engines via a hybrid neural network. Appl. Therm. Eng. 2022, 218, 119269. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, P.; Zhang, C.; Qu, X.; Gao, C.; Xie, Y. Multi-mode fusion BP neural network model with vibration and acoustic emission signals for process pipeline crack location. Ocean. Eng. 2022, 264, 112384. [Google Scholar] [CrossRef]
- Hopfield, J.J.; Tank, D.W. “Neural” computation of decisions in optimization problems. Biol. Cybern. 1985, 52, 141–152. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Ye, X. A new fractional-order chaos system of Hopfield neural network and its application in image encryption. Chaos Solitons Fractals 2022, 157, 111889. [Google Scholar] [CrossRef]
- Boykov, I.; Roudnev, V.; Boykova, A. Stability of Solutions to Systems of Nonlinear Differential Equations with Discontinuous Right-Hand Sides: Applications to Hopfield Artificial Neural Networks. Mathematics 2022, 10, 1524. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S. An Optical Image Encryption Method Using Hopfield Neural Network. Entropy 2022, 24, 521. [Google Scholar] [CrossRef]
- Mai, W.; Lee, R.S. An Application of the Associate Hopfield Network for Pattern Matching in Chart Analysis. Appl. Sci. 2021, 11, 3876. [Google Scholar] [CrossRef]
- Folli, V.; Leonetti, M.; Ruocco, G. On the maximum storage capacity of the Hopfield model. Front. Comput. Neurosci. 2017, 10, 144. [Google Scholar] [CrossRef]
- Lee, D.L. Pattern sequence recognition using a time-varying Hopfield network. IEEE Trans. Neural Netw. 2002, 13, 330–342. [Google Scholar] [CrossRef]
- Abdullah, W.A.T.W. Logic programming on a neural network. Int. J. Intell. Syst. 1992, 7, 513–519. [Google Scholar] [CrossRef]
- Abdullah, W.A.T.W. Logic Programming in neural networks. Malays. J. Comput. Sci. 1996, 9, 1–5. Available online: https://ijps.um.edu.my/index.php/MJCS/article/view/2888 (accessed on 1 June 1996). [CrossRef]
- Kasihmuddin, M.M.S.; Mansor, M.A.; Md Basir, M.F.; Sathasivam, S. Discrete mutation Hopfield neural network in propositional satisfiability. Mathematics 2019, 7, 1133. [Google Scholar] [CrossRef]
- Sathasivam, S.; Mansor, M.A.; Ismail, A.I.M.; Jamaludin, S.Z.M.; Kasihmuddin, M.S.M.; Mamat, M. Novel Random k Satisfiability for k ≤ 2 in Hopfield Neural Network. Sains Malays. 2020, 49, 2847–2857. [Google Scholar] [CrossRef]
- Karim, S.A.; Zamri, N.E.; Alway, A.; Kasihmuddin, M.S.M.; Ismail, A.I.M.; Mansor, M.A.; Hassan, N.F.A. Random satisfiability: A higher-order logical approach in discrete Hopfield Neural Network. IEEE Access 2021, 9, 50831–50845. [Google Scholar] [CrossRef]
- Sidik, M.S.S.; Zamri, N.E.; Mohd Kasihmuddin, M.S.; Wahab, H.A.; Guo, Y.; Mansor, M.A. Non-Systematic Weighted Satisfiability in Discrete Hopfield Neural Network Using Binary Artificial Bee Colony Optimization. Mathematics 2022, 10, 1129. [Google Scholar] [CrossRef]
- Zamri, N.E.; Azhar, S.A.; Mansor, M.A.; Alway, A.; Kasihmuddin, M.S.M. Weighted Random k Satisfiability for k = 1, 2 (r2SAT) in Discrete Hopfield Neural Network. Appl. Soft Comput. 2022, 126, 109312. [Google Scholar] [CrossRef]
- Guo, Y.; Kasihmuddin, M.S.M.; Gao, Y.; Mansor, M.A.; Wahab, H.A.; Zamri, N.E.; Chen, J. YRAN2SAT: A novel flexible random satisfiability logical rule in discrete hopfield neural network. Adv. Eng. Softw. 2022, 171, 103169. [Google Scholar] [CrossRef]
- Gao, Y.; Guo, Y.; Romli, N.A.; Kasihmuddin, M.S.M.; Chen, W.; Mansor, M.A.; Chen, J. GRAN3SAT: Creating Flexible Higher-Order Logic Satisfiability in the Discrete Hopfield Neural Network. Mathematics 2022, 10, 1899. [Google Scholar] [CrossRef]
- Bonet, M.L.; Buss, S.; Ignatiev, A.; Morgado, A.; Marques-Silva, J. Propositional proof systems based on maximum satisfiability. Artif. Intell. 2021, 300, 103552. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.M.; Mansor, M.A.; Sathasivam, S. Discrete Hopfield neural network in restricted maximum k-satisfiability logic programming. Sains Malays. 2018, 47, 1327–1335. [Google Scholar] [CrossRef]
- Sathasivam, S.; Mamat, M.; Kasihmuddin, M.S.M.; Mansor, M.A. Metaheuristics approach for maximum k satisfiability in restricted neural symbolic integration. Pertanika J. Sci. Technol. 2020, 28, 545–564. [Google Scholar]
- Tembine, H. Dynamic robust games in mimo systems. IEEE Trans. Syst. Man Cybern. Part B 2011, 41, 990–1002. [Google Scholar] [CrossRef]
- Aissi, H.; Bazgan, C.; Vanderpooten, D. Min–max and min–max regret versions of combinatorial optimization problems: A survey. Eur. J. Oper. Res. 2009, 197, 427–438. [Google Scholar] [CrossRef]
- Emami, H.; Derakhshan, F. Election algorithm: A new socio-politically inspired strategy. AI Commun. 2015, 28, 591–603. [Google Scholar] [CrossRef]
- Sathasivam, S.; Mansor, M.; Kasihmuddin, M.S.M.; Abubakar, H. Election Algorithm for Random k Satisfiability in the Hopfield Neural Network. Processes 2020, 8, 568. [Google Scholar] [CrossRef]
- Bazuhair, M.M.; Jamaludin, S.Z.M.; Zamri, N.E.; Kasihmuddin, M.S.M.; Mansor, M.A.; Alway, A.; Karim, S.A. Novel Hopfield neural network model with election algorithm for random 3 satisfiability. Processes 2021, 9, 1292. [Google Scholar] [CrossRef]
- Sathasivam, S. Upgrading logic programming in Hopfield network. Sains Malays. 2010, 39, 115–118. [Google Scholar]
- Zhi, H.; Liu, S. Face recognition based on genetic algorithm. J. Vis. Commun. Image Represent. 2019, 58, 495–502. [Google Scholar] [CrossRef]
- Mansor, M.A.; Sathasivam, S. Accelerating activation function for 3-satisfiability logic programming. Int. J. Intell. Syst. Appl. 2016, 8, 44–50. [Google Scholar] [CrossRef]
- Sherrington, D.; Kirkpatrick, S. Solvable model of a spin-glass. Phys. Rev. Lett. 1975, 35, 1792. [Google Scholar] [CrossRef]
- Zhang, T.; Bai, H.; Sun, S. Intelligent Natural Gas and Hydrogen Pipeline Dispatching Using the Coupled Thermodynamics-Informed Neural Network and Compressor Boolean Neural Network. Processes 2022, 10, 428. [Google Scholar] [CrossRef]
- Jiang, W.; Luo, J. Graph neural network for traffic forecasting: A survey. Expert Syst. Appl. 2022, 207, 117921. [Google Scholar] [CrossRef]
- Yang, B.S.; Han, T.; Kim, Y.S. Integration of ART-Kohonen neural network and case-based reasoning for intelligent fault diagnosis. Expert Syst. Appl. 2004, 26, 387–395. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Trojovský, P. A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Sci. Rep. 2022, 12, 9924. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Zainuddin, Z.; Lai, K.H.; Ong, P. An enhanced harmony search based algorithm for feature selection: Applications in epileptic seizure detection and prediction. Comput. Electr. Eng. 2016, 53, 143–162. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Hu, L.; Sun, F.; Xu, H.; Liu, H.; Zhang, X. Mutation Hopfield neural network and its applications. Inf. Sci. 2011, 181, 92–105. [Google Scholar] [CrossRef]
- Wu, A.; Zhang, J.; Zeng, Z. Dynamic behaviors of a class of memristor-based Hopfield networks. Phys. Lett. A 2011, 375, 1661–1665. [Google Scholar] [CrossRef]
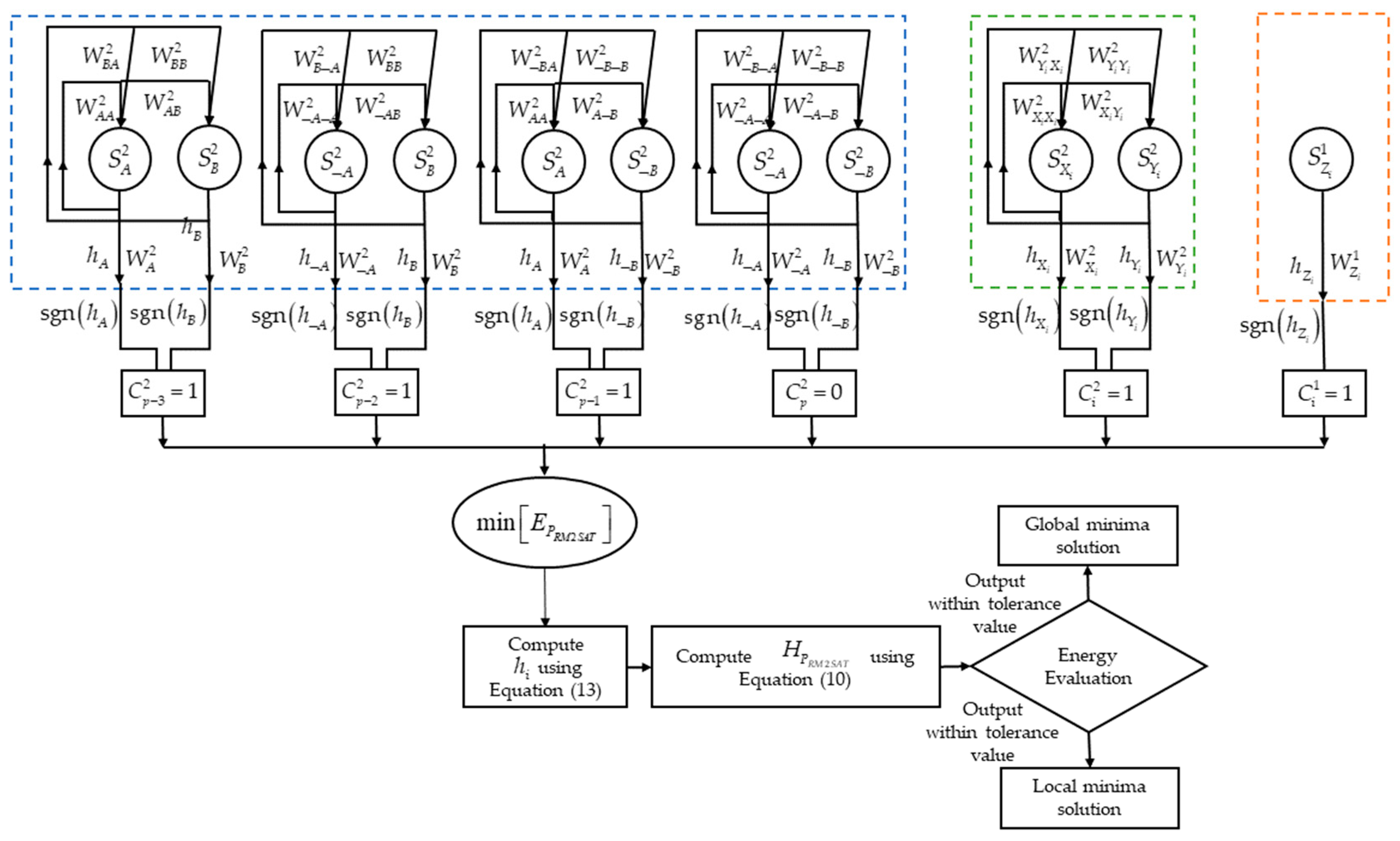





| Author(s) | Detail of the Studies | Summary and Findings |
|---|---|---|
| Hopfield and Tank [6] | The authors proposed non-linear analog neurons. | The authors used DHNN to solve the optimization of the Traveling Salesman Problem (TSP). |
| Abdullah [13] | The author proposed the Wan Abdullah method to solve logic programming in DHNN. | This author proposed a new method in retrieving the synaptic weight of Horn clause. The new method has outperformed Hebbian learning. |
| Kasihmuddin et al. [23] | The authors proposed Restricted Maximum k Satisfiability in DHNN. | The performance of MAXkSAT in DHNN outperformed MAXkSAT in Kernel Hopfield Neural Network (KHNN). |
| Sathasivam et al. [16] | The authors proposed a RAN2SAT has been developed to represent the non-systematic logical rule in DHNN. | RAN2SAT is embedded in DHNN by retrieving maximum outcomes of global solutions. |
| Zamri et al. [19] | The author proposed Implemented Imperialist Competitive Algorithm (ICA) in 3 Satisfiability (3 SAT) and compared with ES and GA. | This paper shows the comparison of the proposed model done by two real data sets and ICA has outperformed ES and GA. |
| Bazuhair et al. [29] | This paper proposed EA in training phase of RAN3SAT. | Incorporation of RAN3SAT with EA in DHNN has the ability to achieve the optimal training phase. |
| Gao et al. [21] | This paper utilized DHNN in explaining G-Type Random k Satisfiable. | This paper emphasizes on the formulation of first, second, and third order of clauses in the logical structure. The proposed logic structure produces higher solution diversity. |
| Karim et al. [17] | The author proposed a new novel of multi-objective HEA for higher order Random Satisfiability in DHNN. | HEA achieves highest fitness value. The HEA is able to yield a high quality of global optimal solution with higher accuracy and outperformed GA, ABC, EA, and ES. |
| Parameter | Parameter Value |
|---|---|
| Tolerance value () | 0.001 [28] |
| Number of combinations () | 100 [28] |
| Number of learnings () | 10,000 |
| Number of trials () | 100 [28] |
| Order of clauses (k) | 1,2 |
| Number of neurons () | (50, 300) |
| Threshold time simulation | 24 h |
| Relaxation rate () | 3 [30] |
| Activation function | Hyperbolic Tangent Activation Function (HTAF) [32] |
| Parameter | Parameter Value |
|---|---|
| Number of generations | 100 |
| Selection rate | 0.1 [19] |
| Crossover rate | 1 [19] |
| Mutation rate | 0.01 [19] |
| Type of selection | Random |
| Parameter | Parameter Value |
|---|---|
| Number of populations | 120 [28] |
| Number of parties | 4 [28] |
| Positive advertisement rate | 0.5 [27] |
| Negative advertisement rate | 0.5 [27] |
| Candidate selection | Highest fitness |
| Type of voter’s attraction | Random |
| Type of state flipping | Random |
| Number of strings on election day | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Someetheram, V.; Marsani, M.F.; Mohd Kasihmuddin, M.S.; Zamri, N.E.; Muhammad Sidik, S.S.; Mohd Jamaludin, S.Z.; Mansor, M.A. Random Maximum 2 Satisfiability Logic in Discrete Hopfield Neural Network Incorporating Improved Election Algorithm. Mathematics 2022, 10, 4734. https://doi.org/10.3390/math10244734
Someetheram V, Marsani MF, Mohd Kasihmuddin MS, Zamri NE, Muhammad Sidik SS, Mohd Jamaludin SZ, Mansor MA. Random Maximum 2 Satisfiability Logic in Discrete Hopfield Neural Network Incorporating Improved Election Algorithm. Mathematics. 2022; 10(24):4734. https://doi.org/10.3390/math10244734
Chicago/Turabian StyleSomeetheram, Vikneswari, Muhammad Fadhil Marsani, Mohd Shareduwan Mohd Kasihmuddin, Nur Ezlin Zamri, Siti Syatirah Muhammad Sidik, Siti Zulaikha Mohd Jamaludin, and Mohd. Asyraf Mansor. 2022. "Random Maximum 2 Satisfiability Logic in Discrete Hopfield Neural Network Incorporating Improved Election Algorithm" Mathematics 10, no. 24: 4734. https://doi.org/10.3390/math10244734
APA StyleSomeetheram, V., Marsani, M. F., Mohd Kasihmuddin, M. S., Zamri, N. E., Muhammad Sidik, S. S., Mohd Jamaludin, S. Z., & Mansor, M. A. (2022). Random Maximum 2 Satisfiability Logic in Discrete Hopfield Neural Network Incorporating Improved Election Algorithm. Mathematics, 10(24), 4734. https://doi.org/10.3390/math10244734








