Abstract
A mathematical model is created to analyze the impact of Thompson and Troian slip boundaries over a contracting/expanding surface sustaining nanofluid-containing carbon nanotubes along a stagnation point flow. Both multi-wall (MWCNTs) and single-wall (SWCNTs) carbon nanotubes are taken into consideration, with water serving as the base liquid. The flow is obtained due to the stretching or contracting of the surface. The thermal radiation, activation energy, buoyancy impacts, and chemical processes called quartic autocatalysis are additionally added to the original mathematical model. The MATLAB-constructed bvp4c function involving the three-stage Lobatto IIIa formula for the numerical results of dimensionless velocity, concentration, and temperature profiles are used. By contrasting it against a published paper in this limited instance, it is determined whether the suggested mathematical model is legitimate. In this sense, a remarkable consensus is achieved. Graphical representations are used to depict the behavior of many non-dimensional flow variables, such as the slip velocity parameter, the inertia coefficient, the porosity parameter, and the solid volume fraction. Surface drag force computations are reported to examine the effects at the permeable stretching surface. It has been shown that increasing the slip velocity factor increases the fluid streaming velocity while decreasing the surface drag force. If the endothermic/exothermic coefficient increases, the local thermal transfer efficiency falls. For nanofluids, the changing viscosity factor increases axial velocity while decreasing temperature distribution. Additionally, the solid volumetric fraction improves the temperature distributions by lowering the concentration profile and speed.
Keywords:
stagnation point; magnetohydrodynamics; endothermic and exothermic reaction; heat generation/absorption; activation energy; carbon nano tubes MSC:
76W05; 76D05; 7604
1. Introduction
When industries and scientists were seeking out greater and better thermal characteristics in fluids used on a regular basis for diverse tasks, Mesuda et al. [1] suggested the introduction of nano-sized particles in ordinary fluids in 1993. Later, the term nanofluid was officially defined by Choi and Eastman [2], and these fluids became a prime focus of researchers. Nanoparticles are typically 1–100 nm in size, but this might vary significantly depending on their sizes and shapes. Water, ethylene glycol, and oil are commonly used base fluids. A nanofluid is a combination of nanosized materials and a base liquid. These nanoparticles are suspended in a base fluid that is colloidal in nature and has weaker thermal conductivity. The major goal of nanosized particles is intended to improve the thermal conductivity of fluids, as well as increase heat transmission. Because of their structure, nanosized particles have unique physical and chemical features and contribute to the development of thermophysical systems. Nanofluids have a wide range of applications, such as in nano-drug delivery, pharmaceutical operations, heating/cooling appliances, fuel cells, and microelectronics. Nanofluids are utilized as coolants in the thermal exchange systems of automobiles and nuclear reactors. However, they are also useful due to their regulated optical features.
Carbon nanotubes are cylinder-type shapes that are formed by rolling or folding a graphite sheet. They have unique mechanical, thermophysical, and chemical properties. Because of their cylindrical form, huge surface area, and small size, carbon nanotubes offer advantages over other macro/nanoparticles. Carbon nanotubes are categorized as SWCNTs or MWCNTs based on their number of graphene layers. The effects of the nanofluid in the physiological examination of cilia were highlighted by Sadaf and Nadeem [3]. Sivasankaran et al. [4] investigated the heat production of nanofluids in the cavity. Ahmed et al. [5] investigated the flow of multi-walled and single-walled carbon nanotubes (MWCNT and SWCNT) across a circular stretchable semi-infinite zone containing water as the base fluid. Hosseinzadeh et al. [6] concentrated on the MWCNTs and SWCNTs combined in ethylene glycol flowing between the two rotating discs with extensible qualities in it; the effects of MHD and thermal radiations were considered, and findings revealed that the fluid system’s instability and the volume fraction of the nanosized particles decreases as the radiation increases. Ramzan et al. [7] investigated a physical system of gyrotactic microorganisms and CNTs submerged in water that was flowing on the top of a vertical cone immersed in a permeable medium by using the bvp4c MATLAB software and discovered that increasing the suction parameter reduces the nanofluid stream velocity. They also considered chemical reactions, thermal radiation, and species stratification. Khan et al. [8] examined the flow at the stagnation point of carbon nanotubes moving across an extended surface in the applied magnetic field, as well as thermal radiation, homogeneous and heterogeneous reactions, and heat absorption/generation. By applying the shooting method, numerical consequences revealed that MWCNTs had a greater induced magnetic field than SWCNTs. Ramazan et al. [9] studied CNTs and gyrotactic microorganisms in a fluid moving through a vertical cone enclosed by porous media. Joule heating, thermal radiation, MHD, and the homogeneous and heterogeneous reactions were all thought to be important inside the fluid system. According to the results obtained by using bvp4c MATLAB software, the flow of the fluid decreases with increasing magnetic force. Khan et al. [10] used the homotopy analysis method (HAM) to study a radiant bioconvective MHD nanofluid flow across an elongated oscillating plane and discovered that the temperature of the nanofluid increases as the buoyancy ratio increases. Sergii et al. [11] presented an analytical theory for the electrostatic interactions between two spherical dielectric particles with arbitrary charge distributions expanded in multipolar terms submerged in a polarizable ionic solvent and with arbitrary radii and dielectric constants. Yu [12] presented a new formalism regarding reciprocity and arbitrarily accommodated many dielectric spheres of different dielectric constants and sizes while being rigorous at the Debye–Hückel level. Some further prominent articles highlighting the use of nanofluid are as follows: refs. [13,14,15,16,17]. A chemical reaction is the interaction of two or more chemicals, which leads to the composition of one or more new chemical substances. A chemical reaction is the breaking of old bonds in order to form a new bond chemically. This is also known as the chemical change caused by the interaction of two or more chemical substances. The temperature of the system rises or decreases when energy is transferred to or from the environment during a chemical process. Exothermic reactions are chemical processes for which energy is discharged into the atmosphere (i.e., outside of the system). Energy is typically conveyed as heat energy, which causes the atmosphere to heat up. The burning process is an illustrative example of an exothermic reaction. Endothermic reactions are chemical reactions that extract energy from their environment. Normally, the energy is shifted as heat, raising the temperature of the reaction mixture. Chemically reactive models, such as biological systems and combustion, are represented by homogeneous/heterogeneous reactions. The surfaces of the catalysts experience heterogeneous reactions, but the fluid itself experiences homogenous reactions. In practice, homogeneous and heterogeneous reactions can be observed in a number of different fields, including air pollution, food processing, ignition, and biological processes. The species of chemical reactions together with the activation energy phenomenon plays a major role in various engineering fields. Mass transport and chemical processes can be seen in the consumption as well as production of reactant species. Regarding the existence of thermal dissipation, Maleque [18] was interested in the study of the impact of endothermic/exothermic chemical processes having Arrhenius activation energy on magnetohydrodynamic-free convective and the mass transfer flow. Recently, Bejawada et al. [19] investigated a magnetohydrodynamic Casson fluid flow with chemical reaction properties along with a porous Forchheimer medium over a non-linear sheet. Suleman et al. [20] used the shooting technique to show how the concentration of nanoparticles in a silver-water nanofluid mixture decayed due to upsurging homogeneous and heterogeneous reactions influenced by viscous dissipation, MHD, thermal radiation that was not linear, and Joule heating moving through a non-linear extending cylinder. Imtiaz et al. [21] explored the streaming of the two-dimensional magnetohydrodynamic viscous fluid flow passing over a stretched sheet. The solution was approximated with the use of a quasi-linearization method and the implicit finite difference approach, taking into account the significant impact of homogeneous and heterogeneous reactions, thermal radiation, and Joule heating. The study discovered that viscous fluids had lower fluid speed and concentration than viscoelastic fluids, and both homogeneous and heterogeneous reactions have a negative effect on fluid viscosity. Suleman et al. [22] used the shooting approach to analyze silver-water nanofluids with MHD, nonlinear heat radiation, and homogeneous and heterogeneous reactions through a nonlinear extended cylinder. Despite a greater radiation impact, the results showed better thermal conditions. Doh et al. [23] further investigated homogeneous and heterogeneous reactions with silver water nanofluids on a revolving permeable disc with changing disc thickness.
During fluid flow research, it is frequently thought that small-scale slips can happen at a fluid-solid interface as a result of uncertainty at the intense stress levels in methodologies such as polymer extraction. Fluid motion at a geometry surface is affected by such fluid slip impacts. Khan et al. [24] investigated the viscous hydromagnetic fluid flow across the permeable rotatable disk with non-linear thermal radiation and partial slip by considering the shooting method. The findings revealed a clear decline in surface friction as slip estimation increased. Using the Crank–Nicolson approach, Hamid et al. [25] investigated the natural convection of the Prandtl fluid, which was flowing at a point of stagnation across an infinite elongated plate. The geometry of the model is presented on the Figure 1. When studying slip at the sheet surface and MHD, it was discovered that when a slip impact was combined with a low magnetic field, the velocity increased dramatically. Reddy et al. [26] investigated magnetohydrodynamic Eyring–Powell fluid flow regarding nonlinear radiation, solutal slippage, temperature, velocity, and chemical processes using a Range–Kutta 4th order scheme. Kiyasatfar [27] investigated the convective slip flow of a non-Newtonian fluid among parallel plates with circular microchannels using the power-law model. The results show that for both geometries, lowered fluid stream speed and increased heat exchange rates and molecule stability occurred in rising slip situations.
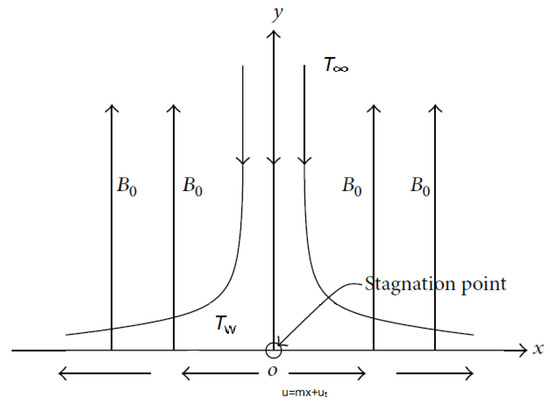
Figure 1.
Geometry of the model [25].
According to the aforementioned studies, fewer expeditions are explored for the study of the Thompson and Troian slip forms. In the existence of suction/injection, for nanofluids based on the Yamada and Ota model consisting of two nanoparticles, i.e., single and multi-wall carbon nanotubes suspended in a base fluid (water), the flow velocity, temperature, and concentration of nanofluid in the presence of the Cattaneo–Christov heat flux model are taken into account. Stagnation point flow is taken over the infinitely expanding sheet. Chemical reactions, nonlinear heat generation, and activation energy are the main key points that are focused on the current problem. The modeled equations are solved by the bvp4c technique. Graphs are drawn for the different parameters to better understand their impact on velocity and temperature.
2. Mathematical Model
Here, we consider the two-dimensional Newtonian nanofluid flowing over the sheet which is linearly stretched along the x-axis. A stagnation point flow is considered along with a magnetic field which is applied normally to the flow. Heat generation, chemical reaction, activation energy, and convection are also prominent impacts that are taken into account. Importantly Thompson and Troian slip mechanisms are employed on the surface. Single and multi-wall carbon nanotubes are taken as nanoparticles which are mixed in water. The fluid flow is compressible, and the Boussinesq approximation is valid for the case of the present problem. Free convection behavior is taken due to buoyancy forces. The momentum equation comprises the buoyancy phenomenon, stagnation point, and free convection phenomenon. Heat transfer is determined in a more precise manner with the utilization of the Cattaneo–Christov heat flux expression instead of classical Fourier law expression in the energy equation. Sometimes, extra energy is required to proceed with a chemical reaction due to the slow collision of fluid molecules. This is why an activation energy expression is utilized in energy as well as concentration equations. The governing modeled PDEs are derived from the law of conservation of mass, Newton’s second law of motion, the second law of thermodynamics, and Fick’s second law of diffusion. After accounting for the boundary layer estimation, the system can be represented as follows [6,7,8,18].
where T represents the fluid temperature, C represents the concentration, and reresents the velocity components in the . The parameter stands for the mass diffusion coefficient, which is the rate of limiting factor for the chemical process, is the endothermic/exothermic factor, and represents the Arrhenius expression, where n represents a unit-less rate constant . The thermophysical characteristics of the nanofluid are presented in Table 1. The corresponding boundary conditions are as follows:

Table 1.
Thermophysical characteristics of nanofluid and base.
The thermophysical properties are represented as defined from the Yamada and Ota model:
Introducing dimensionless variables, we obtain:
After simplification, we convert the system of PDEs into the following ODEs:
The transformed boundary conditions of (5) are:
The different non-dimensional parameters seen in Equations (8)–(11) are explained as:
The skin friction coefficient and local Nusselt number are explained as:
The dimensionless form of the surface drag and the heat transfer rate is given below:
3. Numerical Solution
With the help of the bvp4c technique, which is a built-in function in MATLAB, the mathematical Equations (8)–(10) subject to condition (11) are solved numerically after setting , where is different for different combinations of the physical parameters. Alternatively, the [0, ∞) domain is restricted to [0, ]. For the purpose of the solution, we first convert the system of equations into first-order ODEs. The following variables are used for the purposes of conversion.
Hence, the system of equations are transformed as:
Every numerical solution is obtained by putting , where is defined as the tolerance.
4. Step-by-Step Graphical Detail of the Problem
4.1. Problem Formulation
The governing modeled PDEs are highly nonlinear in nature and derived from the law of conservation, Newton’s second law of motion, the second law of thermodynamics, and Fick’s second law of diffusion. Yamada and Ota’s nanofluid has been employed in the case of SWCNT and MWCNT in order to check the behavior of nanoparticles on fluid flow. The momentum of fluid flow is scrutinized with the inclusion of MHD, stagnation point, and buoyancy effects. A heat transfer analysis has been carried out with the inclusion of heat generation, Cattaneo–Christov and activation energy effects, whereas mass transfer analysis is studied with the utilization of the activation energy phenomenon.
4.2. Modeling
The governing modeled PDEs are highly nonlinear in nature and embedded with various physical effects. The PDEs are renovated into ODEs with the utilization of similarity transformations in order to dimensionalize the PDEs. It is easy to understand the behavior of fluid in the case of dimensionless parameters such as the Prandtl number , Schmidt number , Nusselt number , etc.
4.3. Numerical Process
The dimensionless system of equations can be handled numerically with the utilization of the Lobatto IIIA scheme incorporated with the MATLAB built-in bvp4c scheme. During this procedure, the nonlinear modeled PDEs with the inclusion of various effects in momentum, energy, and concentration equations are transformed into ODEs with the help of similarity variables. In the second step, these dimensionless ODEs are stepped down into first-order ODEs for the Lobatto IIIA scheme. The tolerance level for the case of the present problem was , with an interval of computation of [0, 4] instead of [0, ∞]. All the numerical results have been obtained by considering = 4. The detailed procedure of the proposed numerical scheme is presented in the table mentioned below.
4.4. Numerical Results
The behavior of the obtained numerical outcomes was scrutinized in terms of its impact on velocity, temperature, and concentration fields. The physical quantities of interest, such as heat transfer, Nusselt number, and Sherwood number, were computed as a result of magnification in various dimensionless numbers obtained during the numerical simulation of the problem. The impact of the dimensionless parameters on the velocity, temperature, and concentration fields is portrayed in terms of figures and tables.
4.5. Analysis
The accuracy and convergence of the proposed numerical scheme have been checked with the comparison of obtained numerical results with the existing literature. In order to obtain the convergence criterion, the tolerance level for the case of the present problem was , and the domain for the case of the numerical solution was taken to be = 4 instead of = ∞. The convergence criterion was achieved if the value of the obtained outcome was less than the tolerance level.
5. Results and Discussions
After employing the bvp4c model, we obtained the required results in the form of graphs and tables that highlight the impact of various parameters on the velocity, temperature, concentration, skin friction, and Nusselt number. The values of the dimensionless parameters used in this study are in the range of ; for the magnetic number, the range is , while the range for the shear rate is . The volume fraction of nanoparticles is in the range of , the Schmidt number is in the range of , the Prandtl number has a value in , the velocity ratio parameter is in the range of , the velocity slip lies in , the chemical reaction effect is in the range of , the activation energy lies in , the power law index is in the range of , and the fitted rate constant is in the range of .
Figure 2 and Figure 3 show the impact of the solid volume fraction of CNTs on the thermal situation and axial velocity. For higher , the fluid stream speed decreases, while temperature increases because of the direct relationship between the concentration of nanoparticles and their thermal conductivity. Higher values of the parameter have a favorable influence on a system having higher thermal conductivity, resulting in an improved temperature profile. Figure 4 shows the influence of a velocity ratio parameter on the fluid speed. The velocity profile improves as a result of the direct impact of based on the stream flow rate. Figure 5 shows the effect of a slip velocity parameter on , indicating the positive influence of on the stream velocity of the fluid. As the slip effects on a wall become more significant, there is a small amount of friction and hence small resistance to fluid motion. Figure 6 shows an increasing behavior in the velocity field against increasing magnetic parameters. Usually, the magnetic field acts as an opposing agent and resists the fluid motion due to the presence of external Lorentz forces, but here, due to the employed slip mechanism, the behavior reverses, and an inclination in fluid velocity is observed.

Figure 2.
Problem formulation of the proposed model.

Figure 3.
Modelling of the proposed modeled PDEs and their conversion into ODEs.
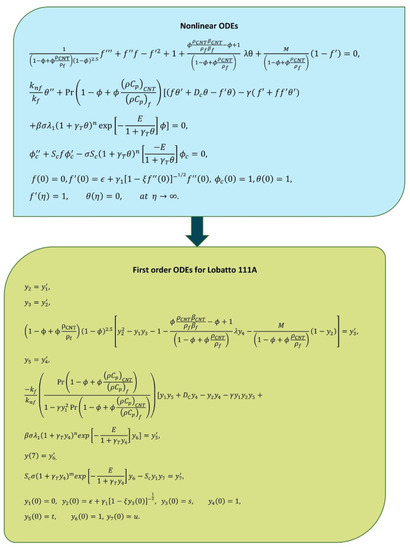
Figure 4.
Conversion of PDEs into first-order ODEs and Lobatto111a scheme.
Figure 5.
Impact of obtained numerical results on velocity, temperature and concentration fields.

Figure 6.
Analysis of obtained results.
Figure 7 shows the thermal behavior caused by heat generation through . The heat transfer surrounded by the adjoining fluid layers and surface improves as increases. Higher parameters ultimately generate more heat internally, which causes an increase in the temperature of the nanofluid. Figure 8 shows the effect of the Prandtl number on the temperature profile. The temperature is found to be decreased for expanding . The Prandtl number is the quotient of momentum to thermal diffusivity, and it is used to measure the heat transfer within the solid surface and moving liquid. As the Prandtl number rises, the thermal diffusivity becomes weaker as the fluid temperature decreases. The thermal relaxation parameter has an effect on temperature distribution, as shown in Figure 9. For greater values of , the temperature, as well as the thickness of the boundary layer, is found to decrease. Figure 10 depicts the effect of the shear rate on a velocity. A high shear rate indicates a lower viscosity, which increases the fluid velocity. Because of the inverse relationship between the mass diffusivity and Schmidt number , Figure 11 shows an increasing trend in the nanoparticle concentration for increasing values of .
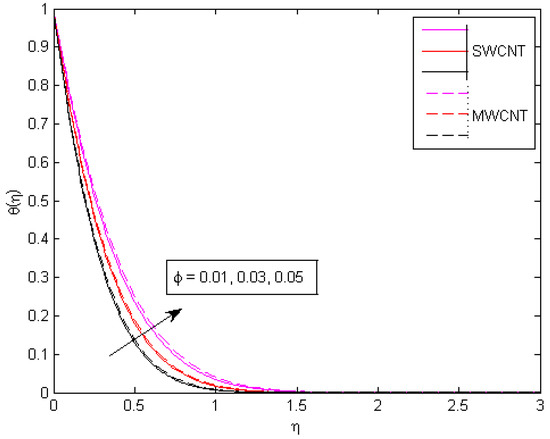
Figure 7.
Influence of on temperature pattern.
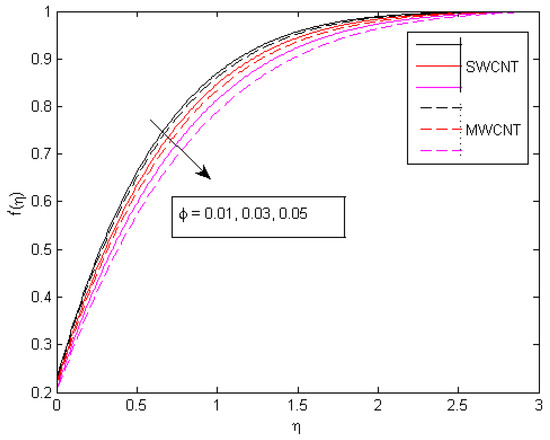
Figure 8.
Influence of on velocity behavior.
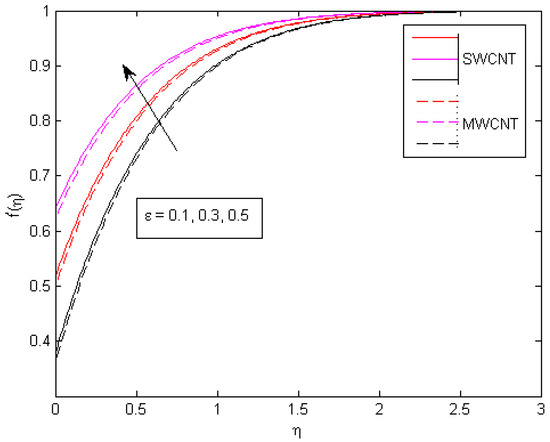
Figure 9.
Influence of on velocity profile.
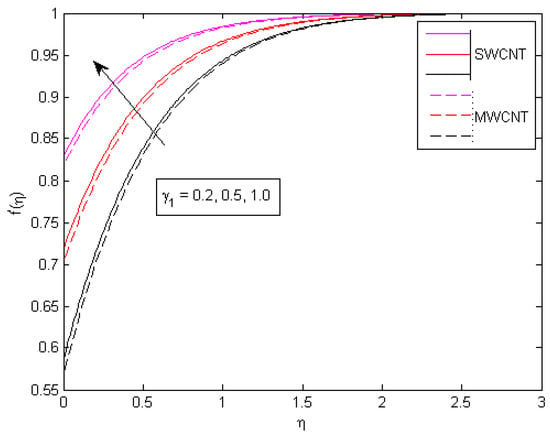
Figure 10.
Impact of on .
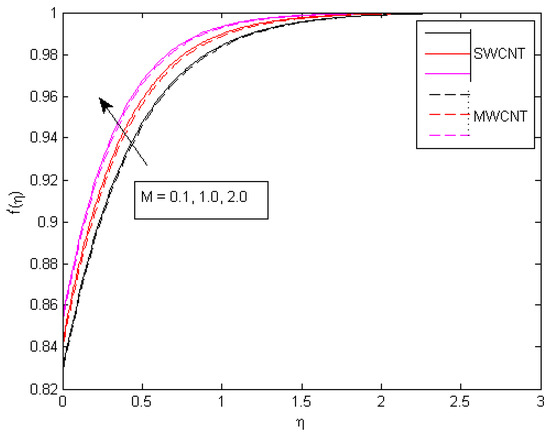
Figure 11.
Consequences of M on velocity pattern.
As seen in Figure 12, the value of , which represents the strength of the chemical reaction, increases as the concentration field decreases. The chemical reaction reduces the movement of the mass of the fluid. Physically, this is accurate since a chemical reaction is called an exothermic reaction when energy is released into the environment, and an endothermic reaction is when energy is taken from the environment. Figure 13 shows how the concentration profile improves as the activation energy parameter increases. The species B, which contains nanoparticles embedded in it, is amplified by the chemical reaction factor . Therefore, the manufacturing of nanoparticles increases. This explains why the system is increased, as shown in Figure 14. The concentration profile decreases as the rate constant increases, as shown in Figure 15. This is owing to the fact that as increases, so does the destructive intensity of chemical reactions. As can be seen in Figure 16, the concentration profile declines as m is magnified.
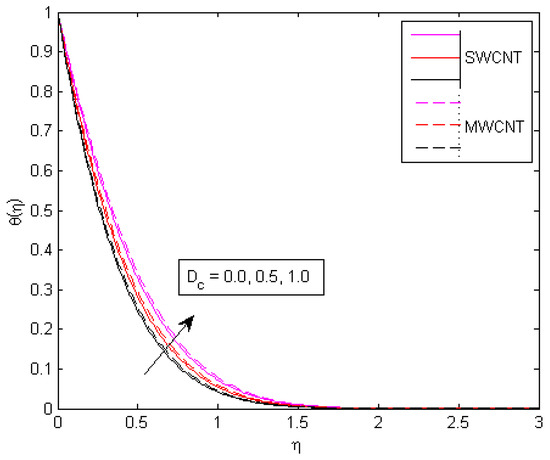
Figure 12.
Consequences of on temperature pattern.
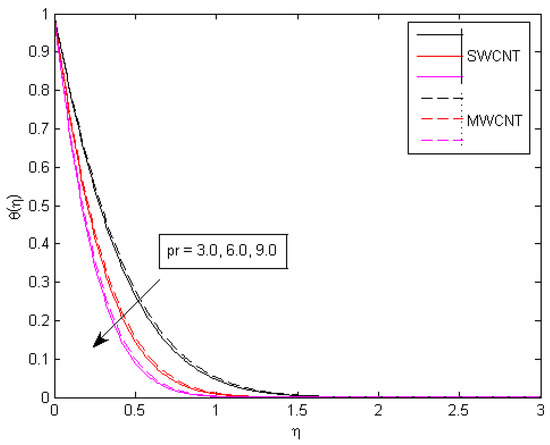
Figure 13.
Consequences of on temperature behavior.
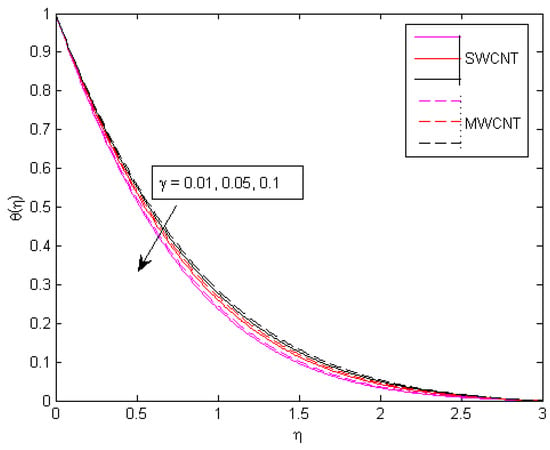
Figure 14.
Consequences of on temperature pattern.
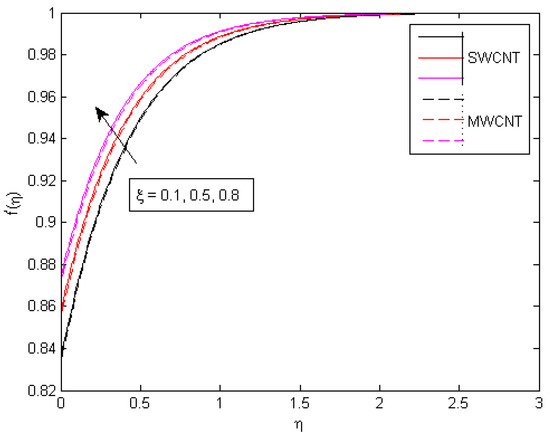
Figure 15.
Consequences of on velocity profile.
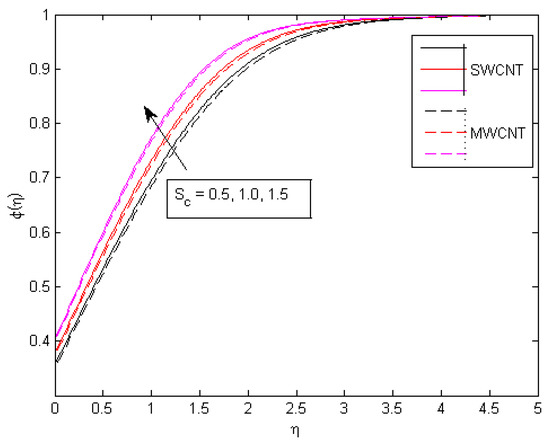
Figure 16.
Consequences of on concentration pattern.
Figure 17, Figure 18 and Figure 19 show the velocity and thermal behavior caused by exothermic/ endothermic parameters through . Exothermic reactions are when energy is released due to the interference of two chemical species, while in endothermic reactions, energy is absorbed. If the ratio of energy absorption versus energy release is the same, then the state of this chemical reaction is called isothermic because, in it, the overall energy is balanced. Heat transfer surrounded by the adjoining fluid layers and surface improves as increases, leading to a velocity profile that rises. The effect of a velocity ratio parameter on the skin friction coefficient is seen in Figure 20. A decreasing behavior in skin friction when increasing the values of is noted, and a reverse pattern is observed for the augmented values in . The value of increases and the free stream velocity overpowers the extending velocity, generating an enlarged motion about the stagnation point, lowering the drag force on a surface and causing to drop.
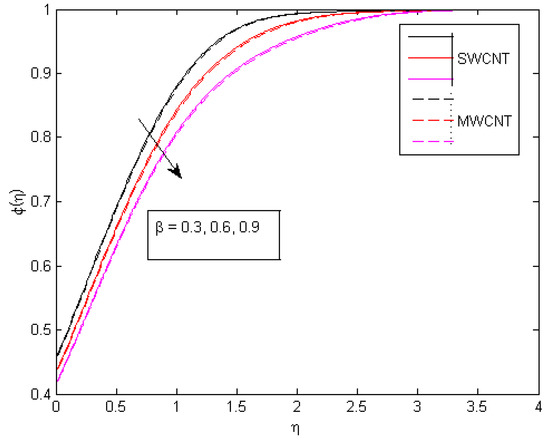
Figure 17.
Consequences of on concentration behavior.
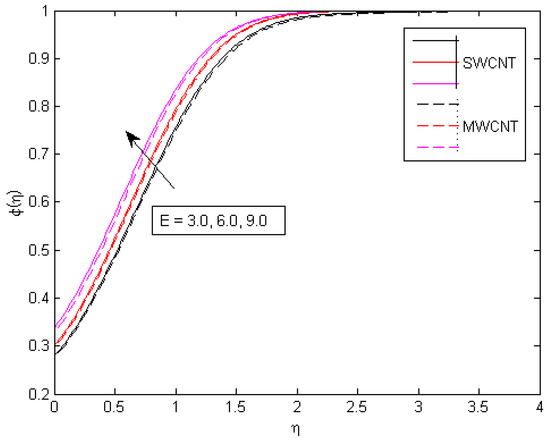
Figure 18.
Consequences of E on concentration behavior.
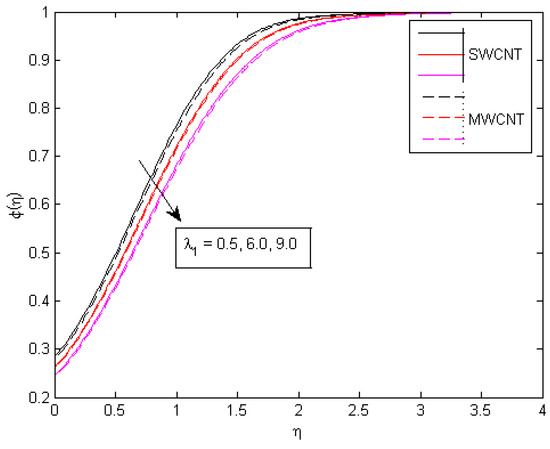
Figure 19.
Consequences of on concentration behavior.
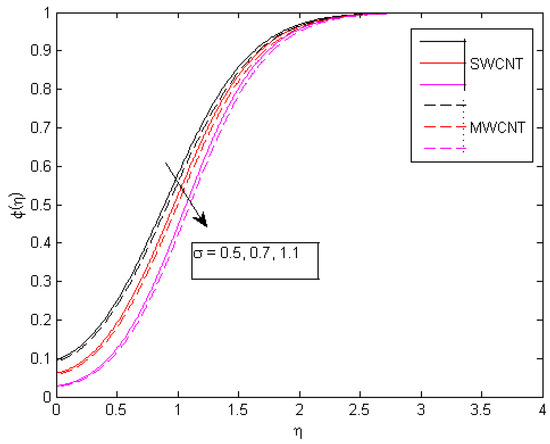
Figure 20.
Consequences of on concentration behavior.
The effect of the thermal relaxing time and velocity ratio parameter on the Nusselt number is shown in Figure 21. becomes higher for escalating . With increasing , the time it would take to transport heat between neighboring particles increases, resulting in a decrement in heat transfer characteristics. On the other hand, an opposing relationship is noted for , which improves the rate of heat transfer characteristics by increasing the fluid speed. The idea behind the plotting of the Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26 is inspired from the following references [13,15,16].
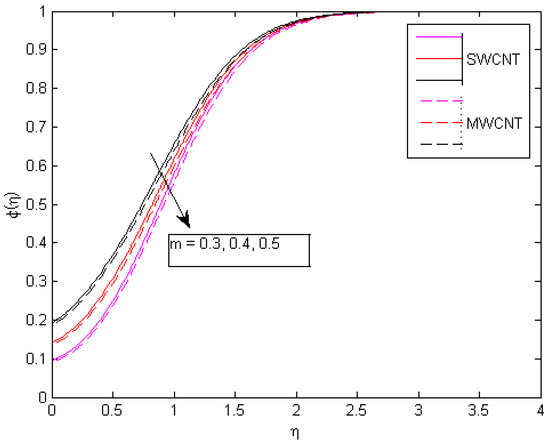
Figure 21.
Consequences of m on concentration behavior.
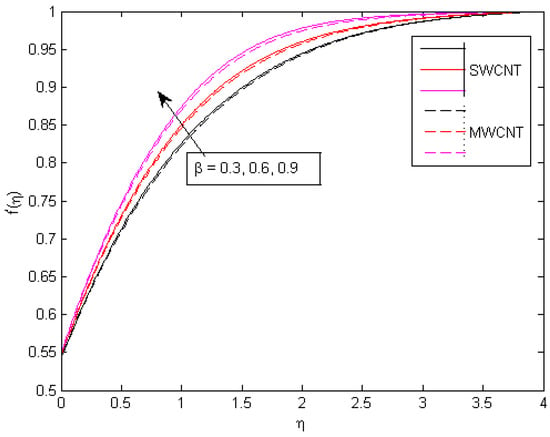
Figure 22.
Consequences of on velocity portfolio.
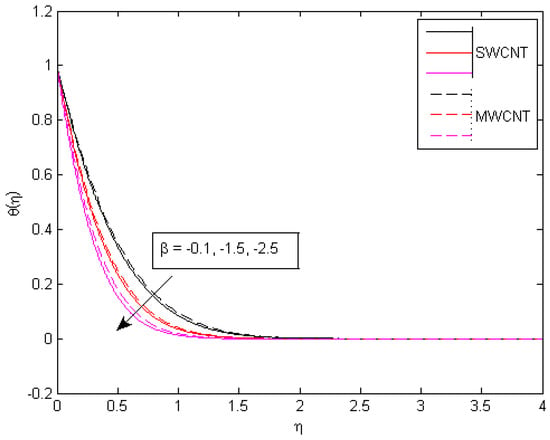
Figure 23.
Consequences of on temperature portfolio.
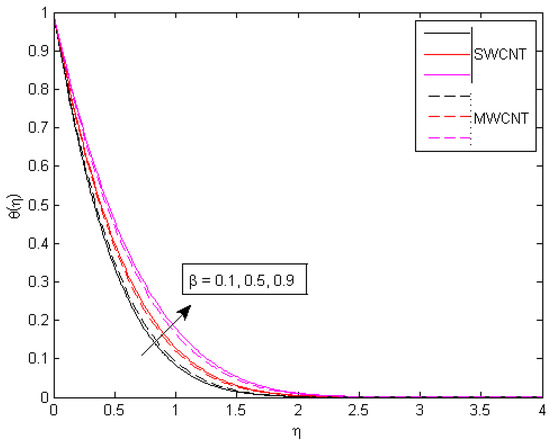
Figure 24.
Consequences of on temperature portfolio.
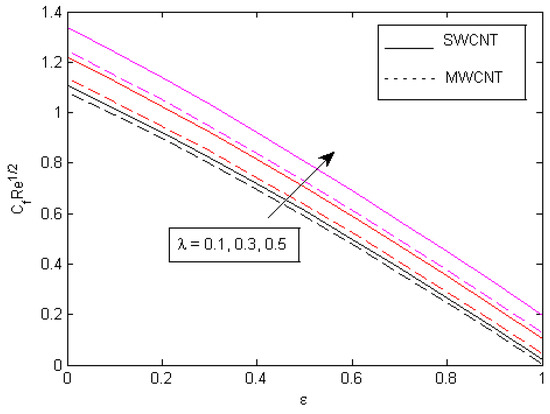
Figure 25.
Consequences of on skin friction.
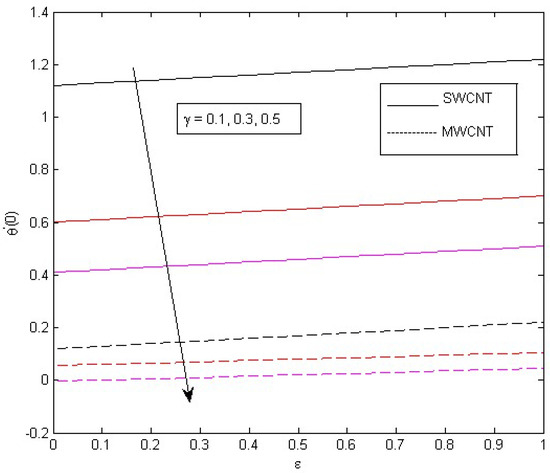
Figure 26.
Consequences of on temperature gradient.
The findings from bvp4c MATLAB software and the earlier work of Ramzan et al. [7] for increasing values exhibit great consistency, as shown in Table 2. From comparison analysis, it is quite clear that the obtained results are quite reliable.

Table 2.
The work of Ramzan et al. [7]’s limited case is compared with statistical data on surface drag force as well as local Nusselt number versus Prandtl number.
Table 3 displays a comparison of numerically achieved outcomes with Othman et al. [28] and Wang [29] for diverse values of by keeping other parameters M = = = = 0. From the comparison analysis, it is quite evident the proposed numerical is quite trustworthy, and the obtained outcomes are quite accurate.

Table 3.
Comparison of current numerical outcomes with Othman et al. [28] and Wang [29].
The effects of the volume fraction of the nano-size particle , non-dimensional velocity profile parameter , slip factor , Schmidt number , exothermic/endothermic parameter , activation energy E, dimensionless chemical reaction rate constant and , unitless rate constant m and n, as well as , are statistically shown in Table 4, which refers to . The pattern shows increasing drag force corresponding to , E, and , but decreases as the influence of m, n, , , and increases.

Table 4.
Rheological numerics of and .
6. Conclusions
The bvp4c MATLAB software was used to examine the buoyant flow of a nanofluid containing carbon nanotubes, including homogeneous and heterogeneous reactions as well as heat absorption/generation. The fluid is in a stagnation point flow past a porous shrinking/expanding plane, and the Thompson and Torian slip situations have also been taken into consideration at the boundary. Through naturally occurring factors, the fluid streaming speed, thermodynamic conditions, CNT nano-size particle density, heat transfer rates, and surface drag were investigated. The main observations are summarised as follows:
- ▪
- Larger magnetic parameters, slip parameters, and velocity ratio factors all cause fluid flow to speed up, but the solid volume fraction causes it to slow down.
- ▪
- As with the measurements of the heat generation and solid volume ratio, the system is observed to gradually cool down.
- ▪
- When increasing the slip parameters and velocity ratio, fluid tends to flow smoothly, whereas for the solid volume fractions, surface roughness increased.
- ▪
- The concentration profile decreases for the larger values of activation energy and exothermic/endothermic parameters.
- ▪
- The process of heat transmission inside the system was influenced in opposing ways by the velocity ratio parameter as well as the thermal expansion parameter.
Author Contributions
Conceptualization, Y.M.; Data curation, T.A.; Formal analysis, T.S.; Funding acquisition, I.E.S.; Investigation, R.S.; Resources, R.S.; Software, Y.M.; Supervision, I.E.S.; Validation, R.S.; Visualization, T.S.; Writing-review and editing, M.B.; Methodology, M.B.; Writing original draft, T.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work is not funded by the government or any private agency.
Data Availability Statement
No new data have been created for this study.
Acknowledgments
The authors would like to acknowledge The University of Lahore for the provision of the research plate form to complete this research work.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
| Symbols | |
| Velocity component along the x and y directions | |
| Volumetric rate of a heat source | |
| Prandtl number | |
| Free-stream velocity of the fluid | |
| Schmidt number | |
| Surface drag force | |
| Local heat transfer | |
| Dimensionless stream velocity | |
| E | Activation energy |
| Dimensionless heat generation parameter | |
| Unitless rate constants | |
| Greek Symbols | |
| Density of nanofluid | |
| Density of fluid | |
| Navier slip length density | |
| Velocity ratio parameter | |
| Dynamic viscosity shear stress | |
| Dynamic viscosity shear stress | |
| Dynamic viscosity shear stress | |
| Thermal diffusivity of nanofluid | |
| Ratio of specific heats | |
| Reciprocal of some critical shear rate | |
| Critical shear rate | |
| Heat capacity of nanofluid | |
| Coefficient of thermal expansion | |
| Heat capacity of fluid | |
| Non-dimensional slip velocity parameter | |
| Electric conductivity of fluid | |
| Electric conductivity of fluid | |
| Electric conductivity of nanofluid | |
| Coefficient of thermal expansion of carbon nanotubes | |
| Nanofluid volume fraction | |
| Dimensionless thermal relaxation time | |
| Exothermic/endothermic parameter | |
| Dimensionless chemical reaction rate | |
| Thermal conductivity of nanofluid | |
| Thermal conductivity of fluid | |
| Kinematic viscosity of nanofluid | |
| Thermal conductivity of carbon nanotubes | |
| Density of carbon nanotubes | |
| Heat capacity of carbon nanotubes | |
| Magnetic field strength |
References
- Masuda, H.; Ebata, A.; Teramae, K. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles. Sci. Inf. Database 1993. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab: Argonne, IL, USA, 1995. [Google Scholar]
- Sadaf, H.; Nadeem, S. Influences of slip and Cu-blood nanofluid in a physiological study of cilia. Comput. Methods Programs Biomed. 2016, 131, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Sivasankaran, S.; Alsabery, A.; Hashim, I. Internal heat generation effect on transient natural convection in a nanofluid-saturated local thermal non-equilibrium porous inclined cavity. Phys. A Stat. Mech. Its Appl. 2018, 509, 275–293. [Google Scholar] [CrossRef]
- Ahmed, N.; Khan, U.; Mohyud-Din, S.T. Modified heat transfer flow model for SWCNTs-H2O and MWCNTs-H2O over a curved stretchable semi-infinite region with thermal jump and velocity slip: A numerical simulation. Phys. A Stat. Mech. Its Appl. 2020, 545, 123431. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Asadi, A.; Mogharrebi, A.R.; Khalesi, J.; Mousavisani, S.M.; Ganji, D.D. Entropy generation analysis of (CH2OH)2 containing CNTs nanofluid flow under effect of MHD and thermal radiation. Case Stud. Therm. Eng. 2019, 14, 100482. [Google Scholar] [CrossRef]
- Ramzan, M.; Mohammad, M.; Howari, F.; Chung, J.D. Entropy analysis of carbon nanotubes based nanofluid flow past a vertical cone with thermal radiation. Entropy 2019, 21, 642. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Shah, F.; Haq, F. Physical aspects of CNTs and induced magnetic flux in stagnation point flow with quartic chemical reaction. Int. J. Heat Mass Transf. 2019, 135, 561–568. [Google Scholar] [CrossRef]
- Ramzan, M.; Mohammad, M.; Howari, F. Magnetized suspended carbon nanotubes based nanofluid flow with bio-convection and entropy generation past a vertical cone. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef]
- Khan, S.U.; Rauf, A.; Shehzad, S.A.; Abbas, Z.; Javed, T. Study of bioconvection flow in Oldroyd-B nanofluid with motile organisms and effective Prandtl approach. Phys. A Stat. Mech. Its Appl. 2019, 527, 121179. [Google Scholar] [CrossRef]
- Siryk, S.V.; Bendandi, A.; Diaspro, A.; Rocchia, W. Charged dielectric spheres interacting in electrolytic solution: A linearized Poisson–Boltzmann equation model. J. Chem. Phys. 2021, 155, 114114. [Google Scholar] [CrossRef]
- Yu, Y.K. Electrostatics of charged dielectric spheres with application to biological systems. III. Rigorous ionic screening at the Debye-Hückel level. Phys. Rev. E 2020, 102, 1–5. [Google Scholar] [CrossRef]
- Bilal, M.; Mazhar, S.Z.; Ramzan, M.; Mehmood, Y. Time-dependent hydromagnetic stagnation point flow of a Maxwell nanofluid with melting heat effect and amended Fourier and Fick’s laws. Heat Transf. 2021, 50, 4417–4434. [Google Scholar] [CrossRef]
- Bilal, M.; Arshad, H.; Ramzan, M.; Shah, Z.; Kumam, P. Unsteady hybrid-nanofluid flow comprising ferrousoxide and CNTs through porous horizontal channel with dilating/squeezing walls. Sci. Rep. 2021, 11, 12637. [Google Scholar] [CrossRef] [PubMed]
- Bilal, M.; Ramzan, M.; Mehmood, Y.; Alaoui, M.K.; Chinram, R. An entropy optimization study of non-Darcian magnetohydrodynamic Williamson nanofluid with nonlinear thermal radiation over a stratified sheet. Proc. IMechE Part E J. Process. Mech. Eng. 2021, 235, 1883–1894. [Google Scholar] [CrossRef]
- Bilal, M.; Ramzan, M.; Mehmood, Y.; Sajid, T.; Shah, S.; Malik, M.Y. A novel approach for EMHD Williamson nanofluid over nonlinear sheet with double stratification and Ohmic dissipation. Proc. IMechE Part E J. Process. Mech. Eng. 2021, 1–16. [Google Scholar] [CrossRef]
- Bilal, M.; Ramzan, M.; Siddique, I.; Anum, A. A numerical simulation of electrically conducting micro-channel nanofluid flow with thermal slip effects. Waves Random Complex Media 2022, 1–25. [Google Scholar] [CrossRef]
- Maleque, K. Effects of exothermic/endothermic chemical reactions with Arrhenius activation energy on MHD free convection and mass transfer flow in presence of thermal radiation. J. Thermodyn. 2013, 2013, 692516. [Google Scholar] [CrossRef]
- Bejawada, S.G.; Reddy, Y.D.; Jamshed, W.; Nisar, K.S.; Alharbi, A.N.; Chouikh, R. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alex. Eng. J. 2022, 61, 8207–8220. [Google Scholar] [CrossRef]
- Suleman, M.; Ramzan, M.; Ahmad, S.; Lu, D.C. Numerical simulation for homogeneous–heterogeneous reactions and Newtonian heating in the silver-water nanofluid flow past a nonlinear stretched cylinder. Phys. Scr. 2019, 94, 085702. [Google Scholar] [CrossRef]
- Imtiaz, M.; Mabood, F.; Hayat, T.; Alsaedi, A. Homogeneous-heterogeneous reactions in MHD radiative flow of second grade fluid due to a curved stretching surface. Int. J. Heat Mass Transf. 2019, 145, 118781. [Google Scholar] [CrossRef]
- Suleman, M.; Ramzan, M.; Ahmad, S.; Lu, D.C.; Muhammad, T.; Chung, J.D. A numerical simulation of silver-water nanofluid flow with impacts of newtonian heating and homogeneous–heterogeneous reactions past a nonlinear stretched cylinder. Symmetry 2019, 11, 295. [Google Scholar] [CrossRef]
- Doh, D.H.; Muthtamilselvan, M.; Swathene, B.; Ramya, E. Homogeneous and heterogeneous reactions in a nanofluid flow due to a rotating disk of variable thickness using HAM. Math. Comput. Simul. 2020, 168, 90–110. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A. Numerical simulation of hydromagnetic mixed convective radiative slip flow with variable fluid properties: A mathematical model for entropy generation. J. Phys. Chem. Solids 2019, 125, 153–164. [Google Scholar] [CrossRef]
- Hamid, M.; Zubair, T.; Usman, M.; Khan, Z.H.; Wang, W. Natural convection effects on heat and mass transfer of slip flow of time-dependent Prandtl fluid. J. Comput. Des. Eng. 2019, 6, 584–592. [Google Scholar] [CrossRef]
- Reddy, S.R.R.; Reddy, P.B.A.; Bhattacharyya, K. Effect of nonlinear thermal radiation on 3D magneto slip flow of Eyring-Powell nanofluid flow over a slendering sheet with binary chemical reaction and Arrhenius activation energy. Adv. Powder Technol. 2019, 30, 3203–3213. [Google Scholar] [CrossRef]
- Kiyasatfar, M. Convective heat transfer and entropy generation analysis of non-Newtonian power-law fluid flows in parallel-plate and circular microchannels under slip boundary conditions. Int. J. Therm. Sci. 2018, 128, 15–27. [Google Scholar] [CrossRef]
- Othman, M.N.; Jedia, A.; Bakar, N.A.A. MHD Stagnation Point on Nanofluid Flow and Heat Transfer of Carbon Nanotube over a Shrinking Surface with Heat Sink Effect. Molecules 2021, 26, 7441. [Google Scholar] [CrossRef]
- Wang, C. Stagnation flow towards a shrinking sheet. Int. J. -Non-Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).