The Connective Eccentricity Index of Hypergraphs

Abstract

The connective eccentricity index (CEI) of a hypergraph $\mathcal{G}$ is defined as ${\xi }^{ce}\left(\mathcal{G}\right)={\sum }_{v\in V\left(\mathcal{G}\right)}\frac{d_{\mathcal{G}}\left(v\right)}{{\epsilon }_{\mathcal{G}}\left(v\right)}$, where ${\epsilon }_{\mathcal{G}}\left(v\right)$ and $d_{\mathcal{G}}\left(v\right)$ denote the eccentricity and the degree of the vertex v, respectively. In this paper, we determine the maximal and minimal values of the connective eccentricity index among all k-uniform hypertrees on n vertices and characterize the corresponding extremal hypertrees. Finally, we establish some relationships between the connective eccentricity index and the eccentric connectivity index of hypergraphs.

1. Introduction

A hypergraph $\mathcal{G}$ is a pair $\left(V\right(\mathcal{G}),E(\mathcal{G}\left)\right)$, where $V\left(\mathcal{G}\right)$ is the nonempty vertex set, $E\left(\mathcal{G}\right)$ is the edge set, and each edge $e\in E\left(\mathcal{G}\right)$ is a nonempty subset of $V\left(\mathcal{G}\right)$. We call $n=\left|V\right(\mathcal{G}\left)\right|$ and $m=\left|E\right(\mathcal{G}\left)\right|$ the order and the size of the hypergraph $\mathcal{G}$, respectively. For an integer $k\ge 2$, if each edge in $E\left(\mathcal{G}\right)$ has exactly k vertices, then $\mathcal{G}$ is called k-uniform. Hence, a simple graph is called a 2-uniform hypergraph. For a vertex $v\in V\left(\mathcal{G}\right)$, we use $d_{\mathcal{G}}\left(v\right)$ (or just $d\left(v\right)$) to denote the degree of the vertex v, which is the number of edges of $\mathcal{G}$ containing v. The complete hypergraph and k-uniform complete hypergraph with order n are denoted by ${\mathcal{K}}_n$ and ${\mathcal{K}}_n^k$, respectively. A pendant vertex is the vertex with degree 1. A pendant edge e is the edge which contains exactly $\left|e\right|-1$ pendant vertices. Let W be a sub-hypergraph of $\mathcal{G}$ and the vertex $u\in V\left(W\right)$, the degree of the vertex u in the sub-hypergraph W, denoted by $d_W\left(u\right)$. If $W=\left\{u\right\}$, then $d_W\left(u\right)$ = 0.

A path of length q from $v_0$ to $v_q$ in a hypergraph $\mathcal{G}$ is defined as a sequence of vertices and edges $(v_0,e_1,v_1,\cdots ,v_{q-1},e_q,v_q)$, where all $v_i$ are distinct and all $e_i$ are distinct such that $v_{i-1}$, $v_i\in e_i$ for $i=1,\cdots ,q$. If $v_0=v_q$ and $q\ge 2$, then it is called a cycle. For any vertices $u,v\in V\left(\mathcal{G}\right)$, if there exists a path between them, then we say that the hypergraph $\mathcal{G}$ is connected. Otherwise, the hypergraph $\mathcal{G}$ is disconnected. A hypertree is a connected hypergraph without cycles. It is evident that the size of a k-uniform hypertree is $m=\frac{n-1}{k-1}$. For vertices $u,v\in V\left(\mathcal{G}\right)$, the distance between u and v is the length of a shortest path between them in the hypergraph $\mathcal{G}$, denoted by $d_{\mathcal{G}}(u,v)$(or just $d(u,v)$ for short). In particular, $d_{\mathcal{G}}(u,u)=0$. The eccentricity ${\epsilon }_{\mathcal{G}}\left(v\right)$(or just $\epsilon \left(v\right)$) of a vertex v in $\mathcal{G}$ is the maximum distance from v to any other vertex in $\mathcal{G}$, i.e.,

$$\epsilon \left(v\right)=\underset{u\in V\left(\mathcal{G}\right)}{max}d(u,v)$$

and the diameter $D\left(\mathcal{G}\right)$ of a hypergraph $\mathcal{G}$ is the maximum eccentricity of any vertex in $\mathcal{G}$, that is, $D\left(\mathcal{G}\right)={max}_{v\in V\left(\mathcal{G}\right)}\epsilon \left(v\right).$ The diametral path of a hypergraph is the shortest path between two vertices which has a length equal to the diameter of the hypergraph.

In organic chemistry, many topological indices (for example, Balaban’s index [1], Wiener index [2,3,4,5,6], Zagreb index [7]) have been found to be useful for the isomer discrimination and pharmaceutical drug design. Some topological indices have been employed associated with the eccentricity such as eccentric distance sum [8,9,10,11,12,13] and the eccentric connectivity index [14,15,16,17]. In 2000, Gupta et al. [18] introduced another topological index associated with the eccentricity, named as the connective eccentricity index. Through experiments, the authors found that the connective eccentricity index was more effective than Balaban’s mean square distance index in predicting biological activity.

In this paper, we study the connective eccentricity index on hypergraphs. The connective eccentricity index (CEI) of a hypergraph $\mathcal{G}$ is defined as

$${\xi }^{ce}\left(\mathcal{G}\right)=\sum _{v\in V\left(\mathcal{G}\right)}\frac{d_{\mathcal{G}}\left(v\right)}{{\epsilon }_{\mathcal{G}}\left(v\right)}.$$

Many researchers have investigated the connective eccentricity index (CEI) of a simple graph [19,20,21,22]. A hypergraph is the generalization of a simple graph. Hypergraph theory has many applications in chemistry [23,24]. For example, the study in [23] indicated that the hypergraph model has a higher accuracy for molecular description. In order to study the topological and organizational properties of hypergraph models more comprehensively, some topological indices (for example, Eccentric connectivity index (ECI) [25], Wiener index [5,6], Degree [26]) have been extended from graphs to hypergraphs. Hence, it is interesting and meaningful to investigate the connective eccentricity index (CEI) of a hypergraph.

This paper is organized as follows. In Section 2, we study how the connective eccentricity index of hypergraphs changes under two types of graph transformations. In Section 3, we determine the maximal and minimal values of the connective eccentricity index among all k-uniform hypertrees on n vertices. In Section 4, we determine the maximal and minimal values of the connective eccentricity index among all k-uniform hypertrees with given diameter d. In Section 5, we establish some relationships between the connective eccentricity index and the eccentric connectivity index of hypergraphs.

2. Hypertree Transformations and CEI

In this section, we propose two types of transformations on hypertrees and show the changes of the connective eccentricity index under these transformations. These two transformations can simplify the structure of the hypertrees and reveal the change trend of CEI. These can help determine the extremal values of CEI and characterize the extremal graphs.

Theorem 1.

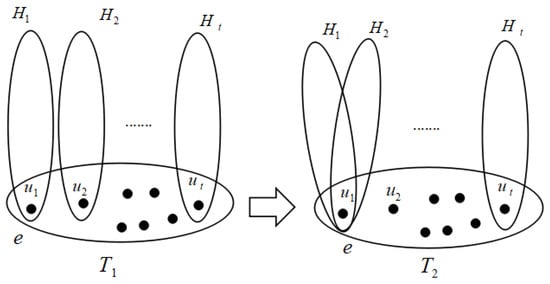
Let $e=\{u_1,u_2,\cdots ,u_{t-1},u_t\}$ ($t\ge 3$) be an edge of a connected hypertree $T_1$, and suppose that e contains at least three non-pendant vertices. Let $u_1,u_2,u_t$ be three non-pendant vertices in e and let $H_i$ be the sub-hypertree of $T_1$ such that $\left\{u_i\right\}=e\cap V\left(H_i\right)$ and $d_{T_1}\left(u_i\right)=1+d_{H_i}\left(u_i\right)$ for $i=1,2,\cdots ,t$. Assume that the eccentricity ${\epsilon }_{H_t}\left(u_t\right)\ge {\epsilon }_{H_i}\left(u_i\right)$ for $i=3,4,\cdots ,t-1$. Let $T_2$ be the hypertree obtained from $T_1$ by moving the sub-hypertree $H_2-u_2$ from $u_2$ to $u_1$ (as depicted in Figure 1). Then, ${\xi }^{ce}\left(T_2\right)\ge {\xi }^{ce}\left(T_1\right)$.

Figure 1. Transformation I.

Proof. 

Note that ${\epsilon }_{T_1}\left(x\right)={\epsilon }_{T_2}\left(x\right)$ and $d_{T_1}\left(x\right)=d_{T_2}\left(x\right)$ for any vertex $x\in V(T_1\backslash (H_1\cup H_2))$, ${\epsilon }_{T_1}\left(y\right)\ge {\epsilon }_{T_2}\left(y\right)$ and $d_{T_1}\left(y\right)=d_{T_2}\left(y\right)$ for any vertex $y\in V(H_1\cup H_2)\backslash \{u_1,u_2\}$.

For vertices $u_1$ and $u_2$, we have

$d_{T_1}\left(u_1\right)=d_{H_1}\left(u_1\right)+1$, ${\epsilon }_{T_1}\left(u_1\right)=max\{{\epsilon }_{H_1}\left(u_1\right),{\epsilon }_{H_2}\left(u_2\right)+1,{\epsilon }_{H_t}\left(u_t\right)+1\}$;

$d_{T_2}\left(u_1\right)=d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1$, ${\epsilon }_{T_2}\left(u_1\right)=max\{{\epsilon }_{H_1}\left(u_1\right),{\epsilon }_{H_2}\left(u_2\right),{\epsilon }_{H_t}\left(u_t\right)+1\}$;

$d_{T_1}\left(u_2\right)=d_{H_2}\left(u_2\right)+1$, ${\epsilon }_{T_1}\left(u_2\right)=max\{{\epsilon }_{H_2}\left(u_2\right),{\epsilon }_{H_1}\left(u_1\right)+1,{\epsilon }_{H_t}\left(u_t\right)+1\}$;

$d_{T_2}\left(u_2\right)=1$, ${\epsilon }_{T_2}\left(u_2\right)=max\{{\epsilon }_{H_1}\left(u_1\right)+1,{\epsilon }_{H_2}\left(u_2\right)+1,{\epsilon }_{H_t}\left(u_t\right)+1\}$.

In this sequel, we divide into four cases to verify the result.

$\mathbf{Case}\mathbf{1}$. ${\epsilon }_{H_1}\left(u_1\right)\ge {\epsilon }_{H_2}\left(u_2\right)+1$ and ${\epsilon }_{H_1}\left(u_1\right)\ge {\epsilon }_{H_t}\left(u_t\right)+1$.

In this case, ${\epsilon }_{T_1}\left(u_1\right)={\epsilon }_{H_1}\left(u_1\right)$, ${\epsilon }_{T_2}\left(u_1\right)={\epsilon }_{H_1}\left(u_1\right)$, ${\epsilon }_{T_1}\left(u_2\right)={\epsilon }_{H_1}\left(u_1\right)+1$, ${\epsilon }_{T_2}\left(u_2\right)={\epsilon }_{H_1}\left(u_1\right)+1$. It follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)& \le & \frac{d_{T_1}\left(u_1\right)}{{\epsilon }_{T_1}\left(u_1\right)}-\frac{d_{T_2}\left(u_1\right)}{{\epsilon }_{T_2}\left(u_1\right)}+\frac{d_{T_1}\left(u_2\right)}{{\epsilon }_{T_1}\left(u_2\right)}-\frac{d_{T_2}\left(u_2\right)}{{\epsilon }_{T_2}\left(u_2\right)}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)+1}{{\epsilon }_{H_1}\left(u_1\right)}-\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)}+\frac{d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)+1}-\frac{1}{{\epsilon }_{H_1}\left(u_1\right)+1}\hfill \\ & =& -\frac{d_{H_2}\left(u_2\right)}{{\epsilon }_{H_1}\left(u_1\right)}+\frac{d_{H_2}\left(u_2\right)}{{\epsilon }_{H_1}\left(u_1\right)+1}<0.\hfill \end{array}$$

$\mathbf{Case}\mathbf{2}$. ${\epsilon }_{H_2}\left(u_2\right)\ge {\epsilon }_{H_1}\left(u_1\right)+1$ and ${\epsilon }_{H_2}\left(u_2\right)\ge {\epsilon }_{H_t}\left(u_t\right)+1.$

In this case, ${\epsilon }_{T_1}\left(u_1\right)={\epsilon }_{H_2}\left(u_2\right)+1$, ${\epsilon }_{T_2}\left(u_1\right)={\epsilon }_{H_2}\left(u_2\right)$, ${\epsilon }_{T_1}\left(u_2\right)={\epsilon }_{H_2}\left(u_2\right)$, ${\epsilon }_{T_2}\left(u_2\right)={\epsilon }_{H_2}\left(u_2\right)+1$. It follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)& \le & \frac{d_{T_1}\left(u_1\right)}{{\epsilon }_{T_1}\left(u_1\right)}-\frac{d_{T_2}\left(u_1\right)}{{\epsilon }_{T_2}\left(u_1\right)}+\frac{d_{T_1}\left(u_2\right)}{{\epsilon }_{T_1}\left(u_2\right)}-\frac{d_{T_2}\left(u_2\right)}{{\epsilon }_{T_2}\left(u_2\right)}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)+1}{{\epsilon }_{H_2}\left(u_2\right)+1}-\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_2}\left(u_2\right)}+\frac{d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_2}\left(u_2\right)}-\frac{1}{{\epsilon }_{H_2}\left(u_2\right)+1}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)}{{\epsilon }_{H_2}\left(u_2\right)+1}-\frac{d_{H_1}\left(u_1\right)}{{\epsilon }_{H_2}\left(u_2\right)}<0.\hfill \end{array}$$

$\mathbf{Case}\mathbf{3}$. ${\epsilon }_{H_1}\left(u_1\right)={\epsilon }_{H_2}\left(u_2\right)\ge {\epsilon }_{H_t}\left(u_t\right)+1.$

In this case, ${\epsilon }_{T_1}\left(u_1\right)={\epsilon }_{H_2}\left(u_2\right)+1={\epsilon }_{H_1}\left(u_1\right)+1$, ${\epsilon }_{T_2}\left(u_1\right)={\epsilon }_{H_1}\left(u_1\right)$, ${\epsilon }_{T_1}\left(u_2\right)={\epsilon }_{H_1}\left(u_1\right)+1$, ${\epsilon }_{T_2}\left(u_2\right)={\epsilon }_{H_1}\left(u_1\right)+1$. It follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)& \le & \frac{d_{T_1}\left(u_1\right)}{{\epsilon }_{T_1}\left(u_1\right)}-\frac{d_{T_2}\left(u_1\right)}{{\epsilon }_{T_2}\left(u_1\right)}+\frac{d_{T_1}\left(u_2\right)}{{\epsilon }_{T_1}\left(u_2\right)}-\frac{d_{T_2}\left(u_2\right)}{{\epsilon }_{T_2}\left(u_2\right)}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)+1}{{\epsilon }_{H_1}\left(u_1\right)+1}-\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)}+\frac{d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)+1}-\frac{1}{{\epsilon }_{H_1}\left(u_1\right)+1}\hfill \\ & =& -\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)}+\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)+1}<0.\hfill \end{array}$$

$\mathbf{Case}\mathbf{4}$. ${\epsilon }_{H_t}\left(u_t\right)\ge {\epsilon }_{H_1}\left(u_1\right)$ and ${\epsilon }_{H_t}\left(u_t\right)\ge {\epsilon }_{H_2}\left(u_2\right).$

In this case, ${\epsilon }_{T_1}\left(u_1\right)={\epsilon }_{H_t}\left(u_t\right)+1$, ${\epsilon }_{T_2}\left(u_1\right)={\epsilon }_{H_t}\left(u_t\right)+1$, ${\epsilon }_{T_1}\left(u_2\right)={\epsilon }_{H_t}\left(u_t\right)+1$, ${\epsilon }_{T_2}\left(u_2\right)={\epsilon }_{H_t}\left(u_t\right)+1$. It follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)& \le & \frac{d_{T_1}\left(u_1\right)}{{\epsilon }_{T_1}\left(u_1\right)}-\frac{d_{T_2}\left(u_1\right)}{{\epsilon }_{T_2}\left(u_1\right)}+\frac{d_{T_1}\left(u_2\right)}{{\epsilon }_{T_1}\left(u_2\right)}-\frac{d_{T_2}\left(u_2\right)}{{\epsilon }_{T_2}\left(u_2\right)}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)+1}{{\epsilon }_{H_t}\left(u_t\right)+1}-\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_t}\left(u_t\right)+1}+\frac{d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_t}\left(u_t\right)+1}-\frac{1}{{\epsilon }_{H_t}\left(u_t\right)+1}\hfill \\ & =& 0.\hfill \end{array}$$

This completes the proof. □

Theorem 2.

Let $e=\{u_1,u_2,\cdots ,u_{t-1},u_t\}$ ($t\ge 2$) be an edge of a connected hypertree $T_1$. Assume that $u_2$ and $u_1$ are the only two non-pendant vertices in e. In addition, $H_1$ and $H_2$ are two sub-hypertrees of $T_1$ such that $\left\{u_i\right\}=e\cap V\left(H_i\right)$ and $d_{T_1}\left(u_i\right)=1+d_{H_i}\left(u_i\right)$ for $i=1,2$. Let $T_2$ be the hypertree obtained from $T_1$ by moving the sub-hypertree $H_2-u_2$ from $u_2$ to $u_1$ (as depicted in Figure 2). Then, ${\xi }^{ce}\left(T_2\right)>{\xi }^{ce}\left(T_1\right)$.

Figure 2. Transformation II.

Proof. 

Note that ${\epsilon }_{T_1}\left(x\right)={\epsilon }_{T_2}\left(x\right)$ and $d_{T_1}\left(x\right)=d_{T_2}\left(x\right)$ for any vertex $x\in V(T_1\backslash (H_1\cup H_2))$, ${\epsilon }_{T_1}\left(y\right)\ge {\epsilon }_{T_2}\left(y\right)$ and $d_{T_1}\left(y\right)=d_{T_2}\left(y\right)$ for any vertex $y\in V(H_1\cup H_2)\backslash \{u_1,u_2\}$.

For vertices $u_1$ and $u_2$, we have

$d_{T_1}\left(u_1\right)=d_{H_1}\left(u_1\right)+1$, ${\epsilon }_{T_1}\left(u_1\right)=max\{{\epsilon }_{H_1}\left(u_1\right),{\epsilon }_{H_2}\left(u_2\right)+1\}$;

$d_{T_2}\left(u_1\right)=d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1$, ${\epsilon }_{T_2}\left(u_1\right)=max\{{\epsilon }_{H_1}\left(u_1\right),{\epsilon }_{H_2}\left(u_2\right)\}$;

$d_{T_1}\left(u_2\right)=d_{H_2}\left(u_2\right)+1$, ${\epsilon }_{T_1}\left(u_2\right)=max\{{\epsilon }_{H_2}\left(u_2\right),{\epsilon }_{H_1}\left(u_1\right)+1\}$;

$d_{T_2}\left(u_2\right)=1$, ${\epsilon }_{T_2}\left(u_2\right)=max\{{\epsilon }_{H_1}\left(u_1\right)+1,{\epsilon }_{H_2}\left(u_2\right)+1\}$.

In this sequel, we divide into three cases to verify the result.

$\mathbf{Case}\mathbf{1}$. ${\epsilon }_{H_1}\left(u_1\right)\ge {\epsilon }_{H_2}\left(u_2\right)+1$.

In this case, ${\epsilon }_{T_1}\left(u_1\right)={\epsilon }_{H_1}\left(u_1\right)$, ${\epsilon }_{T_2}\left(u_1\right)={\epsilon }_{H_1}\left(u_1\right)$, ${\epsilon }_{T_1}\left(u_2\right)={\epsilon }_{H_1}\left(u_1\right)+1$, ${\epsilon }_{T_2}\left(u_2\right)={\epsilon }_{H_1}\left(u_1\right)+1$. It follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)& \le & \frac{d_{T_1}\left(u_1\right)}{{\epsilon }_{T_1}\left(u_1\right)}-\frac{d_{T_2}\left(u_1\right)}{{\epsilon }_{T_2}\left(u_1\right)}+\frac{d_{T_1}\left(u_2\right)}{{\epsilon }_{T_1}\left(u_2\right)}-\frac{d_{T_2}\left(u_2\right)}{{\epsilon }_{T_2}\left(u_2\right)}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)+1}{{\epsilon }_{H_1}\left(u_1\right)}-\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)}+\frac{d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)+1}-\frac{1}{{\epsilon }_{H_1}\left(u_1\right)+1}\hfill \\ & =& -\frac{d_{H_2}\left(u_2\right)}{{\epsilon }_{H_1}\left(u_1\right)}+\frac{d_{H_2}\left(u_2\right)}{{\epsilon }_{H_1}\left(u_1\right)+1}<0.\hfill \end{array}$$

$\mathbf{Case}\mathbf{2}$. ${\epsilon }_{H_1}\left(u_1\right)={\epsilon }_{H_2}\left(u_2\right)$.

In this case, ${\epsilon }_{T_1}\left(u_1\right)={\epsilon }_{H_2}\left(u_2\right)+1={\epsilon }_{H_1}\left(u_1\right)+1$, ${\epsilon }_{T_2}\left(u_1\right)={\epsilon }_{H_1}\left(u_1\right)$, ${\epsilon }_{T_2}\left(u_2\right)={\epsilon }_{H_1}\left(u_1\right)+1$, ${\epsilon }_{T_2}\left(u_2\right)={\epsilon }_{H_1}\left(u_1\right)+1$. It follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)& \le & \frac{d_{T_1}\left(u_1\right)}{{\epsilon }_{T_1}\left(u_1\right)}-\frac{d_{T_2}\left(u_1\right)}{{\epsilon }_{T_2}\left(u_1\right)}+\frac{d_{T_1}\left(u_2\right)}{{\epsilon }_{T_1}\left(u_2\right)}-\frac{d_{T_2}\left(u_2\right)}{{\epsilon }_{T_2}\left(u_2\right)}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)+1}{{\epsilon }_{H_1}\left(u_1\right)+1}-\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)}+\frac{d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)+1}-\frac{1}{{\epsilon }_{H_1}\left(u_1\right)+1}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)+1}-\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_1}\left(u_1\right)}<0.\hfill \end{array}$$

$\mathbf{Case}\mathbf{3}$. ${\epsilon }_{H_1}\left(u_1\right)<{\epsilon }_{H_2}\left(u_2\right).$

In this case, ${\epsilon }_{T_1}\left(u_1\right)={\epsilon }_{H_2}\left(u_2\right)+1$, ${\epsilon }_{T_2}\left(u_1\right)={\epsilon }_{H_2}\left(u_2\right)$, ${\epsilon }_{T_1}\left(u_2\right)={\epsilon }_{H_2}\left(u_2\right)$, ${\epsilon }_{T_2}\left(u_2\right)={\epsilon }_{H_2}\left(u_2\right)+1$. It follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)& \le & \frac{d_{T_1}\left(u_1\right)}{{\epsilon }_{T_1}\left(u_1\right)}-\frac{d_{T_2}\left(u_1\right)}{{\epsilon }_{T_2}\left(u_1\right)}+\frac{d_{T_1}\left(u_2\right)}{{\epsilon }_{T_1}\left(u_2\right)}-\frac{d_{T_2}\left(u_2\right)}{{\epsilon }_{T_2}\left(u_2\right)}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)+1}{{\epsilon }_{H_2}\left(u_2\right)+1}-\frac{d_{H_1}\left(u_1\right)+d_{H_2}\left(u_2\right)+1}{{\epsilon }_{H_2}\left(u_2\right)}+\frac{1+d_{H_2}\left(u_2\right)}{{\epsilon }_{H_2}\left(u_2\right)}-\frac{1}{{\epsilon }_{H_2}\left(u_2\right)+1}\hfill \\ & =& \frac{d_{H_1}\left(u_1\right)}{{\epsilon }_{H_2}\left(u_2\right)+1}-\frac{d_{H_1}\left(u_1\right)}{{\epsilon }_{H_2}\left(u_2\right)}<0.\hfill \end{array}$$

This completes the proof. □

In order to better demonstrate the influence of hypertree transformations I and II on CEI, we apply them on 3-uniform hypertree $T_3$ (Figure 3) and 3-uniform hypertree $T_6$ (Figure 4), respectively, and calculate the corresponding CEI before and after the structural change of the corresponding hypertree.

Figure 3. Transformation I on $T_3$.

Figure 4. Transformation II on $T_6$.

Applying Transformation I, we calculate and compare the CEI of hypertrees $T_3$, $T_4$, and $T_5$ as follows.

$$\begin{array}{c}\hfill {\xi }^{ce}\left(T_3\right)={\xi }^{ce}\left(T_5\right)=\frac{29}{6}<{\xi }^{ce}\left(T_4\right)=\frac{31}{6}.\end{array}$$

Applying Transformation II, we calculate and compare the CEI of hypertrees $T_6$ and $T_7$ as follows.

$$\begin{array}{c}\hfill {\xi }^{ce}\left(T_6\right)=\frac{23}{6}<{\xi }^{ce}\left(T_7\right)=6.\end{array}$$

3. The Maximal and Minimal Values of CEI of $\mathit{k}$-Uniform Hypertrees with Size $\mathit{m}$

In this section, we shall determine the maximal and minimal values of CEI among all k-uniform hypertrees on n vertices with size m.

Firstly, we recall the concept of a loose path introduced in [27,28]. For a connected k-uniform hypertree T with vertex set $V\left(T\right)=\{v_1,v_2,\cdots ,v_n\}$ and edge set $E\left(T\right)=\{e_1,e_2,\cdots ,e_m\}$, if $e_i=\{v_{(i-1)(k-1)+1},v_{(i-1)(k-1)+2},\dots ,v_{(i-1)(k-1)+k}\}$ for $i=1,\cdots ,m,$ then T is called a k-uniform loose path, denoted by $P_{n,k}$.

For a connected hypertree T on n vertices with m edges, if all edges of T are pendant edges at a common vertex u, then T is called a hyperstar (with center u), denoted by $S_{n,m}$. If the hypertree $S_{n,m}$ is k-uniform, then it is called a k-uniform hypertree, denoted by $S_{n,k}$.

Theorem 3.

Let T be a connected hypertree on n vertices with $m(m\ge 3)$ edges. Then,

$${\xi }^{ce}\left(T\right)\le {\xi }^{ce}\left(S_{n,m}\right).$$

The equality holds if and only if $T\cong S_{n,m}.$

Proof. 

Suppose on the contrary that $T\ncong S_{n,m}$, then at least one edge of T is a non-pendant edge. Without loss of generality, we denote a non-pendant edge of T by $e_i$.

By applying the transformations of Theorems 1 and 2 on T, we move all the sub-hypertrees $H_i-\left\{x\right\}$ on one common edge $e_i$ of T from different vertices x to a common vertex v, $x\in e_i$, $v\in e_i$. The resulting hypertree is denoted by $T_1$. By Theorems 1 and 2, we conclude that ${\xi }^{ce}\left(T\right)<{\xi }^{ce}\left(T_1\right)$. After finitely performing the transformations of Theorems 1 and 2, we can get a hypertree $T^{*}$ such that $T^{*}\cong S_{n,m}$ and ${\xi }^{ce}\left(T\right)<{\xi }^{ce}\left(T^{*}\right)={\xi }^{ce}\left(S_{n,m}\right)$. □

Theorem 4.

Let T be a connected k-uniform hypertree on n vertices with size $m=\frac{n-1}{k-1}\ge 3$. Then,

$${\xi }^{ce}\left(T\right)\le \frac{nk+n-k-1}{2(k-1)}.$$

The equality holds if and only if $T\cong S_{n,k}.$

Proof. 

From Theorem 3, we conclude that the equality holds if and only if $T\cong S_{n,k}.$ Note that $d_{S_{n,k}}\left(u\right)=\frac{n-1}{k-1}=m$, ${\epsilon }_{S_{n,k}}\left(u\right)=1$, $d_{S_{n,k}}\left(x\right)=1$ and ${\epsilon }_{S_{n,k}}\left(x\right)=2$ for $x\in V\left(S_{n,k}\right)\backslash \left\{u\right\}$. Therefore, it follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(S_{n,k}\right)& =& \sum _{x\in V\left(S_{n,k}\right)\backslash \left\{u\right\}}\frac{d_{S_{n,k}}\left(x\right)}{{\epsilon }_{S_{n,k}}\left(x\right)}+\frac{d_{S_{n,k}}\left(u\right)}{{\epsilon }_{S_{n,k}}\left(u\right)}\hfill \\ & =& \sum _{x\in V\left(S_{n,k}\right)\backslash \left\{u\right\}}\frac{1}{2}+\frac{n-1}{k-1}\hfill \\ & =& \frac{n-1}{2}+\frac{n-1}{k-1}\hfill \\ & =& \frac{nk+n-k-1}{2(k-1)}.\hfill \end{array}$$

□

The following lemma is immediate, and so we omit its proof.

Lemma 1.

Let T be a k-uniform hypertree on n vertices. Then, ${\sum }_{v\in V\left(T\right)}{d}_T\left(v\right)=\frac{(n-1)k}{k-1}$.

Theorem 5.

Let T be a connected k-uniform hypertree on n vertices with size $m=\frac{n-1}{k-1}\ge 3$. Then,

$${\xi }^{ce}\left(T\right)\ge \left\{\begin{array}{cc}\sum _{i=1}^{\frac{m-1}{2}}\frac{4}{m-i}+\sum _{i=0}^{\frac{m-1}{2}-1}\frac{2(k-2)}{m-i}+\frac{2}{m}+\frac{2(k-2)}{m+1},& if m is odd,\\ \\ \sum _{i=1}^{\frac{m}{2}-1}\frac{4}{m-i}+\sum _{i=0}^{\frac{m}{2}-1}\frac{2(k-2)}{m-i}+\frac{2}{m}+\frac{4}{m},& if m is even.\end{array}\right.$$

The equality holds if and only if $T\cong P_{n,k}.$

Proof. 

It is evident that the diameter of $P_{n,k}$ is $m=\frac{n-1}{k-1}$, i.e., the number of the edges of $P_{n,k}$. Let $T_1$ be a connected k-uniform hypertree on n vertices. Suppose on the contrary that $T_1\ncong P_{n,k}$. Let d be the diameter of $T_1$ and $P=(v_{1,1},e_1,v_{1,k},\cdots ,v_{d-1,k},e_d$,$v_{d,k})$ be the diametral path of $T_1$, where $e_i=\{v_{i,1},v_{i,2},\cdots ,v_{i,k}\}$ ($i=1,2,\cdots ,d$) and $v_{j,k}=v_{j+1,1}$ for $j=1,2,\cdots ,d-1$. Then, $d<m$ and $|E\left(T_1\right)\backslash E\left(P\right)|\ge 1$.

Next, we move a pendant edge in $E\left(T_1\right)\backslash E\left(P\right)$ to $v_{d,k}$ and produce a new hypertree. It means that we delete this pendant edge and organize $v_{d,k}$ and $k-1$-pendant vertices in the pendant edge to build a new edge. We denote the new hypertree by $T_1^{\prime }$. In fact, we can repeat the above operation by finite steps to get a new hypertree $T_2$ such that $T_2\cong P_{n,k}$.

Note that ${\epsilon }_{T_2}\left(x\right)\ge d+1>{\epsilon }_{T_1}\left(x\right)$ for $x\in V(E\left(T_1\right)\backslash E\left(P\right))$, ${\epsilon }_{T_2}\left(y\right)\ge {\epsilon }_{T_1}\left(y\right)$ for $y\in V\left(P\right)$. It is evident that $d_{T_2}\left(v_{1,1}\right)=1$, $d_{T_2}\left(v_{d,k}\right)=2$, $d_{T_2}\left(v_{i,k}\right)=2$ for $i=1,2\cdots ,d-1$, $d_{T_2}\left(v_{j,s}\right)=1$ for $j=1,2,\cdots ,d$ and $s=2,3,\cdots ,k-1$.

Let $D_{T_1}\left(P^{\prime }\right)={\sum }_{v\in V\left(T_1\right)\backslash V\left(P\right)}{d}_{T_1}\left(v\right)+\left|E^{\prime }\right|$, where $E^{\prime }=\left\{e_i\right|e_i$ is incident to one vertex in $V\left(P\right)$ and $k-1$ vertices in $V\left(T_1\right)\backslash V\left(P\right)\}$. Let $D_{T_2}\left(P^{\prime }\right)={\sum }_{v\in V\left(T_2\right)\backslash V\left(P\right)}{d}_{T_2}\left(v\right)+\frac{1}{2}{d}_{T_2}\left(v_{d,k}\right)={\sum }_{v\in V\left(T_2\right)\backslash V\left(P\right)}{d}_{T_2}\left(v\right)+1$. By Lemma 1, we have $D_{T_1}\left(P^{\prime }\right)={\sum }_{v\in V\left(T_1\right)\backslash V\left(P\right)}{d}_{T_1}\left(v\right)+\left|E^{\prime }\right|={\sum }_{v\in V\left(T_2\right)\backslash V\left(P\right)}{d}_{T_2}\left(v\right)+1=D_{T_2}\left(P^{\prime }\right)$. From the definition of CEI, it follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(P_{n,k}\right)& =& {\xi }^{ce}\left(T_2\right)=\sum _{v\in V\left(T_2\right)}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_2}\left(v\right)}=\sum _{v\in V\left(T_2\right)\backslash V\left(P\right)}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_2}\left(v\right)}+\sum _{v\in V\left(P\right)}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_2}\left(v\right)}\hfill \\ & \le & \sum _{v\in V\left(T_2\right)\backslash V\left(P\right)}\frac{d_{T_2}\left(v\right)}{d+1}+\sum _{v\in V\left(P\right)}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_2}\left(v\right)}\hfill \\ & <& \sum _{v\in V\left(T_2\right)\backslash V\left(P\right)}\frac{d_{T_2}\left(v\right)}{d}+\sum _{v\in V\left(P\right)}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_2}\left(v\right)}\hfill \\ & =& \frac{{\sum }_{v\in V\left(T_2\right)\backslash V\left(P\right)}{d}_{T_2}\left(v\right)}{d}+\sum _{v\in V\left(P\right)}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_2}\left(v\right)}\hfill \\ & =& \frac{D_{T_2}\left(P^{\prime }\right)-1}{d}+\sum _{v\in V\left(P\right)}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_2}\left(v\right)}\hfill \\ & \le & \frac{D_{T_2}\left(P^{\prime }\right)-1}{d}+\sum _{v\in V\left(P\right)}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\hfill \\ & =& \frac{D_{T_2}\left(P^{\prime }\right)-1}{d}+\frac{d_{T_2}\left(v_{d,k}\right)}{{\epsilon }_{T_1}\left(v_{d,k}\right)}+\sum _{v\in V\left(P\right)\backslash \left\{v_{d,k}\right\}}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\hfill \\ & =& \frac{D_{T_2}\left(P^{\prime }\right)-1}{d}+\frac{2}{d}+\sum _{v\in V\left(P\right)\backslash \left\{v_{d,k}\right\}}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\hfill \\ & =& \frac{D_{T_2}\left(P^{\prime }\right)}{d}+\frac{1}{d}+\sum _{v\in V\left(P\right)\backslash \left\{v_{d,k}\right\}}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\hfill \\ & =& \frac{D_{T_1}\left(P^{\prime }\right)}{d}+\frac{d_{T_1}\left(v_{d,k}\right)}{{\epsilon }_{T_1}\left(v_{d,k}\right)}+\sum _{v\in V\left(P\right)\backslash \left\{v_{d,k}\right\}}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\hfill \\ & =& \frac{{\sum }_{v\in V\left(T_1\right)\backslash V\left(P\right)}{d}_{T_1}\left(v\right)+\left|E^{\prime }\right|}{d}+\frac{d_{T_1}\left(v_{d,k}\right)}{{\epsilon }_{T_1}\left(v_{d,k}\right)}+\sum _{v\in V\left(P\right)\backslash \left\{v_{d,k}\right\}}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\hfill \\ & =& \frac{{\sum }_{v\in V\left(T_1\right)\backslash V\left(P\right)}{d}_{T_1}\left(v\right)}{d}+\frac{|E^{\prime }|}{d}+\frac{d_{T_1}\left(v_{d,k}\right)}{{\epsilon }_{T_1}\left(v_{d,k}\right)}+\sum _{v\in V\left(P\right)\backslash \left\{v_{d,k}\right\}}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\hfill \\ & <& \frac{{\sum }_{v\in V\left(T_1\right)\backslash V\left(P\right)}{d}_{T_1}\left(v\right)}{d}+\frac{|E^{\prime }|}{d-1}+\frac{d_{T_1}\left(v_{d,k}\right)}{{\epsilon }_{T_1}\left(v_{d,k}\right)}+\sum _{v\in V\left(P\right)\backslash \left\{v_{d,k}\right\}}\frac{d_{T_2}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\hfill \\ & \le & \sum _{v\in V\left(T_1\right)}\frac{d_{T_1}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}={\xi }^{ce}\left(T_1\right).\hfill \end{array}$$

Therefore, ${\xi }^{ce}\left(P_{n,k}\right)<{\xi }^{ce}\left(T_1\right)$ if $T_1\ncong P_{n,k}$, and for any k-uniform hypertrees T with size $m\ge 3$, we conclude that ${\xi }^{ce}\left(P_{n,k}\right)={\xi }^{ce}\left(T\right)$ if and only if $T\cong P_{n,k}$. By direct calculation, we get the CEI of $P_{n,k}$. □

For a k-uniform hypertree T, if $k=2$, then T is a tree. From Theorems 4 and 5, we can deduce the following known theorem.

Theorem 6 

([22]). Let T be a tree on n vertices. Then,

$$\frac{3n}{2}-\frac{3}{2}\ge {\xi }^{ce}\left(T\right)\ge \left\{\begin{array}{cc}\sum _{i=1}^{\frac{n-2}{2}}\frac{4}{n-1-i}+\frac{2}{n-1},& if n is even,\\ \\ \sum _{i=1}^{\frac{n-3}{2}}\frac{4}{n-1-i}+\frac{6}{n-1},& if n is odd.\end{array}\right.$$

The right equality holds if and only if $T\cong P_n$ and the left equality holds if and only if $T\cong S_n$.

4. The Maximal and Minimal Values of CEI of $\mathit{k}$-Uniform Hypertrees with Given Diameter

In this section, we shall determine the maximal and minimal values of CEI of k-uniform hypertrees with a given diameter. Firstly, we introduce two kinds of k-uniform hypertrees of order n with diameter d.

Let $P=(v_{1,1},e_1,v_{1,k},\cdots ,v_{d-1,k},e_d$,$v_{d,k})$ be a path where $e_i=\{v_{i,1},v_{i,2},\cdots ,v_{i,k}\}$ ($i=1,2,3,\cdots ,d$) such that $v_{i,k}=v_{i+1,1}$ and $e_i\cap e_{i+1}=\left\{v_{i,k}\right\}$ for $i=1,2,3,\cdots ,d-1$. For even d, let $T_{n,d}$ be a k-uniform hypertree obtained from a path P by attaching t pendant edges at vertex $v_{\frac{d}{2},k}$, where $t=\frac{n-d(k-1)-1}{k-1}$ is a nonnegative integer. It means that all edges of $E\left(T_{n,d}\right)\backslash E\left(P\right)$ are pendant edges at $v_{\frac{d}{2},k}$. For odd d, let $T_{n,d}^t$ be the hypertree obtained from the path P by attaching $t=\frac{n-d(k-1)-1}{k-1}$ pendant edges at some vertices in $e_{\frac{d+1}{2}}$. Note that $T_{n,d}^t$ is not unique. We denote by ${\mathbb{T}}_{n,d}^t$ the set of hypertrees of the form $T_{n,d}^t$ for odd d.

Theorem 7.

Let T be a connected k-uniform hypertree on n vertices with diameter $d\ge 2$, and let $t=\frac{n-\left[d\right(k-1)+1]}{k-1}$ be a nonnegative integer. Then,

$${\xi }^{ce}\left(T\right)\le \left\{\begin{array}{cc}\sum _{i=1}^{\frac{d}{2}-1}\frac{4}{d-i}+\sum _{i=1}^{\frac{d}{2}-1}\frac{2(k-2)}{d-i}+\frac{6+2t}{d}+\frac{2t(k-1)}{d+2},& if d is even,\\ \\ \sum _{i=1}^{\frac{d-1}{2}}\frac{4}{d-i}+\frac{2}{d}+\sum _{i=0}^{\frac{d-1}{2}-1}\frac{2(k-2)}{d-i}+\frac{2(k-2)+2t}{d+1}+\frac{2t(k-1)}{d+3},& if d is odd.\end{array}\right.$$

The equality holds if and only if $T\cong T_{n,d}$ for even d, or $T\in {\mathbb{T}}_{n,d}^t$ for odd d.

Proof. 

Let $T_1$ be the extremal k-uniform hypertree which has the maximal CEI among all k-uniform hypertrees on n vertices with diameter $d.$ Let $P=(v_{1,1},e_1,v_{1,k},\cdots ,v_{d-1,k},e_d$,$v_{d,k})$ be the diametral path of $T_1$, where $e_i=\{v_{i,1},v_{i,2},\cdots ,v_{i,k}\}$ ($i=1,2,3,\cdots ,d$) such that $v_{i,k}=v_{i+1,1}$ and $e_i\cap e_{i+1}=\left\{v_{i,k}\right\}$ for $i=1,2,3,\cdots ,d-1$. By Theorems 1 and 2, we conclude that all edges of $E\left(T_1\right)\backslash E\left(P\right)$ must be pendant edges at some vertices in $V\left(P\right)\backslash V_1$ where $V_1=(e_1\cup e_d)\backslash \{v_{1,k},v_{d-1,k}\}$. For convenience, we denote $V\left(P\right)\backslash V_1$ by $V_0$.

We now consider the case when d is even. Assume that $e_1^{\prime },e_2^{\prime },\cdots ,e_r^{\prime }$ be pendant edges attached a vertex in $V_0\backslash \left\{v_{\frac{d}{2},k}\right\}$ and $e_{r+1}^{\prime },e_{r+2}^{\prime },\cdots ,e_t^{\prime }$ attached at $v_{\frac{d}{2},k}$. If $r\ge 1$, then $T_1\ncong T_{n,d}$. We build a new hypertree $T_2$ which is obtained from $T_1$ by moving these pendant edges $e_1^{\prime },e_2^{\prime },\cdots ,e_r^{\prime }$ to $v_{\frac{d}{2},k}$. Assume that $u^{\prime }=e_i^{\prime }\cap V\left(P\right)$, $w_i^{\prime }\in e_i^{\prime }\backslash \left\{u^{\prime }\right\}$ for $i=1,2,\cdots ,r$. It is evident that all vertices in $e_i^{\prime }\backslash \left\{u^{\prime }\right\}$ have the same eccentricity in $T_1$( $i=1,2,\cdots ,r$). The same result holds in $T_2$. From the definition of CEI, one has

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)& =& \sum _{i=1}^r\left((k-1)\frac{1}{{\epsilon }_{T_1}\left(w_i^{\prime }\right)}+\frac{1}{{\epsilon }_{T_1}\left(u^{\prime }\right)}\right)-\sum _{i=1}^r\left((k-1)\frac{1}{{\epsilon }_{T_2}\left(w_i^{\prime }\right)}+\frac{1}{{\epsilon }_{T_2}\left(v_{\frac{d}{2},k}\right)}\right)\hfill \\ & =& \frac{r(k-1)}{{\epsilon }_{T_1}\left(w_i^{\prime }\right)}+\frac{r}{{\epsilon }_{T_1}\left(u^{\prime }\right)}-\frac{r(k-1)}{{\epsilon }_{T_2}\left(w_i^{\prime }\right)}-\frac{r}{{\epsilon }_{T_2}\left(v_{\frac{d}{2},k}\right)}.\hfill \end{array}$$

Since ${\epsilon }_{T_1}\left(w_i^{\prime }\right)>{\epsilon }_{T_2}\left(w_i^{\prime }\right)=\frac{d}{2}+1$, ${\epsilon }_{T_1}\left(u^{\prime }\right)>{\epsilon }_{T_2}\left(v_{\frac{d}{2},k}\right)=\frac{d}{2}$, ${\xi }^{ce}\left(T_1\right)-{\xi }^{ce}\left(T_2\right)<0$, which contradicts to the fact that $T_1$ has the maximal CEI. Then, $r=0$. We conclude that all edges of $E\left(T_1\right)\backslash E\left(P\right)$ are pendant edges attaching at $v_{\frac{d}{2},k}$, i.e., $T_1\cong T_{n,d}$. By direct calculation, we get the CEI of $T_{n,d}$.

For odd d, these vertices in $e_{\frac{d+1}{2}}$ have the same eccentricity $\frac{d+1}{2}$, and the eccentricities of the vertices in $V\left(P\right)\backslash e_{\frac{d+1}{2}}$ are more than $\frac{d+1}{2}$. Similarly to the above proof, we get that all edges of $E\left(T_1\right)\backslash E\left(P\right)$ are pendant edges at some vertices in $e_{\frac{d+1}{2}}$, i.e., $T_1\in {\mathbb{T}}_{n,d}^t$. By direct calculation, we get the CEI of the hypertrees in ${\mathbb{T}}_{n,d}^t$. □

Lemma 2.

Let T be a connected k-uniform hypertree with diameter d and the diameter path $P=(v_{1,1},e_1,v_{1,k},\cdots ,v_{d-1,k},e_d$,$v_{d,k})$. Let $\omega \notin V\left(P\right)$ be a vertex with some pendant edges attached. Let $T_1$ be the hypertree obtained by moving these pendant edges from ω to some vertices in $(e_2\backslash \left\{v_{2,k}\right\})\cup (e_{d-1}\backslash \left\{v_{d-2,k}\right\})$. Then, ${\xi }^{ce}\left(T\right)\ge {\xi }^{ce}\left(T_1\right).$

Proof. 

Let $e_i^{\prime }$ ($i=1,2,\cdots ,t$) be all pendant edges attached at $\omega$. Let ${\omega }_{i,j}$ ($j=1,2,\cdots ,k$) be the vertices in $e_i^{\prime }$ and ${\omega }_{i,1}=\omega$ for $i=1,2,\cdots ,t$. For convenience, we set $V_0=(e_2\backslash \left\{v_{2,k}\right\})\cup (e_{d-1}\backslash \left\{v_{d-2,k}\right\})$. It is evident that these vertices in $V_0$ have the same eccentricity $d-1$. Therefore, it follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T\right)-{\xi }^{ce}\left(T_1\right)& =& \left(\frac{d_T\left(\omega \right)}{{\epsilon }_T\left(\omega \right)}-\frac{d_{T_1}\left(\omega \right)}{{\epsilon }_{T_1}\left(\omega \right)}\right)+\left(\sum _{j=2}^k\sum _{i=1}^t\frac{1}{{\epsilon }_T\left({\omega }_{i,j}\right)}-\sum _{j=2}^k\sum _{i=1}^t\frac{1}{{\epsilon }_{T_1}\left({\omega }_{i,j}\right)}\right)\hfill \\ & & +\left(\sum _{v\in V_0}\frac{d_T\left(v\right)}{{\epsilon }_T\left(v\right)}-\sum _{v\in V_0}\frac{d_{T_1}\left(v\right)}{{\epsilon }_{T_1}\left(v\right)}\right)\hfill \\ & =& \frac{t}{{\epsilon }_T\left(\omega \right)}+\left((k-1)\frac{t}{{\epsilon }_T\left({\omega }_{i,j}\right)}-(k-1)\frac{t}{{\epsilon }_{T_1}\left({\omega }_{i,j}\right)}\right)-\frac{t}{d-1}.\hfill \end{array}$$

Note that ${\epsilon }_T\left(\omega \right)={\epsilon }_{T_1}\left(\omega \right)\le d-1={\epsilon }_{T_1}\left(v\right)={\epsilon }_T\left(v\right)$ for $v\in V_0$, ${\epsilon }_T\left({\omega }_{i,j}\right)\le {\epsilon }_{T_1}\left({\omega }_{i,j}\right)=d$ for $i=1,2,\cdots ,t$; $j=2,3\cdots ,k$. Therefore, ${\xi }^{ce}\left(T\right)-{\xi }^{ce}\left(T_1\right)\ge 0$. □

In the rest of this section, we shall deal with the minimal CEI of k-uniform hypertrees with a given diameter. For nonegative integers p, q, let $T_n^d(p,q)$ be the k-uniform hypertree obtained from the diametral path $P=(v_{1,1},e_1,v_{1,k},\cdots ,v_{d-1,k},e_d$,$v_{d,k})$ by attaching p and q pendant edges at some vertices in $e_2\backslash \left\{v_{2,k}\right\}$ and some vertices in $e_{d-1}\backslash \left\{v_{d-2,k}\right\}$, respectively. It is evident that $\left|V\right(P\left)\right|=d(k-1)+1$ and $p+q=\frac{n-\left[d\right(k-1)+1]}{k-1}$. Let ${\mathbb{T}}_n^d(p,q)$ be the set of hypertrees of the form $T_n^d(p,q)$.

Theorem 8.

Let T be a connected k-uniform hypertree on n vertices with diameter $d\ge 3$ and $t=\frac{n-\left[d\right(k-1)+1]}{k-1}$ be a nonnegative integer. Then,

$${\xi }^{ce}\left(T\right)\ge \left\{\begin{array}{cc}\sum _{i=1}^{\frac{d}{2}-1}\frac{4}{d-i}+\sum _{i=0}^{\frac{d}{2}-1}\frac{2(k-2)}{d-i}+\frac{t(k-1)+6}{d}+\frac{t}{d-1},& if d is even,\\ \\ \sum _{i=1}^{\frac{d-1}{2}}\frac{4}{d-i}+\frac{t(k-1)+2}{d}+\sum _{i=0}^{\frac{d-1}{2}-1}\frac{2(k-2)}{d-i}+\frac{t}{d-1},& if d is odd.\end{array}\right.$$

The equality holds if and only if $T\in {\mathbb{T}}_n^d(p,q)$.

Proof. 

Let $T_1$ be the hypertree that has the minimal CEI among all hypertrees on n vertices with diameter d. Let $P=(v_{1,1},e_1,v_{1,k},\cdots ,v_{d-1,k},e_d$,$v_{d,k})$ be the diametral path of $T_0$, where $e_i=\{v_{i,1},v_{i,2},\cdots ,v_{i,k}\}$ ($i=1,2,3,\cdots ,d$) such that $v_{i,k}=v_{i+1,1}$ and $e_i\cap e_{i+1}=\left\{v_{i,k}\right\}$ for $i=1,2,3,\cdots ,d-1$. We only need to verify that all edges of $E\left(T_1\right)\backslash E\left(P\right)$ are pendant edges attaching at some vertices in $(e_{d-1}\backslash \left\{v_{d-2,k}\right\})\cup (e_2\backslash \left\{v_{2,k}\right\})$.

By Lemma 2, $T_1$ has the following form: some pendant edges are attached at some vertices in $(e_2\backslash \left\{v_{2,k}\right\})\cup (e_{d-1}\backslash \left\{v_{d-2,k}\right\})$ while others are attached at some vertices in $e_3\cup e_4\cup \cdots \cup e_{d-2}$. Assume that there exists a vertex $u\in e_3\cup e_4\cup \cdots \cup e_{d-2}$ with a pendant edge $e_u$ attached in $T_1$. For a vertex $w\in (e_2\backslash \left\{v_{2,k}\right\})\cup (e_{d-1}\backslash \left\{v_{d-2,k}\right\})$ and $v^{\prime }\in (e_u\backslash \left\{u\right\})$. It is evident that these vertices in $e_u\backslash \left\{u\right\}$ have the same eccentricity and $|e_u\backslash \left\{u\right\}|=k-1$. Let $T_2$ be the hypertree obtained from $T_1$ by moving $e_u$ from u to w. Next, we compare the CEI of $T_1$ and $T_2$. By the definition of CEI, it follows that

$$\begin{array}{ccc}\hfill {\xi }^{ce}\left(T_2\right)-{\xi }^{ce}\left(T_1\right)& =& \frac{d_{T_2}\left(u\right)}{{\epsilon }_{T_2}\left(u\right)}+\frac{d_{T_2}\left(w\right)}{{\epsilon }_{T_2}\left(w\right)}+(k-1)\frac{d_{T_2}\left(v^{\prime }\right)}{{\epsilon }_{T_2}\left(v^{\prime }\right)}\hfill \\ & & -\left(\frac{d_{T_1}\left(u\right)}{{\epsilon }_{T_1}\left(u\right)}+\frac{d_{T_1}\left(w\right)}{{\epsilon }_{T_1}\left(w\right)}+(k-1)\frac{d_{T_1}\left(v^{\prime }\right)}{{\epsilon }_{T_1}\left(v^{\prime }\right)}\right)\hfill \\ & =& \left(\frac{d_{T_2}\left(u\right)}{{\epsilon }_{T_2}\left(u\right)}-\frac{d_{T_1}\left(u\right)}{{\epsilon }_{T_1}\left(u\right)}\right)+\left(\frac{d_{T_2}\left(w\right)}{{\epsilon }_{T_2}\left(w\right)}-\frac{d_{T_1}\left(w\right)}{{\epsilon }_{T_1}\left(w\right)}\right)\hfill \\ & & +\left((k-1)\frac{d_{T_2}\left(v^{\prime }\right)}{{\epsilon }_{T_2}\left(v^{\prime }\right)}-(k-1)\frac{d_{T_1}\left(v^{\prime }\right)}{{\epsilon }_{T_1}\left(v^{\prime }\right)}\right)\hfill \\ & =& -\frac{1}{{\epsilon }_{T_2}\left(u\right)}+\frac{1}{{\epsilon }_{T_2}\left(w\right)}+\frac{k-1}{{\epsilon }_{T_2}\left(v^{\prime }\right)}-\frac{k-1}{{\epsilon }_{T_1}\left(v^{\prime }\right)}.\hfill \end{array}$$

Note that ${\epsilon }_{T_1}\left(u\right)={\epsilon }_{T_2}\left(u\right)<{\epsilon }_{T_1}\left(w\right)={\epsilon }_{T_2}\left(w\right)=d-1$, ${\epsilon }_{T_2}\left(v^{\prime }\right)=d>{\epsilon }_{T_1}\left(v^{\prime }\right)$. Then, ${\xi }^{ce}\left(T_2\right)-{\xi }^{ce}\left(T_1\right)<0$. This contradicts to the fact that $T_1$ has the minimal CEI. Therefore, we conclude that all edges of $E\left(T_1\right)\backslash E\left(P\right)$ are pendant edges attaching at some vertices in $(e_{d-1}\backslash \left\{v_{d-2,k}\right\})\cup (e_2\backslash \left\{v_{2,k}\right\})$, then $T_1\in {\mathbb{T}}_n^d(p,q)$. By direct calculation, we get the CEI of $T_n^d(p,q)$. □

From Theorems 7 and 8, we can deduce the following known theorems, respectively.

Theorem 9 

([22]). Let T be a tree on n vertices with diameter $d(d\ge 2)$. Then,

$${\xi }^{ce}\left(T\right)\le \left\{\begin{array}{cc}\frac{2n-2d-2}{d+2}+\frac{2n-2d+4}{d}+\sum _{i=1}^{\frac{d}{2}-1}\frac{4}{d-i},& if d is even,\\ \\ \frac{2n-2d-2}{d+3}+\frac{2}{d}+\frac{2n-2d+6}{d+1}+\sum _{i=1}^{\frac{d-1}{2}-1}\frac{4}{d-i},& if d is odd.\end{array}\right.$$

This equality holds if and only if $T\cong T_{n,d}$ for even d, or $T\in {\mathbb{T}}_{n,d}^t$ for odd d.

Theorem 10 

([22]). Let T be a tree of order n with diameter $d(d\ge 3)$. Then,

$${\xi }^{ce}\left(T\right)\ge \left\{\begin{array}{cc}\frac{n-d+5}{d}+\frac{n-d-1}{d-1}+\sum _{i=1}^{\frac{d}{2}-1}\frac{4}{d-i},& if d is even,\\ \\ \frac{n-d+1}{d}+\frac{n-d-1}{d-1}+\sum _{i=1}^{\frac{d-1}{2}}\frac{4}{d-i},& if d is odd.\end{array}\right..$$

This equality holds if and only if $T\in {\mathbb{T}}_n^d(p,q)$.

5. Some Relations between CEI and ECI of Hypergraphs

The first Zagreb index [7,29,30] on simple graphs was widely studied. In this paper, we generalize the first Zagreb index to hypergraphs. In addition, we establish some relationships between the connective eccentricity index (CEI) and the eccentric connectivity index (ECI).

The eccentric connectivity index (ECI) of a hypergraph $\mathcal{G}$ is defined as

$${\xi }^c\left(\mathcal{G}\right)=\sum _{u\in V\left(\mathcal{G}\right)}{\epsilon }_{\mathcal{G}}\left(u\right)d_{\mathcal{G}}\left(u\right).$$

The first Zagreb index of a hypergraph $\mathcal{G}$ is defined as

$$M_1\left(\mathcal{G}\right)=\sum _{u\in V\left(\mathcal{G}\right)}{d}_{\mathcal{G}}^2\left(u\right).$$

Theorem 11.

Let $\mathcal{G}$ be a k-uniform hypergraph on n vertices with m edges. Then,

$${\xi }^{ce}\left(\mathcal{G}\right)\le mk.$$

This equality holds if and only if $\mathcal{G}\cong {\mathcal{K}}_n^k.$

Proof. 

Since ${\epsilon }_{\mathcal{G}}\left(u\right)\ge 1$ for all $u\in V\left(\mathcal{G}\right)$, then

$${\xi }^{ce}\left(\mathcal{G}\right)=\sum _{u\in V\left(\mathcal{G}\right)}\frac{d_{\mathcal{G}}\left(u\right)}{{\epsilon }_{\mathcal{G}}\left(u\right)}\le \sum _{u\in V\left(\mathcal{G}\right)}{d}_{\mathcal{G}}\left(u\right)=mk.$$

This equality holds if and only if ${\epsilon }_{\mathcal{G}}\left(u\right)=1$ for all $u\in V\left(\mathcal{G}\right)$, i.e., $\mathcal{G}$ is a k-uniform complete hypergraph. □

Theorem 12.

Let $\mathcal{G}$ be a hypergraph of order n. Then,

$${\xi }^{ce}\left(\mathcal{G}\right)\le {\xi }^c\left(\mathcal{G}\right).$$

This equality holds if and only if $\mathcal{G}\cong {\mathcal{K}}_n.$

Proof. 

Evidently, $\frac{1}{{\epsilon }_{\mathcal{G}}\left(u\right)}\le {\epsilon }_{\mathcal{G}}\left(u\right)$ for any vertex $u\in V\left(\mathcal{G}\right)$. Then, we have

$${\xi }^{ce}\left(\mathcal{G}\right)=\sum _{u\in V\left(\mathcal{G}\right)}\frac{d_{\mathcal{G}}\left(u\right)}{{\epsilon }_{\mathcal{G}}\left(u\right)}\le \sum _{u\in V\left(\mathcal{G}\right)}{d}_{\mathcal{G}}\left(u\right){\epsilon }_{\mathcal{G}}\left(u\right)={\xi }^c\left(\mathcal{G}\right).$$

This equality holds if and only if ${\epsilon }_{\mathcal{G}}\left(u\right)=1$ for any vertex $u\in V\left(\mathcal{G}\right)$, i.e., $\mathcal{G}$ is a complete hypergraph. □

Theorem 13.

Let $\mathcal{G}$ be a k-uniform hypergraph on n vertices with m edges. Then,

$${\xi }^{ce}\left(\mathcal{G}\right)\ge \frac{m^2{k}^2}{{\xi }^c\left(\mathcal{G}\right)}.$$

This equality holds if and only if ${\epsilon }_{\mathcal{G}}\left(u\right)$ is a constant for any vertex $u\in V\left(\mathcal{G}\right)$.

Proof. 

By the Cauchy inequality, we have

$$\sum _{u\in V\left(\mathcal{G}\right)}\frac{d_{\mathcal{G}}\left(u\right)}{{\epsilon }_{\mathcal{G}}\left(u\right)}\sum _{u\in V\left(\mathcal{G}\right)}{d}_{\mathcal{G}}\left(u\right){\epsilon }_{\mathcal{G}}\left(u\right)\ge {\left(\sum _{u\in V\left(\mathcal{G}\right)}{d}_{\mathcal{G}}\left(u\right)\right)}^2.$$

Therefore,

$${\xi }^{ce}\left(\mathcal{G}\right)\ge \frac{m^2{k}^2}{{\xi }^c\left(\mathcal{G}\right)}.$$

This equality holds if and only if ${\epsilon }_{\mathcal{G}}\left(u\right)$ is equal to a constant for any vertex $u\in V\left(\mathcal{G}\right)$. □

We introduce the self-centered hypergraph as follows. For a hypergraph $\mathcal{G}$ with the vertex set $V\left(\mathcal{G}\right)=\{u_1,u_2,\cdots ,u_n\}$, $\mathcal{G}$ is called a self-centered hypergraph (or $\mathcal{SC}$ hypergraph for short) if ${\epsilon }_{\mathcal{G}}\left(u_1\right)={\epsilon }_{\mathcal{G}}\left(u_2\right)=\cdots ={\epsilon }_{\mathcal{G}}\left(u_n\right)$. Evidently, a hypergraph $\mathcal{G}$ is a $\mathcal{SC}$ hypergraph if and only if $r\left(\mathcal{G}\right)=d\left(\mathcal{G}\right)$, where $r\left(\mathcal{G}\right)$ is the radius and $d\left(\mathcal{G}\right)$ is the diameter of $\mathcal{G}$.

Lemma 3 

([20]). Let $c_1,c_2,\cdots ,c_n$ and $z_1,z_2,\cdots ,z_n$ be two sets of real numbers. Then,

$$\sum _{j=1}^n{c}_j^2\sum _{i=1}^n{z}_i^2-{\left(\sum _{j=1}^n{c}_j{z}_j\right)}^2=\sum _{j<i}{(c_j{z}_i-c_i{z}_j)}^2.$$

(1)

Theorem 14.

Let $\mathcal{G}$ be a connected k-uniform hypergraph on n vertices with size $m(m\ge 2)$, diameter d and radius r. Then,

$${\xi }^{ce}\left(\mathcal{G}\right){\xi }^c\left(\mathcal{G}\right)-m^2{k}^2\le \frac{{(d-r)}^2}{2rd}(m^2{k}^2-M_1\left(\mathcal{G}\right)).$$

(2)

This equality holds if and only if $\mathcal{G}$ is a k-uniform $\mathcal{SC}$ hypergraph.

Proof. 

Set $c_i=\sqrt{d_{\mathcal{G}}\left(u_i\right){\epsilon }_{\mathcal{G}}\left(u_i\right)}$ and $z_i=\sqrt{\frac{d_{\mathcal{G}}\left(u_i\right)}{{\epsilon }_{\mathcal{G}}\left(u_i\right)}}(i=1,2,\cdots ,n)$. By Lemma 3, we have

$$\sum _{j=1}^n{d}_{\mathcal{G}}\left(u_j\right){\epsilon }_{\mathcal{G}}\left(u_j\right)\sum _{i=1}^n\frac{d_{\mathcal{G}}\left(u_i\right)}{{\epsilon }_{\mathcal{G}}\left(u_i\right)}-{\left(\sum _{j=1}^n{d}_{\mathcal{G}}\left(u_j\right)\right)}^2=\sum _{j<i}{\left(\sqrt{d_{\mathcal{G}}\left(u_j\right){\epsilon }_{\mathcal{G}}\left(u_j\right)}\sqrt{\frac{d_{\mathcal{G}}\left(u_i\right)}{{\epsilon }_{\mathcal{G}}\left(u_i\right)}}-\sqrt{d_{\mathcal{G}}\left(u_i\right){\epsilon }_{\mathcal{G}}\left(u_i\right)}\sqrt{\frac{d_{\mathcal{G}}\left(u_j\right)}{{\epsilon }_{\mathcal{G}}\left(u_j\right)}}\right)}^2.$$

That is,

$${\xi }^{ce}\left(\mathcal{G}\right){\xi }^{ce}\left(\mathcal{G}\right)-m^2{k}^2=\sum _{j<i}{d}_{\mathcal{G}}\left(u_j\right)d_{\mathcal{G}}\left(u_i\right){\left(\sqrt{\frac{{\epsilon }_{\mathcal{G}}\left(u_j\right)}{{\epsilon }_{\mathcal{G}}\left(u_i\right)}}-\sqrt{\frac{{\epsilon }_{\mathcal{G}}\left(u_i\right)}{{\epsilon }_{\mathcal{G}}\left(u_j\right)}}\right)}^2.$$

Note that

$$\sqrt{\frac{{\epsilon }_{\mathcal{G}}\left(u_j\right)}{{\epsilon }_{\mathcal{G}}\left(u_i\right)}}-\sqrt{\frac{{\epsilon }_{\mathcal{G}}\left(u_i\right)}{{\epsilon }_{\mathcal{G}}\left(u_j\right)}}\le \sqrt{\frac{d}{r}}-\sqrt{\frac{r}{d}}\mathrm{for} \mathrm{any} i=1,2,\cdots ,n; j=1,2,\cdots ,n).$$

So, it follows that

$${\xi }^{ce}\left(\mathcal{G}\right){\xi }^c\left(\mathcal{G}\right)-m^2{k}^2\le \frac{{(d-r)}^2}{rd}\sum _{j<i}{d}_{\mathcal{G}}\left(u_j\right)d_{\mathcal{G}}\left(u_i\right).$$

Since

$$m^2{k}^2={\left(\sum _{j=1}^n{d}_{\mathcal{G}}\left(u_j\right)\right)}^2=\sum _{j=1}^n{d}_{\mathcal{G}}^2\left(u_j\right)+2\sum _{j<i}{d}_{\mathcal{G}}\left(u_j\right)d_{\mathcal{G}}\left(u_i\right),$$

we have

$${\xi }^{ce}\left(\mathcal{G}\right){\xi }^c\left(\mathcal{G}\right)-m^2{k}^2\le \frac{{(d-r)}^2}{2rd}(m^2{k}^2-M_1\left(\mathcal{G}\right)).$$

The first part of the proof is done.

If $d=r$, then ${\epsilon }_{\mathcal{G}}\left(u_j\right)=d=r$ for all $u_j\in V\left(\mathcal{G}\right)$. Therefore, ${\xi }^{ce}\left(\mathcal{G}\right){\xi }^c\left(\mathcal{G}\right)=m^2{k}^2$ and the equality holds in (2). If $d\ne r$, then there exist at least two vertices $u_j$ and $u_i$ that have the same eccentricity d in $\mathcal{G}$, then for $(u_j,u_i)$, we have

$$\sqrt{\frac{{\epsilon }_{\mathcal{G}}\left(u_j\right)}{{\epsilon }_{\mathcal{G}}\left(u_i\right)}}-\sqrt{\frac{{\epsilon }_{\mathcal{G}}\left(u_i\right)}{{\epsilon }_{\mathcal{G}}\left(u_j\right)}}=0<\sqrt{\frac{d}{r}}-\sqrt{\frac{r}{d}}.$$

Therefore, the inequality in (2) is strict. This completes the proof. □

We introduce the $R-D$ hypergraph as follows. A hypergraph $\mathcal{G}$ is called an $R-D$ hypergraph if ${\epsilon }_{\mathcal{G}}\left(u\right)=r$ or d for any $u\in V\left(\mathcal{G}\right)$, where r is the radius and d is the diameter of $\mathcal{G}$.

Lemma 4 

([31]). Let a and b be two real constants. If the real numbers $c_j\ne 0$ and $z_j(j=1,2,\cdots ,n)$ satisfy $a\le \frac{z_j}{c_j}\le b$, then

$$ab\sum _{j=1}^n{c}_j^2+\sum _{j=1}^n{z}_j^2\le (a+b)\sum _{j=1}^n{z}_j{c}_j.$$

(3)

This equality holds if and only if $z_j=a{c}_j$ or $b{c}_j$ for any $j=1,2,\cdots ,n.$

Theorem 15.

Let $\mathcal{G}$ be a connected k-uniform hypergraph of order n with size $m(m\ge 2)$, diameter d and radius r. Then,

$$dr{\xi }^{ce}\left(\mathcal{G}\right)+{\xi }^c\left(\mathcal{G}\right)\le mk(d+r).$$

(4)

This equality holds if and only if $\mathcal{G}$ is a k-uniform $R-D$ hypergraph.

Proof. 

Set $c_j=\sqrt{\frac{d_{\mathcal{G}}\left(u_j\right)}{{\epsilon }_{\mathcal{G}}\left(u_j\right)}}$ and $z_j=\sqrt{d_{\mathcal{G}}\left(u_j\right){\epsilon }_{\mathcal{G}}\left(u_j\right)}$ for $j=1,2,3,\cdots ,n$. Since $r\le {\epsilon }_{\mathcal{G}}\left(u_j\right)\le d$ and ${\epsilon }_{\mathcal{G}}\left(u_j\right)=\frac{z_j}{c_j}$ for $j=1,2,3,\cdots ,n$, we get

$$dr\sum _{j=1}^n\frac{d_{\mathcal{G}}\left(u_j\right)}{{\epsilon }_{\mathcal{G}}\left(u_j\right)}+\sum _{j=1}^n{d}_{\mathcal{G}}\left(u_j\right){\epsilon }_{\mathcal{G}}\left(u_j\right)\le (d+r)\sum _{j=1}^n{d}_{\mathcal{G}}\left(u_j\right).$$

For one vertex $u_j$, if ${\epsilon }_{\mathcal{G}}\left(u_j\right)=r$, then

$$dr\frac{d_{\mathcal{G}}\left(u_j\right)}{r}+d_{\mathcal{G}}\left(u_j\right)r=(d+r)d_{\mathcal{G}}\left(u_j\right).$$

If ${\epsilon }_{\mathcal{G}}\left(u_j\right)=d$, then

$$dr\frac{d_{\mathcal{G}}\left(u_j\right)}{d}+d_{\mathcal{G}}\left(u_j\right)d=(d+r)d_{\mathcal{G}}\left(u_j\right).$$

Therefore, from Lemma 4, we conclude that the equality holds if and only if ${\epsilon }_{\mathcal{G}}\left(u_j\right)=r$ or d for any $u_j\in V\left(\mathcal{G}\right)$, i.e., $\mathcal{G}$ is a k-uniform $R-D$ hypergraph. □

6. Conclusions

We have determined the maximal and minimal values of the connective eccentricity index among all k-uniform hypertrees on n vertices. We have also determined the maximal and minimal values of the connective eccentricity index among all k-uniform hypertrees with given diameter further and established some relationships between the connective eccentricity index and the eccentric connectivity index of hypergraphs. Different topological indices can reflect the topological properties of hypergraph models from different perspectives, and more different topological indices are worth further study. Determining the extreme values of these topological indices and the relationships between different topological indices will help us to design the structure of some chemical molecules and networks more rationally.