Research on the Lightweight Design of an Aircraft Support Based on Lattice-Filled Structures
Abstract
1. Introduction
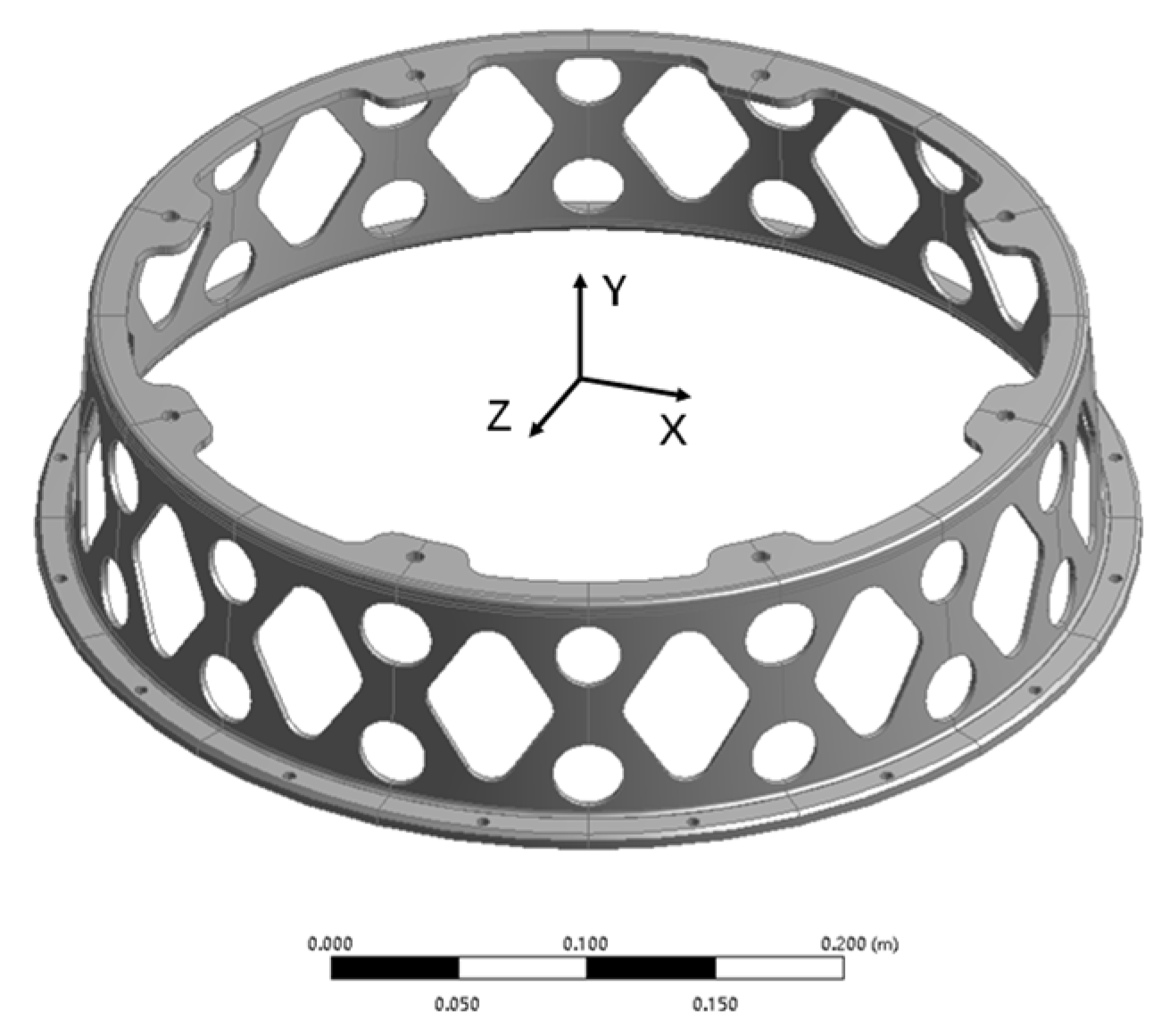
2. Design Problem
3. Design Process and Implementation of Lattice-Filled Structures
3.1. Design Process and Corresponding Theories
3.1.1. Design Process
- (1)
- Finite element model modeling: model the design domain, specify the types and parameters of the filled lattice, calculate the equivalent material parameters of the specified lattice, mesh the design domain, define the material parameters as the calculated equivalent parameters, define boundary conditions, etc.;
- (2)
- Topology optimization: define the objective function, design the variables and constraints of the topology optimization formulation, carry out the topology optimization problem;
- (3)
- Geometric modeling of topology optimized results: choose several control nodes and the surface of the optimized design, build NURBS surfaces surrounding the topology optimized designs, modify the locations of control nodes, add bolt holes;
- (4)
- Lattice filling: define the filling parameters and filling domain, uniformly fill the lattices in the filling domain;
- (5)
- Structural response verification: perform structural analysis; if the performance was not satisfactory, modify the local geometric model or return to (1) to modify the filling parameters.
3.1.2. Finite Element Model Modeling
3.1.3. Topology Optimization
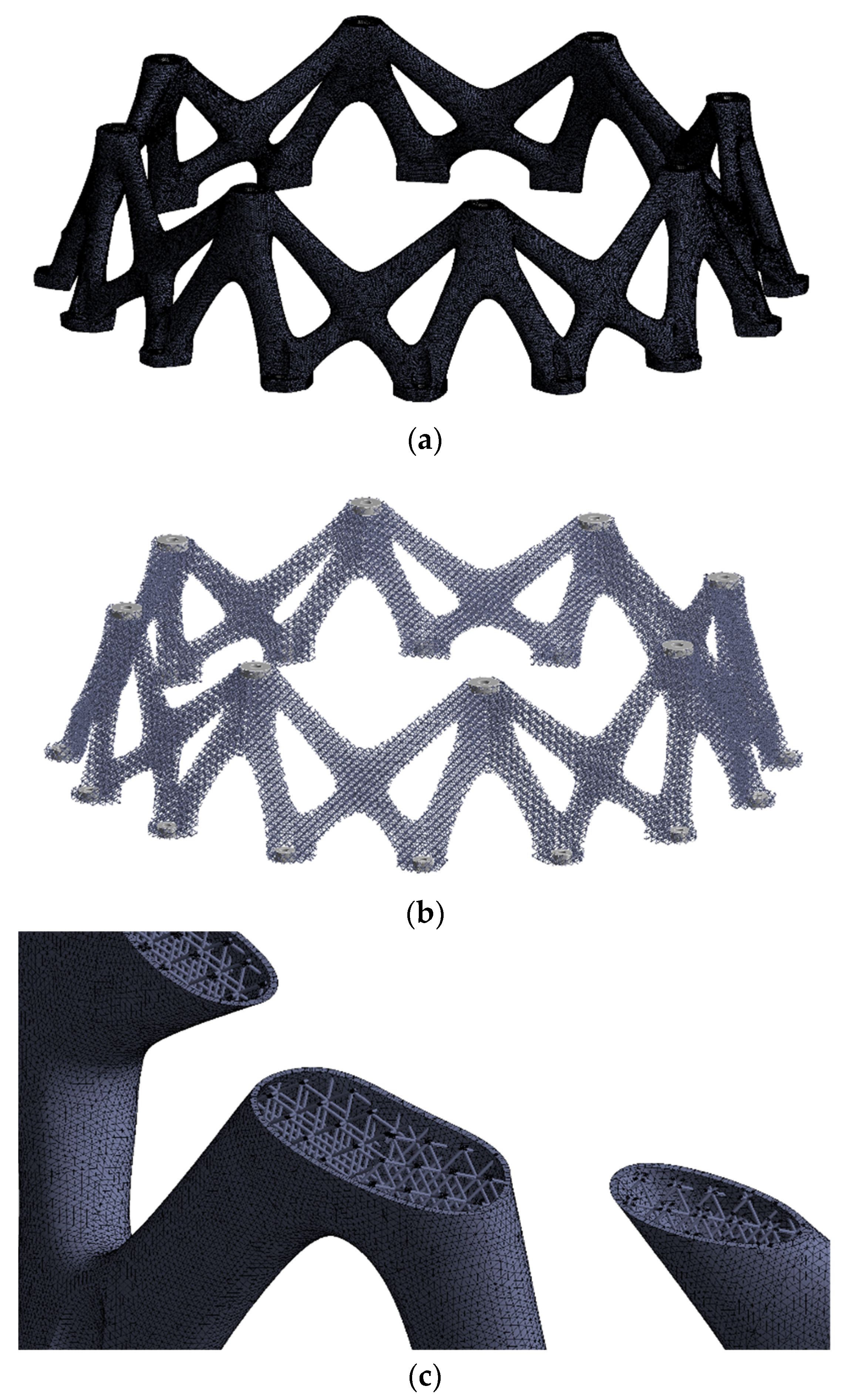
3.1.4. Geometric Modeling of the Topology Optimized Results
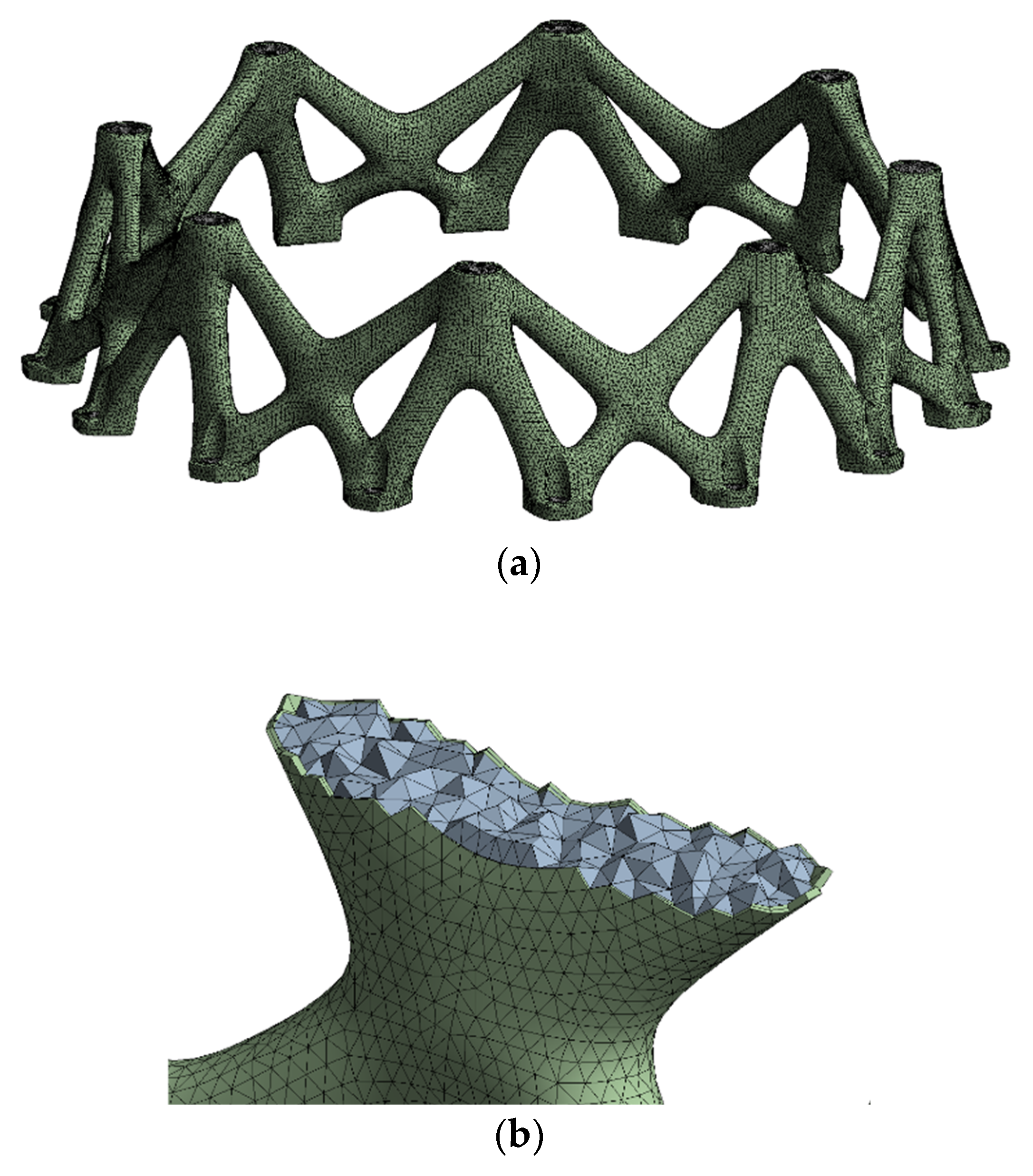
3.1.5. Lattice Filling
3.2. Lightweight Design of Lattice SkinFilling for the Support Structure
3.3. Machinability Verification
4. Numerical Simulations of the Lattice-Filled Structure
4.1. Numerical Simulation Model
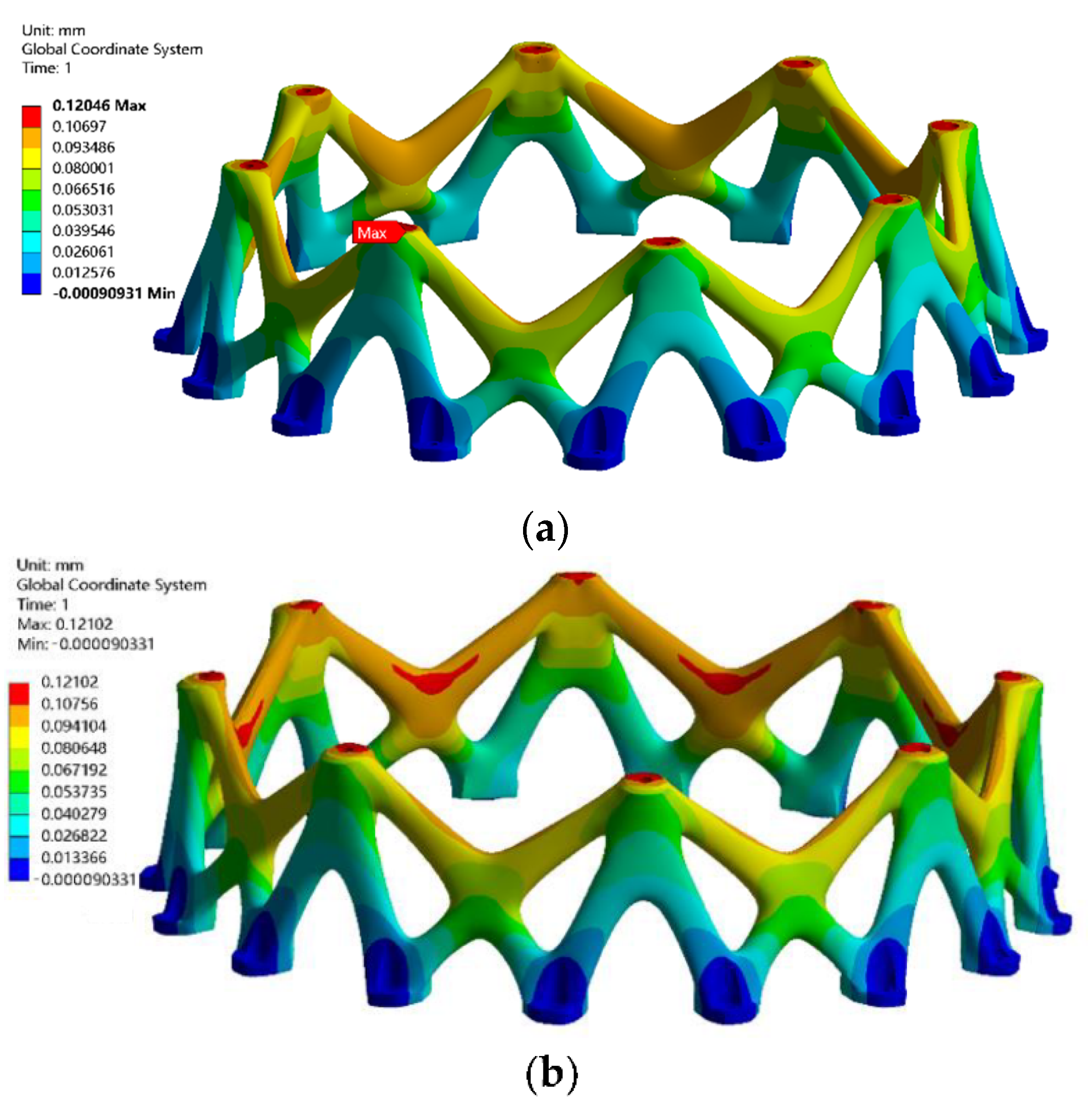
4.2. Static Responses and Discussion
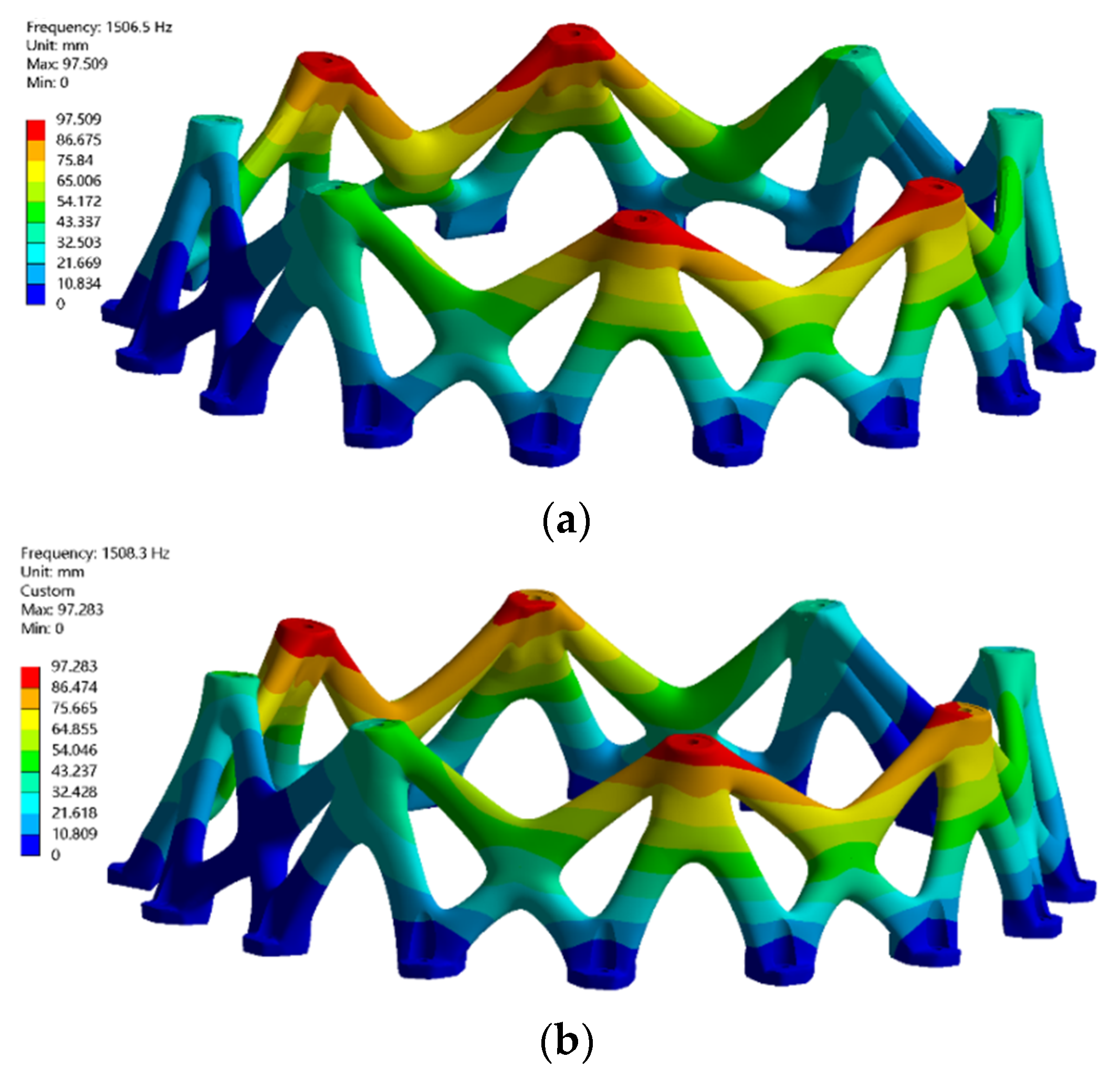
4.3. Dynamic Characteristics and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smith, B.H.; Szyniszewski, S.; Hajjar, J.F.; Schafer, B.W.; Arwade, S.R. Steel Foam for Structures: A Review of Applications, Manufacturing and Material Properties. J. Constr. Steel Res. 2012, 71, 1–10. [Google Scholar] [CrossRef]
- He, M.; Hu, W. A study on composite honeycomb sandwich panel structure. Mater. Des. 2008, 29, 709–713. [Google Scholar] [CrossRef]
- Wadley, H.N.G.; Fleck, N.A.; Evans, A.G. Fabrication and structural performance of periodic cellular metal sandwich structures. Compos. Sci. Technol. 2003, 63, 2331–2343. [Google Scholar] [CrossRef]
- Hao, P.; Wang, B.; Li, G. Surrogate-based optimum design for stiffened shells with adaptive sampling. AIAA J. 2012, 50, 2389–2407. [Google Scholar] [CrossRef]
- Evans, A.G.; Hutchinsona, J.W.; Ashby, M.F. Multifunctionality of cellular metal systems. Prog. Mater. Sci. 1998, 43, 171–221. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal foams: A design guide. Appl. Mech. Rev. 2012, 23, 119. [Google Scholar]
- Ashby, M.F. Designing Hybrid Materials. Acta Mater. 2003, 51, 5801–5821. [Google Scholar] [CrossRef]
- Kooistra, G.W.; Deshpande, V.S.; Wadley, H.N.G. Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminium. Acta Mater. 2004, 52, 4229–4237. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, C.G.; Huo, S.X.; Chai, X.H.; Liu, Z.H.; Yan, K. Experimental and numerical simulation of bird-strike performance of lattice-material-infilled curved plate. Chin. J. Aeronaut. 2021, 34, 245–257. [Google Scholar] [CrossRef]
- Liu, X.; Gao, L.; Xiao, M.; Zhang, Y. Kriging-assisted design of functionally graded cellular structures with smoothly-varying lattice unit cells. Comput. Methods Appl. Mech. Eng. 2022, 390, 114466. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, J.; Yuan, Z.; Xu, S.; Zou, B.; Li, L.; Ma, Y. A novel lattice structure topology optimization method with extreme anisotropic lattice properties. J. Comput. Des. Eng. 2021, 5, 1367–1390. [Google Scholar] [CrossRef]
- Khalil, M.A.; Lebaal, N.; Demoly, F.; Roth, S. A design and optimization framework of variable-density lattice structures for additive manufacturing. Mech. Adv. Mater. Struct. 2021, 3, 1–15. [Google Scholar] [CrossRef]
- Abate, K.M.; Nazir, A.; Yeh, Y.-P.; Chen, J.-E.; Jeng, J.-Y. Design, optimization, and validation of mechanical properties of different cellular structures for biomedical application. Int. J. Adv. Manuf. Technol. 2019, 106, 1253–1265. [Google Scholar] [CrossRef]
- Bian, Y.; Yang, F.; Li, P.; Wang, P.; Li, W.; Fan, H. Energy absorption properties of macro triclinic lattice structures with twin boundaries inspired by microstructure of feldspar twinning crystals. Compos. Struct. 2021, 271, 114103. [Google Scholar] [CrossRef]
- Liu, L.; Yan, J.; Cheng, G. Optimum structure with homogeneous optimum truss-like material. Comput. Struct. 2008, 86, 1417–1425. [Google Scholar] [CrossRef]
- Niu, B.; Yan, J.; Cheng, G. Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency. Struct. Multidiscip. Optim. 2009, 39, 115–132. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sharma, A.; Maute, K.; Sciacovelli, A.; Verda, V. Multi-scale topology optimization of multi-material structures with controllable geometric complexity—Applications to heat transfer problems. Comput. Methods Appl. Mech. Eng. 2019, 357, 112552. [Google Scholar] [CrossRef]
- Yan, J.; Yang, S.; Duan, Z.; Yang, C. Minimum compliance optimization of a thermoelastic lattice structure with size-coupled effects. J. Therm. Stresses 2015, 38, 338–357. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in MATLAB. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Yang, X.Y.; Xie, Y.M.; Steven, G.P.; Querin, O.M. Bidirectional evolutionary method for stiffness optimization. AIAA J. 1999, 37, 1483–1488. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, S. Synthesis of shape and topology of multi-material structures with a phase-field method. J. Comput. Aided Mater. Des. 2004, 11, 117–138. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, J.; Zhang, J.; Guo, X. A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model. Struct. Multidisc. Optim. 2016, 53, 1243–1260. [Google Scholar] [CrossRef]
- Kalamkarov, A.L.; Kolpakov, A.G. Analysis, Design, and Optimization of Composite Structures, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Zhang, H.W.; Liu, Y.; Zhang, S.; Tao, J.; Wu, J.K.; Chen, B.S. Extended multiscale finite element method: Its basis and applications for mechanical analysis of heterogeneous materials. Comput. Mech. 2014, 53, 659–685. [Google Scholar] [CrossRef]
- Yan, J.; Huo, S.; Yu, T.; Zhang, C.; Chai, X.; Hu, D.; Yan, K. Multiscale analysis for 3D lattice structures based on parallel computing. Int. J. Numer. Methods Eng. 2021, 122, 6756–6776. [Google Scholar] [CrossRef]
- Cheng, G.D.; Cai, Y.W.; Xu, L. Novel implementation of homogenization method to predict effective properties of periodic materials. Acta Mech. Sin. 2013, 29, 550–556. [Google Scholar] [CrossRef]
- Cai, Y.; Xu, L.; Cheng, G.D. Novel numerical implementation of asymptotic homogenization method for periodic plate structures. Int. J. Solids Struct. 2014, 51, 284–292. [Google Scholar] [CrossRef]
- Xu, L.; Cheng, G.D. Shear stiffness prediction of reissner-mindlin plates with periodic microstructures. Mech. Adv. Mater. Struct. 2017, 24, 271–286. [Google Scholar] [CrossRef]
- Wang, B.; Tian, K.; Hao, P.; Zheng, Y.; Ma, Y.; Wang, J. Numerical-based smeared stiffener method for global buckling analysis of grid-stiffened composite cylindrical shells. Compos. Struct. 2016, 15, 807–815. [Google Scholar] [CrossRef]
- Yan, K.; Wang, Y.Y.; Pan, Y.; Sun, G.; Chen, J.; Cai, X.H.; Cheng, G.D. Topology Optimization of Simplified Convective Heat Transfer problems using the Finite Volume Method. Sci. China. Technol. Sc. 2022, 4, 1–34. [Google Scholar]
- Tang, Y.; Dong, G.; Zhao, Y.F. A hybrid geometric modeling method for lattice structures fabricated by additive manufacturing. Int. J. Adv. Manuf. Technol. 2019, 102, 4011–4030. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, H.; Shi, W.; Zeng, F.; Zeng, H.; Chen, G. Vibration Tests of 3D Printed Satellite Structure Made of Lattice Sandwich Panels. AIAA J. 2018, 56, 4213–4217. [Google Scholar] [CrossRef]











| Method | Stiffness Coefficients (MPa) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| D11 | D22 | D33 | D12 | D13 | D23 | D44 | D55 | D66 | |
| Analytical formulation | 435 | 435 | 435 | 435 | 435 | 435 | 435 | 435 | 435 |
| NIAH | 431 | 431 | 431 | 419 | 419 | 419 | 425 | 425 | 425 |
| Laser Power/W | Scan Rate/mm | Open Space/mm | Thickness/μm |
|---|---|---|---|
| 120 | 3500 | 0.10–0.19 | 30 |
| Mode | Detailed Model | Homogenization Model | Relative Error |
|---|---|---|---|
| 1 | 1508.3 | 1506.5 | 0.1% |
| 2 | 1508.6 | 1506.6 | 0.1% |
| 3 | 1522.9 | 1517.1 | 0.3% |
| 4 | 1526.8 | 1527.7 | 0.0% |
| 5 | 1527.9 | 1527.7 | 0.0% |
| 6 | 1665.6 | 1658.9 | 0.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Liu, Y.; Huang, X.; Mu, D. Research on the Lightweight Design of an Aircraft Support Based on Lattice-Filled Structures. Mathematics 2022, 10, 4576. https://doi.org/10.3390/math10234576
Huang Z, Liu Y, Huang X, Mu D. Research on the Lightweight Design of an Aircraft Support Based on Lattice-Filled Structures. Mathematics. 2022; 10(23):4576. https://doi.org/10.3390/math10234576
Chicago/Turabian StyleHuang, Zhou, Yong Liu, Xin Huang, and Dong Mu. 2022. "Research on the Lightweight Design of an Aircraft Support Based on Lattice-Filled Structures" Mathematics 10, no. 23: 4576. https://doi.org/10.3390/math10234576
APA StyleHuang, Z., Liu, Y., Huang, X., & Mu, D. (2022). Research on the Lightweight Design of an Aircraft Support Based on Lattice-Filled Structures. Mathematics, 10(23), 4576. https://doi.org/10.3390/math10234576








