On the BiHom-Type Nonlinear Equations

Abstract

In this paper, the Heisenberg doubles and Long dimodules of a BiHom-Hopf algebra are introduced. Then, we discussed the relation between BiHom-Hopf equation and BiHom-pentagon equation, and we obtain the solutions of BiHom-Hopf equation from Heisenberg doubles. We also showed that the parametric generalized Long dimodules can provide the solutions of BiHom-Yang-Baxter equation and generalized $\mathcal{D}$-equation.

1. Introduction

The theory of Hom-type algebras arises from the q-deformations of Witt and Virasoro algebras (see [1,2]). Then, the theory of Hom-type algebras is rapidly developing into a hot topic in algebra theory [3,4,5,6,7,8]. In 2008, Makhlouf and Silvestrov introduced the definition of Hom-associative algebras [4]. In 2012, Caenepeel and Goyvaerts introduced the monoidal Hom–Hopf algebras [9] in order to provide a categorical approach to Hom-type algebras. In 2015, as the generalization of both Hom-(co)algebras and monoidal Hom-(co)algebras, BiHom-(co)algebras and BiHom-bialgebras were investigated by Graziani, Makhlouf, Menini, and Panaite in [10]. Note that a BiHom-algebra is an algebra in which the identities defining the structure are twisted by two homomorphisms. This class of algebras was introduced from a categorical approach in [10] which can be viewed as an extension of the class of Hom-algebras. Further research on BiHom-type algebras could be found in [11,12,13,14,15] and so on.

It is well known that some classical nonlinear equations in Hopf algebra theory, such as the quantum Yang-Baxter equation, the Hopf equation, the pentagon equation, and the $\mathcal{D}$-equation. In [16], the algebraic solutions of Hopf equation and pentagon equation are discussed. In [17], Militaru proved that each Long dimodule gave rise to a solution for the $\mathcal{D}$-equation. Long dimodules are the building stones of the Brauer-Long group [18]. The discussion of solutions of BiHom-type Yang-Baxter equation can be seen in [11,19]. The natural consideration is to ask: does there exist algebraic solutions of BiHom-Hopf equation, BiHom-pentagon equation, and BiHom-type $\mathcal{D}$-equation? That is the motivation of our paper.

In order to obtain the algebraic solutions of the above BiHom-type nonlinear equations, we introduced the Heisenberg doubles and the parametric generalized BiHom-Long dimodules of a BiHom-Hopf algebra. We also generalized Theorem 3.1 and Theorem 5.10 in [20].

The paper is organized as follows. In Section 2, we first recall some notions of BiHom-Hopf algebras. In Section 3, we describe the BiHom-Hopf equation and BiHom-pentagon equation, and provide the algebraic solutions of BiHom-Hopf equation through Heisenberg doubles. In Section 4, we introduce the parametric generalized BiHom-Long dimodules, and provide the algebraic solutions of the BiHom–Yang-Baxter equation and generalized $\mathcal{D}$-equation.

2. Preliminaries

Throughout the paper, $\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d},\mathfrak{e},\cdots$ always mean integers in $\mathbb{Z}$. Let $\mathbb{k}$ be a fixed field and $char\left(\mathbb{k}\right)=0$, and $Ve{c}_{\mathbb{k}}$ be the category of finite dimensional $\mathbb{k}$-spaces. All algebras are supposed to be over $\mathbb{k}$. For the comultiplication $\Delta$ of a $\mathbb{k}$-space C, we use the Sweedler–Heyneman’s notation (see [21]): $\Delta \left(c\right)=c_1\otimes c_2,$ for any $c\in C$. When we say a “BiHom-algebra” or a “BiHom-coalgebra”, we mean the unital BiHom-algebra and counital BiHom-coalgebra. We always assume that the BiHom-structure maps are invertible.

2.1. BiHom-Hopf Algebras

In this section, we will review several definitions and notations related to BiHom-bialgebras.

Recall from [10] or [15] that a BiHom-algebra A over $\mathbb{k}$ is a 5-tuple $(A,{\mu }_A,1_H$, ${\alpha }_A,{\beta }_A)$, where A is a $\mathbb{k}$-linear space, $1_A\in A$ is an element (the unit), ${\alpha }_A,{\beta }_A:A\to A$ are both bijective linear maps, ${\mu }_A:A\otimes A\to A$ is a linear map, with notation $\mu (a\otimes b)=ab$, satisfying the following conditions, for all $a,b,c\in A$:

$$\begin{array}{cc}& {\alpha }_A\left(1_A\right)={\beta }_A\left(1_A\right)=1_A,a{1}_A={\alpha }_A\left(a\right),1_{A}a={\beta }_A\left(a\right),{\alpha }_A\left(a\right)\left(bc\right)=\left(ab\right){\beta }_A\left(c\right),\\ & {\alpha }_A\circ {\beta }_A={\beta }_A\circ {\alpha }_A,{\alpha }_A\left(ab\right)={\alpha }_A\left(a\right){\alpha }_A\left(b\right),{\beta }_A\left(ab\right)={\beta }_A\left(a\right){\beta }_A\left(b\right).\end{array}$$

Remark 1.

Note that the second line of the above identities can be derived from the first line. See [15], (Proposition 2.9).

Example 1.

(1)

If $A=(A,{\mu }_A,1_A)$ is an associative algebra, $\alpha ,\beta :A\to A$ are both algebra isomorphisms, then $(A,{\mu }_A\circ (\alpha \otimes \beta ),1_A,\alpha ,\beta )$ is a BiHom-algebra.

(2)

If $\alpha =\beta$, then A becomes a Hom-algebra.

A BiHom-coalgebra C over $\mathbb{k}$ is a 5-tuple $(C,{\Delta }_C,{\epsilon }_C,{\varphi }_C,{\psi }_C)$, in which C is a linear space, ${\varphi }_C,{\psi }_C:C\to C$ are linear isomorphisms, ${\epsilon }_C:C\to k$ and ${\Delta }_C:C\to C\otimes C$ are linear maps, such that

$$\begin{array}{cc}& c_1{\epsilon }_C\left(c_2\right)={\varphi }_C\left(c\right),{\epsilon }_C\left(c_1\right)c_2={\psi }_C\left(c\right),\\ & {\epsilon }_C\left({\varphi }_C\left(c\right)\right)={\epsilon }_C\left({\psi }_C\left(c\right)\right)={\epsilon }_C\left(c\right),{\varphi }_C\left(c_1\right)\otimes {\Delta }_C\left(c_2\right)={\Delta }_C\left(c_1\right)\otimes {\psi }_C\left(c_2\right),\\ & {\varphi }_C\circ {\psi }_C={\psi }_C\circ {\varphi }_C,{\Delta }_C\left({\varphi }_C\left(c\right)\right)={\varphi }_C\left(c_1\right)\otimes {\varphi }_C\left(c_2\right),{\Delta }_C\left({\psi }_C\left(c\right)\right)={\psi }_C\left(c_1\right)\otimes {\psi }_C\left(c_2\right).\end{array}$$

Remark 2.

Note that the third line of the above identities can be derived from the first two lines. See [15], (Proposition 2.11).

Example 2.

(1)

If $(C,{\Delta }_C,{\epsilon }_C)$ is a coassociative coalgebra, $\varphi ,\psi :C\to C$ are both coalgebra isomorphisms, then $(C,(\varphi \otimes \psi )\circ {\Delta }_C,{\epsilon }_C,\varphi ,\psi )$ is a BiHom-coalgebra.

(2)

If $\varphi =\psi$, then C becomes a Hom-coalgebra.

A BiHom-bialgebra H over $\mathbb{k}$ is a 9-tuple $(H,{\mu }_H,1_H,{\Delta }_H,{\epsilon }_H,{\alpha }_H,{\beta }_H,{\varphi }_H,{\psi }_H)$, with the property that $(H,{\mu }_H,1_H$, ${\alpha }_H$, ${\beta }_H)$ is a BiHom-algebra, $(H,{\Delta }_H,{\epsilon }_H,{\varphi }_H,{\psi }_H)$ is a BiHom-coalgebra, and ${\Delta }_H,{\epsilon }_H$ are all morphisms of BiHom-algebras preserving unit, i.e., for all $h,g\in H$,

$$\begin{array}{cc}& {\Delta }_H\left(hg\right)=h_1{g}_1\otimes h_2{g}_2,{\epsilon }_H\left(hg\right)={\epsilon }_H\left(h\right){\epsilon }_H\left(g\right),\\ & {\Delta }_H\left(1_H\right)=1_H\otimes 1_H,{\epsilon }_H\left(1_H\right)=1_{\mathbb{k}}.\end{array}$$

Moreover, it is easy to check that ${\alpha }_H,{\beta }_H$ are BiHom-coalgebra maps, ${\varphi }_H,{\psi }_H$ are BiHom-algebra maps, and they commute with each other (see [15], Proposition 2.14).

Example 3.

(1)

If $(H,{\mu }_H,1_H,{\Delta }_H,{\epsilon }_H)$ is a bialgebra, $\alpha ,\beta ,\varphi ,\psi :H\to H$ are all bialgebra isomorphisms, then $H^{Bi}=(H,{\mu }_H\circ (\alpha \otimes \beta ),1_H,(\varphi \otimes \psi )\circ {\Delta }_H,{\epsilon }_H,\alpha ,\beta ,\varphi ,\psi )$ is a BiHom-bialgebra.

(2)

If $H=(H,{\mu }_H,1_H,{\Delta }_H,{\epsilon }_H,\alpha ,\beta ,\varphi ,\psi )$ is a finite dimensional BiHom-bialgebra, $H^{*}=hom(H,\mathbb{k})$. Define the multiplication ⋆, the comultiplication ${\Delta }_{H^{*}}$ (with notation ${\Delta }_{H^{*}}\left(p\right)=p_1\otimes p_2$) and ${\epsilon }_{H^{*}}$ by

$$\begin{array}{cc}& (p\star q)\left(h\right)=p\left({\alpha }^{-1}{\varphi }^{-1}\left(h_1\right)\right)q\left({\beta }^{-1}{\psi }^{-1}\left(h_2\right)\right),{\epsilon }_{H^{*}}\left(p\right)=p\left(1_H\right),\\ & (p_1\otimes p_2)(h\otimes g)=p\left({\alpha }^{-1}{\psi }^{-1}\left(h\right){\beta }^{-1}{\varphi }^{-1}\left(g\right)\right),wherep,q\in H^{*},h,g\in H.\end{array}$$

Define ${\alpha }_{H^{*}},{\beta }_{H^{*}},{\varphi }_{H^{*}},{\psi }_{H^{*}}$ by

$$\begin{array}{c}\hfill {\alpha }_{H^{*}}\left(p\right)=p\circ {\alpha }^{-1},{\beta }_{H^{*}}\left(p\right)=p\circ {\beta }^{-1},{\varphi }_{H^{*}}\left(p\right)=p\circ {\psi }^{-1},{\psi }_{H^{*}}\left(p\right)=p\circ {\varphi }^{-1}.\end{array}$$

Then, $H^{\star }=(H^{*},\star ,{\epsilon }_H,{\Delta }_{H^{*}},{\epsilon }_{H^{*}},{\alpha }_{H^{*}},{\beta }_{H^{*}},{\varphi }_{H^{*}},{\psi }_{H^{*}})$ is a BiHom-bialgebra.

(3)

If $\alpha =\beta =\varphi =\psi$, then H becomes a Hom-bialgebra. If ${\alpha }^{-1}={\beta }^{-1}=\varphi =\psi$, then H becomes a monoidal Hom-bialgebra.

Recall from [22] that a BiHom-Hopf algebra H over $\mathbb{k}$ is a 10-tuple $(H,{\mu }_H,1_H,{\Delta }_H,{\epsilon }_H,S_H,{\alpha }_H,{\beta }_H,{\varphi }_H,{\psi }_H$), where $H=(H,\mu ,1_H,\Delta ,\epsilon ,\alpha ,\beta ,\varphi ,\psi )$ is a BiHom-bialgebra, $S:H\to H$ (the antipode) commutes with $\alpha ,\beta ,\varphi ,\psi$, and satisfies, for any $h\in H$,

$$h_{1}S\left(h_2\right)=S\left(h_1\right)h_2=\epsilon \left(h\right)1_H.$$

Proposition 1.

Recall from [22] that, if H is a BiHom-Hopf algebra, then for any $a,b\in H$, the antipode S satisfies

$$\begin{array}{cc}& S\left(ab\right)=S{\alpha }^{-1}\beta \left(b\right)S\alpha {\beta }^{-1}\left(a\right),S\left(1_H\right)=1_H,\end{array}$$

(1)

$$\begin{array}{cc}& \Delta \left(S\left(a\right)\right)=S\varphi {\psi }^{-1}\left(a_2\right)\otimes S{\varphi }^{-1}\psi \left(a_1\right),\epsilon \circ S=\epsilon ,\end{array}$$

(2)

$$\begin{array}{cc}& S{\alpha }^2{\varphi }^2=S{\beta }^2{\psi }^2.\end{array}$$

(3)

Moreover, if S is a bijection, then

$$\begin{array}{cc}& {\alpha }^2{\varphi }^2={\beta }^2{\psi }^2,\end{array}$$

(4)

$$\begin{array}{cc}& S^{-1}\left(ab\right)=S^{-1}{\alpha }^{-1}\beta \left(b\right)S^{-1}\alpha {\beta }^{-1}\left(a\right),S^{-1}\left(1_H\right)=1_H,\end{array}$$

(5)

$$\begin{array}{cc}& \Delta \left(S^{-1}\left(a\right)\right)=S^{-1}\varphi {\psi }^{-1}\left(a_2\right)\otimes S^{-1}{\varphi }^{-1}\psi \left(a_1\right),\epsilon \circ S^{-1}=\epsilon ,\end{array}$$

(6)

$$\begin{array}{cc}& S^{-1}{\alpha }^{-2}{\beta }^2\left(a_2\right)a_1=a_2{S}^{-1}{\alpha }^2{\beta }^{-2}\left(a_1\right)=\epsilon \left(a\right)1_H.\end{array}$$

(7)

Example 4.

(1)

If $(H,S,{\mu }_H,1_H,{\Delta }_H,{\epsilon }_H)$ is a Hopf algebra, $\alpha ,\beta ,\varphi ,\psi :H\to H$ are all Hoppf algebra isomorphisms and satisfying $S{\alpha }^2{\varphi }^2=S{\beta }^2{\psi }^2$, then $H^{BiH}=(H,S,{\mu }_H\circ (\alpha \otimes \beta ),1_H,(\varphi \otimes \psi )\circ {\Delta }_H,{\epsilon }_H,\alpha ,\beta ,\varphi ,\psi )$ is a BiHom-Hopf algebra.

(2)

If $H=(H,S,\mu ,1_H,\Delta ,\epsilon ,\alpha ,\beta ,\varphi ,\psi )$ is a BiHom-Hopf algebra, under the consideration of Example 3 (2), we immediately obtain that ${H^{\star }}^{cop}=(H^{*}$, ⋆, ε, ${\Delta }_{H^{*}}^{cop}$, ${\epsilon }_{H^{*}}$, ${\left(S^{-1}\right)}^{*}$, ${\left({\alpha }^{-1}\right)}^{*}$, ${\left({\beta }^{-1}\right)}^{*},{\left({\psi }^{-1}\right)}^{*},{\left({\varphi }^{-1}\right)}^{*})$ and ${H^{\star }}^{op}=(H^{*}$, ${\star }^{op}$, ε, ${\Delta }_{H^{*}}$, ${\epsilon }_{H^{*}}$, ${\left(S^{-1}\right)}^{*}$, ${\left({\beta }^{-1}\right)}^{*},{\left({\alpha }^{-1}\right)}^{*},{\left({\varphi }^{-1}\right)}^{*}$, (${\psi }^{-1}{)}^{*})$ are all BiHom-Hopf algebras.

(3)

If $\alpha =\beta$ and $\varphi =\psi$, then H becomes the so-called monoidal BiHom-Hopf algebra (see [10], Definition 6.4). If $\alpha =\beta =\varphi =\psi$, then H becomes the usual Hom–Hopf algebra. Similarly, if $\alpha =\beta ={\varphi }^{-1}={\psi }^{-1}$, then H becomes the usual monoidal Hom–Hopf algebra.

2.2. BiHom-Modules and BiHom-Comodules of a BiHom-Bialgebra

Assume that $H=(H,\mu ,1_H$, $\Delta ,\epsilon ,\alpha ,\beta ,\varphi ,\psi )$ is a BiHom-bialgebra. Recall that a $\mathbb{k}$-space M is called a left BiHom-module of H (in short, an H-BiHom-module) if there exist $\mathbb{k}$-linear isomorphisms ${\alpha }_M,{\beta }_M,{\varphi }_M,{\psi }_M:M\to M$ (the Hom-structure maps), and an H action ${\theta }_M:H\otimes M\to M$ (with notation ${\theta }_M(h\otimes m)=h·m$), such that, for any $h,g\in H$, $m\in M$,

$$\begin{array}{cc}& {\alpha }_M,{\beta }_M,{\varphi }_M,{\psi }_M\mathrm{commute}\mathrm{with}\mathrm{each}\mathrm{other},\\ & \alpha \left(h\right)·{\alpha }_M\left(m\right)={\alpha }_M(h·m),\beta \left(h\right)·{\beta }_M\left(m\right)={\beta }_M(h·m),\varphi \left(h\right)·{\varphi }_M\left(m\right)={\varphi }_M(h·m),\\ & \psi \left(h\right)·{\psi }_M\left(m\right)={\psi }_M(h·m),\alpha \left(h\right)·(g·m)=\left(hg\right)·{\beta }_M\left(m\right),1_H·m={\beta }_M\left(m\right).\end{array}$$

If $(M,{\alpha }_M,{\beta }_M,{\varphi }_M,{\psi }_M)$ and $(N,{\alpha }_N,{\beta }_N,{\varphi }_N,{\psi }_N)$ are left H-BiHom-modules with H-actions ${\theta }_M$ and, respectively, ${\theta }_N$, a morphism of H-BiHom-modules$f\in ho{m}_{\mathbb{k}}(M,N)$ is an H-linear map satisfying the conditions

$$\begin{array}{cc}& {\alpha }_N\circ f=f\circ {\alpha }_M,{\beta }_N\circ f=f\circ {\beta }_M,{\varphi }_N\circ f=f\circ {\varphi }_M,{\psi }_N\circ f=f\circ {\psi }_M.\end{array}$$

The category of H-BiHom-modules and morphisms will be denoted by ${}_H\mathcal{BM}$.

Remark 3.

(1)

Obviously, $H\in Obj\left({}_H\mathcal{BM}\right)$.

(2)

The definition of right BiHom-module of H can be defined in a similar way.

(3)

For any integers $\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d},\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}\in \mathbb{Z}$, $M,N,P\in {}_H\mathcal{BM}$, ${}_H\mathcal{BM}$ forms a monoidal category under the following structures:

• the tensor product of $(M,{\alpha }_M,{\beta }_M,{\varphi }_M,{\psi }_M)$ and $(N,{\alpha }_N,{\beta }_N,{\varphi }_N,{\psi }_N)$ is $(M\otimes N,{\alpha }_{M\otimes N}$, ${\alpha }_M\otimes {\alpha }_N,{\beta }_M\otimes {\beta }_N,{\varphi }_M\otimes {\varphi }_N,{\psi }_M\otimes {\psi }_N)$, where the H-action on $M\otimes N$ is given by

  $$h·(m\otimes n)={\alpha }^{\mathfrak{a}}{\beta }^{\mathfrak{b}}{\varphi }^{\mathfrak{c}}{\psi }^{\mathfrak{d}}\left(h_1\right)·m\otimes {\alpha }^{\mathfrak{e}}{\beta }^{\mathfrak{f}}{\varphi }^{\mathfrak{g}}{\psi }^{\mathfrak{h}}\left(h_2\right)·n,wherem\in M,n\in N,h\in H;$$
• the unit object is $(\mathbb{k},i{d}_{\mathbb{k}},i{d}_{\mathbb{k}},i{d}_{\mathbb{k}},i{d}_{\mathbb{k}})$ with the trivial module action;
• for any $m\in M,n\in N,p\in P$, the the associativity and the unit constraints are given by

  $$\begin{array}{cc}& {\mathbf{a}}_{M,N,P}((m\otimes n)\otimes p)={\alpha }_M^{-\mathfrak{a}}{\beta }_M^{-\mathfrak{b}}{\varphi }_M^{-\mathfrak{c}-1}{\psi }_M^{-\mathfrak{d}}\left(m\right)\otimes (n\otimes {\alpha }_P^{\mathfrak{e}}{\beta }_P^{\mathfrak{f}}{\varphi }_P^{\mathfrak{g}}{\psi }_P^{\mathfrak{h}+1}\left(p\right));\\ & {\mathbf{l}}_M(1_{\mathbb{k}}\otimes m)={\alpha }_M^{-\mathfrak{e}}{\beta }_M^{-\mathfrak{f}}{\varphi }_M^{-\mathfrak{g}}{\psi }_M^{-\mathfrak{h}-1}\left(m\right),{\mathbf{r}}_M(m\otimes 1_{\mathbb{k}})={\alpha }_M^{-\mathfrak{a}}{\beta }_M^{-\mathfrak{b}}{\varphi }_M^{-\mathfrak{c}-1}{\psi }_M^{-\mathfrak{d}}\left(m\right).\end{array}$$

We write this monoidal category by ${}_H{\mathcal{BM}}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}}$.

Dually, recall from [15], (Definition 5.3) that a right H-BiHom-comodule is a 5-tuple $(M,{\alpha }_M,{\beta }_M,{\varphi }_M,{\psi }_M)$, where M is a linear space, ${\alpha }_M,{\beta }_M,{\varphi }_M,{\psi }_M:M\to M$ are linear isomorphisms, and we have a linear map (called a coaction) $\rho :M\to M\otimes H$, with notation $\rho \left(m\right)=m_0\otimes m_1$, for all $m\in M$, such that the following conditions are satisfied

$$\begin{array}{cc}& {\varphi }_M,{\psi }_M,{\alpha }_M,{\beta }_M\mathrm{commute}\mathrm{with}\mathrm{each}\mathrm{other},\\ & ({\alpha }_M\otimes \alpha )\circ \rho =\rho \circ {\alpha }_M,({\beta }_M\otimes \beta )\circ \rho =\rho \circ {\beta }_M,({\varphi }_M\otimes \varphi )\circ \rho =\rho \circ {\varphi }_M,\\ & ({\psi }_M\otimes \psi )\circ \rho =\rho \circ {\psi }_M,{\varphi }_M\left(m_0\right)\otimes m_{11}\otimes m_{12}=m_{00}\otimes m_{01}\otimes \psi \left(m_1\right),m_0\epsilon \left(m_1\right)={\varphi }_M\left(m\right).\end{array}$$

If $(M,{\alpha }_M,{\beta }_M,{\varphi }_M,{\psi }_M)$ and $(N,{\alpha }_N,{\beta }_N,{\varphi }_N,{\psi }_N)$ are right H-BiHom-comodules with coactions ${\rho }_M$ and, respectively ${\rho }_N$, a morphism of right H-BiHom-comodules$f:M\to N$ is a linear map satisfying the conditions

$$\begin{array}{cc}& {\alpha }_N\circ f=f\circ {\alpha }_M,{\beta }_N\circ f=f\circ {\beta }_M,{\varphi }_N\circ f=f\circ {\varphi }_M,\\ & {\psi }_N\circ f=f\circ {\psi }_M,{\rho }_N\circ f=(f\otimes i{d}_H)\circ {\rho }_M.\end{array}$$

The category of H-BiHom-comodules and H-colinear morphisms will be denoted by ${\mathcal{BM}}^H$.

Remark 4.

(1)

Obviously, $H\in Obj{\mathcal{BM}}^H$.

(2)

The definition of left BiHom-comodule of H can be defined in a similar way.

(3)

For any integers $\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l},\mathfrak{m},\mathfrak{n},\mathfrak{p},\mathfrak{q}\in \mathbb{Z}$, ${\mathcal{BM}}^H$ forms a monoidal category under the following structures:

• the tensor product of H-BiHom-comodules $(U,{\alpha }_U,{\beta }_U,{\varphi }_U,{\psi }_U)$ and $(V,{\alpha }_V,{\beta }_V,{\varphi }_V,{\psi }_V)$ is $(U\otimes V,{\alpha }_U\otimes {\alpha }_V,{\beta }_U\otimes {\beta }_V,{\varphi }_U\otimes {\varphi }_V,{\psi }_U\otimes {\psi }_V)$ with the H-coaction ${\rho }^{U\otimes V}$:

  $$\begin{array}{c}\hfill u\otimes v\mapsto u_{\left(0\right)}\otimes v_{\left(0\right)}\otimes {\alpha }^{\mathfrak{i}}{\beta }^{\mathfrak{j}}{\varphi }^{\mathfrak{k}}{\psi }^{\mathfrak{l}}\left(u_{\left(1\right)}\right){\alpha }^{\mathfrak{m}}{\beta }^{\mathfrak{n}}{\varphi }^{\mathfrak{p}}{\psi }^{\mathfrak{q}}\left(v_{\left(1\right)}\right);\end{array}$$
• the unit object is $(\mathbb{k},i{d}_{\mathbb{k}},i{d}_{\mathbb{k}},i{d}_{\mathbb{k}},i{d}_{\mathbb{k}})$ with the trivial coaction;
• the associativity constraint $\mathbf{a}$ and the unit constraint $\mathbf{l}$ and $\mathbf{r}$ are given by

  $$\begin{array}{cc}& {\mathbf{a}}_{U,V,W}((u\otimes v)\otimes w)={\alpha }_U^{\mathfrak{i}+1}{\beta }_U^{\mathfrak{j}}{\varphi }_U^{\mathfrak{k}}{\psi }_U^{\mathfrak{l}}\left(u\right)\otimes (v\otimes {\alpha }_W^{-\mathfrak{m}}{\beta }_W^{-\mathfrak{n}-1}{\varphi }_W^{-\mathfrak{p}}{\psi }_W^{-\mathfrak{q}}\left(w\right));\\ & {\mathbf{r}}_U(u\otimes 1_{\mathbb{k}})={\alpha }^{\mathfrak{i}+1}{\beta }_U^{\mathfrak{j}}{\varphi }_U^{\mathfrak{k}}{\psi }_{(}^{\mathfrak{l}}u),{\mathbf{l}}_U(1_{\mathbb{k}}\otimes u)={\alpha }^{\mathfrak{m}}{\beta }_U^{\mathfrak{n}+1}{\varphi }_U^{\mathfrak{p}}{\psi }_{(}^{\mathfrak{q}}u).\end{array}$$

We denote this monoidal category by ${\left({\mathcal{BM}}^H\right)}_{\mathfrak{m},\mathfrak{n},\mathfrak{p},\mathfrak{q}}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}}$.

3. The BiHom-Type Heisenberg Doubles and the BiHom-Hopf Equation

In this section, we will discuss the algebraic solutions of the BiHom-Hopf equation and the BiHom-pentagon equation.

3.1. BiHom-Hopf Equation and BiHom-Pentagon Equation

In this subsection, we will discuss the relation between the BiHom-Hopf equation and BiHom-pentagon equation.

Definition 1.

Let $A=(A,{\mu }_A,1_A,{\alpha }_A,{\beta }_A)$ be a BiHom-algebra over $\mathbb{k}$, $\mathcal{R}=\sum {\mathcal{R}}^{\left(1\right)}\otimes {\mathcal{R}}^{\left(2\right)}$ be an element in $A\otimes A$ and satisfy

$$\begin{array}{c}\hfill ({\alpha }_A\otimes {\alpha }_A)\mathcal{R}=\mathcal{R},({\beta }_A\otimes {\beta }_A)\mathcal{R}=\mathcal{R}.\end{array}$$

(8)

(1) If $\mathcal{R}$ satisfies ${\mathcal{R}}^{23}{\mathcal{R}}^{13}{\mathcal{R}}^{12}={\mathcal{R}}^{12}{\mathcal{R}}^{23}$, i.e.,

$$\begin{array}{c}\hfill \sum {\beta }_A\left({\mathcal{R}}^{\left(1\right)}\right){\mathcal{S}}^{\left(1\right)}\otimes {\mathcal{T}}^{\left(1\right)}{\mathcal{S}}^{\left(2\right)}\otimes {\mathcal{T}}^{\left(2\right)}{\alpha }_A\left({\mathcal{R}}^{\left(2\right)}\right)=\sum {\alpha }_A\left({\mathcal{R}}^{\left(1\right)}\right)\otimes {\mathcal{R}}^{\left(2\right)}{\mathcal{S}}^{\left(1\right)}\otimes {\beta }_A\left({\mathcal{S}}^{\left(2\right)}\right),\end{array}$$

(9)

where $\mathcal{R}=\mathcal{S}=\mathcal{T}$, then we say $\mathcal{R}$ is a solution of the BiHom-Hopf equation.

(2) If $\mathcal{R}$ satisfies ${\mathcal{R}}^{12}{\mathcal{R}}^{13}{\mathcal{R}}^{23}={\mathcal{R}}^{23}{\mathcal{R}}^{12}$, i.e.,

$$\begin{array}{c}\hfill \sum {\mathcal{R}}^{\left(1\right)}{\alpha }_A\left({\mathcal{S}}^{\left(1\right)}\right)\otimes {\mathcal{R}}^{\left(2\right)}{\mathcal{T}}^{\left(1\right)}\otimes {\beta }_A\left({\mathcal{S}}^{\left(2\right)}\right){\mathcal{T}}^{\left(2\right)}=\sum {\beta }_A\left({\mathcal{R}}^{\left(1\right)}\right)\otimes {\mathcal{S}}^{\left(1\right)}{\mathcal{R}}^{\left(2\right)}\otimes {\alpha }_A\left({\mathcal{S}}^{\left(2\right)}\right),\end{array}$$

(10)

then we say $\mathcal{R}$ is a solution of the BiHom-pentagon equation.

Example 5.

(1)

$1_A\otimes 1_A$ is a solution of the BiHom-Hopf equation and the BiHom-pentagon equation.

(2)

For any $a\in A$, $a\otimes 1_A$ is a solution of the BiHom-Hopf equation if and only if ${\alpha }_A\left(a\right)={\beta }_A\left(a\right)$ and ${\alpha }_A\left(a\right)a={\alpha }_A\left(a\right)$, $1_A\otimes a$ is a solution of the BiHom-Hopf equation if and only if ${\alpha }_A\left(a\right)={\beta }_A\left(a\right)$ and $a{\alpha }_A\left(a\right)={\alpha }_A\left(a\right)$.

(3)

If ${\alpha }_A={\beta }_A=i{d}_A$, then A is the usual algebra, and the solution of the BiHom-Hopf equation becomes the solution of usual Hopf equation, the solution of the BiHom-pentagon equation becomes the solution of usual pentagon equation (see [[16], Definition 11] for details).

Proposition 2.

(1)

If $\mathcal{R}=\sum {\mathcal{R}}^{\left(1\right)}\otimes {\mathcal{R}}^{\left(2\right)}\in A\otimes A$ is a solution of the BiHom-Hopf equation, then ${\mathcal{R}}^{21}=\sum {\mathcal{R}}^{\left(2\right)}\otimes {\mathcal{R}}^{\left(1\right)}\in A\otimes A$ is a solution of the BiHom-pentagon equation.

(2)

If $\mathcal{R}\in A\otimes A$ is invertible, then $\mathcal{R}$ is a solution of the BiHom-Hopf equation if and only if ${\mathcal{R}}^{-1}$ is a solution of the BiHom-pentagon equation.

Proof. 

(1)

Self evident.

(2)

Note that ${\mathcal{R}}^{23}{\mathcal{R}}^{13}{\mathcal{R}}^{12}$ and ${\overline{\mathcal{R}}}^{12}{\overline{\mathcal{R}}}^{13}{\overline{\mathcal{R}}}^{23}$ are inverse with each other, ${\mathcal{R}}^{12}{\mathcal{R}}^{23}$ and ${\overline{\mathcal{R}}}^{23}{\overline{\mathcal{R}}}^{12}$ are inverse with each other, where $\overline{\mathcal{R}}$ means the inverse of $\mathcal{R}$. Hence, the conclusion holds.

□

Proposition 3.

Let $A=(A,{\mu }_A,1_A,{\alpha }_A,{\beta }_A)$, $\mathcal{R}\in A\otimes A$ be an invertible solution of the BiHom-Hopf equation. If we define a $\mathbb{k}$-linear map ${\Delta }_L:A\to A\otimes A$, $a\mapsto a_1\otimes a_2$, by

$$\begin{array}{c}\hfill a_1\otimes a_2:=\left(\mathcal{R}(1_A\otimes a)\right){\mathcal{R}}^{-1}=\sum {\alpha }_A\left({\mathcal{R}}^{\left(1\right)}\right){\overline{\mathcal{R}}}^{\left(1\right)}\otimes \left({\mathcal{R}}^{\left(2\right)}a\right){\overline{\mathcal{R}}}^{\left(2\right)},\end{array}$$

where ${\mathcal{R}}^{-1}=\sum {\overline{\mathcal{R}}}^{\left(1\right)}\otimes {\overline{\mathcal{R}}}^{\left(2\right)}$, $a\in A$, then ${\Delta }_L$ is a BiHom-algebra morphism. Furthermore, $(A,{\Delta }_L,{\alpha }_A\circ {\beta }_A)$ forms a Hom-coalgebra without a counit.

Proof. 

For any $a,b\in A$, we compute

$$\begin{array}{ccc}& & {\Delta }_L\left(a\right){\Delta }_L\left(b\right)=\sum ({\alpha }_A\left({\mathcal{R}}^{\left(1\right)}\right){\overline{\mathcal{R}}}^{\left(1\right)}\otimes \left({\mathcal{R}}^{\left(2\right)}a\right){\overline{\mathcal{R}}}^{\left(2\right)})({\alpha }_A\left({\mathcal{S}}^{\left(1\right)}\right){\overline{\mathcal{S}}}^{\left(1\right)}\otimes \left({\mathcal{S}}^{\left(2\right)}b\right){\overline{\mathcal{S}}}^{\left(2\right)})\hfill \\ & =& \left({\alpha }_A\left({\mathcal{R}}^{\left(1\right)}\right)\left({\alpha }_A^{-1}\left({\overline{\mathcal{R}}}^{\left(1\right)}\right){\alpha }_A{\beta }_A^{-1}\left({\mathcal{S}}^{\left(1\right)}\right)\right)\right){\beta }_A\left({\overline{\mathcal{S}}}^{\left(1\right)}\right)\otimes \left(\left({\mathcal{R}}^{\left(2\right)}a\right)\left(\left({\alpha }_A^{-2}\left({\overline{\mathcal{R}}}^{\left(2\right)}\right){\beta }_A^{-1}\left({\mathcal{S}}^{\left(2\right)}\right)\right)b\right)\right){\beta }_A\left({\overline{\mathcal{S}}}^{\left(2\right)}\right)\hfill \\ & \stackrel{\left(8\right)}{=}& {\alpha }_A^2\left({\mathcal{R}}^{\left(1\right)}\right){\overline{\mathcal{S}}}^{\left(1\right)}\otimes \left({\alpha }_A\left({\mathcal{R}}^{\left(2\right)}\right)\left(ab\right)\right){\overline{\mathcal{S}}}^{\left(2\right)}\stackrel{\left(3.1\right)}{=}{\Delta }_L\left(ab\right),\hfill \end{array}$$

which implies ${\Delta }_L$ is a BiHom-algebra morphism.

Moreover, since Proposition 2, ${\mathcal{R}}^{-1}$ is a solution of the BiHom-pentagon equation, then we have

$$\begin{array}{ccc}& & {\Delta }_L\left(a_1\right)\otimes {\alpha }_A{\beta }_A\left(a_2\right)\hfill \\ & \stackrel{\left(8\right)}{=}& \sum {\alpha }_A\left({\mathcal{S}}^{\left(1\right)}\right){\beta }_A\left({\overline{\mathcal{S}}}^{\left(1\right)}\right)\otimes \left({\mathcal{S}}^{\left(2\right)}{\mathcal{R}}^{\left(1\right)}\right)\left({\overline{\mathcal{R}}}^{\left(1\right)}{\overline{\mathcal{S}}}^{\left(2\right)}\right)\otimes \left({\alpha }_A^{-1}{\beta }_A\left({\mathcal{R}}^{\left(2\right)}\right){\alpha }_A{\beta }_A\left(a\right)\right){\alpha }_A\left({\overline{\mathcal{R}}}^{\left(2\right)}\right)\hfill \\ & \stackrel{\left(9\right)}{=}& \sum \left({\beta }_A\left({\mathcal{R}}^{\left(1\right)}\right){\mathcal{T}}^{\left(1\right)}\right){\beta }_A\left({\overline{\mathcal{S}}}^{\left(1\right)}\right)\otimes \left({\mathcal{S}}^{\left(1\right)}{\mathcal{T}}^{\left(2\right)}\right)\left({\overline{\mathcal{R}}}^{\left(1\right)}{\overline{\mathcal{S}}}^{\left(2\right)}\right)\otimes \left(\left({\alpha }_A^{-1}\left({\mathcal{S}}^{\left(2\right)}\right){\mathcal{R}}^{\left(2\right)}\right){\alpha }_A{\beta }_A\left(a\right)\right){\alpha }_A\left({\overline{\mathcal{R}}}^{\left(2\right)}\right)\hfill \\ & \stackrel{\left(10\right)}{=}& \sum \left({\beta }_A\left({\mathcal{R}}^{\left(1\right)}\right){\mathcal{T}}^{\left(1\right)}\right)\left({\overline{\mathcal{R}}}^{\left(1\right)}{\alpha }_A\left({\overline{\mathcal{S}}}^{\left(1\right)}\right)\right)\otimes \left({\mathcal{S}}^{\left(1\right)}{\mathcal{T}}^{\left(2\right)}\right)\left({\overline{\mathcal{R}}}^{\left(2\right)}{\overline{\mathcal{T}}}^{\left(1\right)}\right)\hfill \\ & & \otimes \left(\left({\alpha }_A^{-1}\left({\mathcal{S}}^{\left(2\right)}\right){\mathcal{R}}^{\left(2\right)}\right){\alpha }_A{\beta }_A\left(a\right)\right)\left({\beta }_A\left({\overline{\mathcal{S}}}^{\left(2\right)}\right){\overline{\mathcal{T}}}^{\left(2\right)}\right)\hfill \\ & \stackrel{\left(8\right)}{=}& \sum {\alpha }_A^2{\beta }_A\left({\mathcal{R}}^{\left(1\right)}\right){\alpha }_A{\beta }_A\left({\overline{\mathcal{S}}}^{\left(1\right)}\right)\otimes {\alpha }_A\left({\mathcal{S}}^{\left(1\right)}\right){\beta }_A\left({\overline{\mathcal{T}}}^{\left(1\right)}\right)\otimes \left({\mathcal{S}}^{\left(2\right)}\left(\left({\mathcal{R}}^{\left(2\right)}a\right){\overline{\mathcal{S}}}^{\left(2\right)}\right)\right){\beta }_A\left({\overline{\mathcal{T}}}^{\left(2\right)}\right)\hfill \\ & \stackrel{\left(8\right)}{=}& {\alpha }_A{\beta }_A\left(a_1\right)\otimes {\Delta }_L\left(a_2\right),\hfill \end{array}$$

hence the conclusion holds. □

3.2. Heisenberg Doubles of a BiHom-Hopf Algebra

In this subsection, we will provide the algebraic solutions of BiHom-Hopf equation from Heisenberg doubles. From now on, we assume that $H=(H,S)$ is a finite dimensional BiHom-Hopf algebra, and S is bijective. Recall from Example 3 (2) that

$$H^{\star }=(H^{*},\star ,{\epsilon }_H,{\Delta }_{H^{*}},{\epsilon }_{H^{*}},{\left({\alpha }^{-1}\right)}^{*},{\left({\beta }^{-1}\right)}^{*},{\left({\varphi }^{-1}\right)}^{*},{\left({\psi }^{-1}\right)}^{*})$$

is a BiHom-bialgebra. Then, we obtain the following definition.

Definition 2.

For any $\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}\in \mathbb{Z}$, the $\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}$-th Heisenberg double ${\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)=H\otimes H^{\star }$ of H, in a form containing H and $H^{\star }$, is a BiHom-algebra with the following structure

$$\begin{array}{cc}& (a\otimes p)♯(b\otimes q):=a{\varphi }^{-1}\left(b_1\right)\otimes p\left({\alpha }^{\mathfrak{r}}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}}{\psi }^{\mathfrak{v}}\left(b_2\right){\beta }^{-1}(?)\right)\star q,1_{{\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)}:=1_H\otimes \epsilon ,\\ & {\alpha }_{{\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)}=\alpha \otimes {\left({\alpha }^{-1}\right)}^{*},{\beta }_{{\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)}=\beta \otimes {\left({\beta }^{-1}\right)}^{*},\end{array}$$

where $p,q\in H^{\star }$, $a,b\in H$.

Proof. 

For any $a,b,c,x\in H$, $p,q,f\in H^{\star }$, we have

$$\begin{array}{ccc}& & \left({\alpha }_{{\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)}(a\otimes p)\right)♯((b\otimes q)♯(c\otimes f))\left(x\right)\hfill \\ & =& \alpha \left(a\right)\left({\varphi }^{-1}\left(b_1\right){\varphi }^{-2}\left(c_{11}\right)\right)\otimes (p\left(\left({\alpha }^{\mathfrak{r}-1}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}}{\psi }^{\mathfrak{v}}\left(b_2\right){\alpha }^{\mathfrak{r}-1}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}-1}{\psi }^{\mathfrak{v}}\left(c_{12}\right)\right){\alpha }^{-1}{\beta }^{-1}(?)\right)\hfill \\ & & \star (q\left({\alpha }^{\mathfrak{r}}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}}{\psi }^{\mathfrak{v}}\left(c_2\right){\beta }^{-1}(?)\right)\star f))\left(x\right)\hfill \\ & =& \left(a{\varphi }^{-1}\left(b_1\right)\right)\beta {\varphi }^{-1}\left(c_1\right)\otimes p\left({\alpha }^{\mathfrak{r}}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}}{\psi }^{\mathfrak{v}}\left(b_2\right)\left({\alpha }^{\mathfrak{r}-1}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}-1}{\psi }^{\mathfrak{v}}\left(c_{21}\right){\alpha }^{-2}{\beta }^{-2}{\varphi }^{-2}\left(x_{11}\right)\right)\right)\hfill \\ & & q\left({\alpha }^{\mathfrak{r}}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}}{\psi }^{\mathfrak{v}-1}\left(c_{22}\right){\alpha }^{-1}{\beta }^{-2}{\varphi }^{-1}{\psi }^{-1}\left(x_{12}\right)\right)f\left({\beta }^{-2}{\psi }^{-1}\left(x_2\right)\right)\hfill \\ & =& \left(a{\varphi }^{-1}\left(b_1\right)\right)\beta {\varphi }^{-1}\left(c_1\right)\otimes (p\left({\alpha }^{\mathfrak{r}}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}}{\psi }^{\mathfrak{v}}\left(b_2\right){\beta }^{-1}(?)\right)\star q)\left({\alpha }^{\mathfrak{r}}{\beta }^{\mathfrak{s}+1}{\varphi }^{\mathfrak{u}}{\psi }^{\mathfrak{v}}\left(c_2\right){\alpha }^{-1}{\beta }^{-1}{\varphi }^{-1}\left(x_1\right)\right)\hfill \\ & & f\left({\beta }^{-2}{\psi }^{-1}\left(x_2\right)\right)\hfill \\ & =& (a{\varphi }^{-1}\left(b_1\right)\otimes p\left({\alpha }^{\mathfrak{r}}{\beta }^{\mathfrak{s}}{\varphi }^{\mathfrak{u}}{\psi }^{\mathfrak{v}}\left(b_2\right){\beta }^{-1}(?)\right)\star q)(\beta \left(c\right)\otimes f\circ {\beta }^{-1})\left(x\right)\hfill \\ & =& ((a\otimes p)♯(b\otimes q))♯(\beta \left(c\right)\otimes f\circ {\beta }^{-1})\left(x\right),\hfill \end{array}$$

which implies the BiHom-associative law. Obviously, we have

$$\begin{array}{ccc}& & (a\otimes p)♯(1_H\otimes \epsilon )=(\alpha \otimes {\left({\alpha }^{-1}\right)}^{*})(a\otimes p),(1_H\otimes \epsilon )♯(a\otimes p)=(\beta \otimes {\left({\beta }^{-1}\right)}^{*})(a\otimes p),\hfill \end{array}$$

which implies the BiHom-unit law. Hence, $({\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right),♯,1_H\otimes \epsilon ,\alpha \otimes {\left({\alpha }^{-1}\right)}^{*},\beta \otimes {\left({\beta }^{-1}\right)}^{*})$ is a BiHom-algebra. □

Theorem 1.

$\sum ({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(e_i\right)\otimes \epsilon )\otimes (1_H\otimes e^i)\in {\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)\otimes {\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)$ is a solution of the BiHom-Hopf equation, where $e_i$ and $e^i$ are dual bases of H and $H^{\star }$, respectively.

Proof. 

For any $x,y,z\in H$, we have

$$\begin{array}{ccc}& & \sum (({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+2}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(e_i\right)\otimes \epsilon )♯({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(a_i\right)\otimes \epsilon ))\left(x\right)\hfill \\ & & \otimes (({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(o_i\right)\otimes \epsilon )♯(1_H\otimes a^i))\left(y\right)\otimes ((1_H\otimes o^i)♯(1_H\otimes e^i\left({\alpha }^{-1}(?)\right)))\left(z\right)\hfill \\ & =& \sum ({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+2}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(e_i\right){\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}-1}{\psi }^{-\mathfrak{v}-1}\left({a_i}_1\right)\epsilon \left({a_i}_2\right)\otimes \epsilon )\left(x\right)\hfill \\ & & \otimes ({\alpha }^{-\mathfrak{r}-1}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(o_i\right)\otimes a^i\left({\beta }^{-1}(?)\right))\left(y\right)\otimes (1_H\otimes o^i\star e^i\left({\alpha }^{-1}(?)\right))\left(z\right)\hfill \\ & =& \sum ({\alpha }^{-\mathfrak{r}-3}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-2}\left(z_2\right){\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(y\right)\otimes \epsilon \left(x\right))\hfill \\ & & \otimes ({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}-1}{\psi }^{-\mathfrak{v}-1}\left(z_1\right)\otimes 1_{\mathbb{k}})\otimes (1_H\otimes 1_{\mathbb{k}}),\hfill \end{array}$$

and

$$\begin{array}{ccc}& & \sum ({\alpha }^{-\mathfrak{r}-1}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(e_i\right)\otimes \epsilon )\left(x\right)\hfill \\ & & \otimes ((1_H\otimes e^i)♯({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(o_i\right)\otimes \epsilon ))\left(y\right)\otimes (1_H\otimes o^i\left({\beta }^{-1}(?)\right))\left(z\right)\hfill \\ & =& \sum ({\alpha }^{-\mathfrak{r}-1}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(e_i\right)\otimes \epsilon \left(x\right))\hfill \\ & & \otimes ({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+2}{\varphi }^{-\mathfrak{u}-1}{\psi }^{-\mathfrak{v}-1}\left({o_i}_1\right)\otimes e^i\left({\alpha }^{-2}\beta {\psi }^{-1}\left({o_i}_2\right){\alpha }^{-1}{\beta }^{-1}\left(y\right)\right))\otimes (1_H\otimes o^i\left({\beta }^{-1}\left(z\right)\right))\hfill \\ & =& \sum ({\alpha }^{-\mathfrak{r}-3}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-2}\left(z_2\right){\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(y\right)\otimes \epsilon \left(x\right))\hfill \\ & & \otimes ({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}-1}{\psi }^{-\mathfrak{v}-1}\left(z_1\right)\otimes 1_{\mathbb{k}})\otimes (1_H\otimes 1_{\mathbb{k}}),\hfill \end{array}$$

where $a_i$ and $a^i$ and $o_i$ and $o^i$ are both dual bases of H and $H^{\star }$, respectively. This implies that $\mathcal{R}=\sum ({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}$${\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(e_i\right)\otimes \epsilon )\otimes (1_H\otimes e^i)$ is a solution of the BiHom-Hopf equation. □

Corollary 1.

$\sum (S{\alpha }^{-\mathfrak{r}-1}{\beta }^{-\mathfrak{s}}{\varphi }^{-\mathfrak{u}+1}{\psi }^{-\mathfrak{v}-2}\left(e_i\right)\otimes \epsilon )\otimes (1_H\otimes e^i)\in {\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)\otimes {\mathfrak{H}}_{\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v}}\left(H\right)$ is a solution of the BiHom-pentagon equation.

Proof. 

It is easy to check (by using Equation (3)) that

$$\sum (S{\alpha }^{-\mathfrak{r}-1}{\beta }^{-\mathfrak{s}}{\varphi }^{-\mathfrak{u}+1}{\psi }^{-\mathfrak{v}-2}\left(e_i\right)\otimes \epsilon )\otimes (1_H\otimes e^i)$$

is the inverse of $\mathcal{R}=\sum ({\alpha }^{-\mathfrak{r}-2}{\beta }^{-\mathfrak{s}+1}{\varphi }^{-\mathfrak{u}}{\psi }^{-\mathfrak{v}-1}\left(e_i\right)\otimes \epsilon )\otimes (1_H\otimes e^i)$. Hence, the conclusion holds because of Proposition 2. □

4. The BiHom-Long Dimodules and the BiHom-$\mathcal{D}$ Equation

In this section, we will describe the algebraic solutions of the BiHom–Yang-Baxter equation and BiHom-$\mathcal{D}$ equation.

4.1. The Parametric Generalized BiHom-Long Dimodules

In this subsection, we will introduce the generalized BiHom-Long dimodules which play an important role in the BiHom–Yang-Baxter equation and BiHom-$\mathcal{D}$ equation. Assume that $(H,S_H,{\alpha }_H,{\beta }_H,{\varphi }_H,{\psi }_H)$ and $(B,S_B,{\alpha }_B,{\beta }_B,{\varphi }_B,{\psi }_B)$ are two BiHom-Hopf algebras.

Definition 3.

A $\mathbb{k}$-space U is called a left-right generalized BiHom-Long dimodule of H and B, if there exist morphisms ${\alpha }_U,{\beta }_U,{\varphi }_U,{\psi }_U\in Aut\left(U\right)$ such that $(U,{\alpha }_U,{\beta }_U,{\varphi }_U,{\psi }_U)$ is both a left H-BiHom-module and a right B-BiHom-comodule, and the following compatibility condition is satisfied:

$$\begin{array}{c}\hfill {\underline{h·u}}_0\otimes {\underline{h·u}}_1={\varphi }_H\left(h\right)·u_0\otimes {\beta }_B\left(u_1\right),\end{array}$$

(11)

for all $u\in U$ and $h\in H$. We denote by ${}_H{\mathcal{L}}^B$ the category of generalized BiHom-Long dimodules, with morphisms being H-linear and B-colinear.

Example 6.

(1)

For any $\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v},\mathfrak{t},\mathfrak{w},\mathfrak{x},\mathfrak{y}\in \mathbb{Z}$, define the left H-action ⇀ on $H\otimes B$ by

$$\begin{array}{c}\hfill x\rightharpoonup (h\otimes a)={\alpha }_H^{\mathfrak{r}}{\beta }_H^{\mathfrak{s}}{\varphi }_H^{\mathfrak{u}}{\psi }_H^{\mathfrak{v}}\left(x\right)h\otimes {\beta }_B\left(a\right),\end{array}$$

and define the right B-coaction on $H\otimes B$ by

$$\begin{array}{c}\hfill \rho (h\otimes a)={\varphi }_H\left(h\right)\otimes a_1\otimes {\alpha }_B^{\mathfrak{t}}{\beta }_B^{\mathfrak{w}}{\varphi }_B^{\mathfrak{x}}{\psi }_B^{\mathfrak{y}}\left(a_2\right),\end{array}$$

then it is straightforward to check that $(H\otimes B,\rightharpoonup ,\rho ,{\alpha }_H\otimes {\alpha }_B,{\beta }_H\otimes {\beta }_B,{\varphi }_H\otimes {\varphi }_B,{\psi }_H\otimes {\psi }_B)$ is a generalized BiHom-Long dimodule.

(2)

Similarly, for $\mathfrak{r},\mathfrak{s},\mathfrak{u},\mathfrak{v},\mathfrak{t},\mathfrak{w},\mathfrak{x},\mathfrak{y}\in \mathbb{Z}$, if we define the left H-action ⇁ on $B\otimes H$ by

$$\begin{array}{c}\hfill x\rightharpoondown (a\otimes h)={\beta }_B\left(a\right)\otimes {\alpha }_H^{\mathfrak{r}}{\beta }_H^{\mathfrak{s}}{\varphi }_H^{\mathfrak{u}}{\psi }_H^{\mathfrak{v}}\left(x\right)h,\end{array}$$

and define the right B-coaction on $B\otimes H$ by

$$\begin{array}{c}\hfill \varrho (a\otimes h)=a_1\otimes {\varphi }_H\left(h\right)\otimes {\alpha }_B^{\mathfrak{t}}{\beta }_B^{\mathfrak{w}}{\varphi }_B^{\mathfrak{x}}{\psi }_B^{\mathfrak{y}}\left(a_2\right),\end{array}$$

then, it is straightforward to check that $(B\otimes H,\rightharpoondown ,\varrho ,{\alpha }_H\otimes {\alpha }_B,{\beta }_H\otimes {\beta }_B,{\varphi }_H\otimes {\varphi }_B,{\psi }_H\otimes {\psi }_B)$ is also an object in ${}_H{\mathcal{L}}^B$.

For any $\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d},\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}\in \mathbb{Z}$, we can define the monoidal structures in ${}_H{\mathcal{L}}^B$ as follows:

• the monoidal product of $(U,{\alpha }_U,{\beta }_U,{\varphi }_U,{\psi }_U)$ of $(V,{\alpha }_V,{\beta }_V,{\varphi }_V,{\psi }_V)$ is $(U\otimes V,{\alpha }_U\otimes {\alpha }_V,{\beta }_U\otimes {\beta }_V,{\varphi }_U\otimes {\varphi }_V,{\psi }_U\otimes {\psi }_V)$, where the BiHom-module and BiHom-comodule structures are given by

  $$\begin{array}{cc}& h·(u\otimes v)={\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left(h_1\right)·u\otimes {\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left(h_2\right)·v,\\ & {\rho }^{U\otimes V}(u\otimes v)=u_0\otimes v_0\otimes {\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right){\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right);\end{array}$$
• the unit object is $(\mathbb{k},id,id,id,id)$ with the trivial H-action and trivial B-coaction.

Theorem 2.

For any $\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d},\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}\in \mathbb{Z}$, ${}_H{\mathcal{L}}^B$ forms a monoidal category under the above structures.

Proof. 

First, for any $u\in U$, $v\in V$, we have

$$\begin{array}{ccc}& & \rho (h·(u\otimes v))={\underline{{\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left(h_1\right)·u}}_0\otimes {\underline{{\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left(h_2\right)·v}}_0\hfill \\ & & \otimes {\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left({\underline{{\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left(h_1\right)·u}}_1\right){\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left({\underline{{\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left(h_2\right)·v}}_1\right)\hfill \\ & =& {\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}+1}{\psi }_H^{\mathfrak{d}}\left(h_1\right)·u_0\otimes {\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}+1}{\psi }_H^{\mathfrak{h}}\left(h_2\right)·v_0\otimes {\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}+1}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right){\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right)\hfill \\ & =& {\varphi }_H\left(h\right)·\left({\underline{u\otimes v}}_0\right)\otimes {\varphi }_B\left({\underline{u\otimes v}}_1\right),\hfill \end{array}$$

which implies Equation (11). Hence, $U\otimes V\in {}_H{\mathcal{L}}^B$.

Second, define the the the associativity $\mathbf{a}$ and the unit constraints $\mathbf{l},\mathbf{r}$ by

$$\begin{array}{cc}& {\mathbf{a}}_{U,V,W}((u\otimes v)\otimes w)={\alpha }_U^{-\mathfrak{a}}{\beta }_U^{-\mathfrak{b}}{\varphi }_U^{-\mathfrak{c}-1}{\psi }_U^{-\mathfrak{d}}\left(u\right)\otimes (v\otimes {\alpha }_W^{\mathfrak{e}}{\beta }_W^{\mathfrak{f}}{\varphi }_W^{\mathfrak{g}}{\psi }_W^{\mathfrak{h}+1}\left(w\right)),\\ & {\mathbf{l}}_U(1_{\mathbb{k}}\otimes u)={\alpha }_U^{-\mathfrak{e}}{\beta }_U^{-\mathfrak{f}}{\varphi }_U^{-\mathfrak{g}}{\psi }_U^{-\mathfrak{h}-1}\left(u\right),{\mathbf{r}}_U(u\otimes 1_{\mathbb{k}})={\alpha }_U^{-\mathfrak{a}}{\beta }_U^{-\mathfrak{b}}{\varphi }_U^{-\mathfrak{c}-1}{\psi }_U^{-\mathfrak{d}}\left(u\right);\end{array}$$

where $U,V,W\in {}_H{\mathcal{L}}^B$, then, it is not hard to check that $({}_H{\mathcal{L}}^B,\otimes ,\mathbb{k},\mathbf{a},\mathbf{l},\mathbf{r})$ is a monoidal category. □

Remark 5.

We denote $({}_H{\mathcal{L}}^B,\otimes ,\mathbb{k},\mathbf{a},\mathbf{l},\mathbf{r})$ (under the monoidal structures given above) by ${{}_H{\mathcal{L}}^B}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}}$.

Proposition 4.

For any $\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d},\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h},{\mathfrak{a}}^{\prime },{\mathfrak{b}}^{\prime },{\mathfrak{c}}^{\prime },{\mathfrak{d}}^{\prime },{\mathfrak{e}}^{\prime },{\mathfrak{f}}^{\prime },{\mathfrak{g}}^{\prime },{\mathfrak{h}}^{\prime }\in \mathbb{Z}$, ${{}_H{\mathcal{L}}^B}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}}$ is monoidal isomorphic to ${{}_H{\mathcal{L}}^B}_{{\mathfrak{e}}^{\prime },{\mathfrak{f}}^{\prime },{\mathfrak{g}}^{\prime },{\mathfrak{h}}^{\prime }}^{{\mathfrak{a}}^{\prime },{\mathfrak{b}}^{\prime },{\mathfrak{c}}^{\prime },{\mathfrak{d}}^{\prime }}$.

Proof. 

Define functor $\mathcal{S}=(\mathcal{S},{\mathcal{S}}_2,{\mathcal{S}}_0):{{}_H{\mathcal{L}}^B}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}}\to {{}_H{\mathcal{L}}^B}_{{\mathfrak{e}}^{\prime },{\mathfrak{f}}^{\prime },{\mathfrak{g}}^{\prime },{\mathfrak{h}}^{\prime }}^{{\mathfrak{a}}^{\prime },{\mathfrak{b}}^{\prime },{\mathfrak{c}}^{\prime },{\mathfrak{d}}^{\prime }}$ by

$$\begin{array}{c}\hfill \mathcal{F}\left(U\right)=Uas\mathrm{BiHom}-\mathrm{Long}\mathrm{dimodule},\mathcal{F}\left(f\right)=f,\end{array}$$

where $(U,{\alpha }_U,{\beta }_U,{\varphi }_U,{\psi }_U)\in {}_H{\mathcal{L}}^B$, $f\in Mor\left({}_H{\mathcal{L}}^B\right)$, and ${{\mathcal{S}}_2}_{U,U}$ is given by

$$\begin{array}{c}\hfill {{\mathcal{S}}_2}_{U,V}(u\otimes v)={\alpha }_U^{\mathfrak{a}-{\mathfrak{a}}^{\prime }}{\beta }_U^{\mathfrak{b}-{\mathfrak{b}}^{\prime }}{\varphi }_U^{\mathfrak{c}-{\mathfrak{c}}^{\prime }}{\psi }_U^{\mathfrak{d}-{\mathfrak{d}}^{\prime }}\left(u\right)\otimes {\alpha }_V^{\mathfrak{e}-{\mathfrak{e}}^{\prime }}{\beta }_V^{\mathfrak{f}-{\mathfrak{f}}^{\prime }}{\varphi }_V^{\mathfrak{g}-{\mathfrak{g}}^{\prime }}{\psi }_V^{\mathfrak{h}-{\mathfrak{h}}^{\prime }}\left(v\right),\end{array}$$

for any $U,V\in {}_H{\mathcal{L}}^B$, $u\in U$, $v\in V$. Obviously, $\mathcal{S}=(\mathcal{S},{\mathcal{S}}_2,{\mathcal{S}}_0)$ is a monoidal isomorphic functor. □

4.2. BiHom-Type Yang-Baxter Equation

In this subsection, we will show that the generalized BiHom-Long dimodules will provide the algebraic solutions of the BiHom–Yang-Baxter equation.

Definition 4.

Let H be a BiHom-Hopf algebra. Recall from [22] that a quasitriangular structure of His an invertible element $\mathrm{R}\in H\otimes H$, such that the following conditions hold:

$\left\{\begin{array}{c}\left(Q1\right)(\alpha \otimes \alpha )\mathrm{R}=(\beta \otimes \beta )\mathrm{R}=(\varphi \otimes \varphi )\mathrm{R}=(\psi \otimes \psi )\mathrm{R}=\mathrm{R};\hfill \\ \left(Q2\right)\sum {\mathrm{R}}^{\left(1\right)}{\varphi }^{-1}\psi \left(h_1\right)\otimes {\mathrm{R}}^{\left(2\right)}\varphi {\psi }^{-1}\left(h_2\right)=\sum {\alpha }^{-1}\beta \left(h_2\right){\mathrm{R}}^{\left(1\right)}\otimes {\alpha }^{-1}\beta \left(h_1\right){\mathrm{R}}^{\left(2\right)};\hfill \\ \left(Q3\right)\sum {\mathrm{R}}_1^{\left(1\right)}\otimes {\mathrm{R}}_2^{\left(1\right)}\otimes {\mathrm{R}}^{\left(2\right)}=\sum \alpha \varphi \left({\dot{\mathrm{R}}}^{\left(1\right)}\right)\otimes \beta \psi \left({\mathrm{R}}^{\left(1\right)}\right)\otimes {\dot{\mathrm{R}}}^{\left(2\right)}{\mathrm{R}}^{\left(2\right)};\hfill \\ \left(Q4\right)\sum {\mathrm{R}}^{\left(1\right)}\otimes {\mathrm{R}}_1^{\left(2\right)}\otimes {\mathrm{R}}_2^{\left(2\right)}=\sum {\dot{\mathrm{R}}}^{\left(1\right)}{\mathrm{R}}^{\left(1\right)}\otimes \beta \varphi \left({\mathrm{R}}^{\left(2\right)}\right)\otimes \alpha \psi \left({\dot{\mathrm{R}}}^{\left(2\right)}\right),\hfill \end{array}\right.$for any $h\in H$, where $\dot{\mathrm{R}}=\mathrm{R}=\sum {\mathrm{R}}^{\left(1\right)}\otimes {\mathrm{R}}^{\left(2\right)}=\sum {\dot{\mathrm{R}}}^{\left(1\right)}\otimes {\dot{\mathrm{R}}}^{\left(2\right)}$.

Remark 6.

Let $\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d},\mathfrak{g},\mathfrak{h},\mathfrak{i},\mathfrak{j}$ be integers, $\mathrm{R}$ and ${\mathrm{R}}^{\prime }$ be two elements in $H\otimes H$. Recall from [22], (Section 3.2) that, for any $M,N\in {}_H{\mathcal{BM}}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}}$, if we define families of maps $\mathbf{T}:\otimes \Rightarrow {\otimes }^{op}$ and ${\mathbf{T}}^{\prime }:{\otimes }^{op}\Rightarrow \otimes$ as follows:

• ${\mathbf{T}}_{M,N}:M\otimes N\to N\otimes M$ is given by

  $$\begin{array}{ccc}& & m\otimes n\mapsto \sum {\alpha }^{\mathfrak{a}}{\beta }^{\mathfrak{b}}{\varphi }^{\mathfrak{c}}{\psi }^{\mathfrak{d}}\left({\mathrm{R}}^{\left(2\right)}\right)·{\alpha }_N^{\mathfrak{a}-\mathfrak{e}}{\beta }_N^{\mathfrak{b}-\mathfrak{f}-1}{\varphi }_N^{\mathfrak{c}-\mathfrak{g}+1}{\psi }_N^{\mathfrak{d}-\mathfrak{h}-1}\left(n\right)\hfill \\ & & \otimes {\alpha }^{\mathfrak{e}}{\beta }^{\mathfrak{f}}{\varphi }^{\mathfrak{g}}{\psi }^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}\right)·{\alpha }_M^{-\mathfrak{a}+\mathfrak{e}}{\beta }_M^{-\mathfrak{b}+\mathfrak{f}-1}{\varphi }_M^{-\mathfrak{c}+\mathfrak{g}-1}{\psi }_M^{-\mathfrak{d}+\mathfrak{h}+1}\left(m\right),\hfill \end{array}$$
• ${{\mathbf{T}}^{\prime }}_{M,N}:N\otimes M\to M\otimes N$ is given by

  $$\begin{array}{ccc}& & n\otimes m\mapsto \sum {\alpha }^{\mathfrak{a}}{\beta }^{\mathfrak{b}}{\varphi }^{\mathfrak{c}+1}{\psi }^{\mathfrak{d}-1}\left({{\mathrm{R}}^{\prime }}^{\left(1\right)}\right)·{\alpha }_M^{\mathfrak{a}-\mathfrak{e}}{\beta }_M^{\mathfrak{b}-\mathfrak{f}-1}{\varphi }_M^{\mathfrak{c}-\mathfrak{g}+1}{\psi }_M^{\mathfrak{d}-\mathfrak{h}-1}\left(m\right)\hfill \\ & & \otimes {\alpha }^{\mathfrak{e}}{\beta }^{\mathfrak{f}}{\varphi }^{\mathfrak{g}-1}{\psi }^{\mathfrak{h}+1}\left({{\mathrm{R}}^{\prime }}^{\left(2\right)}\right)·{\alpha }_N^{-\mathfrak{a}+\mathfrak{e}}{\beta }_N^{-\mathfrak{b}+\mathfrak{f}-1}{\varphi }_N^{-\mathfrak{c}+\mathfrak{g}-1}{\psi }_N^{-\mathfrak{d}+\mathfrak{h}+1}\left(n\right),\hfill \end{array}$$
  then $\mathbf{T}$ is a braiding in ${}_H{\mathcal{BM}}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}}$ with the inverse ${\mathbf{T}}^{\prime }$ if and only if $\mathrm{R}$ is a quasitriangular structure of H with the inverse element ${\mathrm{R}}^{\prime }$.

Lemma 1.

If $\mathrm{R}$ is a quasitriangular structure of H, then

$$\begin{array}{c}\hfill \sum \epsilon \left({\mathrm{R}}^{\left(1\right)}\right){\mathrm{R}}^{\left(2\right)}=\sum {\mathrm{R}}^{\left(1\right)}\epsilon \left({\mathrm{R}}^{\left(2\right)}\right)=1_H.\end{array}$$

(12)

Proof. 

Be similar to [23], (Lemma 2.1.2). □

Lemma 2.

If $\mathrm{R}$ is a quasitriangular structure of H, then, for any $h\in H$, we have

$$\begin{array}{c}\hfill \sum {\varphi }^{-1}\psi \left(h_1\right){\mathrm{r}}^{\left(1\right)}\otimes \varphi {\psi }^{-1}\left(h_2\right){\mathrm{r}}^{\left(2\right)}=\sum {\mathrm{r}}^{\left(1\right)}\alpha {\beta }^{-1}\left(h_2\right)\otimes {\mathrm{r}}^{\left(2\right)}\alpha {\beta }^{-1}\left(h_1\right),\end{array}$$

(13)

where $\mathrm{r}=\sum {\mathrm{r}}^{\left(1\right)}\otimes {\mathrm{r}}^{\left(2\right)}={\mathrm{R}}^{-1}$.

Proof. 

Equation (13) holds because of Equation (Q2). Actually,

$$\begin{array}{ccc}& & \sum {\mathrm{R}}^{\left(1\right)}{\varphi }^{-1}\psi \left(h_1\right)\otimes {\mathrm{R}}^{\left(2\right)}\varphi {\psi }^{-1}\left(h_2\right)=\sum {\alpha }^{-1}\beta \left(h_2\right){\mathrm{R}}^{\left(1\right)}\otimes {\alpha }^{-1}\beta \left(h_1\right){\mathrm{R}}^{\left(2\right)}\hfill \\ & \iff & \sum \left({\mathrm{r}}^{\left(1\right)}\alpha \left({\mathrm{R}}^{\left(1\right)}\right)\right)\left(\beta {\varphi }^{-1}\psi \left(h_1\right){\beta }^{-1}\left({\mathrm{s}}^{\left(1\right)}\right)\right)\otimes \left({\mathrm{r}}^{\left(2\right)}\alpha \left({\mathrm{R}}^{\left(2\right)}\right)\right)\left(\beta \varphi {\psi }^{-1}\left(h_2\right){\beta }^{-1}\left({\mathrm{s}}^{\left(2\right)}\right)\right)\hfill \\ & & =\sum \left({\mathrm{r}}^{\left(1\right)}\beta \left(h_2\right)\right)\left(\beta \left({\mathrm{R}}^{\left(1\right)}\right){\beta }^{-1}\left({\mathrm{s}}^{\left(1\right)}\right)\right)\otimes \left({\mathrm{r}}^{\left(2\right)}\beta \left(h_1\right)\right)\left(\beta \left({\mathrm{R}}^{\left(2\right)}\right){\beta }^{-1}\left({\mathrm{s}}^{\left(2\right)}\right)\right)\hfill \\ & \stackrel{\left(Q1\right)}{\iff }& \sum 1_H\left(\beta {\varphi }^{-1}\psi \left(h_1\right){\mathrm{s}}^{\left(1\right)}\right)\otimes 1_H\left(\beta \varphi {\psi }^{-1}\left(h_2\right){\mathrm{s}}^{\left(2\right)}\right)=\sum \left({\mathrm{r}}^{\left(1\right)}\beta \left(h_2\right)\right)1_H\otimes \left({\mathrm{r}}^{\left(2\right)}\beta \left(h_1\right)\right)1_H\hfill \\ & \stackrel{\left(Q1\right)}{\iff }& \sum {\varphi }^{-1}\psi \left(h_1\right){\mathrm{r}}^{\left(1\right)}\otimes \varphi {\psi }^{-1}\left(h_2\right){\mathrm{r}}^{\left(2\right)}=\sum {\mathrm{r}}^{\left(1\right)}\alpha {\beta }^{-1}\left(h_2\right)\otimes {\mathrm{r}}^{\left(2\right)}\alpha {\beta }^{-1}\left(h_1\right),\hfill \end{array}$$

which implies the conclusion. □

Lemma 3.

If H is a BiHom-Hopf algebra with bijective antipode S, and $\mathrm{R}$ is a quasitriangular structure of H, then we have

$$\begin{array}{c}\hfill (S{\alpha }^{-1}\beta {\varphi }^{-1}\psi \otimes id)\mathrm{R}=(id\otimes S^{-1}{\alpha }^{-1}\beta {\varphi }^{-1}\psi )\mathrm{R}={\mathrm{R}}^{-1},\end{array}$$

(14)

and hence

$$\begin{array}{c}\hfill (S\otimes S)\mathrm{R}=\mathrm{R}.\end{array}$$

(15)

Proof. 

Firstly, due to Equation (12), we immediately obtain that

$$\begin{array}{c}\hfill \sum {\mathrm{R}}_1^{\left(1\right)}S\left({\mathrm{R}}_2^{\left(1\right)}\right)\otimes {\mathrm{R}}^{\left(2\right)}=1_H\otimes 1_H.\end{array}$$

thus, from Equation (Q3), we have

$$\begin{array}{c}\hfill \sum {\dot{\mathrm{R}}}^{\left(1\right)}S{\alpha }^{-1}\beta {\varphi }^{-1}\psi \left({\mathrm{R}}^{\left(1\right)}\right)\otimes {\dot{\mathrm{R}}}^{\left(2\right)}{\mathrm{R}}^{\left(2\right)}=1_H\otimes 1_H,\end{array}$$

which implies $(S{\alpha }^{-1}\beta {\varphi }^{-1}\psi \otimes id)\mathrm{R}={\mathrm{R}}^{-1}$.

Secondly, we can obtain $(id\otimes S^{-1}{\alpha }^{-1}\beta {\varphi }^{-1}\psi )\mathrm{R}={\mathrm{R}}^{-1}$ in a similar way.

Finally, one can easily obtain that Equation (15) holds because of Equation (3). □

Definition 5.

Recall from [22], (Definition 3.18) that a coquasitriangular structure on a BiHom-Hopf algebra His a bilinear form $\sigma :H\otimes H\to \mathbb{k}$, such that σ is invertible under the convolution invertible, and the following formulae are satisfied:

$\left\{\begin{array}{c}\left(CQ1\right)\sigma \left(\alpha \right(a),\alpha (b\left)\right)=\sigma \left(\beta \right(a),\beta (b\left)\right)=\sigma \left(\varphi \right(a),\varphi (b\left)\right)=\sigma \left(\psi \right(a),\psi (b\left)\right)=\sigma (a,b);\hfill \\ \left(CQ2\right)\sigma (a_1,b_1)\varphi {\psi }^{-1}\left(a_2\right)\varphi {\psi }^{-1}\left(b_2\right)={\alpha }^{-1}\beta \left(b_1\right)\alpha {\beta }^{-1}\left(a_1\right)\sigma (a_2,b_2);\hfill \\ \left(CQ3\right)\sigma (\alpha \beta \left(a\right),bc)=\sigma (\alpha \left(a_1\right),\varphi \left(c\right))\sigma (\beta \left(a_2\right),\psi \left(b\right));\hfill \\ \left(CQ4\right)\sigma (ab,\varphi \psi \left(c\right))=\sigma (\alpha \left(a\right),\psi \left(c_1\right))\sigma (\beta \left(b\right),\varphi \left(c_2\right)).\hfill \end{array}\right.$

Remark 7.

For any bilinear form $\sigma \in hom(H\otimes H,\mathbb{k})$, $U,V\in {\left({\mathcal{BM}}^H\right)}_{\mathfrak{m},\mathfrak{n},\mathfrak{p},\mathfrak{q}}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}}$ (where $\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l},\mathfrak{m},\mathfrak{n},\mathfrak{p},\mathfrak{q}$ mean any integers), define the families of maps ${\mathbf{B}}_{U,V}:U\otimes V\to V\otimes U$ by

$$\begin{array}{ccc}& & u\otimes v\mapsto {\alpha }_V^{-\mathfrak{i}+\mathfrak{m}-1}{\beta }_V^{-\mathfrak{j}+\mathfrak{n}+1}{\varphi }_V^{-\mathfrak{k}+\mathfrak{p}-1}{\psi }_V^{-\mathfrak{l}+\mathfrak{q}}\left(v_0\right)\otimes {\alpha }_U^{\mathfrak{i}-\mathfrak{m}+1}{\beta }_U^{\mathfrak{j}-\mathfrak{n}-1}{\varphi }_U^{\mathfrak{k}-\mathfrak{p}-1}{\psi }_U^{\mathfrak{l}-\mathfrak{q}}\left(u_0\right)\hfill \\ & & \sigma \left({\alpha }^{\mathfrak{i}}{\beta }^{\mathfrak{j}}{\varphi }^{\mathfrak{k}}{\psi }^{\mathfrak{l}}\left(u_{\left(1\right)}\right){\alpha }^{\mathfrak{m}}{\beta }^{\mathfrak{n}}{\varphi }^{\mathfrak{p}}{\psi }^{\mathfrak{q}}\left(v_{\left(1\right)}\right)\right).\hfill \end{array}$$

Then, recall from [22], (Theorem 3.20) that σ is a coquasitriangular form of H if and only if ${\left({\mathcal{BM}}^H\right)}_{\mathfrak{m},\mathfrak{n},\mathfrak{p},\mathfrak{q}}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}}$ is a braided category with the braiding $\mathbf{B}$.

Being similar to Lemmas 1 and 3, we have the following property.

Lemma 4.

(1)

If σ is a coquasitriangular form of H, then for any $h\in H$, we have

$$\begin{array}{c}\hfill \sigma (h,1_H)=\sigma (1_H,h)=\epsilon \left(h\right).\end{array}$$

(2)

If H is a BiHom-Hopf algebra with bijective antipode S, and σ is a coquasitriangular form of H, then, for any $h,g\in H$, we have

$$\begin{array}{c}\hfill \sigma (S\alpha {\beta }^{-1}\varphi {\psi }^{-1}\left(h_1\right),g)\sigma (h_2,g_2)=\sigma (h_1,S^{-1}\alpha {\beta }^{-1}\varphi {\psi }^{-1}\left(g_2\right))=\epsilon \left(h\right)\epsilon \left(g\right).\end{array}$$

(16)

Now, assume that $(H,S_H,{\alpha }_H,{\beta }_H,{\varphi }_H,{\psi }_H)$ and $(B,S_B,{\alpha }_B,{\beta }_B,{\varphi }_B,{\psi }_B)$ are two BiHom-Hopf algebras.

Theorem 3.

If H is quasitriangular and B is coquasitriangular, then ${}_H{\mathcal{L}}^B$ forms a braided category.

Proof. 

Suppose that $\mathrm{R}$ is a quasitriangular structure of H, and $\sigma$ is a coquasitriangular structure on B. For any $U,V\in {}_H{\mathcal{L}}^B$, $u\in U$, $v\in V$, define ${\mathbf{C}}_{U,V}(u\otimes v)=:$

$$\begin{array}{ccc}& & \sum \sigma ({\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right)){\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left({\mathrm{R}}^{\left(2\right)}\right)\hfill \\ & & ·{\alpha }_V^{\mathfrak{a}-\mathfrak{e}}{\beta }_V^{\mathfrak{b}-\mathfrak{f}-1}{\varphi }_V^{\mathfrak{c}-\mathfrak{g}}{\psi }_V^{\mathfrak{d}-\mathfrak{h}-1}\left(v_0\right)\otimes {\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}\right)·{\alpha }_U^{\mathfrak{e}-\mathfrak{a}}{\beta }_U^{\mathfrak{f}-\mathfrak{b}-1}{\varphi }_U^{\mathfrak{g}-\mathfrak{c}-2}{\psi }_U^{\mathfrak{h}-\mathfrak{d}+1}\left(u_0\right).\hfill \end{array}$$

Obviously, $\mathbf{C}$ is compatible with the BiHom-structure maps. Since we have

$$\begin{array}{ccc}& & {\mathbf{C}}_{U,V}(h·(u\otimes v))\hfill \\ & \stackrel{\left(CQ1\right)}{=}& \sum \sigma ({\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right))\hfill \\ & & {\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left({\mathrm{R}}^{\left(2\right)}\right)·({\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}-1}{\varphi }_H^{\mathfrak{c}+1}{\psi }_H^{\mathfrak{d}-1}\left(h_2\right)·{\alpha }_V^{\mathfrak{a}-\mathfrak{e}}{\beta }_V^{\mathfrak{b}-\mathfrak{f}-1}{\varphi }_V^{\mathfrak{c}-\mathfrak{g}}{\psi }_V^{\mathfrak{d}-\mathfrak{h}-1}\left(v_0\right))\hfill \\ & & \otimes {\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}\right)·({\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}-1}{\varphi }_H^{\mathfrak{g}-1}{\psi }_H^{\mathfrak{h}+1}\left(h_1\right)·{\alpha }_V^{\mathfrak{e}-\mathfrak{a}}{\beta }_V^{\mathfrak{f}-\mathfrak{b}-1}{\varphi }_V^{\mathfrak{g}-\mathfrak{c}-2}{\psi }_V^{\mathfrak{h}-\mathfrak{d}+1}\left(u_0\right))\hfill \\ & \stackrel{\left(Q1\right)}{=}& \sum \sigma ({\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right))\hfill \\ & & {\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}-1}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left({\mathrm{R}}^{\left(2\right)}{\varphi }_H{\psi }_H^{-1}\left(h_2\right)\right)·{\alpha }_V^{\mathfrak{a}-\mathfrak{e}}{\beta }_V^{\mathfrak{b}-\mathfrak{f}}{\varphi }_V^{\mathfrak{c}-\mathfrak{g}}{\psi }_V^{\mathfrak{d}-\mathfrak{h}-1}\left(v_0\right)\hfill \\ & & \otimes {\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}-1}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}{\varphi }_H^{-1}{\psi }_H\left(h_1\right)\right)·{\alpha }_V^{\mathfrak{e}-\mathfrak{a}}{\beta }_V^{\mathfrak{f}-\mathfrak{b}}{\varphi }_V^{\mathfrak{g}-\mathfrak{c}-2}{\psi }_V^{\mathfrak{h}-\mathfrak{d}+1}\left(u_0\right)\hfill \\ & \stackrel{\left(Q2\right)}{=}& \sum \sigma ({\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right))\hfill \\ & & \left({\alpha }_H^{\mathfrak{a}-1}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left(h_1\right){\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}-1}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left({\mathrm{R}}^{\left(2\right)}\right)\right)·{\alpha }_V^{\mathfrak{a}-\mathfrak{e}}{\beta }_V^{\mathfrak{b}-\mathfrak{f}}{\varphi }_V^{\mathfrak{c}-\mathfrak{g}}{\psi }_V^{\mathfrak{d}-\mathfrak{h}-1}\left(v_0\right)\hfill \\ & & \otimes \left({\alpha }_H^{\mathfrak{e}-1}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left(h_2\right){\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}-1}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}\right)\right)·{\alpha }_V^{\mathfrak{e}-\mathfrak{a}}{\beta }_V^{\mathfrak{f}-\mathfrak{b}}{\varphi }_V^{\mathfrak{g}-\mathfrak{c}-2}{\psi }_V^{\mathfrak{h}-\mathfrak{d}+1}\left(u_0\right)\hfill \\ & \stackrel{\left(Q1\right)}{=}& \sum \sigma ({\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right))\hfill \\ & & {\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left(h_1\right)·({\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left({\mathrm{R}}^{\left(2\right)}\right)·{\alpha }_V^{\mathfrak{a}-\mathfrak{e}}{\beta }_V^{\mathfrak{b}-\mathfrak{f}-1}{\varphi }_V^{\mathfrak{c}-\mathfrak{g}}{\psi }_V^{\mathfrak{d}-\mathfrak{h}-1}\left(v_0\right))\hfill \\ & & \otimes {\alpha }_H^{\mathfrak{e}-1}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left(h_2\right)·({\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}\right)·{\alpha }_V^{\mathfrak{e}-\mathfrak{a}}{\beta }_V^{\mathfrak{f}-\mathfrak{b}-1}{\varphi }_V^{\mathfrak{g}-\mathfrak{c}-2}{\psi }_V^{\mathfrak{h}-\mathfrak{d}+1}\left(u_0\right))\hfill \\ & =& h·{\mathbf{C}}_{U,V}\left((u\otimes v)\right),\hfill \end{array}$$

$\mathbf{C}$ is H-linear. Similarly, we have

$$({\mathbf{C}}_{U,V}\otimes i{d}_B)\circ {\rho }^{U\otimes V}={\rho }^{V\otimes U}\circ {\mathbf{C}}_{U,V},$$

which implies $\mathbf{C}$ is B-colinear. Moreover, we also have

$$\begin{array}{ccc}& & ((i{d}_V\otimes {\mathbf{C}}_{U,W})\circ {\mathbf{a}}_{V,U,W}\circ ({\mathbf{C}}_{U,V}\otimes i{d}_W))((u\otimes v)\otimes w)\hfill \\ & =& (i{d}_V\otimes {\mathbf{C}}_{U,W})(\sum \sigma ({\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right)){\varphi }_H^{-1}\left({\mathrm{R}}^{\left(2\right)}\right)\hfill \\ & & ·{\alpha }_V^{-\mathfrak{e}}{\beta }_V^{-\mathfrak{f}-1}{\varphi }_V^{-\mathfrak{g}-1}{\psi }_V^{-\mathfrak{h}-1}\left(v_0\right)\otimes ({\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}\right)·{\alpha }_U^{\mathfrak{e}-\mathfrak{a}}{\beta }_U^{\mathfrak{f}-\mathfrak{b}-1}{\varphi }_U^{\mathfrak{g}-\mathfrak{c}-2}{\psi }_U^{\mathfrak{h}-\mathfrak{d}+1}\left(u_0\right)\hfill \\ & & \otimes {\alpha }_W^{\mathfrak{e}}{\beta }_W^{\mathfrak{f}}{\varphi }_W^{\mathfrak{g}}{\psi }_W^{\mathfrak{h}+1}\left(w\right)\left)\right)\hfill \\ & \stackrel{\left(CQ1\right),\left(Q1\right)}{=}& \sum \sigma ({\alpha }_B\left(u_{11}\right),{\alpha }_B^{2\mathfrak{a}-\mathfrak{e}+2}{\beta }_B^{2\mathfrak{b}-\mathfrak{f}-1}{\varphi }_B^{2\mathfrak{c}-\mathfrak{g}+3}{\psi }_B^{2\mathfrak{d}-\mathfrak{h}-1}\left(w_1\right))\hfill \\ & & \sigma ({\beta }_B\left(u_{12}\right),{\alpha }_B^{\mathfrak{a}-\mathfrak{e}+1}{\beta }_B^{\mathfrak{b}-\mathfrak{f}}{\varphi }_B^{\mathfrak{c}-\mathfrak{g}+1}{\psi }_B^{\mathfrak{d}-\mathfrak{h}}\left(v_1\right))\hfill \\ & & {\alpha }_H^{\mathfrak{a}-2\mathfrak{e}}{\beta }_H^{\mathfrak{b}-2\mathfrak{f}+1}{\varphi }_H^{\mathfrak{c}-2\mathfrak{g}}{\psi }_H^{\mathfrak{d}-2\mathfrak{h}-1}\left({\mathrm{R}}^{\left(2\right)}\right)·{\alpha }_V^{-\mathfrak{e}}{\beta }_V^{-\mathfrak{f}-1}{\varphi }_V^{-\mathfrak{g}-1}{\psi }_V^{-\mathfrak{h}-1}\left(v_0\right)\hfill \\ & & \otimes ({\alpha }_H^{\mathfrak{a}-\mathfrak{e}+1}{\beta }_H^{\mathfrak{b}-\mathfrak{f}}{\varphi }_H^{\mathfrak{c}-\mathfrak{g}}{\psi }_H^{\mathfrak{d}-\mathfrak{h}}\left({\dot{\mathrm{R}}}^{\left(2\right)}\right)·{\alpha }_W^{\mathfrak{a}}{\beta }_W^{\mathfrak{b}-1}{\varphi }_W^{\mathfrak{c}}{\psi }_W^{\mathfrak{d}}\left(w_0\right)\hfill \\ & & \otimes \left({\dot{\mathrm{R}}}^{\left(1\right)}{\mathrm{R}}^{\left(1\right)}\right)·{\alpha }_U^{2\mathfrak{e}-2\mathfrak{a}}{\beta }_U^{2\mathfrak{f}-2\mathfrak{b}-1}{\varphi }_U^{2\mathfrak{g}-2\mathfrak{c}-3}{\psi }_U^{2\mathfrak{h}-2\mathfrak{d}+2}\left(u_0\right))\hfill \\ & \stackrel{\left(CQ3\right),\left(Q4\right)}{=}& \sum \sigma ({\alpha }_B{\beta }_B\left(u_1\right),{\alpha }_B^{\mathfrak{a}-\mathfrak{e}+1}{\beta }_B^{\mathfrak{b}-\mathfrak{f}}{\varphi }_B^{\mathfrak{c}-\mathfrak{g}+1}{\psi }_B^{\mathfrak{d}-\mathfrak{h}-1}\left(v_1\right){\alpha }_B^{2\mathfrak{a}-\mathfrak{e}+2}{\beta }_B^{2\mathfrak{b}-\mathfrak{f}-1}{\varphi }_B^{2\mathfrak{c}-\mathfrak{g}+2}{\psi }_B^{2\mathfrak{d}-\mathfrak{h}-1}\left(w_1\right))\hfill \\ & & {\alpha }_H^{\mathfrak{a}-2\mathfrak{e}}{\beta }_H^{\mathfrak{b}-2\mathfrak{f}}{\varphi }_H^{\mathfrak{c}-2\mathfrak{g}-1}{\psi }_H^{\mathfrak{d}-2\mathfrak{h}-1}\left({\mathrm{R}}_1^{\left(2\right)}\right)·{\alpha }_V^{-\mathfrak{e}}{\beta }_V^{-\mathfrak{f}-1}{\varphi }_V^{-\mathfrak{g}-1}{\psi }_V^{-\mathfrak{h}-1}\left(v_0\right)\hfill \\ & & \otimes ({\alpha }_H^{\mathfrak{a}-\mathfrak{e}}{\beta }_H^{\mathfrak{b}-\mathfrak{f}}{\varphi }_H^{\mathfrak{c}-\mathfrak{g}}{\psi }_H^{\mathfrak{d}-\mathfrak{h}-1}\left({\mathrm{R}}_2^{\left(2\right)}\right)·{\alpha }_W^{\mathfrak{a}}{\beta }_W^{\mathfrak{b}-1}{\varphi }_W^{\mathfrak{c}}{\psi }_W^{\mathfrak{d}}\left(w_0\right)\hfill \\ & & \otimes {\mathrm{R}}^{\left(1\right)}·{\alpha }_U^{2\mathfrak{e}-2\mathfrak{a}}{\beta }_U^{2\mathfrak{f}-2\mathfrak{b}-1}{\varphi }_U^{2\mathfrak{g}-2\mathfrak{c}-3}{\psi }_U^{2\mathfrak{h}-2\mathfrak{d}+2}\left(u_0\right))\hfill \\ & \stackrel{\left(CQ1\right),\left(Q1\right)}{=}& \sum \sigma ({\alpha }_B^{-2\mathfrak{a}-1}{\beta }_B^{-2\mathfrak{b}}{\varphi }_B^{-2\mathfrak{c}-2}{\psi }_B^{-2\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{a}-\mathfrak{e}-1}{\beta }_B^{-\mathfrak{b}-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{c}-\mathfrak{g}-1}{\psi }_B^{-\mathfrak{d}-\mathfrak{h}-1}\left(v_1\right)\hfill \\ & & {\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-2}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(w_1\right)){\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}-1}{\psi }_H^{\mathfrak{d}}\left({\mathrm{R}}_1^{\left(2\right)}\right)·{\alpha }_V^{-\mathfrak{e}}{\beta }_V^{-\mathfrak{f}-1}{\varphi }_V^{-\mathfrak{g}-1}{\psi }_V^{-\mathfrak{h}-1}\left(v_0\right)\hfill \\ & & \otimes ({\alpha }_H^{\mathfrak{a}+\mathfrak{e}}{\beta }_H^{\mathfrak{b}+\mathfrak{f}}{\varphi }_H^{\mathfrak{c}+\mathfrak{g}}{\psi }_H^{\mathfrak{d}+\mathfrak{h}}\left({\mathrm{R}}_2^{\left(2\right)}\right)·{\alpha }_W^{\mathfrak{a}}{\beta }_W^{\mathfrak{b}-1}{\varphi }_W^{\mathfrak{c}}{\psi }_W^{\mathfrak{d}}\left(w_0\right)\hfill \\ & & \otimes {\alpha }_H^{2\mathfrak{e}}{\beta }_H^{2\mathfrak{f}}{\varphi }_H^{2\mathfrak{g}}{\psi }_H^{2\mathfrak{h}+1}\left({\mathrm{R}}^{\left(1\right)}\right)·{\alpha }_U^{2\mathfrak{e}-2\mathfrak{a}}{\beta }_U^{2\mathfrak{f}-2\mathfrak{b}-1}{\varphi }_U^{2\mathfrak{g}-2\mathfrak{c}-3}{\psi }_U^{2\mathfrak{h}-2\mathfrak{d}+2}\left(u_0\right))\hfill \end{array}$$

$$\begin{array}{ccc}& =& {\mathbf{a}}_{V,W,U}(\sum \sigma ({\alpha }_B^{-2\mathfrak{a}-1}{\beta }_B^{-2\mathfrak{b}}{\varphi }_B^{-2\mathfrak{c}-2}{\psi }_B^{-2\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{e}-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{f}-\mathfrak{b}-1}{\varphi }_B^{-\mathfrak{g}-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{h}-\mathfrak{d}-1}\left(v_1\right)\hfill \\ & & {\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-2}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(w_1\right)\left)\right({\alpha }_H^{2\mathfrak{a}}{\beta }_H^{2\mathfrak{b}}{\varphi }_H^{2\mathfrak{c}}{\psi }_H^{2\mathfrak{d}}\left({\mathrm{R}}_1^{\left(2\right)}\right)·{\alpha }_V^{\mathfrak{a}-\mathfrak{e}}{\beta }_V^{\mathfrak{b}-\mathfrak{f}-1}{\varphi }_V^{\mathfrak{c}-\mathfrak{g}}{\psi }_V^{\mathfrak{d}-\mathfrak{h}-1}\left(v_0\right)\hfill \\ & & \otimes {\alpha }_H^{\mathfrak{a}+\mathfrak{e}}{\beta }_H^{\mathfrak{b}+\mathfrak{f}}{\varphi }_H^{\mathfrak{c}+\mathfrak{g}}{\psi }_H^{\mathfrak{d}+\mathfrak{h}}\left({\mathrm{R}}_2^{\left(2\right)}\right)·{\alpha }_W^{\mathfrak{a}}{\beta }_W^{\mathfrak{b}-1}{\varphi }_W^{\mathfrak{c}}{\psi }_W^{\mathfrak{d}}\left(w_0\right))\hfill \\ & & \otimes {\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}\right)·{\alpha }_U^{\mathfrak{e}-2\mathfrak{a}}{\beta }_U^{\mathfrak{f}-2\mathfrak{b}-1}{\varphi }_U^{\mathfrak{g}-2\mathfrak{c}-3}{\psi }_U^{\mathfrak{h}-2\mathfrak{d}+1}\left(u_0\right)\hfill \\ & =& ({\mathbf{a}}_{V,W,U}\circ {\mathbf{C}}_{U,V\otimes W}\circ {\mathbf{a}}_{U,V,W})((u\otimes v)\otimes w),\hfill \end{array}$$

and similarly we can obtain ${\mathbf{a}}_{W,U,V}^{-1}\circ {\mathbf{C}}_{U\otimes V,W}\circ {\mathbf{a}}_{U,V,W}^{-1}=({\mathbf{C}}_{U,W}\otimes i{d}_V)\circ {\mathbf{a}}_{U,W,V}^{-1}\circ (i{d}_U\otimes {\mathbf{C}}_{V,W})$.

Now, for any $U,V\in {}_H{\mathcal{L}}^B$, consider ${\mathbf{C}}^{\prime }:{\otimes }^{op}\Rightarrow \otimes$, where ${{\mathbf{C}}^{\prime }}_{U,V}(v\otimes u):=$

$$\begin{array}{ccc}& & \sum \sigma (S{\alpha }_B^{\mathfrak{a}}{\beta }_B^{\mathfrak{b}}{\varphi }_B^{\mathfrak{c}+2}{\psi }_B^{\mathfrak{d}-2}\left(u_1\right),{\alpha }_B^{\mathfrak{e}}{\beta }_B^{\mathfrak{f}}{\varphi }_B^{\mathfrak{g}}{\psi }_B^{\mathfrak{h}}\left(v_1\right))S{\alpha }_H^{\mathfrak{a}-1}{\beta }_H^{\mathfrak{b}+1}{\varphi }_H^{\mathfrak{c}+1}{\psi }_H^{\mathfrak{d}-1}\left({\mathrm{R}}^{\left(1\right)}\right)\hfill \\ & & ·{\alpha }_U^{\mathfrak{a}-\mathfrak{e}}{\beta }_U^{\mathfrak{b}-\mathfrak{f}-1}{\varphi }_U^{\mathfrak{c}-\mathfrak{g}}{\psi }_U^{\mathfrak{d}-\mathfrak{h}-1}\left(u_0\right)\otimes {\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(2\right)}\right)·{\alpha }_V^{\mathfrak{e}-\mathfrak{a}}{\beta }_V^{\mathfrak{f}-\mathfrak{b}-1}{\varphi }_V^{\mathfrak{g}-\mathfrak{c}-2}{\psi }_V^{\mathfrak{h}-\mathfrak{d}+1}\left(v_0\right).\hfill \end{array}$$

Next, we will show ${\mathbf{C}}^{\prime }$ is the inverse of $\mathbf{C}$. Indeed, we have

$$\begin{array}{ccc}& & ({\mathbf{C}}_{U,V}^{\prime }\circ {\mathbf{C}}_{U,V})(u\otimes v)\hfill \\ & =& {\mathbf{C}}_{U,V}^{\prime }(\sum \sigma ({\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_1\right),{\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_1\right)){\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}}{\psi }_H^{\mathfrak{d}}\left({\mathrm{R}}^{\left(2\right)}\right)\hfill \\ & & ·{\alpha }_V^{\mathfrak{a}-\mathfrak{e}}{\beta }_V^{\mathfrak{b}-\mathfrak{f}-1}{\varphi }_V^{\mathfrak{c}-\mathfrak{g}}{\psi }_V^{\mathfrak{d}-\mathfrak{h}-1}\left(v_0\right)\otimes {\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(1\right)}\right)·{\alpha }_U^{\mathfrak{e}-\mathfrak{a}}{\beta }_U^{\mathfrak{f}-\mathfrak{b}-1}{\varphi }_U^{\mathfrak{g}-\mathfrak{c}-2}{\psi }_U^{\mathfrak{h}-\mathfrak{d}+1}\left(u_0\right))\hfill \\ & \stackrel{\left(CQ1\right),\left(Q1\right)}{=}& \sum \sigma ({\alpha }_B^{-\mathfrak{a}-1}{\beta }_B^{-\mathfrak{b}}{\varphi }_B^{-\mathfrak{c}-1}{\psi }_B^{-\mathfrak{d}}\left(u_{12}\right),{\alpha }_B^{-\mathfrak{e}}{\beta }_B^{-\mathfrak{f}-1}{\varphi }_B^{-\mathfrak{g}}{\psi }_B^{-\mathfrak{h}-1}\left(v_{12}\right))\hfill \\ & & \sigma (S{\alpha }_B^{\mathfrak{e}}{\beta }_B^{\mathfrak{f}}{\varphi }_B^{\mathfrak{g}}{\psi }_B^{\mathfrak{h}}\left(u_{11}\right),{\alpha }_B^{\mathfrak{a}}{\beta }_B^{\mathfrak{b}}{\varphi }_B^{\mathfrak{c}}{\psi }_B^{\mathfrak{d}}\left(v_1\right))\hfill \\ & & \left(S{\alpha }_H^{\mathfrak{a}-1}{\beta }_H^{\mathfrak{b}+1}{\varphi }_H^{\mathfrak{c}+1}{\psi }_H^{\mathfrak{d}-1}\left({\dot{\mathrm{R}}}^{\left(1\right)}\right){\alpha }_H^{\mathfrak{a}}{\beta }_H^{\mathfrak{b}}{\varphi }_H^{\mathfrak{c}+2}{\psi }_H^{\mathfrak{d}-2}\left({\mathrm{R}}^{\left(1\right)}\right)\right)·{\beta }_U^{-1}{\varphi }_U^{-1}\left(u_0\right)\hfill \\ & & \otimes \left({\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\dot{\mathrm{R}}}^{\left(2\right)}\right){\alpha }_H^{\mathfrak{e}}{\beta }_H^{\mathfrak{f}}{\varphi }_H^{\mathfrak{g}}{\psi }_H^{\mathfrak{h}}\left({\mathrm{R}}^{\left(2\right)}\right)\right)·{\beta }_V^{-1}{\varphi }_V^{-1}\left(v_0\right)\hfill \\ & \stackrel{\left(CQ1\right),\left(4.4\right)}{=}& \sigma ({\alpha }_B^{\mathfrak{e}-1}{\beta }_B^{\mathfrak{f}+1}{\varphi }_B^{\mathfrak{g}-1}{\psi }_B^{\mathfrak{h}+1}\left(u_{12}\right),{\alpha }_B^{\mathfrak{a}}{\beta }_B^{\mathfrak{b}}{\varphi }_B^{\mathfrak{c}}{\psi }_B^{\mathfrak{d}}\left(v_{12}\right))\hfill \\ & & \sigma (S{\alpha }_B^{\mathfrak{e}}{\beta }_B^{\mathfrak{f}}{\varphi }_B^{\mathfrak{g}}{\psi }_B^{\mathfrak{h}}\left(u_{11}\right),{\alpha }_B^{\mathfrak{a}}{\beta }_B^{\mathfrak{b}}{\varphi }_B^{\mathfrak{c}}{\psi }_B^{\mathfrak{d}}\left(v_1\right)){\varphi }_U^{-1}\left(u_0\right)\otimes {\varphi }_V^{-1}\left(v_0\right)\hfill \\ & \stackrel{\left(CQ1\right),\left(4.6\right)}{=}& u\otimes v,\hfill \end{array}$$

and similarly we can obtain ${\mathbf{C}}_{U,V}\circ {\mathbf{C}}_{U,V}^{\prime }=id$. This means that $({{}_H{\mathcal{L}}^B}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}},\otimes ,\mathbb{k},\mathbf{a},\mathbf{l},\mathbf{r},\mathbf{C})$ is a braided category. □

Under the consideration above, we obtain the following result.

Corollary 2.

The family of maps ${\mathbf{C}}_{U,V}$ for any $U,V\in {{}_H{\mathcal{L}}^B}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}}$ is a solution of the following BiHom-type Yang-Baxter Equation:

$$\begin{array}{ccc}& & (i{d}_W\otimes {\mathbf{C}}_{U,V})\circ {\mathbf{a}}_{W,U,V}\circ ({\mathbf{C}}_{U,W}\otimes i{d}_V)\circ {\mathbf{a}}_{U,W,V}^{-1}\circ (i{d}_U\otimes {\mathbf{C}}_{V,W})\circ {\mathbf{a}}_{U,V,W}\hfill \\ & & ={\mathbf{a}}_{W,V,U}\circ ({\mathbf{C}}_{W,V}\otimes i{d}_U)\circ {\mathbf{a}}_{W,V,U}^{-1}\circ (i{d}_V\otimes {\mathbf{C}}_{U,W})\circ {\mathbf{a}}_{V,U,W}\circ ({\mathbf{C}}_{U,V}\otimes i{d}_W).\hfill \end{array}$$

Proof. 

Straightforward. □

4.3. Generalized $\mathcal{D}$-Equation

In this section, we will show that the generalized BiHom-Long dimodules will provide the algebraic solutions of BiHom-type $\mathcal{D}$-equation. From now on, we always assume that $H=(H,\mu ,1_H,\Delta ,\epsilon ,S,\alpha ,\beta ,\varphi ,\psi )$ is a BiHom-Hopf algebra over $\mathbb{k}$.

Definition 6.

Let $\xi :\otimes \Rightarrow \otimes$ be a natural transformation in $Ve{c}_{\mathbb{k}}$. If the following diagram is commutative

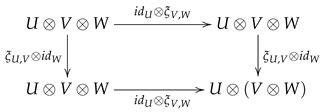in $Ve{c}_{\mathbb{k}}$, then we say ξ is a solution of the $\mathcal{D}$-equation.

Theorem 4.

For any integer $\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d},\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h},\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}\in \mathbb{Z}$, the following $\mathbb{k}$-linear maps

$$\begin{array}{cc}\hfill {\xi }_{U,V}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}}:U\otimes V& ⟶U\otimes V\hfill \\ \hfill u\otimes v& ⟼{\alpha }^{\mathfrak{i}}{\beta }^{\mathfrak{j}}{\varphi }^{\mathfrak{k}}{\psi }^{\mathfrak{l}}\left(v_1\right)·{\beta }_U^{-1}\left(u\right)\otimes {\varphi }_V^{-1}\left(v_0\right),\hfill \end{array}$$

where $U,V\in {}_H{\mathcal{L}}^H$ satisfies the following generalized BiHom-type $\mathcal{D}$-equation in ${{}_H{\mathcal{L}}^H}_{\mathfrak{e},\mathfrak{f},\mathfrak{g},\mathfrak{h}}^{\mathfrak{a},\mathfrak{b},\mathfrak{c},\mathfrak{d}}$:

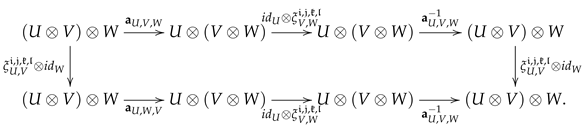
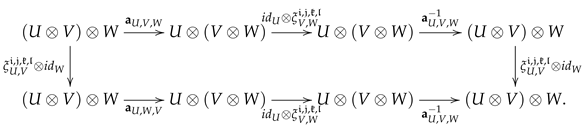
Proof. 

For any $u\in U$, $v\in V$, $w\in W$, since the following identities

$$\begin{array}{ccc}& & (({\xi }_{U,V}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}}\otimes i{d}_W)\circ {\mathbf{a}}_{U,W,V}^{-1}\circ (i{d}_U\otimes {\xi }_{V,W}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}})\circ {\mathbf{a}}_{U,V,W})((u\otimes v)\otimes w)\hfill \\ & =& (({\xi }_{U,V}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}}\otimes i{d}_W)\circ {\mathbf{a}}_{U,W,V}^{-1})({\alpha }_U^{\mathfrak{a}}{\beta }_U^{\mathfrak{b}}{\pi }_U^{\mathfrak{c}}{\psi }_U^{\mathfrak{d}}\left(u\right)\hfill \\ & & \otimes ({\alpha }^{\mathfrak{e}+\mathfrak{i}}{\beta }^{\mathfrak{f}+\mathfrak{j}}{\varphi }^{\mathfrak{g}+\mathfrak{k}}{\psi }^{\mathfrak{h}+\mathfrak{l}}\left(w_1\right)·{\beta }_V^{-1}\left(v\right)\otimes {\alpha }_W^{\mathfrak{e}}{\beta }_W^{\mathfrak{f}}{\varphi }_W^{\mathfrak{g}-1}{\psi }_W^{\mathfrak{h}+1}\left(w_0\right)))\hfill \\ & =& {\alpha }^{\mathfrak{i}}{\beta }^{\mathfrak{j}}{\varphi }^{\mathfrak{k}}{\psi }^{\mathfrak{l}}\left(v_1\right)·{\beta }_U^{-1}\left(u\right)\otimes ({\alpha }^{\mathfrak{e}+\mathfrak{i}}{\beta }^{\mathfrak{f}+\mathfrak{j}}{\varphi }^{\mathfrak{g}+\mathfrak{k}}{\psi }^{\mathfrak{h}+\mathfrak{l}+1}\left(w_1\right)·{\beta }_V^{-1}{\varphi }_V^{-1}\left(v_0\right)\otimes {\varphi }_W^{-1}\left(w_0\right))\hfill \\ & =& ({\mathbf{a}}_{U,V,W}^{-1}\circ (i{d}_U\otimes {\xi }_{V,W}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}}))({\alpha }^{-\mathfrak{a}+\mathfrak{i}}{\beta }^{-\mathfrak{b}+\mathfrak{j}}{\varphi }^{-\mathfrak{c}+\mathfrak{k}-1}{\psi }^{-\mathfrak{d}+\mathfrak{l}}\left(v_1\right)·{\alpha }_U^{-\mathfrak{a}}{\beta }_U^{-\mathfrak{b}-1}{\varphi }_U^{-\mathfrak{c}-1}{\psi }_U^{-\mathfrak{d}}\left(u\right)\hfill \\ & & \otimes ({\varphi }_V^{-1}\left(v_0\right)\otimes {\alpha }_W^{\mathfrak{e}}{\beta }_W^{\mathfrak{f}}{\varphi }_W^{\mathfrak{g}}{\psi }_W^{\mathfrak{h}+1}\left(w\right)))\hfill \\ & =& ({\mathbf{a}}_{U,V,W}^{-1}\circ (i{d}_U\otimes {\xi }_{V,W}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}})\circ {\mathbf{a}}_{U,W,V}\circ ({\xi }_{U,V}^{\mathfrak{i},\mathfrak{j},\mathfrak{k},\mathfrak{l}}\otimes i{d}_W))((u\otimes v)\otimes w),\hfill \end{array}$$

the conclusion holds. □

Remark 8.

As a special case of Theorem 4, if $\alpha =\beta =\varphi =\psi$, then H is a Hom–Hopf algebra, and we immediately obtain [8], (Proposition 5.11).

5. Conclusions

For a BiHom-Hopf algebra H, we first introduced the parametric Heisenberg doubles of H, and show that they can provide the solutions of the BiHom-Hopf equation and BiHom-pentagon equation. Then, we investigated the generalized BiHom-type Long-dimodules, and the solution of BiHom-$\mathcal{D}$-equation derived from them. Moreover, if H is both quasitriangular and coquasitriangular, then BiHom-type Long-dimodules also provide the solutions of BiHom-Yang-Baxter equation.