Abstract
This paper focuses on cooperative multi-task assignment and re-assignment problems when multiple unmanned aerial vehicles (UAVs) attack multiple known targets. A unified multi-objective optimization framework for UAV cooperative task assignment and re-assignment is studied in this paper. In order to simultaneously optimize the losses and benefits of the UAVs, we establish a multi-objective optimization model. The amount of tasks that each UAV can perform and the number of attacks on each target are limited according to the ammunition capacity of each UAV and the value of each target. To solve this multi-objective optimization problem, a multi-objective genetic algorithm suitable for UAV cooperative task assignment is constructed based on the NSGA-II algorithm. At the same time, a selection strategy is used to assist decision-makers in choosing one or more solutions from the Pareto-optimal front. Moreover, to deal with emergencies such as UAV damage and to detect of new targets, a task re-assignment algorithm based on the contract network protocol (CNP) is developed. It can be implemented in real-time while only slightly sacrificing the ability to seek the optimal solution. Simulation results demonstrate that the methods developed in this paper are effective.
Keywords:
unmanned aerial vehicle; cooperative task assignment; multi-objective optimization; genetic algorithm; contract network protocol MSC:
90C29
1. Introduction
Unmanned aerial vehicles (UAVs) refer to aircraft without pilots; such aircraft can fly autonomously or can be remotely controlled by an operator [1]. They can completely reduce casualties and costs when performing high-risk missions [2]. At present, UAVs have become very popular in many fields, such as infrastructure inspection, coastal border surveillance, military applications, and others fields [3,4,5,6]. In the increasingly complex battlefield situation, a single UAV cannot quickly adapt to the changing battlefield environment due to lack of information interaction. At the same time, the effectiveness of a single UAV in perform tasks is not high due to the limited ammunition capacity of a single UAV. However, when a team composed of multiple UAVs performs tasks cooperatively it can overcome the shortcomings of a single UAV. The UAV team can share information and fully allocate internal resources, allowing tasks to be completed efficiently [7,8].
In order to take the advantage of multiple UAVs when performing tasks realize improvements in efficiency, cooperative task assignment is important. In recent years, results have been achieved in research on task assignment in different fields [9,10]. According to the different factors considered by researchers, the task assignment problem of multiple UAVs can be categorized into different models, and many related algorithms have been proposed as well. Swarm intelligence optimization algorithms are widely used in this field, particularly genetic algorithms [11]. The UAV team can be composed of either homogeneous UAVs or heterogeneous UAVs. For cooperative task assignment of homogeneous UAVs considering the limitations on the total flight distance of UAVs, Wang et al. [12] established a combinatorial optimization problem with the total weighted cost of target value and distance cost as the objective, and presented an improved genetic algorithm based on the beetle antennae search algorithm. Venugopalan et al. [13] presented a team search-based decentralized task assignment scheme for homogeneous UAVs. Velhal et al. [14] formulated the restricted airspace protection problem as a multi-UAV spatio-temporal multi-task allocation problem, and proposed a modified consensus-based bundled auction method to solve it. For cooperative task assignment of heterogeneous UAVs, Fatemeh Afghah et al. [15] proposed a coalition formation approach to solve the problem of adversary target detection and subsequent task completion. Schwarzrock et al. [16] proposed a method to increase the amount of tasks performed within the problem of task allocation among agents representing UAVs. Taking the minimization of the task execution time of UAVs as the objective, Ye et al. [17] established a task assignment model and proposed a modified genetic algorithm with a multi-type-gene chromosome encoding method. Considering a coupled task allocation and path planning problem, Yan et al. [18] proposed a task allocation algorithm and a cooperative particle swarm algorithm. Uncertain factors are considered in the cooperative task assignment problem as well. Considering the parameter and time-sensitive uncertainties in the task assignment problem, Chen et al. [19] proposed an algorithm that combines the interior point method and the modified two-part wolf pack search algorithm. Jia et al. [20] established a two-stage stochastic programming model of the cooperative task assignment problem incorporating the stochastic velocities of UAVs, and proposed a novel metaheuristic based on a modified genetic algorithm.
However, only a single goal is considered by the above task assignment problems. In order to simultaneously optimize the losses and benefits of the UAV team, it is necessary to study the multi-objective optimization problem for multi-UAV task assignment. NSGA-II and its variants are widely used in the study of multi-objective optimization for UAV mission assignment [21,22]. Cheng et al. [23] considered the multi-objective optimization of task assignment, with minimization of cost and maximization of the value of destroyed targets regarded as the objectives. Taking into account the relationship between the UAVs and the ground control stations, Cristian et al. [24] proposed a new multi-objective genetic algorithm for solving complex mission planning problems be formulating mission planning as a constraint satisfaction problem [25]. Chen et al. [26] studied the task assignment problem for UAVs with different sensor capacities, and proposed a modified multi-objective symbiotic organism search algorithm. Wang et al. [27] considered a high-dimensional multi-objective optimization problem containing four objectives for task assignment, then used an improved multi-objective quantum-behaved particle swarm optimization algorithm to solve the problem. Pohl et al. [28] developed an innovative algorithm for multi-UAV mission routing. Phiboon et al. [29] studied multi-fidelity multi-objective airfoil design optimization for fixed-wing UAVs. However, the above studies have not explained how decision-makers are to choose a solution from the Pareto-optimal front. At the same time, the above literature does not consider the emergencies that may occur on the battlefield. The complexity of the battlefield environment inevitably causes emergencies; for example, damage to UAVs, the appearance of new targets, etc. The problem of UAV task re-assignment needs to be considered when such emergencies occur. Unlike the general task assignment problem, task re-assignment in emergencies must be completed in a short time. Therefore, the task re-assignment problem has higher requirements with respect to the calculation speed of the algorithm. A contract network algorithm [30] based on the auction mechanism has been applied to the real-time task assignment problem. Zhen et al. [31] proposed an improved contract network protocol-based cooperative target assignment scheme to deal with heterogeneous overloading and time sequence problems. Zhang et al. [32] established a model of real-time assignment of tasking based on reconnaissance benefits and reconnaissance costs, and proposed an improved contract network algorithm. Xiang et al. [33] studied the cooperation target assignment of multiple agents, and proposed an improved contract network protocol according to the characteristics and restrictions of target assignment.
The contributions of the present article are provided as follows:
- (1)
- Based on the idea of the NSGA-II algorithm, an algorithm suitable for solving the multi-objective optimization problem of multi-UAV task assignment is presented, and the encoding format and genetic operators therein are specially designed.
- (2)
- A method for aiding commanders in choosing an operation plan from among the Pareto solution set is provided.
- (3)
- A highly efficient CNP-based algorithm is developed for real-time task re-assignment in emergencies.
The remainder of this paper is organized as follows. Section 2 presents a multi-objective optimization model of cooperative task assignment. Section 3 provides the multi-objective optimization strategy. Section 4 provides the method of selecting solutions from the Pareto solution set. The problem of task re-assignment in emergencies is studied in Section 5. Numerical examples are provided in Section 6. Finally, Section 7 concludes the paper.
2. Multi-Objective Optimization Model of Cooperative Task Assignment
For convenience, let , , . On the battlefield, UAVs with attack capabilities are required to attack multiple known targets in coordination to improve efficiency. Assume that UAVs coordinately attack targets in the combat area. Let be the set of UAVs, where represents the i-th UAV. The target set is recorded as , where represents the j-th target. When a UAV attacks a target, the UAV may be destroyed, and different UAVs have different probabilities of being destroyed when they attack different targets. Let , respectively denote the probability that and are destroyed when attacks . Let and represent the value of and , respectively.
Because the previous single-objective optimization cannot achieve simultaneous optimization of two conflicting objectives, i.e., simultaneous optimization of the costs and benefits in terms of UAVs, it is necessary to establish a multi-objective optimization model for the cooperative task assignment problem. Considering the respective probabilities of UAVs and targets being destroyed, the following two objectives are used to maximize the value of the destroyed targets while incurring the minimum cost in damaged UAVs.
- (i)
- Maximizing the total value of the targets destroyed by UAVs:
- (ii)
- Minimizing the total cost of the damaged UAVs:
The UAVs have a limited amount of ammunition, which makes it impossible to allocate more tasks to each UAV than its ammunition capacity. Targets have different values, and are divided into high-value targets and low-value targets. In this paper, the values of enemy targets are known in advance. Multiple attack missions are assigned to the same high-value target in order to increase the probability of success. To decrease the time that UAVs must stay within the enemy’s threat range, the following assumption is made.
Hypothesis 1 (H1).
Different tasks for the same target are performed by different UAVs.
The implicit constraint in is that the same UAV can only attack the same target once. This constraint not being taken into account can cause the limited ammunition to be distributed unevenly, which can affect efficiency. For this reason, the number of high-value targets to be attacked needs to be limited. According to the above description, the task assignment problem needs to satisfy the following constraints.
- (i)
- The amount of tasks assigned to each UAV cannot exceed its own ammunition capacity:
- (ii)
- The number of tasks for each target is limited:
- (iii)
- The same UAV can only attack the same target once:
Let . The multi-objective optimization problem of the cooperative task assignment (CTAMOP) is expressed as follows.
3. Multi-Objective Optimization Strategy
In order to solve CTAMOP, an improved multi-objective genetic algorithm based on the NSGA-II algorithm [34] is constructed in this section. Based on the characteristics of the task assignment problem, the chromosome encoding method along with the crossover and mutation operators are specially designed and constructed.
3.1. Chromosome Encoding
The task assignment problem has two characteristics. First, the problem is that multiple UAVs may attack multiple targets; second, whether attacks is represented by 0 and 1. Considering the above factors, we use the binary matrix encoding method to encode the chromosomes in order to accurately describe the situation of UAVs performing tasks.
For the scenario of UAVs attacking targets, the generated chromosomes should be order matrices, which only contain 0 and 1 elements. Constraints (3)–(5) need to be satisfied, i.e., the sum of the i-th row of each generated matrix is less than or equal to , and the sum of the j-th column is less than or equal to . The i-th row represents the situation of the targets attacked by , and the j-th column represents the situation of UAVs attacking .
The chromosome encoding method is suitable for all combat situations, i.e., when ammunition is sufficient and when ammunition is insufficient. In order to ensure randomness, the chromosomes are generated in the following way. First, a UAV and a target are randomly selected; then, it is determined whether constraints (3)–(5) are satisfied. If both constraints are satisfied, a variable (0 or 1) is randomly assigned to ; otherwise, . This process is executed repeatedly. When all UAVs do not satisfy constraint (3) or all targets do not satisfy constraint (4) or (5), the process is terminated. At the same time, all that have not been assigned a value receive a value of 0.
Here, a specific example is provided to illustrate how chromosomes are encoded considering the case of and . The ammunition capacity of UAVs is and , and the maximum number of targets that can be attacked is . For the scenario in Figure 1a, , , are assigned to , , , are assigned to , , , are assigned to , and , are assigned to . The values of the corresponding positions of the chromosome are set to 1, and the remaining positions are set to 0, as shown in Figure 1b.
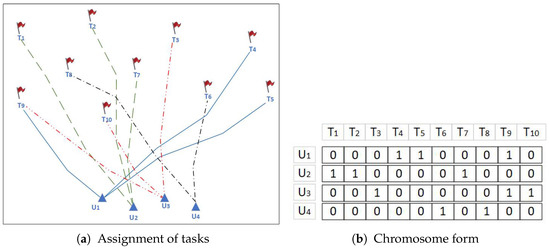
Figure 1.
Assignment of tasks and the chromosome encoding method.
In the evolution process, the offspring are composed of the retained elite individuals and the individuals obtained by crossover and mutation operations. The crossover and mutation operators play key roles. Because the chromosomes are binary matrix, it is necessary to design the crossover and mutation operators for algorithm.
3.2. The Crossover Operator
Two chromosomes and are selected from the parents, then a crossover operation is performed on and with crossover probability . The specific crossover steps are as follows. First, the -th row and the -th row from and , respectively, are randomly selected. Then, the -th row of and the -th row of are swapped to obtain two new chromosomes and . If the task assignment of the obtained chromosome satisfies constraints (3) and (4) and there is no idle UAV, then the obtained chromosome is the crossover offspring. It is common that and do not satisfy the constraints, and the following cases may exist as well.
- Task assignment satisfies constraint (4) while not satisfying constraint (3). If the -th row of does not satisfy constraint (3), that is, the number of tasks assigned to exceeds the ammunition capacity of , we sort the tasks of according to the number of tasks attacked, then delete the corresponding tasks from the task set of according to their number, from high to low. When the -th row satisfies constraint (3), then the operation is stopped.
- Task assignment satisfies constraint (3) while not satisfying constraint (4). If the j-th column of does not satisfy constraint (4), that is, the number of attacks on exceeds the upper limit , the attack task of is randomly deleted from the rows that have not been exchanged. If satisfies the constraint (4), then the operation is stopped.
If both constraints (3) and (4) are satisfied and there is an idle UAV, then as many tasks as possible are assigned to the idle UAV under the premise that constraints (3)–(4) are satisfied; targets that have not yet been attacked are prioritized.
The example provided in Section 3.1 is used to illustrate the construction of the crossover operator. The two selected parent chromosomes are shown in Figure 2. Let the rows randomly selected from and be the second and fourth rows, respectively. It can be seen from Figure 2 that (i.e., the third column marked in yellow) in the offspring chromosome obtained by does not satisfy constraint (4). As this scenario belongs to the first case, an attack task of is randomly deleted from the first or fourth row. If the task of (i.e., the first row marked in yellow) is randomly deleted, becomes an idle UAV. Thus, as many tasks as possible are assigned to under the premise that the constraints are satisfied, and the crossover offspring can be obtained. Here, and (i.e., the fourth column and fourth row marked in yellow) in the offspring chromosome obtained by fail to satisfy constraints (4) and (3), respectively. This belongs to the third case. According to the method used in the third case, the attack task of is deleted. Then, as the chromosome satisfies the constraints and there are no idle UAVs, we have the crossover offspring .
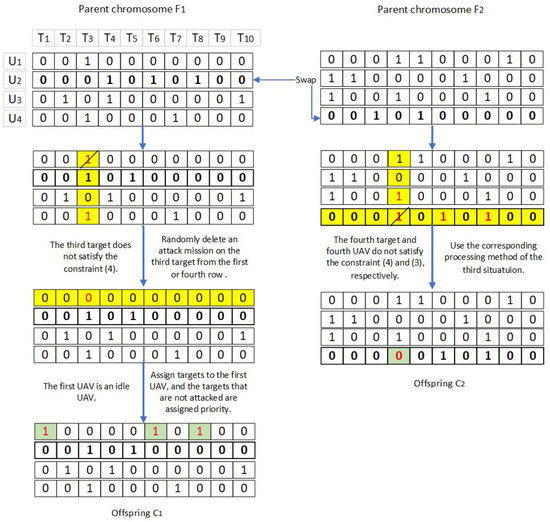
Figure 2.
Example of crossover operator.
3.3. The Mutation Operator
A mutation operation is performed on crossover offspring with a mutation probability of . There are three situations that may occur with respect to the crossover offspring, and different mutation operations are used for different situations.
- If there are targets in the chromosome that have not been attacked and there are UAVs with ammunition that can perform tasks, then the mutation operation seeks to assign the targets to these UAVs under the premise that constraint (3) is satisfied.
- If there are targets in the chromosome that have not been attacked and the UAVs have no remaining ammunition, then the mutation operation randomly selects the task sets of two UAVs from the chromosome and exchanges them.
- If all targets are attacked, then the task sets of two UAVs from the chromosome are randomly selected and exchanged.
3.4. The Improved Multi-Objective Genetic Algorithm
Based on the methods used to construct the chromosomes, crossover operators and mutation operators, the following multi-objective optimization algorithm (i.e., Algorithm 1) suitable for UAV cooperative task assignment is developed.
| Algorithm 1 Multi-objective optimization algorithm. | |
| 1: | Initialize the values of the following parameters: the population size N, crossover probability , mutation probability , and maximum number of evolutions G; |
| 2: | ; |
| 3: | Randomly generate an initial population of size N. The chromosome encoding method and chromosome generation method are based on the methods described in Section 3.1; |
| 4: | while g < G do |
| 5: | Calculate the objective function values of each chromosome in population using (1) and (2); |
| 6: | Sort population using the fast non-dominated sorting approach, then determine the front of each chromosome; |
| 7: | Perform crossover operations on the selected parents according to the crossover probability , then mutate the obtained crossover offspring with probability . Proceed to the next step when a progeny population with N chromosomes is obtained; |
| 8: | Combine the parent population with the offspring population to obtain a new population ; then, the size of population is 2N; |
| 9: | Perform the process in lines 5–6 on population to obtain the front of each chromosome in ; |
| 10: | Select chromosomes from the front; |
| 11: | while the number of chromosomes selected is less than N do |
| 12: | First, the chromosome is selected from the first front, then, the chromosome is selected from the second front, and so on; |
| 13: | if the number of chromosomes required is less than the number of chromosomes in the l-th front then |
| 14: | Calculate the crowded distances; |
| 15: | Select the chromosomes based on the crowding distance from large to small; |
| 16: | end if |
| 17: | end while |
| 18: | and |
| 19: | if then |
| 20: | Sort using the fast non-dominated sorting approach, then output the chromosomes in the first front; |
| 21: | end if |
| 22: | end while |
4. Selection Strategy
Because the decision-maker needs to select one or more solutions from the Pareto solution set in order to perform specific operations, it is necessary to have a strategy for selecting non-dominated solutions from the Pareto-optimal front. Let denote the j-th objective function, n denote the number of objective functions, and m denote the number of non-dominated solution on the Pareto-optimal front. The specific selection steps are shown in Algorithm 2.
| Algorithm 2 The strategy for selecting solutions. | |
| 1: | Convert all objective functions into a form that minimizes or maximizes the function . |
| 2: | Solve the problem using the improved NSGA-II algorithm to obtain the Pareto-optimal front. |
| 3: | If the dimensions of any two objective functions are different or the orders of magnitude of the values of any two objective functions are different, then normalize the objective function values; otherwise, the objective function values are not normalized. The j-th objective function of the i-th non-dominated solution on the Pareto-optimal front is denoted as . |
| 4: | Weight and sum each group of objective function values obtained in step 3 to obtain the following set:
|
| 5: | In step 1, if the objective functions are transformed into the form of seeking the minimum value, then the solution corresponding to the minimum value in set S obtained in step 4 is selected; otherwise, the solution corresponding to the maximum value in set S is selected. |
The specific value of () depends on the degree of preference of the decision-maker for the objective function . Let , where represents the degree of preference of the decision-maker for . The rules for setting the value of are as follows:
- If , then , and , .
- If , then , . In particular, if , then .
Finally, the flowchart diagram of the improved genetic algorithm together with the selection strategy is shown in Figure 3.
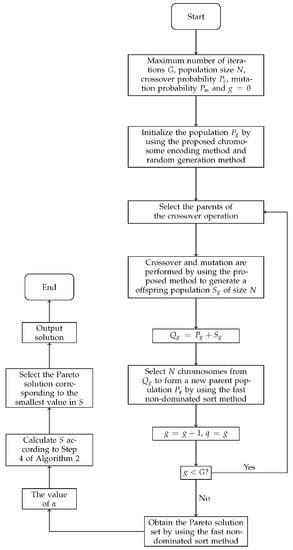
Figure 3.
The flowchart of task assignment.
5. Task Re-Assignment for Emergencies
The task assignment process is carried out on the enemy targets found on the battlefield. However, there are many uncertain factors due to the complexity of the battlefield environment. For example, after assigning the discovered targets, new enemy targets may be found on the battlefield again, or certain UAVs in the task assignment may suddenly malfunction and be unable to continue performing combat tasks. Both new targets and targets in the task sets of damaged UAVs need to be re-assigned. There are two methods of assigning tasks. The first method is to assign all tasks according to the current health status of the UAVs, and the second is to assign tasks that need to be assigned based on the obtained task assignment plan. In combat, efficiency issues are more important when solving unexpected situations. Compared with the first method, the second method takes less time and has a higher task assignment efficiency.
In this paper, the re-assignment strategy for new tasks is constructed based on the idea of the contract network protocol and the characteristics of the task assignment problem. Smith first proposed the idea of a contract network protocol [30]. The principle idea of a contract network protocol is to assign tasks through a process of tendering and bidding between agents. There are three types of agents in a contract network protocol: the tender agent, bidding agent, and winning agent. In the problem of UAV task re-assignment, the tender agent is the reconnaissance UAV that discovers a new task or the UAVs that becomes damaged, the bidding agents are UAVs with the ability to perform the newly available tasks, and the winning agent is the UAV corresponding to the bid with the best function value.
5.1. Task Re-Assignment Model
Based on the above description, there are two trigger conditions for task reassignment: (1) new enemy targets are discovered and (2) one or more UAVs are damaged. Suppose that the number of new targets found on the battlefield is , and the number of destroyed UAVs is . Let denote the set of targets that need to be assigned,
where represents the i-th task that needs to be assigned. Let denote the set of UAVs that can perform tasks,
where () represents the -th damaged UAV. Based on (1) and (2), an objective function is constructed with the following form:
where and represents the target replaced by ; is only considered in an interchange contract, which is described along with sales contracts in the next section. The values of and are the same as the values of and in Algorithm 2 in Section 4. Thus, the model of task re-assignment (TRAM) is as follows:
where .
5.2. Task Re-Assignment Algorithm
In the CNP-based algorithm, sales contracts and interchange contracts are considered. The idea of a sales contract is that a new task is added to the task set of the bidding agent. The specific form of a sales contract of a UAV for a target is represented as follows:
where, , . The sales contract (9) indicates that the revenue obtained by adding target to the task set of is . An interchange contract, on the other hand, replaces a target in the UAV task set with a target that needs to be assigned. The specific form of an interchange contract of a UAV for a target is represented as follows:
where , , and . The interchange contract (10) indicates that the revenue obtained by replacing in the task set of with is . If UAV has ammunition remaining, then can execute both the sales contract and the interchange contract; otherwise, can only execute the interchange contract. The steps for assigning target are provided in Algorithm 3.
| Algorithm 3 Task re-assignment algorithm . | |
| 1: | Initialize the information of UAV , the values of parameters , , , and the number of iterations of interchange contract . |
| 2: | Calculate the remaining ammunition of . |
| 3: | If , then executes the interchange contract and sales contract for ; otherwise, only executes the interchange contract for . Then, bidding agent chooses the contract with the largest value of . |
| 4: | The bidding agent evaluates the received contracts and selects the contract with the largest value of as the winning contract, then broadcasts the information of winning agent. |
The flowchart diagram of the CNP-based algorithm is shown in Figure 4.
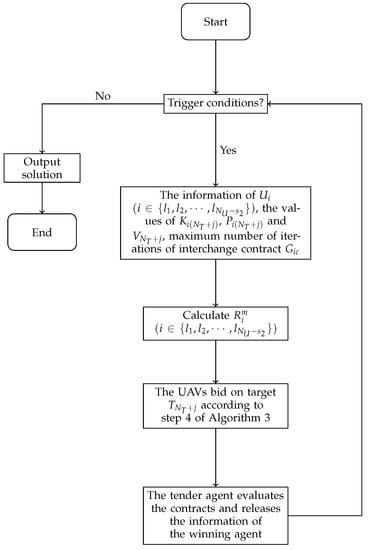
Figure 4.
The flowchart of task re-assignment.
6. Numerical Experiments
In order to verify the effectiveness of Algorithms 1–3, simulation examples of various battle situations are analyzed in this section. Examples of the improved multi-objective genetic algorithm and selection strategy are provided in Section 6.1. In Section 6.1.1 and Section 6.1.2, examples where the total amount of ammunition is less than or equal to the total number of tasks are considered, and the effectiveness of Algorithm 1 is verified. In Section 6.1.3, a large-scale example where the total amount of ammunition is greater than the total number of tasks is provided. Examples of task re-assignment in emergencies are laid out in Section 6.2. In Section 6.2.1, an example is used to illustrate the process of Algorithm 3. A large-scale example considering emergencies is provided in Section 6.2.2 to verify the effectiveness and advantages of Algorithm 3. In Section 6.2.3, we analyze why the CNP-based method is not directly used to solve the task assignment problem. All numerical experiments were implemented using Python 3.8 on a computer with an Intel Core i5-10210U CPU @ 1.60GHz, 2.11 GHz, and 4.00 GB RAM. The code for the algorithms can be found at the URL (accessed on 14 September 2022) https://github.com/gaoxh-github/multi-objetive-task-assignment-source-code. For the different examples provided in this paper, the reader only needs to change the corresponding parameters in the code.
6.1. Test of the Improved Multi-Objective Genetic Algorithm
6.1.1. Case 1: Total Amount of Ammunition = Total Number of Tasks
First, we consider a case in which and . The ammunition capacity of each UAV is , and the upper limit of each target being attacked is . When attacks , the probability of being destroyed and the probability of being destroyed are shown in Table 1. The values of and are shown in Table 2. To verify the effectiveness of Algorithm 1, we compare it with the Multiple Objective Particle Swarm Optimization (MOPSO) algorithm using the example in this section. In Algorithm 1, the crossover probability is and the mutation probability is . In MOPSO, the values of the parameters are , and . The population size and maximum number of iterations of the two algorithms are and , respectively.

Table 1.
Probabilities of UAVs and targets being destroyed.

Table 2.
Values of UAVs and targets.
The comparison results of the obtained Pareto-optimal fronts and CPU runtime are shown in Figure 5. According to the definition of the Pareto solution [34], it can be seen from Figure 5a that all the non-dominated solutions obtained by Algorithm 1 dominate the non-dominated solution obtained by MOPSO. As can be seen from Figure 5b, the CPU runtime of GA-CTAP is significantly shorter than that of MOPSO. The convergence curves of the objective functions are shown in Figure 6. Clearly, thte GA-CTAP algorithm achieves better convergence performance compared to MOPSO. For convenient description, the task assignment corresponding to the non-dominated solutions A, B, and C are provided in Table 3.
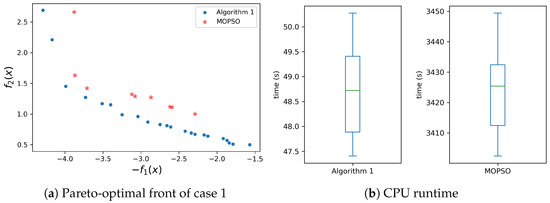
Figure 5.
Comparison of results.
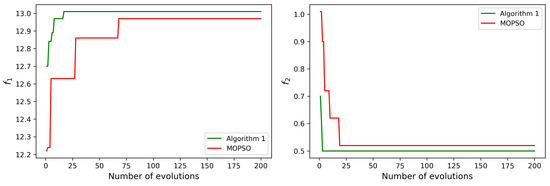
Figure 6.
Convergence curves of objective functions for case 1.

Table 3.
Specific task assignment of non-dominated solutions A, B, C.
Case 1 considers a situation in which the total amount of ammunition is equal to the number of tasks. However, in actual combat it is possible that the number of tasks is more or less than the amount of ammunition.
6.1.2. Case 2: Total Amount of Ammunition < Total Number of Tasks
In this section, we analyze a case in which four UAVs attack twenty targets. For convenience of calculation, it is assumed that each UAV has the same amount of ammunition . At the same time, in order to simplify the description, the parameter information of multiple UAVs carrying out attacking tasks on the first eight targets takes the values in Table 1 and Table 2. When attacks , the probability of being destroyed, the probability of being destroyed, and the value of are provided in Table 4.

Table 4.
Probabilities of UAVs and targets being destroyed and target values.
The obtained Pareto-optimal front is shown in Figure 7. It can be seen that the non-dominated solutions are evenly distributed and the population diversity is good. Figure 8 shows the changes of the maximum value of and the minimum value of in each iteration over the course of the entire iteration when . It can be seen that as the evolutionary algebra increases, the values of the two functions converge.
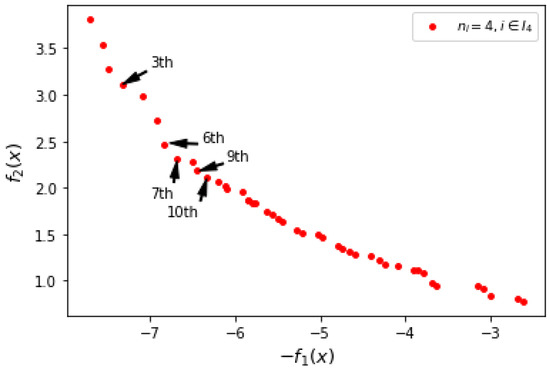
Figure 7.
Pareto-optimal front of case 2.
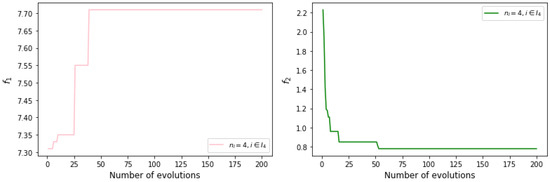
Figure 8.
Convergence curves of objective functions for case 2.
The process of selecting solutions from the Pareto solution set using the selection strategy is as follows. Let represent the result obtained in Step 4 of Algorithm 2, where , , , , and represent the weights and represents the i-th non-dominated solution in the Pareto-optimal front. Based on this example and the description of weights in Section 4, the rules for setting the values of are as follows:
- If , then .
- If , then .
- If , then .
For the Pareto-optimal front shown in Figure 7, the solutions from the upper left corner to the lower right corner are the 0th to the 44th non-dominated solutions. In this example, the objective function values are not normalized because the dimensions of and are the same, and the order of magnitude of the values of and is the same at and , respectively. Assuming the weights , , the results obtained by selection strategy are shown in Table 5.

Table 5.
The order of selection of non-dominated solutions.
As can be seen from Table 5, the sixth and seventh non-dominated solutions on the Pareto-optimal front are the best choices, while the 44th non-dominated solution is the worst choice. For the sake of simplifying the description, only the non-dominated solution information and the specific task assignment corresponding to the first five choices are shown. The positions of the five solutions are shown in Figure 7, and the corresponding specific task assignments are shown in Table 6.

Table 6.
The information of the first five non-dominated solutions.
The above description represents the process of selecting solutions of the multi-objective task assignment problem containing two objective functions. For general multi-objective optimization problems, the process of selecting solutions from the Pareto-optimal front is similar to the above process, and the values of weights are set according to the rules in Section 4.
Let denote the task set of UAV . According to the meaning of chromosomes, the task assignment information corresponding to the five non-dominated solutions in Table 6 is provided in Table 7.

Table 7.
The task assignment schemes of the solutions in Table 6.
6.1.3. Case 3: Total Amount of Ammunition > Total Number of Tasks
In this section, a large-scale task assignment example of 15 UAVs attacking 100 targets is considered. The ammunition capacity of each UAV is , and the upper limit of each target being attacked is . Considering the length of the paper, the values of parameters , , , and are not provided. The values of these parameters can be downloaded from the website (accessed on 14 September 2022) https://github.com/gaoxh-github/Values-of-parameters. In Algorithm 1, the values of the parameters are as follows: , , , . The obtained Pareto-optimal front is shown in Figure 9. The average time for this scale of experiment is about 60 min.
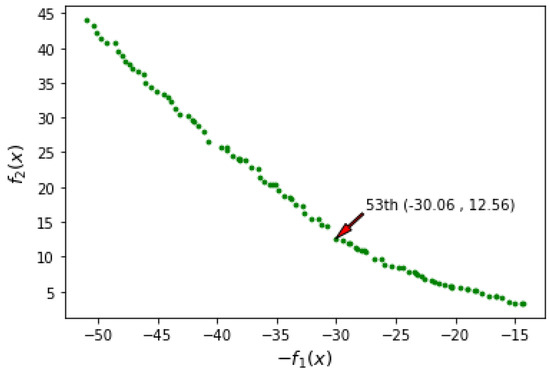
Figure 9.
Pareto-optimal front of case 3.
Algorithm 2 is used to select the solution from the Pareto solution set in Figure 9. In Algorithm 2, the values of weights and are . The obtained results are shown in Table 8. It can be seen from Table 8 that the 53rd non-dominated solution should be selected. The information of the 53rd non-dominated solution is shown in Figure 9 and the task assignment scheme of the 53rd non-dominated solution is shown in Table 9.

Table 8.
The order of selecting non-dominated solutions.

Table 9.
Task assignment of the 53rd non-dominated solution in Figure 9.
To further verify the effectiveness of the proposed task assignment algorithm combined with the solution selection strategy, in this section we compare the algorithms developed in this paper with the well-developed Gurobi optimization solver. There are three methods for solving multi-objective optimization problems in the Gurobi solver, namely, Blend, Hierarchical, and a combination of these two methods. In this paper, after obtaining the Pareto front of the task assignment problem using Algorithm 1, the decision-maker can be assisted in selecting a solution from the set of non-dominated solutions based on Algorithm 2, which is constructed based on the weights. Considering the idea behind the construction of Algorithm 2, we compared Algorithm 1 and Algorithm 2 with the Blend method in Gurobi in order to better reflect the comparison results. The comparison process is as follows. First, given nine different sets of weights, the solution of the example provided in this section is solved for each set of weights using Blend in Gurobi. Second, the Pareto front of the example is solved using Algorithm 1, then the solution is selected from the Pareto front under each set of weights using Algorithm 2. Finally, the solutions obtained by the two methods are compared for each case of weights. Table 10 shows the results of the comparison between Gurobi and the algorithms in this paper under nine sets of weights. As can be seen in Table 10, for each set of weights, the solutions developed this paper and those obtained by Gurobi are not dominated by each other, i.e., both are non-dominated solutions of the problem. Although it cannot be proven that the algorithms in this paper are better than the Gurobi solver, it can be seen that the proposed algorithms are not inferior to Gurobi in terms of solution quality.

Table 10.
Comparison results of the proposed algorithms and the multi-objective method in Gurobi.
6.2. Test of the CNP-Based Task Re-Assignment Algorithm
6.2.1. Case 1: A Small-Scale Scenario Involving the Task Re-Assignment Problem
In order to introduce the specific steps of Algorithm 3 in detail, the process of task re-assignment is explained based on the sixth non-dominated solution selected in Section 6.1.2. Suppose that four new targets are found on the battlefield. The probability of UAVs successfully attacking these targets, the probability of UAVs being destroyed, and the values of these new targets are shown in Table 11. In Algorithm 3, the value of the parameter is 10 and .

Table 11.
Probabilities of UAVs and new targets being destroyed and the value of new targets.
Targets are assigned using Algorithm 3; the bidding process is shown in Table 12. The results of task re-assignment are shown in Figure 10, where Figure 10a shows the results for the initial assignment and Figure 10b the results for task re-assignment in emergencies. From Figure 10 and Table 12, the following can be determined. The winning agents of and are and , respectively, and the contracts of and are all sales contracts. The winning agents of and are and , respectively, and the contracts of and are all interchange contracts. In the contract of and , the replaced targets are and , respectively, while in the bidding processes of and , no UAV bids for or .

Table 12.
The bidding process and results.
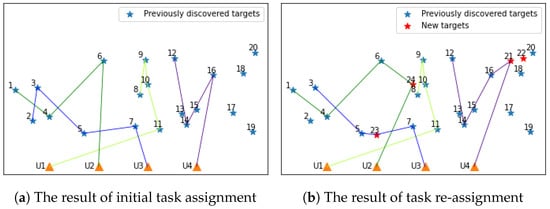
Figure 10.
Results of initial task assignment and task re-assignment in emergencies.
6.2.2. Case 2: A Large-Scale Scenario involving the Task Re-Assignment Problem
The primary advantage of the CNP-based method is that it can shorten the time requried for task assignment. The effectiveness of this method can be fully reflected in large-scale calculation examples. In a large-scale problem, to assign all the current tasks again takes a lot of time. However, if only new tasks are assigned using the CNP-based method, a large amount of time can be saved. In this section, the large-scale calculation example in Section 6.1.3 is used to discuss the effectiveness of the task re-assignment method in emergencies.
Suppose that ten new targets are found. The values of the parameters , , of the new targets can be downloaded from the website (accessed on 14 September 2022) https://github.com/gaoxh-github/Values-of-parameters. In Algorithm 3, the value of the parameter is 50. The results of the assignment of ten new targets based on the original assignment results are shown in Table 13. It can be seen from Table 13 that the task sets of UAVs , , , and have changed. The task assignment results obtained using Algorithms 1 and 2 to assign all 110 targets are shown in Table 14. Through calculation, the values of corresponding to the task assignment schemes in Table 13 and Table 14 are and , respectively. The performance of the assignment scheme obtained using Algorithms 1 and 2 to assign all tasks is better than the performance of the assignment scheme obtained using Algorithm 3 to assign new tasks. However, the calculation time of Algorithm 3 is lower than that of Algorithm 1 combined with Algorithm 2. Figure 11 shows the time of ten task re-assignment experiments under these two assignment methods. It can be seen from Figure 11 that Algorithm 3 requires less time to solve the problem of task re-assignment in emergencies than Algorithm 1 combined with Algorithm 2. Therefore, in emergency situations, Algorithm 3 can perform real-time task re-assignment by slightly sacrificing the ability to seek global optimization.

Table 13.
Results of task re-assignment using Algorithm 3.

Table 14.
Results of task re-assignment using Algorithm 1 and Algorithm 2.
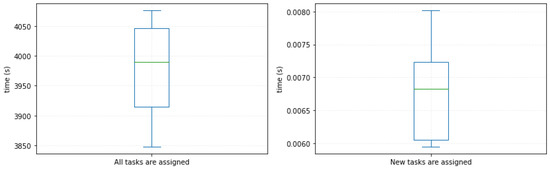
Figure 11.
CPU runtime required for the task re-assignment process. (a) Algorithm 1 combined with Algorithm 2. (b) Algorithm 3.
6.2.3. Case 3: Attempting to Solve the Task Assignment Problem Directly Using the CNP-Based Method
Considering that Algorithm 3 can quickly solve the task re-assignment problem, it may be possible to use this algorithm directly to solve the task assignment problem. An analysis of this problem is provided in this section. In the task assignment problem before the battle, the main goal of assignment is to find an assignment plan that achieves better performance. Taking the 15 UAVs attacking 100 targets in Section 6.1.3 as an example. Let , the calculation time of Algorithm 3 is about 1 s. The task assignment plan obtained using the CNP-based algorithm is shown in Table 15. The values of corresponding to the task assignment schemes in Table 9 and Table 15 are and , respectively. Obviously, the calculation result of the improved multi-objective genetic algorithm combined with selection strategy is much better than the calculation result of the CNP-based method. For the task assignment problem, the CNP-based method is much faster than the improved multi-objective genetic algorithm combined with selection strategy. However, the result obtained by the improved multi-objective genetic algorithm combined with selection strategy is much better than the result obtained by the CNP-based algorithm. Therefore, according to the above analysis, Algorithms 1 and 2 should be used in the task assignment phase with high requirements for the performance of the task assignment scheme, and Algorithm 3 should be used in the task re-assignment phase in emergencies with high requirements related to assignment time.

Table 15.
The result of Case 3 in Section 6.1.3 based on the CNP-based method.
7. Conclusions
In this paper, we have provided a unified multi-objective optimization framework for the cooperative task assignment and re-assignment of multiple UAVs. First, we propose a multi-objective optimization problem in which the minimization of the cost and the maximization of the benefits are regarded as the objectives. To solve the problem, a multi-objective genetic algorithm suitable for UAV cooperative task assignment is proposed and the encoding format and genetic operators in the proposed algorithm are specially designed. Then, we provide a selection strategy to facilitate the choice of an operation plan from the Pareto solution set by the decision-maker. Finally, taking into account the possible emergencies in the complex combat environment, the task re-assignment problem in emergencies before the battle is studied and a task re-assignment algorithm based on a contract network protocol is proposed. Simulation examples are used to verify the effectiveness of the proposed algorithms.
When the battlefield environment is more complex, a single target may contain multiple different tasks. For multiple types of tasks, heterogeneous UAVs have higher efficiency in performing their tasks compared to homogeneous UAVs. At the same time, there may be multiple obstacles in the environment that affect UAV flight. In addition, it is important to study the performance of the algorithm. Therefore, in our next work we intend to focus on the performance of the algorithm and task assignment of heterogeneous UAVs in complex environments containing obstacles.
Author Contributions
Data curation, Y.D.; Funding acquisition, L.W. and X.W.; Investigation, X.S. and Y.D.; Methodology, X.G., L.W., C.W. and X.W.; Project administration, L.W. and X.W.; Resources, C.L., C.W. and X.W.; Supervision, C.L., Y.D., C.W. and H.P.; Validation, X.S.; Writing—original draft, X.G.; Writing—review and editing, X.G. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Plan (2021YFB3302501); the National Natural Science Foundation of China (12102077); and the Fundamental Research Funds for the Central Universities (DUT22LAB305, DUT22RC(3)010).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Contact the first/corresponding author please.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Newcome, L.R. Unmanned Aviation: A Brief History of Unmanned Aerial Vehicles; Library of Flight Series; AIAA: Reston, VA, USA, 2004. [Google Scholar] [CrossRef]
- Sarris, Z. Survey of UAV applications in civil markets (June 2001). In Proceedings of the IEEE Mediterranean Conference on Control and Automation, Dubrovnik, Croatia, June 2001; Available online: https://www.researchgate.net/publication/229091536_Survey_of_UAV_applications_in_civil_markets_June_2001 (accessed on 14 September 2022).
- Nonami, K.; Kendoul, F.; Suzuki, S.; Wang, W.; Nakazawa, D. Autonomous Flying Robots: Unmanned Aerial Vehicles and Micro Aerial Vehicles; Springer: Tokyo, Japan, 2010; Available online: https://dl.acm.org/doi/abs/10.5555/1941802 (accessed on 14 September 2022).
- Qu, X.B.; Zhang, W.G.; Wang, X.G. Research of UAVs’ attack strategy under uncertain condition. Flight Dyn. 2015, 33, 381–384. Available online: http://en.cnki.com.cn/Article_en/CJFDTOTAL-FHLX201504021.htm (accessed on 14 September 2022).
- Máthé, K.; Busoniu, L. Vision and Control for UAVs: A Survey of General Methods and of Inexpensive Platforms for Infrastructure Inspection. Sensors 2015, 15, 14887–14916. [Google Scholar] [CrossRef] [PubMed]
- Turner, I.L.; Harley, M.D.; Drummond, C.D. UAVs for coastal surveying. Coast. Eng. 2016, 114, 19–24. [Google Scholar] [CrossRef]
- Fu, X.; Feng, P.; Gao, X. Swarm UAVs Task and Resource Dynamic Assignment Algorithm Based on Task Sequence Mechanism. IEEE Access 2019, 7, 41090–41100. [Google Scholar] [CrossRef]
- Zhen, Z.; Xing, D.; Gao, C. Cooperative search-attack mission planning for multi-UAV based on intelligent self-organized algorithm. Aerosp. Sci. Technol. 2018, 76, 402–411. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, J.; Guo, C.; Zhang, H. A Multi-swarm Competitive Algorithm Based on Dynamic Task Allocation Particle Swarm Optimization. Arab. J. Sci. Eng. 2018, 43, 8255–8274. [Google Scholar] [CrossRef]
- Issac, T.; Silas, S.; Rajsingh, E.B. Prototyping a Scalable P-system-Inspired Dynamic Task Assignment Algorithm for a Centralized Heterogeneous Wireless Sensor Network. Arab. J. Sci. Eng. 2020, 45, 10353–10380. [Google Scholar] [CrossRef]
- Takahashi, M.; Kita, H. A crossover operator using independent component analysis for real-coded genetic algorithms. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), Seoul, Korea, 27–30 May 2001; Volume 1, pp. 643–649. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, B.; Wei, Y.L.; Liu, P.F.; Zhang, L. Cooperative multi-task assignment of multiple UAVs with improved genetic algorithm based on beetle antennae search. In Proceedings of the 2020 39th Chinese Control Conference, Shenyang, China, 27–29 July 2020; pp. 1065–1610. [Google Scholar] [CrossRef]
- Venugopalan, T.K.; Subramanian, K.; Sundaram, S. Multi-UAV task allocation: A team-based approach. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015; pp. 45–50. [Google Scholar] [CrossRef]
- Velhal, S.; Sundaram, S. Restricted airspace protection using multi-UAV spatio-temporal multi-task allocation. arXiv 2020, arXiv:2011.11247. [Google Scholar]
- Afghah, F.; Zaeri-Amirani, M.; Razi, A.; Chakareski, J.; Bentley, E. A coalition formation approach to coordinated task allocation in heterogeneous UAV networks. In Proceedings of the 2018 Annual American Control Conference, Milwaukee, WI, USA, 27–29 June 2018; pp. 5968–5975. [Google Scholar] [CrossRef]
- Schwarzrock, J.; Zacarias, I.; Bazzan, A.L.; Fernandes, R.Q.D.A.; Moreira, L.H.; de Freitas, E.P. Solving task allocation problem in multi Unmanned Aerial Vehicles systems using Swarm intelligence. Eng. Appl. Artif. Intell. 2018, 72, 10–20. [Google Scholar] [CrossRef]
- Ye, F.; Chen, J.; Tian, Y.; Jiang, T. Cooperative Multiple Task Assignment of Heterogeneous UAVs Using a Modified Genetic Algorithm with Multi-type-gene Chromosome Encoding Strategy. J. Intell. Robot. Syst. 2020, 100, 615–627. [Google Scholar] [CrossRef]
- Yan, F.; Zhu, X.; Zhou, Z.; Tang, Y. Real-time task allocation for a heterogeneous multi-UAV simultaneous attack. Sci. Sin. Inf. 2019, 49, 555–569. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, D.; Yu, J. Multi-UAV Task Assignment With Parameter and Time-Sensitive Uncertainties Using Modified Two-Part Wolf Pack Search Algorithm. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2853–2872. [Google Scholar] [CrossRef]
- Jia, Z.; Yu, J.; Ai, X.; Xu, X.; Yang, D. Cooperative multiple task assignment problem with stochastic velocities and time windows for heterogeneous unmanned aerial vehicles using a genetic algorithm. Aerosp. Sci. Technol. 2018, 76, 112–125. [Google Scholar] [CrossRef]
- Singh, M.K.; Choudhary, A.; Gulia, S.; Verma, A. Multi-objective NSGA-II optimization framework for UAV path planning in an UAV-assisted WSN. J. Supercomput. 2022, 1–35. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Huang, H.; Cheng, S.; Wu, M. A NSGA-II Algorithm for Task Scheduling in UAV-Enabled MEC System. IEEE Trans. Intell. Transp. Syst. 2021, 23, 9414–9429. [Google Scholar] [CrossRef]
- Cheng, C.; Wu, X.Q.; Liu, M.; Chen, M. Research on task allocation for UCAVs cooperatively attacking multiple targets. J. Jilin Univ. (Inf. Sci. Ed.) 2012, 30, 609–615. [Google Scholar]
- Ramirez-Atencia, C.; Bello-Orgaz, G.; R-Moreno, M.; Camacho, D. Solving complex multi-UAV mission planning problems using multi-objective genetic algorithms. Soft Comput. 2016, 21, 4883–4900. [Google Scholar] [CrossRef]
- Ramirez-Atencia, C.; Camacho, D. Constrained multi-objective optimization for multi-UAV planning. J. Ambient. Intell. Humaniz. Comput. 2019, 10, 2467–2484. [Google Scholar] [CrossRef]
- Chen, H.-X.; Nan, Y.; Yang, Y. Multi-UAV Reconnaissance Task Assignment for Heterogeneous Targets Based on Modified Symbiotic Organisms Search Algorithm. Sensors 2019, 19, 734. [Google Scholar] [CrossRef]
- Wang, J.-F.; Jia, G.-W.; Lin, J.-C.; Hou, Z.-X. Cooperative task allocation for heterogeneous multi-UAV using multi-objective optimization algorithm. J. Central South Univ. 2020, 27, 432–448. [Google Scholar] [CrossRef]
- Pohl, A.J.; Lamont, G.B. Multi-objective UAV mission planning using evolutionary computation. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 1268–1279. [Google Scholar] [CrossRef]
- Phiboon, T.; Khankwa, K.; Petcharat, N.; Phoksombat, N.; Kanazaki, M.; Kishi, Y.; Bureerat, S.; Ariyarit, A. Experiment and computation multi-fidelity multi-objective airfoil design optimization of fixed-wing UAV. J. Mech. Sci. Technol. 2021, 35, 4065–4072. [Google Scholar] [CrossRef]
- Smith, R.G. The contract net protocol: High-level communication and control in a distributed problem solver. IEEE Trans. Comput. 1980, 29, 1104–1113. [Google Scholar] [CrossRef]
- Zhen, Z.; Wen, L.; Wang, B.; Hu, Z.; Zhang, D. Improved contract network protocol algorithm based cooperative target allocation of heterogeneous UAV swarm. Aerosp. Sci. Technol. 2021, 119, 107054. [Google Scholar] [CrossRef]
- Zhang, K.W.; Zhao, X.L.; Li, Z.Z.; Zhao, B.X.; Xiao, Z.H. Real-time reconnaissance task assignment of multi-UAV based on improved contract network. In Proceedings of the 2020 International Conference on Artificial Intelligence and Computer Engineering, Beijing, China, 23–25 October 2020. [Google Scholar] [CrossRef]
- Xiang, J.Q.; Dong, X.W.; Li, Q.D.; Ren, Z. Cooperation target assignment of missiles based on multi-agent technique and improved contract net protocol. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference, Xiamen, China, 10–12 August 2018. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).