Abstract
Cable robots are a type of parallel robot in which cables have replaced the usual rigid arms. In cable robots, due to the tensile strength of the cable, the workspace analysis is much more complex than in conventional robots. In this paper, we design an adaptive fuzzy controller for a cable-driven parallel robot (CDPR). In the proposed controller, the results show that the accuracy of the system performance in tracking the reference value as well as the controller performance speed is better than that of the robust method. In one of the simulation modes, the performance speed of the control system for convergence is reduced and its error is very small, which indicates the proper performance of the proposed adaptive fuzzy method. It should be noted that all simulations are performed in a MATLAB software environment.
MSC:
70E60; 03B52; 93C42; 94D05; 93C40; 93C10
1. Introduction
The widespread use of robots in various applications has led to the fact that many common industrial robots today are not able to meet all requirements [1,2,3,4]. This has led to the design and construction of new structures of robots to meet the vast amount of human needs. One of these types of robots is mobile or cable-driven robots [5]. Due to the unique features of cable mechanisms, their application is increasing day by day. This has a wide range of new applications in a variety of industries, from the transport of heavy objects to rehabilitation and space applications. The crane robot is one of the most widely used cable mechanisms in the transport of objects and has the aim of increasing safety and control over conventional cranes. The aerial imaging of stadiums is another useful application of these mechanisms to the general public worldwide. Replacing the cable with rigid arms in parallel robots makes these robots a good alternative to deal with the inherent and structural shortcomings of conventional series and parallel robots. However, this raises new challenges and horizons for researchers [6]. One of the challenges in cable robots is the possibility of cables colliding with each other and the body of the robot, and this leads to a constraint in the optimal design of the robot. In addition to the above, the number of cables, the geometry of the robot body, and the location of the cable connections must be considered during the design process. Compared to the large volume of work conducted in the field of control of series and parallel robots, less has discussed the control of cable robots. The purpose of this paper is to control a cable-driven parallel robot (CDPR) that, as its name implies, has parallel and flexible cables [7]. Figure 1 shows the structure of a cable-driven parallel robot.
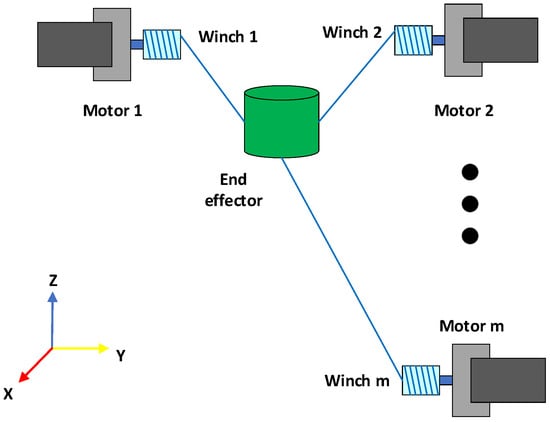
Figure 1.
The structure of a cable-driven parallel robot.
CDPRs are a type of parallel robot that has high accuracy, high acceleration, and a high load-carrying capacity. In fact, CDPRs are a type of skilled arm in which the actuator connection is supported using n cables parallel to the traction motors. In addition to the advantages of parallel robots over other robots, CDPRs can have lower mass and better rigidity (high rigidity causes less environmental noise to affect the robot) than other parallel robots. CDPRs were first used for forklifts in the 1980s and were developed by the Institute of Standards and Technology (NIST) for use in loading bays. This robot has been in use for many years, with new concepts for robotic lifts being developed. These concepts use the basic idea of the Stewart platform, which is similar to an arm. NIST’s achievement is the use of cables as parallel connections and the use of towing devices as actuators instead of hydraulic cylinder legs. In this system, gravity ensures that the cables are stretched at all times [8]. In [9], the Newton–Euler method is used for the dynamic analysis of parallel robots. In this method, a better intuitive understanding of the physics of a problem can be achieved because all internal forces, constraints, etc., can be seen in this method; however, the complexity of equations and their large volume make it impossible to achieve the desired equations even for simple problems. In [10], a new modeling method for cable robots, which considers the elastic properties of the cable, is presented. In this research, the obtained model has a higher accuracy than other models. In [11], a Proportional–Integral–Derivative (PID) controller was introduced to control the cable robot. In this study, first the dynamic equations of the robot are presented, and then the proportional controller for the control of the robot is presented, the results of which, for the controller, were acceptable. In [12], a reverse controller was proposed to control the cable robot in question, which used the type 2 neural-fuzzy network algorithm. The results of this study show that the use of the neural-fuzzy type 2 algorithm has a very good performance due to its lack of sensitivity to the parameters and system model. In [13], the same method was performed on another type of cable robot. In [14], a robust sliding mode control was used to track the dynamic path of the cable robot. A comparison between the results of the previous studies shows the superiority of the proposed robust controller over other controllers.
In [15], a method is proposed to optimize the design and modeling of a parallel cable robot, which actually optimizes and improves the movement and routing of the robot. In [16], an adaptive controller is provided to control the flexible cable robot. In this paper, some control constraints are also considered, and the results show that the designed controller has a much better performance than other studies conducted in this field. In [17], the routing programming of a suspended cable robot using the optimized linearized feedback approach is presented. It can be seen that the proposed control system has several separate control sections that control the different parts of the robot for routing. In [18], dynamic modeling, optimal path design, and the control of a cable robot are presented. Path design in parallel robots requires a consideration of the kinematic characteristics of the robot to detect the technique and an examination of its dynamic structure to determine operating constraints. Route design and control algorithms have been implemented on an Aras Laboratory cable robot, and the laboratory results indicate the efficiency of the proposed solution. In [19], a two-stage controller is proposed, which consists of two control loops including (1) a voltage control loop and (2) a control loop. In this reference, the control structure for a parallel cable robot is presented, which shows the simulation results and high-accuracy tracking of the reference path for this control method. In [20], a cable robot with three degrees of freedom is modeled and controlled. The control method in this paper is based on fuzzy adaptive torque control. Reference [21] provides an adaptive controller for controlling a parallel cable robot. In this reference, the issue of uncertainty in these robots and its effect on robot performance is mentioned. In [22], a robust sliding mode control is used for the dynamic routing of the cable robot. First, the robot dynamic equations are extracted; then, the sliding mode control algorithm is implemented in the presence of perturbation. Due to the limitations of cable robots that can only withstand tension and not pressure, an algorithm is applied that binds the system inputs from the controller to the positive tension of the cable. Finally, a plate robot is simulated to track the path, and the results of motor torque and dynamic response of the final operator are presented. A comparison between the results of previous studies shows the superiority of the proposed robust controller over other controllers.
Reviewing various sources, it can be seen that controlling cable robots has always been one of the challenges in this field; moreover, due to the novelty of this type of robot, methods beyond classical controllers have been used, and research is limited. For this reason, this study presents an adaptive fuzzy controller that is expected to have high accuracy. Because adaptive controllers have been recently used in many systems, and due to their adaptability to different operating conditions and high accuracy, they are suitable for controlling cable robots. In this research, the adaptive controller is improved by the fuzzy method, which is utilized to increase the accuracy of the controller operation. The first step in designing a controller is to have a complete model of the robot. Therefore, in this paper, we first model the system under study and obtain the system equations. The main purpose of this paper is to use an adaptive fuzzy robust control method to control the position of a parallel cable robot. Therefore, first, the control algorithm and its related relations are presented, and then the proposed controller is designed and simulated.
2. Dynamic Analysis of Cable Parallel Robot
The workspaces defined in the field of parallel cable robots can be divided into four main groups: available workspace [23], static workspace [24], dynamic workspace [25], and controllable workspace [26]. The available workspace is obtained by considering the real and physical demands of the robot, such as the minimum and maximum limits on the force of the cables or the application of a specific set of external forces to the final executor of the mechanism. Some researchers have introduced this type of workspace, sometimes referred to as a rotating work space, force-workable space, or acceptable work space. One of the defined workspaces is the dynamic workspace in which the linear and angular accelerations of the final performer of the mechanism are considered. In fact, this type of space is a subset of the available workspace where the external force is due to the determined accelerations. Researchers have studied this type of workspace for space robots and have claimed that it can be extended to space robots as well. One of the most common workspaces in cable mechanisms is the controllable workspace. In this workspace, external force vectors are a set of all force vectors in any direction and of any size. One of the important points in this type of space is the requirement of cable redundancy in the mechanism, and this can be considered in fully restricted mechanisms. Since there is no limit other than the positive force of the cable in this type of attitude, this workspace depends only on the geometry of the robot and how the connection points to the stationary and moving frame are located in the robot. The design of a fully restricted cable mechanism is very important. Because of this, relatively extensive research has been conducted in this type of workspace than in other workspaces. In reference [27], the collision of the cable with the end-effector is also considered, and an effective algorithm is presented in this regard. In this method, by examining the cable near the end-effector, the method of collision is considered. Although the proposed algorithm is an efficient and effective method allowing the cable to deal with the end-effector, the end-effector is only considered through cubic geometry. Although significant studies have been conducted on the working space of cable mechanisms, it is still one of the most challenging issues for this type of mechanism.
Unlike skilled mechanical arms, the dynamic modeling of parallel mechanical arms is very complex. Unlike much research on the kinematics of parallel robots, the work performed on the dynamics of these robots is limited. The most common method for obtaining dynamic equations of motion in parallel robots is the Newton–Euler method. With this method, a better intuitive understanding of the physics of the problem can be achieved, because all the internal forces, constraints, etc., can be seen in this method; however, the complexity of the equations and their large volume make it impossible to make arbitrary equations even for simple problems. In [28], this method has been used for the analysis of parallel plane and space robots. In this reference, the Newton–Euler method has been used to obtain the dynamic equations of the motion of the Stuart–Go robot, which is the most famous parallel mechanism. To do this, the author obtained the equations of motion of all the branches and the moving platform, taking into account the forces of constraints, the volume of which is high. The Lagrange method, which describes system dynamics using the concepts of work and energy, has also been used to model parallel robots. Because constraint forces are removed and not seen in this method, this method is computationally more efficient than the Newton–Euler method. In [29], this method is used to model a parallel mechanism of six degrees of freedom, and the dynamic equations of motion in closed form are obtained. In this model, they considered branches as point masses. Of course, it should be noted that, in this method, due to the existence of multiple kinematic circles, it is very difficult to obtain explicit equations of motion in terms of generalized independent coordinates. Other methods used in the dynamic modeling of parallel robots include the virtual work method [30]. In this method, by using the linear and angular accelerations of each object, forces and moments of inertia are calculated, and there is no need to calculate the constraint forces. Other common methods for obtaining dynamic equations for systems with closed kinematic loops have reduced system use. This idea was first proposed in the study of the dynamics of mechanisms with closed kinematic loops [31]. In this method, first, the kinematic closed-loop mechanism is transformed into an open-loop mechanism with a tree structure; then, all the open torques of the open-structure mechanism are calculated based on the desired motion of the closed-loop mechanism, before the same is performed for the joint torques. The open-loop system is obtained by considering the constraints. Using cable instead of the usual rigid arms in parallel cable robots, despite its simplicity in design and cost, poses new challenges for researchers, especially in the field of dynamics and control. In addition, due to the inherent nature of the cable, which is only able to apply tensile forces, in the dynamic design of these robots, how to apply and distribute these forces should be considered properly.
In many cable robots, the mass of the cables is ignored and the cable is considered as a solid element without mass [32]; this simplistic assumption in applications with a large workspace such as giant telescopes, due to a lack of a proper description of behavior cable dynamics, cannot be used; moreover, the problem of cable bending and stretching must be addressed in some way, and appropriate solutions must be provided to deal with this problem. Assuming the mass of the cable is considerable, the bending due to the cable is significant; therefore, the cable must be well understood from a static point of view. As noted, most of the cable models studied are static models used in kinematic analysis and system stiffness matrices. From a dynamic point of view, different models have been studied for cable modeling in parallel cable mechanisms. In the vast majority of these studies, cables are considered as solid, non-massive elements. With this assumption, the robot dynamics simplifier will depend on the dynamic characteristics of the final executor. However, in applications with high accuracy and speed, this simplifying assumption can no longer be applied, and more accurate models must be used. The dynamic modeling of a system is a useful way to study the behavior of that system before construction operations and thus reduces construction time and cost. In this section, the dynamic equations of the CDPR are obtained. The CDPR studied in this study is seen in Figure 2.
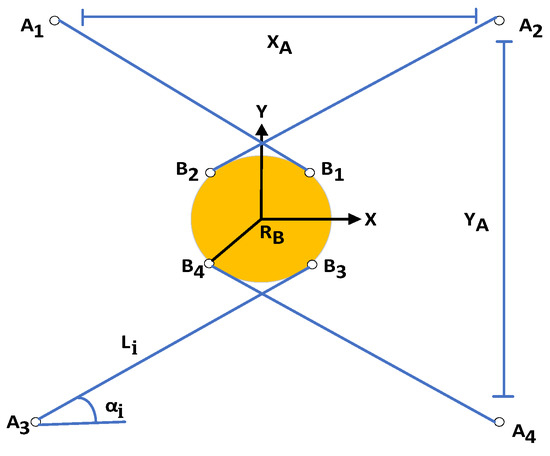
Figure 2.
The schematics of the CDPR.
According to Figure 2, the dynamic model of the cable robot can be written as the following equation [33]:
in which,
where x is the position vector of the robot, M(x) is robot mass, C(x, ) are Coriolis and centrifugal terms, G(x) is the gravity term, Fd is the viscosity friction coefficient matrix, Fs is the Columbine friction matrix, and Td is turbulence. Moreover, L2 and L1 are the cable length and the voltage cable length of vector, or an estimate is provided by solving the robot’s inverse kinematic problem; L0 is the cable length vector at x = 0 and j is the Jacobin matrix. In addition, q is the angular vector of the actuators, Im is the inertia coefficient matrix, u is the input torque vector, r is the actuator radius, and K is the cable stiffness matrix.
3. Proposed Adaptive Fuzzy Controller
In this section, an adaptive fuzzy controller is proposed to control the position of the cable-driven parallel robot and all the dynamic and kinematic terms of the robot model are uncertain. There is no information about its accuracy for their end boundaries. With this assumption, the control law is expressed as follows [34]:
where is a term of control and Kv is a symmetric definite matrix with positive diagonal elements. Let us define ur as follows:
In this equation, is the Jacobin matrix, and Q is the physical interpretation of the external force. It should be noted that, to keep the cables under the stress of the robot, external forces are used in this control structure. The term F in Equation (4) is the law of Cartesian force, and this is expressed as
in which,
where S = [S1, …, Sn]T is the sliding surface vector, є = diag(є1, …, єn) is the threshold width on the boundary layer of S, and xd is the reference signal. Λ = diag(Λ1, …, Λn) is a positive definite matrix, and Km = diag(kd1, …, kdn) is a positive-definite matrix in which is the control gain and denotes estimation of the uncertainties upper bound [29]:
where i is the diagonal element of Γ = diag(Γ1, …, Γn). Moreover, , , and in Equation (5) are estimates of the following dynamic matrices:
The above matrix is used in the analysis of the stability of the adaptive fuzzy controller.
4. Lyapunov Stability Analysis
The studies show that controlling the cable-driven robots is more challenging than controlling other robots due to the unique nature of the cables, which only need to be in tension, and the control rules cannot be directly applied to these robots. This inherent limitation not only causes worse performance but may also cause system instability; therefore, it is necessary to use a proper control method to control such robots. In this section, the Lyapunov method is used to analyze the stability of the system with the proposed adaptive fuzzy controller. According to the robot dynamic equations and control rules, the following equations can be written:
If and , , where and are in order of , the following equations can be written:
According to theorem of Tikhonov [28]:
Considering this result, the elastic system (9) and (10) can be estimated to by
If , we have:
Considering the following equations:
the following equation can be expressed:
The Lyapunov function is constructed as:
where is the upper bound of the robot uncertainties and is an estimation of . Using (18), we can write:
in which,
Applying Cartesian force control law (5):
in which,
Given the uncertainty and Rayleigh–Ritz inequality, the following limitations can be considered:
in which,
where denotes a positive definite matrix and and are the minimum of eigenvalue and maximum singular value of the matrices.
By considering Rayleigh–Ritz, Equation (23) can be rewritten as follows:
in which,
Inequality (25) can be written as:
Therefore, the proposed controller presented in this paper can stabilize the system, and the position error is ultimately uniformly limited.
5. Structure of Proposed Adaptive Fuzzy Control System
The fuzzy logic approach has been employed on various problems, such as image encryption [35], stabilization [36], tracking control [37], exoskeleton robots [38], humanoid robots [39], photo-voltaic inverters [40,41], electric vehicles [42], nonlinear estimation [43], data security [44], etc. In this paper, the adaptive control technique is improved using the fuzzy method. In fact, in this case, the coefficients of the adaptive control system are obtained by the fuzzy method, and this can help increase the accuracy and speed of the controller operation and reduce the control error. Table 1 shows the fuzzy rules for adjusting the adaptive fuzzy controller coefficient.

Table 1.
Fuzzy rules to adjust the coefficient of the adaptive controller.
Three-dimensional curves related to fuzzy rules for calculating coefficients are shown in Figure 3. The proposed controller block diagram is shown in Figure 4. The proposed control system has various parts, such as an adaptive robust controller, fast-fuzzy control, adaptation law, cable-driven parallel robot, and internal force blocks. By using the sliding surface S, the adaptation laws are used for design of the coefficient of adaptive robust controller (). The fuzzy rules of the fast-fuzzy control block are used to calculate some of the parameters of the adaptive robust controller. Finally, the adaptive robust fast-fuzzy controller is applied on the cable-driven parallel robot. By using the feedback loop, the state variables x of the cable-driven parallel robot are compared with the desired trajectories xd at each moment. In the next section, a cable robot is introduced, and the values of its related parameters are specified and simulated along with the control section in MATLAB software, the results of which are then discussed. The proposed controller structure in MATLAB/Simulink is shown in Figure 5, which demonstrates the connections between the inputs, control blocks, and outputs.
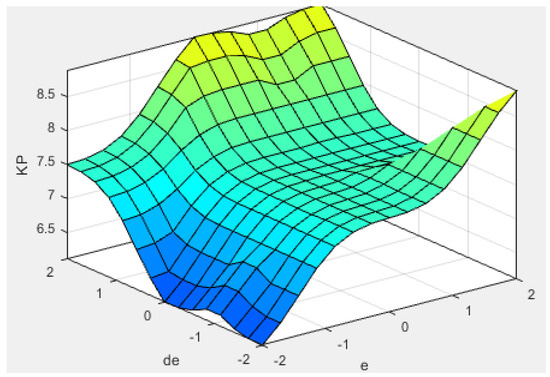
Figure 3.
Three-dimensional curves related to fuzzy rules used in research.
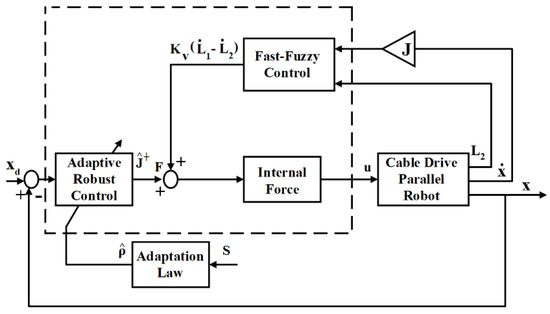
Figure 4.
Proposed controller block diagram.
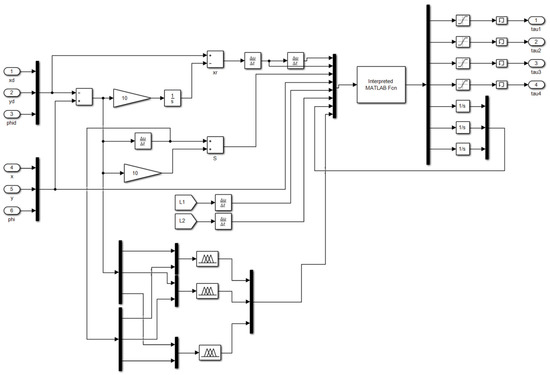
Figure 5.
Proposed controller structure in MATLAB/Simulink.
6. Simulation Results
The schematic of the robot in this paper is shown in Figure 2, and the values of the parameters in this simulation are given in Table 2. The robot used in this simulation has three degrees of freedom in the form of [x, y, φ], which are shown in Figure 2. The equations for the robot model are in accordance with Equations (1) and (2). In what follows, for two scenarios, the results of the adaptive fuzzy controller design are evaluated and compared.

Table 2.
Values of robot parameters and control section.
6.1. Case A
In Case A, the following reference trajectories are considered in the X, Y, and φ directions.
The input signals to the modeled cable robot, which are in fact the signals from the output of the designed controller, are shown in Figure 6. Figure 6 shows performance of the adaptive fuzzy controller in three directions using the proposed controller. According to Figure 7, the control system works well and follows the reference value, and the system is completely stable. The position errors are shown in Figure 8. As shown in Figure 7, the adaptive fuzzy controller can successfully track the circular trajectory with accuracy in the order of 10−3 m.
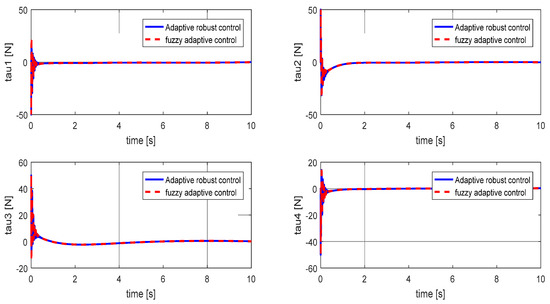
Figure 6.
Force applied to cables: Case A.
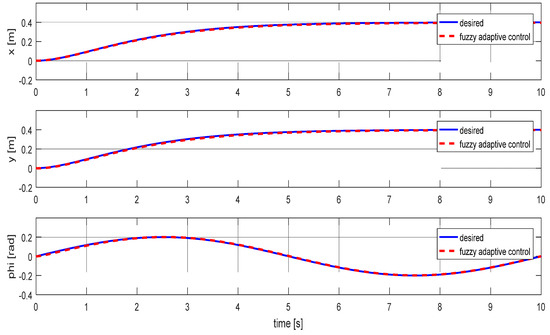
Figure 7.
Evaluate the performance of the controller in three directions: Case A.
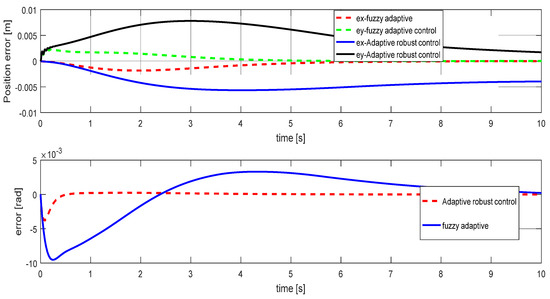
Figure 8.
Position errors of the parallel cable robot: Case A.
According to Figure 8, the error values for the situation, in which the proposed adaptive fuzzy controller is used, are much lower than the results of the other method, which indicates the high accuracy of the proposed method.
6.2. Case B
In Case B, a circular path with a radius of 0.2 m is considered to examine how the system works with the proposed controller, while the final effect always tries to maintain φ = 0. Therefore, the following reference paths are considered:
In this case, the input signals to the cable robot are modeled, and these signals, which are due to the output of the designed controller, are shown in Figure 9.
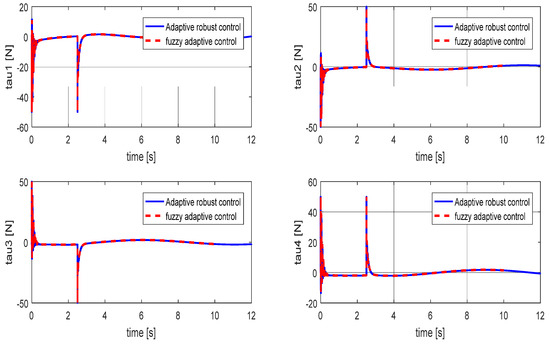
Figure 9.
Force applied to cables: Case B.
It should be noted that the input signals which enter into the modeled parallel cable robot determine the amount of tensile force of the cables, through which the cable robot is placed in the desired position. The operation of the control system is shown in Figure 10, which shows how the simulated cable robot follows the reference control signal. As shown in Figure 9, the simulated parallel cable robot using a well-designed adaptive fuzzy controller was able to follow the reference value. The system error value in this case for adaptive fuzzy controllers is shown in Figure 11.
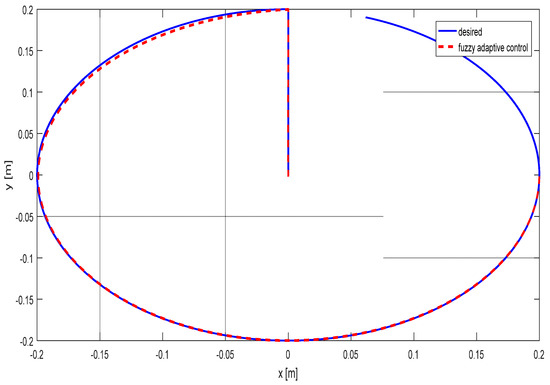
Figure 10.
Tracking of the parallel cable robot: Case B.
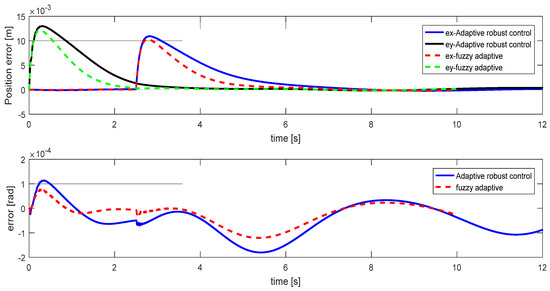
Figure 11.
Position errors of the parallel cable robot: Case B.
As can be seen, in the second case, the control error related to the fuzzy-adaptive method is low, which indicates the high accuracy of the controller designed in this paper to control the parallel cable robot. In the continuation of this section, according to the curves for the proposed adaptive fuzzy and adaptive robust controller, we made a numerical comparison between these two methods. Table 3 shows the comparison of the results obtained from the adaptive fuzzy controller with the adaptive robust controller. According to Table 3, the performance speed of the fuzzy-adaptive controller is higher than the robust controller in following the reference value, and this shows the superiority of the proposed method.

Table 3.
Comparison of results obtained from fuzzy-adaptive controller with adaptive robust controller.
7. Conclusions
In cable robots, due to the tensile strength of the cable, workspace analysis is much more complex than conventional robots. For this reason, this issue is considered to be one of the most important parts in the field of cable robots. Another challenge in the field of cable robots is the possibility of cables colliding with each other and the body of the robot, which leads to a constraint in the optimal design of the robot. In addition to the above-mentioned point, the number of cables, geometry of the robot body, and location of the cable connections should be considered during the design process. This paper designs the robot model and simulates a proposed adaptive fuzzy controller for cable-centric parallel robots. The adaptive fuzzy controller can control the complexity, lack of accurate modeling, and extreme performance specifications. Moreover, using these controllers, it is possible to control the multivariate systems much better, and, for this reason, this control method has been used to control the parallel robot in this article. The simulation results for the two scenarios studied in this paper show that the control method and structure presented in this paper work well. The simulation results show that the control signal follows the reference value well and that the control error is less than 1%, which is a very small value. In addition to the accuracy of the controller, its speed is so high that it follows the reference signal quickly and in less than a millisecond, and, through this, the parallel cable robot reaches the intended location. The results show that, in the proposed controller, the accuracy of the system performance in following the reference value as well as the controller performance speed is better than the robust method. In one of the simulation modes, the performance speed of the control system for convergence is reduced and its error is very low, which indicates the proper performance of the proposed adaptive fuzzy method. The main limitation of this research is the application of the control method for cable robots with non-stretching axes, and it is not used for other robots. The extension of the adaptive robust fuzzy control technique on the cable-driven parallel robot with time-delay and input saturation is the topic of our future research.
Author Contributions
Conceptualization, M.-T.V., K.-H.H. and F.F.M.E.-S.; formal analysis, S.M., T.R. and R.R.; funding acquisition, M.-T.V.; investigation, S.M., M.-T.V., K.-H.H. and T.R.; methodology, F.F.M.E.-S. and S.M.; writing—original draft, M.-T.V., K.-H.H. and R.R.; writing—review and editing, and supervision, S.M. and M.-T.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Chiang Mai University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest in preparing this article.
References
- Jafari, M.; Mobayen, S.; Bayat, F.; Roth, H. A Nonsingular Terminal Sliding Algorithm for Swing and Stance Control of a Prosthetic Leg Robot. Appl. Math. Model. 2022, 113, 13–29. [Google Scholar] [CrossRef]
- Vu, M.T.; Alattas, K.A.; Bouteraa, Y.; Rahmani, R.; Fekih, A.; Mobayen, S.; Assawinchaichote, W. Optimized Fuzzy Enhanced Robust Control Design for a Stewart Parallel Robot. Mathematics 2022, 10, 1917. [Google Scholar] [CrossRef]
- Mobayen, S.; Alattas, K.A.; Assawinchaichote, W. Adaptive continuous barrier function terminal sliding mode control technique for disturbed robotic manipulator. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4403–4412. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Mobayen, S.; Asad, J.H.; Vu, M.T.; Chang, A.; Puangmalai, J. Fast terminal sliding control of underactuated robotic systems based on disturbance observer with experimental validation. Mathematics 2021, 9, 1935. [Google Scholar] [CrossRef]
- Li, D.; Fu, L.; Wang, L.; Fan, W.; Li, Y. Cable-Driven Parallel Robot in the Hardware-in-the-Loop Simulation for GNC System. In Advances in Guidance, Navigation and Control; Springer: Berlin/Heidelberg, Germany, 2022; pp. 3393–3403. [Google Scholar]
- Xiong, H.; Diao, X. A review of cable-driven rehabilitation devices. Disabil. Rehabil. Assist. Technol. 2020, 15, 885–897. [Google Scholar] [CrossRef]
- Ennaiem, F.; Chaker, A.; Sandoval, J.; Bennour, S.; Mlika, A.; Romdhane, L.; Zeghloul, S.; Laribi, M.A. Cable-Driven Parallel Robot Workspace Identification and Optimal Design Based on the Upper Limb Functional Rehabilitation. J. Bionic Eng. 2022, 19, 1–13. [Google Scholar] [CrossRef]
- Schneier, M.; Schneier, M.; Bostelman, R. Literature Review of Mobile Robots for Manufacturing; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Gosselin, C. Parallel computational algorithms for the kinematics and dynamics of planar and spatial parallel manipulators. J. Dyn. Syst. Meas. Control Mar. 1996, 118, 22–28. [Google Scholar] [CrossRef]
- Martin, S.; Hillier, N. Characterisation of the Novint Falcon haptic device for application as a robot manipulator. In Proceedings of the Australasian Conference on Robotics and Automation (ACRA), Adelaide, Australia, 9–11 December 2019; pp. 291–292. [Google Scholar]
- Shen, W.; Norrie, D.H. Agent-based systems for intelligent manufacturing: A state-of-the-art survey. Knowl. Inf. Syst. 1999, 1, 129–156. [Google Scholar] [CrossRef]
- Merlet, J.-P. Wire-driven parallel robot: Open issues. In Romansy 19–Robot Design, Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–10. [Google Scholar]
- Du, J.; Bao, H.; Cui, C.; Yang, D. Dynamic analysis of cable-driven parallel manipulators with time-varying cable lengths. Finite Elem. Anal. Des. 2012, 48, 1392–1399. [Google Scholar] [CrossRef]
- Seriani, S.; Gallina, P. A storable tubular extendible member (STEM) parallel robot: Modelization and evaluation. Mech. Mach. Theory 2015, 90, 95–107. [Google Scholar] [CrossRef]
- Trevisani, A.; Gallina, P.; Williams, R.L. Cable-direct-driven robot (CDDR) with passive SCARA support: Theory and simulation. J. Intell. Robot. Syst. 2006, 46, 73–94. [Google Scholar] [CrossRef]
- Williams, R.L.; Gallina, P. Planar cable-direct-driven robots: Design for wrench exertion. J. Intell. Robot. Syst. 2002, 35, 203–219. [Google Scholar] [CrossRef]
- Williams Ii, R.L.; Gallina, P. Translational planar cable-direct-driven robots. J. Intell. Robot. Syst. 2003, 37, 69–96. [Google Scholar] [CrossRef]
- Gallina, P.; Rossi, A.; Williams, R.L. Planar Cable-Direct-Driven Robots: Part II—Dynamics and Control. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, 18–21 August 2021; pp. 1241–1247. [Google Scholar]
- Zhang, B.; Shang, W.; Cong, S.; Li, Z. Dual-Loop Dynamic Control of Cable-Driven Parallel Robots without Online Tension Distribution. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6555–6568. [Google Scholar] [CrossRef]
- Jiesinuer, A.; Shangfeng, P.; Yang, C. Research on a 3-DOF Planar Cable-Driven Parallel Robot Based on Fuzzy Adaptive PD Computed Torque Control. J. Phys. Conf. Ser. 2021, 1986, 012124. [Google Scholar] [CrossRef]
- Barhaghtalab, M.H.; Bayani, H.; Nabaei, A.; Zarrabi, H.; Amiri, A. On the design of the robust neuro-adaptive controller for cable-driven parallel robots. Automatika 2016, 57, 724–735. [Google Scholar] [CrossRef][Green Version]
- Jafarlou, F.; Peimani, M.; Lotfivand, N. Fractional order adaptive sliding-mode finite time control for cable-suspended parallel robots with unknown dynamics. Int. J. Dyn. Control 2022, 10, 1–11. [Google Scholar] [CrossRef]
- Cheng, H.H.; Lau, D. Ray-based cable and obstacle interference-free workspace for cable-driven parallel robots. Mech. Mach. Theory 2022, 172, 104782. [Google Scholar] [CrossRef]
- Jiang, X.; Barnett, E.; Gosselin, C. Periodic trajectory planning beyond the static workspace for 6-DOF cable-suspended parallel robots. IEEE Trans. Robot. 2018, 34, 1128–1140. [Google Scholar] [CrossRef]
- Gagliardini, L.; Gouttefarde, M.; Caro, S. Determination of a dynamic feasible workspace for cable-driven parallel robots. In Advances in Robot Kinematics 2016; Springer: Berlin/Heidelberg, Germany, 2018; pp. 361–370. [Google Scholar]
- Choi, H.; Piao, J.; Kim, E.-S.; Jung, J.; Choi, E.; Park, J.-O.; Kim, C.-S. Intuitive bilateral teleoperation of a cable-driven parallel robot controlled by a cable-driven parallel robot. Int. J. Control Autom. Syst. 2020, 18, 1792–1805. [Google Scholar] [CrossRef]
- Aref, M.M.; Taghirad, H.D. Geometrical workspace analysis of a cable-driven redundant parallel manipulator: KNTU CDRPM. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 1958–1963. [Google Scholar]
- Gosselin, C.M. Parallel computational algorithms for the kinematics and dynamics of parallel manipulators. In Proceedings of the [1993] IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; pp. 883–888. [Google Scholar]
- Nguyen, C.C.; Pooran, F.J. Dynamic analysis of a 6 DOF CKCM robot end-effector for dual-arm telerobot systems. Robot. Auton. Syst. 1989, 5, 377–394. [Google Scholar] [CrossRef]
- Wang, J.; Gosselin, C.M. A new approach for the dynamic analysis of parallel manipulators. Multibody Syst. Dyn. 1998, 2, 317–334. [Google Scholar] [CrossRef]
- Karbasizadeh, N.; Zarei, M.; Aflakian, A.; Masouleh, M.T.; Kalhor, A. Experimental dynamic identification and model feed-forward control of Novint Falcon haptic device. Mechatronics 2018, 51, 19–30. [Google Scholar] [CrossRef]
- Cohen, A.; Or, Y. Modeling the dynamics and control of rehabilitative exoskeleton with robotic crutches. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418761137. [Google Scholar] [CrossRef]
- Khosravi, M.A.; Taghirad, H.D. Dynamic modeling and control of parallel robots with elastic cables: Singular perturbation approach. IEEE Trans. Robot. 2014, 30, 694–704. [Google Scholar] [CrossRef]
- González, J.A.; Barreiro, A.; Dormido, S. A practical approach to adaptive sliding mode control. Int. J. Control Autom. Syst. 2019, 17, 2452–2461. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Synchronization of Delayed Fuzzy Neural Networks with Probabilistic Communication Delay and Its Application to Image Encryption. IEEE Trans. Fuzzy Syst. 2022. [Google Scholar] [CrossRef]
- Xie, X.; Yang, F.; Wan, L.; Xia, J.; Shi, K. Enhanced Local Stabilization of Constrained N-TS Fuzzy Systems With Lighter Computational Burden. IEEE Trans. Fuzzy Syst. 2022. [Google Scholar] [CrossRef]
- Shen, M.; Ma, Y.; Park, J.H.; Wang, Q.-G. Fuzzy tracking control for Markov jump systems with mismatched faults by iterative proportional-integral observers. IEEE Trans. Fuzzy Syst. 2020, 30, 542–554. [Google Scholar] [CrossRef]
- Aly, A.A.; The Vu, M.; El-Sousy, F.F.; Alotaibi, A.; Mousa, G.; Le, D.-N.; Mobayen, S. Fuzzy-Based Fixed-Time Nonsingular Tracker of Exoskeleton Robots for Disabilities Using Sliding Mode State Observer. Mathematics 2022, 10, 3147. [Google Scholar] [CrossRef]
- Cetin, O. Present Applications of Humanoid Robots and Fuzzy Control. In Toward Humanoid Robots: The Role of Fuzzy Sets; Springer: Berlin/Heidelberg, Germany, 2021; pp. 237–251. [Google Scholar]
- Stonier, A.A.; Murugesan, S.; Samikannu, R.; Krishnamoorthy, V.; Subburaj, S.K.; Chinnaraj, G.; Mani, G. Fuzzy logic control for solar PV fed modular multilevel inverter towards marine water pumping applications. IEEE Access 2021, 9, 88524–88534. [Google Scholar] [CrossRef]
- Zand, S.J.; Mobayen, S.; Gul, H.Z.; Molashahi, H.; Nasiri, M.; Fekih, A. Optimized Fuzzy Controller Based on Cuckoo Optimization Algorithm for Maximum Power-Point Tracking of Photovoltaic Systems. IEEE Access 2022, 10, 71699–71716. [Google Scholar] [CrossRef]
- Ta, M.C.; Nguyen, B.-M.; Vo-Duy, T. Fuzzy Logic Control for Motor Drive Performance Improvement in EV Applications. In Intelligent Control and Smart Energy Management; Springer: Berlin/Heidelberg, Germany, 2022; pp. 395–427. [Google Scholar]
- Sepestanaki, M.A.; Bahmani, H.; Ali, M.A.; Jalilvand, A.; Mobayen, S.; Fekih, A. Fuzzy Estimator Indirect Terminal Sliding Mode Control of Nonlinear Systems Based on Adaptive Continuous Barrier Function. IEEE Access 2022, 10, 34296–34305. [Google Scholar] [CrossRef]
- Li, J.-F.; Jahanshahi, H.; Kacar, S.; Chu, Y.-M.; Gómez-Aguilar, J.; Alotaibi, N.D.; Alharbi, K.H. On the variable-order fractional memristor oscillator: Data security applications and synchronization using a type-2 fuzzy disturbance observer-based robust control. Chaos Solitons Fractals 2021, 145, 110681. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).