On Two Outer Independent Roman Domination Related Parameters in Torus Graphs

Abstract

In a graph $G=(V,E)$, where every vertex is assigned 0, 1 or 2, f is an assignment such that every vertex assigned 0 has at least one neighbor assigned 2 and all vertices labeled by 0 are independent, then f is called an outer independent Roman dominating function (OIRDF). The domination is strengthened if every vertex is assigned 0, 1, 2 or 3, f is such an assignment that each vertex assigned 0 has at least two neighbors assigned 2 or one neighbor assigned 3, each vertex assigned 1 has at least one neighbor assigned 2 or 3, and all vertices labeled by 0 are independent, then f is called an outer independent double Roman dominating function (OIDRDF). The weight of an (OIDRDF) OIRDF f is the sum of $f\left(v\right)$ for all $v\in V$. The outer independent (double) Roman domination number (${\gamma }_{oidR}\left(G\right)$) ${\gamma }_{oiR}\left(G\right)$ is the minimum weight taken over all (OIDRDFs) OIRDFs of G. In this article, we investigate these two parameters ${\gamma }_{oiR}\left(G\right)$ and ${\gamma }_{oidR}\left(G\right)$ of regular graphs and present lower bounds on them. We improve the lower bound on ${\gamma }_{oiR}\left(G\right)$ for a regular graph presented by Ahangar et al. (2017). Furthermore, we present upper bounds on ${\gamma }_{oiR}\left(G\right)$ and ${\gamma }_{oidR}\left(G\right)$ for torus graphs. Furthermore, we determine the exact values of ${\gamma }_{oiR}(C_3\square C_n)$ and ${\gamma }_{oiR}(C_m\square C_n)$ for $m\equiv 0\left(\mathrm{mod}4\right)$ and $n\equiv 0\left(\mathrm{mod}4\right)$, and the exact value of ${\gamma }_{oidR}(C_3\square C_n)$. By our result, ${\gamma }_{oidR}(C_m\square C_n)\le 5mn/4$ which verifies the open question is correct for $C_m\square C_n$ that was presented by Ahangar et al. (2020).

1. Introduction

In graph theory, problems on vertex domination and independence are attractive research topics. There have been many achievements on this topic, and still some open problems remain that have not been completely solved in this area. In this work, we focus on two parameters which are the combinations of (double) Roman domination and vertex independence in graphs, and they are the outer independent Roman domination number and the outer independent double Roman domination number.

In this paper, $G=(V,E)$ is a finite simple connected graph with vertex set V and edge set E. $\left|V\right|$ is the order of G. For a vertex $v\in V$, $N\left(v\right)$ is the open neighborhood of v, i.e., $N\left(v\right)=\left\{w\right|w\mathrm{is}\mathrm{joined}\mathrm{to}v\}$ and ${deg}_G\left(v\right)$ is the degree of v. If both the maximum and minimum degrees are k, then G is k-regular.

Roman domination is a very famous domination on a graph introduced by Cockayne et al. [1]. In a graph $G=(V,E)$, every vertex is considered as a city that needs legion protection and every city can be assigned zero, one, or two legions, f is an assignment such that each vertex without legions must be adjacent to at least one vertex with two legions. Then, the assignment f is called a Roman dominating function (RDF) of G. The weight of an RDF f is $w\left(f\right)={\sum }_{v\in V}f\left(v\right)$. The Roman domination number is the minimum weight taken over all RDFs of G, denoted as ${\gamma }_R\left(G\right)$. Since Roman domination was proposed, many papers on Roman domination have been published and there are several variations such as weak Roman domination [2], Roman {2}-domination [3], perfect Roman domination [4], signed Roman domination [5], Roman {3}-domination (double Italian domination) [6], triple Roman domination [7], and double Roman domination [8].

Double Roman domination is a strengthened Roman domination, which can provide double the defense for less than twice the cost. In double Roman domination, every vertex can have no more than three legions, f is an assignment such that each vertex without legion must be adjacent to at least one vertex with three legions or two vertices with two legions, and each vertex with one legion must have at least one neighbor with two or three legions. Then, the assignment f is called a double Roman dominating function (DRDF) of G. The weight of a DRDF f is $w\left(f\right)={\sum }_{v\in V\left(G\right)}f\left(v\right)$. The double Roman domination number is the minimum weight of DRDFs on G, denoted as ${\gamma }_{dR}\left(G\right)$.

Ahangar et al. combined Roman domination and double Roman domination with vertex independence and introduced the outer independent Roman domination [9] and the outer independent double Roman domination [10]. A function f is an outer independent (double) Roman dominating function on G, abbreviated as (OIDRDF) OIRDF, if f is a (DRDF) RDF and the set of vertexes assigned 0 under f is independent. The outer independent (double) Roman domination number is the minimum weight of (OIDRDFs) OIRDFs on G, denoted as (${\gamma }_{oidR}\left(G\right)$) ${\gamma }_{oiR}\left(G\right)$. For an (OIDRDF) OIRDF f on G, if $w\left(f\right)=\left({\gamma }_{oidR}\left(G\right)\right){\gamma }_{oiR}\left(G\right)$, then f is called a (${\gamma }_{oidR}\left(G\right)$)${\gamma }_{oiR}\left(G\right)$-function.

After the two papers [9,10] were published, the topic attracted many researchers. Poureidi et al. [11] proposed an algorithm to compute ${\gamma }_{oiR}\left(G\right)$ in $O\left(\right|V\left|\right)$ time. Martínez et al. [12] obtained some bounds on ${\gamma }_{oiR}\left(G\right)$ in terms of other parameters. Nazari-Moghaddam et al. [13] provided a constructive characterization of trees T with ${\gamma }_{oiR}\left(T\right)={\gamma }_R\left(T\right)$. Mojdeh et al. [14] characterized a connected graph G with small ${\gamma }_{oidR}\left(G\right)$, gave lower and upper bounds on this parameter in terms of domination number $\gamma$, independence number $\alpha$, and vertex cover number $\beta$, proved the decision problem associated with ${\gamma }_{oidR}\left(G\right)$ was NP-complete, and proved $2\beta \left(T\right)+1\le {\gamma }_{oidR}\left(T\right)\le 3\beta \left(T\right)$ for a tree T. Some variations related to these two parameters have been presented and studied [15,16,17,18,19].

The purpose of this paper was to study two parameters, ${\gamma }_{oiR}\left(G\right)$ and ${\gamma }_{oidR}\left(G\right)$, of regular graphs. We improve the lower bound on ${\gamma }_{oiR}\left(G\right)$ presented by Ahangar et al. [9] and present a lower bound on ${\gamma }_{oidR}\left(G\right)$. For torus graphs (the Cartesian product of cycles) $G=C_m\square C_n$, we obtain upper bounds of ${\gamma }_{oiR}\left(G\right)$ and ${\gamma }_{oidR}\left(G\right)$ by constructing some OIRDFs and OIDRDFs. We determine the exact values of ${\gamma }_{oiR}(C_3\square C_n)$, ${\gamma }_{oiR}(C_m\square C_n)$ for $m\equiv 0\left(\mathrm{mod}4\right)$ and $n\equiv 0\left(\mathrm{mod}4\right)$ and ${\gamma }_{oidR}(C_3\square C_n)$. Ahangar et al. [10] provided an open question: Is it true that, for any graph G of order $n\ge 4$, ${\gamma }_{oidR}\left(G\right)\le 5n/4$? For the Cartesian product of cycles $C_m\square C_n$, we find ${\gamma }_{oidR}(C_m\square C_n)\le \lfloor \frac{7mn+3m+3n}{8}\rfloor <5mn/4$, which partially answers the open question.

2. The Outer Independent Roman Domination Number of Regular Graphs

2.1. The Lower Bound on ${\gamma }_{oiR}$ of Regular Graphs

For any regular graph $G=(V,E)$, f is an outer independent Roman dominating function of G. Let $V_i=\{v\in V|f\left(v\right)=i,i=0,1,2\}$, then $(V_0,V_1,V_2)$ is a partition of V induced by f. There is a one-to-one correspondence between $(V_0,V_1,V_2)$ and f, thus we also write $f=(V_0,V_1,V_2)$. Let $E_{ij}=\{\left(uv\right)\in E|u\in V_i,v\in V_j,0\le i,j\le 2\}$, obviously $E_{ij}=E_{ji}$, then $(E_{01},E_{02},E_{11},E_{12},E_{22})$ is a partition of E.

Lemma 1.

For any k-regular graph $G=(V,E)$, let $f=(V_0,V_1,V_2)$ be an outer independent Roman dominating function of G and $E_{ij}=\{\left(uv\right)\in E|u\in V_i,v\in V_j,0\le i,j\le 2\}$, then

(a) 

$k|V_0|=|E_{01}|+|E_{02}|$.

(b) 

$k|V_1|=|E_{10}|+|E_{11}|+|E_{12}|$.

(c) 

$k|V_2|=|E_{20}|+|E_{21}|+|E_{22}|$.

(d) 

$(k-1)|E_{02}|\ge |E_{01}|$.

Proof. 

Since $G=(V,E)$ is a k-regular graph, $V=V_0\cup V_1\cup V_2$ and $V_0$ is an independent set, then $\left(a\right)$, $\left(b\right)$, and $\left(c\right)$ hold.

For $\left(d\right)$, since every $v\in V_0$ has at least one neighbor which is in $V_2$ and all other neighbors are in $V_1$, then $(k-1)|E_{02}|\ge |E_{01}|$. □

Theorem 1.

For a k-regular graph G of order n, ${\gamma }_{oiR}\left(G\right)\ge \lceil \frac{(k+1)n}{2k}\rceil$.

Proof. 

Let $f=(V_0,V_1,V_2)$ be an arbitrary ${\gamma }_{oiR}\left(G\right)$-function and $E_{ij}=\{\left(uv\right)\in E\left(G\right)|u\in V_i,v\in V_j,0\le i,j\le 2\}$. By Lemma 1 $\left(b\right)$ and $\left(c\right)$,

$$|E_{10}|=k|V_1|-|E_{11}|-|E_{12}|,|E_{20}|=k|V_2|-|E_{12}|-|E_{22}|.$$

Since $|V_0|=|V|-|V_1|-|V_2|$, $E_{ij}=E_{ji}$, then by Lemma 1 $\left(a\right)$,

$$\begin{array}{ccc}\hfill & \hfill k\left(\right|V|-|V_1|-|V_2\left|\right)& =|E_{10}|+|E_{20}|\hfill \\ \Rightarrow \hfill & \hfill k\left(\right|V|-|V_1|-|V_2\left|\right)& =k|V_1|-|E_{11}|-|E_{12}|+k|V_2|-|E_{12}|-|E_{22}|\hfill \\ \Rightarrow \hfill & \hfill 2k|V_1|+2k|V_2|& =k\left|V\right|+|E_{11}|+2|E_{12}|+|E_{22}|\hfill \\ \Rightarrow \hfill & \hfill 2(k+1)\left(\right|V_1|+|V_2\left|\right)& =k\left|V\right|+2|V_1|+2|V_2|+|E_{11}|+2|E_{12}|+|E_{22}|\hfill \\ \Rightarrow \hfill & \hfill 2(k+1)\left(\right|V_1|+|V_2\left|\right)& =(k+1)\left|V\right|-|V_0|+|V_1|+|V_2|+|E_{11}|+2|E_{12}|+|E_{22}|\hfill \end{array}$$

By Lemma 1 $\left(a\right)$–$\left(c\right)$, $k\left(\right|V_1|+|V_2|-|V_0\left|\right)=|E_{11}|+2|E_{12}|+|E_{22}|$, then

$$2(k+1)\left(\right|V_1|+|V_2\left|\right)=(k+1)\left|V\right|+\frac{(k+1)\left(\right|E_{11}|+2|E_{12}|+|E_{22}\left|\right)}{k}.$$

(1)

By Lemma 1 $\left(d\right)$, $(k-1)|E_{20}|\ge |E_{10}|$, then

$$\begin{array}{ccc}\hfill & \hfill (k-1)\left(k\right|V_2|-|E_{12}|-|E_{22}\left|\right)& \ge k|V_1|-|E_{11}|-|E_{12}|\hfill \\ \Rightarrow \hfill & \hfill (k-1)k|V_2|-k|V_1|& \ge (k-1)\left(\right|E_{12}|+|E_{22}\left|\right)-|E_{11}|-|E_{12}|\hfill \end{array}$$

Then,

$$2(k-1)|V_2|-2|V_1|\ge \frac{2(k-2)|E_{12}|+2(k-1)|E_{22}|-2|E_{11}|}{k}$$

(2)

Add both sides of Equation (1) and Inequality (2),

$$2k|V_1|+4k|V_2|\ge (k+1)|V|+\frac{(k-1)|E_{11}|+2(2k-1)|E_{12}|+(3k-1)|E_{22}|}{k}$$

Since $k\ge 1$, then the last term on the right side is non-negative. Therefore,

$$2k\left(\right|V_1|+2|V_2\left|\right)\ge (k+1)\left|V\right|.$$

Thus,

$$w\left(f\right)=|V_1|+2|V_2|\ge \frac{(k+1)\left|V\right|}{2k}.$$

Since ${\gamma }_{oiR}$ is an integer, we have ${\gamma }_{oiR}\left(G\right)\ge \lceil \frac{(k+1)n}{2k}\rceil$. □

Ahangar et al. ([9]) presented ${\gamma }_{oiR}\left(G\right)\ge \lceil \frac{n}{2}\rceil +1$ for a regular graph G of order n. We improve this lower bound to $\lceil \frac{(k+1)n}{2k}\rceil$. In fact, for an arbitrary k-regular graph G, $k\ge 1$, then we have $\frac{1}{2}<\frac{k+1}{2k}\le 1$. Furthermore, since $\left|V\right(G\left)\right|=n\ge k+1$, then $\lceil \frac{(k+1)n}{2k}\rceil =\lceil \frac{n}{2}+\frac{n}{2k}\rceil \ge \lceil \frac{n}{2}+\frac{k+1}{2k}\rceil =\lceil \frac{n}{2}+1\rceil =\lceil \frac{n}{2}\rceil +1$.

2.2. Outer Independent Roman Domination in Torus Graphs

In this subsection, we investigate the outer independent Roman domination number of $C_m\square C_n$ (torus graph). We determine the exact values of ${\gamma }_{oiR}(C_m\square C_n)$ for $m\equiv 0\left(\mathrm{mod}4\right)$ and $n\equiv 0\left(\mathrm{mod}4\right)$ and the exact value of ${\gamma }_{oiR}(C_3\square C_n)$. Furthermore, we present bounds on the outer independent Roman domination number of other torus graphs.

We denote the vertex set of $C_m\square C_n$ as $V=\left\{v_{i,j}\right|0\le i\le m-1,0\le j\le n-1\}$; Figure 1a shows the graph of $C_4\square C_6$ where vertices $v_{i,0}$ are joined to $v_{i,5}$ and $v_{0,j}$ are joined to $v_{3,j}$. Figure 1b shows an OIRDF on $C_4\square C_6$.

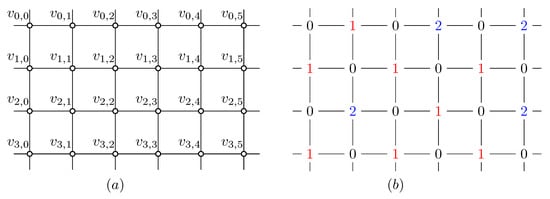
Figure 1. The graph of $C_4\square C_6$ (a) and an OIRDF on $C_4\square C_6$ (b).

To save space, thoughout this paper we use an m-by-n matrix to show the OIRDF on $C_m\square C_n$ in which entry $m_{i,j}$ is $f\left(v_{i,j}\right)$ and the following is an OIRDF f on $C_4\square C_6$,

$$\begin{array}{c}\hfill f(C_4\square C_6)=\left(\begin{array}{c}010202\\ 101010\\ 020102\\ 101010\end{array}\right).\end{array}$$

Theorem 2.

For $m\equiv 0\left(\mathrm{mod}4\right)$ and $n\equiv 0\left(\mathrm{mod}4\right)$, ${\gamma }_{oiR}(C_m\square C_n)=\frac{5mn}{8}$.

Proof. 

Let $G=C_m\square C_n$, then G is 4-regular, $k=4$, $\left|V\right|=mn$, by Theorem 1, ${\gamma }_{oiR}(C_m\square C_n)\ge \frac{5mn}{8}$. To prove $\frac{5mn}{8}$ is the upper bound, we define an OIRDF g on $C_4\square C_4$,

$$\begin{array}{c}\hfill g(C_4\square C_4)=\left(\begin{array}{c}0101\\ 1020\\ 0101\\ 2010\end{array}\right).\end{array}$$

Then, defining an OIRDF f on $C_m\square C_n$, $f\left(v_{i,j}\right)=g\left(v_{i\mathrm{mod}4,j\mathrm{mod}4}\right)$. Thus, ${\gamma }_{oiR}(C_m\square C_n)\le w\left(f\right)=\frac{m}{4}\times \frac{n}{4}\times 10=\frac{5mn}{8}$. □

Fact.${\gamma }_{oiR}(C_3\square C_3)=8$.

Theorem 3.

For any integer $n\ge 4$, ${\gamma }_{oiR}(C_3\square C_n)=\lceil \frac{7n}{3}\rceil$.

Proof. 

We define an OIRDF f on $C_3\square C_n$ as follows.

$$\begin{array}{c}\hfill \begin{array}{cccc}n\equiv 0(\mathrm{mod} 6),\hfill & & & n\equiv 1(\mathrm{mod} 6),\hfill \\ f=\left(\begin{array}{c}010102\cdots 010102\\ 102010\cdots 102010\\ 111111\cdots 111111\end{array}\right),\hfill & & & f=\left(\begin{array}{cc}010102\cdots 010102& 2\\ 102010\cdots 102010& 1\\ 111111\cdots 111111& 0\end{array}\right),\hfill \\ n\equiv 2(\mathrm{mod} 6),\hfill & & & n\equiv 3(\mathrm{mod} 6),\hfill \\ f=\left(\begin{array}{cc}010102\cdots 010102& 02\\ 102010\cdots 102010& 10\\ 111111\cdots 111111& 11\end{array}\right),\hfill & & & f=\left(\begin{array}{cc}020101\cdots 020101& 101\\ 101020\cdots 101020& 111\\ 111111\cdots 111111& 020\end{array}\right),\hfill \\ n\equiv 4(\mathrm{mod} 6),\hfill & & & n\equiv 5(\mathrm{mod} 6),\hfill \\ f=\left(\begin{array}{cc}010102\cdots 010102& 0102\\ 102010\cdots 102010& 1020\\ 111111\cdots 111111& 1111\end{array}\right),\hfill & & & f=\left(\begin{array}{cc}010102\cdots 010102& 01012\\ 102010\cdots 102010& 10201\\ 111111\cdots 111111& 11110\end{array}\right).\hfill \end{array}\end{array}$$

Then,

$$w\left(f\right)=\left\{\begin{array}{cc}14\times \frac{n}{6}=\frac{7n}{3}=\lceil \frac{7n}{3}\rceil ,\hfill & n\equiv 0(\mathrm{mod} 6),\hfill \\ 14\times \frac{n-1}{6}+3=\frac{7n+2}{3}=\lceil \frac{7n}{3}\rceil ,\hfill & n\equiv 1(\mathrm{mod} 6),\hfill \\ 14\times \frac{n-2}{6}+5=\frac{7n+1}{3}=\lceil \frac{7n}{3}\rceil ,\hfill & n\equiv 2(\mathrm{mod} 6),\hfill \\ 14\times \frac{n-3}{6}+7=\frac{7n}{3}=\lceil \frac{7n}{3}\rceil ,\hfill & n\equiv 3(\mathrm{mod} 6),\hfill \\ 14\times \frac{n-4}{6}+10=\frac{7n+2}{3}=\lceil \frac{7n}{3}\rceil ,\hfill & n\equiv 4(\mathrm{mod} 6),\hfill \\ 14\times \frac{n-5}{6}+12=\frac{7n+1}{3}=\lceil \frac{7n}{3}\rceil ,\hfill & n\equiv 5(\mathrm{mod} 6).\hfill \end{array}\right.$$

So, ${\gamma }_{oiR}(C_3\square C_n)\le \lceil \frac{7n}{3}\rceil$.

Then, we prove ${\gamma }_{oiR}(C_3\square C_n)\ge \lceil \frac{7n}{3}\rceil$. Let f be an arbitrary ${\gamma }_{oiR}(C_3\square C_n)$-function and $w\left(f_i\right)=f\left(v_{0,i}\right)+f\left(v_{1,i}\right)+f\left(v_{2,i}\right)$$(0\le i\le n-1)$. Since every vertex $v\in V(C_3\square C_n)$ with $f\left(v\right)=0$ has no neighbor assigned 0 under f, then $w\left(f_i\right)\ge 2$ for $0\le i\le n-1$.

We claim $w\left(f_{i-1}\right)+w\left(f_i\right)+w\left(f_{i+1}\right)\ge 7$ for $0\le i\le n-1$, where subscripts are taken modulo n. In fact, if $w\left(f_i\right)=2$, without loss of generality, let $f\left(v_{0,i}\right)=0$, $f\left(v_{1,i}\right)=f\left(v_{2,i}\right)=1$, then $f\left(v_{0,i-1}\right)+f\left(v_{0,i+1}\right)\ge 3$, $f\left(v_{1,i-1}\right)+f\left(v_{2,i-1}\right)\ge 1$, and $f\left(v_{1,i+1}\right)+f\left(v_{2,i+1}\right)\ge 1$. It follows that $w\left(f_{i-1}\right)+w\left(f_i\right)+w\left(f_{i+1}\right)\ge 7$. If $w\left(f_i\right)\ge 3$, by $w\left(f_{i-1}\right)\ge 2$ and $w\left(f_{i+1}\right)\ge 2$, it follows $w\left(f_{i-1}\right)+w\left(f_i\right)+w\left(f_{i+1}\right)\ge 7$.

Thus, $3w\left(f\right)=3{\sum }_{0\le i\le n-1}w\left(f_i\right)={\sum }_{0\le i\le n-1}(w\left(f_{i-1}\right)+w\left(f_i\right)+w\left(f_{i+1}\right))\ge 7n$.

Hence, ${\gamma }_{oiR}(C_3\square C_n)=w\left(f\right)\ge \lceil \frac{7n}{3}\rceil$. □

For every connected graph G of order n, ${\gamma }_{oiR}\left(G\right)\le n$ (see Ahangar et al. [9]). For torus graphs, we obtain a smaller upper bound presented by the following theorem.

Theorem 4.

For any integers $m,n\ge 4$, $m\not\equiv 0\left(\mathrm{mod}4\right)$ or $n\not\equiv 0\left(\mathrm{mod}4\right)$,

$$\lceil \frac{5mn}{8}\rceil \le {\gamma }_{oiR}(C_m\square C_n)\le \lfloor \frac{5mn+5m+5n}{8}\rfloor .$$

Proof. 

By Theorem 1, ${\gamma }_{oiR}(C_m\square C_n)\ge \lceil \frac{5mn}{8}\rceil$. Then, we define some recursive OIRDFs and obtain ${\gamma }_{oiR}(C_m\square C_n)\le \lfloor \frac{5mn+5m+5n}{8}\rfloor$.

Case 1. $m\equiv 0(\mathrm{mod} 4)$. For $n\not\equiv 0(\mathrm{mod} 4)$, we define an OIRDF f on $C_m\square C_n$ by repeating the first four rows in the OIRDF $f(C_4\square C_n)$ as m increases by 4 and $f(C_4\square C_n)$ is defined as follows.

$$\begin{array}{c}\hfill \begin{array}{cc}n\equiv 1(\mathrm{mod} 4),\hfill & n\equiv 2(\mathrm{mod} 4),\hfill \\ f(C_4\square C_n)=\left(\begin{array}{cc}0101\cdots 0101& 01011\\ 1020\cdots 1020& 10201\\ 0101\cdots 0101& 01011\\ 2010\cdots 2010& 20110\end{array}\right),\hfill & f(C_4\square C_n)=\left(\begin{array}{cc}0102\cdots 0102& 02\\ 1010\cdots 1010& 10\\ 0201\cdots 0201& 02\\ 1010\cdots 1010& 10\end{array}\right),\hfill \\ n\equiv 3(\mathrm{mod} 4),\hfill \\ f(C_4\square C_n)=\left(\begin{array}{cc}0102\cdots 0102& 012\\ 1010\cdots 1010& 101\\ 0201\cdots 0201& 021\\ 1010\cdots 1010& 101\end{array}\right).\hfill \end{array}\end{array}$$

The weight of f is

$$w\left(f\right)=\left\{\begin{array}{cc}\frac{m}{4}\times \frac{n-5}{4}\times 10+\frac{m}{4}\times 14=\frac{5mn+3m}{8},\hfill & n\equiv 1(\mathrm{mod} 4),\hfill \\ \frac{m}{4}\times \frac{n-2}{4}\times 10+\frac{m}{4}\times 6=\frac{5mn+2m}{8},\hfill & n\equiv 2(\mathrm{mod} 4),\hfill \\ \frac{m}{4}\times \frac{n-3}{4}\times 10+\frac{m}{4}\times 10=\frac{5mn+5m}{8},\hfill & n\equiv 3(\mathrm{mod} 4).\hfill \end{array}\right.$$

Case 2. $m\equiv 1(\mathrm{mod} 4)$. For $n\equiv 0,1,2,3(\mathrm{mod} 4)$, $m\ge 13$, an OIRDF f on $C_m\square C_n$ is defined by repeating the first four rows in the OIRDF $f(C_9\square C_n)$ as m increases by 4 and $f(C_9\square C_n)$ is defined as follows. An OIRDF $f(C_5\square C_n)$ is defined by deleting the first four rows of $f(C_9\square C_n)$.

$$\begin{array}{c}\hfill \begin{array}{cc}n\equiv 0(\mathrm{mod} 4),\hfill & n\equiv 1(\mathrm{mod} 4),\hfill \\ f(C_9\square C_n)=\left(\begin{array}{c}0102\cdots 0102\\ 1010\cdots 1010\\ 0201\cdots 0201\\ 1010\cdots 1010\\ 0102\cdots 0102\\ 1010\cdots 1010\\ 0201\cdots 0201\\ 1011\cdots 1011\\ 1110\cdots 1110\end{array}\right),\hfill & f(C_9\square C_n)=\left(\begin{array}{cc}1020\cdots 1020& 10201\\ 0101\cdots 0101& 01011\\ 2010\cdots 2010& 20110\\ 0101\cdots 0101& 01011\\ 1020\cdots 1020& 10201\\ 0101\cdots 0101& 01011\\ 2010\cdots 2010& 20110\\ 0111\cdots 0111& 01102\\ 1101\cdots 1101& 11010\end{array}\right),\hfill \\ n\equiv 2(\mathrm{mod} 4),\hfill & n\equiv 3(\mathrm{mod} 4),\hfill \\ f(C_9\square C_n)=\left(\begin{array}{cc}0102\cdots 0102& 02\\ 1010\cdots 1010& 10\\ 0201\cdots 0201& 02\\ 1010\cdots 1010& 10\\ 0102\cdots 0102& 02\\ 1010\cdots 1010& 10\\ 0201\cdots 0201& 02\\ 1011\cdots 1011& 10\\ 1110\cdots 1110& 11\end{array}\right),\hfill & f(C_9\square C_n)=\left(\begin{array}{cc}0102\cdots 0102& 012\\ 1010\cdots 1010& 110\\ 0201\cdots 0201& 101\\ 1010\cdots 1010& 120\\ 0102\cdots 0102& 012\\ 1010\cdots 1010& 110\\ 0201\cdots 0201& 101\\ 1011\cdots 1011& 020\\ 1110\cdots 1110& 101\end{array}\right).\hfill \end{array}\end{array}$$

Then the weight of f is

$$w\left(f\right)=\left\{\begin{array}{cc}\frac{m-5}{4}·\frac{n}{4}·10+\frac{n}{4}·14=\frac{5mn+3n}{8},\hfill & n\equiv 0(\mathrm{mod} 4),\hfill \\ \frac{(m-5)(n-5)}{16}·10+\frac{m-5}{4}·14+\frac{n-5}{4}·14+18=\frac{5mn+3m+3n-11}{8},\hfill & n\equiv 1(\mathrm{mod} 4),\hfill \\ \frac{(m-5)(n-2)}{16}·10+\frac{m-5}{4}·6+\frac{n-2}{4}·14+8=\frac{5mn+2m+3n-2}{8},\hfill & n\equiv 2(\mathrm{mod} 4),\hfill \\ \frac{(m-5)(n-3)}{16}·10+\frac{m-5}{4}·10+\frac{n-3}{4}·14+11=\frac{5mn+5m+3n-21}{8},\hfill & n\equiv 3(\mathrm{mod} 4).\hfill \end{array}\right.$$

Case 3. $m\equiv 2(\mathrm{mod} 4)$. For $n\equiv 0,1,2,3(\mathrm{mod} 4)$, an OIRDF $f(C_m\square C_n)$ is defined by repeating the first four rows of the OIRDF $f(C_6\square C_n)$ as m increases by 4.

$$\begin{array}{c}\hfill \begin{array}{cc}n\equiv 0(\mathrm{mod} 4),\hfill & n\equiv 1(\mathrm{mod} 4),\hfill \\ f(C_6\square C_n)=\left(\begin{array}{c}0102\cdots 0102\\ 1010\cdots 1010\\ 0201\cdots 0201\\ 1010\cdots 1010\\ 0102\cdots 0102\\ 1020\cdots 1020\end{array}\right),\hfill & f(C_6\square C_n)=\left(\begin{array}{cc}0101\cdots 0101& 01011\\ 1020\cdots 1020& 10201\\ 0101\cdots 0101& 01011\\ 2010\cdots 2010& 20110\\ 0101\cdots 0101& 01011\\ 2020\cdots 2020& 20201\end{array}\right),\hfill \\ n\equiv 2(\mathrm{mod} 4),\hfill & n\equiv 3(\mathrm{mod} 4),\hfill \\ f(C_6\square C_n)=\left(\begin{array}{cc}0102\cdots 0102& 010202\\ 1010\cdots 1010& 101010\\ 0201\cdots 0201& 020101\\ 1010\cdots 1010& 101020\\ 0202\cdots 0202& 020101\\ 1010\cdots 1010& 101010\end{array}\right),\hfill & f(C_6\square C_n)=\left(\begin{array}{cc}0102\cdots 0102& 0102012\\ 1010\cdots 1010& 1010110\\ 0201\cdots 0201& 0201011\\ 1010\cdots 1010& 1010201\\ 0202\cdots 0202& 0201011\\ 1010\cdots 1010& 1010110\end{array}\right).\hfill \end{array}\end{array}$$

The weight of f is

$$w\left(f\right)=\left\{\begin{array}{cc}\frac{m-2}{4}·\frac{n}{4}·10+\frac{n}{4}·6=\frac{5mn+2n}{8},\hfill & n\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-2)(n-5)}{16}·10+\frac{m-2}{4}·14+\frac{n-5}{4}·6+8=\frac{5mn+3m+2n-2}{8},\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-2)(n-2)}{16}·10+\frac{m-2}{4}·6+\frac{n-6}{4}·6+7=\frac{5mn+2m+2n-20}{8},\hfill & n\equiv 2\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-2)(n-3)}{16}·10+\frac{m-2}{4}·10+\frac{n-7}{4}·6+9=\frac{5mn+5m+2n-22}{8},\hfill & n\equiv 3\left(\mathrm{mod}4\right).\hfill \end{array}\right.$$

Case 4. $m\equiv 3\left(\mathrm{mod}4\right)$. For $n\equiv 0,1,2,3\left(\mathrm{mod}4\right)$, an OIRDF $f(C_m\square C_n)$ is defined by repeating the first four rows of the OIRDF $f(C_7\square C_n)$ as m increases by 4 and $f(C_7\square C_n)$ is defined as follows.

$$\begin{array}{c}\hfill \begin{array}{cc}n\equiv 0\left(\mathrm{mod}4\right),\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ f(C_7\square C_n)=\left(\begin{array}{c}0102\cdots 0102\\ 1010\cdots 1010\\ 0201\cdots 0201\\ 1010\cdots 1010\\ 0102\cdots 0102\\ 1020\cdots 1020\\ 1111\cdots 1111\end{array}\right),\hfill & f(C_7\square C_n)=\left(\begin{array}{cc}0101\cdots 0101& 01011\\ 1020\cdots 1020& 10201\\ 0101\cdots 0101& 01011\\ 2010\cdots 2010& 20110\\ 0111\cdots 0111& 01101\\ 1102\cdots 1102& 11020\\ 2010\cdots 2010& 20101\end{array}\right),\hfill \\ n\equiv 2\left(\mathrm{mod}4\right),\hfill & n\equiv 3\left(\mathrm{mod}4\right),\hfill \\ f(C_7\square C_n)=\left(\begin{array}{cc}0102\cdots 0102& 010202\\ 1010\cdots 1010& 101010\\ 0201\cdots 0201& 020101\\ 1010\cdots 1010& 101020\\ 0202\cdots 0202& 020101\\ 1010\cdots 1010& 101111\\ 1111\cdots 1111& 111010\end{array}\right),\hfill & f(C_7\square C_n)=\left(\begin{array}{cc}0102\cdots 0102& 102\\ 1010\cdots 1010& 110\\ 0201\cdots 0201& 102\\ 1010\cdots 1010& 110\\ 0202\cdots 0202& 011\\ 1010\cdots 1010& 101\\ 1111\cdots 1111& 020\end{array}\right).\hfill \end{array}\end{array}$$

The weight of f is

$$w\left(f\right)=\left\{\begin{array}{cc}\frac{m-3}{4}·\frac{n}{4}·10+\frac{n}{4}·10=\frac{5mn+5n}{8},\hfill & n\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-3)(n-5)}{16}·10+\frac{m-3}{4}·14+\frac{n-5}{4}·10+11=\frac{5mn+3m+5n-21}{8},\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-3)(n-2)}{16}·10+\frac{m-3}{4}·6+\frac{n-6}{4}·10+13=\frac{5mn+2m+5n-22}{8},\hfill & n\equiv 2\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-3)(n-3)}{16}·10+\frac{m-3}{4}·10+\frac{n-3}{4}·10+6=\frac{5mn+5m+5n-27}{8},\hfill & n\equiv 3\left(\mathrm{mod}4\right).\hfill \end{array}\right.$$

Hence, ${\gamma }_{oiR}(C_m\square C_n)\le \lfloor \frac{5mn+5m+5n}{8}\rfloor$. □

3. The Outer Independent Double Roman Domination Number of Regular Graphs

3.1. The Lower Bound on ${\gamma }_{oidR}$ of Regular Graphs

For any regular graph $G=(V,E)$, f is an outer independent double Roman dominating function (OIDRDF) of G. Let $V_i=\{v\in V|f\left(v\right)=i,i=0,1,2,3\}$, then $(V_0,V_1,V_2,V_3)$ is a partition of V induced by f. We also write $f=(V_0,V_1,V_2,V_3)$.

Since every vertex $v\in V_0$ must have at least two neighbors assigned 2 or one neighbor assigned 3 under f, then we write $V_0=V_{02}\cup V_{03}$, where $V_{02}=\{v\in V_0:|N\left(v\right)\cap V_3|=0\wedge |N\left(v\right)\cap V_2|\ge 2\}$ and $V_{03}=\{v\in V_0:|N\left(v\right)\cap V_3|\ge 1\}$. Since every vertex $v\in V_1$ must have at least one neighbor in $V_2\cup V_3$, then we write $V_1=V_{12}\cup V_{13}$, where $V_{12}=\{v\in V_1:|N\left(v\right)\cap V_3|=0\wedge |N\left(v\right)\cap V_2|\ge 1\}$ and $V_{13}=\{v\in V_1:|N\left(v\right)\cap V_3|\ge 1\}$. Then, we write $f=(V_0,V_1,V_2,V_3)=(V_{02}\cup V_{03},V_{12}\cup V_{13},V_2,V_3)$. Let $E_{a,b}=\{\left(uv\right)\in E\left(G\right):u\in V_a,v\in V_b\}$ where $V_a,V_b\in \{V_0,V_1,V_2,V_3,V_{02},V_{03},V_{12},V_{13}\}$ and $e_{a,b}=\left|E_{a,b}\right|$. Obviously, $e_{a,b}=e_{b,a}$ and $e_{1,2}+e_{1,3}\ge \left|V_1\right|$.

Lemma 2.

Let $f=(V_0,V_1,V_2,V_3)=(V_{02}\cup V_{03},V_{12}\cup V_{13},V_2,V_3)$ be an arbitrary OIDRDF of a k-regular graph G and $e_{a,b}$ be the cardinality of $E_{a,b}=\{\left(uv\right)\in E\left(G\right):u\in V_a,v\in V_b\mathit{where}{V}_a,V_b\in \{V_0,V_1,V_2,V_3,V_{02},V_{03},V_{12},V_{13}\}\}$, then we have

(a) 

$k|V_0|=e_{1,02}+e_{1,03}+e_{2,02}+e_{2,03}+e_{3,03}$,

$k|V_1|=e_{1,02}+e_{1,03}+e_{1,1}+e_{1,2}+e_{1,3}$,

$k|V_2|=e_{2,02}+e_{2,03}+e_{2,1}+e_{2,2}+e_{2,3}$,

$k|V_3|=e_{3,03}+e_{3,1}+e_{3,2}+e_{3,3}$.

(b) 

$e_{1,02}\le \frac{k-2}{2}{e}_{2,02}$ and $e_{1,03}\le (k-1)e_{3,03}$.

Proof. 

$\left(a\right)$ Since $k|V_0|=e_{0,1}+e_{0,2}+e_{0,3}$, $e_{0,1}=e_{02,1}+e_{03,1}$, $e_{0,2}=e_{02,2}+e_{03,2}$ and $e_{0,3}=e_{03,3}$, then

$k|V_0|=e_{02,1}+e_{03,1}+e_{02,2}+e_{03,2}+e_{03,3}=e_{1,02}+e_{1,03}+e_{2,02}+e_{2,03}+e_{3,03}$.

$k|V_1|=e_{1,0}+e_{1,1}+e_{1,2}+e_{1,3}=e_{1,02}+e_{1,03}+e_{1,1}+e_{1,2}+e_{1,3}$.

$k|V_2|=e_{2,0}+e_{2,1}+e_{2,2}+e_{2,3}=e_{2,02}+e_{2,03}+e_{2,1}+e_{2,2}+e_{2,3}$.

$k|V_3|=e_{3,0}+e_{3,1}+e_{3,2}+e_{3,3}=e_{3,03}+e_{3,1}+e_{3,2}+e_{3,3}$.

$\left(b\right)$ Since every vertex $v\in V_{02}$ has at least two neighbors in $V_2$ and other neighbors in $V_1$, then $e_{1,02}\le \frac{k-2}{2}{e}_{2,02}$. Every vertex $v\in V_{03}$ has at least one neighbor in $V_3$ and other neighbors in $V_1\cup V_2$, then $e_{1,03}\le e_{1,03}+e_{2,03}\le (k-1)e_{3,03}$. □

Theorem 5.

Let G be a k-regular graph with order of n and $k\ge 2$, then

$${\gamma }_{oidR}\left(G\right)\ge \lceil \frac{(k^2+4k-8)n}{2k^2-4}\rceil .$$

Proof. 

Let $f=(V_0,V_1,V_2,V_3)=(V_{02}\cup V_{03},V_{12}\cup V_{13},V_2,V_3)$ be a ${\gamma }_{oidR}$-function of G and $e_{a,b}$ be the cardinality of $E_{a,b}$, i.e., $e_{a,b}=\left|E_{a,b}\right|$ where $E_{a,b}=\{\left(uv\right)\in E\left(G\right):u\in V_a,v\in V_b\}$, $V_a,V_b\in \{V_0,V_1,V_2,V_3,V_{02},V_{03},V_{12},V_{13}\}$. By Lemma 2 $\left(a\right)$,

$$\begin{array}{cc}\hfill k|V_0|& =e_{1,02}+e_{1,03}+e_{2,02}+e_{2,03}+e_{3,03},\hfill \\ \hfill e_{1,02}+e_{1,03}& =k|V_1|-e_{1,1}-e_{1,2}-e_{1,3},\hfill \\ \hfill e_{2,02}+e_{2,03}& =k|V_2|-e_{2,1}-e_{2,2}-e_{2,3},\hfill \\ \hfill e_{3,03}& =k|V_3|-e_{3,1}-e_{3,2}-e_{3,3}.\hfill \end{array}$$

Since $|V_0|=|V\left(G\right)|-|V_1|-|V_2|-|V_3|$, then

$$\begin{array}{cc}\hfill & k\left(\right|V\left(G\right)|-|V_1|-|V_2|-|V_3\left|\right)\hfill \\ \hfill & =k|V_1|-e_{1,1}-e_{1,2}-e_{1,3}+k|V_2|-e_{2,1}-e_{2,2}-e_{2,3}+k\left|V_3\right|-e_{3,1}-e_{3,2}-e_{3,3}\hfill \\ \hfill & =k\left(\right|V_1|+|V_2|+|V_3\left|\right)-{\displaystyle \sum _{a=1}^3}{\displaystyle \sum _{b=1}^3}{e}_{a,b}\hfill \\ \hfill \Rightarrow & 2k\left(\right|V_1|+|V_2|+|V_3\left|\right)=k\left|V\left(G\right)\right|+{\displaystyle \sum _{a=1}^3}{\displaystyle \sum _{b=1}^3}{e}_{a,b}.\hfill \end{array}$$

Multiply both sides of the above equation by $(k^2+4k-8)/k$, we have the following equation.

$$2(k^2+4k-8)\left(\right|V_1|+|V_2|+|V_3\left|\right)=(k^2+4k-8)\left|V\left(G\right)\right|+\frac{k^2+4k-8}{k}\sum _{a=1}^3\sum _{b=1}^3{e}_{a,b}$$

(3)

By Lemma 2 $\left(a\right)$ and $\left(b\right)$,

$$\begin{array}{cc}\hfill & \frac{(k-2)}{2}{e}_{2,02}+(k-1)e_{3,03}\ge e_{1,02}+e_{1,03},\hfill \\ \hfill & e_{2,02}=k\left|V_2\right|-e_{2,03}-e_{2,1}-e_{2,2}-e_{2,3},\hfill \\ \hfill & e_{3,03}=k\left|V_3\right|-e_{3,1}-e_{3,2}-e_{3,3},\hfill \\ \hfill & e_{1,02}+e_{1,03}=k\left|V_1\right|-e_{1,1}-e_{1,2}-e_{1,3}.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill & (k-2)\left(k\right|V_2|-e_{2,03}-e_{2,1}-e_{2,2}-e_{2,3})+2(k-1)(k|V_3|-e_{3,1}-e_{3,2}-e_{3,3})\hfill \\ \hfill & \ge 2\left(k\right|V_1|-e_{1,1}-e_{1,2}-e_{1,3})\hfill \\ \hfill \Rightarrow & k(k-2)|V_2|-(k-2)(e_{2,03}+{\displaystyle \sum _{b=1}^3}{e}_{2,b})+2k(k-1)\left|V_3\right|-2(k-1){\displaystyle \sum _{b=1}^3}{e}_{3,b}\hfill \\ \hfill & \ge 2k|V_1|-2{\displaystyle \sum _{b=1}^3}{e}_{1,b}\hfill \\ \hfill \Rightarrow & k(k-2)|V_2|+2k(k-1)|V_3|-2k|V_1|\hfill \\ \hfill & \ge (k-2)(e_{2,03}+{\displaystyle \sum _{b=1}^3}{e}_{2,b})+2(k-1){\displaystyle \sum _{b=1}^3}{e}_{3,b}-2{\displaystyle \sum _{b=1}^3}{e}_{1,b}\hfill \end{array}$$

Multiply both sides of the above inequality by $2(k-2)/k$. Since $k\ge 2$, the direction of the inequality is reversed. Then, we have the following inequality.

$$\begin{array}{cc}\hfill & 2{(k-2)}^2|V_2|+4(k-2)(k-1)|V_3|-4(k-2)|V_1|\hfill \\ \hfill & \ge \frac{2(k-2)}{k}[(k-2)(e_{2,03}+{\displaystyle \sum _{b=1}^3}{e}_{2,b})+2(k-1){\displaystyle \sum _{b=1}^3}{e}_{3,b}-2{\displaystyle \sum _{b=1}^3}{e}_{1,b}]\hfill \end{array}$$

(4)

Add both sides of Equation (3) and Inequality (4),

$$\begin{array}{cc}\hfill & 2(k^2+4k-8)\left(\right|V_1|+|V_2|+|V_3\left|\right)+2{(k-2)}^2|V_2|+4(k-2)(k-1)|V_3|-4(k-2)\left|V_1\right|\hfill \\ \hfill & \ge (k^2+4k-8)\left|V\left(G\right)\right|+\frac{k^2+4k-8}{k}{\displaystyle \sum _{a=1}^3}{\displaystyle \sum _{b=1}^3}{e}_{a,b}\hfill \\ \hfill & +\frac{2(k-2)}{k}[(k-2)(e_{2,03}+{\displaystyle \sum _{b=1}^3}{e}_{2,b})+2(k-1){\displaystyle \sum _{b=1}^3}{e}_{3,b}-2{\displaystyle \sum _{b=1}^3}{e}_{1,b}]\hfill \\ \hfill \Rightarrow & (2k^2+4k-8)|V_1|+(4k^2-8)|V_2|+(6k^2-4k-8)\left|V_3\right|\hfill \\ \hfill & \ge (k^2+4k-8)\left|V\left(G\right)\right|+\frac{k^2+4k-8}{k}{\displaystyle \sum _{a=1}^3}{\displaystyle \sum _{b=1}^3}{e}_{a,b}\hfill \\ \hfill & +\frac{1}{k}[(2k^2-8k+8)(e_{2,03}+{\displaystyle \sum _{b=1}^3}{e}_{2,b})+(4k^2-12k+8){\displaystyle \sum _{b=1}^3}{e}_{3,b}-(4k-8){\displaystyle \sum _{b=1}^3}{e}_{1,b}]\hfill \end{array}$$

The left-hand side of above inequality is

$$\mathrm{LHS}=(2k^2+4k-8)|V_1|+(4k^2-8)|V_2|+(6k^2-4k-8)\left|V_3\right|.$$

The right-hand side is

$$\begin{array}{cc}\hfill \mathrm{RHS}=& (k^2+4k-8)\left|V\left(G\right)\right|\hfill \\ \hfill & +\frac{k^2+4k-8}{k}(e_{1,1}+e_{1,2}+e_{1,3}+e_{2,1}+e_{2,2}+e_{2,3}+e_{3,1}+e_{3,2}+e_{3,3})\hfill \\ \hfill & +\frac{2k^2-8k+8}{k}(e_{2,03}+e_{2,1}+e_{2,2}+e_{2,3})+\frac{4k^2-12k+8}{k}(e_{3,1}+e_{3,2}+e_{3,3})\hfill \\ \hfill & -\frac{4k-8}{k}(e_{1,1}+e_{1,2}+e_{1,3}).\hfill \end{array}$$

Since $e_{a,b}=e_{b,a}$, then

$$\begin{array}{cc}\hfill \mathrm{RHS}=& (k^2+4k-8)\left|V\left(G\right)\right|+k{e}_{1,1}+(4k-4)e_{1,2}+(6k-8)e_{1,3}\hfill \\ \hfill & +\frac{2k^2-8k+8}{k}{e}_{2,03}+(3k-4)e_{2,2}+(8k-12)e_{2,3}+(5k-8)e_{3,3}\hfill \\ \hfill =& (k^2+4k-8)\left|V\left(G\right)\right|+k{e}_{1,1}+(4k-4)(e_{2,1}+e_{3,1})+(3k-4)(e_{2,2}+e_{2,3})\hfill \\ \hfill & +(2k-4)e_{3,1}+(5k-8)(e_{3,2}+e_{3,3})+\frac{2k^2-8k+8}{k}{e}_{2,03}.\hfill \end{array}$$

Since $e_{1,2}+e_{1,3}\ge \left|V_1\right|$, then

$$\begin{array}{c}\mathrm{LHS}\ge \mathrm{RHS}\ge (k^2+4k-8)|V\left(G\right)|+k{e}_{1,1}+(4k-4)\left|V_1\right|+(3k-4)(e_{2,2}+e_{2,3})\hfill \\ +(2k-4)e_{3,1}+(5k-8)(e_{3,2}+e_{3,3})+\frac{2k^2-8k+8}{k}{e}_{2,03}.\hfill \\ \Rightarrow (2k^2-4)|V_1|+(4k^2-8)|V_2|+(6k^2-4k-8)\left|V_3\right|\hfill \\ \ge (k^2+4k-8)\left|V\left(G\right)\right|+k{e}_{1,1}+(3k-4)(e_{2,2}+e_{2,3})\hfill \\ +(2k-4)e_{3,1}+(5k-8)(e_{3,2}+e_{3,3})+\frac{2k^2-8k+8}{k}{e}_{2,03}.\hfill \\ \Rightarrow (2k^2-4)|V_1|+(4k^2-8)|V_2|+(6k^2-12)\left|V_3\right|\hfill \\ \ge (k^2+4k-8)\left|V\left(G\right)\right|+k{e}_{1,1}+(3k-4)(e_{2,2}+e_{2,3})\hfill \\ +(2k-4)e_{3,1}+(5k-8)(e_{3,2}+e_{3,3})+\frac{2k^2-8k+8}{k}{e}_{2,03}+(4k-4)\left|V_3\right|.\hfill \\ \Rightarrow (2k^2-4)\left(\right|V_1|+2|V_2|+3|V_3\left|\right)\ge (k^2+4k-8)\left|V\left(G\right)\right|.\hfill \\ \Rightarrow |V_1|+2|V_2|+3|V_3|\ge \frac{(k^2+4k-8)}{2k^2-4}\left|V\left(G\right)\right|.\hfill \end{array}$$

Since $w\left(f\right)=|V_1|+2|V_2|+3|V_3|$, then $w\left(f\right)\ge \frac{(k^2+4k-8)}{2k^2-4}\left|V\left(G\right)\right|$. Furthermore, ${\gamma }_{oidR}$ is an integer, then

$${\gamma }_{oidR}\left(G\right)\ge \lceil \frac{(k^2+4k-8)n}{2k^2-4}\rceil .$$

□

3.2. Outer Independent Double Roman Domination in Torus Graphs

In this subsection, we investigate the outer independent double Roman domination number of $C_m\square C_n$ (torus graph). We determine the exact values of ${\gamma }_{oidR}(C_3\square C_n)$ and present bounds of ${\gamma }_{oidR}(C_m\square C_n)$ for $m\ge 4$.

We denote the vertex set of $C_m\square C_n$ as $V=\left\{v_{i,j}\right|0\le i\le m-1,0\le j\le n-1\}$, and use an m-by-n matrix to show the OIDRDF on $C_m\square C_n$ in which entry $m_{i,j}$ is $f\left(v_{i,j}\right)$ and the following is an OIDRDF f on $C_3\square C_4$,

$$\begin{array}{c}\hfill f(C_3\square C_4)=\left(\begin{array}{c}0202\\ 1020\\ 2111\end{array}\right).\end{array}$$

Theorem 6.

For any integer $n\ge 3$, ${\gamma }_{oidR}(C_3\square C_n)=3n$.

Proof. 

We define an OIDRDF f on $C_3\square C_3$ by: $f\left(v_{0,2}\right)=f\left(v_{1,1}\right)=f\left(v_{2,0}\right)=2$, $f\left(v_{0,1}\right)=f\left(v_{1,0}\right)=f\left(v_{2,2}\right)=1$ and $f\left(v_{0,0}\right)=f\left(v_{1,2}\right)=f\left(v_{2,1}\right)=0$. For $n\ge 4$, define an OIDRDF f as follows.

$$\begin{array}{c}\hfill \begin{array}{cccc}n\equiv 0\left(\mathrm{mod}4\right),\hfill & & & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ f=\left(\begin{array}{c}0202\cdots 0202\\ 1020\cdots 1020\\ 2111\cdots 2111\end{array}\right),\hfill & & & f=\left(\begin{array}{cc}0202\cdots 0202& 02012\\ 1020\cdots 1020& 10201\\ 2111\cdots 2111& 21120\end{array}\right),\hfill \\ n\equiv 2\left(\mathrm{mod}4\right),\hfill & & & n\equiv 3\left(\mathrm{mod}4\right),\hfill \\ f=\left(\begin{array}{cc}0202\cdots 0202& 02\\ 1020\cdots 1020& 11\\ 2111\cdots 2111& 20\end{array}\right),\hfill & & & f=\left(\begin{array}{cc}0202\cdots 0202& 0201022\\ 1020\cdots 1020& 1020201\\ 2111\cdots 2111& 2112110\end{array}\right).\hfill \end{array}\end{array}$$

Then,

$$w\left(f\right)=\left\{\begin{array}{cc}12\times \frac{n}{4}=3n,\hfill & n\equiv 0\left(\mathrm{mod}4\right),\hfill \\ 12\times \frac{n-5}{4}+15=3n,\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ 12\times \frac{n-2}{4}+6=3n,\hfill & n\equiv 2\left(\mathrm{mod}4\right),\hfill \\ 12\times \frac{n-7}{4}+21=3n,\hfill & n\equiv 3\left(\mathrm{mod}4\right),n\ge 7.\hfill \end{array}\right.$$

Thus, ${\gamma }_{oidR}(C_3\square C_n)\le 3n$.

Next we prove ${\gamma }_{oidR}(C_3\square C_n)\ge 3n$. Let f be an arbitrary ${\gamma }_{oidR}(C_3\square C_n)$-function, $V_i=\{v_{0,i},v_{1,i},v_{2,i}\}$ and $w\left(f_i\right)=f\left(v_{0,i}\right)+f\left(v_{1,i}\right)+f\left(v_{2,i}\right)$$(0\le i\le n-1)$, then f has the properties:

(1) $w\left(f_i\right)\ge 2$. Since every vertex $v\in V(C_3\square C_n)$ with $f\left(v\right)=0$ has no neighbor assigned 0 under f, then $w\left(f_i\right)\ge 2$ for $0\le i\le n-1$.

(2) If $w\left(f_i\right)=2$, then $w\left(f_{i-1}\right)+w\left(f_{i+1}\right)\ge 8$ where subscripts are taken modulo n. If $w\left(f_i\right)=2$, by symmetry, let $f\left(v_{0,i}\right)=f\left(v_{1,i}\right)=1$ and $f\left(v_{2,i}\right)=0$. Then, by the definition of OIDRDF, $f\left(v_{0,i-1}\right)+f\left(v_{0,i+1}\right)\ge 2$, $f\left(v_{1,i-1}\right)+f\left(v_{1,i+1}\right)\ge 2$, and $f\left(v_{2,i-1}\right)+f\left(v_{2,i+1}\right)\ge 4$, it follows $w\left(f_{i-1}\right)+w\left(f_{i+1}\right)\ge 8$.

For $0\le i\le n-1$, we put the columns $V_i$ into different sets $B_s$$(0\le s\le t)$.

Initialization: $t=0$ and $D\left[i\right]=0$ for $i=0$ up to $n-1$.

S1. For i from 0 to $n-1$ with $w\left(f_i\right)\ge 5$ and $D\left[i\right]=0$, do:

$t=t+1$, $D\left[i\right]=1$, $B_t=\left\{V_j\right\}$.

If $w\left(f_{i+1}\right)=2$ and $D[i+1]=0$, then $D[i+1]=1$, $B_t=B_t\cup \left\{V_{i+1}\right\}$.

If $w\left(f_{i-1}\right)=2$ and $D[i-1]=0$, then $D[i-1]=1$, $B_t=B_t\cup \left\{V_{i-1}\right\}$.

S2. For i from 0 to $n-1$ with $w\left(f_i\right)=4$ and $D\left[i\right]=0$, do:

$t=t+1$, $D\left[i\right]=1$, $B_t=\left\{V_i\right\}$.

If $w\left(f_{i+1}\right)=2$, then $D[i+1]=1$, $B_t=B_t\cup \left\{V_{i+1}\right\}$.

By (2), if $w\left(f_i\right)=2$, then $w\left(f_{i-1}\right)\ge 4$ or $w\left(f_{i+1}\right)\ge 4$. Therefore $w\left(f_i\right)=3$ for all

$D\left[i\right]=0$ after S1 and S2.

S3. For i from 0 to $n-1$ with $w\left(f_i\right)=3$ and $D\left[i\right]=0$, do:

$t=t+1$, $D\left[i\right]=1$, $B_t=\left\{V_i\right\}$.

Notice that ${\sum }_{V_i\in B_t}w\left(f_i\right)\ge 3\times \left|B_t\right|$.

Thus, we have

$$\begin{array}{c}w\left(f\right)={\displaystyle \sum _{0\le i\le n-1}}w\left(f_i\right)={\displaystyle \sum _{1\le s\le t}}{\displaystyle \sum _{V_i\in B_s}}w\left(f_i\right)\ge {\displaystyle \sum _{1\le s\le t}}3\left|B_s\right|=3n.\hfill \end{array}$$

Hence, ${\gamma }_{oidR}(C_3\square C_n)\ge 3n$. □

Ahangar et al. [10] proved ${\gamma }_{oidR}\left(T\right)\le 5n/4$ for tree T of order n and provided an open problem: “Is it true that, for any graph G on $n\ge 4$ vertices, ${\gamma }_{oidR}\left(G\right)\le 5n/4$?” We say this is true for the Cartesian product of cycles $C_m\square C_n$, since we obtain ${\gamma }_{oidR}(C_m\square C_n)\le \lfloor \frac{7mn+3m+3n}{8}\rfloor$ by constructing some OIDRDFs described in the following theorem.

Theorem 7.

For any integers $m,n\ge 4$,

$$\lceil \frac{6mn}{7}\rceil \le {\gamma }_{oidR}(C_m\square C_n)\le \lfloor \frac{7mn+3m+3n}{8}\rfloor .$$

Proof. 

By Theorem 5, ${\gamma }_{oidR}(C_m\square C_n)\ge \lceil \frac{6mn}{7}\rceil$. Then, we define some recursive OIDRDFs and obtain ${\gamma }_{oidR}(C_m\square C_n)\le \lfloor \frac{7mn+3m+3n}{8}\rfloor$.

Case 1. $m\equiv 0\left(\mathrm{mod}4\right)$. For $n\equiv 0,1,2,3\left(\mathrm{mod}4\right)$, we define an OIDRDF $f(C_m\square C_n)$ by repeating the first four rows in $f(C_4\square C_n)$ as m increases by 4.

$$\begin{array}{c}\hfill \begin{array}{cc}n\equiv 0\left(\mathrm{mod}4\right),\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ f(C_4\square C_n)=\left(\begin{array}{c}0202\cdots 0202\\ 1020\cdots 1020\\ 2101\cdots 2101\\ 1020\cdots 1020\end{array}\right),\hfill & f(C_4\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 02012\\ 1020\cdots 1020& 10201\\ 2101\cdots 2101& 21020\\ 1020\cdots 1020& 10201\end{array}\right),\hfill \\ n\equiv 2\left(\mathrm{mod}4\right),\hfill & n\equiv 3\left(\mathrm{mod}4\right),\hfill \\ f(C_4\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 02\\ 1020\cdots 1020& 10\\ 2101\cdots 2101& 22\\ 1020\cdots 1020& 10\end{array}\right),\hfill & f(C_4\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 022\\ 1020\cdots 1020& 101\\ 2101\cdots 2101& 220\\ 1020\cdots 1020& 101\end{array}\right).\hfill \end{array}\end{array}$$

The weight of f is

$$w\left(f\right)=\left\{\begin{array}{cc}\frac{m}{4}·\frac{n}{4}·14=\frac{7mn}{8},\hfill & n\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{m}{4}·\frac{n-5}{4}·14+\frac{m}{4}\times 18=\frac{7mn+m}{8},\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{m}{4}·\frac{n-2}{4}·14+\frac{m}{4}\times 8=\frac{7mn+2m}{8},\hfill & n\equiv 2\left(\mathrm{mod}4\right),\hfill \\ \frac{m}{4}·\frac{n-3}{4}·14+\frac{m}{4}\times 12=\frac{7mn+3m}{8},\hfill & n\equiv 3\left(\mathrm{mod}4\right).\hfill \end{array}\right.$$

Case 2. $m\equiv 1\left(\mathrm{mod}4\right)$. For $n\equiv 0,1,2,3\left(\mathrm{mod}4\right)$ and $m\ge 13$, an OIDRDF is defined by repeating the first four rows in $f(C_9\square C_n)$ as m increases by 4. For $f(C_5\square C_n)$ is defined by deleting the first four rows in $f(C_9\square C_n)$.

$$\begin{array}{c}\hfill \begin{array}{cc}n\equiv 0\left(\mathrm{mod}4\right),\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ f(C_9\square C_n)=\left(\begin{array}{c}0202\cdots 0202\\ 1020\cdots 1020\\ 2101\cdots 2101\\ 1020\cdots 1020\\ 0202\cdots 0202\\ 1020\cdots 1020\\ 2101\cdots 2101\\ 0121\cdots 0121\\ 2010\cdots 2010\end{array}\right),\hfill & f(C_9\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 02012\\ 1020\cdots 1020& 10201\\ 2101\cdots 2101& 21020\\ 1020\cdots 1020& 10201\\ 0202\cdots 0202& 02012\\ 1020\cdots 1020& 10201\\ 2101\cdots 2101& 21020\\ 0121\cdots 0121& 01201\\ 2010\cdots 2010& 20112\end{array}\right),\hfill \\ n\equiv 2\left(\mathrm{mod}4\right),\hfill & n\equiv 3\left(\mathrm{mod}4\right),\hfill \\ f(C_9\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 02\\ 1020\cdots 1020& 10\\ 2101\cdots 2101& 22\\ 1020\cdots 1020& 10\\ 0202\cdots 0202& 02\\ 1020\cdots 1020& 10\\ 2101\cdots 2101& 22\\ 0121\cdots 0121& 01\\ 2010\cdots 2010& 20\end{array}\right),\hfill & f(C_9\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 102\\ 1020\cdots 1020& 120\\ 2101\cdots 2101& 201\\ 1020\cdots 1020& 120\\ 0202\cdots 0202& 102\\ 1020\cdots 1020& 120\\ 2101\cdots 2101& 201\\ 0121\cdots 0121& 012\\ 2010\cdots 2010& 210\end{array}\right).\hfill \end{array}\end{array}$$

Then, the weight of f is

$$w\left(f\right)=\left\{\begin{array}{cc}\frac{m-5}{4}·\frac{n}{4}·14+\frac{n}{4}·18=\frac{7mn+n}{8},\hfill & n\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-5)(n-5)}{16}·14+\frac{n-5}{4}·18+\frac{m-5}{4}·18+24=\frac{7mn+m+n+7}{8},\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-5)(n-2)}{16}·14+\frac{n-2}{4}·18+\frac{m-5}{4}·8+10=\frac{7mn+2m+n-2}{8},\hfill & n\equiv 2\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-5)(n-3)}{16}·14+\frac{n-3}{4}·18+\frac{m-5}{4}·12+15=\frac{7mn+3m+n-3}{8},\hfill & n\equiv 3\left(\mathrm{mod}4\right).\hfill \end{array}\right.$$

Case 3. $m\equiv 2\left(\mathrm{mod}4\right)$. For $n\equiv 0,1,2,3\left(\mathrm{mod}4\right)$, an OIDRDF f on $C_m\square C_n$ is defined by repeating the first four rows of $f(C_6\square C_n)$ as m increases by 4.

$$\begin{array}{c}\hfill \begin{array}{cc}n\equiv 0\left(\mathrm{mod}4\right),\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ f(C_6\square C_n)=\left(\begin{array}{c}0202\cdots 0202\\ 1020\cdots 1020\\ 2101\cdots 2101\\ 1020\cdots 1020\\ 0202\cdots 0202\\ 1012\cdots 1012\end{array}\right),\hfill & f(C_6\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 02012\\ 1020\cdots 1020& 10201\\ 2101\cdots 2101& 21020\\ 1020\cdots 1020& 10201\\ 0202\cdots 0202& 02012\\ 2020\cdots 2020& 20210\end{array}\right),\hfill \\ n\equiv 2\left(\mathrm{mod}4\right),\hfill & n\equiv 3\left(\mathrm{mod}4\right),\hfill \\ f(C_6\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 02\\ 1020\cdots 1020& 10\\ 2101\cdots 2101& 22\\ 1020\cdots 1020& 10\\ 0202\cdots 0202& 02\\ 2020\cdots 2020& 20\end{array}\right),\hfill & f(C_6\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 102\\ 1020\cdots 1020& 120\\ 2101\cdots 2101& 201\\ 1020\cdots 1020& 120\\ 0202\cdots 0202& 102\\ 1210\cdots 1210& 120\end{array}\right).\hfill \end{array}\end{array}$$

The weight of f is

$$w\left(f\right)=\left\{\begin{array}{cc}\frac{m-2}{4}·\frac{n}{4}·14+\frac{n}{4}·8=\frac{7mn+2n}{8},\hfill & n\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-2)(n-5)}{16}·14+\frac{n-5}{4}·8+\frac{m-2}{4}·18+10=\frac{7mn+m+2n-2}{8},\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-2)(n-2)}{16}·14+\frac{n-2}{4}·8+\frac{m-2}{4}·8+4=\frac{7mn+2m+2n-4}{8},\hfill & n\equiv 2\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-2)(n-3)}{16}·14+\frac{n-3}{4}·8+\frac{m-2}{4}·12+6=\frac{7mn+3m+2n-6}{8},\hfill & n\equiv 3\left(\mathrm{mod}4\right).\hfill \end{array}\right.$$

Case 4. $m\equiv 3\left(\mathrm{mod}4\right)$. For $n\equiv 0,1,2,3\left(\mathrm{mod}4\right)$, an OIDRDF f on $C_m\square C_n$ is defined by repeating the first four rows of the OIDRDF $f(C_7\square C_n)$ as m increases by 4.

$$\begin{array}{c}\hfill \begin{array}{cc}n\equiv 0\left(\mathrm{mod}4\right),\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ f(C_7\square C_n)=\left(\begin{array}{c}0202\cdots 0202\\ 1020\cdots 1020\\ 2101\cdots 2101\\ 1020\cdots 1020\\ 0202\cdots 0202\\ 1020\cdots 1020\\ 2111\cdots 2111\end{array}\right),\hfill & f(C_7\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 02012\\ 1020\cdots 1020& 10201\\ 2101\cdots 2101& 21020\\ 1020\cdots 1020& 10201\\ 0202\cdots 0202& 02012\\ 1020\cdots 1020& 10201\\ 2111\cdots 2111& 21120\end{array}\right),\hfill \\ n\equiv 2\left(\mathrm{mod}4\right),\hfill & n\equiv 3\left(\mathrm{mod}4\right),\hfill \\ f(C_7\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 02\\ 1020\cdots 1020& 11\\ 2101\cdots 2101& 20\\ 1020\cdots 1020& 11\\ 0202\cdots 0202& 02\\ 1020\cdots 1020& 11\\ 2111\cdots 2111& 20\end{array}\right),\hfill & f(C_7\square C_n)=\left(\begin{array}{cc}0202\cdots 0202& 0201022\\ 1020\cdots 1020& 1020201\\ 2101\cdots 2101& 2101020\\ 1020\cdots 1020& 1022101\\ 0202\cdots 0202& 0201022\\ 1020\cdots 1020& 1020201\\ 2111\cdots 2111& 2112110\end{array}\right).\hfill \end{array}\end{array}$$

The weight of f is

$$w\left(f\right)=\left\{\begin{array}{cc}\frac{m-3}{4}·\frac{n}{4}·14+\frac{n}{4}·12=\frac{7mn+3n}{8},\hfill & n\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-3)(n-5)}{16}·14+\frac{n-5}{4}·12+\frac{m-3}{4}·18+15=\frac{7mn+m+3n-3}{8},\hfill & n\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-3)(n-2)}{16}·14+\frac{n-2}{4}·12+\frac{m-3}{4}·8+6=\frac{7mn+2m+3n-6}{8},\hfill & n\equiv 2\left(\mathrm{mod}4\right),\hfill \\ \frac{(m-3)(n-7)}{16}·14+\frac{n-7}{4}·12+\frac{m-3}{4}·26+21=\frac{7mn+3m+3n-9}{8},\hfill & n\equiv 3\left(\mathrm{mod}4\right).\hfill \end{array}\right.$$

Hence, ${\gamma }_{oidR}(C_m\square C_n)\le \lfloor \frac{7mn+3m+3n}{8}\rfloor$. □

4. Conclusions

For the outer independent Roman domination number of regular graph G, we improved the lower bound on ${\gamma }_{oiR}\left(G\right)$ presented by Ahangar et al. ([9]), determined the exact values of ${\gamma }_{oiR}(C_3\square C_n)$, ${\gamma }_{oiR}(C_m\square C_n)$ for $m\equiv 0\left(\mathrm{mod}4\right)$ and $n\equiv 0\left(\mathrm{mod}4\right)$, and presented bounds on ${\gamma }_{oiR}(C_m\square C_n)$ for $m\not\equiv 0\left(\mathrm{mod}4\right)$ or $n\not\equiv 0\left(\mathrm{mod}4\right)$. For the outer independent double Roman domination number of regular graph G, we presented a lower bound on ${\gamma }_{oidR}\left(G\right)$, determined the exact values of ${\gamma }_{oidR}(C_3\square C_n)$, and presented bounds on ${\gamma }_{oidR}(C_m\square C_n)$ for $m,n\ge 4$. By our results, ${\gamma }_{oidR}(C_m\square C_n)\le \lfloor \frac{7mn+3m+3n}{8}\rfloor$, which verifies ${\gamma }_{oidR}\left(G\right)\le 5\left|V\left(G\right)\right|/4$ is correct for $G=C_m\square C_n$.