Using a Separable Mathematical Entropy to Construct Entropy-Stable Schemes for a Reduced Blood Flow Model

Abstract

The aim of this paper is to derive a separable entropy for a one-dimensional reduced blood flow model, which will be used to treat the symmetrizability of the model in full generality and for constructing entropy conservative fluxes, which are one of the essential building blocks of designing entropy-stable schemes. Time discretization is conducted by implicit–explicit (IMEX) Runge–Kutta schemes, but solutions for nonlinear systems will not be required due to the particular form of the source term. To validate the numerical schemes obtained, some numerical tests are presented.

1. Introduction

This paper is concerned with a well-known reduced blood flow model described by a nonlinear hyperbolic system of conservation laws in one space dimension [1], which is used to model the flow of blood in axisymmetric vessels with compliant walls. The governing equations in terms of the vessel cross-sectional area $A(x,t)$ and the mean blood velocity $U(x,t)$ in the axial direction x are given by

$$\left\{\begin{array}{c}{A}_t+{\left(AU\right)}_x=0\hfill \\ U_t+{\left({\displaystyle \frac{U^2}{2}}+{\displaystyle \frac{P}{\rho }}\right)}_x=-C_f{\displaystyle \frac{U}{A}}\hfill \end{array}\right.$$

(1)

where $\rho$ is the blood density, assumed to be constant for blood, which is essentially incompressible, $C_f$ is the skin friction coefficient and $P=P\left(A\right)$ is the internal pressure, which is taken here as (see, for instance, [2])

$$P=P_0+\beta (\sqrt{A}-\sqrt{A_0}).$$

(2)

Here $A_0$ is the vessel cross-sectional at rest and $P_0$ is the pressure when $A=A_0$. Hereafter, it is assumed that $\beta$ and $A_0$ are constants, but in reality, they may depend on x in the case of some pathologies.

The system of Equation (1) is known as the $(A,U)$-system. The velocity U is not a conservative quantity, in contrast to $Q=AU$ within the so-called $(A,Q)$-system (see [3] for a complete discussion). For continuous solutions, the two formulations are equivalent. However, we will restrict our attention to the $(A,U)$-system, which can be written in the vector form as

$${\mathit{u}}_t+\mathit{f}{\left(\mathit{u}\right)}_x=\mathit{s}\left(\mathit{u}\right),$$

(3)

where

$$\mathit{u}=\left. [\begin{array}{c}A\\ U\end{array}\right],\mathit{f}\left(\mathit{u}\right)=\left. [\begin{array}{c}AU\\ {\displaystyle \frac{U^2}{2}}+{\displaystyle \frac{P}{\rho }}\end{array}\right]\mathrm{and}\mathit{s}\left(\mathit{u}\right)=\left. [\begin{array}{c}0\\ -C_f{\displaystyle \frac{U}{A}}\end{array}\right]$$

(4)

and the corresponding quasilinear form is

$${\mathit{u}}_t+H\left(\mathit{u}\right){\mathit{u}}_x=\mathit{s}\left(\mathit{u}\right),$$

(5)

where

$$H\left(\mathit{u}\right)=\left. [\begin{array}{cc}U& A\\ c^2/A& U\end{array}\right]$$

is the Jacobian of the flux function $\mathit{f}$. Here $c=c\left(A\right)$ is the Moens–Korteweg wave speed and corresponds to the speed of pulse waves in an artery:

$$c={\left(\frac{\beta \sqrt{A}}{2\rho }\right)}^{1/2}.$$

(6)

The Jacobian matrix H has two real eigenvalues, namely ${\lambda }_1=U-c$ and ${\lambda }_2=U+c$ with corresponding right eigenvectors

$${\mathit{r}}_1=\left. [\begin{array}{c}-1\\ c/A\end{array}\right]\mathrm{and}{\mathit{r}}_2=\left. [\begin{array}{c}1\\ c/A\end{array}\right].$$

(7)

Let us define the Shapiro number $S_h$ as [4]

$$S_h=\frac{U}{c}.$$

(8)

The quantity $S_h$ is the analog of the Froude number for the shallow water equations. A state $\mathit{u}$ is said to be subcritical if $S_h<1$, critical if $S_h=1$, and supercritical if $S_h>1$. The system is strictly hyperbolic in subcritical and supercritical regimes. In physiological conditions, blood flow is almost always subcritical. Nevertheless, very specific pathologies may lead to supercritical flows [5].

One-dimensional models are notably recognized to be computationally inexpensive in comparison with 3D models. In addition, 1D models are not suitable for describing blood flow in complicated morphological regions, and they can be coupled with 3D models to obtain a considerable reduction in the computational complexity [6].

The system (1) without friction, that is, with $C_f=0$, admits the following steady-state solution, known as the (non-zero pressure) man-at-eternal-rest steady state or dead-man equilibrium [3] (by analogy to the lake at rest in the shallow water equations):

$$\begin{array}{c}\hfill U=0\mathrm{and}\sqrt{A}-\sqrt{A_0}=\mathrm{constant}.\end{array}$$

(9)

In particular, the (zero pressure) man-at-eternal-rest steady state is given by

$$\begin{array}{c}\hfill U=0\mathrm{and}A=A_0.\end{array}$$

(10)

Let us also recall that a convex scalar function $\eta =\eta \left(\mathit{u}\right)$ is the entropy for the system of conservation laws

$${\mathit{u}}_t+\mathit{f}{\left(\mathit{u}\right)}_x=0,$$

(11)

with associated entropy flux $G=G\left(\mathit{u}\right)$ if

$${\nabla }_{\mathit{u}}G\left(\mathit{u}\right)={\mathit{v}}^{\mathrm{T}}H\left(\mathit{u}\right),$$

(12)

where

$$\mathit{v}={\nabla }_{\mathit{u}}\eta \left(\mathit{u}\right)$$

is the vector of entropy variables. $(\eta ,G)$ is called an entropy pair for the conservation law (11). When $\eta$ is strictly convex, the entropy variables $\mathit{v}$ symmetrize the system (11) by making the change of variables $\mathit{u}=\mathit{u}\left(\mathit{v}\right)$ [7], which puts the system into its equivalent symmetric form

$$\mathit{u}{\left(\mathit{v}\right)}_t+\mathit{g}{\left(\mathit{v}\right)}_x=0,\mathit{g}\left(\mathit{v}\right):=\mathit{f}\left(\mathit{u}\left(\mathit{v}\right)\right).$$

(13)

Note that the Jacobian of $\mathit{g}\left(\mathit{v}\right)$ is the Hessian of the function

$$\psi \left(\mathit{v}\right):={\mathit{v}}^{\mathrm{T}}\mathit{f}\left(\mathit{u}\left(\mathit{v}\right)\right)-G\left(\mathit{u}\left(\mathit{v}\right)\right).$$

(14)

The function $\psi$ is called entropy potential and plays an important role in the construction of entropy conservative fluxes.

In Reference [6], an entropy pair for the inviscid $(A,U)$ system (1) was derived, namely

$$\eta =\frac{1}{2}\rho A{U}^2+\frac{2\beta A^{3/2}}{3\rho },G=\frac{1}{2}A{U}^3+\frac{\beta U{A}^{3/2}}{\rho }.$$

(15)

This entropy pair was used in [8] for constructing a well-balanced and entropy-stable scheme for the inviscid $(A,U)$-system but with $A_0$ depending on x.

The remainder of the paper is organized as follows: in Section 2, a separable entropy pair for the inviscid model (1) is derived and then employed to prove the symmetrizability of the last-mentioned model. In Section 3, another application of the last-mentioned entropy pair is obtained, namely, the construction of entropy conservative fluxes, which in turn, are used to obtain entropy-stable schemes by adding numerical diffusion [9]. After dealing with spatial discretization, we end this section with the treatment of the friction source term by using IMEX schemes. In Section 4, the obtained numerical schemes are validated with some benchmark tests taken from the literature. At last, some conclusions are drawn in Section 5.

2. Theoretical Results

Entropy Pair and Simmetrizability

It is well-known (see [10]) that symmetrizability is equivalent to the existence of a convex entropy function. Using the entropy given by (15), a result on the symmetrizability of the inviscid form of the system (1) was conducted in [11] to the subcritical case, that is, under the assumption $U(x,t)<c\left(A\right(x,t\left)\right)$ for $(x,t)\in [0,L]\times [0,T]$. We next follow the idea used in [12] to construct a separable entropy function for the inviscid $(A,U)$ system, which allows us to obtain symmetrizability without the aforementioned assumption.

If $\eta \left(\mathit{u}\right)$ is an additively separable function, that is, $\eta \left(\mathit{u}\right)=e_1\left(A\right)+e_2\left(U\right)$, then the Hessian matrix of $\eta$, denoted by ${\eta }_{\mathit{u}\mathit{u}}\left(\mathit{u}\right)$, is a diagonal matrix. Now, it is fairly easy to see that ${\eta }_{\mathit{u}\mathit{u}}\left(\mathit{u}\right)H\left(\mathit{u}\right)$ is symmetric if

$$e_1^{″}\left(A\right)=e_2^{″}\frac{P^{\prime }\left(A\right)}{\rho }.$$

Thus, $e_1\left(A\right)=-2\beta \sqrt{A}$ and $e_2\left(U\right)=\rho U^2/2$. Accordingly,

$$\eta \left(\mathit{u}\right)=\frac{\rho U^2}{2}-2\beta \sqrt{A}$$

(16)

is an entropy function for the inviscid $(A,U)$ system, and the associated entropy flux is

$$G\left(\mathit{u}\right)=\frac{\rho U^3}{3}-\beta U\sqrt{A}.$$

(17)

From the entropy pair (16) and (17), we obtain the entropy potential

$$\psi \left(\mathit{u}\right)=\frac{\rho U^3}{6}+UP\left(A\right).$$

(18)

Next, we use the entropy function given above to demonstrate the symmetrizability of the inviscid $(A,U)$ system (compare with the hypothesis in [11] (Lemma 2)).

Lemma 1.

If $A(x,t)>\delta >0$, the inviscid $(A,U)$ system is symmetrizable.

Proof. 

From (16) it follows that the entropy variables are $\mathit{v}={\nabla }_{\mathit{u}}\eta \left(\mathit{u}\right)={[-\beta /\sqrt{A},\rho U]}^T$. Let $\mathit{u}\left(\mathit{v}\right)$ denote the inverse of the transformation $\mathit{u}\to \mathit{v}\left(\mathit{u}\right)$. Then the Jacobian

$${\mathit{u}}_{\mathit{v}}=\left. [\begin{array}{cc}2\sqrt{A^3}/\beta & 0\\ 0& 1/\rho \end{array}\right]$$

(19)

is clearly symmetric positive definite and

$$H{\mathit{u}}_{\mathit{v}}=\left. [\begin{array}{cc}U& A\\ c^2/A& U\end{array}\right]\left. [\begin{array}{cc}2\sqrt{A^3}/\beta & 0\\ 0& 1/\rho \end{array}\right]=\left. [\begin{array}{cc}2U\sqrt{A^3}/\beta & A/\rho \\ A/\rho & U/\rho \end{array}\right]$$

is symmetric, which proves the lemma. □

In [11,13,14], the authors point out the fundamental importance of the numerical analysis with symmetrizability, in particular, to study the error estimates of the Runge–Kutta discontinuous Galerkin method.

Using the entropy function (16) and the eigenvector rescaling theorem [15] (Theorem 4), we obtain the lemma below, which provides a scaling of the eigenvectors $R=\left[{\mathit{r}}_1\right|{\mathit{r}}_2]\to \tilde{R}=\left[{\tilde{\mathit{r}}}_1\right|{\tilde{\mathit{r}}}_2]$ such that $\tilde{R}{\tilde{R}}^T={\mathit{u}}_{\mathit{v}}$.

Lemma 2.

Consider the model (3) along with the entropy function $\eta \left(\mathit{v}\right)=\frac{\rho U^2}{2}-2\beta \sqrt{A}$ and the entropy variables $\mathit{v}={[-\beta /\sqrt{A},\rho U]}^T$. Let ${\mathit{u}}_j$ and ${\mathit{u}}_{j+1}$ be two adjacent states. Let $\tilde{R}$ be the scaled right eigenvectors matrix of H given by

$$\tilde{R}=\frac{1}{\sqrt{2\rho }}\left. [\begin{array}{cc}-A/c& A/c\\ 1& 1\end{array}\right].$$

(20)

Then we have

$$\tilde{R}{\tilde{R}}^T={\mathit{u}}_{\mathit{v}},$$

where ${\mathit{u}}_{\mathit{v}}$ is the symmetric positive definite change-of-variables matrix given by (19).

Proof. 

The result can be obtained directly by insertion. □

This lemma will be used in the next section to construct a numerical diffusion operator.

3. Numerical Method

3.1. Entropy Conservative and Entropy-Stable Numerical Schemes

For the homogeneous system (11) (until Section 3.2, we take $C_f=0$), a semi-discrete conservative scheme on a uniform spatial mesh $x_j=j\mathsf{\Delta }x$, $j\in \mathbb{Z}$ writes as

$$\frac{\mathrm{d}{\mathit{u}}_j\left(t\right)}{\mathrm{d}t}=-\frac{1}{\mathsf{\Delta }x}\left({\mathit{F}}_{j+1/2}-{\mathit{F}}_{j-1/2}\right),j\in \mathbb{Z},$$

(21)

where ${\mathit{u}}_j\left(t\right)$ denotes the numerical approximation of $\mathit{u}(x_j,t)$ and the numerical flux ${\mathit{F}}_{j+1/2}$ is an approximation of the flux function at the cell interface $j+1/2$.

The scheme (21) is called entropy stable with respect to the entropy pair $(\eta ,G)$ if it satisfies a discrete entropy inequality

$$\frac{\mathrm{d}}{\mathrm{d}t}\eta \left({\mathit{u}}_j\left(t\right)\right)+\frac{1}{\mathsf{\Delta }x}\left({\tilde{G}}_{j+1/2}-{\tilde{G}}_{j-1/2}\right)\le 0$$

(22)

for some numerical entropy flux ${\tilde{G}}_{j+1/2}$ consistent with the entropy flux G. If equality holds in (22), then the scheme (21) is called entropy conservative.

We focus on entropy-stable numerical fluxes of the form [9]

$${\mathit{F}}_{j+1/2}={\tilde{\mathit{F}}}_{j+1/2}-\frac{1}{2}{D}_{j+1/2}{⟨⟨\mathit{v}⟩⟩}_{j+1/2},$$

(23)

where ${\tilde{\mathit{F}}}_{j+1/2}$ is an entropy conservative flux, ${⟨⟨\mathit{v}⟩⟩}_{j+1/2}={\mathit{v}}_{j+1}^{-}-{\mathit{v}}_j^{+}$, ${\mathit{v}}_j^{\pm }$ being the cell interface values of a reconstructed function ${\mathit{v}}_j\left(x\right)$ and $D_{j+1/2}$ is a suitable numerical diffusion matrix, which will be specified later.

The following general procedure to define entropy conservative fluxes ${\tilde{\mathit{F}}}_{j+1/2}$ appears in [16]. In what follows, ${\left[\left[a\right]\right]}_{j+1/2}$ denotes the jump of a across the interface at $x_{j+1/2}$, that is, ${\left[\left[a\right]\right]}_{j+1/2}:=a_{j+1}-a_j$, and ${\overline{a}}_{j+1/2}:=\frac{1}{2}(a_{j+1}+a_j)$.

Theorem 1

([16]). If the numerical flux ${\tilde{\mathit{F}}}_{j+1/2}$ satisfies

$${\left[\left[\mathit{v}\right]\right]}_{j+1/2}^T{\tilde{\mathit{F}}}_{j+1/2}={\left[\left[\psi \right]\right]}_{j+1/2},j\in \mathbb{Z},$$

(24)

then the scheme

$$\begin{array}{c}\hfill \frac{\mathrm{d}{\mathit{u}}_j\left(t\right)}{\mathrm{d}t}=-\frac{1}{\mathsf{\Delta }x}\left({\tilde{\mathit{F}}}_{j+1/2}-{\tilde{\mathit{F}}}_{j-1/2}\right),j\in \mathbb{Z},\end{array}$$

is second-order accurate and entropy conservative.

Observe that the existence of an explicitly given entropy pair is an important ingredient in designing entropy conservative schemes. For the scalar case, the solution of (24) is unique. However, for systems of conservation laws, this is no longer true.

Tadmor also proposed (see [16] for more details) the following solution of (24):

$${\tilde{\mathit{F}}}_{j+1/2}={\int }_{-1/2}^{1/2}\mathit{f}\left({\mathit{v}}_{j+1/2}\left(\xi \right)\right)\mathrm{d}\xi ,$$

(25)

where ${\mathit{v}}_{j+1/2}\left(\xi \right)$ denotes the straight line connecting ${\mathit{v}}_j$ and ${\mathit{v}}_{j+1}$, i.e.,

$$\begin{array}{c}\hfill {\mathit{v}}_{j+1/2}\left(\xi \right)=\frac{1}{2}({\mathit{v}}_j+{\mathit{v}}_{j+1})+\xi ({\mathit{v}}_{j+1}-{\mathit{v}}_j),\xi \in [-1/2,1/2].\end{array}$$

The flux (25) is sometimes called Averaged Energy Conservative (AEC for short) flux [17]. A straightforward computation of the integral in (25) for the $(A,U)$ system yields the following components of the numerical flux ${\tilde{\mathit{F}}}_{j+1/2}$:

$$\begin{array}{cc}\hfill {\tilde{F}}_{j+1/2}^{\left(1\right)}& ={\int }_{-1/2}^{1/2}{f}_1\left({\mathit{v}}_{j+1/2}\left(\xi \right)\right)\mathrm{d}\xi ={\overline{A}}_{j+1/2}{\overline{U}}_{j+1/2}+\frac{1}{12}{\left[\left[A\right]\right]}_{j+1/2}{\left[\left[U\right]\right]}_{j+1/2}\hfill \\ \hfill {\tilde{F}}_{j+1/2}^{\left(2\right)}& ={\int }_{-1/2}^{1/2}{f}_2\left({\mathit{v}}_{j+1/2}\left(\xi \right)\right)\mathrm{d}\xi \hfill \\ \hfill & =\frac{1}{6}\left(U_{j+1}^2+U_{j+1}{U}_j+U_j^2\right)+\frac{1}{\rho }\left(P_0-\beta \sqrt{A_0}+\frac{2\beta \left(A_{j+1}\sqrt{A_{j+1}}-A_j\sqrt{A_j}\right)}{3(A_{j+1}-A_{j+1})}\right).\hfill \end{array}$$

(26)

It is easy to check that the flux (26) is consistent. To do this, it is sufficient to recall that

$$\frac{A_{j+1}\sqrt{A_{j+1}}-A_j\sqrt{A_j}}{A_{j+1}-A_j}⟶\frac{3}{2}\sqrt{A_j}.$$

as $A_{j+1}\to A_j$.

Another way of solving (24) is based on different paths in the phase space of the entropy variables [18]. This is described as follows: Let ${\left\{{\mathit{r}}_i\right\}}_{i=1}^n$ be an arbitrary set of n linearly independent vectors, and let ${\left\{{\mathit{l}}_i\right\}}_{i=1}^n$ be the corresponding orthogonal set. At an interface $x_{j+1/2}$, we define the paths

$$\begin{array}{c}\hfill {\mathit{v}}^0:={\mathit{v}}_j,{\mathit{v}}^i:={\mathit{v}}^{i-1}+\left({\left[\left[\mathit{v}\right]\right]}_{j+1/2}^{\mathrm{T}}{\mathit{l}}_i\right){\mathit{r}}_i\mathrm{for}i=1,\cdots ,n-1,{\mathit{v}}^n:={\mathit{v}}_{j+1}.\end{array}$$

Then the entropy conservative flux is given by

$${\tilde{\mathit{F}}}_{j+1/2}=\sum _{i=1}^n\frac{\psi \left({\mathit{v}}^i\right)-\psi \left({\mathit{v}}^{i-1}\right)}{{\left[\left[\mathit{v}\right]\right]}_{j+1/2}^{\mathrm{T}}{\mathit{l}}_i}{\mathit{l}}_i.$$

(27)

This flux is termed the Pathwise Energy Conservative (PEC) flux. In [17], it was reported that the computation of (27) may be numerically unstable.

A third strategy to construct the entropy conservative flux at the interface $x_{j+1/2}$ was proposed in [17]. In this reference, an explicit solution of (24) for the shallow water equations was obtained by using the identity

$${\left[\left[ab\right]\right]}_{j+1/2}={\overline{b}}_{j+1/2}{\left[\left[a\right]\right]}_{j+1/2}+{\left[\left[b\right]\right]}_{j+1/2}{\overline{a}}_{j+1/2}.$$

(28)

The strategy is called Explicit Energy Conservative (EEC) flux, and we employ this approach to the $(A,u)$ blood flow model.

Using (28), the jump of the entropy potential (18) across $x_{j+1/2}$ can be expressed as

$$\begin{array}{cc}\hfill & {\left[\left[\psi \right]\right]}_{j+1/2}={\left[\left[\rho U^3/6+UP\left(A\right)\right]\right]}_{j+1/2}\hfill \\ \hfill & =\frac{\rho }{6}{\left[\left[U\right]\right]}_{j+1/2}(U_{j+1}^2+U_{j+1}{U}_j+U_j^2)+{\overline{U}}_{j+1/2}{\left[\left[P\left(A\right)\right]\right]}_{j+1/2}+{\left[\left[U\right]\right]}_{j+1/2}{\overline{P\left(A\right)}}_{j+1/2}.\hfill \end{array}$$

Under the assumptions that $A_0$ and $\beta$ are constants, the jump of entropy variables can be written as

$${\left[\left[\mathit{v}\right]\right]}_{j+1/2}^T=\left. [\frac{{\left[\left[P\left(A\right)\right]\right]}_{j+1/2}}{\sqrt{A_{j+1}{A}_j}},\rho {\left[\left[U\right]\right]}_{j+1/2}\right].$$

(29)

Writing down the desired flux componentwise as ${\tilde{\mathit{F}}}_{j+1/2}={[{\tilde{F}}_{j+1/2}^{\left(1\right)},{\tilde{F}}_{j+1/2}^{\left(2\right)}]}^T$, inserting the above two quantities into (24), equating jumps in U and $P\left(A\right)$ and then solving the resulting system, we obtain

$$\begin{array}{cc}\hfill {\tilde{F}}_{j+1/2}^{\left(1\right)}& ={\overline{U}}_{j+1/2}\sqrt{A_{j+1}{A}_j},\hfill \\ \hfill {\tilde{F}}_{j+1/2}^{\left(2\right)}& =\frac{1}{6}(U_{j+1}^2+U_{j+1}{U}_j+U_j^2)+\frac{1}{\rho }{\overline{P\left(A\right)}}_{j+1/2}.\hfill \end{array}$$

(30)

This flux is clearly consistent, very simple to code and computationally inexpensive.

The two-point entropy conservative fluxes obtained from (24) are only second-order accurate. However, high-order entropy conservative fluxes can be constructed by linear combinations of two-point entropy conservative fluxes $\tilde{\mathit{F}}$ [19]. In this work, we use the fourth-order entropy conservative flux given by

$${\tilde{\mathit{F}}}_{j+1/2}^4=\frac{4}{3}\tilde{\mathit{F}}({\mathit{u}}_j,{\mathit{u}}_{j+1})-\frac{1}{6}\left(\tilde{\mathit{F}}({\mathit{u}}_{j-1},{\mathit{u}}_{j+1})+\tilde{\mathit{F}}({\mathit{u}}_j,{\mathit{u}}_{j+2})\right).$$

(31)

To deal with the numerical diffusion part in (23), the diffusion matrix $D_{j+1/2}$ is taken as [9]

$$D_{j+1/2}={\tilde{R}}_{j+1/2}{\mathsf{\Lambda }}_{j+1/2}{\tilde{R}}_{j+1/2}^T,$$

(32)

where ${\mathsf{\Lambda }}_{j+1/2}=diag\left(\right|{\lambda }_1|,|{\lambda }_2\left|\right)$ is a Roe-type diagonal matrix, and ${\tilde{R}}_{j+1/2}$ is the matrix of scaled right eigenvectors of the flux Jacobian $H\left({\mathit{u}}_{j+1/2}\right)$ that is evaluated at the average state ${\mathit{u}}_{j+1/2}:=({\mathit{u}}_j+{\mathit{u}}_{j+1})/2$.

To complete the description of (23), it only remains to perform a suitable reconstruction of the entropy variables $\mathit{v}$. Let ${\mathit{v}}_j\left(x\right)$ be a $p-$th reconstruction function of the entropy variables $\mathit{v}$. Denoting

$${\mathit{v}}_j^{+}={\mathit{v}}_j\left(x_{j+1/2}\right),{\mathit{v}}_j^{-}={\mathit{v}}_j\left(x_{j-1/2}\right),$$

(33)

and defining the scaled entropy variables

$${\mathit{z}}_j^{\pm }:=R_{j\pm 1/2}^T{\mathit{v}}_j,{\tilde{\mathit{z}}}_j^{\pm }:=R_{j\pm 1/2}^T{\mathit{v}}_j^{\pm },$$

(34)

Instead of reconstructing the entropy variables, we reconstruct the scaled entropy variables such that the so-called sign property

$$\mathrm{sign}{⟨⟨{\tilde{z}}_j^l⟩⟩}_{j+1/2}=\mathrm{sign}{⟨⟨z_j^l⟩⟩}_{j+1/2}$$

will be satisfied. Here, $z_j^l$ and ${\tilde{z}}_j^l$ denote the l-th component of ${\mathit{z}}_j$ and ${\tilde{\mathit{z}}}_j$, respectively. The advantage of using reconstruction procedures satisfying the sign property lies in the fact that they are entropy-stable (see Lemma 3.2 in [9]). On the other hand, the use of high-order nonoscillatory reconstruction is needed in order to avoid large oscillations around shocks; in particular, we use the fourth-order ENO. The crucial fact is that the ENO method satisfies the sign property [20], which in turn, guarantees that the reconstruction does not destroy entropy stability. The combination of entropy conservative fluxes and ENO reconstruction is termed TeCNO schemes [9].

3.2. Friction Source Term Discretization

Up to now, we have restricted our attention to the system (1)–(3) without friction, that is, the homogeneous case. For a treatment of the non-homogeneous case, the spatial semi-discretization of system (3) can be written as

$$\frac{d\mathit{u}}{dt}=𝓛\left(\mathit{u}\right)+𝓢\left(\mathit{u}\right),$$

(35)

where

$$\begin{array}{c}\hfill {\left[𝓛(·)\right]}_j:=-\frac{1}{\mathsf{\Delta }x}\left({\mathit{F}}_{j+1/2}-{\mathit{F}}_{j-1/2}\right)\end{array}$$

is the spatial discretization of the convective term, and $𝓢\left(\mathit{u}\right)$ corresponds to the source term $\mathit{s}\left(\mathit{u}\right)$. To solve (35), an implicit–explicit Runge–Kutta (IMEX-RK) method (see [21] and the references therein) will be used. Let us first recall that an IMEX-RK scheme consists of applying an implicit discretization to the source term and an explicit one to the convective part. An m-stage IMEX-RK scheme applied to system (35) takes the form

$$\begin{array}{cc}\hfill {\mathit{u}}^{\left(i\right)}& ={\mathit{u}}^n+\mathsf{\Delta }t\sum _{l=1}^{i-1}{\tilde{a}}_{il}𝓛({\mathit{u}}^{\left(l\right)})+\mathsf{\Delta }t\sum _{l=1}^i{a}_{il}𝓢({\mathit{u}}^{\left(l\right)}),i=1,\dots ,m,\hfill \\ \hfill {\mathit{u}}^{n+1}& ={\mathit{u}}^n+\mathsf{\Delta }t\sum _{i=1}^m{\tilde{b}}_i𝓛({\mathit{u}}^{\left(i\right)})+\mathsf{\Delta }t\sum _{i=1}^m{b}_i𝓢({\mathit{u}}^{\left(i\right)}).\hfill \end{array}$$

This scheme is characterized by $m\times m$ matrices $\tilde{\mathcal{A}}=\left({\tilde{a}}_{il}\right)$ (with ${\tilde{a}}_{il}=0$ for $l\ge i$) and $\mathcal{A}=\left(a_{il}\right)$ that correspond to the explicit (ERK) and (diagonally) implicit (DIRK) parts of the method, respectively, while $\tilde{b}={({\tilde{b}}_1,\cdots ,{\tilde{b}}_m)}^T$ and $b={(b_1,\cdots ,b_m)}^T$ are m-dimensional vectors of real coefficients.

In this work, we employ a second-order IMEX-RK scheme based on the Heun method coupled with the L-stable DIRK method, namely the scheme H-LDIRK3(2,2,2) [21,22], which is defined by

$$\tilde{\mathcal{A}}=\left. [\begin{array}{cc}0& 0\\ 1& 0\end{array}\right],\mathcal{A}=\left. [\begin{array}{cc}\gamma & 0\\ 1-2\gamma & \gamma \end{array}\right],\tilde{b}=b=\left. [\begin{array}{c}1/2\\ 1/2\end{array}\right],\gamma =\frac{3+\sqrt{3}}{6}.$$

The particular value of $\gamma$ guarantees that the implicit part is a third-order DIRK scheme with the best dampening properties (see [22,23] and references given there).

Applying the H-LDIRK3(2,2,2) scheme to (35) and taking into account the particular form of the source term $\mathit{s}\left(\mathit{u}\right)={(0,-C_{f}U/A)}^T$, we obtain that the required computations to advance ${\mathit{u}}^n$ from time $t^n$ to $t^{n+1}=t^n+\mathsf{\Delta }t$ are given by

$${\mathit{u}}^{\left(1\right)}=\left. [\begin{array}{c}{A}^n\\ \frac{A^n{U}^n}{A^n+a_{11}\mathsf{\Delta }t{C}_f}\end{array}\right]$$

(36)

and

$${\mathit{u}}^{\left(2\right)}=\left. [\begin{array}{c}\widehat{A}\\ \frac{\widehat{A}\widehat{U}}{\widehat{A}+a_{22}\mathsf{\Delta }t{C}_f}\end{array}\right],$$

(37)

where

$$\widehat{\mathit{u}}={\mathit{u}}^n+\mathsf{\Delta }t{\tilde{a}}_{21}{\tilde{K}}_1+\mathsf{\Delta }t{a}_{21}{K}_1,$$

with

$${\tilde{K}}_1=𝓛({\mathit{u}}^{\left(1\right)}),K_1=𝓢({\mathit{u}}^{\left(1\right)})=\left. [\begin{array}{c}0\\ -C_f\frac{U^n}{A^n+a_{11}\mathsf{\Delta }t{C}_f}\end{array}\right].$$

Finally, evaluate

$${\mathit{u}}^{n+1}={\mathit{u}}^n+\mathsf{\Delta }t({\tilde{b}}_1{\tilde{K}}_1+{\tilde{b}}_2{\tilde{K}}_2)+\mathsf{\Delta }t(b_1{K}_1+b_2{K}_2),$$

(38)

where

$${\tilde{K}}_2=𝓛({\mathit{u}}^{\left(2\right)}),K_2=𝓢({\mathit{u}}^{\left(2\right)})=\frac{{\mathit{u}}^{\left(2\right)}-\widehat{\mathit{u}}}{a_{22}\mathsf{\Delta }t}.$$

It is worth pointing out that solutions for nonlinear systems are not required, reducing computational costs and making this method much simpler to implement. Let us also mention that (36) corresponds to the formula obtained in [3] (with $a_{11}=1$) by using the so-called semi-implicit treatment (SI).

Notice that when $C_f=0$, the method described above reduces to the Heun method, which is an explicit strong stability preserving Runge–Kutta method (SSPRK) [24]:

$$\begin{array}{cc}\hfill {\mathit{u}}^{\left(1\right)}& ={\mathit{u}}^n+\mathsf{\Delta }t𝓛\left({\mathit{u}}^n\right),\hfill \\ \hfill {\mathit{u}}^{\left(2\right)}& ={\mathit{u}}^{\left(1\right)}+\mathsf{\Delta }t𝓛\left({\mathit{u}}^{\left(1\right)}\right),\hfill \\ \hfill {\mathit{u}}^{n+1}& =\frac{1}{2}\left({\mathit{u}}^n+{\mathit{u}}^{\left(2\right)}\right).\hfill \end{array}$$

The time step $\mathsf{\Delta }t$ is computed adaptatively in order for the CFL condition to be satisfied. We use the value $\mathsf{\Delta }t=\kappa \ast \mathsf{\Delta }x/a$, where a is an estimate of the maximal characteristic velocity. Here, the CFL number $\kappa$ is taken as $0.5$.

4. Numerical Results

In this section, we present some numerical examples by testing the numerical flux (23) with $\tilde{\mathit{F}}$ given by (26) and (30) for the inviscid $(A,U)$ system as well as for the viscous case. In the latter case, the scheme H-LDIRK3(2,2,2) is employed and compared with the SI scheme. For all the tests, the blood density is taken as $\rho =1060\mathrm{kg}/{\mathrm{m}}^3$.

4.1. Example 1: The Ideal Tourniquet

This example is proposed by Delestre and Lagrée [3], and it resembles the dam break problem in shallow water equations. A tourniquet is applied, and we remove it instantaneously. When the tourniquet is removed, the blood flows from upstream to downstream in the vessel. The initial conditions are

$$A(x,0)=\left\{\begin{array}{cc}\pi R_{\mathrm{L}}^2\hfill & \mathrm{for}x\le 0,\hfill \\ \pi R_{\mathrm{R}}^2\hfill & \mathrm{for}x>0\hfill \end{array}\right.\mathrm{and}U(x,0)=0,$$

with $R_{\mathrm{L}}=5\times {10}^{-3}\mathrm{m}$ and $R_{\mathrm{R}}=4\times {10}^{-3}\mathrm{m}$. The computational domain is $[-0.04,0.04]$ (in meters), we choose $\beta ={\pi }^{-1}\times {10}^7\mathrm{Pa}/\mathrm{m}$, and the radius of the artery at rest is taken as constant. Transmissive boundary conditions are imposed. The solution profiles consists of a left-moving rarefaction wave and right-moving shock wave, as shown in Figure 1. Numerical solutions are computed on a mesh with 200 cells at simulated time $t=0.005\mathrm{s}$ by using the flux (26) (termed as TeCNO4-AEC) and the flux (30) (termed as TeCNO4-EEC). It can be reported that both fluxes are capable of capturing discontinuous solutions. No significant differences are observed between the solutions obtained with TeCNO4-EEC and TeCNO4-AEC.

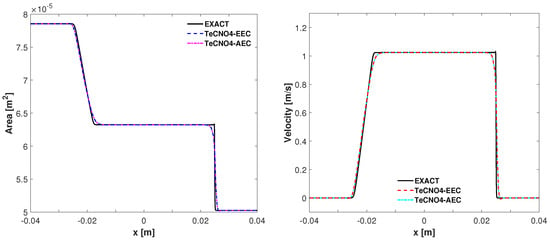
Figure 1. Example-1: Numerical solutions of the ideal tourniquet problem at $t=0.005$ s on a mesh with 200 cells: area (left) and velocity (right).

4.2. Example 2: Wave Equation

We consider the system without friction and constant cross-section at rest to validate the capability of the proposed scheme to approximate the perturbed steady-state solutions. The cross section at rest is given by $A_0\left(x\right)=\pi R_0^2$ with $R_0=4\times {10}^{-3}\mathrm{m}$, and the initial conditions are

$$A(x,0)=\left\{\begin{array}{cc}\pi R_0^2\hfill & \mathrm{for}x\in [0,x_2]\cup [x_3,L],\hfill \\ \pi R_0^2{\left(1+\epsilon sin(\pi (x-x_2)/x_1)\right)}^2\hfill & \mathrm{for}x\in [x_2,x_3],\hfill \end{array}\right.U(x,0)=0,$$

with $L=0.16\mathrm{m}$, $x_1=0.2L$, $x_2=0.4L$, $x_3=0.6L$ and $\epsilon =5\times {10}^{-3}$. The computational domain is $[0,L]$ and $\beta ={\pi }^{-1}\times {10}^8$ Pa/m. The exact solution (see [3] for more details) can be expressed as

$$R(x,t)=R_0+\frac{\epsilon }{2}\left(\varphi (x-c_{0}t)+\varphi (x+c_{0}t)\right),U(x,t)=-\epsilon \frac{c_0}{R_0}\left(-\varphi (x-c_{0}t)+\varphi (x+c_{0}t)\right),$$

(39)

where $c_0=c\left(A_0\right)$ and $\varphi \left(x\right)=R_{0}sin(\pi (x-x_2)/x_1){\chi }_{[x_2,x_3]}\left(x\right)$, where $\chi$ is the indicator function. Numerical solutions obtained using TeCNO4 with TeCNO4-AEC and TeCNO4-EEC are displayed in Figure 2 (for radius) and Figure 3 (for velocity), respectively. It can be observed that the results obtained with both fluxes are in good agreement with the exact solutions, but the EEC flux provides a slightly better performance.

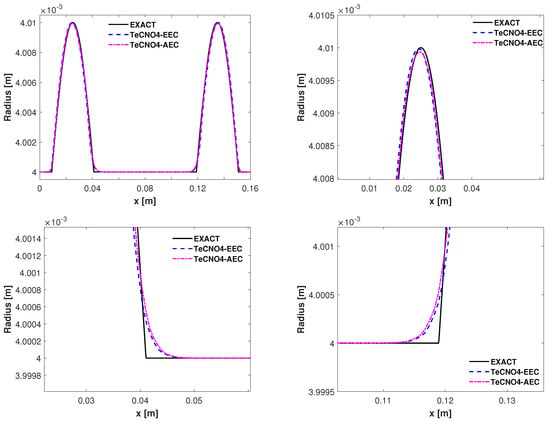
Figure 2. Example-2: Numerical solutions (for radius) of the wave equation at $t=0.004$ s on a mesh with 200 cells with enlarged views in selected regions.

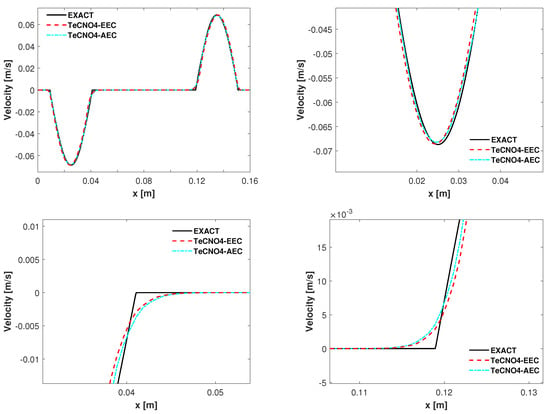
Figure 3. Example-2: Numerical solutions (for velocity) of the wave equation at $t=0.004$ s on a mesh with 200 cells with enlarged views in selected regions.

4.3. Example 3: Wave Damping

In this last test [3], the viscous damping term is investigated in the linearized momentum equation. This is the analog of the Womersley problem [25], and a periodic signal at the inflow is considered with a constant section at rest. System (1), in terms of the variables $(R,U)$ with the friction term, takes the form

$$\left\{\begin{array}{c}{R}_t+U{R}_x+\frac{R}{2}{U}_x=0\hfill \\ U_t+U{U}_x+\frac{\beta \sqrt{\pi }}{\rho }{R}_x=-C_f{\displaystyle \frac{U}{\pi R^2}}\hfill \end{array}\right.$$

In the above model, the skin friction coefficient $C_f$ is $8\pi \nu$, with $\nu$ being the viscosity of the blood. We consider this example on the computational domain $[0,3]$ subject to the given initial conditions

$$R(x,0)=R_0,U(x,0)=0\mathrm{m}/\mathrm{s},$$

along with the following parameters: $\beta ={\pi }^{-1}\times {10}^8$ Pa/m, $R_0=4\times {10}^{-3}\mathrm{m}$. The incoming discharge is

$$Q_b(0,t)=Q_{amp}sin\left(\omega t\right){\mathrm{m}}^3/\mathrm{s},$$

where $Q_{amp}=3.45\times {10}^{-7}{\mathrm{m}}^3/\mathrm{s}$ is the amplitude of the inflow discharge and $\omega =2\pi /T_{pulse}$ being $T_{pulse}=0.5\mathrm{s}$ the time length of a pulse. A damping wave is obtained in the domain (see [3] for more details)

$$Q(x,t)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if} k_{r}x>\omega t\hfill \\ Q_{amp}sin(\omega t-k_{r}x)e^{k_{i}x},\hfill & \mathrm{if} k_{r}x\le \omega t,\hfill \end{array}\right.$$

(40)

with

$$\begin{array}{cc}\hfill k_r& ={\left. [\frac{{\omega }^4}{c_0^4}+{\left(\frac{\omega C_f}{\pi R_0^2{c}_0^2}\right)}^2\right]}^{1/4}cos\left(\frac{1}{2}arctan\left(-\frac{C_f}{\pi R_0^2\omega }\right)\right),\hfill \\ \hfill k_i& ={\left. [\frac{{\omega }^4}{c_0^4}+{\left(\frac{\omega C_f}{\pi R_0^2{c}_0^2}\right)}^2\right]}^{1/4}sin\left(\frac{1}{2}arctan\left(-\frac{C_f}{\pi R_0^2\omega }\right)\right),\hfill \\ \hfill c_0& =\sqrt{\frac{\beta \sqrt{\pi }{R}_0}{2\rho }}.\hfill \end{array}$$

Exact and numerical solutions of the damping of a discharge wave are depicted in Figure 4. Enlarged views are included to compare the performance of the H-LDIRK3(2,2,2) method and the SI method used for the discretization of the friction source term.

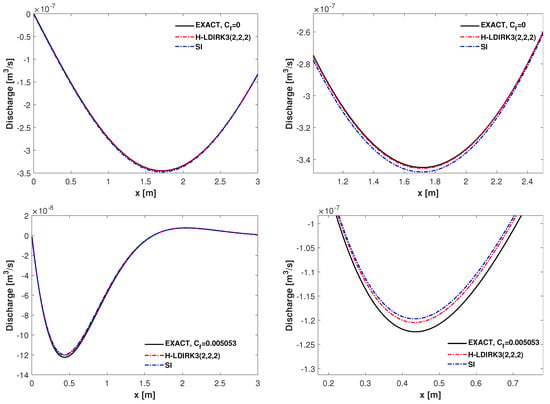
Figure 4. Example-3: Numerical solutions of the wave damping at $t=25$ s with $C_f=0$ (top) and $C_f=0.005053$ (bottom) and the corresponding enlarged views. The friction term has been treated with either the H-LDIRK3(2,2,2) method or the SI method.

5. Conclusions

In this paper, we have presented a separable entropy pair for a 1D reduced blood flow model. We have used the proposed entropy pair to show the symmetrizability of the model and for constructing explicit, computationally inexpensive and easy-to-implement entropy conservative fluxes. After adding numerical diffusion to the entropy conservative fluxes (as recommended in [9]) along with a suitable reconstruction of the entropy variables, we obtained entropy-stable schemes. No significant differences were found between the numerical solutions obtained with the EEC flux and the AEC flux. However, small differences observed in the second numerical example were favorable for the EEC flux. Finally, we have solved the friction source term by IMEX-RK methods, with the advantage that it was unnecessary to solve nonlinear systems. In fact, the particular form of the friction term allowed us to derive a fully explicit scheme.