Inertial Tseng Method for Solving the Variational Inequality Problem and Monotone Inclusion Problem in Real Hilbert Space

Abstract

The main aim of this research is to introduce and investigate an inertial Tseng iterative method to approximate a common solution for the variational inequality problem for $\gamma$-inverse strongly monotone mapping and monotone inclusion problem in real Hilbert spaces. We establish a strong convergence theorem for our suggested iterative method to approximate a common solution for our proposed problems under some certain mild conditions. Furthermore, we deduce a consequence from the main convergence result. Finally, a numerical experiment is presented to demonstrate the effectiveness of the iterative method. The method and methodology described in this paper extend and unify previously published findings in this field.

1. Introduction

Let $\mathcal{H}$ be a real Hibert space equipped with the inner product $⟨·,·⟩$ and the induced norm $\parallel ·\parallel$ and let $\mathcal{D}$ be a nonempty, closed, and convex subset of $\mathcal{H}$.

In 1966, Hartman and Stampacchia [1] proposed and studied the variational inequality problem (VIP), which is described as follows:

$$\mathrm{Find}{\mathfrak{p}}^{*}\in \mathcal{D}\mathrm{such}\mathrm{that}⟨\mathcal{T}{\mathfrak{p}}^{*},{\mathfrak{q}}^{*}-{\mathfrak{p}}^{*}⟩\ge 0,\forall {\mathfrak{q}}^{*}\in \mathcal{D},$$

(1)

where $\mathcal{T}:\mathcal{D}\to \mathcal{H}$ is a nonlinear mapping. The solution set of VIP (1) is represented by $\mathrm{VI}(\mathcal{D},\mathcal{T}).$ Variational inequality is a useful tool in many domains including economics, engineering, mathematical programming, transportation, and others (see, for example, [2,3,4,5,6,7,8,9]). Many numerical approaches for solving variational inequalities and associated optimization problems have been developed; see [10,11,12,13,14,15] and references therein.

On the other hand, the monotone inclusion problem (MIP), which is described as follows:

$$\mathrm{Find}{\mathfrak{z}}^{*}\in \mathcal{H}\mathrm{such}\mathrm{that}0\in (\mathcal{P}+\mathcal{Q}){\mathfrak{z}}^{*},$$

(2)

where $\mathcal{P}:\mathcal{H}\to \mathcal{H}$ and $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ are singlevalued and multivalued mappings, respectively. The solution set of MIP (2) is represented by $\Gamma$.

This problem has received significant attention because it is at the core of many mathematical problems, including convex programming, variational inequalities, split feasibility problem, and minimization problems (see [16,17,18,19]), which have applications in machine learning, image processing, and linear inverse problems. Due to the importance and interest of the problem, many researchers have developed iterative methods for solving (2) (see [16,20,21,22]).

In 1979, Lions and Mercier [23] proposed and studied the forward–backward splitting method. It is described by the following iterative scheme:

$$\left\{\begin{array}{c}{v}_1\in \mathcal{H},\hfill \\ v_{m+1}={(I+{\lambda }_m\mathcal{Q})}^{-1}(I-{\lambda }_m\mathcal{P})v_m,\forall m\ge 1,\hfill \end{array}\right.$$

(3)

where $I:\mathcal{H}\to \mathcal{H}$ denotes the identity operator and ${\lambda }_m>0$. Operators $\mathcal{P}$ and $\mathcal{Q}$ are referred to as forward and backward operators, respectively. The forward–backward splitting method has recently been investigated and extended by a number of authors (see [20,24,25,26,27]).

In 1964, Polyak [28] introduced the inertial extrapolation process as a useful tool for speeding up the convergence rate of iterative methods. This method is well known as the heavy-ball method. In recent years, many academicians have extensively used this beneficial concept to combine their algorithms with an inertial term in order to accelerate the speed of convergence (see [29,30]).

Alvarez and Attouch [29] introduced and constructed the heavy-ball method with the proximal point algorithm to solve a problem of maximal monotone operator. It is defined as follows:

$$\left\{\begin{array}{c}{v}_0,v_1\in \mathcal{H},\hfill \\ w_m=v_m+{\theta }_m(v_m-v_{m-1}),\hfill \\ v_{m+1}={(I+{\lambda }_m\mathcal{Q})}^{-1}{w}_m,\forall m\ge 1,\hfill \end{array}\right.$$

(4)

where $\left\{{\theta }_m\right\}\subset [0,1)$ and $\left\{{\lambda }_m\right\}$ is nondecreasing with ${\sum }_{m=1}^{\infty }{\theta }_m\parallel v_m-v_{m-1}\parallel <\infty .$ They established that the sequence induced by (4) converges weakly to a zero of the monotone operator $\mathcal{Q}$.

There are numerous approaches for solving the monotone inclusion problem by using an algorithm combined with the heavy-ball idea (see [26,31]).

In 2000, Tseng [22] proposed and studied the following iterative method, known as the Tseng splitting method, which is defined as follows:

$$\left\{\begin{array}{c}{v}_1\in \mathcal{H},\hfill \\ y_m={(I+{\lambda }_m\mathcal{Q})}^{-1}(I-{\lambda }_m\mathcal{P})v_m,\hfill \\ v_{m+1}=y_m-{\lambda }_m(\mathcal{P}{y}_m-\mathcal{P}{v}_m),\forall m\ge 1.\hfill \end{array}\right.$$

(5)

Tseng established that the sequence induced by (5) converges weakly to a point of the solution set $\Gamma$ under some acceptable assumptions.

In 2021, Padcharoen et al. [32] developed and analyzed the following iterative method, known as the inertial Tseng method, for solving monotone inclusion problem, which is defined as follows:

$$\left\{\begin{array}{c}{v}_0,v_1\in \mathcal{H},\hfill \\ w_m=v_m+{\theta }_m(v_m-v_{m-1}),\hfill \\ y_m={(I+{\lambda }_m\mathcal{Q})}^{-1}(I-{\lambda }_m\mathcal{P})w_m,\hfill \\ v_{m+1}=y_m-{\lambda }_m(\mathcal{P}{y}_m-\mathcal{P}{w}_m),\forall m\ge 1.\hfill \end{array}\right.$$

(6)

They established that the sequence induced by (6) converges weakly to a point of the solution set $\Gamma$ under some certain assumptions.

In 2021, Tan and Cho [33] introduced and investigated the following iterative method, known as the inertial viscosity-type Tseng method, for solving monotone inclusion problem, which is defined as follows:

$$\left\{\begin{array}{c}{v}_0,v_1\in \mathcal{H},\hfill \\ w_m=v_m+{\theta }_m(v_m-v_{m-1}),\hfill \\ y_m={(I+{\lambda }_m\mathcal{Q})}^{-1}(I-{\lambda }_m\mathcal{P})w_m,\hfill \\ z_m=y_m-{\lambda }_m(\mathcal{P}{y}_m-\mathcal{P}{w}_m),\hfill \\ v_{m+1}={\xi }_m\psi \left(v_m\right)+(1-{\xi }_m)z_m,\forall m\ge 1,\hfill \end{array}\right.$$

(7)

where $\psi :\mathcal{H}\to \mathcal{H}$ is a $\tau$-contraction with constant $\tau \in [0,1)$, $\mathcal{P}:\mathcal{H}\to \mathcal{H}$ is $\mathcal{L}$-Lipschitz continuous and monotone, and $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ is a multivalued maximal monotone mapping. They established that the sequence induced by (7) converges strongly to a point of the solution set $\Gamma$ under some mild conditions.

Motivated and inspired by the above research studies, in this paper, we suggest and analyze an iterative method to approximate a common solution of variational inequality problem (1) and monotone inclusion problem (2) in a real Hilbert space; i.e., we propose and investigate the following problem:

$$\mathrm{Find}{\mathfrak{g}}^{*}\in \mathcal{D}\mathrm{such}\mathrm{that}{\mathfrak{g}}^{*}\in \mathcal{J}=\mathrm{VI}(\mathcal{D},\mathcal{T})\cap \Gamma \ne \varphi .$$

2. Preliminaries

In this section, we review some fundamental definitions, results, and lemmas that will be applied in the subsequent sections. We denote the symbols ⇀ and → for weak and strong convergences, respectively.

A mapping $\mathcal{P}:\mathcal{H}\to \mathcal{H}$ is said to be

(i)

monotone if

$$⟨\mathcal{P}{\mathfrak{g}}^{*}-\mathcal{P}{\mathfrak{q}}^{*},{\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}⟩\ge 0,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H};$$

(ii)

nonexpansive if

$$\parallel \mathcal{P}{\mathfrak{g}}^{*}-\mathcal{P}{\mathfrak{q}}^{*}\parallel \le \parallel {\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}\parallel ,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H};$$

(iii)

firmly nonexpansive if

$$⟨\mathcal{P}{\mathfrak{g}}^{*}-\mathcal{P}{\mathfrak{q}}^{*},{\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}⟩\ge {\parallel \mathcal{P}{\mathfrak{g}}^{*}-\mathcal{P}{\mathfrak{q}}^{*}\parallel }^2,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H};$$

(iv)

$\gamma$-strongly monotone if there exists $\gamma >0$ such that

$$⟨\mathcal{P}{\mathfrak{g}}^{*}-\mathcal{P}{\mathfrak{q}}^{*},{\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}⟩\ge \gamma {\parallel {\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}\parallel }^2,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H};$$

(v)

$\gamma$-inverse strongly monotone if there exists $\gamma >0$ such that

$$⟨\mathcal{P}{\mathfrak{g}}^{*}-\mathcal{P}{\mathfrak{q}}^{*},{\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}⟩\ge \gamma {\parallel \mathcal{P}{\mathfrak{g}}^{*}-\mathcal{P}{\mathfrak{q}}^{*}\parallel }^2,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H};$$

(vi)

$\mathcal{L}$-Lipschitz continuous with $\mathcal{L}>0$ such that

$$\parallel \mathcal{P}{\mathfrak{g}}^{*}-\mathcal{P}{\mathfrak{q}}^{*}\parallel \le \mathcal{L}\parallel {\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}\parallel ,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H}.$$

A mapping $P_{\mathcal{D}}$ is said to be metric projection from $\mathcal{H}$ onto $\mathcal{D}$ if for every point ${\mathfrak{g}}^{*}\in \mathcal{H}$, there exists a unique nearest point in $\mathcal{D}$ denoted by $P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right)$ such that

$$\parallel {\mathfrak{g}}^{*}-P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right)\parallel \le \parallel {\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}\parallel ,\forall {\mathfrak{q}}^{*}\in \mathcal{D}.$$

It is well known that $P_{\mathcal{D}}$ is nonexpansive and satisfies

$$⟨{\mathfrak{g}}^{*}-{\mathfrak{q}}^{*},P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right)-P_{\mathcal{D}}\left({\mathfrak{q}}^{*}\right)⟩\ge {\parallel P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right)-P_{\mathcal{D}}\left({\mathfrak{q}}^{*}\right)\parallel }^2,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H}.$$

Furthermore, $P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right)$ is characterized by the fact $P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right)\in \mathcal{D}$ and

$$⟨{\mathfrak{g}}^{*}-P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right),{\mathfrak{q}}^{*}-P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right)⟩\le 0,\forall {\mathfrak{q}}^{*}\in \mathcal{D}.$$

(8)

This implies that

$$\parallel {\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}{\parallel }^2\ge \parallel {\mathfrak{g}}^{*}-P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right){\parallel }^2+{\parallel {\mathfrak{q}}^{*}-P_{\mathcal{D}}\left({\mathfrak{g}}^{*}\right)\parallel }^2,\forall {\mathfrak{g}}^{*}\in \mathcal{H},\forall {\mathfrak{q}}^{*}\in \mathcal{D}.$$

A multivalued mapping $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ is said to be monotone, if for all ${\mathfrak{g}}_1^{*},{\mathfrak{g}}_2^{*}\in \mathcal{H},{\mathfrak{q}}_1^{*}\in \mathcal{Q}{\mathfrak{g}}_1^{*}$ and ${\mathfrak{q}}_2^{*}\in \mathcal{Q}{\mathfrak{g}}_2^{*}$ such that

$$⟨{\mathfrak{g}}_1^{*}-{\mathfrak{g}}_2^{*},{\mathfrak{q}}_1^{*}-{\mathfrak{q}}_2^{*}⟩\ge 0.$$

A monotone mapping $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ is at the maximum if $G\left(\mathcal{Q}\right)$, the graph of $\mathcal{Q}$ defined as $G\left(\mathcal{Q}\right)=\{({\mathfrak{g}}_1^{*},{\mathfrak{q}}_1^{*}):{\mathfrak{q}}_1^{*}\in \mathcal{Q}{\mathfrak{g}}_1^{*}\},$ is not properly contained in the graph of any other monotone mapping.

Remark 1.

It is well known that a monotone mapping $\mathcal{Q}$ is maximal if and only if for $({\mathfrak{g}}_1^{*},{\mathfrak{q}}_1^{*})\in \mathcal{H}\times \mathcal{H},⟨{\mathfrak{g}}_1^{*}-{\mathfrak{g}}_2^{*},{\mathfrak{q}}_1^{*}-{\mathfrak{q}}_2^{*}⟩\ge 0,$ for each $({\mathfrak{g}}_2^{*},{\mathfrak{q}}_2^{*})\in G\left(\mathcal{Q}\right)$ implies that ${\mathfrak{q}}_1^{*}\in \mathcal{Q}{\mathfrak{g}}_1^{*}.$

Let $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ be a multivalued maximal monotone mapping. Then, the resolvent operator $J_{\lambda }^{\mathcal{Q}}:\mathcal{H}\to \mathcal{H}$ associated with $\mathcal{Q}$ is defined by

$$J_{\lambda }^{\mathcal{Q}}\left({\mathfrak{g}}^{*}\right)={(I+\lambda \mathcal{Q})}^{-1}\left({\mathfrak{g}}^{*}\right),\forall {\mathfrak{g}}^{*}\in \mathcal{H},\lambda >0,$$

where $I:\mathcal{H}\to \mathcal{H}$ denotes the identity operator. We notice that the resolvent operator $J_{\lambda }^{\mathcal{Q}}$ is single-valued, nonexpansive, and firmly nonexpansive (see [34]).

Let $\mathcal{T}:\mathcal{D}\to \mathcal{H}$ be a monotone mapping and let $N_{\mathcal{D}}z$ be the normal cone to $\mathcal{D}$ at $z\in \mathcal{D}$, which is defined by $N_{\mathcal{D}}\left(z\right)=\{v\in \mathcal{H}:⟨z-u,v⟩\ge 0,\forall u\in \mathcal{D}\}$. Define

$$\mathcal{Q}\left(z\right)=\left\{\begin{array}{cc}\mathcal{T}\left(z\right)+N_{\mathcal{D}}\left(z\right),\hfill & \mathit{if}z\in \mathcal{D}\hfill \\ \varphi ,\hfill & \mathit{if}z\notin \mathcal{D},\hfill \end{array}\right.$$

Then, $\mathcal{Q}$ is maximal monotone and $0\in \mathcal{Q}\left(z\right)$ iff $z\in V(\mathcal{D},\mathcal{T});$ for more details, see [35,36,37].

Lemma 1

([38]). Let$\mathcal{H}$ be a real Hilbert space. The following properties hold:

(i)

$\parallel {\mathfrak{g}}^{*}+{\mathfrak{q}}^{*}{\parallel }^2\le {\parallel {\mathfrak{g}}^{*}\parallel }^2+2⟨{\mathfrak{q}}^{*},{\mathfrak{g}}^{*}+{\mathfrak{q}}^{*}⟩,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H};$

(ii)

$\parallel {\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}{\parallel }^2\le \parallel {\mathfrak{g}}^{*}{\parallel }^2-{\parallel {\mathfrak{q}}^{*}\parallel }^2-2⟨{\mathfrak{g}}^{*}-{\mathfrak{q}}^{*},{\mathfrak{q}}^{*}⟩,\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H};$

(iii)

$\parallel \xi {\mathfrak{g}}^{*}+(1-\xi ){\mathfrak{q}}^{*}{\parallel }^2=\xi \parallel {\mathfrak{g}}^{*}{\parallel }^2+(1-\xi )\parallel {\mathfrak{q}}^{*}{\parallel }^2-\xi (1-\xi ){\parallel {\mathfrak{g}}^{*}-{\mathfrak{q}}^{*}\parallel }^2,\xi \in [0,1],\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathcal{H}.$

Lemma 2

([39]). Let $\mathcal{H}$ be a real Hilbert space. Let $\mathcal{P}:\mathcal{H}\to \mathcal{H}$ be a γ-inverse strongly monotone and $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ be a maximal monontone mapping. Then, the following relation hold:

$$\mathrm{Fix}\left(J_{\lambda }^{\mathcal{Q}}(I-\lambda \mathcal{P})\right)={(\mathcal{P}+\mathcal{Q})}^{-1}\left(0\right),\lambda >0.$$

Lemma 3

([40]). Let $\left\{{\zeta }_m\right\}$ be a sequence of non-negative real numbers such that

$${\zeta }_{m+1}\le (1-{\delta }_m){\zeta }_m+{\zeta }_m{\tau }_m+{\gamma }_m,m\ge 0,$$

where $\left\{{\delta }_m\right\}\subset (0,1)$ and $\left\{{\tau }_m\right\}$ is a sequence in $\mathbb{R}$ satisfy the following conditions:

(i)

${\displaystyle \sum _{m=1}^{\infty }}{\delta }_m=\infty ;$

(ii)

$\underset{m\to \infty }{lim\; sup}{\tau }_m\le 0$;

(iii)

${\gamma }_m\ge 0(m\ge 1$), ${\displaystyle \sum _{m=1}^{\infty }}{\gamma }_m<\infty$.

Then, $\underset{m\to \infty }{lim}{\zeta }_m=0$.

Lemma 4

([41]). Let $\left\{l_m\right\}$ be a sequence of real numbers that does not decrease at infinity in the sense that a subsequence $\left\{l_{m_i}\right\}$ of $\left\{l_m\right\}$ exists such that $l_{m_i}<l_{m_i+1},$ $\forall i\ge 0.$ Additionally, consider the sequence of integers ${\left\{f\left(m\right)\right\}}_{m\ge m_0}$ defined by

$$f\left(m\right)=\max \{k\le m:l_k\le l_{k+1}\}.$$

Then, ${\left\{f\left(m\right)\right\}}_{m\ge m_0}$ is a non-decreasing sequence that verifies $\underset{m\to \infty }{lim}f\left(m\right)=\infty$ and for all $m\ge m_0$,

$$\max \{l_{f\left(m\right)},l_m\}\le l_{f\left(m\right)+1}.$$

3. Main Result

In this section, we prove a strong convergence theorem based on the inertial Tseng splitting iterative method to compute a common solution of the variational inequality problem (1) and monotone inclusion problem (2).

Theorem 1.

Let $\mathcal{H}$ be a real Hilbert space and $\mathcal{D}$ be a nonempty, closed and convex subset of $\mathcal{H}$. Let $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ be a multivalued maximal monotone mapping, $\mathcal{P}:\mathcal{H}\to \mathcal{H}$ be monotone and $\mathcal{L}$-Lipschitz continuous and $\mathcal{T}:\mathcal{D}\to \mathcal{H}$ be a γ-inverse strongly monotone mapping. Let $\psi :\mathcal{H}\to \mathcal{H}$ be τ-Lipschitz continuous with $\tau \in [0,1)$ such that $\mathcal{J}=\mathrm{VI}(\mathcal{D},\mathcal{T})\cap \Gamma \ne \varphi .$ For given $v_0,v_1\in \mathcal{D},$ let the sequences $\left\{v_m\right\}$, $\left\{w_m\right\}$, $\left\{z_m\right\}$, $\left\{y_m\right\}$, and $\left\{s_m\right\}$ be generated as follows:

$$\left\{\begin{array}{c}{w}_m=v_m+{\theta }_m(v_m-v_{m-1}),\hfill \\ z_m=P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T})w_m,\hfill \\ y_m={(I+{\lambda }_m\mathcal{Q})}^{-1}(I-{\lambda }_m\mathcal{P})z_m,\hfill \\ s_m=y_m-{\lambda }_m(\mathcal{P}{y}_m-\mathcal{P}{z}_m),\hfill \\ v_{m+1}={\xi }_m\psi \left(v_m\right)+(1-{\xi }_m)s_m,\forall m\ge 1,\hfill \end{array}\right.$$

(9)

where

$${\lambda }_{m+1}=\left\{\begin{array}{cc}\min \left\{\frac{\mu \parallel z_m-y_m\parallel }{\parallel \mathcal{P}{z}_m-\mathcal{P}{y}_m\parallel },{\lambda }_m\right\}\hfill & \mathit{if}\parallel \mathcal{P}{z}_m-\mathcal{P}{y}_m\parallel \ne 0;\hfill \\ {\lambda }_m\hfill & else,\hfill \end{array}\right.$$

(10)

where $\left\{{\xi }_m\right\},\left\{{\theta }_m\right\}$ are two sequences in (0,1), $\lambda >0,$ and $\mu \in (0,1)$. Moreover, let the following conditions hold:

(i)

$\underset{m\to \infty }{lim}{\xi }_m=0$ and ${\displaystyle \sum _{m=0}^{\infty }}{\xi }_m=\infty ;$

(ii)

$0<\underset{m\to \infty }{lim\; inf}{\lambda }_m\le \underset{m\to \infty }{lim\; sup}{\lambda }_m<2\gamma ;$

(iii)

$\underset{m\to \infty }{lim}\frac{{\theta }_m}{{\xi }_m}\parallel v_m-v_{m-1}\parallel =0$ and $\underset{m\to \infty }{lim}{\theta }_m\parallel v_m-v_{m-1}\parallel =0.$

Then, the sequence $\left\{v_m\right\}$ converges strongly to an element ${\mathfrak{g}}^{*}\in \mathcal{J}$, where ${\mathfrak{g}}^{*}=P_{\mathcal{J}}\psi \left({\mathfrak{g}}^{*}\right).$

We also need the following lemma to prove Theorem 1.

Lemma 5

([42]). Let $\left\{y_m\right\}$ be a sequence induced by (9). Then, for all ${\mathfrak{g}}^{*}\in \Gamma$

$$\parallel s_m-{\mathfrak{g}}^{*}{\parallel }^2\le \parallel z_m-{\mathfrak{g}}^{*}{\parallel }^2-\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right){\parallel z_m-y_m\parallel }^2,$$

(11)

and

$$\parallel s_m-y_m\parallel \le \mu \frac{{\lambda }_m}{{\lambda }_{m+1}}\parallel z_m-y_m\parallel .$$

(12)

Proof of Theorem 1.

Let ${\mathfrak{g}}^{*}\in \mathcal{J}$; by Lemma 5, we have

$$\parallel s_m-{\mathfrak{g}}^{*}{\parallel }^2\le \parallel z_m-{\mathfrak{g}}^{*}{\parallel }^2-\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right){\parallel z_m-y_m\parallel }^2,$$

(13)

and

$$\parallel s_m-y_m\parallel \le \mu \frac{{\lambda }_m}{{\lambda }_{m+1}}\parallel z_m-y_m\parallel .$$

(14)

From (13), it can be written as

$$\parallel s_m-{\mathfrak{g}}^{*}\parallel \le \parallel z_m-{\mathfrak{g}}^{*}\parallel .$$

(15)

Moreover, we observe that

$$\begin{array}{cc}\hfill \parallel w_m-{\mathfrak{g}}^{*}\parallel & =\parallel v_m+{\theta }_m(v_m-v_{m-1})-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le \parallel v_m-{\mathfrak{g}}^{*}\parallel +{\theta }_m\parallel v_m-v_{m-1}\parallel ,\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill \parallel z_m-{\mathfrak{g}}^{*}\parallel & =\parallel P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T})w_m-{\mathfrak{g}}^{*}\parallel \hfill \end{array}$$

$$\begin{array}{cc}\hfill & \le \parallel w_m-{\mathfrak{g}}^{*}\parallel \hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \le \parallel v_m-{\mathfrak{g}}^{*}\parallel +{\theta }_m\parallel v_m-v_{m-1}\parallel ,\hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill \parallel y_m-{\mathfrak{g}}^{*}\parallel & =\parallel J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})z_m-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le \parallel z_m-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le \parallel v_m-{\mathfrak{g}}^{*}\parallel +{\theta }_m\parallel v_m-v_{m-1}\parallel .\hfill \end{array}$$

(19)

Consider

$$\begin{array}{cc}\hfill \parallel v_{m+1}-{\mathfrak{g}}^{*}\parallel & =\parallel {\xi }_m\psi \left(v_m\right)+(1-{\xi }_m)s_m-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le {\xi }_m\parallel \psi \left(v_m\right)-{\mathfrak{g}}^{*}\parallel +(1-{\xi }_m)\parallel s_m-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le {\xi }_m\parallel \psi \left(v_m\right)-\psi \left({\mathfrak{g}}^{*}\right)\parallel +{\xi }_m\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel +(1-{\xi }_m)\parallel s_m-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le {\xi }_m\parallel \psi \left(v_m\right)-\psi \left({\mathfrak{g}}^{*}\right)\parallel +{\xi }_m\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel +(1-{\xi }_m)\parallel z_m-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le {\xi }_m\tau \parallel v_m-{\mathfrak{g}}^{*}\parallel +{\xi }_m\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel +(1-{\xi }_m)(\parallel v_m-{\mathfrak{g}}^{*}\parallel +{\theta }_m\parallel v_m-v_{m+1}\parallel )\hfill \\ \hfill & \le (1-{\xi }_m(1-\tau ))\parallel v_m-{\mathfrak{g}}^{*}\parallel +{\xi }_m(1-\tau )\frac{\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel }{(1-\tau )}\hfill \\ \hfill & +(1-{\xi }_m(1-\tau )){\theta }_m\parallel v_m-v_{m-1}\parallel \hfill \\ \hfill & \le \max \left\{\parallel v_m-{\mathfrak{g}}^{*}\parallel +{\theta }_m\parallel v_m-v_{m-1}\parallel ,(1-\tau )\frac{\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel }{(1-\tau )}\right\}\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le \max \left\{\parallel v_1-{\mathfrak{g}}^{*}\parallel +{\theta }_1\parallel v_1-v_0\parallel ,(1-\tau )\frac{\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel }{(1-\tau )}\right\}.\hfill \end{array}$$

Thus, sequence $\left\{v_m\right\}$ generated by (9) is bounded and so are the sequences $\left\{w_m\right\}$, $\left\{z_m\right\}$, $\left\{y_m\right\}$, and $\left\{s_m\right\}$.

Next, we observe that

$$\begin{array}{cc}\hfill \parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2& =\parallel v_m+{\theta }_m(v_m-v_{m-1})-{\mathfrak{g}}^{*}{\parallel }^2\hfill \\ \hfill & =\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+2{\theta }_m⟨v_m-v_{m-1},v_m-{\mathfrak{g}}^{*}⟩+{\theta }_m^2{\parallel v_m-v_{m-1}\parallel }^2.\hfill \end{array}$$

(20)

It follows that

$$\begin{array}{cc}\hfill \parallel (v_m-v_{m-1})-(v_m-{\mathfrak{g}}^{*}){\parallel }^2& =\parallel v_m-v_{m-1}{\parallel }^2-2⟨v_m-v_{m-1},v_m-{\mathfrak{g}}^{*}⟩+{\parallel v_m-{\mathfrak{g}}^{*}\parallel }^2,\hfill \end{array}$$

and

$$2{\theta }_m⟨v_m-v_{m-1},v_m-{\mathfrak{g}}^{*}⟩={\theta }_m\parallel v_m-v_{m-1}{\parallel }^2+{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2).$$

(21)

Then, by combining (20) with (21), we have

$$\begin{array}{cc}\hfill \parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2& =\parallel v_m+{\theta }_m(v_m-v_{m-1})-{\mathfrak{g}}^{*}{\parallel }^2\hfill \\ \hfill & =\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+2{\theta }_m⟨v_m-v_{m-1},v_m-{\mathfrak{g}}^{*}⟩+{\theta }_m^2{\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & =\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+{\theta }_m\parallel v_m-v_{m-1}{\parallel }^2+{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & +{\theta }_m^2{\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & \le \parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+{\theta }_m(1+{\theta }_m)\parallel v_m-v_{m-1}{\parallel }^2+{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & \le \parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+2{\theta }_m\parallel v_m-v_{m-1}{\parallel }^2+{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2).\hfill \end{array}$$

(22)

From (13) and (17) and (22), we have

$$\begin{array}{cc}\hfill \parallel s_m-{\mathfrak{g}}^{*}{\parallel }^2& \le \parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+2{\theta }_m\parallel v_m-v_{m-1}{\parallel }^2+{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & -\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right){\parallel z_m-y_m\parallel }^2.\hfill \end{array}$$

(23)

Consider

$$\begin{array}{cc}\hfill \parallel v_{m+1}-{\mathfrak{g}}^{*}{\parallel }^2& =⟨v_{m+1}-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & =⟨{\xi }_m\psi \left(v_m\right)+(1-{\xi }_m)s_m-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & ={\xi }_m⟨\psi \left(v_m\right)-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩+(1-{\xi }_m)⟨s_m-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & \le \frac{{\xi }_m}{2}\left(\parallel \psi \left(v_m\right)-\psi \left({\mathfrak{g}}^{*}\right){\parallel }^2+{\parallel v_{m+1}-{\mathfrak{g}}^{*}\parallel }^2\right)+{\xi }_m⟨\psi \left(v_m\right)-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & +\frac{(1-{\xi }_m)}{2}\left(\parallel s_m-{\mathfrak{g}}^{*}{\parallel }^2+{\parallel v_{m+1}-{\mathfrak{g}}^{*}\parallel }^2\right)\hfill \\ \hfill & \le \frac{{\xi }_m}{2}\left(\parallel \psi \left(v_m\right)-\psi \left({\mathfrak{g}}^{*}\right){\parallel }^2+{\parallel v_{m+1}-{\mathfrak{g}}^{*}\parallel }^2\right)+{\xi }_m⟨\psi \left(v_m\right)-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & +\frac{(1-{\xi }_m)}{2}(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+2{\theta }_m{\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & +{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & -\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right)\parallel z_m-y_m{\parallel }^2+{\parallel v_{m+1}-{\mathfrak{g}}^{*}\parallel }^2)\hfill \\ \hfill & \le \frac{(1-{\xi }_m(1-{\tau }^2))}{2}\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+\frac{1}{2}{\parallel v_{m+1}-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +{\xi }_m⟨\psi \left(v_m\right)-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & +{\theta }_m(1-{\xi }_m)\parallel v_m-v_{m-1}{\parallel }^2+\frac{(1-{\xi }_m)}{2}{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & -\frac{(1-{\xi }_m)}{2}\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right){\parallel z_m-y_m\parallel }^2.\hfill \end{array}$$

(24)

It follows that

$$\begin{array}{cc}\hfill \parallel v_{m+1}-{\mathfrak{g}}^{*}{\parallel }^2& =(1-{\xi }_m(1-{\tau }^2)){\parallel v_m-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +{\xi }_m(1-{\tau }^2)\left(\frac{2}{(1-{\tau }^2)}⟨\psi \left(v_m\right)-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\right)\hfill \\ \hfill & +2{\theta }_m(1-{\xi }_m)\parallel v_m-v_{m-1}{\parallel }^2+(1-{\xi }_m){\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & -(1-{\xi }_m)\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right){\parallel z_m-y_m\parallel }^2.\hfill \end{array}$$

(25)

Therefore, we obtain

$$\begin{array}{cc}\hfill (1-{\xi }_m)\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right){\parallel z_m-y_m\parallel }^2& \le \parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-{\parallel v_{m+1}-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +2{\theta }_m(1-{\xi }_m){\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & +(1-{\xi }_m){\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & +{\xi }_m(1-{\tau }^2)\left(\frac{2}{(1-{\tau }^2)}⟨\psi \left(v_m\right)-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\right).\hfill \end{array}$$

(26)

Moreover, by using (25), we obtain

$$\begin{array}{cc}\hfill \parallel v_{m+1}-{\mathfrak{g}}^{*}{\parallel }^2& \le (1-{\xi }_m(1-{\tau }^2)){\parallel v_m-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +{\xi }_m(1-{\tau }^2)\{\frac{2}{(1-{\tau }^2)}⟨\psi \left(v_m\right)-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & +\left(\frac{2{\theta }_m(1-{\xi }_m)}{(1-{\tau }^2){\xi }_m}\right){\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & +\left(\frac{(1-{\xi }_m){\theta }_m}{(1-{\tau }^2){\xi }_m}\right)\parallel v_m-v_{m-1}\parallel (\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\}\hfill \\ \hfill & -(1-{\xi }_m)\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right){\parallel z_m-y_m\parallel }^2.\hfill \end{array}$$

(27)

Now, we suppose two possible cases to show that $\underset{m\to \infty }{lim}\parallel v_m-{\mathfrak{g}}^{*}\parallel =0.$

Case I: Assume that the sequence $\left\{l_m\right\}=\{\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2\}$ is non-increasing; then, there exists $m_0\in \mathbb{N}$ such that $l_{m+1}\le l_m$ for every $m\ge m_0$. Hence, $l_m$ converges.

Since $\underset{m\to \infty }{lim}{\xi }_m=0,$ and $\underset{m\to \infty }{lim}\left(1-{\mu }^2\frac{{\lambda }_m^2}{{\lambda }_{m+1}^2}\right)>0,$ we obtain from (26) that

$$\underset{m\to \infty }{lim}\parallel z_m-y_m\parallel =0.$$

(28)

Thus, from (14), we have

$$\underset{m\to \infty }{lim}\parallel s_m-y_m\parallel =0.$$

(29)

If we consider

$$\parallel s_m-z_m\parallel \le \parallel s_m-y_m\parallel +\parallel y_m-z_m\parallel ,$$

from (28) and (29), we obtain

$$\underset{m\to \infty }{lim}\parallel s_m-z_m\parallel =0.$$

(30)

Now, from (9), we have

$$\begin{array}{cc}\hfill \parallel z_m-{\mathfrak{g}}^{*}{\parallel }^2& =\parallel P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T})w_m-{\mathfrak{g}}^{*}{\parallel }^2\hfill \\ \hfill & =\parallel P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T})w_m-P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T}){\mathfrak{g}}^{*}{\parallel }^2\hfill \\ \hfill & \le \parallel (w_m-{\lambda }_m\mathcal{T}{w}_m)-({\mathfrak{g}}^{*}-{\lambda }_m\mathcal{T}{\mathfrak{g}}^{*}){\parallel }^2\hfill \\ \hfill & =\parallel (w_m-{\mathfrak{g}}^{*})-{\lambda }_m(\mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}){\parallel }^2\hfill \\ \hfill & =\parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2-2{\lambda }_m⟨\mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*},w_m-{\mathfrak{g}}^{*}⟩+{\lambda }_m^2{\parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & \le \parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2-2{\lambda }_m\gamma \parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}{\parallel }^2+{\lambda }_m^2{\parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & =\parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2+{\lambda }_m({\lambda }_m-2\gamma ){\parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel }^2.\hfill \end{array}$$

(31)

It follows from (22) that

$$\begin{array}{cc}\hfill \parallel v_{m+1}-{\mathfrak{g}}^{*}{\parallel }^2& =\parallel {\xi }_m\psi \left(v_m\right)+(1-{\xi }_m)s_m-{\mathfrak{g}}^{*}{\parallel }^2\hfill \\ \hfill & \le {\xi }_m\parallel \psi \left(v_m\right)-{\mathfrak{g}}^{*}{\parallel }^2+(1-{\xi }_m){\parallel s_m-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & \le {\xi }_m\parallel \psi \left(v_m\right)-\psi \left({\mathfrak{g}}^{*}\right){\parallel }^2+{\xi }_m\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}{\parallel }^2+(1-{\xi }_m){\parallel z_m-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +2{\xi }_m\parallel v_m-{\mathfrak{g}}^{*}\parallel \parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le {\xi }_m{\parallel v_m-{\mathfrak{g}}^{*}\parallel }^2+{\xi }_m\left(\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}{\parallel }^2+2\parallel v_m-{\mathfrak{g}}^{*}\parallel \parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel \right)\hfill \\ \hfill & +(1-{\xi }_m)\left(\parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2+{\lambda }_m({\lambda }_m-2\gamma ){\parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel }^2\right)\hfill \\ \hfill & \le {\xi }_m{\parallel v_m-{\mathfrak{g}}^{*}\parallel }^2+{\xi }_m\left(\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}{\parallel }^2+2\parallel v_m-{\mathfrak{g}}^{*}\parallel \parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel \right)\hfill \\ \hfill & +(1-{\xi }_m)(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+2{\theta }_m{\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & +{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)+{\lambda }_m({\lambda }_m-2\gamma ){\parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel }^2),\hfill \end{array}$$

(32)

which implies

$$\begin{array}{cc}\hfill {\lambda }_m(2\gamma -{\lambda }_m){\parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel }^2& \le \parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m+1}-{\mathfrak{g}}^{*}{\parallel }^2+{\xi }_m({\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +2\parallel v_m-{\mathfrak{g}}^{*}\parallel \parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel )+2(1-{\xi }_m){\theta }_m{\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & +(1-{\xi }_m){\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2).\hfill \end{array}$$

(33)

Using conditions (i) and (iii) and fact that $\underset{m\to \infty }{lim}\parallel v_m-{\mathfrak{g}}^{*}\parallel$ exists, we have

$$\underset{m\to \infty }{lim}\parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel =0.$$

(34)

From Lemma 1 (i), we compute

$$\begin{array}{cc}\hfill \parallel z_m-{\mathfrak{g}}^{*}{\parallel }^2& =\parallel P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T})w_m-{\mathfrak{g}}^{*}{\parallel }^2\hfill \\ \hfill & =\parallel P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T})w_m-P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T}){\mathfrak{g}}^{*}{\parallel }^2\hfill \\ \hfill & \le ⟨z_m-{\mathfrak{g}}^{*},(w_m-{\lambda }_m\mathcal{T}{w}_m)-({\mathfrak{g}}^{*}-{\lambda }_m\mathcal{T}{\mathfrak{g}}^{*})⟩\hfill \\ \hfill & \le \frac{1}{2}\{\parallel z_m-{\mathfrak{g}}^{*}{\parallel }^2+{\parallel (w_m-{\lambda }_m\mathcal{T}{w}_m)-({\mathfrak{g}}^{*}-{\lambda }_m\mathcal{T}{\mathfrak{g}}^{*})\parallel }^2\hfill \\ \hfill & -\parallel (z_m-w_m)+{\lambda }_m(\mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}){\parallel }^2\}\hfill \\ \hfill & \le \frac{1}{2}\left\{\parallel z_m-{\mathfrak{g}}^{*}{\parallel }^2+\parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2-{\parallel (z_m-w_m)+{\lambda }_m(\mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*})\parallel }^2\right\}\hfill \\ \hfill & \le \parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel z_m-w_m{\parallel }^2-{\lambda }_m^2{\parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +2{\lambda }_m⟨z_m-w_m,\mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & \le \parallel z_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel z_m-w_m{\parallel }^2+2{\lambda }_m\parallel z_m-w_m\parallel \parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le \parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel z_m-w_m{\parallel }^2+2{\lambda }_m\parallel z_m-w_m\parallel \parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}\parallel .\hfill \end{array}$$

(35)

It follows from (22) and (35) that

$$\begin{array}{cc}\hfill \parallel v_{m+1}-{\mathfrak{g}}^{*}{\parallel }^2& =\parallel {\xi }_m\psi \left(v_m\right)+(1-{\xi }_m)s_m-{\mathfrak{g}}^{*}{\parallel }^2\hfill \\ \hfill & \le {\xi }_m\parallel \psi \left(v_m\right)-\psi \left({\mathfrak{g}}^{*}\right){\parallel }^2+{\xi }_m\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}{\parallel }^2+(1-{\xi }_m){\parallel z_m-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +2{\xi }_m\parallel v_m-{\mathfrak{g}}^{*}\parallel \parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel \hfill \\ \hfill & \le {\xi }_m{\parallel v_m-{\mathfrak{g}}^{*}\parallel }^2+{\xi }_m\left(\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}{\parallel }^2+2\parallel v_m-{\mathfrak{g}}^{*}\parallel \parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel \right)\hfill \\ \hfill & +(1-{\xi }_m)\left(\parallel w_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel z_m-w_m{\parallel }^2+2{\lambda }_m\parallel z_m-w_m\parallel \parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}{\parallel }^2\right)\hfill \\ \hfill & \le {\xi }_m{\parallel v_m-{\mathfrak{g}}^{*}\parallel }^2+{\xi }_m\left(\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}{\parallel }^2+2\parallel v_m-{\mathfrak{g}}^{*}\parallel \parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel \right)\hfill \\ \hfill & +(1-{\xi }_m)(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2+2{\theta }_m{\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & +{\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & -\parallel z_m-w_m{\parallel }^2+2{\lambda }_m\parallel z_m-w_m\parallel \parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}{\parallel }^2),\hfill \end{array}$$

(36)

which implies

$$\begin{array}{cc}\hfill (1-{\xi }_m)\parallel z_m-w_m\parallel & \le \parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m+1}-{\mathfrak{g}}^{*}{\parallel }^2+{\xi }_m({\parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel }^2\hfill \\ \hfill & +2\parallel v_m-{\mathfrak{g}}^{*}\parallel \parallel \psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*}\parallel )+2(1-{\xi }_m){\theta }_m{\parallel v_m-v_{m-1}\parallel }^2\hfill \\ \hfill & +(1-{\xi }_m){\theta }_m(\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{m-1}-{\mathfrak{g}}^{*}{\parallel }^2)\hfill \\ \hfill & +2{\lambda }_m(1-{\xi }_m)\parallel z_m-w_m\parallel \parallel \mathcal{T}{w}_m-\mathcal{T}{\mathfrak{g}}^{*}{\parallel }^2.\hfill \end{array}$$

As $\underset{m\to \infty }{lim}\parallel v_m-{\mathfrak{g}}^{*}\parallel$ exists, then using conditions (i), (iii), and (34), we have

$$\underset{m\to \infty }{lim}\parallel z_m-w_m\parallel =0.$$

(37)

Using (iii), we observe that

$$\underset{m\to \infty }{lim}\parallel w_m-v_m\parallel =\underset{m\to \infty }{lim}{\theta }_m\parallel v_m-v_{m-1}\parallel =0.$$

(38)

We can write

$$\begin{array}{cc}\hfill \parallel v_{m+1}-v_m\parallel & \le \parallel v_{m+1}-s_m\parallel +\parallel s_m-y_m\parallel +\parallel y_m-z_m\parallel +\parallel z_m-w_m\parallel +\parallel w_m-v_m\parallel \hfill \\ \hfill & \le {\xi }_m\parallel \psi \left(v_m\right)-s_m\parallel +\parallel s_m-y_m\parallel +\parallel y_m-z_m\parallel +\parallel z_m-w_m\parallel +\parallel w_m-v_m\parallel .\hfill \end{array}$$

(39)

This implies that

$$\underset{m\to \infty }{lim}\parallel v_{m+1}-v_m\parallel =0.$$

(40)

Since $\left\{v_m\right\}$ is bounded, take a subsequence $\left\{v_{m_k}\right\}$ of $\left\{v_m\right\}$ such that $v_{m_k}$ ⇀ ${\mathfrak{q}}^{*}$. Then, we have

$$\begin{array}{cc}\hfill \parallel (I-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})){\mathfrak{q}}^{*}{\parallel }^2& =⟨(I-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})){\mathfrak{q}}^{*},(I-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})){\mathfrak{q}}^{*}⟩\hfill \\ \hfill & =⟨(I-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})){\mathfrak{q}}^{*},{\mathfrak{q}}^{*}-z_{m_k}⟩\hfill \\ \hfill & +⟨(I-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})){\mathfrak{q}}^{*},z_{m_k}-w_{m_k}⟩\hfill \\ \hfill & +⟨(I-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})){\mathfrak{q}}^{*},w_{m_k}-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})w_{m_k}⟩\hfill \\ \hfill & +⟨(I-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})){\mathfrak{q}}^{*},J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})w_{m_k}-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P}){\mathfrak{q}}^{*}⟩.\hfill \end{array}$$

Using the fact that $\parallel w_m-v_m\parallel \to 0$, $\parallel z_m-w_m\parallel \to 0$, and $\parallel z_m-y_m\parallel \to 0,$ we obtain

$$\underset{m\to \infty }{lim}{\parallel (I-J_{{\lambda }_m}^B(I-{\lambda }_m\mathcal{P})){\mathfrak{q}}^{*}\parallel }^2=0.$$

Therefore ${\mathfrak{q}}^{*}\in \Gamma$. Next we show that ${\mathfrak{q}}^{*}\in \mathrm{VI}(\mathcal{D},\mathcal{T}).$

Since $\underset{m\to \infty }{lim}\parallel z_m-w_m\parallel =0$ and $\underset{m\to \infty }{lim}\parallel w_m-v_m\parallel =0$, there exist subsequences $\left\{z_{m_i}\right\}$ and $\left\{w_{m_i}\right\}$ of $\left\{z_m\right\}$ and $\left\{w_m\right\}$, respectively, such that $z_{m_i}\rightharpoonup {\mathfrak{q}}^{*}$ and $w_{m_i}\rightharpoonup {\mathfrak{q}}^{*}$. Define the mapping $\mathcal{Q}$ as follows:

$$\mathcal{Q}\left(z\right)=\left\{\begin{array}{cc}\mathcal{T}\left(z\right)+N_{\mathcal{D}}\left(z\right),\hfill & \mathrm{if}z\in \mathcal{D}\hfill \\ \varphi ,\hfill & \mathrm{if}z\notin \mathcal{D},\hfill \end{array}\right.$$

where $N_{\mathcal{D}}\left(z\right)=\{v\in \mathcal{H}:⟨z-u,v⟩\ge 0,\forall u\in \mathcal{D}\}$ is the normal cone to $\mathcal{D}$ at $z\in \mathcal{H}$. In this case, mapping $\mathcal{Q}$ is maximal monotone and $0\in \mathcal{Q}z$ mapping iff $z\in \mathrm{Sol}(\mathrm{VIP}\left(1\right))$. Let $(z,v)\in \mathrm{graph}\left(\mathcal{Q}\right)$, we have $v\in \mathcal{Q}z=\mathcal{T}z+N_{\mathcal{D}}\left(z\right)$ and, hence, $v-\mathcal{T}z\in N_{\mathcal{D}}\left(z\right)$. By the definition of $N_{\mathcal{D}}$, we have $⟨z-u,v-\mathcal{T}z⟩\ge 0,\forall u\in \mathcal{D}$. On the other hand, since $z_m=P_{\mathcal{D}}(w_m-{\lambda }_m\mathcal{T}{w}_m)$ and $z\in \mathcal{D}$, we have

$$⟨(w_m-{\lambda }_m\mathcal{T}{w}_m)-z_m,z_m-z⟩\ge 0.$$

This implies that

$$⟨z-z_m,\frac{z_m-w_m}{{\lambda }_m}+\mathcal{T}{w}_m⟩\ge 0.$$

Since $⟨z-u,v-\mathcal{T}z⟩\ge 0,\forall u\in \mathcal{D}$ and $z_{m_i}\in \mathcal{D}$, using the monotonicity of $\mathcal{T}$, we have

$$\begin{array}{cc}\hfill ⟨z-z_{m_i}⟩& \ge ⟨z-z_{m_i},\mathcal{T}z⟩\hfill \\ \hfill & \ge ⟨z-z_{m_i},\mathcal{T}z⟩-⟨z-z_{m_i},\frac{z_{m_i}-w_{m_i}}{{\lambda }_m}+\mathcal{T}{w}_{m_i}⟩\hfill \\ \hfill & =⟨z-z_{m_i},\mathcal{T}z-\mathcal{T}{z}_{m_i}⟩+⟨z-z_{m_i},\mathcal{T}{z}_{m_i}-\mathcal{T}{w}_{m_i}⟩\hfill \\ \hfill & -⟨z-z_{m_i},\frac{z_{m_i}-w_{m_i}}{{\lambda }_m}⟩\hfill \\ \hfill & \ge ⟨z-z_{m_i},\mathcal{T}{z}_{m_i}-\mathcal{T}{w}_{m_i}⟩-⟨z-z_{m_i},\frac{z_{m_i}-w_{m_i}}{{\lambda }_m}⟩.\hfill \end{array}$$

Since $\mathcal{T}$ is continuous, therefore, on taking limit $i\to \infty$, we have $⟨z-{\mathfrak{q}}^{*},v⟩\ge 0.$ Since $\mathcal{Q}$ is maximal monotone, we have ${\mathfrak{q}}^{*}\in {\mathcal{Q}}^{-1}\left(0\right)$ and, hence, ${\mathfrak{q}}^{*}\in \mathrm{VI}(\mathcal{D},\mathcal{T}).$ We obtain

$$\begin{array}{cc}\hfill \underset{m\to \infty }{lim\; sup}\frac{2}{1-{\tau }^2}⟨\psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*},v_{m+1}-{\mathfrak{g}}^{*}⟩& =\underset{m\to \infty }{lim\; sup}\frac{2}{1-{\tau }^2}⟨\psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*},v_{m_k}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & \le \frac{2}{1-{\tau }^2}⟨\psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*},{\mathfrak{q}}^{*}-{\mathfrak{g}}^{*}⟩\le 0.\hfill \end{array}$$

(41)

By Lemma 3 and using (27) and (41) and condition of paprameters, we can claim that the sequence $\left\{v_m\right\}$ strongly converges to ${\mathfrak{g}}^{*}=P_{\mathcal{J}}\psi \left({\mathfrak{g}}^{*}\right)$.

Case II: Assume that the sequence $\left\{l_m\right\}=\{\parallel v_m-{\mathfrak{g}}^{*}{\parallel }^2\}$ is increasing. Let $f:\mathbb{N}\to \mathbb{N}$ be a mapping for all $m\ge m_0$ values (where $m_0$ is large enough). This is defined by

$$f\left(m\right)=\max \{k\in \mathbb{N}:l_m\le l_{m+1}\}.$$

Then, $f\left(m\right)\to \infty \mathrm{as}m\to \infty$ and $l_{f\left(m\right)}\le l_{f\left(m\right)+1},$ for all $m\ge m_0$. By using (26) and the conditions of the parameters for each $m\ge m_0$, we have

$$\begin{array}{cc}\hfill \parallel z_{f\left(m\right)}-y_{f\left(m\right)}{\parallel }^2& \le l_{f\left(m\right)}-l_{f\left(m\right)+1}+2(1-{\xi }_{f\left(m\right)}){\theta }_{f\left(m\right)}{\parallel v_{f\left(m\right)}-v_{f\left(m\right)+1}\parallel }^2\hfill \\ \hfill & +{\xi }_{f\left(m\right)}(1-{\tau }^2)\left(\frac{2}{(1-{\tau }^2)}⟨f\left(m\right)-{\mathfrak{g}}^{*},v_{f\left(m\right)+1}-{\mathfrak{g}}^{*}⟩\right)\hfill \\ \hfill & +(1-{\xi }_{f\left(m\right)}){\theta }_{f\left(m\right)}(l_{f\left(m\right)}-l_{f\left(m\right)-1}).\hfill \end{array}$$

Using 3.1 (i), we conclude that

$$\underset{m\to \infty }{lim}\parallel z_{f\left(m\right)}-y_{f\left(m\right)}\parallel =0.$$

Furthermore, by following the proof in Case I, we obtain

$$\underset{m\to \infty }{lim}\parallel z_{f\left(m\right)}-w_{f\left(m\right)}\parallel =0,$$

and

$$\underset{m\to \infty }{lim\; sup}⟨\psi \left({\mathfrak{g}}^{*}\right)-{\mathfrak{g}}^{*},v_{f\left(m\right)+1}-{\mathfrak{g}}^{*}⟩\le 0.$$

(42)

From (27), we have

$$\begin{array}{cc}\hfill l_{f\left(m\right)+1}& \le (1-{\xi }_{f\left(m\right)}(1-{\tau }^2))l_{f\left(m\right)}+{\xi }_{f\left(m\right)}(1-{\tau }^2)\{\frac{2}{(1-{\tau }^2)}⟨\psi \left(v_m\right)-{\mathfrak{g}}^{*},v_{f\left(m\right)+1}-{\mathfrak{g}}^{*}⟩\hfill \\ \hfill & +\left(\frac{2{\theta }_{f\left(m\right)}(1-{\xi }_{f\left(m\right)})}{(1-{\tau }^2){\xi }_{f\left(m\right)}}\right){\parallel v_{f\left(m\right)}-v_{f\left(m\right)-1}\parallel }^2\hfill \\ \hfill & +\left(\frac{(1-{\xi }_{f\left(m\right)}){\theta }_{f\left(m\right)}}{(1-{\tau }^2){\xi }_{f\left(m\right)}}\right)\parallel v_{f\left(m\right)}-v_{f\left(m\right)+1}\parallel (\parallel v_{f\left(m\right)}-{\mathfrak{g}}^{*}{\parallel }^2-\parallel v_{f\left(m\right)+1}-{\mathfrak{g}}^{*}{\parallel }^2)\}\hfill \\ \hfill & -(1-{\xi }_{f\left(m\right)})\left(1-{\mu }^2\frac{{\lambda }_{f\left(m\right)}^2}{{\lambda }_{f\left(m\right)+1}^2}\right){\parallel z_{f\left(m\right)}-y_{f\left(m\right)}\parallel }^2.\hfill \end{array}$$

(43)

Using Lemma 3 to (43), using (42) and the conditions of all parameters, we obtain

$$\underset{m\to \infty }{lim}\parallel v_{f\left(m\right)+1}-{\mathfrak{g}}^{*}\parallel =0.$$

From Lemma 4, we obtain

$$\begin{array}{cc}\hfill 0\le \parallel v_m-{\mathfrak{g}}^{*}\parallel & \le \max \{\parallel v_m-{\mathfrak{g}}^{*}\parallel ,\parallel v_{f\left(m\right)}-{\mathfrak{g}}^{*}\parallel \}\hfill \\ \hfill & \le \parallel v_{f\left(m\right)+1}-{\mathfrak{g}}^{*}\parallel \to 0\mathrm{as}m\to \infty .\hfill \end{array}$$

Therefore $v_m\to {\mathfrak{g}}^{*},$ where ${\mathfrak{g}}^{*}=P_{\mathcal{J}}\psi \left({\mathfrak{g}}^{*}\right).$

4. Consequences

In this section, we deduce a special case from our main convergence theorem.

Setting ${\theta }_m=0$ in Theorem 1, we have the following result.

Corollary 1.

Let $\mathcal{H}$ be a real Hilbert space and let $\mathcal{D}$ be a nonempty, closed, and convex subset of $\mathcal{H}$. Let $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ be a multivalued maximal monotone mapping, $\mathcal{P}:\mathcal{H}\to \mathcal{H}$ be monotone and $\mathcal{L}$-Lipschitz continuous and $\mathcal{T}:\mathcal{D}\to \mathcal{H}$ be a γ-inverse strongly monotone mapping. Let $\psi :\mathcal{H}\to \mathcal{H}$ be τ-Lipschitz continuous with $\tau \in [0,1)$ such that $\mathcal{J}=\mathrm{VI}(\mathcal{D},\mathcal{T})\cap \Gamma \ne \varphi .$ For a given $v_0\in \mathcal{D},$ let the sequences $\left\{v_m\right\}$, $\left\{z_m\right\}$, $\left\{y_m\right\}$, and $\left\{s_m\right\}$ be generated as follows:

$$\left\{\begin{array}{c}{z}_m=P_{\mathcal{D}}(I-{\lambda }_m\mathcal{T})v_m,\hfill \\ y_m={(I+{\lambda }_m\mathcal{Q})}^{-1}(I-{\lambda }_m\mathcal{P})z_m,\hfill \\ s_m=y_m-{\lambda }_m(\mathcal{P}{y}_m-\mathcal{P}{z}_m),\hfill \\ v_{m+1}={\xi }_m\psi \left(v_m\right)+(1-{\xi }_m)s_m,\forall m\ge 1,\hfill \end{array}\right.$$

(44)

where

$${\lambda }_{m+1}=\left\{\begin{array}{cc}\min \left\{\frac{\mu \parallel z_m-y_m\parallel }{\parallel \mathcal{P}{z}_m-\mathcal{P}{y}_m\parallel },{\lambda }_m\right\}\hfill & \mathit{if}\parallel \mathcal{P}{z}_m-\mathcal{P}{y}_m\parallel \ne 0;\hfill \\ {\lambda }_m\hfill & else,\hfill \end{array}\right.$$

(45)

where $\left\{{\xi }_m\right\}$ is a sequence in (0,1), $\lambda >0$ and $\mu \in (0,1)$. Moreover, let the following conditions hold:

(i)

$\underset{m\to \infty }{lim}{\xi }_m=0$ and ${\displaystyle \sum _{m=0}^{\infty }}{\xi }_m=\infty ;$

(ii)

$0<\underset{m\to \infty }{lim\; inf}{\lambda }_m\le \underset{m\to \infty }{lim\; sup}{\lambda }_m<2\gamma .$

Then, the sequence $\left\{v_m\right\}$ converges strongly to an element ${\mathfrak{g}}^{*}\in \mathcal{J}$, where ${\mathfrak{g}}^{*}=P_{\mathcal{J}}\psi \left({\mathfrak{g}}^{*}\right).$

5. Numerical Experiment

In this section, we present a numerical result to demonstrate the applicability of our main result.

Let $\mathcal{H}=\mathcal{D}=\mathbb{R}$ be the set of all real numbers with the inner product represented by $⟨{\mathfrak{g}}^{*},{\mathfrak{q}}^{*}⟩={\mathfrak{g}}^{*}{\mathfrak{q}}^{*}$, $\forall {\mathfrak{g}}^{*},{\mathfrak{q}}^{*}\in \mathbb{R},$ and the equipped with usual norm $|·|$. Let $\mathcal{Q}:\mathcal{H}\to 2^{\mathcal{H}}$ be defined by $\mathcal{Q}=\left\{3{\mathfrak{g}}^{*}\right\},\forall {\mathfrak{g}}^{*}\in \mathcal{H}$ and let $\mathcal{P}:\mathcal{H}\to \mathcal{H}$ be defined by $\mathcal{P}\left({\mathfrak{g}}^{*}\right)=\frac{{\mathfrak{g}}^{*}}{3},\forall {\mathfrak{g}}^{*}\in \mathcal{H}.$ Let the mapping $\mathcal{T}:\mathcal{D}\to \mathcal{H}$ be defined by $\mathcal{T}\left({\mathfrak{g}}^{*}\right)=2{\mathfrak{g}}^{*},\forall {\mathfrak{g}}^{*}\in \mathcal{D};$ let the mapping $\psi :\mathcal{H}\to \mathcal{H}$ be defined by $\psi \left({\mathfrak{g}}^{*}\right)=\frac{{\mathfrak{g}}^{*}}{5},\forall {\mathfrak{g}}^{*}\in \mathcal{H}.$

It is easy to see that $\mathcal{P}$ is $\mathcal{L}$- Lipschitz continuous and monotone with $\mathcal{L}=\frac{1}{3}$, $\psi$ is a $\tau$-Lipschitz continuous with $\tau =\frac{1}{5}$, and $\mathcal{T}$ is $\gamma$-inverse strongly monotone mapping with $\gamma =\frac{1}{2}$. Let us choose ${\lambda }_m=0.4$, ${\theta }_m=0.9$ and ${\xi }_m=\frac{1}{m+4},\forall m\ge 1$. Furthermore, we observe that $\mathrm{VI}(\mathcal{D},\mathcal{T})=\left\{0\right\}$ and $\Gamma =\left\{0\right\}$; hence, $\mathcal{J}=\mathrm{VI}(\mathcal{D},\mathcal{T})\cap \Gamma =\left\{0\right\}$.

From Table 1 and Figure 1, it can be very well visualized that the sequence of iteration $\left\{v_m\right\}$ converges weakly to 0.

Table 1. Numerical results for different initial values $v_0$ and $v_1$.

No. of Iterations	${\mathit{v}}_0=5,{\mathit{v}}_1=4$	${\mathit{v}}_0=-5,{\mathit{v}}_1=-8$
1	5.000000	−5.000000
2	4.000000	−8.000000
3	0.378620	−1.113300
4	−0.223623	0.382014
5	−0.069201	0.153097
6	0.004352	−0.001065
7	0.006116	−0.011969
8	0.000776	−0.002098
9	−0.000338	0.000556
10	−0.000123	0.000267
11	0.000005	0.000004
12	0.000011	−0.000020
13	0.000002	−0.000004
14	−0.000001	0.000001
15	0.000000	0.000000

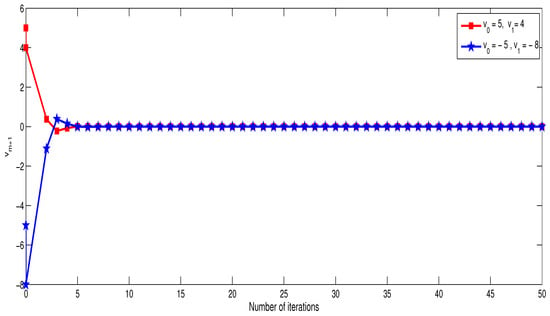
Figure 1. Convergence of sequence $\left\{v_m\right\}$.

6. Conclusions

In this paper, we developd and analyzed an inertial Tseng iterative method to find a common solution for the variational inequality problem and monotone inclusion problem with the help of the inertial Tseng method in the setting of real Hilbert spaces. Furthermore, we show that the sequences induced by the proposed iterative method converge strongly to an element of common solution of these problems. We also discuss a special cases deduced from our main convergence result. Finally, we present a numerical experiment to justify the main convergence theorem.