Bayesian Estimation Using MCMC Method of System Reliability for Inverted Topp–Leone Distribution Based on Ranked Set Sampling

Abstract

The current work focuses on ranked set sampling and a simple random sample as sampling approaches for determining stress–strength reliability from the inverted Topp–Leone distribution. Asymptotic confidence intervals are established, along with a maximum likelihood estimator of the parameters and stress–strength reliability. The reliability of such a system is assessed using the Bayesian approach under symmetric and asymmetric loss functions. The highest posterior density credible interval is constructed successively. The results are extracted using Monte Carlo simulation to compare the proposed estimators performance with different sample sizes. Finally, by looking at waiting time data and failure times of insulating fluid, the usefulness of the suggested technique is demonstrated.

1. Introduction

In reliability theory, the life of a component is described using stress–strength models, which include a random strength Y that is subjected to a random stress X. When the stress level applied to a component exceeds the strength level, the component fails instantly. Thus, $R=P(X<Y)$ is used to calculate component reliability. This measurement has a wide range of applications, most notably in the engineering industry, where it is used to monitor the degradation of rocket motors and structures, the fatigue failure of aircraft structures, the ageing of concrete pressure vessels, and the static fatigue of ceramic components. As a result, the estimation of $R=P(X<Y)$ is critical in practical applications.

Many authors presented a lot of papers about the estimation of $R=P(X<Y)$ for various distributions due to the practical point of view of reliability stress–strength model. For instance, the reader can see [1,2,3,4,5]. Multlak et al. [6] used Ranked-set sampling (RSS) in the case of the exponential distribution for estimating a stress–strength model. Dong et al. [7] used RSS to evaluate $R=P(Y<X)$ for an exponential distribution with unequal samples. It was used by Akgul et al. [8] for the Weibull distribution. Al-Omari et al. [9] investigated $R=P(Y<X)$ estimation in the case of exponentiated Pareto distribution, and Hassan et al. [10] analysed $R=P(Y<X)$ estimation in the case of generalized inverted exponential distribution. For more examples, see [11,12,13,14,15]. Different papers discussed inference on reliability estimation for a multi-component stress–strength model as [16,17] and Almetwally et al. [18] discussed $P(X<Y<Z)$ for the alpha power exponential model using progressive first failure. For a comprehensive review of studies of the stress–strength modeling, see Kotz et al. [19].

The most popular sampling strategy for data collection is simple random sampling (SRS). Ranking a number of sampling units without actually measuring them can be done reasonably simply and inexpensively in many applications (for example, in fisheries and medical research) when actual measurement of the variable of interest would be either time-consuming or expensive. In these situations, rank-based sampling designs may be used to obtain more representative samples from the underlying population and improve the efficiency of the statistical inference. RSS was initially proposed by McIntyre [20,21]. Several studies, either numerically or theoretically, have demonstrated the superiority of RSS-based statistical techniques over their analogues in SRS scheme. The one-cycle RSS involves an initial ranking of n samples of size n as follows:

$$\begin{array}{c}\hfill \begin{array}{cccc}1.& \underline{Z_{(1:n)1}}{Z}_{(2:n)1}& \cdots & Z_{(n:n)1}\to X_1=Z_{(1:n)1}\\ 2.& Z_{(1:n)2}\underline{Z_{(2:n)2}}& \cdots & Z_{(n:n)2}\to X_2=Z_{(2:n)2}\\ & ⋮& \ddots & ⋮\\ n.& Z_{(1:n)n}{Z}_{(2:n)n}& \cdots & \underline{Z_{(n:n)n}}\to X_n=Z_{(n:n)n}\end{array}\end{array}$$

where $Z_{(i:n)j}$ represents the ith order statistic from the jth SRS of size n. The resulting sample is known as one-cycle RSS of size n and it is denoted by $\underline{X}=(X_1,X_2,\dots ,X_n)$. $X_i$ has the same distribution as $Z_{\left(i\right)i}$, which is the ith order statistic in a set of size n obtained from the ith sample with probability density function (PDF) under the assumption of perfect judgment ranking, see Takahasi and Wakimoto [22].

$$\begin{array}{c}\hfill f_{\left(i\right)}\left(z\right)=\frac{n!}{(i-1)!(n-i)!}{\left[F\left(z\right)\right]}^{i-1}{[1-F\left(z\right)]}^{n-i}f\left(z\right),-\infty <z<\infty .\end{array}$$

(1)

The cycle can be repeated an m of times until $nm$ units are quantified.

Following that, several extensions to the original RSS were proposed. Extreme RSS–ERSS (Samawi et al. [23]) is based solely on units ranked at the extremes, whereas median RSS–MRSS (Muttlak [24]) only takes into account units ranked as the median for each set. Double RSS–DRSS (Al-Saleh and Al-Kadiri [25]) is a more efficient, but also more expensive, version of RSS that ranks a larger number of sets in two ordering stages, whereas paired RSS–PRSS (Hossain and Muttlak [26]) is a less expensive option that ranks a smaller number of units. A recently proposed sampling scheme can be found for different probability distributions including [27,28,29,30,31,32,33,34].

Inverted distributions are very important due to their applicability in many fields such as medical sciences, biological sciences, life test problems, and so on. In terms of density and hazard functions, inverted conformation distributions differ from non-inverted conformation distributions. Many researchers have discussed the applications of inverted distributions.

Hassan et al. [35] presented an inverted Topp–Leone (ITL) distribution with only one shape parameter $(\theta \ge 0)$, which is a recent significant model among the well-known inverted distributions. Its density and hazard functions take various shapes depending on the value of $\theta$, such as unimodal, right skewed, increasing, decreasing, and upside down. PDF and the cumulative distribution function (CDF) and the PDF of the ITL distribution with shape parameter $\theta$ are defined as follows:

$$\begin{array}{cc}\hfill f_X\left(x;\theta \right)& =2\theta x{(1+x)}^{(-2\theta -1)}{(1+2x)}^{\theta -1},x\ge 0,\theta >0,\hfill \end{array}$$

(2)

and

$$\begin{array}{cc}\hfill F_X\left(x;\theta \right)& =1-\frac{{(1+2x)}^{\theta }}{{(1+x)}^{2\theta }},x\ge 0,\theta >0.\hfill \end{array}$$

(3)

Plots of the PDF and CDF are represented in Figure 1. Aijaz et al. [36] obtained the Bayes posterior distribution and estimation of parameter of ITL distribution under both gamma (informative prior (IP)) and uniform (non-informative prior(NIP)).

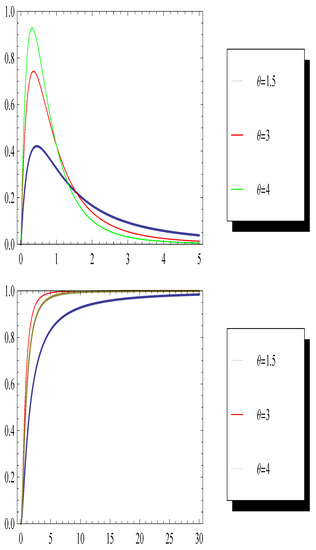
Figure 1. Plots of PDF and CDF distribution.

The reliability $R=P(X<Y)$ is derived, under the assumption that the random stress $X\sim ITL\left({\theta }_1\right)$ and the random strength $Y\sim ITL\left({\theta }_2\right)$ as follows:

$$\begin{array}{cc}\hfill R=P(X<Y)& ={\int }_0^{\infty }{F}_X\left(x;{\theta }_1\right)f_Y\left(x;{\theta }_2\right)dx\hfill \\ \hfill & =1-\sum _{j=0}^{\infty }\left(\genfrac{}{}{0pt}{}{{\theta }_1+{\theta }_2-1}{j}\right)2{\theta }_2\beta (j+2,{\theta }_1+{\theta }_2).\hfill \end{array}$$

(4)

where, β(j + 2, θ₁ + θ₂) is beta function, note that the reliability R depends on parameters ${\theta }_1$ and ${\theta }_2$, see Figure 2.

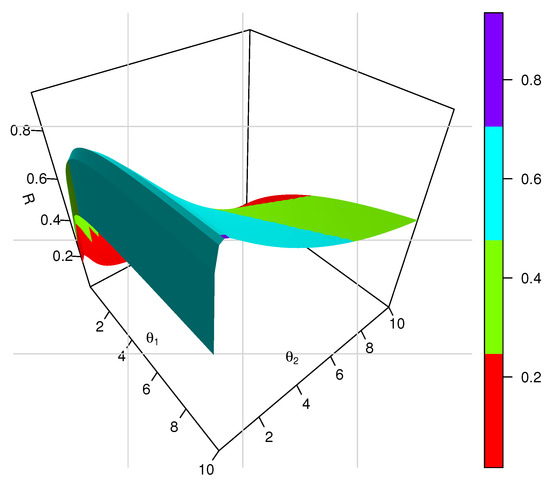
Figure 2. The reliability $R=P(X<Y)$.

The main objective of this paper is to obtain the maximum likelihood (ML) estimators (MLEs) and Bayesian estimators (BEs) of ${\theta }_1$, ${\theta }_2$, and R based on X and Y being two independent random variables, where $X\sim ITL\left({\theta }_1\right)$ and $Y\sim ITL\left({\theta }_2\right)$ using RSS. To determine how well the parameters and R estimators perform under SRS and RSS, a Monte Carlo simulation study is presented and then applied to the waiting times (in minutes) prior to customer service in two different banks as well as failure times of insulating fluid data.

This essay may be stated as follows. The present section introduces, justifies, obtains expression for the R and describes the subject of the current essay. In Section 2, we calculate the MLEs and construct asymptotic confidence intervals (ACI) for parameters and R based on SRS and RSS. The BEs and highest posterior density (HPD) credible intervals for R are derived based on SRS and RSS in Section 3. Section 4 considers a Monte Carlo simulation study to illustrate the performance of parameters and R estimators under SRS via RSS. In Section 5, waiting time data and failure times of insulating fluid data are used to indicate the proposed method’s application. Finally, Section 6 provides conclusions.

2. Maximum Likelihood Estimation of $\mathbf{R}$

In this section, we obtain the reliability estimator of R as well as the parameter estimator of ${\theta }_1$ and ${\theta }_2$ based on SRS and RSS. In addition, we display their ACI using the asymptotic distribution of MLE.

2.1. MLE Based on SRS

Here, using SRS, we obtain the MLE of R. To do this, we first need to get the MLE of ${\theta }_1$ and ${\theta }_2$. Let $X_i$, $i=(1,\dots ,n^{*})$ and $Y_j$, $j=(1,\dots ,m^{*})$ as independent SRS drawn from $X\sim ITL\left({\theta }_1\right)$ and $Y\sim ITL\left({\theta }_2\right)$, respectively. The likelihood function based on SRS is:

$$\begin{array}{cc}\hfill L& =\prod _{i=1}^{n^{*}}{f}_X\left(x_i\right)\prod _{j=1}^{m^{*}}{f}_Y\left(y_j\right)\hfill \\ \hfill & ={\left(2{\theta }_1\right)}^{n^{*}}{\left(2{\theta }_2\right)}^{m^{*}}\prod _{i=1}^{n^{*}}{x}_i{(1+x_i)}^{(-2{\theta }_1-1)}{(1+2x_i)}^{{\theta }_1-1}\prod _{j=1}^{m^{*}}{y}_j{(1+y_j)}^{(-2{\theta }_2-1)}{(1+2y_j)}^{{\theta }_2-1}.\hfill \end{array}$$

(5)

The log-likelihood function of the observed samples

$$\begin{array}{cc}\hfill l& =(n^{*}+m^{*})\ln 2+n^{*}\ln {\theta }_1+m^{*}\ln {\theta }_2+\sum _{i=1}^{n^{*}}\ln x_i-(2{\theta }_1+1)\sum _{i=1}^{n^{*}}\ln (1+x_i)\hfill \\ \hfill & +({\theta }_1-1)\sum _{i=1}^{n^{*}}\ln (1+2x_i)+\sum _{j=1}^{m^{*}}\ln y_j-(2{\theta }_2+1)\sum _{j=1}^{m^{*}}\ln (1+y_j)\hfill \\ \hfill & +({\theta }_2-1)\sum _{j=1}^{m^{*}}\ln (1+2y_j).\hfill \end{array}$$

(6)

The partial derivatives of (6) with respect to ${\theta }_1$ and ${\theta }_2$ to get the likelihood equations

$$\begin{array}{cc}\hfill \frac{\partial l}{\partial {\theta }_1}& =\frac{n^{*}}{{\theta }_1}-2\sum _{i=1}^{n^{*}}\ln (1+x_i)+\sum _{i=1}^{n^{*}}\ln (1+2x_i),\hfill \\ \hfill \frac{\partial l}{\partial {\theta }_2}& =\frac{m^{*}}{{\theta }_2}-2\sum _{j=1}^{m^{*}}\ln (1+y_j)+\sum _{j=1}^{m^{*}}\ln (1+2y_j).\hfill \end{array}$$

The MLEs of the parameters, say ${\widehat{\theta }}_{1SRS}$ and ${\widehat{\theta }}_{2SRS}$ have been obtained as follows

$$\begin{array}{cc}\hfill {\widehat{\theta }}_{1SRS}& =\frac{n^{*}}{{\displaystyle \sum _{i=1}^{n^{*}}\left[\ln \frac{{(1+x_i)}^2}{(1+2x_i)}\right]}},\hfill \\ \hfill {\widehat{\theta }}_{2SRS}& =\frac{m^{*}}{{\displaystyle \sum _{j=1}^{m^{*}}\left[\ln \frac{{(1+y_j)}^2}{(1+2y_j)}\right]}}.\hfill \end{array}$$

Thus, the MLE of reliability R based on SRS is obtained as

$$\begin{array}{c}\hfill {\widehat{R}}_{ML.SRS}=1-\sum _{j=0}^{\infty }\left(\genfrac{}{}{0pt}{}{{\widehat{\theta }}_{1SRS}+{\widehat{\theta }}_{2SRS}-1}{j}\right)2{\widehat{\theta }}_{2SRS}\beta (j+2,{\widehat{\theta }}_{1SRS}+{\widehat{\theta }}_{2SRS}).\end{array}$$

(7)

2.2. ACI Based on SRS

Deriving the asymptotic distribution of the MLE, R, yields the ACI for R as a function of parameters. First, we obtained the asymptotic distribution of ${\widehat{\theta }}_{1SRS}$ and ${\widehat{\theta }}_{2SRS}$ for this purpose.

$$\begin{array}{c}\hfill (\sqrt{n^{*}}\left({\widehat{\theta }}_{1SRS}-{\theta }_1\right),\sqrt{m^{*}}\left({\widehat{\theta }}_{2SRS}-{\theta }_2\right))\to N(0,I_{SRS}^{-1}\left(\mathit{\theta }\right)),\end{array}$$

(8)

where $I\left(\mathit{\theta }\right)=(-\frac{\partial l}{\partial {\theta }_i\partial {\theta }_j}),i,j=1,2,\mathit{\theta }=({\theta }_1,{\theta }_2)$, we obtained the elements of $I\left(\mathit{\theta }\right)$ by using the second partial derivatives of log-likelihood function (6) as follows.

$$\begin{array}{c}\hfill I_{SRS}(\theta )=\left[\begin{array}{cc}{I}_{11}& 0\\ 0& I_{22}\end{array}\right].\end{array}$$

where

$$\begin{array}{cc}\hfill I_{11}=\frac{{\partial }^{2}l}{\partial {\theta }_1^2}& =\frac{-n^{*}}{{\theta }_1^2},I_{22}=\frac{{\partial }^{2}l}{\partial {\theta }_2^2}=\frac{-m^{*}}{{\theta }_2^2},I_{12}=I_{21}=0.\hfill \end{array}$$

As $n^{*}\to \infty$ and $m^{*}\to \infty$, the asymptotic distribution of ${\widehat{R}}_{ML.SRS}$ is formulated by

$$\begin{array}{c}\hfill \frac{{\widehat{R}}_{ML.SRS}-R}{\sqrt{\frac{a_1^2}{n^{*}{I}_{11}}+\frac{a_2^2}{m^{*}{I}_{22}}}}\to N(0,1).\end{array}$$

(9)

where

$$\begin{array}{c}\hfill a_1=\frac{\partial R}{\partial {\theta }_1},a_2=\frac{\partial R}{\partial {\theta }_2}.\end{array}$$

Using the asymptotic distribution of $\widehat{R}$, $100(1-\zeta )\%$ ACI for the system reliability R is constructed as follows:

$$\begin{array}{c}\hfill \left({\widehat{R}}_{ML.SRS}-z_{\frac{\zeta }{2}}\sqrt{\frac{{\widehat{a}}_1^2}{n^{*}{\widehat{I}}_{11}}+\frac{{\widehat{a}}_2^2}{m^{*}{\widehat{I}}_{22}}},{\widehat{R}}_{ML.SRS}+z_{\frac{\zeta }{2}}\sqrt{\frac{{\widehat{a}}_1^2}{n^{*}{\widehat{I}}_{11}}+\frac{{\widehat{a}}_2^2}{m^{*}{\widehat{I}}_{22}}}\right).\end{array}$$

(10)

where $z_{\frac{\zeta }{2}}$ is the $100\zeta$th percentile of standard normal distribution.

2.3. MLE Based on RSS

Let $X_{i(i:n)s},i=1,\dots ,n,s=1,\dots ,p$ be s-cycle of RSS from the ITL(${\theta }_1$) and let $Y_{j(j:m)t},j=1,\dots ,m,t=1,\dots ,q$ be the t-cycle of RSS from the ITL(${\theta }_2$). In this case, n and m are the set sizes for X and Y, respectively. Also, p and q are the X and Y cycle sizes, respectively. Consequently, $n^{*}=np$ and $m^{*}=mq$ are the sample sizes of X and Y, respectively. We denote $X_{i(i:n)s}$ by $X_{is}$ and $Y_{j(j:m)t}$ by $Y_{jt}$ to simplify the notations. The likelihood function based on RSS is:

$$\begin{array}{cc}\hfill L(x_{is},y_{jt}|{\theta }_1,{\theta }_2)& =f_i\left(x_{is}\right|{\theta }_1)f_j\left(y_{jt}\right|{\theta }_2)=\sum _{k=0}^{i-1}{a}_k\left(i\right)h_k\left(x_{is}\right|{\theta }_1)\sum _{l=0}^{j-1}{b}_l\left(j\right)g_l\left(y_{jt}\right|{\theta }_2).\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill a_k\left(i\right)& =\sum _{k=0}^{i-1}i\left(\genfrac{}{}{0pt}{}{n}{i}\right)\left(\genfrac{}{}{0pt}{}{i-1}{k}\right){(-1)}^k,\hfill \\ \hfill h_k\left(x_{is}\right|{\theta }_1)& =2{\theta }_1\frac{x_{is}}{(1+x_{is})(1+2x_{is})}{\left[\frac{{(1+2x_{is})}^{{\theta }_1}}{{(1+x_{is})}^{2{\theta }_1}}\right]}^{n-i+k+1},\hfill \\ \hfill b_l\left(j\right)& =\sum _{l=0}^{j-1}j\left(\genfrac{}{}{0pt}{}{m}{j}\right)\left(\genfrac{}{}{0pt}{}{j-1}{l}\right){(-1)}^l,\hfill \\ \hfill g_l\left(y_{jt}\right|{\theta }_2)& =2{\theta }_2\frac{y_{jt}}{(1+y_{jt})(1+2y_{jt})}{\left[\frac{{(1+2y_{jt})}^{{\theta }_2}}{{(1+y_{jt})}^{2{\theta }_2}}\right]}^{m-j+l+1}.\hfill \end{array}$$

Then, the joint density of the RSS in this case is given by

$$\begin{array}{cc}\hfill L(\underline{x},\underline{y}|{\theta }_1,{\theta }_2)& =\prod _{s=1}^p\prod _{i=1}^n{f}_i\left(x_{is}\right|{\theta }_1)\prod _{t=1}^q\prod _{j=1}^m{f}_j\left(y_{jt}\right|{\theta }_2)\hfill \\ \hfill & =\left[\sum _{c_1^1=0}^0\sum _{c_2^1=0}^1...\sum _{c_n^1=0}^{n-1}\right]...\left[\sum _{c_1^p=0}^0\sum _{c_2^p=0}^1...\sum _{c_n^p=0}^{n-1}\right]\left[\prod _{s=1}^p\prod _{i=1}^n\frac{2a_{c_i^s}\left(i\right)x_{is}}{(1+x_{is})(1+2x_{is})}\right]{\theta }_1^{np}\hfill \\ \hfill & \times e^{{\theta }_1{\sum }_{s=1}^p{\sum }_{i=1}^{n}A\left(x_{is}\right)}\hfill \\ \hfill & \times \left[\sum _{d_1^1=0}^0\sum _{d_2^1=0}^1...\sum _{d_m^1=0}^{m-1}\right]...\left[\sum _{d_1^q=0}^0\sum _{d_2^q=0}^1...\sum _{d_m^q=0}^{m-1}\right]\left[\prod _{t=1}^q\prod _{j=1}^m\frac{2b_{d_j^t}\left(j\right)y_{jt}}{(1+y_{jt})(1+2y_{jt})}\right]{\theta }_2^{mq}\hfill \\ \hfill & \times e^{{\theta }_2{\sum }_{t=1}^q{\sum }_{j=1}^{m}B\left(y_{jt}\right)},\hfill \end{array}$$

(11)

where

$$\begin{array}{c}\hfill A\left(x_{is}\right)=(n-i+c_i+1)\ln \left(\frac{(1+2x_{is})}{{(1+x_{is})}^2}\right),\\ \hfill B\left(y_{jt}\right)=(m-j+d_j+1)\ln \left(\frac{(1+2y_{jt})}{{(1+y_{jt})}^2}\right).\end{array}$$

The log likelihood is given by

$$\begin{array}{cc}\hfill l(\underline{x},\underline{y}|{\theta }_1,{\theta }_2)& \propto np\ln {\theta }_1+{\theta }_1\sum _{s=1}^p\sum _{i=1}^{n}A\left(x_{is}\right)+mq\ln {\theta }_2+{\theta }_2\sum _{t=1}^q\sum _{j=1}^{m}B\left(y_{jt}\right).\hfill \end{array}$$

(12)

Calculating the first partial derivatives of (12) with respect to ${\theta }_1$ and ${\theta }_2$.

$$\begin{array}{cc}\hfill \frac{\partial l(\underline{x},\underline{y}|{\theta }_1,{\theta }_2)}{\partial {\theta }_1}& =\frac{np}{{\theta }_1}+\sum _{s=1}^p\sum _{i=1}^{n}A\left(x_{is}\right),\hfill \\ \hfill \frac{\partial l(\underline{x},\underline{y}|{\theta }_1,{\theta }_2)}{\partial {\theta }_2}& =\frac{mq}{{\theta }_2}+\sum _{t=1}^q\sum _{j=1}^{m}B\left(y_{jt}\right).\hfill \end{array}$$

The MLEs of the parameters, say ${\widehat{\theta }}_{1RSS}$ and ${\widehat{\theta }}_{2RSS}$, have been obtained as follows:

$$\begin{array}{c}\hfill {\widehat{\theta }}_{1RSS}=\frac{-np}{{\displaystyle \sum _{s=1}^p\sum _{i=1}^{n}A\left(x_{is}\right)}},\\ \hfill {\widehat{\theta }}_{2RSS}=\frac{-mq}{{\displaystyle \sum _{t=1}^q\sum _{j=1}^{m}B\left(y_{jt}\right)}}.\end{array}$$

Thus, the MLE of the reliability under RSS is obtained as

$$\begin{array}{c}\hfill {\widehat{R}}_{ML.RSS}=1-\sum _{j=0}^{\infty }\left(\genfrac{}{}{0pt}{}{{\widehat{\theta }}_{1RSS}+{\widehat{\theta }}_{2RSS}-1}{j}\right)2{\widehat{\theta }}_{2RSS}\beta (j+2,{\widehat{\theta }}_{1RSS}+{\widehat{\theta }}_{2RSS}).\end{array}$$

(13)

2.4. ACI Based on RSS

The Fisher information matrix based on RSS is defined below as

$$\begin{array}{c}\hfill I_{RSS}\left(\mathit{\theta }\right)=I_{SRS}\left(\mathit{\theta }\right)+(Q-1)\psi \left(\mathit{\theta }\right),\end{array}$$

(14)

where $Q=(n,m)$ is the set size and $I_{SRS}(\theta )$ is the Fisher information matrix based on SRS. Also,

$$\begin{array}{c}\hfill \psi \left(\mathit{\theta }\right)=E\left(\frac{DF(W;\mathit{\theta }){\left[DF(W;\mathit{\theta })\right]}^T}{F(W;\mathit{\theta })(1-F(W;\mathit{\theta }\left)\right)}\right),\end{array}$$

where $F(W;\mathit{\theta })$ is the CDF and $D=(D_1,D_2)={(\partial /\partial {\theta }_1,\partial /\partial {\theta }_2)}^T$ and $W=(X,Y)$. Thus

$$\left.\begin{array}{cc}\hfill \psi \left({\theta }_1\right)& =E\left(\frac{{\left(\acute{F}(x;{\theta }_1)\right)}^2}{F(x;{\theta }_1)(1-F(x;{\theta }_1))}\right)=E\left(\frac{\frac{{(1+2x)}^{{\theta }_1}}{{(1+x)}^{2{\theta }_1}}{\left(\ln \frac{(1+2x)}{{(1+x)}^2}\right)}^2}{1-\frac{{(1+2x)}^{{\theta }_1}}{{(1+x)}^{2{\theta }_1}}}\right),\hfill \\ \hfill \psi \left({\theta }_2\right)& =E\left(\frac{{\left(\acute{F}(y;{\theta }_2)\right)}^2}{F(y;{\theta }_2)(1-F(y;{\theta }_2))}\right)=E\left(\frac{\frac{{(1+2y)}^{{\theta }_2}}{{(1+y)}^{2{\theta }_2}}{\left(\ln \frac{(1+2y)}{{(1+y)}^2}\right)}^2}{1-\frac{{(1+2y)}^{{\theta }_2}}{{(1+y)}^{2{\theta }_2}}}\right).\hfill \end{array}\right\}$$

(15)

It is clear from (15) that obtaining the expected values’ explicit form is very difficult. Therefore, numerical methods are used. The Fisher information matrix based on RSS given in (14) in explicit form is very difficult. Therefore, numerical methods are used, shown as

$$\begin{array}{c}\hfill I_{RSS}(\theta )=\left(\begin{array}{cc}{I}_{11}& I_{12}\\ I_{21}& I_{22}\end{array}\right)=\left(\begin{array}{cc}{I}_{11}& 0\\ 0& I_{22}\end{array}\right),\end{array}$$

(16)

where

$$\begin{array}{cc}\hfill I_{11}& =\frac{-n}{{\theta }_1^2}+(n-1)\psi \left({\theta }_1\right),\hfill \\ \hfill I_{22}& =\frac{-m}{{\theta }_2^2}+(m-1)\psi \left({\theta }_2\right).\hfill \end{array}$$

The $100(1-\zeta )\%$ confidence interval for the system reliability R is constructed as follows in (10) with ${\widehat{R}}_{ML.RSS}$ replaced by ${\widehat{R}}_{ML.SRS}$.

3. Bayesian Inference of R

The Bayesian viewpoint has received a lot of attention in statistical inference as a powerful and valid alternative to classical estimation, see Korkmaz et al. [37], Aboraya et al. [38], and Elbatal et al. [39]. Its ability to incorporate prior information into the analysis makes it extremely effective in reliability, lifetime study, and other applications associated fields, where one of the major challenges is the limited supply of data.

We consider the Bayesian estimation for R under the assumption that the parameters of ITL distribution are unknown and have independent gamma conjugate prior distributions with the parameters $({\mu }_i,{\nu }_i),i=1,2$.

$$\begin{array}{c}\hfill \pi \left({\theta }_i\right)=\frac{{\theta }_i^{{\mu }_i-1}}{\Gamma \left({\mu }_i\right){\nu }_i^{{\mu }_i}}{e}^{-\frac{{\theta }_i}{{\nu }_i}},{\theta }_i>0,{\mu }_i,{\nu }_i>0,i=1,2.\end{array}$$

(17)

In addition, we derive the corresponding BEs using the symmetric loss function (squared error loss function (SELF)) and asymmetric loss function (LINEX).

3.1. Bayesian Inference of R Based on SRS

Using the prior (17) and the likelihood function (5), the joint posterior density can be derived as follows:

$$\begin{array}{cc}\hfill {\pi }_1^{*}({\theta }_1,{\theta }_2)& \propto {\theta }_1^{n^{*}+{\mu }_1-1}{\theta }_2^{m^{*}+{\mu }_2-1}{e}^{-(\frac{{\theta }_1}{{\nu }_1}+\frac{{\theta }_2}{{\nu }_2})}\prod _{i=1}^{n^{*}}{x}_i{(1+x_i)}^{(-2{\theta }_1-1)}{(1+2x_i)}^{{\theta }_1-1}\hfill \\ & \times \prod _{j=1}^{m^{*}}{y}_j{(1+y_j)}^{(-2{\theta }_2-1)}{(1+2y_j)}^{{\theta }_2-1}.\hfill \end{array}$$

(18)

Then, the Bayes estimator of R under SELF and LINEX loss function can be given as

$$\left.\begin{array}{cc}\hfill {\tilde{R}}_{CSE.SRS}& ={\int }_0^{\infty }{\int }_0^{\infty }R{\pi }_1^{*}({\theta }_1,{\theta }_2)d{\theta }_{1}d{\theta }_2,\hfill \\ \hfill {\tilde{R}}_{CLN.SRS}& =\frac{-1}{e}{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-eR}{\pi }_1^{*}({\theta }_1,{\theta }_2)d{\theta }_{1}d{\theta }_2.\hfill \end{array}\right\}$$

(19)

Clearly, it is not possible to compute (19) analytically, and such estimates are obtained from the Markov Chain Monte Carlo (MCMC) technique to obtain the Bayesian estimates and to construct the HPD.

3.2. Markov Chain Monte Carlo Method

In this subsection, we use MCMC method for deriving Bayesian estimates of parameters and R. The conditional posterior densities of the parameters ${\theta }_1$ and ${\theta }_2$ can be written as

$$\begin{array}{cc}\hfill {\pi }^{*}\left({\theta }_1\right|{\theta }_2)& \propto {\theta }_1^{n^{*}+{\mu }_1-1}{e}^{{\displaystyle -{\theta }_1(\frac{1}{{\nu }_1}+\sum _{i=1}^{n^{*}}\ln \left(\frac{{(1+x_i)}^2}{(1+2x_i)}\right))}},\hfill \\ \hfill {\pi }^{*}\left({\theta }_2\right|{\theta }_1)& \propto {\theta }_2^{m^{*}+{\mu }_2-1}{e}^{{\displaystyle -{\theta }_2(\frac{1}{{\nu }_2}+\sum _{j=1}^{m^{*}}\ln \left(\frac{{(1+y_j)}^2}{(1+2y_j)}\right))}}.\hfill \end{array}$$

It is clear that samples of ${\theta }_1$ and ${\theta }_2$ can be easily generated by using their conditional posterior distributions which are obtained above based on Gibbs sampling algorithm:

Step 1.

Set initial values for ${\theta }_1^{\left(0\right)}$ and ${\theta }_2^{\left(0\right)}$.

Step 2.

Set $k=1$.

Step 3.

Generate ${\theta }_1^{\left(k\right)}$ from ${\displaystyle Gamma(n^{*}+{\mu }_1,1/(\frac{1}{{\nu }_1}+\sum _{i=1}^{n^{*}}\ln \left(\frac{{(1+x_i)}^2}{(1+2x_i)}\right)))}$.

Step 4.

Generate ${\theta }_2^{\left(k\right)}$ from ${\displaystyle Gamma(m^{*}+{\mu }_2,1/(\frac{1}{{\nu }_2}+\sum _{j=1}^{m^{*}}\ln \left(\frac{{(1+y_j)}^2}{(1+2y_j)}\right)))}$.

Step 5.

Compute $R^{\left(k\right)}$ at ${\theta }_1^{\left(k\right)},{\theta }_2^{\left(k\right)}$.

Step 6.

Set $k=k+1$.

Step 7.

Repeat steps 2–6 N times and obtain a posterior sample $R^{\left(k\right)},k=1,\dots ,N$.

Step 8.

The Bayesian estimates of R under SELF and LINEX loss function are computed from following expressions

$$\left.\begin{array}{cc}\hfill {\tilde{R}}_{CSE.SRS}& =\frac{1}{N-M}\sum _{k=M+1}^N{R}^{\left(k\right)},\hfill \\ \hfill {\tilde{R}}_{CLN.SRS}& =\frac{-1}{e}\ln \left[\frac{1}{N-M}\sum _{k=M+1}^N{e}^{-e{R}^{\left(k\right)}}\right].\hfill \end{array}\right\}$$

(20)

Step 9.

Then $100(1-\zeta )\%$ credible interval of R becomes

$$\begin{array}{c}\hfill ({\tilde{R}}_{CSE.SRS\left[N\right(\zeta /2\left)\right]},{\tilde{R}}_{CSE.SRS\left[N\right(1-\zeta /2\left)\right]}).\end{array}$$

(21)

3.3. Bayesian Inference of R Based on RSS

Using the prior (17) and the likelihood function (11), the joint posterior density can be expressed as

$$\begin{array}{cc}\hfill {\pi }_2^{*}({\theta }_1,{\theta }_2)& \propto \left[{\displaystyle \prod _{s=1}^p\sum _{c_1^s=0}^0\sum _{c_2^s=0}^1\cdots \sum _{c_n^s=0}^{n-1}}\right]\left[{\displaystyle \prod _{s=1}^p\prod _{i=1}^n\frac{2a_{c_i^s}\left(i\right)x_{is}}{(1+x_{is})(1+2x_{is})}}\right]{\theta }_1^{np+{\mu }_1-1}{e}^{{\displaystyle -{\theta }_1(\frac{1}{{\nu }_1}-\sum _{s=1}^p\sum _{i=1}^{n}A\left(x_{is}\right))}}\hfill \\ \hfill & \times \left[{\displaystyle \prod _{t=1}^q\sum _{d_1^t=0}^0\sum _{d_2^t=0}^1...\sum _{d_m^t=0}^{m-1}}\right]\left[{\displaystyle \prod _{t=1}^q\prod _{j=1}^m\frac{2b_{d_j^t}\left(j\right)y_{jt}}{(1+y_{jt})(1+2y_{jt})}}\right]{\theta }_2^{mq+{\mu }_2-1}{e}^{{\displaystyle -{\theta }_2(\frac{1}{{\nu }_2}-\sum _{t=1}^q\sum _{j=1}^{m}B\left(y_{jt}\right))}}.\hfill \end{array}$$

(22)

Then, the Bayes estimator of R under SELF and LINEX loss function can be given as

$$\left.\begin{array}{cc}\hfill {\tilde{R}}_{CSE.RSS}& ={\int }_0^{\infty }{\int }_0^{\infty }R{\pi }_2^{*}({\theta }_1,{\theta }_2)d{\theta }_{1}d{\theta }_2,\hfill \\ \hfill {\tilde{R}}_{CLN.RSS}& =\frac{-1}{e}{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-eR}{\pi }_2^{*}({\theta }_1,{\theta }_2)d{\theta }_{1}d{\theta }_2.\hfill \end{array}\right\}$$

(23)

Similarly the integrals given in (23) cannot be calculated analytically. Therefore, we use Gibbs sampling which ${\displaystyle {\theta }_1\sim Gamma(np+{\mu }_1,1/(\frac{1}{{\nu }_1}-\sum _{s=1}^p\sum _{i=1}^{n}A\left(x_{is}\right)))}$ and ${\displaystyle {\theta }_2\sim Gamma(mq+{\mu }_2,1/(\frac{1}{{\nu }_2}-\sum _{t=1}^q\sum _{j=1}^{m}B\left(y_{jt}\right)))}$.

4. Simulation

In the following section, the ML and Bayesian estimations are compared based on SRS and RSS by using a Monte-Carlo simulation study to evaluate how well various approaches work with various sample sizes and parameter values. Due to the fact that we cannot theoretically compare the performances of the various strategies, some simulation findings are offered. We primarily look at how well the various methods for point and interval estimates of the reliability $R=P(X<Y)$ work when all the parameters are unknown. We mainly compute the biases, mean squared errors (MSEs), and length of confidence intervals (LCI) of the ML and Bayesian estimates with IP and NIP. The CIs of parameters and R by two methods as asymptotic CIs and HPD credible intervals of Bayesian estimation are obtained. In the Bayesian with Gamma prior, we select hyper parameters by elective hyper parameters as follows:

Using the known prior parameters ${\mu }_1$ and ${\nu }_1$, the parameter ${\theta }_1$ have been generated from $Gamma({\mu }_1,{\nu }_1)$. Using the known prior parameters ${\mu }_2$ and ${\nu }_2$, the parameter ${\theta }_2$ have been generated from $Gamma({\mu }_2,{\nu }_2)$.

We may utilize the estimate and variance-covariance matrix of the likelihood method to figure out how to elicit hyper-parameters of the independent joint prior. The calculated hyper-parameters can be represented by equating the mean and variance of gamma priors.

$${\mu }_i=\frac{{\left[\frac{1}{N}{\sum }_{j=1}^N\widehat{{\theta }_j^i}\right]}^2}{\frac{1}{N-1}{\sum }_{j=1}^N{\left[\widehat{{\theta }_j^i}-\frac{1}{N}{\sum }_{i=1}^N\widehat{{\theta }_j^i}\right]}^2};i=1,2,$$

$${\nu }_i=\frac{\frac{1}{N}{\sum }_{j=1}^N\widehat{{\theta }_j^i}}{\frac{1}{N-1}{\sum }_{j=1}^N{\left[\widehat{{\theta }_j^i}-\frac{1}{N}{\sum }_{i=1}^N\widehat{{\theta }_j^i}\right]}^2};i=1,2,$$

where N is the number of simulation iterations.

We consider set sizes $n=m$ = 2, 3, 4, 5, and 6 and number of cycles as $p=q=10$ for each stress and strength variable. Under RSS, the regarded sample sizes are $(n^{*},m^{*})=(20,20),$ (30, 30), (40, 40), (50, 50), $(60,60)$, where $n^{*}=np$, and $m^{*}=mq$. It should be noted that we use $(n^{*},m^{*}$) as sample sizes for SRS as 20, 30, 40, 50, and 60 for each stress and strength variable. For parameter values, we assume that ${\theta }_1=$ 0.5 and 3, ${\theta }_2=$ 0.5 and 3. All the results are based on 1000 replications. Under LINEX loss function, the value of e = 1.5 and −1.5. The MCMC Bayesian estimates are based on 10,000 sampling, namely, N = 10,000. In each case, the interval level for the CIs or the credible intervals is 95%. We also obtain the average biases, MSEs and LCI of the ML estimates by comparing SRS and RSS in Table 1. We obtain the average biases, MSEs and LCI of the Bayesian estimation with gamma prior by comparing SRS and RSS in Table 2. We obtain the average biases, MSEs and LCI of the Bayesian estimation with NIP by comparing SRS and RSS in Table 3. We obtain the average biases, MSEs and LCI of the Bayesian estimation with Gamma prior based on LINEX loss function by comparing SRS and RSS in Table 4 and Table 5. Bayesian estimates based on LINEX loss function with NIP is listed in Table 4, Table 5, Table 6 and Table 7, respectively.

Table 1. SRS and RSS by ML Method of Parameter and R of ITL Stress Strength Model.

${\mathit{\theta }}_1$			0.5						3
${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{n},\mathit{m}$		SRS			RSS			SRS			RSS
			Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI
0.5	2, 2	${\theta }_1$	0.0107	0.0139	0.4601	0.0047	0.0102	0.3955	0.0605	0.4885	2.7323	0.0243	0.3560	2.3392
		${\theta }_2$	0.0221	0.0157	0.4840	0.0074	0.0102	0.3954	0.0221	0.0157	0.4840	0.0074	0.0102	0.3954
		R	−0.0089	0.0046	0.2634	−0.0051	0.0036	0.2350	−0.0108	0.0011	0.1254	−0.0079	0.0008	0.1101
	3, 3	${\theta }_1$	0.0006	0.0102	0.3963	−0.0083	0.0049	0.2733	−0.0004	0.3478	2.3141	−0.0500	0.1764	1.6361
		${\theta }_2$	0.0174	0.0110	0.4062	0.0032	0.0045	0.2625	0.0174	0.0110	0.4062	0.0032	0.0045	0.2625
		R	−0.0107	0.0035	0.2292	−0.0078	0.0020	0.1746	−0.0101	0.0009	0.1084	−0.0067	0.0005	0.0802
	4, 4	${\theta }_1$	−0.0013	0.0076	0.3426	−0.0075	0.0026	0.1970	−0.0092	0.2713	2.0434	−0.0447	0.0927	1.1820
		${\theta }_2$	0.0136	0.0078	0.3425	0.0025	0.0028	0.2062	0.0136	0.0078	0.3425	0.0025	0.0028	0.2062
		R	−0.0093	0.0029	0.2093	−0.0060	0.0010	0.1239	−0.0082	0.0007	0.0996	−0.0044	0.0002	0.0558
	5, 5	${\theta }_1$	−0.0081	0.0059	0.2998	−0.0098	0.0019	0.1676	−0.0493	0.2115	1.7943	−0.0589	0.0687	1.0024
		${\theta }_2$	0.0056	0.0057	0.2957	0.0035	0.0020	0.1754	0.0056	0.0057	0.2957	0.0035	0.0020	0.1754
		R	−0.0090	0.0022	0.1813	−0.0072	0.0008	0.1064	−0.0075	0.0005	0.0832	−0.0045	0.0002	0.0476
	6, 6	${\theta }_1$	−0.0082	0.0045	0.2613	−0.0096	0.0015	0.1447	−0.0491	0.1618	1.5666	−0.0580	0.0522	0.8668
		${\theta }_2$	0.0039	0.0048	0.2717	0.0011	0.0014	0.1456	0.0039	0.0048	0.2717	0.0011	0.0014	0.1456
		R	−0.0077	0.0016	0.1545	−0.0060	0.0006	0.0895	−0.0062	0.0004	0.0707	−0.0037	0.0001	0.0401
3	2, 2	${\theta }_1$	0.0107	0.0139	0.4601	0.0047	0.0102	0.3955	0.0642	0.4991	2.7606	0.0281	0.3665	2.3730
		${\theta }_2$	0.1292	0.5566	2.8834	0.0396	0.3541	2.3299	0.1324	0.5651	2.9037	0.0443	0.3675	2.3725
		R	0.0018	0.0015	0.1536	0.0026	0.0012	0.1329	−0.0051	0.0059	0.3002	−0.0015	0.0046	0.2655
	3, 3	${\theta }_1$	0.0006	0.0102	0.3963	−0.0083	0.0049	0.2733	0.0038	0.3673	2.3780	−0.0496	0.1770	1.6396
		${\theta }_2$	0.1006	0.3867	2.4079	0.0191	0.1611	1.5731	0.1045	0.3967	2.4372	0.0194	0.1615	1.5753
		R	−0.0007	0.0011	0.1303	−0.0011	0.0006	0.0976	−0.0080	0.0045	0.2603	−0.0060	0.0026	0.1974
	4, 4	${\theta }_1$	−0.0013	0.0076	0.3426	−0.0075	0.0026	0.1970	−0.0079	0.2745	2.0558	−0.0447	0.0927	1.1820
		${\theta }_2$	0.0797	0.2765	2.0396	0.0148	0.0996	1.2369	0.0816	0.2810	2.0552	0.0148	0.0996	1.2369
		R	−0.0011	0.0009	0.1154	−0.0015	0.0003	0.0689	−0.0075	0.0036	0.2343	−0.0049	0.0013	0.1406
	5, 5	${\theta }_1$	−0.0081	0.0059	0.2998	−0.0098	0.0019	0.1676	−0.0489	0.2125	1.7987	−0.0588	0.0691	1.0054
		${\theta }_2$	0.0331	0.2046	1.7702	0.0203	0.0716	1.0466	0.0337	0.2056	1.7744	0.0211	0.0724	1.0523
		R	−0.0015	0.0007	0.1014	−0.0025	0.0002	0.0585	−0.0070	0.0028	0.2048	−0.0066	0.0010	0.1205
	6, 6	${\theta }_1$	−0.0082	0.0045	0.2613	−0.0096	0.0015	0.1447	−0.0490	0.1620	1.5677	−0.0578	0.0523	0.8681
		${\theta }_2$	0.0229	0.1726	1.6277	0.0065	0.0494	0.8721	0.0232	0.1731	1.6300	0.0066	0.0496	0.8734
		R	−0.0015	0.0005	0.0855	−0.0022	0.0002	0.0492	−0.0059	0.0020	0.1748	−0.0054	0.0007	0.1010

Table 2. SRS and RSS by Bayesian Method with Gamma Prior of Parameters and R of ITL Stress Strength Model.

${\mathit{\theta }}_1$			0.5						3
${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{n},\mathit{m}$		SRS			RSS			SRS			RSS
			Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI
0.5	2, 2	${\theta }_1$	0.0109	0.0041	0.2476	0.0111	0.0034	0.2035	0.0170	0.0053	0.2670	0.0060	0.0030	0.1984
		${\theta }_2$	0.0262	0.0050	0.2454	0.0146	0.0033	0.2146	0.0049	0.0007	0.1004	0.0030	0.0004	0.0759
		R	−0.0062	0.0015	0.1454	−0.0016	0.0012	0.1315	0.0036	0.0003	0.0633	0.0012	0.0002	0.0483
	3, 3	${\theta }_1$	0.0048	0.0023	0.1744	−0.0022	0.0014	0.1555	0.0065	0.0021	0.1709	−0.0005	0.0013	0.1435
		${\theta }_2$	0.0065	0.0021	0.1610	0.0074	0.0015	0.1432	0.0028	0.0003	0.0633	0.0025	0.0002	0.0555
		R	−0.0012	0.0008	0.1021	−0.0046	0.0006	0.0852	0.0013	0.0001	0.0417	−0.0003	0.0001	0.0356
	4, 4	${\theta }_1$	0.0019	0.0013	0.1358	−0.0011	0.0008	0.1152	0.0004	0.0015	0.1503	−0.0011	0.0009	0.1138
		${\theta }_2$	0.0034	0.0014	0.1511	0.0060	0.0008	0.1073	0.0029	0.0002	0.0465	0.0006	0.0001	0.0433
		R	−0.0010	0.0005	0.0842	−0.0032	0.0004	0.0745	−0.0001	0.0001	0.0360	−0.0004	0.0001	0.0283
	5, 5	${\theta }_1$	−0.0015	0.0009	0.1202	−0.0020	0.0007	0.1050	0.0023	0.0010	0.1221	0.0002	0.0006	0.0921
		${\theta }_2$	0.0069	0.0012	0.1290	0.0031	0.0007	0.0970	0.0003	0.0001	0.0429	0.0015	0.0001	0.0438
		R	−0.0038	0.0004	0.0789	−0.0025	0.0003	0.0680	0.0005	0.0001	0.0291	0.0000	0.0000	0.0221
	6, 6	${\theta }_1$	−0.0026	0.0008	0.1132	−0.0043	0.0006	0.0906	−0.0066	0.0008	0.1036	−0.0078	0.0005	0.0758
		${\theta }_2$	0.0025	0.0008	0.1106	0.0032	0.0006	0.0975	−0.0001	0.0001	0.0393	−0.0003	0.0001	0.0390
		R	−0.0027	0.0003	0.0650	−0.0036	0.0002	0.0555	−0.0017	0.0001	0.0255	−0.0019	0.0000	0.0187
3	2, 2	${\theta }_1$	0.0015	0.0006	0.0947	0.0001	0.0004	0.0735	0.0438	0.1524	1.4049	0.0187	0.1051	1.1304
		${\theta }_2$	0.0179	0.0046	0.2779	0.0218	0.0035	0.2148	0.0738	0.1558	1.4515	0.0914	0.0911	1.0847
		R	−0.0040	0.0001	0.0306	−0.0040	0.0001	0.0285	−0.0025	0.0019	0.1766	−0.0063	0.0012	0.1135
	3, 3	${\theta }_1$	−0.0008	0.0002	0.0601	−0.0005	0.0002	0.0566	0.0369	0.0743	0.9954	0.0097	0.0501	0.8981
		${\theta }_2$	0.0087	0.0026	0.2103	0.0032	0.0011	0.1311	0.0389	0.0878	1.1140	0.0361	0.0542	0.9292
		R	−0.0022	0.0001	0.0256	−0.0009	0.0000	0.0152	0.0000	0.0012	0.1337	−0.0021	0.0007	0.1039
	4, 4	${\theta }_1$	−0.0015	0.0001	0.0425	−0.0025	0.0001	0.0437	0.0027	0.0428	0.7874	−0.0306	0.0309	0.6708
		${\theta }_2$	0.0058	0.0015	0.1486	0.0022	0.0012	0.1357	0.0269	0.0414	0.7617	0.0166	0.0285	0.6436
		R	−0.0014	0.0000	0.0168	−0.0009	0.0000	0.0154	−0.0020	0.0006	0.0876	−0.0040	0.0004	0.0736
	5, 5	${\theta }_1$	−0.0011	0.0001	0.0389	−0.0004	0.0001	0.0421	0.0047	0.0352	0.7075	−0.0119	0.0186	0.5470
		${\theta }_2$	0.0058	0.0012	0.1222	0.0047	0.0008	0.1041	0.0193	0.0451	0.8395	0.0060	0.0195	0.5575
		R	−0.0013	0.0000	0.0156	−0.0009	0.0000	0.0125	−0.0011	0.0006	0.0888	−0.0015	0.0002	0.0540
	6, 6	${\theta }_1$	−0.0014	0.0001	0.0366	−0.0019	0.0001	0.0411	−0.0123	0.0294	0.6603	−0.0189	0.0202	0.5171
		${\theta }_2$	0.0012	0.0008	0.1000	0.0007	0.0005	0.0839	0.0156	0.0286	0.6594	0.0093	0.0187	0.4991
		R	−0.0006	0.0000	0.0123	−0.0004	0.0000	0.0107	−0.0023	0.0003	0.0705	−0.0024	0.0003	0.0615

Table 3. SRS and RSS by Bayesian Method with NIP of Parameters and R of ITL Stress Strength Model.

${\mathit{\theta }}_1$			0.5						3
${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{n},\mathit{m}$		SRS			RSS			SRS			RSS
			Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI
0.5	2, 2	${\theta }_1$	−0.3372	0.1582	0.6341	−0.2984	0.1267	0.6040	0.0273	0.0271	0.6646	0.0192	0.0120	0.3767
		${\theta }_2$	−0.3036	0.1432	0.6356	−0.2929	0.1339	0.6647	0.1575	0.8901	3.7239	0.2079	0.4250	2.3099
		R	−0.3893	0.1659	0.4051	−0.3211	0.1297	0.4837	0.0042	0.0021	0.1697	−0.0003	0.0013	0.1318
	3, 3	${\theta }_1$	−0.3001	0.1316	0.6090	−0.0465	0.0154	0.5070	0.0179	0.0121	0.3730	0.0048	0.0058	0.2661
		${\theta }_2$	−0.2810	0.1227	0.6606	−0.0226	0.0125	0.4925	0.2346	0.4798	2.3941	0.1197	0.2516	1.8809
		R	−0.2994	0.1199	0.5106	−0.0317	0.0087	0.3057	−0.0016	0.0011	0.1279	−0.0018	0.0005	0.0879
	4, 4	${\theta }_1$	−0.1882	0.0789	0.6066	−0.0157	0.0036	0.2210	0.0133	0.0080	0.3291	0.0032	0.0033	0.2183
		${\theta }_2$	−0.1781	0.0718	0.6152	−0.0105	0.0034	0.2111	0.1900	0.3166	1.9086	0.0510	0.1005	1.1168
		R	−0.1573	0.0572	0.5433	−0.0058	0.0012	0.1228	−0.0019	0.0008	0.1093	−0.0005	0.0003	0.0652
	5, 5	${\theta }_1$	−0.0887	0.0360	0.6048	−0.0221	0.0024	0.1666	0.0138	0.0054	0.2748	−0.0093	0.0019	0.1578
		${\theta }_2$	−0.0878	0.0299	0.5739	−0.0060	0.0025	0.1946	0.1133	0.2679	1.9653	0.0494	0.0615	0.8621
		R	−0.0641	0.0226	0.5206	−0.0100	0.0010	0.1155	0.0011	0.0007	0.0960	−0.0037	0.0002	0.0529
	6, 6	${\theta }_1$	−0.0437	0.0115	0.4068	−0.0135	0.0017	0.1375	0.0036	0.0051	0.2702	−0.0028	0.0018	0.1532
		${\theta }_2$	−0.0375	0.0122	0.4957	−0.0023	0.0018	0.1578	0.1059	0.1752	1.4985	0.0155	0.0620	0.9827
		R	−0.0215	0.0052	0.2342	−0.0068	0.0007	0.0938	−0.0021	0.0005	0.0859	−0.0007	0.0002	0.0553
3	2, 2	${\theta }_1$	0.1638	0.9759	3.9879	0.1150	0.4315	2.2600	0.3410	0.7718	2.8635	0.2491	0.4934	2.4668
		${\theta }_2$	0.0263	0.0247	0.6207	0.0346	0.0118	0.3850	0.3441	0.7432	3.0275	0.3001	0.4833	2.2820
		R	−0.0217	0.0080	0.1773	−0.0106	0.0029	0.1003	−0.0008	0.0059	0.2741	−0.0045	0.0040	0.2432
	3, 3	${\theta }_1$	0.1072	0.4345	2.2380	0.0288	0.2078	1.5966	0.2588	0.5009	2.4410	0.0573	0.1892	1.6026
		${\theta }_2$	0.0391	0.0133	0.3990	0.0199	0.0070	0.3135	0.2602	0.4744	2.3601	0.0768	0.1885	1.6074
		R	−0.0085	0.0009	0.1079	−0.0058	0.0004	0.0739	−0.0003	0.0044	0.2579	−0.0017	0.0022	0.1676
	4, 4	${\theta }_1$	0.0484	0.2569	1.9749	0.0203	0.1168	1.3261	0.1049	0.2368	1.8624	0.0526	0.1054	1.2037
		${\theta }_2$	0.0338	0.0095	0.3113	0.0109	0.0028	0.1871	0.2017	0.3548	2.0856	0.1137	0.1228	1.3145
		R	−0.0081	0.0007	0.0925	−0.0029	0.0002	0.0589	−0.0067	0.0029	0.1967	−0.0049	0.0014	0.1422
	5, 5	${\theta }_1$	0.1113	0.1970	1.5596	−0.0463	0.0756	0.9306	0.1091	0.2286	1.8539	−0.0041	0.0625	0.9481
		${\theta }_2$	0.0217	0.0070	0.3045	0.0089	0.0023	0.1774	0.1735	0.2620	1.7927	0.0684	0.0756	0.9738
		R	−0.0027	0.0004	0.0722	−0.0047	0.0002	0.0478	−0.0050	0.0024	0.1875	−0.0059	0.0010	0.1202
	6, 6	${\theta }_1$	−0.0011	0.1604	1.3226	−0.0373	0.0624	0.8959	0.0870	0.1619	1.4598	−0.0207	0.0484	0.8722
		${\theta }_2$	0.0130	0.0053	0.2759	0.0053	0.0015	0.1518	0.1157	0.1776	1.5047	0.0884	0.0591	0.9526
		R	−0.0056	0.0004	0.0789	−0.0035	0.0001	0.0424	−0.0022	0.0019	0.1579	−0.0090	0.0008	0.1038

Table 4. SRS and RSS by Bayesian Method with Gamma Prior under LINEX Loss Function of Parameters and R of ITL Stress Strength Model ${\theta }_1=0.5$.

${\mathit{\theta }}_1=0.5$			SRS						RSS
${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{n},\mathit{m}$		e = −1.5			e = 1.5			e = −1.5			e = 1.5
			Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI
0.5	2, 2	${\theta }_1$	0.0209	0.0048	0.2571	0.0013	0.0037	0.2400	0.0184	0.0039	0.2111	0.0184	0.0031	0.1966
		${\theta }_2$	0.0373	0.0061	0.2553	0.0156	0.0042	0.2362	0.0220	0.0037	0.2197	0.0220	0.0030	0.2089
		R	−0.0056	0.0015	0.1499	−0.0070	0.0014	0.1418	−0.0009	0.0013	0.1348	−0.0009	0.0012	0.1286
	3, 3	${\theta }_1$	0.0104	0.0025	0.1802	−0.0007	0.0021	0.1689	0.0014	0.0015	0.1570	0.0014	0.0014	0.1541
		${\theta }_2$	0.0127	0.0023	0.1718	0.0005	0.0019	0.1565	0.0111	0.0016	0.1453	0.0111	0.0014	0.1414
		R	−0.0008	0.0008	0.1043	−0.0016	0.0007	0.1011	−0.0043	0.0006	0.0858	−0.0043	0.0005	0.0843
	4, 4	${\theta }_1$	0.0058	0.0014	0.1375	−0.0020	0.0013	0.1338	0.0012	0.0008	0.1158	0.0012	0.0008	0.1146
		${\theta }_2$	0.0077	0.0015	0.1542	−0.0008	0.0013	0.1480	0.0084	0.0009	0.1089	0.0084	0.0008	0.1058
		R	−0.0007	0.0005	0.0857	−0.0013	0.0005	0.0827	−0.0030	0.0004	0.0751	−0.0030	0.0004	0.0739
	5, 5	${\theta }_1$	0.0015	0.0010	0.1211	−0.0044	0.0009	0.1189	−0.0003	0.0007	0.1059	−0.0003	0.0007	0.1042
		${\theta }_2$	0.0103	0.0013	0.1305	0.0037	0.0011	0.1269	0.0047	0.0007	0.0972	0.0047	0.0007	0.0963
		R	−0.0036	0.0004	0.0794	−0.0040	0.0004	0.0782	−0.0023	0.0003	0.0683	−0.0023	0.0003	0.0676
	6, 6	${\theta }_1$	−0.0002	0.0009	0.1141	−0.0050	0.0008	0.1120	−0.0031	0.0006	0.0907	−0.0031	0.0006	0.0905
		${\theta }_2$	0.0051	0.0009	0.1109	0.0000	0.0008	0.1097	0.0044	0.0006	0.0979	0.0044	0.0006	0.0972
		R	−0.0025	0.0003	0.0656	−0.0029	0.0003	0.0645	−0.0035	0.0002	0.0556	−0.0035	0.0002	0.0554
3	2, 2	${\theta }_1$	0.02687	0.00606	0.27357	0.00751	0.00473	0.25864	0.01309	0.00336	0.20362	0.01309	0.00282	0.19646
		${\theta }_2$	0.02680	0.00143	0.10431	−0.01664	0.00094	0.09959	0.01791	0.00073	0.07771	0.01791	0.00052	0.07707
		R	0.00506	0.00033	0.06466	0.00221	0.00028	0.06248	0.00224	0.00019	0.04942	0.00224	0.00017	0.04768
	3, 3	${\theta }_1$	0.01183	0.00227	0.17441	0.00121	0.00198	0.16766	0.00301	0.00140	0.14609	0.00301	0.00133	0.14135
		${\theta }_2$	0.01394	0.00046	0.06306	−0.00825	0.00033	0.06389	0.00986	0.00034	0.05688	0.00986	0.00025	0.05496
		R	0.00217	0.00013	0.04218	0.00050	0.00012	0.04108	0.00024	0.00008	0.03612	0.00024	0.00008	0.03527
	4, 4	${\theta }_1$	0.00421	0.00158	0.15370	−0.00334	0.00146	0.14753	0.00116	0.00093	0.11573	0.00116	0.00090	0.11212
		${\theta }_2$	0.01040	0.00028	0.04816	−0.00452	0.00019	0.04478	0.00555	0.00017	0.04399	0.00555	0.00015	0.04334
		R	0.00050	0.00009	0.03626	−0.00074	0.00009	0.03575	−0.00001	0.00006	0.02844	−0.00001	0.00005	0.02801
	5, 5	${\theta }_1$	0.00523	0.00103	0.12354	−0.00068	0.00095	0.12000	0.00183	0.00066	0.09372	0.00183	0.00064	0.09145
		${\theta }_2$	0.00575	0.00016	0.04306	−0.00517	0.00015	0.04371	0.00516	0.00016	0.04338	0.00516	0.00014	0.04387
		R	0.00097	0.00006	0.02942	−0.00002	0.00006	0.02880	0.00019	0.00004	0.02239	0.00019	0.00004	0.02208
	6, 6	${\theta }_1$	−0.00422	0.00084	0.10427	−0.00896	0.00087	0.10295	−0.00659	0.00046	0.07627	−0.00659	0.00049	0.07544
		${\theta }_2$	0.00432	0.00013	0.04003	−0.00458	0.00013	0.03878	0.00262	0.00012	0.03867	0.00262	0.00012	0.03858
		R	−0.00126	0.00005	0.02564	−0.00207	0.00005	0.02548	−0.00175	0.00003	0.01867	−0.00175	0.00003	0.01872

Table 5. SRS and RSS by Bayesian Method with Gamma Prior under LINEX Loss Function of Parameters and R of ITL Stress Strength Model ${\theta }_1=3$.

${\mathit{\theta }}_1=3$			SRS						RSS
${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{n},\mathit{m}$		e = −1.5			e = 1.5			e = −1.5			e = 1.5
			Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI
0.5	2, 2	${\theta }_1$	0.02157	0.00104	0.09699	−0.01822	0.00087	0.09364	0.01500	0.00068	0.07795	0.01500	0.00064	0.07100
		${\theta }_2$	0.02830	0.00554	0.29154	0.00792	0.00402	0.25589	0.02937	0.00415	0.22299	0.02937	0.00305	0.20829
		R	−0.00462	0.00011	0.03265	−0.00349	0.00008	0.02818	−0.00444	0.00009	0.03026	−0.00444	0.00007	0.02684
	3, 3	${\theta }_1$	0.00904	0.00031	0.06011	−0.01052	0.00034	0.06167	0.00686	0.00027	0.05780	0.00686	0.00027	0.05631
		${\theta }_2$	0.01458	0.00290	0.21544	0.00304	0.00247	0.20548	0.00671	0.00120	0.13359	0.00671	0.00110	0.12875
		R	−0.00253	0.00006	0.02779	−0.00184	0.00005	0.02356	−0.00106	0.00002	0.01582	−0.00106	0.00002	0.01468
	4, 4	${\theta }_1$	0.00521	0.00015	0.04336	−0.00815	0.00019	0.04096	0.00243	0.00014	0.04278	0.00243	0.00014	0.04320
		${\theta }_2$	0.00988	0.00158	0.15024	0.00173	0.00138	0.14725	0.00450	0.00120	0.13732	0.00450	0.00114	0.13405
		R	−0.00165	0.00003	0.01748	−0.00115	0.00002	0.01623	−0.00098	0.00002	0.01581	−0.00098	0.00002	0.01495
	5, 5	${\theta }_1$	0.00390	0.00012	0.03922	−0.00610	0.00014	0.03863	0.00325	0.00013	0.04205	0.00325	0.00013	0.04236
		${\theta }_2$	0.00898	0.00128	0.12489	0.00257	0.00114	0.12026	0.00636	0.00082	0.10450	0.00636	0.00077	0.10377
		R	−0.00148	0.00002	0.01596	−0.00107	0.00002	0.01507	−0.00101	0.00001	0.01272	−0.00101	0.00001	0.01233
	6, 6	${\theta }_1$	0.00254	0.00010	0.03724	−0.00540	0.00012	0.03669	0.00099	0.00012	0.04011	0.00099	0.00012	0.04183
		${\theta }_2$	0.00380	0.00084	0.10075	−0.00131	0.00079	0.09955	0.00188	0.00047	0.08469	0.00188	0.00045	0.08312
		R	−0.00073	0.00001	0.01263	−0.00042	0.00001	0.01206	−0.00040	0.00001	0.01082	−0.00040	0.00001	0.01054
3	2, 2	${\theta }_1$	0.42656	0.42841	1.94886	−0.25746	0.17117	1.21073	0.30258	0.24725	1.43209	0.30258	0.12330	1.06866
		${\theta }_2$	0.48082	0.49282	1.91554	−0.24286	0.15852	1.18907	0.37858	0.26526	1.30315	0.37858	0.08291	0.94729
		R	−0.00388	0.00250	0.19830	−0.00143	0.00158	0.15663	−0.00610	0.00144	0.13545	−0.00610	0.00104	0.11073
	3, 3	${\theta }_1$	0.24951	0.16188	1.19953	−0.14678	0.07877	0.86102	0.14806	0.08374	0.96422	0.14806	0.05550	0.83786
		${\theta }_2$	0.27405	0.19471	1.30486	−0.15832	0.09286	0.99024	0.17594	0.09374	1.03312	0.17594	0.05383	0.87896
		R	−0.00166	0.00142	0.14573	0.00119	0.00108	0.12536	−0.00220	0.00081	0.10858	−0.00220	0.00067	0.09795
	4, 4	${\theta }_1$	0.14934	0.07650	0.84663	−0.12819	0.05182	0.74317	0.05286	0.03653	0.70441	0.05286	0.03878	0.63306
		${\theta }_2$	0.18445	0.08452	0.82094	−0.11368	0.04703	0.74130	0.10277	0.04228	0.69213	0.10277	0.02954	0.62554
		R	−0.00281	0.00066	0.09608	−0.00127	0.00052	0.08389	−0.00409	0.00040	0.07501	−0.00409	0.00036	0.07170
	5, 5	${\theta }_1$	0.11543	0.05345	0.73126	−0.09774	0.04075	0.68259	0.04717	0.02201	0.56455	0.04717	0.02193	0.51189
		${\theta }_2$	0.14063	0.07250	0.91318	−0.09214	0.04713	0.77507	0.06709	0.02544	0.57698	0.06709	0.02082	0.53583
		R	−0.00186	0.00060	0.09484	−0.00037	0.00052	0.08450	−0.00161	0.00025	0.05650	−0.00161	0.00023	0.05318
	6, 6	${\theta }_1$	0.07713	0.03938	0.71490	−0.09530	0.03501	0.62336	0.02604	0.02182	0.53396	0.02604	0.02256	0.50386
		${\theta }_2$	0.11220	0.04470	0.68742	−0.07378	0.03062	0.61990	0.05504	0.02302	0.51909	0.05504	0.01872	0.47767
		R	−0.00286	0.00038	0.07337	−0.00186	0.00033	0.06778	−0.00240	0.00027	0.06376	−0.00240	0.00026	0.05943

Table 6. SRS and RSS by Bayesian Method with NIP under LINEX Loss Function of Parameters and R of ITL Stress Strength Model ${\theta }_1=0.5$.

${\mathit{\theta }}_1=0.5$			SRS						RSS
${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{n},\mathit{m}$		e = −1.5			e = 1.5			e = −1.5			e = 1.5
			Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI
0.5	2, 2	${\theta }_1$	−0.3258	0.1521	0.6354	−0.3457	0.1626	0.6313	−0.2817	0.1196	0.6295	−0.2817	0.1328	0.5826
		${\theta }_2$	−0.2908	0.1388	0.6845	−0.3133	0.1467	0.6214	−0.2776	0.1274	0.6948	−0.2776	0.1392	0.6374
		R	−0.3674	0.1511	0.4226	−0.4052	0.1774	0.3695	−0.2963	0.1156	0.5105	−0.2963	0.1416	0.4783
	3, 3	${\theta }_1$	−0.2824	0.1229	0.6356	−0.3141	0.1387	0.5834	−0.0381	0.0148	0.5032	−0.0381	0.0162	0.5132
		${\theta }_2$	−0.2632	0.1148	0.6802	−0.2952	0.1292	0.6406	−0.0135	0.0121	0.4689	−0.0135	0.0131	0.5120
		R	−0.2740	0.1057	0.5177	−0.3203	0.1323	0.5055	−0.0293	0.0080	0.2645	−0.0293	0.0094	0.3301
	4, 4	${\theta }_1$	−0.1711	0.0729	0.6210	−0.2034	0.0846	0.5953	−0.0114	0.0036	0.2257	−0.0114	0.0037	0.2167
		${\theta }_2$	−0.1595	0.0648	0.6263	−0.1945	0.0783	0.6029	−0.0061	0.0035	0.2173	−0.0061	0.0034	0.2072
		R	−0.1404	0.0495	0.5436	−0.1737	0.0648	0.5395	−0.0053	0.0012	0.1241	−0.0053	0.0011	0.1215
	5, 5	${\theta }_1$	−0.0773	0.0334	0.6120	−0.0993	0.0385	0.6010	−0.0193	0.0023	0.1683	−0.0193	0.0022	0.1650
		${\theta }_2$	−0.0765	0.0271	0.5798	−0.0984	0.0327	0.5657	−0.0031	0.0026	0.1972	−0.0031	0.0022	0.1921
		R	−0.0561	0.0195	0.5106	−0.0720	0.0258	0.5301	−0.0097	0.0010	0.1167	−0.0097	0.0010	0.1144
	6, 6	${\theta }_1$	−0.0367	0.0109	0.4097	−0.0504	0.0122	0.4031	−0.0115	0.00169	0.1382	−0.0115	0.00163	0.1371
		${\theta }_2$	−0.0297	0.0113	0.4712	−0.0451	0.0131	0.5016	−0.0001	0.0018	0.1590	−0.0001	0.0017	0.1566
		R	−0.0191	0.0045	0.2289	−0.0240	0.0060	0.2302	−0.0065	0.00068	0.0940	−0.0065	0.00067	0.0935
3	2, 2	${\theta }_1$	0.0497	0.0325	0.6697	0.0068	0.0235	0.6544	0.0342	0.0143	0.4079	0.0342	0.0104	0.3604
		${\theta }_2$	0.9861	2.4466	5.0694	−0.4385	0.7702	3.2139	0.8024	1.3757	3.1028	0.8024	0.2855	1.7689
		R	−0.0171	0.0022	0.1646	0.0275	0.0036	0.1979	−0.0153	0.0015	0.1370	−0.0153	0.0015	0.1345
	3, 3	${\theta }_1$	0.0314	0.0143	0.3841	0.0052	0.0106	0.3542	0.0120	0.0063	0.2748	0.0120	0.0054	0.2609
		${\theta }_2$	0.8012	1.4159	3.3080	−0.1963	0.2798	1.8429	0.4116	0.5121	2.2905	0.4116	0.1851	1.6247
		R	−0.0160	0.0014	0.1266	0.0123	0.0013	0.1282	−0.0103	0.0006	0.0874	−0.0103	0.0006	0.0865
	4, 4	${\theta }_1$	0.0233	0.0090	0.3395	0.0038	0.0073	0.3191	0.0075	0.0034	0.2244	0.0075	0.0032	0.2127
		${\theta }_2$	0.5874	0.7887	2.3600	−0.1268	0.2116	1.6292	0.2150	0.1674	1.2411	0.2150	0.0895	1.0500
		R	−0.0127	0.0010	0.1087	0.0083	0.0009	0.1101	−0.0057	0.0003	0.0659	−0.0057	0.0003	0.0654
	5, 5	${\theta }_1$	0.0216	0.0060	0.2860	0.0063	0.0050	0.2636	−0.0065	0.0019	0.1593	−0.0065	0.0019	0.1561
		${\theta }_2$	0.4230	0.5474	2.4251	−0.1421	0.2073	1.7004	0.1614	0.0939	0.9440	0.1614	0.0553	0.8033
		R	−0.0080	0.0007	0.0977	0.0096	0.0008	0.0972	−0.0072	0.0003	0.0526	−0.0072	0.0002	0.0530
	6, 6	${\theta }_1$	0.0099	0.0054	0.2772	−0.0025	0.0048	0.2632	−0.0007	0.0018	0.1543	−0.0007	0.0018	0.1522
		${\theta }_2$	0.3665	0.3599	1.6765	−0.1070	0.1386	1.3142	0.0914	0.0758	1.0294	0.0914	0.0601	0.9433
		R	−0.0098	0.0006	0.0843	0.0050	0.0005	0.0852	−0.0032	0.0002	0.0547	−0.0032	0.0002	0.0559

Table 7. SRS and RSS by Bayesian Method with NIP under LINEX Loss Function of Parameters and R of ITL Stress Strength Model ${\theta }_1=3$.

${\mathit{\theta }}_1=3$			SRS						RSS
${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{n},\mathit{m}$		e = −1.5			e = 1.5			e = −1.5			e = 1.5
			Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI	Bias	MSE	LCI
0.5	2, 2	${\theta }_1$	0.9916	2.7258	4.6140	−0.4219	0.7619	3.4253	0.7022	1.3435	3.3050	0.7022	0.3437	1.8081
		${\theta }_2$	0.0483	0.0286	0.6431	0.0058	0.0222	0.5946	0.0497	0.0142	0.4072	0.0497	0.0101	0.3655
		R	0.0052	0.0042	0.1518	−0.0508	0.0148	0.2680	0.0081	0.0014	0.1070	0.0081	0.0042	0.0994
	3, 3	${\theta }_1$	0.6348	1.2610	3.0849	−0.2814	0.3345	1.7590	0.3046	0.4048	2.0060	0.3046	0.1858	1.3851
		${\theta }_2$	0.0538	0.0161	0.4179	0.0252	0.0112	0.3832	0.0275	0.0078	0.3226	0.0275	0.0064	0.3046
		R	0.0072	0.0009	0.1091	−0.0232	0.0014	0.1101	0.0034	0.0004	0.0759	0.0034	0.0006	0.0717
	4, 4	${\theta }_1$	0.4252	0.5958	2.3837	−0.2505	0.2348	1.6221	0.1846	0.1785	1.4805	0.1846	0.1129	1.2274
		${\theta }_2$	0.0446	0.0112	0.3199	0.0236	0.0082	0.3058	0.0153	0.0030	0.1907	0.0153	0.0026	0.1838
		R	0.0041	0.0007	0.0971	−0.0196	0.0010	0.0927	0.0029	0.0002	0.0588	0.0029	0.0003	0.0576
	5, 5	${\theta }_1$	0.4302	0.4777	2.0503	−0.1447	0.1528	1.3349	0.0576	0.0878	0.9999	0.0576	0.0843	0.8771
		${\theta }_2$	0.0298	0.0079	0.3164	0.0138	0.0063	0.2933	0.0118	0.0024	0.1786	0.0118	0.0022	0.1756
		R	0.0074	0.0005	0.0751	−0.0121	0.0005	0.0695	−0.0009	0.0002	0.0472	−0.0009	0.0002	0.0472
	6, 6	${\theta }_1$	0.2412	0.2803	1.6413	−0.2037	0.1631	1.1498	0.0376	0.0693	0.9414	0.0376	0.0670	0.8625
		${\theta }_2$	0.0195	0.0058	0.2810	0.0067	0.0050	0.2710	0.0074	0.0016	0.1535	0.0074	0.0015	0.1505
		R	0.0028	0.0004	0.0824	−0.0134	0.0006	0.0782	−0.0007	0.0001	0.0432	−0.0007	0.0002	0.0422
3	2, 2	${\theta }_1$	1.1574	2.7472	4.3370	−0.2480	0.3835	2.0203	0.8576	1.5856	3.2337	0.8576	0.2783	1.8797
		${\theta }_2$	1.1438	2.7440	4.3656	−0.2515	0.3427	2.0382	0.8831	1.5223	3.0528	0.8831	0.2422	1.6855
		R	0.0005	0.0079	0.3137	−0.0005	0.0042	0.2381	−0.0028	0.0054	0.2832	−0.0028	0.0031	0.2180
	3, 3	${\theta }_1$	0.8085	1.4579	3.1906	−0.1531	0.2855	1.8476	0.3263	0.3725	1.8470	0.3263	0.1639	1.3747
		${\theta }_2$	0.7991	1.3505	3.2019	−0.1475	0.2742	1.7850	0.3528	0.3858	1.8456	0.3528	0.1582	1.3671
		R	0.0000	0.0056	0.2851	−0.0006	0.0036	0.2255	−0.0021	0.0026	0.1872	−0.0021	0.0019	0.1562
	4, 4	${\theta }_1$	0.4812	0.5846	2.2411	−0.1924	0.1919	1.5724	0.2180	0.1779	1.3538	0.2180	0.0937	1.0694
		${\theta }_2$	0.6068	0.8992	2.5908	−0.1144	0.2223	1.7405	0.2842	0.2172	1.4529	0.2842	0.0925	1.1867
		R	−0.0074	0.0037	0.2177	−0.0062	0.0024	0.1818	−0.0050	0.0015	0.1481	−0.0050	0.0013	0.1356
	5, 5	${\theta }_1$	0.4082	0.4819	2.2751	−0.1358	0.1764	1.5540	0.1015	0.0829	1.0071	0.1015	0.0648	0.8801
		${\theta }_2$	0.4939	0.5847	2.2745	−0.0849	0.1779	1.5644	0.1795	0.1148	1.0751	0.1795	0.0634	0.9253
		R	−0.0060	0.0029	0.1904	−0.0043	0.0022	0.1736	−0.0061	0.0011	0.1262	−0.0061	0.0010	0.1147
	6, 6	${\theta }_1$	0.3344	0.3297	1.6557	−0.1206	0.1325	1.2729	0.0550	0.0565	0.9238	0.0550	0.0517	0.8254
		${\theta }_2$	0.3733	0.3811	1.8682	−0.0963	0.1325	1.2961	0.1694	0.0856	0.9828	0.1694	0.0471	0.8988
		R	−0.0026	0.0023	0.1723	−0.0020	0.0016	0.1506	−0.0092	0.0009	0.1073	−0.0092	0.0008	0.1009

All the computations are performed in the R program based on 1000 Monte-Carlo runs. The simulation results are reported in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7. From these tables, we conclude the following

• The ML estimate of the parameters, and the system reliability R based on RSS have smaller MSE, and shortest CI than those of the others under SRS (see Table 1).
• All suggested estimates perform better as n or m increases.
• The bias, MSE, and LCI of Bayesian estimate of the parameters, and reliability under SELF in case of IP are smaller than the corresponding under NIP for both sampling methods (see Table 2 and Table 3).
• At true value ${\theta }_1=0.5$ and ${\theta }_1=3$, under the LINEX loss function, all accuracy measurements of the computed Bayes estimates of the parameters and the system reliability are lower under RSS than they are under SRS (see Table 4, Table 5, Table 6 and Table 7). Additionally, we draw the conclusion that all Bayes estimates obtained using RSS are more efficient than those produced using SRS.
• For various sample sizes, all Bayes estimates under RSS typically exhibit less MSE and shortest CIs than those under SRS. These measurements of Bayesian estimates reduce as set sizes increase (see Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7).
• Accuracy measures including, MSE, LCI, and bias of all Bayesian estimates using IP are smaller than the others using NIP.
• The Bayesian estimates of R, ${\theta }_1$ and ${\theta }_2$ under LINEX loss function at e = 1.5 are more efficient than the corresponding at e = −1.5 in both sampling methods.
• The best Bayes estimates of R, ${\theta }_1$ and ${\theta }_2$ in case of RSS are those based on the LINEX loss function.
• In the sense of efficiencies, the estimate of R based on RSS is more efficient than its SRS. It is obvious that when the set size increases the efficiency of RSS increases (see Table 1, Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7).
• The LCI for all estimates became narrow with increases sample sizes.
• Interestingly, in most of the cases, the MSEs of the Bayesian estimate are smaller than the MSEs of the MLEs. As the sample size $(n^{*},m^{*})$ increases, the MSEs of the estimates decreases as expected.
• According on the aforementioned comments, we recommend employing both the RSS approach and the Bayesian estimating method to acquire more accurate estimates.
• When the sample is SRS or RSS, it is advised to estimate the unknown parameters and the consistency of stress–strength of the ITL distribution using the Bayes MCMC inference via the Metropolis–Hastings algorithm.

5. Application of Real Data

To demonstrate how the suggested methods have been put into practice, we analyse two actual data sets in this section.

5.1. Time Waiting

The data set pertains to the lengths of time (in minutes) that customers must wait before receiving service from two separate banks. Ghitany et al. [40] are the ones who first conceived of it. In this part, we concentrate on the estimation of reliability $R=P(X<Y)$, where X and Y stand for Bank A’s (Data Set I) and Bank B’s (Data Set II) respective customer service wait times. There are 100 and 60 samples in each of the two data sets, respectively. Al-Mutairi et al. [41] examined waiting times data sets based on the Lindley distribution under SRS in the context of stress–strength reliability. They demonstrated how these data sets can be modelled using the Lindley distribution. For the sake of brevity, we will not repeat the results here.

The following approach is used to choose the RSS units from Data Set I and Data Set II: First, choose 20 observations from Data Sets I and II independently. Then, order the observations in each set from the smallest to the largest after randomly dividing them into 10 cycles of size 2. Furthermore, n = 20 and m = 20 observations from Data Sets I and II, respectively, are randomly chosen to form the SRS units. Table 8 and Table 9 contain data on waiting times based on SRS and RSS designs.

Table 8. SRS for Bank A and Bank B when n = 20, m = 20.

Bank A	1.8	3.2	3.2	4.9	5.3	8	8	8.6	9.8	10.7
	10.7	11	12.5	12.5	15.4	15.4	17.3	18.4	18.4	18.9
Bank B	1.2	1.9	2.3	2.3	2.3	2.3	2.7	3.5	3.5	3.5
	3.5	5.6	5.6	5.6	6.6	7.7	7.7	8.5	10.7	12.1

Table 9. RSS for Bank A and Bank B with set sizes n = m = 2.

Cycle	Bank A		Bank B
p=q	I	II	I	II
1	4.9	12.5	2.7	10.7
2	3.2	12.5	0.3	6.6
3	15.4	18.4	2.2	12.1
4	10.7	18.9	2.2	6.6
5	3.3	3.2	2.3	2.2
6	2.1	4.9	12.1	1.9
7	10.7	8	2	10.7
8	5.3	11.2	1.2	28
9	6.3	7.1	7.7	12.1
10	2.1	21.9	2.3	12.1

It can be concluded from Table 10 that the ML and Bayesian estimates of ${\theta }_1$ and ${\theta }_2$ based on SRS and RSS are both unbiased and best estimators where standard error (SE) is small. It is also obvious that the stress–strength reliability R based on RSS is larger than the other based on SRS.

Table 10. ML and Bayesian methods for SRS and RSS.

		ML		Bayesian SELF		Bayesian NIP
		Estimates	SE	Estimates	SE	Estimates	SE
SRS	${\theta }_1$	0.5895	0.1318	0.5918	0.1114	0.6599	0.2124
	${\theta }_2$	0.9228	0.2064	0.9208	0.1651	1.0046	0.2996
	R	0.3894		0.3908		0.3963
RSS	${\theta }_1$	0.5980	0.1109	0.4999	0.0468	0.6472	0.1695
	${\theta }_2$	0.7924	0.1481	0.7093	0.0660	0.8416	0.2028
	R	0.4289		0.4111		0.4340

Sabry et al. [42] used this data to estimate stress–strength reliability for extension of the exponential distribution by using different methods. Kumar et al. [43] used this data to estimate $P(Y<X)$ in Lindley distribution using progressively first failure censoring. Akgül et al. [44] estimated stress–strength reliability based on RSS data in case of Lindley distribution. Singh et al. [45] estimated system reliability in generalized Lindley stress–strength model.

For each SRS and RSS, we plot the profile likelihood in Figure 3 and Figure 4 to indicate that it has a unique maximum, respectively. The contour plot in Figure 5 to ensure that the ML estimate is unique values with maximum log-likelihood. We present the MCMC trace and posterior function for each model parameter to determine if the Bayesian estimates are converged (see Figure 6 and Figure 7 for SRS and RSS, respectively).

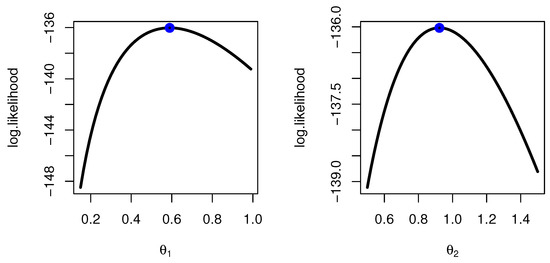
Figure 3. Profile likelihood for parameter estimation by SRS method for banking data.

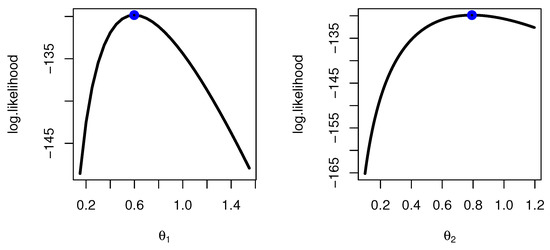
Figure 4. Profile likelihood for parameter estimation by RSS method for banking data.

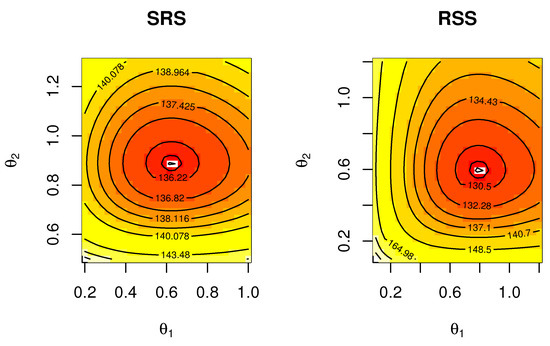
Figure 5. Contour plot of likelihood for parameter estimation by SRS and RSS method for banking data.

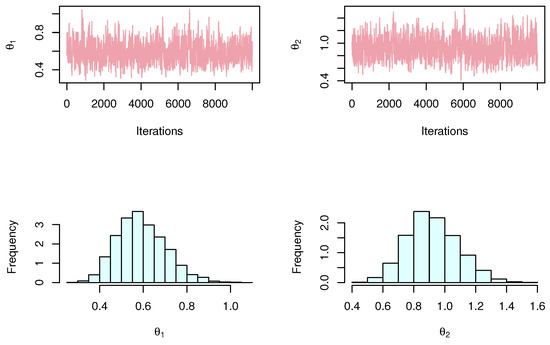
Figure 6. MCMC plot of parameter estimation by SRS method for banking data.

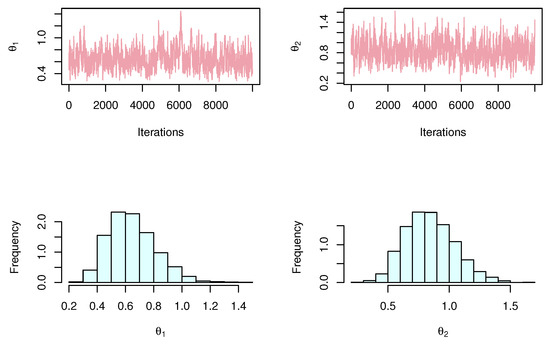
Figure 7. MCMC plot of parameter estimation by RSS method for banking data.

5.2. Failure Times of Insulating Fluid

Times to degrade an insulating fluid between electrodes were measured in two real stress and strength data sets, and these findings have been reviewed by Martino et al. [46]. The failure times (in minutes) for an insulating fluid between two electrodes subjected to a voltage of 34 kV and 36 kV are reported in Data I and Data II as shown in Table 11.

Table 11. Data sets of insulating fluid breakdown periods between electrodes acquired at various voltages.

Voltage	Time
34 kV	0.19 0.78 0.96 1.31 2.78 3.16 4.15 4.67 4.85 6.50 7.35 8.01 8.27
	12.06 31.75 32.52 33.91 36.71 72.89
36 kV	0.35 0.59 0.96 0.99 1.69 1.97 2.07 2.58 2.71 2.90 3.67 3.99 5.35
	13.77 25.50

The following approach is used to choose the RSS units from 34 kV and 36 kV data Sets: Sort the observations in each set from the smallest to the largest after randomly dividing them into 7 cycles of size 2. Furthermore, n = 14 and m = 14 observations from Data Sets I and II, respectively, are randomly chosen to form the SRS units. Table 12 and Table 13 contain data on waiting times based on SRS and RSS.

Table 12. SRS for failure times of insulating fluid data when n = 14, m = 14.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
34 kV	0.96	0.96	2.78	2.78	4.67	4.85	6.5	7.35	12.06	12.06	31.75	36.71	72.89	72.89
34 kV	0.35	0.96	0.99	1.69	2.07	2.07	2.71	2.9	2.9	3.67	3.99	13.77	13.77	25.5

Table 13. RSS for failure times of insulating fluid data with set sizes n = m = 2.

	34 kV		34 kV
$\mathit{p}=\mathit{q}$	I	II	I	II
1	2.78	32.52	2.58	3.67
2	0.78	4.15	1.69	13.77
3	3.16	12.06	0.96	1.97
4	1.31	36.71	0.35	2.71
5	0.96	31.75	0.35	3.67
6	0.78	31.75	1.97	2.71
7	8.01	4.15	0.96	2.9

It can be concluded from Table 14 that the ML and Bayesian estimates of ${\theta }_1$ and ${\theta }_2$ based on SRS and RSS are both unbiased and best estimates where SE is small. Another evident difference between the two is the size of the stress–strength reliability R based on RSS against the other based on SRS.

Table 14. ML and Bayesian methods for SRS and RSS for failure times of insulating fluid data.

		ML		Bayesian SELF		Bayesian NIP
		Estimates	SE	Estimates	SE	Estimates	SE
SRS	${\theta }_1$	1.0470	0.2798	1.0643	0.2199	1.2383	0.2426
	${\theta }_2$	0.5806	0.1552	0.5933	0.1324	0.6674	0.1424
	R	0.6362		0.6357		0.6464
RSS	${\theta }_1$	1.4595	0.3276	1.1873	0.1600	1.8034	0.3155
	${\theta }_2$	0.7104	0.1603	0.6113	0.0815	0.8579	0.1525
	R	0.6703		0.6547		0.6770

Since we don’t have any previous knowledge, we employ NIP in Bayes estimation. Table 14 provides a list of the estimates ML and Bayes with gamma prior as trail and NIP.

To check that the point ML estimate is unique and maximum for failure times of insulating fluid data for each SRS and RSS, we plotted the profile likelihood in Figure 8 and Figure 9, respectively, and we plotted the contour plot in Figure 10. We present the MCMC trace and posterior function for each model parameter to determine if the Bayesian estimates are converged for failure times of insulating fluid data (see Figure 11 and Figure 12 for SRS and RSS, respectively).

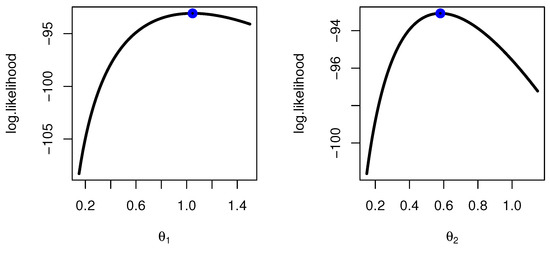
Figure 8. Profile likelihood for parameter estimation by SRS method for failure times of insulating fluid data.

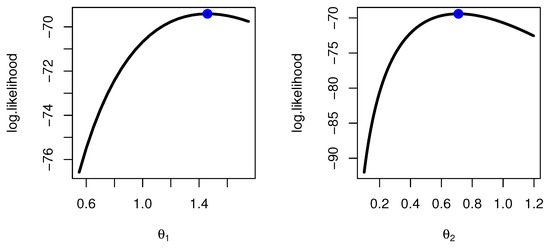
Figure 9. Profile likelihood for parameter estimation by RSS method for failure times of insulating fluid data.

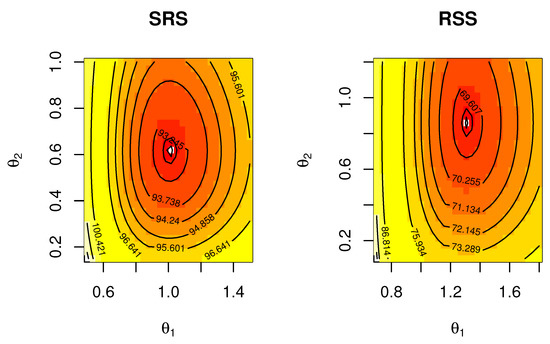
Figure 10. Contour plots of likelihood for parameter estimation by SRS and RSS method for failure times of insulating fluid data.

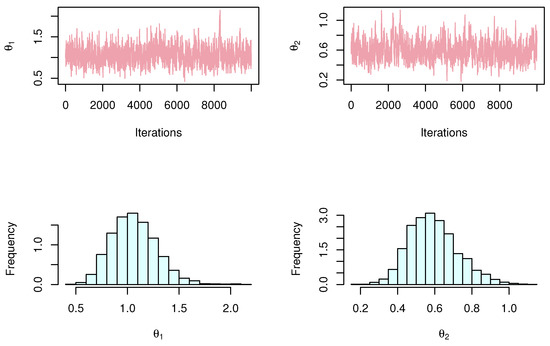
Figure 11. MCMC plots of parameter estimation by SRS method for failure times of insulating fluid data.

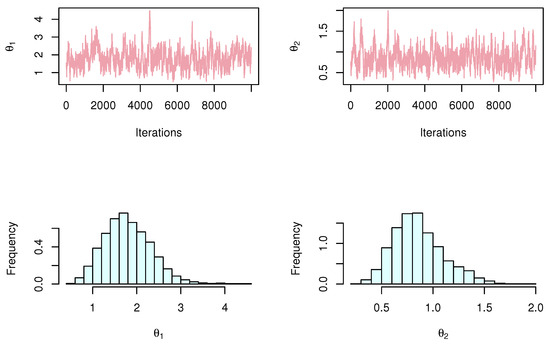
Figure 12. MCMC plots of parameter estimation by RSS method for failure times of insulating fluid data.

In these applications, it is clear that the Bayes with gamma prior and Bayes estimator with respect to NIP behave quite similarly, although the stress–strength reliability of Bayes estimates with NIP is greater than the stress–strength reliability of Bayes estimates with gamma prior. All estimates based on RSS are more efficient than their SRS.

6. Concluding Remarks

In this study, we examined the estimator of parameters as well as strength–stress reliability estimator under ITL distribution. With the support of RSS and SRR, we presented the estimation issue using the ML and Bayesian approaches. Bayesian estimators of parameters and R using gamma and uniform priors approach was employed using symmetric and asymmetric loss functions. Following that, the highest posterior density credible interval of the Bayesian estimate and an approximate confidence interval for the ML estimator were built. In order to assess the performance of the proposed estimators with various sample sizes, the results were analysed using Monte Carlo simulation. In most scenarios, according to the simulation results, the reliability estimate based on RSS is closer to the actual value than the reliability estimate based on SRS for both estimation methods. Notably, most of the MSEs of the Bayesian estimate are lower than the MSEs of the ML estimates. Additionally, for both ML and Bayesian approaches, RSS is found to produce outcomes that are more efficient than SRS as indicated by the MSE values. In order to show how theoretical results are applied in practise, two real datasets were provided.