A Note on Outer-Independent 2-Rainbow Domination in Graphs

Abstract

Let G be a graph with vertex set $V\left(G\right)$ and $f:V\left(G\right)\to \{\varnothing ,\{1\},\{2\},\{1,2\left\}\right\}$ be a function. We say that f is an outer-independent 2-rainbow dominating function on G if the following two conditions hold: $\left(\mathrm{i}\right)$$V_{\varnothing }=\{x\in V\left(G\right):f\left(x\right)=\varnothing \}$ is an independent set of G. $\left(\mathrm{ii}\right)$${\cup }_{u\in N\left(v\right)}f\left(u\right)=\{1,2\}$ for every vertex $v\in V_{\varnothing }$. The outer-independent 2-rainbow domination number of G, denoted by ${\gamma }_{r2}^{oi}\left(G\right)$, is the minimum weight $\omega \left(f\right)={\sum }_{x\in V\left(G\right)}\left|f\left(x\right)\right|$ among all outer-independent 2-rainbow dominating functions f on G. In this note, we obtain new results on the previous domination parameter. Some of our results are tight bounds which improve the well-known bounds $\beta \left(G\right)\le {\gamma }_{r2}^{oi}\left(G\right)\le 2\beta \left(G\right)$, where $\beta \left(G\right)$ denotes the vertex cover number of G. Finally, we study the outer-independent 2-rainbow domination number of the join, lexicographic, and corona product graphs. In particular, we show that, for these three product graphs, the parameter achieves equality in the lower bound of the previous inequality chain.

1. Introduction

Over the last decade, many variants associated with classical domination parameters in graphs have been defined and studied. In particular, variants related to domination and independence in graphs have attracted the attention of many researchers.

One of the most analysed ideas, and from which many parameters have been defined, is considering dominating sets whose complements form independent sets. Some recent references about some of these remarkable variants can be observed in [1,2] for total outer-independent domination, in [3,4] for outer-independent double Roman domination, in [5,6,7,8] for outer-independent (total) Roman domination, and in [9,10,11,12] for outer-independent (total) 2-rainbow domination.

This note mainly deals with providing new results about one of the aforementioned parameters: the outer-independent 2-rainbow domination number (OI2RD number) of a graph. Given a graph G, we say that a function $f:V\left(G\right)\to \{\varnothing ,\{1\},\{2\},\{1,2\left\}\right\}$ is an outer-independent 2-rainbow dominating function (OI2RD function) on G if the following two conditions hold.

(i)

$V_{\varnothing }=\{x\in V\left(G\right):f\left(x\right)=\varnothing \}$ is an independent set of G.

(ii)

${\cup }_{u\in N\left(v\right)}f\left(u\right)=\{1,2\}$ for every vertex $v\in V_{\varnothing }$.

Let $V_X=\{v\in V\left(G\right):f\left(v\right)=X\}$ for $X\in \{\varnothing ,\{1\},\{2\},\{1,2\left\}\right\}$. We will identify an OI2RD function f with the subsets $V_{\varnothing }$, $V_{\left\{1\right\}}$, $V_{\left\{2\right\}}$, and $V_{\{1,2\}}$ of $V\left(G\right)$ associated with it, and so we will use the unified notation $f(V_{\varnothing },V_{\left\{1\right\}},V_{\left\{2\right\}},V_{\{1,2\}})$ for the function and these associated subsets. The OI2RD number of G, denoted by ${\gamma }_{r2}^{oi}\left(G\right)$, is the minimum weight $\omega \left(f\right)={\sum }_{x\in V\left(G\right)}\left|f\left(x\right)\right|$ among all OI2RD functions f on G. A ${\gamma }_{r2}^{oi}\left(G\right)$-function is an OI2RD function with weight ${\gamma }_{r2}^{oi}\left(G\right)$.

As previously mentioned, this parameter has been studied by different researchers. For instance, in [9,10] interesting tight bounds were obtained for general graphs and for the particular case of trees. Moreover, in [9] graphs with small and large OI2RD numbers were characterized. Finally, in [11] the authors studied the OI2RD number for the Cartesian products of paths and cycles.

The note is organised as follows. In Section 2, we provide new tight bounds which improve the well-known bounds $\beta \left(G\right)\le {\gamma }_{r2}^{oi}\left(G\right)\le 2\beta \left(G\right)$ given in [9], where $\beta \left(G\right)$ denotes the vertex cover number of G. Finally, in Section 3 we provide closed formulas for this parameter in the join, lexicographic, and corona product graphs.

Additional Definitions and Tools

In this note, we consider that all graphs are simple and undirected, meaning that they have only undirected edges with no loops and no multiple edges between two fixed vertices. Given a graph $G\left(V\right(G),E(G\left)\right)$ of order $n\left(G\right)=\left|V\right(G\left)\right|$ and a vertex $v\in V\left(G\right)$, the open neighbourhood of v is defined to be $N\left(v\right)=\{u\in V(G):uv\in E(G\left)\right\}$. Now, we consider the following sets of vertices: $\mathcal{L}\left(G\right)=\{v\in V(G):|N\left(v\right)|=1\}$, $\mathcal{S}\left(G\right)=\{v\in V(G):N(v)\cap \mathcal{L}(G)\ne \varnothing \}$, and ${\mathcal{S}}_s\left(G\right)=\{v\in \mathcal{S}\left(G\right):|N\left(v\right)\cap \mathcal{L}\left(G\right)|\ge 2\}$.

A set $D\subseteq V\left(G\right)$ is a dominating set of G if $N\left(v\right)\cap D\ne \varnothing$ for every $v\in V\left(G\right)\backslash D$. The domination number of G, denoted by $\gamma \left(G\right)$, is the minimum cardinality among all dominating sets of G. A dominating set D with $\left|D\right|=\gamma \left(G\right)$ is defined as a $\gamma \left(G\right)$-set. This classical parameter has been extensively studied. From now on, for a parameter $\rho \left(G\right)$ of a graph G, by $\rho \left(G\right)$-set we mean a set of cardinality $\rho \left(G\right)$.

Two of the best-known variants of dominating sets, which they are also related to each other, are the independent sets and the vertex cover sets. A set $I\subseteq V\left(G\right)$ is an independent set of G if $N\left(v\right)\cap I=\varnothing$ for every $v\in I$. The maximum cardinality among all independent sets of G, denoted by $\alpha \left(G\right)$, is the independence number of G. Moreover, a set $D\subseteq V\left(G\right)$ is a vertex cover set of G if $V\left(G\right)\backslash D$ is an independent set of G. The minimum cardinality among all vertex cover sets of G, denoted by $\beta \left(G\right)$, is the vertex cover number of G. In 1959, Gallai established the following well-known relationship.

Theorem 1

([13]). If G is a nontrivial graph, then

$$\beta \left(G\right)+\alpha \left(G\right)=n\left(G\right).$$

Finally, we state the following useful tool. For the remainder of the paper, definitions will be introduced whenever a concept is needed.

Proposition 1.

Let G be a graph with no isolated vertex. Then, there exists a ${\gamma }_{r2}^{oi}\left(G\right)$-function $f(V_{\varnothing },V_{\left\{1\right\}},V_{\left\{2\right\}},V_{\{1,2\}})$ such that ${\mathcal{S}}_s\left(G\right)\subseteq V_{\{1,2\}}$.

Proof. 

Let $f(V_{\varnothing },V_{\left\{1\right\}},V_{\left\{2\right\}},V_{\{1,2\}})$ be a ${\gamma }_{r2}^{oi}\left(G\right)$-function such that $|V_{\varnothing }|$ is maximum among all ${\gamma }_{r2}^{oi}\left(G\right)$-functions. Suppose that there exists a vertex $v\in {\mathcal{S}}_s\left(G\right)\backslash V_{\{1,2\}}$. This implies that $N\left(v\right)\cap \mathcal{L}\left(G\right)\subseteq V_{\left\{1\right\}}\cup V_{\left\{2\right\}}$. Notice that the function $f^{\prime }(V_{\varnothing }^{\prime },V_{\left\{1\right\}}^{\prime },V_{\left\{2\right\}}^{\prime },V_{\{1,2\}}^{\prime })$, defined by $f^{\prime }\left(v\right)=\{1,2\}$, $f^{\prime }\left(h\right)=\varnothing$ for every $h\in N\left(v\right)\cap \mathcal{L}\left(G\right)$ and $f^{\prime }\left(x\right)=f\left(x\right)$ otherwise, is a ${\gamma }_{r2}^{oi}\left(G\right)$-function with $|V_{\varnothing }^{\prime }|>|V_{\varnothing }|$, which is a contradiction. Therefore, ${\mathcal{S}}_s\left(G\right)\subseteq V_{\{1,2\}}$, which completes the proof. □

2. New Bounds on the Outer-Independent 2-Rainbow Domination Number

Kang et al. [9] showed that, for any graph G with no isolated vertex,

$$\beta \left(G\right)\le {\gamma }_{r2}^{oi}\left(G\right)\le 2\beta \left(G\right).$$

(1)

The following theorem shows that the bounds given in (1) have room for improvement, since $|{\mathcal{S}}_s\left(G\right)|\ge 0$ and $\gamma \left(G\right)\le \beta \left(G\right)$.

Theorem 2.

For any graph G with no isolated vertex,

$$\beta \left(G\right)+|{\mathcal{S}}_s\left(G\right)|\le {\gamma }_{r2}^{oi}\left(G\right)\le \beta \left(G\right)+\gamma \left(G\right).$$

Proof. 

We first prove the lower bound. Let $f(V_{\varnothing },V_{\left\{1\right\}},V_{\left\{2\right\}},V_{\{1,2\}})$ be a ${\gamma }_{r2}^{oi}\left(G\right)$-function which satisfies Proposition 1. Hence, $V\left(G\right)\backslash V_{\varnothing }$ is a vertex cover and ${\mathcal{S}}_s\left(G\right)\subseteq V_{\{1,2\}}$, which implies that

$${\gamma }_{r2}^{oi}\left(G\right)=|V_{\left\{1\right\}}|+|V_{\left\{2\right\}}|+2|V_{\{1,2\}}|=|V\left(G\right)\backslash V_{\varnothing }|+|V_{\{1,2\}}|\ge \beta \left(G\right)+|{\mathcal{S}}_s\left(G\right)|.$$

Now, we proceed to prove the upper bound. Let D be a $\gamma \left(G\right)$-set and S a $\beta \left(G\right)$-set. Let $g(W_{\varnothing },W_{\left\{1\right\}},W_{\left\{2\right\}},W_{\{1,2\}})$ be a function defined as follows.

$$W_{\varnothing }=V\left(G\right)\backslash (D\cup S),W_{\left\{1\right\}}=D\backslash S,W_{\left\{2\right\}}=S\backslash D\mathrm{and}{W}_{\{1,2\}}=D\cap S.$$

We claim that g is an OI2RD function on G. If $W_{\varnothing }=\varnothing$, then we are done. Hence, we assume that $W_{\varnothing }\ne \varnothing$. Notice that $W_{\varnothing }$ is an independent set of G because S is a vertex cover set of G. We only need to prove that $g\left(N\left(x\right)\right)={\cup }_{u\in N\left(x\right)}g\left(u\right)=\{1,2\}$ for every $x\in W_{\varnothing }$. Let $v\in W_{\varnothing }$. Since S and D are both dominating sets of G, we deduce that either $N\left(v\right)\cap D\cap S\ne \varnothing$ or $N\left(v\right)\cap D\ne \varnothing$ and $N\left(v\right)\cap S\ne \varnothing$. In both cases, and by definition of g, we obtain that $g\left(N\right(v\left)\right)=\{1,2\}$. Thus, g is an OI2RD function on G, as required.

Therefore, ${\gamma }_{r2}^{oi}\left(G\right)\le \omega \left(g\right)=|S\backslash D|+|D\backslash S|+2|D\cap S|=\beta \left(G\right)+\gamma \left(G\right)$, which completes the proof. □

The following result, which is a direct consequence of Theorem 2, the upper bound given in (1), and the fact that $\gamma \left(G\right)\le \beta \left(G\right)$, provides a necessary condition for the graphs that satisfy the equality ${\gamma }_{r2}^{oi}\left(G\right)=2\beta \left(G\right)$.

Proposition 2.

Let G be a graph with no isolated vertex. If ${\gamma }_{r2}^{oi}\left(G\right)=2\beta \left(G\right)$, then $\beta \left(G\right)=\gamma \left(G\right)$.

The converse of proposition above does not hold. For instance, the graph G given in Figure 1 satisfies $\beta \left(G\right)=\gamma \left(G\right)$ and ${\gamma }_{r2}^{oi}\left(G\right)<2\beta \left(G\right)$.

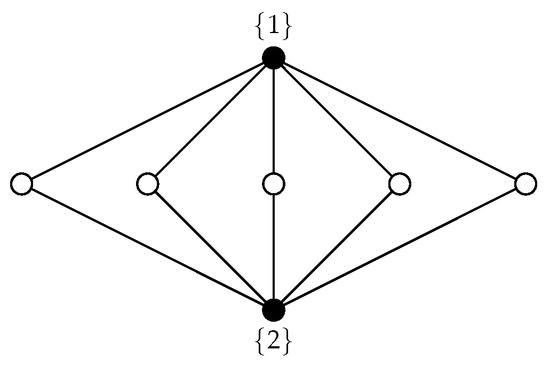
Figure 1. A graph G with ${\gamma }_{r2}^{oi}\left(G\right)=\beta \left(G\right)=\gamma \left(G\right)=2$.

As a second consequence of Theorem 2 we can derive the next proposition.

Proposition 3.

Let G be a graph with no isolated vertex. If ${\mathcal{S}}_s\left(G\right)$ is a dominating set of G, then

$${\gamma }_{r2}^{oi}\left(G\right)=\beta \left(G\right)+\left|{\mathcal{S}}_s\left(G\right)\right|=\beta \left(G\right)+\gamma \left(G\right).$$

Proof. 

If ${\mathcal{S}}_s\left(G\right)$ is a dominating set of G, then $\gamma \left(G\right)\le |{\mathcal{S}}_s\left(G\right)|$. Therefore, Theorem 2 leads to the equality, which completes the proof. □

The next theorem improves the upper bound given in Theorem 2 for the case where G is a tree.

Theorem 3.

For any nontrivial tree T,

$${\gamma }_{r2}^{oi}\left(T\right)\le \beta \left(T\right)+\left|\mathcal{S}\left(T\right)\right|.$$

Proof. 

Let S be a $\beta \left(T\right)$-set such that $\mathcal{S}\left(T\right)\subseteq S$. Now, we construct a partition $\{I,D\}$ of S as follows. Let $u\in \mathcal{S}\left(T\right)$ and $S_i^u=\{w\in S:d(w,u)=i\}$, where $d(w,u)$ represents the distance between w and u. Now, we need to introduce some necessary definitions. Let $ϵ\left(u\right)$ be the eccentricity of u, and, for any vertex $x\ne u$, the $\mathrm{Parent}\left[x\right]$ is the vertex adjacent to x on the unique $x-u$ path.

Let $I={\cup }_{i=0}^{ϵ\left(u\right)}{I}_i$ and $D={\cup }_{i=0}^{ϵ\left(u\right)}{D}_i$, where $I_0=\left\{u\right\}$ and $D_0=\varnothing$ and for $i\ge 1$ we define $I_i$ and $D_i$ as follows. For every $v\in S_i^u$, define the class $\dot{v}\subseteq S_i^u$ such that $v,v^{\prime }\in \dot{v}$ if and only if Parent $\left[v\right]$ = Parent $\left[v^{\prime }\right]$. From $i=1$ to eccentricity $ϵ\left(u\right)$, we consider the next cases for every $\dot{v}\subseteq S_i^u$, where we fix $v\in \dot{v}$.

(i)

$\mathrm{Parent}\left[v\right]\in S$. In this case, we set $\dot{v}\subseteq I_i$.

(ii)

$\mathrm{Parent}\left[v\right]\notin S$ (notice that $i\ge 2$ and $\mathrm{Parent}\left[\mathrm{Parent}\right[v\left]\right]\in S$). If $\mathrm{Parent}\left[\mathrm{Parent}\left[v\right]\right]\in I_{i-2}$, then we set $\dot{v}\subseteq D_i$, otherwise we set $\dot{v}\subseteq I_i$.

It is clear that $\{I,D\}$ is a partition of S. By condition (ii) in the construction above, it follows that $N\left(x\right)\cap I\ne \varnothing$ and $N\left(x\right)\cap D\ne \varnothing$ for every vertex $x\in V\left(T\right)\backslash (S\cup \mathcal{L}(T\left)\right)$. With this property in mind and the fact that $V\left(T\right)\backslash S$ is an independent set, it is easy to deduce that the function f, defined below, is an OI2RD function on T.

$$f\left(x\right)=\left\{\begin{array}{cc}\hfill \varnothing ;& \mathrm{if}x\in V\left(T\right)\backslash S,\hfill \\ \hfill \{1,2\};& \mathrm{if}x\in \mathcal{S}\left(T\right),\hfill \\ \hfill \left\{1\right\};& \mathrm{if}x\in I\backslash \mathcal{S}\left(T\right),\hfill \\ \hfill \left\{2\right\};& \mathrm{if}x\in D\backslash \mathcal{S}\left(T\right).\hfill \end{array}\right.$$

Therefore, ${\gamma }_{r2}^{oi}\left(T\right)\le \omega \left(f\right)=\left|I\right|+\left|D\right|+\left|\mathcal{S}\left(T\right)\right|=\left|S\right|+\left|\mathcal{S}\left(T\right)\right|=\beta \left(T\right)+\left|\mathcal{S}\left(T\right)\right|$, which completes the proof. □

From Theorems 2 and 3, we obtain that for any nontrivial tree T,

$$\beta \left(T\right)+|{\mathcal{S}}_s\left(T\right)|\le {\gamma }_{r2}^{oi}\left(T\right)\le \beta \left(T\right)+\left|\mathcal{S}\left(T\right)\right|.$$

(2)

The following result is a direct consequence of the previous inequality chain.

Proposition 4.

If T is a tree such that $\mathcal{S}\left(T\right)={\mathcal{S}}_s\left(T\right)$, then

$${\gamma }_{r2}^{oi}\left(T\right)=\beta \left(T\right)+\left|\mathcal{S}\left(T\right)\right|.$$

3. The Cases of the Join, Lexicographic, and Corona Product Graphs

In this section, we consider the OI2RD number of three well-known product graphs (join −+, lexicographic −∘, and corona −⊙). If $G_1$ and $G_2$ are any two graphs with no isolated vertex, then

• The join graph $G_1+G_2$ is the graph with vertex set $V(G_1+G_2)=V\left(G_1\right)\cup V\left(G_2\right)$ and edge set $E(G_1+G_2)=E\left(G_1\right)\cup E\left(G_2\right)\cup \{xy:x\in V\left(G_1\right),y\in V\left(G_2\right)\}$. For instance, the graph G given in Figure 1 is isomorphic to the join graph $N_2+N_5$, where $N_r$ is the empty graph of r vertices.
• The lexicographic product graph $G_1\circ G_2$ is the graph with vertex set $V(G_1\circ G_2)=V\left(G_1\right)\times V\left(G_2\right)$, and two vertices $(u,v),(x,y)\in V(G_1\circ G_2)$ are adjacent if and only if $ux\in E\left(G_1\right)$ or $u=x$ and $vy\in E\left(G_2\right)$. Figure 2 shows the graph $P_4\circ P_3$.
  

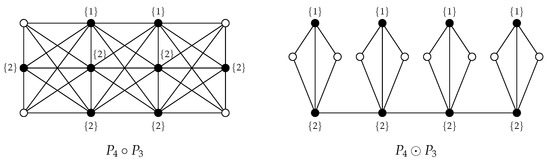  Figure 2. The labels of black-coloured vertices describe the (non-empty) weights of a ${\gamma }_{r2}^{oi}(P_4\circ P_3)$-function and ${\gamma }_{r2}^{oi}(P_4\odot P_3)$-function, respectively.
• The corona product graph $G_1\odot G_2$ is the graph obtained from $G_1$ and $G_2$, by taking one copy of $G_1$ and $n\left(G_1\right)$ copies of $G_2$ and joining by an edge every vertex from the $i^{th}$-copy of $G_2$ with the $i^{th}$-vertex of $G_1$. Figure 2 shows the graph $P_4\odot P_3$.

The following equalities are part of folklore, and these can be found for instance in [14,15,16], respectively.

Theorem 4.

If $G_1$ and $G_2$ are two nontrivial graphs, then

(i)

[14]$\alpha (G_1+G_2)=max\{\alpha \left(G_1\right),\alpha \left(G_2\right)\}.$

(ii)

[15]$\alpha (G_1\circ G_2)=\alpha \left(G_1\right)\alpha \left(G_2\right).$

(iii)

[16]$\alpha (G_1\odot G_2)=n\left(G_1\right)\alpha \left(G_2\right).$

The following results show that the join, lexicographic, and corona product graphs reach the equality in the lower bound given in Theorem 2.

Theorem 5.

If $G_1$ and $G_2$ are two nontrivial graphs, then the following equalities hold.

(i)

${\gamma }_{r2}^{oi}(G_1+G_2)=\beta (G_1+G_2)=n\left(G_1\right)+n\left(G_2\right)-max\{\alpha \left(G_1\right),\alpha \left(G_2\right)\}.$

(ii)

${\gamma }_{r2}^{oi}(G_1\circ G_2)=\beta (G_1\circ G_2)=n\left(G_1\right)n\left(G_2\right)-\alpha \left(G_1\right)\alpha \left(G_2\right).$

Proof. 

We first proceed to prove (i). By Theorem 2, it follows that $\beta (G_1+G_2)\le {\gamma }_{r2}^{oi}(G_1+G_2)$ and Theorems 1 and 4-(i) lead to $\beta (G_1+G_2)=n\left(G_1\right)+n\left(G_2\right)-max\{\alpha \left(G_1\right),\alpha \left(G_2\right)\}.$ We only need to prove that ${\gamma }_{r2}^{oi}(G_1+G_2)\le \beta (G_1+G_2).$ Let D be a $\beta (G_1+G_2)$-set. By definition, $V\left(G_1\right)\subseteq D$ or $V\left(G_2\right)\subseteq D$. Without loss of generality, we consider that $V\left(G_1\right)\subseteq D$. Let $g(W_{\varnothing },W_{\left\{1\right\}},W_{\left\{2\right\}},W_{\{1,2\}})$ be a function defined as follows:

• $W_{\{1,2\}}=\varnothing$, $W_{\left\{1\right\}}\cup W_{\left\{2\right\}}=D$ and $W_{\varnothing }=V(G_1+G_2)\backslash D$.
• $W_{\left\{1\right\}}\cap V\left(G_1\right)\ne \varnothing$ and $W_{\left\{2\right\}}\cap V\left(G_1\right)\ne \varnothing$.

Notice that g is an OI2RD function on $G_1+G_2$. Thus, ${\gamma }_{r2}^{oi}(G_1+G_2)=\omega \left(g\right)=\left|D\right|=\beta (G_1+G_2)$, as required, which completes the proof of (i).

Finally, we proceed to prove (ii). Theorem 2 leads to $\beta (G_1\circ G_2)\le {\gamma }_{r2}^{oi}(G_1\circ G_2)$, and, by Theorems 1 and 4-(ii), it follows that $\beta (G_1\circ G_2)=n\left(G_1\right)n\left(G_2\right)-\alpha \left(G_1\right)\alpha \left(G_2\right).$ In order to conclude the proof, we only need to prove that ${\gamma }_{r2}^{oi}(G_1\circ G_2)\le \beta (G_1\circ G_2).$ For any $x\in V\left(G_1\right)$, $G_2^x\cong G_2$ will denote the copy of $G_2$ in $G_1\circ G_2$ containing x. Let S be a $\beta (G_1\circ G_2)$-set and $S^{*}=\{x\in V\left(G_1\right):V\left(G_2^x\right)\subseteq S\}$. By definition, it follows that $S^{*}$ is a $\beta \left(G_1\right)$-set. Now, let us define a function $f(V_{\varnothing },V_{\left\{1\right\}},V_{\left\{2\right\}},V_{\{1,2\}})$ on $G_1\circ G_2$ as follows.

• $V_{\{1,2\}}=\varnothing$, $V_{\left\{1\right\}}\cup V_{\left\{2\right\}}=S$ and $V_{\varnothing }=V(G_1\circ G_2)\backslash S$.
• $V_{\left\{1\right\}}\cap V\left(G_2^x\right)\ne \varnothing$ and $V_{\left\{2\right\}}\cap V\left(G_2^x\right)\ne \varnothing$ for every vertex $x\in S^{*}$.

Notice that f is an OI2RD function on $G_1\circ G_2$, which implies that ${\gamma }_{r2}^{oi}(G_1\circ G_2)=\omega \left(f\right)=\left|S\right|=\beta (G_1\circ G_2)$, as required. Therefore, the proof is complete. □

Theorem 6.

If $G_1$ and $G_2$ are two graphs with no isolated vertex, then

$${\gamma }_{r2}^{oi}(G_1\odot G_2)=\beta (G_1\odot G_2)=n\left(G_1\right)(n\left(G_2\right)+1)-n\left(G_1\right)\alpha \left(G_2\right).$$

Proof. 

By Theorem 2 it follows that $\beta (G_1\odot G_2)\le {\gamma }_{r2}^{oi}(G_1\odot G_2)$, and Theorems 1 and 4-(iii) lead to $\beta (G_1\odot G_2)=n\left(G_1\right)(n\left(G_2\right)+1)-n\left(G_1\right)\alpha \left(G_2\right).$ We only need to prove that ${\gamma }_{r2}^{oi}(G_1\odot G_2)\le \beta (G_1\odot G_2).$ For any $x\in V\left(G_1\right)$, $G_2^x\cong G_2$ will denote the copy of $G_2$ in $G_1\odot G_2$ associated to x. Let $D_x$ be a $\beta \left(G_2^x\right)$-set for every $x\in V\left(G_1\right)$. Now, we consider the function $f(V_{\varnothing },V_{\left\{1\right\}},V_{\left\{2\right\}},V_{\{1,2\}})$ on $G_1\odot G_2$ as follows.

$$V_{\left\{1\right\}}=\bigcup _{x\in V\left(G_1\right)}{D}_x,V_{\left\{2\right\}}=V\left(G_1\right)\mathrm{and}{V}_{\{1,2\}}=\varnothing .$$

Notice that f is an OI2RD function on $G_1\odot G_2$, which implies that ${\gamma }_{r2}^{oi}(G_1\odot G_2)=\omega \left(f\right)=n\left(G_1\right)(n\left(G_2\right)-\alpha \left(G_2\right)+1)=\beta (G_1\odot G_2)$, as required. Therefore, the proof is complete. □

4. Conclusions and Open Problems

New results concerning the OI2RD number of a graph have been presented in this note. Among the main results, we emphasize the following.

• We have provided new bounds on the OI2RD number of a graph, which improve other well-known bounds.
• We obtained closed formulas for the OI2RD number of the join, lexicographic, and corona product graphs in terms of the independence number of the factor graphs involved in these products.

Finally, and based on the inequality chain $\beta \left(T\right)+|{\mathcal{S}}_s\left(T\right)|\le {\gamma }_{r2}^{oi}\left(T\right)\le \beta \left(T\right)+\left|\mathcal{S}\left(T\right)\right|$ given in Equation (2), we propose the problem of characterizing the trees T that satisfy the equality ${\gamma }_{r2}^{oi}\left(T\right)=\beta \left(T\right)+k$, where $k\in \left\{\right|{\mathcal{S}}_s\left(T\right)|,\dots ,|\mathcal{S}\left(T\right)\left|\right\}$.