Meta-Optimization of Dimension Adaptive Parameter Schema for Nelder–Mead Algorithm in High-Dimensional Problems
Abstract
1. Introduction
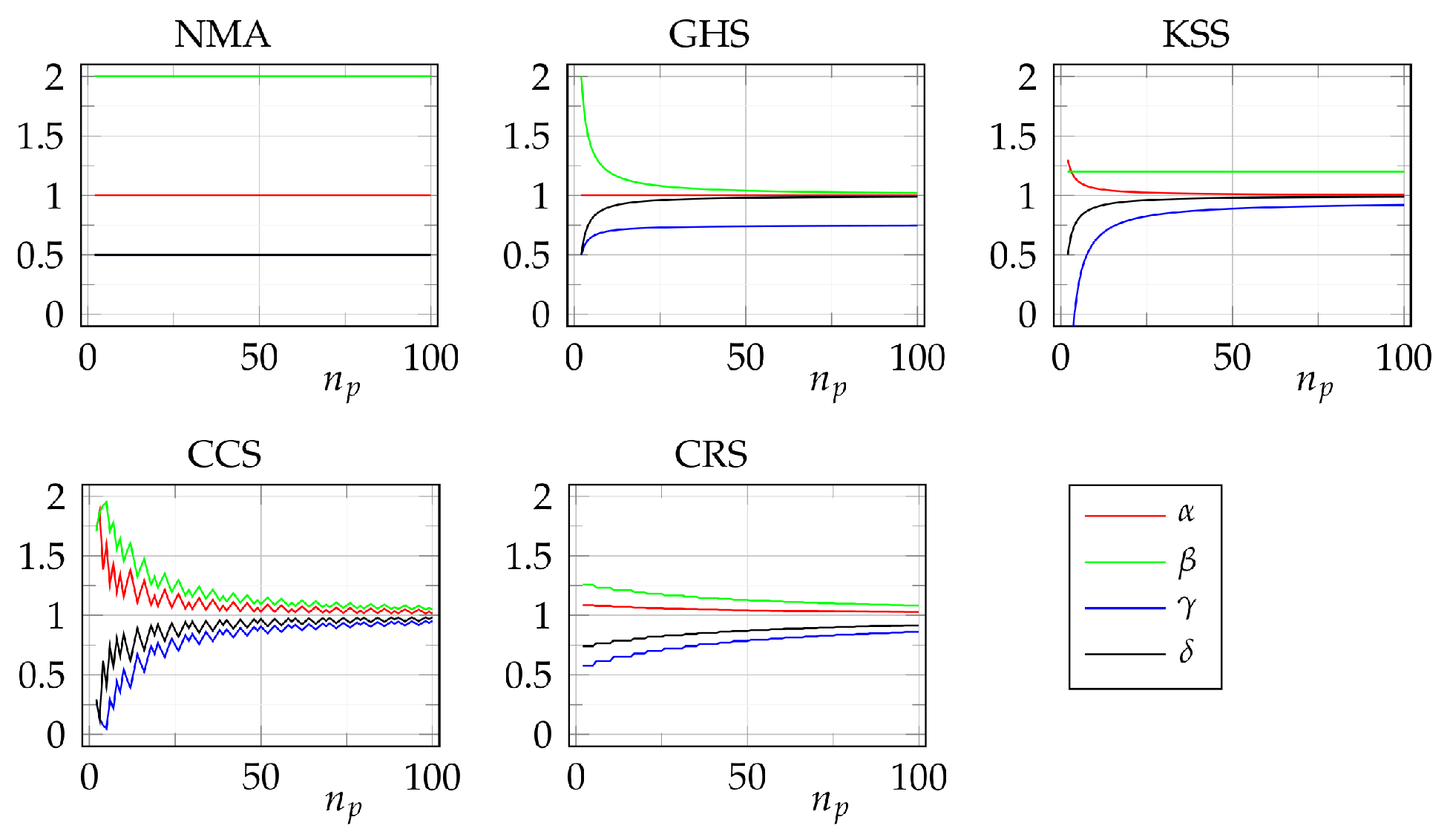
2. Adaptive Parameter Schemas for NMA
- Order and relabel simplex vertices to satisfy . Calculate the centroid point excluding the highest objective function value point.
- Reflect over to obtain the reflected point , .
- If , expand to obtain the expanded point, .If , replace with and end the iteration.
- If , replace with and end the iteration.
- If , contract towards to obtain the contracted point, .If , replace with and end the iteration.
- If , contract towards to obtain the contracted point.If , replace with and end the iteration.
- Shrink the entire simplex towards , , , .
3. Optimization of the Adaptive Parameter Schema
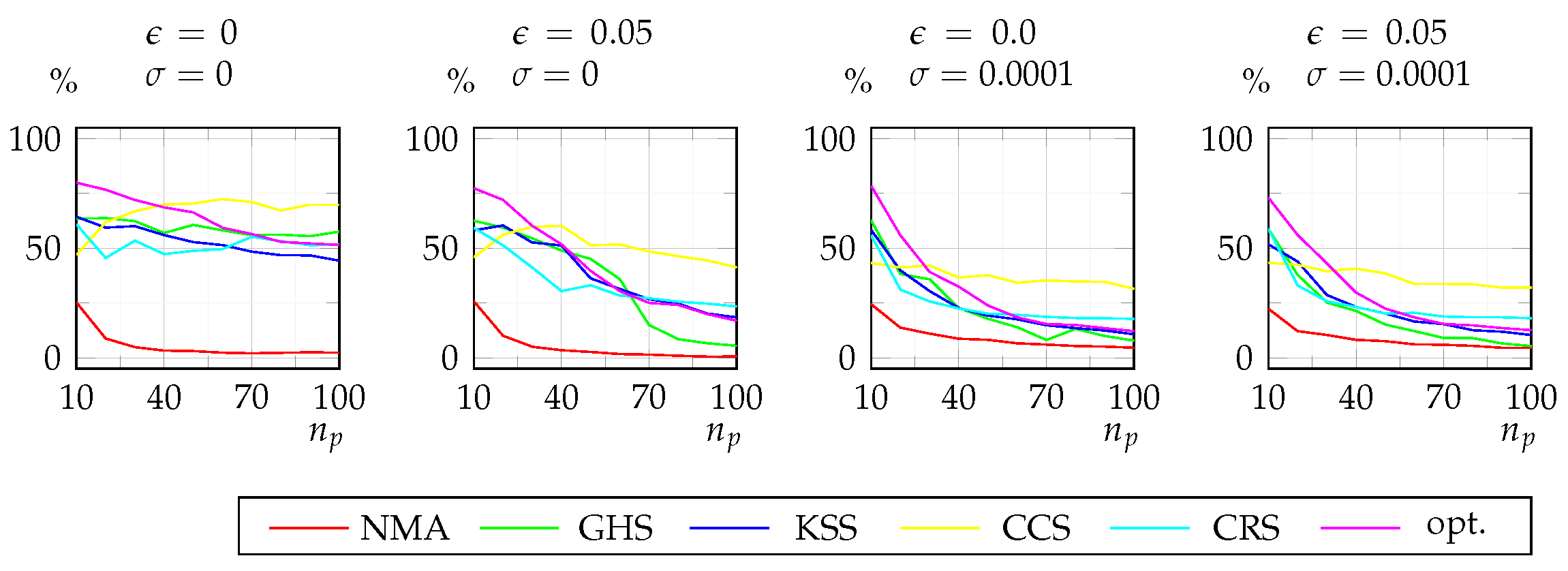
4. Evaluation of the Optimized Schema with Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NMA | Nelder–Mead Algorithm |
| PSADE | Parallel Simulated Annealing with Differential Evolution |
| SC | Schema Candidate |
| GH | Gao–Han |
| MGH | Moré–Garbow–Hilstrom |
| CUTEr | Constrained and Unconstrained Testing Environment, revisited |
| GHS | Gao–Han Schema |
| KSS | Kumar–Suri Schema |
| CCS | Chebyshev Crude Schema |
| CRS | Chebyshev Refined Schema |
| PyPI | Python Package Index |
| f | objective function |
| number of optimized variables or problem dimension | |
| , | ith simplex vertex and centroid of simplex vertices |
| , | reflected point and expanded point |
| , | reflected point and worst point contracted towards centroid |
| , , , | NMA reflection, expansion, contraction, and shrink parameters |
| CRS constant calculated from | |
| , | starting point, an arbitrary point in -dimensional parameter space |
| , | ith component Pfeffer’s constant and unit vector |
| , | simplex flatness and size tolerances |
| jth component of ith simplex vertex | |
| , , , , etc. | meta-optimization variables defining an SC |
| p, | single benchmark problem and set of benchmark problems |
| s, | single parameter schema and set of all parameter schemas |
| r, | reference parameter schema and set of all reference parameter schemas |
| set of sets of GH and MGH benchmark problems | |
| number of simplex gradient estimates | |
| available for schema evaluation per single p | |
| number of objective function evaluations needed on problem p by schema s to satisfy (7) | |
| share of problems from set solved by schema s in simplex gradient estimates | |
| lowest objective function value reached in simplex gradient estimates by any of the schemas on a particular problem | |
| convergence condition tolerance | |
| weight used in meta-optimization objective function when at least one of the reference schemas outperforms the evaluated SC on set of benchmark problems | |
| weight used in meta-optimization objective function when the evaluated SC outperforms all the reference schemas on set of benchmark problems |
References
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- McKinnon, K.I.M. Convergence of the Nelder-Mead simplex method to a non-stationary point. J. Optim. 1998, 9, 148–158. [Google Scholar]
- Galántai, A. A convergence analysis of the Nelder-Mead simplex method. Acta Polytech. Hungarica 2021, 18, 93–105. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder-Mead simplex method in low dimensions. J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Poonen, B.; Wright, M.H. Convergence of the restricted Nelder-Mead algorithm in two dimensions. J. Optim. 2012, 22, 501–532. [Google Scholar] [CrossRef]
- Kelley, C.T. Detection and remediation of stagnation in the Nelder-Mead algorithm using a sufficient decrease condition. J. Optim. 1999, 10, 43–55. [Google Scholar] [CrossRef]
- Tseng, P. Fortified-descent simplicial search method: A general approach. J. Optim. 1999, 10, 269–288. [Google Scholar] [CrossRef]
- Nazareth, L.; Tseng, P. Gilding the lily: A variant of the Nelder-Mead algorithm based on golden-section search. Comput. Optim. Appl. 2002, 22, 133–144. [Google Scholar] [CrossRef]
- Price, C.J.; Coope, I.D.; Byatt, D. A convergent variant of the Nelder-Mead algorithm. J. Optim. Theory. Appl. 2002, 113, 5–19. [Google Scholar] [CrossRef]
- Bűrmen, Á.; Puhan, J.; Tuma, T. Grid restrained Nelder-Mead algorithm. Comput. Optim. Appl. 2006, 34, 359–375. [Google Scholar] [CrossRef][Green Version]
- Bűrmen, Á.; Tuma, T. Unconstrained derivative-free optimization by successive approximation. Comput. Appl. Math. 2009, 223, 62–74. [Google Scholar] [CrossRef]
- Torczon, V.J. Multi-Directional Search: A Direct Search Algorithm for Parallel Machines. Ph.D. Thesis, Rice University, Houston, TX, USA, 1989. [Google Scholar]
- Wright, M. Direct search methods: Once scorned, now respectable. In Proceedings of the 16th Dundee Biennial Conference in Numerical Analysis, Dundee, Scotland, 27–30 June 1996; pp. 191–208. [Google Scholar]
- Han, L.; Neumann, M. Effect of dimensionality on the Nelder-Mead simplex method. Optim. Methods Softw. 2006, 21, 1–16. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259–277. [Google Scholar] [CrossRef]
- Fajfar, I.; Puhan, J.; Bűrmen, Á. Evolving a Nelder-Mead algorithm for optimization with genetic programming. Evol. Comput. 2017, 25, 351–373. [Google Scholar] [CrossRef] [PubMed]
- Musafer, H.A.; Mahmood, A. Dynamic Hassan–Nelder-Mead with simplex free selectivity for unconstrained optimization. IEEE Access 2018, 6, 39015–39026. [Google Scholar] [CrossRef]
- Fajfar, I.; Bűrmen, Á.; Puhan, J. The Nelder-Mead simplex algorithm with perturbed centroid for high-dimensional function optimization. Optim. Lett. 2019, 13, 1011–1025. [Google Scholar] [CrossRef]
- Kumar, G.N.S.; Suri, V.K. Multilevel Nelder-Mead’s simplex method. In Proceedings of the 2014 9th International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014; Volume 9, pp. 1–6. [Google Scholar]
- Mehta, V.K. Improved Nelder-Mead algorithm in high dimensions with adaptive parameters based on Chebyshev spacing points. Eng. Optim. 2020, 52, 1814–1828. [Google Scholar] [CrossRef]
- Olenšek, J.; Tuma, T.; Puhan, J.; Bűrmen, Á. A new asynchronous parallel global optimization method based on simulated annealing and differential evolution. Appl. Soft Comput. 2011, 11, 1481–1489. [Google Scholar] [CrossRef]
- Moré, J.J.; Garbow, B.S.; Hilstrom, K.E. Testing unconstrained optimization software. ACM Trans. Math. Softw. 1981, 7, 17–41. [Google Scholar] [CrossRef]
- Gould, N.I.M.; Orban, D.; Toint, P.L. CUTEr and SifDec: A constrained and unconstrained testing environment, revisited. ACM Trans. Math. Softw. 2003, 29, 373–394. [Google Scholar] [CrossRef]
- Moré, J.J.; Wild, S.M. Benchmarking derivative-free optimization algorithms. SIAM J. Optim. 2009, 20, 172–191. [Google Scholar] [CrossRef]
- Olenšek, J.; Bűrmen, Á.; Puhan, J.; Tuma, T. DESA: A new hybrid global optimization method and its application to analog integrated circuit sizing. J. Glob. Optim. 2009, 44, 53–77. [Google Scholar] [CrossRef]
- Bűrmen, Á. PyOPUS-Simulation, Optimization, and Design. Available online: http://fides.fe.uni-lj.si/pyopus (accessed on 15 May 2022).
- Bűrmen, B.; Locatelli, I.; Bűrmen, Á.; Bogataj, M.; Mrhar, A. Mathematical modeling of individual gastric emptying of pellets in the fed state. J. Drug. Deliv. Sci. Technol 2014, 24, 418–424. [Google Scholar] [CrossRef]
- Rojec, Ž.; Olenšek, J.; Fajfar, I. Analog circuit topology representation for automated synthesis and optimization. Inf. MIDEM 2018, 48, 29–40. [Google Scholar]
- Rojec, Ž.; Bűrmen, Á.; Fajfar, I. Analog circuit topology synthesis by means of evolutionary computation. Eng. Appl. Artif. Intell. 2019, 80, 48–65. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. CCSA: Conscious Neighborhood-based Crow Search Algorithm for Solving Global Optimization Problems. Appl. Soft Comput. 2019, 85, 105583. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H. DMDE: Diversity-maintained multi-trial vector differential evolution algorithm for non-decomposition large-scale global optimization. Expert Syst. Appl. 2022, 98, 116895. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Engrg. 2022, 392, 114616. [Google Scholar] [CrossRef]
- Shanno, D.F.; Phua, K. Matrix conditioning and nonlinear optimization. Math. Program. 1978, 14, 149–160. [Google Scholar] [CrossRef]





| 0.0 | 10 | 3.5 × 10−323 | 0.0 | 0.0 | 3.5 × 10−323 | 0.0 | 0.0 |
| 0.0 | 20 | 2 × 10−322 | 0.0 | 0.0 | 0.0 | 0.0 | 10−323 |
| 30 | 1.14 × 10−11 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 40 | 2.03 × 10−4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 50 | 5.54 × 10−4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 60 | 1.38 × 10−5 | 0.0 | 0.0 | 5 × 10−324 | 0.0 | 5 × 10−324 | |
| 70 | 5.76 × 10−5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 80 | 4.87 × 10−6 | 5 × 10−323 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 90 | 2.75 × 10−6 | 1.4 × 10−322 | 0.0 | 5 × 10−324 | 0.0 | 0.0 | |
| 100 | 3.19 × 10−6 | 6 × 10−323 | 0.0 | 2 × 10−323 | 0.0 | 0.0 | |
| 0.05 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 20 | 6.23 × 10−322 | 0.0 | 0.0 | 0.0 | 5 × 10−324 | 0.0 |
| 30 | 5.31 × 10−3 | 0.0 | 0.0 | 0.0 | 0.0 | 5 × 10−324 | |
| 40 | 1.32 × 10−2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 50 | 1.62 × 10−1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 60 | 12.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 70 | 8.24 | 2 × 10−323 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 80 | 32.2 | 1.24 × 10−322 | 0.0 | 5 × 10−324 | 0.0 | 0.0 | |
| 90 | 3.77 | 5.4 × 10−323 | 5 × 10−324 | 5 × 10−324 | 0.0 | 0.0 | |
| 100 | 278 | 6 × 10−323 | 0.0 | 10−323 | 0.0 | 0.0 | |
| 0.0 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0001 | 20 | 2.05 × 10−3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 30 | 1.91 × 10−5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 40 | 16.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 50 | 2.63 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 60 | 10.9 | 0.0 | 0.0 | 10−323 | 0.0 | 0.0 | |
| 70 | 276 | 5 × 10−324 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 80 | 292 | 8 × 10−323 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 90 | 11.7 | 6 × 10−323 | 5 × 10−324 | 5 × 10−324 | 0.0 | 0.0 | |
| 100 | 48.7 | 7.4 × 10−323 | 0.0 | 10−323 | 0.0 | 0.0 | |
| 0.05 | 10 | 1.5 × 10−323 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0001 | 20 | 1.93 × 10−4 | 0.0 | 0.0 | 0.0 | 5 × 10−324 | 5 × 10−324 |
| 30 | 1.12 × 10−2 | 0.0 | 0.0 | 0.0 | 0.0 | 5 × 10−324 | |
| 40 | 7.31 × 10−1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 50 | 37.2 | 0.0 | 0.0 | 0.0 | 0.0 | 5 × 10−324 | |
| 60 | 179 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 70 | 18.7 | 3 × 10−323 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 80 | 16.4 | 7.4 × 10−323 | 0.0 | 5 × 10−324 | 0.0 | 0.0 | |
| 90 | 1480 | 1.3 × 10−322 | 1.5 × 10−323 | 0.0 | 0.0 | 0.0 | |
| 100 | 3802 | 5 × 10−323 | 0.0 | 10−323 | 0.0 | 0.0 | |
| accurate | 7/40 | 40/40 | 40/40 | 40/40 | 40/40 | 40/40 |
| Function | |||||||
|---|---|---|---|---|---|---|---|
| Extended | 12 | 2.91 × 10−28 | 2.35 × 10−29 | 1.73 × 10−28 | 4.64 × 10−29 | 5.18 × 10−29 | 6.88 × 10−29 |
| Rosenbrock | 18 | 20.0 | 6.97 × 10−29 | 6.51 × 10−29 | 1.44 × 10−28 | 5.66 × 10−28 | 1.35 × 10−28 |
| 24 | 12.5 | 1.72 × 10−28 | 2.58 × 10−28 | 1.86 × 10−28 | 3.72 × 10−28 | 6.21 × 10−28 | |
| 30 | 34.5 | 4.09 × 10−28 | 6.70 × 10−28 | 7.28 × 10−28 | 3.70 × 10−27 | 2.76 × 10−28 | |
| 36 | 49.1 | 8.72 × 10−28 | 6.64 × 10−28 | 6.81 × 10−28 | 4.77 × 10−28 | 1.11 × 10−27 | |
| Extended | 12 | 8.34 × 10−55 | 3.33 × 10−57 | 7.09 × 10−59 | 3.09 × 10−57 | 1.07 × 10−59 | 1.18 × 10−58 |
| Powell | 24 | 1.33 × 10−9 | 1.83 × 10−54 | 3.45 × 10−56 | 5.37 × 10−56 | 1.67 × 10−53 | 3.39 × 10−53 |
| singular | 40 | 1.69 × 10 | 1.06 × 10−50 | 2.34 × 10−52 | 1.46 × 10−52 | 5.22 × 10−52 | 2.33 × 10−53 |
| 60 | 4.16 × 10−4 | 9.71 × 10 | 3.43 × 10−50 | 2.88 × 10−52 | 1.28 × 10−37 | 1.16 × 10−46 | |
| Penalty I | 10 | 7.57 × 10−5 | 7.09 × 10−5 | 7.09 × 10−5 | 7.60 × 10 | 7.09 × 10−5 | 7.09 × 10−5 |
| Penalty II | 10 | 2.98 × 10−4 | 2.94 × 10−4 | 2.94 × 10−4 | 2.98 × 10−4 | 2.95 × 10−4 | 2.94 × 10−4 |
| Variably | 12 | 4.77 | 3.72 × 10−30 | 1.47 × 10−29 | 3.64 × 10−29 | 2.30 × 10−29 | 1.78 × 10−29 |
| dimensioned | 18 | 4.22 | 8.96 × 10−30 | 2.06 × 10−29 | 1.52 × 10−29 | 4.74 × 10−29 | 4.25 × 10−29 |
| 24 | 11.5 | 8.22 × 10−29 | 8.37 × 10−29 | 7.52 × 10−29 | 9.23 × 10−29 | 2.27 × 10−28 | |
| 30 | 40.5 | 8.08 × 10−29 | 1.08 × 10−28 | 1.06 × 10−28 | 3.38 × 10−28 | 4.49 × 10−28 | |
| 36 | 60.1 | 4.21 × 10−28 | 1.46 × 10−28 | 8.82 × 10−29 | 8.35 × 10−28 | 7.60 × 10−28 | |
| Trigonometric | 10 | 2.80 × 10 | 2.80 × 10−5 | 2.80 × 10−5 | 2.80 × 10−5 | 2.80 × 10−5 | 2.80 × 10−5 |
| 20 | 1.35 × 10−6 | 1.35 × 10−6 | 6.03 × 10−6 | 6.86 × 10−6 | 1.35 × 10−6 | 1.35 × 10−6 | |
| 30 | 2.20 × 10−5 | 9.90 × 10−7 | 9.90 × 10−7 | 5.65 × 10−6 | 9.90 × 10−7 | 5.98 × 10−7 | |
| 40 | 1.41 × 10−5 | 1.55 × 10−6 | 3.95 × 10−6 | 1.68 × 10−7 | 5.58 × 10−7 | 1.55 × 10−6 | |
| 50 | 2.52 × 10−5 | 2.24 × 10−7 | 3.41 × 10−6 | 9.23 × 10−7 | 1.11 × 10−6 | 2.24 × 10−7 | |
| 60 | 3.87 × 10−5 | 8.68 × 10−7 | 7.57 × 10−7 | 7.57 × 10−7 | 1.27 × 10−6 | 4.62 × 10−7 | |
| Discrete | 10 | 6.85 × 10−32 | 3.03 × 10−33 | 8.36 × 10−32 | 2.20 × 10−31 | 3.07 × 10−32 | 1.59 × 10−32 |
| boundary | 20 | 4.69 × 10−30 | 7.24 × 10−32 | 2.51 × 10−32 | 2.39 × 10−32 | 1.05 × 10−31 | 3.92 × 10−32 |
| value | 30 | 9.87 × 10−6 | 1.10 × 10−31 | 1.43 × 10−31 | 1.19 × 10−31 | 2.02 × 10−31 | 9.29 × 10−32 |
| 40 | 6.46 × 10−6 | 4.58 × 10−31 | 3.55 × 10−31 | 1.37 × 10−31 | 4.76 × 10−31 | 3.45 × 10−31 | |
| 50 | 5.72 × 10−6 | 6.02 × 10−31 | 5.70 × 10−31 | 2.84 × 10−31 | 5.35 × 10−31 | 4.35 × 10−31 | |
| 60 | 3.19 × 10−6 | 2.46 × 10−30 | 8.09 × 10−31 | 6.64 × 10−31 | 1.11 × 10−30 | 7.39 × 10−31 | |
| Discrete | 10 | 1.91 × 10−31 | 4.24 × 10−33 | 1.44 × 10−32 | 2.27 × 10−31 | 2.56 × 10−32 | 3.08 × 10−33 |
| integral | 20 | 7.69 × 10−30 | 4.62 × 10−32 | 2.90 × 10−32 | 6.27 × 10−32 | 3.40 × 10−32 | 2.37 × 10−32 |
| equation | 30 | 7.11 × 10−4 | 2.22 × 10−31 | 2.50 × 10−31 | 3.45 × 10−31 | 8.55 × 10−32 | 2.50 × 10−31 |
| 40 | 3.63 × 10−4 | 3.82 × 10−31 | 3.07 × 10−31 | 3.21 × 10−31 | 4.25 × 10−31 | 3.04 × 10−31 | |
| 50 | 3.05 × 10−3 | 8.51 × 10−31 | 1.34 × 10−30 | 5.95 × 10−31 | 1.47 × 10−30 | 7.34 × 10−31 | |
| 60 | 4.46 × 10−4 | 2.24 × 10−30 | 1.30 × 10−30 | 1.59 × 10−30 | 9.74 × 10−31 | 6.12 × 10−31 | |
| Broyden | 10 | 3.99 × 10−30 | 3.12 × 10−30 | 7.31 × 10−30 | 3.28 × 10−29 | 2.92 × 10−30 | 2.92 × 10−30 |
| tridiagonal | 20 | 3.20 × 10−26 | 1.63 × 10−29 | 3.34 × 10−29 | 6.15 × 10−29 | 2.45 × 10−29 | 3.15 × 10−29 |
| 30 | 4.70 × 10−26 | 1.68 × 10−28 | 1.19 × 10−28 | 9.66 × 10−29 | 6.50 × 10−29 | 8.18 × 10−29 | |
| 40 | 9.11 × 10−14 | 2.24 × 10−28 | 6.73 × 10−28 | 3.70 × 10−28 | 2.45 × 10−28 | 2.24 × 10−28 | |
| 50 | 2.67 × 10−13 | 5.82 × 10−28 | 6.98 × 10−28 | 4.61 × 10−28 | 6.86 × 10−28 | 4.54 × 10−28 | |
| 60 | 3.78 × 10−11 | 9.12 × 10−28 | 1.69 × 10−27 | 1.01 × 10−27 | 1.34 × 10−27 | 1.10 × 10−27 | |
| Broyden | 10 | 4.18 × 10−28 | 4.61 × 10−30 | 4.81 × 10−30 | 6.82 × 10−29 | 7.43 × 10−30 | 2.36 × 10−30 |
| banded | 20 | 1.85 × 10−26 | 2.63 × 10−29 | 6.04 × 10−29 | 7.47 × 10−29 | 1.60 × 10−28 | 4.77 × 10−29 |
| 30 | 12.2 | 2.25 × 10−28 | 1.34 × 10−28 | 2.08 × 10−28 | 3.15 × 10−28 | 2.89 × 10−28 | |
| 40 | 2.02 × 10 | 3.48 × 10−28 | 7.41 × 10−28 | 9.32 × 10−28 | 1.34 × 10−28 | 3.25 × 10−28 | |
| 50 | 9.33 × 10 | 6.08 × 10−28 | 1.38 × 10−27 | 6.78 × 10−28 | 5.98 × 10−28 | 1.04 × 10−27 | |
| 60 | 5.13 × 10 | 2.93 × 10−27 | 3.44 × 10−27 | 4.09 × 10−27 | 7.98 × 10−28 | 7.59 × 10−28 | |
| accurate | 15/46 | 40/46 | 40/46 | 39/46 | 39/46 | 42/46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojec, Ž.; Tuma, T.; Olenšek, J.; Bűrmen, Á.; Puhan, J. Meta-Optimization of Dimension Adaptive Parameter Schema for Nelder–Mead Algorithm in High-Dimensional Problems. Mathematics 2022, 10, 2288. https://doi.org/10.3390/math10132288
Rojec Ž, Tuma T, Olenšek J, Bűrmen Á, Puhan J. Meta-Optimization of Dimension Adaptive Parameter Schema for Nelder–Mead Algorithm in High-Dimensional Problems. Mathematics. 2022; 10(13):2288. https://doi.org/10.3390/math10132288
Chicago/Turabian StyleRojec, Žiga, Tadej Tuma, Jernej Olenšek, Árpád Bűrmen, and Janez Puhan. 2022. "Meta-Optimization of Dimension Adaptive Parameter Schema for Nelder–Mead Algorithm in High-Dimensional Problems" Mathematics 10, no. 13: 2288. https://doi.org/10.3390/math10132288
APA StyleRojec, Ž., Tuma, T., Olenšek, J., Bűrmen, Á., & Puhan, J. (2022). Meta-Optimization of Dimension Adaptive Parameter Schema for Nelder–Mead Algorithm in High-Dimensional Problems. Mathematics, 10(13), 2288. https://doi.org/10.3390/math10132288






