Lie Symmetry Group, Invariant Subspace, and Conservation Law for the Time-Fractional Derivative Nonlinear Schrödinger Equation
Abstract
:1. Introduction
2. Preliminaries
3. Symmetry Analysis
3.1. Lie Symmetry Group
3.2. Symmetry Reduction
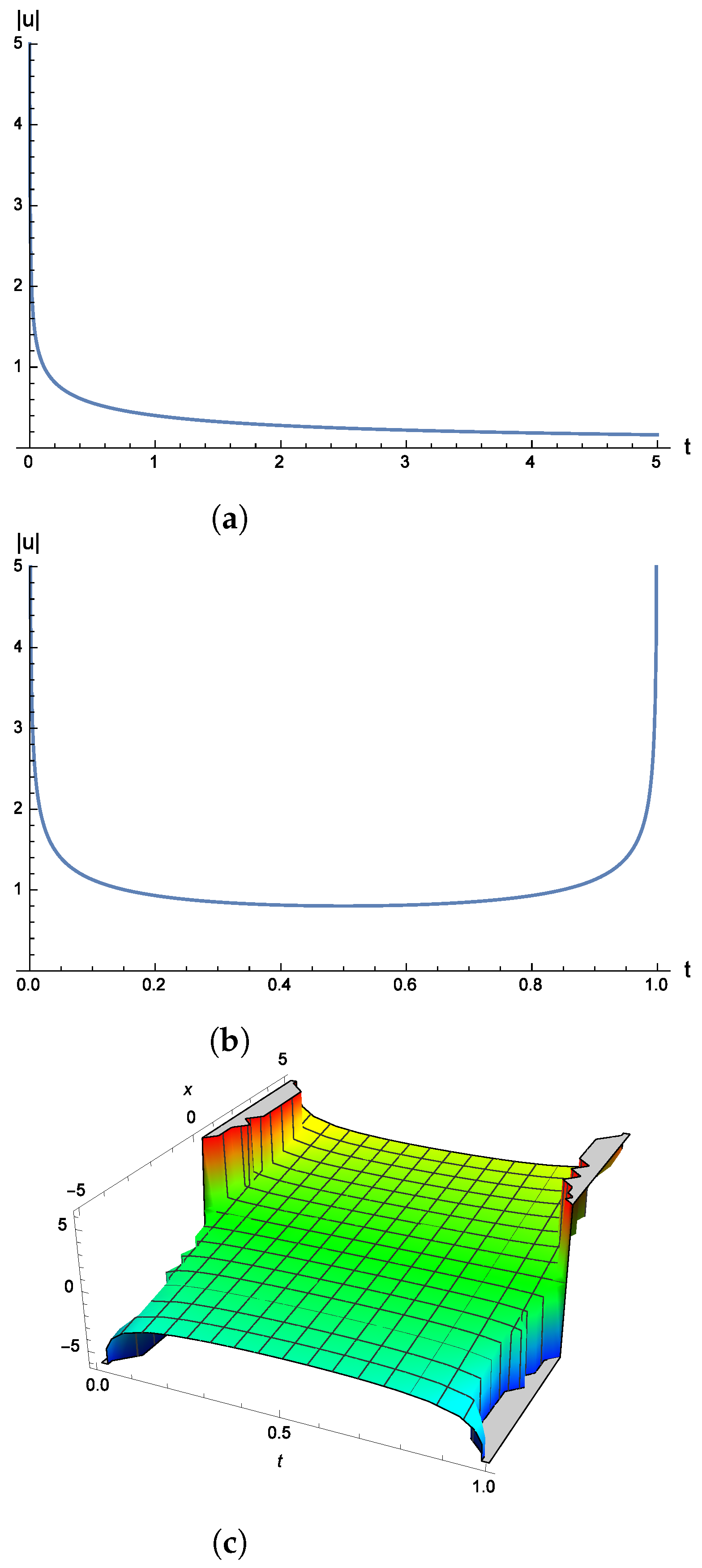
3.2.1. Reduction under
3.2.2. Reduction under
4. Invariant Subspace
5. Conservation Law
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oldham, K.B.; Spanier, F. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujilo, J.J. Theory and Application of Fractional Differential Equation; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Odibat, Z.; Momani, S. A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 2008, 21, 194–199. [Google Scholar] [CrossRef] [Green Version]
- Yuste, S.B.; Acedo, L. An explicit finite difference method and a new von Neumann-type stablity analysis for fractional diffusion equations. SIAM J. Mumer. Anal. 2005, 42, 1862–1874. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A. 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Li, X.C.; Xu, M.Y.; Jiang, X.Y. Homotopy perturbation method to time-fractional diffusion equation with a moving boundary condition. Appl. Math. Comput. 2009, 208, 434–439. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Bluman, G.W.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 2010. [Google Scholar]
- Gazizov, R.K.; Kasatkin, A.A.; Lukashchuk, S.Y. Continuous transformation groups of fractional differential equations. Vestnik USATU 2007, 9, 125–135. [Google Scholar]
- Gazizov, R.K.; Kasatkin, A.A.; Lukashchuk, S.Y. Symmetry Properties of Fractional Diffusion Equations. Phys. Scr. 2009, T136, 014016. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Lukashchuk, S.Y. Higher-order symmetries of a time-fractional anomalous diffusion equation. Mathematics 2020, 9, 216. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Lin, Z.X. Local symmetry structure and potential symmetries of time-fractional partial differential equations. Stud. Appl. Math. 2021, 147, 363–389. [Google Scholar] [CrossRef]
- Lukashchuk, S.Y. Conservation laws for time-fractional subdiffusion and diffusion-wave equations. Nonlinear Dyn. 2015, 80, 791–802. [Google Scholar] [CrossRef] [Green Version]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2017, 333, 311–328. [Google Scholar] [CrossRef] [Green Version]
- Galaktionov, V.A.; Svirshchevski, S. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics; Chapman and Hall: London, UK, 2007. [Google Scholar]
- Gazizov, R.K.; Kasatkin, A.A. Construction of exact solutions for fractional order differential equations by invariant subspace method. Comput. Math. Appl. 2013, 66, 576–584. [Google Scholar] [CrossRef]
- Huang, Q.; Zhdanov, R. Symmetries and exact solutions of the time fractional Harry-Dym equation with Riemann-Liouville derivative. Phys. A 2014, 409, 110–118. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, S.L. Time-fractional inhomogeneous nonlinear diffusion equation: Symmetries, conservation laws, invariant subspaces, and exact solutions. Mod. Phys. Lett. B 2018, 32, 1850401. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Zheng, J. Symmetry structure of multi-dimensional time-fractional partial differential equations. Nonlinearity 2021, 34, 5186. [Google Scholar] [CrossRef]
- Cheng, X.Y.; Wang, L.Z. Invariant analysis, exact solutions and conservation laws of (2+1)-dimensional time fractional Navier-Stokes equations. Proc. R. Soc. A 2021, 477, 1–20. [Google Scholar] [CrossRef]
- Feng, W. Exact solutions and conservation laws of time-fractional Levi equation. Symmetry 2020, 12, 1074. [Google Scholar] [CrossRef]
- Singla, K.; Gupta, R.K. Generalized Lie symmetry approach for fractional order systems of differential equations. III. J. Math. Phys. 2017, 58, 061501. [Google Scholar] [CrossRef]
- Sahadevan, R.; Prakash, P. Exact solutions and maximal dimension of invariant subspaces of time fractional coupled nonlinear partial differential equations. Commun. Nonlinear Sci. Numer. Simulat. 2017, 42, 158–177. [Google Scholar] [CrossRef]
- Feng, W. On symmetry groups and conservation laws for space-time fractional inhomogeneous nonlinear diffusion equation. Rep. Math. Phys. 2019, 84, 375–392. [Google Scholar] [CrossRef]
- Singla, K.; Gupta, R.K. On invariant analysis of space-time fractional nonlinear systems of partial differential equations. II. J. Math. Phys. 2017, 58, 051503. [Google Scholar] [CrossRef]
- Inc, M.; Yusuf, A.; Aliyu, A.I.; Baleanu, D. Lie symmetry analysis, explicit solutions and conservation laws for the space-time fractional nonlinear evolution equations. Phys. A 2018, 496, 371–383. [Google Scholar] [CrossRef]
- Rogister, A. Parallel propagation of nonlinear low-frequency waves in high-β plasma. Phys. Fluids 1971, 14, 2733–2743. [Google Scholar] [CrossRef]
- Agrawal, G.P. Applications of Nonlinear Fiber Optics; Academic Press: New York, NY, USA, 2001. [Google Scholar]
- Kaup, D.J.; Newell, A.C. An exact solution for a derivative nonlinear Schrödinger equation. J. Math. Phys. 1978, 19, 798. [Google Scholar] [CrossRef]
- Kakei, S.; Sasa, N.; Satsuma, J. Bilinearization of a generalized derivative nonlinear schrödinger equation. J. Phys. Soc. Jpn. 1995, 64, 1519–1526. [Google Scholar] [CrossRef] [Green Version]
- Imai, K. Generlization of Kaup-Newell inverse scattering formulation and Darboux transformation. J. Phys. Soc. Jpn. 1999, 68, 355–359. [Google Scholar] [CrossRef]
- Steudel, H. The hierarchy of multi-soliton solutions of the derivative nonlinear Schrödinger equation. J. Phys. A Math. Gen. 2003, 36, 1931–1946. [Google Scholar] [CrossRef]
- Qu, C.Z.; Ji, L.N. Invariant subspaces and conditional Lie-Bäcklund symmetries of inhomogeneous nonlinear diffusion equations. Sci. China Math. 2013, 56, 2187–2203. [Google Scholar] [CrossRef]
| 0 | 0 | ||
| 0 | 0 | 0 | |
| 0 | 0 |
| Ad | |||
|---|---|---|---|
| Invariant Subspace | Conditions | |
|---|---|---|
| 0 | ||
| Invariant Subspace | Conditions | ||
|---|---|---|---|
| 0 | |||
| 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, F.; Feng, W.; Zhao, S. Lie Symmetry Group, Invariant Subspace, and Conservation Law for the Time-Fractional Derivative Nonlinear Schrödinger Equation. Mathematics 2022, 10, 2170. https://doi.org/10.3390/math10132170
Qin F, Feng W, Zhao S. Lie Symmetry Group, Invariant Subspace, and Conservation Law for the Time-Fractional Derivative Nonlinear Schrödinger Equation. Mathematics. 2022; 10(13):2170. https://doi.org/10.3390/math10132170
Chicago/Turabian StyleQin, Fan, Wei Feng, and Songlin Zhao. 2022. "Lie Symmetry Group, Invariant Subspace, and Conservation Law for the Time-Fractional Derivative Nonlinear Schrödinger Equation" Mathematics 10, no. 13: 2170. https://doi.org/10.3390/math10132170
APA StyleQin, F., Feng, W., & Zhao, S. (2022). Lie Symmetry Group, Invariant Subspace, and Conservation Law for the Time-Fractional Derivative Nonlinear Schrödinger Equation. Mathematics, 10(13), 2170. https://doi.org/10.3390/math10132170







