Stochastic Fractal Search Algorithm Improved with Opposition-Based Learning for Solving the Substitution Box Design Problem
Abstract
:1. Introduction
2. State of the Art
3. Substitution Box
Preliminaries
- Let f be a Boolean function defined as , where n is the input bits and m. We can mention several ways to represent a Boolean function: algebraic form, truth table, and hexadecimal form, to name a few.
- The representation in its algebraic normal form is built on the basis of the operations of sum and product of the input variables. We can write f in the following way:where .
- The decimal representation of a Boolean function is based on a vector of length , where n indicates the number of input bits. The elements of the vector are in decimal form.
- The number of 1 present in the truth table representation of a Boolean function is defined as the Hamming weight.
- If the elements present in the decimal representation are unique or the hamming weight is equal to , the Boolean function satisfies the balance property.
- The Hamming distance is calculated by counting all the differences in the output bits of two Boolean functions.
- The maximum of the degrees of the monomials of the algebraic normal form is called the algebraic degree.
- If the algebraic degree of a Boolean function is equal to one, the function is defined as an affine Boolean function. An affine Boolean function can be described aswhere . When is zero, we get a linear Boolean function. A Boolean function of n input bits, can have affine Boolean functions.
- The Walsh–Hadamard transformation of Boolean function f with n variables is defined as:where is the polarity representation of a Boolean function, is the signed function of the linear function , and is known as a spectral walsh coefficient. The real-value vector of all spectral coefficients is referred to as the Walsh–Hadamard transformation spectrum. The maximum absolute value, taken by , is given by: .
- The Hadamard matrix, is a binary matrix of dimensions . For the elements , where i represents the rows and j represents the columns,where .
- In cryptography, one of the critical properties of a Boolean function is the nonlinearity. The nonlinearity is the minimum distance between a Boolean function and any affine Boolean function. A low nonlinearity value implies that a cryptographic algorithm may be weak against linear or differential attacks. The distance between a Boolean function and any affine Boolean function , can be calculated as follows:taking , where w is the coefficient vector; we can rewrite the above result aswhere is the Walsh–Hadamard transform of on w, is the representation of all affine boolean functions and . Finally, the nonlinearity is defined as follows:The objective function to be used by the optimization algorithm is the nonlinearity.
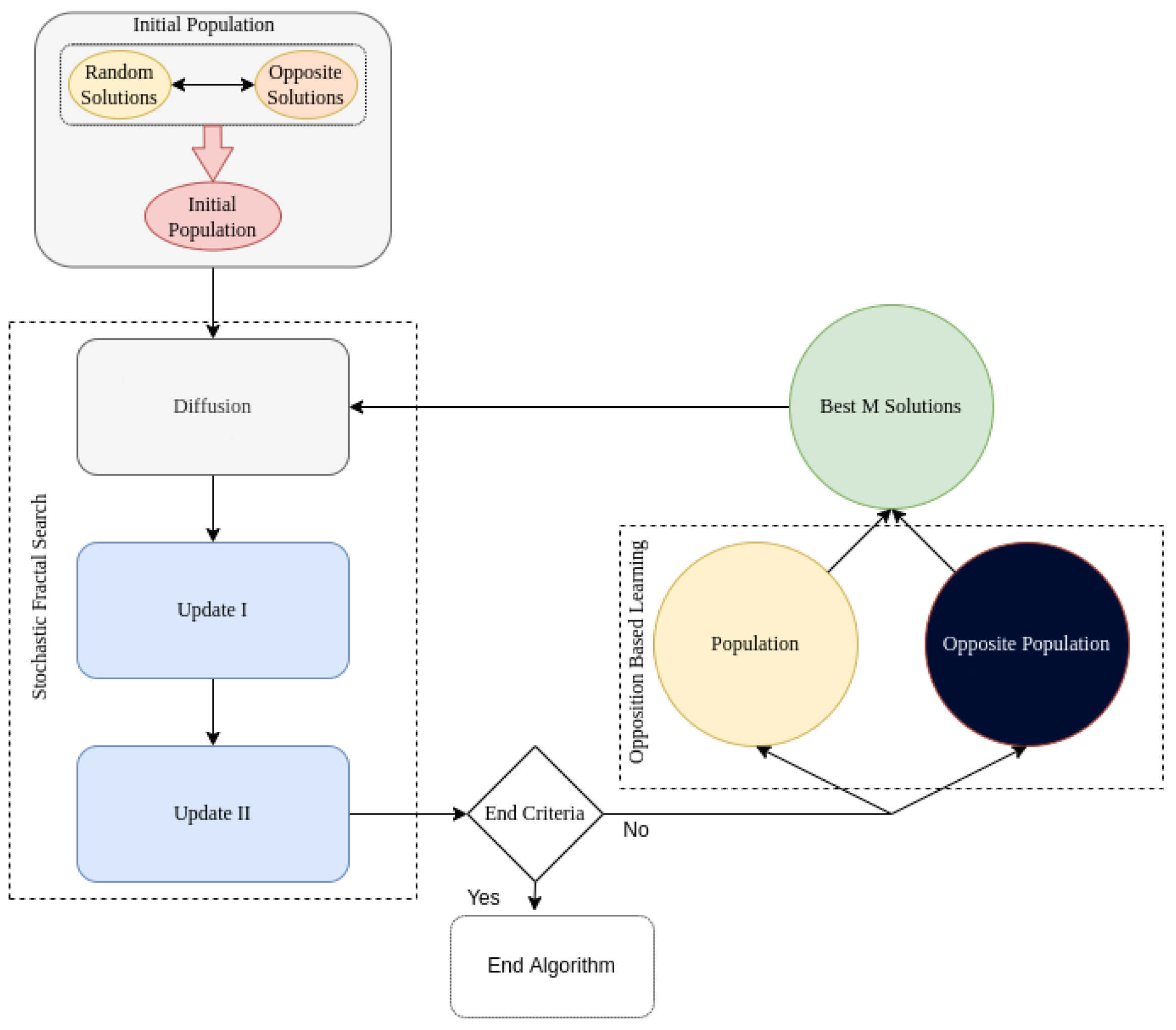
4. Stochastic Fractal Search Algorithm with Opposition Based Learning
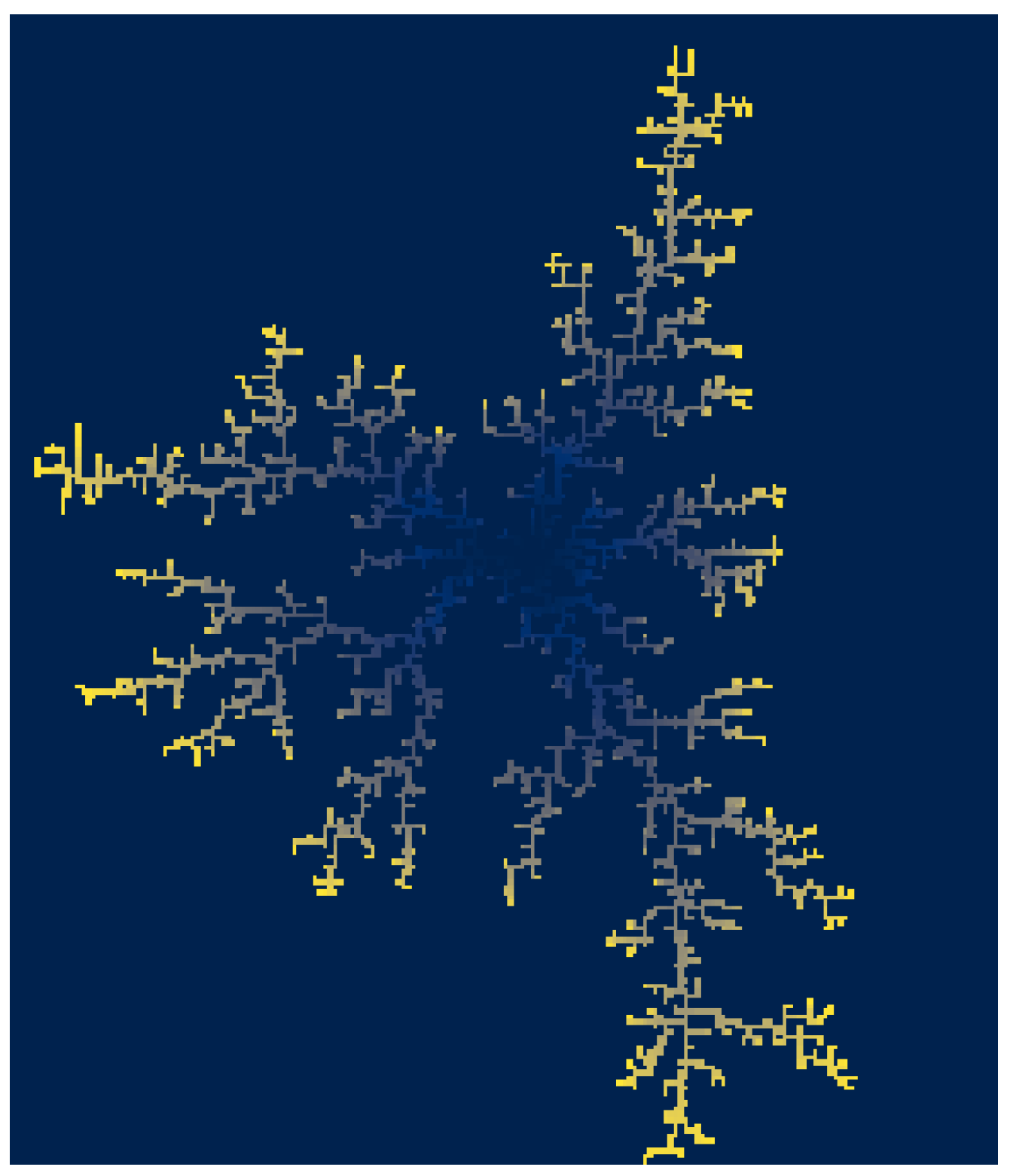
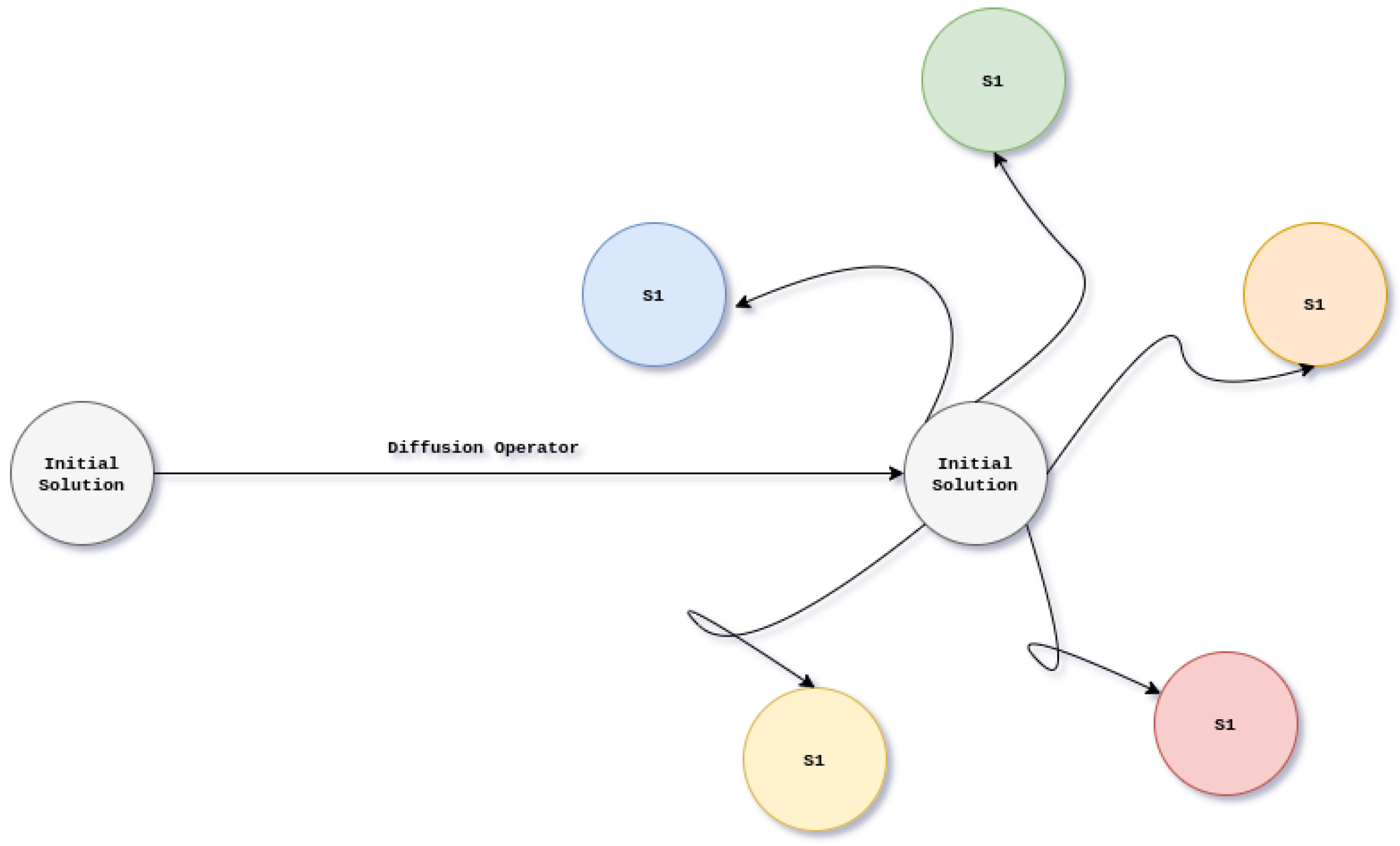
4.1. Stochastic Fractal Search Algorithm
- Using a combination of chaotic maps. The first map is the logistic map (16) which uses the parameter . This map will iterate 1000 times, and the output is used as input for the tent map (17). The tent map uses and also iterates over 1000 times. The result of this operation allows us to form a vector of 256 unique elements in the interval that will be our representation of a Boolean function.
- Standard C++ functions for generating random numbers.
- Generation of random solutions together with the respective opposite solutions and extracting half of each set, whose solutions present the best fitness to form the initial population.
- Generation of random solutions in conjunction with the respective opposite solutions, combining this set and using the best solutions.
- Generating random solutions in conjunction with the respective opposite solutions, combining this set, selecting a subset of good solutions, and extracting a random set from the latter to form the initial population.
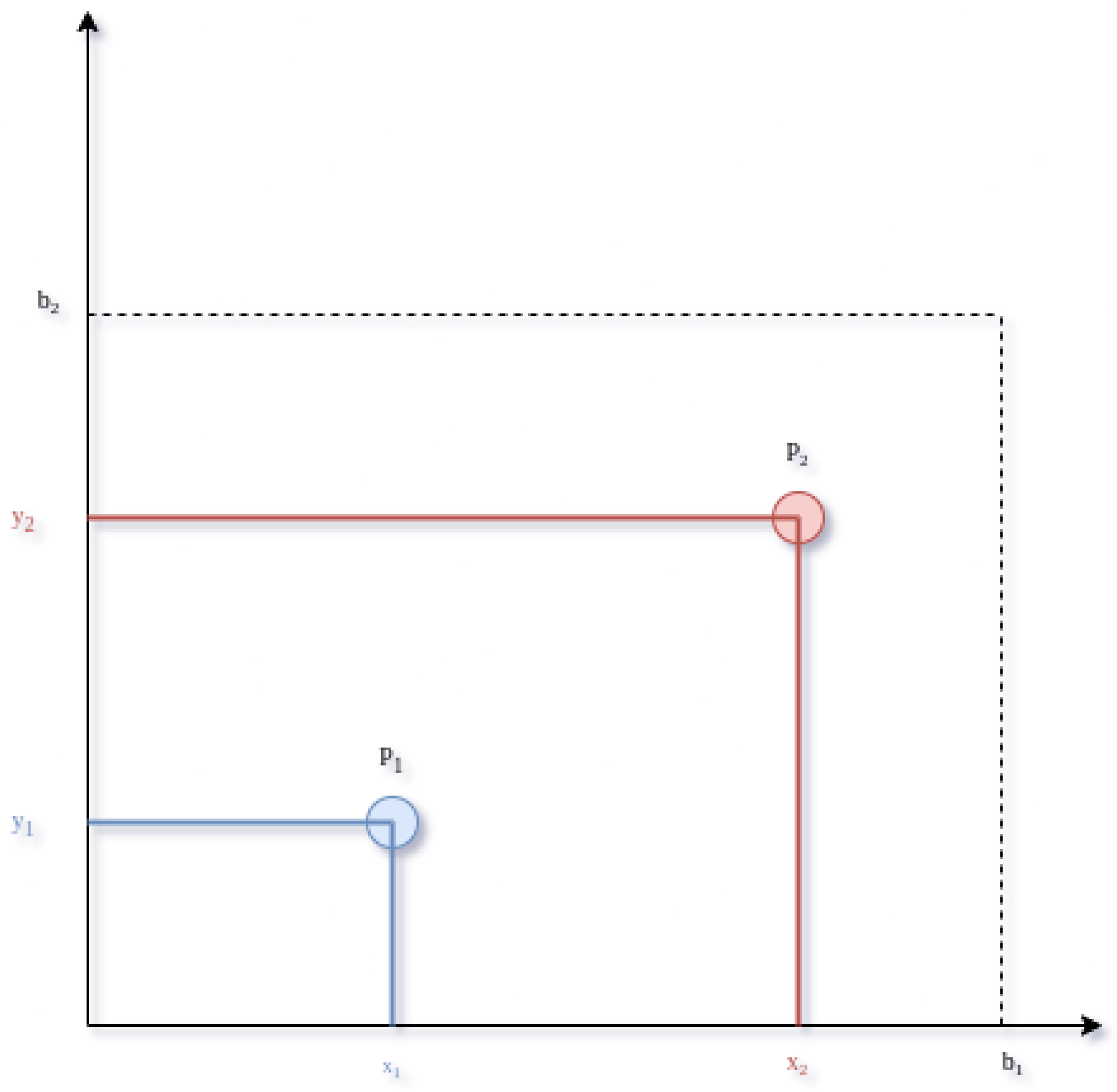
4.2. Opposition Based Learning
4.3. Integration
| Algorithm 1 SFS OBL. |
|
4.4. Sequential Model-Based Algorithm Configuration
5. Results
5.1. Nonlinearity
5.2. Bijectivity
5.3. Algebraic Degree
5.4. Strict Avalanche Criterion
5.5. Bit-Independent Criterion
5.6. Differential Approximation Probability
5.7. Linear Approximation Probability
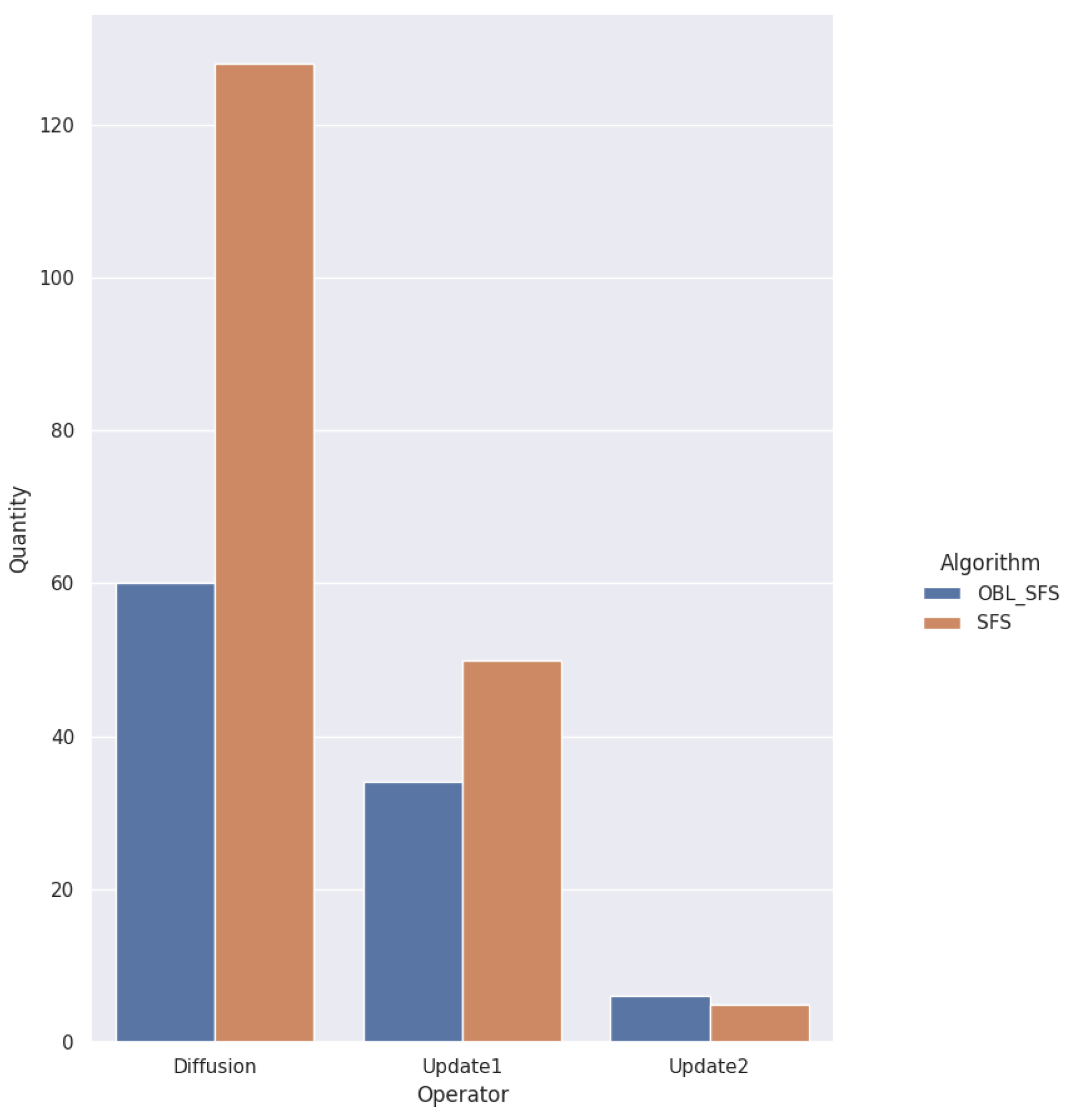
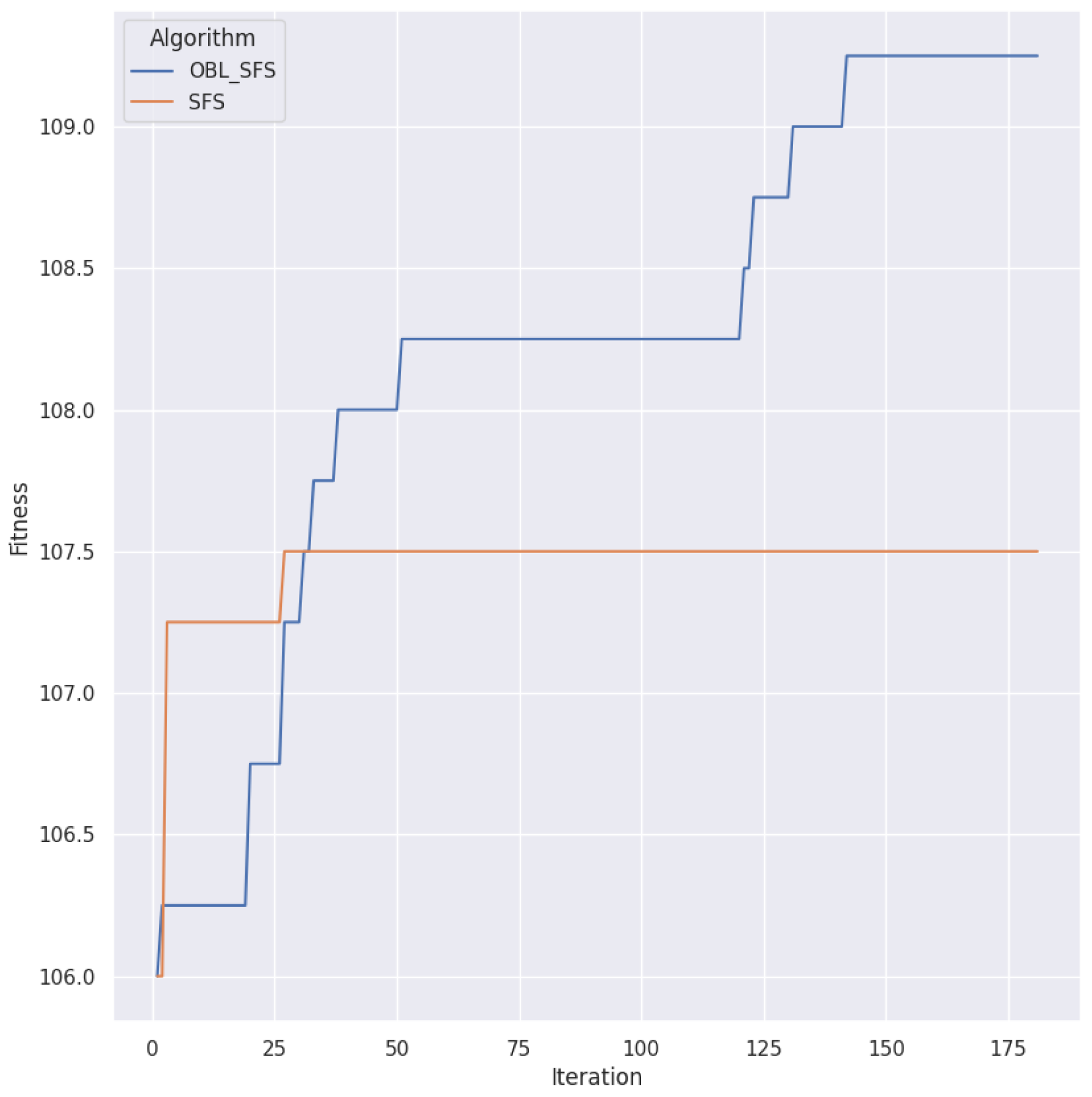
5.8. Comparison without Opposition Based Learning
5.9. Brief Image Analysis
- The randomness of the information present in the encrypted image is measured with entropy. Values close to 8 are preferable.
- Comparing the values between neighboring pixels determines the degree of similarity between them, which is known as correlation.
- The energy is a measure of the localized change of the image.
- Contrast is a measure of luminance that allows one object to be distinguished from another.
- Homogeneity determines the relationship between the elements of the gray level co-occurrence matrix with respect to its diagonal.
- Number of pixel change rate are designed to test the number of changing pixels between two encrypted images.
- Unified average changing intensity is designed to test the number of mean intensities modified between two encrypted images.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Picek, S.; Cupic, M.; Rotim, L. A new cost function for evolution of s-boxes. Evol. Comput. 2016, 24, 695–718. [Google Scholar] [CrossRef]
- Biham, E.; Shamir, A.; Cryptol, J. Differential cryptanalysis of des. Like Cryptosyst. 1991, 4, 3. [Google Scholar]
- Matsui, M. Linear cryptanalysis method for des cipher. In Advances in Cryptology—EUROCRYPT’93; Springer: Berlin/Heidelberg, Germany, 1994; pp. 386–397. [Google Scholar]
- Zahid, A.H.; Arshad, M.J. An innovative design of substitution-boxes using cubic polynomial mapping. Symmetry 2019, 11, 437. [Google Scholar] [CrossRef] [Green Version]
- Zahid, A.H.; Arshad, M.J.; Ahmad, M. A novel construction of efficient substitution-boxes using cubic fractional transformation. Entropy 2019, 21, 245. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.F.; Ahmed, A.; Saleem, K. A novel cryptographic substitution box design using gaussian distribution. IEEE Access 2019, 7, 15999–16007. [Google Scholar] [CrossRef]
- Akhtar, T.; Din, N.; Uddin, J. Substitution box design based on chaotic maps and cuckoo search algorithm. In Proceedings of the 2019 International Conference on Advanced Communication Technologies and Networking (CommNet), Rabat, Morocco, 12–14 April 2019; pp. 1–7. [Google Scholar]
- Jamal, S.S.; Anees, A.; Ahmad, M.; Khan, M.F.; Hussain, I. Construction of cryptographic s-boxes based on mobius transformation and chaotic tent-sine system. IEEE Access 2019, 7, 173273–173285. [Google Scholar] [CrossRef]
- Ahmed, H.A.; Zolkipli, M.F.; Ahmad, M. A novel efficient substitution-box design based on fire fly algorithm and discrete chaotic map. Neural Comput. Appl. 2019, 31, 7201–7210. [Google Scholar] [CrossRef]
- Jamal, S.S.; Shah, T. A novel algebraic technique for the construction of strong substitution box. Wirel. Pers. Commun. 2018, 99, 213–226. [Google Scholar]
- Ullah, A.; Javeed, A.; Shah, T. A scheme based on algebraic and chaotic structures for the construction of substitution box. Multimed. Tools Appl. 2019, 78, 32467–32484. [Google Scholar] [CrossRef]
- Ahmad, M.; Khaja, I.A.; Baz, A.; Alhakami, H.; Alhakami, W. Particle swarm optimization based highly nonlinear substitution-boxes generation for security applications. IEEE Access 2020, 8, 116132–116147. [Google Scholar] [CrossRef]
- Şengel, Ö.; Aydın, M.A.; Sertbaş, A. An efficient generation and security analysis of substitution box using fingerprint patterns. IEEE Access 2020, 8, 160158–160176. [Google Scholar] [CrossRef]
- Malik, M.S.M.; Ali, M.A.; Khan, M.A.; Ehatisham-Ul-Haq, M.; Shah, S.N.M.; Rehman, M.; Ahmad, W. Generation of highly nonlinear and dynamic aes substitution-boxes (s-boxes) using chaos-based rotational matrices. IEEE Access 2020, 8, 35682–35695. [Google Scholar] [CrossRef]
- Ibrahim, S.; Abbas, A.M. A novel optimization method for constructing cryptographically strong dynamic s-boxes. IEEE Access 2020, 8, 225004–225017. [Google Scholar] [CrossRef]
- Ahmad, M.; Al-Solami, E.; Alghamdi, A.M.; Yousaf, M.A. Bijective S-Boxes Method Using Improved Chaotic Map-Based Heuristic Search and Algebraic Group Structures. IEEE Access 2020, 8, 110397–110411. [Google Scholar] [CrossRef]
- Peng, J.; Pang, S.; Zhang, D.; Jin, S.; Feng, L.; Li, Z. S-boxes construction based on quantum chaos and pwlcm chaotic mapping. In Proceedings of the 2019 IEEE 18th International Conference on Cognitive Informatics Cognitive Computing (ICCI*CC), Milan, Italy, 23–25 July 2019; pp. 1–6. [Google Scholar]
- Freyre-Echevarría, A.; Martínez-Díaz, I.; Pérez, C.M.L.; Sosa-Gómez, G.; Rojas, O. Evolving nonlinear s-boxes with improved theoretical resilience to power attacks. IEEE Access 2020, 8, 202728–202737. [Google Scholar] [CrossRef]
- Alhadawi, H.S.; Lambić, D.; Zolkipli, M.F.; Ahmad, M. Globalized firefly algorithm and chaos for designing substitution box. J. Inf. Secur. Appl. 2020, 55, 102671. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Zhang, L.Y.; Feng, J.; Gao, J.; Lei, P. A genetic algorithm for constructing bijective substitution boxes with high nonlinearity. Inf. Sci. 2020, 523, 152–166. [Google Scholar] [CrossRef]
- Farah, M.A.; Farah, A.; Farah, T. An image encryption scheme based on a new hybrid chaotic map and optimized substitution box. Nonlinear Dyn. 2020, 99, 3041–3064. [Google Scholar] [CrossRef]
- Bolufé-Röhler, A.; Tamayo-Vera, D. Machine learning based metaheuristic hybrids for s-box optimization. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 5139–5152. [Google Scholar] [CrossRef]
- Khan, M. A novel image encryption scheme based on multiple chaotic s-boxes. Nonlinear Dyn. 2015, 82, 527–533. [Google Scholar] [CrossRef]
- Alanazi, A.S.; Munir, N.; Khan, M.; Asif, M.; Hussain, I. Cryptanalysis of novel image encryption scheme based on multiple chaotic substitution boxes. IEEE Access 2021, 9, 93795–93802. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Zahid, A.H.; Iliyasu, A.M.; Ahmad, M.; Shaban, M.M.U.; Arshad, M.J.; Alhadawi, H.S.; Abd El-Latif, A.A. A novel construction of dynamic s-box with high nonlinearity using heuristic evolution. IEEE Access 2021, 9, 67797–67812. [Google Scholar] [CrossRef]
- Kim, G.; Kim, H.; Heo, Y.; Jeon, Y.; Kim, J. Generating cryptographic s-boxes using the reinforcement learning. IEEE Access 2021, 9, 83092–83104. [Google Scholar] [CrossRef]
- Khan, L.S.; Hazzazi, M.M.; Khan, M.; Jamal, S.S. A novel image encryption based on rossler map diffusion and particle swarm optimization generated highly non-linear substitution boxes. Chin. J. Phys. 2021, 72, 558–574. [Google Scholar] [CrossRef]
- Zamli, K.Z.; Kader, A.; Din, F.; Alhadawi, H.S. Selective chaotic maps tiki-taka algorithm for the s-box generation and optimization. Neural Comput. Appl. 2021, 33, 16641–16658. [Google Scholar] [CrossRef]
- Siddiqui, N.; Naseer, A.; Ehatisham-ul-Haq, M. A novel scheme of substitution-box design based on modified pascal’s triangle and elliptic curve. Wirel. Pers. Commun. 2021, 116, 3015–3030. [Google Scholar] [CrossRef]
- Alhadawi, H.S.; Majid, M.A.; Lambić, D.; Ahmad, M. A novel method of s-box design based on discrete chaotic maps and cuckoo search algorithm. Multimed. Tools Appl. 2021, 80, 7333–7350. [Google Scholar] [CrossRef]
- Salimi, H. Stochastic fractal search: A powerful metaheuristic algorithm. Knowl.-Based Syst. 2015, 75, 1–18. [Google Scholar] [CrossRef]
- Luo, Q.; Zhang, S.; Zhou, Y. Stochastic fractal search algorithm for template matching with lateral inhibition. Sci. Program. 2017, 2017, 1803934. [Google Scholar] [CrossRef] [Green Version]
- Alomoush, M.I.; Oweis, Z.B. Environmental-economic dispatch using stochastic fractal search algorithm. Int. Trans. Electr. Energy Syst. 2018, 28, e2530. [Google Scholar] [CrossRef]
- Li, W.; Sun, S.; Li, J.; Hu, Y. Stochastic fractal search algorithm and its application in path planning. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–5. [Google Scholar]
- Rezk, H.; Babu, T.S.; Al-Dhaifallah, M.; Ziedan, H.A. A robust parameter estimation approach based on stochastic fractal search optimization algorithm applied to solar pv parameters. Energy Rep. 2021, 7, 620–640. [Google Scholar] [CrossRef]
- Sasmito, A.; Pratiwi, A.B. Stochastic fractal search algorithm in permutation flowshop scheduling problem. Aip Conf. Proc. 2021, 2329, 050003. [Google Scholar]
- Li, Y.; Huang, X.; Zhao, C.; Ding, P. Stochastic fractal search-optimized multi-support vector regression for remaining useful life prediction of bearings. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 414. [Google Scholar] [CrossRef]
- Çelik, E. Incorporation of stochastic fractal search algorithm into efficient design of pid controller for an automatic voltage regulator system. Neural Comput. Appl. 2018, 30, 1991–2002. [Google Scholar] [CrossRef]
- Charef-Khodja, D.; Toumi, A.; Medouakh, S.; Sbaa, S. A novel visual tracking method using stochastic fractal search algorithm. Signal Image Video Process. 2021, 15, 331–339. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Naderi, B.; Khalilpourazary, S. Multi-objective stochastic fractal search: A powerful algorithm for solving complex multi-objective optimization problems. Soft Comput. 2020, 24, 3037–3066. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N.; Jaser, E. Differential evolution with stochastic fractal search algorithm for global numerical optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3154–3161. [Google Scholar]
- Rahman, T.A.; Jalil, N.A.; As’Arry, A.; Ahmad, R.R. Chaos-enhanced stochastic fractal search algorithm for global optimization with application to fault diagnosis. In Materials Science and Engineering Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 210, p. 012060. [Google Scholar]
- Zhou, C.; Sun, C.; Wang, B.; Wang, X. An improved stochastic fractal search algorithm for 3D protein structure prediction. J. Mol. Model. 2018, 24, 125. [Google Scholar] [CrossRef]
- Talbi, E.-G. Machine learning into metaheuristics: A survey and taxonomy. ACM Comput. Surv. 2021, 54, 1–32. [Google Scholar] [CrossRef]
- Ahandani, M.A. Opposition-based learning in the shuffled bidirectional differential evolution algorithm. Swarm Evol. Comput. 2016, 26, 64–85. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M. Opposition-based differential evolution. IEEE Trans. Evol. Comput. 2008, 12, 64–79. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wu, Z.; Rahnamayan, S.; Liu, Y.; Ventresca, M. Enhancing particle swarm optimization using generalized opposition-based learning. Inf. Sci. 2011, 181, 4699–4714. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Liu, Y.; Li, C.; Zeng, S. Opposition-based particle swarm algorithm with cauchy mutation. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4750–4756. [Google Scholar]
- Si, T.; De, A.; Bhattacharjee, A.K. Particle swarm optimization with generalized opposition based learning in particle’s pbest position. In Proceedings of the 2014 International Conference on Circuits, Power and Computing Technologies [ICCPCT-2014], Nagercoil, India, 20–21 March 2014. [Google Scholar]
- Wang, H.; Wu, Z.; Rahnamayan, S. Enhanced opposition-based differential evolution for solving high-dimensional continuous optimization problems. Soft Comput. 2011, 15, 2127–2140. [Google Scholar] [CrossRef]
- Basu, M. Quasi-oppositional differential evolution for optimal reactive power dispatch. Int. J. Electr. Power Energy Syst. 2016, 78, 29–40. [Google Scholar] [CrossRef]
- Yazdani, S.; Shanbehzadeh, J. Balanced cartesian genetic programming via migration and opposition-based learning: Application to symbolic regression. Genet. Program. Evolvable Mach. 2015, 16, 133–150. [Google Scholar] [CrossRef]
- Shankar, G.; Mukherjee, V. Quasi oppositional harmony search algorithm based controller tuning for load frequency control of multi-source multi-area power system. Int. J. Electr. Power Energy Syst. 2016, 75, 289–302. [Google Scholar] [CrossRef]
- Carlet, C.; Dalai, D.K.; Gupta, K.C.; Maitra, S. Algebraic immunity for cryptographically significant boolean functions: Analysis and construction. IEEE Trans. Inf. Theory 2006, 52, 3105–3121. [Google Scholar] [CrossRef]
- Rodríguez-Henríquez, F.; Saqib, N.A.; Pérez, A.D.; Koc, C.K. Cryptographic Algorithms on Reconfigurable Hardware; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Niemeyer, L.; Pietronero, L.; Wiesmann, H. Fractal Dimension of Dielectric Breakdown. Phys. Rev. Lett. 1984, 52, 1033–1036. [Google Scholar] [CrossRef]
- Mahdavi, S.; Rahnamayan, S.; Deb, K. Opposition based learning: A literature review. Swarm Evol. Comput. 2018, 39, 1–23. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; Volume 1, pp. 695–701. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Learning and Intelligent Optimization, Coello, C.A.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar]
- Álvarez-Cubero, J.A.; Zufiria, P.J. Algorithm 959: Vbf: A library of c++ classes for vector boolean functions in cryptography. ACM Trans. Math. Softw. 2016, 42, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Molina, F.G. Stochastic Fractal Search Algorithm improved with Opposition-Based Learning for solving the substitution box design problem. Figshare 2021. [Google Scholar] [CrossRef]
- Dimitrov, M.M. On the design of chaos-based s-boxes. IEEE Access 2020, 8, 117173–117181. [Google Scholar] [CrossRef]
- Khan, M.; Shah, T.; Batool, S.I. Construction of s-box based on chaotic boolean functions and its application in image encryption. Neural Comput. Appl. 2016, 27, 677–685. [Google Scholar] [CrossRef]
- Chen, G.; Chen, Y.; Liao, X. An extended method for obtaining sboxes based on three-dimensional chaotic baker maps. Chaos Solitons Fractals 2007, 31, 571–579. [Google Scholar] [CrossRef]
- Jakimoski, G.; Kocarev, L. Chaos and cryptography: Block encryption ciphers based on chaotic maps. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 163–169. [Google Scholar] [CrossRef]
- Özkaynak, F.; Özer, A.B. A method for designing strong sboxes based on chaotic lorenz system. Phys. Lett. A 2010, 374, 3733–3738. [Google Scholar] [CrossRef]
- Asim, M.; Jeoti, V. Efficient and simple method for designing chaotic s-boxes. ETRI J. 2008, 30, 170–172. [Google Scholar] [CrossRef]
- Tang, G.; Liao, X. A method for designing dynamical s-boxes based on discretized chaotic map. Chaos Solitons Fractals 2005, 23, 1901–1909. [Google Scholar] [CrossRef]
- Khan, M.; Shah, T. A construction of novel chaos base nonlinear component of block cipher. Nonlinear Dyn. 2014, 76, 377–382. [Google Scholar] [CrossRef]
- Khan, M.; Shah, T. An efficient construction of substitution box with fractional chaotic system. Signal Image Video Process 2015, 9, 1335–1338. [Google Scholar] [CrossRef]
- Liu, G.; Yang, W.; Liu, W.; Dai, Y. Designing s-boxes based on 3-d four-wing autonomous chaotic system. Nonlinear Dyn. 2015, 82, 1867–1877. [Google Scholar] [CrossRef]
- Islam, F.U.; Liu, G. Designing sbox based on 4d-4wing hyperchaotic system. 3D Res. 2017, 8, 9. [Google Scholar] [CrossRef]
- Wang, X.; Çavuşoğlu, Ü.; Kacar, S.; Akgul, A.; Pham, V.T.; Jafari, S.; Alsaadi, F.E.; Nguyen, X.Q. S-box based image encryption application using a chaotic system without equilibrium. Appl. Sci. 2019, 9, 781. [Google Scholar] [CrossRef] [Green Version]
- Zengin, A.; Pehlivan, I.; Kaçar, S. A novel approach for strong s-box generation algorithm design based on chaotic scaled zhongtang system. Nonlinear Dyn. 2017, 87, 1081–1094. [Google Scholar] [CrossRef]
- Farah, T.; Rhouma, R.; Belghith, S. A novel method for designing s-box based on chaotic map and teaching learning-based optimization. Nonlinear Dyn. 2017, 88, 1059–1074. [Google Scholar] [CrossRef]
- Lambi, D. S-box design method based on improved one-dimensional discrete chaotic map. J. Inf. Telecommun. 2018, 2, 181–191. [Google Scholar] [CrossRef]
- Soto, R.; Crawford, B.; Molina, F.G.; Olivares, R. Human behaviour based optimization supported with self-organizing maps for solving the s-box design problem. IEEE Access 2021, 9, 84605–84618. [Google Scholar] [CrossRef]
- Özkaynak, F. Construction of robust substitution boxes based on chaotic systems. Neural Comput. Appl. 2019, 31, 3317–3326. [Google Scholar] [CrossRef]
- Lambi, D. A novel method of s-box design based on discrete chaotic map. Nonlinear Dyn. 2017, 87, 2407–2413. [Google Scholar] [CrossRef]
- Ye, T.; Zhimao, L. Chaotic s-box: Six-dimensional fractional lorenz duffing chaotic system and o-shaped path scrambling. Nonlinear Dyn. 2018, 94, 2115–2126. [Google Scholar] [CrossRef]
- Ahmad, M.; Bhatia, D.; Hassan, Y. A novel ant colony optimization based scheme for substitution box design. Procedia Comput. Sci. 2015, 57, 572–580. [Google Scholar] [CrossRef] [Green Version]
- Yi, L.; Tong, X.; Wang, Z.; Zhang, M.; Zhu, H.; Liu, J. A novel block encryption algorithm based on chaotic s-box for wireless sensor network. IEEE Access 2019, 7, 53079–53090. [Google Scholar] [CrossRef]
- Wang, K.-W.; Wong, Y.; Li, C.; Li, Y. A novel method to design sbox based on chaotic map and genetic algorithm. Phys. Lett. A 2012, 376, 827–833. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Z.; Wang, J. Chaotic image encryption based on circular substitution box and key stream buffer. Signal Process. Image Commun. 2014, 29, 902–913. [Google Scholar] [CrossRef]
- Al Solami, E.; Ahmad, M.; Volos, C.; Doja, M.N.; Beg, M.M.S. A new hyperchaotic system-based design for efficient bijective substitution-boxes. Entropy 2018, 20, 525. [Google Scholar] [CrossRef] [Green Version]
- Lambi, D. A novel method of s-box design based on chaotic map and composition method. Chaos Solitons Fractals 2014, 58, 16–21. [Google Scholar] [CrossRef]
- Hussain, I.; Shah, T.; Gondal, M.A.; Mahmood, H. An efficient approach for the construction of lft s-boxes using chaotic logistic map. Nonlinear Dyn. 2013, 71, 133–140. [Google Scholar] [CrossRef]
- Hussain, I.; Shah, T.; Gondal, M.A.; Mahmood, H. Efficient method for designing chaotic s-boxes based on generalized baker’s map and tderc chaotic sequence. Nonlinear Dyn. 2013, 74, 271–275. [Google Scholar] [CrossRef]
- Belazi, A.; Abd El-Latif, A.A.; Diaconu, A.V.; Rhouma, R.; Belghith, S. Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms. Opt. Lasers Eng. 2017, 88, 37–50. [Google Scholar] [CrossRef]
- Boura, C.; Canteaut, A. On the influence of the algebraic degree of f-1 on the algebraic degree of g ∘ f. IEEE Trans. Inf. Theory 2013, 59, 691–702. [Google Scholar] [CrossRef]
- Boura, C.; Canteaut, A.; Cannière, C.D. Higher-order differential properties of keccak and luffa. In Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 2011; pp. 252–269. [Google Scholar]
- Courtois, N.T. Fast algebraic attacks on stream ciphers with linear feedback. In Advances in Cryptology—CRYPTO 2003; Boneh, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 176–194. [Google Scholar]
- Courtois, N.T.; Meier, W. Algebraic attacks on stream ciphers with linear feedback. In Advances in Cryptology—EUROCRYPT 2003, International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 4–8 May 2003; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2656, pp. 345–359. [Google Scholar]
- Webster, A.F.; Tavares, S.E. On the design of s-boxes. In Advances in Cryptology—CRYPTO ’85 Proceedings; Springer: Berlin/Heidelberg, Germany, 1986; pp. 523–534. [Google Scholar]
- Ahmad, M.; Khan, P.M.; Ansari, M.Z. A simple and efficient key-dependent s-box design using fisher-yates shuffle technique. In Recent Trends in Computer Networks and Distributed Systems Security; Martínez Pérez, G., Thampi, S.M., Ko, R., Shu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 540–550. [Google Scholar]
- Gondal, M.A.; Raheem, A.; Hussain, I. A scheme for obtaining secure s-boxes based on chaotic baker’s map. 3D Res. 2014, 5, 17. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Hao, J.L.; Wang, X.Y. An efficient image encryption scheme based on s-boxes and fractional-order differential logistic map. IEEE Access 2020, 8, 54175–54188. [Google Scholar] [CrossRef]
- Bin Faheem, Z.; Ali, A.; Khan, M.A.; Ul-Haq, M.E.; Ahmad, W. Highly dispersive substitution box (s-box) design using chaos. ETRI J. 2020, 42, 619–632. [Google Scholar] [CrossRef] [Green Version]
- Hussain, S.; Jamal, S.S.; Shah, T.; Hussain, I. A power associative loop structure for the construction of non-linear components of block cipher. IEEE Access 2020, 8, 123492–123506. [Google Scholar] [CrossRef]
- El-Latif, A.; Ahmed, A.; Abd-El-Atty, B.; Amin, M.; Iliyasu, A.M. Quantum-inspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic applications. Sci. Rep. 2020, 10, 1930. [Google Scholar] [CrossRef]
- Yong, W.; Peng, L. An improved method to obtaining s-box based on chaos and genetic algorithm. HKIE Trans. 2012, 19, 53–58. [Google Scholar] [CrossRef]
- Ahmad, M.; Doja, M.N.; Beg, M.M. Abc optimization based construction of strong substitution-boxes. Wirel. Pers. Commun. 2018, 101, 1715–1729. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, C.P.; Chen, L.; Xu, X.; Hu, B. Design of highly nonlinear substitution boxes based on i-ching operators. IEEE Trans. Cybern. 2018, 48, 3349–3358. [Google Scholar] [CrossRef] [PubMed]
- Alzaidi, A.A.; Ahmad, M.; Ahmed, H.S.; Solami, E.A. Sine-cosine optimization-based bijective substitution-boxes construction using enhanced dynamics of chaotic map. Complexity 2018, 2018, 9389065. [Google Scholar] [CrossRef]
| Parameter | Range | Default |
|---|---|---|
| iterations | [100, 400] | 150 |
| number population | [10, 50] | 25 |
| walk | [0.1, 1.0] | 0.3 |
| max number diffusion | [1, 5] | 1 |
| Parameter | Value |
|---|---|
| iterations | 183 |
| number population | 36 |
| walk | 0.583946 |
| max number diffusion | 5 |
| 13 | 97 | 252 | 4 | 66 | 245 | 89 | 35 | 170 | 203 | 111 | 128 | 115 | 253 | 241 | 26 |
| 124 | 28 | 139 | 43 | 5 | 134 | 200 | 112 | 210 | 14 | 21 | 148 | 37 | 248 | 205 | 228 |
| 85 | 65 | 151 | 30 | 219 | 25 | 238 | 204 | 96 | 80 | 87 | 232 | 136 | 234 | 2 | 152 |
| 132 | 167 | 49 | 53 | 254 | 197 | 208 | 121 | 84 | 178 | 226 | 38 | 68 | 110 | 130 | 42 |
| 182 | 150 | 186 | 104 | 98 | 94 | 48 | 81 | 56 | 190 | 162 | 165 | 250 | 233 | 156 | 24 |
| 201 | 34 | 140 | 71 | 227 | 63 | 129 | 29 | 240 | 54 | 251 | 196 | 189 | 33 | 93 | 61 |
| 8 | 166 | 79 | 173 | 172 | 138 | 158 | 230 | 239 | 212 | 249 | 123 | 169 | 120 | 183 | 113 |
| 12 | 50 | 214 | 179 | 237 | 194 | 145 | 105 | 3 | 220 | 209 | 222 | 160 | 176 | 159 | 59 |
| 137 | 62 | 213 | 51 | 223 | 181 | 108 | 218 | 247 | 40 | 99 | 242 | 52 | 168 | 69 | 107 |
| 32 | 102 | 188 | 78 | 184 | 163 | 58 | 9 | 74 | 100 | 7 | 109 | 75 | 67 | 57 | 91 |
| 161 | 16 | 20 | 6 | 31 | 149 | 193 | 0 | 216 | 15 | 36 | 86 | 64 | 73 | 44 | 60 |
| 22 | 229 | 144 | 153 | 177 | 198 | 47 | 175 | 125 | 171 | 206 | 221 | 235 | 244 | 18 | 23 |
| 122 | 114 | 146 | 202 | 55 | 11 | 180 | 191 | 77 | 116 | 119 | 103 | 106 | 1 | 41 | 217 |
| 231 | 70 | 83 | 224 | 39 | 199 | 46 | 211 | 27 | 141 | 246 | 225 | 88 | 215 | 45 | 142 |
| 19 | 154 | 118 | 127 | 143 | 101 | 207 | 147 | 157 | 95 | 187 | 164 | 126 | 90 | 82 | 76 |
| 236 | 185 | 117 | 10 | 72 | 133 | 92 | 131 | 155 | 255 | 192 | 135 | 243 | 195 | 174 | 17 |
| 167 | 205 | 46 | 120 | 3 | 20 | 163 | 154 | 96 | 151 | 243 | 197 | 112 | 0 | 25 | 169 |
| 161 | 255 | 190 | 224 | 162 | 26 | 176 | 191 | 79 | 37 | 15 | 216 | 17 | 87 | 35 | 164 |
| 144 | 93 | 81 | 7 | 170 | 28 | 59 | 212 | 137 | 206 | 63 | 19 | 174 | 222 | 214 | 182 |
| 70 | 50 | 113 | 131 | 140 | 51 | 89 | 196 | 72 | 158 | 150 | 127 | 175 | 95 | 129 | 85 |
| 172 | 33 | 4 | 157 | 60 | 142 | 209 | 83 | 244 | 173 | 152 | 156 | 239 | 200 | 147 | 98 |
| 41 | 71 | 238 | 210 | 56 | 32 | 171 | 42 | 220 | 6 | 237 | 159 | 246 | 94 | 69 | 233 |
| 40 | 1 | 68 | 138 | 153 | 229 | 145 | 203 | 67 | 119 | 204 | 143 | 134 | 155 | 61 | 10 |
| 23 | 111 | 193 | 12 | 201 | 242 | 226 | 202 | 109 | 55 | 192 | 107 | 16 | 184 | 236 | 227 |
| 11 | 86 | 62 | 247 | 48 | 245 | 21 | 251 | 44 | 128 | 101 | 18 | 82 | 217 | 223 | 228 |
| 178 | 118 | 194 | 231 | 27 | 165 | 65 | 34 | 47 | 179 | 225 | 248 | 78 | 232 | 102 | 126 |
| 124 | 160 | 74 | 149 | 235 | 75 | 97 | 49 | 141 | 108 | 8 | 185 | 100 | 99 | 254 | 183 |
| 125 | 180 | 57 | 115 | 198 | 133 | 64 | 110 | 148 | 241 | 66 | 234 | 146 | 92 | 73 | 199 |
| 250 | 166 | 117 | 253 | 91 | 53 | 181 | 213 | 22 | 80 | 195 | 9 | 39 | 30 | 186 | 230 |
| 54 | 122 | 24 | 215 | 105 | 130 | 114 | 221 | 168 | 207 | 135 | 36 | 121 | 187 | 123 | 132 |
| 211 | 219 | 58 | 84 | 31 | 177 | 103 | 208 | 43 | 77 | 45 | 188 | 240 | 116 | 38 | 104 |
| 88 | 14 | 139 | 252 | 189 | 5 | 218 | 136 | 29 | 106 | 76 | 90 | 2 | 13 | 52 | 249 |
| Method | Min NL | Max NL | ACNV |
|---|---|---|---|
| [24,67] | 84 | 106 | 100.0 |
| [68] | 100 | 106 | 103.0 |
| [69] | 98 | 108 | 103.2 |
| [70] | 100 | 106 | 103.2 |
| [71] | 96 | 108 | 103.5 |
| [72] | 101 | 108 | 103.8 |
| [73] | 100 | 106 | 104.0 |
| [74] | 100 | 108 | 104.75 |
| [75] | 104 | 108 | 105.7 |
| [76] | 102 | 108 | 106.0 |
| [77] | 106 | 108 | 106.0 |
| [78] | 104 | 110 | 106.2 |
| [79] | 104 | 110 | 106.5 |
| [80] | 106 | 108 | 106.5 |
| [81] | 102 | 110 | 106.5 |
| [82,83] | 106 | 108 | 106.7 |
| [84] | 104 | 108 | 106.7 |
| [85] | 106 | 110 | 107.0 |
| [10] | 106 | 108 | 107.5 |
| [86] | 106 | 110 | 107.75 |
| [87] | 108 | 108 | 108.0 |
| [88] | 104 | 110 | 108.0 |
| [89] | 106 | 110 | 108.5 |
| [90] | 108 | 112 | 109.0 |
| This Work | 106 | 112 | 109.25 |
| [91,92,93] | 112 | 112 | 112.0 |
| [66] | 112 | 112 | 112.0 |
| 0.5000 | 0.4219 | 0.5156 | 0.4688 | 0.4844 | 0.4531 | 0.5469 | 0.4531 |
| 0.4844 | 0.5000 | 0.4844 | 0.5625 | 0.4688 | 0.5313 | 0.5313 | 0.4531 |
| 0.4844 | 0.5313 | 0.4844 | 0.4844 | 0.5469 | 0.5313 | 0.5000 | 0.4531 |
| 0.4531 | 0.4531 | 0.4688 | 0.5781 | 0.4844 | 0.5313 | 0.5469 | 0.5156 |
| 0.4844 | 0.4688 | 0.5156 | 0.4688 | 0.4844 | 0.5625 | 0.4375 | 0.5156 |
| 0.5000 | 0.5000 | 0.5469 | 0.5000 | 0.5000 | 0.4688 | 0.5625 | 0.4844 |
| 0.5000 | 0.5000 | 0.5000 | 0.5781 | 0.4531 | 0.5000 | 0.4688 | 0.4688 |
| 0.5313 | 0.5156 | 0.5781 | 0.5156 | 0.4844 | 0.5000 | 0.4688 | 0.5625 |
| 0 | 104 | 104 | 104 | 104 | 108 | 100 | 106 |
| 104 | 0 | 102 | 102 | 98 | 104 | 102 | 100 |
| 104 | 102 | 0 | 102 | 106 | 106 | 106 | 106 |
| 104 | 102 | 102 | 0 | 100 | 96 | 106 | 108 |
| 104 | 98 | 106 | 100 | 0 | 108 | 106 | 106 |
| 108 | 104 | 106 | 96 | 108 | 0 | 104 | 104 |
| 100 | 102 | 106 | 106 | 106 | 104 | 0 | 102 |
| 106 | 100 | 106 | 108 | 106 | 104 | 102 | 0 |
| S-Box | DAP |
|---|---|
| This work | 0.046 |
| [85] | 0.039 |
| [69] | 0.046 |
| [68] | 0.046 |
| [71] | 0.039 |
| [72] | 0.054 |
| [70] | 0.039 |
| [74] | 0.046 |
| [99] | 0.046 |
| [100] | 0.046 |
| [13] | 0.031 |
| [101] | 0.047 |
| [102] | 0.039 |
| [103] | 0.031 |
| [104] | 0.055 |
| [91] | 0.015 |
| [92] | 0.015 |
| [93] | 0.031 |
| [88] | 0.046 |
| [87] | 0.039 |
| [79] | 0.039 |
| [76] | 0.039 |
| [75] | 0.039 |
| [84] | 0.039 |
| S-Box | LP |
|---|---|
| This work | 0.125 |
| [90] | 0.093 |
| [83] | 0.132 |
| [80] | 0.132 |
| [73] | 0.132 |
| [11] | 0.132 |
| [105] | 0.140 |
| [106] | 0.125 |
| [10] | 0.125 |
| [107] | 0.132 |
| [108] | 0.125 |
| [13] | 0.132 |
| [101] | 0.148 |
| [102] | 0.137 |
| [103] | 0.113 |
| [104] | 0.132 |
| [91] | 0.062 |
| [92] | 0.142 |
| [93] | 0.102 |
| [88] | 0.139 |
| [87] | 0.140 |
| [79] | 0.117 |
| [84] | 0.132 |
| Image | Proposed | AES | Camellia | Safer | Skipjack |
|---|---|---|---|---|---|
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
| Sbox | Image | Entropy | Correlation | Contrast | Homogeneity | Energy | NPCR | UACI |
|---|---|---|---|---|---|---|---|---|
| Proposed | cameraman | 7.8963 | 0.0756 | 14.3905 | 0.0304 | 0.0052 | 0.9957 | 0.3509 |
| house | 7.8023 | 0.3008 | 37.7356 | 0.0798 | 0.0084 | 0.9944 | 0.3257 | |
| lena | 7.9233 | 0.2116 | 25.5224 | 0.0990 | 0.0212 | 0.9946 | 0.3089 | |
| baboon | 7.9107 | 0.1242 | 31.3474 | 0.0412 | 0.0055 | 0.9949 | 0.3009 | |
| Aes | cameraman | 7.8604 | 0.0475 | 14.1664 | 0.0309 | 0.0053 | 0.9982 | 0.3343 |
| house | 7.7912 | 0.2642 | 40.3050 | 0.0794 | 0.0086 | 0.9982 | 0.3301 | |
| lena | 7.9289 | 0.2023 | 29.0630 | 0.1038 | 0.0222 | 0.9979 | 0.2956 | |
| baboon | 7.9108 | 0.0776 | 32.6460 | 0.0408 | 0.0054 | 0.9984 | 0.3039 | |
| Camellia | cameraman | 7.8734 | 0.0440 | 12.3571 | 0.0313 | 0.0052 | 0.9948 | 0.2968 |
| house | 7.8284 | 0.1495 | 36.7644 | 0.0782 | 0.0083 | 0.9980 | 0.3209 | |
| lena | 7.9014 | 0.1687 | 27.5230 | 0.0986 | 0.0214 | 0.9983 | 0.2754 | |
| baboon | 7.9059 | 0.0777 | 28.8319 | 0.0406 | 0.0056 | 0.9978 | 0.2715 | |
| Safer | cameraman | 7.8686 | 0.0992 | 12.2388 | 0.0317 | 0.0053 | 0.9959 | 0.3177 |
| house | 7.7647 | 0.3108 | 32.5408 | 0.0767 | 0.0082 | 0.9878 | 0.3494 | |
| lena | 7.9338 | 0.1927 | 26.0448 | 0.0999 | 0.0216 | 0.9954 | 0.3185 | |
| baboon | 7.8983 | 0.1541 | 27.1982 | 0.0414 | 0.0054 | 0.9919 | 0.3018 | |
| Skipjack | cameraman | 7.8624 | 0.0590 | 9.6959 | 0.0332 | 0.0055 | 0.9976 | 0.3309 |
| house | 7.7418 | 0.2369 | 37.4516 | 0.0822 | 0.0090 | 0.9961 | 0.3553 | |
| lena | 7.9186 | 0.1660 | 23.1028 | 0.1038 | 0.0219 | 0.9946 | 0.2955 | |
| baboon | 7.9046 | 0.1171 | 27.8579 | 0.0438 | 0.0057 | 0.9944 | 0.2995 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez, F.; Soto, R.; Crawford, B. Stochastic Fractal Search Algorithm Improved with Opposition-Based Learning for Solving the Substitution Box Design Problem. Mathematics 2022, 10, 2172. https://doi.org/10.3390/math10132172
Gonzalez F, Soto R, Crawford B. Stochastic Fractal Search Algorithm Improved with Opposition-Based Learning for Solving the Substitution Box Design Problem. Mathematics. 2022; 10(13):2172. https://doi.org/10.3390/math10132172
Chicago/Turabian StyleGonzalez, Francisco, Ricardo Soto, and Broderick Crawford. 2022. "Stochastic Fractal Search Algorithm Improved with Opposition-Based Learning for Solving the Substitution Box Design Problem" Mathematics 10, no. 13: 2172. https://doi.org/10.3390/math10132172
APA StyleGonzalez, F., Soto, R., & Crawford, B. (2022). Stochastic Fractal Search Algorithm Improved with Opposition-Based Learning for Solving the Substitution Box Design Problem. Mathematics, 10(13), 2172. https://doi.org/10.3390/math10132172








