Modified Iterative Schemes for a Fixed Point Problem and a Split Variational Inclusion Problem

Abstract

In this paper, we alter Wang’s new iterative method as well as apply it to find the common solution of fixed point problem (FPP) and split variational inclusion problem ($S_p$VIP) in Hilbert space. We discuss the weak convergence for ($S_p$VIP) and strong convergence for the common solution of ($S_p$VIP) and (FPP) using appropriate assumptions. Some consequences of the proposed methods are studied. We compare our iterative schemes with other existing related schemes.

1. Introduction

Variational inclusions, which are the generalized forms of variational inequalities, are useful to deal with the problems arising in mechanics, optimization, economics, nonlinear programming, and many other problems occuring in pure and applied sciences. The split feasibility problem (SFP) was initially studied by Censor and Elfving [1] for the reconstruction of medical images. This split feasibility problem has also been considered by many researchers (see, for example, [2,3,4,5] and references therein). Furthermore, a novel problem was proposed by Censor et al. [6] by combing both (SFP) and variational inequality problem (VIP) and they call it split variational inequality problem (SVIP).

$$\begin{array}{c}\hfill \mathrm{That}\mathrm{is},\mathrm{the}\mathrm{problem}\mathrm{of}\mathrm{finding}{u}^{\ast }\in C\mathrm{such}\mathrm{that}{u}^{\ast }\in \mathrm{VIP}(f;C) \mathrm{and} A{u}^{\ast }\in \mathrm{VIP}(g;Q),\end{array}$$

(1)

where $H_1$ and $H_2$ are Hilbert spaces, $C\subseteq H_1$, $Q\subseteq H_2$ are closed, convex subsets, $f:H_1\to H_1$ and $g:H_2\to H_2$ are two operators, and $A:H_1\to H_2$ is a bounded linear operator; $\mathrm{VIP}(f;C)=\{y\in C:⟨f(y),u-y⟩\ge 0,\forall u\in C\}$ and $\mathrm{VIP}(g;Q)=\{z\in Q:⟨g(z),u-z⟩\ge 0,\forall u\in Q\}$.

Split variational inclusion problems are applicable in intensity-modulated radiation therapy treatment planning, modeling many inverse problem arising for phase retrieval and many other problems of day-to-day life. For more applications of the related subject, we refer to [7].

Moudafi [8] extended (SVIP) and call it split monotone variational inclusion problem (${\mathrm{S}}_{\mathrm{p}}\mathrm{MVIP}$).

$$\begin{array}{c}\hfill \mathrm{That}\mathrm{is},\mathrm{the}\mathrm{problem}\mathrm{of}\mathrm{finding}{u}^{\ast }\in H_1\mathrm{such}\mathrm{that}{u}^{\ast }\in \mathrm{VI}(f,G_1;H_1) \mathrm{and} A{u}^{\ast }\in \mathrm{VI}(g,G_2;H_2),\end{array}$$

(2)

where $G_1:H_1\to 2^{H_1}$ and $G_2:H_2\to 2^{H_2}$ are set-valued operators, $\mathrm{VI}(f,G_1;H_1)=\{y\in H_1:0\in f(y)+G_1(y)\}$ and $\mathrm{VI}(g,G_2;H_2)=\{z\in H_2:0\in g(z)+G_2(z)\}$.

Moudafi [8] formulated the following iterative scheme to solve (${\mathrm{S}}_{\mathrm{p}}\mathrm{MVIP}$).

For initial point $u_0\in H_1$, compute

$$\begin{array}{c}\hfill u_{n+1}=U[u_n+\gamma A^{\ast }(V-I)A{u}_n],\end{array}$$

(3)

where $\gamma \in (0,1/L),L$ is the spectral radius of the operator $A^{\ast }A$, $A^{\ast }$ is the adjoint of A, $U=J_{\lambda }^{G_1}(I-\lambda f)={(I+\lambda G_1)}^{-1}(I-\lambda f),V=J_{\lambda }^{G_2}(I-\lambda g)={(I+\lambda G_2)}^{-1}(I-\lambda g)$ and $\lambda >0$.

Let $N_C(u)=\left\{z\in H_1:⟨z,y-u⟩\le 0,\forall y\in C\right\}$ and $N_Q(u)=\left\{w\in H_2:⟨w,y-u⟩\le 0,\forall y\in Q\right\}$ be the normal cones. If $G_1=N_C$ and $G_2=N_Q$, then (${\mathrm{S}}_{\mathrm{p}}\mathrm{MVIP}$) reduces to split variational inequality problem (SVIP). If $f=g=0$, then (${\mathrm{S}}_{\mathrm{p}}\mathrm{MVIP}$) coincides with the split variational inclusion problem (S${}_{\mathrm{p}}$VIP) studied by Byrne et al. [9].

$$\begin{array}{c}\hfill \mathrm{That}\mathrm{is},\mathrm{find}{u}^{\ast }\in H_1\mathrm{such}\mathrm{that}{u}^{\ast }\in \mathrm{VI}(G_1;H_1) \mathrm{and} A{u}^{\ast }\in \mathrm{VI}(G_2;H_2),\end{array}$$

(4)

where $\mathrm{VI}(G_1;H_1)=\{y\in H_1:0\in G_1(y)\}$ and $\mathrm{VI}(G_2;H_2)=\{z\in H_2:0\in G_2(z)\}$, $G_1,G_2$ are the same as in (2). We denote the solution set of (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$) by $\Delta$. Moreover, Byrne et al. [9] furnished the following scheme to investigate (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$).

For initial point $u_0\in H_1$, compute

$$\begin{array}{c}\hfill u_{n+1}=J_{\lambda }^{G_1}[u_n-\gamma A^{\ast }(I-J_{\lambda }^{G_2})A{u}_n],\end{array}$$

(5)

where $\lambda >0,\gamma \in (0,\frac{2}{L}$) and $L=||A{A}^{\ast }||$.

Let $T:H_1\to H_1$ be a nonexpansive mapping, then (FPP) is to find $x^{\ast }\in H_1$ so that $T(x^{\ast })=x^{\ast }$ and Fix$(S)$ means the set of fixed points of S.

Kazmi and Rizvi [10] investigated the common solution of (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$) and (FPP). They obtain the common solution of (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$) by using the following scheme:

$$\left\{\begin{array}{c}{w}_n=J_{\lambda }^{G_1}[u_n+\mu A^{\ast }(J_{\lambda }^{G_2}-I)A{u}_n],\hfill \\ u_{n+1}={\alpha }_n\psi (u_n)+(1-{\alpha }_n)T(w_n),\hfill \end{array}\right.$$

where $\psi$ is a contraction mapping, $\alpha \in (0,1)$, $\mu \in (0,\frac{1}{L})$, L is the spectral radius of $A^{\ast }A$, ${\alpha }_n\in (0,1)$ is a real sequence, and $\lambda >0$. Inspired by the work of [8,9,10], many authors have studied (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$) and ($\mathrm{FPP}$) in diverse directions using different techniques (see, for example, [11,12,13,14,15,16,17,18,19,20]).

In view of calculation of $||A||$, which is not easy to calculate in practice, Yang [21] studied the (SFP) such that prior calculation of $||A||$ is not required.

In 2017, Wang [22,23] studied the split common fixed point problem (SCFP).

$$\begin{array}{c}\hfill \mathrm{That}\mathrm{is},\mathrm{find}{u}^{\ast }\in \mathrm{Fix}(\mathrm{S})\mathrm{such}\mathrm{that}A{u}^{\ast }\in \mathrm{Fix}(\mathrm{T}).\end{array}$$

(6)

However, Wang [23] discussed Yang’s step size ${\tau }_n$ related to the scheme (3) with $U=S$ and $V=T$ and stated that it is inconvenient to establish the convergence of (3) with the following step size:

$${\tau }_n=\frac{{\rho }_n}{||A^{\ast }(I-T)A{u}_n||},$$

(7)

where $\left\{{\rho }_n\right\}$ is a positive real sequence such that

$$\sum _{n=1}^{\infty }{\rho }_n=\infty \mathrm{and} \sum _{n=1}^{\infty }{\rho }_n^2<\infty .$$

(8)

To overcome this difficulty, Wang [23] analyzed the weak convergence to the (SCFP) by setting up following scheme with step size ${\tau }_n={\rho }_n$.

Wang [22] studied the weak convergence of Algorithm 1 to investigate the solution of (SCFP) with the step size ${\tau }_n=\frac{||u_n-S{u}_n{||}^2+{||A^{\ast }(I-T)A{u}_n||}^2}{||u_n-S{u}_n+A^{\ast }(I-T)A{u}_n{||}^2}$, such that precalculation of $||A||$ is not required.

Algorithm 1 Weak convergence.

Choose arbitrary initial point $x_0$ and assume that $x_n$ has been calculated. If $||u_n-S{u}_n+A^{\ast }(I-T)A{u}_n||=0$, then stop; otherwise, continue and compute the next iteration by the formula: $$\begin{array}{ccc}\hfill u_{n+1}& =& u_n-{\tau }_n\left[(I-S)u_n+A^{\ast }(I-T)A{u}_n\right],\mathrm{for}\mathrm{all}n\ge 0.\hfill \end{array}$$ (9)

Motivated and inspired by the work of [8,9,10,22,23], we propose two iterative schemes by modifying the Wang’s scheme (9) with a new step size $\tau =\frac{1}{1+{||A||}^2}$.

We inspect the weak convergence of suggested scheme for (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$), which is a viscosity type iterative scheme for the common solution of (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$) and ($\mathrm{FPP}$). We also prove the strong convergence of our scheme. Some consequences of the proposed schemes are given. We demonstrate our methods by a numerical example and showing the efficiency of step size $\tau$ in comparison of ${\tau }_n$ and ${\rho }_n$. Our results can be seen as different version of Wang’s methods studied in [22,23].

2. Preliminaries

Throughout the paper, we assume that H is a real Hilbert space with the norm $||·||$ and inner product $⟨·,·⟩$. Let C be a nonempty, closed, and convex subset of H. We denote the set of all weak cluster points of the sequence $\left\{x_n\right\}$ by ${\omega }_W(x_n)$.

The following concepts and results are essential for the proof of the main result.

Definition 1.

A mapping $T:H\to H$ is said to be contraction if

$$||T(u)-T(v)||\le \kappa ||u-v||,\kappa \in (0,1),\mathit{for}\mathit{all}u,v\in H.$$

T is nonexpansive if $\kappa =1$.

Definition 2.

The mapping $T:H\to H$ is said to be firmly nonexpansive if

$${||T(u)-T(v)||}^2\le ⟨u-v,T(u)-T(v)⟩,\mathit{for}\mathit{all}u,v\in H.$$

Definition 3.

The mapping $T:H\to H$ is said to be μ-inverse strongly monotone if there exists a constant $\mu >0$ such that

$$⟨T(u)-T(v),u-v⟩\ge \mu {||T(u)-T(v)||}^2,for all u,v\in H.$$

Definition 4.

A nonexpansive mapping $T:C\to H$ is said to be α-averaged, if there exists a nonexpansive operator $R:C\to H$ such that $T=(1-\alpha )I+\alpha R,\alpha \in (0,1)$. Clearly, if T is averaged, then it is nonexpansive.

Definition 5.

An operator $P_C$ is said to be a metric projection of H onto C if

$$||u-P_C(u)||\le ||u-v||,for any u\in Handv\in C.$$

Note that $P_C$ is firmly nonexpansive and characterized by $⟨u-P_C(v),v-P_C(u)⟩\le 0$ for all $u\in H$ and $v\in C$.

For any $t_1,t_2\in H$ and $\alpha \in (0,1)$, the following equation holds:

$$\begin{array}{c}\hfill ||\alpha t_1-(1-\alpha )t_2{||}^2=\alpha ||t_1{||}^2+(1-\alpha )||t_2{||}^2-\alpha (1-\alpha ){||t_1-t_2||}^2.\end{array}$$

(10)

Let $G:H\to 2^H$ be a set-valued operator. Then,

(i)

The set $\{(u,y):y\in G(u)\}$ denotes the graph of G,

(ii)

$J_{\lambda }^G={(I+\lambda G)}^{-1}$, $\lambda >0$ denotes the resolvent of G,

(iii)

$G^{-1}(u)=\{x\in H:u\in G(x)\}$ denotes the inverse of G.

Definition 6.

A set-valued mapping $G:H\to 2^H$ is said to be monotone, if

$$⟨x-y,u-v⟩\ge 0,\mathit{for}\mathit{all}x\in G(u),y\in G(v).$$

It is well known that resolvent operator of a maximal monotone operator is single-valued and firmly nonexpansive.

Definition 7.

A mapping $T:H\to H$ is said to be demiclosed at zero if, for any sequence $\left\{x_n\right\}$ in H, $x_n\rightharpoonup x_0$ such that $T(x_n)\to 0$ imply $T(x_0)=0$.

Definition 8

([24]). (Demiclosedness Principle): Let $T:H\to H$ be an operator with $\mathrm{Fix}(T)\ne \varphi$. If $\left\{u_n\right\}$ is a sequence in C, $u_n\rightharpoonup u\in C$ such that $\left\{(I-T)u_n\right\}\to 0$ imply $(I-T)(u)=0$.

Remark 1

([25]). If $T:H\to H$ is nonexpansive, then $I-T$ is demiclosed at zero. Moreover, if T is firmly nonexpansive, then $I-T$ is firmly nonexpansive.

Lemma 1

([25], Corollary 23.10). If $G:H\to 2^H$ is a maximal monotone operator, then $J_{\lambda }^G$ and $I-J_{\lambda }^G$ are firmly nonexpansive.

Definition 9

([22]). A sequence $\left\{u_n\right\}$ in a Hilbert space H is said to be Féjer monotone with respect to C, if

$$||u_{n+1}-p||\le ||u_n-p||,foralln\ge 0 and p\in C, where C is a closed convex subset of H.$$

Lemma 2

([26]). Let the sequence $\left\{u_n\right\}$ be Féjer monotone with respect to C; then,

(i) 

$u_n\rightharpoonup u^{\ast }\in C,ifandonlyif{\omega }_W(u_n)\subseteq C,$

(ii) 

$\left\{P_C(u_n)\right\}$ converges strongly,

(iii) 

if $u_n\rightharpoonup u^{\ast }\in C$, then $u^{\ast }=\underset{n\to \infty }{lim}{P}_C(u_n)$.

Lemma 3

([27]). If $\left\{{\zeta }_n\right\}$ is a nonnegative real sequence satisfying ${\zeta }_{n+1}\le (1-{\mu }_n){\zeta }_n+{\delta }_n,$ for all $n\ge 0,$ where $\left\{{\mu }_n\right\}$ is a sequence in $(0,1)$ and $\left\{{\delta }_n\right\}$ is a real sequence such that:

(i) 

$\sum _{n=1}^{\infty }{\mu }_n=\infty ,$

(ii) 

$\underset{n\to \infty }{lim\; sup}\frac{{\delta }_n}{{\mu }_n}\le 0$ or $\underset{n\to \infty }{lim\; sup}\left|{\delta }_n\right|<\infty .$

Then, $\underset{n\to \infty }{lim}{\zeta }_n=0.$

Lemma 4.

If $\alpha ,\beta$, and γ are positive real numbers, then ${\alpha }^2+\frac{{\beta }^2}{\gamma }\ge \frac{{(\alpha +\beta )}^2}{1+\gamma }$ holds.

Proof. 

For any positive real numbers $\alpha ,\beta$, and $\gamma$, we estimate

$$\begin{array}{ccc}\hfill {\displaystyle 0\le \frac{1}{\gamma +1}{\left(\sqrt{\gamma }\alpha -\frac{\beta }{\sqrt{\gamma }}\right)}^2}& =& \frac{\gamma }{\gamma +1}{\alpha }^2+\frac{1}{\gamma (\gamma +1)}{\beta }^2-\frac{1}{\gamma +1}2\alpha \beta \hfill \\ & =& (1-\frac{1}{\gamma +1}){\alpha }^2+(\frac{1}{\gamma }-\frac{1}{\gamma +1}){\beta }^2-\frac{2}{1+\gamma }\alpha \beta \hfill \\ & =& {\alpha }^2+\frac{{\beta }^2}{\gamma }-\frac{{(\alpha +\beta )}^2}{1+\gamma },\hfill \end{array}$$

which implies that ${\alpha }^2+\frac{{\beta }^2}{\gamma }\ge \frac{{(\alpha +\beta )}^2}{1+\gamma }$. □

Lemma 5.

A mapping $M:H\to H$ is τ-inverse strongly monotone, if and only if $(I-\tau M)$ is firmly nonexpansive, for $\tau >0$.

Proof. 

Let $(I-\tau M)$ be firmly nonexpansive, that is,

$$\begin{array}{ccc}\hfill ⟨(I-\tau M)x-(I-\tau M)y,x-y⟩& \ge & {||(I-\tau M)x-(I-\tau M)y||}^2\hfill \\ \hfill ⟨x-y,x-y⟩-\tau ⟨M(x)-M(y),x-y⟩& \ge & {||x-y||}^2-2\tau ⟨M(x)-M(y),x-y⟩+{\tau }^2{||M(x)-M(y)||}^2\hfill \\ \hfill {||x-y||}^2-\tau ⟨M(x)-M(y),x-y⟩& \ge & {||x-y||}^2-2\tau ⟨M(x)-M(y),x-y⟩+{\tau }^2{||M(x)-M(y)||}^2,\hfill \\ \hfill \mathrm{which} \mathrm{implies} \mathrm{that}\\ \hfill ⟨M(x)-M(y),x-y⟩& \ge & {\tau ||M(x)-M(y)||}^2.\hfill \end{array}$$

Thus, $M:H\to H$ is $\tau$-inverse strongly monotone.

Conversely, it is easy to show that if $M:H\to H$ is $\tau$-inverse strongly monotone, then $(I-\tau M)$ is firmly nonexpansive. □

Theorem 1

([28]). (Krasnosel’skii–Mann theorem) Let $M:H\to H$ be an averaged operator such that $\mathrm{Fix}(M)\ne \varphi$. Then, for initial point $u_0$, we have $M^n{u}_0\rightharpoonup u\in$$\mathrm{Fix}(M)$.

3. Main Results

Unless otherwise specified, we assume that $H_1$ and $H_2$ are real Hilbert spaces, $A:H_1\to H_2$ is a bounded linear operator, $A^{\ast }$ is the adjoint of A, $G_1:H_1\to 2^{H_1}$, $G_2:H_2\to 2^{H_2}$ are the set-valued maximal monotone operators, and $T:H_1\to H_1$ is a nonexpansive mapping.

We consider the following problem:

$$\begin{array}{c}\hfill \mathrm{Find}\theta \in H_1\mathrm{such}\mathrm{that}\theta \in \mathrm{Fix}(T)\cap \Delta .\end{array}$$

(11)

We mention some necessary results below:

Lemma 6

([10]). $x^{\ast }\in H_1$ and $y^{\ast }=A{x}^{\ast }\in H_2$ solve (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$), if and only if

$$x^{\ast }=J_{{\lambda }_1}^{G_1}(x^{\ast })\mathrm{and}{y}^{\ast }=J_{{\lambda }_2}^{G_2}(y^{\ast }),forsome{\lambda }_1,{\lambda }_2>0.$$

Lemma 7

([13]). $x^{\ast }\in H_1$ solves (${\mathrm{S}}_{\mathrm{p}}\mathrm{VIP}$), if and only if

$$||x^{\ast }-J_{{\lambda }_1}^{G_1}(x^{\ast })+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}^{\ast }||=0,forall{\lambda }_1,{\lambda }_2>0.$$

Lemma 8

([13]). Let $\left\{x_n\right\}$ be a bounded sequence. If for any ${\lambda }_1,{\lambda }_2>0$

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}||x_n-J_{{\lambda }_1}^{G_1}(x_n)+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||=0,}\end{array}$$

(12)

then

$${\displaystyle \underset{n\to \infty }{lim}||(I-J_{{\lambda }_1}^{G_1})x_n||=\underset{n\to \infty }{lim}||(I-J_{{\lambda }_2}^{G_2})A{x}_n||=0.}$$

Lemma 9.

Let $G_1:H_1\to 2^{H_1}$ and $G_2:H_2\to 2^{H_2}$ be set-valued maximal monotone operators. Then, for ${\lambda }_1,{\lambda }_2>0$, the operator $\left[I-\tau [(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]\right]$is firmly nonexpansive, where $\tau =\frac{1}{1+{||A||}^2}$, A is a bounded linear operator and $A^{\ast }$ is adjoint of A.

Proof. 

Let $M=[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]$. Since $G_1$ and $G_2$ are maximal monotone, by Lemma 1, it follows that the operators $(I-J_{{\lambda }_1}^{G_1})$ and $(I-J_{{\lambda }_2}^{G_2})$ are firmly nonexpansive. As A is a bounded linear operator and $A^{\ast }$ is adjoint of A, we have

$$\begin{array}{cc}\hfill ⟨M(x)-& M(y),x-y⟩\hfill \\ \hfill & =⟨[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]x-[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]y,x-y⟩\hfill \\ \hfill & =⟨(I-J_{{\lambda }_1}^{G_1})x-(I-J_{{\lambda }_1}^{G_1})y,x-y⟩+⟨A^{\ast }(I-J_{{\lambda }_2}^{G_2})Ax-A^{\ast }(I-J_{{\lambda }_2}^{G_2})Ay,x-y⟩\hfill \\ \hfill & =⟨(I-J_{{\lambda }_1}^{G_1})x-(I-J_{{\lambda }_1}^{G_1})y,x-y⟩+⟨(I-J_{{\lambda }_2}^{G_2})Ax-(I-J_{{\lambda }_2}^{G_2})Ay,A(x)-A(y)⟩.\hfill \end{array}$$

Using firmly nonexpansiveness of the operators $(I-J_{{\lambda }_1}^{G_1})$ and $(I-J_{{\lambda }_2}^{G_2})$, we have

$$\begin{array}{cc}\hfill ⟨M(x)-& M(y),x-y⟩\hfill \\ \hfill & \ge ||(I-J_{{\lambda }_1}^{G_1})x-(I-J_{{\lambda }_1}^{G_1}){y||}^2+{||(I-J_{{\lambda }_2}^{G_2})Ax-(I-J_{{\lambda }_2}^{G_2})Ay||}^2.\hfill \end{array}$$

As $||A^{\ast }||=||A||$, we have $||A^{\ast }(I-J_{{\lambda }_2}^{G_2})Ax-A^{\ast }(I-J_{{\lambda }_2}^{G_2}){Ay||}^2\le ||A^{\ast }{||}^2{||(I-J_{{\lambda }_2}^{G_2})Ax-(I-J_{{\lambda }_2}^{G_2})Ay||}^2$.

Thus, the above inequality implies that

$$\begin{array}{cc}\hfill ⟨M(x)-& M(y),x-y⟩\hfill \\ \hfill & \ge ||(I-J_{{\lambda }_1}^{G_1})x-(I-J_{{\lambda }_1}^{G_1}){y||}^2+\frac{||A^{\ast }(I-J_{{\lambda }_2}^{G_2})Ax-A^{\ast }(I-J_{{\lambda }_2}^{G_2}){Ay||}^2}{{||A||}^2}.\hfill \end{array}$$

By the Lemma 4, we obtain

$$\begin{array}{cc}\hfill ⟨M(x)-& M(y),x-y⟩\hfill \\ \hfill & \ge \frac{||[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]x-[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]{y||}^2}{1+{||A||}^2}\hfill \\ \hfill & ={\tau ||M(x)-M(y)||}^2,\hfill \end{array}$$

which shows that M is $\tau$-inverse strongly monotone, and hence, by Lemma 5, $I-\tau M$ is firmly nonexpansive for $\tau =\frac{1}{1+{||A||}^2}$. □

Lemma 10.

If $M=[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]\mathit{for}\mathit{all}{\lambda }_1,{\lambda }_2>0$, then $\mathrm{Fix}(I-\tau M)=\Delta$, for every $\tau >0$.

Proof. 

Let $\Delta \ne \varphi$; then, $\Delta \subset \mathrm{Fix}(I-\tau M)$. Let $p\in \mathrm{Fix}(I-\tau M)$, so $M(p)=0$ and $\theta \in \Delta$, then $J_{{\lambda }_1}^{G_1}(\theta )=\theta$, $J_{{\lambda }_2}^{G_2}(A\theta )=A\theta$ and $M(\theta )=0$. By using firmly nonexpansive property of operators $(I-J_{{\lambda }_1}^{G_1})$ and $(I-J_{{\lambda }_2}^{G_2})$, we obtain

$$\begin{array}{cc}\hfill 0& =⟨M(p)-M(\theta ),p-\theta ⟩\hfill \\ \hfill & =⟨[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]p-[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]\theta ,p-\theta ⟩\hfill \\ \hfill & =⟨(I-J_{{\lambda }_1}^{G_1})p-(I-J_{{\lambda }_1}^{G_1})\theta ,p-\theta ⟩+⟨A^{\ast }(I-J_{{\lambda }_2}^{G_2})Ap-A^{\ast }(I-J_{{\lambda }_2}^{G_2})A\theta ,p-\theta ⟩\hfill \\ \hfill & =⟨(I-J_{{\lambda }_1}^{G_1})p-(I-J_{{\lambda }_1}^{G_1})\theta ,p-\theta ⟩+⟨(I-J_{{\lambda }_2}^{G_2})Ap-(I-J_{{\lambda }_2}^{G_2})A\theta ,A(p)-A(\theta )⟩\hfill \\ \hfill & \ge ||(I-J_{{\lambda }_1}^{G_1})p-(I-J_{{\lambda }_1}^{G_1}){\theta ||}^2+{||(I-J_{{\lambda }_2}^{G_2})Ap-(I-J_{{\lambda }_2}^{G_2})A\theta ||}^2,\hfill \\ \hfill & \ge ||(I-J_{{\lambda }_1}^{G_1}){p||}^2+{||(I-J_{{\lambda }_2}^{G_2})Ap||}^2,\hfill \end{array}$$

that is, $J_{{\lambda }_1}^{G_1}(p)=p$ and $J_{{\lambda }_2}^{G_2}(Ap)=Ap$. Thus, $p\in \Delta$. □

Theorem 2.

Let $G_1:H_1\to 2^{H_1}$ and $G_2:H_2\to 2^{H_2}$ be the set-valued maximal monotone operators and $A:H_1\to H_2$ be a bounded linear operator. Then, the sequence $\left\{x_n\right\}$ such that

$$\begin{array}{ccc}\hfill x_{n+1}& =& x_n-\tau \left[(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n\right],\mathit{for}\mathit{all}n\ge 0,\hfill \end{array}$$

(13)

where ${\lambda }_1,{\lambda }_2>0$ and $\tau =\frac{1}{1+{||A||}^2}$ converges weakly to the solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$.

Proof. 

Let $\theta \in \Delta$; then, by (13), we have

$$\begin{array}{cc}\hfill ||x_{n+1}{-\theta ||}^2& =||x_n-\tau [(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})]A{x}_n{-\theta ||}^2\hfill \\ \hfill & =||x_n{-\theta ||}^2+{\tau }^2{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2\hfill \\ \hfill & -2\tau ⟨x_n-\theta ,(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n⟩.\hfill \end{array}$$

(14)

By Lemma 9, the operator $M=(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A$ is $\tau$-inverse strongly monotone for $\tau =\frac{1}{1+{||A||}^2}$. Using the fact that $[(I-J_{{\lambda }_1}^{G_1})\theta +A^{\ast }(I-J_{{\lambda }_2}^{G_2})A\theta ]=0$, we have

$$\begin{array}{cc}\hfill 2\tau ⟨x_n-\theta & ,(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n⟩\hfill \\ \hfill & =2\tau ⟨x-\theta ,[(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n]-[(I-J_{{\lambda }_1}^{G_1})\theta +A^{\ast }(I-J_{{\lambda }_2}^{G_2})A\theta ]⟩\hfill \\ \hfill & \ge 2\tau (\tau )||[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]x_n{]-[(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]\theta ||}^2\hfill \\ \hfill & =2{\tau }^2{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2.\hfill \end{array}$$

(15)

Using (15), (14) becomes

$$\begin{array}{cc}\hfill ||x_{n+1}{-\theta ||}^2& \le ||x_n{-\theta ||}^2+{\tau }^2{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2\hfill \\ \hfill & -2{\tau }^2{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2\hfill \\ \hfill & \le ||x_n{-\theta ||}^2-{\tau }^2{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2.\hfill \end{array}$$

(16)

From (16), it is clear that

$$\begin{array}{c}\hfill ||x_{n+1}{-\theta ||}^2\le {||x_n-\theta ||}^2.\end{array}$$

(17)

Thus, $\left\{x_n\right\}$ is Féjer monotone and bounded, and consequently, $\left\{A(x_n)\right\}$ is also bounded. In view of Lemma 2, it is required to show that ${\omega }_W(x_n)\in \Delta$. From (16), we have

$$\begin{array}{c}\hfill ||x_{n+1}{-\theta ||}^2\le ||x_0{-\theta ||}^2-{\tau }^2\sum _{n=0}^n{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2.\end{array}$$

Boundedness of $\left\{x_n\right\}$ implies that

$$\begin{array}{c}\hfill \sum _{n=0}^{\infty }{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2<\infty .\end{array}$$

It follows that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2=0.\end{array}$$

(18)

By Lemma 8, we have $||(I-J_{{\lambda }_1}^{G_1})x_n||\to 0$ and $||(I-J_{{\lambda }_2}^{G_2})A{x}_n||\to 0$, as $n\to \infty$. Since the nonexpansive operators $J_{{\lambda }_1}^{G_1}$ and $J_{{\lambda }_2}^{G_2}$ are demiclosed at zero, by Lemma 2, we deduce that $x_n\rightharpoonup w\in \Delta$. □

Making use of the Krasnosel’skii–Mann Theorem [28], we have the following weak convergence result.

Theorem 3.

Suppose that the operators $G_1,G_2$, and A are the same as in Theorem 2 and M is same as in Lemma 9. Then, the sequence $\left\{{(I-\tau M)}^n{x}_0\right\}$ converges weakly to the solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$.

Proof. 

It follows from Lemma 9 that $[I-\tau M]=\left[I-\tau [(I-J_{{\lambda }_1}^{G_1})+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A]\right]$ is firmly nonexpansive and hence averaged. Applying Theorem 1, for arbitrary $x_0\in H_1$, the sequence $\left\{{(I-\tau M)}^n{x}_0\right\}$ converges weakly to the fixed point of $[I-\tau M]$. It follows from Lemma 10 that the fixed point of $[I-\tau M]$ is the solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$. □

We prove a viscosity type convergence result to approximate the common solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$ and $(\mathrm{FPP})$ using Theorem 2.

Theorem 4.

Suppose that the operators $G_1,G_2$, and A are the same as in Theorem 2 and $T:H_1\to H_1$ is a self-nonexpansive mapping. Then, the sequence $\left\{x_n\right\}$ defined by

$$\left\{\begin{array}{cc}{y}_n\hfill & :=x_n-\tau \left[(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n\right],\hfill \\ x_{n+1}\hfill & :={\alpha }_n\psi (x_n)+(1-{\alpha }_n)T(y_n),\forall n\ge 0,\hfill \end{array}\right.$$

(19)

converges strongly to a common solution s of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$ and $(\mathrm{FPP})$, where ψ is an α-contraction mapping, ${\lambda }_1,{\lambda }_2>0,\tau =\frac{1}{1+{||A||}^2}$, $\left\{{\alpha }_n\right\}$ is a sequence in $(0,1)$ such that $\underset{n\to \infty }{lim}{\alpha }_n=0$, ${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty ,$${\displaystyle \sum _{n=1}^{\infty }}|{\alpha }_n-{\alpha }_{n-1}|<\infty$, and $s:=P_{\mathrm{Fix}(\mathrm{T})\cap \Delta }\psi (s)$.

Proof. 

The proof is divided into following easy steps for the convenience of readers.

Step 1. We show that the sequence $\left\{x_n\right\}$ is bounded. Let $\theta \in \mathrm{Fix}(T)\cap \Delta$; then, $J_{\lambda }^{G_1}\theta =\theta$, $J_{\lambda }^{G_2}(A\theta )=A\theta$ and $T(\theta )=\theta$. Applying (16) and (17), we obtain

$$\begin{array}{c}\hfill ||y_n{-\theta ||}^2\le ||x_n{-\theta ||}^2-{\tau }^2{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2,\end{array}$$

(20)

and

$$\begin{array}{c}\hfill ||y_n{-\theta ||}^2\le {||x_n-\theta ||}^2.\end{array}$$

(21)

From (19), we get

$$\begin{array}{cc}\hfill ||x_{n+1}-\theta ||& =||{\alpha }_n\psi (x_n)+(1-{\alpha }_n)T(y_n)-\theta ||\hfill \\ \hfill & \le {\alpha }_n||\psi (x_n)-\theta ||+(1-{\alpha }_n)||T(y_n)-\theta ||\hfill \\ \hfill & \le {\alpha }_n||\psi (x_n)-\psi (\theta )||+{\alpha }_n||\psi (\theta )-\theta ||+(1-{\alpha }_n)||T(y_n)-T(\theta )||\hfill \\ \hfill & \le {\alpha }_n\alpha ||x_n-\theta ||+{\alpha }_n||\psi (\theta )-\theta ||+(1-{\alpha }_n)||y_n-\theta ||\hfill \\ \hfill & \le {\alpha }_n\alpha ||x_n-\theta ||+{\alpha }_n||\psi (\theta )-\theta ||+(1-{\alpha }_n)||x_n-\theta ||\hfill \\ \hfill & =[1-{\alpha }_n(1-\alpha )]||x_n-\theta ||+{\alpha }_n||\psi (\theta )-\theta ||\hfill \\ \hfill & \le max\left\{||x_n-\theta ||,\frac{||\psi (\theta )-\theta ||}{1-\alpha }\right\}.\hfill \end{array}$$

Continuing in the same way as above, we have

$$\begin{array}{cc}\hfill ||x_{n+1}-\theta ||& \le \left\{||x_0-\theta ||,\frac{||\psi (\theta )-\theta ||}{1-\alpha }\right\}.\hfill \end{array}$$

(22)

Hence, $\left\{x_n\right\}$ is bounded, and consequently, $\left\{y_n\right\},\left\{\psi (x_n)\right\}$ and $\left\{T(y_n)\right\}$ are also bounded.

Step 2.$||x_{n+1}-x_n||\to 0$, as $n\to \infty$. By Lemma 9, $I-\tau M$ is firmly nonexpansive and consequently nonexpansive, that is,

$$\begin{array}{c}\hfill ||y_n-y_{n-1}||=||(I-\tau M)x_n-(I-\tau M)x_{n-1}||\le ||x_n-x_{n-1}||.\end{array}$$

(23)

From (19), we conclude that

$$\begin{array}{cc}\hfill ||x_{n+1}-x_n& ||\hfill \\ \hfill & =||{\alpha }_n\psi (x_n)+(1-{\alpha }_n)T(y_n)-{\alpha }_{n-1}\psi (x_{n-1})+(1-{\alpha }_{n-1})T(y_{n-1})||\hfill \\ \hfill & =||{\alpha }_n\psi (x_n)-{\alpha }_n\psi (x_{n-1})+{\alpha }_n\psi (x_{n-1})+(1-{\alpha }_n)T(y_{n-1})-(1-{\alpha }_n)T(y_{n-1})\hfill \\ \hfill & +(1-{\alpha }_n)T(y_n)-{\alpha }_{n-1}\psi (x_{n-1})+(1-{\alpha }_{n-1})T(y_{n-1})||\hfill \\ \hfill & \le {\alpha }_n||\psi (x_n)-\psi (x_{n-1})||+||\psi (x_{n-1})|||{\alpha }_n-{\alpha }_{n-1}|+(1-{\alpha }_n)||T(y_n)-T(y_{n-1})||\hfill \\ \hfill & +||T(y_{n-1})|||{\alpha }_{n-1}-{\alpha }_n|\hfill \\ \hfill & \le {\alpha }_n\alpha ||x_n-x_{n-1}||+||\psi (x_{n-1})|||{\alpha }_n-{\alpha }_{n-1}|+(1-{\alpha }_n)||y_n-y_{n-1}||\hfill \\ \hfill & +||T(y_{n-1})|||{\alpha }_{n-1}-{\alpha }_n|\hfill \\ \hfill & \le {\alpha }_n\alpha ||x_n-x_{n-1}||+||\psi (x_{n-1})|||{\alpha }_n-{\alpha }_{n-1}|+(1-{\alpha }_n)||x_n-x_{n-1}||\hfill \\ \hfill & +||T(y_{n-1})|||{\alpha }_{n-1}-{\alpha }_n|,\hfill \end{array}$$

(24)

that is,

$$\begin{array}{c}\hfill ||x_{n+1}-x_n||\le [1-{\alpha }_n(1-\alpha )]||x_n-x_{n-1}||+|{\alpha }_n-{\alpha }_{n-1}|K,\end{array}$$

(25)

where $K:=sup\{||\psi (x_{n-1})||+||T(y_{n-1})||:n\ge 0\}$. By Lemma 3, it follows that

$$\begin{array}{c}\hfill ||x_{n+1}-x_n||\to 0,\mathrm{as}n\to \infty .\end{array}$$

(26)

Step 3.$||T(y_n)-y_n||\to 0$, as $n\to \infty$. Again using (19), we have

$$\begin{array}{cc}\hfill ||x_{n+1}& {-\theta ||}^2\hfill \\ \hfill & =||{\alpha }_n\psi (x_n)+(1-{\alpha }_n)T(y_n){-\theta ||}^2\hfill \\ \hfill & \le {\alpha }_n||\psi (x_n){-\theta ||}^2+(1-{\alpha }_n){||T(y_n)-\theta ||}^2\hfill \\ \hfill & \le {\alpha }_n||\psi (x_n){-\theta ||}^2+(1-{\alpha }_n){||y_n-\theta ||}^2\hfill \\ \hfill & \le {\alpha }_n{||\psi (x_n)-\theta ||}^2+(1-{\alpha }_n)\left[||x_n{-\theta ||}^2-{\tau }^2{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2\right]\hfill \\ \hfill & \le {\alpha }_n||\psi (x_n){-\theta ||}^2+||x_n{-\theta ||}^2-{\tau }^2{||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||}^2,\hfill \end{array}$$

(27)

and so,

$$\begin{array}{cc}\hfill {\tau }^2||(I-J_{{\lambda }_1}^{G_1})x_n& +A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n{||}^2\hfill \\ \hfill & \le {\alpha }_n||\psi (x_n){-\theta ||}^2+||x_n{-\theta ||}^2-{||x_{n+1}-\theta ||}^2\hfill \\ \hfill & \le {\alpha }_n||\psi (x_n){-\theta ||}^2+||x_{n+1}-x_n||\left(||x_n-\theta ||+||x_{n+1}-\theta ||\right).\hfill \end{array}$$

(28)

Taking limit $n\to \infty$, we obtain

$$\begin{array}{c}\hfill ||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||\to 0.\end{array}$$

(29)

From (19), we have

$$\begin{array}{c}\hfill y_n=x_n-\tau \left[(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n\right],\end{array}$$

or, equivalently

$$\begin{array}{c}\hfill \frac{x_n-y_n}{\tau }=\left[(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n\right].\end{array}$$

Using (29), we obtain

$$\begin{array}{c}\hfill \frac{1}{\tau }||x_n-y_n||=||(I-J_{{\lambda }_1}^{G_1})x_n+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_n||\to 0.\end{array}$$

that is,

$$\begin{array}{c}\hfill ||x_n-y_n||\to 0,\mathrm{as}n\to \infty .\end{array}$$

(30)

Again, by (19), we can write

$$\begin{array}{cc}\hfill x_{n+1}-x_n& ={\alpha }_n\psi (x_n)+(1-{\alpha }_n)T(y_n)-x_n\hfill \\ \hfill & ={\alpha }_n(\psi (x_n)-x_n)+(1-{\alpha }_n)(T(y_n)-x_n),\hfill \end{array}$$

or

$$(1-{\alpha }_n)||T(y_n)-x_n||\le ||x_{n+1}-x_n||+{\alpha }_n||\psi (x_n)-x_n||.$$

Thus, $||T(y_n)-x_n||\to 0$, as $n\to \infty$. That is,

$$\begin{array}{ccc}\hfill ||T(y_n)-y_n||& \le & ||T(y_n)-x_n||+||x_n-y_n||,\hfill \end{array}$$

taking limit as $n\to \infty$, it follows that $||T(y_n)-y_n||\to 0$.

Step 4.$x_n\to s$, where $s=P_{\mathrm{Fix}(\mathrm{T})\cap \Delta }\psi (s).$

It follows from the boundedness of $\left\{x_n\right\}$ that there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $\left\{x_{n_k}\right\}$ converges to r. By step 3 and demiclosedness of nonexpansive mapping T, we get $r\in \mathrm{Fix}(T)$. From (29), we have

$$\begin{array}{c}\hfill ||(I-J_{{\lambda }_1}^{G_1})x_{n_k}+A^{\ast }(I-J_{{\lambda }_2}^{G_2})A{x}_{n_k}||\to 0,\mathrm{as}n\to \infty .\end{array}$$

(31)

By Lemma 8, we have

$$||(I-J_{{\lambda }_1}^{G_1})x_{n_k}||\to 0and||(I-J_{{\lambda }_2}^{G_2})A{x}_{n_k}||\to 0.$$

Since $\left\{x_n\right\}$ and $\left\{y_n\right\}$ have the same asymptotic behavior, $A(x_n)\rightharpoonup A(r)$ and by demiclosedness of nonexpansive operators $J_{{\lambda }_1}^{G_1}$ and $J_{{\lambda }_2}^{G_2}$, we get $0\in G_1(r)$ and $0\in G_2(Ar)$. We have $r\in \mathrm{Fix}(\mathrm{T})\cap \Delta$. Applying the definition of s, we have $⟨\psi (s)-s,r-s⟩\le 0$. Thus,

$$\begin{array}{cc}\hfill lim\underset{n\to \infty }{sup}⟨\psi (s)-s,x_{n+1}-s⟩& =\underset{k\to \infty }{lim}⟨\psi (s)-s,x_{n_k+1}-s⟩\hfill \\ \hfill & =⟨\psi (s)-s,r-s⟩\le 0.\hfill \end{array}$$

(32)

Therefore,

$$\begin{array}{cc}\hfill ||x_{n+1}-& {s||}^2\hfill \\ & =||{\alpha }_n\psi (x_n)+(1-{\alpha }_n)T(y_n){-s||}^2\hfill \\ \hfill & =⟨{\alpha }_n\psi (x_n)+(1-{\alpha }_n)T(y_n)-s,x_{n+1}-s⟩\hfill \\ \hfill & ={\alpha }_n⟨\psi (x_n)-s,x_{n+1}-s⟩+(1-{\alpha }_n)⟨T(y_n)-s,x_{n+1}-s⟩\hfill \\ \hfill & \le {\alpha }_n⟨\psi (x_n)-s,x_{n+1}-s⟩+(1-{\alpha }_n)⟨y_n-s,x_{n+1}-s⟩\hfill \\ \hfill & \le {\alpha }_n⟨\psi (x_n)-\psi (s),x_{n+1}-s⟩+{\alpha }_n⟨\psi (s)-s,x_{n+1}-s⟩+(1-{\alpha }_n)⟨y_n-s,x_{n+1}-s⟩\hfill \\ \hfill & \le \frac{{\alpha }_n}{2}\left\{||\psi (x_n)-\psi (s){||}^2+{||x_{n+1}-s||}^2\right\}+{\alpha }_n⟨\psi (s)-s,x_{n+1}-s⟩\hfill \\ \hfill & +\frac{(1-{\alpha }_n)}{2}\left\{||y_n{-s||}^2+{||x_{n+1}-s||}^2\right\}\hfill \\ \hfill & \le \frac{{\alpha }_n}{2}\left\{{\alpha }^2||x_n{-s||}^2+{||x_{n+1}-s||}^2\right\}+{\alpha }_n⟨\psi (s)-s,x_n-s⟩\hfill \\ \hfill & +\frac{(1-{\alpha }_n)}{2}\left\{||x_n{-s||}^2+{||x_{n+1}-s||}^2\right\},\hfill \end{array}$$

that is,

$$\begin{array}{cc}\hfill ||x_{n+1}{-s||}^2& \le {\alpha }_n{\alpha }^2||x_n{-s||}^2+{\alpha }_n⟨\psi (s)-s,x_n-s⟩+(1-{\alpha }_n){||x_n-s||}^2\hfill \\ \hfill & =[1-{\alpha }_n(1-{\alpha }^2)]{||x_n-s||}^2+{\alpha }_n⟨\psi (s)-s,x_{n+1}-s⟩.\hfill \end{array}$$

By using (32) and Lemma 3, we have $x_n\to s$, as $n\to \infty$. □

4. Consequences

4.1. Split Equilibrium Problem

The equilibrium problem (EP) is to find $\overline{u}\in C$ such that

$$F(\overline{u},v)\ge 0,forallv\in C,$$

(33)

where $F:C\times C\to \mathbb{R}$ is a bifunction. In 2012, He [29] studied the concept of split equilibrium problem (SEP), that is, to find

$$u^{\ast }\in C \mathrm{such} \mathrm{that} u^{\ast }\in EP(F_1;C) \mathrm{and} A{u}^{\ast }\in EP(F_2;Q),$$

(34)

where the bifunctions $F_1$ and $F_2$ are defined over closed convex subsets $C(\ne \varphi )\subseteq H_1$ and $Q(\ne \varphi )\subseteq H_2$, respectively. He studied weak convergence of (SEP). Furthermore, Dinh et al. [30] and Dinh and Kim [31] studied (SEP) and (FPP) involving monotone and nonmonotone bifunctions and discussed the weak as well as strong convergence. For more details of EPs, see [31,32,33].

The resolvent of a bifunction F is defined as

$$R_{\lambda }^F(u)=\left\{z\in C:F(z,y)-\frac{1}{\lambda }⟨u-z,y-z⟩\ge 0,\mathrm{for}\mathrm{all}y\in C\right\},\mathrm{for}\mathrm{all}u\in H.$$

(35)

Blum and Oettli [32] have shown that the resolvent $R_{\lambda }^F$ is properly defined, that is, $R_{\lambda }^F(u)\ne \varnothing ,\mathrm{for}\mathrm{all}u\in H$ and $\mathrm{Fix}(R_{\lambda }^F)=\mathrm{EP}(F)$. Takahashi et al. [34] defined the following set-valued mapping

$$G_F(u):=\left\{\begin{array}{cc}\left\{z\in H:F(u,y)\ge ⟨z,y-u⟩,\mathrm{for}\mathrm{all}y\in C\right\},\hfill & u\in C,\hfill \\ \varnothing ,\hfill & u\notin C,\hfill \end{array}\right.$$

(36)

and stated that $\mathrm{EP}(F)=G_F^{-1}(0)$. Additionally, Takahashi et al. [34] have shown that for any $x\in H$ and $\lambda >0$, the resolvents of F and $G_F$ are identical, that is, $R_{\lambda }^F=J_{\lambda }^{G_F}$. It is shown in [32,34], the problem $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$ reduces to (SEP).

Remark 2.

If $G_1=G_{F_1}$ and $G_2=G_{F_2}$, then the following assertions are true.

(i) 

The sequence generated by scheme (13) converges weakly to the solution of (SEP).

(ii) 

The sequence $\left\{{(I-\tau M)}^n{x}_0\right\}$ defined in Theorem 3, converges weakly to the solution of (SEP).

(iii) 

The sequence generated by scheme (19) converges strongly to the common solution of (SEP) and (FPP).

4.2. Split Common Fixed Point Problem

If $J_{{\lambda }_1}^{G_1}=S$ and $J_{{\lambda }_2}^{G_2}=T$, then the following assertions for (SCFP) are true.

(i)

The scheme (13) defined in the Theorem 2 converges weakly to the solution of (SCFP).

(ii)

The sequence $\left\{{(I-\tau M)}^n{x}_0\right\}$ obtained in Theorem 3, converges weakly to the solution of (SCFP).

5. Numerical Example

The convergence graph of $||x_n||$ and $||x_{n+1}-x_n||$ obtained from the scheme (19) with step size $\tau$ is shown in Figure 1 and Figure 2, and a comparison of $||x_n||$ and $||x_{n+1}-x_n||$ is shown in Table 1. Later, a comparison of the convergence of scheme (19) with step size $\tau$, ${\rho }_n$, and ${\tau }_n$ is shown in Figure 3 and Figure 4. Figure 3 and Figure 4 ensure that the convergence of $||x_n||$ and $||x_{n+1}-x_n||$ obtained from the scheme (19) with step size $\tau$ is better than with the step sizes ${\rho }_n$ and ${\tau }_n$. Moreover, Table 2 shows that the proposed method takes few number of steps and time with the step size $\tau$ in comparison of ${\rho }_n$ and ${\tau }_n$. The stopping criterion is $||x_{n+1}-x_n||<{10}^{-6}$. All of the codes are written in MATLAB r2013a. The step sizes and control parameters are chosen as follows:

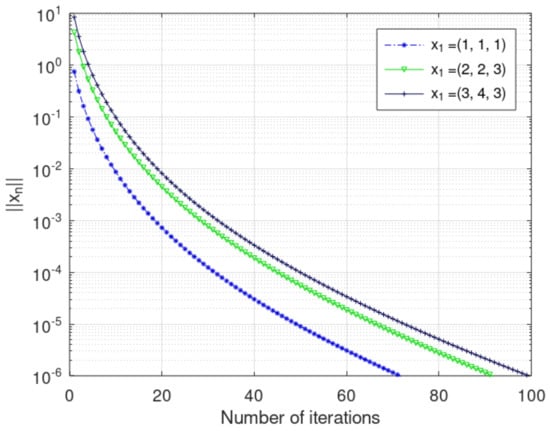
Figure 1. Convergence graph of $||x_n||$.

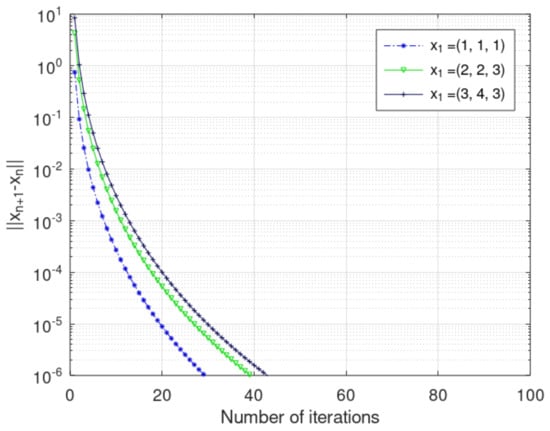
Figure 2. Convergence graph of $||x_{n+1}-x_n||$.

Table 1. Comparison table of Figure 1 and Figure 2.

${\mathit{s}}_1$		$||{\mathit{x}}_{\mathit{n}}||$	$||{\mathit{x}}_{\mathit{n}+1}-{\mathit{x}}_{\mathit{n}}||$
$s_1=(1,1,1)$	VCTA	1.12163182 × 10−6	1.20231424 × 10−6
	No. Iter.	55	27
	CPU Time (s)	0.00005	0.00001
$s_1=(2,2,3)$	VCTA	1.07080608 × 10−6	1.16727778 × 10−6
	No. Iter.	69	35
	CPU Time (s)	0.00019	0.00001
$s_1=(3,4,3)$	VCTA	1.01097722 × 10−6	1.04270864 × 10−6
	No. Iter.	75	39
	CPU Time (s)	0.00035	0.00001

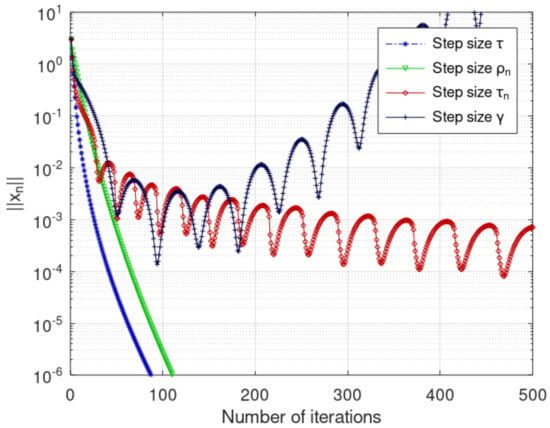
Figure 3. Comparison of $||x_n||$ for different step sizes.

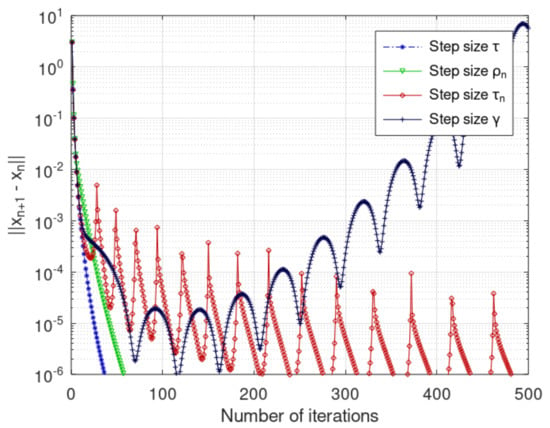
Figure 4. Comparison of $||x_{n+1}-x_n||$ with different step sizes.

Table 2. Comparison table of Figure 3 and Figure 4.

${\mathit{s}}_1$		WGM1	WGM2	VCTA
$s_1=(2,2,2)$	$||x_n||$	1.02734625 × 10−6	2.61940737 × 10−4	1.06138607 × 10−6
	No. Iter.	110	1000	66
	CPU Time (s)	0.00019	3	0.00001
$s_1=(2,2,2)$	$||x_{n+1}-x_n||$	1.04342385 × 10−6	1.01232329 × 10−6	1.00378988 × 10−6
	No. Iter.	57	969	35
	CPU Time (s)	0.00006	2.35	0.00001

WGM1:

Scheme (19) with the Wang’s step size ${\rho }_n=1/n$, $S=J_{{\lambda }_1}^{G_1}$ and $T=J_{{\lambda }_1}^{G_2}$.

WGM2:

Scheme (19) with the Yang’s step size ${\tau }_n=\frac{{\rho }_n}{||A^{\ast }(I-T)A{x}_n||}$, $S=J_{{\lambda }_1}^{G_1}$ and $T=J_{{\lambda }_1}^{G_2}$.

WGM3:

Scheme (19) with the Byrne’s [9] step size $\gamma =\frac{2}{{||A||}^2}=0.2000$.

VCTA:

Viscosity type Scheme (19) with the step size $\tau =\frac{1}{1+{||A||}^2}=0.0156$ and the parameter ${\alpha }_n=1/\sqrt{n}$ for all $n\ge 1$.

Let $H_1=H_2={\mathbb{R}}^3$ with the inner product defined by

$$⟨s,t⟩=s_1{t}_1+s_2{t}_2+s_3{t}_3,$$

and

$${||s||}^2=|s_1{|}^2+|s_2{|}^2+{\left|s_3\right|}^2,\mathrm{for}\mathrm{all}s=(s_1,s_2,s_3)\in {\mathbb{R}}^3\mathrm{and}t=(t_1,t_2,t_3)\in {\mathbb{R}}^3.$$

Also,

$${||s-t||}^2=|s_1-t_1{|}^2+|s_2-t_2{|}^2+{|s_3-t_3|}^2,\mathrm{for}\mathrm{all}s=(s_1,s_2,s_3)\mathrm{and}t=(t_1,t_2,t_3)\in {\mathbb{R}}^3.$$

We define the operators $G_1$ and $G_2$ by

$$G_1=\left(\begin{array}{ccc}1/3& 0& 0\\ 0& 1/2& 0\\ 0& 0& 1\end{array}\right)\mathrm{and}{G}_2=\left(\begin{array}{ccc}1/4& 0& 0\\ 0& 1/5& 0\\ 0& 0& 1/6\end{array}\right).$$

(37)

Clearly, $G_1$ and $G_2$ are maximal monotone operators and their resolvents are given by

$$J_{{\lambda }_1}^{G_1}=\left(\begin{array}{ccc}\frac{3}{3-{\lambda }_1}& 0& 0\\ 0& \frac{2}{2-{\lambda }_1}& 0\\ 0& 0& \frac{1}{1-{\lambda }_1}\end{array}\right)\mathrm{and}{J}_{{\lambda }_2}^{G_2}=\left(\begin{array}{ccc}\frac{4}{4-{\lambda }_2}& 0& 0\\ 0& \frac{5}{5-{\lambda }_2}& 0\\ 0& 0& \frac{6}{6-{\lambda }_2}\end{array}\right).$$

(38)

Now, consider a bounded linear operator A and its adjoint operator $A^{\ast }$ such that

$$A=\left(\begin{array}{ccc}4& 3& 3\\ 2& 4& 1\\ 3& 1& 2\end{array}\right)\mathrm{and}{A}^{\ast }=\left(\begin{array}{ccc}7& -3& -9\\ -1& -1& 2\\ -10& 5& 10\end{array}\right).$$

We define the mappings T and $\psi$ by

$$T=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)\mathrm{and}\psi =\left(\begin{array}{ccc}1/2& 0& 0\\ 0& 1/2& 0\\ 0& 0& 1/2\end{array}\right).$$

(39)

Clearly, T is nonexpansive and $\psi$ is a contraction mapping with $\alpha =1/2$. Choose the scalars ${\lambda }_1=1/2$, ${\lambda }_2=1/3$, and ${\alpha }_n=1/\sqrt{n}$, for all $n\ge 1$, $\tau =\frac{1}{1+{||A||}^2}=0.0156$ with $||A||=7.9465$, $\gamma =\frac{2}{{||A||}^2}=0.2000$, and ${\rho }_n=1/n$. We consider arbitrary initial points $x_1=(1,1,1),(2,2,3)$, and $(3,4,3)$ in scheme (19) of Theorem 4. Then, the sequence generated by suggested scheme converges to a solution $(0,0,0)$ of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$ and $(\mathrm{FPP})$.

6. Conclusions

In this paper, we modified Wang’s new iterative method using a different stepsize to solve $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$ and $(\mathrm{FPP})$ in Hilbert space. We analyzed the weak convergence of the modified scheme to investigate the approximate solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$ and extended it to a viscosity type iterative scheme to obtain the common solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$ and $(\mathrm{FPP})$ in Hilbert space with some mild assumptions. In support of our results, a numerical example with comparison tables and convergence graphs is constructed. We remark that one can further study weak and strong convergence of common solutions of $({\mathrm{S}}_{\mathrm{p}}\mathrm{VIP})$ and $(\mathrm{FPP})$ in higher dimensional spaces.