Abstract
Many of the applied algorithms that have been developed for solving a system of logical equations or the Boolean satisfiability problem have solved the problem in the Boolean domain. However, other approaches have recently been developed and improved. One of these developments is the transformation of a system of logical equations to a real continuous domain. The essence of this development is that a system of logical equations is transformed into a system in a real domain and the solution is sought in a real continuous domain. A real continuous domain is a richer domain, as it involves many well-developed algorithms. In this paper, we have constructively transformed the solution of any system of logical equations with a unique solution into an optimization problem for a polylinear target function in a unit -dimensional cube . The resulting polylinear target function in does not have a local minimum. We proved that only once by calculating the gradient of the polylinear target function at any interior point of the cube, we can determine the solution to the system of logical equations.
Keywords:
polylinear functions; global optimization; algorithms; Zhegalkin polynomials; logical operations; systems of Boolean algebraic equations; algebraic cryptanalysis MSC:
06E30; 03G05; 90C26; 65H10; 90C09; 90C23; 90C26
1. Introduction
For many years, the system of logical equations has been an important research topic. The solution of logical equations penetrates into many areas of modern science, such as logical design, biology, grammar, chemistry, law, medicine, spectroscopy, graph theory, military affairs, automation, control, and experiment planning [1,2]. Many problems in operations research, recognizing objects, and phenomena come down to solving a system of logical equations. Solutions of logical equations also serve as an important tool in the processing of pseudo-Boolean equations and inequalities and associated problems of integer linear programming [2,3].
Another important and promising area in which the solution of a system of logical equations is used is algebraic cryptanalysis. For a specific cipher, algebraic cryptanalysis consists of two stages: transforming the cipher into a system of polynomial equations (usually over a Boolean ring) and solving the resulting system of polynomial equations [4]. One of the first successful applications of solving a system of logical equations in a cryptographic problem was demonstrated in [5]. Thereafter, many new directions and algorithms for solving systems of logical equations have been developed and adapted [6,7,8,9,10,11,12,13]. One such development is the transformation of a system of logical equations to a real contiguous domain, since a real contiguous domain is a richer area that includes many well-developed methods and algorithms. The essence of this development lies in the fact that the system of logical equations is transformed into a system in a real domain and the solution is sought in a real continuous domain [14]. The transformed system can be reduced to a numerical optimization problem, which makes it possible to apply, analyze, and combine methods such as the steepest descent algorithm, Newton’s method, and the coordinate descent algorithm [12,15,16,17,18,19,20,21,22]. In addition, another constructive idea was recently proposed in [22], the essence of which is that the transformed system can be converted to an equivalent system of polynomial equations, which means that any symbolic methods for solving polynomial systems can be used to solve and analyze the equivalent system of polynomial equations.
There are many ways to transform a system of logical equations into a minimization problem in a real continuous domain. However, one of the main problems with this transformation is that the target function in the desired continuous domain can have many local minimums; this greatly hinders the suitability of the method in practice. Currently, as far as we know, all numerical optimization algorithms find only a local minimum, and, in general, there is no effective method for finding the global minimum of the target function.
Very recently, in [20,21], an interesting idea was proposed, i.e., an arbitrary system of logical equations was transformed into the corresponding unique system of polylinear-polynomial equations in a unit -dimensional cube . In , the solution of a system of polylinear-polynomial equations was reduced to the problem of optimizing a polylinear target function. The authors found that, according to the system of equations, the composed polylinear target function did not have a local extremum either inside, on the edges, or on the faces of the . Rather, it obtains the minimum value at the vertices of .
This was a significant result in terms of reducing the number of local minima of the target function. However, because the proposed idea was new and was being improved, on the set of vertices of the cube there were local minimums of the polylinear target function. How to deal with them? In work [21] this question was not investigated and it remained an open problem.
In this paper, the idea of the authors D.N. Barotov and R.N. Barotov, which was recently proposed in [20,21], was improved both theoretically and algorithmically. Specifically, any system of logical equations with a single solution may be constructively reduced to the optimization problem of a polylinear target function in a unit -dimensional cube . According to the system of logical equations, the composed polylinear target function in does not have a local minimum; that is, neither inside, nor on the edges, nor on the faces of , nor at the vertices of the -dimensional cube , is there a local minimum. It was proved that only once by calculating the gradient of the polylinear target function at any internal point of the cube , it is possible to determine the solution to the system of logical equations.
Our work is divided into several sections. In the Section 2, we describe the essence of the method and prove the corresponding theorem. In the Section 3, we show the result of the theorem in one simple system of two logical equations. In the Section 4, we explain and provide appropriate corrections for some typographical errors that were made in our previous work. Finally, in the Section 5, we present our findings and plans for further research.
2. A Constructive Method for Transforming a System of Logical Equations into the Problem of Minimizing a Polylinear Target Function
First, we define the necessary notation and formulas for further use.
Let be an -dimensional unit cube and let be the vertices of .
Let be the logical operation (addition by mod 2), i.e., .
Let be the logical operation (logical multiplication), i.e.,
Definition 1.
A functionis called a polylinear function inif.
According to Definition 1, any harmonic function, in each of its variables [20], is a polylinear function, and vice versa.
Consider the following arbitrary system of logical equations:
where is a Zhegalkin polynomial, .
First, it is obvious that system (1) is equivalent to the following system:
Second, it is easy to see that system (2) is equivalent to one equation in the following form:
We understand that the last polynomial obtained is also a Zhegalkin polynomial in the variables , denoted by ; i.e.,
According to the lemma of D.N. Barotov and R.N. Barotov, set out in [21], for the Zhegalkin polynomial there exists a unique non-negative polylinear function in , such that
The function can be found algorithmically. For example, it can be found by using the algorithm of D.N. Barotov and R.N. Barotov, which was set out in the [21] (which is included below for convenience, see Appendix A).
If system (1) has a unique solution (b1, b2, …, bn), then Equations (3)–(5) imply the following:
To find a solution to system (1) in , we minimize the polylinear target function f(x1, x2, …, xn).
Regarding the minimization of the polylinear target function f(x1, x2, …, xn), we managed to obtain an interesting (and at least a theoretical) result. Now, we formulate this process in the form of a theorem and provide proof in detail.
Theorem 1.
If system (1) has a unique solution, then only once by calculating the gradient of the target function f(x1, x2, …, xn) at any interior point of the cube , this solution can be found.
Proof of Theorem 1.
Let some Boolean vector be the only solution to system (1). Then, we first prove that
(i) Let us first show that the values f(x1, x2, …, xn) and p(x1, x2, …, xn) are equal at the vertices of the cube . Indeed:
If , then . Calculate the value of the function:
(ii) Let us show that f(x1, x2, …, xn) is a polylinear function.
(iii) From (i) and (ii), it is implied that f(x1, x2, …, xn) is a non-negative function in .
(iv) Let us prove uniqueness. Proof by contradiction: let there exist another non-negative polylinear function f1(x1, x2, …, xn) in and such that . Then consider the function . On the one hand, it is clear that if , than , on the other hand, is also a polylinear function, since . From these considerations and the maximum principle [23,24], it follows that
—this is a contradiction, which was to be proved.
Second, based on the appropriate form of the function f(x1, x2, …, xn), we prove that if , then the solution of system (1) can be determined as follows:
Indeed, means that . Then . We differentiate the function and find .
or
□
As a result, the presented idea [20,21] with reliable proofs was constructively and algorithmically improved in terms of reducing the number of local minimums. However, we acknowledge that for the suitability of the proposed result in practice, we still need to modify the algorithm to obtain a polylinear target function that does not have a local minimum from a given system of logical equations.
3. Illustration of the Result of a Theorem in One Simple Two-Dimensional System
For clarity, using one simple two-dimensional example, we show the method of applying the proved theorem and the graph of the corresponding target function.
Consider a system of two logical equations:
We construct an equivalent equation:
We transform the polynomial and obtain the corresponding non-negative polylinear function that is unique in , so that
For clarity, we present the graph of the function in (see Figure 1a).
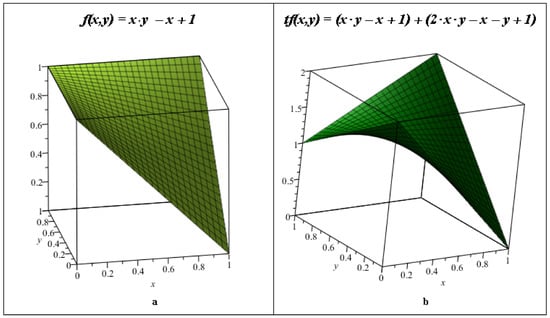
Figure 1.
The left graph (a) is the graph of the function . The right graph (b) is the graph of the function .
Everything is obvious from the graph, but for the sake of completeness, we will find a solution to the system by Theorem 1. Let .
It is easy to see that (x, y) = (1, 0) is the only solution to this system of two logical equations.
For comparison, we reduce this system of two logical equations to another problem of minimizing the polylinear target function , asdefined in [21]. For clarity, we present the graph of the function in (see Figure 1b).
Thus, the following results are obtained:
- As was proved in [21], the function has no local minima either inside, on the faces, or on the edges of the cube . However, this example shows that there can be local minima among the vertices of the cube (see Figure 1b). Therefore, as in this example, the gradient of the function from any interior point of the cube can be directed, not to the solution but to another vertex of the cube , or the gradient may not indicate any direction.
- In the current work, we have proved that there is no local minimum on the first graph (see Figure 1a); we can determine the solution to the system of logical equations only once by calculating the gradient of the function at any interior point of the cube .
4. Correcting Typing Errors
Some typographical errors were made in [20,21]. The important typographical errors were the following: the first error was in [20] (see page 10) showing the results not of coordinate descent, but of gradient descent; the second error was in [21] (see page 8, line 12), where the word “only” was redundant and needed to be removed.
5. Conclusions
We have constructively transformed the solution of any system of logical equations with a unique solution of an optimization problem for a polylinear target function in a unit -dimensional cube . The resulting polylinear target function in does not have a local minimum; that is, neither inside, nor on the edges, nor on the faces of , nor at the vertices of the -dimensional cube , is there a local minimum. We proved that only once by calculating the gradient of the polylinear target function at any interior point of the cube, we can determine the solution to the system of logical equations.
Based on this result, in future studies we will work on improving the algorithm for transforming a system of logical equations with a unique solution into the problem of minimizing the corresponding polylinear target function without a local minimum in . Second, we will study the possibility of transforming a system of logical equations with non-unique solutions of the minimization problem for the corresponding polylinear target function without a local minimum in .
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author is very grateful to his parents and family members and thanks them for their all-round support. The author is grateful to anonymous reviewers for valuable comments and suggestions that helped improve the manuscript.
Conflicts of Interest
The author declares there is no conflict of interest.
Appendix A
Let be any Zhegalkin polynomial.
Let be the set of all variables such that each variable is included in at least two monomials of the polynomial .
We construct the corresponding intermediate function based on the polynomial :
We are ready to write an algorithm for obtaining from the polynomial (Algorithm A1).
| Algorithm A1: Obtaining from the polynomial |
| Input: polynomial and set . Output: polynomial for from to do end for return |
The result of Algorithm A1 is —in a non-negative unique polylinear function such that . This result was proved in detail in [21].
References
- Brown, F.M. Boolean Reasoning: The Logic of Boolean Equations; Kluwer Academic Publishers: Boston, MA, USA, 1990. [Google Scholar]
- Ashurov, A. Solution of systems of nonlinear Boolean equations. Int. J. Appl. Math. 2021, 34, 595. [Google Scholar] [CrossRef]
- Hammer, P.L.; Rudeanu, S. Boolean Methods in Operations Research and Related Areas; Springer: Berlin, Germany, 1968. [Google Scholar] [CrossRef]
- Bard, G.V. Algorithms for Solving Linear and Polynomial Systems of Equations over Finite Fields, with Applications to Cryptanalysis; University of Maryland: College Park, MD, USA, 2007. [Google Scholar]
- Faugere, J.C.; Joux, A. Algebraic cryptanalysis of hidden field equation (HFE) cryptosystems using Gröbner bases. In Advances in Cryptology—CRYPTO 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 44–60. [Google Scholar]
- Armknecht, F. Improving fast algebraic attacks. In Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 2004; pp. 65–82. [Google Scholar]
- Bardet, M.; Faugère, J.-C.; Salvy, B.; Spaenlehauer, P.-J. On the complexity of solving quadratic Boolean systems. J. Complex. 2013, 29, 53–75. [Google Scholar] [CrossRef]
- Courtois, N. Fast algebraic attacks on stream ciphers with linear feedback. In Advances in Cryptology—CRYPTO 2003; Lecture Notes in Computer Science; Boneh, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2729, pp. 176–194. [Google Scholar]
- Faugére, J.-C. A new efficient algorithm for computing Gröbner bases (F4). J. Pure Appl. Algebra 1999, 139, 61–88. [Google Scholar] [CrossRef]
- Faugere, J.C. A new efficient algorithm for computing Gröbner bases without reduction to zero (F5). In Proceedings of the 2002 International Symposium on Symbolic and Algebraic Computation, Lille, France, 7–10 July 2002; pp. 75–83. [Google Scholar]
- Liu, M.; Lin, D.; Pei, D. Fast algebraic attacks and decomposition of symmetric Boolean functions. IEEE Trans. Inf. Theory 2011, 57, 4817–4821. [Google Scholar] [CrossRef][Green Version]
- Abdel-Gawad, A.H.; Atiya, A.F.; Darwish, N.M. Solution of systems of Boolean equations via the integer domain. Inf. Sci. 2010, 180, 288–300. [Google Scholar] [CrossRef]
- Kyrillidis, A.; Shrivastava, A.; Vardi, M.Y.; Zhang, Z. Solving hybrid Boolean constraints in continuous space via multilinear Fourier expansions. Artif. Intell. 2021, 299, 103559. [Google Scholar] [CrossRef]
- Pakhomchik, A.I.; Voloshinov, V.V.; Vinokur, V.M.; Lesovik, G.B. Converting of Boolean expression to linear equations, inequalities and QUBO penalties for cryptanalysis. Algorithms 2022, 15, 33. [Google Scholar] [CrossRef]
- Gu, J. How to Solve Very Large-Scale Satisfiability (VLSS) Problems; Technical Report UCECETR-90-002; University of Calgary: Calgary, AB, Canada, 1990. [Google Scholar]
- Gu, J. On optimizing a search problem. In Artificial Intelligence Methods and Applications; Bourbakis, N.G., Ed.; World Scientific Publishers: Singapore, 1992. [Google Scholar]
- Gu, J. Global optimization for satisfiability (SAT) problem. IEEE Trans. Knowl. Data Eng. 1994, 6, 361–381. [Google Scholar] [CrossRef]
- Gu, J.; Gu, Q.; Du, D. On optimizing the satisfiability (SAT) problem. J. Comput. Sci. Technol. 1999, 14, 1–17. [Google Scholar] [CrossRef]
- Barotov, D.N.; Muzafarov, D.Z.; Barotov, R.N. On one method for solving systems of Boolean algebraic equations. Mod. Math. Concept Innov. Math. Educ. 2021, 8, 17–23. [Google Scholar]
- Barotov, D.; Osipov, A.; Korchagin, S.; Pleshakova, E.; Muzafarov, D.; Barotov, R.; Serdechnyy, D. Transformation method for solving system of Boolean algebraic equations. Mathematics 2021, 9, 3299. [Google Scholar] [CrossRef]
- Barotov, D.N.; Barotov, R.N. Polylinear transformation method for solving systems of logical equations. Mathematics 2022, 10, 918. [Google Scholar] [CrossRef]
- Barotov, D.N.; Barotov, R.N.; Soloviev, V.; Feklin, V.; Muzafarov, D.; Ergashboev, T.; Egamov, K. The development of suitable inequalities and their application to systems of logical equations. Mathematics 2022, 10, 1851. [Google Scholar] [CrossRef]
- Axler, S.; Bourdon, P.; Wade, R. Harmonic Function Theory, 2nd ed.; Springer: New York, NY, USA, 2001; Volume 137. [Google Scholar]
- Mukhsinov, A.; Boboev, E.D.; Barotov, D.N. Formula presentation the solutions of the initial-boundary problem for one a many-dimtnsional parabolic equation with singular coefficients. Sci. Notes Khujand State Univ. Named After Acad. B. Gafurov. Ser. Nat. Sci. Econ. 2016, 4, 18–25. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).