Dialogues in Play: Conversational AI and Early Mathematical Thinking

Abstract

As conversational artificial intelligence (CAI), including smart speakers, social robots, and dialogic learning apps, becomes increasingly present in children’s lives, its potential to support early mathematical thinking warrants closer attention. While existing research largely concentrates on literacy and language development, the role of CAI in early numeracy remains underexplored. This paper examines how voice-based CAI might contribute to informal mathematical thinking in early childhood. Adopting a conceptual lens, this paper synthesises existing theory and research to examine the potential roles of CAI in early mathematical learning. Grounded in sociocultural theory and dialogic pedagogy, this paper positions CAI as a potential mediator of early mathematical thinking through responsive dialogue. Four interrelated dimensions (child agency, cognitive scaffolding, mathematical language quality, and responsiveness and timing) are identified as a conceptual lens for evaluating how dialogue-based interactions with CAI may support or constrain young children’s mathematical thinking. Rather than framing CAI as a direct teaching tool, this paper explores its potential role as a dialogic partner in play-based numeracy and inquiry. The framework contributes to early mathematics education by highlighting both the promise and the limitations of CAI, offering guidance for research, technology design, and educational practice. It underscores the need for intentional, ethically informed integration of CAI that approximates the qualities of human dialogue while acknowledging current constraints in real-world use.

1. Introduction

Digital technologies are increasingly shaping the experiences of young children worldwide, transforming how they play, communicate, and learn. Among these technologies, artificial intelligence (AI) is gaining increasing attention in education, supporting teaching practices, enabling personalised learning experiences, and offering adaptive feedback to learners (Du Boulay et al., 2023; Holmes & Tuomi, 2022; Zawacki-Richter et al., 2019). In recent years, many AI tools, especially AI-powered technology products, have expanded beyond the adult-oriented context to become part of children’s everyday environments, both at home and in educational settings (Su & Yang, 2022; Voulgari et al., 2024).

Among these, conversational AI (CAI) systems are gaining increasing presence. Broadly speaking, CAI is a subfield of AI that enables machines to interact with humans using natural language, either through text or voice, for back-and-forth communication (Freed, 2021; Ibrahim & Bilquise, 2025; Khatri et al., 2018). It encompasses tools like ChatGPT, which is built on large language models (LLMs), as well as voice-based interfaces that support spoken dialogue. These systems are designed to support spoken, naturalistic exchanges between users and machines through technologies (Holmes & Tuomi, 2022; Kong & Wang, 2021). The introduction of Apple’s Siri in 2010 is widely considered a watershed moment in the proliferation of CAI into consumer technology, as it uses natural language processing (NLP) to facilitate voice-based interaction (Saka et al., 2023). Subsequent advancements in neural networks and LLMs further enhanced the ability of voice assistants to comprehend context, manage complex conversations, and personalise responses (Jampala et al., 2024; Lin et al., 2023). These improvements have led to the proliferation of voice assistants like Google Assistant and Amazon Alexa, which now support a wide range of applications from customer service to healthcare and education (Ji et al., 2023; Li et al., 2023). Although CAI is now commonly associated with adult productivity (such as customer service) or teacher-facing applications (like automated grading), it is important to recognise its growing direct interaction with young children (Andries & Roberston, 2023; McTear & Ashurkina, 2024).

In this paper, CAI refers specifically to the voice-based dialogue systems that support spoken, naturalistic exchanges between young children and machine. These voice-based dialogue CAI systems are often embedded in tools like Amazon Alexa, Siri, Google Assistant, and educational social robots, all of which are increasingly accessible in both homes and classrooms (Andries & Roberston, 2023; Festerling et al., 2024). Unlike many digital applications that require reading or typing, these, voice-based dialogue CAI systems allow children to engage in turn-taking dialogue-based exchanges with machines (Jeon et al., 2023; Joyner, 2024; Kong & Wang, 2021).

From smart speakers in family homes to voice-enabled toys and classroom robots, CAI is becoming increasingly present in both domestic and early years education settings. While current CAI systems still face challenges, such as recognising non-verbal cues, responding to emotional nuance, or adapting spontaneously to children’s shifting language, these limitations are increasingly being addressed through advances in NLP and adaptive interface design (Kossack & Unger, 2024; Kurian, 2023). As these systems become more refined, their potential to act as dialogic partners in early learning grows considerably. They enable even pre-literate children to independently interact using spoken language. This makes them particularly developmentally appropriate for early childhood settings, where learning is grounded in talk, play, and social interaction (Bruce, 2015; Thunder et al., 2023). While these advances expand CAI’s potential as a dialogic partner in early learning, it is important to acknowledge that current CAI systems still grapple with interpreting the fluid, non-verbal, and emotionally nuanced nature of young children’s communication – elements that are often central to early learning experiences.

Nevertheless, recent studies have begun to explore how these voice-based CAI systems can support young children’s development, particularly in the domains of language and literacy (Holmes & Tuomi, 2022; Su & Yang, 2022). A growing body of research has examined the role of CAI in supporting early language and literacy development. Studies show that CAI-powered tools such as smart speakers, voice-enabled apps, and social robots can play a valuable role in supporting early language and literacy development. These technologies have been found to enhance vocabulary acquisition, foster storytelling and narrative comprehension, and facilitate bilingual communication by providing responsive, engaging, and developmentally accessible dialogue experiences for young children (Jeon et al., 2023; Joyner, 2024; Su et al., 2023). They enable children to engage in responsive, dialogue-based interactions that involve turn-taking, questioning, and immediate verbal feedback. In second-language learning contexts, CAI has been found to support pronunciation, listening skills, and conversational confidence (W. Huang et al., 2022; Jeon et al., 2023). These studies highlight the value of responsive CAI systems in promoting oral language development, sustained attention, and active participation. Furthermore, they suggest that young children are not only capable of engaging in meaningful exchanges with CAI but may also benefit from its dialogic structure and consistent language exposure. Crucially, such work challenges the common perception of young children as passive recipients of AI technologies. Instead, emerging studies increasingly portray them as active conversational partners, co-constructing meaning through interactions with CAI in ways that align with the inherently social, verbal, and interactive nature of early learning (Aslan et al., 2024; Yi & Rieh, 2024). Such findings invite further inquiry into how similar affordances might support other foundational domains of early learning, particularly mathematical thinking, which also develops through rich verbal and social engagement.

However, despite the growing momentum in language and literacy-related research, relatively little attention has been given to the potential of CAI to support early mathematical thinking. This gap underscores the need for critical reflection on how emerging technologies like CAI might shape children’s mathematical experiences in informal learning contexts, including at home and in play-based early education settings. Given the strong evidence that early mathematics is a critical predictor of later academic achievement, not only in mathematics, but also in literacy and general cognitive development, this area of inquiry warrants urgent attention (Duncan et al., 2007; Platas et al., 2022). Foundational mathematical competencies such as number sense, comparison, counting, and spatial reasoning begin developing well before formal schooling and are deeply embedded in children’s everyday experiences that are inherently social, verbal, and contextual (Bennett & Weidner, 2012; Montague-Smith et al., 2018). Importantly, these early mathematical ideas are shaped through social interaction, language use, and play-based exploration. Just as language learning is supported through rich verbal exchanges, early numeracy also depends on opportunities for children to talk about quantities, patterns, problems, and relationships (Cross et al., 2009; Knaus, 2017). Given that CAI tools offer verbal, interactive, and context-sensitive engagement, they present significant potential as dialogic partners in children’s early mathematical learning. Yet, compared to literacy and language development, the role of CAI in mediating mathematical dialogue, thinking, reasoning, and exploration remains significantly under-theorised and under-researched.

This conceptual paper aims to address this gap by examining how voice-based conversational AI might participate in children’s early mathematical thinking, particularly within informal, play-based contexts. To develop a structured understanding of this potential, this study adopts a conceptual synthesis approach, drawing on relevant theory and the literature to develop a framework for future research and design. This structured process of conceptual synthesis, involving an iterative thematic analysis of scholarly literature across sociocultural theory, dialogic pedagogy, and early mathematics education. Rather than attempting an exhaustive review of all available studies, we employed an interpretive conceptual synthesis approach, closely reading key texts to identify recurring pedagogical patterns, affordances, and tensions in how voice-based CAI is theorised in early learning environments. Particular attention was given to the literature that examined how CAI mediates interaction, scaffolds children’s reasoning, supports or limits learner agency, and shapes the use of mathematical language in dialogic settings. Given the nascent nature of this research area and the limited number of empirical studies focused specifically on voice-based CAI in early mathematics education, a systematic review was not feasible nor appropriate (Barnett-Page & Thomas, 2009; Thomas et al., 2023). Instead, conceptual synthesis offers a suitable methodology for emerging fields, where the goal is to build interpretive frameworks that can guide future inquiry (Sokolowski, 2018). Building on the sociocultural view that learning is mediated through tools and interaction, and informed by dialogic pedagogy’s emphasis on meaning-making through responsive dialogue, as well as through successive cycles of analysis, synthesis, and refinement, the paper considers how CAI might function as a dialogic partner in early numeracy experiences (Mercer & Howe, 2012; Townley, 2020). By mapping existing insights onto four pedagogical dimensions, this study contributes both a conceptual tool and a foundation for future empirical investigation.

In doing so, it brings together research from early mathematical thinking and technology-mediated interaction, framed through sociocultural theory and dialogic pedagogy, to examine how CAI might support, constrain, or reshape numeracy dialogue in informal early learning contexts.

Specifically, it asks: What pedagogical dimensions are required for voice-based CAI to effectively support early mathematical thinking in informal learning contexts?

To address this question, the paper proceeds in three parts. First, it outlines the background and theoretical foundations that inform early mathematical thinking in the context of mediated, dialogue-rich learning, drawing on sociocultural theory and dialogic pedagogy. Second, it develops a four-part conceptual lens for analysing how voice-based CAI might influence children’s engagement with mathematical ideas. This lens focuses on (1) child agency; (2) cognitive scaffolding; (3) mathematical language quality; and (4) responsiveness and timing. The final sections consider implications for educational research, technology design, and early years pedagogy, highlighting the need for more intentional and ethically informed integration of dialogic learning principles in future research and practice concerning how CAI can mediate early mathematical thinking through dialogic interaction.

2. Background and Theoretical Foundations

Understanding how CAI might contribute to early mathematical thinking requires integrating insights from multiple disciplines. Research in mathematics education, sociocultural learning theory, dialogic pedagogy, and emergent numeracy frameworks each offer important perspectives on how young children develop mathematical thinking through social interaction, dialogue, and language-rich play (Mercer & Howe, 2012; Montague-Smith et al., 2018). These combined perspectives provide a foundation for analysing how voice-based CAI might influence and mediate learning in early childhood contexts.

2.1. Sociocultural Theory and Learning Mediation

Sociocultural Theory, primarily developed by Vygotsky (1978), posits that learning and cognitive development are fundamentally social and cultural processes, mediated by tools, language, and interaction with others. It offers a foundational lens for understanding how children learn through interaction, communication, and the use of tools. The theory emphasises that child cognitive development (such as early mathematical thinking), is fundamentally shaped by social interaction, cultural context, and the use of mediational tools, especially through the use of language (Göncü, 1999; Klüver, 2002; Tzuriel, 2021). From this perspective, cognitive development is not an isolated, internal process but one that emerges through social participation, particularly within the Zone of Proximal Development (ZPD), which is the space between what a child can do independently and what they can achieve with the support of a more knowledgeable other (John-Steiner & Mahn, 1996; Vygotsky, 1978).

Learning is thus mediated through dialogue, shared activity, and cultural artefacts, with language playing a central role in shaping thought and meaning. Learning mediation refers to the process by which learning is facilitated, supported, or enhanced through the use of tools, strategies, or interactions that help learners construct knowledge, develop skills, and achieve deeper understanding (John-Steiner & Mahn, 1996; Kozulin, 2002). During the learning process, individuals use cultural artefacts, symbols, and social relationships to assist their thinking and regulate their behaviours. This concept highlights the relationship between culture, cognitive tools, and intellectual growth (Kozulin, 2023; Presseisen & Kozulin, 1992). Essentially, mediation acts as a bridge between the learner and new information, making learning more meaningful and effective. It is a process that empowers learners to engage with tools, strategies, and social interactions to build knowledge, cultivate deeper thinking, and gain meaningful understanding.

In the context of early mathematics, sociocultural theory emphasises that children’s mathematical thinking is shaped through interaction, the use of mathematical language, and engagement with tools within culturally embedded activities (Kinard & Kozulin, 2008; Renshaw, 1996). Mathematical learning often emerges and develop through everyday routines such as cooking, sorting, organising, or storytelling, where adults or peers model strategies, pose questions, and invite children to reason about numbers, shapes, patterns, or comparisons (Montague-Smith et al., 2018; Stott, 2016). Through these shared experiences, children begin to internalise not only mathematical content but also the underlying processes of mathematical thinking and communication. Learning mediation enables them to move from concrete, socially grounded experiences toward more abstract and independent reasoning. The mathematical language used during these exchanges, such as naming quantities, describing spatial relationships, or comparing attributes, which plays a critical role in supporting concept development and structuring the thinking process (Hiltrimartin et al., 2024; Sarama & Clements, 2009).

Importantly, the integrated lens of sociocultural theory and learning mediation also applies to understanding how tools and technologies support learning processes. Vygotsky (1978) viewed tools as essential to cognitive development. He included both symbolic tools, such as language, and technical tools, such as artefacts. In contemporary educational contexts, digital tools such as tablets, apps, and increasingly, voice-based CAI systems, function as educational cultural mediators that can structure and extend children’s engagement with mathematical learning (Jorgensen et al., 2020; Larkin et al., 2015). While human mediators can adapt their responses based on children’s gestures, emotional cues, or changing needs, current CAI systems operate with limited sensitivity to such contingencies. Its effectiveness depends not only on its ability to deliver content, but more critically, on how well it can replicate the contingent, language-rich, and meaning-making nature of social interaction that drives learning within the ZPD (Hewitt, 2023; Stott, 2016). When designed responsively, such technologies have the potential to support the kinds of dialogic interaction that sociocultural theory identifies as central to learning.

Yet, as mentioned, given that young children often communicate through gesture, tone, or context-dependent meaning, CAI systems still face limitations in recognising and responding appropriately (Aslan et al., 2025; Kurian, 2023; McTear & Ashurkina, 2024). This raises important questions about the extent to which CAI can authentically serve as a mediational agent in early mathematics. Accordingly, sociocultural theory and learning mediation together provide both a rationale and a critical framework for understanding and evaluating CAI’s role in mathematical learning. By foregrounding dialogue as a central means of mediation, they lay the foundation for dialogic pedagogy, which further elaborates how conversation functions as a key driver of learning and mathematical thinking.

2.2. Dialogic Pedagogy and Learning Through Conversation

Emerging from philosophical traditions of Socratic dialogue and developed further through the works of Bakhtin, Vygotsky, and others, dialogic pedagogy builds on sociocultural principles by emphasising dialogue as a primary driver of learning (Belknap, 1982; Kim & Wilkinson, 2019; Laird-Gentle et al., 2023; White, 2016). It has since gained prominence as an educational approach that positions conversation at the centre of teaching practice.

Fundamentally, dialogic pedagogy is characterised by the co-construction of knowledge through open-ended, reciprocal exchanges between teachers and students, as well as among peers. Unlike monologic or transmission-based models of instruction, it values multiple voices, diverse perspectives, and the dynamic interplay of ideas (Nesari & Miljkovic, 2015; White, 2021). Drawing on Bakhtin’s concept of dialogism, which views meaning as emerging from the interaction of different voices, and on Vygotsky’s sociocultural theory, which highlights the central role of social interaction in cognitive development, dialogic pedagogy positions learning as a socially situated, meaning-making process (Holquist, 2002; White, 2014). Rather than functioning as a fixed method, dialogic pedagogy provides guiding principles that orient teaching and learning toward joint meaning-making and the recognition of learners as active participants.

A key feature of dialogic pedagogy is the use of talk to stimulate thinking, problem-solving, and deeper understanding. Scholars such as Mercer and Littleton (2007) and Alexander (2018) argue that learning is co-constructed through open, reciprocal dialogue in which participants share, question, and refine ideas collaboratively. Dialogue is thus not simply the transmission of information, but a dynamic process of reasoning, negotiation, and shared meaning-making. In this way, dialogic pedagogy shifts the focus from one-way knowledge delivery to a participatory learning process where learners actively contribute to the co-construction of understanding through conversation (Kim & Wilkinson, 2019; Wells, 1999).

In mathematics education, productive dialogue is particularly important to facilitate children’s learning. Mathematical talk allows children to articulate their thinking, listen to alternative viewpoints, and compare strategies, all of which contributes to the development of conceptual understanding and reasoning (Kazemi & Hintz, 2014; Sfard, 2008). Research shows that when children explain their strategies aloud, they not only consolidate their own understanding but also create opportunities for peers to engage in joint sense-making (Mercer & Sams, 2006; Webb et al., 2014). Effective dialogic teaching relies on several interrelated practices, such as the following:

• Open-ended questioning that invites reasoning and justification (e.g., “How do you know?” or “Can you explain your thinking?”).
• Creating opportunities for multiple solutions or strategies, encouraging flexibility and creativity in mathematical problem solving (e.g., asking children to show different ways to make the number 10, such as 5 + 5, 6 + 4, or 2 + 2 + 2 + 2 + 2, then comparing the strategies).
• Introducing rich mathematical vocabulary within authentic contexts, supporting children’s conceptual and linguistic development (e.g., using terms like more than, equal to, pattern, symmetry during block play or cooking activities where children naturally encounter quantities and shapes).
• Providing scaffolding that challenges and extends thinking, while still providing appropriate support to sustain engagement and confidence (e.g., when a child counts objects correctly, the adult prompts with a slightly harder task such as “What if we had two more blocks? How many would we have now?”).

Within dialogic pedagogy, these practices serve not only to strengthen mathematical knowledge but also to nurture dispositions such as curiosity, persistence, and collaborative reasoning (Alexander, 2018; Mercer & Littleton, 2007). Traditionally, such forms of dialogue have been fostered in interaction with adults and peers, yet emerging technologies raise the possibility that CAI might also contribute to children’s mathematical experiences. CAI theoretically has the potential to extend opportunities for such dialogue beyond human interactions. A well-designed CAI system could, for example, prompt a child to elaborate on their reasoning, ask probing follow-up questions, or model problem-solving strategies during numeracy-related play. In this way, CAI might begin to approximate some of the dialogic moves that typically support children’s engagement in talk-rich mathematical exploration (Holmes & Tuomi, 2022; Jeon et al., 2023). However, most current CAI systems remain limited to scripted exchanges or factual responses, which restricts their ability to support sustained, reasoning-based conversation (McTear & Ashurkina, 2024). They often lack the adaptability and contextual awareness needed to respond contingently to children’s expressive nuances that are necessary for dialogic learning. Such challenges underscore the importance of intentionally designing CAI so that it supports the qualities of productive dialogue identified as central to mathematical development (Aslan et al., 2024; Kong & Wang, 2021; Kusal et al., 2022).

This discussion highlights the paper’s conceptual focus: examining how voice-based CAI might influence and reshape children’s mathematical thinking in informal learning contexts. This requires moving beyond transactional question–answer exchanges toward systems that can sustain genuinely dialogic interaction, where the technology not only responds to surface-level inputs but also engages with children’s reasoning, prompts further reflection, and nurtures shared inquiry. This, in turn, calls for examining how CAI might approximate the qualities of productive mathematical dialogue. A conceptual lens is therefore needed to evaluate both the potential and the limitations of CAI in early mathematics learning, requiring a reimagining of CAI as a potential dialogic partner rather than a static source of knowledge.

2.3. Early Mathematical Thinking Through Dialogue with CAI

In education, early mathematics learning is increasingly understood as a multifaceted, socially grounded process. It involves a range of interrelated skills, such as reasoning, problem-solving, spatial awareness, measurement, patterning, and classification (Aunio & Räsänen, 2016; Chen, 2025). These skills develop alongside key mathematical strands like number and operations, spatial and geometric thinking, measurement, patterning, and data handling or classification, with each strand contributing uniquely to the development of young children’s mathematical learning (McLennan, 2014; Rittle-Johnson et al., 2019). Crucially, early mathematical learning is best supported through rich, interactive experiences. It often emerges through play, exploration, and dialogue in everyday contexts with adults, peers, and, increasingly, with digital tools (Thunder et al., 2023). Understanding early mathematics as socially situated and interactive foregrounds communication and social interaction as central, providing the foundation for exploring how dialogue, and increasingly technological tools, contribute to the development of mathematical thinking.

From sociocultural and dialogic perspectives, early mathematical thinking refers to the foundational reasoning processes such as counting, comparing, spatial reasoning, and recognising patterns that emerge through talk, exploration, and shared activity in everyday contexts (Hiltrimartin et al., 2024; Kazemi & Hintz, 2014; Wolf & Neugebauer, 2005). Dialogic pedagogy highlights the central role of language, questioning, and reasoning in co-constructing mathematical understanding (Alexander, 2018; Mercer & Littleton, 2007). Building on this emphasis on dialogue as a driver of learning, an important question is whether and how such processes might also be supported through technology. While most of the existing research has focused on human-mediated interaction, a growing line of inquiry in language and literacy education has begun to examine how CAI can participate in dialogic learning (Holmes & Tuomi, 2022; Jeon et al., 2023; Su et al., 2023). These developments suggest important possibilities for extending similar affordances into mathematics learning.

Early mathematical competencies, such as number sense, comparison, counting, spatial reasoning, and pattern recognition, are now well established as predictors of later academic achievement (Duncan et al., 2007; Platas et al., 2022). These skills are not acquired in isolation; they are also socially constructed through language-rich play and interaction (Montague-Smith et al., 2018; van Oers, 2010). Early mathematical language refers to the words and concepts young children use to describe numbers, quantities, shapes, sizes, positions, and patterns. This includes both numerical terms (like “more,” “less,” and “count”) and non-numerical terms related to geometry, measurement, and spatial relations (such as “big,” “small,” “next to,” and “middle”) (H.-H. Huang, 2024; Turan & De Smedt, 2022). During play, children naturally encounter and use mathematical language as they explore, build, sort, and interact with objects and peers. They engage with mathematics, for example, when comparing quantities at snack time, identifying patterns in music and dance, or reasoning spatially while building with blocks (Cohrssen et al., 2017; Gillanders & Casal De La Fuente, 2020). Mathematical language-rich, reasoning-oriented dialogue provides the mechanism through which these informal experiences are transformed into deeper mathematical ideas, as children articulate strategies, negotiate meanings, and internalise concepts (Sfard, 2008; Webb et al., 2014).

Traditionally, these dialogic processes have been mediated by teachers, caregivers, or peers who act as more knowledgeable others with the skills to guide children’s mathematical talk and reasoning. Supporting such interactions requires pedagogical sensitivity, including the ability to pose questions, model strategies, and scaffold problem-solving in ways that extend children’s participation in mathematical dialogue (Bálint, 2024; McLennan, 2014; Vygotsky et al., 2012). While this role has historically depended on human expertise, emerging technologies raise important questions for early mathematics education. As stated earlier, the aim of this paper is to explore how voice-based CAI might participate in children’s mathematical learning, with the guiding question: how might CAI support, constrain, or transform mathematical thinking in informal early learning contexts?

Research on CAI has highlighted both its potential and its limitations in supporting children’s learning. Across education, CAI has been shown to prompt reflection, offer contingent feedback, and model reasoning moves that enhance engagement and self-efficacy (Holmes & Tuomi, 2022; Jeon et al., 2023). Emerging work in mathematics education reports similar promise. For example, AI chatbots have been used with preservice teachers to rehearse responsive questioning strategies around fractions, providing low-stakes opportunities to practice dialogic techniques (Lee & Yeo, 2022). In school classrooms, CAI has been linked to increased attention, motivation, and conceptual understanding when integrated into inquiry- and problem-based tasks (Van Doc et al., 2023). Broader reviews of AI in mathematics also highlight the potential of AI-driven systems to model inductive reasoning, exemplification, and problem-solving pathways that support conceptual development (Choukade, 2025). Collectively, these findings, though still emerging, suggest that CAI can extend opportunities for mathematical dialogue beyond human-to-human exchanges, particularly when embedded in playful and interactive contexts.

Importantly, CAI is not limited to supporting procedural knowledge but may also influence broader beliefs and dispositions toward mathematics. For instance, studies using fuzzy logic, neuro-fuzzy inference, and neural networks demonstrate that AI can model learners’ problem-solving beliefs and dispositions, opening new possibilities for understanding and supporting children’s mathematical mindsets (Göktepe Körpeoğlu et al., 2025). Research on generative AI also suggests potential for capturing cognitive styles, such as analytic versus narrative thinking, from language data, pointing toward new ways of analysing how learners approach mathematical tasks (Markowitz, 2024). Such findings resonate with early childhood perspectives that position mathematics as exploratory, multimodal, and meaning-driven, rather than narrowly procedural (Oughton et al., 2024).

Although emerging research highlights CAI’s potential to enrich children’s mathematical dialogue by prompting reasoning and fostering engagement, several limitations temper this promise. Many current systems rely on scripted or transactional exchanges, which restrict their ability to sustain reasoning-based conversation (McTear & Ashurkina, 2024). For young children in particular, CAI often struggles to interpret non-verbal communication, contextual nuance, or affective signals that are central to early learning (Aslan et al., 2025). Concerns have also been raised about the risks of narrowing dialogue when AI prioritises efficiency over exploration or inadvertently privileges certain language forms (Holmes & Tuomi, 2022). Beyond these pedagogical issues, broader ethical considerations include data privacy, equity of access, and the implications of embedding AI into children’s everyday environments (Andries & Roberston, 2023; Holmes & Tuomi, 2022).

Seen together, this body of work suggests that while CAI has significant potential to complement human dialogue in early mathematics education, its effectiveness depends on intentional design that prioritises responsiveness, openness, and child agency. The challenge is not only technical but also pedagogical, as it concerns whether CAI systems can genuinely sustain the qualities of productive mathematical dialogue instead of collapsing into scripted question and answer routines. Addressing this challenge requires a structured lens for understanding how CAI can support, constrain, or transform mathematical thinking in dialogic contexts. The next section proposes a conceptual lens to examine how CAI might support, constrain, or transform children’s mathematical thinking.

3. A Conceptual Lens for Evaluating Conversational AI in Early Mathematical Thinking

Despite the growing presence of CAI in children’s everyday environments, its potential to shape early mathematical thinking remains insufficiently examined. To address this gap, this paper proposes a conceptual lens that brings together four interrelated dimensions: child agency, cognitive scaffolding, mathematical language quality, and responsiveness and timing. These four pedagogical dimensions proposed in this framework emerged through the synthesis of sociocultural theory and dialogic pedagogy, with careful consideration of the affordances and challenges specific to voice-based CAI in early childhood mathematical learning contexts.

As illustrated in Figure 1, these pedagogical dimensions are represented as quadrants of a circle to highlight their interconnectedness and collective role in shaping dialogue-based interactions with CAI. Together, they provide a structured framework for evaluating how CAI might support, constrain, or transform children’s mathematical thinking in informal learning contexts.

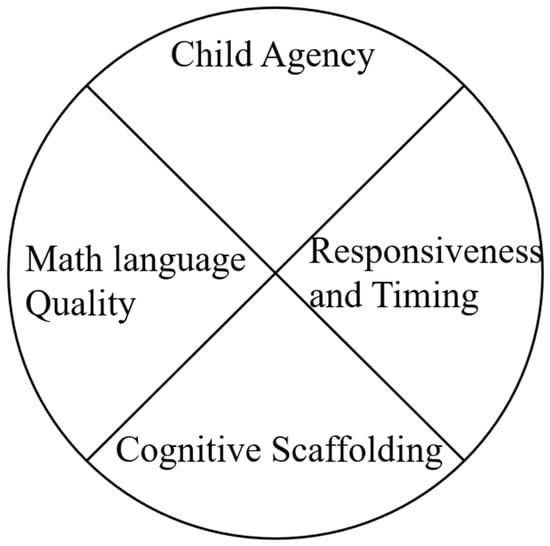
Figure 1. The P4CAI Framework: A conceptual lens for evaluating conversational AI in early mathematical thinking. (created by the authors based on the conceptual synthesis presented in the study).

The lens consists of four interconnected pedagogical dimensions: child agency, cognitive scaffolding, mathematical language quality, and responsiveness and timing. These dimensions emphasise that effective conversational technologies must approximate key qualities of human mathematical interactions: rich language, contingent responsiveness, adaptive support, and opportunities for child-led exploration. Considering these aspects is essential for understanding both the potential and the current limitations of Conversational AI as a partner in fostering early mathematical thinking.

3.1. Child Agency

Child agency refers to the capacity of young children to act intentionally, make choices, and influence their own learning and environment (Baker et al., 2021; Burr & Degotardi, 2021). Rather than viewing children as passive recipients of adult direction, research increasingly recognises them as active participants who shape their learning experiences and contribute to shared activities (Hygum & Hygum, 2023; Wood, 2014). In early childhood education, this means children can influence what and how they learn, express preferences, initiate activities, and contribute to decision-making (Sairanen et al., 2020). Agency is not just about autonomy; it is visible in children’s everyday actions like asking questions, suggesting ideas, or negotiating roles during play. Studies show that children’s initiatives may be expressed verbally, through gesture, or through action, and that the ways adults respond to these initiatives are crucial in either supporting or constraining agency. Recognising agency means acknowledging children as competent and capable of co-constructing learning, with their contributions central not only to the development of mathematical thinking but also to their broader educational engagement and emerging identities as learners (Biesta & Tedder, 2007; Hygum & Hygum, 2023).

In early mathematics learning, agency can be understood in relation to how learning environments are designed to position children as active participants (Cobb et al., 2003) and how classroom interactions and structures can either support or suppress students’ engagement and persistence in mathematical activity (Turner et al., 2002). Dialogic interactions that respect children’s choices and perspectives promote motivation, curiosity, and deeper understanding. CAI could, in principle, support these forms of agency by allowing free-form questioning, responding flexibly, and adapting dialogue to a child’s interests. For instance, a child might ask a voice assistant “Can we count the toys on the table together?” If the CAI responds only with “There are ten toys,” the child’s initiative is curtailed. In contrast, if the system replies “Let’s count them. Do you want to count by twos or one by one?”, the child’s agency is recognised, and the dialogue becomes a co-constructed exploration shaped by the child’s choices.

At present, however, many CAI systems are designed around command-based or adult-directed logics, expecting specific input formats and offering little scope for deviation (Holmes & Tuomi, 2022; Plowman & Stephen, 2005). When children introduce novel ideas or playful variations, they often encounter errors or rigid responses that close down the interaction. Such limitations not only risk frustrating children but also undermine their agency in meaning-making. Instead of enabling co-construction, poorly designed systems may inadvertently position children as passive consumers of information (Aslan et al., 2025; Jeon et al., 2023). Evaluating CAI through the dimension of child agency therefore requires careful attention to whether technologies create space for children’s contributions, questions, and initiatives. Systems that genuinely support agency will allow children to guide interactions, pursue self-generated problems, and take ownership of their mathematical explorations. Designing for agency means building CAI that is flexible, responsive, and open-ended, aligning with broader child-centred pedagogies in early years education.

3.2. Cognitive Scaffolding

Cognitive scaffolding refers to the structured support that helps learners accomplish tasks and develop understandings that they might not achieve alone (Doo et al., 2020; Kusmaryono & Wijayanti, 2020). In early mathematics, this often involves breaking down complex ideas, modelling strategies, or prompting children to explain and extend their reasoning. Such support bridges the gap between children’s informal intuitions and more formal mathematical concepts, gradually transferring responsibility to the learner as competence grows (Bakker et al., 2015).

Research shows that effective scaffolding in mathematics reduces cognitive load, increases persistence, and supports conceptual development by sustaining engagement in reasoning processes. Adults scaffold in many ways: by asking guiding questions, encouraging estimation, modelling counting strategies, or highlighting relationships between numbers and operations (Hou & Keng, 2020). Similarly, peer or computer-based scaffolding can provide opportunities for joint sense-making, though these require sensitivity to timing and adaptability (Plowman & Stephen, 2005).

CAI could, in principle, provide this type of scaffolding if designed to go beyond supplying answers. For instance, when a child asks “What is two plus three?”, a simple reply of “five” closes the interaction. In contrast, an AI that says “Let’s count together: two apples and three more apples. How many now?” turns the moment into an interactive reasoning process. Vignette: A child using a learning app points to a picture of four blocks and asks “What if I add one more?”. A command-based AI might reply “That makes five.” A scaffolded design could instead respond “Yes, that makes five. Can you show me another way to see it—maybe by taking one away from six?” In this version, the system encourages the child to connect strategies, reflect, and generalise across contexts, echoing how teachers extend reasoning in play-based mathematics (Bakker et al., 2015; Hou & Keng, 2020).

Yet most current CAI systems lack this adaptive capacity (Aslan et al., 2025; Ibrahim & Bilquise, 2025). They typically provide direct, scripted responses that do not probe children’s thinking or adjust to their developmental level (Plowman & Stephen, 2005). Unlike human teachers who can detect hesitation, vary their support, and prompt elaboration, CAI tends to follow fixed pathways. This risk reducing children to passive consumers of information rather than active problem-solvers (Bakker et al., 2015; Y.-P. Huang et al., 2024). Evaluating CAI through this dimension highlights the need to assess whether systems can provide graduated support, pose open-ended questions, and prompt strategy articulation. Designing for scaffolding means creating technologies that not only deliver answers but also guide children’s reasoning in ways that promote independence, resilience, and conceptual depth.

3.3. Mathematical Language Quality

The quality of mathematical language is central to how children construct meaning in mathematics. It is not only the presence of terms such as “more than,” “equal to,” or “altogether” that matters, but also how these terms are modelled, contextualised, and connected to reasoning processes (Turan & De Smedt, 2022). In natural interactions, adults introduce mathematical vocabulary fluidly during everyday activities, such as counting steps while climbing stairs, comparing toy sizes, or discussing shapes while drawing, which allows children to encounter words in context and link them to conceptual understanding (Bittner & Degotardi, 2022; Purpura & Reid, 2016).

Research consistently demonstrates that mathematical language proficiency in the preschool years predicts concurrent and later mathematical ability, above and beyond general language skills (Purpura et al., 2017; Zhang et al., 2017). Differences in children’s exposure to mathematical language, often shaped by socioeconomic background, contribute to disparities in early numeracy development. Intervention studies further show that high-quality adult–child interactions that deliberately use mathematical vocabulary lead to measurable gains in children’s mathematical performance and even better keep the questions and dialogue going to facilitate children’s thinking (Besser et al., 2025). These interactions also benefit from keeping questions and dialogue going to facilitate children’s thinking. A vignette illustrates this point: A child asks a voice assistant while pointing to the table “Do I have more biscuits than you?” A basic reply might be “Yes, you have more.” A higher-quality response could be “You have five biscuits, and I have three. Five is two more than three. What if I eat one, then who will have more then?”

The quality of mathematical language is also linked to child agency. Dialogic teaching, where children are prompted to explain their strategies, empowers them to participate actively in learning rather than passively receive answers (Cheung et al., 2023). When teachers or parents encourage children to clarify and articulate their thinking, children develop a stronger sense of ownership over their problem-solving. Similarly, in terms of cognitive scaffolding, structured support that gradually fades as competence increases, becomes more powerful when it incorporates precise mathematical terms (Hiltrimartin et al., 2024; Oughton et al., 2024).

Despite these opportunities, research indicates that many AI systems still generate language of inconsistent quality, with responses often factual, fragmented, or overly scripted, and tend to omit the comparative and inferential vocabulary that supports extended reasoning and dialogic depth (Davar et al., 2025; Holmes & Tuomi, 2022; Jacobsen & Weber, 2025). Speech recognition errors further risk providing inaccurate or confusing feedback Without careful design, AI dialogue reduces mathematical talk to rote memorisation rather than conceptual exploration (Kusal et al., 2022; Lin et al., 2023). Evaluating CAI through this dimension, therefore, requires attention to whether the language generated is precise, developmentally appropriate, and contextually relevant. It should also include open-ended questions and ongoing dialogue to provoke thinking. High-quality mathematical dialogue should extend beyond vocabulary exposure to include comparative, inferential, and explanatory terms that support reasoning. Only by approximating the richness of adult-mediated “math talk” with quality mathematical language can AI systems foster children’s conceptual understanding and, importantly, promote both agency and scaffolded independence in mathematical thinking (Aslan et al., 2025).

3.4. Responsiveness and Timing

Responsiveness and timing are critical dimensions in the use of CAI for early mathematical learning and thinking. Responsiveness refers to the system’s ability to provide accurate, relevant, and contextually appropriate replies that build on a child’s contributions, while timing concerns the promptness and sequencing of those responses (Jančařík et al., 2023; Lee & Yeo, 2022). Together, they determine whether dialogue supports learning in ways that feel natural, engaging, and pedagogically effective.

Well-trained educators who know dialogic strategies are often more adept at managing responsiveness and timing. They adjust their pace, pause to give children thinking time, repeat or rephrase when needed, and adapt questions based on a child’s contributions. This kind of responsive interaction helps sustain engagement, encourages reasoning, and keeps children active participants in the learning and thinking process. In contrast, CAI often struggles with these qualities. Speech recognition errors (particularly with children’s variable pronunciation, accents, or non-standard grammar) frequently lead to interruptions or irrelevant answers. Delays in response or abrupt turn-taking can also break conversational flow (Jeon et al., 2023; Kurian, 2023). For instance, if a child says “I think there are more red blocks,” and the AI pauses several seconds before replying, “I didn’t understand that,” the opportunity to scaffold comparative reasoning is lost.

Research suggests that the effectiveness of AI in mathematics education depends not only on what feedback is provided but also on when. Well-timed responses can sustain attention, prompt persistence, and encourage deeper reasoning. Conversely, poorly timed or generic replies risk reducing motivation and closing down dialogue. Studies with AI chatbots in teacher education illustrate this point: when the systems simulated misconceptions and responded promptly to preservice teachers’ queries, they helped foster responsive questioning skills and clarification strategies. Similarly, analysis of solution-time data shows that response timing can shape engagement and learning trajectories, with support being most effective when neither too delayed nor too immediate (Yi & Rieh, 2024).

Effective CAI in mathematics education must recognise and adapt to diverse educational contexts and instructional needs. High responsiveness means the AI can interpret student queries, identify misconceptions, and offer tailored guidance or scaffolding that aligns with the learner’s current understanding (Cheng et al., 2018). Studies show that educators value AI tools that provide actionable, context-specific feedback, and that the quality of AI responsiveness can vary depending on how well the system is designed to differentiate and adapt its responses to individual learners (Jampala et al., 2024; Joyner, 2024). For CAI to support early mathematical thinking, its responsiveness must extend beyond recognising keywords to interpreting intent, identifying misconceptions, and tailoring scaffolding in ways that align with a child’s current understanding. Timing, in turn, should approximate the pacing of human conversation, allowing pauses for children to process but avoiding disruptive delays. This kind of sequential, well-calibrated exchange is especially important in mathematics, where reasoning develops step by step and each contribution provides the foundation for the next. In summary, high-quality responsiveness and sensitive timing are essential if CAI is to function as a dialogic partner in early mathematics learning.

These dimensions influence whether children remain engaged, whether reasoning is extended, and whether the system can approximate the qualities of productive human dialogue. Evaluating CAI through this lens requires attention not only to the accuracy of mathematical content but also to its ability to sustain smooth, contingent, and meaningful exchanges in real time.

4. Implications for Research, Technology Design, and Educational Practice

The four dimensions of the P4CAI framework highlight critical directions for research, technology development, and educational practice. Together, these dimensions extend current theoretical discussions by providing a structured lens for empirical investigation, helping researchers identify observable indicators of productive child–AI dialogue. Table 1 summarises how each dimension can support, constrain, or transform early mathematical thinking during interactions with CAI. This synthesis not only clarifies the conceptual contribution of the framework but also provides a concrete reference point for future applications in design and pedagogy.

Table 1. Author-developed conceptual lens outlining four pedagogical dimensions of CAI in early mathematical thinking (author-developed table based on the conceptual synthesis presented in the study).

Dimension	Focus	Support	Constraint	Transformative Potential
Child Agency	Opportunities for choice, initiative, and control in dialogue	Encourages exploration, multiple strategies, and child-led questioning	Limits interaction to fixed scripts or adult-directed pathways	Positions children as co-constructors of learning, shaping dialogue and directing mathematical inquiry
Cognitive Scaffolding	Structured support that extends children’s reasoning	Guides strategy use, connects ideas, and prompts reflection	Reduces interaction to factual recall or procedural answers	Encourages children to articulate strategies, generalise ideas, and gradually take ownership of problem-solving
Mathematical Language Quality	Precision, richness, and contextual use of mathematical vocabulary	Expands vocabulary and models comparative, inferential, and explanatory terms	Simplified, scripted, or inaccurate responses restrict reasoning and reinforce rote learning	Enables rich math talk with precise, developmentally appropriate language that sustains dialogue and deepens conceptual understanding
Responsiveness and Timing	Accuracy, contingency, and pacing of replies	Provides Contingent prompts, timely feedback, and sustained engagement	Errors, interruptions, or delays disrupt conversational flow and reduce learning opportunities	Approximates human-like turn-taking, allowing pauses and sequenced dialogue that supports reasoning step by step

Table 1 highlights how each dimension can inform not only how CAI tools are evaluated, but also how they are developed and implemented in practice. For research, the P4CAI framework draws attention to unexplored questions about how children engage in mathematical dialogue with CAI in real time. Such as how systems respond to misconceptions, whether they promote or suppress reasoning, and how agency is negotiated in dialogic interactions. For technology development, the framework underscores the need for dialogic principles to shape system design. Developers must attend to the quality of language, responsiveness, and scaffolding opportunities while respecting children’s agency. Finally, for educational practice, the framework provides a tool for practitioners and researchers to assess the pedagogical affordances and limitations of CAI in early learning settings. It encourages intentional design and use of CAI tools that extend, rather than replace, human interaction, and foregrounds ethical use that supports children’s conceptual development.

5. Conclusions

This paper has proposed a conceptual lens for examining how conversational AI might contribute to early mathematical thinking. By foregrounding four dimensions of child agency, cognitive scaffolding, mathematical language quality, and responsiveness and timing, the framework highlights what is required for CAI to move beyond scripted answers toward supporting genuine dialogue that fosters reasoning, curiosity, and problem-solving. Drawing on sociocultural and dialogic perspectives, the argument is that mathematics learning is inherently social and language-rich, and that AI tools must approximate the qualities of effective human interaction if they are to add value. At the same time, this work remains conceptual. Empirical studies are urgently needed to explore how children engage with CAI in real settings, how responsive systems shape mathematical dialogue, and what inequities may arise across diverse groups. By recognising both possibilities and limitations, this paper calls for interdisciplinary efforts to design and evaluate CAI that meaningfully enriches children’s early numeracy experiences. In doing so, it directly addresses the guiding research question by demonstrating how the four pedagogical dimensions—child agency, cognitive scaffolding, mathematical language quality, and responsiveness—together define the conditions under which voice-based CAI can effectively support or constrain children’s mathematical thinking.